文档内容
2020年辽宁省鞍山市中考数学试卷
一、选择题(本题共8个小题,每小题3分,共24分.在每小题给出的四个选项中,只有
一项是符合题目要求的)
1.(3分)﹣ 的绝对值是( )
A.﹣2020 B.﹣ C. D.2020
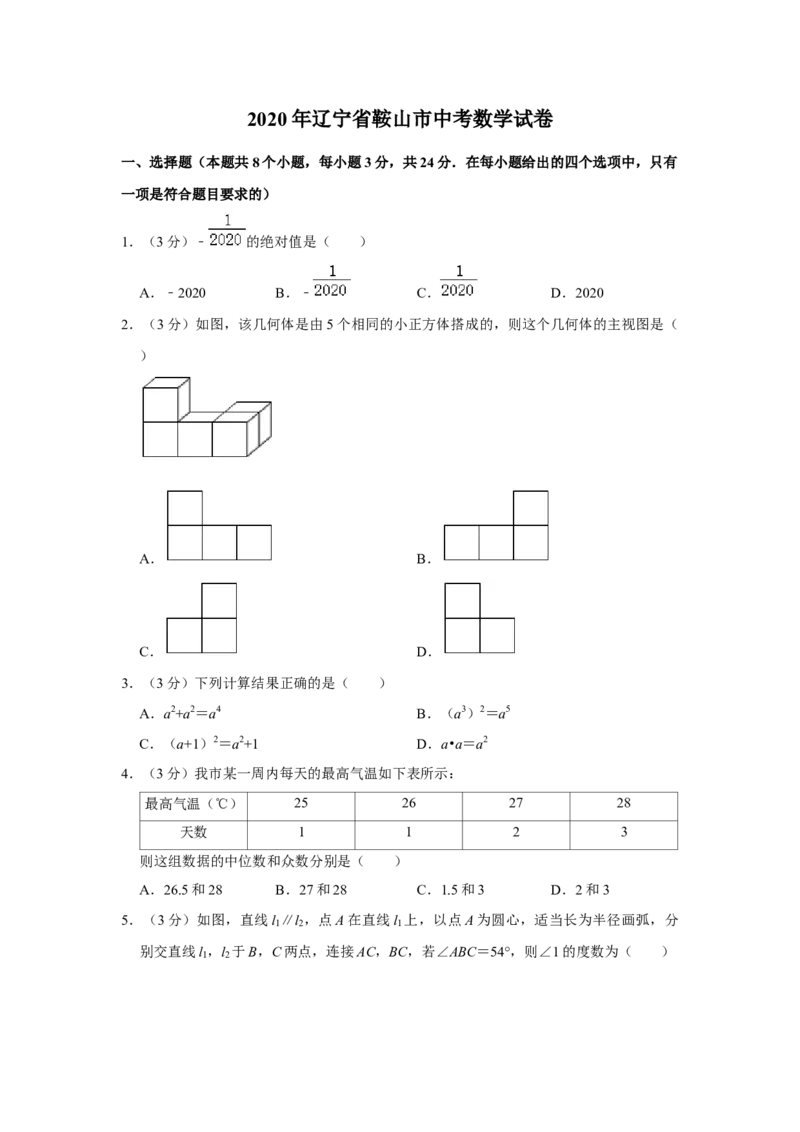
2.(3分)如图,该几何体是由5个相同的小正方体搭成的,则这个几何体的主视图是(
)
A. B.
C. D.
3.(3分)下列计算结果正确的是( )
A.a2+a2=a4 B.(a3)2=a5
C.(a+1)2=a2+1 D.a•a=a2
4.(3分)我市某一周内每天的最高气温如下表所示:
最高气温(℃) 25 26 27 28
天数 1 1 2 3
则这组数据的中位数和众数分别是( )
A.26.5和28 B.27和28 C.1.5和3 D.2和3
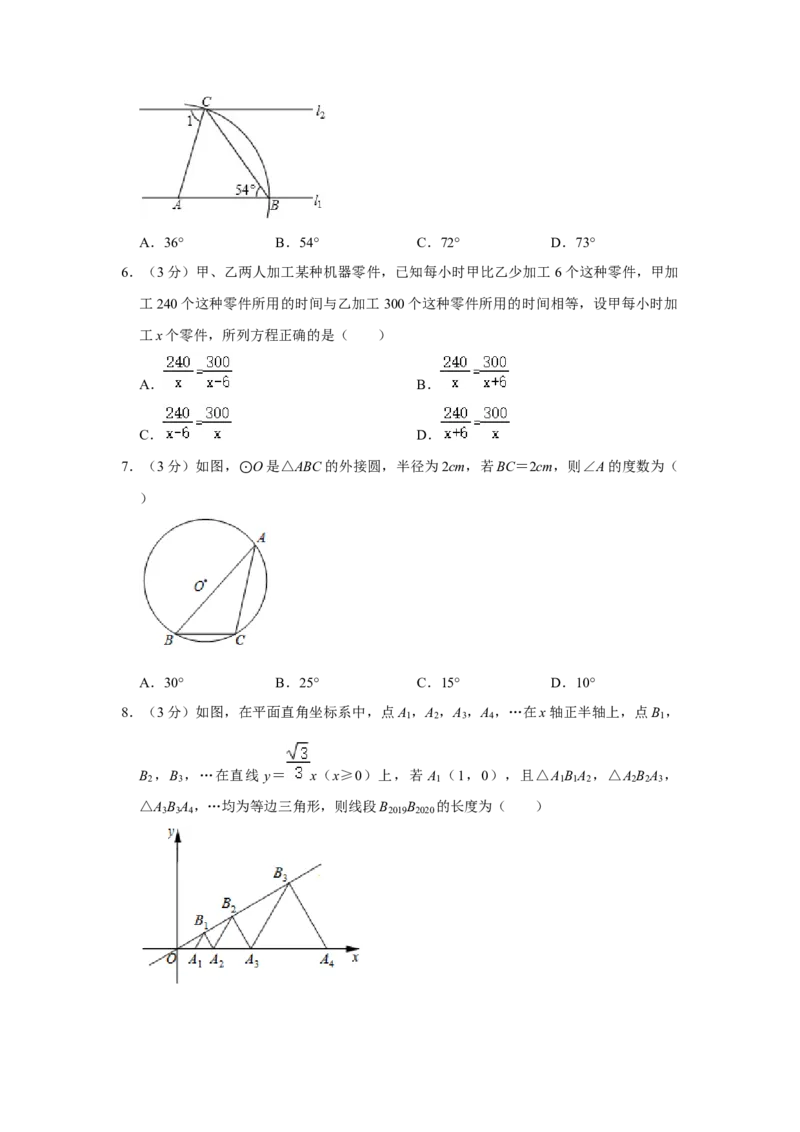
5.(3分)如图,直线l ∥l ,点A在直线l 上,以点A为圆心,适当长为半径画弧,分
1 2 1
别交直线l ,l 于B,C两点,连接AC,BC,若∠ABC=54°,则∠1的度数为( )
1 2A.36° B.54° C.72° D.73°
6.(3分)甲、乙两人加工某种机器零件,已知每小时甲比乙少加工6个这种零件,甲加
工240个这种零件所用的时间与乙加工300个这种零件所用的时间相等,设甲每小时加
工x个零件,所列方程正确的是( )
A. B.
C. D.
7.(3分)如图, O是△ABC的外接圆,半径为2cm,若BC=2cm,则∠A的度数为(
) ⊙
A.30° B.25° C.15° D.10°
8.(3分)如图,在平面直角坐标系中,点A ,A ,A ,A ,…在x轴正半轴上,点B ,
1 2 3 4 1
B ,B ,…在直线 y= x(x≥0)上,若 A (1,0),且△A B A ,△A B A ,
2 3 1 1 1 2 2 2 3
△A B A ,…均为等边三角形,则线段B B 的长度为( )
3 3 4 2019 2020A.22021 B.22020 C.22019 D.22018
二、填空题(本题共8个小题,每小题3分,共24分)
9.(3分)据《光明日报》报道:截至2020年5月31日,全国参与新冠肺炎疫情防控的
志愿者约为8810000,将数据8810000科学记数法表示为 .
10.(3分)分解因式:a3﹣2a2b+ab2= .
11.(3分)在一个不透明的袋子中装有6个红球和若干个白球,这些球除颜色外都相同,
将球搅匀后随机摸出一个球,记下颜色后放回,不断重复这一过程,共摸球100次,发
现有20次摸到红球,估计袋子中白球的个数约为 .
12.(3分)如果关于x的一元二次方程x2﹣3x+k=0有两个相等的实数根,那么实数k的
值是 .
13.(3分)不等式组 的解集为 .
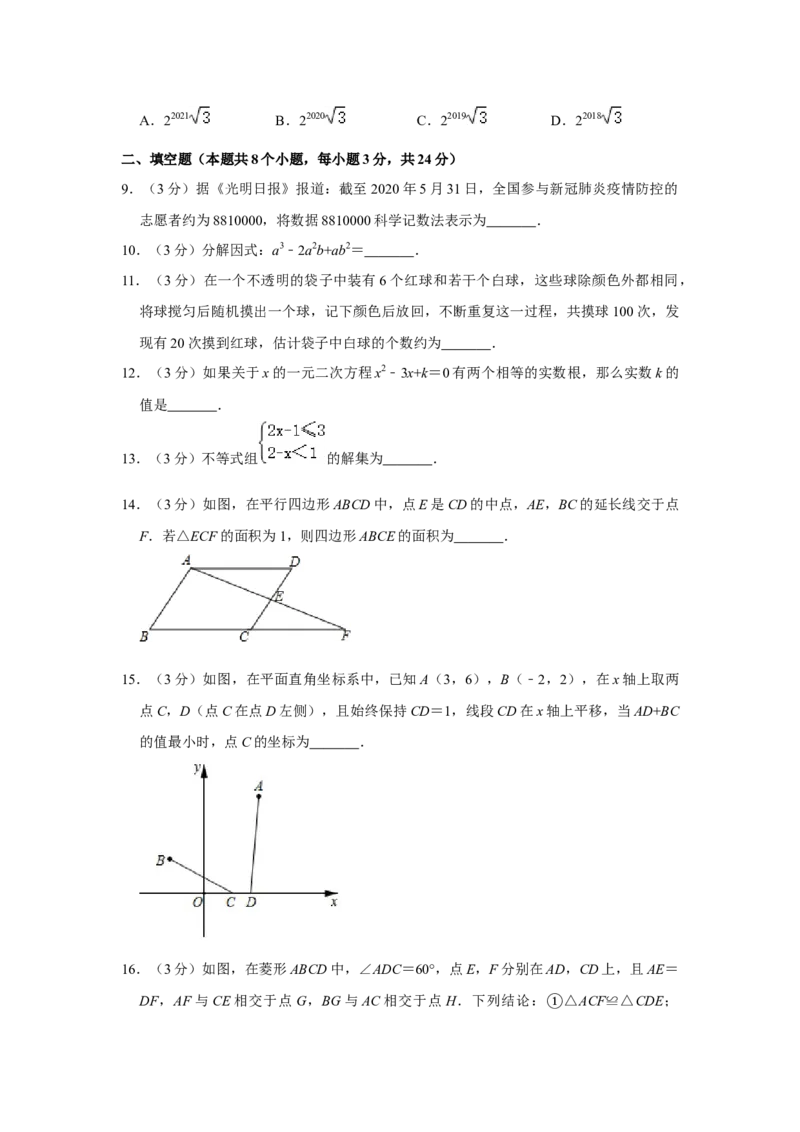
14.(3分)如图,在平行四边形ABCD中,点E是CD的中点,AE,BC的延长线交于点
F.若△ECF的面积为1,则四边形ABCE的面积为 .
15.(3分)如图,在平面直角坐标系中,已知A(3,6),B(﹣2,2),在x轴上取两
点C,D(点C在点D左侧),且始终保持CD=1,线段CD在x轴上平移,当AD+BC
的值最小时,点C的坐标为 .
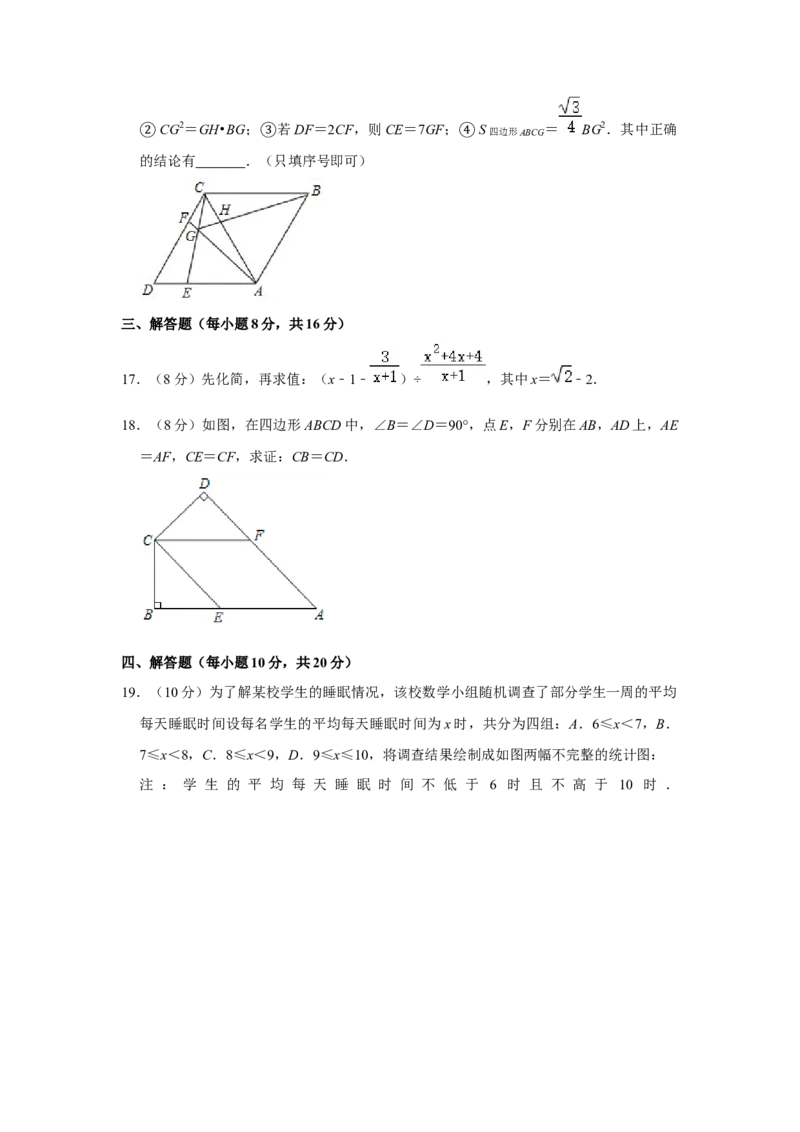
16.(3分)如图,在菱形ABCD中,∠ADC=60°,点E,F分别在AD,CD上,且AE=
DF,AF与CE相交于点G,BG与AC相交于点H.下列结论: △ACF≌△CDE;
①CG2=GH•BG; 若DF=2CF,则CE=7GF; S四边形ABCG = BG2.其中正确
②的结论有 .(③只填序号即可) ④
三、解答题(每小题8分,共16分)
17.(8分)先化简,再求值:(x﹣1﹣ )÷ ,其中x= ﹣2.
18.(8分)如图,在四边形ABCD中,∠B=∠D=90°,点E,F分别在AB,AD上,AE
=AF,CE=CF,求证:CB=CD.
四、解答题(每小题10分,共20分)
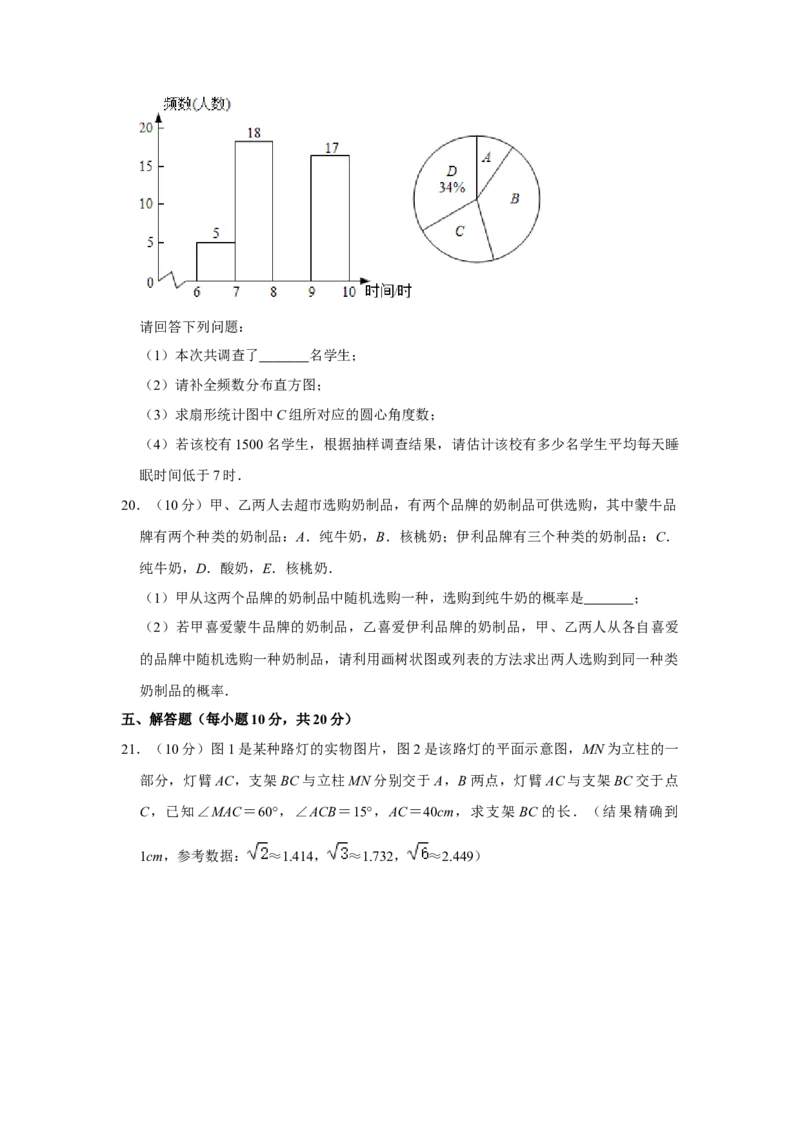
19.(10分)为了解某校学生的睡眠情况,该校数学小组随机调查了部分学生一周的平均
每天睡眠时间设每名学生的平均每天睡眠时间为x时,共分为四组:A.6≤x<7,B.
7≤x<8,C.8≤x<9,D.9≤x≤10,将调查结果绘制成如图两幅不完整的统计图:
注 : 学 生 的 平 均 每 天 睡 眠 时 间 不 低 于 6 时 且 不 高 于 10 时 .请回答下列问题:
(1)本次共调查了 名学生;
(2)请补全频数分布直方图;
(3)求扇形统计图中C组所对应的圆心角度数;
(4)若该校有1500名学生,根据抽样调查结果,请估计该校有多少名学生平均每天睡
眠时间低于7时.
20.(10分)甲、乙两人去超市选购奶制品,有两个品牌的奶制品可供选购,其中蒙牛品
牌有两个种类的奶制品:A.纯牛奶,B.核桃奶;伊利品牌有三个种类的奶制品:C.
纯牛奶,D.酸奶,E.核桃奶.
(1)甲从这两个品牌的奶制品中随机选购一种,选购到纯牛奶的概率是 ;
(2)若甲喜爱蒙牛品牌的奶制品,乙喜爱伊利品牌的奶制品,甲、乙两人从各自喜爱
的品牌中随机选购一种奶制品,请利用画树状图或列表的方法求出两人选购到同一种类
奶制品的概率.
五、解答题(每小题10分,共20分)
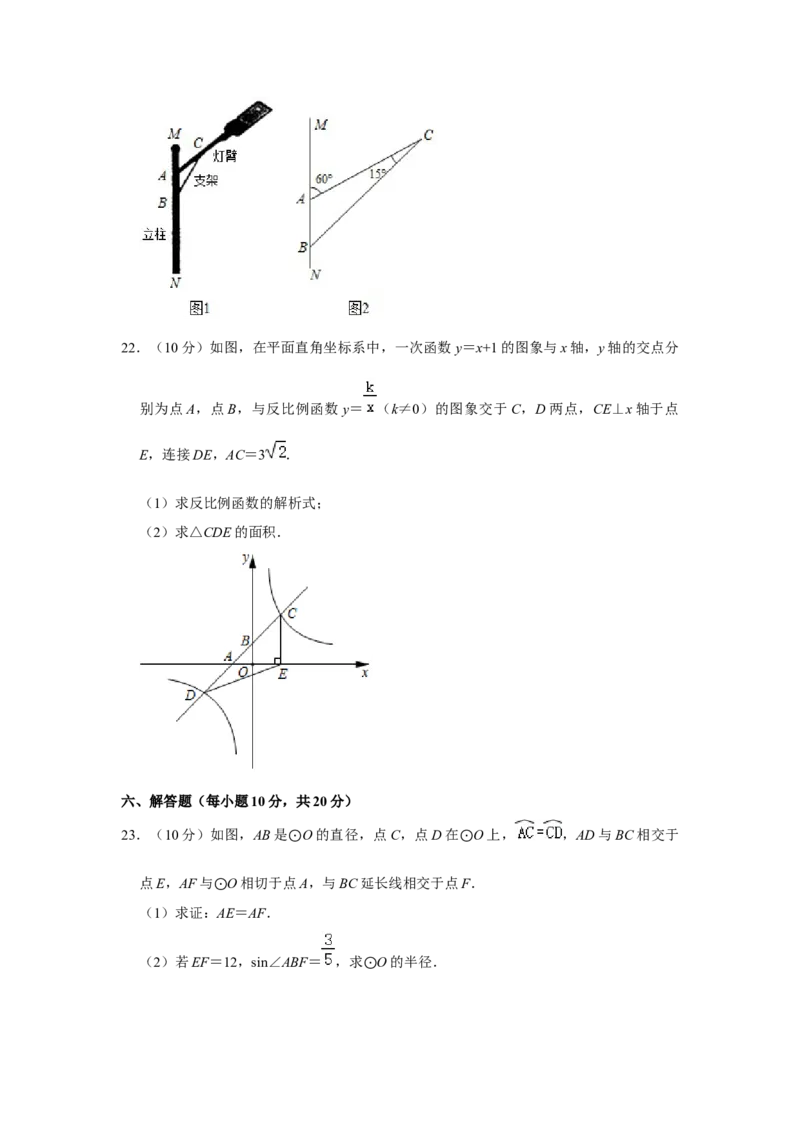
21.(10分)图1是某种路灯的实物图片,图2是该路灯的平面示意图,MN为立柱的一
部分,灯臂AC,支架BC与立柱MN分别交于A,B两点,灯臂AC与支架BC交于点
C,已知∠MAC=60°,∠ACB=15°,AC=40cm,求支架 BC 的长.(结果精确到
1cm,参考数据: ≈1.414, ≈1.732, ≈2.449)22.(10分)如图,在平面直角坐标系中,一次函数y=x+1的图象与x轴,y轴的交点分
别为点A,点B,与反比例函数y= (k≠0)的图象交于C,D两点,CE⊥x轴于点
E,连接DE,AC=3 .
(1)求反比例函数的解析式;
(2)求△CDE的面积.
六、解答题(每小题10分,共20分)
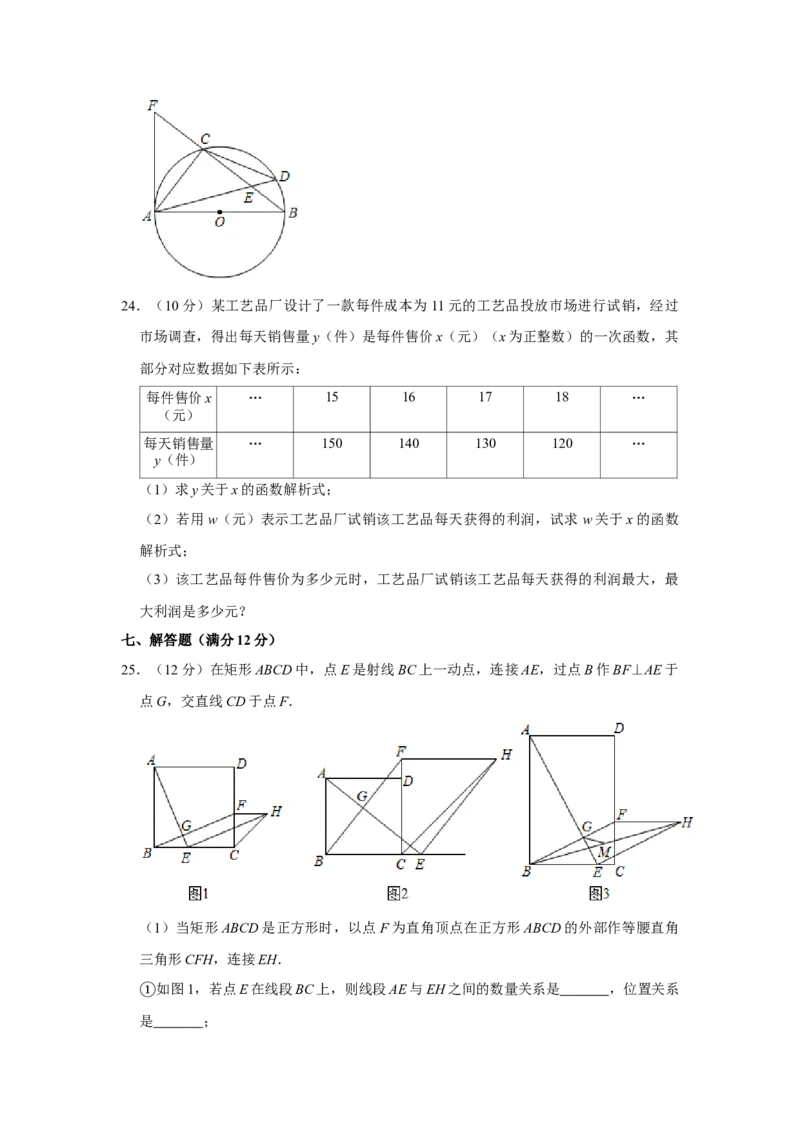
23.(10分)如图,AB是 O的直径,点C,点D在 O上, ,AD与BC相交于
⊙ ⊙
点E,AF与 O相切于点A,与BC延长线相交于点F.
(1)求证:⊙AE=AF.
(2)若EF=12,sin∠ABF= ,求 O的半径.
⊙24.(10分)某工艺品厂设计了一款每件成本为11元的工艺品投放市场进行试销,经过
市场调查,得出每天销售量y(件)是每件售价x(元)(x为正整数)的一次函数,其
部分对应数据如下表所示:
每件售价x … 15 16 17 18 …
(元)
每天销售量 … 150 140 130 120 …
y(件)
(1)求y关于x的函数解析式;
(2)若用w(元)表示工艺品厂试销该工艺品每天获得的利润,试求 w关于x的函数
解析式;
(3)该工艺品每件售价为多少元时,工艺品厂试销该工艺品每天获得的利润最大,最
大利润是多少元?
七、解答题(满分12分)
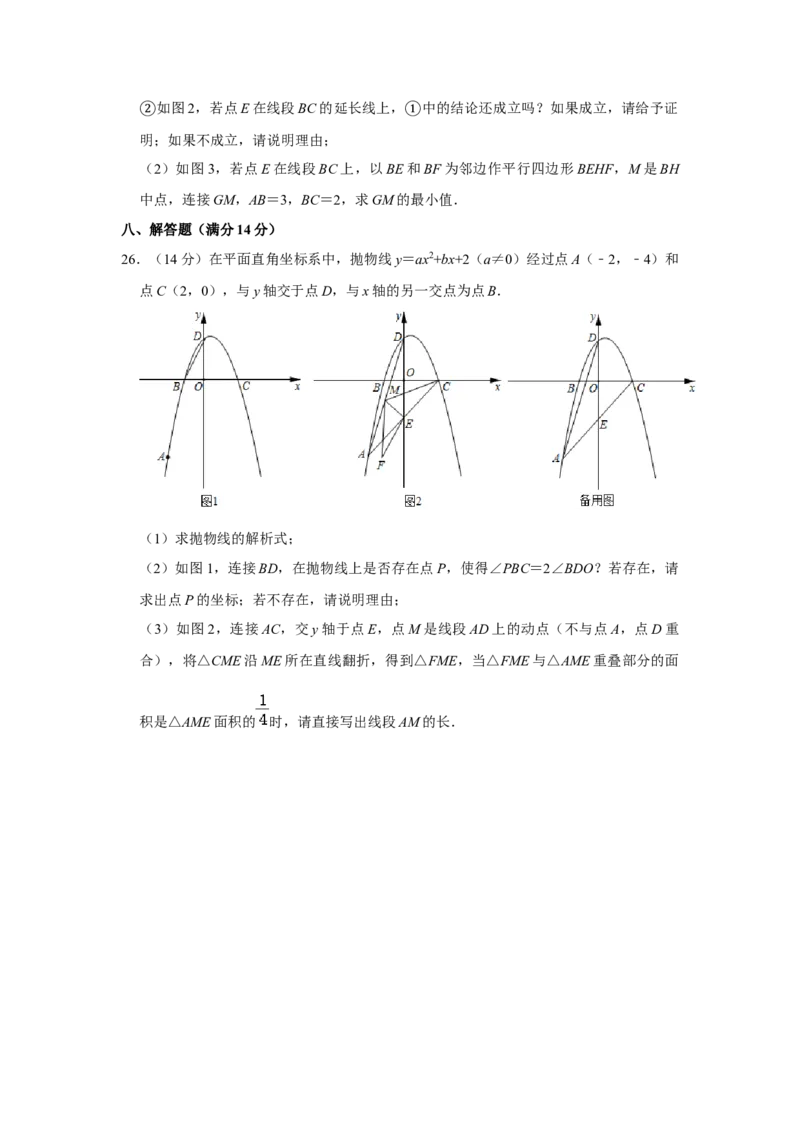
25.(12分)在矩形ABCD中,点E是射线BC上一动点,连接AE,过点B作BF⊥AE于
点G,交直线CD于点F.
(1)当矩形ABCD是正方形时,以点F为直角顶点在正方形ABCD的外部作等腰直角
三角形CFH,连接EH.
如图1,若点E在线段BC上,则线段AE与EH之间的数量关系是 ,位置关系
①是 ;如图2,若点E在线段BC的延长线上, 中的结论还成立吗?如果成立,请给予证
②明;如果不成立,请说明理由; ①
(2)如图3,若点E在线段BC上,以BE和BF为邻边作平行四边形BEHF,M是BH
中点,连接GM,AB=3,BC=2,求GM的最小值.
八、解答题(满分14分)
26.(14分)在平面直角坐标系中,抛物线y=ax2+bx+2(a≠0)经过点A(﹣2,﹣4)和
点C(2,0),与y轴交于点D,与x轴的另一交点为点B.
(1)求抛物线的解析式;
(2)如图1,连接BD,在抛物线上是否存在点P,使得∠PBC=2∠BDO?若存在,请
求出点P的坐标;若不存在,请说明理由;
(3)如图2,连接AC,交y轴于点E,点M是线段AD上的动点(不与点A,点D重
合),将△CME沿ME所在直线翻折,得到△FME,当△FME与△AME重叠部分的面
积是△AME面积的 时,请直接写出线段AM的长.