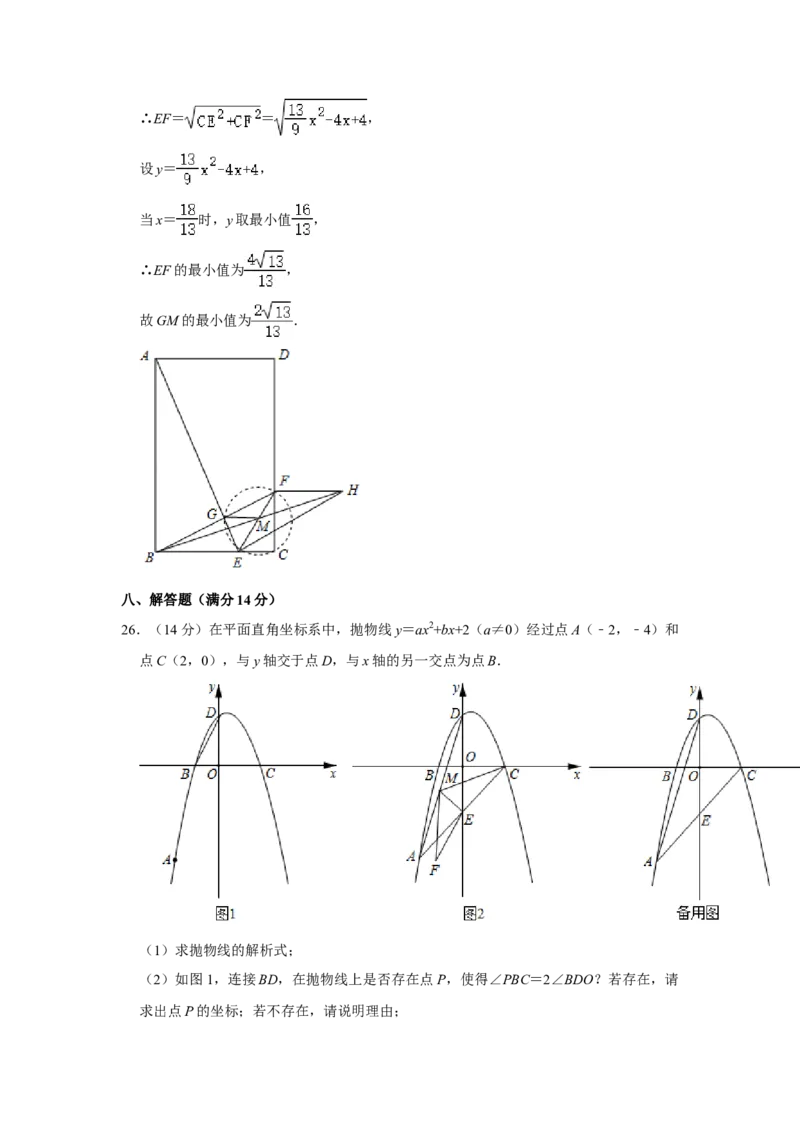
文档内容
2020年辽宁省鞍山市中考数学试卷
参考答案与试题解析
一、选择题(本题共8个小题,每小题3分,共24分.在每小题给出的四个选项中,只有
一项是符合题目要求的)
1.(3分)﹣ 的绝对值是( )
A.﹣2020 B.﹣ C. D.2020
【分析】﹣ 的绝对值等于它的相反数,据此求解即可.
【解答】解:|﹣ |= .
故选:C.
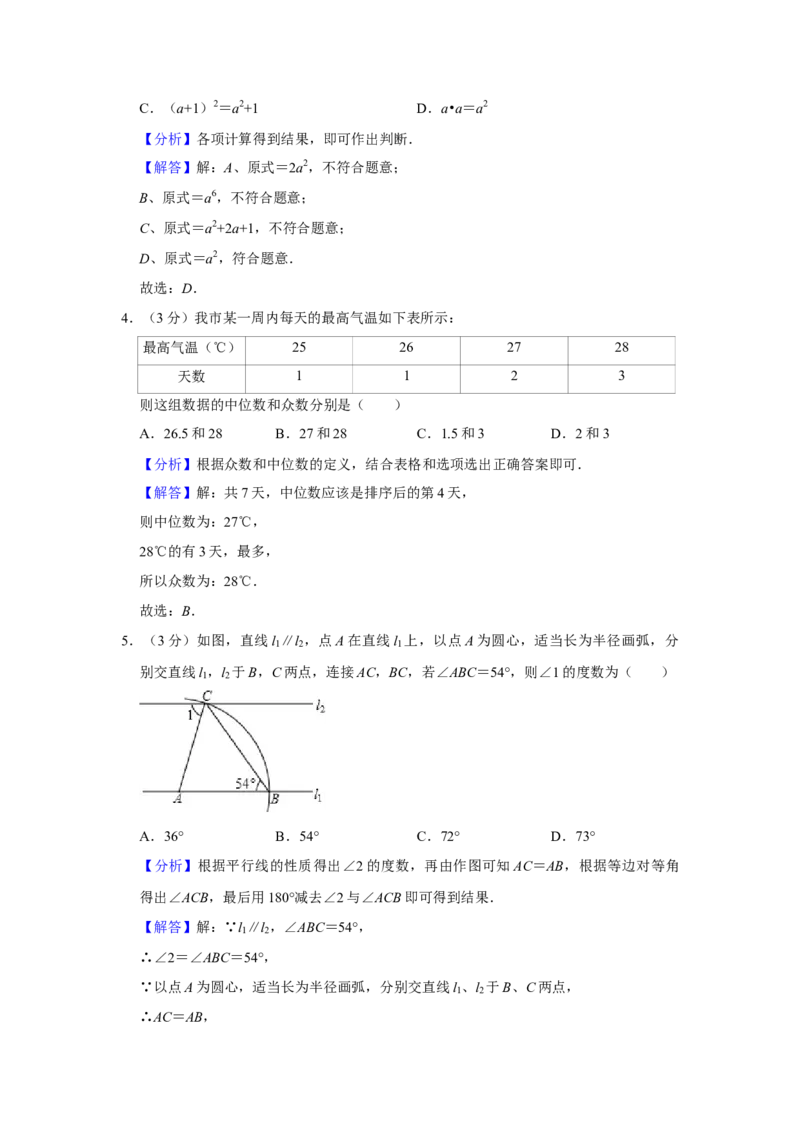
2.(3分)如图,该几何体是由5个相同的小正方体搭成的,则这个几何体的主视图是(
)
A. B.
C. D.
【分析】从正面看所得到的图形是主视图,从左面看到的图形是左视图,从上面看到的
图象是俯视图,画出从正面看所得到的图形即可.
【解答】解:从正面看,底层是三个小正方形,上层左边是一个小正方形.
故选:A.
3.(3分)下列计算结果正确的是( )
A.a2+a2=a4 B.(a3)2=a5C.(a+1)2=a2+1 D.a•a=a2
【分析】各项计算得到结果,即可作出判断.
【解答】解:A、原式=2a2,不符合题意;
B、原式=a6,不符合题意;
C、原式=a2+2a+1,不符合题意;
D、原式=a2,符合题意.
故选:D.
4.(3分)我市某一周内每天的最高气温如下表所示:
最高气温(℃) 25 26 27 28
天数 1 1 2 3
则这组数据的中位数和众数分别是( )
A.26.5和28 B.27和28 C.1.5和3 D.2和3
【分析】根据众数和中位数的定义,结合表格和选项选出正确答案即可.
【解答】解:共7天,中位数应该是排序后的第4天,
则中位数为:27℃,
28℃的有3天,最多,
所以众数为:28℃.
故选:B.
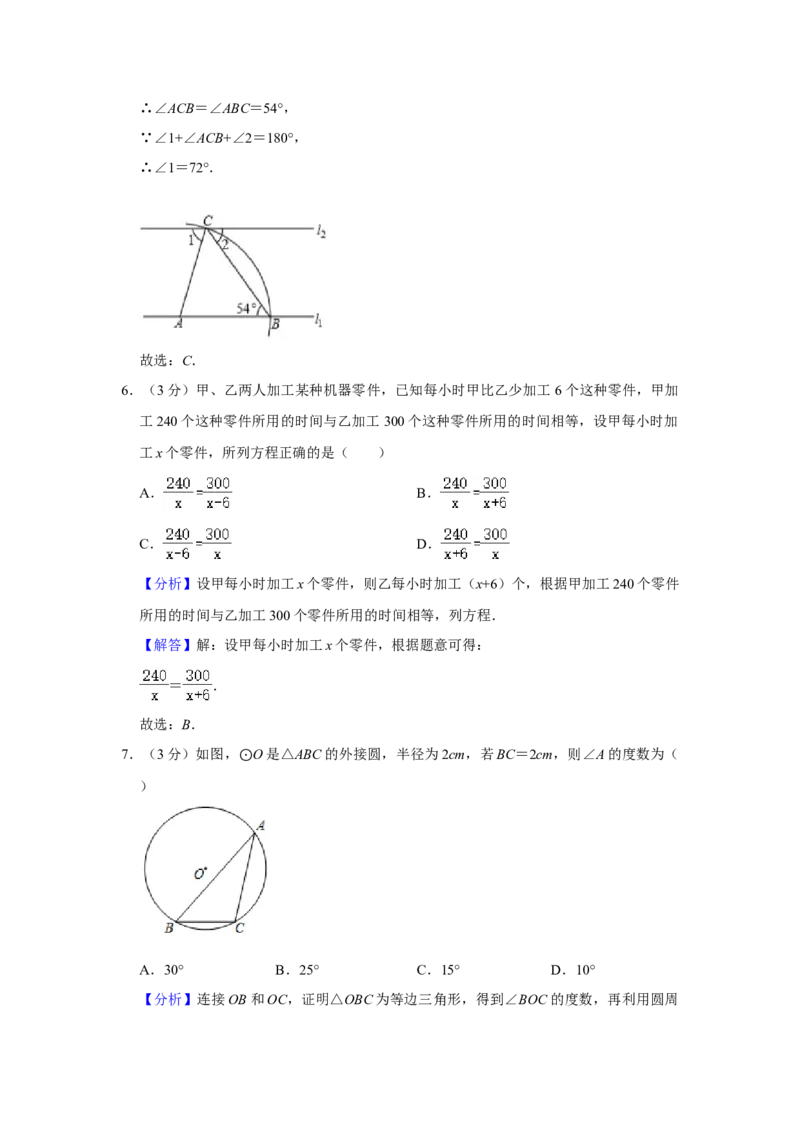
5.(3分)如图,直线l ∥l ,点A在直线l 上,以点A为圆心,适当长为半径画弧,分
1 2 1
别交直线l ,l 于B,C两点,连接AC,BC,若∠ABC=54°,则∠1的度数为( )
1 2
A.36° B.54° C.72° D.73°
【分析】根据平行线的性质得出∠2的度数,再由作图可知AC=AB,根据等边对等角
得出∠ACB,最后用180°减去∠2与∠ACB即可得到结果.
【解答】解:∵l ∥l ,∠ABC=54°,
1 2
∴∠2=∠ABC=54°,
∵以点A为圆心,适当长为半径画弧,分别交直线l 、l 于B、C两点,
1 2
∴AC=AB,∴∠ACB=∠ABC=54°,
∵∠1+∠ACB+∠2=180°,
∴∠1=72°.
故选:C.
6.(3分)甲、乙两人加工某种机器零件,已知每小时甲比乙少加工6个这种零件,甲加
工240个这种零件所用的时间与乙加工300个这种零件所用的时间相等,设甲每小时加
工x个零件,所列方程正确的是( )
A. B.
C. D.
【分析】设甲每小时加工x个零件,则乙每小时加工(x+6)个,根据甲加工240个零件
所用的时间与乙加工300个零件所用的时间相等,列方程.
【解答】解:设甲每小时加工x个零件,根据题意可得:
= .
故选:B.
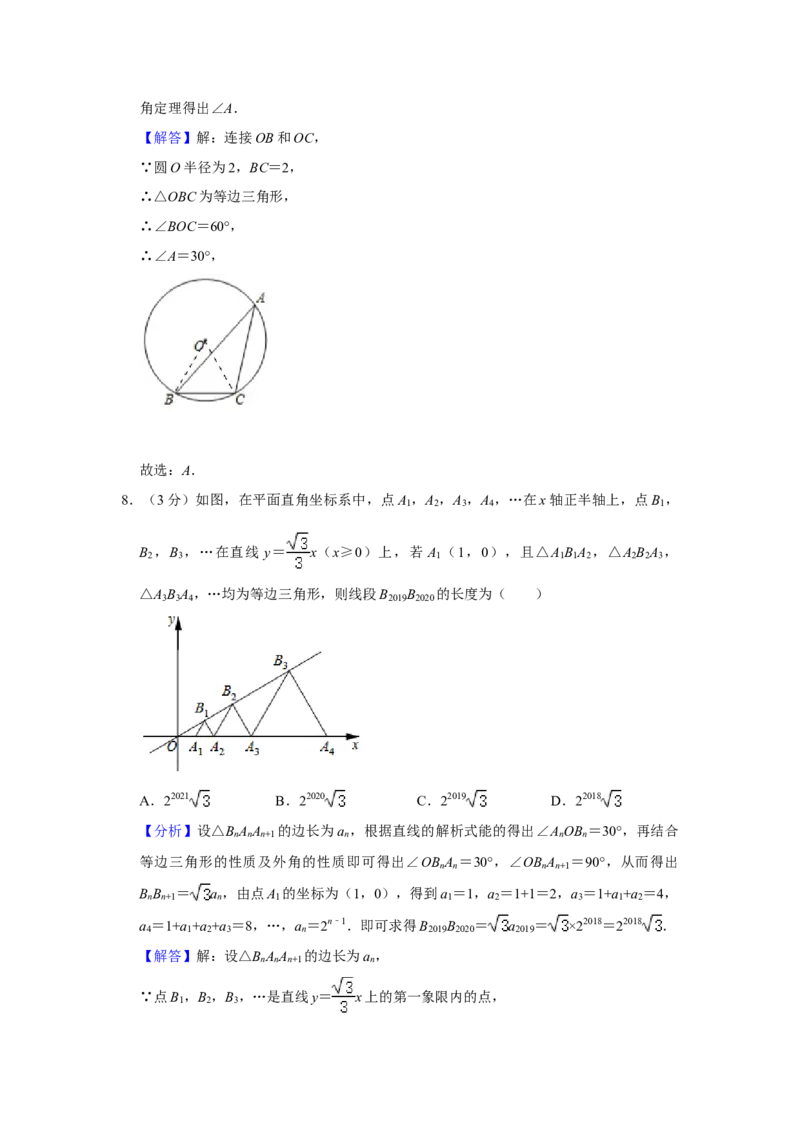
7.(3分)如图, O是△ABC的外接圆,半径为2cm,若BC=2cm,则∠A的度数为(
) ⊙
A.30° B.25° C.15° D.10°
【分析】连接OB和OC,证明△OBC为等边三角形,得到∠BOC的度数,再利用圆周角定理得出∠A.
【解答】解:连接OB和OC,
∵圆O半径为2,BC=2,
∴△OBC为等边三角形,
∴∠BOC=60°,
∴∠A=30°,
故选:A.
8.(3分)如图,在平面直角坐标系中,点A ,A ,A ,A ,…在x轴正半轴上,点B ,
1 2 3 4 1
B ,B ,…在直线 y= x(x≥0)上,若 A (1,0),且△A B A ,△A B A ,
2 3 1 1 1 2 2 2 3
△A B A ,…均为等边三角形,则线段B B 的长度为( )
3 3 4 2019 2020
A.22021 B.22020 C.22019 D.22018
【分析】设△B A A 的边长为a ,根据直线的解析式能的得出∠A OB =30°,再结合
n n n+1 n n n
等边三角形的性质及外角的性质即可得出∠OB A =30°,∠OB A =90°,从而得出
n n n n+1
B B = a ,由点A 的坐标为(1,0),得到a =1,a =1+1=2,a =1+a +a =4,
n n+1 n 1 1 2 3 1 2
a =1+a +a +a =8,…,a =2n﹣1.即可求得B B = a = ×22018=22018 .
4 1 2 3 n 2019 2020 2019
【解答】解:设△B A A 的边长为a ,
n n n+1 n
∵点B ,B ,B ,…是直线y= x上的第一象限内的点,
1 2 3∴∠A OB =30°,
n n
又∵△B A A 为等边三角形,
n n n+1
∴∠B A A =60°,
n n n+1
∴∠OB A =30°,∠OB A =90°,
n n n n+1
∴B B =OB = a ,
n n+1 n n
∵点A 的坐标为(1,0),
1
∴a =1,a =1+1=2,a =1+a +a =4,a =1+a +a +a =8,…,
1 2 3 1 2 4 1 2 3
∴a =2n﹣1.
n
∴B B = a = ×22018=22018 ,
2019 2020 2019
故选:D.
二、填空题(本题共8个小题,每小题3分,共24分)
9.(3分)据《光明日报》报道:截至2020年5月31日,全国参与新冠肺炎疫情防控的
志愿者约为8810000,将数据8810000科学记数法表示为 8.81×1 0 6 .
【分析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的
值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相
同.当原数绝对值≥10时,n是正数;当原数的绝对值<1时,n是负数.
【解答】解:8810000=8.81×106,
故答案为:8.81×106.
10.(3分)分解因式:a3﹣2a2b+ab2= a ( a ﹣ b ) 2 .
【分析】先提取公因式a,再对余下的多项式利用完全平方公式继续分解.
【解答】解:a3﹣2a2b+ab2,
=a(a2﹣2ab+b2),
=a(a﹣b)2.
11.(3分)在一个不透明的袋子中装有6个红球和若干个白球,这些球除颜色外都相同,
将球搅匀后随机摸出一个球,记下颜色后放回,不断重复这一过程,共摸球100次,发
现有20次摸到红球,估计袋子中白球的个数约为 2 4 个 .
【分析】估计利用频率估计概率可估计摸到白球的概率为 0.2,然后根据概率公式构建
方程求解即可.
【解答】解:设白球有x个,
根据题意得: =0.2,解得:x=24,
经检验:x=24是分式方程的解,
即白球有24个,
故答案为24个
12.(3分)如果关于x的一元二次方程x2﹣3x+k=0有两个相等的实数根,那么实数k的
值是 .
【分析】利用判别式的意义得到△=(﹣3)2﹣4k=0,然后解关于k的方程即可.
【解答】解:根据题意得△=(﹣3)2﹣4k=0,
解得k= .
故答案为 .
13.(3分)不等式组 的解集为 1 < x ≤ 2 .
【分析】首先解每个不等式,两个不等式的解集的公共部分就是不等式组的解集.
【解答】解:解不能等式2x﹣1≤3,得:x≤2,
解不等式2﹣x<1,得:x>1,
则不等式组的解集为1<x≤2,
故答案为:1<x≤2.
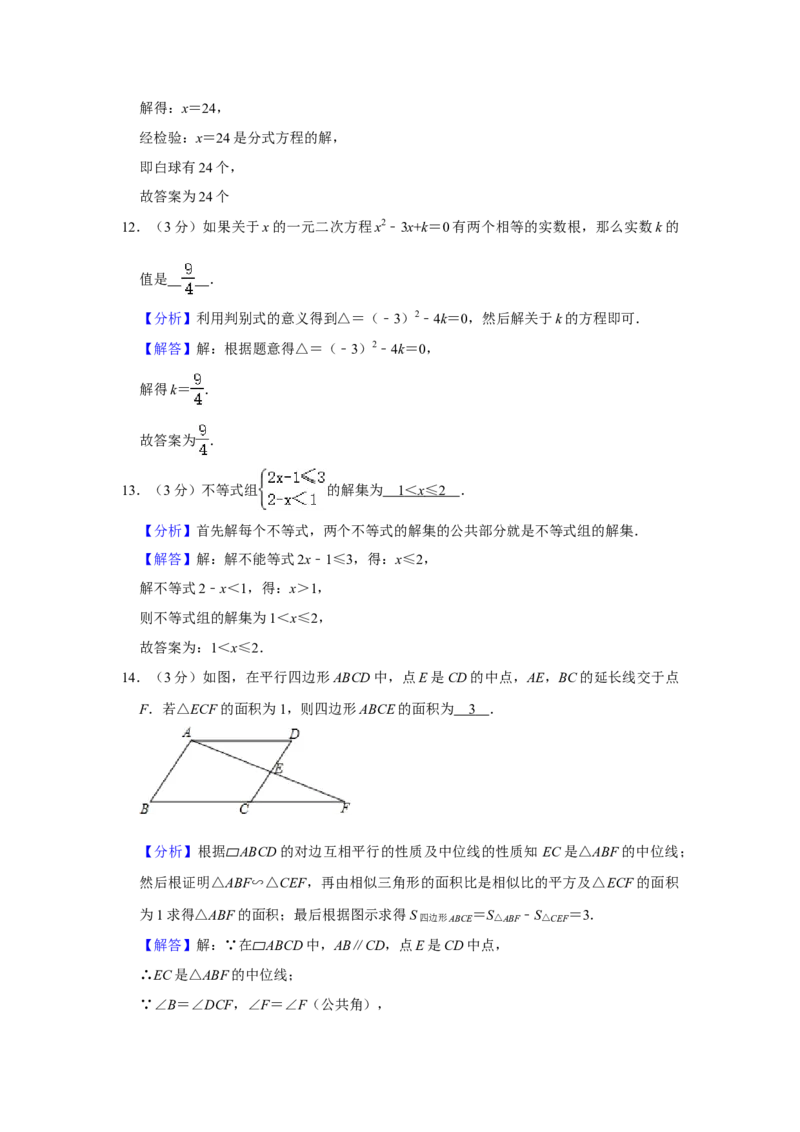
14.(3分)如图,在平行四边形ABCD中,点E是CD的中点,AE,BC的延长线交于点
F.若△ECF的面积为1,则四边形ABCE的面积为 3 .
【分析】根据 ABCD的对边互相平行的性质及中位线的性质知 EC是△ABF的中位线;
然后根证明△A▱BF∽△CEF,再由相似三角形的面积比是相似比的平方及△ECF的面积
为1求得△ABF的面积;最后根据图示求得S四边形ABCE =S△ABF ﹣S△CEF =3.
【解答】解:∵在 ABCD中,AB∥CD,点E是CD中点,
∴EC是△ABF的中▱位线;
∵∠B=∠DCF,∠F=∠F(公共角),∴△ABF∽△ECF,
∵ ,
∴S△ABF :S△CEF =1:4;
又∵△ECF的面积为1,
∴S△ABF =4,
∴S四边形ABCE =S△ABF ﹣S△CEF =3.
故答案为:3.
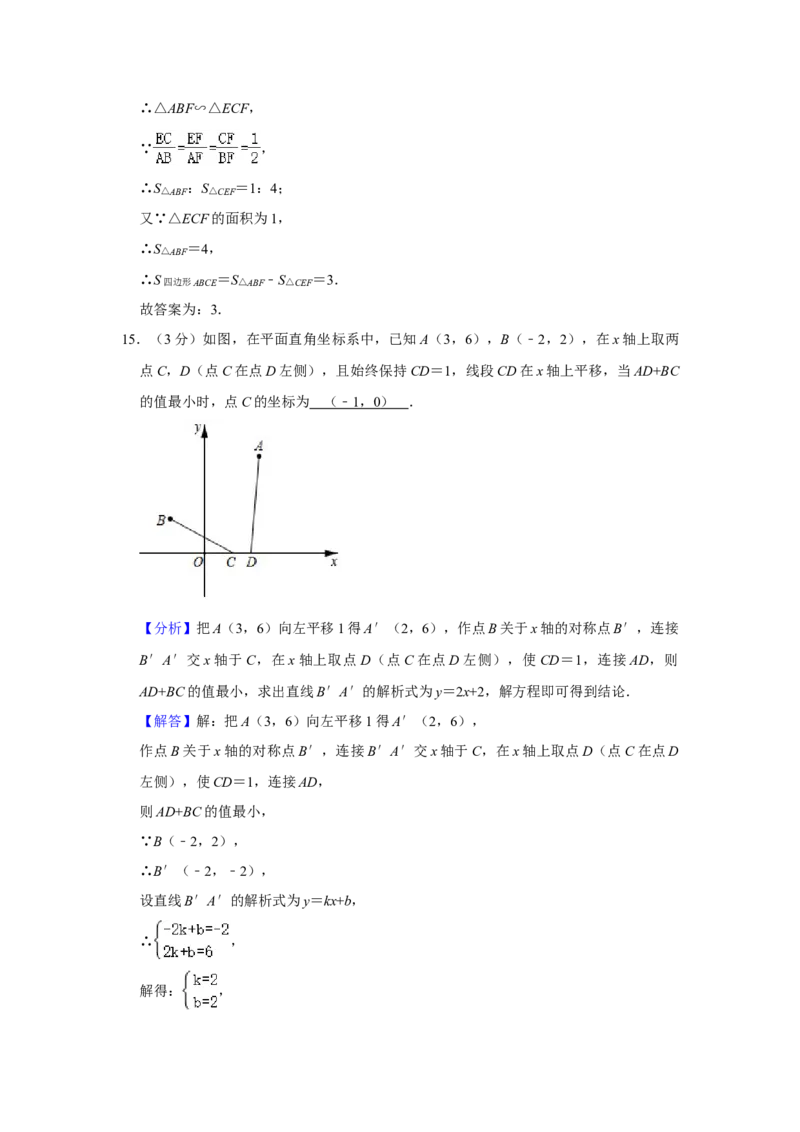
15.(3分)如图,在平面直角坐标系中,已知A(3,6),B(﹣2,2),在x轴上取两
点C,D(点C在点D左侧),且始终保持CD=1,线段CD在x轴上平移,当AD+BC
的值最小时,点C的坐标为 (﹣ 1 , 0 ) .
【分析】把A(3,6)向左平移1得A′(2,6),作点B关于x轴的对称点B′,连接
B′A′交x轴于C,在x轴上取点D(点C在点D左侧),使CD=1,连接AD,则
AD+BC的值最小,求出直线B′A′的解析式为y=2x+2,解方程即可得到结论.
【解答】解:把A(3,6)向左平移1得A′(2,6),
作点B关于x轴的对称点B′,连接B′A′交x轴于C,在x轴上取点D(点C在点D
左侧),使CD=1,连接AD,
则AD+BC的值最小,
∵B(﹣2,2),
∴B′(﹣2,﹣2),
设直线B′A′的解析式为y=kx+b,
∴ ,
解得: ,∴直线B′A′的解析式为y=2x+2,
当y=0时,x=﹣1,
∴C(﹣1,0),
故答案为:(﹣1,0).
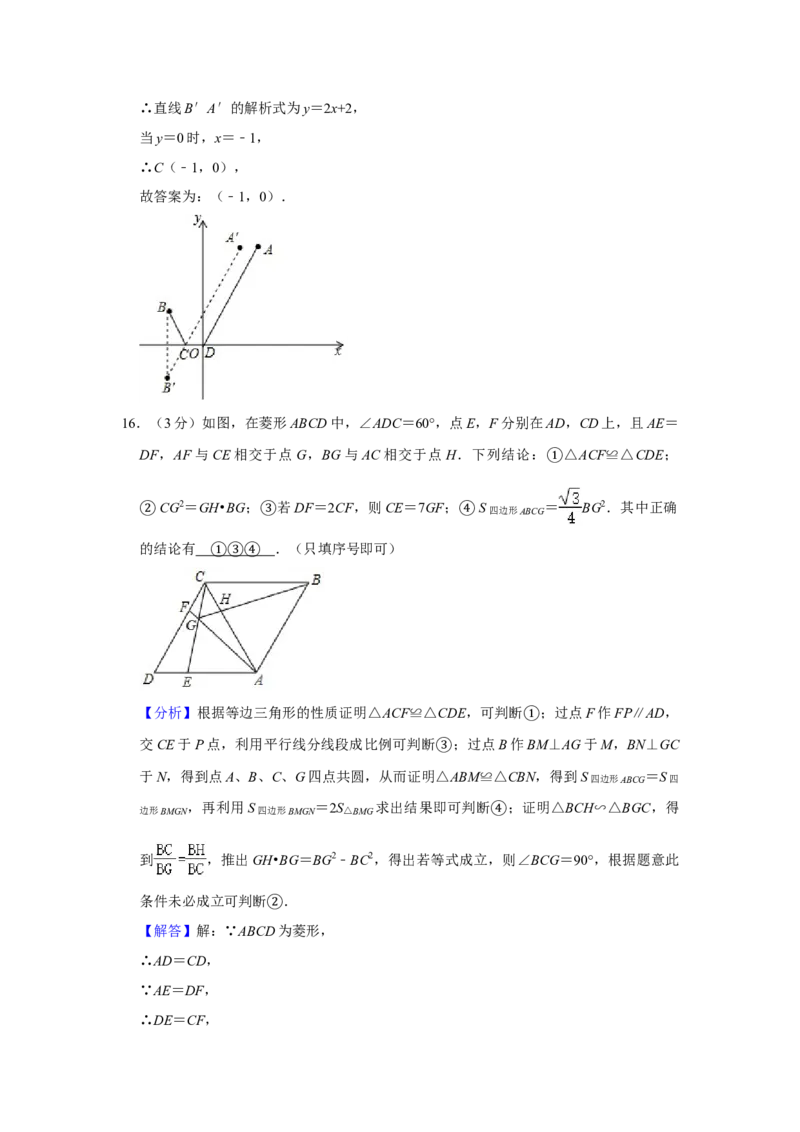
16.(3分)如图,在菱形ABCD中,∠ADC=60°,点E,F分别在AD,CD上,且AE=
DF,AF与CE相交于点G,BG与AC相交于点H.下列结论: △ACF≌△CDE;
①
CG2=GH•BG; 若DF=2CF,则CE=7GF; S四边形ABCG = BG2.其中正确
② ③ ④
的结论有 .(只填序号即可)
①③④
【分析】根据等边三角形的性质证明△ACF≌△CDE,可判断 ;过点F作FP∥AD,
交CE于P点,利用平行线分线段成比例可判断 ;过点B作①BM⊥AG于M,BN⊥GC
于N,得到点A、B、C、G四点共圆,从而证明△③ABM≌△CBN,得到S四边形ABCG =S四
边形BMGN
,再利用S四边形BMGN =2S△BMG 求出结果即可判断 ;证明△BCH∽△BGC,得
④
到 ,推出GH•BG=BG2﹣BC2,得出若等式成立,则∠BCG=90°,根据题意此
条件未必成立可判断 .
【解答】解:∵ABCD②为菱形,
∴AD=CD,
∵AE=DF,
∴DE=CF,∵∠ADC=60°,
∴△ACD为等边三角形,
∴∠D=∠ACD=60°,AC=CD,
∴△ACF≌△CDE(SAS),故 正确;
过点F作FP∥AD,交CE于P点①.
∵DF=2CF,
∴FP:DE=CF:CD=1:3,
∵DE=CF,AD=CD,
∴AE=2DE,
∴FP:AE=1:6=FG:AG,
∴AG=6FG,
∴CE=AF=7GF,故 正确;
过点B作BM⊥AG于③M,BN⊥GC于N,
∵∠AGE=∠ACG+∠CAF=∠ACG+∠GCF=60°=∠ABC,
即∠AGC+∠ABC=180°,
∴点A、B、C、G四点共圆,
∴∠AGB=∠ACB=60°,∠CGB=∠CAB=60°,
∴∠AGB=∠CGB=60°,
∴BM=BN,又AB=BC,
∴△ABM≌△CBN(HL),
∴S四边形ABCG =S四边形BMGN ,
∵∠BGM=60°,
∴GM= BG,BM= BG,
∴S四边形BMGN =2S△BMG =2× × = BG2,故 正确;
④
∵∠CGB=∠ACB=60°,∠CBG=∠HBC,
∴△BCH∽△BGC,
∴ ,
则BG•BH=BC2,
则BG•(BG﹣GH)=BC2,则BG2﹣BG•GH=BC2,
则GH•BG=BG2﹣BC2,
当∠BCG=90°时,BG2﹣BC2=CG2,此时GH•BG=CG2,
而题中∠BCG未必等于90°,故 不成立,
故正确的结论有 , ②
故答案为: ①③.④
①③④
三、解答题(每小题8分,共16分)
17.(8分)先化简,再求值:(x﹣1﹣ )÷ ,其中x= ﹣2.
【分析】先根据分式混合运算的法则把原式进行化简,再将x的值代入进行计算即可
【解答】解:(x﹣1﹣ )÷ ,
=[ ﹣ ] ,
= ,
= ,
当x= ﹣2时,原式= = = =1﹣2 .
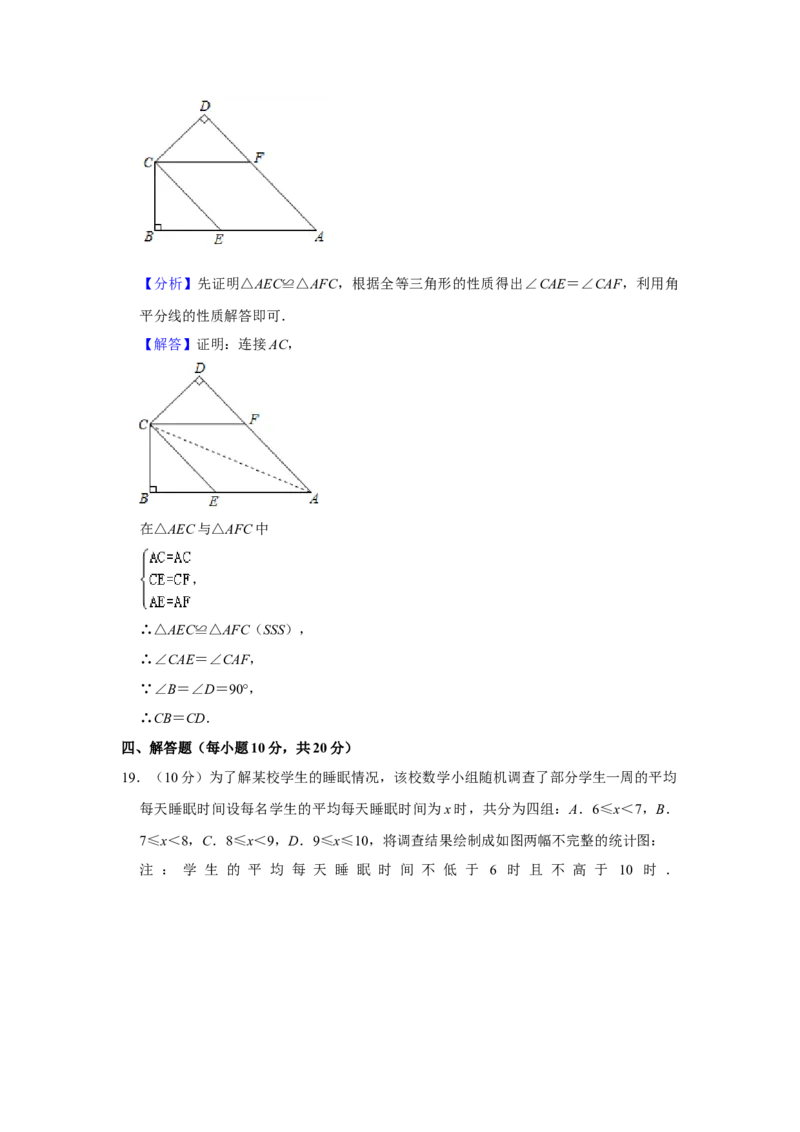
18.(8分)如图,在四边形ABCD中,∠B=∠D=90°,点E,F分别在AB,AD上,AE
=AF,CE=CF,求证:CB=CD.【分析】先证明△AEC≌△AFC,根据全等三角形的性质得出∠CAE=∠CAF,利用角
平分线的性质解答即可.
【解答】证明:连接AC,
在△AEC与△AFC中
,
∴△AEC≌△AFC(SSS),
∴∠CAE=∠CAF,
∵∠B=∠D=90°,
∴CB=CD.
四、解答题(每小题10分,共20分)
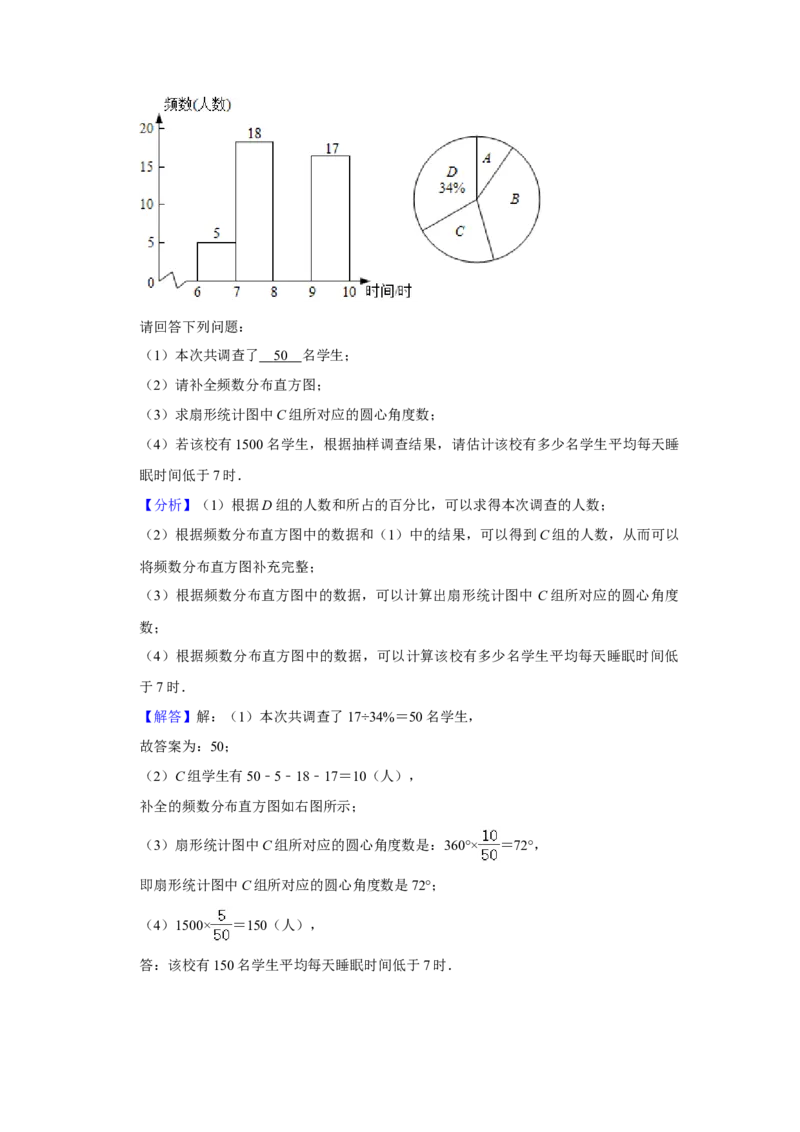
19.(10分)为了解某校学生的睡眠情况,该校数学小组随机调查了部分学生一周的平均
每天睡眠时间设每名学生的平均每天睡眠时间为x时,共分为四组:A.6≤x<7,B.
7≤x<8,C.8≤x<9,D.9≤x≤10,将调查结果绘制成如图两幅不完整的统计图:
注 : 学 生 的 平 均 每 天 睡 眠 时 间 不 低 于 6 时 且 不 高 于 10 时 .请回答下列问题:
(1)本次共调查了 5 0 名学生;
(2)请补全频数分布直方图;
(3)求扇形统计图中C组所对应的圆心角度数;
(4)若该校有1500名学生,根据抽样调查结果,请估计该校有多少名学生平均每天睡
眠时间低于7时.
【分析】(1)根据D组的人数和所占的百分比,可以求得本次调查的人数;
(2)根据频数分布直方图中的数据和(1)中的结果,可以得到C组的人数,从而可以
将频数分布直方图补充完整;
(3)根据频数分布直方图中的数据,可以计算出扇形统计图中 C组所对应的圆心角度
数;
(4)根据频数分布直方图中的数据,可以计算该校有多少名学生平均每天睡眠时间低
于7时.
【解答】解:(1)本次共调查了17÷34%=50名学生,
故答案为:50;
(2)C组学生有50﹣5﹣18﹣17=10(人),
补全的频数分布直方图如右图所示;
(3)扇形统计图中C组所对应的圆心角度数是:360°× =72°,
即扇形统计图中C组所对应的圆心角度数是72°;
(4)1500× =150(人),
答:该校有150名学生平均每天睡眠时间低于7时.20.(10分)甲、乙两人去超市选购奶制品,有两个品牌的奶制品可供选购,其中蒙牛品
牌有两个种类的奶制品:A.纯牛奶,B.核桃奶;伊利品牌有三个种类的奶制品:C.
纯牛奶,D.酸奶,E.核桃奶.
(1)甲从这两个品牌的奶制品中随机选购一种,选购到纯牛奶的概率是 ;
(2)若甲喜爱蒙牛品牌的奶制品,乙喜爱伊利品牌的奶制品,甲、乙两人从各自喜爱
的品牌中随机选购一种奶制品,请利用画树状图或列表的方法求出两人选购到同一种类
奶制品的概率.
【分析】(1)用纯牛奶的个数除以总牛奶的个数即可得出答案;
(2)根据题意画出树状图得出所有等可能的情况数和两人选购到同一种类奶制品的情
况数,然后根据概率公式即可得出答案.
【解答】解:(1)∵蒙牛品牌有两个种类的奶制品:A.纯牛奶,B.核桃奶;伊利品
牌有三个种类的奶制品:C.纯牛奶,D.酸奶,E.核桃奶,
∴甲从这两个品牌的奶制品中随机选购一种,选购到纯牛奶的概率是: ;
故答案为: ;
(2)根据题意画树状图如下:
共有6种等可能的情况数,其中两人选购到同一种类奶制品的有2种,则两人选购到同一种类奶制品的概率是 = .
五、解答题(每小题10分,共20分)
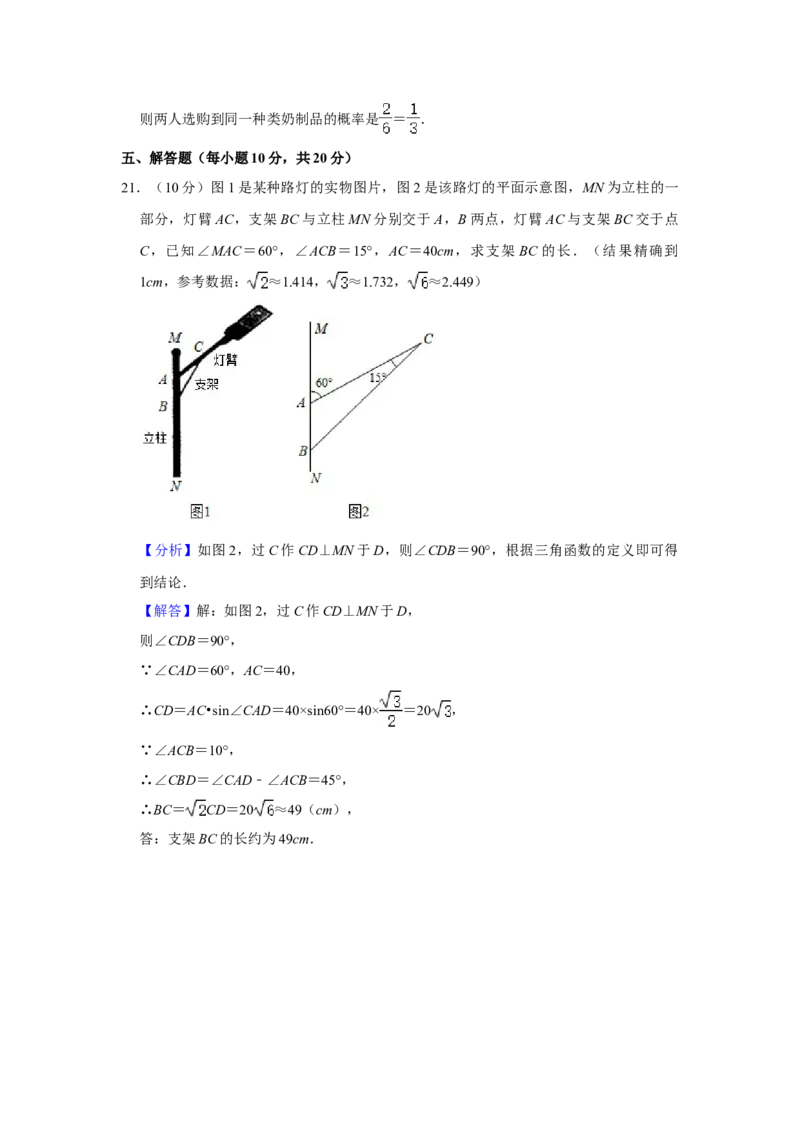
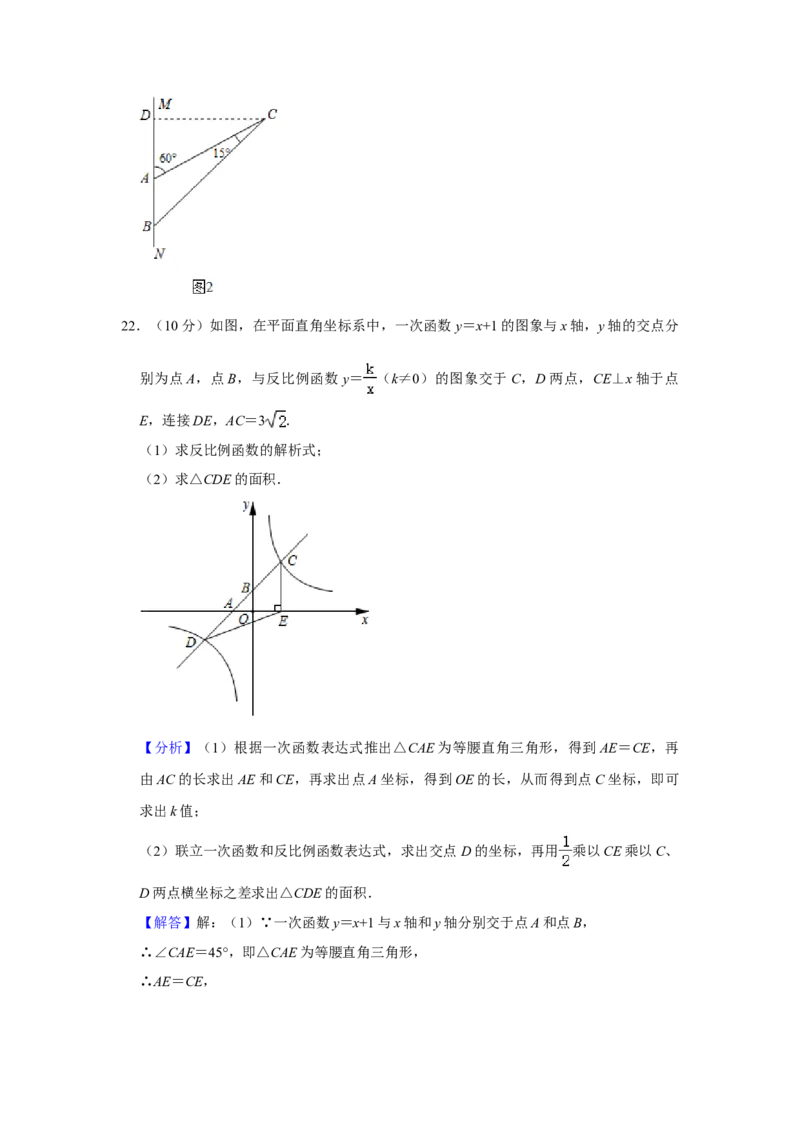
21.(10分)图1是某种路灯的实物图片,图2是该路灯的平面示意图,MN为立柱的一
部分,灯臂AC,支架BC与立柱MN分别交于A,B两点,灯臂AC与支架BC交于点
C,已知∠MAC=60°,∠ACB=15°,AC=40cm,求支架 BC 的长.(结果精确到
1cm,参考数据: ≈1.414, ≈1.732, ≈2.449)
【分析】如图2,过C作CD⊥MN于D,则∠CDB=90°,根据三角函数的定义即可得
到结论.
【解答】解:如图2,过C作CD⊥MN于D,
则∠CDB=90°,
∵∠CAD=60°,AC=40,
∴CD=AC•sin∠CAD=40×sin60°=40× =20 ,
∵∠ACB=10°,
∴∠CBD=∠CAD﹣∠ACB=45°,
∴BC= CD=20 ≈49(cm),
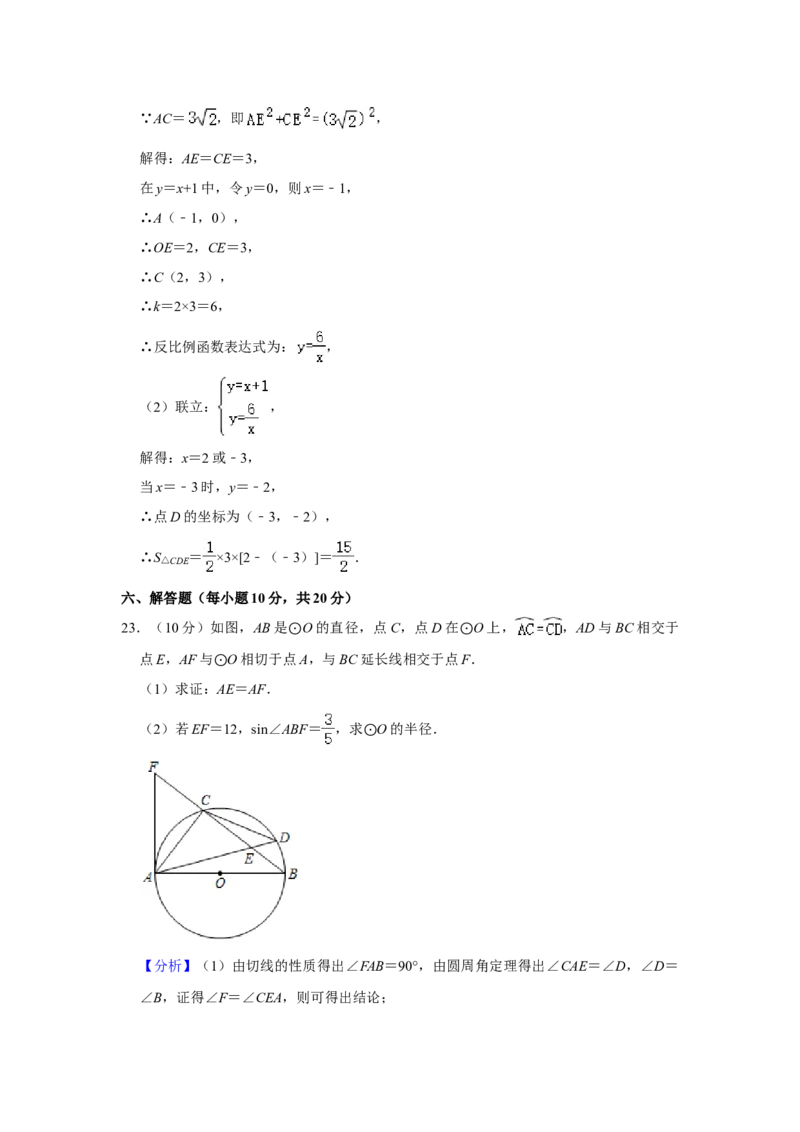
答:支架BC的长约为49cm.22.(10分)如图,在平面直角坐标系中,一次函数y=x+1的图象与x轴,y轴的交点分
别为点A,点B,与反比例函数y= (k≠0)的图象交于C,D两点,CE⊥x轴于点
E,连接DE,AC=3 .
(1)求反比例函数的解析式;
(2)求△CDE的面积.
【分析】(1)根据一次函数表达式推出△CAE为等腰直角三角形,得到AE=CE,再
由AC的长求出AE和CE,再求出点A坐标,得到OE的长,从而得到点C坐标,即可
求出k值;
(2)联立一次函数和反比例函数表达式,求出交点 D的坐标,再用 乘以CE乘以C、
D两点横坐标之差求出△CDE的面积.
【解答】解:(1)∵一次函数y=x+1与x轴和y轴分别交于点A和点B,
∴∠CAE=45°,即△CAE为等腰直角三角形,
∴AE=CE,∵AC= ,即 ,
解得:AE=CE=3,
在y=x+1中,令y=0,则x=﹣1,
∴A(﹣1,0),
∴OE=2,CE=3,
∴C(2,3),
∴k=2×3=6,
∴反比例函数表达式为: ,
(2)联立: ,
解得:x=2或﹣3,
当x=﹣3时,y=﹣2,
∴点D的坐标为(﹣3,﹣2),
∴S△CDE = ×3×[2﹣(﹣3)]= .
六、解答题(每小题10分,共20分)
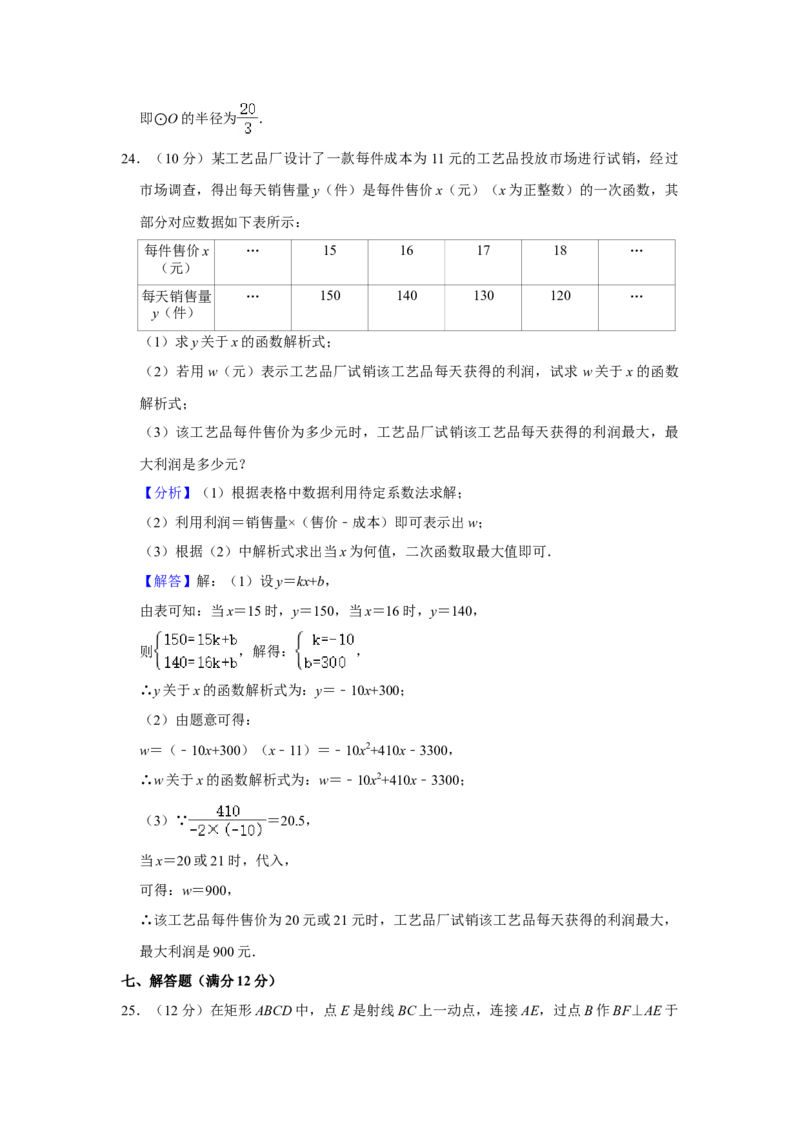
23.(10分)如图,AB是 O的直径,点C,点D在 O上, ,AD与BC相交于
点E,AF与 O相切于点⊙A,与BC延长线相交于点⊙F.
(1)求证:⊙AE=AF.
(2)若EF=12,sin∠ABF= ,求 O的半径.
⊙
【分析】(1)由切线的性质得出∠FAB=90°,由圆周角定理得出∠CAE=∠D,∠D=
∠B,证得∠F=∠CEA,则可得出结论;(2)由锐角三角函数的定义得出 ,求出AE=10,由勾股定理求出AC,则
可求出AB的长.
【解答】(1)证明:∵AF与 O相切于点A,
∴FA⊥AB, ⊙
∴∠FAB=90°,
∴∠F+∠B=90°,
∵AB是 O的直径,
∴∠ACB⊙=90°,
∴∠CAE+∠CEA=90°,
∵ = ,
∴∠CAE=∠D,
∴∠D+∠CEA=90°,
∵∠D=∠B,
∴∠B+∠CEA=90°,
∴∠F=∠CEA,
∴AE=AF.
(2)解:∵AE=AF,∠ACB=90°,
∴CF=CE= EF=6,
∵∠ABF=∠D=∠CAE,
∴sin∠ABF=sin∠CAE= ,
∴ ,
∴AE=10,
∴AC= = =8,
∵sin∠ABC= = = ,
∴AB= ,
∴OA= AB= .即 O的半径为 .
⊙
24.(10分)某工艺品厂设计了一款每件成本为11元的工艺品投放市场进行试销,经过
市场调查,得出每天销售量y(件)是每件售价x(元)(x为正整数)的一次函数,其
部分对应数据如下表所示:
每件售价x … 15 16 17 18 …
(元)
每天销售量 … 150 140 130 120 …
y(件)
(1)求y关于x的函数解析式;
(2)若用w(元)表示工艺品厂试销该工艺品每天获得的利润,试求 w关于x的函数
解析式;
(3)该工艺品每件售价为多少元时,工艺品厂试销该工艺品每天获得的利润最大,最
大利润是多少元?
【分析】(1)根据表格中数据利用待定系数法求解;
(2)利用利润=销售量×(售价﹣成本)即可表示出w;
(3)根据(2)中解析式求出当x为何值,二次函数取最大值即可.
【解答】解:(1)设y=kx+b,
由表可知:当x=15时,y=150,当x=16时,y=140,
则 ,解得: ,
∴y关于x的函数解析式为:y=﹣10x+300;
(2)由题意可得:
w=(﹣10x+300)(x﹣11)=﹣10x2+410x﹣3300,
∴w关于x的函数解析式为:w=﹣10x2+410x﹣3300;
(3)∵ =20.5,
当x=20或21时,代入,
可得:w=900,
∴该工艺品每件售价为20元或21元时,工艺品厂试销该工艺品每天获得的利润最大,
最大利润是900元.
七、解答题(满分12分)
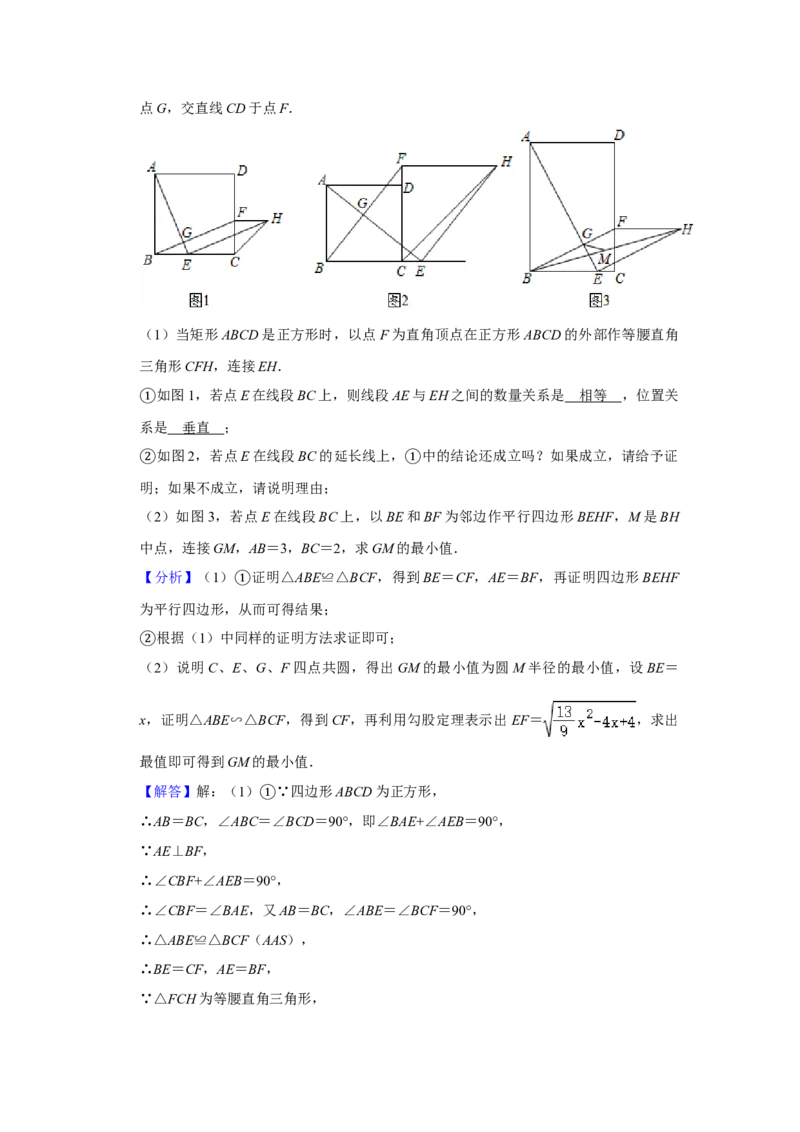
25.(12分)在矩形ABCD中,点E是射线BC上一动点,连接AE,过点B作BF⊥AE于点G,交直线CD于点F.
(1)当矩形ABCD是正方形时,以点F为直角顶点在正方形ABCD的外部作等腰直角
三角形CFH,连接EH.
如图1,若点E在线段BC上,则线段AE与EH之间的数量关系是 相等 ,位置关
①系是 垂直 ;
如图2,若点E在线段BC的延长线上, 中的结论还成立吗?如果成立,请给予证
②明;如果不成立,请说明理由; ①
(2)如图3,若点E在线段BC上,以BE和BF为邻边作平行四边形BEHF,M是BH
中点,连接GM,AB=3,BC=2,求GM的最小值.
【分析】(1) 证明△ABE≌△BCF,得到BE=CF,AE=BF,再证明四边形BEHF
为平行四边形,①从而可得结果;
根据(1)中同样的证明方法求证即可;
②(2)说明C、E、G、F四点共圆,得出GM的最小值为圆M半径的最小值,设BE=
x,证明△ABE∽△BCF,得到CF,再利用勾股定理表示出EF= ,求出
最值即可得到GM的最小值.
【解答】解:(1) ∵四边形ABCD为正方形,
∴AB=BC,∠ABC=①∠BCD=90°,即∠BAE+∠AEB=90°,
∵AE⊥BF,
∴∠CBF+∠AEB=90°,
∴∠CBF=∠BAE,又AB=BC,∠ABE=∠BCF=90°,
∴△ABE≌△BCF(AAS),
∴BE=CF,AE=BF,
∵△FCH为等腰直角三角形,∴FC=FH=BE,FH⊥FC,而CD⊥BC,
∴FH∥BC,
∴四边形BEHF为平行四边形,
∴BF∥EH且BF=EH,
∴AE=EH,AE⊥EH,
故答案为:相等;垂直;
成立,理由是:
②当点E在线段BC的延长线上时,
同理可得:△ABE≌△BCF(AAS),
∴BE=CF,AE=BF,
∵△FCH为等腰直角三角形,
∴FC=FH=BE,FH⊥FC,而CD⊥BC,
∴FH∥BC,
∴四边形BEHF为平行四边形,
∴BF∥EH且BF=EH,
∴AE=EH,AE⊥EH;
(2)∵∠EGF=∠BCD=90°,
∴C、E、G、F四点共圆,
∵四边形BCHF是平行四边形,M为BH中点,
∴M也是EF中点,
∴M是四边形BCHF外接圆圆心,
则GM的最小值为圆M半径的最小值,
∵AB=3,BC=2,
设BE=x,则CE=2﹣x,
同(1)可得:∠CBF=∠BAE,
又∵∠ABE=∠BCF=90°,
∴△ABE∽△BCF,
∴ ,即 ,
∴CF= ,∴EF= = ,
设y= ,
当x= 时,y取最小值 ,
∴EF的最小值为 ,
故GM的最小值为 .
八、解答题(满分14分)
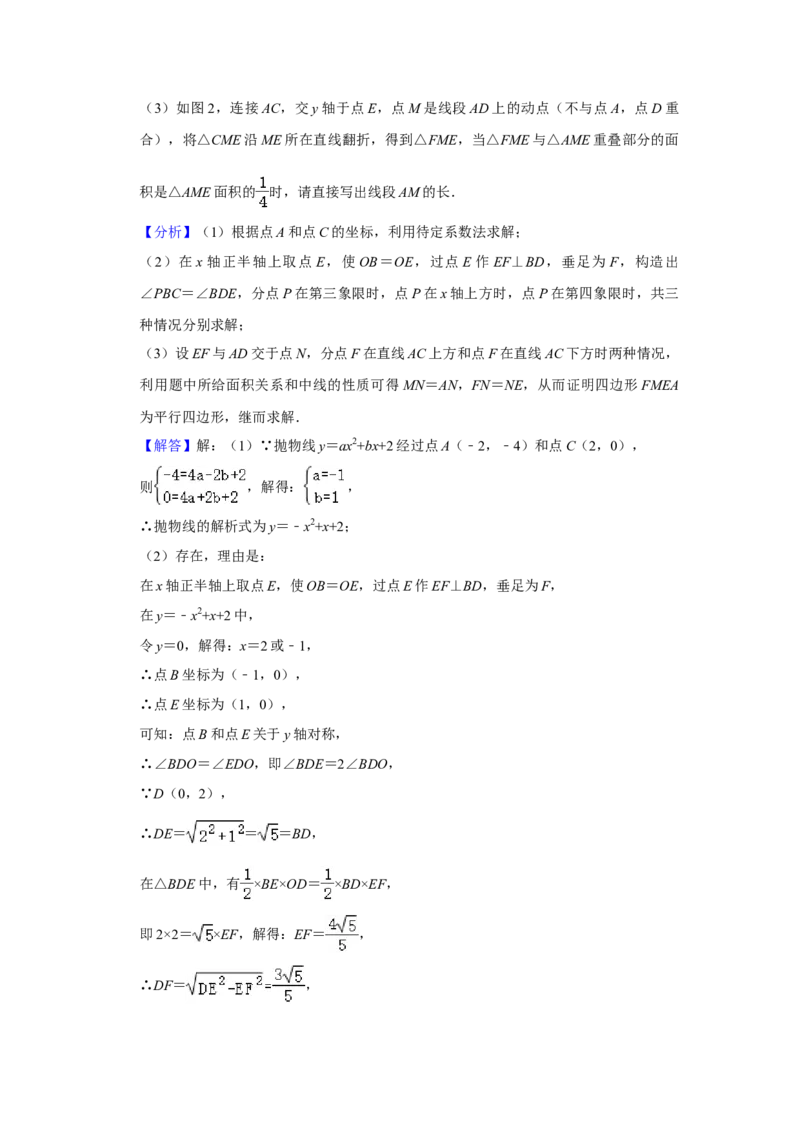
26.(14分)在平面直角坐标系中,抛物线y=ax2+bx+2(a≠0)经过点A(﹣2,﹣4)和
点C(2,0),与y轴交于点D,与x轴的另一交点为点B.
(1)求抛物线的解析式;
(2)如图1,连接BD,在抛物线上是否存在点P,使得∠PBC=2∠BDO?若存在,请
求出点P的坐标;若不存在,请说明理由;(3)如图2,连接AC,交y轴于点E,点M是线段AD上的动点(不与点A,点D重
合),将△CME沿ME所在直线翻折,得到△FME,当△FME与△AME重叠部分的面
积是△AME面积的 时,请直接写出线段AM的长.
【分析】(1)根据点A和点C的坐标,利用待定系数法求解;
(2)在x轴正半轴上取点E,使OB=OE,过点E作EF⊥BD,垂足为F,构造出
∠PBC=∠BDE,分点P在第三象限时,点P在x轴上方时,点P在第四象限时,共三
种情况分别求解;
(3)设EF与AD交于点N,分点F在直线AC上方和点F在直线AC下方时两种情况,
利用题中所给面积关系和中线的性质可得MN=AN,FN=NE,从而证明四边形FMEA
为平行四边形,继而求解.
【解答】解:(1)∵抛物线y=ax2+bx+2经过点A(﹣2,﹣4)和点C(2,0),
则 ,解得: ,
∴抛物线的解析式为y=﹣x2+x+2;
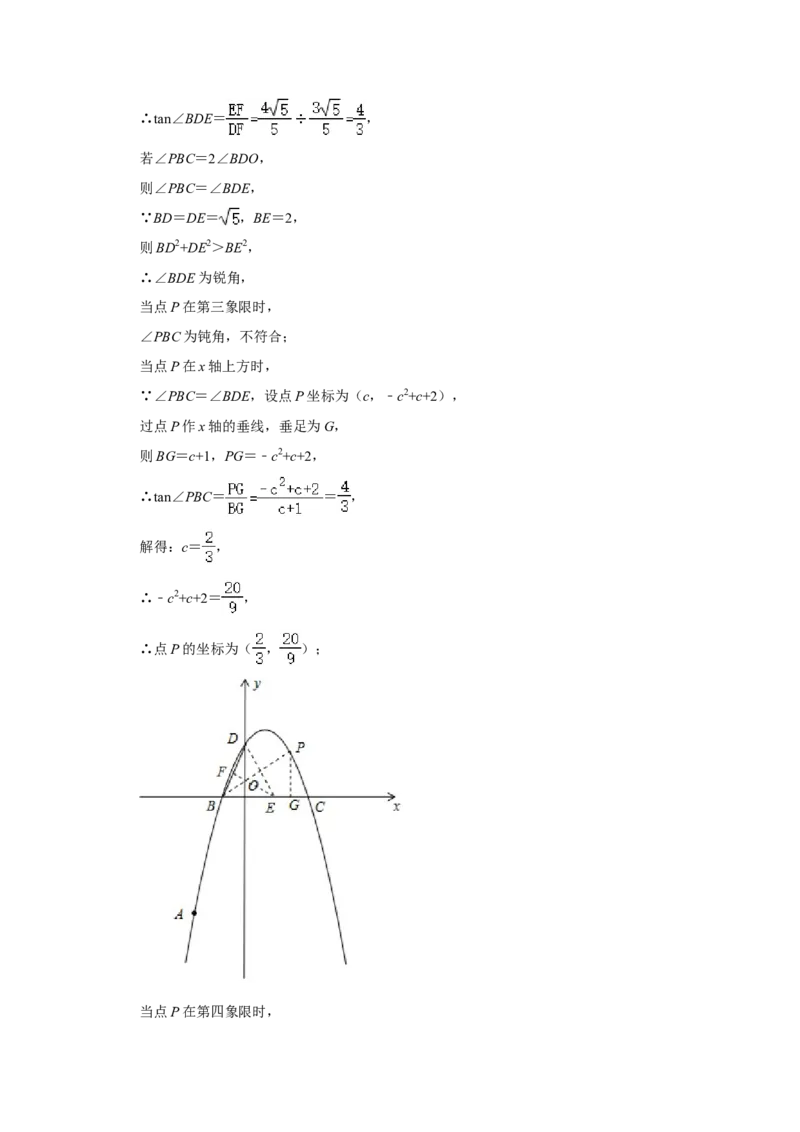
(2)存在,理由是:
在x轴正半轴上取点E,使OB=OE,过点E作EF⊥BD,垂足为F,
在y=﹣x2+x+2中,
令y=0,解得:x=2或﹣1,
∴点B坐标为(﹣1,0),
∴点E坐标为(1,0),
可知:点B和点E关于y轴对称,
∴∠BDO=∠EDO,即∠BDE=2∠BDO,
∵D(0,2),
∴DE= = =BD,
在△BDE中,有 ×BE×OD= ×BD×EF,
即2×2= ×EF,解得:EF= ,
∴DF= ,∴tan∠BDE= ,
若∠PBC=2∠BDO,
则∠PBC=∠BDE,
∵BD=DE= ,BE=2,
则BD2+DE2>BE2,
∴∠BDE为锐角,
当点P在第三象限时,
∠PBC为钝角,不符合;
当点P在x轴上方时,
∵∠PBC=∠BDE,设点P坐标为(c,﹣c2+c+2),
过点P作x轴的垂线,垂足为G,
则BG=c+1,PG=﹣c2+c+2,
∴tan∠PBC= = ,
解得:c= ,
∴﹣c2+c+2= ,
∴点P的坐标为( , );
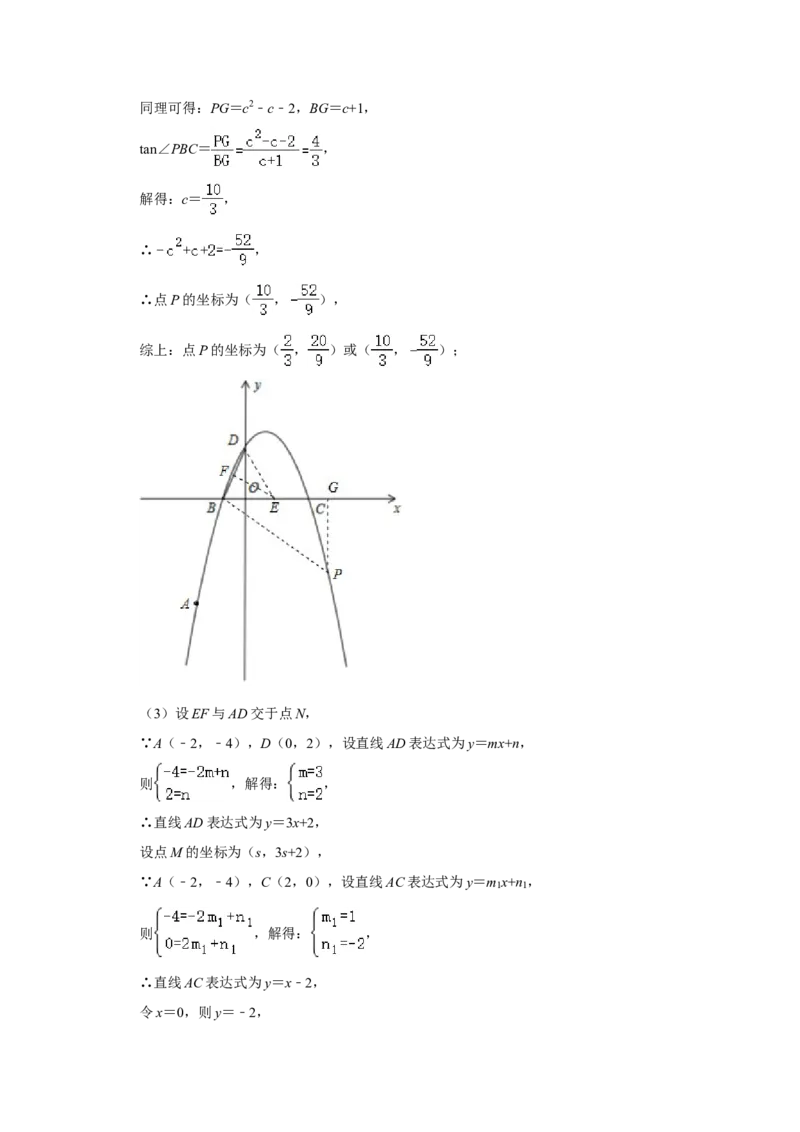
当点P在第四象限时,同理可得:PG=c2﹣c﹣2,BG=c+1,
tan∠PBC= ,
解得:c= ,
∴ ,
∴点P的坐标为( , ),
综上:点P的坐标为( , )或( , );
(3)设EF与AD交于点N,
∵A(﹣2,﹣4),D(0,2),设直线AD表达式为y=mx+n,
则 ,解得: ,
∴直线AD表达式为y=3x+2,
设点M的坐标为(s,3s+2),
∵A(﹣2,﹣4),C(2,0),设直线AC表达式为y=m x+n ,
1 1
则 ,解得: ,
∴直线AC表达式为y=x﹣2,
令x=0,则y=﹣2,∴点E坐标为(0,﹣2),
可得:点E是线段AC中点,
∴△AME和△CME的面积相等,
由于折叠,
∴△CME≌△FME,即S△CME =S△FME ,
由题意可得:
当点F在直线AC上方时,
∴S△MNE = S△AMC = S△AME = S△FME ,
即S△MNE =S△ANE =S△MNF ,
∴MN=AN,FN=NE,
∴四边形FMEA为平行四边形,
∴CM=FM=AE= AC= ,
∵M(s,3s+2),
∴ ,
解得:s= 或0(舍),
∴M( , ),
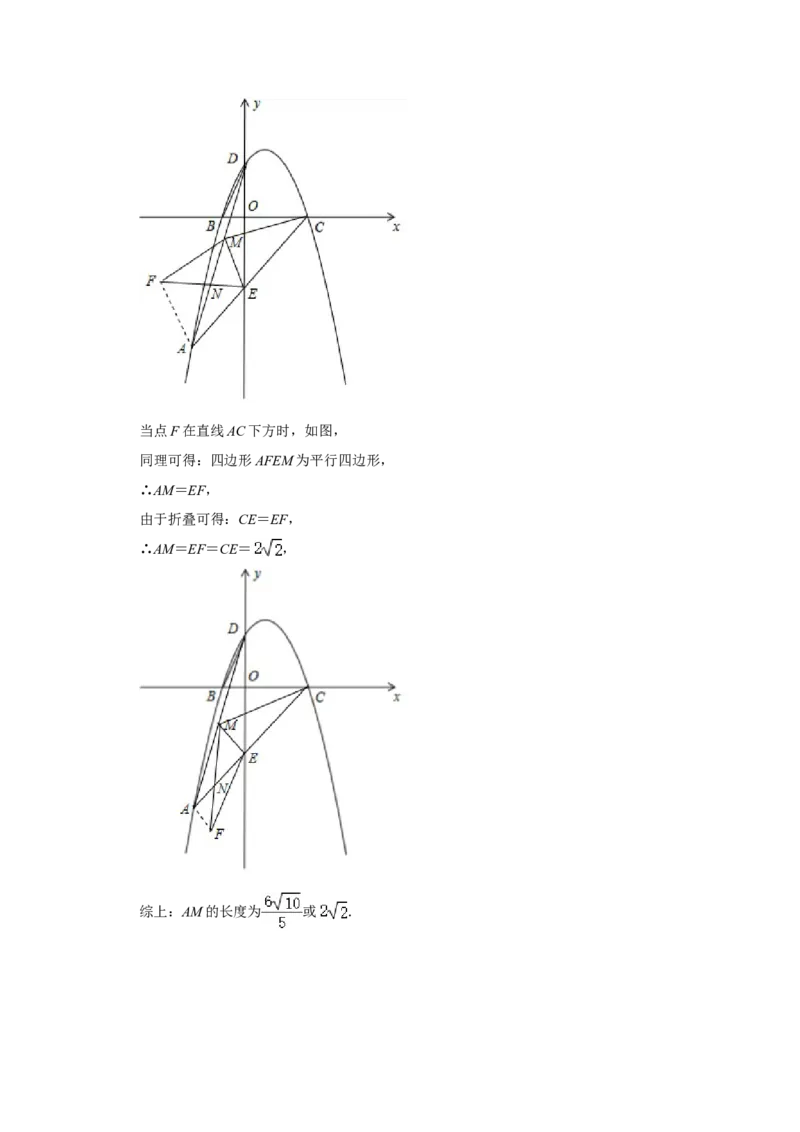
∴AM= ,当点F在直线AC下方时,如图,
同理可得:四边形AFEM为平行四边形,
∴AM=EF,
由于折叠可得:CE=EF,
∴AM=EF=CE= ,
综上:AM的长度为 或 .