文档内容
2021年山东省滨州市中考数学试卷
一、选择题:本大题共12个小题,在每小题的四个选项中只有一个是正确的,请把正确的
选项选出来,用2B铅笔把答题卡上对应题目的答案标号涂黑。每小题涂对得3分,满分
36分.
1.(3分)(2021•滨州)在数轴上,点 表示 .若从点 出发,沿数轴的正方向移动
4个单位长度到达点 ,则点 表示的数是
A. B. C.2 D.4
2.(3分)(2021•滨州)在 中,若 , , ,则点 到直线
的距离为
A.3 B.4 C.5 D.2.4
3.(3分)(2021•滨州)下列计算中,正确的是
A. B. C. D.
4.(3 分)(2021•滨州)如图,在 中, 平分 交 于点 .若
,则 的大小为
A. B. C. D.
5.(3分)(2021•滨州)如图所示的几何体,是由几个相同的小正方体组合而成的,其
俯视图为
第1页(共8页)A. B. C. D.
6.(3分)(2021•滨州)把不等式组 中每个不等式的解集在同一条数轴上表
示出来,正确的为
A. B.
C. D.
7.(3分)(2021•滨州)下列一元二次方程中,无实数根的是
A. B. C. D.
8.(3分)(2021•滨州)在四张反面无差别的卡片上,其正面分别印有线段、等边三角
形、平行四边形和正六边形.现将四张卡片的正面朝下放置,混合均匀后从中随机抽取两
张,则抽到的卡片正面图形都是轴对称图形的概率为
A. B. C. D.
9.(3分)(2021•滨州)如图, 是 的外接圆, 是 的直径.若 ,
弦 ,则 的值为
第2页(共8页)A. B. C. D.
10.(3分)(2021•滨州)对于二次函数 ,有以下结论:①当 时,
随 的增大而增大;②当 时, 有最小值3;③图象与 轴有两个交点;④图象是
由抛物线 向左平移6个单位长度,再向上平移3个单位长度得到的.其中结论正确
的个数为
A.1 B.2 C.3 D.4
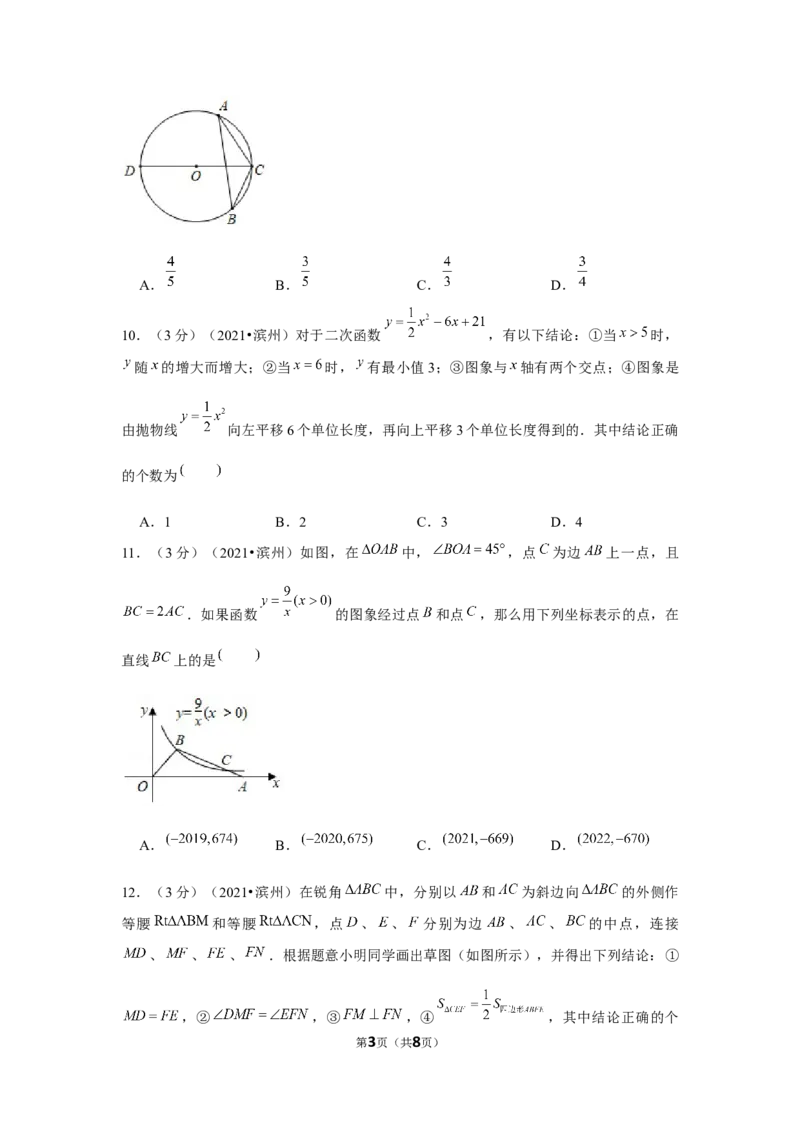
11.(3分)(2021•滨州)如图,在 中, ,点 为边 上一点,且
.如果函数 的图象经过点 和点 ,那么用下列坐标表示的点,在
直线 上的是
A. B. C. D.
12.(3分)(2021•滨州)在锐角 中,分别以 和 为斜边向 的外侧作
等腰 和等腰 ,点 、 、 分别为边 、 、 的中点,连接
、 、 、 .根据题意小明同学画出草图(如图所示),并得出下列结论:①
,② ,③ ,④ ,其中结论正确的个
第3页(共8页)数为
A.4 B.3 C.2 D.1
二、填空题:本大题共6个小题,每小题4分,满分24分.
13.(4分)(2021•滨州)若代数式 有意义,则 的取值范围为 .
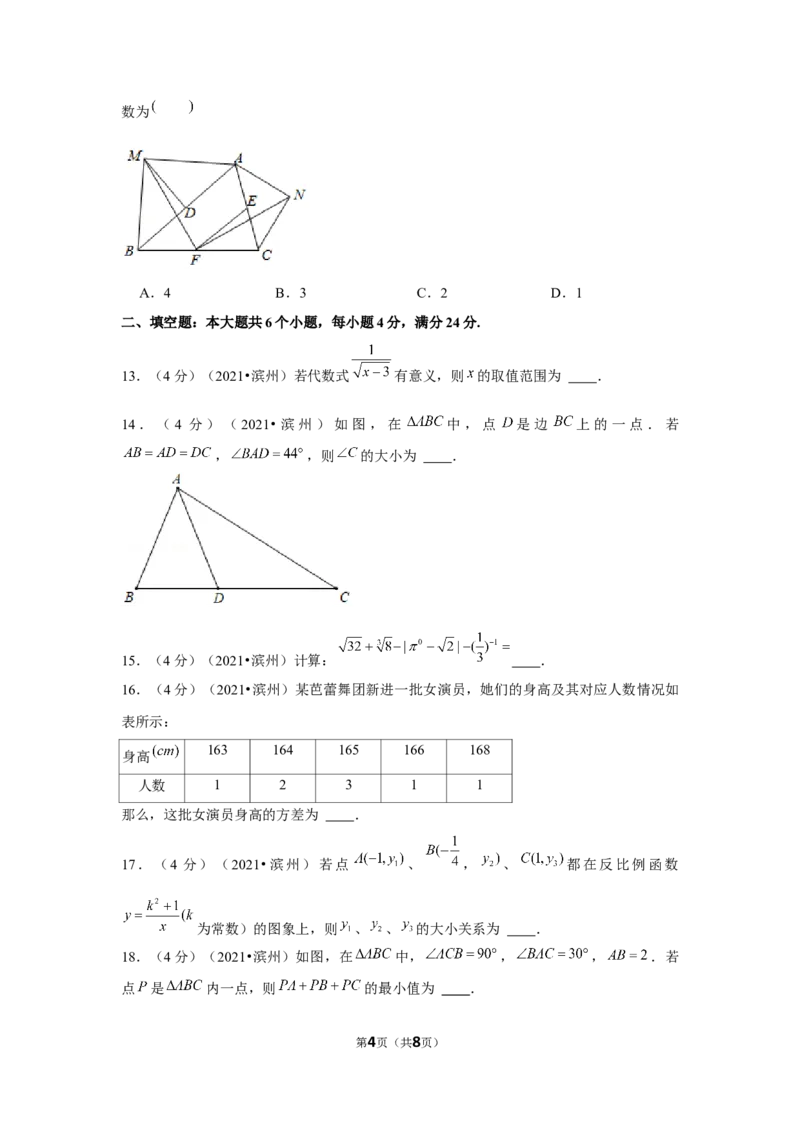
14.(4 分)(2021•滨州)如图,在 中,点 是边 上的一点.若
, ,则 的大小为 .
15.(4分)(2021•滨州)计算: .
16.(4分)(2021•滨州)某芭蕾舞团新进一批女演员,她们的身高及其对应人数情况如
表所示:
163 164 165 166 168
身高
人数 1 2 3 1 1
那么,这批女演员身高的方差为 .
17.(4 分)(2021•滨州)若点 、 , 、 都在反比例函数
为常数)的图象上,则 、 、 的大小关系为 .
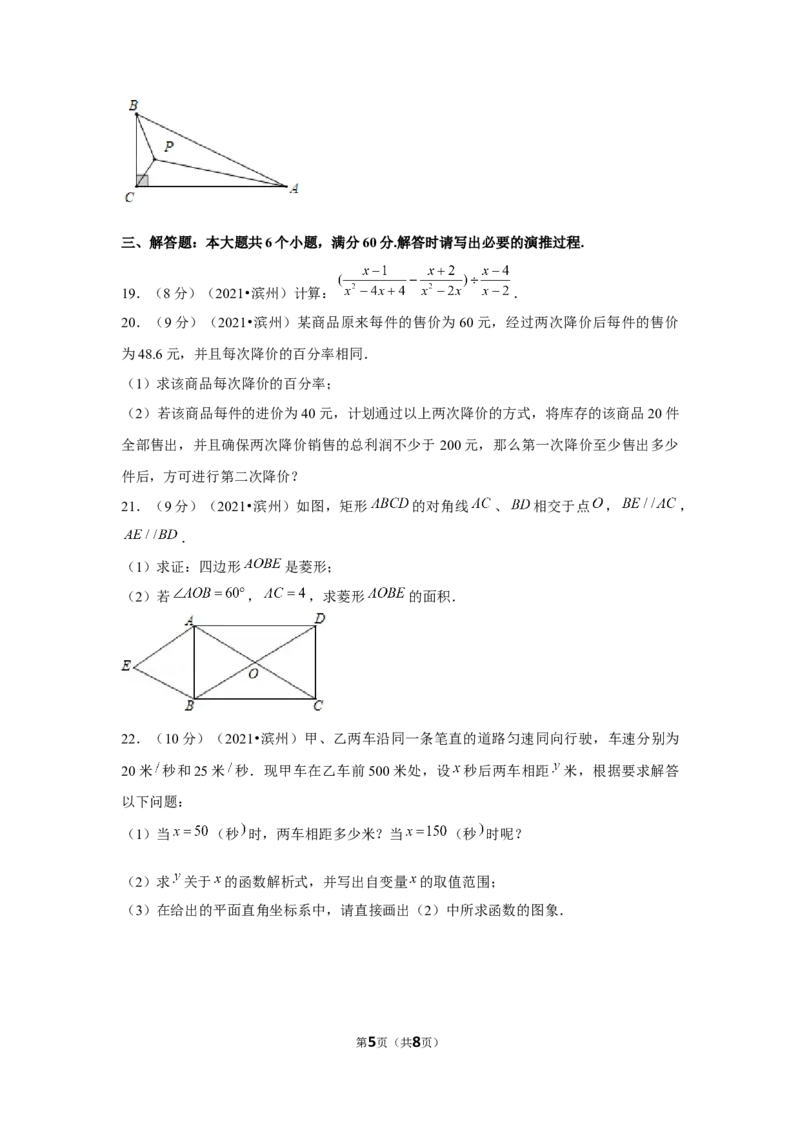
18.(4分)(2021•滨州)如图,在 中, , , .若
点 是 内一点,则 的最小值为 .
第4页(共8页)三、解答题:本大题共6个小题,满分60分.解答时请写出必要的演推过程.
19.(8分)(2021•滨州)计算: .
20.(9分)(2021•滨州)某商品原来每件的售价为60元,经过两次降价后每件的售价
为48.6元,并且每次降价的百分率相同.
(1)求该商品每次降价的百分率;
(2)若该商品每件的进价为40元,计划通过以上两次降价的方式,将库存的该商品20件
全部售出,并且确保两次降价销售的总利润不少于 200元,那么第一次降价至少售出多少
件后,方可进行第二次降价?
21.(9分)(2021•滨州)如图,矩形 的对角线 、 相交于点 , ,
.
(1)求证:四边形 是菱形;
(2)若 , ,求菱形 的面积.
22.(10分)(2021•滨州)甲、乙两车沿同一条笔直的道路匀速同向行驶,车速分别为
20米 秒和25米 秒.现甲车在乙车前500米处,设 秒后两车相距 米,根据要求解答
以下问题:
(1)当 (秒 时,两车相距多少米?当 (秒 时呢?
(2)求 关于 的函数解析式,并写出自变量 的取值范围;
(3)在给出的平面直角坐标系中,请直接画出(2)中所求函数的图象.
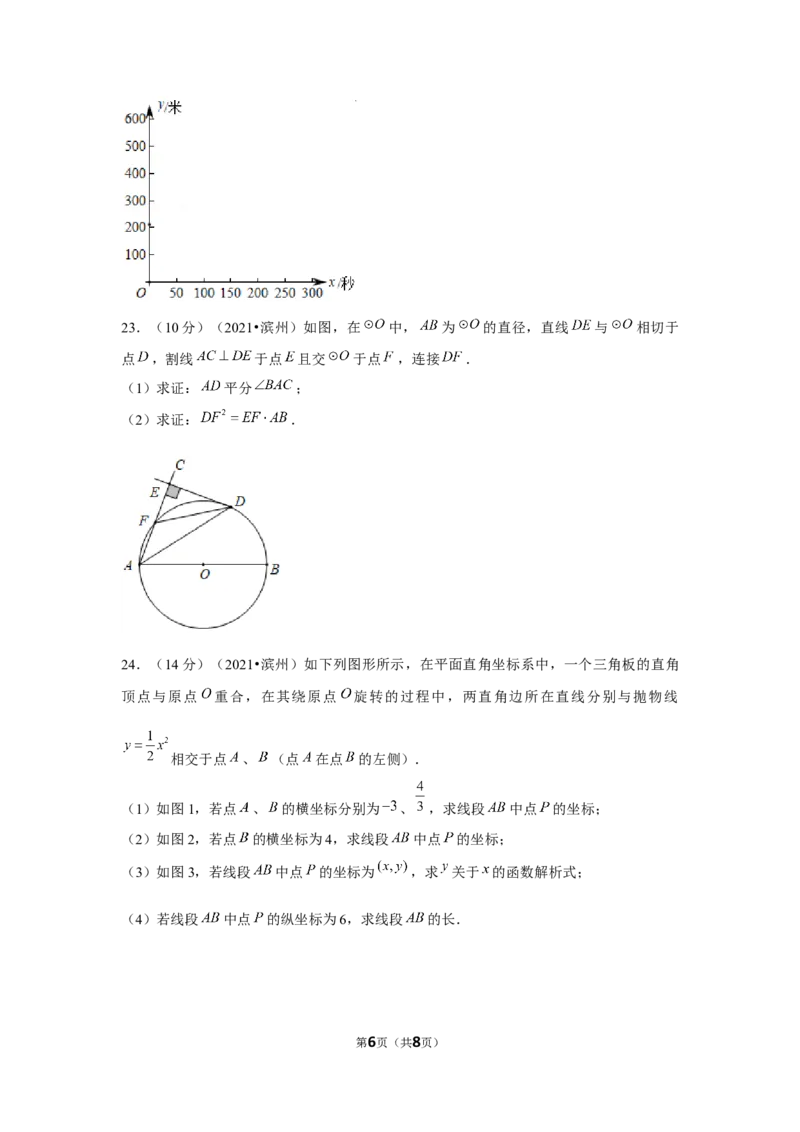
第5页(共8页)23.(10分)(2021•滨州)如图,在 中, 为 的直径,直线 与 相切于
点 ,割线 于点 且交 于点 ,连接 .
(1)求证: 平分 ;
(2)求证: .
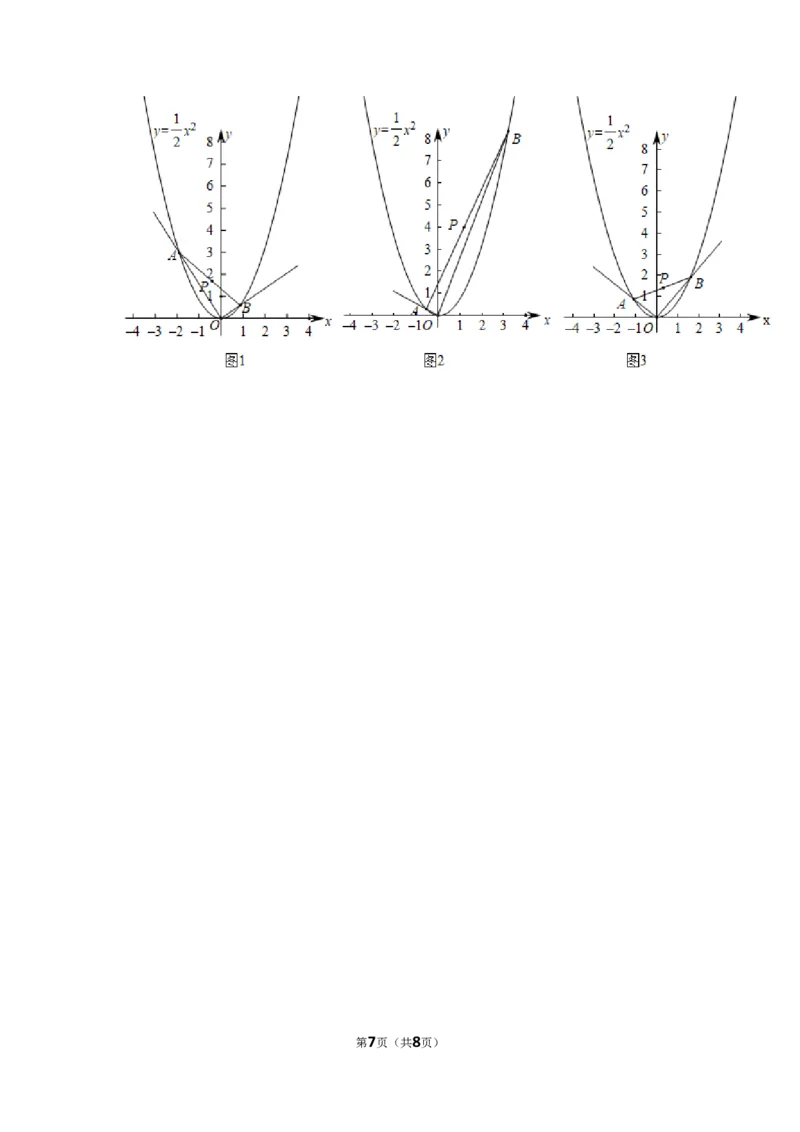
24.(14分)(2021•滨州)如下列图形所示,在平面直角坐标系中,一个三角板的直角
顶点与原点 重合,在其绕原点 旋转的过程中,两直角边所在直线分别与抛物线
相交于点 、 (点 在点 的左侧).
(1)如图1,若点 、 的横坐标分别为 、 ,求线段 中点 的坐标;
(2)如图2,若点 的横坐标为4,求线段 中点 的坐标;
(3)如图3,若线段 中点 的坐标为 ,求 关于 的函数解析式;
(4)若线段 中点 的纵坐标为6,求线段 的长.
第6页(共8页)第7页(共8页)第8页(共8页)