文档内容
山东省潍坊市 2021 年中考数学真题
一、单项选择题(共8小题,每小题3分,共24分.每小题四个选项只有一项
正确.)
1. 下列各数的相反数中,最大的是( )
A. 2 B. 1 C. ﹣1 D. ﹣2
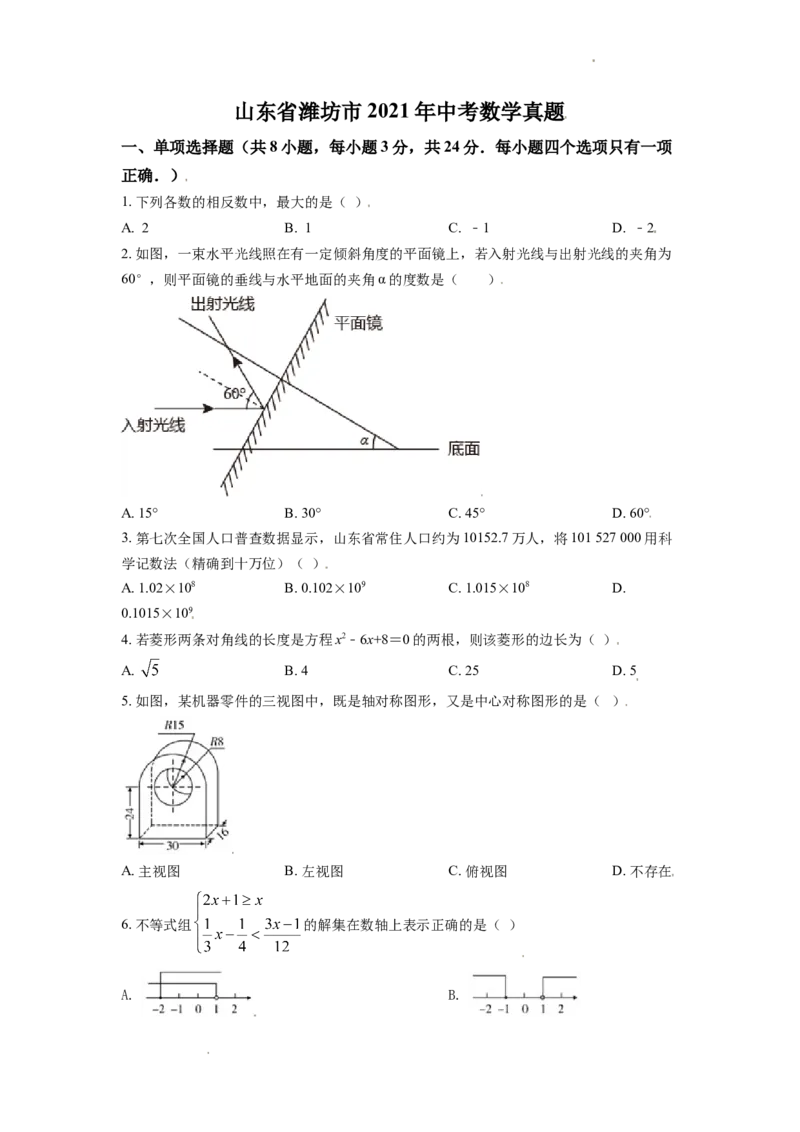
2. 如图,一束水平光线照在有一定倾斜角度的平面镜上,若入射光线与出射光线的夹角为
60°,则平面镜的垂线与水平地面的夹角α的度数是( )
A. 15° B. 30° C. 45° D. 60°
3. 第七次全国人口普查数据显示,山东省常住人口约为10152.7万人,将101 527 000用科
学记数法(精确到十万位)( )
A. 1.02×108 B. 0.102×109 C. 1.015×108 D.
0.1015×109
4. 若菱形两条对角线的长度是方程x2﹣6x+8=0的两根,则该菱形的边长为( )
A. B. 4 C. 25 D. 5
5. 如图,某机器零件的三视图中,既是轴对称图形,又是中心对称图形的是( )
A. 主视图 B. 左视图 C. 俯视图 D. 不存在
6. 不等式组 的解集在数轴上表示正确的是( )
A. B.
学科网(北京)股份有限公司C. D.
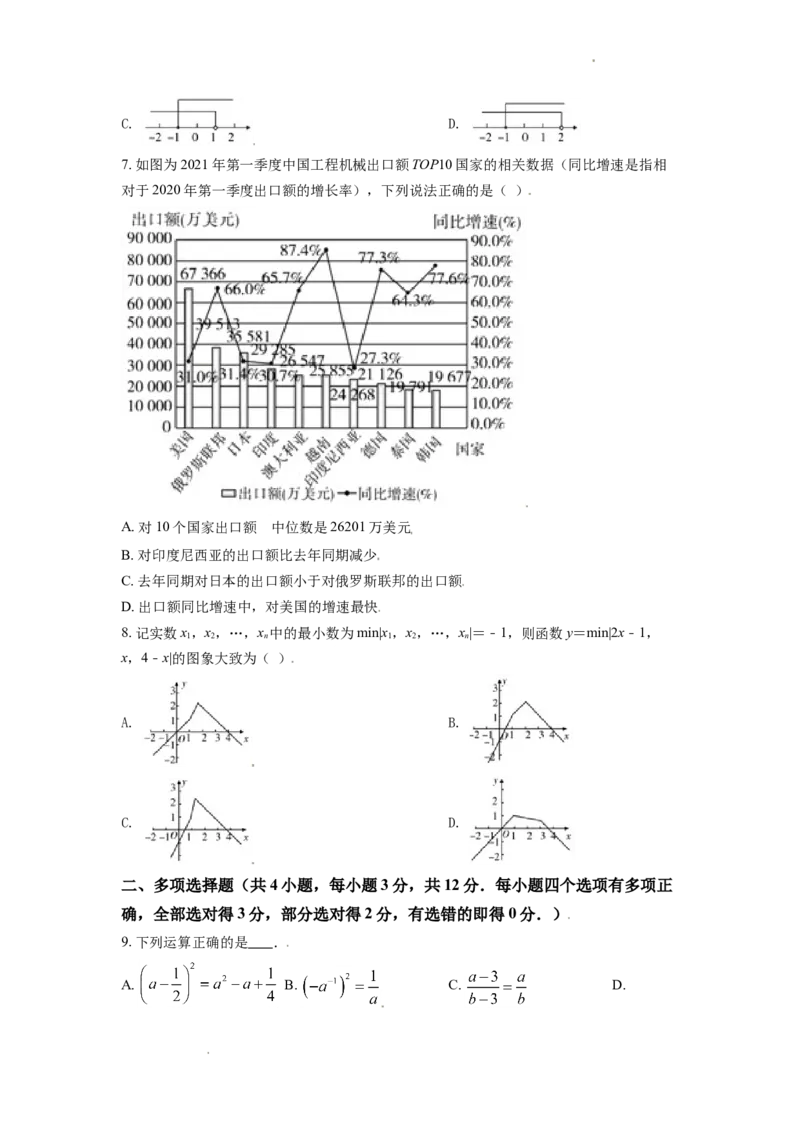
7. 如图为2021年第一季度中国工程机械出口额TOP10国家的相关数据(同比增速是指相
对于2020年第一季度出口额的增长率),下列说法正确的是( )
A. 对10个国家出口额 的中位数是26201万美元
B. 对印度尼西亚的出口额比去年同期减少
C. 去年同期对日本的出口额小于对俄罗斯联邦的出口额
D. 出口额同比增速中,对美国的增速最快
8. 记实数x,x,…,x 中的最小数为min|x,x,…,x|=﹣1,则函数y=min|2x﹣1,
1 2 n 1 2 n
x,4﹣x|的图象大致为( )
A. B.
C. D.
二、多项选择题(共4小题,每小题3分,共12分.每小题四个选项有多项正
确,全部选对得3分,部分选对得2分,有选错的即得0分.)
9. 下列运算正确的是 .
A. B. C. D.
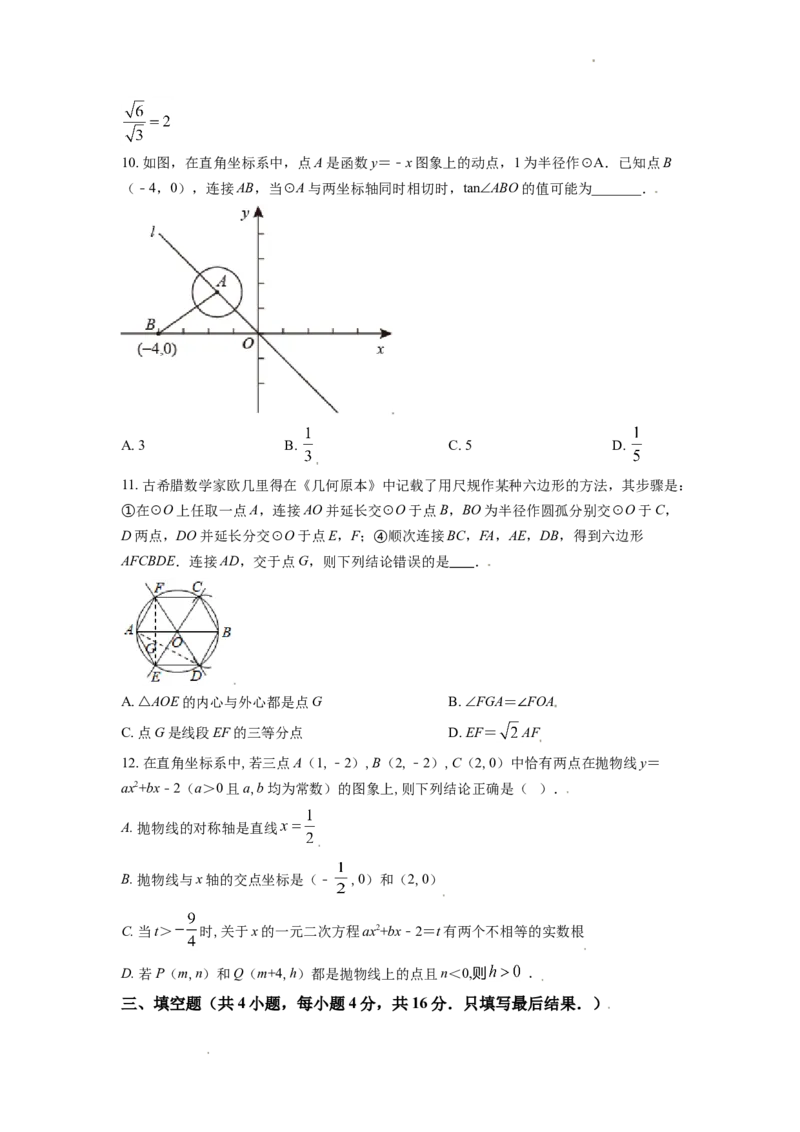
学科网(北京)股份有限公司10. 如图,在直角坐标系中,点A是函数y=﹣x图象上的动点,1为半径作⊙A.已知点B
(﹣4,0),连接AB,当⊙A与两坐标轴同时相切时,tan∠ABO的值可能为_______.
A. 3 B. C. 5 D.
11. 古希腊数学家欧几里得在《几何原本》中记载了用尺规作某种六边形的方法,其步骤是:
①在⊙O上任取一点A,连接AO并延长交⊙O于点B,BO为半径作圆孤分别交⊙O于C,
D两点,DO并延长分交⊙O于点E,F;④顺次连接BC,FA,AE,DB,得到六边形
AFCBDE.连接AD,交于点G,则下列结论错误的是 .
A. △AOE的内心与外心都是点G B. ∠FGA=∠FOA
C. 点G是线段EF的三等分点 D. EF= AF
12. 在直角坐标系中,若三点A(1,﹣2),B(2,﹣2),C(2,0)中恰有两点在抛物线y=
ax2+bx﹣2(a>0且a,b均为常数)的图象上,则下列结论正确是( ).
A. 抛物线的对称轴是直线
B. 抛物线与x轴的交点坐标是(﹣ ,0)和(2,0)
C. 当t> 时,关于x的一元二次方程ax2+bx﹣2=t有两个不相等的实数根
D. 若P(m,n)和Q(m+4,h)都是抛物线上的点且n<0,则 .
三、填空题(共4小题,每小题4分,共16分.只填写最后结果.)
学科网(北京)股份有限公司13. 甲、乙、丙三名同学观察完某个一次函数的图象,各叙述如下:
甲:函数的图象经过点(0,1);
乙:y随x的增大而减小;
丙:函数 的图象不经过第三象限.
根据他们的叙述,写出满足上述性质的一个函数表达式为 _______.
14. 若x<2,且 ,则x=_______.
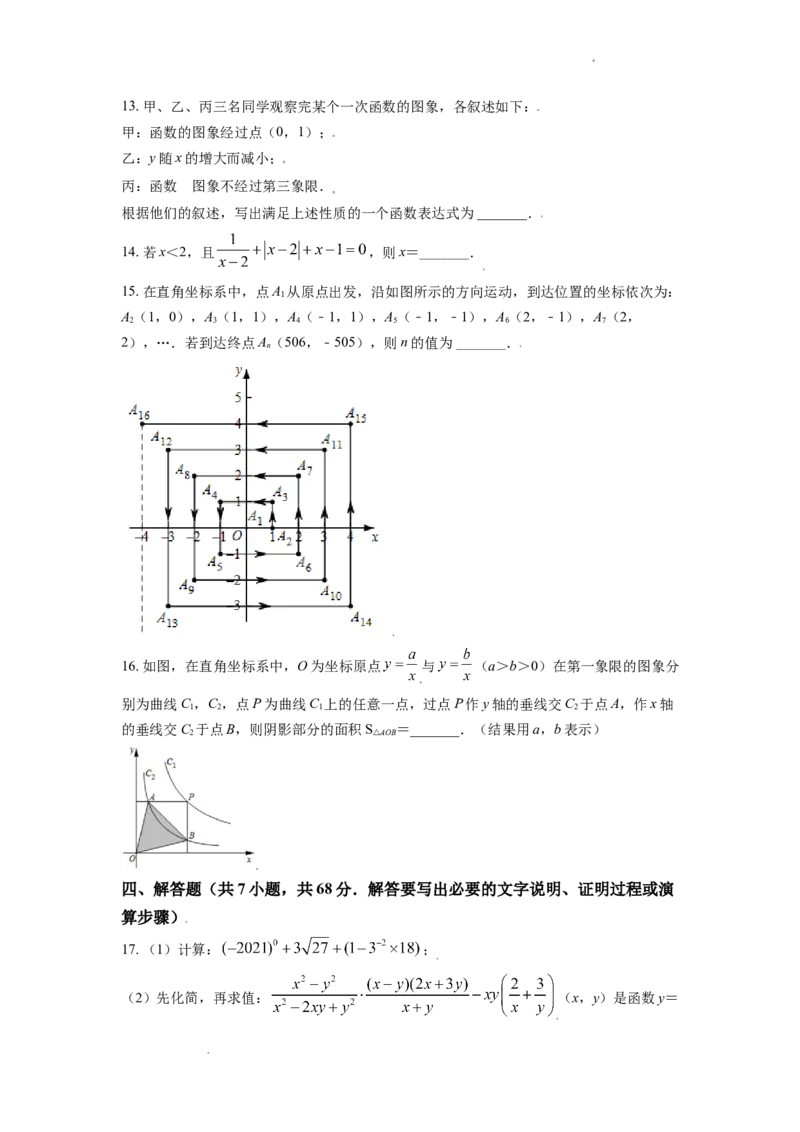
15. 在直角坐标系中,点A 从原点出发,沿如图所示的方向运动,到达位置的坐标依次为:
1
A(1,0),A(1,1),A(﹣1,1),A(﹣1,﹣1),A(2,﹣1),A(2,
2 3 4 5 6 7
2),….若到达终点A(506,﹣505),则n的值为 _______.
n
16. 如图,在直角坐标系中,O为坐标原点 与 (a>b>0)在第一象限的图象分
别为曲线C ,C ,点P为曲线C 上的任意一点,过点P作y轴的垂线交C 于点A,作x轴
1 2 1 2
的垂线交C 于点B,则阴影部分的面积S =_______.(结果用a,b表示)
2 △AOB
四、解答题(共7小题,共68分.解答要写出必要的文字说明、证明过程或演
算步骤)
17. (1)计算: ;
(2)先化简,再求值: (x,y)是函数y=
学科网(北京)股份有限公司2x与 的图象的交点坐标.
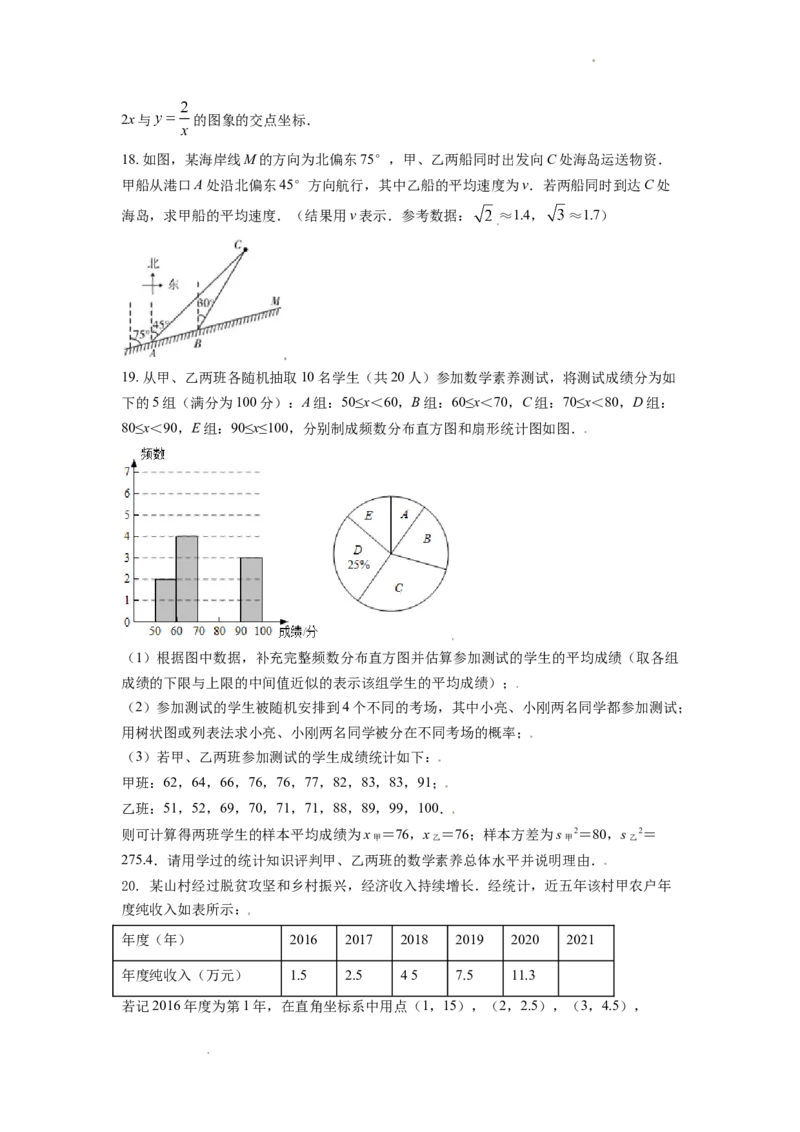
18. 如图,某海岸线M的方向为北偏东75°,甲、乙两船同时出发向C处海岛运送物资.
甲船从港口A处沿北偏东45°方向航行,其中乙船的平均速度为v.若两船同时到达C处
海岛,求甲船的平均速度.(结果用v表示.参考数据: ≈1.4, ≈1.7)
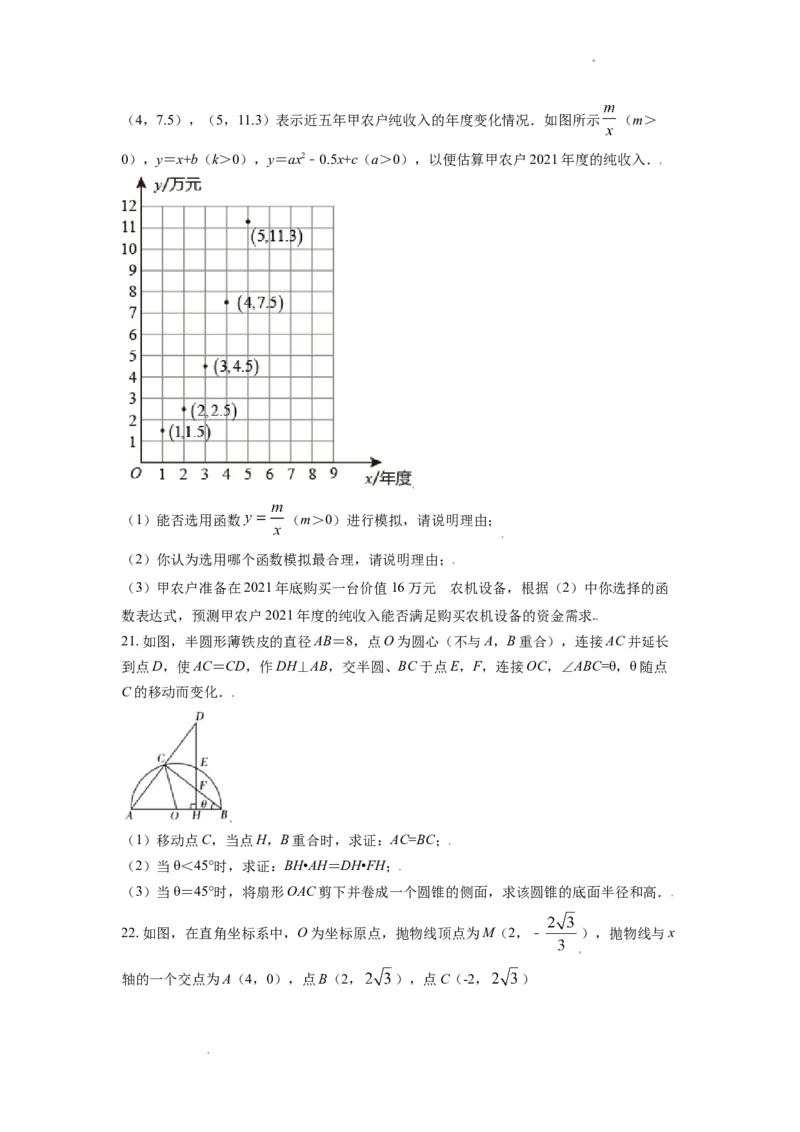
19. 从甲、乙两班各随机抽取10名学生(共20人)参加数学素养测试,将测试成绩分为如
下的5组(满分为100分):A组:50≤x<60,B组:60≤x<70,C组:70≤x<80,D组:
80≤x<90,E组:90≤x≤100,分别制成频数分布直方图和扇形统计图如图.
(1)根据图中数据,补充完整频数分布直方图并估算参加测试的学生的平均成绩(取各组
成绩的下限与上限的中间值近似的表示该组学生的平均成绩);
(2)参加测试的学生被随机安排到4个不同的考场,其中小亮、小刚两名同学都参加测试;
用树状图或列表法求小亮、小刚两名同学被分在不同考场的概率;
(3)若甲、乙两班参加测试的学生成绩统计如下:
甲班:62,64,66,76,76,77,82,83,83,91;
乙班:51,52,69,70,71,71,88,89,99,100.
则可计算得两班学生的样本平均成绩为x =76,x =76;样本方差为s 2=80,s 2=
甲 乙 甲 乙
275.4.请用学过的统计知识评判甲、乙两班的数学素养总体水平并说明理由.
20. 某山村经过脱贫攻坚和乡村振兴,经济收入持续增长.经统计,近五年该村甲农户年
度纯收入如表所示:
年度(年) 2016 2017 2018 2019 2020 2021
.
年度纯收入(万元) 1.5 2.5 45 7.5 11.3
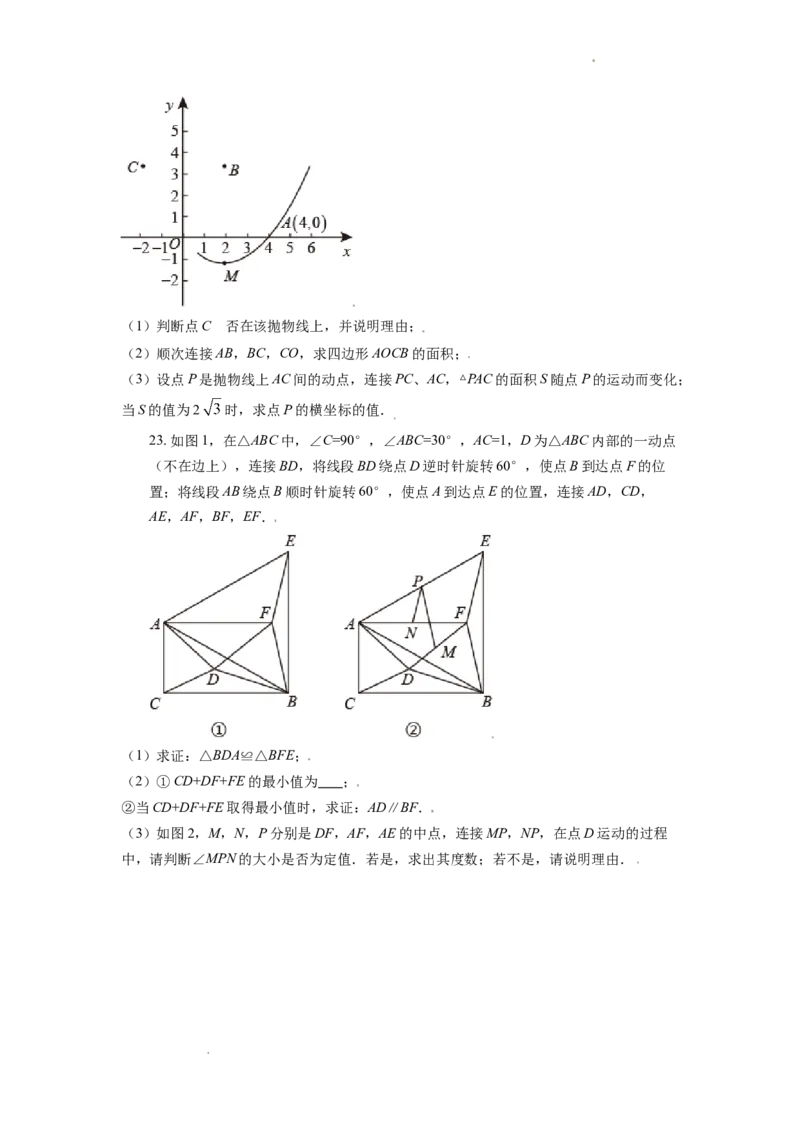
若记2016年度为第1年,在直角坐标系中用点(1,15),(2,2.5),(3,4.5),
学科网(北京)股份有限公司(4,7.5),(5,11.3)表示近五年甲农户纯收入的年度变化情况.如图所示 (m>
0),y=x+b(k>0),y=ax2﹣0.5x+c(a>0),以便估算甲农户2021年度的纯收入.
(1)能否选用函数 (m>0)进行模拟,请说明理由;
(2)你认为选用哪个函数模拟最合理,请说明理由;
(3)甲农户准备在2021年底购买一台价值16万元 的农机设备,根据(2)中你选择的函
数表达式,预测甲农户2021年度的纯收入能否满足购买农机设备的资金需求.
21. 如图,半圆形薄铁皮的直径AB=8,点O为圆心(不与A,B重合),连接AC并延长
到点D,使AC=CD,作DH⊥AB,交半圆、BC于点E,F,连接OC,∠ABC=θ,θ随点
C的移动而变化.
(1)移动点C,当点H,B重合时,求证:AC=BC;
(2)当θ<45°时,求证:BH•AH=DH•FH;
(3)当θ=45°时,将扇形OAC剪下并卷成一个圆锥的侧面,求该圆锥的底面半径和高.
22. 如图,在直角坐标系中,O为坐标原点,抛物线顶点为M(2,﹣ ),抛物线与x
轴的一个交点为A(4,0),点B(2, ),点C(-2, )
学科网(北京)股份有限公司(1)判断点C 是否在该抛物线上,并说明理由;
(2)顺次连接AB,BC,CO,求四边形AOCB的面积;
(3)设点P是抛物线上AC间的动点,连接PC、AC,△PAC的面积S随点P的运动而变化;
当S的值为2 时,求点P的横坐标的值.
23. 如图1,在△ABC中,∠C=90°,∠ABC=30°,AC=1,D为△ABC内部的一动点
(不在边上),连接BD,将线段BD绕点D逆时针旋转60°,使点B到达点F的位
置;将线段AB绕点B顺时针旋转60°,使点A到达点E的位置,连接AD,CD,
AE,AF,BF,EF.
(1)求证:△BDA≌△BFE;
(2)①CD+DF+FE的最小值为 ;
②当CD+DF+FE取得最小值时,求证:AD∥BF.
(3)如图2,M,N,P分别是DF,AF,AE的中点,连接MP,NP,在点D运动的过程
中,请判断∠MPN的大小是否为定值.若是,求出其度数;若不是,请说明理由.
学科网(北京)股份有限公司学科网(北京)股份有限公司