文档内容
2021年山东省烟台市中考数学试卷
一、选择题(本题共12个小题,每小题3分,满分36分)每小题都给出标号为A,B,C,D
四个备选答案,其中有且只有一个是正确的
1.若x的相反数是3,则x的值是( )
A.﹣3 B.﹣ C.3 D.±3
2.下列数学符号中,既是轴对称图形又是中心对称图形的是( )
A. B. C. D.
3.下列计算正确的是( )
A.a2•a3=a6 B.a2+a3=a5 C.(a2)3=a6 D.a2÷a3=a
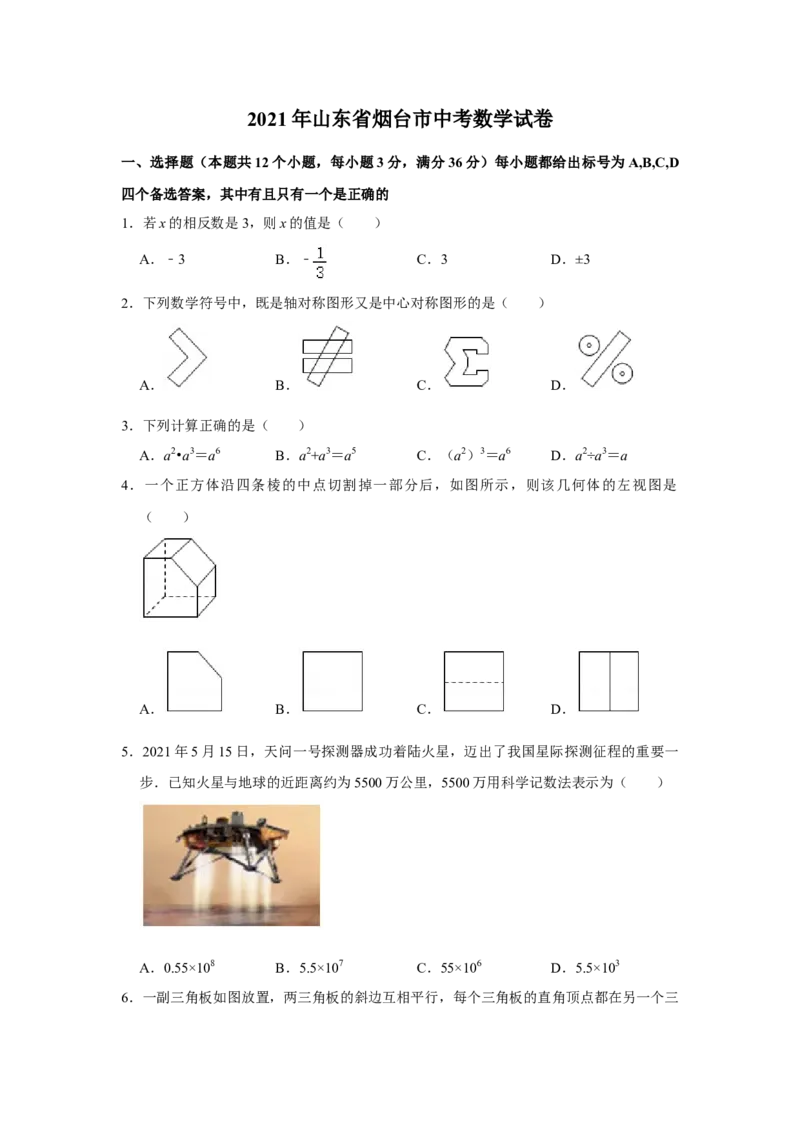
4.一个正方体沿四条棱的中点切割掉一部分后,如图所示,则该几何体的左视图是
( )
A. B. C. D.
5.2021年5月15日,天问一号探测器成功着陆火星,迈出了我国星际探测征程的重要一
步.已知火星与地球的近距离约为5500万公里,5500万用科学记数法表示为( )
A.0.55×108 B.5.5×107 C.55×106 D.5.5×103
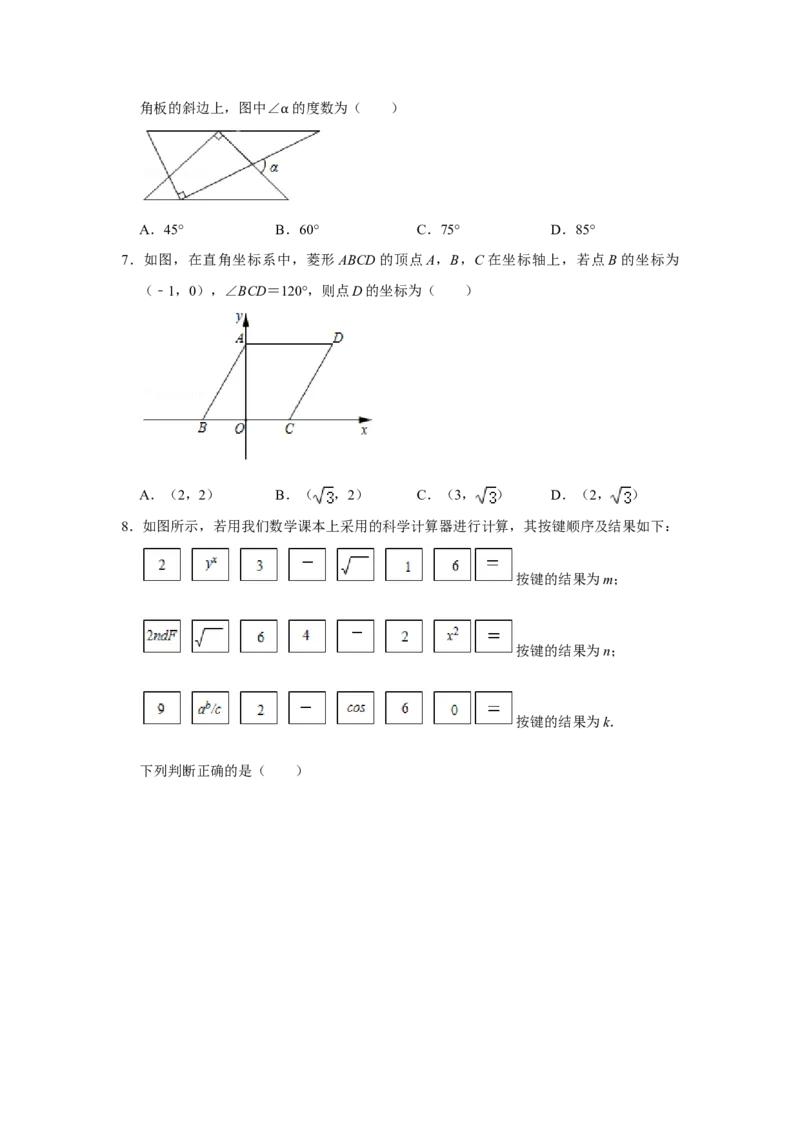
6.一副三角板如图放置,两三角板的斜边互相平行,每个三角板的直角顶点都在另一个三角板的斜边上,图中∠ 的度数为( )
α
A.45° B.60° C.75° D.85°
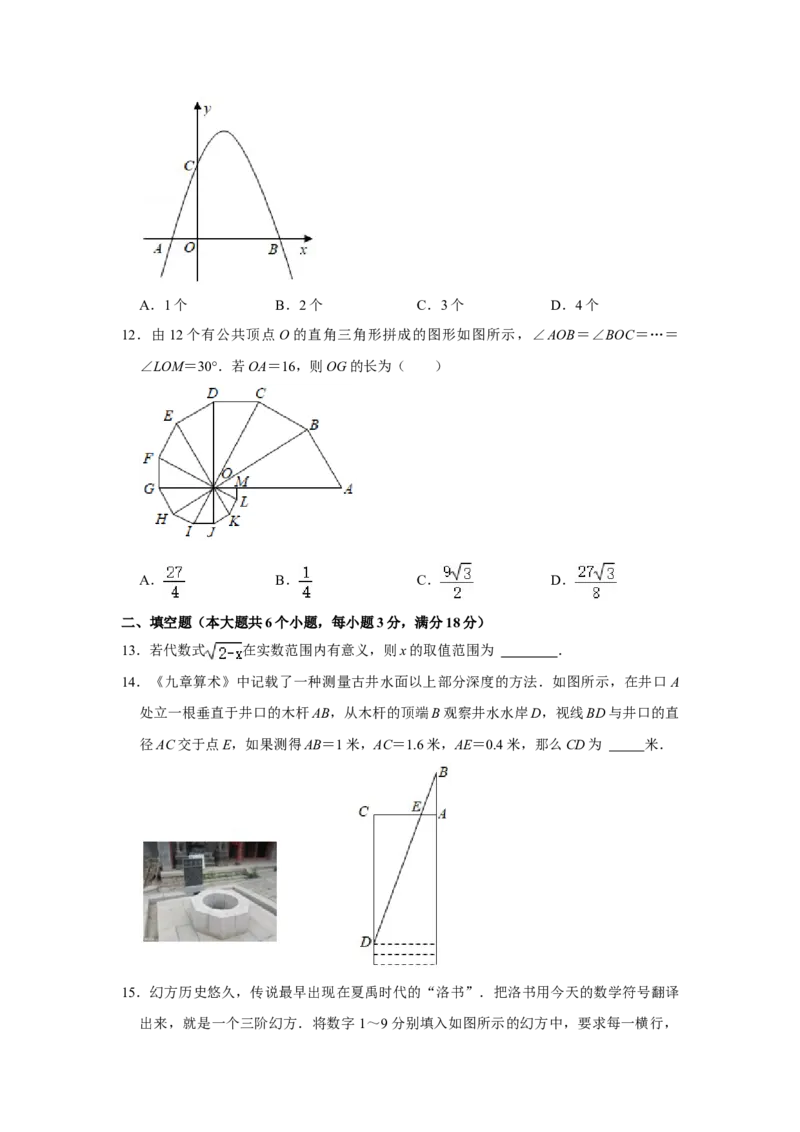
7.如图,在直角坐标系中,菱形ABCD的顶点A,B,C在坐标轴上,若点B的坐标为
(﹣1,0),∠BCD=120°,则点D的坐标为( )
A.(2,2) B.( ,2) C.(3, ) D.(2, )
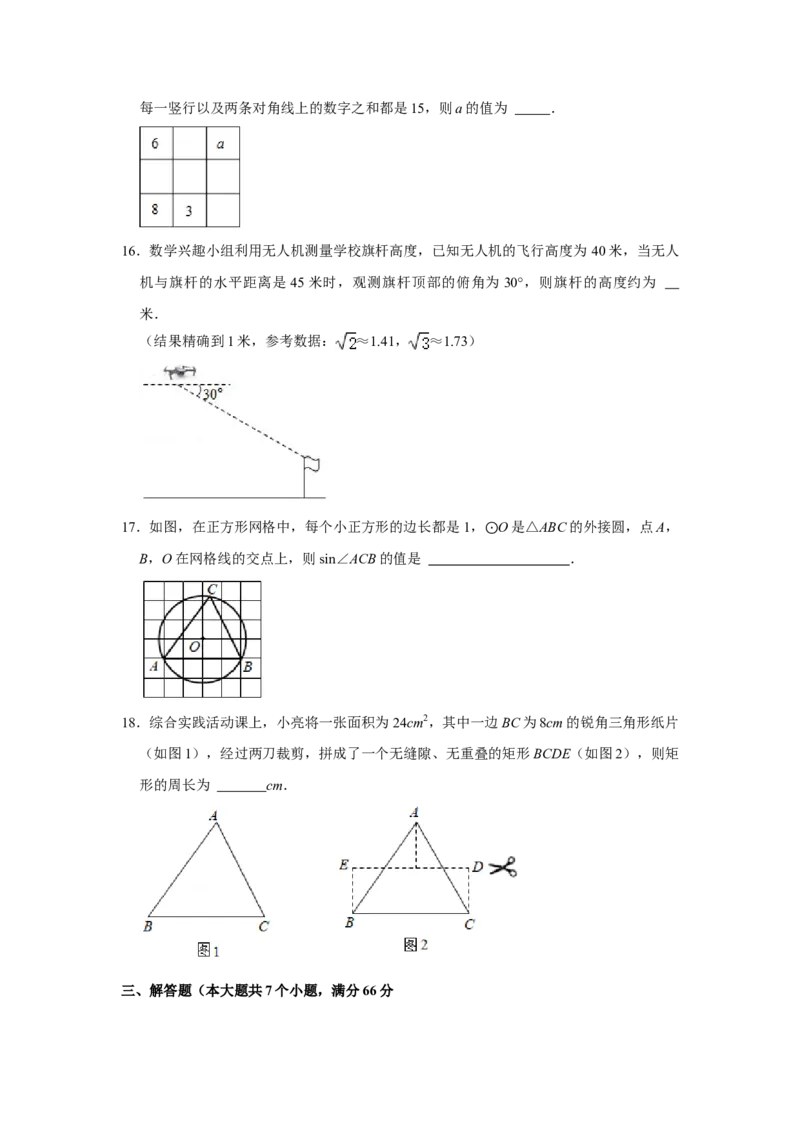
8.如图所示,若用我们数学课本上采用的科学计算器进行计算,其按键顺序及结果如下:
按键的结果为m;
按键的结果为n;
按键的结果为k.
下列判断正确的是( )A.m=n B.n=k C.m=k D.m=n=k
9.已知关于x的一元二次方程x2﹣mnx+m+n=0,其中m,n在数轴上的对应点如图所示,
则这个方程的根的情况是( )
A.有两个不相等的实数根 B.有两个相等的实数根
C.没有实数根 D.无法确定
10.连接正六边形不相邻的两个顶点,并将中间的六边形涂成黑色,制成如图所示的镖盘
将一枚飞镖任意投掷到镖盘上,飞镖落在黑色区域的概率为( )
A. B. C. D.
11.如图,二次函数y=ax2+bx+c的图象经过点A(﹣1,0),B(3,0),与y轴交于点
C.下列结论:
①ac>0;
②当x>0时,y随x的增大而增大;
③3a+c=0;
④a+b≥am2+bm.
其中正确的个数有( )A.1个 B.2个 C.3个 D.4个
12.由12个有公共顶点 O的直角三角形拼成的图形如图所示,∠AOB=∠BOC=…=
∠LOM=30°.若OA=16,则OG的长为( )
A. B. C. D.
二、填空题(本大题共6个小题,每小题3分,满分18分)
13.若代数式 在实数范围内有意义,则x的取值范围为 .
14.《九章算术》中记载了一种测量古井水面以上部分深度的方法.如图所示,在井口A
处立一根垂直于井口的木杆AB,从木杆的顶端B观察井水水岸D,视线BD与井口的直
径AC交于点E,如果测得AB=1米,AC=1.6米,AE=0.4米,那么CD为 米.
15.幻方历史悠久,传说最早出现在夏禹时代的“洛书”.把洛书用今天的数学符号翻译
出来,就是一个三阶幻方.将数字1~9分别填入如图所示的幻方中,要求每一横行,每一竖行以及两条对角线上的数字之和都是15,则a的值为 .
16.数学兴趣小组利用无人机测量学校旗杆高度,已知无人机的飞行高度为 40米,当无人
机与旗杆的水平距离是45米时,观测旗杆顶部的俯角为30°,则旗杆的高度约为
米.
(结果精确到1米,参考数据: ≈1.41, ≈1.73)
17.如图,在正方形网格中,每个小正方形的边长都是1, O是△ABC的外接圆,点A,
B,O在网格线的交点上,则sin∠ACB的值是 ⊙ .
18.综合实践活动课上,小亮将一张面积为24cm2,其中一边BC为8cm的锐角三角形纸片
(如图1),经过两刀裁剪,拼成了一个无缝隙、无重叠的矩形BCDE(如图2),则矩
形的周长为 cm.
三、解答题(本大题共7个小题,满分66分19.(6分)先化简,再求值: ,从﹣2<x≤2中选出合适的
x的整数值代入求值.
20.(8分)2021年是中国共产党成立100周年.为普及党史知识,培养爱国主义精神,
今年五月份,某市党校举行党史知识竞赛,每个班级各选派 15名学员参加了网上测试,
现对甲、乙两班学员的分数进行整理分析如下:
甲班15名学员测试成绩(满分100分)统计如下:
87,84,88,76,93,87,73,98,86,87,79,85,84,85,98.
乙班15名学员测试成绩(满分100分)统计如下:
77,88,92,85,76,90,76,91,88,81,85,88,98,86,89
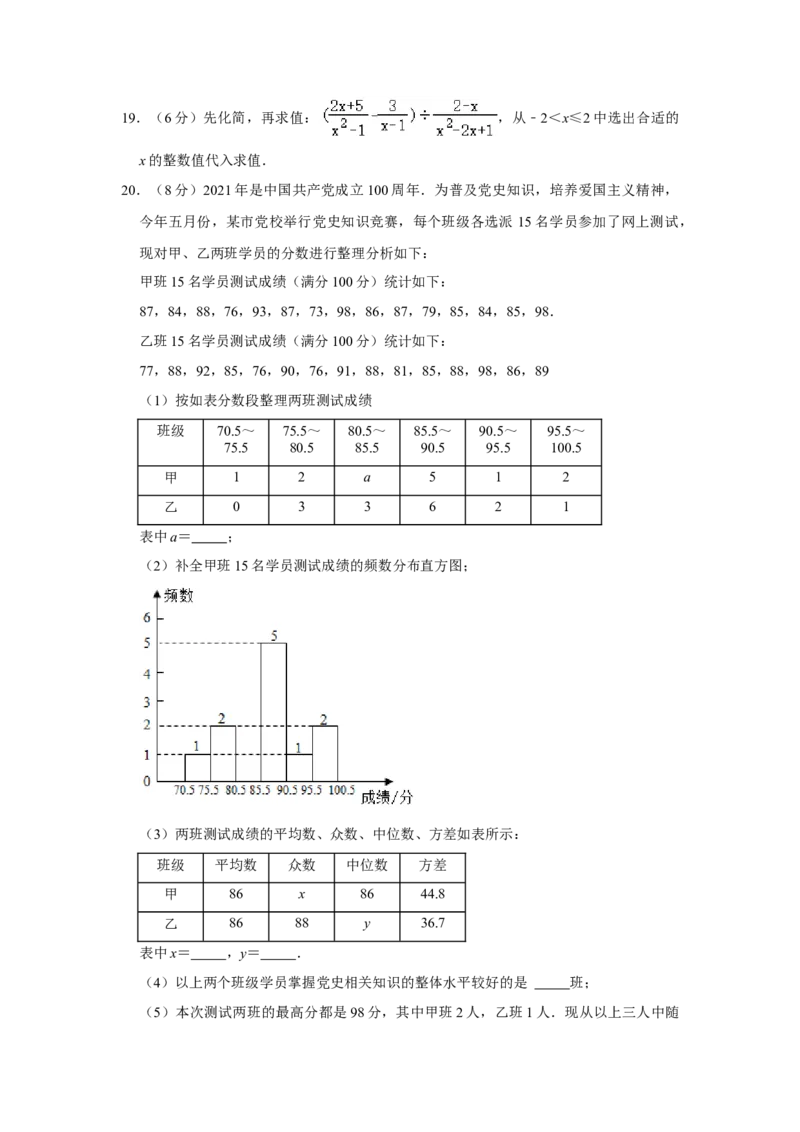
(1)按如表分数段整理两班测试成绩
班级 70.5~ 75.5~ 80.5~ 85.5~ 90.5~ 95.5~
75.5 80.5 85.5 90.5 95.5 100.5
甲 1 2 a 5 1 2
乙 0 3 3 6 2 1
表中a= ;
(2)补全甲班15名学员测试成绩的频数分布直方图;
(3)两班测试成绩的平均数、众数、中位数、方差如表所示:
班级 平均数 众数 中位数 方差
甲 86 x 86 44.8
乙 86 88 y 36.7
表中x= ,y= .
(4)以上两个班级学员掌握党史相关知识的整体水平较好的是 班;
(5)本次测试两班的最高分都是98分,其中甲班2人,乙班1人.现从以上三人中随机抽取两人代表党校参加全市党史知识竞赛,利用树状图或表格求出恰好抽取甲、乙两
班各一人参加全市党史知识竞赛的概率.
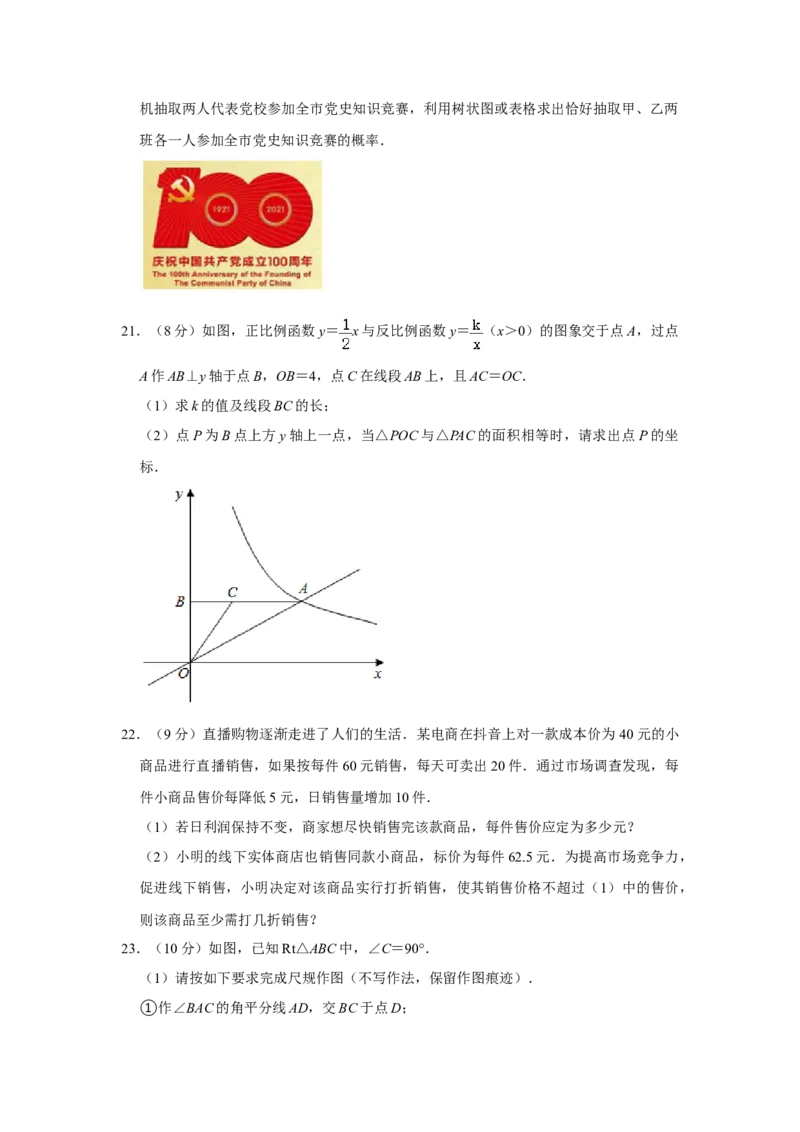
21.(8分)如图,正比例函数y= x与反比例函数y= (x>0)的图象交于点A,过点
A作AB⊥y轴于点B,OB=4,点C在线段AB上,且AC=OC.
(1)求k的值及线段BC的长;
(2)点P为B点上方y轴上一点,当△POC与△PAC的面积相等时,请求出点P的坐
标.
22.(9分)直播购物逐渐走进了人们的生活.某电商在抖音上对一款成本价为40元的小
商品进行直播销售,如果按每件60元销售,每天可卖出20件.通过市场调查发现,每
件小商品售价每降低5元,日销售量增加10件.
(1)若日利润保持不变,商家想尽快销售完该款商品,每件售价应定为多少元?
(2)小明的线下实体商店也销售同款小商品,标价为每件62.5元.为提高市场竞争力,
促进线下销售,小明决定对该商品实行打折销售,使其销售价格不超过(1)中的售价,
则该商品至少需打几折销售?
23.(10分)如图,已知Rt△ABC中,∠C=90°.
(1)请按如下要求完成尺规作图(不写作法,保留作图痕迹).
①作∠BAC的角平分线AD,交BC于点D;②作线段AD的垂直平分线EF与AB相交于点O;
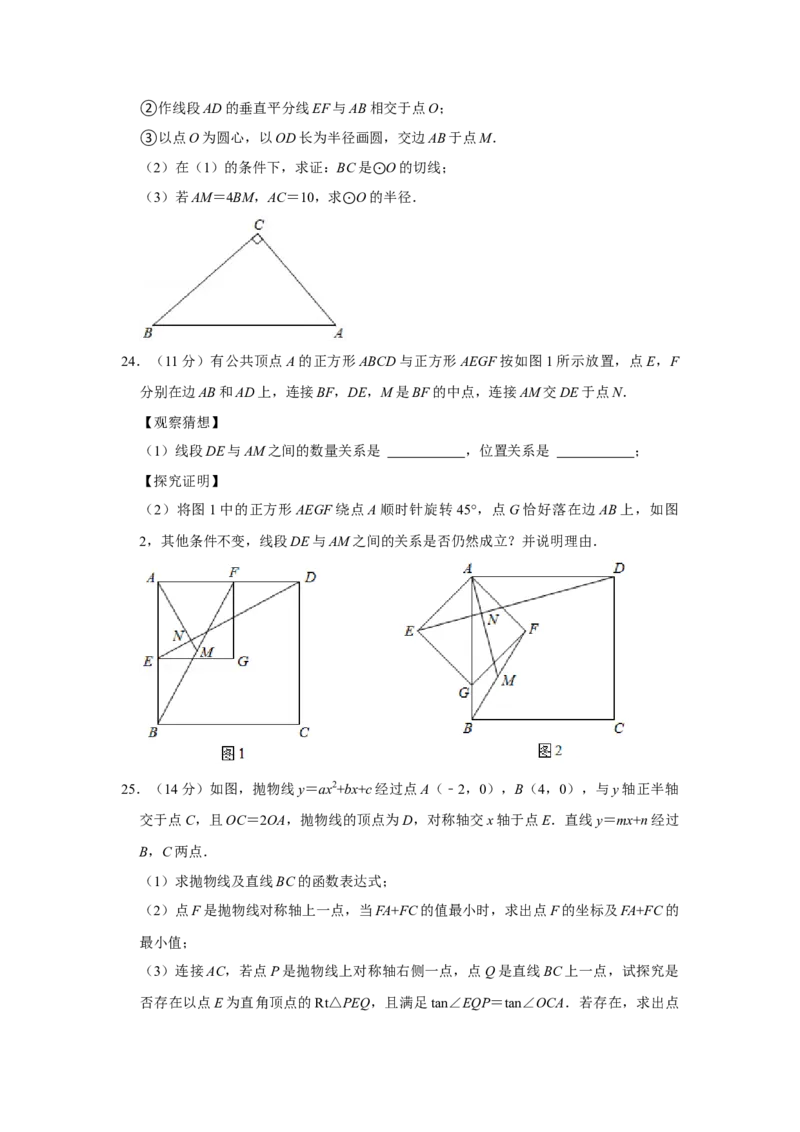
③以点O为圆心,以OD长为半径画圆,交边AB于点M.
(2)在(1)的条件下,求证:BC是 O的切线;
(3)若AM=4BM,AC=10,求 O的⊙半径.
⊙
24.(11分)有公共顶点A的正方形ABCD与正方形AEGF按如图1所示放置,点E,F
分别在边AB和AD上,连接BF,DE,M是BF的中点,连接AM交DE于点N.
【观察猜想】
(1)线段DE与AM之间的数量关系是 ,位置关系是 ;
【探究证明】
(2)将图1中的正方形AEGF绕点A顺时针旋转45°,点G恰好落在边AB上,如图
2,其他条件不变,线段DE与AM之间的关系是否仍然成立?并说明理由.
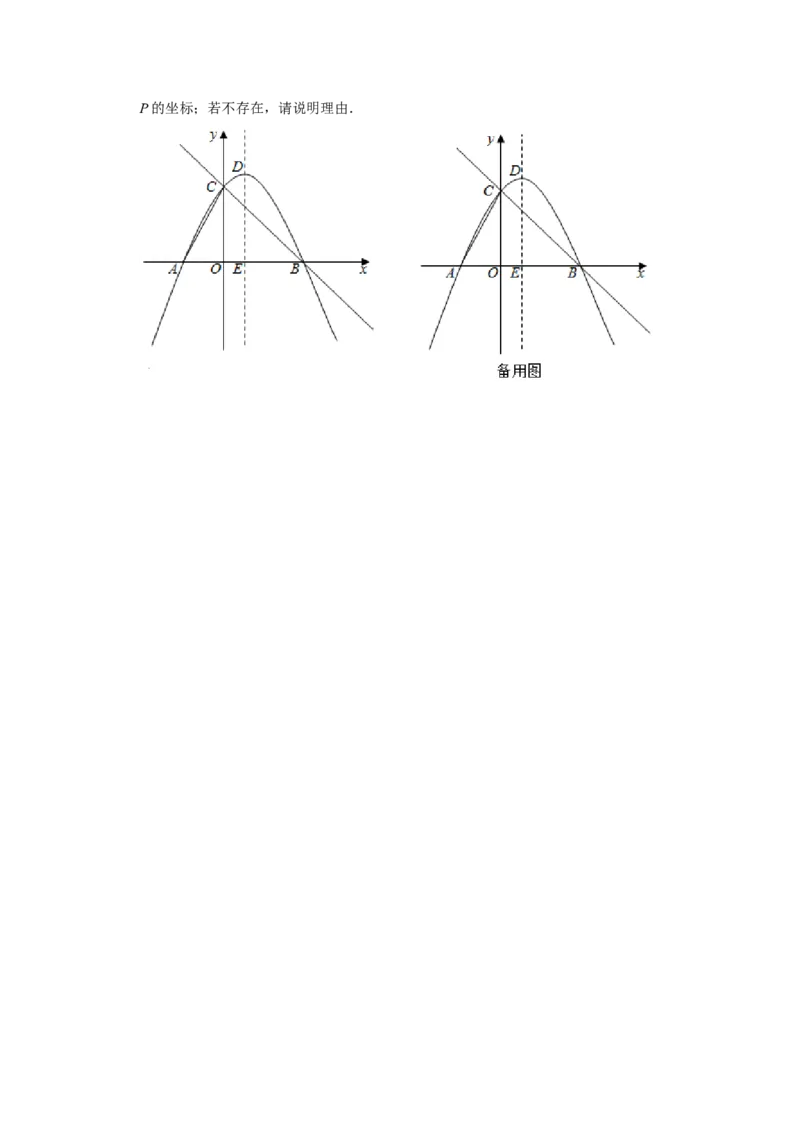
25.(14分)如图,抛物线y=ax2+bx+c经过点A(﹣2,0),B(4,0),与y轴正半轴
交于点C,且OC=2OA,抛物线的顶点为D,对称轴交x轴于点E.直线y=mx+n经过
B,C两点.
(1)求抛物线及直线BC的函数表达式;
(2)点F是抛物线对称轴上一点,当FA+FC的值最小时,求出点F的坐标及FA+FC的
最小值;
(3)连接AC,若点P是抛物线上对称轴右侧一点,点Q是直线BC上一点,试探究是
否存在以点E为直角顶点的Rt△PEQ,且满足tan∠EQP=tan∠OCA.若存在,求出点P的坐标;若不存在,请说明理由.