文档内容
2021年山东省菏泽市中考数学试卷
一、选择题(本大题共8个小题,每小题3分,共24分,在每小题给出的四个选项中,只
有一个选项是正确的,请把正确选项的序号涂在答题卡的相应位置.)
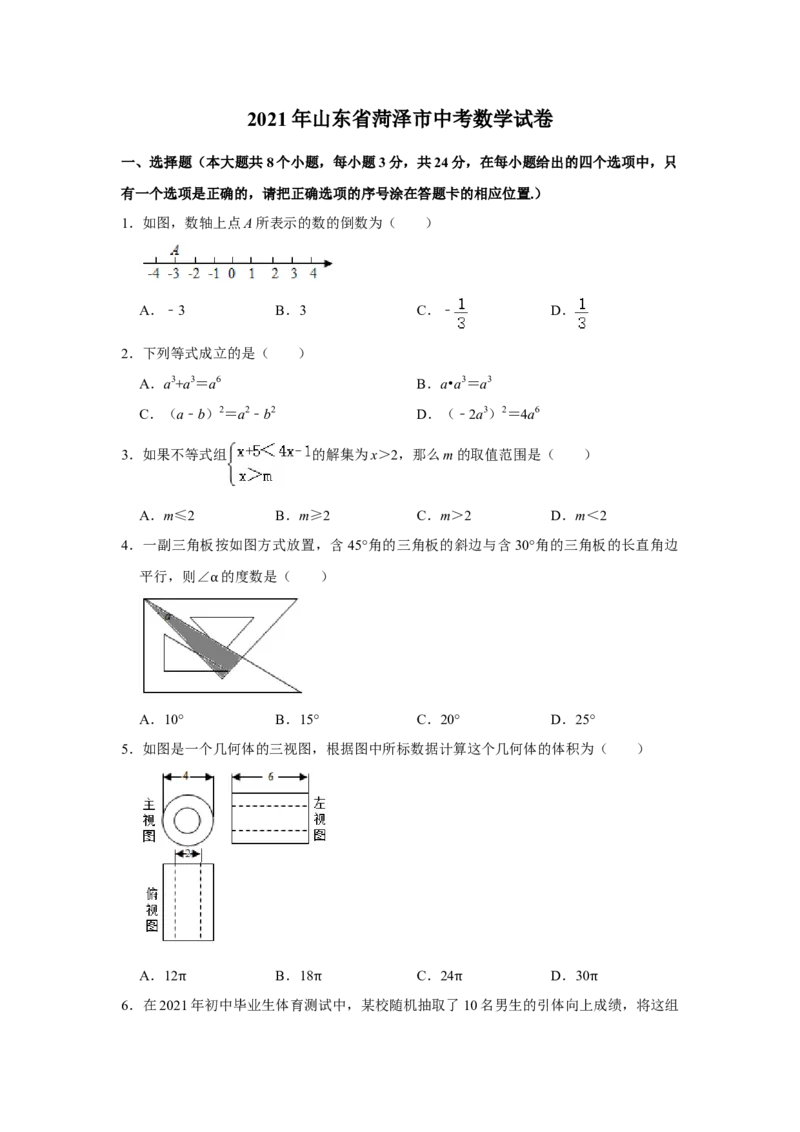
1.如图,数轴上点A所表示的数的倒数为( )
A.﹣3 B.3 C.﹣ D.
2.下列等式成立的是( )
A.a3+a3=a6 B.a•a3=a3
C.(a﹣b)2=a2﹣b2 D.(﹣2a3)2=4a6
3.如果不等式组 的解集为x>2,那么m的取值范围是( )
A.m≤2 B.m≥2 C.m>2 D.m<2
4.一副三角板按如图方式放置,含 45°角的三角板的斜边与含30°角的三角板的长直角边
平行,则∠ 的度数是( )
α
A.10° B.15° C.20° D.25°
5.如图是一个几何体的三视图,根据图中所标数据计算这个几何体的体积为( )
A.12 B.18 C.24 D.30
6.在202π1年初中毕业生体育测π试中,某校随机抽取了π10名男生的引体向上π成绩,将这组数据整理后制成如下统计表:
成绩(次) 12 11 10 9
人数(名) 1 3 4 2
关于这组数据的结论不正确的是( )
A.中位数是10.5 B.平均数是10.3
C.众数是10 D.方差是0.81
7.关于x的方程(k﹣1)2x2+(2k+1)x+1=0有实数根,则k的取值范围是( )
A.k 且k≠1 B.k≥ 且k≠1 C.k D.k≥
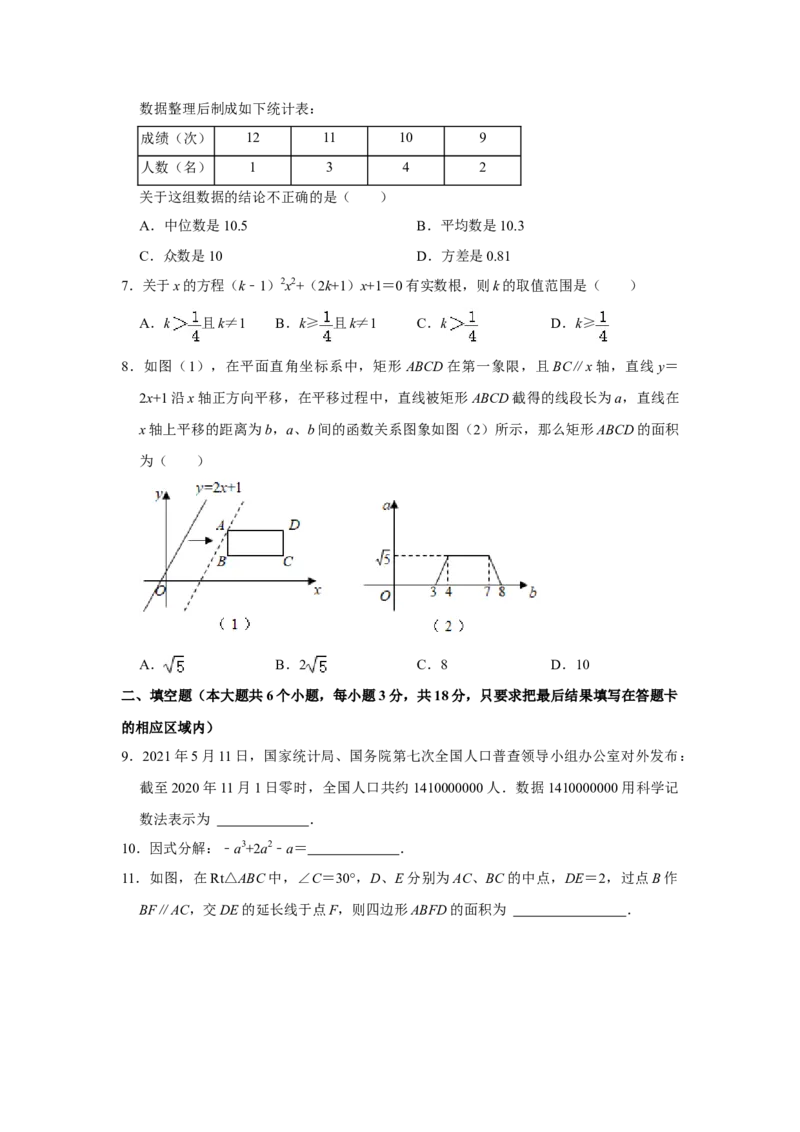
8.如图(1),在平面直角坐标系中,矩形 ABCD在第一象限,且BC∥x轴,直线y=
2x+1沿x轴正方向平移,在平移过程中,直线被矩形ABCD截得的线段长为a,直线在
x轴上平移的距离为b,a、b间的函数关系图象如图(2)所示,那么矩形ABCD的面积
为( )
A. B.2 C.8 D.10
二、填空题(本大题共6个小题,每小题3分,共18分,只要求把最后结果填写在答题卡
的相应区域内)
9.2021年5月11日,国家统计局、国务院第七次全国人口普查领导小组办公室对外发布:
截至2020年11月1日零时,全国人口共约1410000000人.数据1410000000用科学记
数法表示为 .
10.因式分解:﹣a3+2a2﹣a= .
11.如图,在Rt△ABC中,∠C=30°,D、E分别为AC、BC的中点,DE=2,过点B作
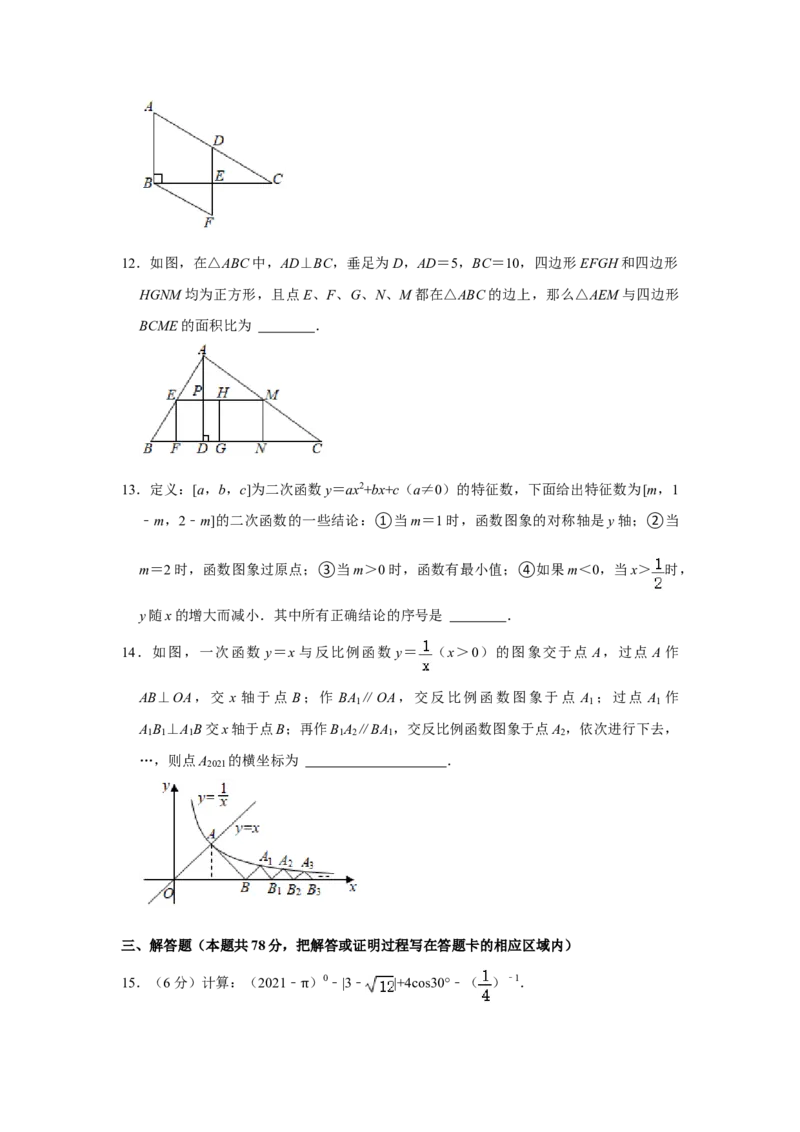
BF∥AC,交DE的延长线于点F,则四边形ABFD的面积为 .12.如图,在△ABC中,AD⊥BC,垂足为D,AD=5,BC=10,四边形EFGH和四边形
HGNM均为正方形,且点E、F、G、N、M都在△ABC的边上,那么△AEM与四边形
BCME的面积比为 .
13.定义:[a,b,c]为二次函数y=ax2+bx+c(a≠0)的特征数,下面给出特征数为[m,1
﹣m,2﹣m]的二次函数的一些结论:①当m=1时,函数图象的对称轴是y轴;②当
m=2时,函数图象过原点;③当m>0时,函数有最小值;④如果m<0,当x> 时,
y随x的增大而减小.其中所有正确结论的序号是 .
14.如图,一次函数 y=x 与反比例函数 y= (x>0)的图象交于点 A,过点 A 作
AB⊥OA,交 x 轴于点 B;作 BA ∥OA,交反比例函数图象于点 A ;过点 A 作
1 1 1
A B ⊥A B交x轴于点B;再作B A ∥BA ,交反比例函数图象于点A ,依次进行下去,
1 1 1 1 2 1 2
…,则点A 的横坐标为 .
2021
三、解答题(本题共78分,把解答或证明过程写在答题卡的相应区域内)
15.(6分)计算:(2021﹣ )0﹣|3﹣ |+4cos30°﹣( )﹣1.
π16.(6分)先化简,再求值:1+ ÷ ,其中m,n满足 =﹣ .
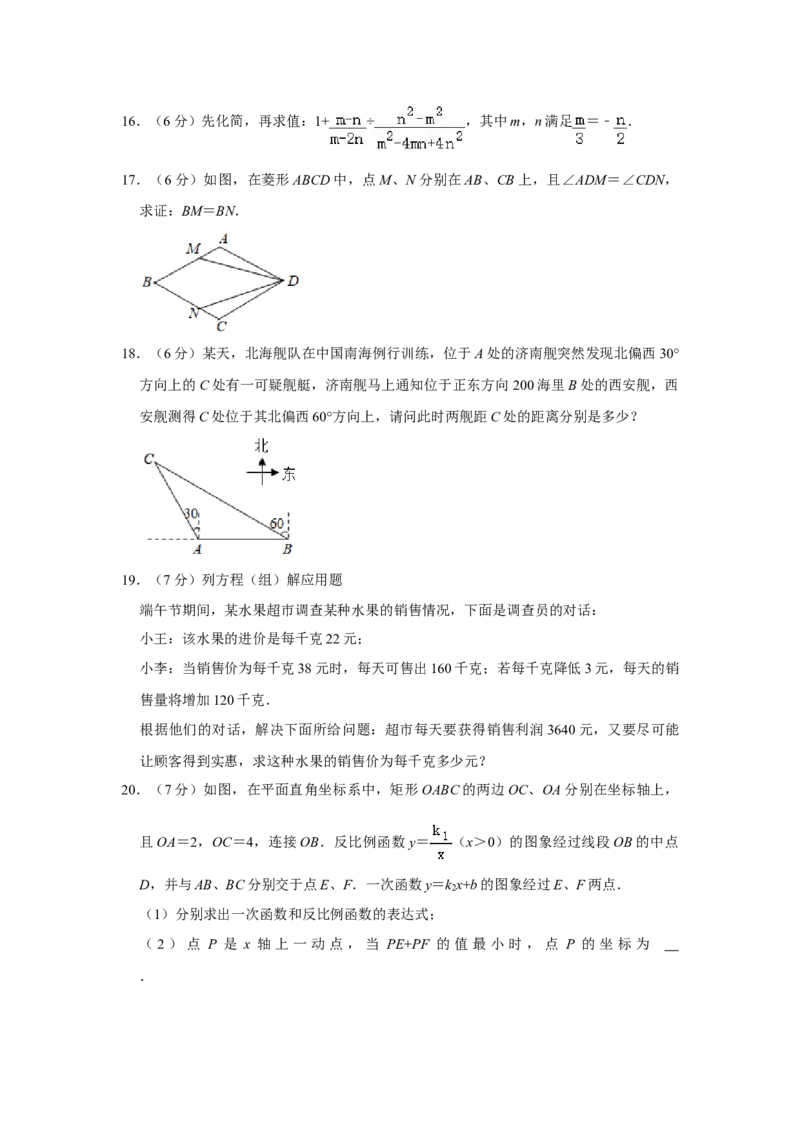
17.(6分)如图,在菱形ABCD中,点M、N分别在AB、CB上,且∠ADM=∠CDN,
求证:BM=BN.
18.(6分)某天,北海舰队在中国南海例行训练,位于A处的济南舰突然发现北偏西30°
方向上的C处有一可疑舰艇,济南舰马上通知位于正东方向200海里B处的西安舰,西
安舰测得C处位于其北偏西60°方向上,请问此时两舰距C处的距离分别是多少?
19.(7分)列方程(组)解应用题
端午节期间,某水果超市调查某种水果的销售情况,下面是调查员的对话:
小王:该水果的进价是每千克22元;
小李:当销售价为每千克38元时,每天可售出160千克;若每千克降低3元,每天的销
售量将增加120千克.
根据他们的对话,解决下面所给问题:超市每天要获得销售利润3640元,又要尽可能
让顾客得到实惠,求这种水果的销售价为每千克多少元?
20.(7分)如图,在平面直角坐标系中,矩形OABC的两边OC、OA分别在坐标轴上,
且OA=2,OC=4,连接OB.反比例函数y= (x>0)的图象经过线段OB的中点
D,并与AB、BC分别交于点E、F.一次函数y=k x+b的图象经过E、F两点.
2
(1)分别求出一次函数和反比例函数的表达式;
(2)点 P 是 x 轴上一动点,当 PE+PF 的值最小时,点 P 的坐标为
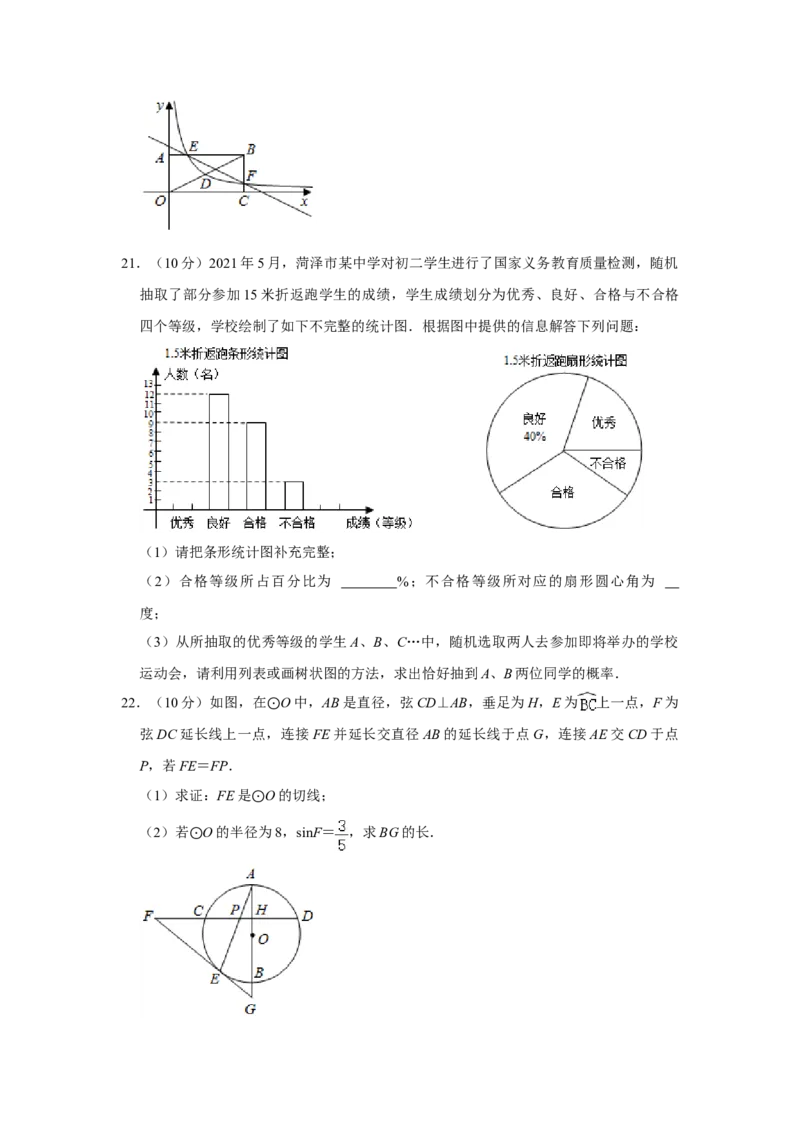
.21.(10分)2021年5月,菏泽市某中学对初二学生进行了国家义务教育质量检测,随机
抽取了部分参加15米折返跑学生的成绩,学生成绩划分为优秀、良好、合格与不合格
四个等级,学校绘制了如下不完整的统计图.根据图中提供的信息解答下列问题:
(1)请把条形统计图补充完整;
(2)合格等级所占百分比为 %;不合格等级所对应的扇形圆心角为
度;
(3)从所抽取的优秀等级的学生A、B、C…中,随机选取两人去参加即将举办的学校
运动会,请利用列表或画树状图的方法,求出恰好抽到A、B两位同学的概率.
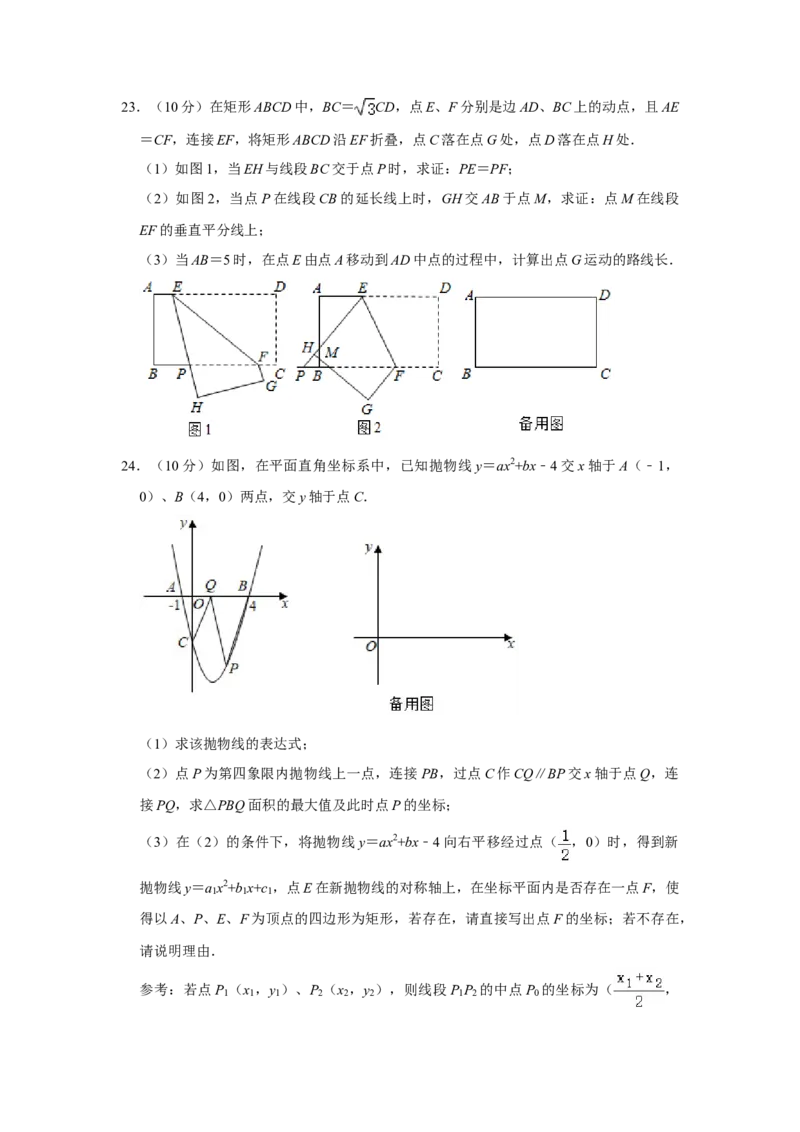
22.(10分)如图,在 O中,AB是直径,弦CD⊥AB,垂足为H,E为 上一点,F为
弦DC延长线上一点,⊙连接FE并延长交直径AB的延长线于点G,连接AE交CD于点
P,若FE=FP.
(1)求证:FE是 O的切线;
(2)若 O的半径⊙为8,sinF= ,求BG的长.
⊙23.(10分)在矩形ABCD中,BC= CD,点E、F分别是边AD、BC上的动点,且AE
=CF,连接EF,将矩形ABCD沿EF折叠,点C落在点G处,点D落在点H处.
(1)如图1,当EH与线段BC交于点P时,求证:PE=PF;
(2)如图2,当点P在线段CB的延长线上时,GH交AB于点M,求证:点M在线段
EF的垂直平分线上;
(3)当AB=5时,在点E由点A移动到AD中点的过程中,计算出点G运动的路线长.
24.(10分)如图,在平面直角坐标系中,已知抛物线y=ax2+bx﹣4交x轴于A(﹣1,
0)、B(4,0)两点,交y轴于点C.
(1)求该抛物线的表达式;
(2)点P为第四象限内抛物线上一点,连接PB,过点C作CQ∥BP交x轴于点Q,连
接PQ,求△PBQ面积的最大值及此时点P的坐标;
(3)在(2)的条件下,将抛物线y=ax2+bx﹣4向右平移经过点( ,0)时,得到新
抛物线y=a x2+b x+c ,点E在新抛物线的对称轴上,在坐标平面内是否存在一点F,使
1 1 1
得以A、P、E、F为顶点的四边形为矩形,若存在,请直接写出点F的坐标;若不存在,
请说明理由.
参考:若点P (x ,y )、P (x ,y ),则线段P P 的中点P 的坐标为( ,
1 1 1 2 2 2 1 2 0).