文档内容
2021年辽宁省铁岭市中考数学试卷
参考答案与试题解析
一、选择题(本题共10个小题,每小题3分,共30分。在每小题给出的四个选项中,只有一项
是符合题目要求的。
1.【分析】有理数大小比较的法则:①正数都大于0;②负数都小于0;③正数大于一切负数;
④两个负数,绝对值大的其值反而小,据此判断即可.
【解答】解:∵﹣3<﹣1,﹣2<﹣1,﹣1=﹣1,0>﹣1,
∴所给的各数中,比﹣1大的数是0.
故选:D.
【点评】此题主要考查了有理数大小比较的方法,解答此题的关键是要明确:①正数都大
于0;②负数都小于0;③正数大于一切负数;④两个负数,绝对值大的其值反而小.
2.【分析】左视图是从物体的左边观察得到的图形,结合选项进行判断即可.
【解答】解:从左边看,有两列,从左到右第一列是两个正方形,第二列底层是一个正方形.
故选:A.
【点评】本题考查了简单组合体的三视图,属于基础题,解答本题的关键是掌握左视图的
定义.
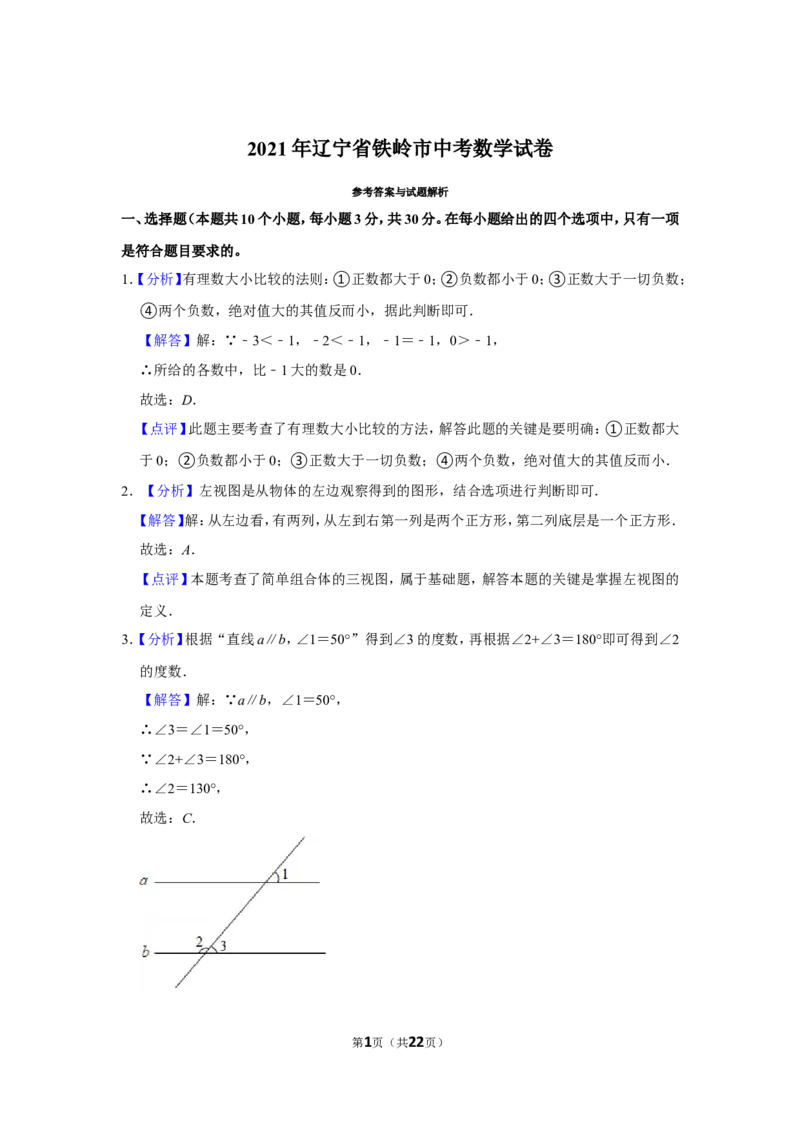
3.【分析】根据“直线a∥b,∠1=50°”得到∠3的度数,再根据∠2+∠3=180°即可得到∠2
的度数.
【解答】解:∵a∥b,∠1=50°,
∴∠3=∠1=50°,
∵∠2+∠3=180°,
∴∠2=130°,
故选:C.
第1页(共22页)【点评】本题考查平行线的性质,解题的关键是能够利用平行线的性质求得∠3的度数.
4.【分析】根据合并同类项,积的乘方,同底数幂的除法,同底数幂的乘法法则进行计算,从
而作出判断.
【解答】解:A、x5+x5=2x5,故此选项不符合题意;
B、(x3y2)2=x6y4,故此选项不符合题意;
C、x6÷x2=x4,故此选项不符合题意;
D、x2•x3=x5,正确,故此选项符合题意;
故选:D.
【点评】本题考查合并同类项,积的乘方,同底数幂的除法,同底数幂的乘法运算,掌握运
算法则是解题关键.
5.【分析】根据中位数、众数的意义分别求出中位数、众数即可.
【解答】解:将这15名学生成绩从小到大排列,处在中间位置的一个数,即第8个数是96,
因此中位数是96,
这15名学生成绩出现次数最多的是96,共出现4次,因此众数是96,
故选:C.
【点评】本题考查中位数、众数,理解中位数、众数的意义是解决问题的前提,掌握众数、中
位数的计算方法是解决问题的关键.
6.【分析】根据加权平均数的定义列式计算即可.
【解答】解:他的最终成绩为80×40%+90×60%=86(分),
故选:D.
【点评】本题主要考查加权平均数,解题的关键是掌握加权平均数的定义.
7.【分析】首先利用函数解析式y=2x求出m的值,然后再根据两函数图象的交点横坐标就
是关于x的方程kx+b=2的解可得答案.
【解答】解:∵直线y=2x与y=kx+b相交于点P(m,2),
∴2=2m,
∴m=1,
∴P(1,2),
∴当x=1时,y=kx+b=2,
∴关于x的方程kx+b=2的解是x=1,
故选:B.
【点评】此题主要考查了一次函数与一元一次方程,关键是求得两函数图象的交点坐标.
第2页(共22页)8.【分析】根据三角形的外角性质求出∠D,根据圆周角定理得出∠D= COB,求出
∠COB=2∠D,再代入求出答案即可.
【解答】解:∵∠ABD=20°,∠AED=80°,
∴∠D=∠AED﹣∠ABD=80°﹣20°=60°,
∴∠COB=2∠D=120°,
故选:C.
【点评】本题考查了三角形外角性质,圆周角定理等知识点,能熟记一条弧所对的圆周角
等于它所对的圆心角的一半是解此题的关键.
9.【分析】设甲种水杯的单价为x元,则乙种水杯的单价为(x﹣15)元,利用数量=总价÷单价,
结合用720元购买甲种水杯的数量和用540元购买乙种水杯的数量相同,即可得出关于x
的分式方程,此题得解.
【解答】解:设甲种水杯的单价为x元,则乙种水杯的单价为(x﹣15)元,
依题意得: = .
故选:A.
【点评】本题考查了由实际问题抽象出分式方程,找准等量关系,正确列出分式方程是解
题的关键.
10.【分析】先证明△ADE≌△FCE得到,BF=8,由勾股定理求出AF=10.当点M在AB上时,
根据三角函数求出NM= ,
从而得到△AMN的面积S= = ;当点M在BF上时,先利用三角函数求
出MN,再求出此时S关于x的函数关系式,即可得到答案.
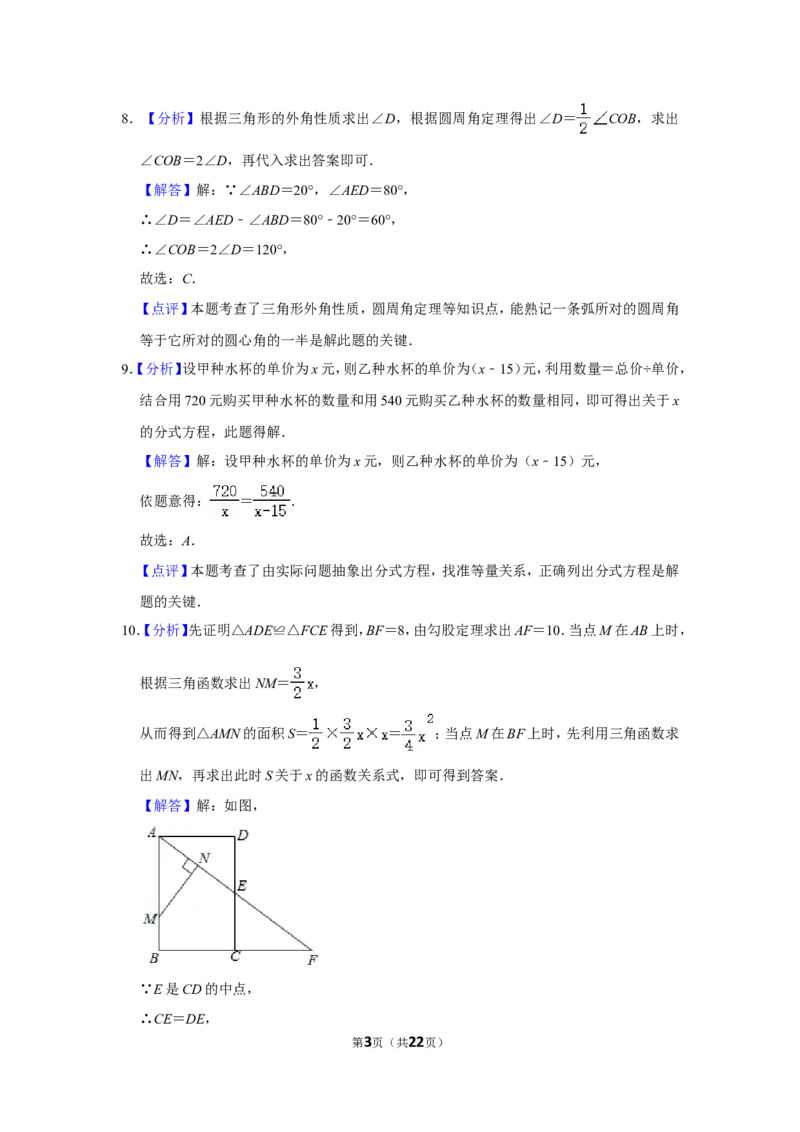
【解答】解:如图,
∵E是CD的中点,
∴CE=DE,
第3页(共22页)∵四边形ABCD是矩形,
∴∠D=∠DCF=90°,AD=BC=4,
在△ADE与△FCE中,
,
∴△ADE≌△FCE(SAS),
∴CF=AD=4,
∴BF=CF+BC=8,
∴AF= ,
当点M在AB上时,
在Rt△AMN和Rt△AFB中,
tan∠NAM= ,
∴NM= x= x,
∴△AMN的面积S= × x×x= x2,
∴当点M在AB上时,函数图象是开口向上、经过原点的抛物线的一部分;
当点M在BF上时,如图,
AN=x,NF=10﹣x,
在Rt△FMN和Rt△FBA中,
tan∠F= ,
∴ =﹣ ,
∴△AMN的面积S=
=﹣ ,
∴当点M在BF上时,函数图象是开口向下的抛物线的一部分;
故选:B.
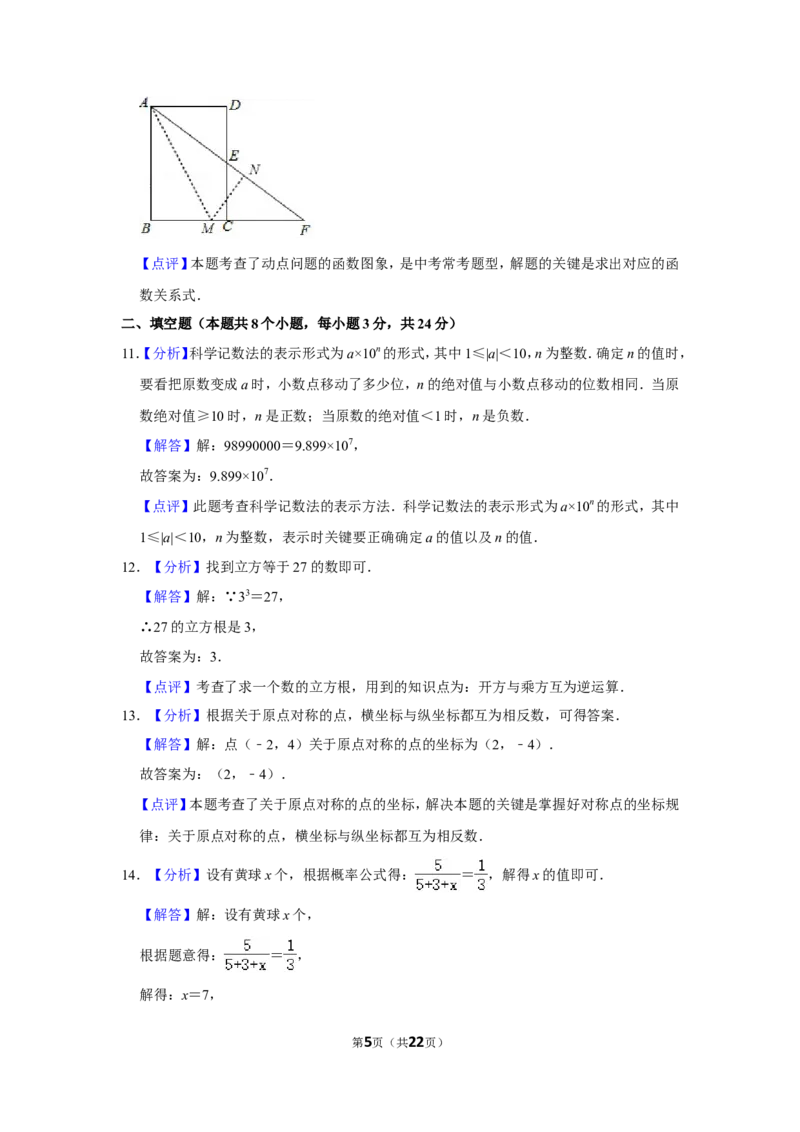
第4页(共22页)【点评】本题考查了动点问题的函数图象,是中考常考题型,解题的关键是求出对应的函
数关系式.
二、填空题(本题共8个小题,每小题3分,共24分)
11.【分析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,
要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原
数绝对值≥10时,n是正数;当原数的绝对值<1时,n是负数.
【解答】解:98990000=9.899×107,
故答案为:9.899×107.
【点评】此题考查科学记数法的表示方法.科学记数法的表示形式为a×10n的形式,其中
1≤|a|<10,n为整数,表示时关键要正确确定a的值以及n的值.
12.【分析】找到立方等于27的数即可.
【解答】解:∵33=27,
∴27的立方根是3,
故答案为:3.
【点评】考查了求一个数的立方根,用到的知识点为:开方与乘方互为逆运算.
13.【分析】根据关于原点对称的点,横坐标与纵坐标都互为相反数,可得答案.
【解答】解:点(﹣2,4)关于原点对称的点的坐标为(2,﹣4).
故答案为:(2,﹣4).
【点评】本题考查了关于原点对称的点的坐标,解决本题的关键是掌握好对称点的坐标规
律:关于原点对称的点,横坐标与纵坐标都互为相反数.
14.【分析】设有黄球x个,根据概率公式得: = ,解得x的值即可.
【解答】解:设有黄球x个,
根据题意得: = ,
解得:x=7,
第5页(共22页)经检验x=7是原方程的解,
故答案为:7.
【点评】此题考查了概率公式的应用.用到的知识点为:概率=所求情况数与总情况数之
比.
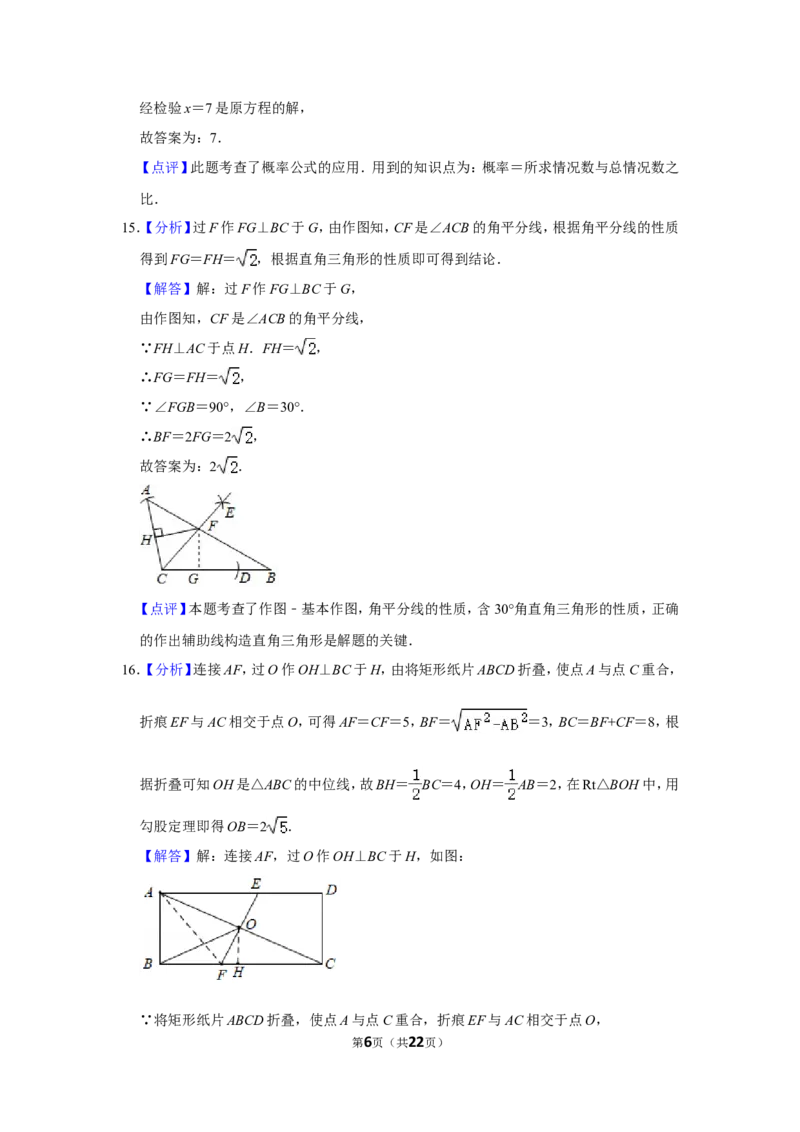
15.【分析】过F作FG⊥BC于G,由作图知,CF是∠ACB的角平分线,根据角平分线的性质
得到FG=FH= ,根据直角三角形的性质即可得到结论.
【解答】解:过F作FG⊥BC于G,
由作图知,CF是∠ACB的角平分线,
∵FH⊥AC于点H.FH= ,
∴FG=FH= ,
∵∠FGB=90°,∠B=30°.
∴BF=2FG=2 ,
故答案为:2 .
【点评】本题考查了作图﹣基本作图,角平分线的性质,含30°角直角三角形的性质,正确
的作出辅助线构造直角三角形是解题的关键.
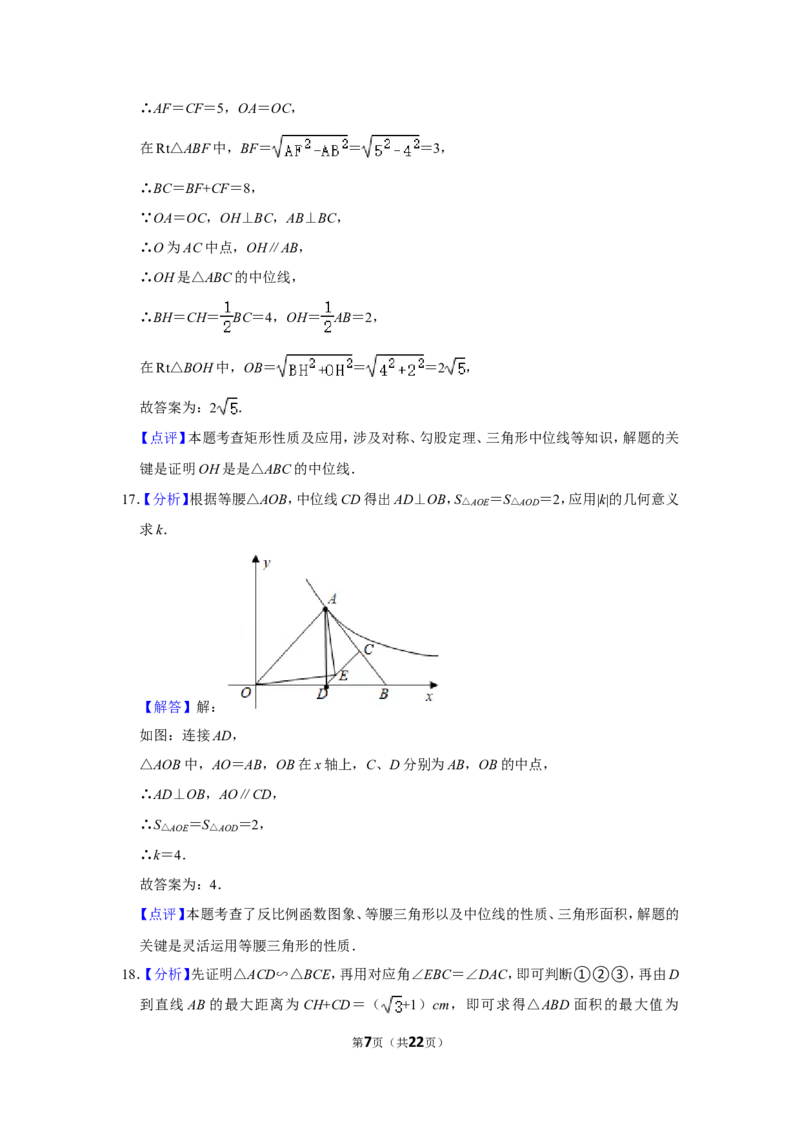
16.【分析】连接AF,过O作OH⊥BC于H,由将矩形纸片ABCD折叠,使点A与点C重合,
折痕EF与AC相交于点O,可得AF=CF=5,BF= =3,BC=BF+CF=8,根
据折叠可知OH是△ABC的中位线,故BH= BC=4,OH= AB=2,在Rt△BOH中,用
勾股定理即得OB=2 .
【解答】解:连接AF,过O作OH⊥BC于H,如图:
∵将矩形纸片ABCD折叠,使点A与点C重合,折痕EF与AC相交于点O,
第6页(共22页)∴AF=CF=5,OA=OC,
在Rt△ABF中,BF= = =3,
∴BC=BF+CF=8,
∵OA=OC,OH⊥BC,AB⊥BC,
∴O为AC中点,OH∥AB,
∴OH是△ABC的中位线,
∴BH=CH= BC=4,OH= AB=2,
在Rt△BOH中,OB= = =2 ,
故答案为:2 .
【点评】本题考查矩形性质及应用,涉及对称、勾股定理、三角形中位线等知识,解题的关
键是证明OH是是△ABC的中位线.
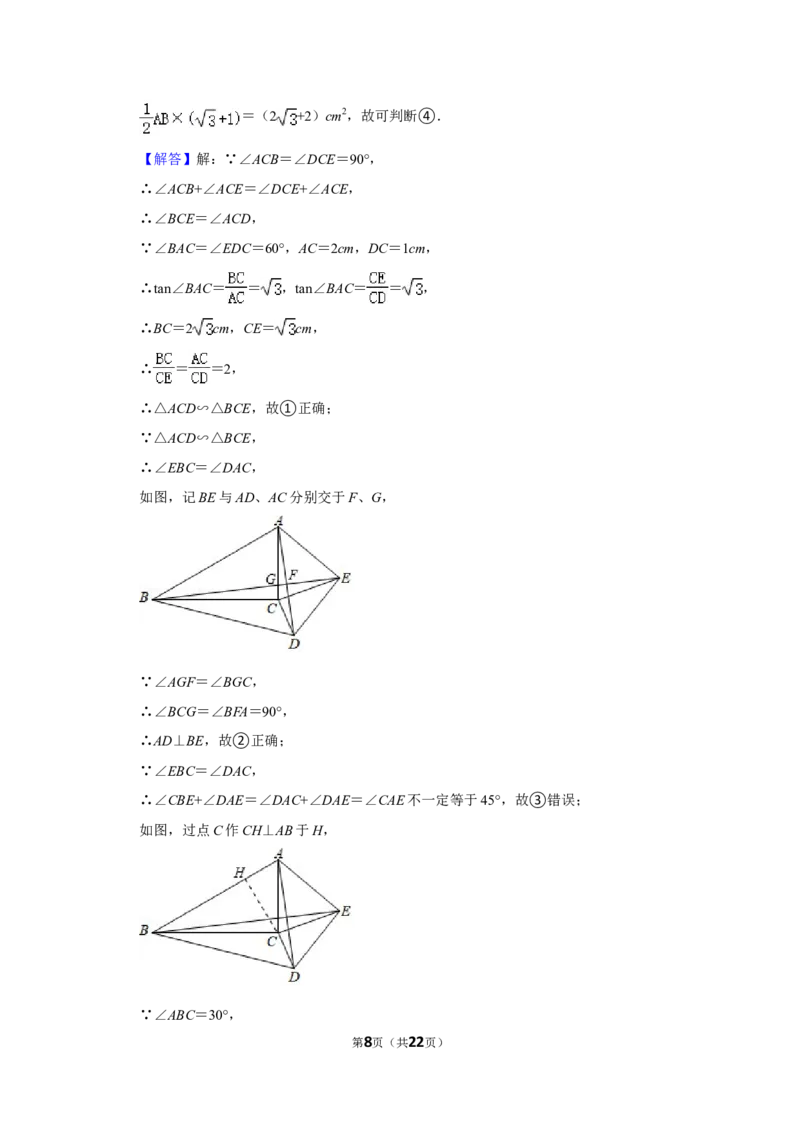
17.【分析】根据等腰△AOB,中位线CD得出AD⊥OB,S△AOE =S△AOD =2,应用|k|的几何意义
求k.
【解答】解:
如图:连接AD,
△AOB中,AO=AB,OB在x轴上,C、D分别为AB,OB的中点,
∴AD⊥OB,AO∥CD,
∴S△AOE =S△AOD =2,
∴k=4.
故答案为:4.
【点评】本题考查了反比例函数图象、等腰三角形以及中位线的性质、三角形面积,解题的
关键是灵活运用等腰三角形的性质.
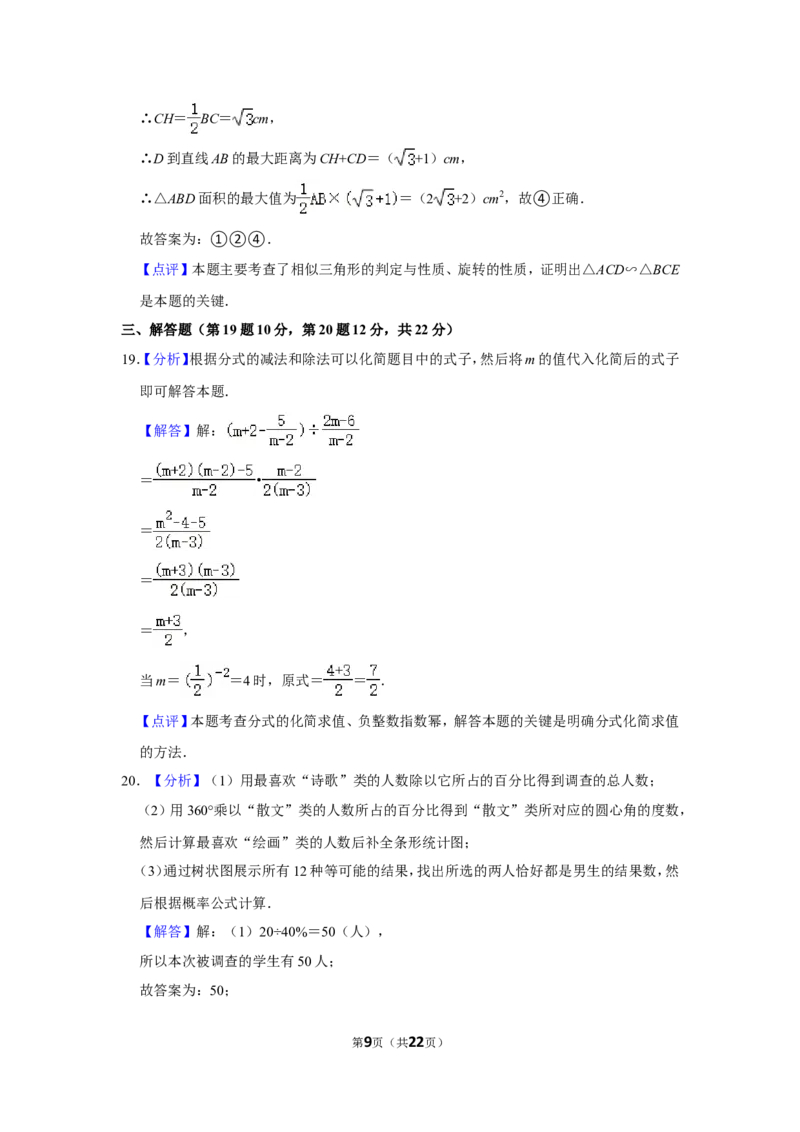
18.【分析】先证明△ACD∽△BCE,再用对应角∠EBC=∠DAC,即可判断①②③,再由D
到直线 AB的最大距离为 CH+CD=( +1)cm,即可求得△ABD面积的最大值为
第7页(共22页)=(2 +2)cm2,故可判断④.
【解答】解:∵∠ACB=∠DCE=90°,
∴∠ACB+∠ACE=∠DCE+∠ACE,
∴∠BCE=∠ACD,
∵∠BAC=∠EDC=60°,AC=2cm,DC=1cm,
∴tan∠BAC= = ,tan∠BAC= = ,
∴BC=2 cm,CE= cm,
∴ = =2,
∴△ACD∽△BCE,故①正确;
∵△ACD∽△BCE,
∴∠EBC=∠DAC,
如图,记BE与AD、AC分别交于F、G,
∵∠AGF=∠BGC,
∴∠BCG=∠BFA=90°,
∴AD⊥BE,故②正确;
∵∠EBC=∠DAC,
∴∠CBE+∠DAE=∠DAC+∠DAE=∠CAE不一定等于45°,故③错误;
如图,过点C作CH⊥AB于H,
∵∠ABC=30°,
第8页(共22页)∴CH= BC= cm,
∴D到直线AB的最大距离为CH+CD=( +1)cm,
∴△ABD面积的最大值为 =(2 +2)cm2,故④正确.
故答案为:①②④.
【点评】本题主要考查了相似三角形的判定与性质、旋转的性质,证明出△ACD∽△BCE
是本题的关键.
三、解答题(第19题10分,第20题12分,共22分)
19.【分析】根据分式的减法和除法可以化简题目中的式子,然后将m的值代入化简后的式子
即可解答本题.
【解答】解:
= •
=
=
= ,
当m= =4时,原式= = .
【点评】本题考查分式的化简求值、负整数指数幂,解答本题的关键是明确分式化简求值
的方法.
20.【分析】(1)用最喜欢“诗歌”类的人数除以它所占的百分比得到调查的总人数;
(2)用360°乘以“散文”类的人数所占的百分比得到“散文”类所对应的圆心角的度数,
然后计算最喜欢“绘画”类的人数后补全条形统计图;
(3)通过树状图展示所有12种等可能的结果,找出所选的两人恰好都是男生的结果数,然
后根据概率公式计算.
【解答】解:(1)20÷40%=50(人),
所以本次被调查的学生有50人;
故答案为:50;
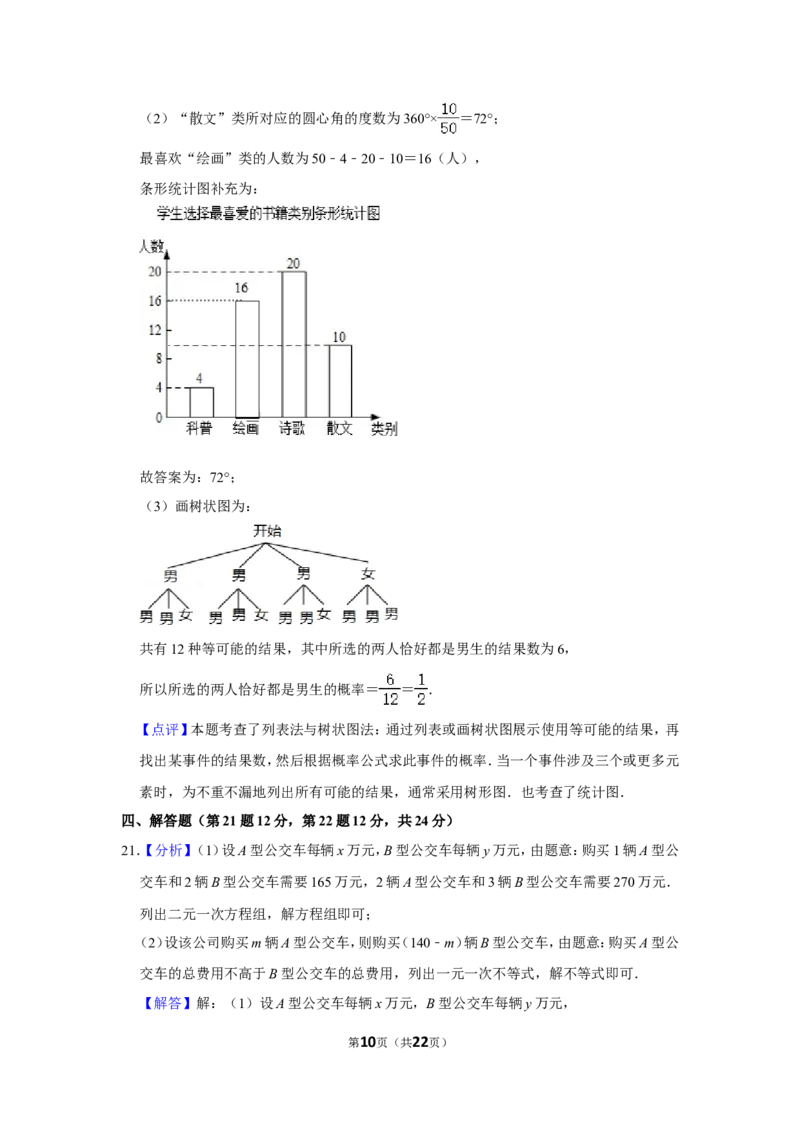
第9页(共22页)(2)“散文”类所对应的圆心角的度数为360°× =72°;
最喜欢“绘画”类的人数为50﹣4﹣20﹣10=16(人),
条形统计图补充为:
故答案为:72°;
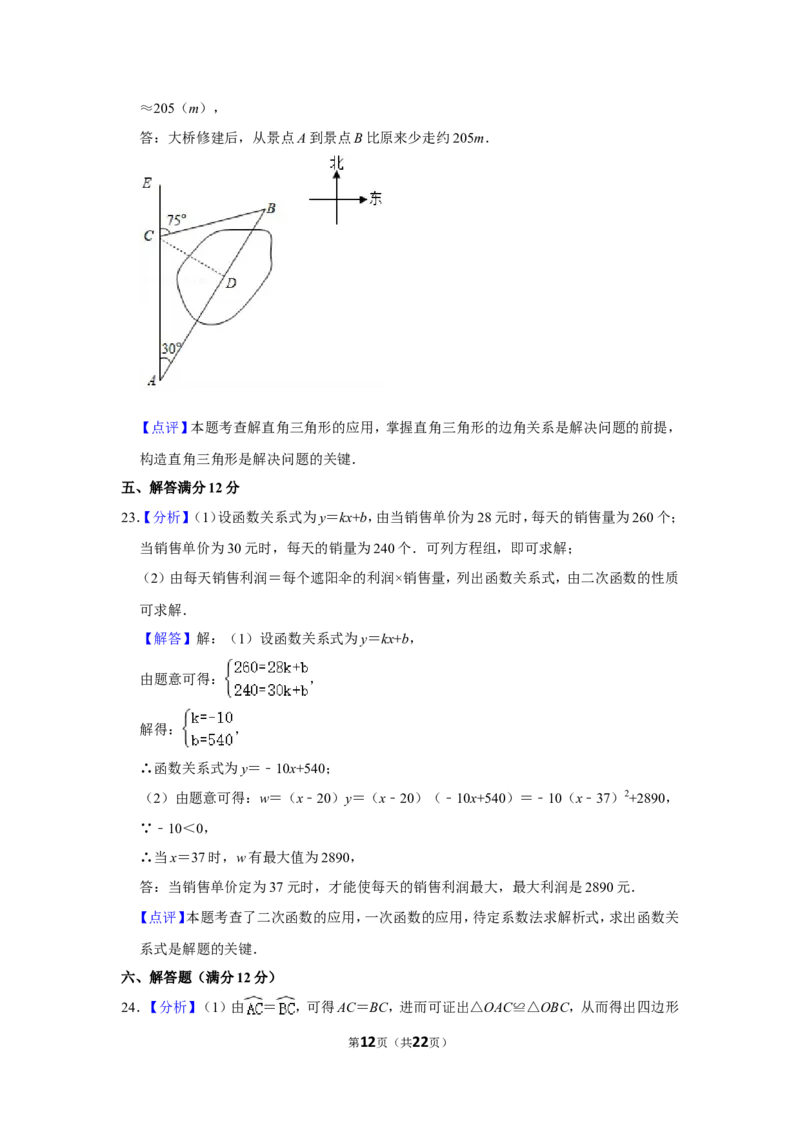
(3)画树状图为:
共有12种等可能的结果,其中所选的两人恰好都是男生的结果数为6,
所以所选的两人恰好都是男生的概率= = .
【点评】本题考查了列表法与树状图法:通过列表或画树状图展示使用等可能的结果,再
找出某事件的结果数,然后根据概率公式求此事件的概率.当一个事件涉及三个或更多元
素时,为不重不漏地列出所有可能的结果,通常采用树形图.也考查了统计图.
四、解答题(第21题12分,第22题12分,共24分)
21.【分析】(1)设A型公交车每辆x万元,B型公交车每辆y万元,由题意:购买1辆A型公
交车和2辆B型公交车需要165万元,2辆A型公交车和3辆B型公交车需要270万元.
列出二元一次方程组,解方程组即可;
(2)设该公司购买m辆A型公交车,则购买(140﹣m)辆B型公交车,由题意:购买A型公
交车的总费用不高于B型公交车的总费用,列出一元一次不等式,解不等式即可.
【解答】解:(1)设A型公交车每辆x万元,B型公交车每辆y万元,
第10页(共22页)由题意得: ,
解得: ,
答:A型公交车每辆45万元,B型公交车每辆60万元;
(2)设该公司购买m辆A型公交车,则购买(140﹣m)辆B型公交车,
由题意得:45m≤60(140﹣m),
解得:m≤80,
答:该公司最多购买80辆A型公交车.
【点评】本题考查了二元一次方程组的应用以及一元一次不等式组的应用,解题的关键是:
(1)找准等量关系,正确列出二元一次方程组;(2)根据各数量之间的关系,正确列出一元
一次不等式.
22.【分析】(1)通过作辅助线,构造直角三角形,在Rt△ACD中,可求出CD、AD,根据外角
的性质可求出∠B的度数,在Rt△BCD中求出BC即可;
(2)计算AC+BC和AB的长,计算可得答案.
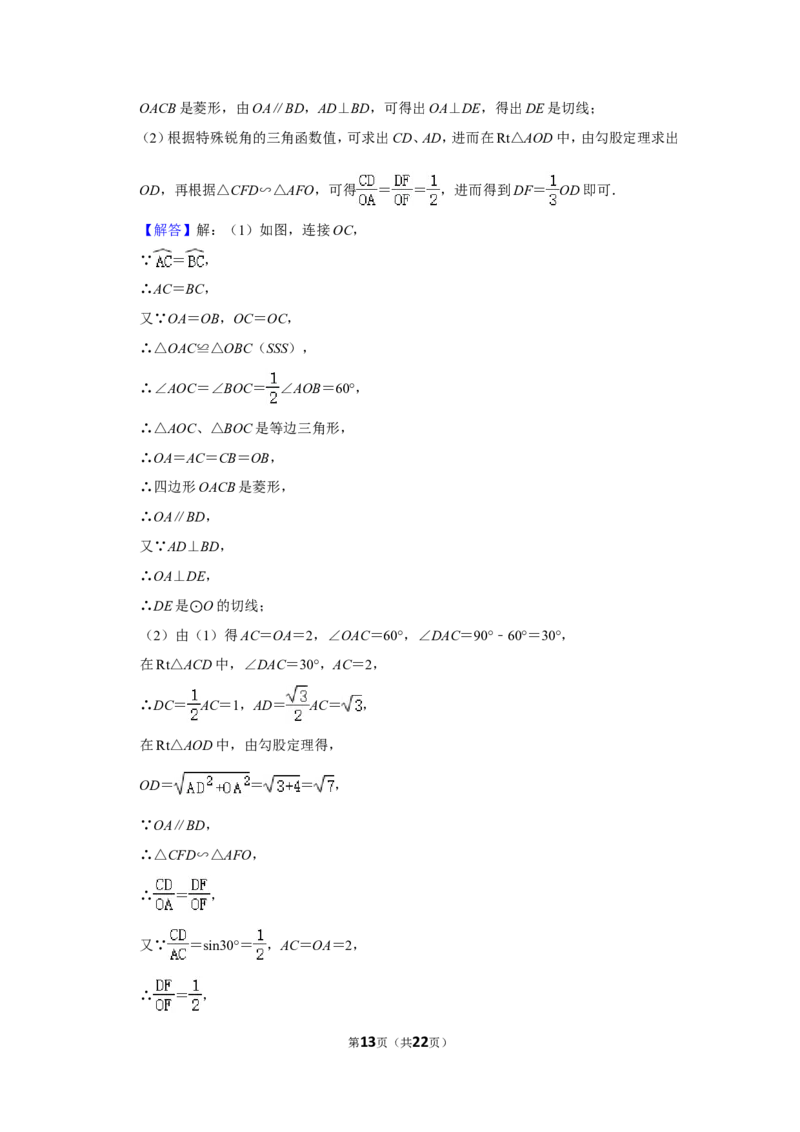
【解答】解:(1)过点C作CD⊥AB于点D,
由题意得,∠A=30°,∠BCE=75°,AC=600m,
在Rt△ACD中,∠A=30°,AC=600,
∴CD= AC=300(m),
AD= AC=300 (m),
∵∠BCE=75°=∠A+∠B,
∴∠B=75°﹣∠A=45°,
∴CD=BD=300(m),
BC= CD=300 (m),
答:景点B和C处之间的距离为300 m;
(2)由题意得.
AC+BC=(600+300 )m,
AB=AD+BD=(300+300 )m,
AC+BC﹣AB=(600+300 )﹣(300+300 )
≈204.6
第11页(共22页)≈205(m),
答:大桥修建后,从景点A到景点B比原来少走约205m.
【点评】本题考查解直角三角形的应用,掌握直角三角形的边角关系是解决问题的前提,
构造直角三角形是解决问题的关键.
五、解答满分12分
23.【分析】(1)设函数关系式为y=kx+b,由当销售单价为28元时,每天的销售量为260个;
当销售单价为30元时,每天的销量为240个.可列方程组,即可求解;
(2)由每天销售利润=每个遮阳伞的利润×销售量,列出函数关系式,由二次函数的性质
可求解.
【解答】解:(1)设函数关系式为y=kx+b,
由题意可得: ,
解得: ,
∴函数关系式为y=﹣10x+540;
(2)由题意可得:w=(x﹣20)y=(x﹣20)(﹣10x+540)=﹣10(x﹣37)2+2890,
∵﹣10<0,
∴当x=37时,w有最大值为2890,
答:当销售单价定为37元时,才能使每天的销售利润最大,最大利润是2890元.
【点评】本题考查了二次函数的应用,一次函数的应用,待定系数法求解析式,求出函数关
系式是解题的关键.
六、解答题(满分12分)
24.【分析】(1)由 = ,可得AC=BC,进而可证出△OAC≌△OBC,从而得出四边形
第12页(共22页)OACB是菱形,由OA∥BD,AD⊥BD,可得出OA⊥DE,得出DE是切线;
(2)根据特殊锐角的三角函数值,可求出CD、AD,进而在Rt△AOD中,由勾股定理求出
OD,再根据△CFD∽△AFO,可得 = = ,进而得到DF= OD即可.
【解答】解:(1)如图,连接OC,
∵ = ,
∴AC=BC,
又∵OA=OB,OC=OC,
∴△OAC≌△OBC(SSS),
∴∠AOC=∠BOC= ∠AOB=60°,
∴△AOC、△BOC是等边三角形,
∴OA=AC=CB=OB,
∴四边形OACB是菱形,
∴OA∥BD,
又∵AD⊥BD,
∴OA⊥DE,
∴DE是 O的切线;
(2)由(⊙1)得AC=OA=2,∠OAC=60°,∠DAC=90°﹣60°=30°,
在Rt△ACD中,∠DAC=30°,AC=2,
∴DC= AC=1,AD= AC= ,
在Rt△AOD中,由勾股定理得,
OD= = = ,
∵OA∥BD,
∴△CFD∽△AFO,
∴ = ,
又∵ =sin30°= ,AC=OA=2,
∴ = ,
第13页(共22页)∴ = ,
即DF= OD= .
【点评】本题考查切线的判定和性质,证出OA⊥DE,是判断DE是圆的切线的关键.
七、解答题(满分12分)
25.【分析】(1)结论:EF=BE.利用线段的垂直平分线的性质证明即可.
(2)结论:AF2+BE2=EF2如图2中,过点A作AJ⊥AC交ED的延长线于J,连接FJ.证明
△AJD≌△BED(AAS),推出AJ=BE,DJ=DE,再证明FJ=EF,可得结论.
(3)分两种情形:如图3﹣1中,当点E在线段BC上时,如图3﹣2中,当点E在线段BC的
延长线上时,设AF=x,则CF=5﹣x.构建方程求解即可.
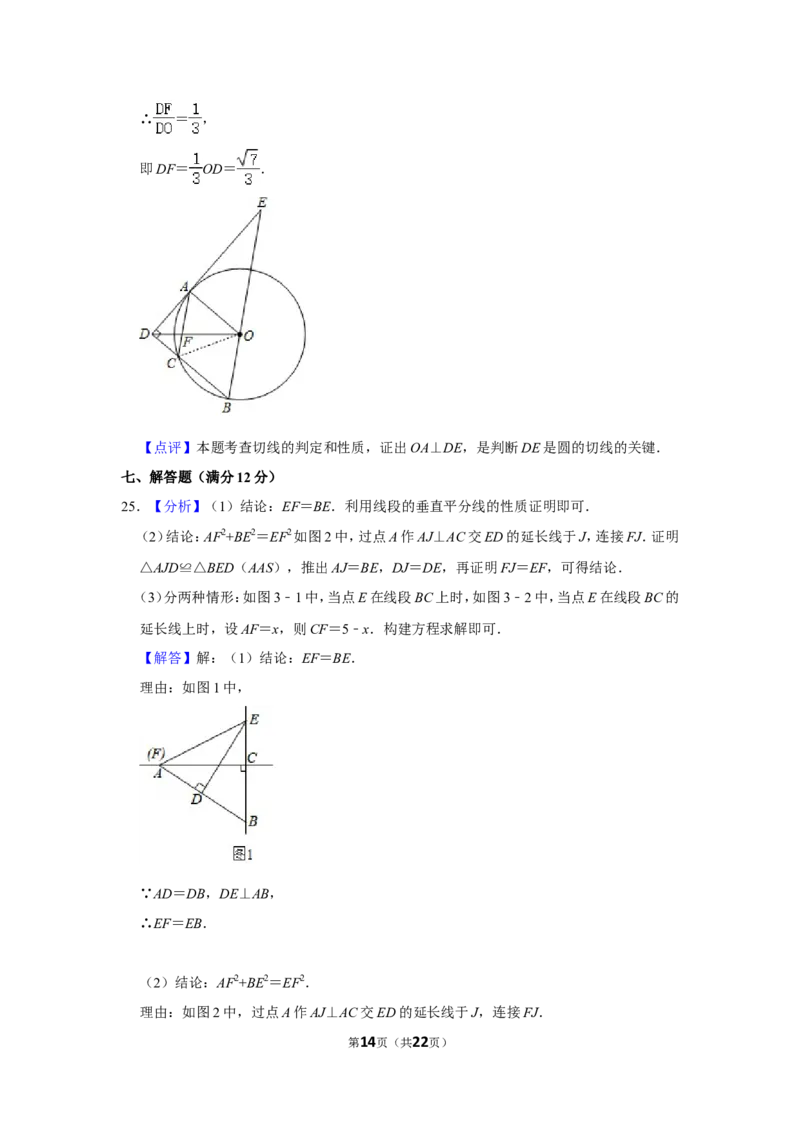
【解答】解:(1)结论:EF=BE.
理由:如图1中,
∵AD=DB,DE⊥AB,
∴EF=EB.
(2)结论:AF2+BE2=EF2.
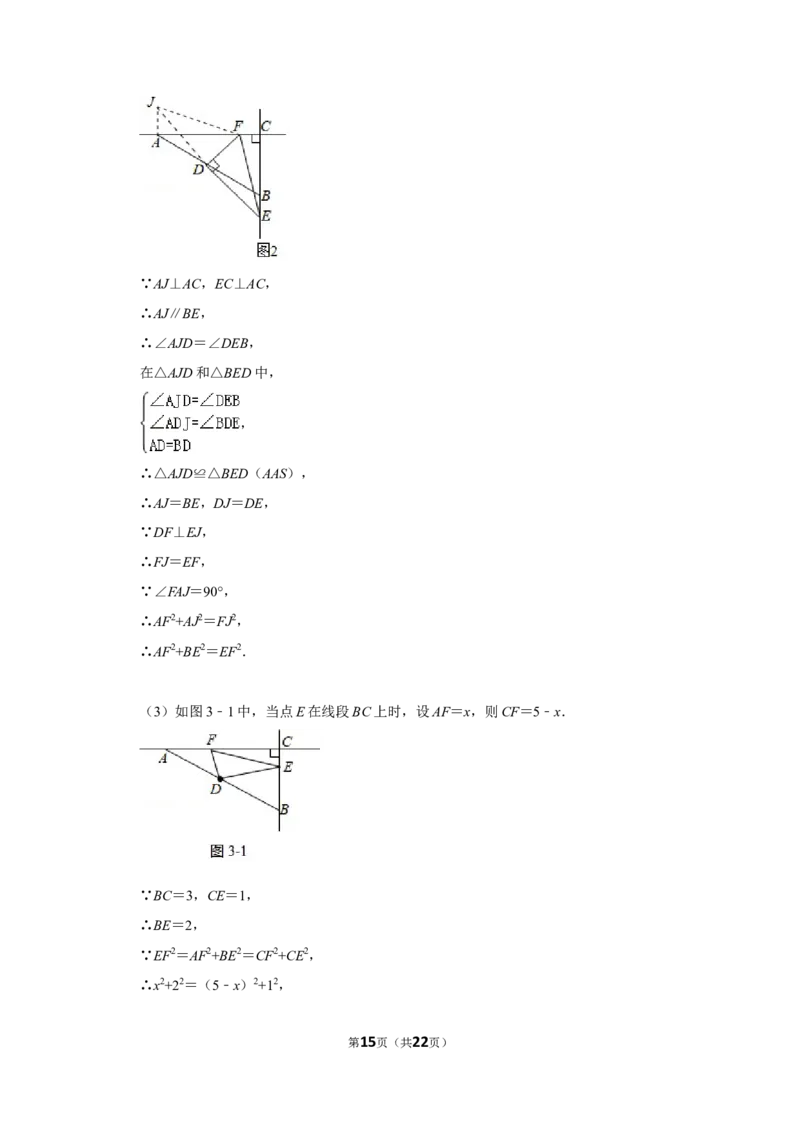
理由:如图2中,过点A作AJ⊥AC交ED的延长线于J,连接FJ.
第14页(共22页)∵AJ⊥AC,EC⊥AC,
∴AJ∥BE,
∴∠AJD=∠DEB,
在△AJD和△BED中,
,
∴△AJD≌△BED(AAS),
∴AJ=BE,DJ=DE,
∵DF⊥EJ,
∴FJ=EF,
∵∠FAJ=90°,
∴AF2+AJ2=FJ2,
∴AF2+BE2=EF2.
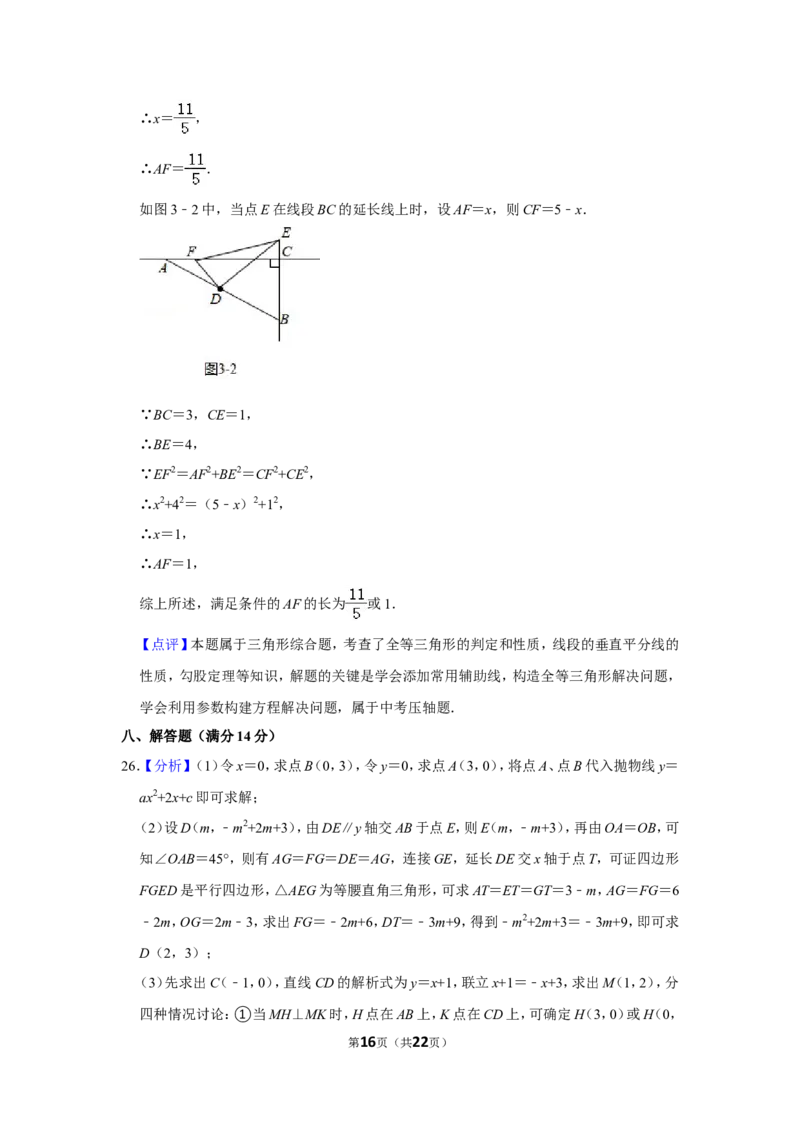
(3)如图3﹣1中,当点E在线段BC上时,设AF=x,则CF=5﹣x.
∵BC=3,CE=1,
∴BE=2,
∵EF2=AF2+BE2=CF2+CE2,
∴x2+22=(5﹣x)2+12,
第15页(共22页)∴x= ,
∴AF= .
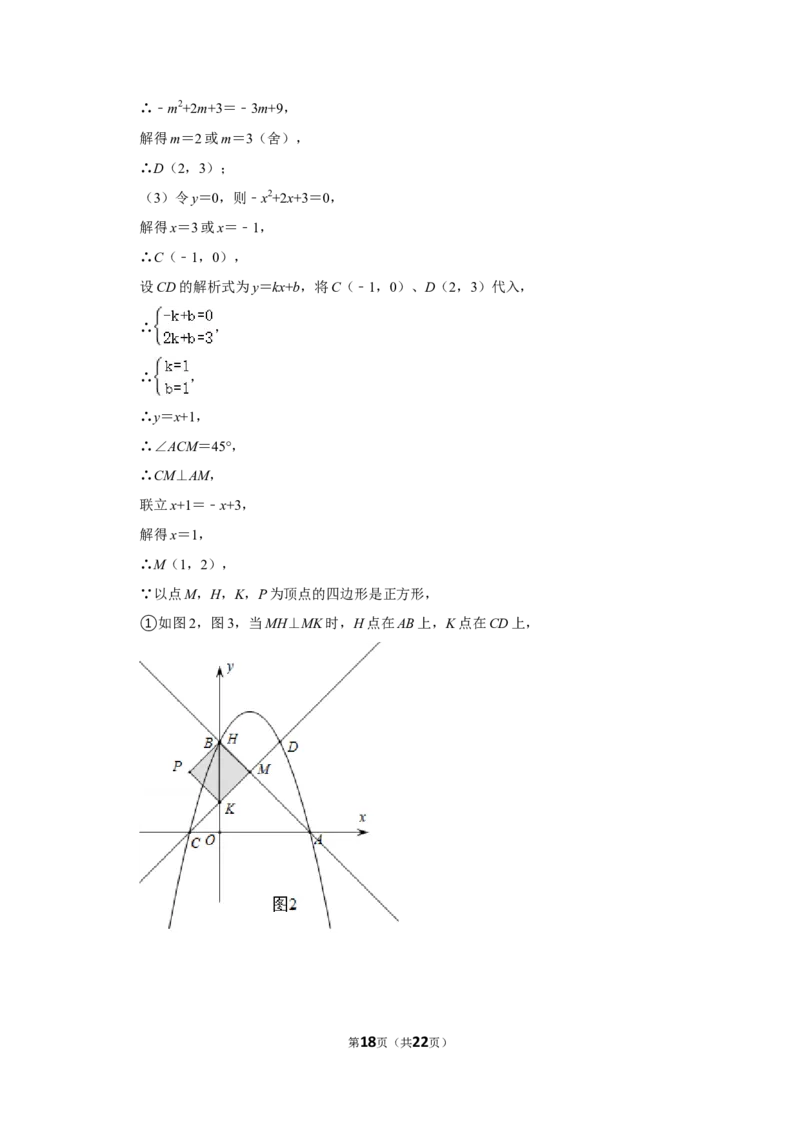
如图3﹣2中,当点E在线段BC的延长线上时,设AF=x,则CF=5﹣x.
∵BC=3,CE=1,
∴BE=4,
∵EF2=AF2+BE2=CF2+CE2,
∴x2+42=(5﹣x)2+12,
∴x=1,
∴AF=1,
综上所述,满足条件的AF的长为 或1.
【点评】本题属于三角形综合题,考查了全等三角形的判定和性质,线段的垂直平分线的
性质,勾股定理等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,
学会利用参数构建方程解决问题,属于中考压轴题.
八、解答题(满分14分)
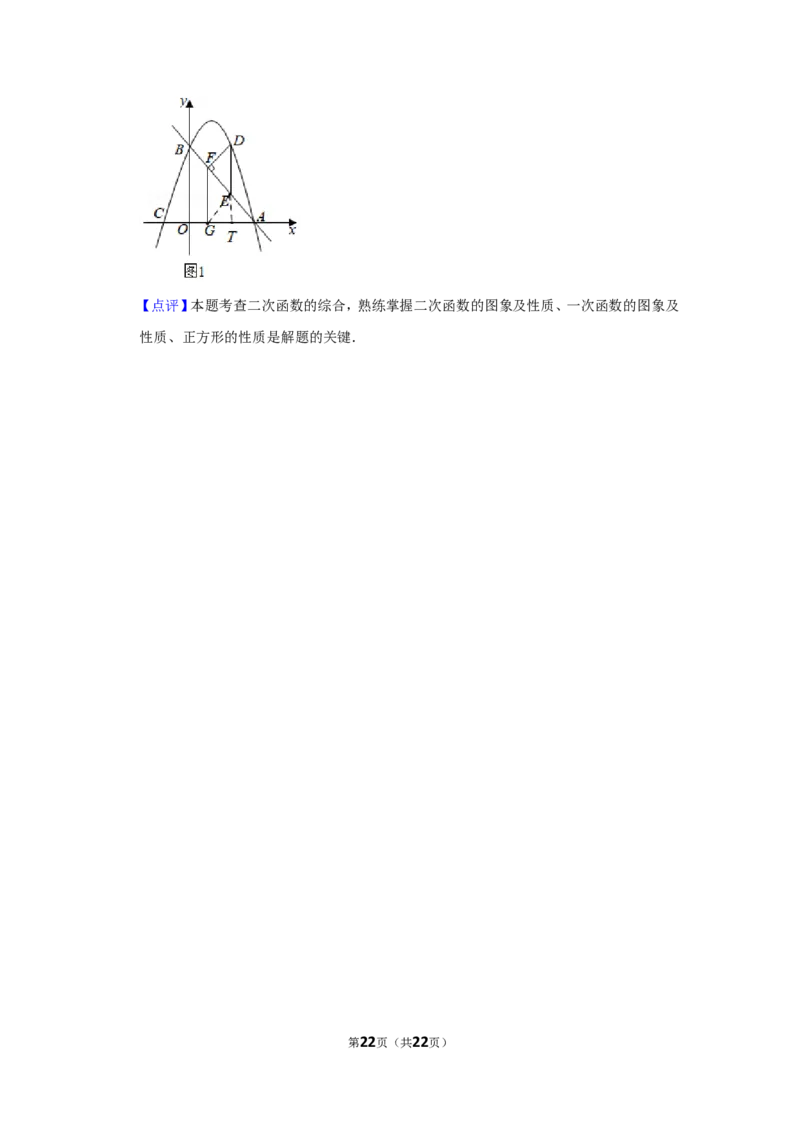
26.【分析】(1)令x=0,求点B(0,3),令y=0,求点A(3,0),将点A、点B代入抛物线y=
ax2+2x+c即可求解;
(2)设D(m,﹣m2+2m+3),由DE∥y轴交AB于点E,则E(m,﹣m+3),再由OA=OB,可
知∠OAB=45°,则有AG=FG=DE=AG,连接GE,延长DE交x轴于点T,可证四边形
FGED是平行四边形,△AEG为等腰直角三角形,可求AT=ET=GT=3﹣m,AG=FG=6
﹣2m,OG=2m﹣3,求出FG=﹣2m+6,DT=﹣3m+9,得到﹣m2+2m+3=﹣3m+9,即可求
D(2,3);
(3)先求出C(﹣1,0),直线CD的解析式为y=x+1,联立x+1=﹣x+3,求出M(1,2),分
四种情况讨论:①当MH⊥MK时,H点在AB上,K点在CD上,可确定H(3,0)或H(0,
第16页(共22页)3),当H(3,0)时,K(3,4),P(5,2);②当MH⊥HK时,此时MH⊥y轴,H(1+ ,2)或
H(1﹣ ,2),当H(1+ ,2)时,P(1,2+ );当H(1﹣ ,2)时,P(1,2﹣ );③当
H点与C点重合时,P(﹣3,2);④当H点与点D重合时,P(3,2).
【解答】解:(1)令x=0,则y=3,
∴B(0,3),
令y=0,则x=3,
∴A(3,0),
∵抛物线y=ax2+2x+c经过点A,B,
∴ ,
∴ ,
∴抛物线解析式为y=﹣x2+2x+3;
(2)设D(m,﹣m2+2m+3),
∵DE∥y轴交AB于点E,
∴E(m,﹣m+3),
∵OA=OB,
∴∠OAB=45°,
∴AG=FG,
∵DE=FG,
∴DE=AG,
连接GE,延长DE交x轴于点T,
∴四边形FGED是平行四边形,
∵DF⊥AB,
∴EG⊥AB,
∴△AEG为等腰直角三角形,
∴AT=ET=GT=3﹣m,
∴AG=FG=6﹣2m,
∴OG=3﹣(6﹣2m)=2m﹣3,
∴F点横坐标为2m﹣3,
∴FG=﹣2m+6,
∴DT=﹣2m+6+3﹣m=﹣3m+9,
第17页(共22页)∴﹣m2+2m+3=﹣3m+9,
解得m=2或m=3(舍),
∴D(2,3);
(3)令y=0,则﹣x2+2x+3=0,
解得x=3或x=﹣1,
∴C(﹣1,0),
设CD的解析式为y=kx+b,将C(﹣1,0)、D(2,3)代入,
∴ ,
∴ ,
∴y=x+1,
∴∠ACM=45°,
∴CM⊥AM,
联立x+1=﹣x+3,
解得x=1,
∴M(1,2),
∵以点M,H,K,P为顶点的四边形是正方形,
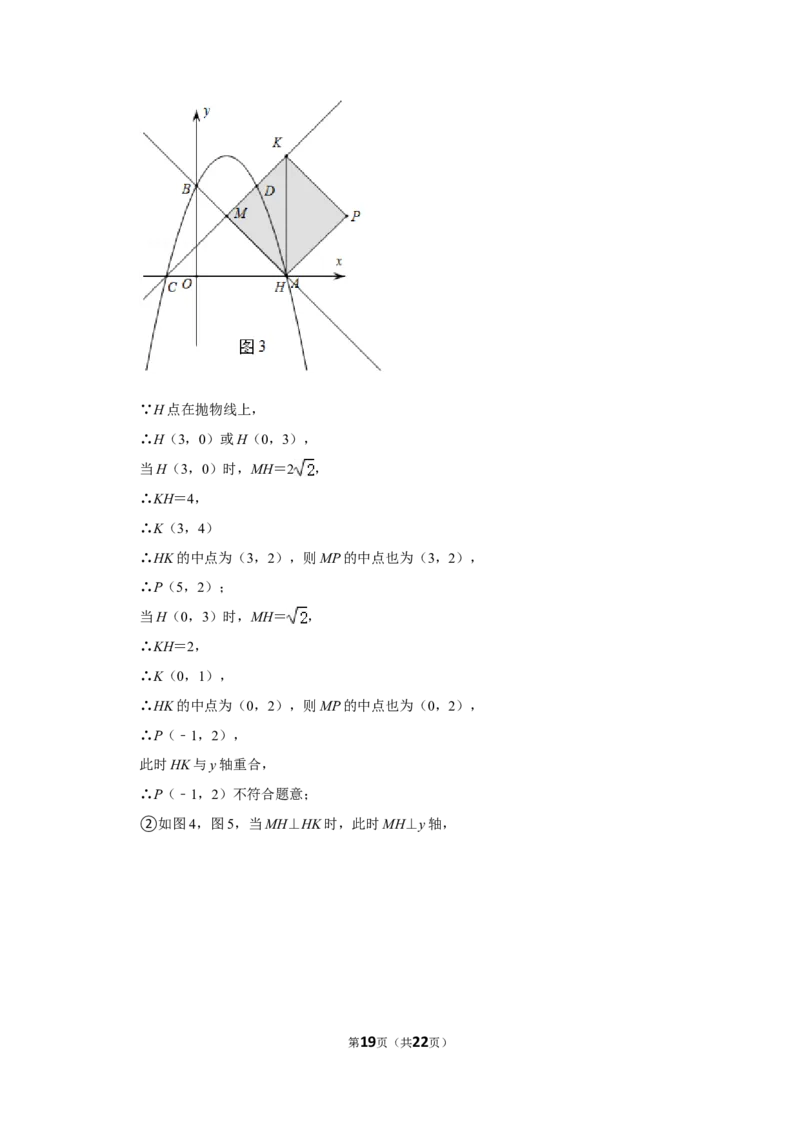
①如图2,图3,当MH⊥MK时,H点在AB上,K点在CD上,
第18页(共22页)∵H点在抛物线上,
∴H(3,0)或H(0,3),
当H(3,0)时,MH=2 ,
∴KH=4,
∴K(3,4)
∴HK的中点为(3,2),则MP的中点也为(3,2),
∴P(5,2);
当H(0,3)时,MH= ,
∴KH=2,
∴K(0,1),
∴HK的中点为(0,2),则MP的中点也为(0,2),
∴P(﹣1,2),
此时HK与y轴重合,
∴P(﹣1,2)不符合题意;
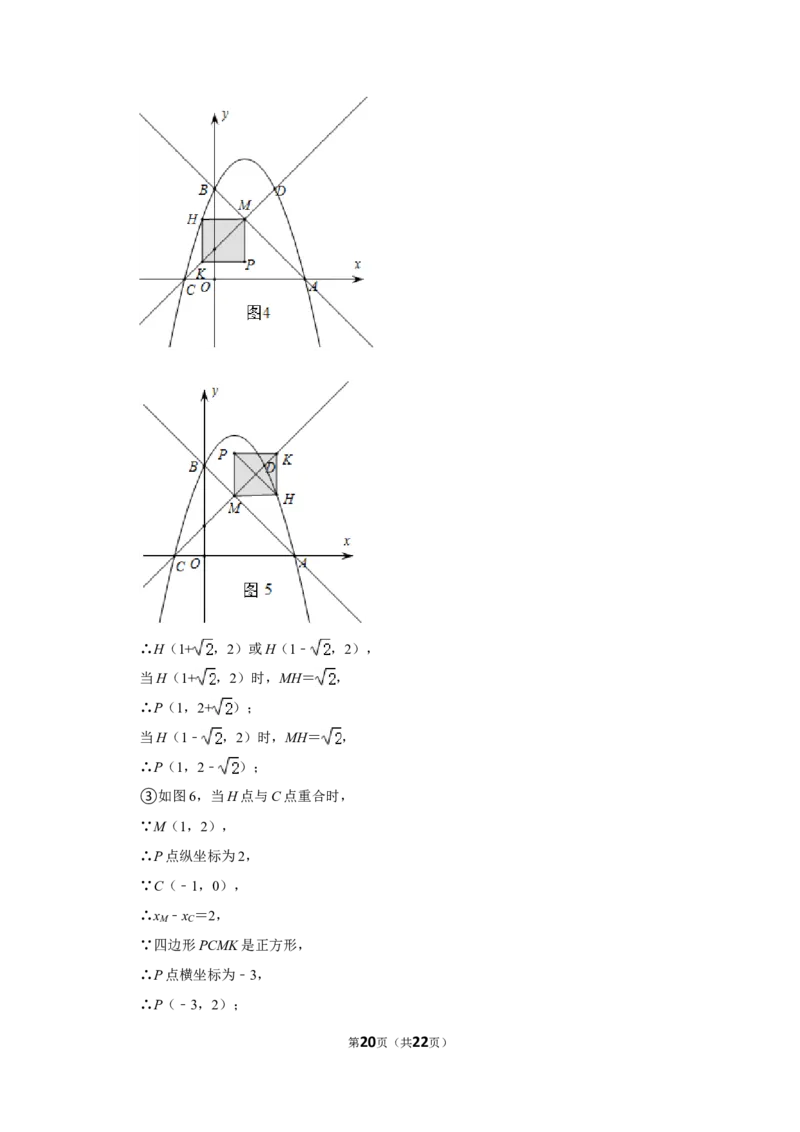
②如图4,图5,当MH⊥HK时,此时MH⊥y轴,
第19页(共22页)∴H(1+ ,2)或H(1﹣ ,2),
当H(1+ ,2)时,MH= ,
∴P(1,2+ );
当H(1﹣ ,2)时,MH= ,
∴P(1,2﹣ );
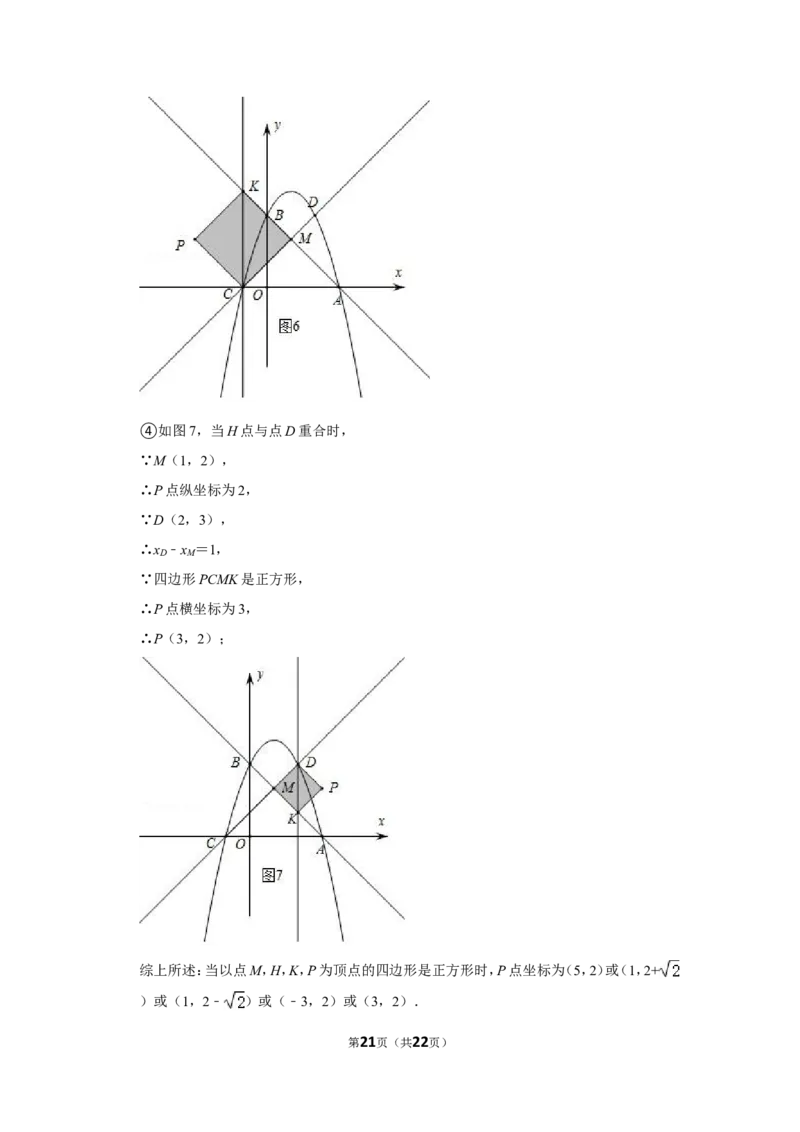
③如图6,当H点与C点重合时,
∵M(1,2),
∴P点纵坐标为2,
∵C(﹣1,0),
∴x ﹣x =2,
M C
∵四边形PCMK是正方形,
∴P点横坐标为﹣3,
∴P(﹣3,2);
第20页(共22页)④如图7,当H点与点D重合时,
∵M(1,2),
∴P点纵坐标为2,
∵D(2,3),
∴x ﹣x =1,
D M
∵四边形PCMK是正方形,
∴P点横坐标为3,
∴P(3,2);
综上所述:当以点M,H,K,P为顶点的四边形是正方形时,P点坐标为(5,2)或(1,2+
)或(1,2﹣ )或(﹣3,2)或(3,2).
第21页(共22页)【点评】本题考查二次函数的综合,熟练掌握二次函数的图象及性质、一次函数的图象及
性质、正方形的性质是解题的关键.
声明:试题解析著作权属菁优网所有,未经书面同意,不得复制发布
日期:2022/1/22 23:18:31;用户:我不叫王海宁;邮箱:orFmNtygTZdeoRRXtaD47YJRzPg0@weixin.jyeoo.com;学号:39962365
第22页(共22页)