2021年山西中考数学解析_中考真题_2.数学中考真题2015-2024年_2021中考数学真题86份_2021年山西中考数学

2021山西中考·数学·试卷解析 2021 年山西中考数学试卷解析 第一卷 选择题（共30分） 一、选择题（本大题共10个小题，每小题3分，共30分.在每个小题给出的四个选项中，只有一项符合题 目要求，请选出并在答题卡上将该项涂黑） 1.计算28的结果是（ ） A.6 B.6 C.10 D.10 【考点】有理数运算 【难度星级】★ 【答案】B 【解析】28826 2.为推动世界冰雪运动的发展，我国将于2022年举办北京冬奥会.在此之前进行了冬奥会会标的征集活动， 以下是部分参选作品，其文字上方的图案既是轴对称图形又是中心对称图形的是（ ） 【考点】中心对称图形 【难度星级】★ 【答案】B 【解析】A选项既不是中心对称图形，也不是轴对称图形；C、D选项不是中心对称图形 3.下列运算正确的是（ ） A.  m2n 3 m6n3 B.m5 m3 m2 C.m22 m2 4 D.  12m4 3m  3m4m3 【考点】整式运算 【难度星级】★ 【答案】A 【解析】B选项中m5和m3不是同类项，无法合并；C选项中m22 m2 4m4； D选项中 12m4 3m  3m4m3 12021山西中考·数学·试卷解析 4.《中国核能发展报告2021》蓝皮书显示，2020年我国核能发电量为3662.43亿千瓦时，相当于造林77.14 万公顷.已知1公顷=104平方米，则数据77.14万公顷用科学记数法表示为（ ） A.77.14104平方米 B.7.714107平方米 C.77.14108平方米 D.7.714109平方米 【考点】科学记数法 【难度星级】★ 【答案】D 【解析】科学记数法a10n中的a满足1a10，注意单位换算 6 5.已知反比例函数y ，则下列描述不正确的是（ ） x 3 A.图象位于第一、第三象限 B.图象必经过点（4， ） 2 C.图象不可能与坐标轴相交 D.y随x的增大而减小 【考点】反比例函数 【难度星级】★ 【答案】D 【解析】双曲线的每一支都是y随x的增大而减小，但整个图象并不是y随x的增大而减小 6.每天登录“学习强国”App进行学习，在获得积分的同时，还可获得“点点通”附加奖励，李老师最近一周每 日“点点通”收入明细如下表，则这组数据的中位数和众数分别是（ ） A.27点，21点 B.21点，27点 C.21点，21点 D.24点，21点 【考点】数据分析 【难度星级】★ 【答案】C 【解析】对数据进行排序如下：15，21，21，21，27，27，30，所以中位数是21，众数是21 7.如图，在O中，AB切O于点A，连接OB交O于点C，过点A作AD//OB交O 于点D，连接CD.若B50，则OCD为（ ） A.15 B.20 C.25 D.30 【考点】圆中倒角2021山西中考·数学·试卷解析 【难度星级】★ 【答案】B 1 【解析】连接 OA，则 OAB90 ，易得 AOB40 ，ADC  AOB20 ；  AD//OB， 2 OCDADC 20 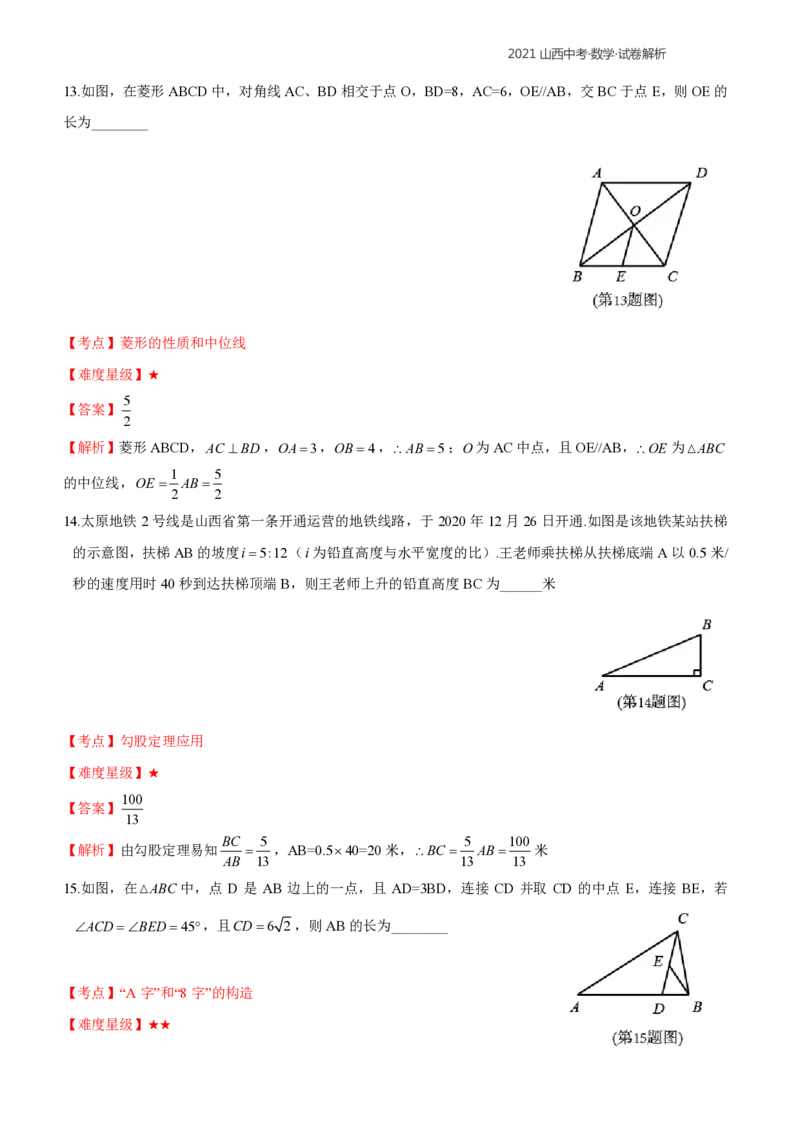8.在勾股定理的学习过程中，我们已经学会了运用以下图形，验证著名的勾股定理.这种根据图形直观推论或 验证数学规律和公式的方法，简称为“无字证明”.实际上它也可用于验证数与代数，图形与几何等领域中的 许多数学公式和规律，它体现的数学思想是（ ） A.统计思想 B.分类思想 C.数形结合思想 D.函数思想 【考点】数学思想 【难度星级】★ 【答案】C 9.如图，正六边形ABCDEF的边长为2，以A为圆心，AC的长为半径画弧，得E  C，连接AC、AE，则图中 阴影部分的面积为（ ） 3 2 3 A.2 B.4 C.  D.  3 3 【考点】圆中面积计算 【难度星级】★ 【答案】A 【解析】正六边形的每个内角为120，易得EAC 60；在等腰AEF 中，AE 3AF 2 3，则图中阴2021山西中考·数学·试卷解析 1  2 影部分的面积为S   2 3 2 6 10.抛物线的函数表达式为y3x22 1，若将x轴向上平移2个单位长度，将y轴向左平移3个单位长度， 则该抛物线在新的平面直角坐标系中的函数表达式为（ ） A. y3x12 3 B. y3x52 3 C. y3x52 1 D. y3x12 1 【考点】二次函数图象变换 【难度星级】★ 【答案】C 【解析】原题等价的一种说法是“在原坐标系中，抛物线向下平移2个单位长度，再向右平移3个单位长度”， 水平方向平移，对 x 左加右减，竖直方向平移，对解析式上加下减，所以新抛物线表达式为 y3x322 123x52 1. 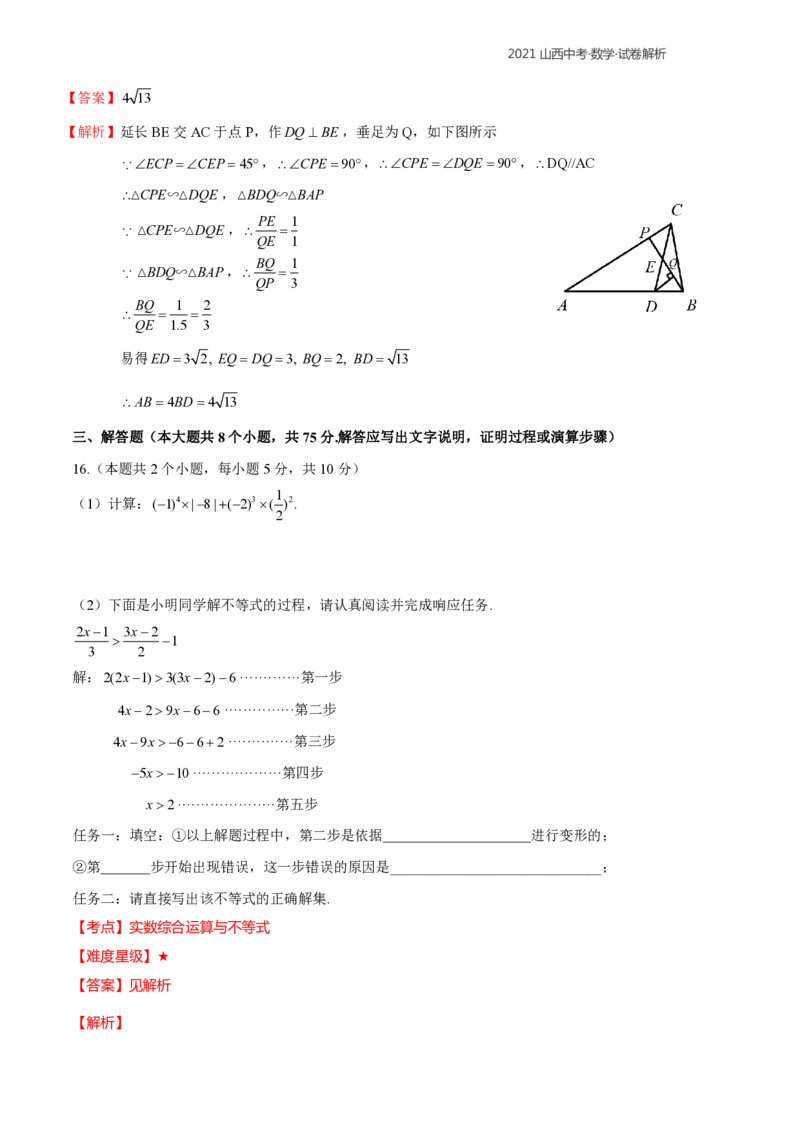第II卷 非选择题（共90分） 二、填空题（本大题共5个小题，每小题3分，共15分） 11.计算： 12 27 _______ 【考点】二次根式运算 【难度星级】★ 【答案】5 3 【解析】原式=2 33 35 3 12.如图是一片枫叶标本，其形状呈“掌状五裂型”，裂片具有少数突出的齿，将其放在平面直角坐标系中， 表示叶片“顶部”A，B两点的坐标分别为2,2，3,0，则叶杆“底部”点C的坐标为_________ 【考点】平面直角坐标系 【难度星级】★ 【答案】2,3 【解析】由题意易知，每个格代表一个单位长度，将点B向右平移5个单位长度，向下平移3个单位长度， 可得到点C，横坐标左减右加，纵坐标上加下减，则点C的坐标为2,32021山西中考·数学·试卷解析 13.如图，在菱形ABCD中，对角线AC、BD相交于点O，BD=8，AC=6，OE//AB，交BC于点E，则OE的 长为________ 【考点】菱形的性质和中位线 【难度星级】★ 5 【答案】 2 【解析】菱形ABCD，AC BD，OA3，OB4，AB5；O为AC中点，且OE//AB，OE 为ABC 1 5 的中位线，OE AB 2 2 14.太原地铁2号线是山西省第一条开通运营的地铁线路，于2020年12月26日开通.如图是该地铁某站扶梯 的示意图，扶梯AB的坡度i5:12（i为铅直高度与水平宽度的比）.王老师乘扶梯从扶梯底端A以0.5米/ 秒的速度用时40秒到达扶梯顶端B，则王老师上升的铅直高度BC为______米 【考点】勾股定理应用 【难度星级】★ 100 【答案】 13 BC 5 5 100 【解析】由勾股定理易知  ，AB=0.540=20米，BC  AB 米 AB 13 13 13 15.如图，在ABC中，点 D 是 AB 边上的一点，且 AD=3BD，连接 CD 并取 CD 的中点 E，连接 BE，若 ACDBED45，且CD6 2，则AB的长为________ 【考点】“A字”和“8字”的构造 【难度星级】★★2021山西中考·数学·试卷解析 【答案】4 13 【解析】延长BE交AC于点P，作DQBE，垂足为Q，如下图所示 ECPCEP45，CPE90，CPEDQE90，DQ//AC CPE∽DQE，BDQ∽BAP PE 1  CPE∽DQE，  QE 1 BQ 1  BDQ∽BAP，  QP 3 BQ 1 2    QE 1.5 3 易得ED3 2, EQDQ3, BQ2, BD 13 AB4BD4 13 三、解答题（本大题共8个小题，共75分.解答应写出文字说明，证明过程或演算步骤） 16.（本题共2个小题，每小题5分，共10分） 1 （1）计算：(1)4|8|(2)3( )2. 2 （2）下面是小明同学解不等式的过程，请认真阅读并完成响应任务. 2x1 3x2  1 3 2 解：2(2x1)3(3x2)6·············第一步 4x29x66···············第二步 4x9x662··············第三步 5x10···················第四步 x2·····················第五步 任务一：填空：①以上解题过程中，第二步是依据 进行变形的； ②第 步开始出现错误，这一步错误的原因是______________________________； 任务二：请直接写出该不等式的正确解集. 【考点】实数综合运算与不等式 【难度星级】★ 【答案】见解析 【解析】2021山西中考·数学·试卷解析 1 （1）解：原式=18+(8) 4 =8+(2) =6 （2）任务一：填空：①以上解题过程中，第二步是依据乘法分配律（或分配律）（运算律）进行变形的；··· （7分 ） ②第五步开始出现错误，这一步错误的原因是不等式两边都除以-5，不等号的方向没有改变（或不符合不 等式的性质3）；·········································································（9分 ） 任务二：请直接写出该不等式的正确解集. 解：x2············································································（10分） 17.（本题6分）2021年7月1日是建党100周年纪念日，在本月日历表上可以用一个方框圈出4个数(如图 所示)，若圈出的四个数中，最小数与最大数的乘积为65，求这个最小数(请用方程知识解答). 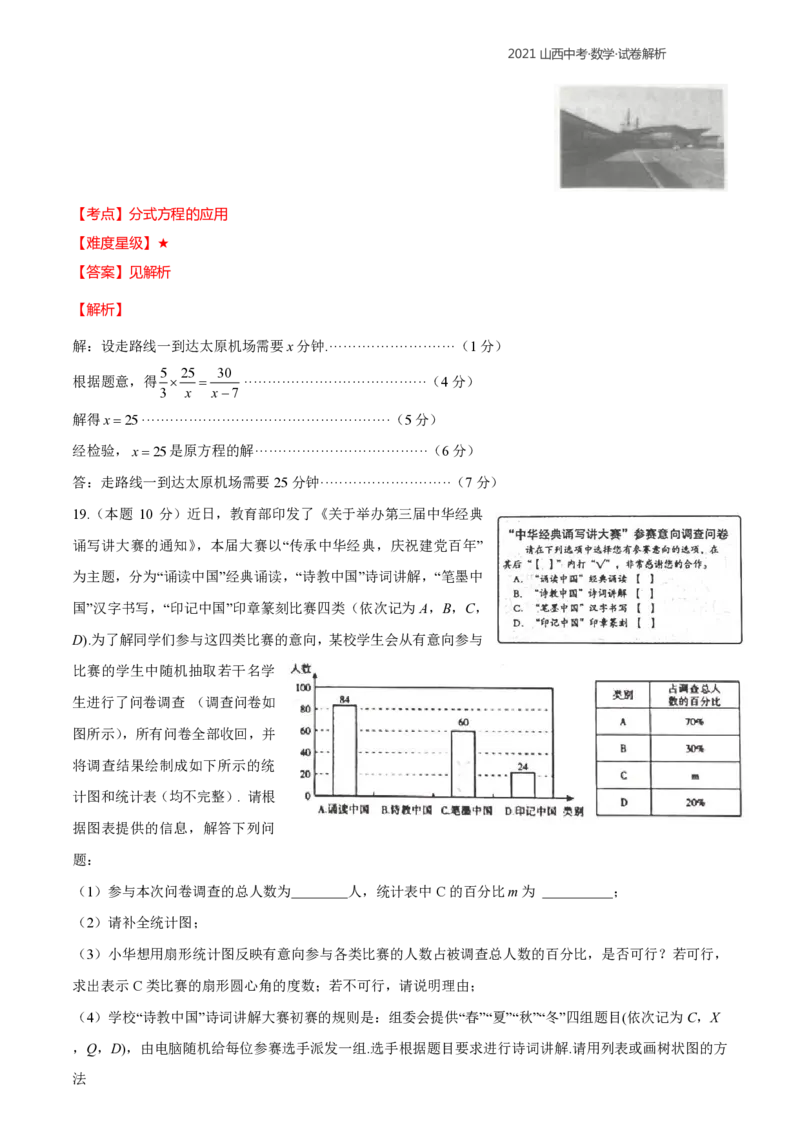【考点】一元二次方程的应用 【难度星级】★ 【答案】见解析 【解析】 解：设这个最小数为x·········································（1分） 根据题意，得x(x8)65······································（3分） 解得x 5,x 13 （不符合题意，舍去）························（5分） 1 2 答:这个最小数为5.············································（6分） 18.（本题 7 分）太原武宿国际机场简称"太原机场"，是山西省开通的首条定期国际客运航线.游客从太原某 景区乘车到太原机场，有两条路线可供选择，路线一：走迎宾路经太榆路全程是25千米，但交通比较拥堵； 5 路线二：走太原环城高速全程是30千米，平均速度是路线一的 倍，因此到达太原机场的时间比走路线一 3 少用7分钟，求走路线一到达太原机场需要多长时间.2021山西中考·数学·试卷解析 【考点】分式方程的应用 【难度星级】★ 【答案】见解析 【解析】 解：设走路线一到达太原机场需要x分钟.···························（1分） 5 25 30 根据题意，得   ·······································（4分） 3 x x7 解得x25·····················································（5分） 经检验，x25是原方程的解·····································（6分） 答：走路线一到达太原机场需要25分钟····························（7分） 19.（本题 10 分）近日，教育部印发了《关于举办第三届中华经典 诵写讲大赛的通知》，本届大赛以“传承中华经典，庆祝建党百年” 为主题，分为“诵读中国”经典诵读，“诗教中国”诗词讲解，“笔墨中 国”汉字书写，“印记中国”印章篆刻比赛四类（依次记为A，B，C， D).为了解同学们参与这四类比赛的意向，某校学生会从有意向参与 比赛的学生中随机抽取若干名学 生进行了问卷调查 （调查问卷如 图所示），所有问卷全部收回，并 将调查结果绘制成如下所示的统 计图和统计表（均不完整）. 请根 据图表提供的信息，解答下列问 题： （1）参与本次问卷调查的总人数为 人，统计表中C的百分比m为 ； （2）请补全统计图； （3）小华想用扇形统计图反映有意向参与各类比赛的人数占被调查总人数的百分比，是否可行？若可行， 求出表示C类比赛的扇形圆心角的度数；若不可行，请说明理由； （4）学校“诗教中国”诗词讲解大赛初赛的规则是：组委会提供“春”“夏”“秋”“冬”四组题目(依次记为C，X ，Q，D)，由电脑随机给每位参赛选手派发一组.选手根据题目要求进行诗词讲解.请用列表或画树状图的方 法2021山西中考·数学·试卷解析 求甲，乙两名选手抽到的题目在同一组的概率. 【考点】统计与概率 【难度星级】★ 【答案】见解析 【解析】（1）120； 50% ；……………………(2分) （2）请补全统计图； …………………………………(3分) （3）小华想用扇形统计图反映有意向参与各类比赛的人数占被调查总人数的百分比，是否可行？若可行 ，求出表示C类比赛的扇形圆心角的度数；若不可行，请说明理由； 解：不可行.…………………………………………(4分) 理由：答案不唯一.如：由统计表可知 70%+30%+ 50%+ 20%>1.即有意向参与比赛的人数占调查总人数的 百分比之和大于1；或84+60>120，即有意向参与A类 与C类的人数之和大于总人数120等.…………(5 分) （4）学校“诗教中国”诗词讲解大赛初赛的规则是：组委会提供“春”“夏”“秋”“冬”四组题目(依次记为C ，X，Q，D)，由电脑随机给每位参赛选手派发一组.选手根据题目要求进行诗词讲解.请用列表或画树状图 的方法求甲，乙两名选手抽到的题目在同一组的 概率. 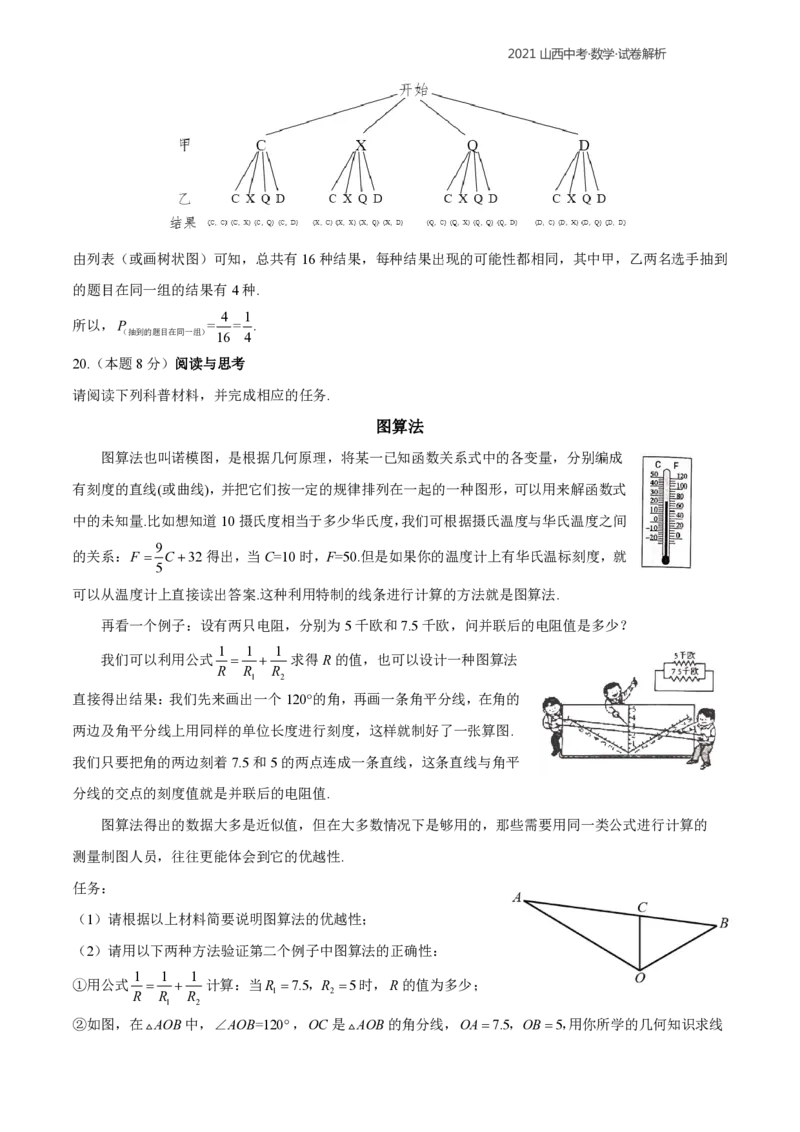解：列表如下： 乙 C X Q D 甲 C （C，C） （C，X） （C，Q） （C，D） X （X，C） （X，X） （X，Q） （X，D） Q （Q，C） （Q，X） （Q，Q） （Q，D） D （D，C） （D，X） （D，Q） （D，D） 或画树状图如下：2021山西中考·数学·试卷解析 由列表（或画树状图）可知，总共有16种结果，每种结果出现的可能性都相同，其中甲，乙两名选手抽到 的题目在同一组的结果有4种. 4 1 所以，P = = . （抽到的题目在同一组） 16 4 20.（本题8分）阅读与思考 请阅读下列科普材料，并完成相应的任务. 图算法 图算法也叫诺模图，是根据几何原理，将某一已知函数关系式中的各变量，分别编成 有刻度的直线(或曲线)，并把它们按一定的规律排列在一起的一种图形，可以用来解函数式 中的未知量.比如想知道10摄氏度相当于多少华氏度，我们可根据摄氏温度与华氏温度之间 9 的关系：F  C32得出，当C=10时，F=50.但是如果你的温度计上有华氏温标刻度，就 5 可以从温度计上直接读出答案.这种利用特制的线条进行计算的方法就是图算法. 再看一个例子：设有两只电阻，分别为5千欧和7.5千欧，问并联后的电阻值是多少？ 1 1 1 我们可以利用公式   求得R的值，也可以设计一种图算法 R R R 1 2 直接得出结果：我们先来画出一个120°的角，再画一条角平分线，在角的 两边及角平分线上用同样的单位长度进行刻度，这样就制好了一张算图. 我们只要把角的两边刻着7.5和5的两点连成一条直线，这条直线与角平 分线的交点的刻度值就是并联后的电阻值. 图算法得出的数据大多是近似值，但在大多数情况下是够用的，那些需要用同一类公式进行计算的 测量制图人员，往往更能体会到它的优越性 . 任务： （1）请根据以上材料简要说明图算法的优越性； （2）请用以下两种方法验证第二个例子中图算法的正确性： 1 1 1 ①用公式   计算：当R 7.5，R 5时，R的值为多少； R R R 1 2 1 2 ②如图，在AOB中，∠AOB=120，OC是AOB的角分线，OA7.5，OB5，用你所学的几何知识求线2021山西中考·数学·试卷解析 段OC的长. 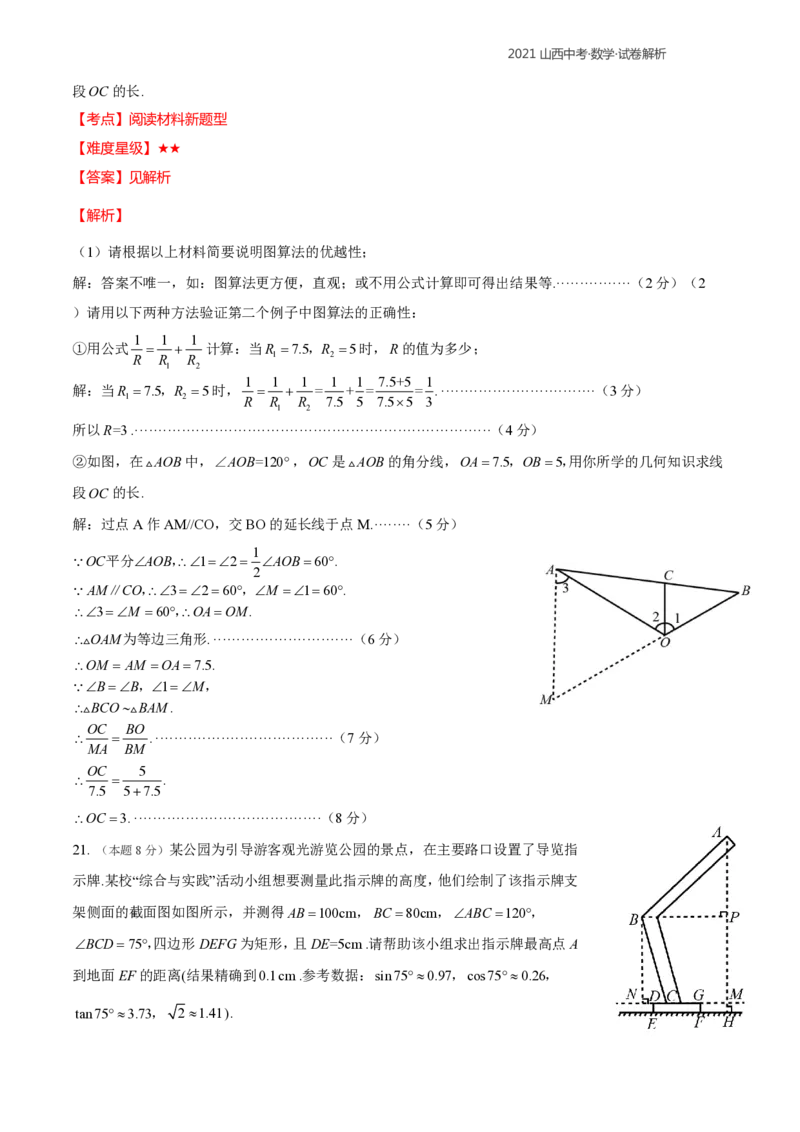【考点】阅读材料新题型 【难度星级】★★ 【答案】见解析 【解析】 （1）请根据以上材料简要说明图算法的优越性； 解：答案不唯一，如：图算法更方便，直观；或不用公式计算即可得出结果等.················（2分） （2 ）请用以下两种方法验证第二个例子中图算法的正确性： 1 1 1 ①用公式   计算：当R 7.5，R 5时，R的值为多少； R R R 1 2 1 2 1 1 1 1 1 7.5+5 1 解：当R 7.5，R 5时，   = + = = .·································（3分） 1 2 R R R 7.5 5 7.55 3 1 2 所以R=3.············································································（4分） ②如图，在AOB中，∠AOB=120，OC是AOB的角分线，OA7.5，OB5，用你所学的几何知识求线 段OC的长. 解：过点A作AM//CO，交BO的延长线于点M.········（5分） 1 OC平分AOB，12 AOB60. 2 AM∥CO，3260，M 160. 3M 60，OAOM. OAM为等边三角形.······························（6分） OM  AM OA7.5. BB，1M， BCOBAM. OC BO   .······································（7分） MA BM OC 5   . 7.5 57.5 OC 3.········································（8分） 21. （本题8分）某公园为引导游客观光游览公园的景点，在主要路口设置了导览指 示牌.某校“综合与实践”活动小组想要测量此指示牌的高度，他们绘制了该指示牌支 架侧面的截面图如图所示，并测得AB100cm， BC80cm， ABC 120， BCD75，四边形DEFG为矩形，且DE=5cm .请帮助该小组求出指示牌最高点A 到地面EF的距离(结果精确到0.1cm .参考数据：sin750.97， cos750.26， tan753.73， 2 1.41).2021山西中考·数学·试卷解析 【考点】锐角三角函数的应用 【难度星级】★★ 【答案】153.1cm 【解析】 解：过点A作AH EF 于点H ，交直线DG于点M.过点B作BN DG于点N，BP AH 于点P.则四边形 BNMP和四边形DEHM 均为矩形.······································（2分） PM BN，MH DE5cm, BP∥DG. CBPBCD75.···············································（3分） ABPABCCBP1207545.······························（4分） AP 在RtABP中，APB90，sin45 . AB 2 AP ABsin45100 50 2.·····································（5分） 2 BN 在RtBCN中，BNC 90，sin75 . BC BN BCsin75800.9777.6.·······································（6分） PM BN 77.6. AH  APPM MH 50 277.65501.4177.65153.1.············（7分） 答：指示牌最高点A到地面EF的距离为153.1cm. 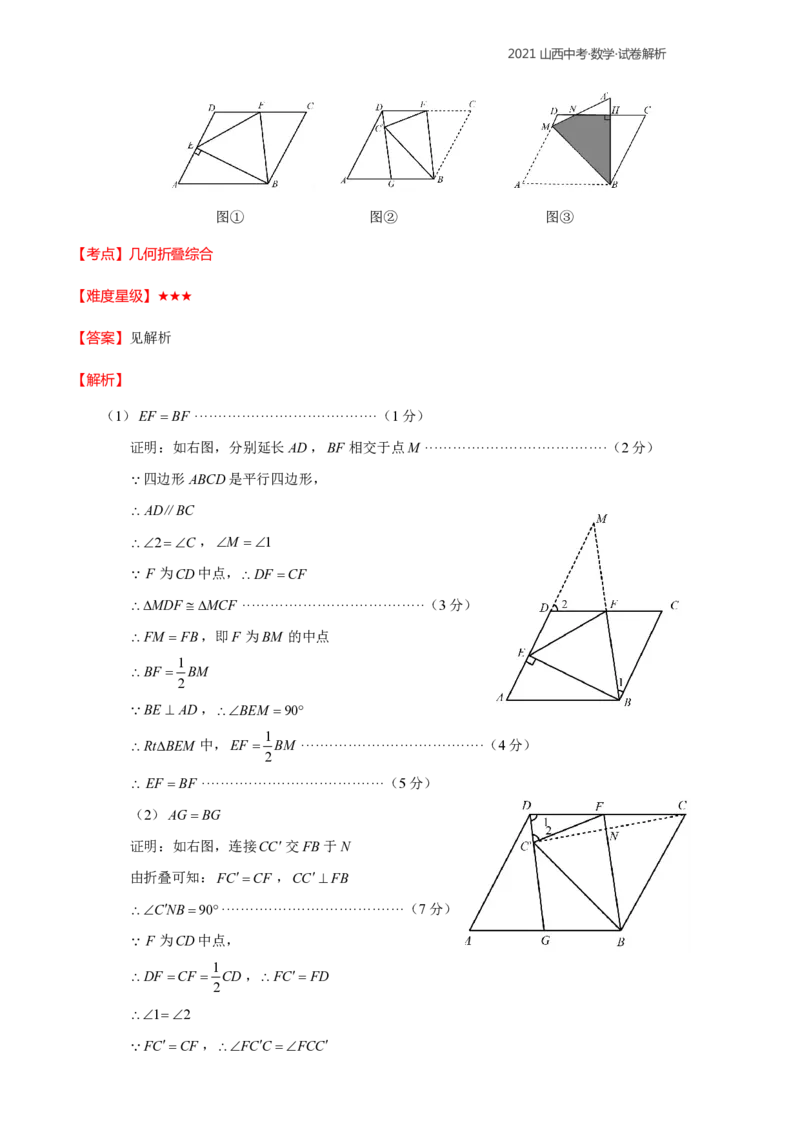22.（本题13分）综合与实践 问题情景：数学活动课上，老师出示了一个问题：如图①，在ABCD中，BE  AD，垂足为E，F 为 CD的中点，连接EF，BF，试猜想EF与BF的数量关系，并加以证明； 独立思考：（1）请解答老师提出的问题； 实践探究：（2）希望小组受此问题的启发，将ABCD沿着BF（F 为CD的中点）所在直线折叠，如 图②，点C的对应点为C，连接DC并延长交AB于点G ，请判断AG与BG 的数量关系，并加以证 明； 问题解决：（3）智慧小组突发奇想，将ABCD沿过点B的直线折叠，如图③，点A的对应点A，使 ABCD于点M ，连接AM ，交CD于点N.该小组提出一个向题：若此ABCD的面积为20，边长 AB5，BC 2 5，求图中阴影部分（四边形BHNM)的面积.请你思考此问题，直接写出结果.2021山西中考·数学·试卷解析 图① 图② 图③ 【考点】几何折叠综合 【难度星级】★★★ 【答案】见解析 【解析】 （1）EF BF ·······································（1分） 证明：如右图，分别延长AD，BF相交于点M ·······································（2分） 四边形ABCD是平行四边形， AD∥BC 2C ，M 1  F 为CD中点，DF CF MDF MCF ·······································（3分） FM FB，即F 为BM 的中点 1 BF  BM 2 BE AD，BEM 90 1 RtBEM 中，EF  BM ·······································（4分） 2 EF BF ·······································（5分） （2）AGBG 证明：如右图，连接CC交FB于N 由折叠可知：FCCF ，CCFB CNB90·······································（7分）  F 为CD中点， 1 DF CF  CD，FCFD 2 12 FCCF ，FCCFCC2021山西中考·数学·试卷解析 在DCC中，1DCCDCC180 12FCCFCC180 222FCC 180 2FCC 90，DCC 90 DCC CNB=90，DG∥FB·······································（8分） 四边形ABCD是平行四边形，DC∥AB，DC=AB 四边形DGBF是平行四边形，BGFD 1 BG AB 2 AGBG ·······································（10分） （3）如右图，过点M作MG⊥AB于点G A' ∵S BHCD，即20BH5，∴BH 4 C ABCD D H N M 在RtBHC中：CH  BC2 BH2 2 由折叠知：AB AB5，AAC 易知：AHN CHB HN AH HN 1 B   ，即  A G BH CH 4 2 ∴HN 2 1 ∴S  121 AHN 2 易知：AGM CHB MG BH ∴  2 AG CH 设AGa，则MG2a 1 由折叠知：ABM ABM  ABA45 2 在RtBGM 中：BGMG2a AB AGBG3a 5 3a5，a 3 10 ∴MG2a 3 1 1 10 25 ∴S S  ABMG 5  ABM ABM 2 2 3 3 25 22 S S S  1 ·······································（13分） BMNH ABM AHN 3 32021山西中考·数学·试卷解析 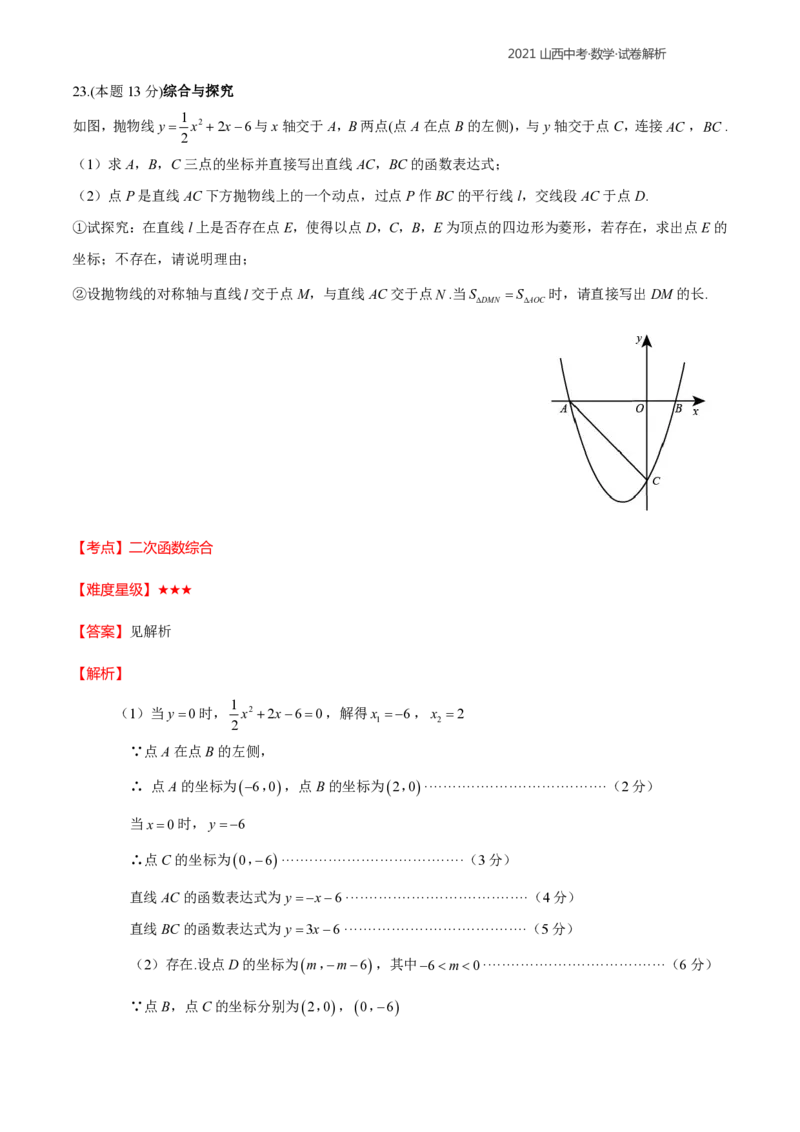23.(本题13分)综合与探究 1 如图，抛物线y x2 2x6与x轴交于A，B两点(点A在点B的左侧)，与y轴交于点C，连接AC，BC. 2 （1）求A，B，C三点的坐标并直接写出直线AC，BC的函数表达式； （2）点P是直线AC下方抛物线上的一个动点，过点P作BC的平行线l，交线段AC于点D. ①试探究：在直线l上是否存在点E，使得以点D，C，B，E为顶点的四边形为菱形，若存在，求出点E的 坐标；不存在，请说明理由； ②设抛物线的对称轴与直线l交于点M，与直线AC交于点N.当S S 时，请直接写出DM的长. 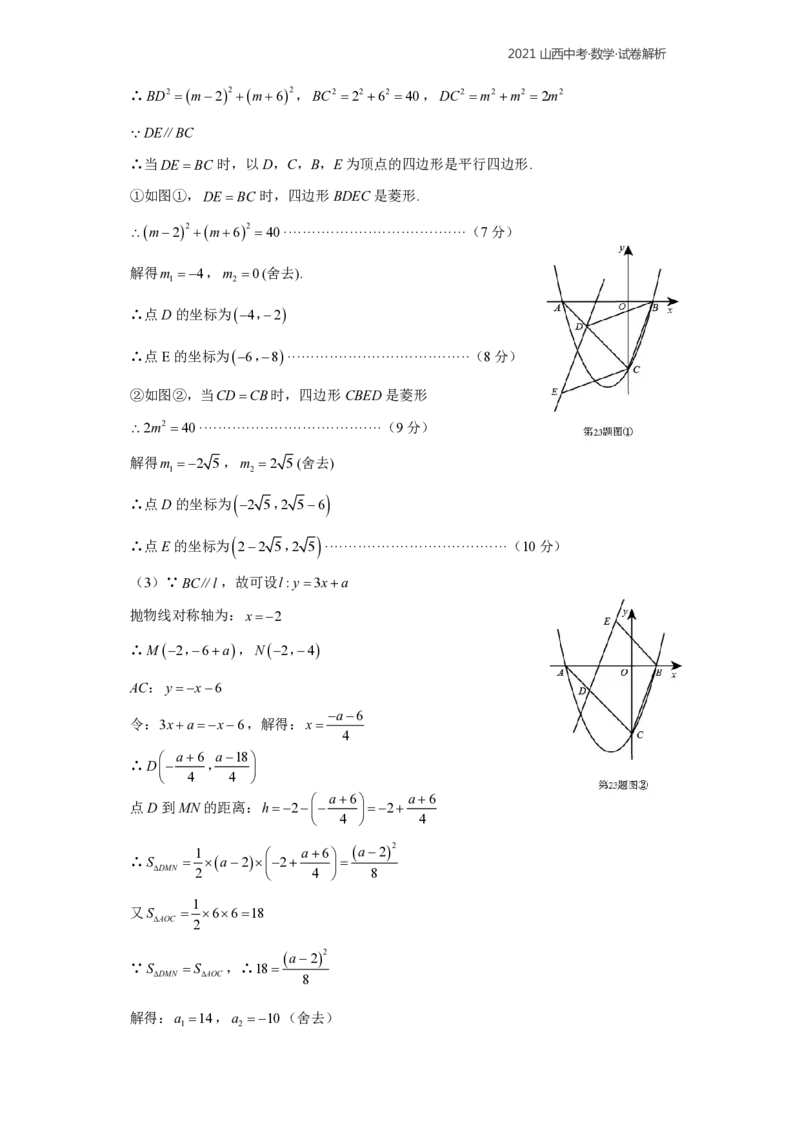DMN AOC 【考点】二次函数综合 【难度星级】★★★ 【答案】见解析 【解析】 1 （1）当y0时， x2 2x60，解得x 6，x 2 2 1 2 ∵点A在点B的左侧， ∴ 点A的坐标为6，0，点B的坐标为2，0·······································（2分） 当x0时，y6 ∴点C的坐标为0，6·······································（3分） 直线AC的函数表达式为yx6·······································（4分） 直线BC的函数表达式为y3x6·······································（5分） （2）存在.设点D的坐标为m，m6，其中6m0·······································（6分） ∵点B，点C的坐标分别为2，0，0，62021山西中考·数学·试卷解析 ∴BD2 m22 m62，BC2 22 62 40，DC2 m2 m2 2m2 DE∥BC ∴当DEBC时，以D，C，B，E为顶点的四边形是平行四边形. ①如图①，DEBC时，四边形BDEC是菱形. m22 m62 40·······································（7分） 解得m 4，m 0(舍去). 1 2 ∴点D的坐标为4，2 ∴点E的坐标为6，8·······································（8分） ②如图②，当CDCB时，四边形CBED是菱形 2m2 40·······································（9分） 解得m 2 5，m 2 5(舍去) 1 2   ∴点D的坐标为 2 5，2 56   ∴点E的坐标为 22 5，2 5 ·······································（10分） （3）∵BC∥l，故可设l:y3xa 抛物线对称轴为：x2 ∴M2，6a，N2，4 AC：yx6 a6 令：3xax6，解得：x 4  a6 a18 ∴D ，   4 4   a6 a6 点D到MN的距离：h2 2  4  4 1  a6 a22 ∴S  a22  DMN 2  4  8 1 又S  6618 AOC 2 a22 ∵S S ，∴18 DMN AOC 8 解得：a 14，a 10（舍去） 1 22021山西中考·数学·试卷解析 ∴M2，8，D5，1 DM  252 182 3 10·······································（13分）