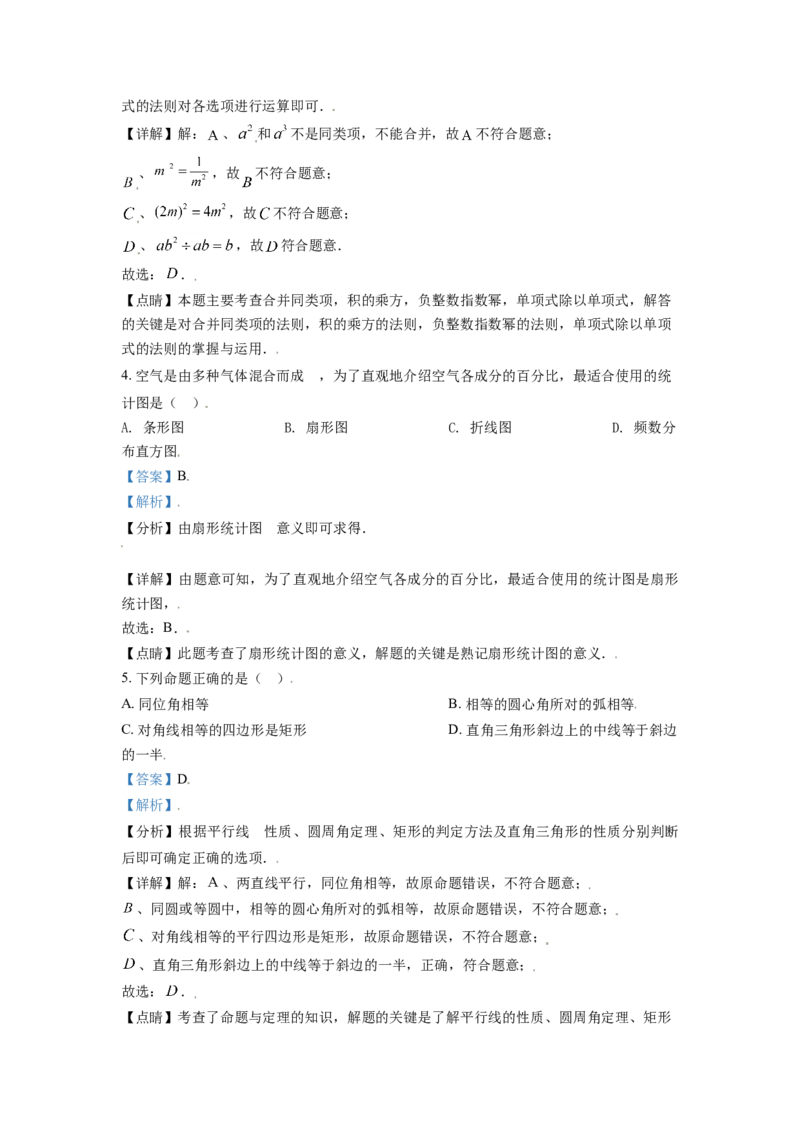文档内容
辽宁省盘锦市 2021 年中考数学真题试卷
一、选择题(本题有10小题,每小题3分,共30分)
1. 3的相反数是( )
A. 3 B. -3 C. D.
【答案】B
【解析】
【分析】根据相反数的定义进行解答即可.
【详解】解:3的相反数是-3,
故选B.
【点睛】本题考查的是相反数的定义,即只有符号不同的两个数叫做互为相反数.
2. 图中三视图对应的正三棱柱是( )
A. B. C. D.
【答案】A
【解析】
【分析】由俯视图得到正三棱柱两个底面在竖直方向,由主视图得到有一条侧棱在正前方
从而求解
【详解】解:由俯视图得到正三棱柱两个底面在竖直方向,由主视图得到有一条侧棱在正
前方,于是可判定A选项正确.
故选A.
【点睛】本题考查由三视图判断几何体,掌握几何体 的三视图是本题的解题关键.
3. 下列运算正确的是( )
A. B. C. D.
【答案】D
【解析】
【分析】利用合并同项类,负整数指数幂的运算法则,积的乘方的法则,单项式除以单项式的法则对各选项进行运算即可.
【详解】解: 、 和 不是同类项,不能合并,故 不符合题意;
、 ,故 不符合题意;
、 ,故 不符合题意;
、 ,故 符合题意.
故选: .
【点睛】本题主要考查合并同类项,积的乘方,负整数指数幂,单项式除以单项式,解答
的关键是对合并同类项的法则,积的乘方的法则,负整数指数幂的法则,单项式除以单项
式的法则的掌握与运用.
4. 空气是由多种气体混合而成 的,为了直观地介绍空气各成分的百分比,最适合使用的统
计图是( )
A. 条形图 B. 扇形图 C. 折线图 D. 频数分
布直方图
【答案】B
【解析】
【分析】由扇形统计图 的意义即可求得.
【详解】由题意可知,为了直观地介绍空气各成分的百分比,最适合使用的统计图是扇形
统计图,
故选:B.
【点睛】此题考查了扇形统计图的意义,解题的关键是熟记扇形统计图的意义.
5. 下列命题正确的是( )
A. 同位角相等 B. 相等的圆心角所对的弧相等
C. 对角线相等的四边形是矩形 D. 直角三角形斜边上的中线等于斜边
的一半
【答案】D
【解析】
【分析】根据平行线 的性质、圆周角定理、矩形的判定方法及直角三角形的性质分别判断
后即可确定正确的选项.
【详解】解: 、两直线平行,同位角相等,故原命题错误,不符合题意;
、同圆或等圆中,相等的圆心角所对的弧相等,故原命题错误,不符合题意;
、对角线相等的平行四边形是矩形,故原命题错误,不符合题意;
、直角三角形斜边上的中线等于斜边的一半,正确,符合题意;
故选: .
【点睛】考查了命题与定理的知识,解题的关键是了解平行线的性质、圆周角定理、矩形的判定方法及直角三角形的性质等知识,难度不大.
6. 下列调查中,适宜采用抽样调查的是( )
A. 调查某班学生的身高情况
B. 调查亚运会100m游泳决赛运动员兴奋剂的使用情况
C. 调查某批汽车的抗撞击能力
D. 调查一架“歼10”隐形战斗机各零部件的质量
【答案】C
【解析】
【分析】根据普查得到的调查结果比较准确,但所费人力、物力和时间较多,而抽样调查
得到的调查结果比较近似解答.
【详解】解:A.调查某班学生的身高情况,适合全面调查,故本选项不符合题意;
B.调查亚运会100m游泳决赛运动员兴奋剂的使用情况,适合全面调查,故本选项不符合
题意;
C.调查某批汽车的抗撞击能力,适合抽样调查,故本选项符合题意;
D.调查一架“歼10”隐形战斗机各零部件的质量,适合全面调查,故本选项不符合题意.
故选:C.
【点睛】本题考查的是抽样调查和全面调查的区别,选择普查还是抽样调查要根据所要考
查的对象的特征灵活选用,一般来说,对于具有破坏性的调查、无法进行普查、普查的意
义或价值不大,应选择抽样调查,对于精确度要求高的调查,事关重大的调查往往选用普
查.
7. 如图,已知直线AB和AB上的一点C,过点C作直线AB的垂线,步骤如下:
第一步:以点C为圆心,以任意长为半径作弧,交直线AB于点D和点E;
第二步:分别以点D和点E为圆心,以 为半径作弧,两弧交于点F;
第三步:作直线CF,直线CF即为所求.
下列关于 的说法正确的是( )
A. ≥ B. ≤ C. D.
【答案】C
【解析】
【分析】根据过直线外一点作已知直线的垂线的步骤,结合三角形三边关系判断即可.【详解】解:由作图可知,分别以点 和点 为圆心,以 为半径作弧,两弧交于点 ,
此时 ,
故选: .
【点睛】本题考查作图 基本作图,解题的关键是理解题意,灵活运用所学知识解决问题.
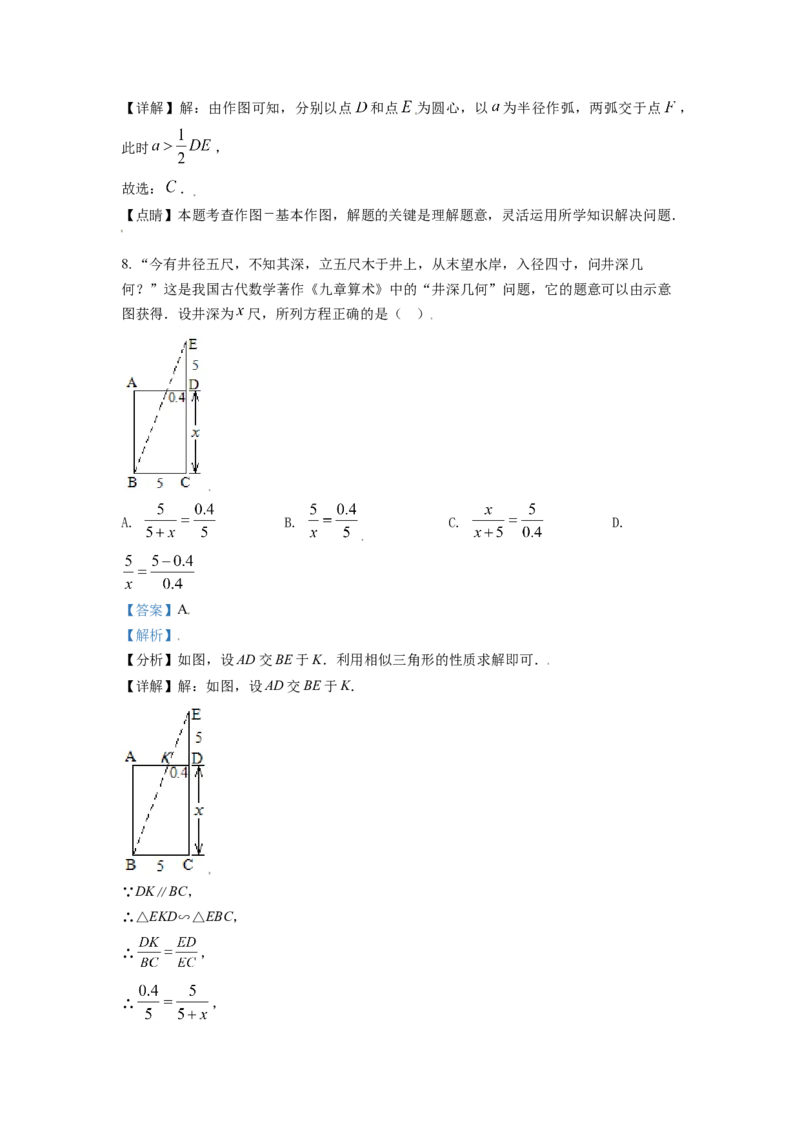
8. “今有井径五尺,不知其深,立五尺木于井上,从末望水岸,入径四寸,问井深几
何?”这是我国古代数学著作《九章算术》中的“井深几何”问题,它的题意可以由示意
图获得.设井深为 尺,所列方程正确的是( )
A. B. C. D.
【答案】A
【解析】
【分析】如图,设AD交BE于K.利用相似三角形的性质求解即可.
【详解】解:如图,设AD交BE于K.
∵DK∥BC,
∴△EKD∽△EBC,
∴ ,
∴ ,故选:A.
【点睛】本题考查相似三角形的应用,解题的关键是正确寻找相似三角形解决问题.
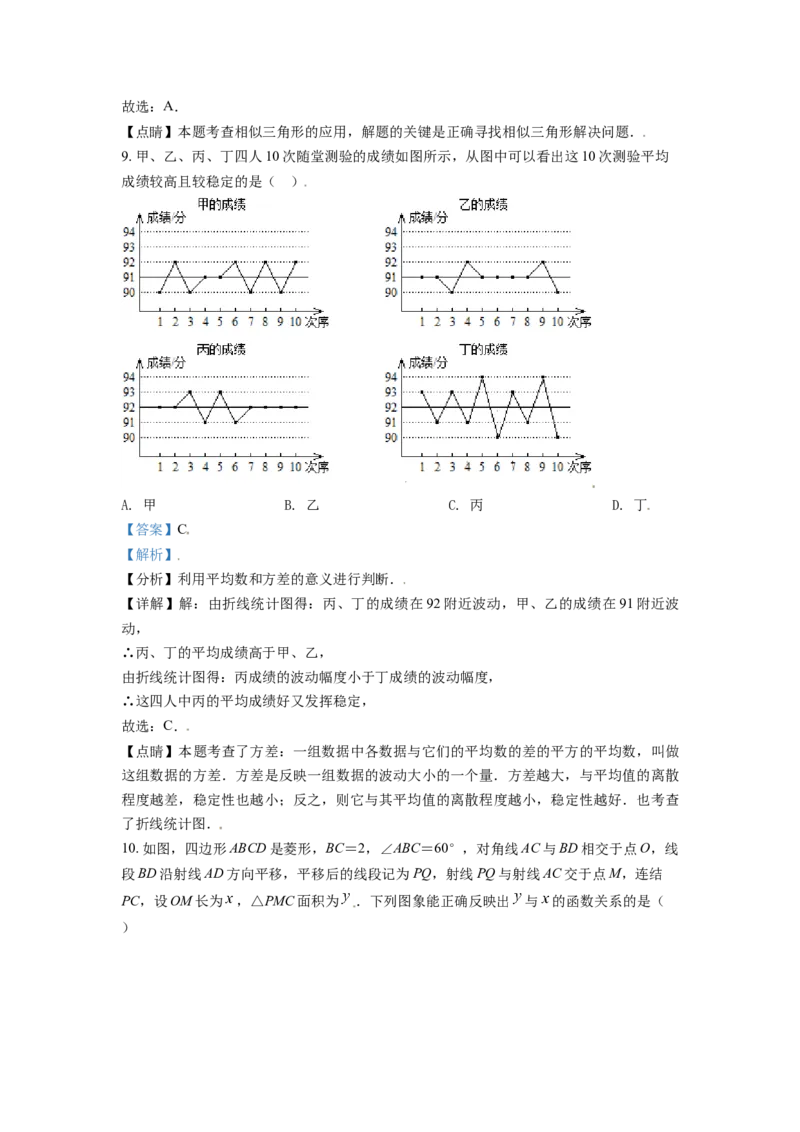
9. 甲、乙、丙、丁四人10次随堂测验的成绩如图所示,从图中可以看出这10次测验平均
成绩较高且较稳定的是( )
A. 甲 B. 乙 C. 丙 D. 丁
【答案】C
【解析】
【分析】利用平均数和方差的意义进行判断.
【详解】解:由折线统计图得:丙、丁的成绩在92附近波动,甲、乙的成绩在91附近波
动,
∴丙、丁的平均成绩高于甲、乙,
由折线统计图得:丙成绩的波动幅度小于丁成绩的波动幅度,
∴这四人中丙的平均成绩好又发挥稳定,
故选:C.
【点睛】本题考查了方差:一组数据中各数据与它们的平均数的差的平方的平均数,叫做
这组数据的方差.方差是反映一组数据的波动大小的一个量.方差越大,与平均值的离散
程度越差,稳定性也越小;反之,则它与其平均值的离散程度越小,稳定性越好.也考查
了折线统计图.
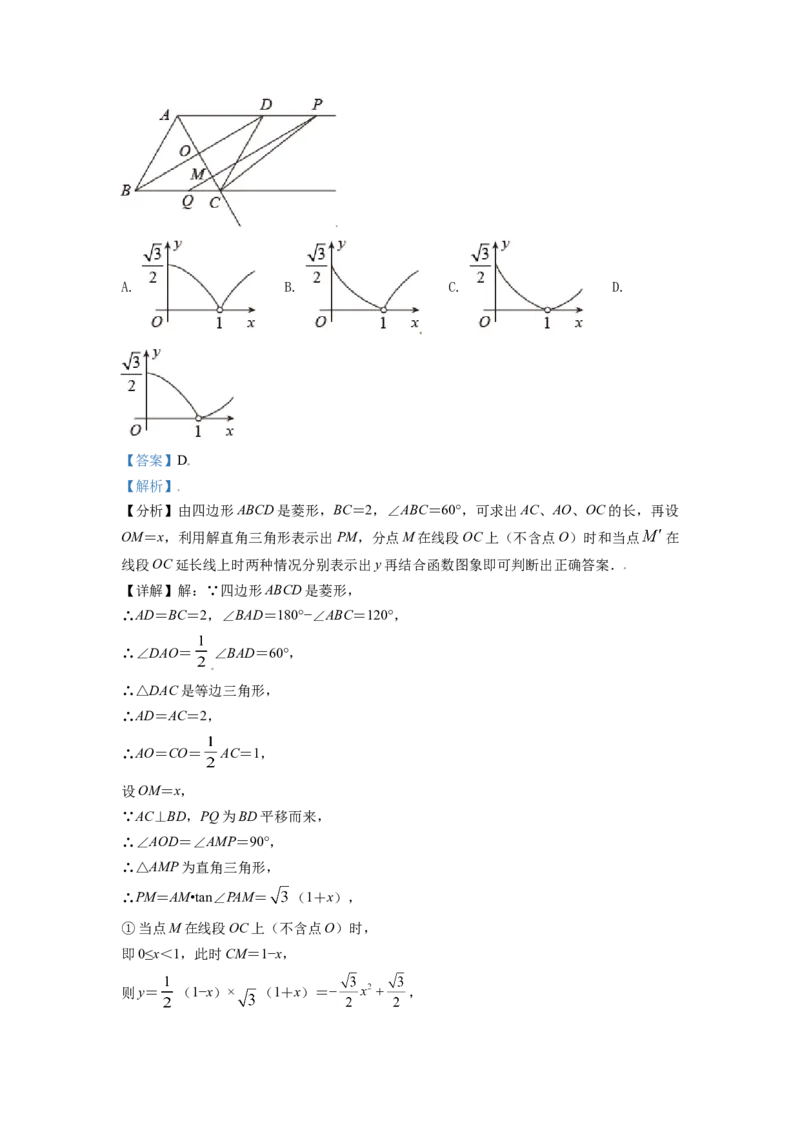
10. 如图,四边形ABCD是菱形,BC=2,∠ABC=60°,对角线AC与BD相交于点O,线
段BD沿射线AD方向平移,平移后的线段记为PQ,射线PQ与射线AC交于点M,连结
PC,设OM长为 ,△PMC面积为 .下列图象能正确反映出 与 的函数关系的是(
)A. B. C. D.
【答案】D
【解析】
【分析】由四边形ABCD是菱形,BC=2,∠ABC=60°,可求出AC、AO、OC的长,再设
OM=x,利用解直角三角形表示出PM,分点M在线段OC上(不含点O)时和当点 在
线段OC延长线上时两种情况分别表示出y再结合函数图象即可判断出正确答案.
【详解】解:∵四边形ABCD是菱形,
∴AD=BC=2,∠BAD=180°−∠ABC=120°,
∴∠DAO= ∠BAD=60°,
∴△DAC是等边三角形,
∴AD=AC=2,
∴AO=CO= AC=1,
设OM=x,
∵AC⊥BD,PQ为BD平移而来,
∴∠AOD=∠AMP=90°,
∴△AMP为直角三角形,
∴PM=AM•tan∠PAM= (1+x),
①当点M在线段OC上(不含点O)时,
即0≤x<1,此时CM=1−x,
则y= (1−x)× (1+x)=− ,∴0≤x<1,函数图象开口应朝下,
故B、C不符合题意,
②当点 在线段OC延长线上时,即x>1,如图所示:
此时C =x−1,
则y= (x−1)× (x+1)= ,
∴只有D选项符合题意,
故选:D.
【点睛】本题考查了菱形的性质,三角形面积,解直角三角形,二次函数图象等知识,熟
练掌握上述知识并能分点M在线段OC上(不含点O)时和当点 在线段OC延长线上时
两种情况分别表示出y再结合函数图象进行判断是解题的关键.
二、填空题(本题有8小题,每小题3分,共24分)
11. 建党100周年期间,我市人社系统不断提升服务能力和水平,让我市约1 300 000参保
人员获得更高质量的社会保障福祉.数据1 300 000用科学记数法表示为________
【答案】1.3×106
【解析】
【分析】科学记数法的表现形式为 的形式,其中 ,n为整数,确定n的
值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同,
当原数绝对值大于等于10时,n是正数,当原数绝对值小于1时n是负数;由此进行求解
即可得到答案.
【详解】解: 1300000=
故答案为: .
【点睛】本题主要考查了科学记数法,解题的关键在于能够熟练掌握科学记数法的定义.
12. 分解因式: =________
【答案】
【解析】
【分析】先提取公因式2,然后利用平方差公式求解即可得到答案.
【详解】解:故答案为: .
【点睛】本题主要考查了分解因式,解题的关键在于能够熟练掌握分解因式的方法.
13. 计算: =________
【答案】
【解析】
【分析】直接利用绝对值的性质以及二次根式的性质分别化简得出答案.
【详解】解:原式
.
故答案为: .
【点睛】此题主要考查了绝对值的性质以及二次根式的性质,正确化简各数是解题关键.
14. 从不等式组 的所有整数解中任取一个数,它是偶数的概率是________
【答案】
【解析】
【分析】首先求得不等式组 的所有整数解,然后由概率公式求得答案.
【详解】解:∵ ,
由①得:x≥1,
由②得:x≤5,
∴不等式组的解集为:1≤x≤5,
∴整数解有:1,2,3,4,5;
∴它是偶数的概率是 .
故答案为: .
【点睛】此题考查了概率公式的应用以及不等式组的解集.用到的知识点为:概率=所求情况数与总情况数之比.
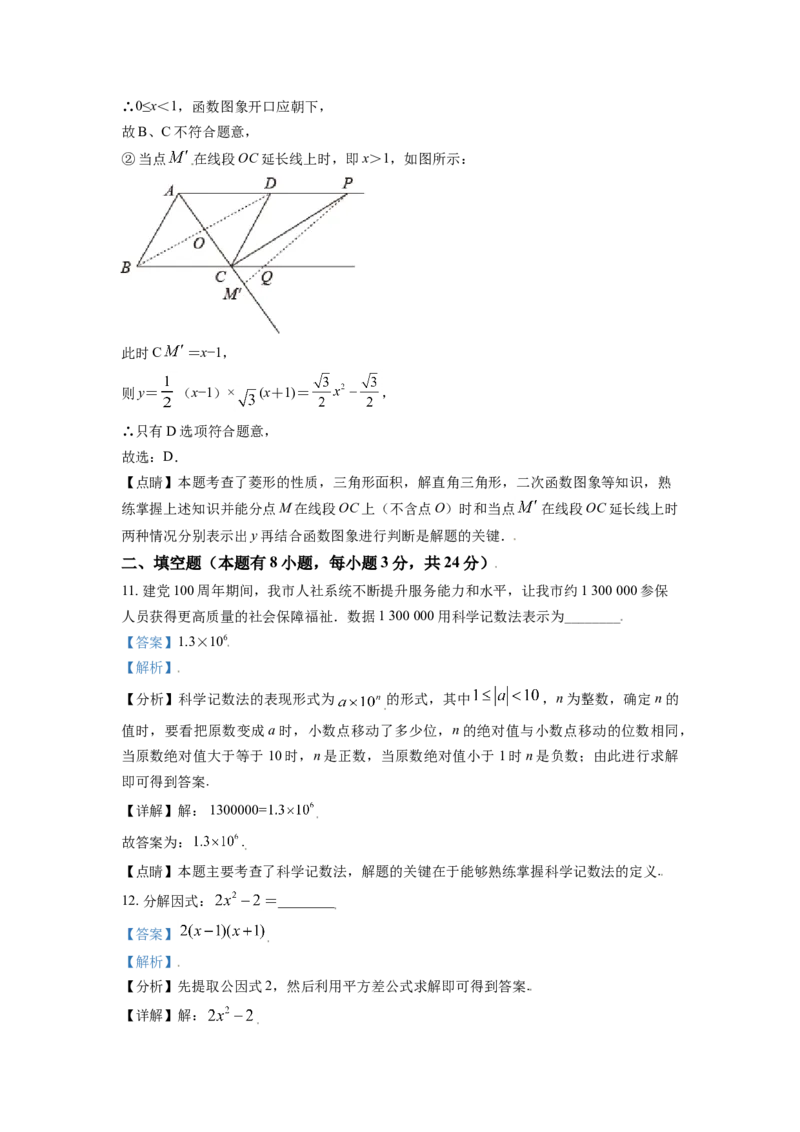
15. 如图,⊙A、⊙B、⊙C两两不相交,且半径都是2cm,则图中三个扇形(即阴影部分)面积
之和是_____cm2
【答案】2π
【解析】
【分析】因为三个小扇形所在圆半径相等,根据三角形的内角和是 180度,将三个小扇形
组合成一个半圆,即可求面积.
【详解】解:S = =2π.
阴影
故答案是:2π.
【点睛】本题考查了扇形面积的计算;三角形内角和定理.熟记公式是关键.
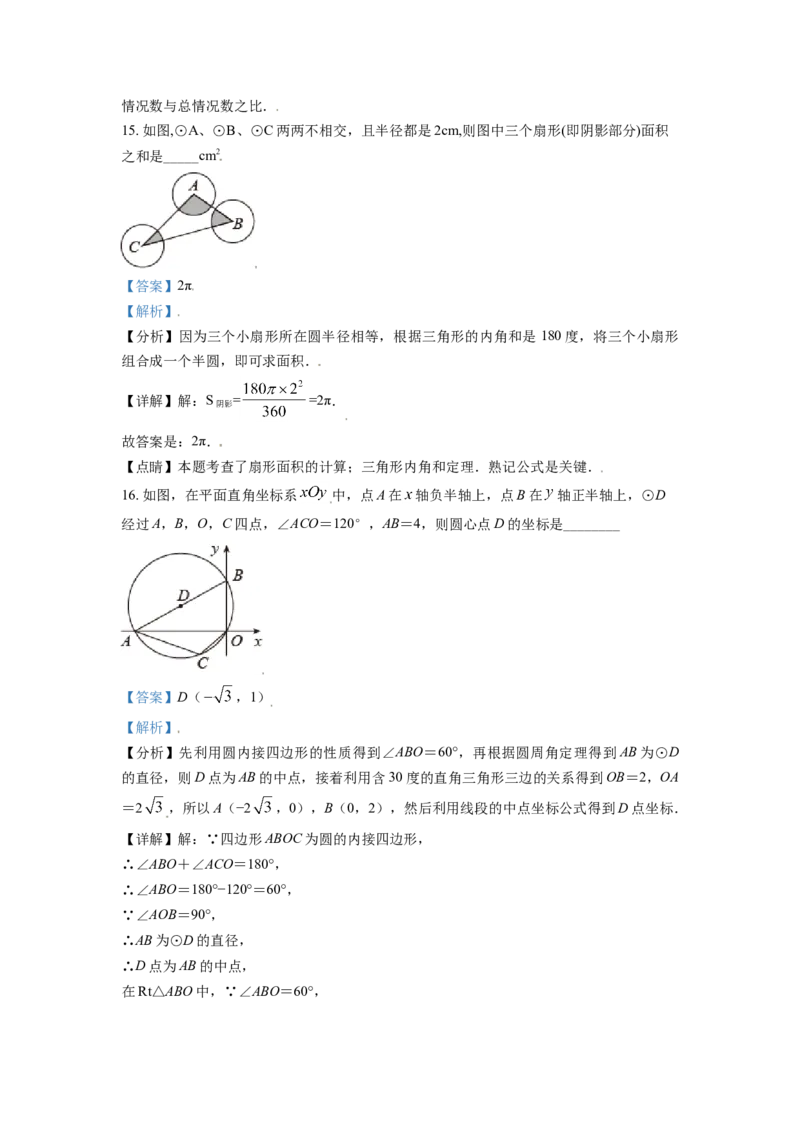
16. 如图,在平面直角坐标系 中,点A在 轴负半轴上,点B在 轴正半轴上,⊙D
经过A,B,O,C四点,∠ACO=120°,AB=4,则圆心点D的坐标是________
【答案】D( ,1)
【解析】
【分析】先利用圆内接四边形的性质得到∠ABO=60°,再根据圆周角定理得到AB为⊙D
的直径,则D点为AB的中点,接着利用含30度的直角三角形三边的关系得到OB=2,OA
=2 ,所以A(−2 ,0),B(0,2),然后利用线段的中点坐标公式得到D点坐标.
【详解】解:∵四边形ABOC为圆的内接四边形,
∴∠ABO+∠ACO=180°,
∴∠ABO=180°−120°=60°,
∵∠AOB=90°,
∴AB为⊙D的直径,
∴D点为AB的中点,
在Rt△ABO中,∵∠ABO=60°,∴OB= AB=2,
∴OA= OB=2 ,
∴A(−2 ,0),B(0,2),
∴D点坐标为(− ,1).
故答案为(− ,1).
【点睛】本题考查了圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等
于这条弧所对的圆心角的一半.半圆(或直径)所对的圆周角是直角,90°的圆周角所对的
弦是直径.也考查了坐标与图形性质.
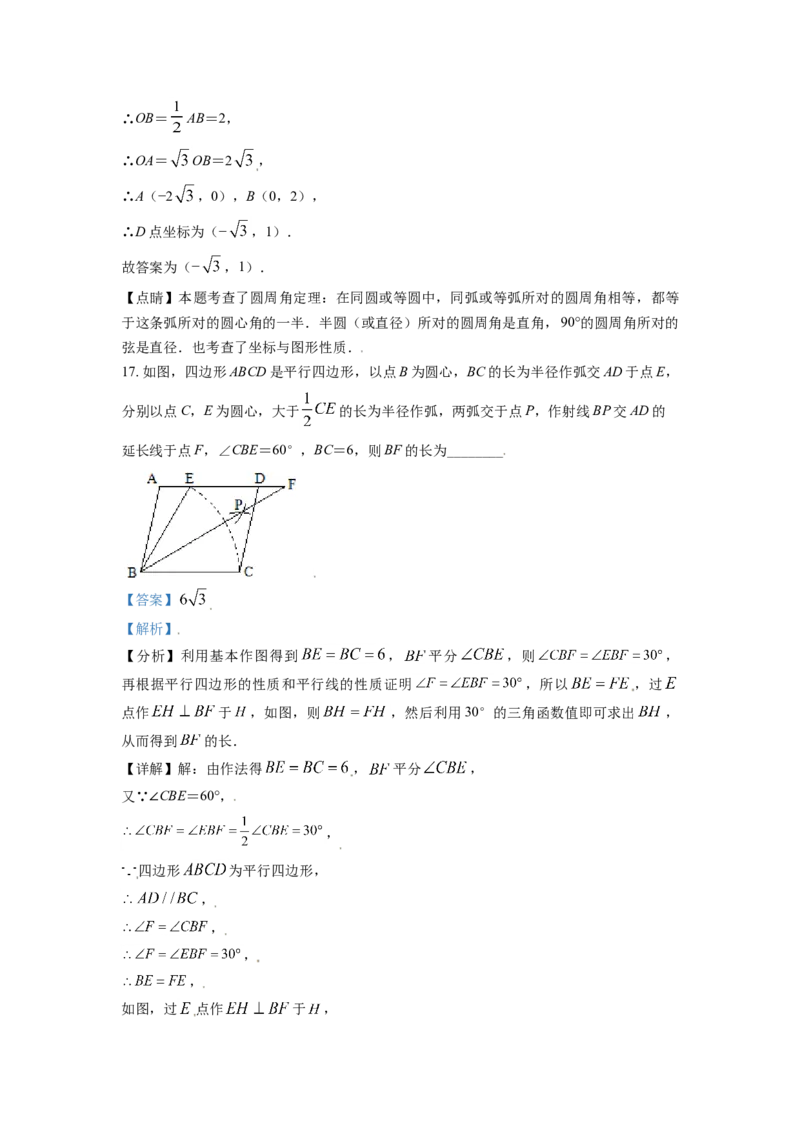
17. 如图,四边形ABCD是平行四边形,以点B为圆心,BC的长为半径作弧交AD于点E,
分别以点C,E为圆心,大于 的长为半径作弧,两弧交于点P,作射线BP交AD的
延长线于点F,∠CBE=60°,BC=6,则BF的长为________
【答案】
【解析】
【分析】利用基本作图得到 , 平分 ,则 ,
再根据平行四边形的性质和平行线的性质证明 ,所以 ,过
点作 于 ,如图,则 ,然后利用30°的三角函数值即可求出 ,
从而得到 的长.
【详解】解:由作法得 , 平分 ,
又∵∠CBE=60°,
,
四边形 为平行四边形,
,
,
,
,
如图,过 点作 于 ,∵ , ,
∴ ,
在 中, ,
,
.
故答案为: .
【点睛】本题考查了作图 复杂作图:解决此类题目的关键是熟悉基本几何图形的性质,
结合几何图形的基本性质把复杂作图拆解成基本作图,逐步操作.也考查了平行四边形的
性质、等腰三角形的判定及性质以及解直角三角形的应用.
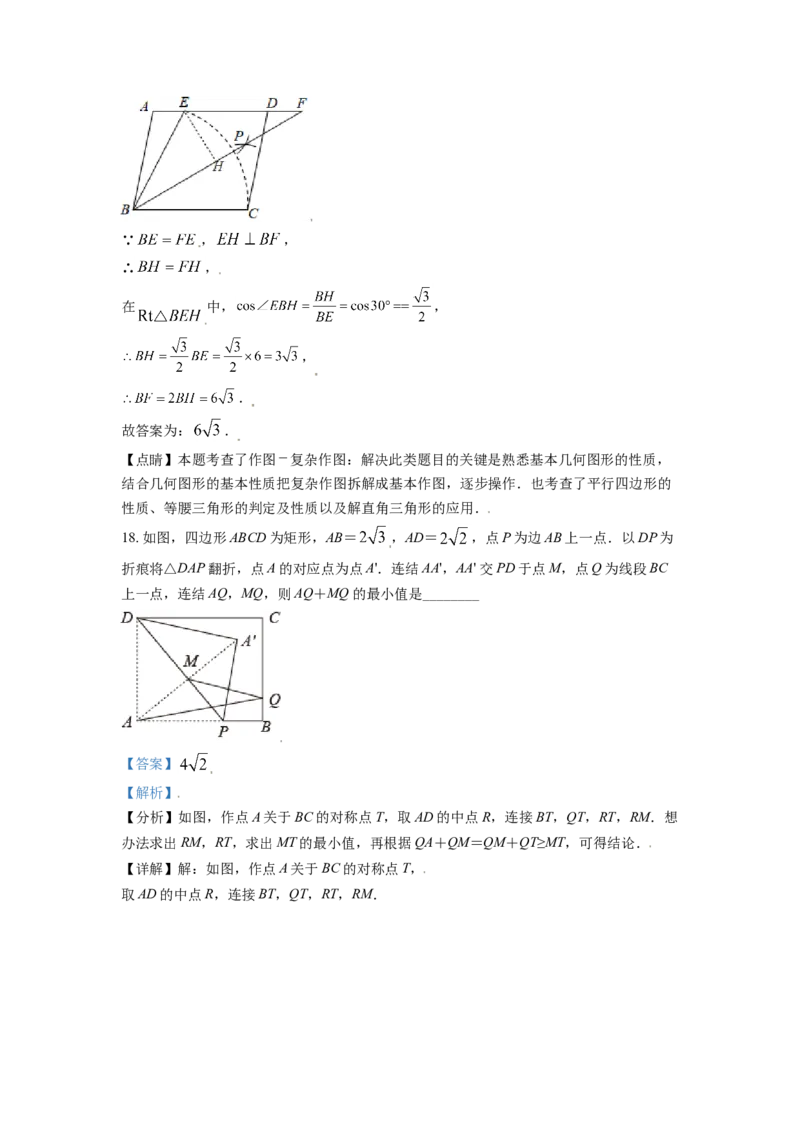
18. 如图,四边形ABCD为矩形,AB= ,AD= ,点P为边AB上一点.以DP为
折痕将△DAP翻折,点A的对应点为点A'.连结AA',AA' 交PD于点M,点Q为线段BC
上一点,连结AQ,MQ,则AQ+MQ的最小值是________
【答案】
【解析】
【分析】如图,作点A关于BC的对称点T,取AD的中点R,连接BT,QT,RT,RM.想
办法求出RM,RT,求出MT的最小值,再根据QA+QM=QM+QT≥MT,可得结论.
【详解】解:如图,作点A关于BC的对称点T,
取AD的中点R,连接BT,QT,RT,RM.∵四边形ABCD是矩形,
∴∠RAT=90°,
∵AR=DR= ,AT=2AB=4 ,
∴RT= ,
∵A,A′关于DP对称,
∴AA′⊥DP,
∴∠AMD=90°,
∵AR=RD,
∴RM= AD= ,
∵MT≥RT−RM,
∴MT≥4 ,
∴MT的最小值为4 ,
∵QA+QM=QT+QM≥MT,
∴QA+QM≥4 ,
∴QA+QM的最小值为4 .
故答案为:4 .
【点睛】本题考查翻折变换,矩形的性质,解直角三角形等知识,解题的关键是求出MT
的最小值,属于中考常考题型.
三、解答题(共96分)
19. 先化简,再求值: ,其中
【答案】 ,
【解析】
【分析】先利用平方差公式和完全平方公式对原式进行分解因式化简,然后代入值计算即
可得到答案.【详解】解:原式=
=
当 时,
原式=
【点睛】本题主要考查了因式分解,分式的化简求解,解题的关键在于能够熟练掌握因式
分解的方法.
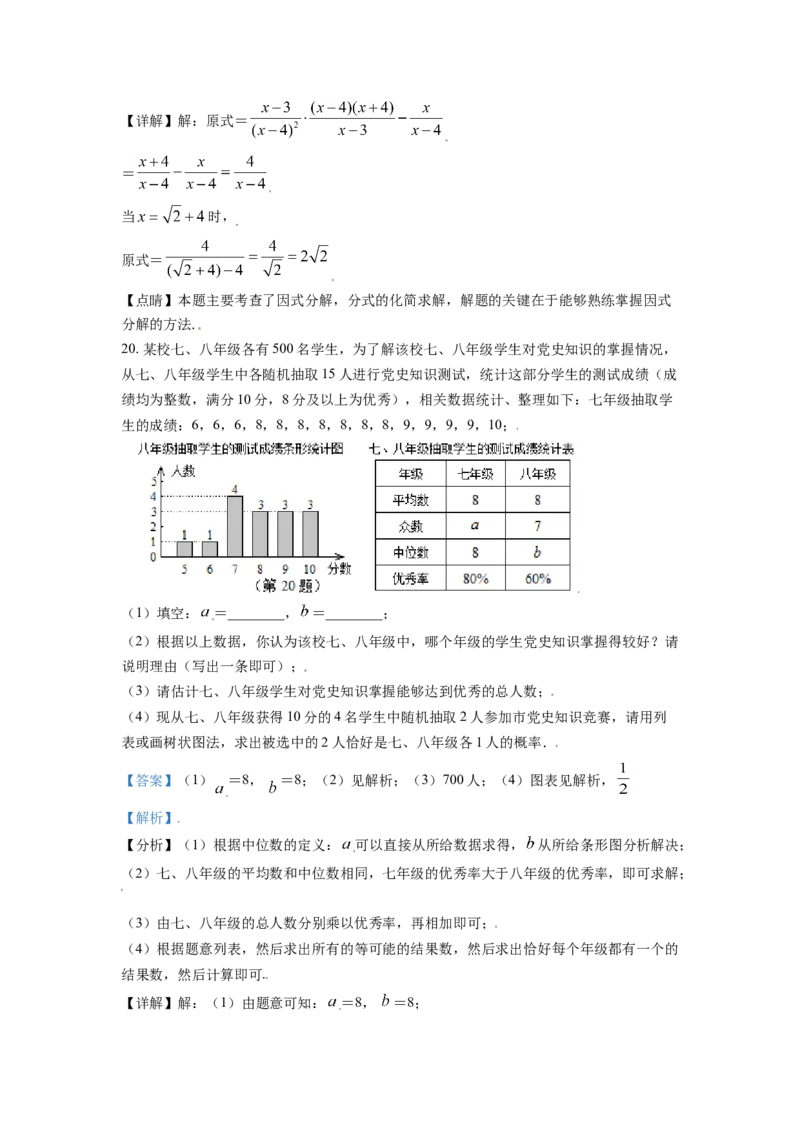
20. 某校七、八年级各有500名学生,为了解该校七、八年级学生对党史知识的掌握情况,
从七、八年级学生中各随机抽取15人进行党史知识测试,统计这部分学生的测试成绩(成
绩均为整数,满分10分,8分及以上为优秀),相关数据统计、整理如下:七年级抽取学
生的成绩:6,6,6,8,8,8,8,8,8,8,9,9,9,9,10;
(1)填空: =________, =________;
(2)根据以上数据,你认为该校七、八年级中,哪个年级的学生党史知识掌握得较好?请
说明理由(写出一条即可);
(3)请估计七、八年级学生对党史知识掌握能够达到优秀的总人数;
(4)现从七、八年级获得10分的4名学生中随机抽取2人参加市党史知识竞赛,请用列
表或画树状图法,求出被选中的2人恰好是七、八年级各1人的概率.
【答案】(1) =8, =8;(2)见解析;(3)700人;(4)图表见解析,
【解析】
【分析】(1)根据中位数的定义: 可以直接从所给数据求得, 从所给条形图分析解决;
(2)七、八年级的平均数和中位数相同,七年级的优秀率大于八年级的优秀率,即可求解;
(3)由七、八年级的总人数分别乘以优秀率,再相加即可;
(4)根据题意列表,然后求出所有的等可能的结果数,然后求出恰好每个年级都有一个的
结果数,然后计算即可.
【详解】解:(1)由题意可知: =8, =8;(2)七年级学生的党史知识掌握得较好,理由如下:
∵七年级和八年级的平均数相同,但是七年级的优秀率大于八年级的优秀率
∴七年级学生 的党史知识掌握得较好;
(3)从现有样本估计全年级,七年级达到优秀的人数可能有500人×80%=400人,
八年级达到优秀的人数可能有500人×60%=300人,
所以两个年级能达优秀的总人数可能会有700人;
(4)把七年级的学生记做A,八年级的三名学生即为B、C、D,列表如下:
A B C D
A (A,B) (A,C) (A,D)
B (B,A) (B,C) (B,D)
C (C,A) (C,B) (C,D)
D (D,A) (D,B) (D,C)
由表知,一共有12种等可能性的结果,恰好每个年级都有一个的结果数是6,
两人中恰好是七八年级各1人的概率是 .
【点睛】本题主要考查了统计与概率,用样本估计总体,列表或画树状图求概率,中位数
的定义等等,解题的关键在于能够熟练掌握相关知识进行求解.
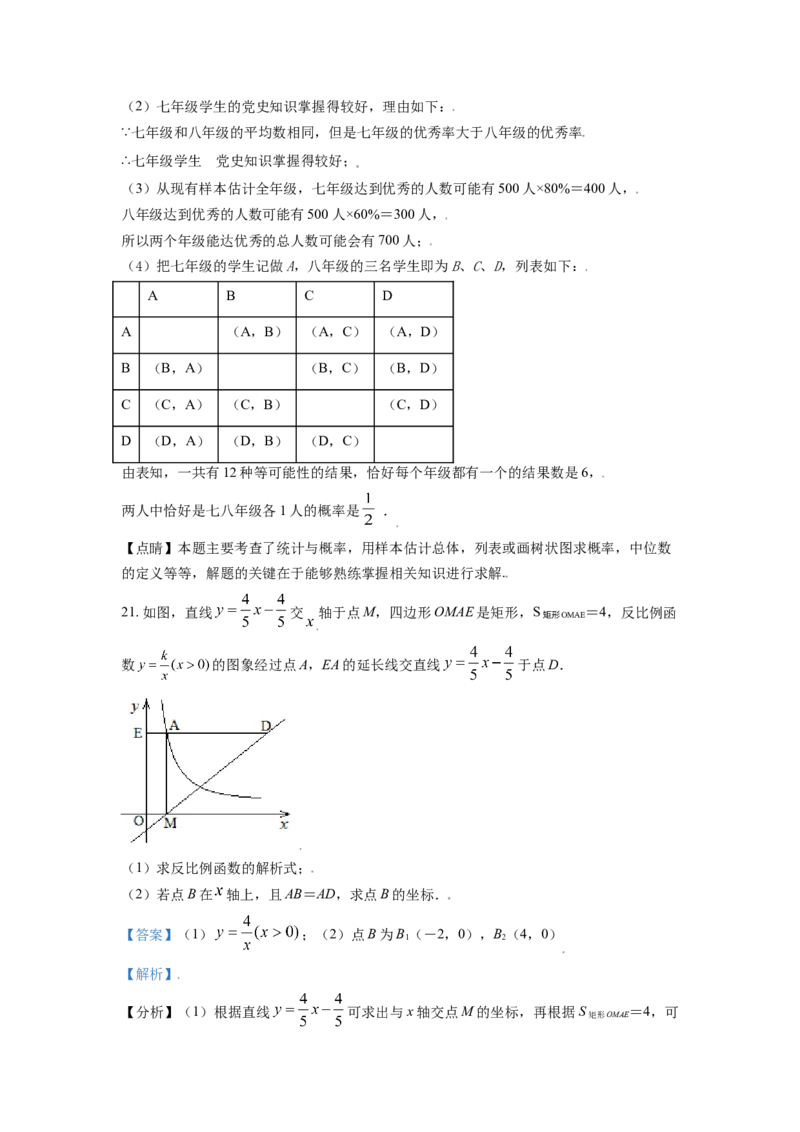
21. 如图,直线 交 轴于点M,四边形OMAE是矩形,S =4,反比例函
矩形OMAE
数 的图象经过点A,EA的延长线交直线 于点D.
(1)求反比例函数的解析式;
(2)若点B在 轴上,且AB=AD,求点B的坐标.
【答案】(1) ;(2)点B为B(-2,0),B(4,0)
1 2
【解析】
【分析】(1)根据直线 可求出与x轴交点M的坐标,再根据S =4,可
矩形OMAE以确定点A的坐标,进而求出k的值,确定反比例函数关系式;
(2)根据一次函数的关系式求出点D的坐标,得出AD的长,于是分两种情况进行解答,
即点B在点M的左侧和右侧,由勾股定理求解即可.
【详解】解:(1)求得直线 与 轴交点坐标为M(1,0),则OM=1,
而S =4,即OM·AM=4,
矩形OMAE
∴AM=4,
∴A(1,4);
∵反比例函数的图象过点A(1,4),
∴ ,
∴所求函数为 ;
(2)∵点D在EA延长线上,
∴直线AD: ,
求得直线 与直线 的交点坐标为D(6,4),
∴AD=5;
设B( ,0),则BM= ,
Rt△ABM中,AB=AD=5,AM=4,
∴BM=3,即 =3,则 , ,
∴所求点B为B(-2,0),B(4,0).
1 2
【点睛】本题考查一次函数、反比例函数的交点,理解一次函数、反比例函数图象的意义
是解决问题的前提,将点的坐标代入是常用的方法.
22. 如图,小华遥控无人机从点A处飞行到对面大厦MN的顶端M,无人机飞行方向与水平
方向的夹角为37°,小华在点A测得大厦底部N的俯角为31°,两楼之间一棵树EF的顶
点E恰好在视线AN上,已知树的高度为6米,且 ,楼AB,MN,树EF均垂直于
地面,问:无人机飞行的距离AM约是多少米?(结果保留整数.参考数据:
cos31°≈0.86, tan31°≈0.60, cos37°≈0.80, tan37°≈0.75)【答案】38米
【解析】
【分析】过 作 于 ,易证 ,得 ,则
,再由锐角三角函数求出 ,然后在 中,由锐角三角函数定
义求出 的长即可.
【详解】解:过 作 于 ,如图所示:
则 , ,
,
,
由题意得: , , ,
,
,
,
,
,
在 中, ,
,
在 中, ,
,
即无人机飞行的距离 约是 .
【点睛】本题考查了解直角三角形的应用 仰角俯角问题,相似三角形的应用等知识,正
确作出辅助线构造直角三角形,证明 是解题的关键.
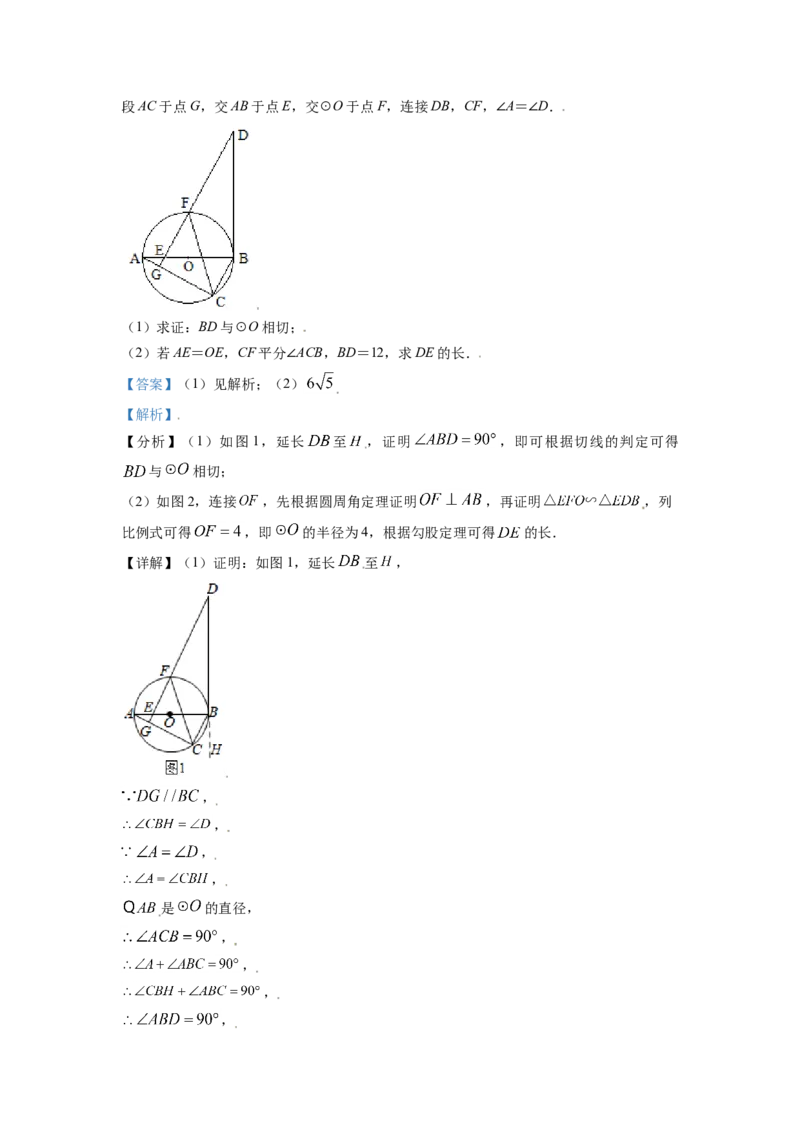
23. 如图,△ABC内接于⊙O,AB是⊙O的直径,过⊙O外一点D作 ,DG交线段AC于点G,交AB于点E,交⊙O于点F,连接DB,CF,∠A=∠D.
(1)求证:BD与⊙O相切;
(2)若AE=OE,CF平分∠ACB,BD=12,求DE的长.
【答案】(1)见解析;(2)
【解析】
【分析】(1)如图1,延长 至 ,证明 ,即可根据切线的判定可得
与 相切;
(2)如图2,连接 ,先根据圆周角定理证明 ,再证明 ,列
比例式可得 ,即 的半径为4,根据勾股定理可得 的长.
【详解】(1)证明:如图1,延长 至 ,
,
,
,
,
是 的直径,
,
,
,
,∴AB⊥BD,
与 相切;
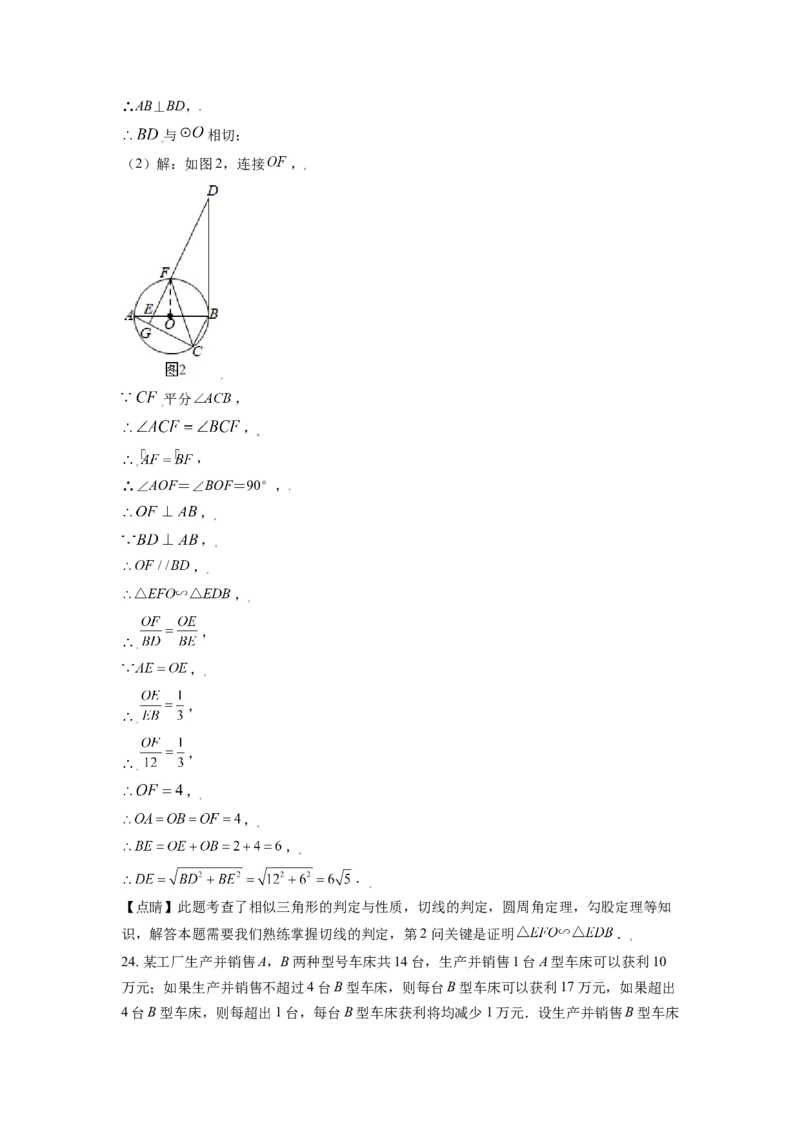
(2)解:如图2,连接 ,
平分 ,
,
,
∴∠AOF=∠BOF=90°,
,
,
,
,
,
,
,
,
,
,
,
.
【点睛】此题考查了相似三角形的判定与性质,切线的判定,圆周角定理,勾股定理等知
识,解答本题需要我们熟练掌握切线的判定,第2问关键是证明 .
24. 某工厂生产并销售A,B两种型号车床共14台,生产并销售1台A型车床可以获利10
万元;如果生产并销售不超过4台B型车床,则每台B型车床可以获利17万元,如果超出
4台B型车床,则每超出1台,每台B型车床获利将均减少1万元.设生产并销售B型车床台.
(1)当 时,完成以下两个问题:
①请补全下面的表格:
A型 B型
车床数量/台 ________
每台车床获利/万元 10 ________
②若生产并销售B型车床比生产并销售A型车床获得的利润多70万元,问:生产并销售B
型车床多少台?
(2)当0< ≤14时,设生产并销售A,B两种型号车床获得的总利润为W万元,如何分
配生产并销售A,B两种车床的数量,使获得的总利润W最大?并求出最大利润.
【答案】(1)① , ;②10台;(2)分配产销A型车床9台、B型车床5台;
或产销A型车床8台、B型车床6台,此时可获得总利润最大值170万元
【解析】
【分析】(1)①由题意可知,生产并销售B型车床x台时,生产A型车床(14-x)台,当
时,每台就要比17万元少( )万元,所以每台获利 ,也就是(
)万元;
②根据题意可得根据题意: 然后解方程即可;
(2)当0≤ ≤4时,W= + = ,当4< ≤14时,
W= ,分别求出两个范围内的最大值即可得到答案.
【详解】解:(1)当 时,每台就要比17万元少( )万元
所以每台获利 ,也就是( )万元
①补全表格如下面:
A型 B型
车床数量/台
每台车床获利/万元 10
②此时,由A型获得的利润是10( )万元,
由B型可获得利润为 万元,
根据题意: , ,
,∵0≤ ≤14, ∴ ,
即应产销B型车床10台;
(2)当0≤ ≤4时,当0≤ ≤4 A型 B型
车床数量/台
每台车床获利/万元 10 17
利润
此时,W= + = ,
该函数值随着 的增大而增大,当 取最大值4时,W =168(万元);
最大1
当4< ≤14时,
当4< ≤14 A型 B型
车床数量/台
每台车床获利/万元 10
利润
则W= + = = ,
当 或 时(均满足条件4< ≤14),W达最大值W =170(万元),
最大2
∵W > W ,
最大2 最大1
∴应分配产销A型车床9台、B型车床5台;或产销A型车床8台、B型车床6台,此时可
获得总利润最大值170万元.
【点睛】本题主要考查了一元二次方程的实际应用,一次函数和二次函数的实际应用,解
题的关键在于能够根据题意列出合适的方程或函数关系式求解.
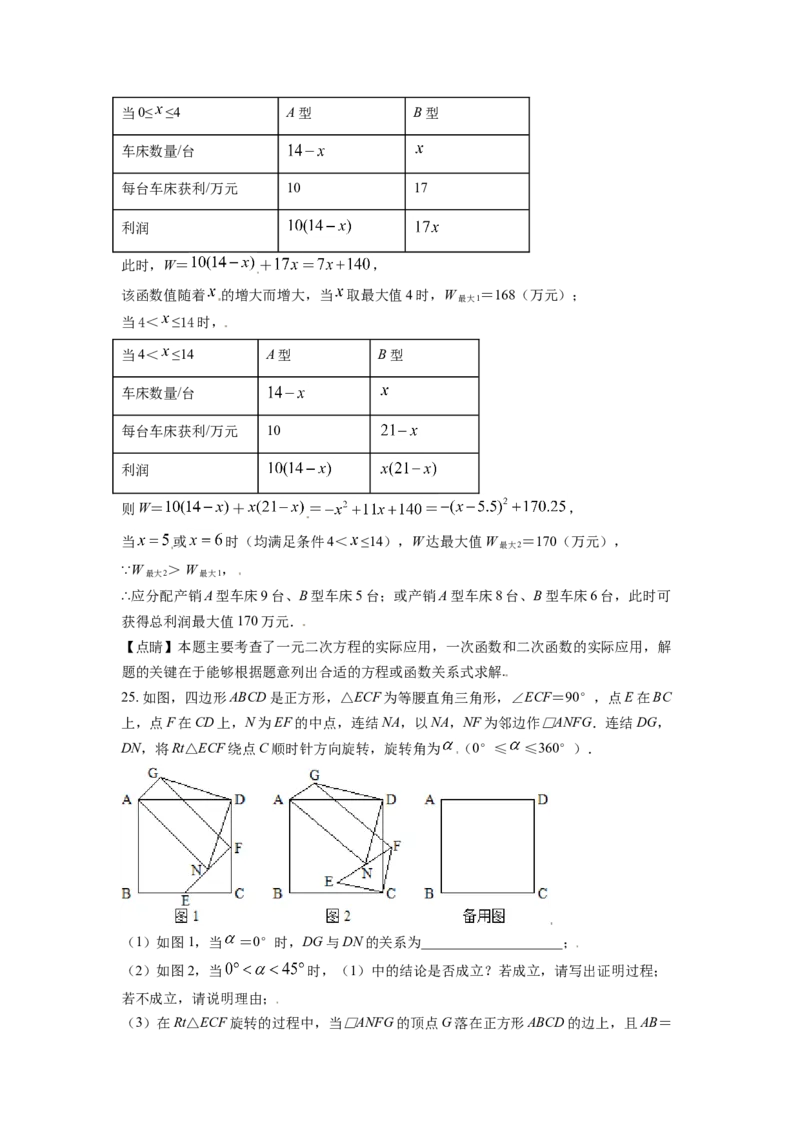
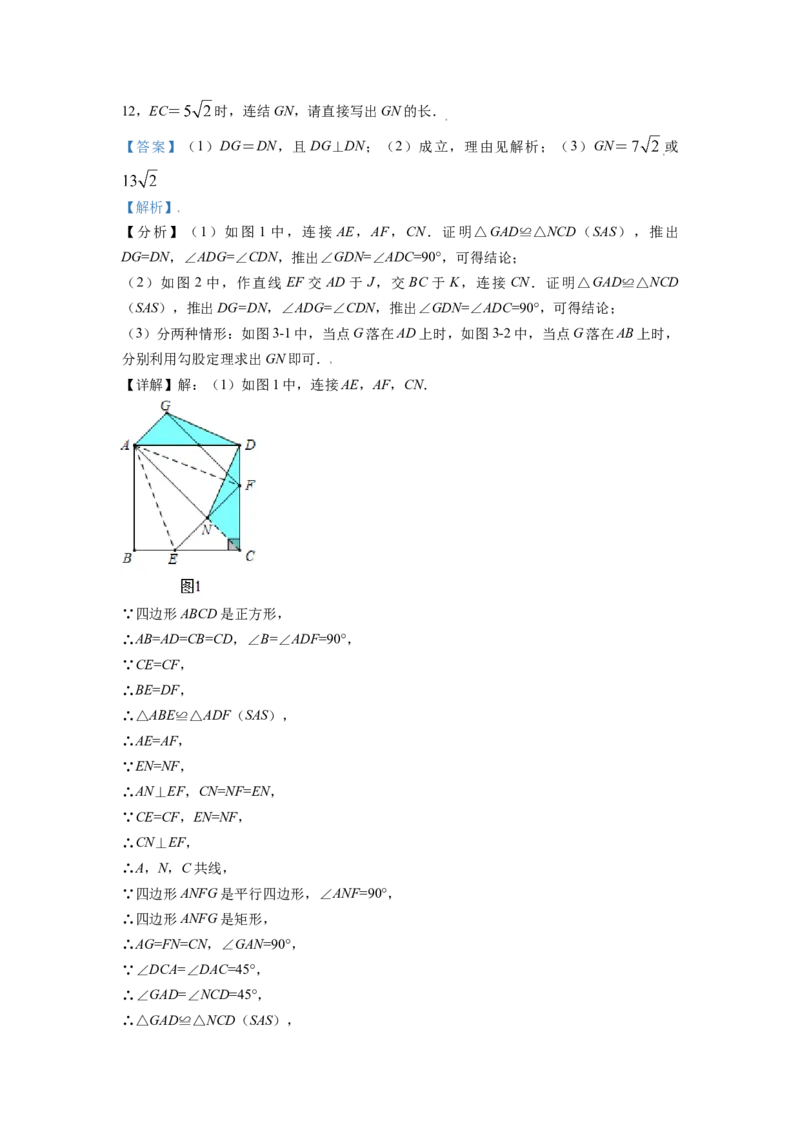
25. 如图,四边形ABCD是正方形,△ECF为等腰直角三角形,∠ECF=90°,点E在BC
上,点F在CD上,N为EF的中点,连结NA,以NA,NF为邻边作□ANFG.连结DG,
DN,将Rt△ECF绕点C顺时针方向旋转,旋转角为 (0°≤ ≤360°).
(1)如图1,当 =0°时,DG与DN的关系为____________________;
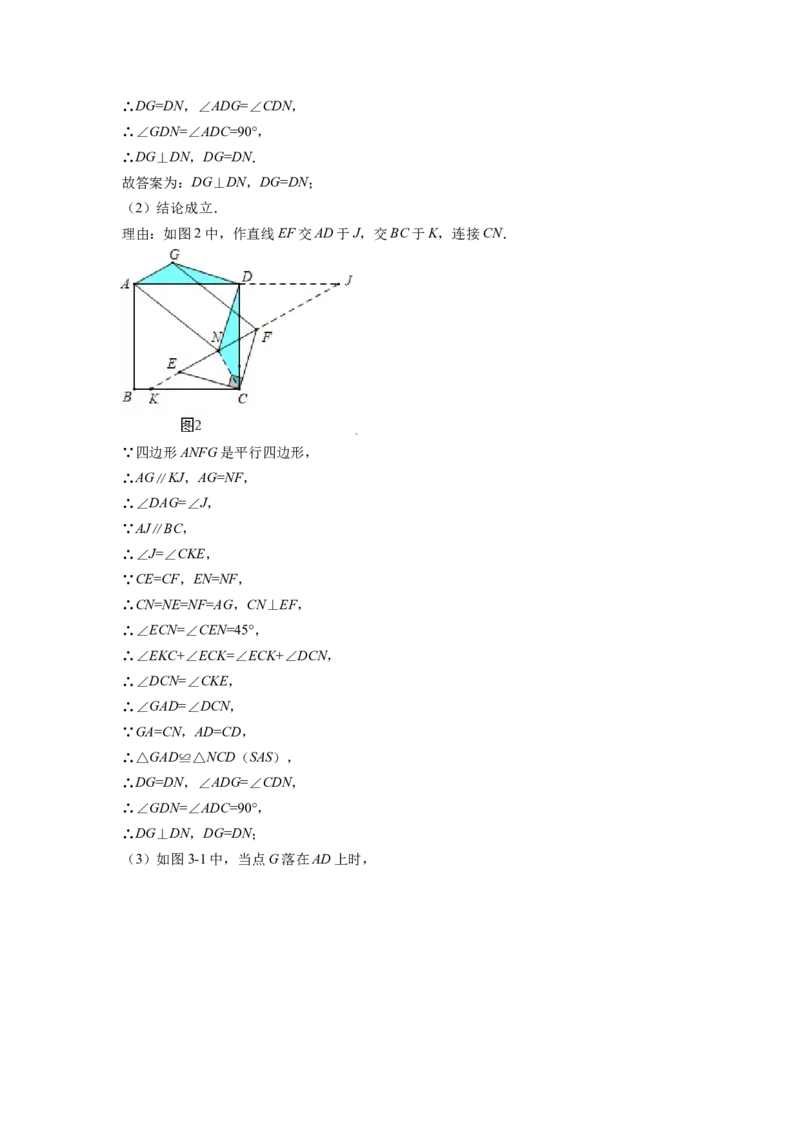
(2)如图2,当 时,(1)中的结论是否成立?若成立,请写出证明过程;
若不成立,请说明理由;
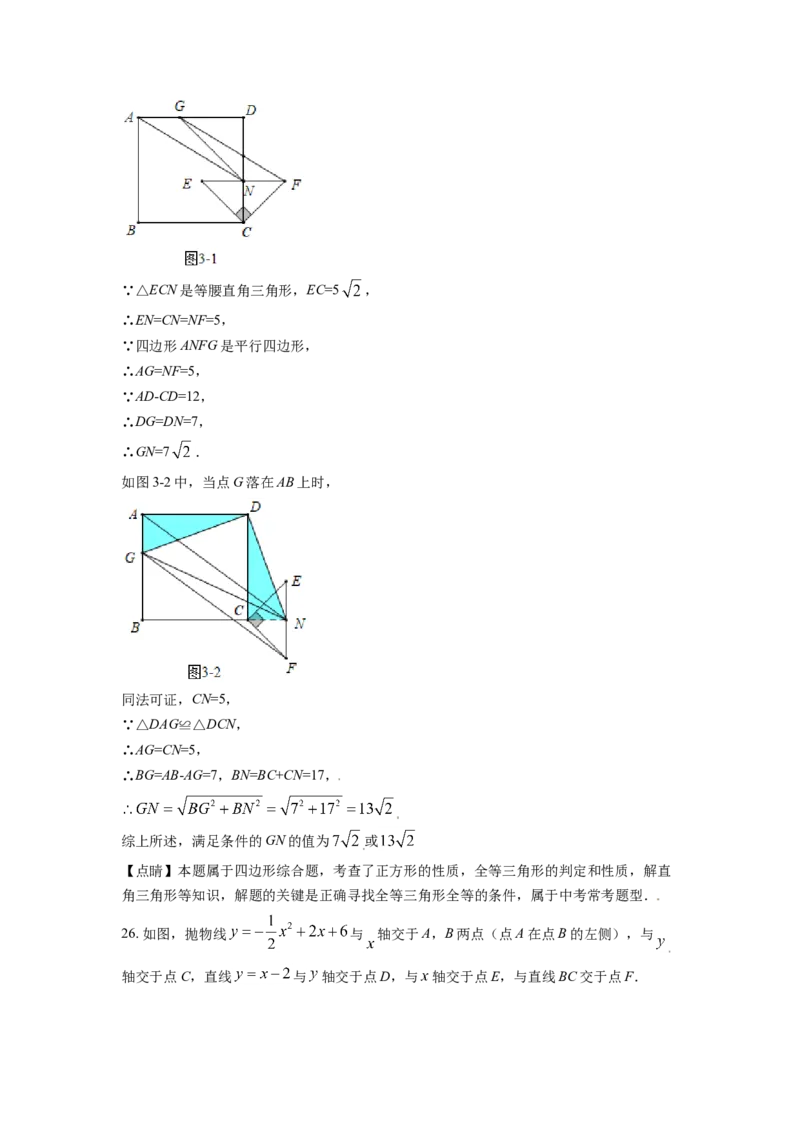
(3)在Rt△ECF旋转的过程中,当□ANFG的顶点G落在正方形ABCD的边上,且AB=12,EC= 时,连结GN,请直接写出GN的长.
【答案】(1)DG=DN,且DG⊥DN;(2)成立,理由见解析;(3)GN= 或
【解析】
【分析】(1)如图 1 中,连接 AE,AF,CN.证明△GAD≌△NCD(SAS),推出
DG=DN,∠ADG=∠CDN,推出∠GDN=∠ADC=90°,可得结论;
(2)如图 2 中,作直线 EF 交 AD 于 J,交 BC 于 K,连接 CN.证明△GAD≌△NCD
(SAS),推出DG=DN,∠ADG=∠CDN,推出∠GDN=∠ADC=90°,可得结论;
(3)分两种情形:如图3-1中,当点G落在AD上时,如图3-2中,当点G落在AB上时,
分别利用勾股定理求出GN即可.
【详解】解:(1)如图1中,连接AE,AF,CN.
∵四边形ABCD是正方形,
∴AB=AD=CB=CD,∠B=∠ADF=90°,
∵CE=CF,
∴BE=DF,
∴△ABE≌△ADF(SAS),
∴AE=AF,
∵EN=NF,
∴AN⊥EF,CN=NF=EN,
∵CE=CF,EN=NF,
∴CN⊥EF,
∴A,N,C共线,
∵四边形ANFG是平行四边形,∠ANF=90°,
∴四边形ANFG是矩形,
∴AG=FN=CN,∠GAN=90°,
∵∠DCA=∠DAC=45°,
∴∠GAD=∠NCD=45°,
∴△GAD≌△NCD(SAS),∴DG=DN,∠ADG=∠CDN,
∴∠GDN=∠ADC=90°,
∴DG⊥DN,DG=DN.
故答案为:DG⊥DN,DG=DN;
(2)结论成立.
理由:如图2中,作直线EF交AD于J,交BC于K,连接CN.
∵四边形ANFG是平行四边形,
∴AG∥KJ,AG=NF,
∴∠DAG=∠J,
∵AJ∥BC,
∴∠J=∠CKE,
∵CE=CF,EN=NF,
∴CN=NE=NF=AG,CN⊥EF,
∴∠ECN=∠CEN=45°,
∴∠EKC+∠ECK=∠ECK+∠DCN,
∴∠DCN=∠CKE,
∴∠GAD=∠DCN,
∵GA=CN,AD=CD,
∴△GAD≌△NCD(SAS),
∴DG=DN,∠ADG=∠CDN,
∴∠GDN=∠ADC=90°,
∴DG⊥DN,DG=DN;
(3)如图3-1中,当点G落在AD上时,∵△ECN是等腰直角三角形,EC=5 ,
∴EN=CN=NF=5,
∵四边形ANFG是平行四边形,
∴AG=NF=5,
∵AD-CD=12,
∴DG=DN=7,
∴GN=7 .
如图3-2中,当点G落在AB上时,
同法可证,CN=5,
∵△DAG≌△DCN,
∴AG=CN=5,
∴BG=AB-AG=7,BN=BC+CN=17,
综上所述,满足条件的GN的值为 或
【点睛】本题属于四边形综合题,考查了正方形的性质,全等三角形的判定和性质,解直
角三角形等知识,解题的关键是正确寻找全等三角形全等的条件,属于中考常考题型.
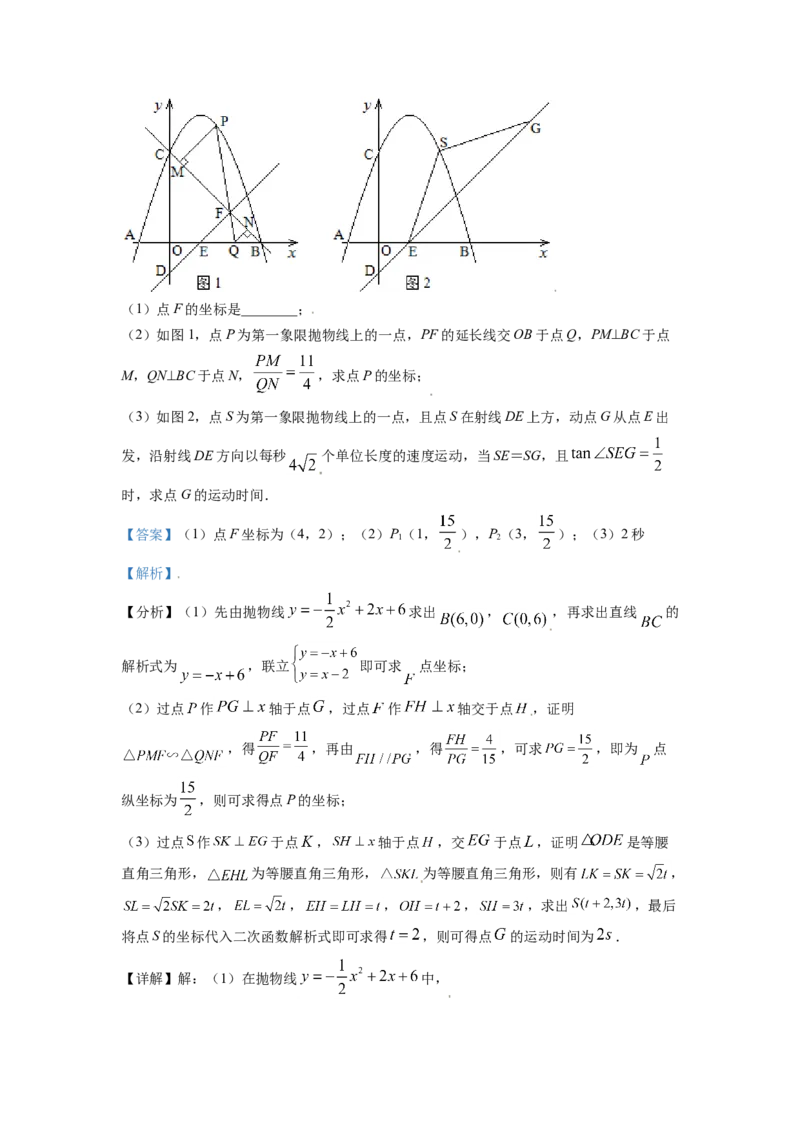
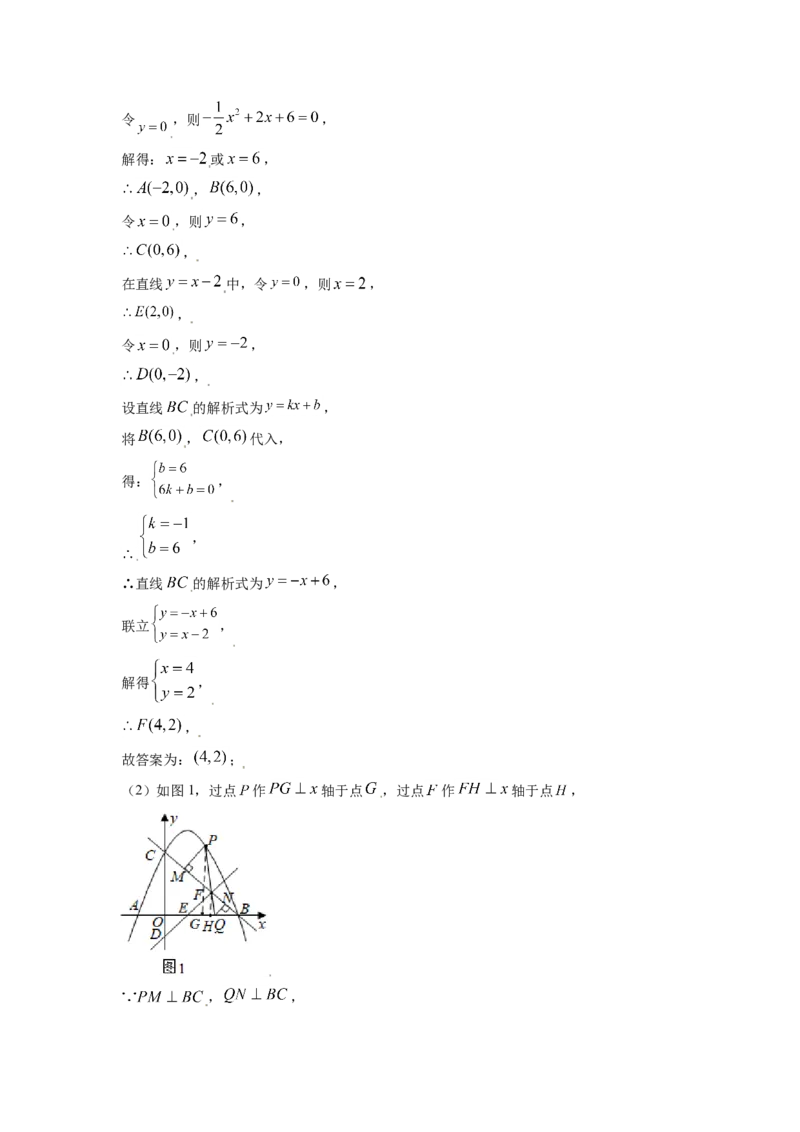
26. 如图,抛物线 与 轴交于A,B两点(点A在点B的左侧),与
轴交于点C,直线 与 轴交于点D,与 轴交于点E,与直线BC交于点F.(1)点F的坐标是________;
(2)如图1,点P为第一象限抛物线上的一点,PF的延长线交OB于点Q,PM⊥BC于点
M,QN⊥BC于点N, ,求点P的坐标;
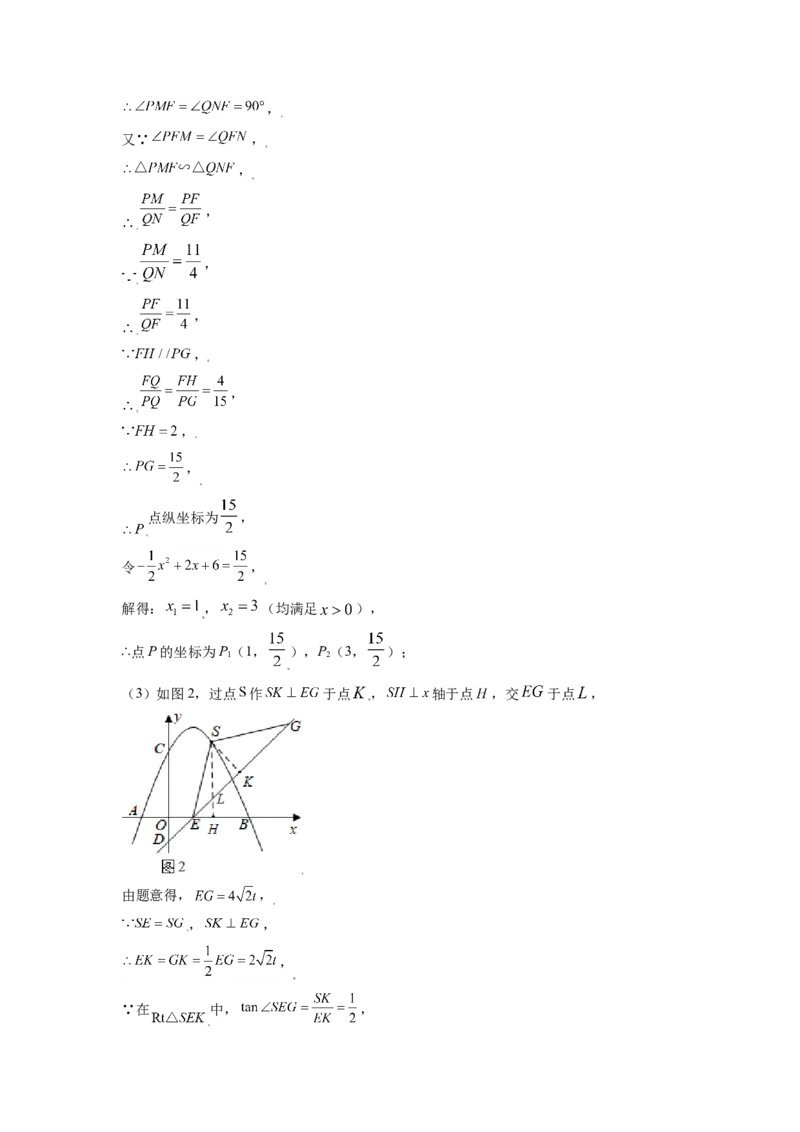
(3)如图2,点S为第一象限抛物线上的一点,且点S在射线DE上方,动点G从点E出
发,沿射线DE方向以每秒 个单位长度的速度运动,当SE=SG,且
时,求点G的运动时间.
【答案】(1)点F坐标为(4,2);(2)P(1, ),P(3, );(3)2秒
1 2
【解析】
【分析】(1)先由抛物线 求出 , ,再求出直线 的
解析式为 ,联立 即可求 点坐标;
(2)过点 作 轴于点 ,过点 作 轴交于点 ,证明
,得 ,再由 ,得 ,可求 ,即为 点
纵坐标为 ,则可求得点P的坐标;
(3)过点 作 于点 , 轴于点 ,交 于点 ,证明 是等腰
直角三角形, 为等腰直角三角形, 为等腰直角三角形,则有 ,
, , , , ,求出 ,最后
将点S的坐标代入二次函数解析式即可求得 ,则可得点 的运动时间为 .
【详解】解:(1)在抛物线 中,令 ,则 ,
解得: 或 ,
, ,
令 ,则 ,
,
在直线 中,令 ,则 ,
,
令 ,则 ,
,
设直线 的解析式为 ,
将 , 代入,
得: ,
,
∴直线 的解析式为 ,
联立 ,
解得 ,
,
故答案为: ;
(2)如图1,过点 作 轴于点 ,过点 作 轴于点 ,
, ,,
又∵ ,
,
,
,
,
,
,
,
,
点纵坐标为 ,
令 ,
解得: , (均满足 ),
∴点P的坐标为P(1, ),P(3, );
1 2
(3)如图2,过点 作 于点 , 轴于点 ,交 于点 ,
由题意得, ,
, ,
,
∵在 中, ,,
, ,
,
是等腰直角三角形,
,
,
为等腰直角三角形,
,
为等腰直角三角形,
, ,
,
,
, ,
,
将 代入 ,
得 ,
解得: 或 (舍),
点 的运动时间为 .
【点睛】本题考查二次函数的图象及性质,熟练掌握二次函数的图象及性质,灵活运用平
移、三角形相似、解直角三角形等相关知识是解题的关键.