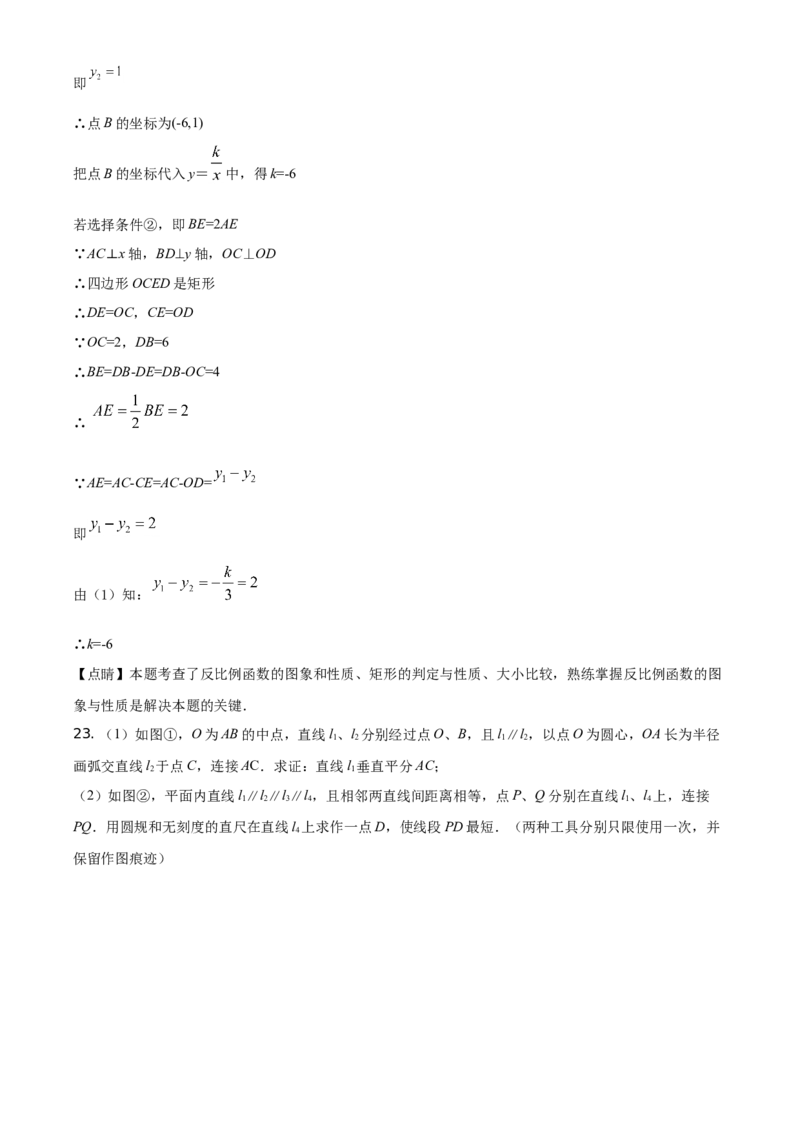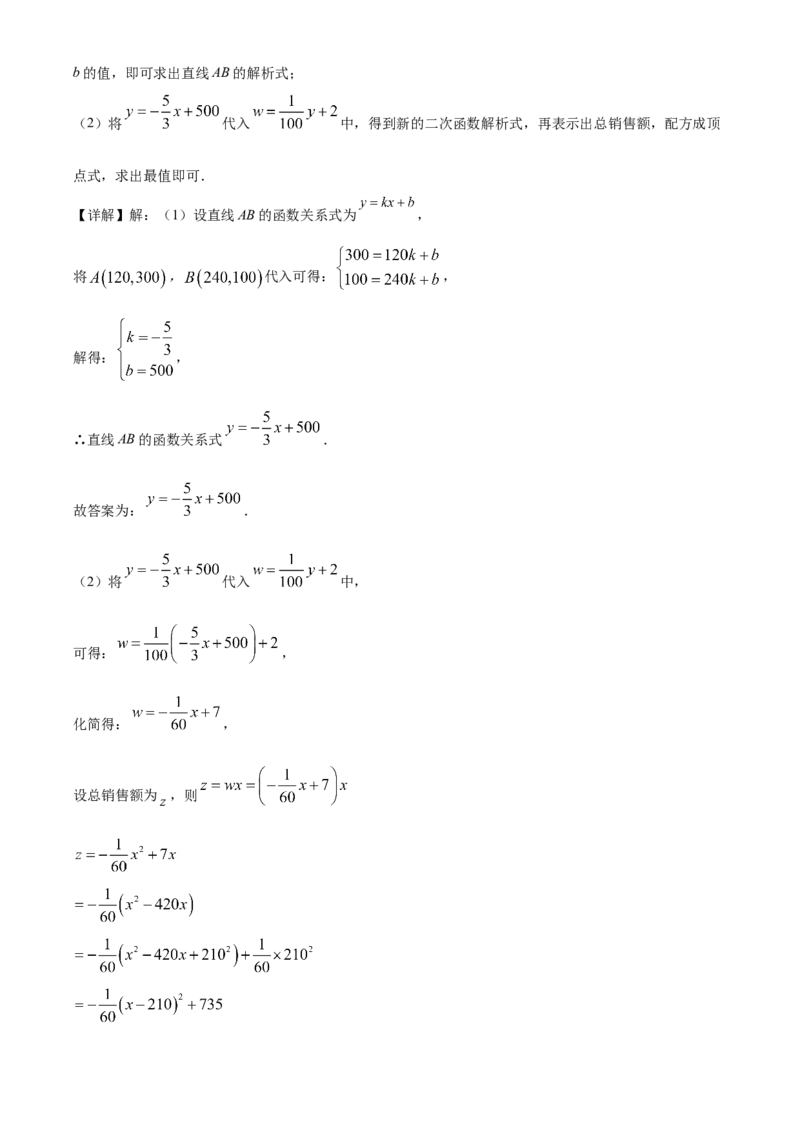文档内容
2021 年江苏省泰州市中考数学试卷
一、选择题(本大题共有6小题,每小题3分,共18分)
1. (﹣3)0等于( )
A. 0 B. 1 C. 3 D. ﹣3
【答案】B
【解析】
【分析】根据任何不为0的数的零次幂都等于1,可得答案.
【详解】解: ,
故选:B.
【点睛】本题主要考查了零指数幂的性质,正确掌握相关定义是解题关键.
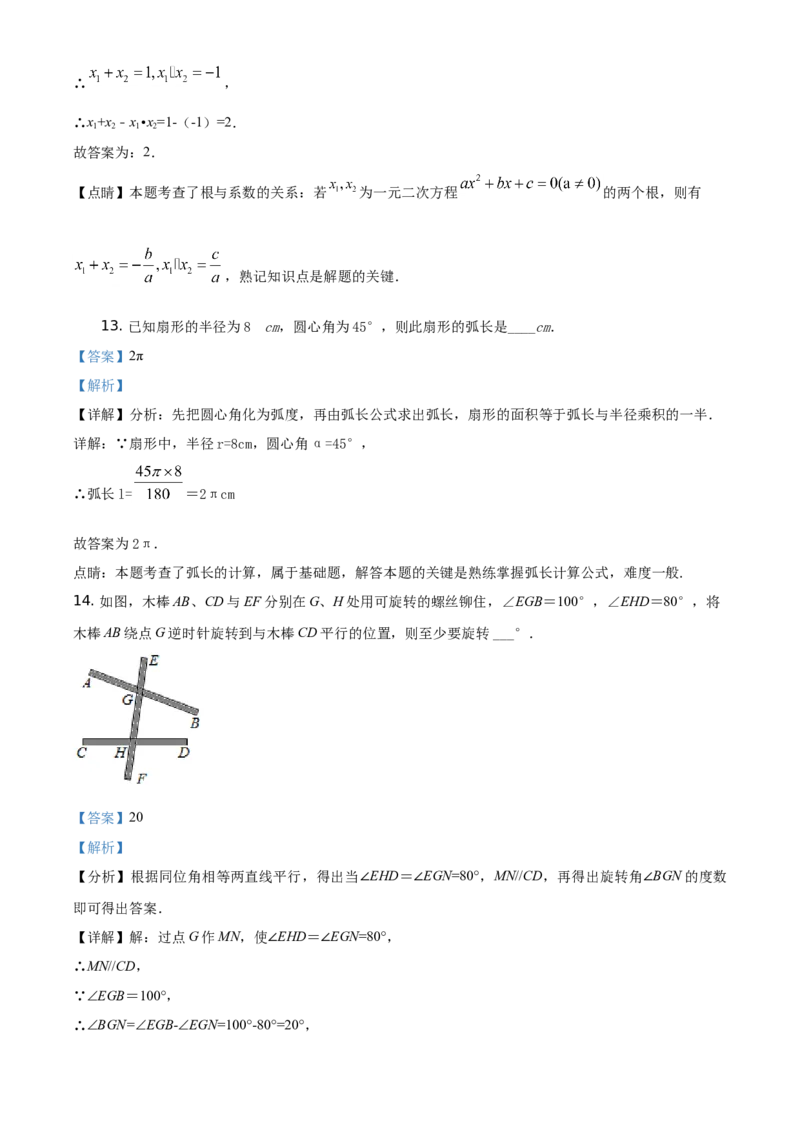
2. 如图所示几何体的左视图是( )
A. B.
C. D.
【答案】C
【解析】
【分析】根据从左面看得到的图形是左视图,可得答案.
【详解】解:如图所示,几何体的左视图是:
故选:C.
【点睛】本题考查了简单组合体的三视图,从左面看得到的图形是左视图.3. 下列各组二次根式中,化简后是同类二次根式的是( )
A. 与 B. 与 C. 与 D. 与
【答案】D
【解析】
【分析】把每个选项中的不是最简二次根式化为最简二次根式即可作出判断.
【详解】A、 , 与 不是同类二次根式,故此选项错误;
B、 , 与 不是同类二次根式,故此选项错误;
C、 与 不是同类二次根式,故此选项错误;
D、 , , 与3 是同类二次根式,故此选项正确.
故选:D.
【点睛】本题考查了二次根式的化简,同类二次根式的识别等知识,注意二次根式必须化成最简二次根式.
4. “14人中至少有2人在同一个月过生日”这一事件发生的概率为P,则( )
A. P=0 B. 0<P<1 C. P=1 D. P>1
【答案】C
【解析】
【分析】根据不可能事件的概率为 ,随机事件的概率大于 而小于 ,必然事件的概率为1,即可判断.
【详解】解:∵一年有12个月,14个人中有12个人在不同的月份过生日,剩下的两人不论哪个月生日,
都和前12人中的一个人同一个月过生日
∴“14人中至少有2人在同一个月过生日”是必然事件,
即这一事件发生的概率为 .
故选: .
【点睛】本题考查了概率的初步认识,确定此事件为必然事件是解题的关键.
5. 如图,P为AB上任意一点,分别以AP、PB为边在AB同侧作正方形APCD、正方形PBEF,设 ,
则 为( )A. 2α B. 90°﹣α C. 45°+α D. 90°﹣ α
【答案】B
【解析】
【分析】根据题意可得 ,从而 即可.
【详解】∵四边形APCD和四边形PBEF是正方形,
∴AP=CP,PF=PB, ,
∴ ,
∴∠AFP=∠CBP,
又∵ ,
∴ ,
故选:B.
【点睛】本题主要考查了正方形的性质,全等三角形的判定,熟练掌握正方形的性质,全等三角形的判定
方法是解题的关键.
6. 互不重合的A、B、C三点在同一直线上,已知AC=2a+1,BC=a+4,AB=3a,这三点的位置关系是(
)
A. 点A在B、C两点之间 B. 点B在A、C两点之间
C. 点C在A、B两点之间 D. 无法确定
【答案】A
【解析】
【分析】分别对每种情况进行讨论,看a的值是否满足条件再进行判断.
【详解】解:①当点A在B、C两点之间,则满足 ,
即 ,
解得: ,符合题意,故选项A正确;
②点B在A、C两点之间,则满足 ,
即 ,解得: ,不符合题意,故选项B错误;
③点C在A、B两点之间,则满足 ,
即 ,
解得:a无解,不符合题意,故选项C错误;
故选项D错误;
故选:A.
【点睛】本题主要考查了线段 的和与差及一元一次方程的解法,分类讨论并列出对应的式子是解本题的关
键.
二、填空题(本大题共有10小题,每小题3分,共30分)
7. 计算:﹣(﹣2)=___.
【答案】2
【解析】
【分析】根据相反数的定义即可得答案.
【详解】﹣(﹣2)=2,
故答案为:2
【点睛】本题考查相反数的定义,只有符号不同的两个数互为相反数;熟练掌握定义是解题关键.
8. 函数: 中,自变量x的取值范围是_____.
【答案】
【解析】
【详解】求函数自变量的取值范围,就是求函数解析式有意义的条件,根据分式分母不为 0的条件,要使
在实数范围内有意义,必须 ,即 .
9. 2021年5月,中国首个火星车“祝融号”成功降落在火星上直径为3200km的乌托邦平原.把数据3200
用科学记数法表示为 ___.
【答案】
【解析】【分析】用科学记数法表示较大的数时,一般形式为 ,其中 ,n为正整数.
【详解】解: .
故答案为: .
【点睛】本题考查了科学记数法较大数的表示,确定a与n是解题的关键.
10. 在函数 中,当x>1时,y随x的增大而 ___.(填“增大”或“减小”)
【答案】增大
【解析】
【分析】根据其顶点式函数 可知,抛物线开口向上,对称轴为 ,在对称轴右侧y随x的增大
而增大,可得到答案.
【详解】由题意可知: 函数 ,开口向上,在对称轴右侧y随x的增大而增大,又∵对称轴为 ,
∴当 时,y随的增大而增大,
故答案为:增大.
【点睛】本题主要考查了二次函数的对称轴及增减性,掌握当二次函数开口向上时,在对称轴的右侧y随x的
增大而增大,在对称轴的左侧y随x的增大而减小是解题的关键.
11. 某班按课外阅读时间将学生分为3组,第1、2组的频率分别为0.2、0.5,则第3组的频率是 ___.
【答案】0.3
【解析】
【分析】利用1减去第1、2组的频率即可得出第3组的频率.
【详解】解:1-0.2-0.5=0.3,
∴第3组的频率是0.3;
故答案为:0.3
【点睛】本题考查了频率,熟练掌握频率的定义和各小组的频率之和为1是解题的关键.
12. 关于x的方程x2﹣x﹣1=0的两根分别为x、x 则x+x﹣x•x 的值为 ___.
1 2 1 2 1 2
【答案】2.
【解析】
【分析】先根据根与系数 的关系得到 ,然后利用整体代入的方法计算即可.
【详解】解:∵关于x的方程x2﹣x﹣1=0的两根分别为x、x,
1 2∴ ,
∴x+x﹣x•x=1-(-1)=2.
1 2 1 2
故答案为:2.
【点睛】本题考查了根与系数的关系:若 为一元二次方程 的两个根,则有
,熟记知识点是解题的关键.
13. 已知扇形的半径为8 cm,圆心角为45°,则此扇形的弧长是____cm.
【答案】2π
【解析】
【详解】分析:先把圆心角化为弧度,再由弧长公式求出弧长,扇形的面积等于弧长与半径乘积的一半.
详解:∵扇形中,半径r=8cm,圆心角α=45°,
∴弧长l= =2πcm
故答案为2π.
点睛:本题考查了弧长的计算,属于基础题,解答本题的关键是熟练掌握弧长计算公式,难度一般.
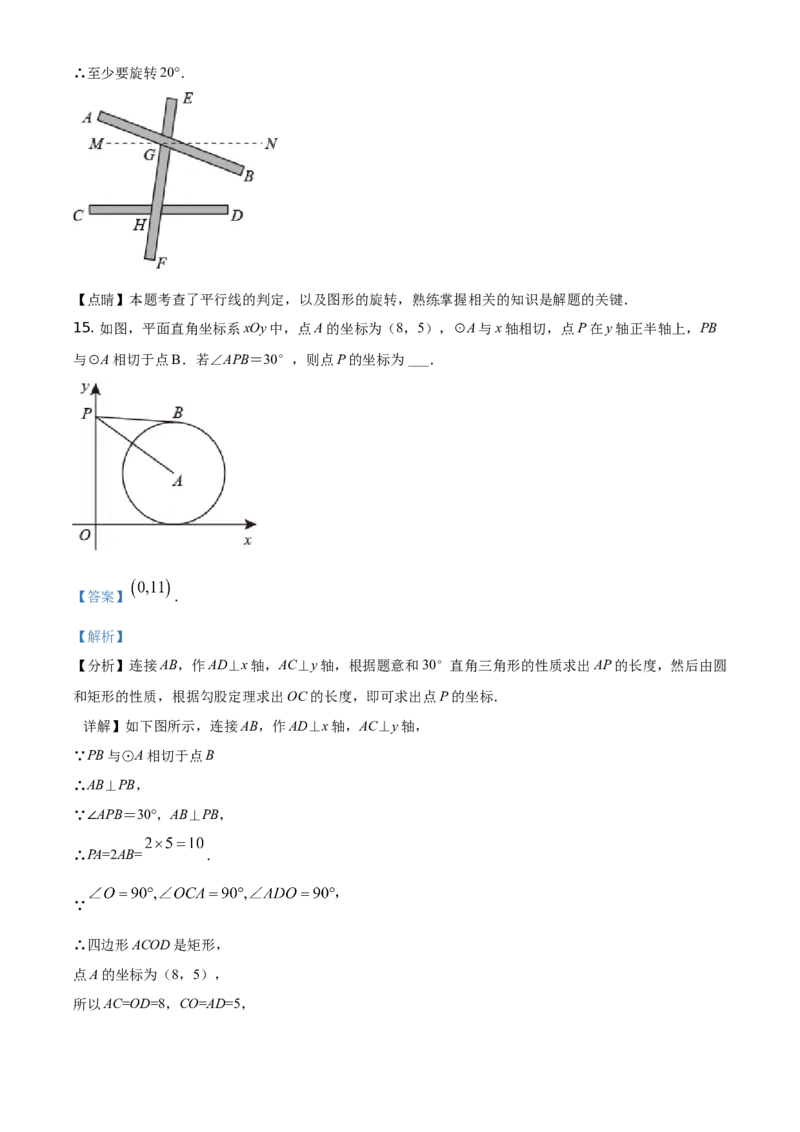
14. 如图,木棒AB、CD与EF分别在G、H处用可旋转的螺丝铆住,∠EGB=100°,∠EHD=80°,将
木棒AB绕点G逆时针旋转到与木棒CD平行的位置,则至少要旋转 ___°.
【答案】20
【解析】
【分析】根据同位角相等两直线平行,得出当∠EHD=∠EGN=80°,MN//CD,再得出旋转角∠BGN的度数
即可得出答案.
【详解】解:过点G作MN,使∠EHD=∠EGN=80°,
∴MN//CD,
∵∠EGB=100°,
∴∠BGN=∠EGB-∠EGN=100°-80°=20°,∴至少要旋转20°.
【点睛】本题考查了平行线的判定,以及图形的旋转,熟练掌握相关的知识是解题的关键.
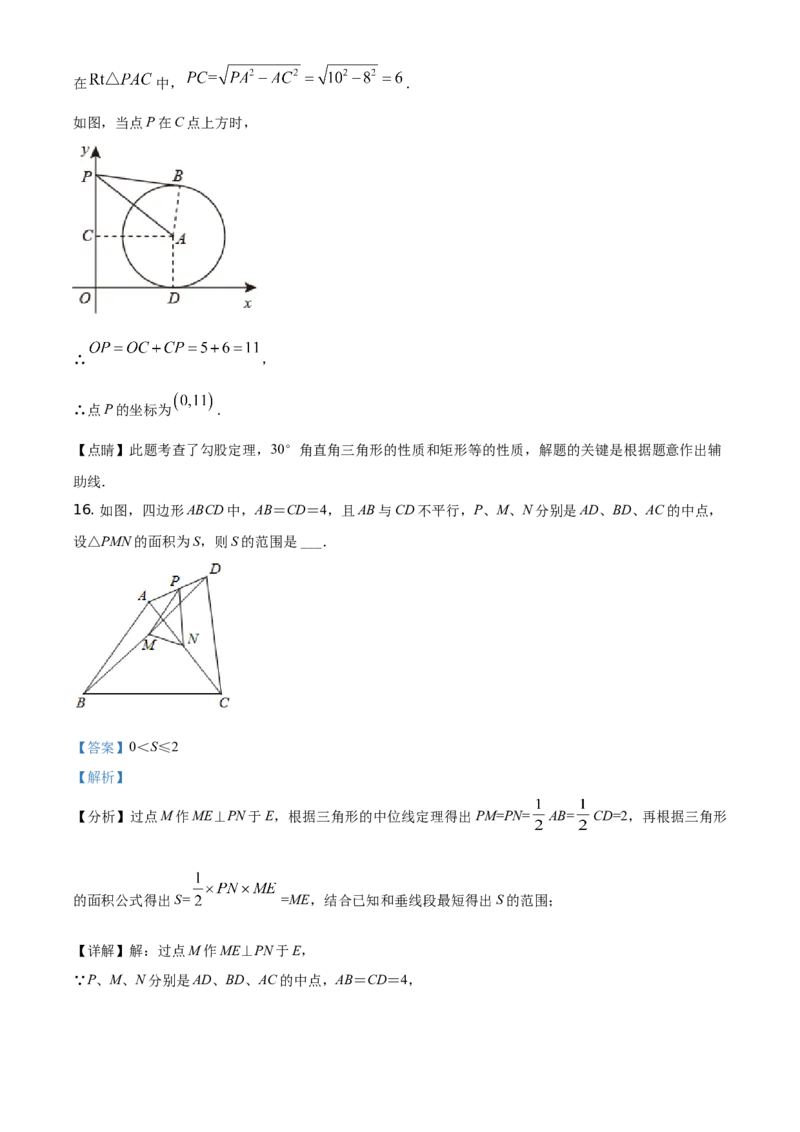
15. 如图,平面直角坐标系xOy中,点A的坐标为(8,5),⊙A与x轴相切,点P在y轴正半轴上,PB
与⊙A相切于点B.若∠APB=30°,则点P的坐标为 ___.
【答案】 .
【解析】
【分析】连接AB,作AD⊥x轴,AC⊥y轴,根据题意和30°直角三角形的性质求出AP的长度,然后由圆
和矩形的性质,根据勾股定理求出OC的长度,即可求出点P的坐标.
【详解】如下图所示,连接AB,作AD⊥x轴,AC⊥y轴,
∵PB与⊙A相切于点B
∴AB⊥PB,
∵∠APB=30°,AB⊥PB,
∴PA=2AB= .
∵
∴四边形ACOD是矩形,
点A的坐标为(8,5),
所以AC=OD=8,CO=AD=5,在 中, .
如图,当点P在C点上方时,
∴ ,
∴点P的坐标为 .
【点睛】此题考查了勾股定理,30°角直角三角形的性质和矩形等的性质,解题的关键是根据题意作出辅
助线.
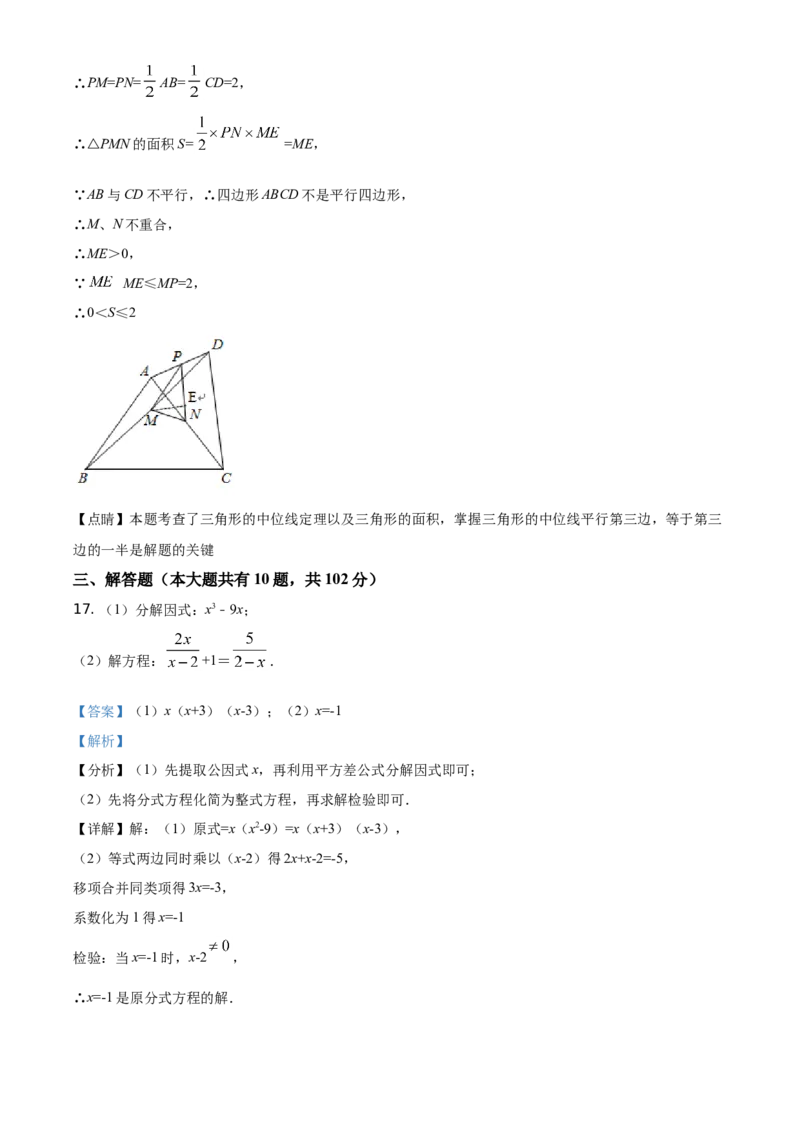
16. 如图,四边形ABCD中,AB=CD=4,且AB与CD不平行,P、M、N分别是AD、BD、AC的中点,
设△PMN的面积为S,则S的范围是 ___.
【答案】0<S≤2
【解析】
【分析】过点M作ME⊥PN于E,根据三角形的中位线定理得出PM=PN= AB= CD=2,再根据三角形
的面积公式得出S= =ME,结合已知和垂线段最短得出S的范围;
【详解】解:过点M作ME⊥PN于E,
∵P、M、N分别是AD、BD、AC的中点,AB=CD=4,∴PM=PN= AB= CD=2,
∴△PMN的面积S= =ME,
∵AB与CD不平行,∴四边形ABCD不是平行四边形,
∴M、N不重合,
∴ME>0,
∵ ME≤MP=2,
∴0<S≤2
【点睛】本题考查了三角形的中位线定理以及三角形的面积,掌握三角形的中位线平行第三边,等于第三
边的一半是解题的关键
三、解答题(本大题共有10题,共102分)
17. (1)分解因式:x3﹣9x;
(2)解方程: +1= .
【答案】(1)x(x+3)(x-3);(2)x=-1
【解析】
【分析】(1)先提取公因式x,再利用平方差公式分解因式即可;
(2)先将分式方程化简为整式方程,再求解检验即可.
【详解】解:(1)原式=x(x2-9)=x(x+3)(x-3),
(2)等式两边同时乘以(x-2)得2x+x-2=-5,
移项合并同类项得3x=-3,
系数化为1得x=-1
检验:当x=-1时,x-2 ,
∴x=-1是原分式方程的解.【点睛】本题考查了因式分解和解分式方程,解题关键是熟练掌握因式分解的方法及注意解分式方程要检
验.
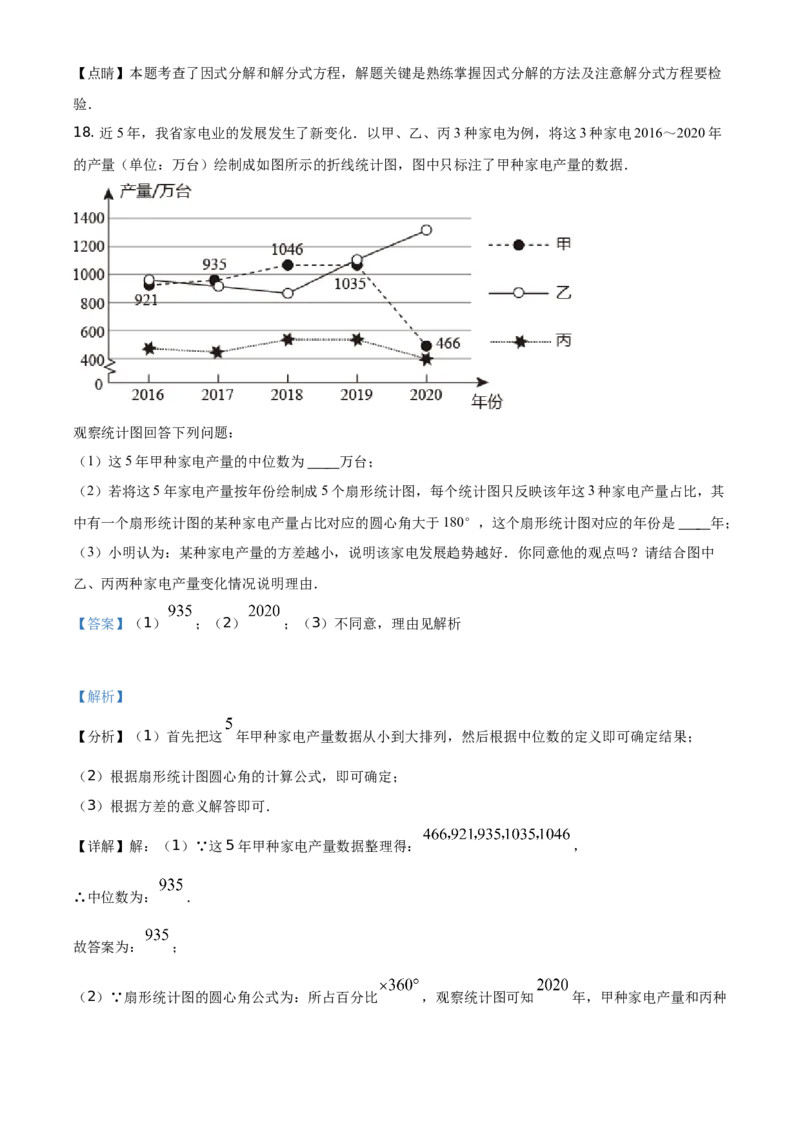
18. 近5年,我省家电业的发展发生了新变化.以甲、乙、丙3种家电为例,将这3种家电2016~2020年
的产量(单位:万台)绘制成如图所示的折线统计图,图中只标注了甲种家电产量的数据.
观察统计图回答下列问题:
(1)这5年甲种家电产量的中位数为 万台;
(2)若将这5年家电产量按年份绘制成5个扇形统计图,每个统计图只反映该年这3种家电产量占比,其
中有一个扇形统计图的某种家电产量占比对应的圆心角大于180°,这个扇形统计图对应的年份是 年;
(3)小明认为:某种家电产量的方差越小,说明该家电发展趋势越好.你同意他的观点吗?请结合图中
乙、丙两种家电产量变化情况说明理由.
【答案】(1) ;(2) ;(3)不同意,理由见解析
【解析】
【分析】(1)首先把这 年甲种家电产量数据从小到大排列,然后根据中位数的定义即可确定结果;
(2)根据扇形统计图圆心角的计算公式,即可确定;
(3)根据方差的意义解答即可.
【详解】解:(1)∵这5年甲种家电产量数据整理得: ,
∴中位数为: .
故答案为: ;
(2)∵扇形统计图的圆心角公式为:所占百分比 ,观察统计图可知 年,甲种家电产量和丙种家电产量之和小于乙种产量,
∴ 年乙种家电产量占比对应的圆心角大于 .
故答案为: ;
(3)不同意,理由如下:
因为方差只是反映一组数据的离散程度,方差越小说明数据波动越小,越稳定;从图中乙、丙两种家电产
量的变化情况来看,丙种家电产量较为稳定,即方差较小,乙种家电产量波动较大,即方差较大,但是从
年起丙种家电的产量在逐年降低,而乙种家电的产量在逐年提高,所以乙种家电发展趋势更好,即
家电产量的方差越小,不能说明该家电发展趋势越好.
【点睛】本题考查了中位数、扇形统计图、方差等,掌握相关知识是解题的关键.
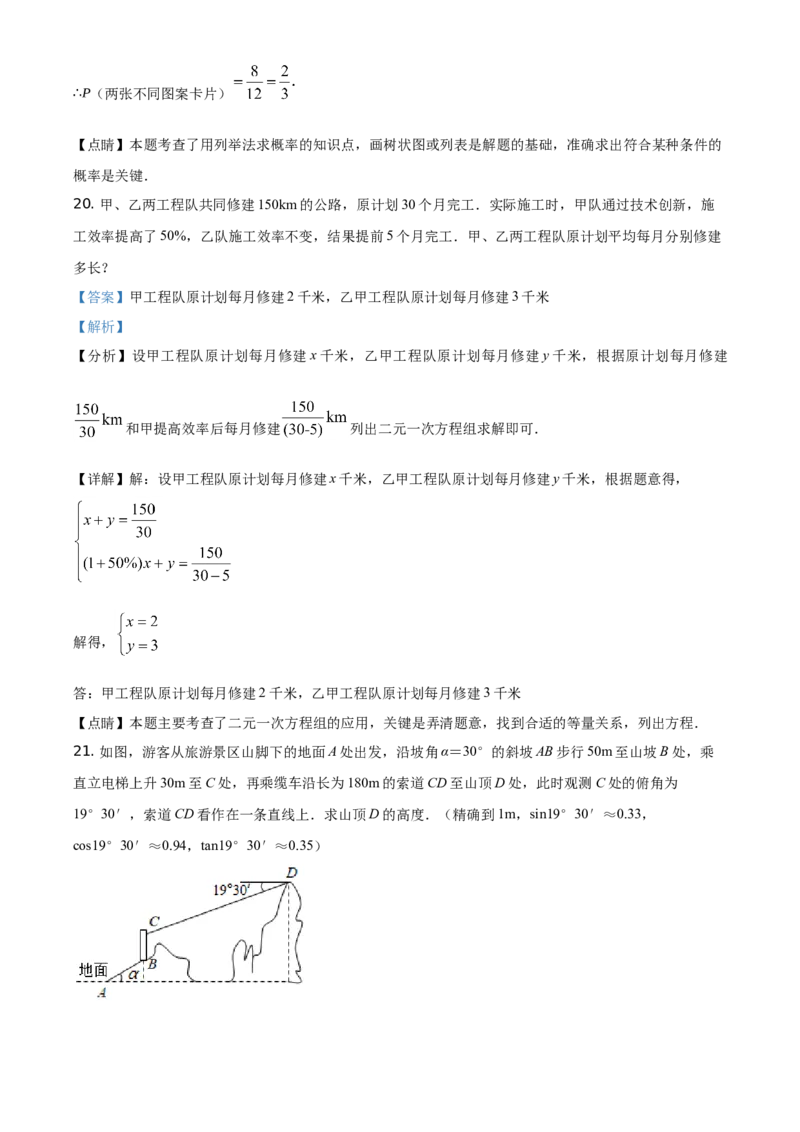
19. 江苏省第20届运动会将在泰州举办,“泰宝”和“凤娃”是运动会吉祥物.在一次宣传活动中,组织
者将分别印有这两种吉祥物图案的卡片各2张放在一个不透明的盒子中并搅匀,卡片除图案外其余均相同.
小张从中随机抽取2张换取相应的吉祥物,抽取方式有两种:第一种是先抽取1张不放回,再抽取1张;
第二种是一次性抽取2张.
(1)两种抽取方式抽到不同图案卡片的概率 (填“相同”或“不同”);
(2)若小张用第一种方式抽取卡片,求抽到不同图案卡片的概率.
【答案】(1)相同;(2)
【解析】
【分析】(1)画树状图即可判断;
(2)结合第(1)题所画树状图可求概率.
【详解】解:(1)设两张“泰宝”图案卡片为 ,两张“凤娃”图案卡片为
画出两种方式的树状图,是相同的,所以抽到不同图案卡片的概率是相同的.
故答案为:相同
(2)由(1)中的树状图可知,抽取到的两张卡片,共有12种等可能的结果,其中抽到不同图案卡片的
结果有8种.∴P(两张不同图案卡片)
【点睛】本题考查了用列举法求概率的知识点,画树状图或列表是解题的基础,准确求出符合某种条件的
概率是关键.
20. 甲、乙两工程队共同修建150km的公路,原计划30个月完工.实际施工时,甲队通过技术创新,施
工效率提高了50%,乙队施工效率不变,结果提前5个月完工.甲、乙两工程队原计划平均每月分别修建
多长?
【答案】甲工程队原计划每月修建2千米,乙甲工程队原计划每月修建3千米
【解析】
【分析】设甲工程队原计划每月修建x千米,乙甲工程队原计划每月修建y千米,根据原计划每月修建
和甲提高效率后每月修建 列出二元一次方程组求解即可.
【详解】解:设甲工程队原计划每月修建x千米,乙甲工程队原计划每月修建y千米,根据题意得,
解得,
答:甲工程队原计划每月修建2千米,乙甲工程队原计划每月修建3千米
【点睛】本题主要考查了二元一次方程组的应用,关键是弄清题意,找到合适的等量关系,列出方程.
21. 如图,游客从旅游景区山脚下的地面A处出发,沿坡角α=30°的斜坡AB步行50m至山坡B处,乘
直立电梯上升30m至C处,再乘缆车沿长为180m的索道CD至山顶D处,此时观测C处的俯角为
19°30′,索道CD看作在一条直线上.求山顶D的高度.(精确到1m,sin19°30′≈0.33,
cos19°30′≈0.94,tan19°30′≈0.35)【答案】114m
【解析】
【分析】过点C作CE⊥DG于E,CB的延长线交AG于F,在Rt△BAF中可求得BF的长,从而可得CF
的长;在Rt△DCE中,利用锐角三角函数可求得DE的长,从而由DG=DE+CF即可求得山顶D的高度.
【详解】过点C作CE⊥DG于E,CB的延长线交AG于F,设山顶的所在线段为DG,如图所示
在Rt△BAF中,α=30°,AB=50m
则BF= (m)
∴CF=BC+BF=30+25=55(m)
在Rt△DCE中,∠DCE ,CD=180m
∴ (m)
∵四边形CFGE是矩形
∴EG=CF
∴DG=DE+EG=DE+CF=59+55=114(m)
即山顶D的高度为114m.
【点睛】本题考查了解直角三角形在实际测量中的应用,题目较简单,但这里出现了坡角、俯角等概念,
要理解其含义,另外通过作适当的辅助线,把问题转化为在直角三角形中解决.
22. 如图,点A(﹣2,y)、B(﹣6,y)在反比例函数y= (k<0)的图象上,AC⊥x轴,BD⊥y轴,
1 2
垂足分别为C、D,AC与BD相交于点E.(1)根据图象直接写出y、y 的大小关系,并通过计算加以验证;
1 2
(2)结合以上信息,从①四边形OCED的面积为2,②BE=2AE这两个条件中任选一个作为补充条件,
求k的值.你选择的条件是 (只填序号).
【答案】(1) ,见解析;(2)见解析,①(也可以选择②)
【解析】
【分析】(1)观察函数的图象即可作出判断,再根据A、B两点在反比例函数图象上,把两点的坐标代入
后作差比较即可;
(2)若选择条件①,由面积的值及OC的长度,可得OD的长度,从而可得点B的坐标,把此点坐标代入函
数解析式中,即可求得k;若选择条件②,由DB=6及OC=2,可得BE的长度,从而可得AE长度,此长度即
为A、B两点纵坐标的差,(1)所求得的差即可求得k.
【详解】(1)由于图象从左往右是上升的,即自变量增大,函数值也随之增大,故 ;
当x=-6时, ;当x=-2时,
∵ ,k<0
∴
即
(2)选择条件①
∵AC⊥x轴,BD⊥y轴,OC⊥OD
∴四边形OCED是矩形
∴ODOC=2
∵OC=∙2
∴OD=1即
∴点B的坐标为(-6,1)
把点B的坐标代入y= 中,得k=-6
若选择条件②,即BE=2AE
∵AC⊥x轴,BD⊥y轴,OC⊥OD
∴四边形OCED是矩形
∴DE=OC,CE=OD
∵OC=2,DB=6
∴BE=DB-DE=DB-OC=4
∴
∵AE=AC-CE=AC-OD=
即
由(1)知:
∴k=-6
【点睛】本题考查了反比例函数的图象和性质、矩形的判定与性质、大小比较,熟练掌握反比例函数的图
象与性质是解决本题的关键.
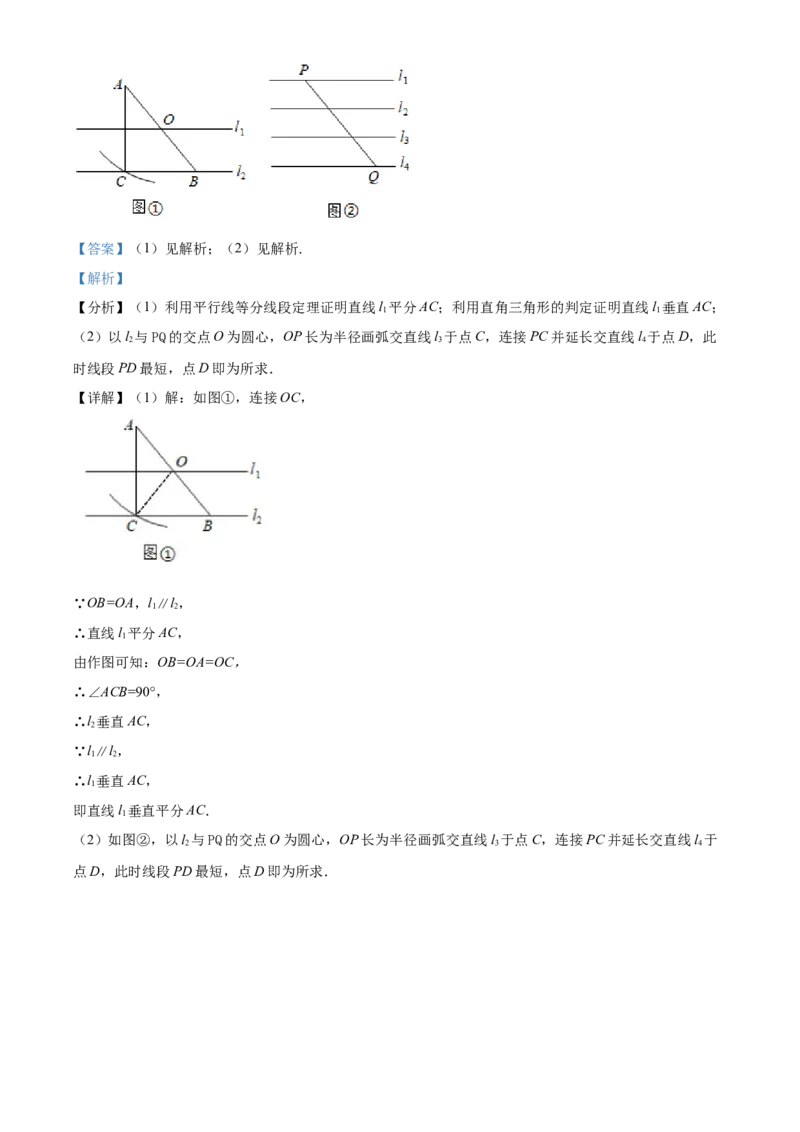
23. (1)如图①,O为AB的中点,直线l、l 分别经过点O、B,且l∥l,以点O为圆心,OA长为半径
1 2 1 2
画弧交直线l 于点C,连接AC.求证:直线l 垂直平分AC;
2 1
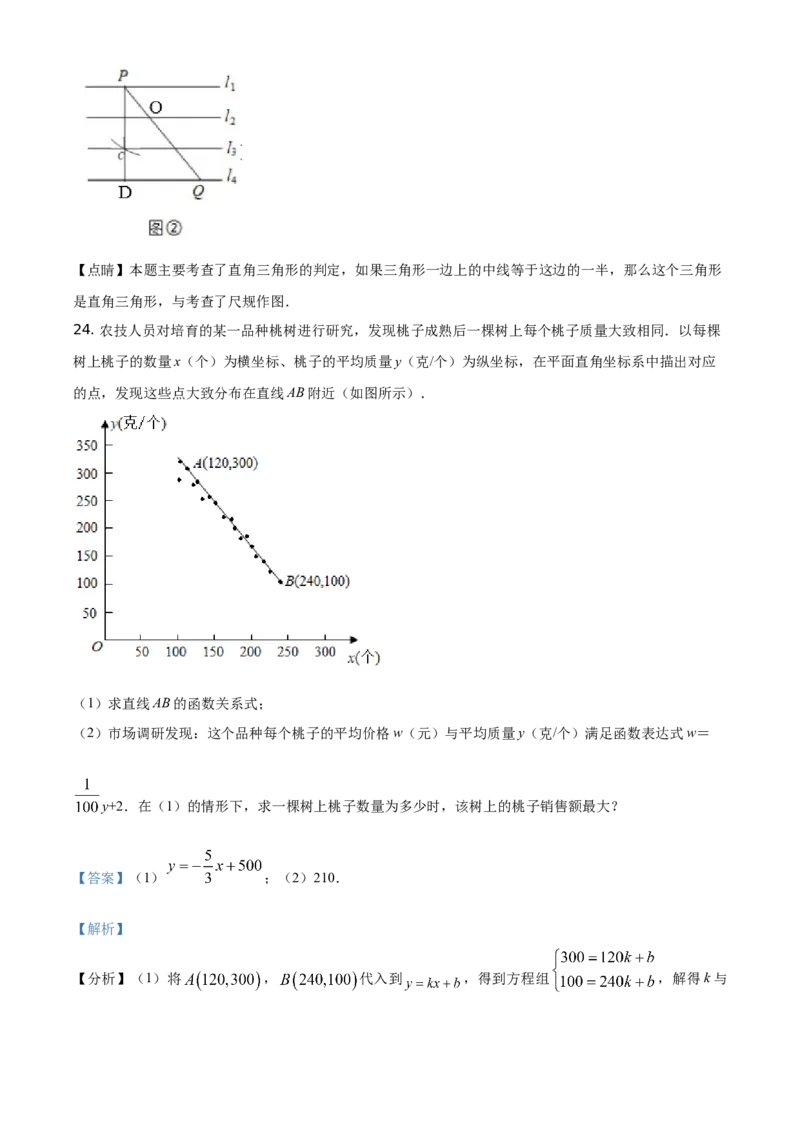
(2)如图②,平面内直线l∥l∥l∥l,且相邻两直线间距离相等,点P、Q分别在直线l、l 上,连接
1 2 3 4 1 4
PQ.用圆规和无刻度的直尺在直线l 上求作一点D,使线段PD最短.(两种工具分别只限使用一次,并
4
保留作图痕迹)【答案】(1)见解析;(2)见解析.
【解析】
【分析】(1)利用平行线等分线段定理证明直线l 平分AC;利用直角三角形的判定证明直线l 垂直AC;
1 1
(2)以l 与PQ的交点O为圆心,OP长为半径画弧交直线l 于点C,连接PC并延长交直线l 于点D,此
2 3 4
时线段PD最短,点D即为所求.
【详解】(1)解:如图①,连接OC,
∵OB=OA,l∥l,
1 2
∴直线l 平分AC,
1
由作图可知:OB=OA=OC,
∴∠ACB=90°,
∴l 垂直AC,
2
∵l∥l,
1 2
∴l 垂直AC,
1
即直线l 垂直平分AC.
1
(2)如图②,以l 与PQ的交点O为圆心,OP长为半径画弧交直线l 于点C,连接PC并延长交直线l 于
2 3 4
点D,此时线段PD最短,点D即为所求.【点睛】本题主要考查了直角三角形的判定,如果三角形一边上的中线等于这边的一半,那么这个三角形
是直角三角形,与考查了尺规作图.
24. 农技人员对培育的某一品种桃树进行研究,发现桃子成熟后一棵树上每个桃子质量大致相同.以每棵
树上桃子的数量x(个)为横坐标、桃子的平均质量y(克/个)为纵坐标,在平面直角坐标系中描出对应
的点,发现这些点大致分布在直线AB附近(如图所示).
(1)求直线AB的函数关系式;
(2)市场调研发现:这个品种每个桃子的平均价格w(元)与平均质量y(克/个)满足函数表达式w=
y+2.在(1)的情形下,求一棵树上桃子数量为多少时,该树上的桃子销售额最大?
【答案】(1) ;(2)210.
【解析】
【分析】(1)将 , 代入到 ,得到方程组 ,解得k与b的值,即可求出直线AB的解析式;
(2)将 代入 中,得到新的二次函数解析式,再表示出总销售额,配方成顶
点式,求出最值即可.
【详解】解:(1)设直线AB的函数关系式为 ,
将 , 代入可得: ,
解得: ,
∴直线AB的函数关系式 .
故答案为: .
(2)将 代入 中,
可得: ,
化简得: ,
设总销售额为 ,则∵ ,
∴ 有最大值,当 时, 取到最大值,最大值为735.
故答案为:210.
【点睛】本题考查了一次函数解析式的求解,二次函数的应用,能理解题意,并表示出其解析式是解题关
键.
25. 二次函数y=﹣x2+(a﹣1)x+a(a为常数)图象的顶点在y轴右侧.
(1)写出该二次函数图象的顶点横坐标(用含a的代数式表示);
(2)该二次函数表达式可变形为y=﹣(x﹣p)(x﹣a)的形式,求p的值;
(3)若点A(m,n)在该二次函数图象上,且n>0,过点(m+3,0)作y轴的平行线,与二次函数图象
的交点在x轴下方,求a的范围.
【答案】(1) ;(2)p=-1;(3)1< <2.
【解析】
【分析】(1)根据顶点坐标公式即可得答案;
(2)利用十字相乘法分解因式即可得答案;
(3)利用(2)的结果可得抛物线与x轴的交点坐标,根据顶点在y轴右侧,过点(m+3,0)作y轴的平
行线,与二次函数图象的交点在x轴下方可得关于a的不等式,解不等式即可得答案.
【详解】(1)∵二次函数解析式y=﹣x2+(a﹣1)x+a,
∴顶点横坐标为 = .
(2)∵y=﹣x2+(a﹣1)x+a= =﹣(x﹣p)(x﹣a),
∴p=-1.
(3)∵y=﹣x2+(a﹣1)x+a= ,
∴抛物线与x轴的交点坐标为(-1,0),(a,0),
∵-1<0,
∴该二次函数的图象开口向下,
∵图象的顶点在y轴右侧,∴ >0,
∴ ,
∵点A(m,n)在该二次函数图象上,且n>0,
∴-1<m<a,
∵过点(m+3,0)作y轴的平行线,与二次函数图象的交点在x轴下方,
∴ <3,
解得: ,
∴a的范围为1< <2.
【点睛】本题考查二次函数、因式分解及解一元一次不等式,熟练掌握二次函数顶点坐标公式是解题关键.
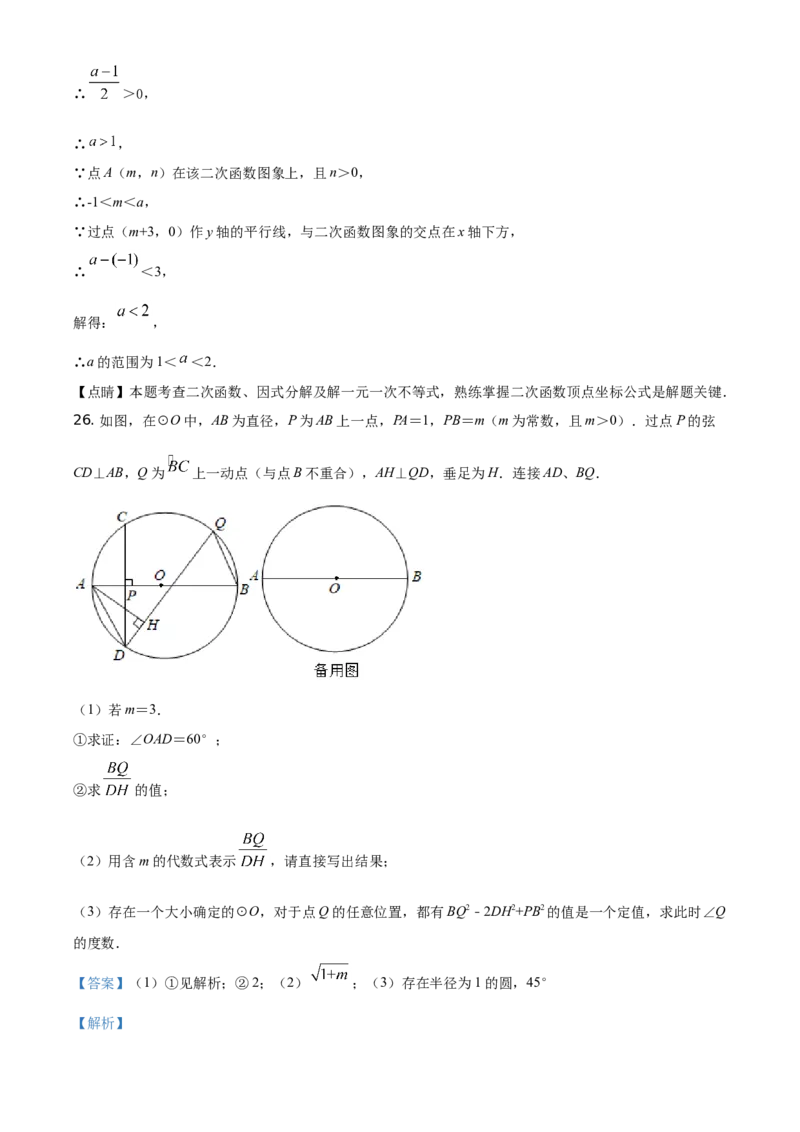
26. 如图,在⊙O中,AB为直径,P为AB上一点,PA=1,PB=m(m为常数,且m>0).过点P的弦
CD⊥AB,Q为 上一动点(与点B不重合),AH⊥QD,垂足为H.连接AD、BQ.
(1)若m=3.
①求证:∠OAD=60°;
②求 的值;
(2)用含m的代数式表示 ,请直接写出结果;
(3)存在一个大小确定的⊙O,对于点Q的任意位置,都有BQ2﹣2DH2+PB2的值是一个定值,求此时∠Q
的度数.
【答案】(1)①见解析;②2;(2) ;(3)存在半径为1的圆,45°
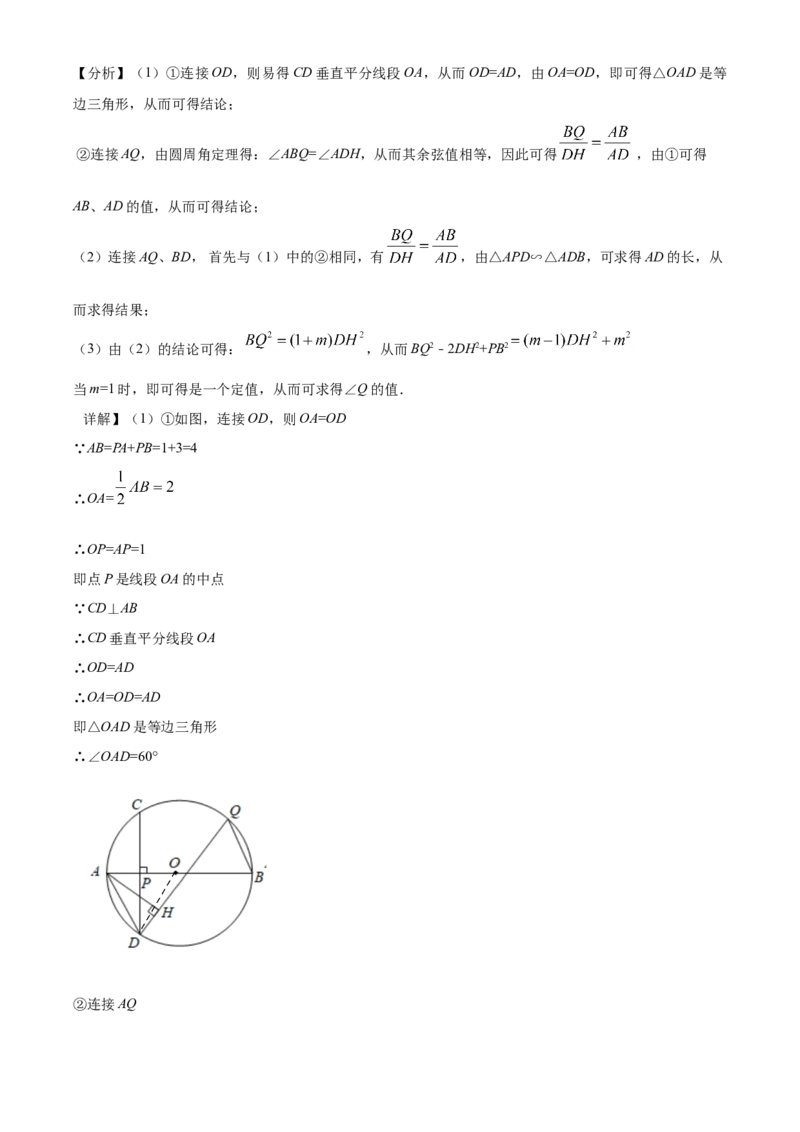
【解析】【分析】(1)①连接OD,则易得CD垂直平分线段OA,从而OD=AD,由OA=OD,即可得△OAD是等
边三角形,从而可得结论;
②连接AQ,由圆周角定理得:∠ABQ=∠ADH,从而其余弦值相等,因此可得 ,由①可得
AB、AD的值,从而可得结论;
(2)连接AQ、BD, 首先与(1)中的②相同,有 ,由△APD∽△ADB,可求得AD的长,从
而求得结果;
(3)由(2)的结论可得: ,从而BQ2﹣2DH2+PB2
当m=1时,即可得是一个定值,从而可求得∠Q的值.
【详解】(1)①如图,连接OD,则OA=OD
∵AB=PA+PB=1+3=4
∴OA=
∴OP=AP=1
即点P是线段OA的中点
∵CD⊥AB
∴CD垂直平分线段OA
∴OD=AD
∴OA=OD=AD
即△OAD是等边三角形
∴∠OAD=60°
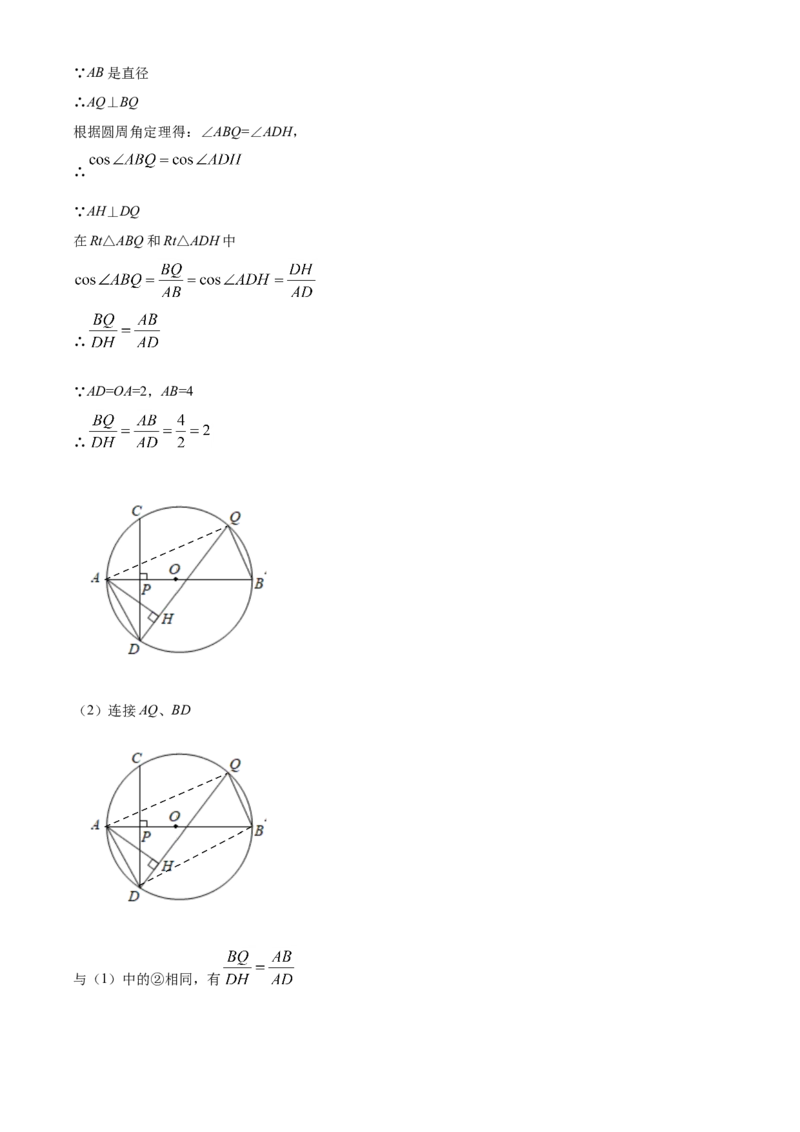
②连接AQ∵AB是直径
∴AQ⊥BQ
根据圆周角定理得:∠ABQ=∠ADH,
∴
∵AH⊥DQ
在Rt△ABQ和Rt△ADH中
∴
∵AD=OA=2,AB=4
∴
(2)连接AQ、BD
与(1)中的②相同,有∵AB是直径
∴AD⊥BD
∴∠DAB+∠ADP=∠DAB+∠ABD=90°
∴∠ADP=∠ABD
∴Rt△APD∽Rt△ADB
∴
∵AB=PA+PB=1+m
∴
∴
(3)由(2)知,
∴BQ=
即
∴BQ2﹣2DH2+PB2=
当m=1时,BQ2﹣2DH2+PB2是一个定值,且这个定值为1,此时PA=PB=1,即点P与圆心O重合
∵CD⊥AB,OA=OD=1
∴△AOD是等腰直角三角形
∴∠OAD=45°
∵∠OAD与∠Q对着同一条弧
∴∠Q=∠OAD=45°
故存在半径为1的圆,对于点Q的任意位置,都有BQ2﹣2DH2+PB2的值是一个定值1,此时∠Q的度数为
45.
【点睛】本题是圆的综合,它考查了圆的基本性质,锐角三角函数,相似三角形的判定与性质,等边三角
形的判定与性质等知识,难点是第(3)问,得出BQ2﹣2DH2+PB2 后,当m=1即可得
出BQ2﹣2DH2+PB2是一个定值.