文档内容
2021年浙江省嘉兴市中考数学试卷
一、选择题(本题有10小题,每题3分,共30分,请选出各题中唯一的正确选项,不选、
多选错选,均不得分)
1.2021年5月22日,我国自主研发的“祝融号”火星车成功到达火星表面.已知火星与
地球的最近距离约为55000000千米,数据55000000用科学记数法表示为( )
A.55×106 B.5.5×107 C.5.5×108 D.0.55×108
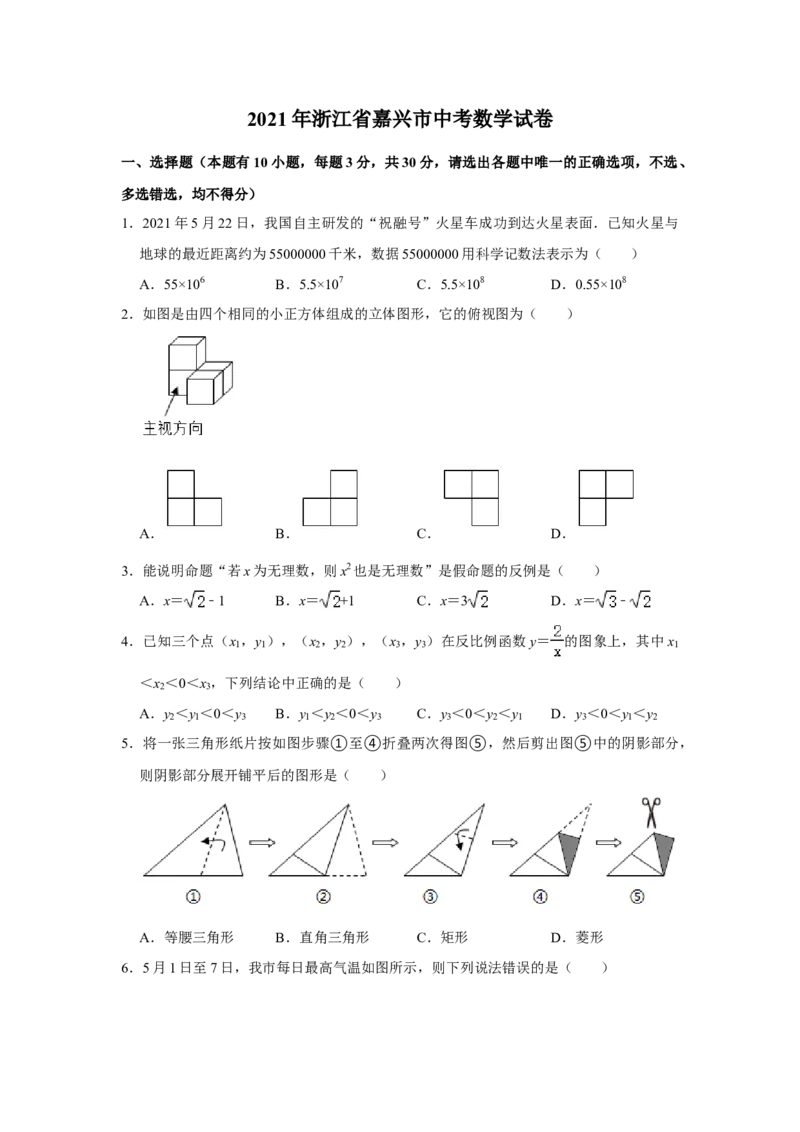
2.如图是由四个相同的小正方体组成的立体图形,它的俯视图为( )
A. B. C. D.
3.能说明命题“若x为无理数,则x2也是无理数”是假命题的反例是( )
A.x= ﹣1 B.x= +1 C.x=3 D.x= ﹣
4.已知三个点(x ,y ),(x ,y ),(x ,y )在反比例函数y= 的图象上,其中x
1 1 2 2 3 3 1
<x <0<x ,下列结论中正确的是( )
2 3
A.y <y <0<y B.y <y <0<y C.y <0<y <y D.y <0<y <y
2 1 3 1 2 3 3 2 1 3 1 2
5.将一张三角形纸片按如图步骤①至④折叠两次得图⑤,然后剪出图⑤中的阴影部分,
则阴影部分展开铺平后的图形是( )
A.等腰三角形 B.直角三角形 C.矩形 D.菱形
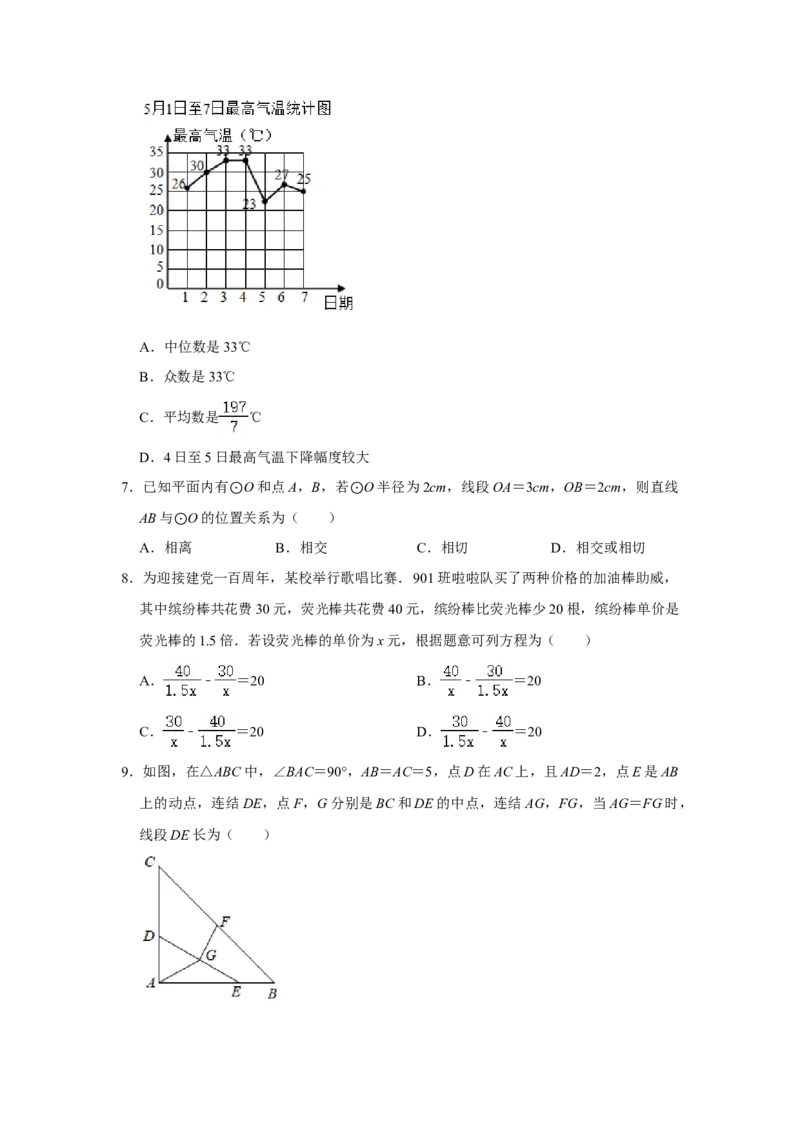
6.5月1日至7日,我市每日最高气温如图所示,则下列说法错误的是( )A.中位数是33℃
B.众数是33℃
C.平均数是 ℃
D.4日至5日最高气温下降幅度较大
7.已知平面内有 O和点A,B,若 O半径为2cm,线段OA=3cm,OB=2cm,则直线
AB与 O的位置⊙关系为( ) ⊙
A.相⊙离 B.相交 C.相切 D.相交或相切
8.为迎接建党一百周年,某校举行歌唱比赛.901班啦啦队买了两种价格的加油棒助威,
其中缤纷棒共花费30元,荧光棒共花费40元,缤纷棒比荧光棒少20根,缤纷棒单价是
荧光棒的1.5倍.若设荧光棒的单价为x元,根据题意可列方程为( )
A. ﹣ =20 B. ﹣ =20
C. ﹣ =20 D. ﹣ =20
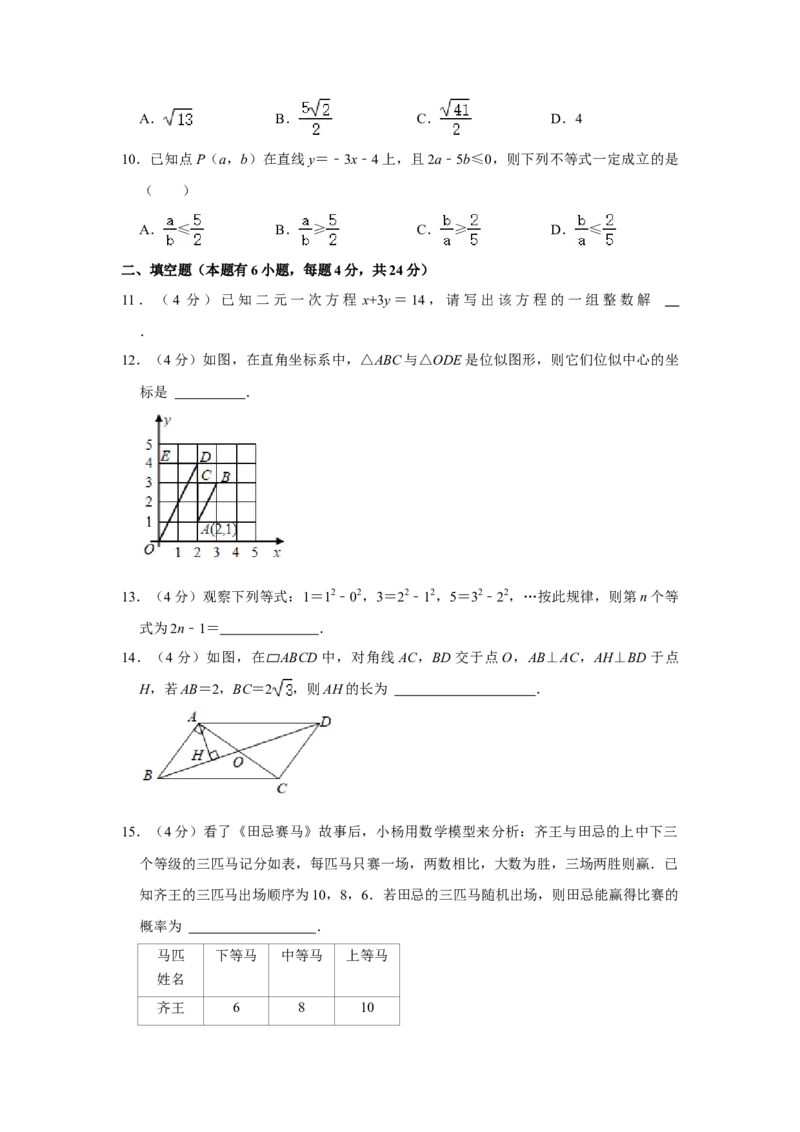
9.如图,在△ABC中,∠BAC=90°,AB=AC=5,点D在AC上,且AD=2,点E是AB
上的动点,连结DE,点F,G分别是BC和DE的中点,连结AG,FG,当AG=FG时,
线段DE长为( )A. B. C. D.4
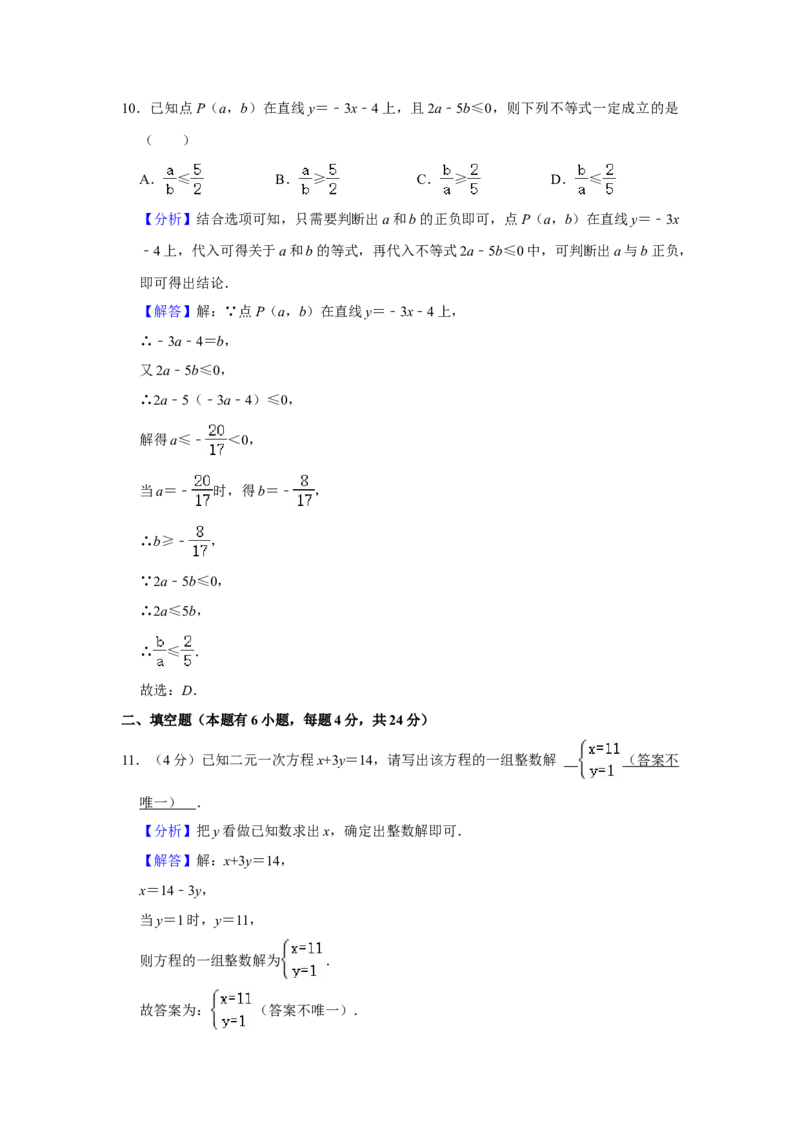
10.已知点P(a,b)在直线y=﹣3x﹣4上,且2a﹣5b≤0,则下列不等式一定成立的是
( )
A. ≤ B. ≥ C. ≥ D. ≤
二、填空题(本题有6小题,每题4分,共24分)
11.(4 分)已知二元一次方程 x+3y=14,请写出该方程的一组整数解
.
12.(4分)如图,在直角坐标系中,△ABC与△ODE是位似图形,则它们位似中心的坐
标是 .
13.(4分)观察下列等式:1=12﹣02,3=22﹣12,5=32﹣22,…按此规律,则第n个等
式为2n﹣1= .
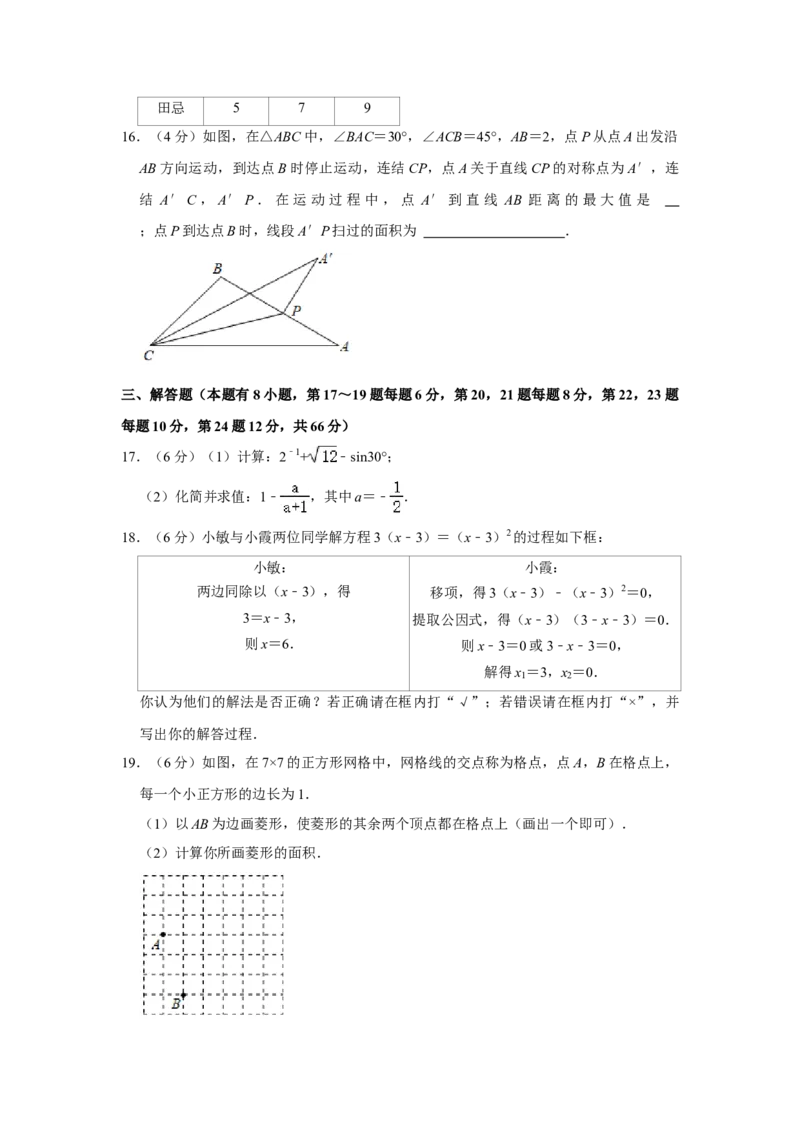
14.(4分)如图,在 ABCD中,对角线AC,BD交于点O,AB⊥AC,AH⊥BD于点
H,若AB=2,BC=2▱ ,则AH的长为 .
15.(4分)看了《田忌赛马》故事后,小杨用数学模型来分析:齐王与田忌的上中下三
个等级的三匹马记分如表,每匹马只赛一场,两数相比,大数为胜,三场两胜则赢.已
知齐王的三匹马出场顺序为10,8,6.若田忌的三匹马随机出场,则田忌能赢得比赛的
概率为 .
马匹 下等马 中等马 上等马
姓名
齐王 6 8 10田忌 5 7 9
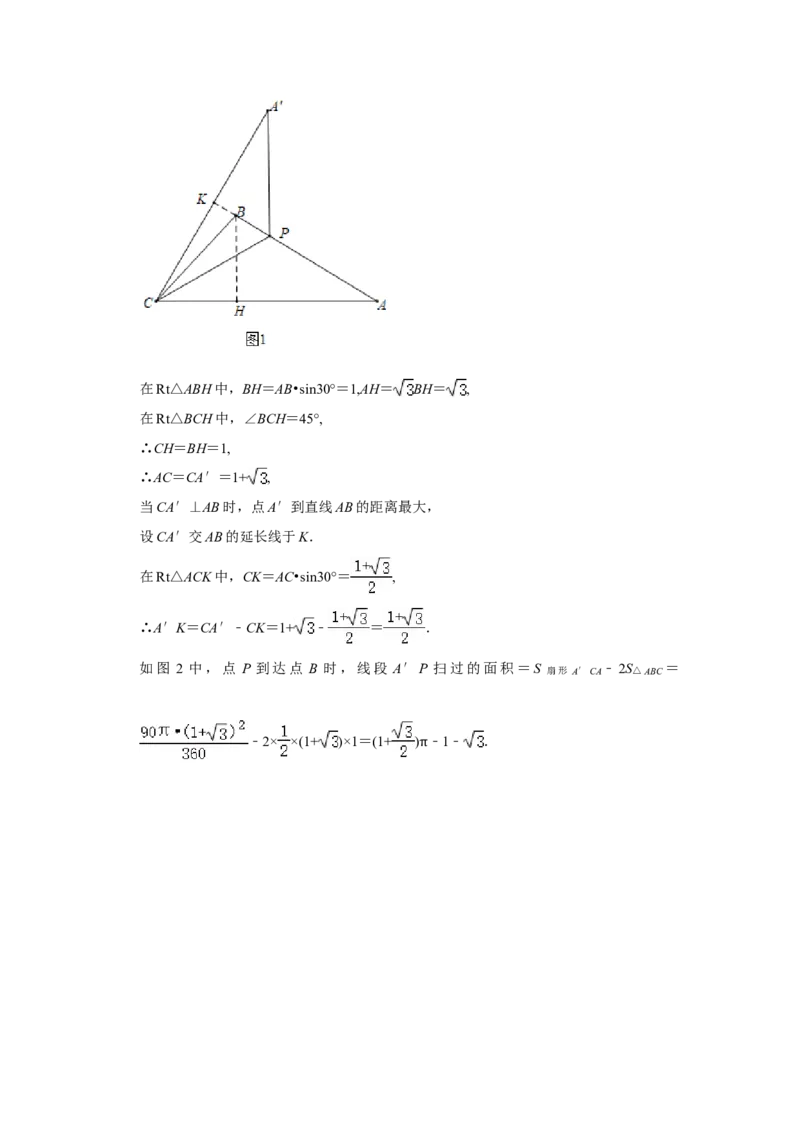
16.(4分)如图,在△ABC中,∠BAC=30°,∠ACB=45°,AB=2,点P从点A出发沿
AB方向运动,到达点B时停止运动,连结CP,点A关于直线CP的对称点为A′,连
结 A′C,A′P.在运动过程中,点 A′到直线 AB 距离的最大值是
;点P到达点B时,线段A′P扫过的面积为 .
三、解答题(本题有8小题,第17~19题每题6分,第20,21题每题8分,第22,23题
每题10分,第24题12分,共66分)
17.(6分)(1)计算:2﹣1+ ﹣sin30°;
(2)化简并求值:1﹣ ,其中a=﹣ .
18.(6分)小敏与小霞两位同学解方程3(x﹣3)=(x﹣3)2的过程如下框:
小敏: 小霞:
两边同除以(x﹣3),得 移项,得3(x﹣3)﹣(x﹣3)2=0,
3=x﹣3, 提取公因式,得(x﹣3)(3﹣x﹣3)=0.
则x=6. 则x﹣3=0或3﹣x﹣3=0,
解得x =3,x =0.
1 2
你认为他们的解法是否正确?若正确请在框内打“√”;若错误请在框内打“×”,并
写出你的解答过程.
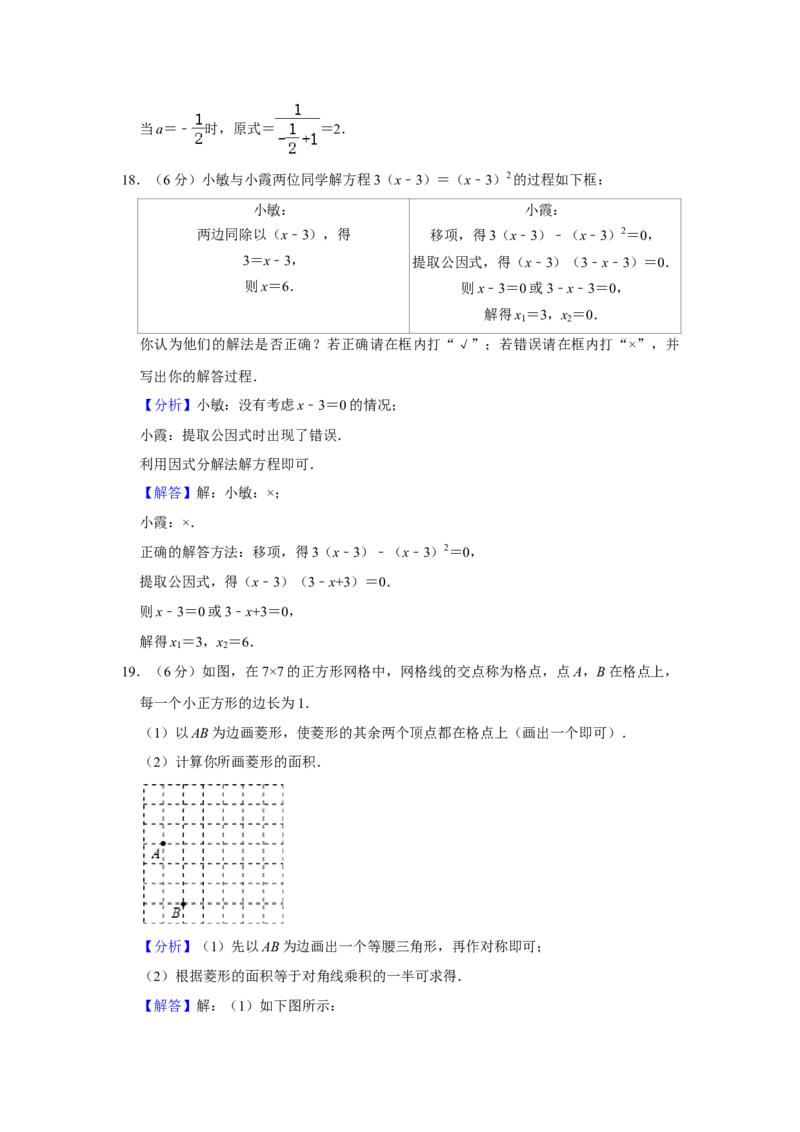
19.(6分)如图,在7×7的正方形网格中,网格线的交点称为格点,点A,B在格点上,
每一个小正方形的边长为1.
(1)以AB为边画菱形,使菱形的其余两个顶点都在格点上(画出一个即可).
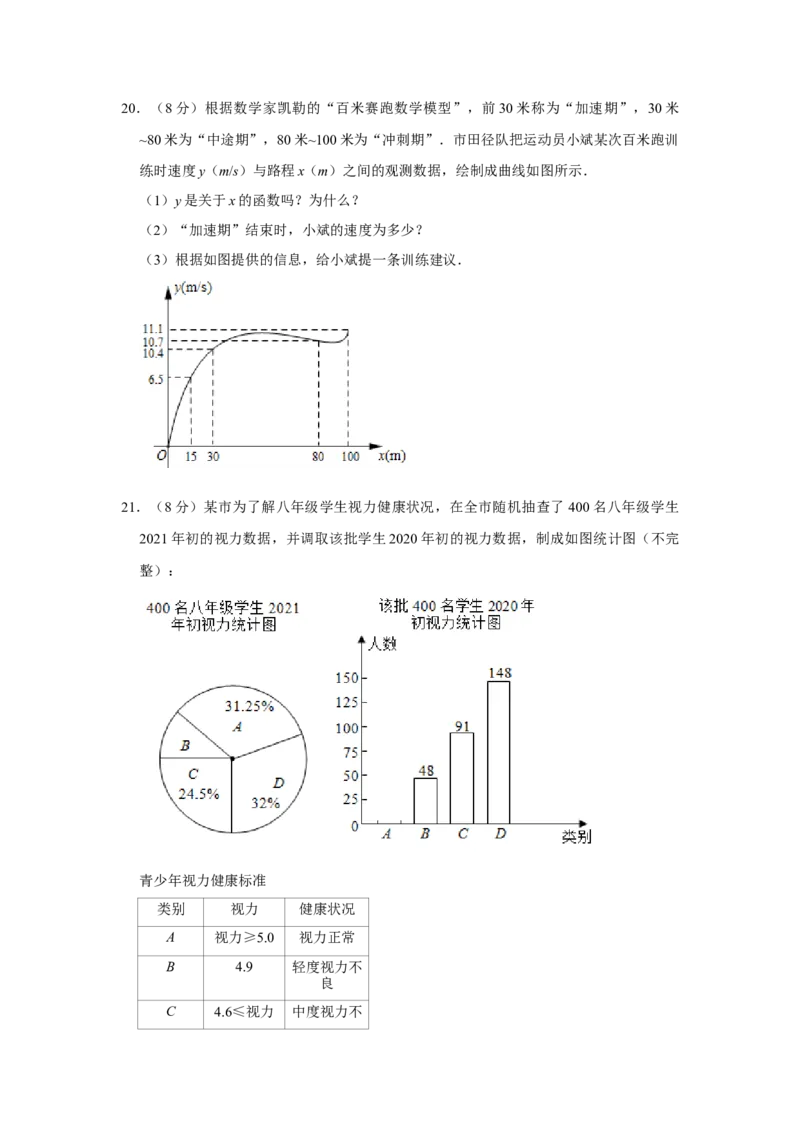
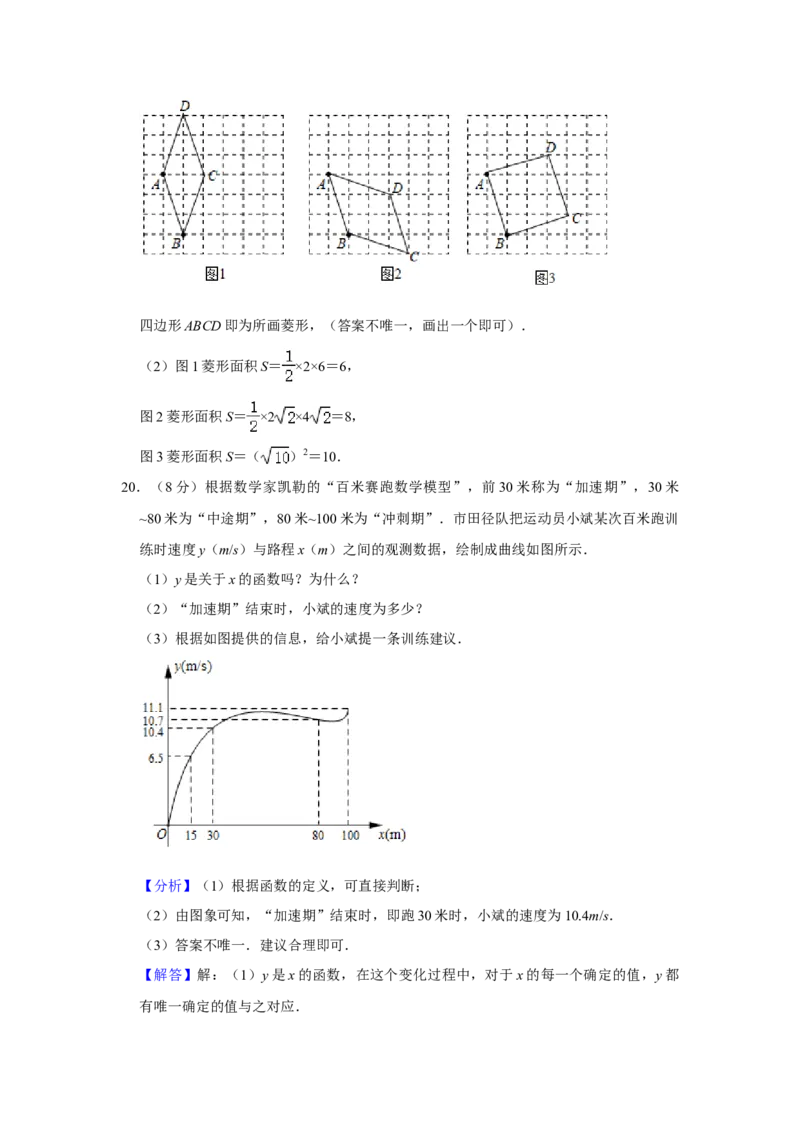
(2)计算你所画菱形的面积.20.(8分)根据数学家凯勒的“百米赛跑数学模型”,前30米称为“加速期”,30米
~80米为“中途期”,80米~100米为“冲刺期”.市田径队把运动员小斌某次百米跑训
练时速度y(m/s)与路程x(m)之间的观测数据,绘制成曲线如图所示.
(1)y是关于x的函数吗?为什么?
(2)“加速期”结束时,小斌的速度为多少?
(3)根据如图提供的信息,给小斌提一条训练建议.
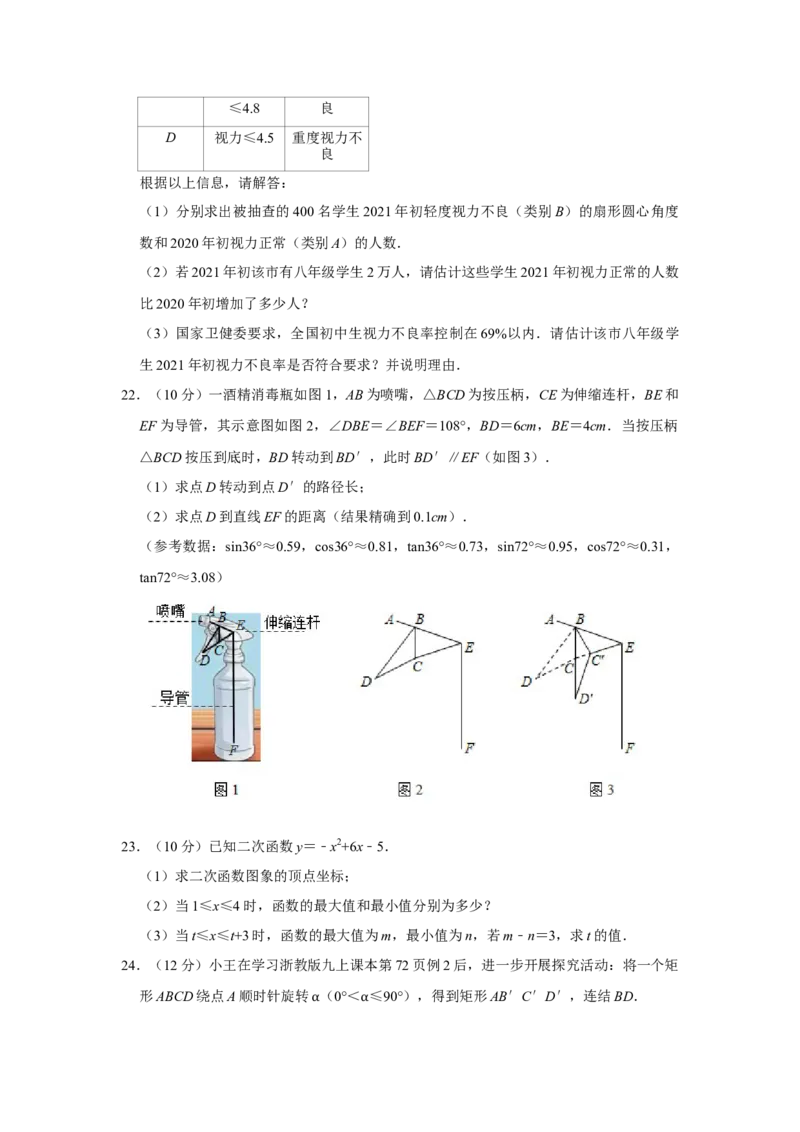
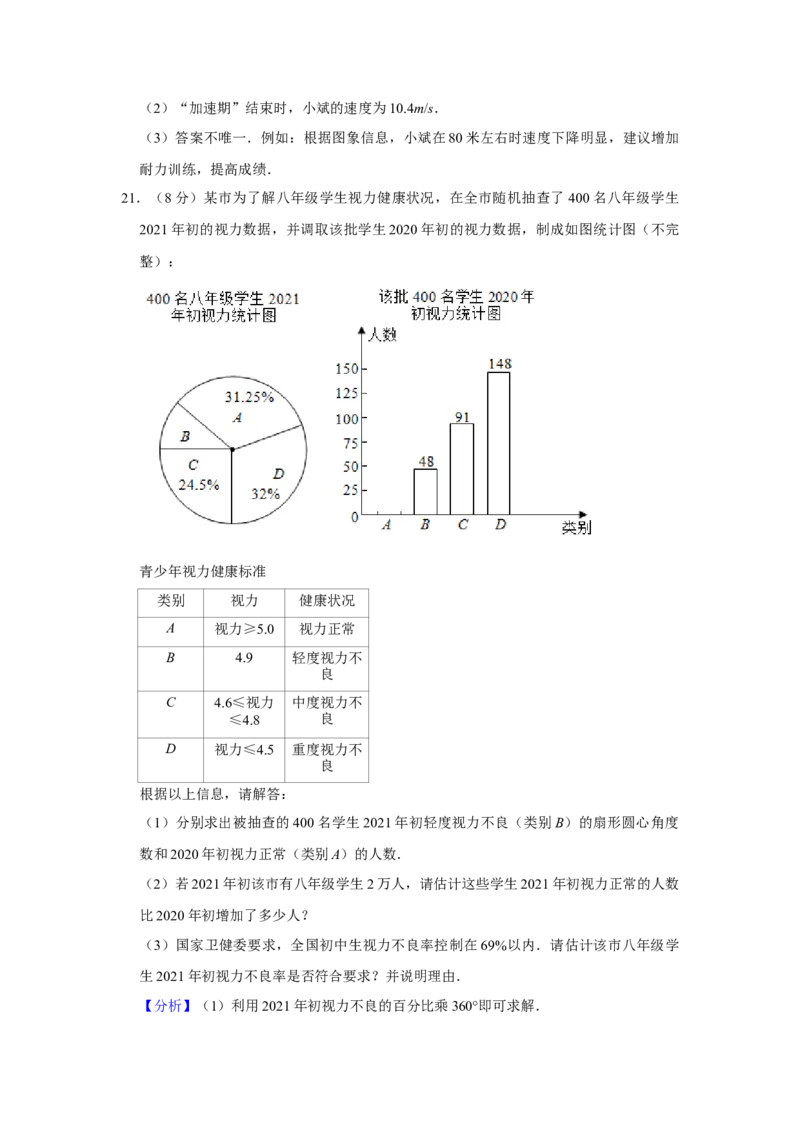
21.(8分)某市为了解八年级学生视力健康状况,在全市随机抽查了400名八年级学生
2021年初的视力数据,并调取该批学生2020年初的视力数据,制成如图统计图(不完
整):
青少年视力健康标准
类别 视力 健康状况
A 视力≥5.0 视力正常
B 4.9 轻度视力不
良
C 4.6≤视力 中度视力不≤4.8 良
D 视力≤4.5 重度视力不
良
根据以上信息,请解答:
(1)分别求出被抽查的400名学生2021年初轻度视力不良(类别B)的扇形圆心角度
数和2020年初视力正常(类别A)的人数.
(2)若2021年初该市有八年级学生2万人,请估计这些学生2021年初视力正常的人数
比2020年初增加了多少人?
(3)国家卫健委要求,全国初中生视力不良率控制在69%以内.请估计该市八年级学
生2021年初视力不良率是否符合要求?并说明理由.
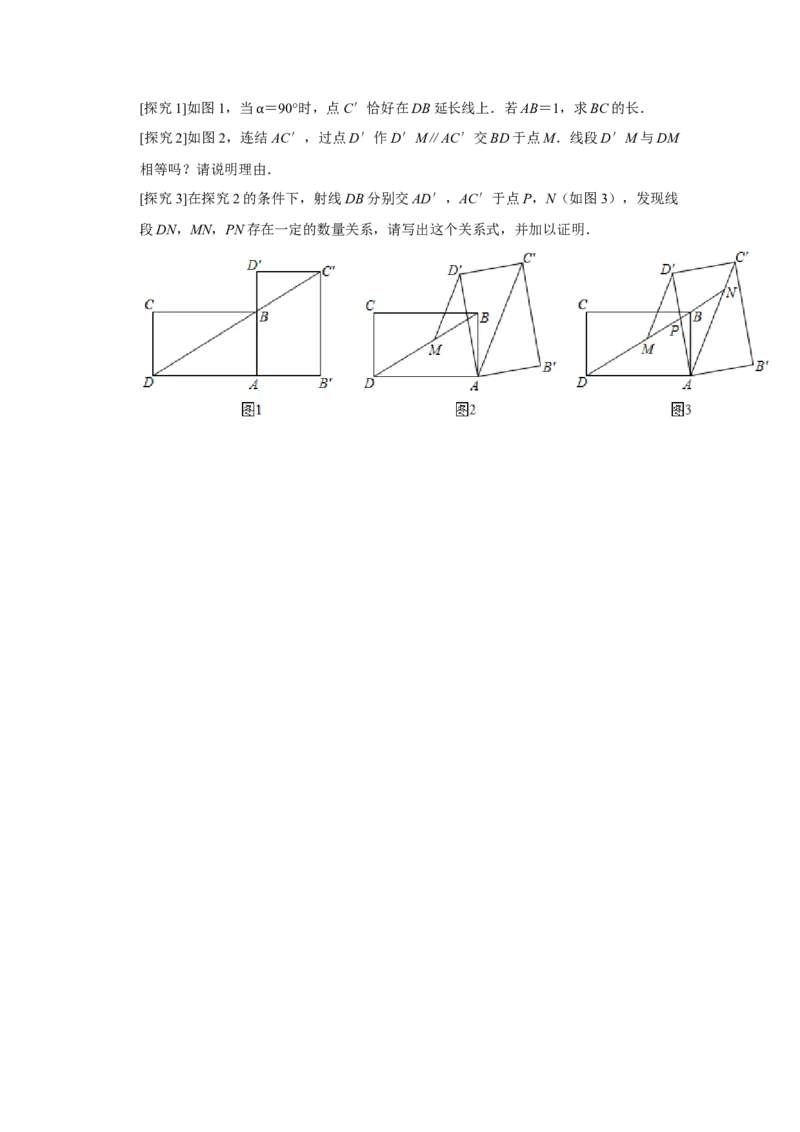
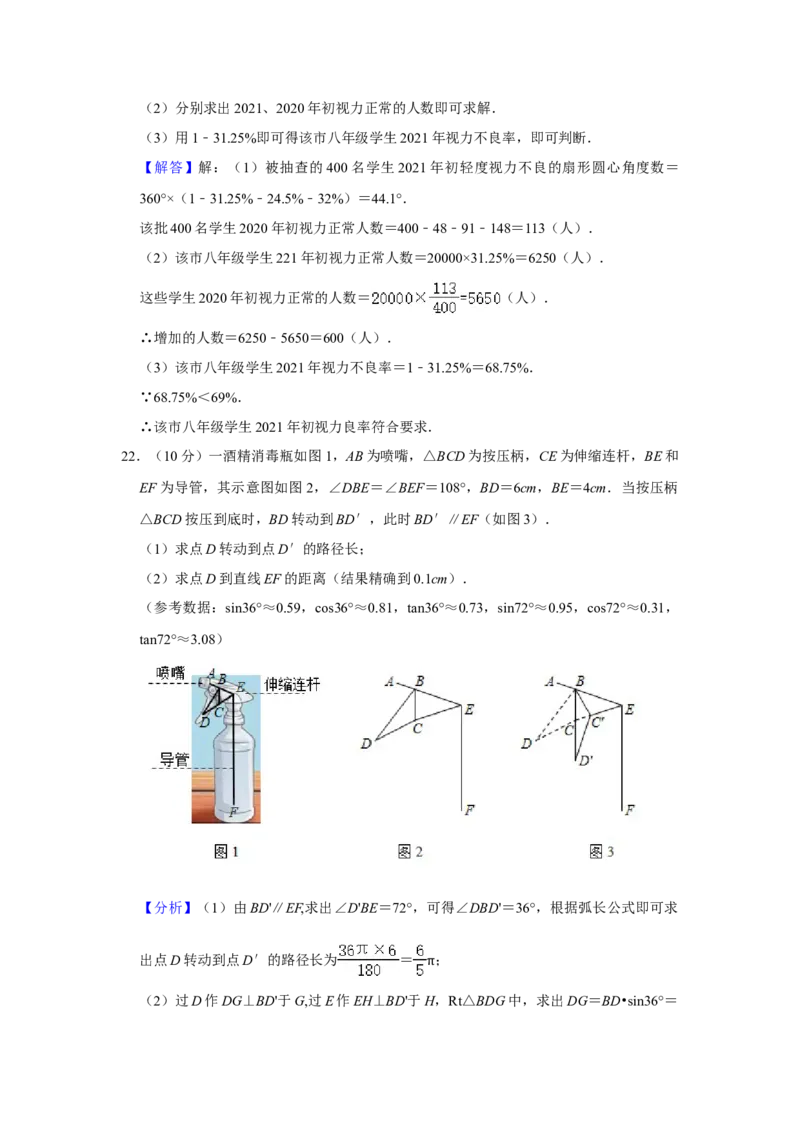
22.(10分)一酒精消毒瓶如图1,AB为喷嘴,△BCD为按压柄,CE为伸缩连杆,BE和
EF为导管,其示意图如图2,∠DBE=∠BEF=108°,BD=6cm,BE=4cm.当按压柄
△BCD按压到底时,BD转动到BD′,此时BD′∥EF(如图3).
(1)求点D转动到点D′的路径长;
(2)求点D到直线EF的距离(结果精确到0.1cm).
(参考数据:sin36°≈0.59,cos36°≈0.81,tan36°≈0.73,sin72°≈0.95,cos72°≈0.31,
tan72°≈3.08)
23.(10分)已知二次函数y=﹣x2+6x﹣5.
(1)求二次函数图象的顶点坐标;
(2)当1≤x≤4时,函数的最大值和最小值分别为多少?
(3)当t≤x≤t+3时,函数的最大值为m,最小值为n,若m﹣n=3,求t的值.
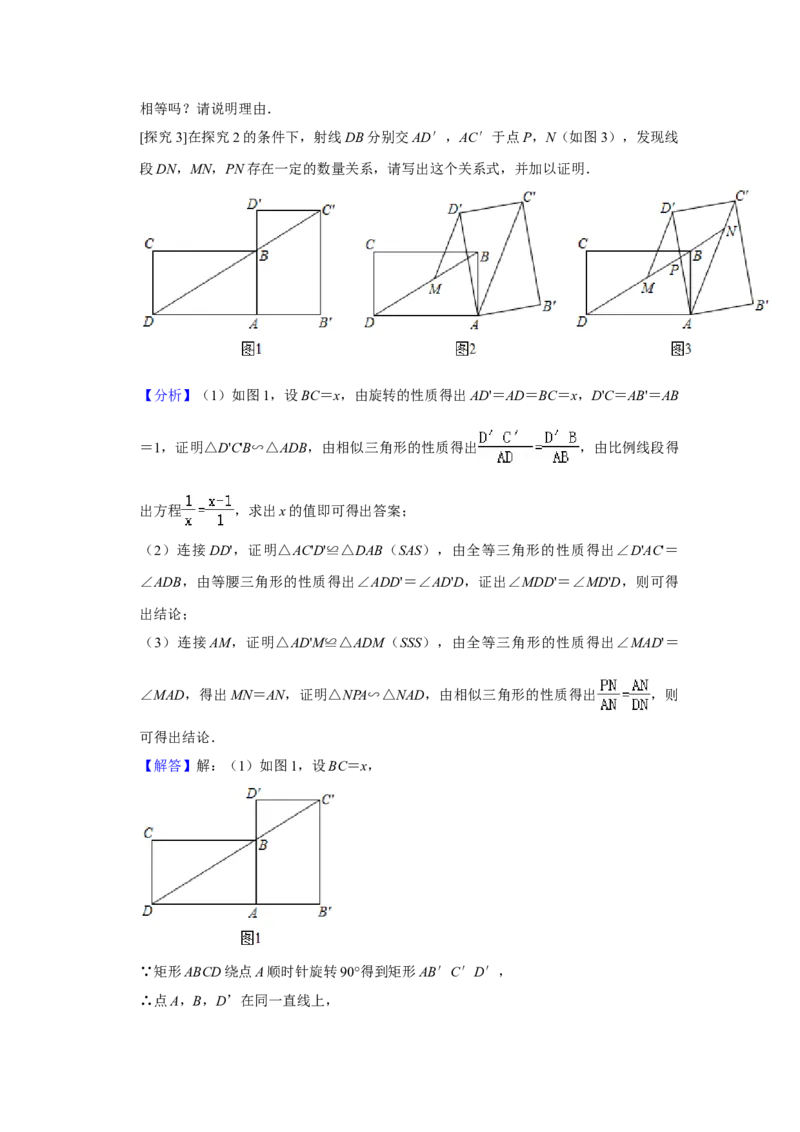
24.(12分)小王在学习浙教版九上课本第72页例2后,进一步开展探究活动:将一个矩
形ABCD绕点A顺时针旋转 (0°< ≤90°),得到矩形AB′C′D′,连结BD.
α α[探究1]如图1,当 =90°时,点C′恰好在DB延长线上.若AB=1,求BC的长.
[探究2]如图2,连结α AC′,过点D′作D′M∥AC′交BD于点M.线段D′M与DM
相等吗?请说明理由.
[探究3]在探究2的条件下,射线DB分别交AD′,AC′于点P,N(如图3),发现线
段DN,MN,PN存在一定的数量关系,请写出这个关系式,并加以证明.2021年浙江省嘉兴市中考数学试卷
参考答案与试题解析
一、选择题(本题有10小题,每题3分,共30分,请选出各题中唯一的正确选项,不选、
多选错选,均不得分)
1.2021年5月22日,我国自主研发的“祝融号”火星车成功到达火星表面.已知火星与
地球的最近距离约为55000000千米,数据55000000用科学记数法表示为( )
A.55×106 B.5.5×107 C.5.5×108 D.0.55×108
【分析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.当原数绝
对值≥10时,n是正数.
【解答】解:55000000=5.5×107.
故选:B.
2.如图是由四个相同的小正方体组成的立体图形,它的俯视图为( )
A. B. C. D.
【分析】找到从上面看所得到的图形即可,注意所有的看到的棱都应表现在主视图中.
【解答】解:从上面看,底层右边是一个小正方形,上层是两个小正方形,右齐.
故选:C.
3.能说明命题“若x为无理数,则x2也是无理数”是假命题的反例是( )
A.x= ﹣1 B.x= +1 C.x=3 D.x= ﹣
【分析】根据题意,只要x2是有理数,即求出各个选项中x2的值,再判断即可.
【解答】解:( ﹣1)2=3﹣2 ,是无理数,不符合题意;
( +1)2=3+2 ,是无理数,不符合题意;
(3 )2=18,是有理数,符合题意;
( ﹣ )2=5﹣2 ,是无理数,不符合题意;故选:C.
4.已知三个点(x ,y ),(x ,y ),(x ,y )在反比例函数y= 的图象上,其中x
1 1 2 2 3 3 1
<x <0<x ,下列结论中正确的是( )
2 3
A.y <y <0<y B.y <y <0<y C.y <0<y <y D.y <0<y <y
2 1 3 1 2 3 3 2 1 3 1 2
【分析】先根据反比例函数的解析式判断出函数图象所在的象限,再根据x <x <0<x
1 2 3
即可得出结论
【解答】解:∵反比例函数y= 中,k=2>0,
∴函数图象的两个分支分别位于一、三象限,且在每一象限内,y随x的增大而减小.
∵x <x <0<x ,
1 2 3
∴A、B两点在第三象限,C点在第一象限,
∴y <y <0<y .
2 1 3
故选:A.
5.将一张三角形纸片按如图步骤①至④折叠两次得图⑤,然后剪出图⑤中的阴影部分,
则阴影部分展开铺平后的图形是( )
A.等腰三角形 B.直角三角形 C.矩形 D.菱形
【分析】对折是轴对称得到的图形,根据最后得到的图形可得是沿对角线折叠2次后,
剪去一个三角形得到的,按原图返回即可.
【解答】解:如图,由题意可知,剪下的图形是四边形BACD,
由折叠可知CA=AB,
∴△ABC是等腰三角形,
又△ABC和△BCD关于直线CD对称,∴四边形BACD是菱形,
故选:D.
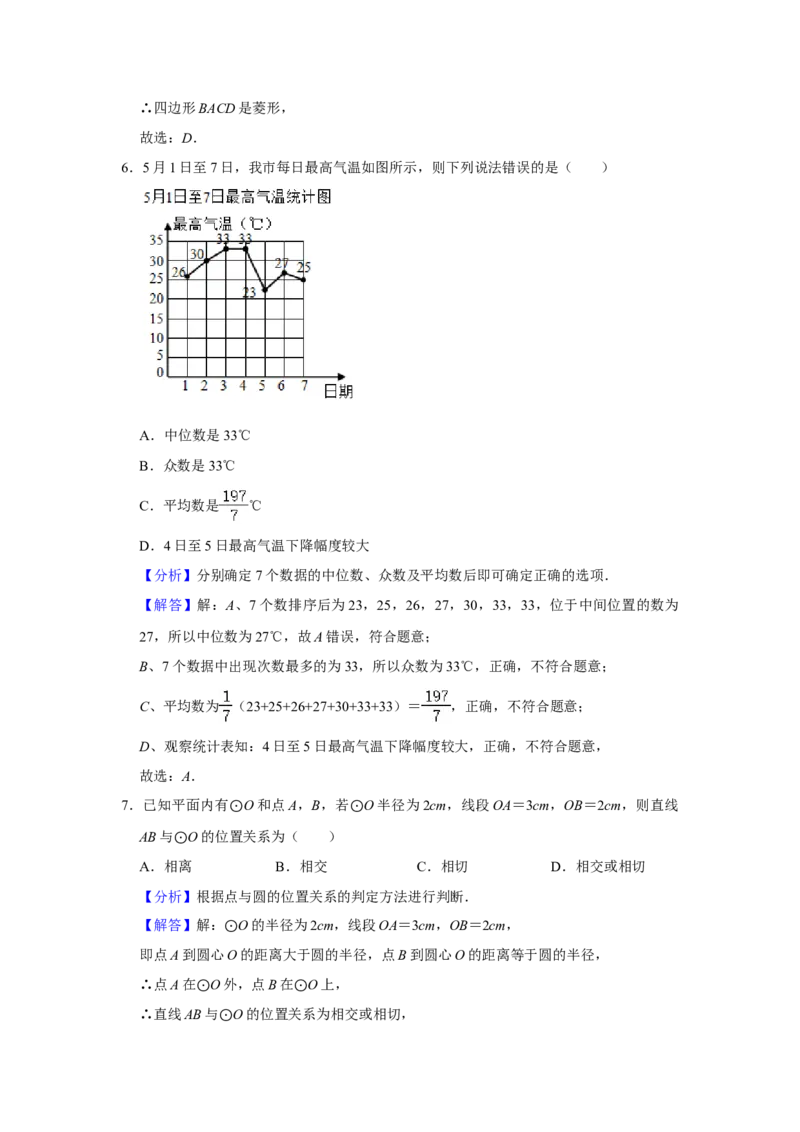
6.5月1日至7日,我市每日最高气温如图所示,则下列说法错误的是( )
A.中位数是33℃
B.众数是33℃
C.平均数是 ℃
D.4日至5日最高气温下降幅度较大
【分析】分别确定7个数据的中位数、众数及平均数后即可确定正确的选项.
【解答】解:A、7个数排序后为23,25,26,27,30,33,33,位于中间位置的数为
27,所以中位数为27℃,故A错误,符合题意;
B、7个数据中出现次数最多的为33,所以众数为33℃,正确,不符合题意;
C、平均数为 (23+25+26+27+30+33+33)= ,正确,不符合题意;
D、观察统计表知:4日至5日最高气温下降幅度较大,正确,不符合题意,
故选:A.
7.已知平面内有 O和点A,B,若 O半径为2cm,线段OA=3cm,OB=2cm,则直线
AB与 O的位置⊙关系为( ) ⊙
A.相⊙离 B.相交 C.相切 D.相交或相切
【分析】根据点与圆的位置关系的判定方法进行判断.
【解答】解: O的半径为2cm,线段OA=3cm,OB=2cm,
即点A到圆心⊙O的距离大于圆的半径,点B到圆心O的距离等于圆的半径,
∴点A在 O外,点B在 O上,
∴直线AB⊙与 O的位置关⊙系为相交或相切,
⊙故选:D.
8.为迎接建党一百周年,某校举行歌唱比赛.901班啦啦队买了两种价格的加油棒助威,
其中缤纷棒共花费30元,荧光棒共花费40元,缤纷棒比荧光棒少20根,缤纷棒单价是
荧光棒的1.5倍.若设荧光棒的单价为x元,根据题意可列方程为( )
A. ﹣ =20 B. ﹣ =20
C. ﹣ =20 D. ﹣ =20
【分析】若设荧光棒的单价为x元,则缤纷棒单价是1.5x元,根据等量关系“缤纷棒比
荧光棒少20根”可列方程即可.
【解答】解:若设荧光棒的单价为x元,则缤纷棒单价是1.5x元,
根据题意可得: ﹣ =20.
故选:B.
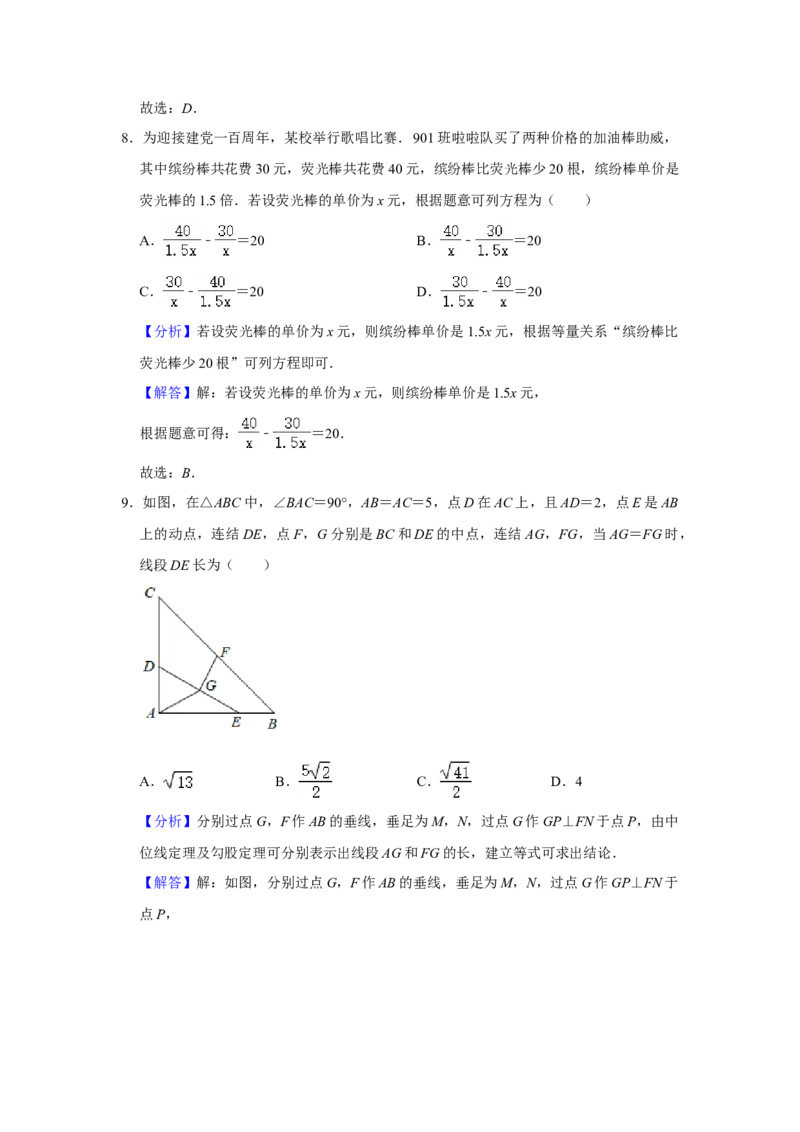
9.如图,在△ABC中,∠BAC=90°,AB=AC=5,点D在AC上,且AD=2,点E是AB
上的动点,连结DE,点F,G分别是BC和DE的中点,连结AG,FG,当AG=FG时,
线段DE长为( )
A. B. C. D.4
【分析】分别过点G,F作AB的垂线,垂足为M,N,过点G作GP⊥FN于点P,由中
位线定理及勾股定理可分别表示出线段AG和FG的长,建立等式可求出结论.
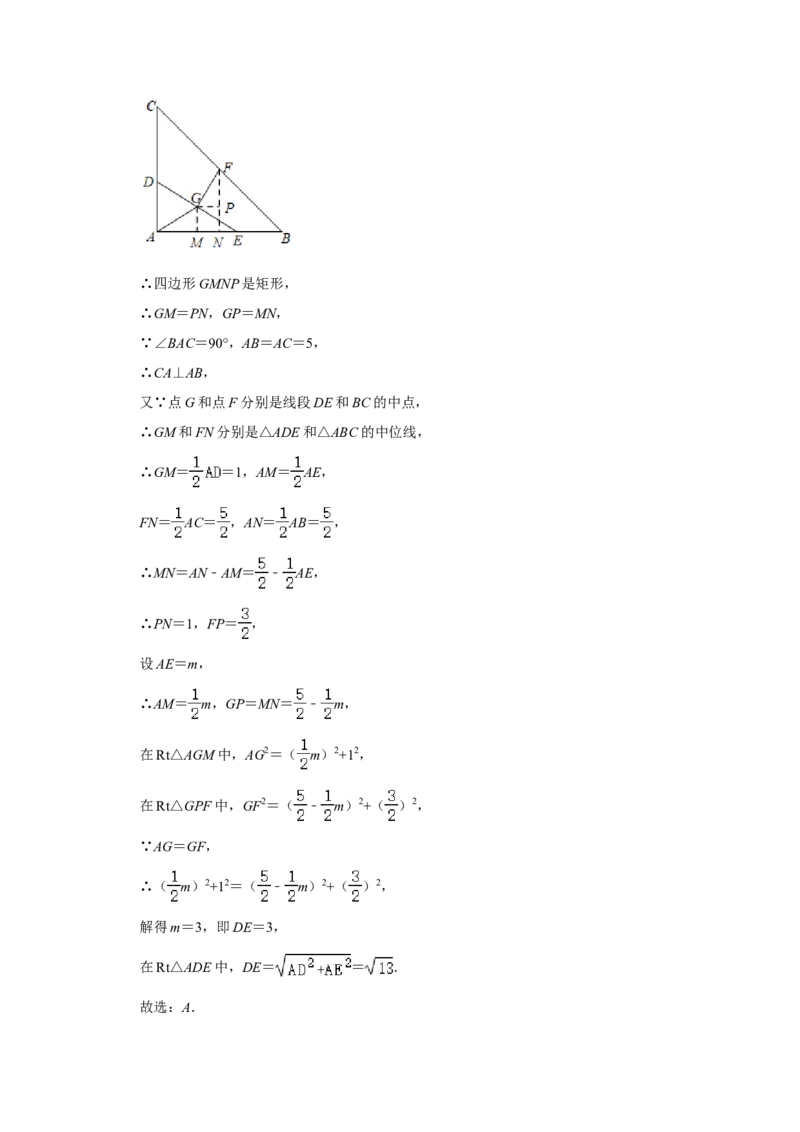
【解答】解:如图,分别过点G,F作AB的垂线,垂足为M,N,过点G作GP⊥FN于
点P,∴四边形GMNP是矩形,
∴GM=PN,GP=MN,
∵∠BAC=90°,AB=AC=5,
∴CA⊥AB,
又∵点G和点F分别是线段DE和BC的中点,
∴GM和FN分别是△ADE和△ABC的中位线,
∴GM= =1,AM= AE,
FN= AC= ,AN= AB= ,
∴MN=AN﹣AM= ﹣ AE,
∴PN=1,FP= ,
设AE=m,
∴AM= m,GP=MN= ﹣ m,
在Rt△AGM中,AG2=( m)2+12,
在Rt△GPF中,GF2=( ﹣ m)2+( )2,
∵AG=GF,
∴( m)2+12=( ﹣ m)2+( )2,
解得m=3,即DE=3,
在Rt△ADE中,DE= = .
故选:A.10.已知点P(a,b)在直线y=﹣3x﹣4上,且2a﹣5b≤0,则下列不等式一定成立的是
( )
A. ≤ B. ≥ C. ≥ D. ≤
【分析】结合选项可知,只需要判断出a和b的正负即可,点P(a,b)在直线y=﹣3x
﹣4上,代入可得关于a和b的等式,再代入不等式2a﹣5b≤0中,可判断出a与b正负,
即可得出结论.
【解答】解:∵点P(a,b)在直线y=﹣3x﹣4上,
∴﹣3a﹣4=b,
又2a﹣5b≤0,
∴2a﹣5(﹣3a﹣4)≤0,
解得a≤﹣ <0,
当a=﹣ 时,得b=﹣ ,
∴b≥﹣ ,
∵2a﹣5b≤0,
∴2a≤5b,
∴ ≤ .
故选:D.
二、填空题(本题有6小题,每题4分,共24分)
11.(4分)已知二元一次方程x+3y=14,请写出该方程的一组整数解 (答案不
唯一) .
【分析】把y看做已知数求出x,确定出整数解即可.
【解答】解:x+3y=14,
x=14﹣3y,
当y=1时,y=11,
则方程的一组整数解为 .
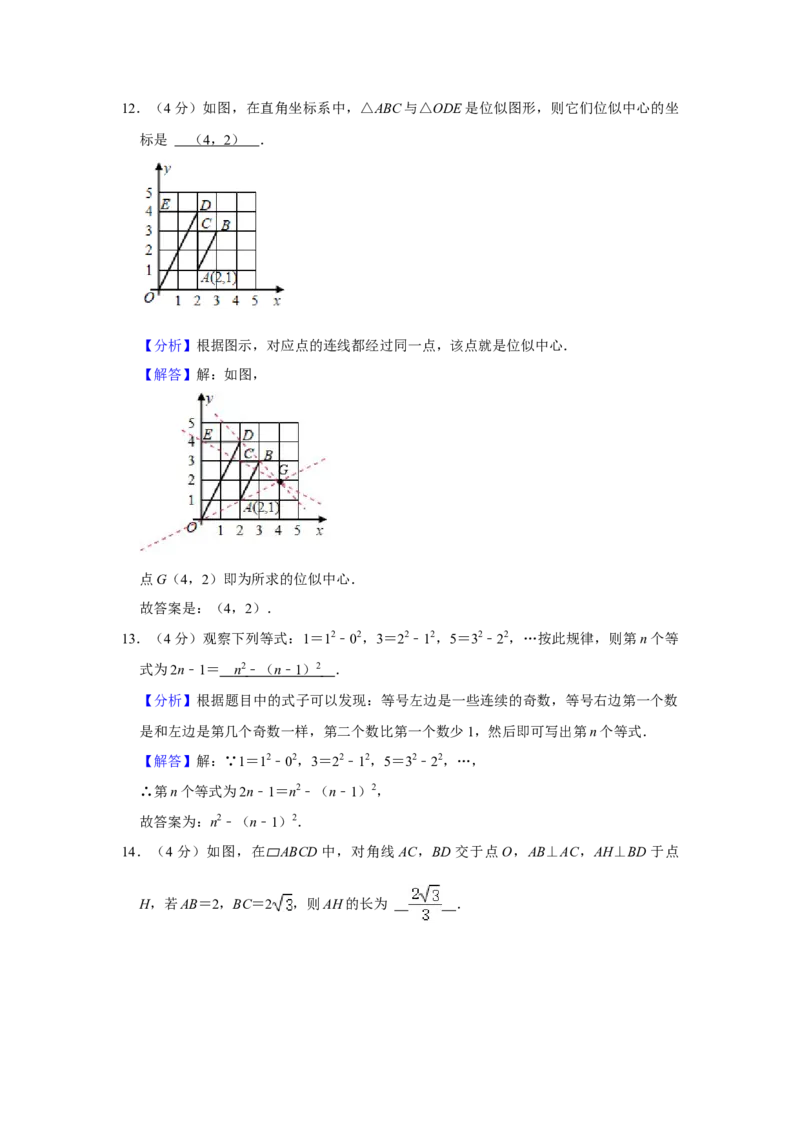
故答案为: (答案不唯一).12.(4分)如图,在直角坐标系中,△ABC与△ODE是位似图形,则它们位似中心的坐
标是 ( 4 , 2 ) .
【分析】根据图示,对应点的连线都经过同一点,该点就是位似中心.
【解答】解:如图,
点G(4,2)即为所求的位似中心.
故答案是:(4,2).
13.(4分)观察下列等式:1=12﹣02,3=22﹣12,5=32﹣22,…按此规律,则第n个等
式为2n﹣1= n 2 ﹣( n ﹣ 1 ) 2 .
【分析】根据题目中的式子可以发现:等号左边是一些连续的奇数,等号右边第一个数
是和左边是第几个奇数一样,第二个数比第一个数少1,然后即可写出第n个等式.
【解答】解:∵1=12﹣02,3=22﹣12,5=32﹣22,…,
∴第n个等式为2n﹣1=n2﹣(n﹣1)2,
故答案为:n2﹣(n﹣1)2.
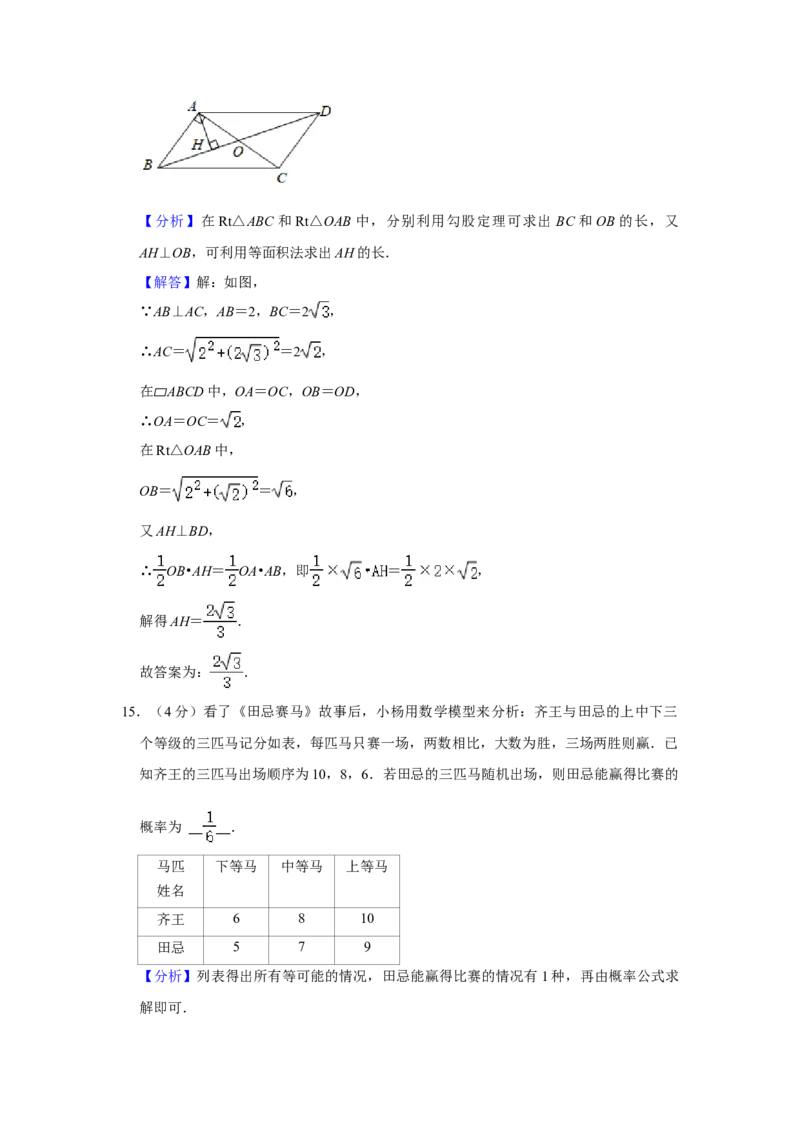
14.(4分)如图,在 ABCD中,对角线AC,BD交于点O,AB⊥AC,AH⊥BD于点
▱
H,若AB=2,BC=2 ,则AH的长为 .【分析】在Rt△ABC和Rt△OAB中,分别利用勾股定理可求出 BC和OB的长,又
AH⊥OB,可利用等面积法求出AH的长.
【解答】解:如图,
∵AB⊥AC,AB=2,BC=2 ,
∴AC= =2 ,
在 ABCD中,OA=OC,OB=OD,
∴▱OA=OC= ,
在Rt△OAB中,
OB= = ,
又AH⊥BD,
∴ OB•AH= OA•AB,即 = ,
解得AH= .
故答案为: .
15.(4分)看了《田忌赛马》故事后,小杨用数学模型来分析:齐王与田忌的上中下三
个等级的三匹马记分如表,每匹马只赛一场,两数相比,大数为胜,三场两胜则赢.已
知齐王的三匹马出场顺序为10,8,6.若田忌的三匹马随机出场,则田忌能赢得比赛的
概率为 .
马匹 下等马 中等马 上等马
姓名
齐王 6 8 10
田忌 5 7 9
【分析】列表得出所有等可能的情况,田忌能赢得比赛的情况有1种,再由概率公式求
解即可.【解答】解:由于田忌的上、中等马分别比齐王的中、下等马强,当齐王的三匹马出场
顺序为10,8,6时,田忌的马按5,9,7的顺序出场,田忌才能赢得比赛,
当田忌的三匹马随机出场时,双方马的对阵情况如下:
双方马的对阵中,只有一种对阵情况田忌能赢,
∴田忌能赢得比赛的概率为 .
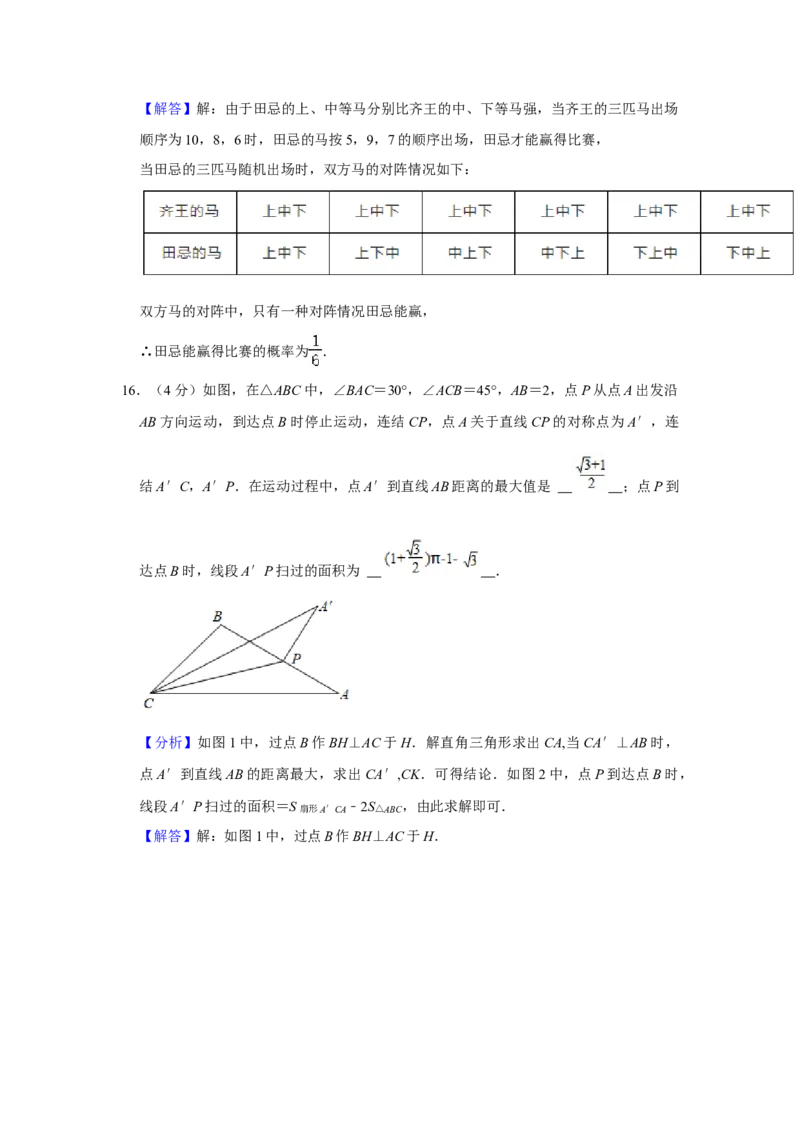
16.(4分)如图,在△ABC中,∠BAC=30°,∠ACB=45°,AB=2,点P从点A出发沿
AB方向运动,到达点B时停止运动,连结CP,点A关于直线CP的对称点为A′,连
结A′C,A′P.在运动过程中,点A′到直线AB距离的最大值是 ;点P到
达点B时,线段A′P扫过的面积为 .
【分析】如图1中,过点B作BH⊥AC于H.解直角三角形求出CA,当CA′⊥AB时,
点A′到直线AB的距离最大,求出CA′,CK.可得结论.如图2中,点P到达点B时,
线段A′P扫过的面积=S扇形A′CA ﹣2S△ABC ,由此求解即可.
【解答】解:如图1中,过点B作BH⊥AC于H.在Rt△ABH中,BH=AB•sin30°=1,AH= BH= ,
在Rt△BCH中,∠BCH=45°,
∴CH=BH=1,
∴AC=CA′=1+ ,
当CA′⊥AB时,点A′到直线AB的距离最大,
设CA′交AB的延长线于K.
在Rt△ACK中,CK=AC•sin30°= ,
∴A′K=CA′﹣CK=1+ ﹣ = .
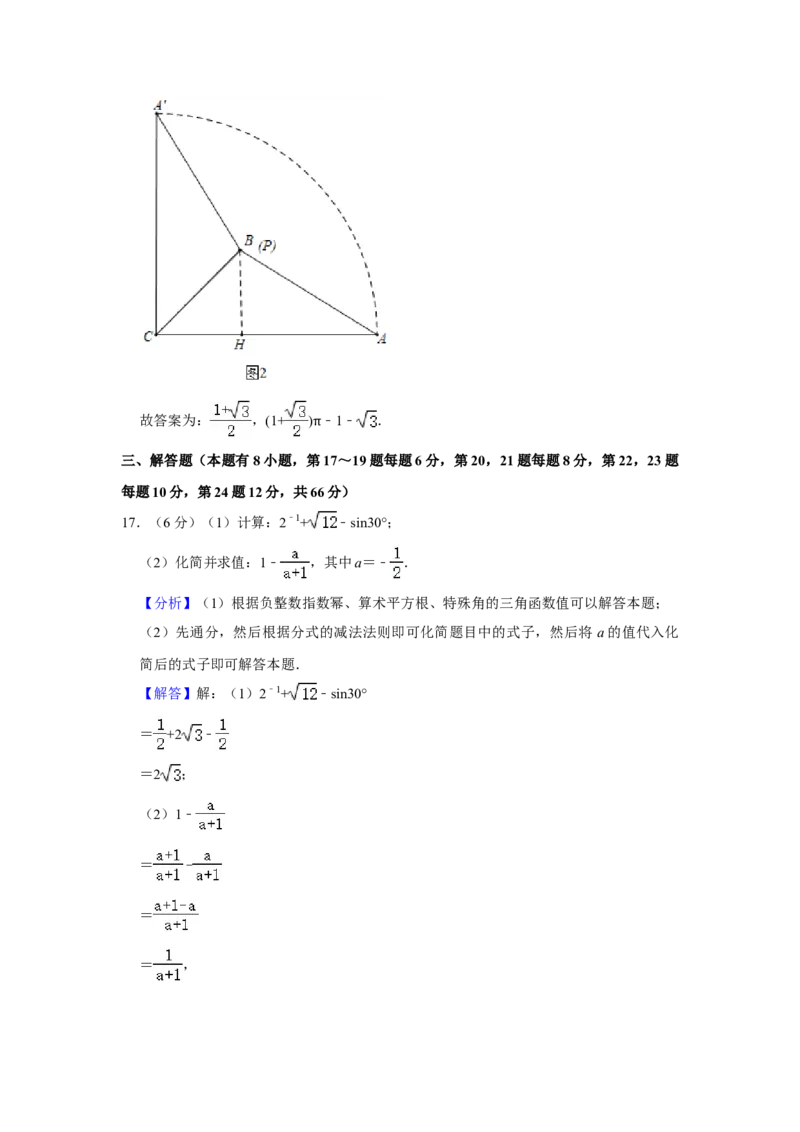
如图 2 中,点 P 到达点 B 时,线段 A′P 扫过的面积=S 扇形 A′CA ﹣2S△ABC =
﹣2× ×(1+ )×1=(1+ ) ﹣1﹣ .
π故答案为: ,(1+ ) ﹣1﹣ .
π
三、解答题(本题有8小题,第17~19题每题6分,第20,21题每题8分,第22,23题
每题10分,第24题12分,共66分)
17.(6分)(1)计算:2﹣1+ ﹣sin30°;
(2)化简并求值:1﹣ ,其中a=﹣ .
【分析】(1)根据负整数指数幂、算术平方根、特殊角的三角函数值可以解答本题;
(2)先通分,然后根据分式的减法法则即可化简题目中的式子,然后将 a的值代入化
简后的式子即可解答本题.
【解答】解:(1)2﹣1+ ﹣sin30°
= +2 ﹣
=2 ;
(2)1﹣
=
=
= ,当a=﹣ 时,原式= =2.
18.(6分)小敏与小霞两位同学解方程3(x﹣3)=(x﹣3)2的过程如下框:
小敏: 小霞:
两边同除以(x﹣3),得 移项,得3(x﹣3)﹣(x﹣3)2=0,
3=x﹣3, 提取公因式,得(x﹣3)(3﹣x﹣3)=0.
则x=6. 则x﹣3=0或3﹣x﹣3=0,
解得x =3,x =0.
1 2
你认为他们的解法是否正确?若正确请在框内打“√”;若错误请在框内打“×”,并
写出你的解答过程.
【分析】小敏:没有考虑x﹣3=0的情况;
小霞:提取公因式时出现了错误.
利用因式分解法解方程即可.
【解答】解:小敏:×;
小霞:×.
正确的解答方法:移项,得3(x﹣3)﹣(x﹣3)2=0,
提取公因式,得(x﹣3)(3﹣x+3)=0.
则x﹣3=0或3﹣x+3=0,
解得x =3,x =6.
1 2
19.(6分)如图,在7×7的正方形网格中,网格线的交点称为格点,点A,B在格点上,
每一个小正方形的边长为1.
(1)以AB为边画菱形,使菱形的其余两个顶点都在格点上(画出一个即可).
(2)计算你所画菱形的面积.
【分析】(1)先以AB为边画出一个等腰三角形,再作对称即可;
(2)根据菱形的面积等于对角线乘积的一半可求得.
【解答】解:(1)如下图所示:四边形ABCD即为所画菱形,(答案不唯一,画出一个即可).
(2)图1菱形面积S= ×2×6=6,
图2菱形面积S= ×2 ×4 =8,
图3菱形面积S=( )2=10.
20.(8分)根据数学家凯勒的“百米赛跑数学模型”,前30米称为“加速期”,30米
~80米为“中途期”,80米~100米为“冲刺期”.市田径队把运动员小斌某次百米跑训
练时速度y(m/s)与路程x(m)之间的观测数据,绘制成曲线如图所示.
(1)y是关于x的函数吗?为什么?
(2)“加速期”结束时,小斌的速度为多少?
(3)根据如图提供的信息,给小斌提一条训练建议.
【分析】(1)根据函数的定义,可直接判断;
(2)由图象可知,“加速期”结束时,即跑30米时,小斌的速度为10.4m/s.
(3)答案不唯一.建议合理即可.
【解答】解:(1)y是x的函数,在这个变化过程中,对于x的每一个确定的值,y都
有唯一确定的值与之对应.(2)“加速期”结束时,小斌的速度为10.4m/s.
(3)答案不唯一.例如:根据图象信息,小斌在80米左右时速度下降明显,建议增加
耐力训练,提高成绩.
21.(8分)某市为了解八年级学生视力健康状况,在全市随机抽查了400名八年级学生
2021年初的视力数据,并调取该批学生2020年初的视力数据,制成如图统计图(不完
整):
青少年视力健康标准
类别 视力 健康状况
A 视力≥5.0 视力正常
B 4.9 轻度视力不
良
C 4.6≤视力 中度视力不
≤4.8 良
D 视力≤4.5 重度视力不
良
根据以上信息,请解答:
(1)分别求出被抽查的400名学生2021年初轻度视力不良(类别B)的扇形圆心角度
数和2020年初视力正常(类别A)的人数.
(2)若2021年初该市有八年级学生2万人,请估计这些学生2021年初视力正常的人数
比2020年初增加了多少人?
(3)国家卫健委要求,全国初中生视力不良率控制在69%以内.请估计该市八年级学
生2021年初视力不良率是否符合要求?并说明理由.
【分析】(1)利用2021年初视力不良的百分比乘360°即可求解.(2)分别求出2021、2020年初视力正常的人数即可求解.
(3)用1﹣31.25%即可得该市八年级学生2021年视力不良率,即可判断.
【解答】解:(1)被抽查的400名学生2021年初轻度视力不良的扇形圆心角度数=
360°×(1﹣31.25%﹣24.5%﹣32%)=44.1°.
该批400名学生2020年初视力正常人数=400﹣48﹣91﹣148=113(人).
(2)该市八年级学生221年初视力正常人数=20000×31.25%=6250(人).
这些学生2020年初视力正常的人数= (人).
∴增加的人数=6250﹣5650=600(人).
(3)该市八年级学生2021年视力不良率=1﹣31.25%=68.75%.
∵68.75%<69%.
∴该市八年级学生2021年初视力良率符合要求.
22.(10分)一酒精消毒瓶如图1,AB为喷嘴,△BCD为按压柄,CE为伸缩连杆,BE和
EF为导管,其示意图如图2,∠DBE=∠BEF=108°,BD=6cm,BE=4cm.当按压柄
△BCD按压到底时,BD转动到BD′,此时BD′∥EF(如图3).
(1)求点D转动到点D′的路径长;
(2)求点D到直线EF的距离(结果精确到0.1cm).
(参考数据:sin36°≈0.59,cos36°≈0.81,tan36°≈0.73,sin72°≈0.95,cos72°≈0.31,
tan72°≈3.08)
【分析】(1)由BD'∥EF,求出∠D'BE=72°,可得∠DBD'=36°,根据弧长公式即可求
出点D转动到点D′的路径长为 = ;
π
(2)过D作DG⊥BD'于G,过E作EH⊥BD'于H,Rt△BDG中,求出DG=BD•sin36°=3.54,Rt△BEH中,HE=3.80,故DG+HE≈7.3,即点D到直线EF的距离为7.3cm,
【解答】解:∵BD'∥EF,∠BEF=108°,
∴∠D'BE=180°﹣∠BEF=72°,
∵∠DBE=108°,
∴∠DBD'=∠DBE﹣∠D'BE=108°﹣72°=36°,
∵BD=6,
∴点D转动到点D′的路径长为 = ;
π
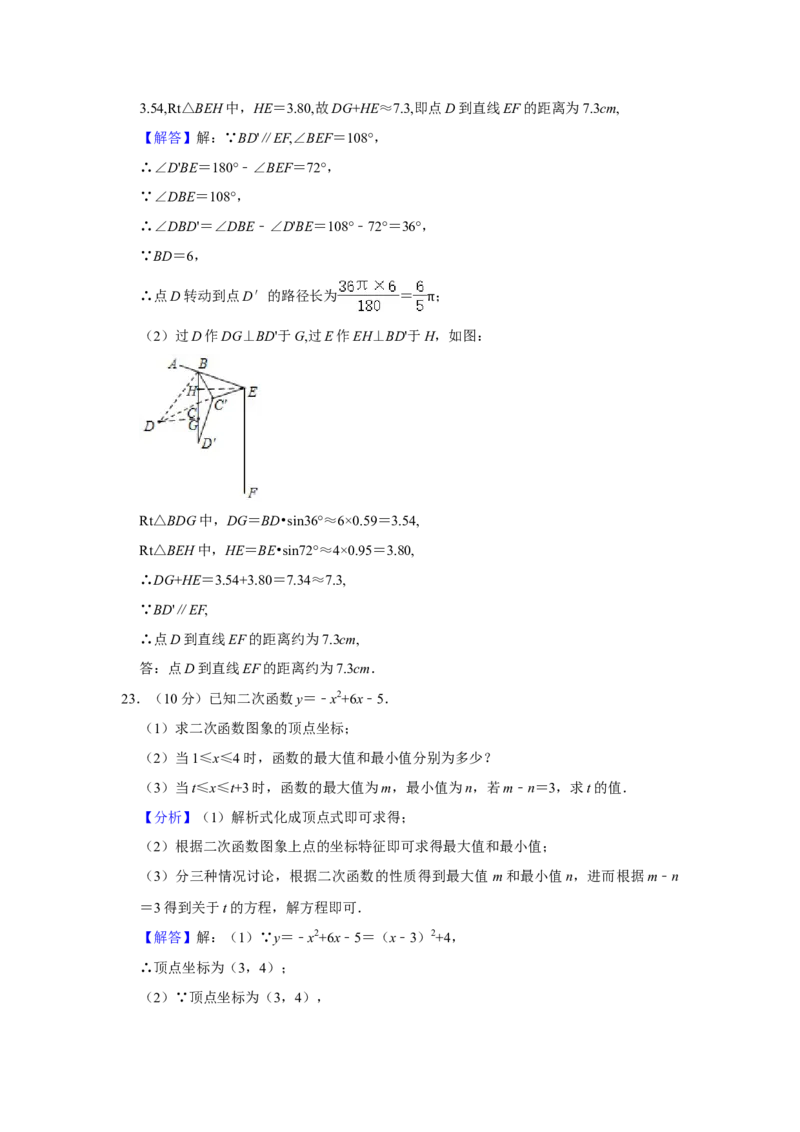
(2)过D作DG⊥BD'于G,过E作EH⊥BD'于H,如图:
Rt△BDG中,DG=BD•sin36°≈6×0.59=3.54,
Rt△BEH中,HE=BE•sin72°≈4×0.95=3.80,
∴DG+HE=3.54+3.80=7.34≈7.3,
∵BD'∥EF,
∴点D到直线EF的距离约为7.3cm,
答:点D到直线EF的距离约为7.3cm.
23.(10分)已知二次函数y=﹣x2+6x﹣5.
(1)求二次函数图象的顶点坐标;
(2)当1≤x≤4时,函数的最大值和最小值分别为多少?
(3)当t≤x≤t+3时,函数的最大值为m,最小值为n,若m﹣n=3,求t的值.
【分析】(1)解析式化成顶点式即可求得;
(2)根据二次函数图象上点的坐标特征即可求得最大值和最小值;
(3)分三种情况讨论,根据二次函数的性质得到最大值 m和最小值n,进而根据m﹣n
=3得到关于t的方程,解方程即可.
【解答】解:(1)∵y=﹣x2+6x﹣5=(x﹣3)2+4,
∴顶点坐标为(3,4);
(2)∵顶点坐标为(3,4),∴当x=3时,y最大值 =4,
∵当1≤x≤3时,y随着x的增大而增大,
∴当x=1时,y最小值 =0,
∵当3<x≤4时,y随着x的增大而减小,
∴当x=4时,y最小值 =3.
∴当1≤x≤4时,函数的最大值为4,最小值为0;
(3)当t≤x≤t+3时,对t进行分类讨论,
①当t+3<3时,即t<0,y随着x的增大而增大,
当x=t+3时,m=(t+3)2+6(t+3)﹣5=﹣t2+4,
当x=t时,n=﹣t2+6t﹣5,
∴m﹣n=﹣=﹣t2+4﹣(﹣t2+6t﹣5)=﹣6t+9,
∴﹣6t+9=3,解得t=1(不合题意,舍去),
②当0≤t<3时,顶点的横坐标在取值范围内,
∴m=4,
i)当0≤t≤ 时,在x=t时,n=﹣t2+6t﹣5,
∴m﹣n=4﹣(﹣t2+6t﹣5)=t2﹣6t+9,
∴t2﹣6t+9=3,解得t =3﹣ ,t =3+ (不合题意,舍去);
1 2
ii)当 <t<3时,在x=t+3时,n=﹣t2+4,
∴m﹣n=4﹣(﹣t2+4)=t2,
∴t2=3,解得t = ,t =﹣ (不合题意,舍去),
1 2
③当t≥3时,y随着x的增大而减小,
当x=t时,m=﹣t2+6t﹣5,
当x=t+3时,n=﹣(t+3)2+6(t+3)﹣5=﹣t2+4,
.m﹣n=﹣t2+6t﹣5﹣(﹣t2+4)=6t﹣9,
∴6t﹣9=3,解得t=2(不合题意,舍去),
综上所述,t=3﹣ 或 .
24.(12分)小王在学习浙教版九上课本第72页例2后,进一步开展探究活动:将一个矩
形ABCD绕点A顺时针旋转 (0°< ≤90°),得到矩形AB′C′D′,连结BD.
[探究1]如图1,当 =90°时α,点C′α恰好在DB延长线上.若AB=1,求BC的长.
[探究2]如图2,连结α AC′,过点D′作D′M∥AC′交BD于点M.线段D′M与DM相等吗?请说明理由.
[探究3]在探究2的条件下,射线DB分别交AD′,AC′于点P,N(如图3),发现线
段DN,MN,PN存在一定的数量关系,请写出这个关系式,并加以证明.
【分析】(1)如图1,设BC=x,由旋转的性质得出AD'=AD=BC=x,D'C=AB'=AB
=1,证明△D'C'B∽△ADB,由相似三角形的性质得出 ,由比例线段得
出方程 ,求出x的值即可得出答案;
(2)连接DD',证明△AC'D'≌△DAB(SAS),由全等三角形的性质得出∠D'AC'=
∠ADB,由等腰三角形的性质得出∠ADD'=∠AD'D,证出∠MDD'=∠MD'D,则可得
出结论;
(3)连接AM,证明△AD'M≌△ADM(SSS),由全等三角形的性质得出∠MAD'=
∠MAD,得出MN=AN,证明△NPA∽△NAD,由相似三角形的性质得出 ,则
可得出结论.
【解答】解:(1)如图1,设BC=x,
∵矩形ABCD绕点A顺时针旋转90°得到矩形AB′C′D′,
∴点A,B,D’在同一直线上,∴AD'=AD=BC=x,D'C=AB'=AB=1,
∴D'B=AD'﹣AB=x﹣1,
∵∠BAD=∠D'=90°,
∴D'C'∥DA,
又∵点C'在DB的延长线上,
∴△D'C'B∽△ADB,
∴ ,
∴ ,
解得x = ,x = (不合题意,舍去),
1 2
∴BC= .
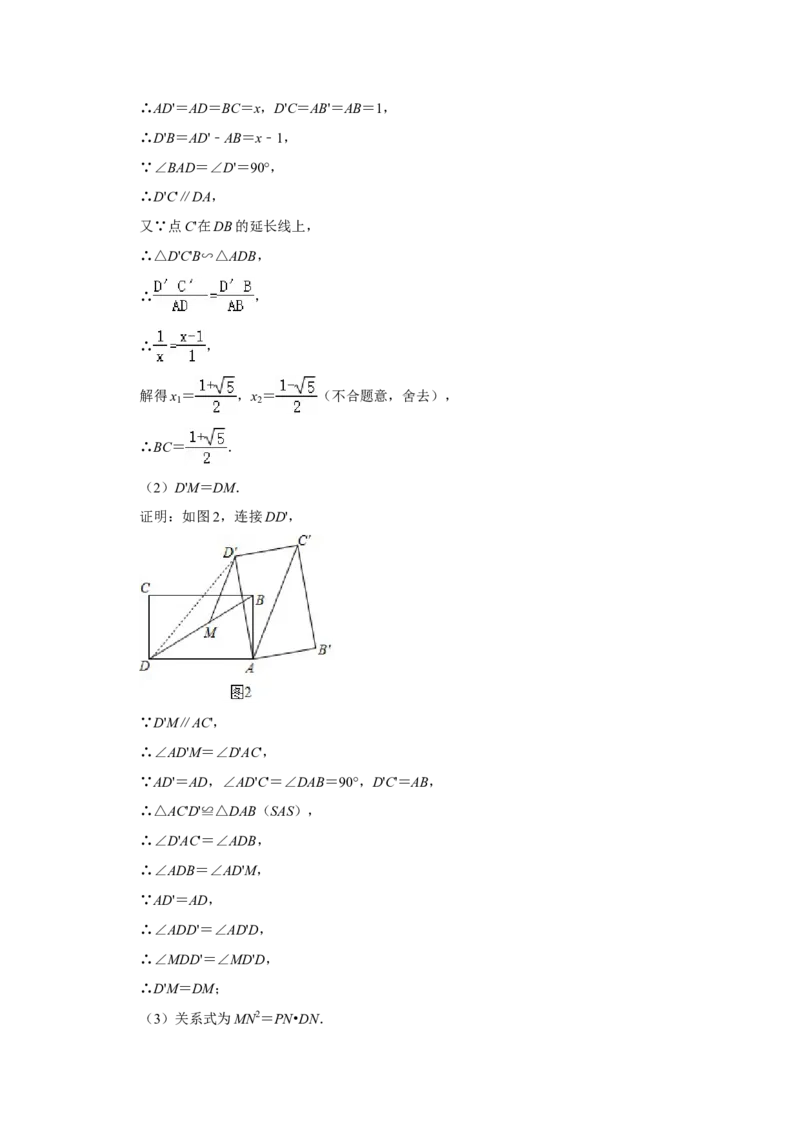
(2)D'M=DM.
证明:如图2,连接DD',
∵D'M∥AC',
∴∠AD'M=∠D'AC',
∵AD'=AD,∠AD'C'=∠DAB=90°,D'C'=AB,
∴△AC'D'≌△DAB(SAS),
∴∠D'AC'=∠ADB,
∴∠ADB=∠AD'M,
∵AD'=AD,
∴∠ADD'=∠AD'D,
∴∠MDD'=∠MD'D,
∴D'M=DM;
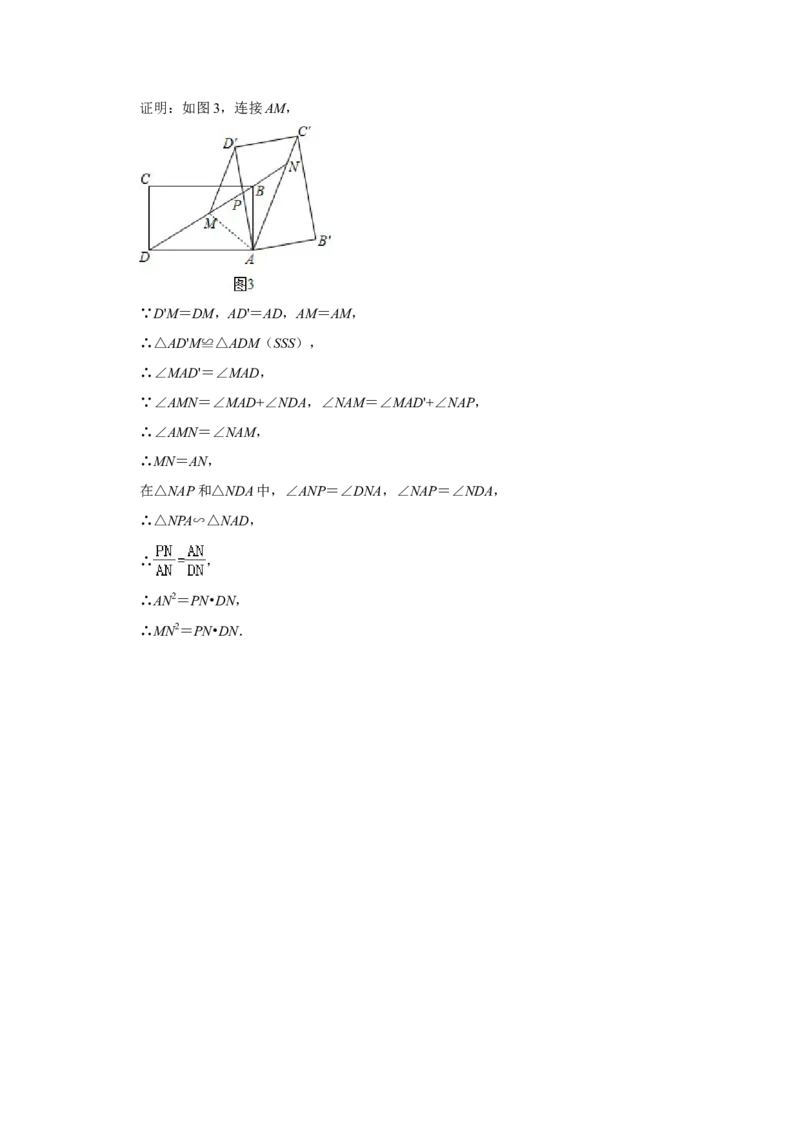
(3)关系式为MN2=PN•DN.证明:如图3,连接AM,
∵D'M=DM,AD'=AD,AM=AM,
∴△AD'M≌△ADM(SSS),
∴∠MAD'=∠MAD,
∵∠AMN=∠MAD+∠NDA,∠NAM=∠MAD'+∠NAP,
∴∠AMN=∠NAM,
∴MN=AN,
在△NAP和△NDA中,∠ANP=∠DNA,∠NAP=∠NDA,
∴△NPA∽△NAD,
∴ ,
∴AN2=PN•DN,
∴MN2=PN•DN.