文档内容
【淘宝搜索店铺:中小学教辅资源店 微信:mlxt2022】
2021年浙江省杭州市中考数学试卷
一、选择题:本大题有10个小题,每小题3分,共30分。在每小题给出的四个选项中,
只有一项是符合题目要求的.
1.﹣(﹣2021)=( )
A.﹣2021 B.2021 C.﹣ D.
2.“奋斗者”号载人潜水器此前在马里亚纳海沟创造了 10909米的我国载人深潜记录.数
据10909用科学记数法可表示为( )
A.0.10909×105 B.1.0909×104
C.10.909×103 D.109.09×102
3.因式分解:1﹣4y2=( )
A.(1﹣2y)(1+2y) B.(2﹣y)(2+y)
C.(1﹣2y)(2+y) D.(2﹣y)(1+2y)
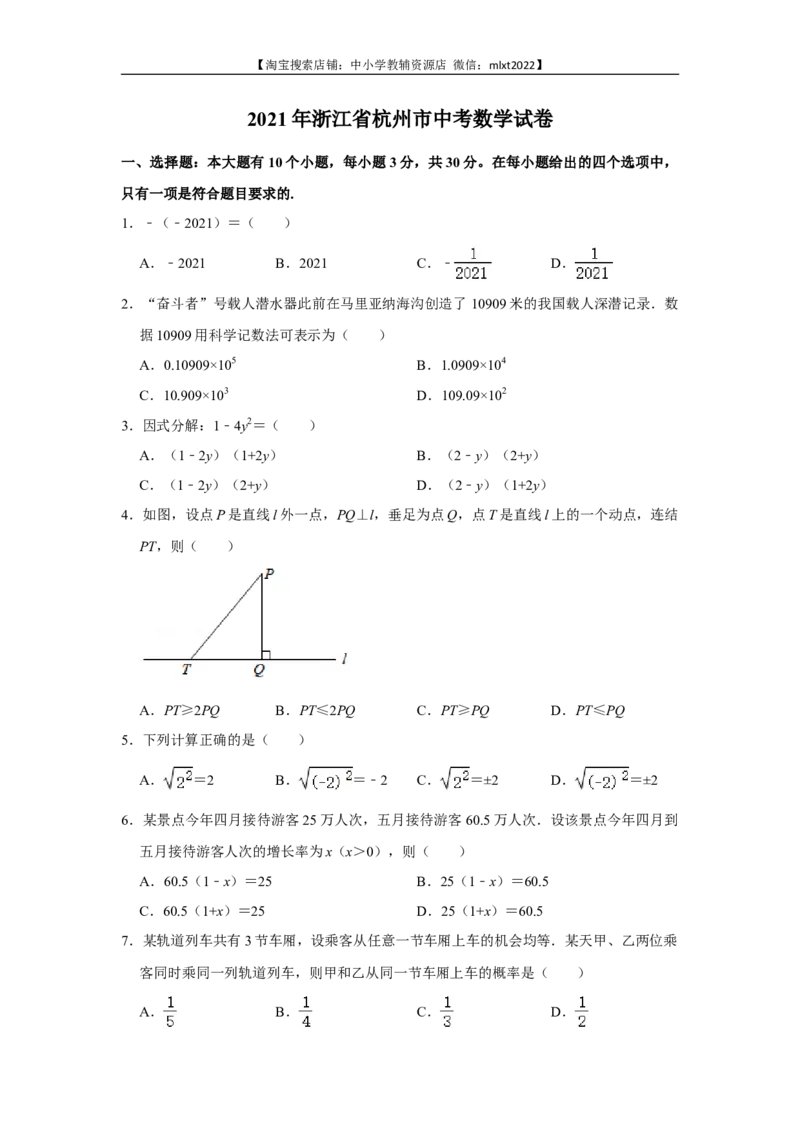
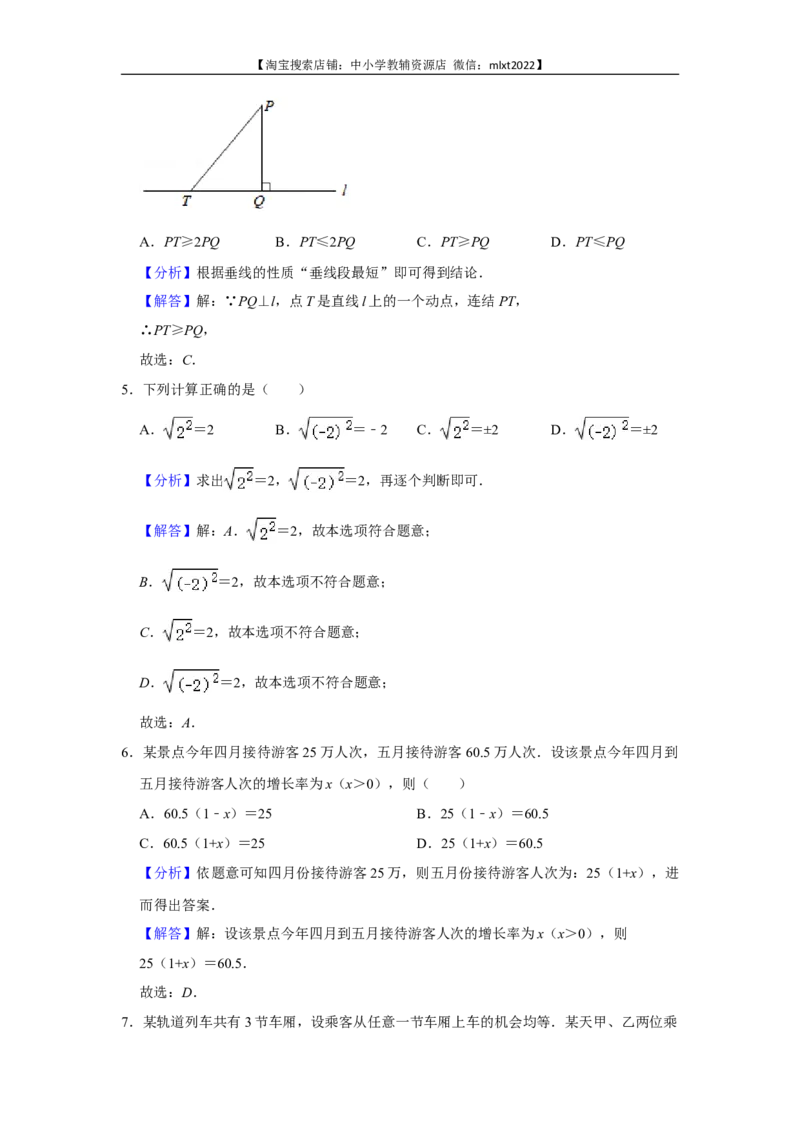
4.如图,设点P是直线l外一点,PQ⊥l,垂足为点Q,点T是直线l上的一个动点,连结
PT,则( )
A.PT≥2PQ B.PT≤2PQ C.PT≥PQ D.PT≤PQ
5.下列计算正确的是( )
A. =2 B. =﹣2 C. =±2 D. =±2
6.某景点今年四月接待游客25万人次,五月接待游客60.5万人次.设该景点今年四月到
五月接待游客人次的增长率为x(x>0),则( )
A.60.5(1﹣x)=25 B.25(1﹣x)=60.5
C.60.5(1+x)=25 D.25(1+x)=60.5
7.某轨道列车共有3节车厢,设乘客从任意一节车厢上车的机会均等.某天甲、乙两位乘
客同时乘同一列轨道列车,则甲和乙从同一节车厢上车的概率是( )
A. B. C. D.【淘宝搜索店铺:中小学教辅资源店 微信:mlxt2022】
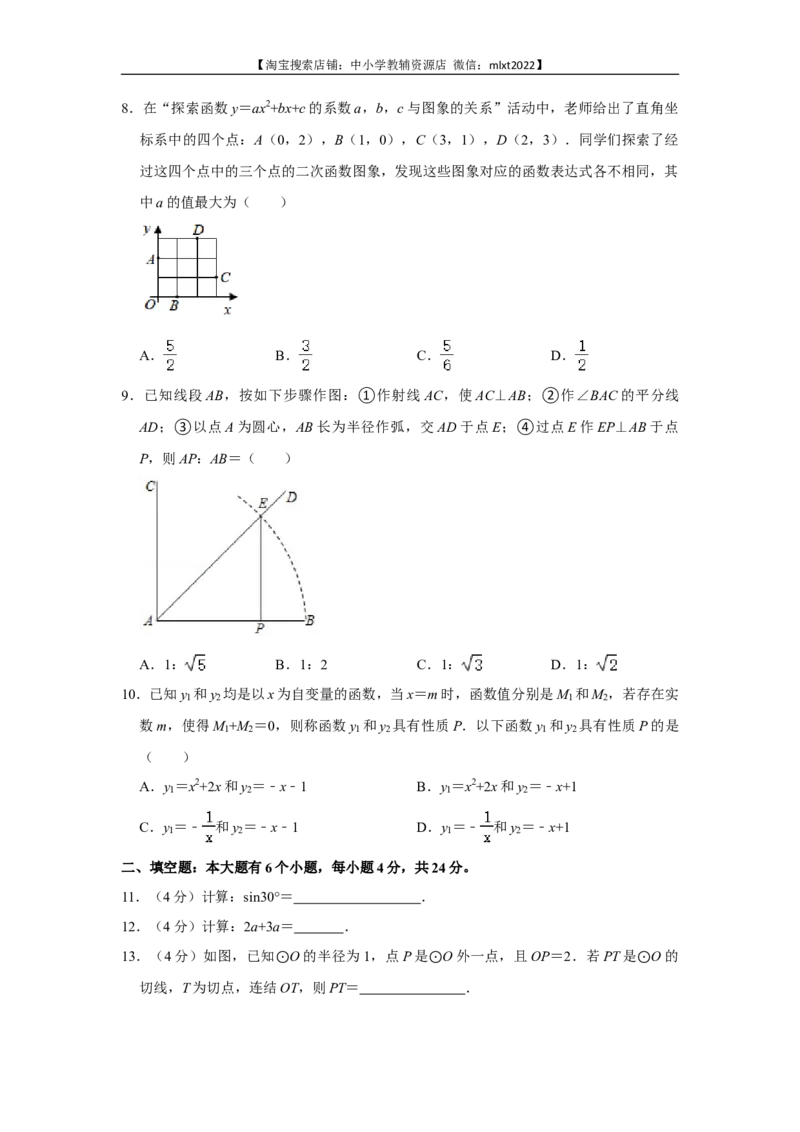
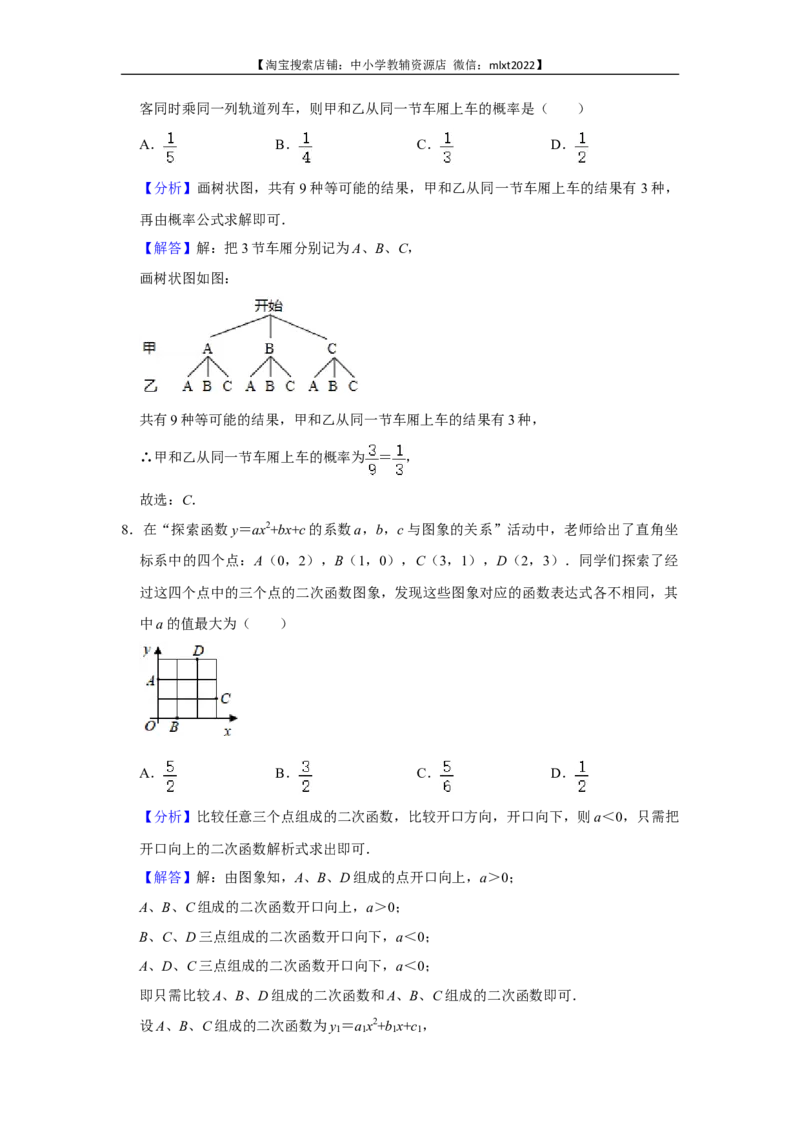
8.在“探索函数y=ax2+bx+c的系数a,b,c与图象的关系”活动中,老师给出了直角坐
标系中的四个点:A(0,2),B(1,0),C(3,1),D(2,3).同学们探索了经
过这四个点中的三个点的二次函数图象,发现这些图象对应的函数表达式各不相同,其
中a的值最大为( )
A. B. C. D.
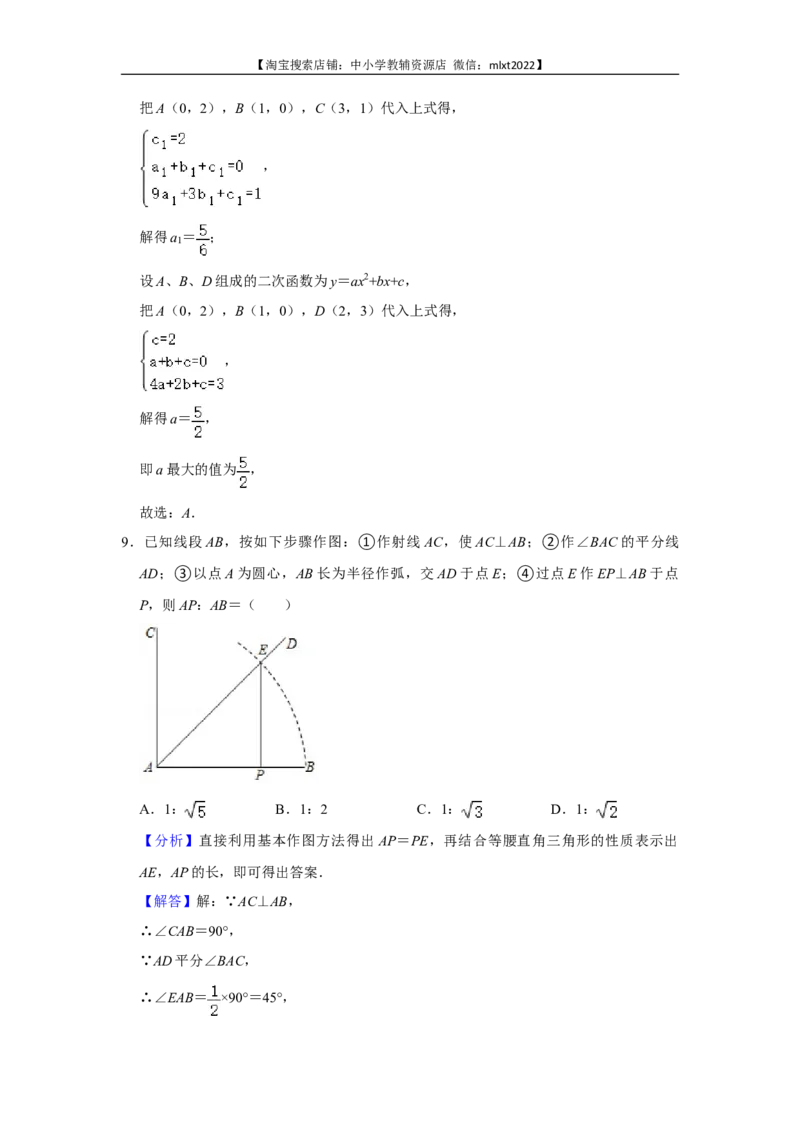
9.已知线段AB,按如下步骤作图:①作射线AC,使AC⊥AB;②作∠BAC的平分线
AD;③以点A为圆心,AB长为半径作弧,交AD于点E;④过点E作EP⊥AB于点
P,则AP:AB=( )
A.1: B.1:2 C.1: D.1:
10.已知y 和y 均是以x为自变量的函数,当x=m时,函数值分别是M 和M ,若存在实
1 2 1 2
数m,使得M +M =0,则称函数y 和y 具有性质P.以下函数y 和y 具有性质P的是
1 2 1 2 1 2
( )
A.y =x2+2x和y =﹣x﹣1 B.y =x2+2x和y =﹣x+1
1 2 1 2
C.y =﹣ 和y =﹣x﹣1 D.y =﹣ 和y =﹣x+1
1 2 1 2
二、填空题:本大题有6个小题,每小题4分,共24分。
11.(4分)计算:sin30°= .
12.(4分)计算:2a+3a= .
13.(4分)如图,已知 O的半径为1,点P是 O外一点,且OP=2.若PT是 O的
切线,T为切点,连结⊙OT,则PT= ⊙ . ⊙【淘宝搜索店铺:中小学教辅资源店 微信:mlxt2022】
14.(4分)现有甲、乙两种糖果的单价与千克数如下表所示.
甲种糖果 乙种糖果
单价(元/千克) 30 20
千克数 2 3
将这2千克甲种糖果和3千克乙种糖果混合成5千克什锦糖果,若商家用加权平均数来
确定什锦糖果的单价,则这5千克什锦糖果的单价为 元/千克.
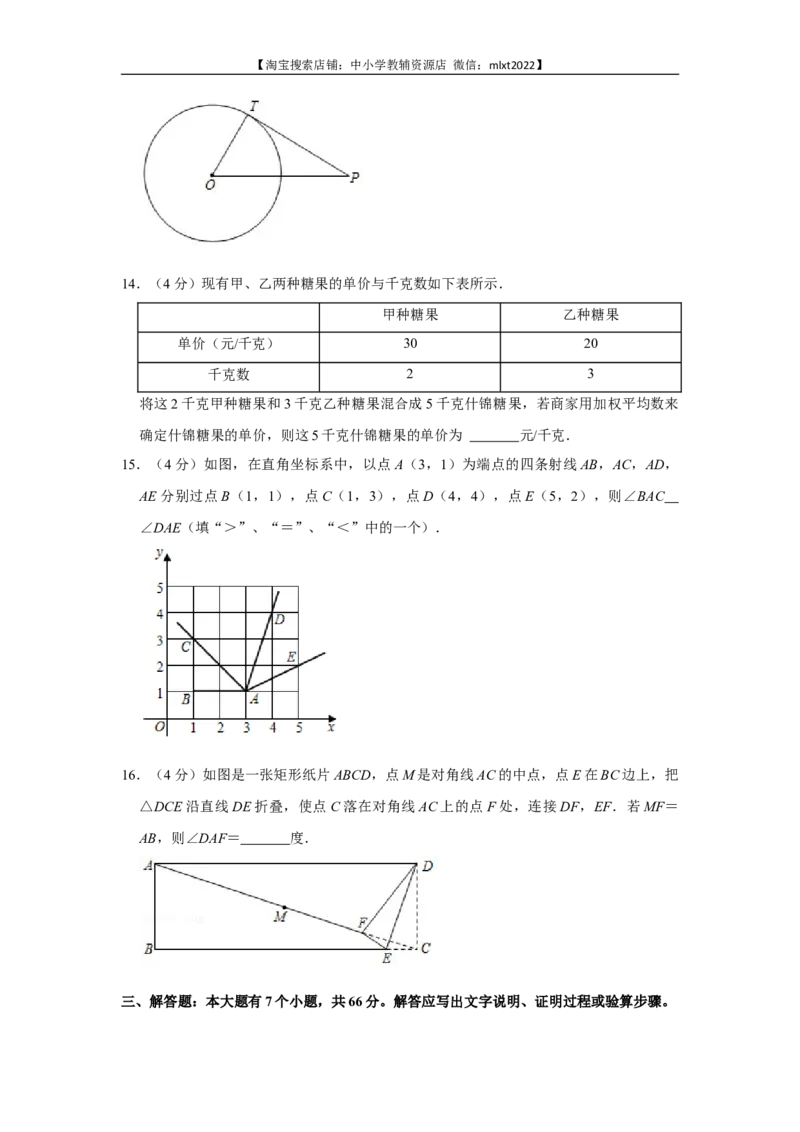
15.(4分)如图,在直角坐标系中,以点A(3,1)为端点的四条射线AB,AC,AD,
AE分别过点B(1,1),点C(1,3),点D(4,4),点E(5,2),则∠BAC
∠DAE(填“>”、“=”、“<”中的一个).
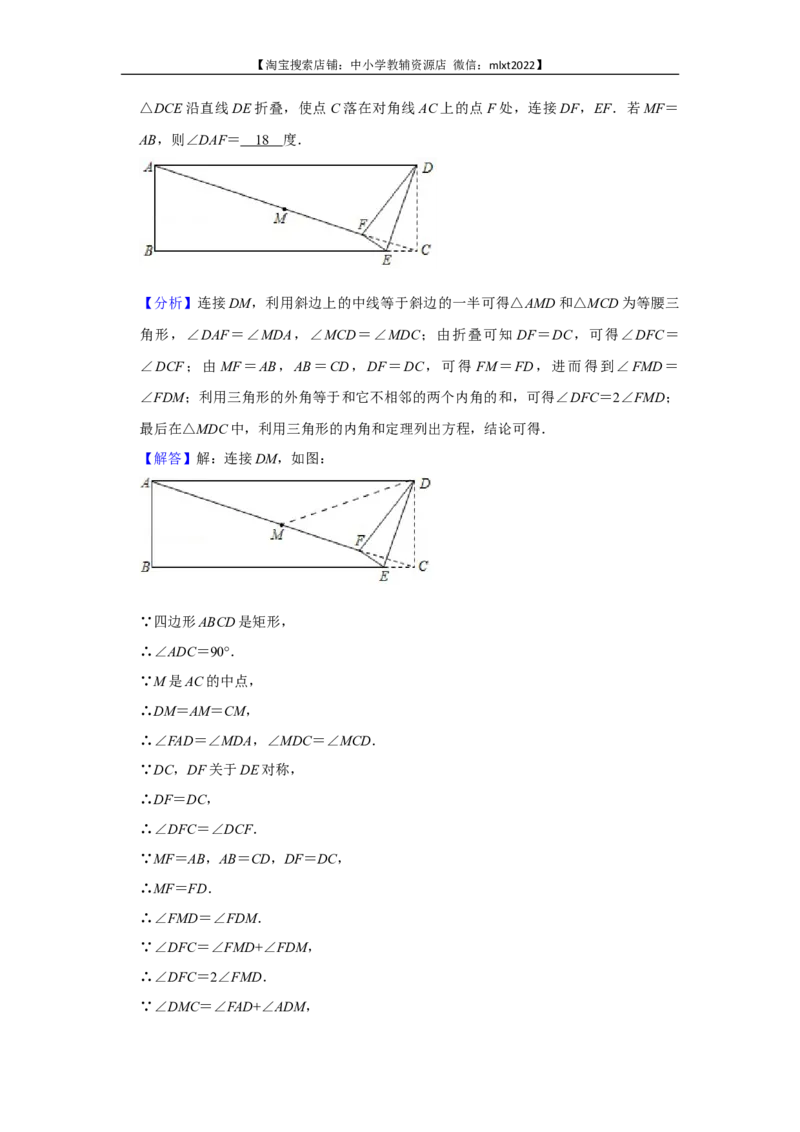
16.(4分)如图是一张矩形纸片ABCD,点M是对角线AC的中点,点E在BC边上,把
△DCE沿直线DE折叠,使点C落在对角线AC上的点F处,连接DF,EF.若MF=
AB,则∠DAF= 度.
三、解答题:本大题有7个小题,共66分。解答应写出文字说明、证明过程或验算步骤。【淘宝搜索店铺:中小学教辅资源店 微信:mlxt2022】
17.(6分)以下是圆圆解不等式组 的解答过程:
解:由①,得2+x>﹣1,
所以x>﹣3.
由②,得1﹣x>2,
所以﹣x>1,
所以x>﹣1.
所以原不等式组的解集是x>﹣1.
圆圆的解答过程是否有错误?如果有错误,请写出正确的解答过程.
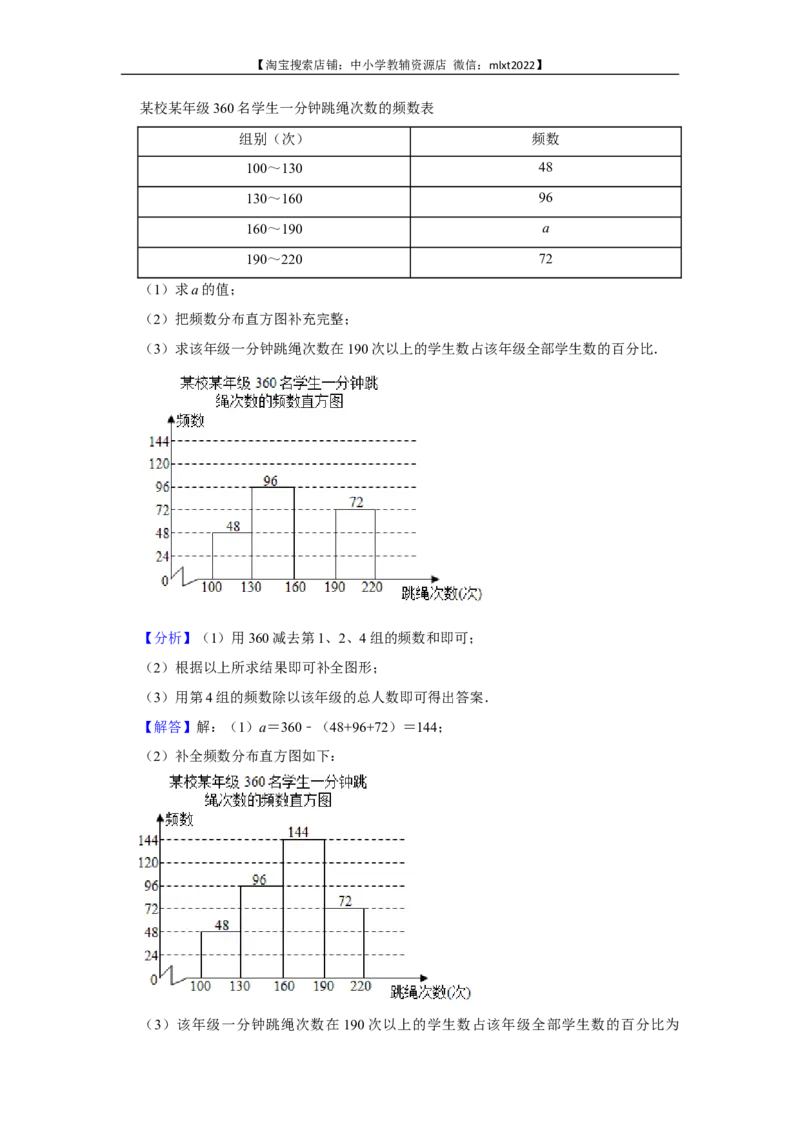
18.(8分)为了解某校某年级学生一分钟跳绳情况,对该年级全部360名学生进行一分
钟跳绳次数的测试,并把测得数据分成四组,绘制成如图所示的频数表和未完成的频数
分布直方图(每一组不含前一个边界值,含后一个边界值).
某校某年级360名学生一分钟跳绳次数的频数表
组别(次) 频数
100~130 48
130~160 96
160~190 a
190~220 72
(1)求a的值;
(2)把频数分布直方图补充完整;
(3)求该年级一分钟跳绳次数在190次以上的学生数占该年级全部学生数的百分比.
19.(8分)在①AD=AE,②∠ABE=∠ACD,③FB=FC这三个条件中选择其中一个,【淘宝搜索店铺:中小学教辅资源店 微信:mlxt2022】
补充在下面的问题中,并完成问题的解答.
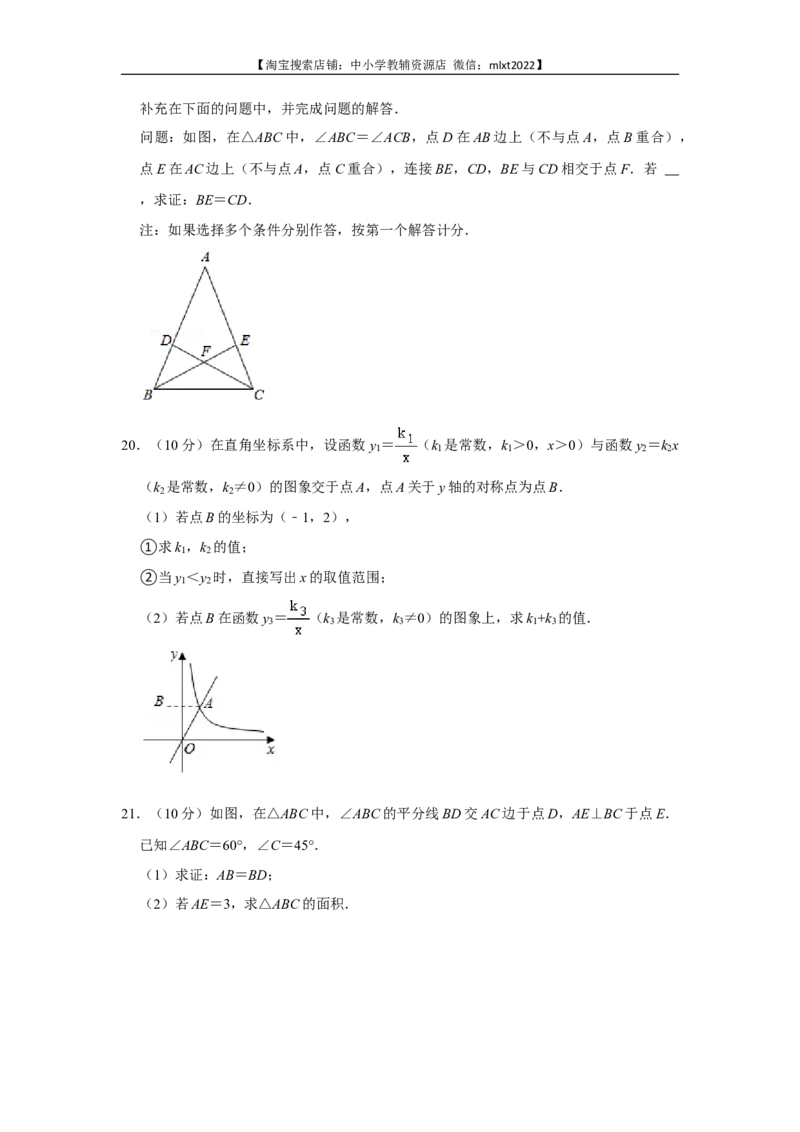
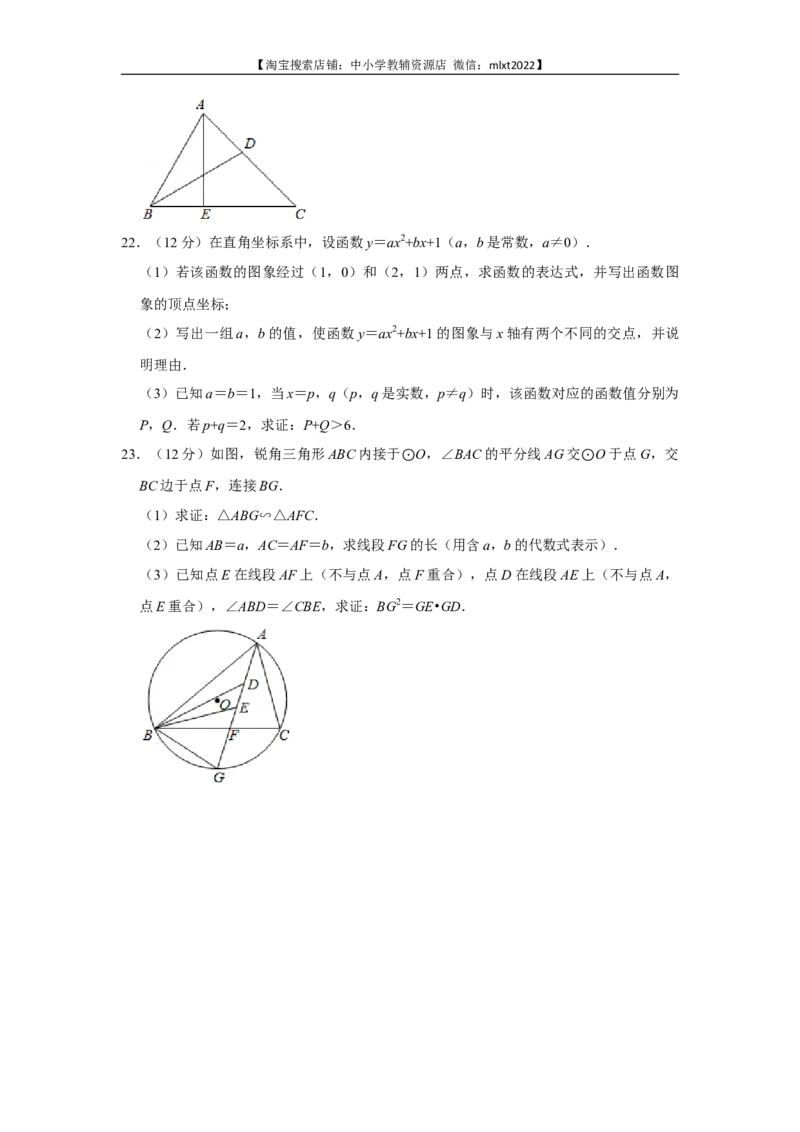
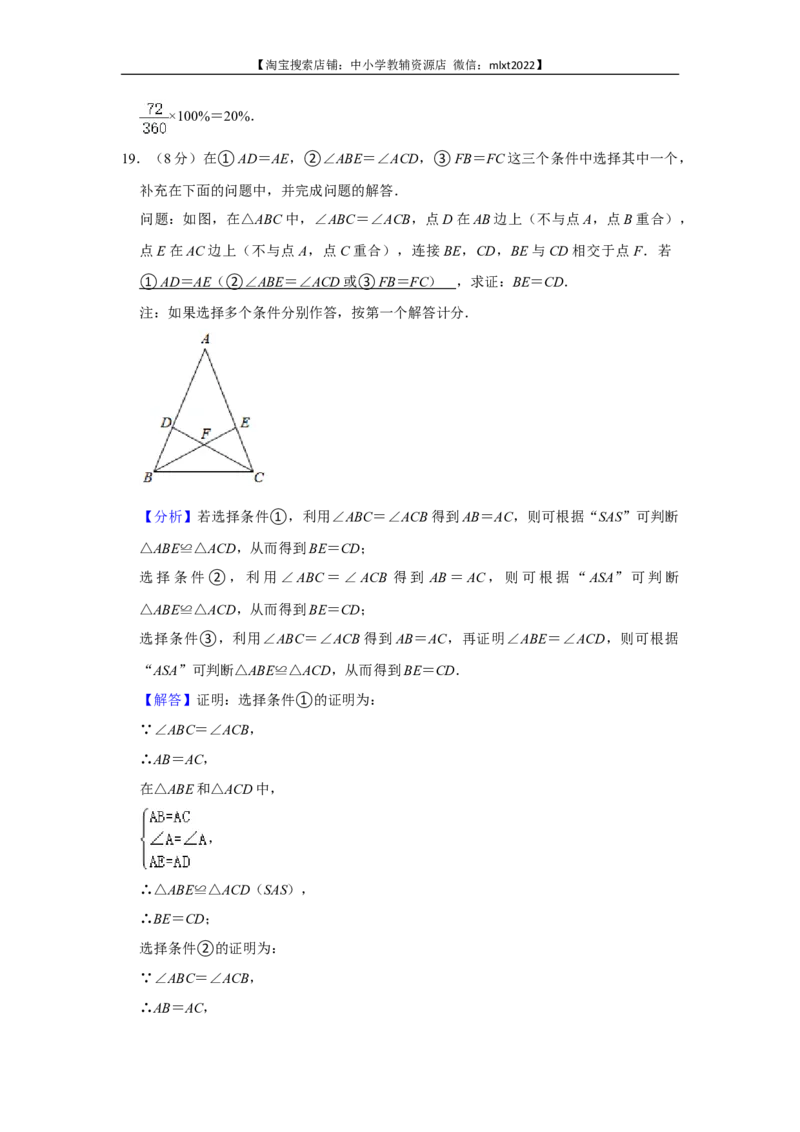
问题:如图,在△ABC中,∠ABC=∠ACB,点D在AB边上(不与点A,点B重合),
点E在AC边上(不与点A,点C重合),连接BE,CD,BE与CD相交于点F.若
,求证:BE=CD.
注:如果选择多个条件分别作答,按第一个解答计分.
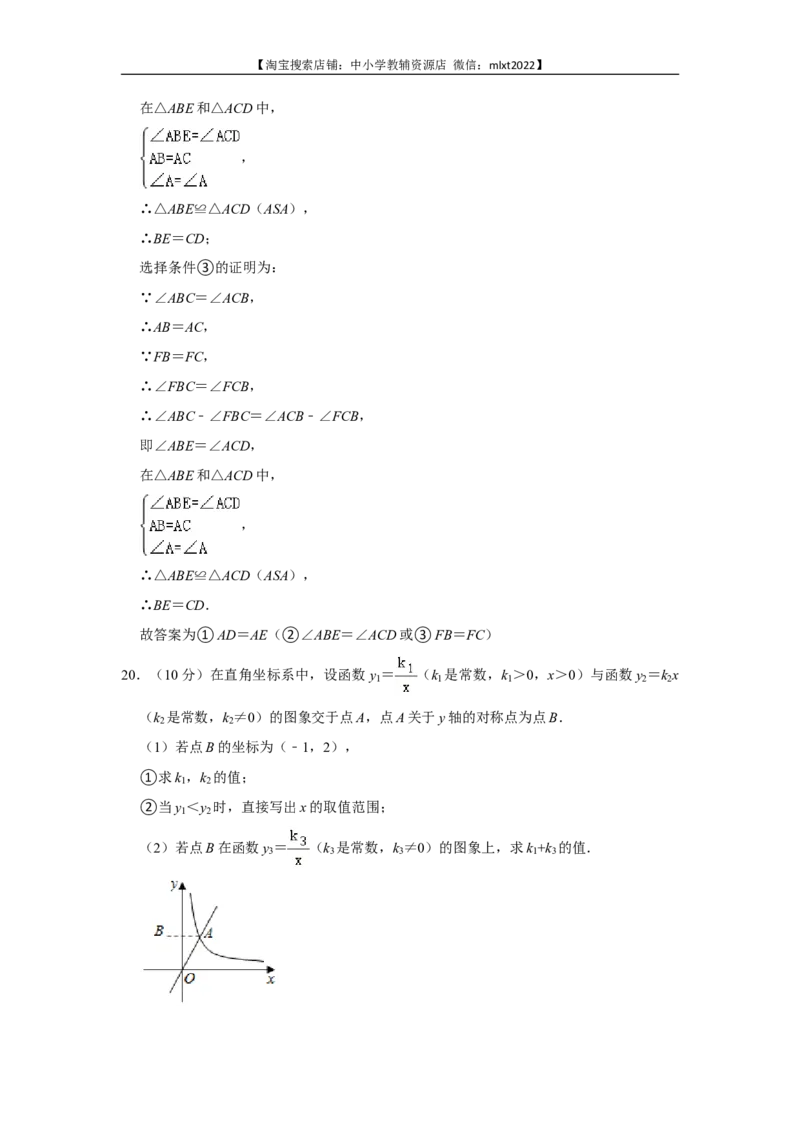
20.(10分)在直角坐标系中,设函数y = (k 是常数,k >0,x>0)与函数y =k x
1 1 1 2 2
(k 是常数,k ≠0)的图象交于点A,点A关于y轴的对称点为点B.
2 2
(1)若点B的坐标为(﹣1,2),
①求k ,k 的值;
1 2
②当y <y 时,直接写出x的取值范围;
1 2
(2)若点B在函数y = (k 是常数,k ≠0)的图象上,求k +k 的值.
3 3 3 1 3
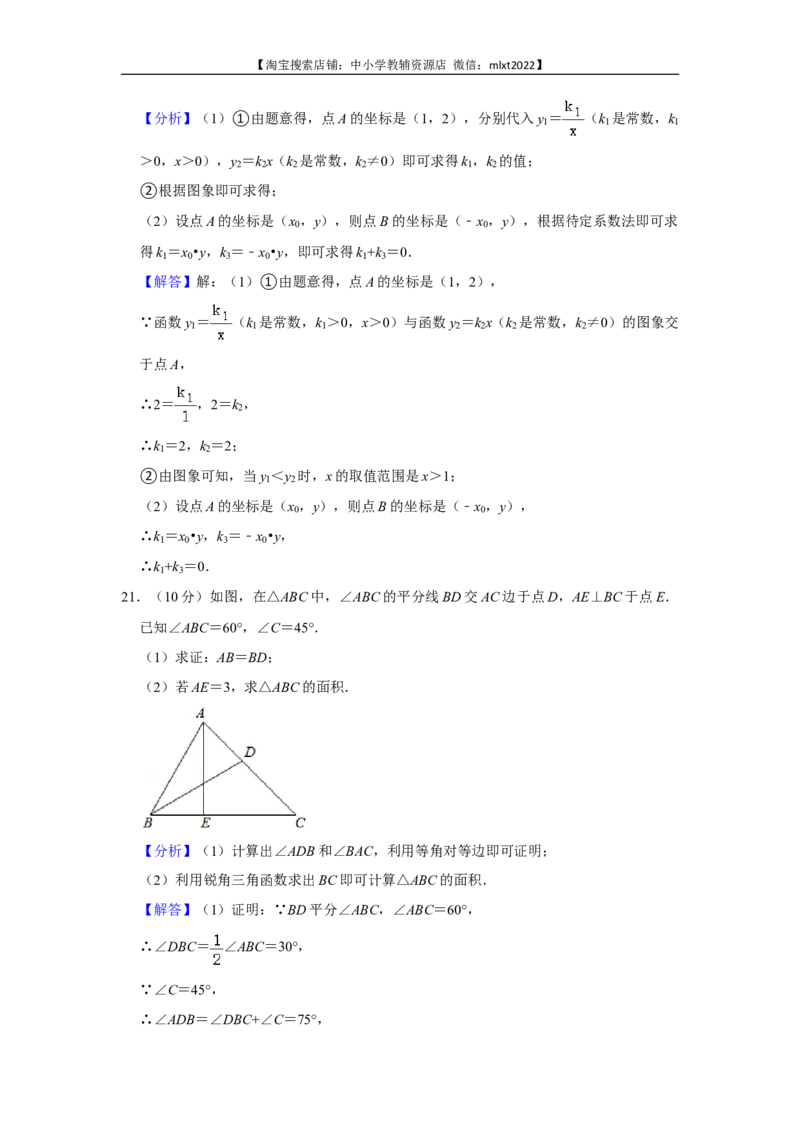
21.(10分)如图,在△ABC中,∠ABC的平分线BD交AC边于点D,AE⊥BC于点E.
已知∠ABC=60°,∠C=45°.
(1)求证:AB=BD;
(2)若AE=3,求△ABC的面积.【淘宝搜索店铺:中小学教辅资源店 微信:mlxt2022】
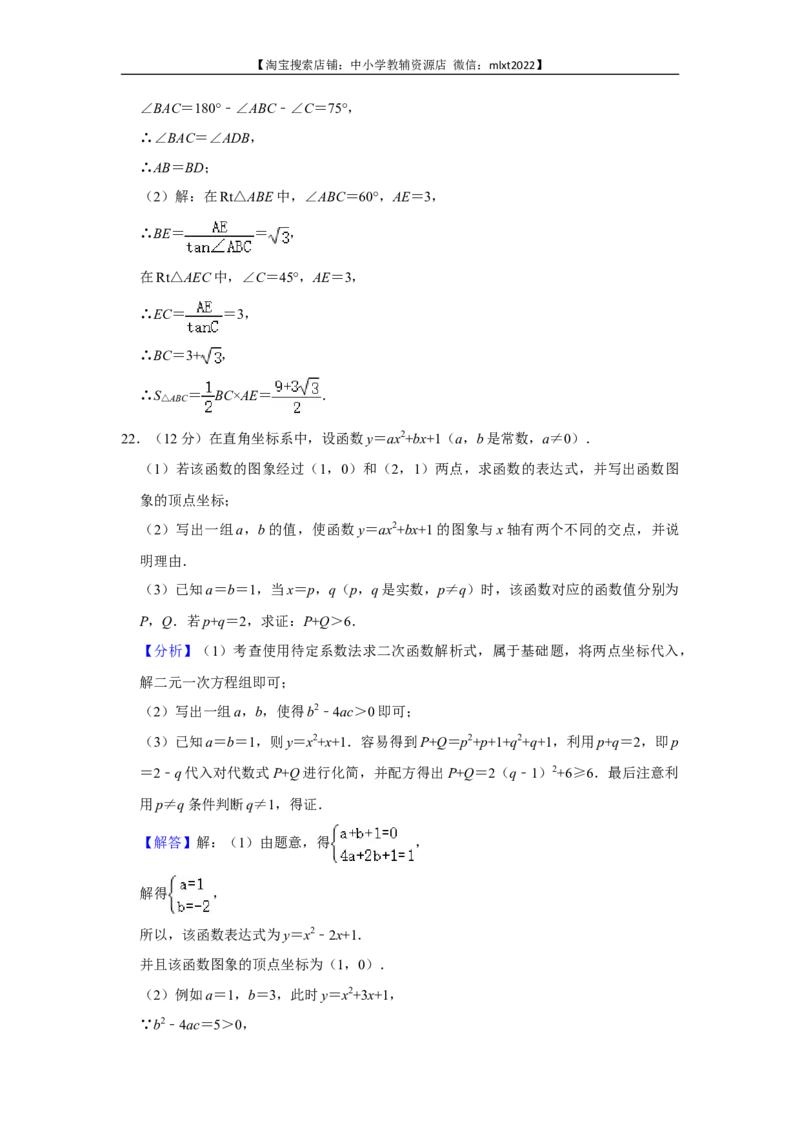
22.(12分)在直角坐标系中,设函数y=ax2+bx+1(a,b是常数,a≠0).
(1)若该函数的图象经过(1,0)和(2,1)两点,求函数的表达式,并写出函数图
象的顶点坐标;
(2)写出一组a,b的值,使函数y=ax2+bx+1的图象与x轴有两个不同的交点,并说
明理由.
(3)已知a=b=1,当x=p,q(p,q是实数,p≠q)时,该函数对应的函数值分别为
P,Q.若p+q=2,求证:P+Q>6.
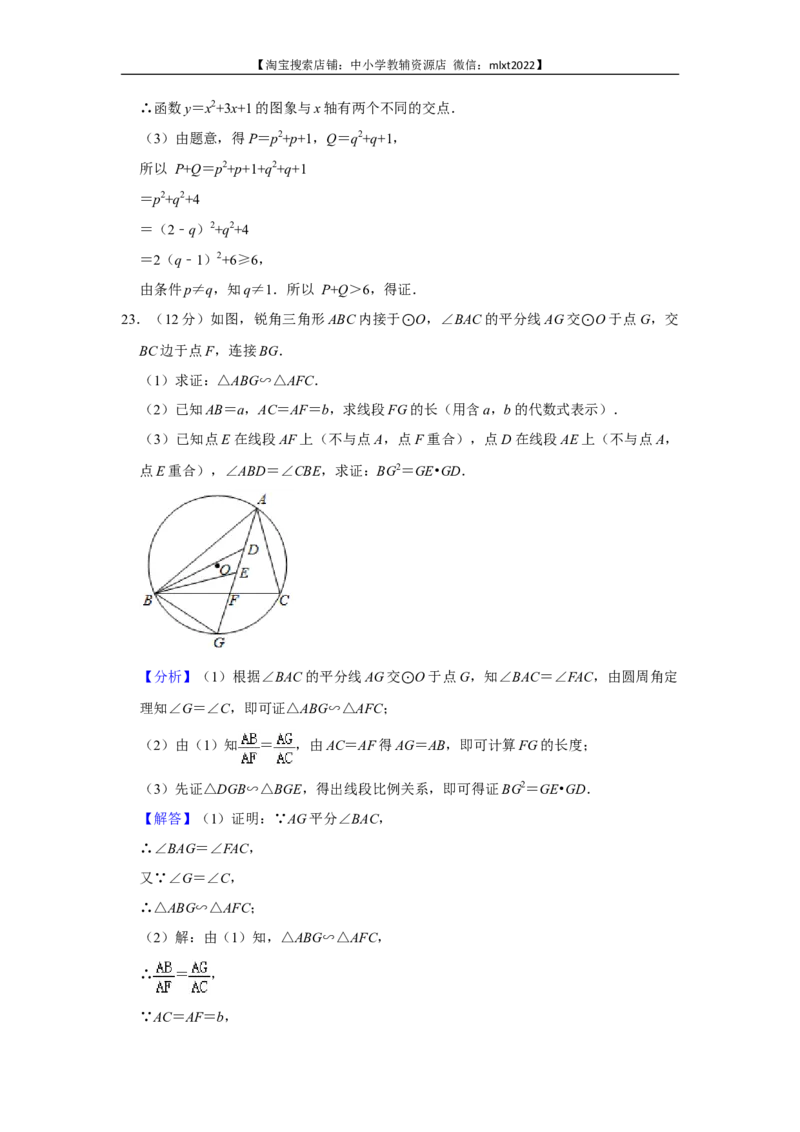
23.(12分)如图,锐角三角形ABC内接于 O,∠BAC的平分线AG交 O于点G,交
BC边于点F,连接BG. ⊙ ⊙
(1)求证:△ABG∽△AFC.
(2)已知AB=a,AC=AF=b,求线段FG的长(用含a,b的代数式表示).
(3)已知点E在线段AF上(不与点A,点F重合),点D在线段AE上(不与点A,
点E重合),∠ABD=∠CBE,求证:BG2=GE•GD.【淘宝搜索店铺:中小学教辅资源店 微信:mlxt2022】
2021年浙江省杭州市中考数学试卷
参考答案与试题解析
一、选择题:本大题有10个小题,每小题3分,共30分。在每小题给出的四个选项中,
只有一项是符合题目要求的.
1.﹣(﹣2021)=( )
A.﹣2021 B.2021 C.﹣ D.
【分析】直接利用相反数的概念:只有符号不同的两个数互为相反数,即可得出答案.
【解答】解:﹣(﹣2021)=2021.
故选:B.
2.“奋斗者”号载人潜水器此前在马里亚纳海沟创造了 10909米的我国载人深潜记录.数
据10909用科学记数法可表示为( )
A.0.10909×105 B.1.0909×104
C.10.909×103 D.109.09×102
【分析】用科学记数法表示较大的数时,一般形式为a×10n,其中1≤|a|<10,n为整数,
据此判断即可.
【解答】解:10909=1.0909×104.
故选:B.
3.因式分解:1﹣4y2=( )
A.(1﹣2y)(1+2y) B.(2﹣y)(2+y)
C.(1﹣2y)(2+y) D.(2﹣y)(1+2y)
【分析】直接利用平方差公式分解因式得出答案.
【解答】解:1﹣4y2
=1﹣(2y)2
=(1﹣2y)(1+2y).
故选:A.
4.如图,设点P是直线l外一点,PQ⊥l,垂足为点Q,点T是直线l上的一个动点,连结
PT,则( )【淘宝搜索店铺:中小学教辅资源店 微信:mlxt2022】
A.PT≥2PQ B.PT≤2PQ C.PT≥PQ D.PT≤PQ
【分析】根据垂线的性质“垂线段最短”即可得到结论.
【解答】解:∵PQ⊥l,点T是直线l上的一个动点,连结PT,
∴PT≥PQ,
故选:C.
5.下列计算正确的是( )
A. =2 B. =﹣2 C. =±2 D. =±2
【分析】求出 =2, =2,再逐个判断即可.
【解答】解:A. =2,故本选项符合题意;
B. =2,故本选项不符合题意;
C. =2,故本选项不符合题意;
D. =2,故本选项不符合题意;
故选:A.
6.某景点今年四月接待游客25万人次,五月接待游客60.5万人次.设该景点今年四月到
五月接待游客人次的增长率为x(x>0),则( )
A.60.5(1﹣x)=25 B.25(1﹣x)=60.5
C.60.5(1+x)=25 D.25(1+x)=60.5
【分析】依题意可知四月份接待游客25万,则五月份接待游客人次为:25(1+x),进
而得出答案.
【解答】解:设该景点今年四月到五月接待游客人次的增长率为x(x>0),则
25(1+x)=60.5.
故选:D.
7.某轨道列车共有3节车厢,设乘客从任意一节车厢上车的机会均等.某天甲、乙两位乘【淘宝搜索店铺:中小学教辅资源店 微信:mlxt2022】
客同时乘同一列轨道列车,则甲和乙从同一节车厢上车的概率是( )
A. B. C. D.
【分析】画树状图,共有9种等可能的结果,甲和乙从同一节车厢上车的结果有3种,
再由概率公式求解即可.
【解答】解:把3节车厢分别记为A、B、C,
画树状图如图:
共有9种等可能的结果,甲和乙从同一节车厢上车的结果有3种,
∴甲和乙从同一节车厢上车的概率为 = ,
故选:C.
8.在“探索函数y=ax2+bx+c的系数a,b,c与图象的关系”活动中,老师给出了直角坐
标系中的四个点:A(0,2),B(1,0),C(3,1),D(2,3).同学们探索了经
过这四个点中的三个点的二次函数图象,发现这些图象对应的函数表达式各不相同,其
中a的值最大为( )
A. B. C. D.
【分析】比较任意三个点组成的二次函数,比较开口方向,开口向下,则a<0,只需把
开口向上的二次函数解析式求出即可.
【解答】解:由图象知,A、B、D组成的点开口向上,a>0;
A、B、C组成的二次函数开口向上,a>0;
B、C、D三点组成的二次函数开口向下,a<0;
A、D、C三点组成的二次函数开口向下,a<0;
即只需比较A、B、D组成的二次函数和A、B、C组成的二次函数即可.
设A、B、C组成的二次函数为y =a x2+b x+c ,
1 1 1 1【淘宝搜索店铺:中小学教辅资源店 微信:mlxt2022】
把A(0,2),B(1,0),C(3,1)代入上式得,
,
解得a = ;
1
设A、B、D组成的二次函数为y=ax2+bx+c,
把A(0,2),B(1,0),D(2,3)代入上式得,
,
解得a= ,
即a最大的值为 ,
故选:A.
9.已知线段AB,按如下步骤作图:①作射线AC,使AC⊥AB;②作∠BAC的平分线
AD;③以点A为圆心,AB长为半径作弧,交AD于点E;④过点E作EP⊥AB于点
P,则AP:AB=( )
A.1: B.1:2 C.1: D.1:
【分析】直接利用基本作图方法得出AP=PE,再结合等腰直角三角形的性质表示出
AE,AP的长,即可得出答案.
【解答】解:∵AC⊥AB,
∴∠CAB=90°,
∵AD平分∠BAC,
∴∠EAB= ×90°=45°,【淘宝搜索店铺:中小学教辅资源店 微信:mlxt2022】
∵EP⊥AB,
∴∠APE=90°,
∴∠EAP=∠AEP=45°,
∴AP=PE,
∴设AP=PE=x,
故AE=AB= x,
∴AP:AB=x: x=1: .
故选:D.
10.已知y 和y 均是以x为自变量的函数,当x=m时,函数值分别是M 和M ,若存在实
1 2 1 2
数m,使得M +M =0,则称函数y 和y 具有性质P.以下函数y 和y 具有性质P的是
1 2 1 2 1 2
( )
A.y =x2+2x和y =﹣x﹣1 B.y =x2+2x和y =﹣x+1
1 2 1 2
C.y =﹣ 和y =﹣x﹣1 D.y =﹣ 和y =﹣x+1
1 2 1 2
【分析】根据题干信息可知,直接令y +y =0,若方程有解,则具有性质P,若无解,
1 2
则不具有性质P.
【解答】解:A.令y +y =0,则x2+2x﹣x﹣1=0,解得x= 或x= ,即
1 2
函数y 和y 具有性质P,符合题意;
1 2
B.令y +y =0,则x2+2x﹣x+1=0,整理得,x2+x+1=0,方程无解,即函数y 和y 不
1 2 1 2
具有性质P,不符合题意;
C.令y +y =0,则﹣ ﹣x﹣1=0,整理得,x2+x+1=0,方程无解,即函数y 和y 不
1 2 1 2
具有性质P,不符合题意;
D.令y +y =0,则﹣ ﹣x+1=0,整理得,x2﹣x+1=0,方程无解,即函数y 和y 不
1 2 1 2
具有性质P,不符合题意;
故选:A.
二、填空题:本大题有6个小题,每小题4分,共24分。
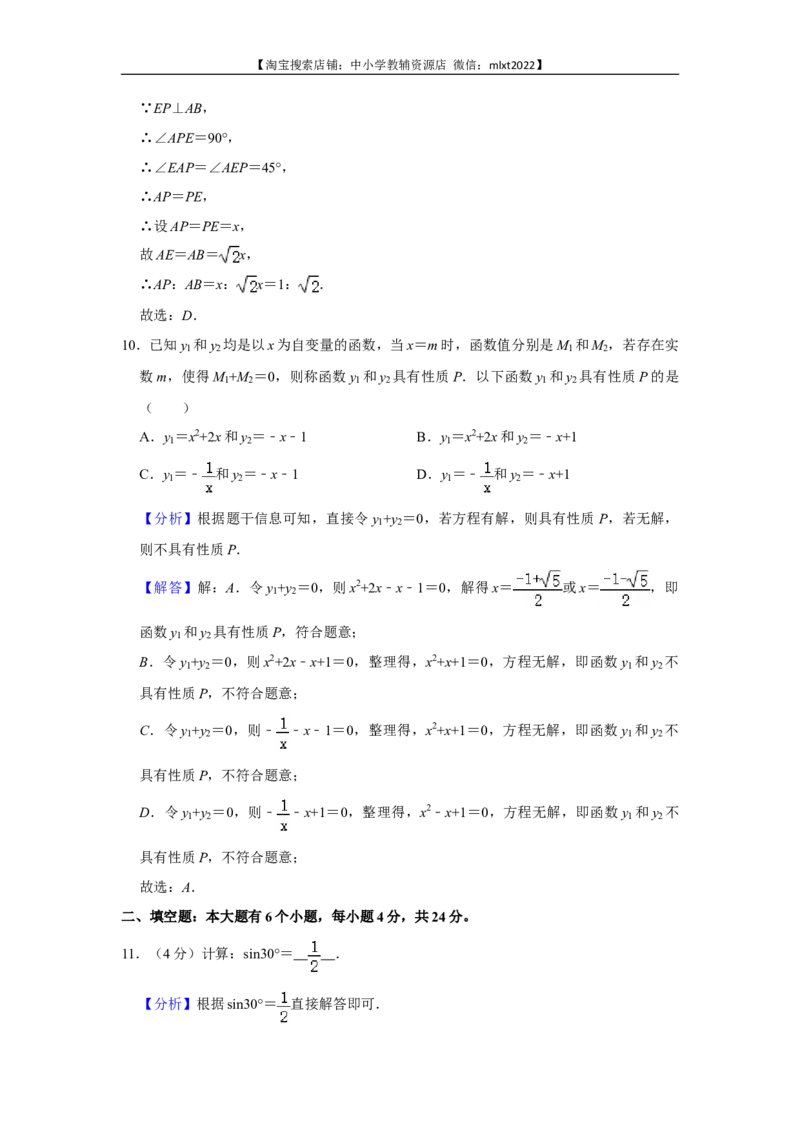
11.(4分)计算:sin30°= .
【分析】根据sin30°= 直接解答即可.【淘宝搜索店铺:中小学教辅资源店 微信:mlxt2022】
【解答】解:sin30°= .
12.(4分)计算:2a+3a= 5 a .
【分析】根据合并同类项的法则:把同类项的系数相加,所得结果作为系数,字母和字
母的指数不变求解.
【解答】解:2a+3a=5a,故答案为5a.
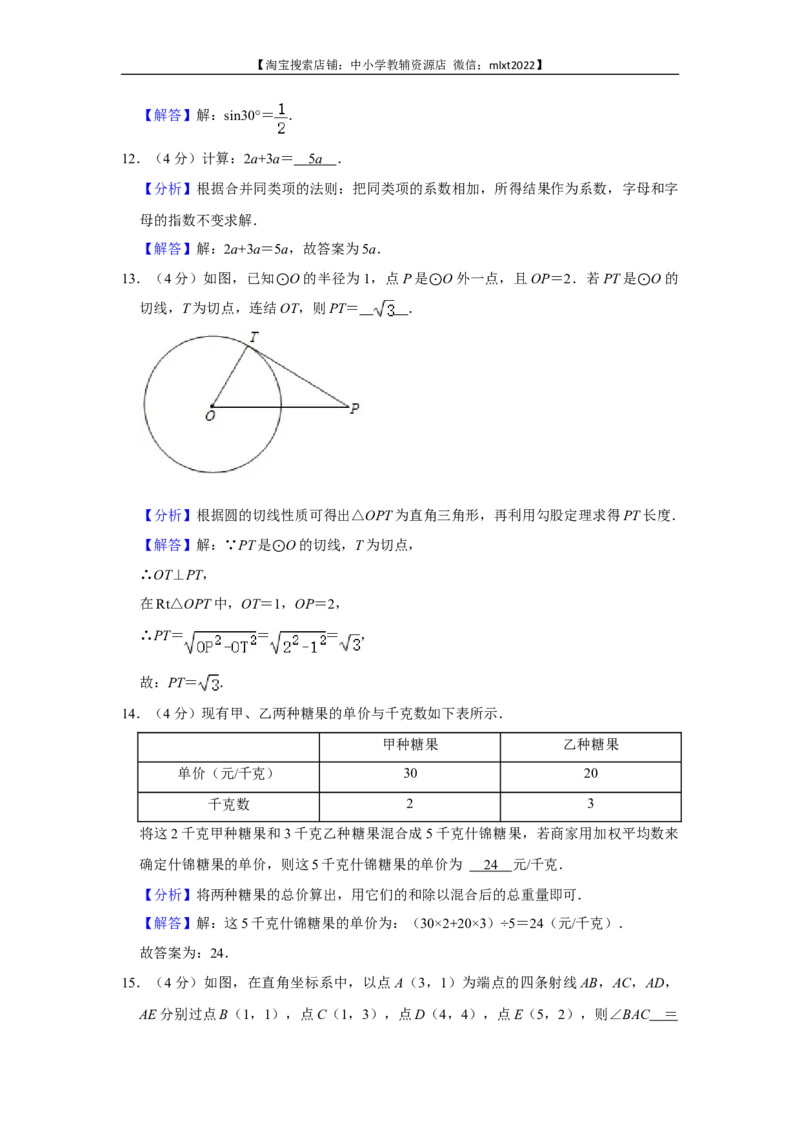
13.(4分)如图,已知 O的半径为1,点P是 O外一点,且OP=2.若PT是 O的
切线,T为切点,连结⊙OT,则PT= . ⊙ ⊙
【分析】根据圆的切线性质可得出△OPT为直角三角形,再利用勾股定理求得PT长度.
【解答】解:∵PT是 O的切线,T为切点,
∴OT⊥PT, ⊙
在Rt△OPT中,OT=1,OP=2,
∴PT= = = ,
故:PT= .
14.(4分)现有甲、乙两种糖果的单价与千克数如下表所示.
甲种糖果 乙种糖果
单价(元/千克) 30 20
千克数 2 3
将这2千克甲种糖果和3千克乙种糖果混合成5千克什锦糖果,若商家用加权平均数来
确定什锦糖果的单价,则这5千克什锦糖果的单价为 2 4 元/千克.
【分析】将两种糖果的总价算出,用它们的和除以混合后的总重量即可.
【解答】解:这5千克什锦糖果的单价为:(30×2+20×3)÷5=24(元/千克).
故答案为:24.
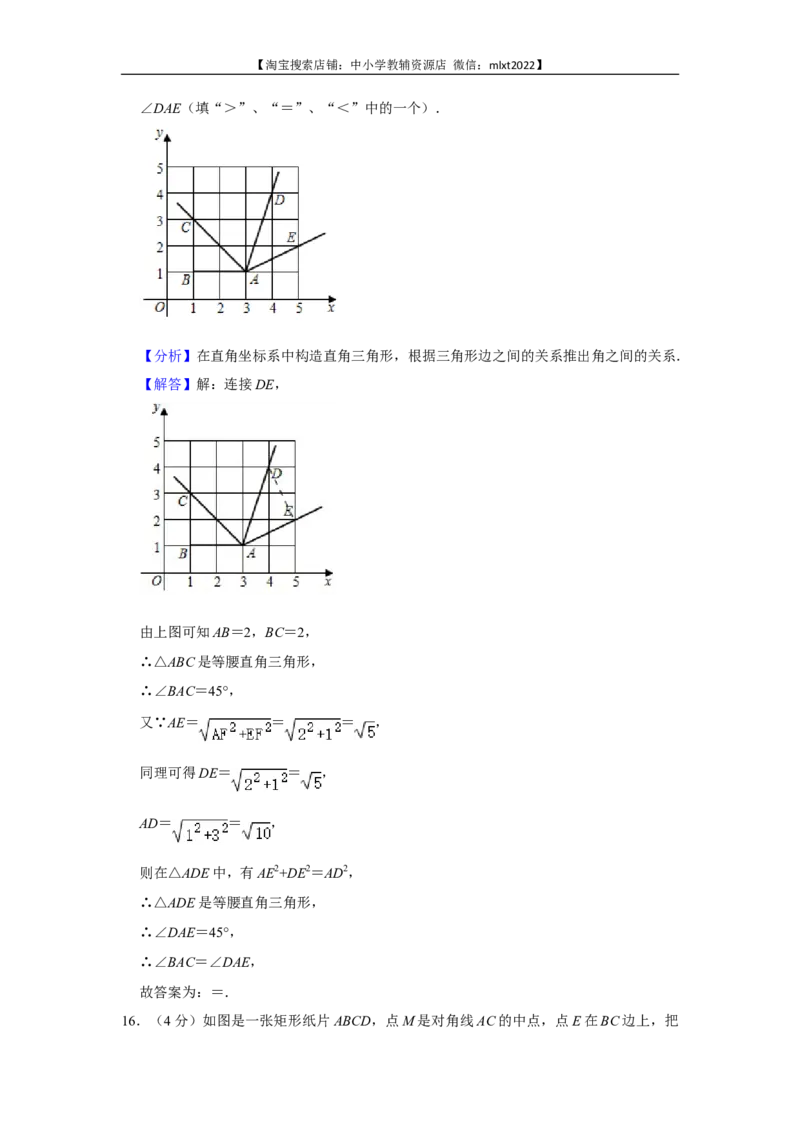
15.(4分)如图,在直角坐标系中,以点A(3,1)为端点的四条射线AB,AC,AD,
AE分别过点B(1,1),点C(1,3),点D(4,4),点E(5,2),则∠BAC =【淘宝搜索店铺:中小学教辅资源店 微信:mlxt2022】
∠DAE(填“>”、“=”、“<”中的一个).
【分析】在直角坐标系中构造直角三角形,根据三角形边之间的关系推出角之间的关系.
【解答】解:连接DE,
由上图可知AB=2,BC=2,
∴△ABC是等腰直角三角形,
∴∠BAC=45°,
又∵AE= = = ,
同理可得DE= = ,
AD= = ,
则在△ADE中,有AE2+DE2=AD2,
∴△ADE是等腰直角三角形,
∴∠DAE=45°,
∴∠BAC=∠DAE,
故答案为:=.
16.(4分)如图是一张矩形纸片ABCD,点M是对角线AC的中点,点E在BC边上,把【淘宝搜索店铺:中小学教辅资源店 微信:mlxt2022】
△DCE沿直线DE折叠,使点C落在对角线AC上的点F处,连接DF,EF.若MF=
AB,则∠DAF= 1 8 度.
【分析】连接DM,利用斜边上的中线等于斜边的一半可得△AMD和△MCD为等腰三
角形,∠DAF=∠MDA,∠MCD=∠MDC;由折叠可知 DF=DC,可得∠DFC=
∠DCF;由 MF=AB,AB=CD,DF=DC,可得 FM=FD,进而得到∠FMD=
∠FDM;利用三角形的外角等于和它不相邻的两个内角的和,可得∠DFC=2∠FMD;
最后在△MDC中,利用三角形的内角和定理列出方程,结论可得.
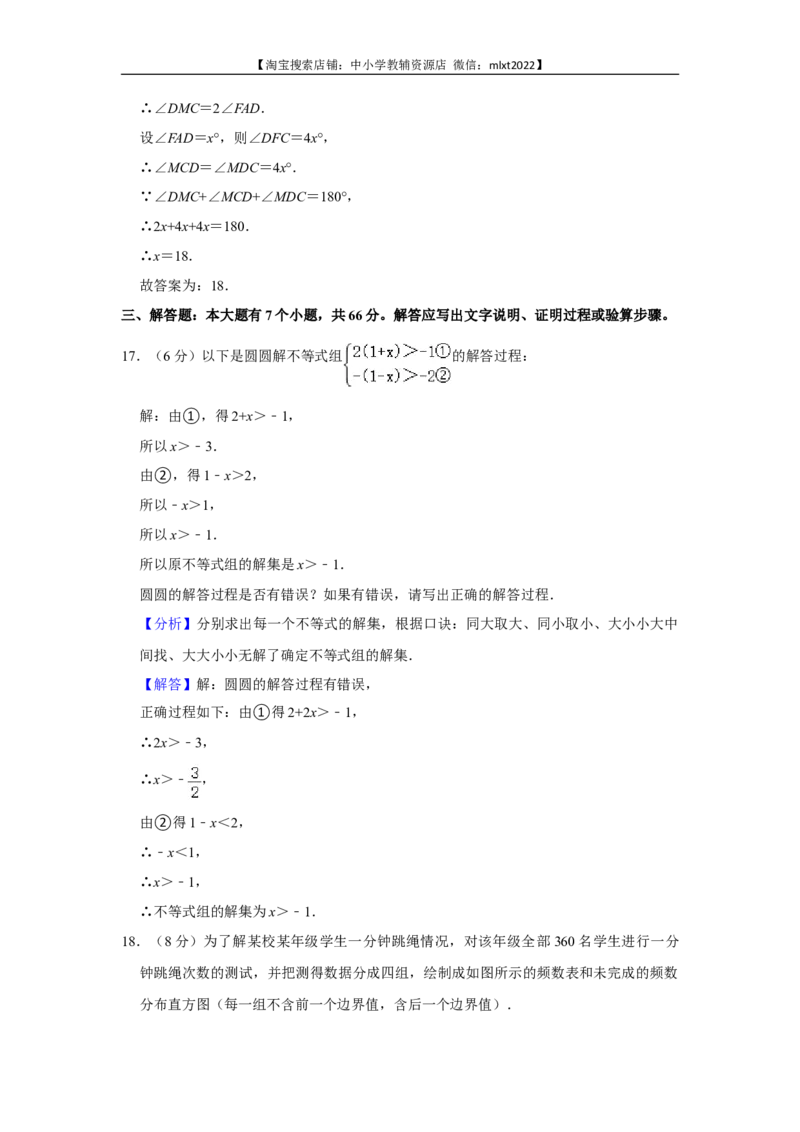
【解答】解:连接DM,如图:
∵四边形ABCD是矩形,
∴∠ADC=90°.
∵M是AC的中点,
∴DM=AM=CM,
∴∠FAD=∠MDA,∠MDC=∠MCD.
∵DC,DF关于DE对称,
∴DF=DC,
∴∠DFC=∠DCF.
∵MF=AB,AB=CD,DF=DC,
∴MF=FD.
∴∠FMD=∠FDM.
∵∠DFC=∠FMD+∠FDM,
∴∠DFC=2∠FMD.
∵∠DMC=∠FAD+∠ADM,【淘宝搜索店铺:中小学教辅资源店 微信:mlxt2022】
∴∠DMC=2∠FAD.
设∠FAD=x°,则∠DFC=4x°,
∴∠MCD=∠MDC=4x°.
∵∠DMC+∠MCD+∠MDC=180°,
∴2x+4x+4x=180.
∴x=18.
故答案为:18.
三、解答题:本大题有7个小题,共66分。解答应写出文字说明、证明过程或验算步骤。
17.(6分)以下是圆圆解不等式组 的解答过程:
解:由①,得2+x>﹣1,
所以x>﹣3.
由②,得1﹣x>2,
所以﹣x>1,
所以x>﹣1.
所以原不等式组的解集是x>﹣1.
圆圆的解答过程是否有错误?如果有错误,请写出正确的解答过程.
【分析】分别求出每一个不等式的解集,根据口诀:同大取大、同小取小、大小小大中
间找、大大小小无解了确定不等式组的解集.
【解答】解:圆圆的解答过程有错误,
正确过程如下:由①得2+2x>﹣1,
∴2x>﹣3,
∴x>﹣ ,
由②得1﹣x<2,
∴﹣x<1,
∴x>﹣1,
∴不等式组的解集为x>﹣1.
18.(8分)为了解某校某年级学生一分钟跳绳情况,对该年级全部360名学生进行一分
钟跳绳次数的测试,并把测得数据分成四组,绘制成如图所示的频数表和未完成的频数
分布直方图(每一组不含前一个边界值,含后一个边界值).【淘宝搜索店铺:中小学教辅资源店 微信:mlxt2022】
某校某年级360名学生一分钟跳绳次数的频数表
组别(次) 频数
100~130 48
130~160 96
160~190 a
190~220 72
(1)求a的值;
(2)把频数分布直方图补充完整;
(3)求该年级一分钟跳绳次数在190次以上的学生数占该年级全部学生数的百分比.
【分析】(1)用360减去第1、2、4组的频数和即可;
(2)根据以上所求结果即可补全图形;
(3)用第4组的频数除以该年级的总人数即可得出答案.
【解答】解:(1)a=360﹣(48+96+72)=144;
(2)补全频数分布直方图如下:
(3)该年级一分钟跳绳次数在190次以上的学生数占该年级全部学生数的百分比为【淘宝搜索店铺:中小学教辅资源店 微信:mlxt2022】
×100%=20%.
19.(8分)在①AD=AE,②∠ABE=∠ACD,③FB=FC这三个条件中选择其中一个,
补充在下面的问题中,并完成问题的解答.
问题:如图,在△ABC中,∠ABC=∠ACB,点D在AB边上(不与点A,点B重合),
点E在AC边上(不与点A,点C重合),连接BE,CD,BE与CD相交于点F.若
① AD = AE ( ② ∠ ABE =∠ ACD 或 ③ FB = FC ) ,求证:BE=CD.
注:如果选择多个条件分别作答,按第一个解答计分.
【分析】若选择条件①,利用∠ABC=∠ACB得到AB=AC,则可根据“SAS”可判断
△ABE≌△ACD,从而得到BE=CD;
选择条件②,利用∠ABC=∠ACB 得到 AB=AC,则可根据“ASA”可判断
△ABE≌△ACD,从而得到BE=CD;
选择条件③,利用∠ABC=∠ACB得到AB=AC,再证明∠ABE=∠ACD,则可根据
“ASA”可判断△ABE≌△ACD,从而得到BE=CD.
【解答】证明:选择条件①的证明为:
∵∠ABC=∠ACB,
∴AB=AC,
在△ABE和△ACD中,
,
∴△ABE≌△ACD(SAS),
∴BE=CD;
选择条件②的证明为:
∵∠ABC=∠ACB,
∴AB=AC,【淘宝搜索店铺:中小学教辅资源店 微信:mlxt2022】
在△ABE和△ACD中,
,
∴△ABE≌△ACD(ASA),
∴BE=CD;
选择条件③的证明为:
∵∠ABC=∠ACB,
∴AB=AC,
∵FB=FC,
∴∠FBC=∠FCB,
∴∠ABC﹣∠FBC=∠ACB﹣∠FCB,
即∠ABE=∠ACD,
在△ABE和△ACD中,
,
∴△ABE≌△ACD(ASA),
∴BE=CD.
故答案为①AD=AE(②∠ABE=∠ACD或③FB=FC)
20.(10分)在直角坐标系中,设函数y = (k 是常数,k >0,x>0)与函数y =k x
1 1 1 2 2
(k 是常数,k ≠0)的图象交于点A,点A关于y轴的对称点为点B.
2 2
(1)若点B的坐标为(﹣1,2),
①求k ,k 的值;
1 2
②当y <y 时,直接写出x的取值范围;
1 2
(2)若点B在函数y = (k 是常数,k ≠0)的图象上,求k +k 的值.
3 3 3 1 3【淘宝搜索店铺:中小学教辅资源店 微信:mlxt2022】
【分析】(1)①由题意得,点A的坐标是(1,2),分别代入y = (k 是常数,k
1 1 1
>0,x>0),y =k x(k 是常数,k ≠0)即可求得k ,k 的值;
2 2 2 2 1 2
②根据图象即可求得;
(2)设点A的坐标是(x ,y),则点B的坐标是(﹣x ,y),根据待定系数法即可求
0 0
得k =x •y,k =﹣x •y,即可求得k +k =0.
1 0 3 0 1 3
【解答】解:(1)①由题意得,点A的坐标是(1,2),
∵函数y = (k 是常数,k >0,x>0)与函数y =k x(k 是常数,k ≠0)的图象交
1 1 1 2 2 2 2
于点A,
∴2= ,2=k ,
2
∴k =2,k =2;
1 2
②由图象可知,当y <y 时,x的取值范围是x>1;
1 2
(2)设点A的坐标是(x ,y),则点B的坐标是(﹣x ,y),
0 0
∴k =x •y,k =﹣x •y,
1 0 3 0
∴k +k =0.
1 3
21.(10分)如图,在△ABC中,∠ABC的平分线BD交AC边于点D,AE⊥BC于点E.
已知∠ABC=60°,∠C=45°.
(1)求证:AB=BD;
(2)若AE=3,求△ABC的面积.
【分析】(1)计算出∠ADB和∠BAC,利用等角对等边即可证明;
(2)利用锐角三角函数求出BC即可计算△ABC的面积.
【解答】(1)证明:∵BD平分∠ABC,∠ABC=60°,
∴∠DBC= ∠ABC=30°,
∵∠C=45°,
∴∠ADB=∠DBC+∠C=75°,【淘宝搜索店铺:中小学教辅资源店 微信:mlxt2022】
∠BAC=180°﹣∠ABC﹣∠C=75°,
∴∠BAC=∠ADB,
∴AB=BD;
(2)解:在Rt△ABE中,∠ABC=60°,AE=3,
∴BE= = ,
在Rt△AEC中,∠C=45°,AE=3,
∴EC= =3,
∴BC=3+ ,
∴S△ABC = BC×AE= .
22.(12分)在直角坐标系中,设函数y=ax2+bx+1(a,b是常数,a≠0).
(1)若该函数的图象经过(1,0)和(2,1)两点,求函数的表达式,并写出函数图
象的顶点坐标;
(2)写出一组a,b的值,使函数y=ax2+bx+1的图象与x轴有两个不同的交点,并说
明理由.
(3)已知a=b=1,当x=p,q(p,q是实数,p≠q)时,该函数对应的函数值分别为
P,Q.若p+q=2,求证:P+Q>6.
【分析】(1)考查使用待定系数法求二次函数解析式,属于基础题,将两点坐标代入,
解二元一次方程组即可;
(2)写出一组a,b,使得b2﹣4ac>0即可;
(3)已知a=b=1,则y=x2+x+1.容易得到P+Q=p2+p+1+q2+q+1,利用p+q=2,即p
=2﹣q代入对代数式P+Q进行化简,并配方得出P+Q=2(q﹣1)2+6≥6.最后注意利
用p≠q条件判断q≠1,得证.
【解答】解:(1)由题意,得 ,
解得 ,
所以,该函数表达式为y=x2﹣2x+1.
并且该函数图象的顶点坐标为(1,0).
(2)例如a=1,b=3,此时y=x2+3x+1,
∵b2﹣4ac=5>0,【淘宝搜索店铺:中小学教辅资源店 微信:mlxt2022】
∴函数y=x2+3x+1的图象与x轴有两个不同的交点.
(3)由题意,得P=p2+p+1,Q=q2+q+1,
所以 P+Q=p2+p+1+q2+q+1
=p2+q2+4
=(2﹣q)2+q2+4
=2(q﹣1)2+6≥6,
由条件p≠q,知q≠1.所以 P+Q>6,得证.
23.(12分)如图,锐角三角形ABC内接于 O,∠BAC的平分线AG交 O于点G,交
BC边于点F,连接BG. ⊙ ⊙
(1)求证:△ABG∽△AFC.
(2)已知AB=a,AC=AF=b,求线段FG的长(用含a,b的代数式表示).
(3)已知点E在线段AF上(不与点A,点F重合),点D在线段AE上(不与点A,
点E重合),∠ABD=∠CBE,求证:BG2=GE•GD.
【分析】(1)根据∠BAC的平分线AG交 O于点G,知∠BAC=∠FAC,由圆周角定
理知∠G=∠C,即可证△ABG∽△AFC; ⊙
(2)由(1)知 = ,由AC=AF得AG=AB,即可计算FG的长度;
(3)先证△DGB∽△BGE,得出线段比例关系,即可得证BG2=GE•GD.
【解答】(1)证明:∵AG平分∠BAC,
∴∠BAG=∠FAC,
又∵∠G=∠C,
∴△ABG∽△AFC;
(2)解:由(1)知,△ABG∽△AFC,
∴ = ,
∵AC=AF=b,【淘宝搜索店铺:中小学教辅资源店 微信:mlxt2022】
∴AB=AG=a,
∴FG=AG﹣AF=a﹣b;
(3)证明:∵∠CAG=∠CBG,∠BAG=∠CAG,
∴∠BAG=∠CBG,
∵∠ABD=∠CBE,
∴∠BDG=∠BAG+∠ABD=∠CBG+∠CBE=∠EBG,
又∵∠DGB=∠BGE,
∴△DGB∽△BGE,
∴ = ,
∴BG2=GE•GD.【淘宝搜索店铺:中小学教辅资源店 微信:mlxt2022】