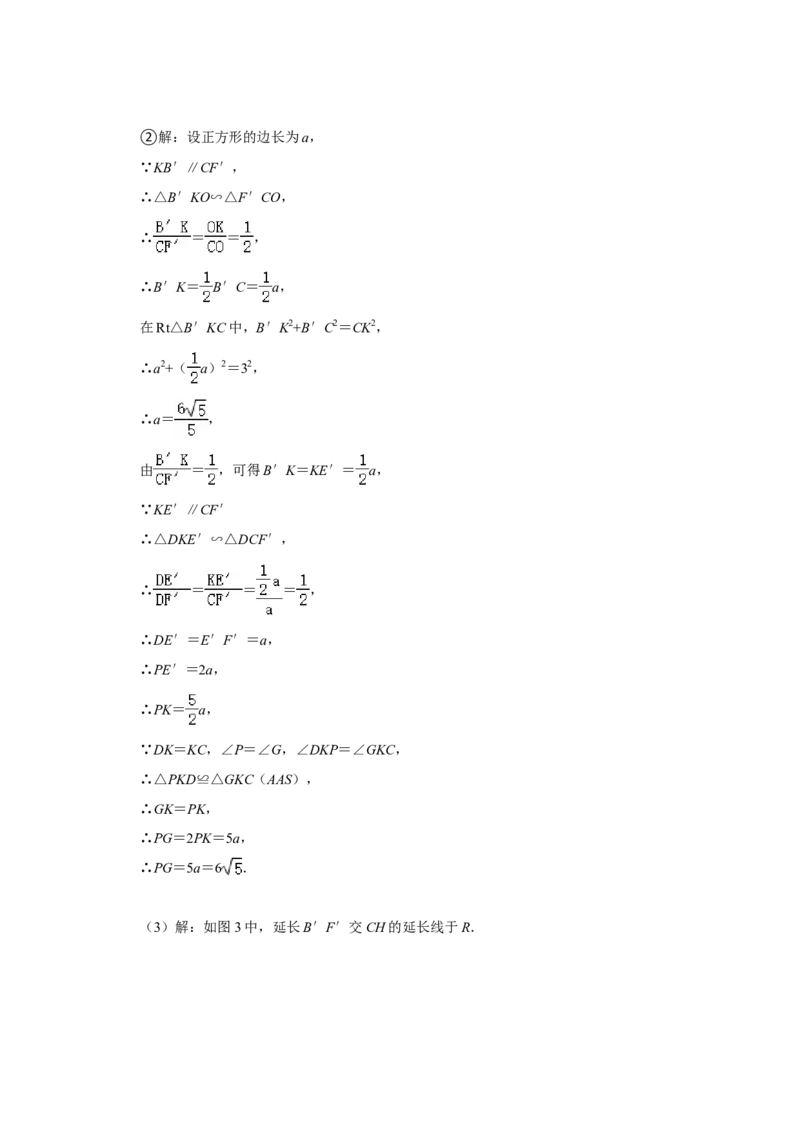文档内容
2021年湖北省宜昌市中考数学试卷
一、选择题(下列各小题中,只有一个选项是符合题目要求的,请在答题卡上指定的位置
填涂符合要求的选项前面的字母代号,每小题3分,计33分)
1.﹣2021的倒数是( )
A.2021 B.﹣2021 C. D.﹣
2.下列四幅图案是四所大学校徽的主体标识,其中是中心对称图形的是( )
A. B.
C. D.
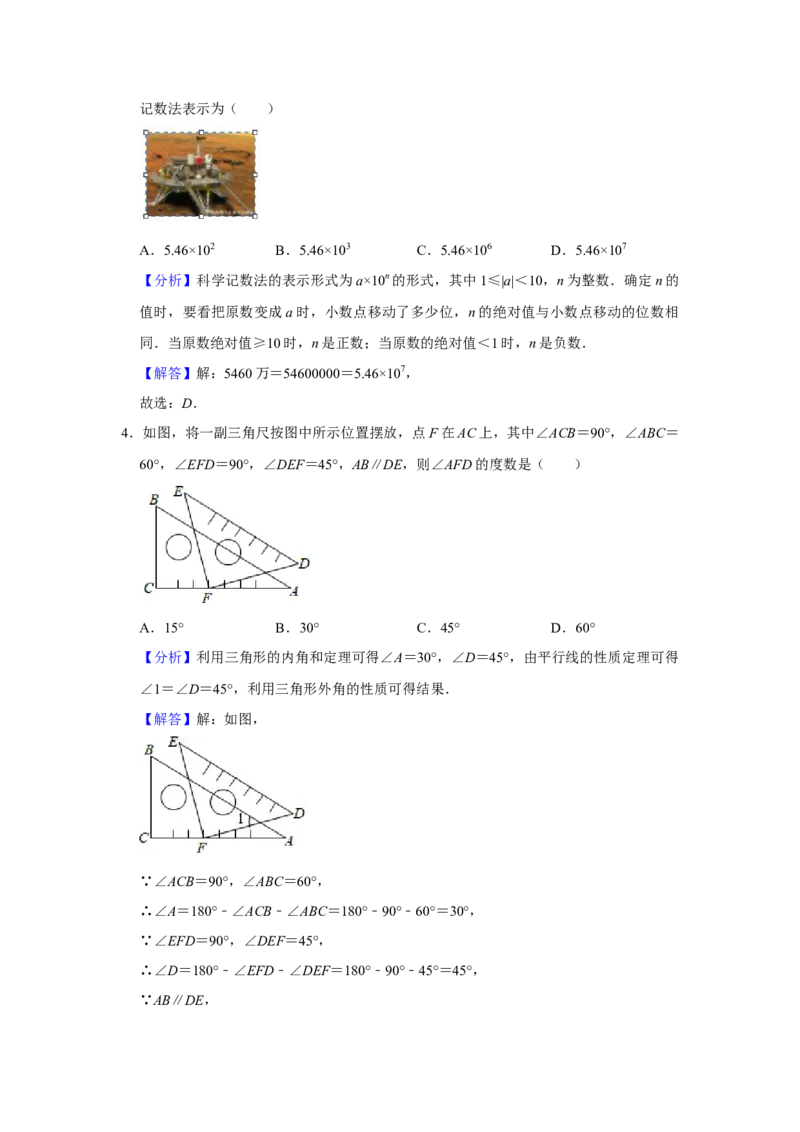
3.2021年5月15日07时18分,“天问一号”火星探测器成功登陆火星表面,开启了中
国人自主探测火星之旅.地球与火星的最近距离约为5460万公里.“5460万”用科学
记数法表示为( )
A.5.46×102 B.5.46×103 C.5.46×106 D.5.46×107
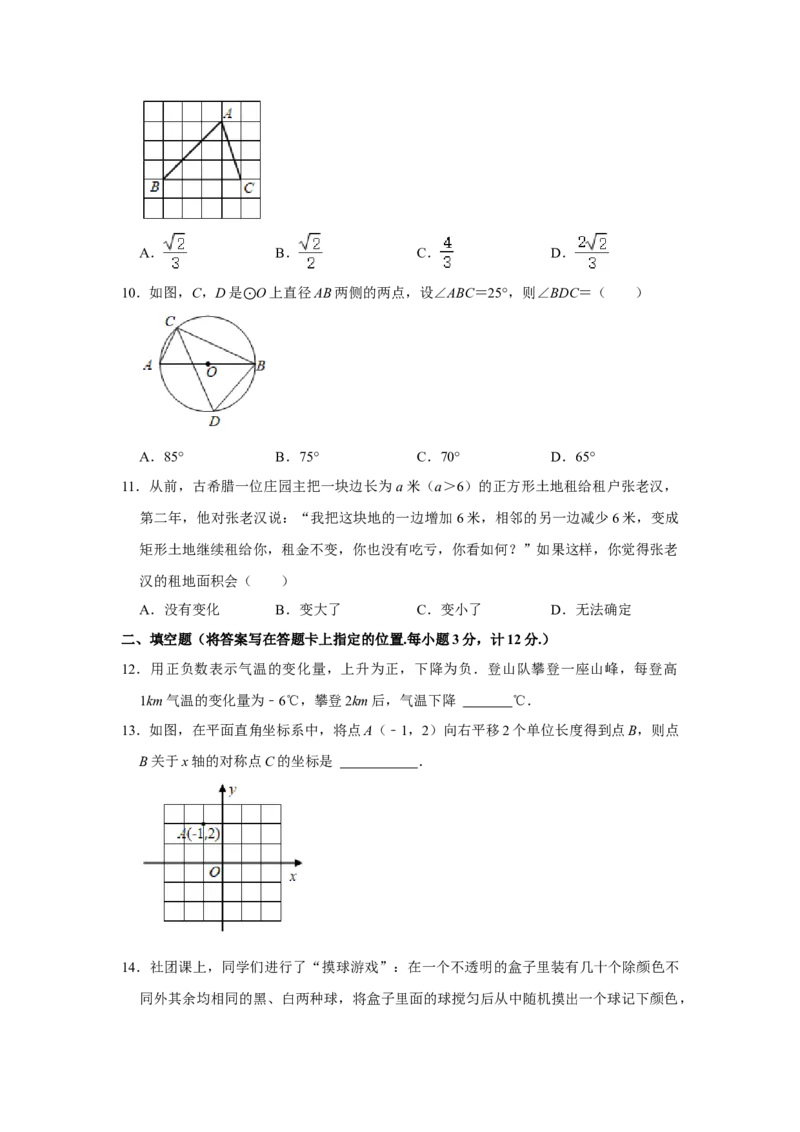
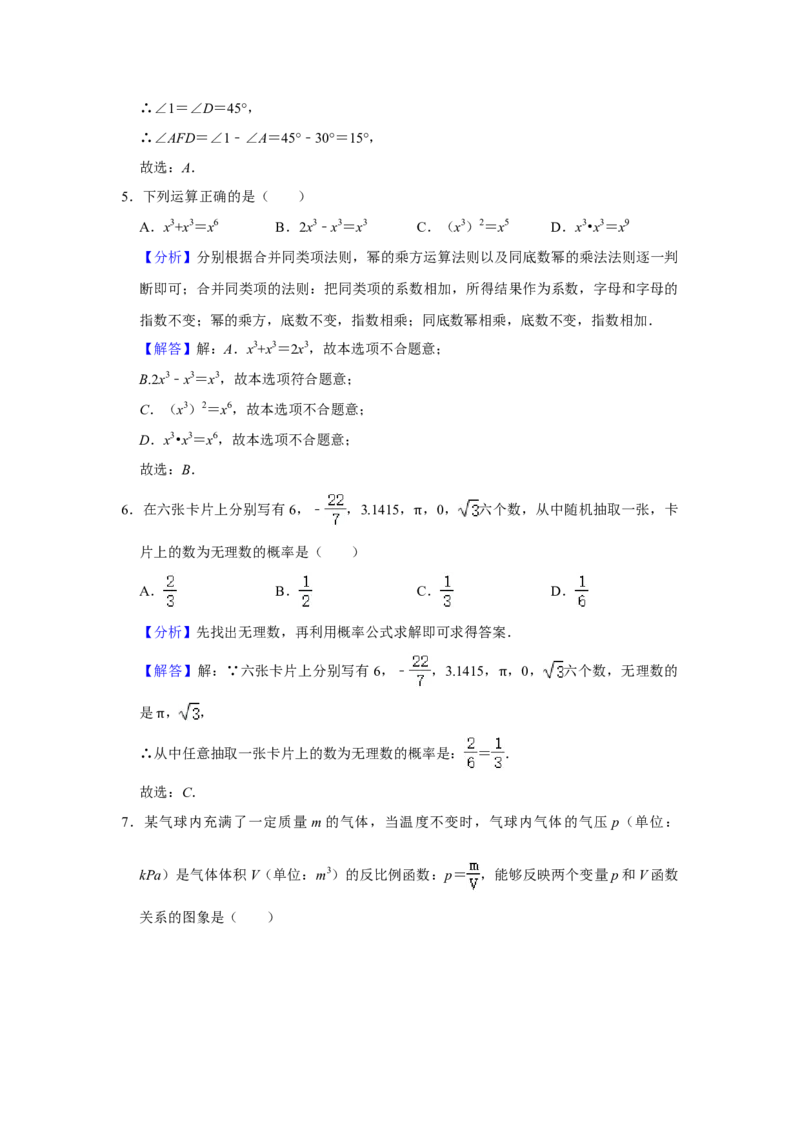
4.如图,将一副三角尺按图中所示位置摆放,点F在AC上,其中∠ACB=90°,∠ABC=
60°,∠EFD=90°,∠DEF=45°,AB∥DE,则∠AFD的度数是( )A.15° B.30° C.45° D.60°
5.下列运算正确的是( )
A.x3+x3=x6 B.2x3﹣x3=x3 C.(x3)2=x5 D.x3•x3=x9
6.在六张卡片上分别写有6,﹣ ,3.1415, ,0, 六个数,从中随机抽取一张,卡
π
片上的数为无理数的概率是( )
A. B. C. D.
7.某气球内充满了一定质量 m的气体,当温度不变时,气球内气体的气压 p(单位:
kPa)是气体体积V(单位:m3)的反比例函数:p= ,能够反映两个变量p和V函数
关系的图象是( )
A. B.
C. D.
8.我国古代数学经典著作《九章算术》中有这样一题,原文是:“今有共买物,人出八,
盈三;人出七,不足四.问人数、物价各几何?”意思是:今有人合伙购物,每人出八
钱,会多三钱;每人出七钱,又差四钱.问人数、物价各多少?设人数为x人,物价为
y钱,下列方程组正确的是( )
A. B.
C. D.
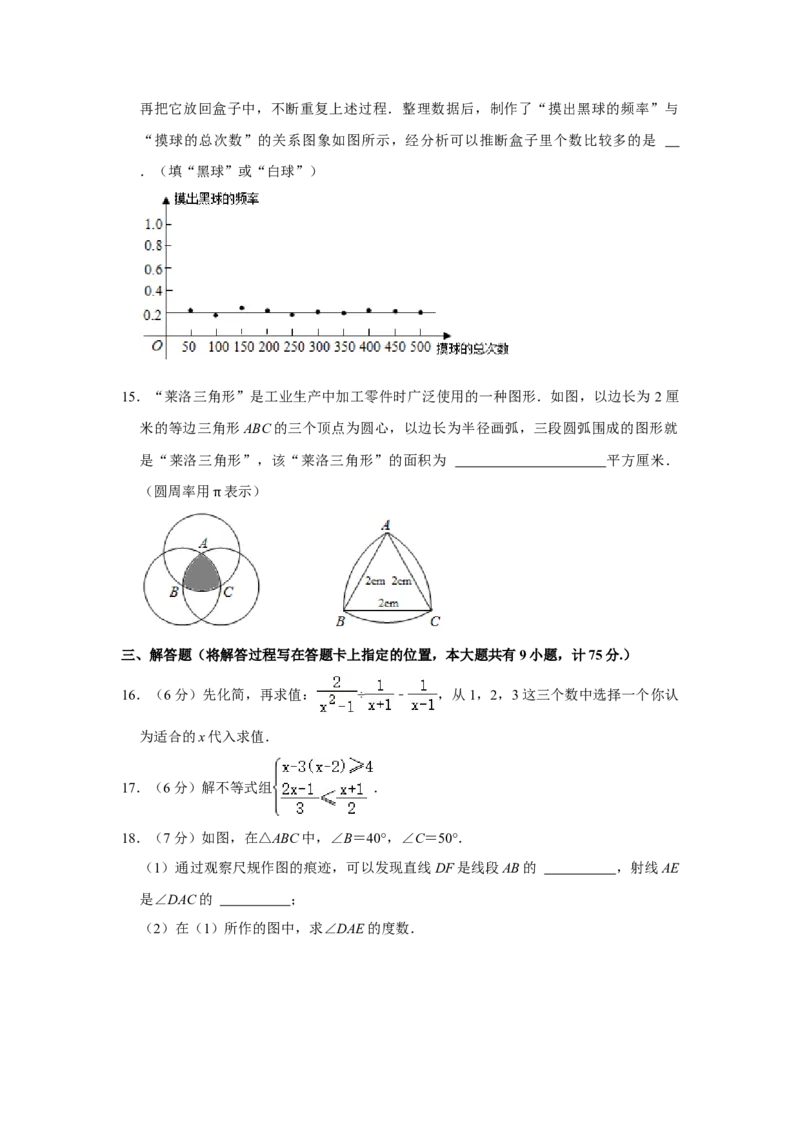
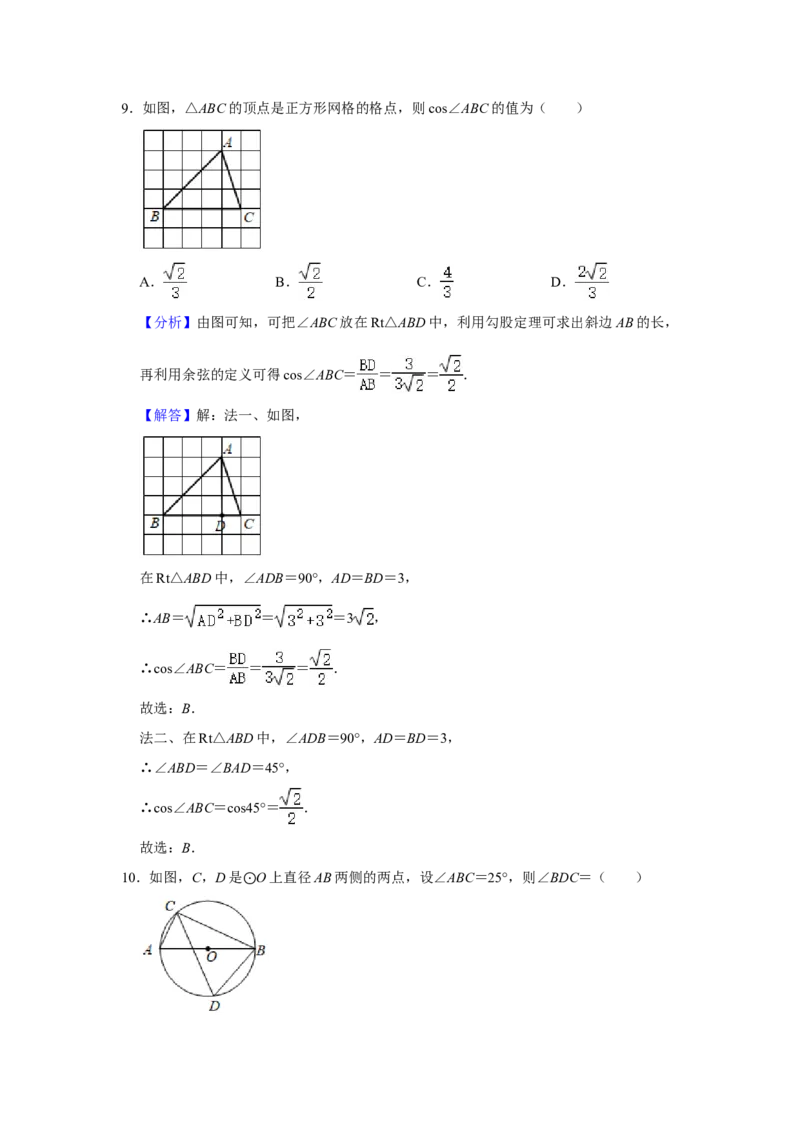
9.如图,△ABC的顶点是正方形网格的格点,则cos∠ABC的值为( )A. B. C. D.
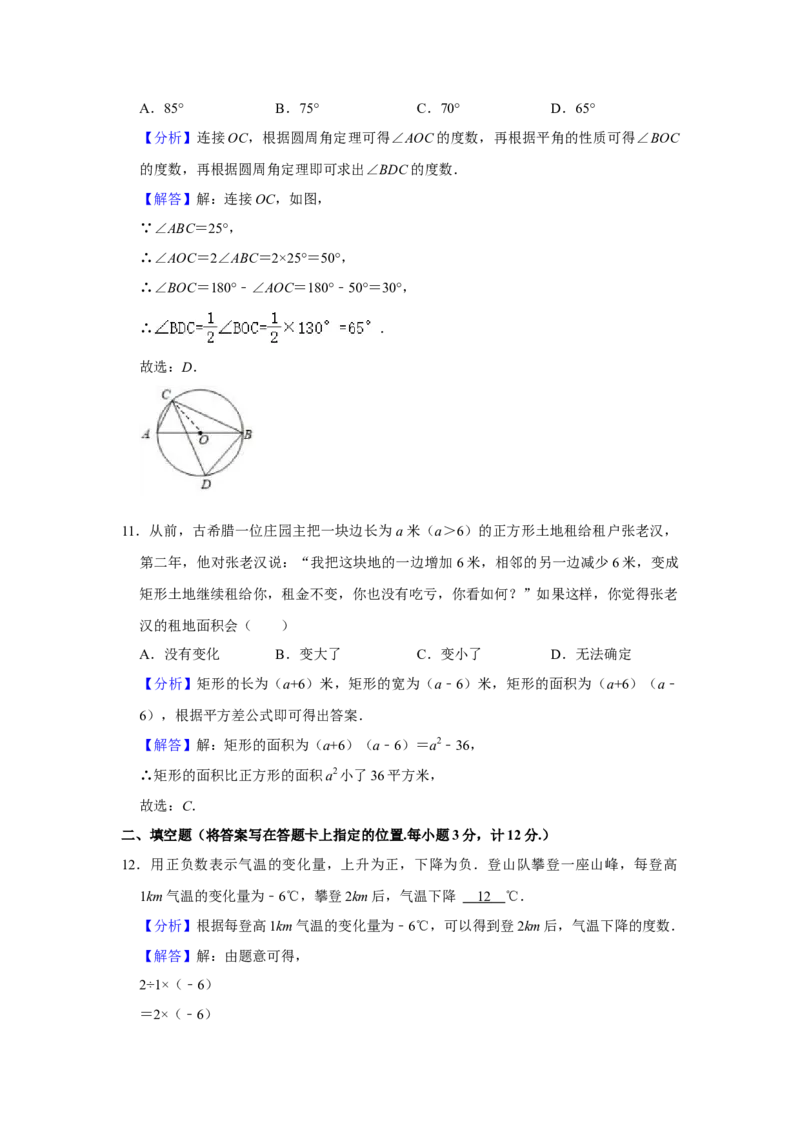
10.如图,C,D是 O上直径AB两侧的两点,设∠ABC=25°,则∠BDC=( )
⊙
A.85° B.75° C.70° D.65°
11.从前,古希腊一位庄园主把一块边长为 a米(a>6)的正方形土地租给租户张老汉,
第二年,他对张老汉说:“我把这块地的一边增加6米,相邻的另一边减少6米,变成
矩形土地继续租给你,租金不变,你也没有吃亏,你看如何?”如果这样,你觉得张老
汉的租地面积会( )
A.没有变化 B.变大了 C.变小了 D.无法确定
二、填空题(将答案写在答题卡上指定的位置.每小题3分,计12分.)
12.用正负数表示气温的变化量,上升为正,下降为负.登山队攀登一座山峰,每登高
1km气温的变化量为﹣6℃,攀登2km后,气温下降 ℃.
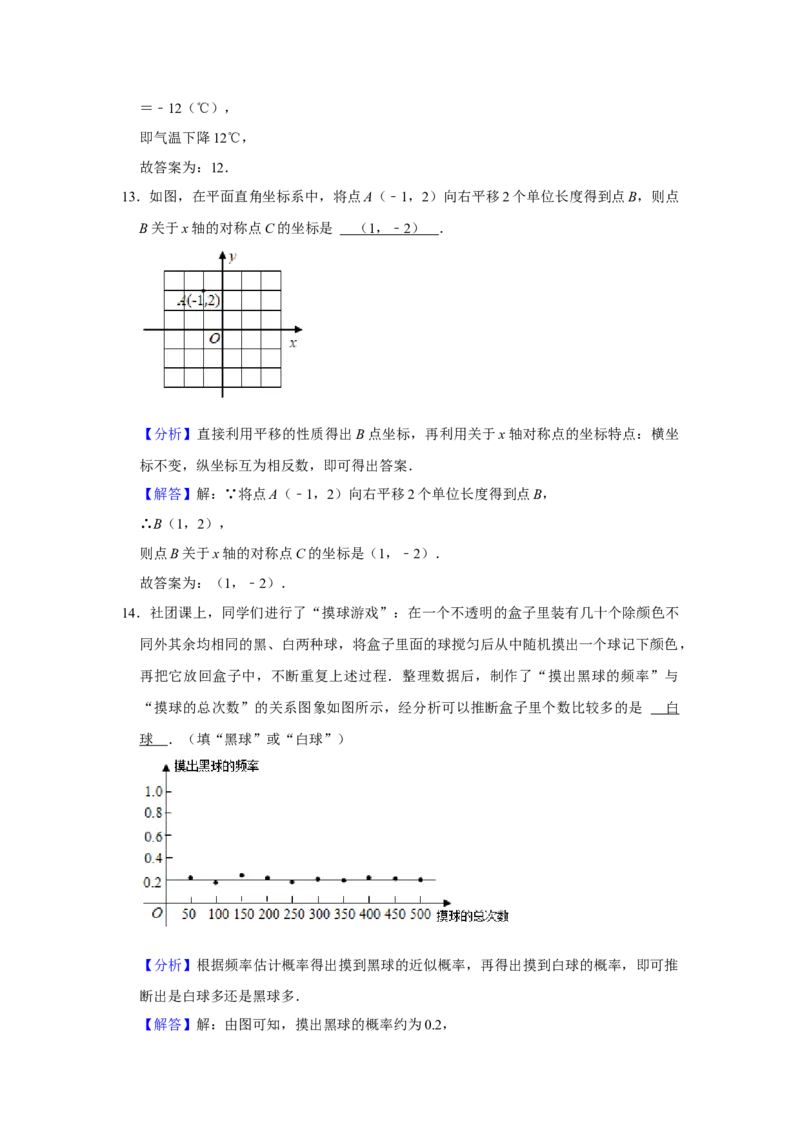
13.如图,在平面直角坐标系中,将点A(﹣1,2)向右平移2个单位长度得到点B,则点
B关于x轴的对称点C的坐标是 .
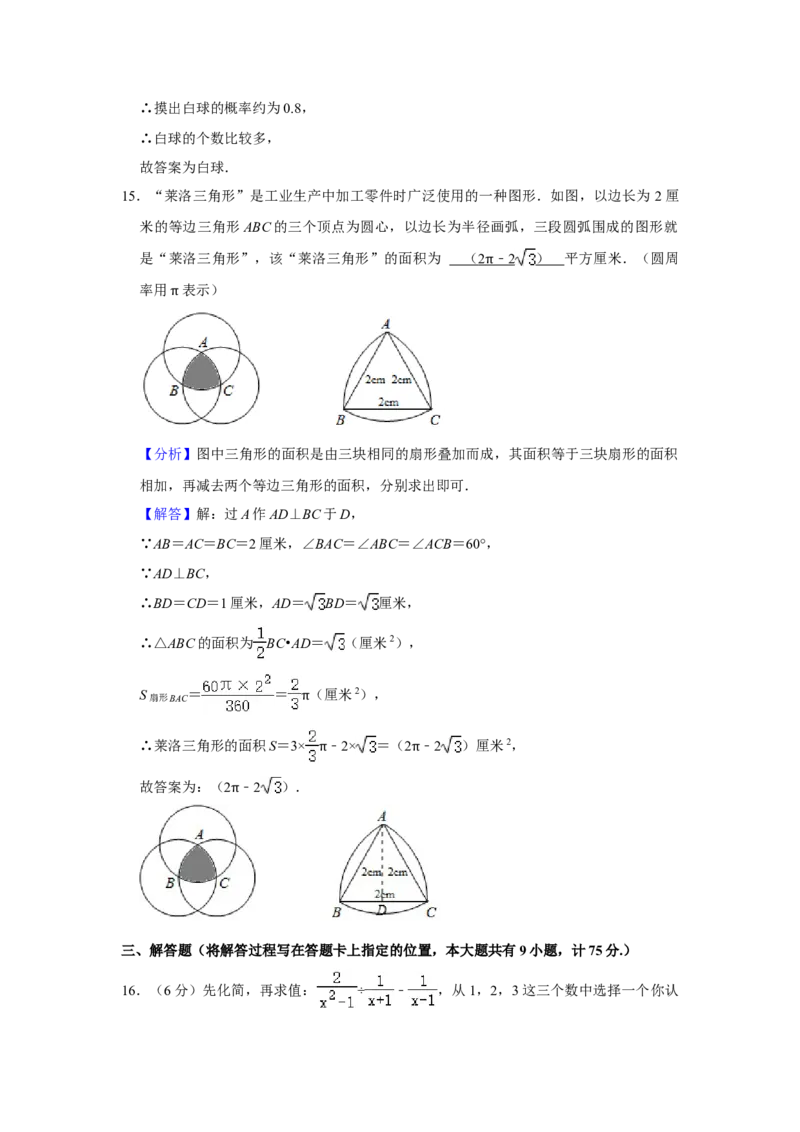
14.社团课上,同学们进行了“摸球游戏”:在一个不透明的盒子里装有几十个除颜色不
同外其余均相同的黑、白两种球,将盒子里面的球搅匀后从中随机摸出一个球记下颜色,再把它放回盒子中,不断重复上述过程.整理数据后,制作了“摸出黑球的频率”与
“摸球的总次数”的关系图象如图所示,经分析可以推断盒子里个数比较多的是
.(填“黑球”或“白球”)
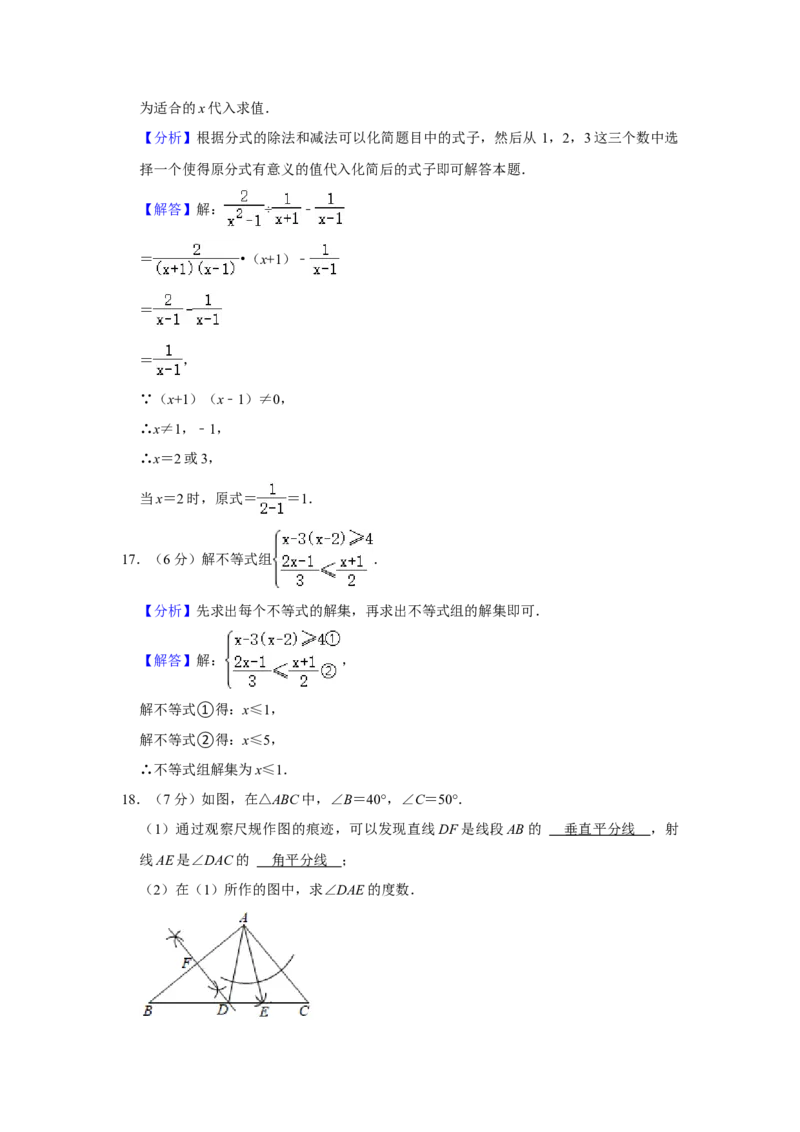
15.“莱洛三角形”是工业生产中加工零件时广泛使用的一种图形.如图,以边长为 2厘
米的等边三角形ABC的三个顶点为圆心,以边长为半径画弧,三段圆弧围成的图形就
是“莱洛三角形”,该“莱洛三角形”的面积为 平方厘米.
(圆周率用 表示)
π
三、解答题(将解答过程写在答题卡上指定的位置,本大题共有9小题,计75分.)
16.(6分)先化简,再求值: ÷ ﹣ ,从1,2,3这三个数中选择一个你认
为适合的x代入求值.
17.(6分)解不等式组 .
18.(7分)如图,在△ABC中,∠B=40°,∠C=50°.
(1)通过观察尺规作图的痕迹,可以发现直线DF是线段AB的 ,射线AE
是∠DAC的 ;
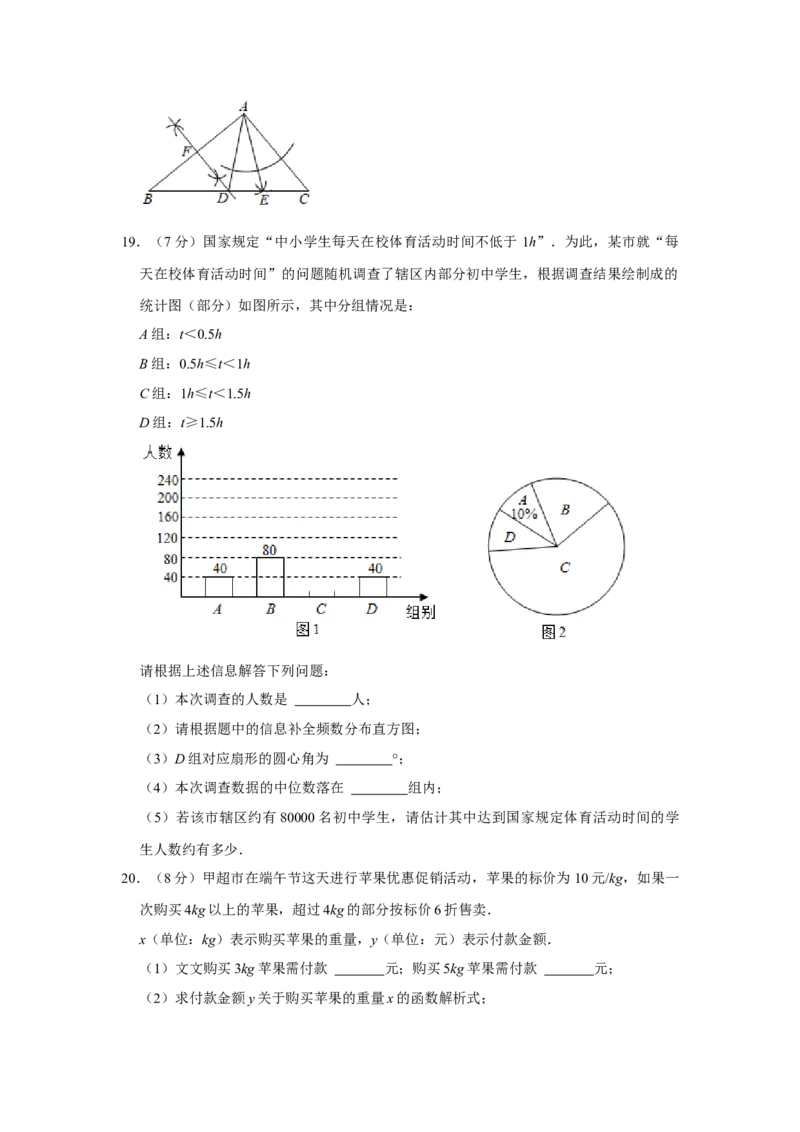
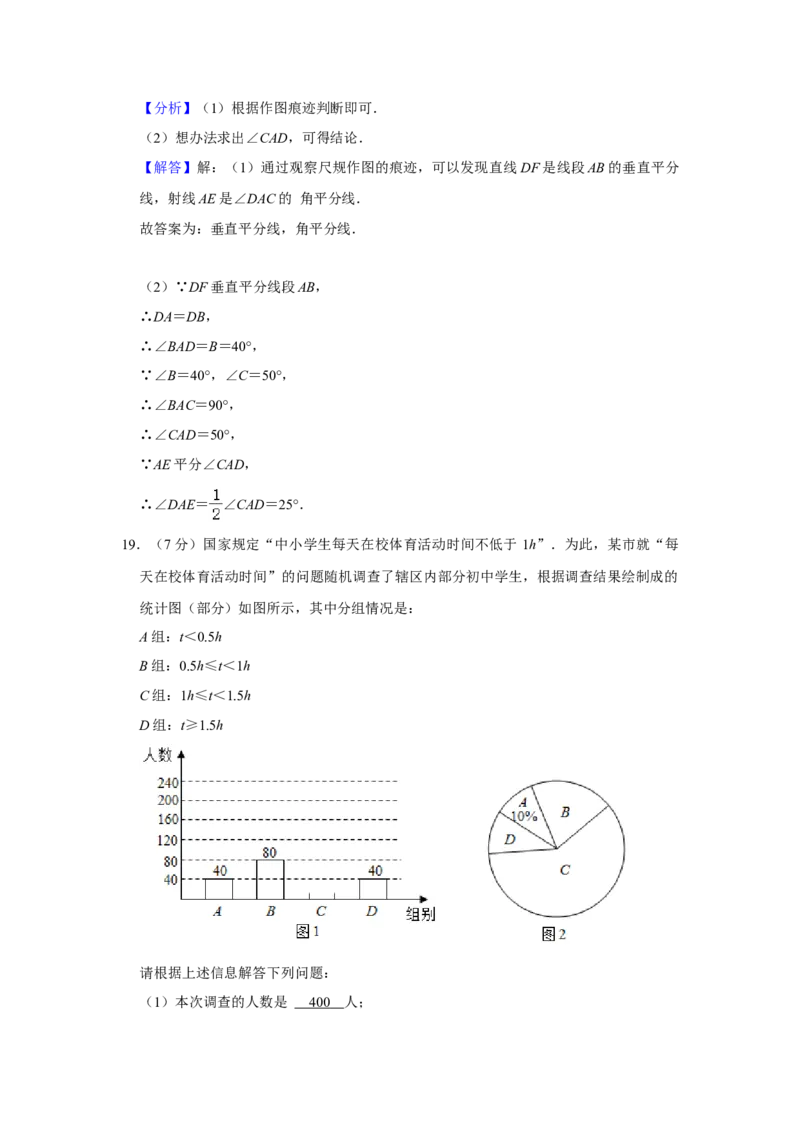
(2)在(1)所作的图中,求∠DAE的度数.19.(7分)国家规定“中小学生每天在校体育活动时间不低于 1h”.为此,某市就“每
天在校体育活动时间”的问题随机调查了辖区内部分初中学生,根据调查结果绘制成的
统计图(部分)如图所示,其中分组情况是:
A组:t<0.5h
B组:0.5h≤t<1h
C组:1h≤t<1.5h
D组:t≥1.5h
请根据上述信息解答下列问题:
(1)本次调查的人数是 人;
(2)请根据题中的信息补全频数分布直方图;
(3)D组对应扇形的圆心角为 °;
(4)本次调查数据的中位数落在 组内;
(5)若该市辖区约有80000名初中学生,请估计其中达到国家规定体育活动时间的学
生人数约有多少.
20.(8分)甲超市在端午节这天进行苹果优惠促销活动,苹果的标价为10元/kg,如果一
次购买4kg以上的苹果,超过4kg的部分按标价6折售卖.
x(单位:kg)表示购买苹果的重量,y(单位:元)表示付款金额.
(1)文文购买3kg苹果需付款 元;购买5kg苹果需付款 元;
(2)求付款金额y关于购买苹果的重量x的函数解析式;(3)当天,隔壁的乙超市也在进行苹果优惠促销活动,同样的苹果的标价也为10元/
kg,且全部按标价的8折售卖,文文如果要购买10kg苹果,请问她在哪个超市购买更划
算?
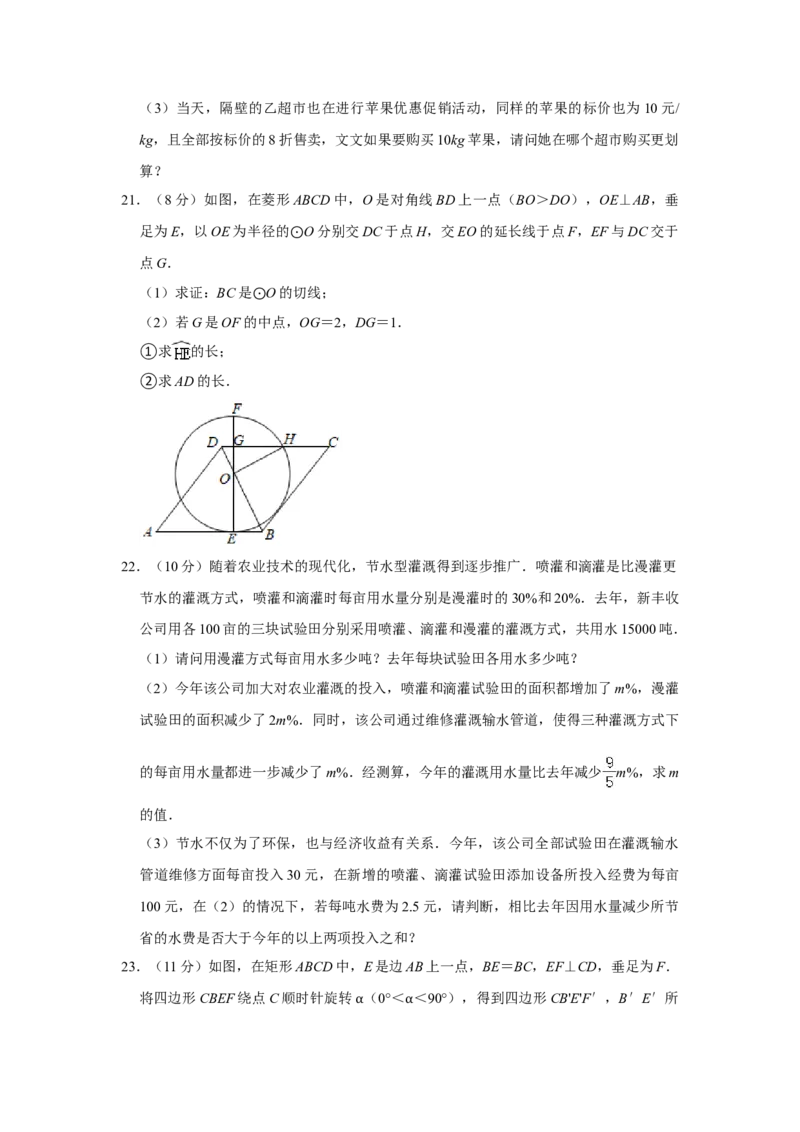
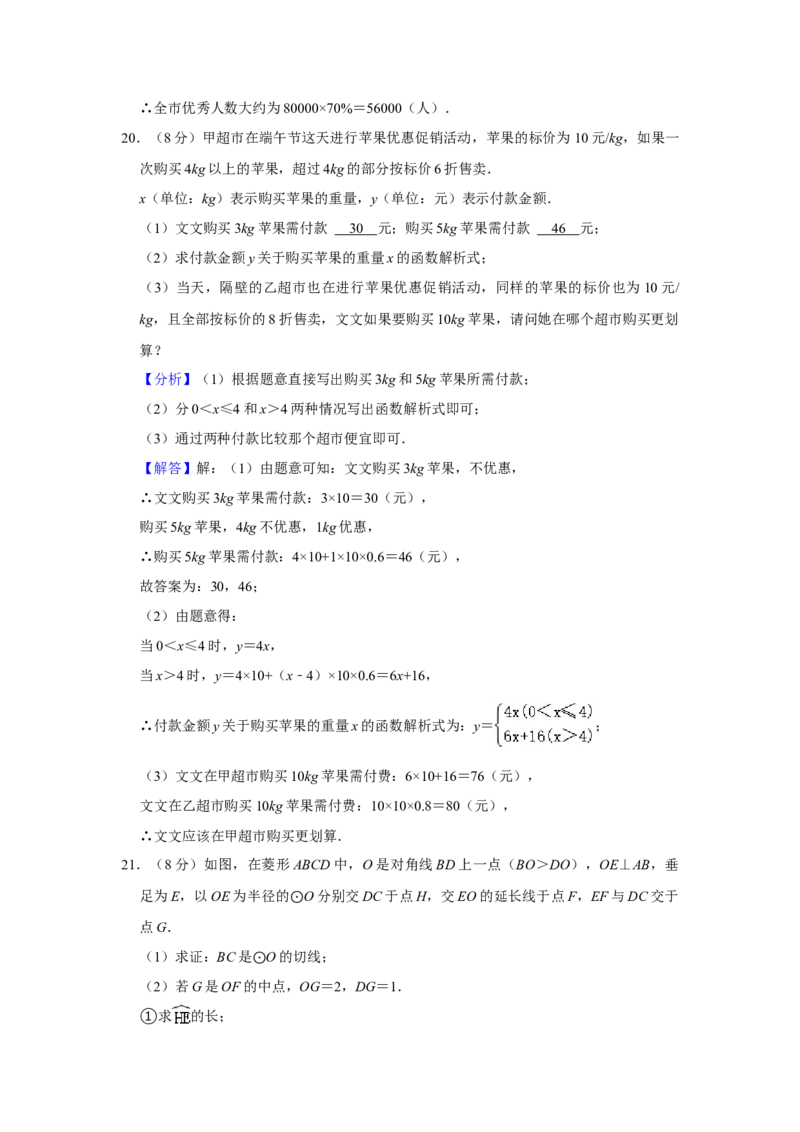
21.(8分)如图,在菱形ABCD中,O是对角线BD上一点(BO>DO),OE⊥AB,垂
足为E,以OE为半径的 O分别交DC于点H,交EO的延长线于点F,EF与DC交于
点G. ⊙
(1)求证:BC是 O的切线;
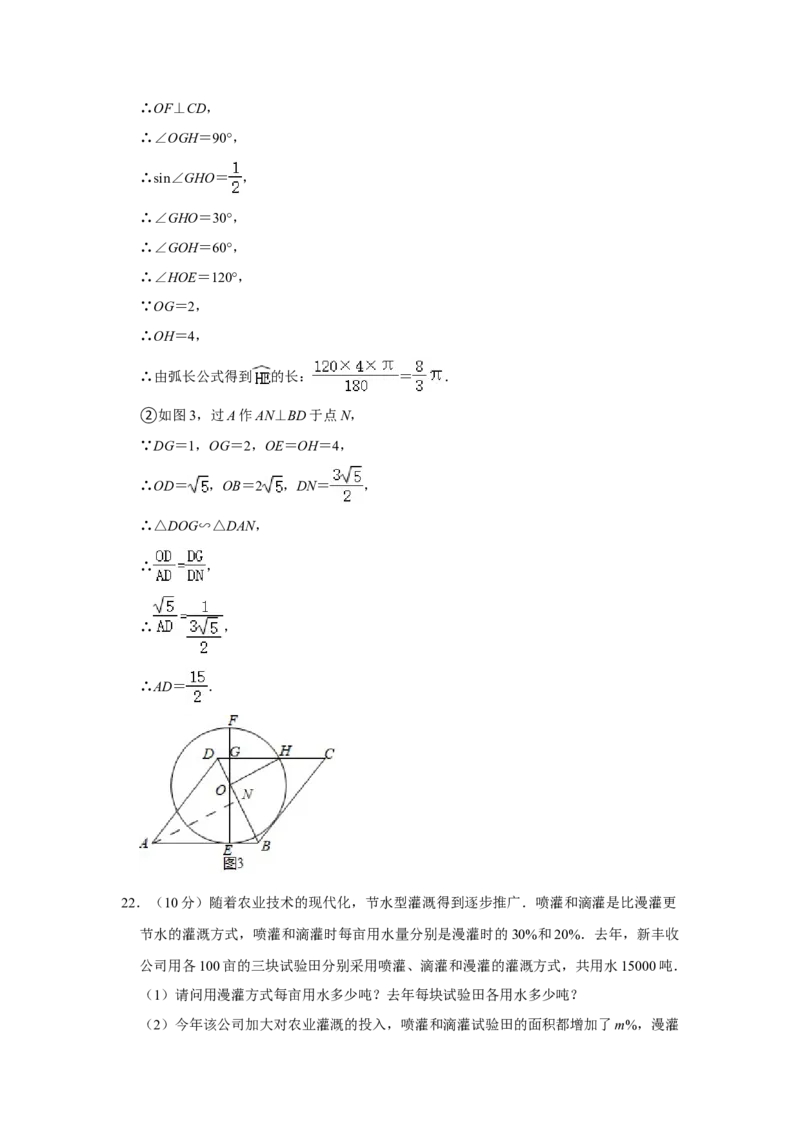
(2)若G是OF的⊙中点,OG=2,DG=1.
①求 的长;
②求AD的长.
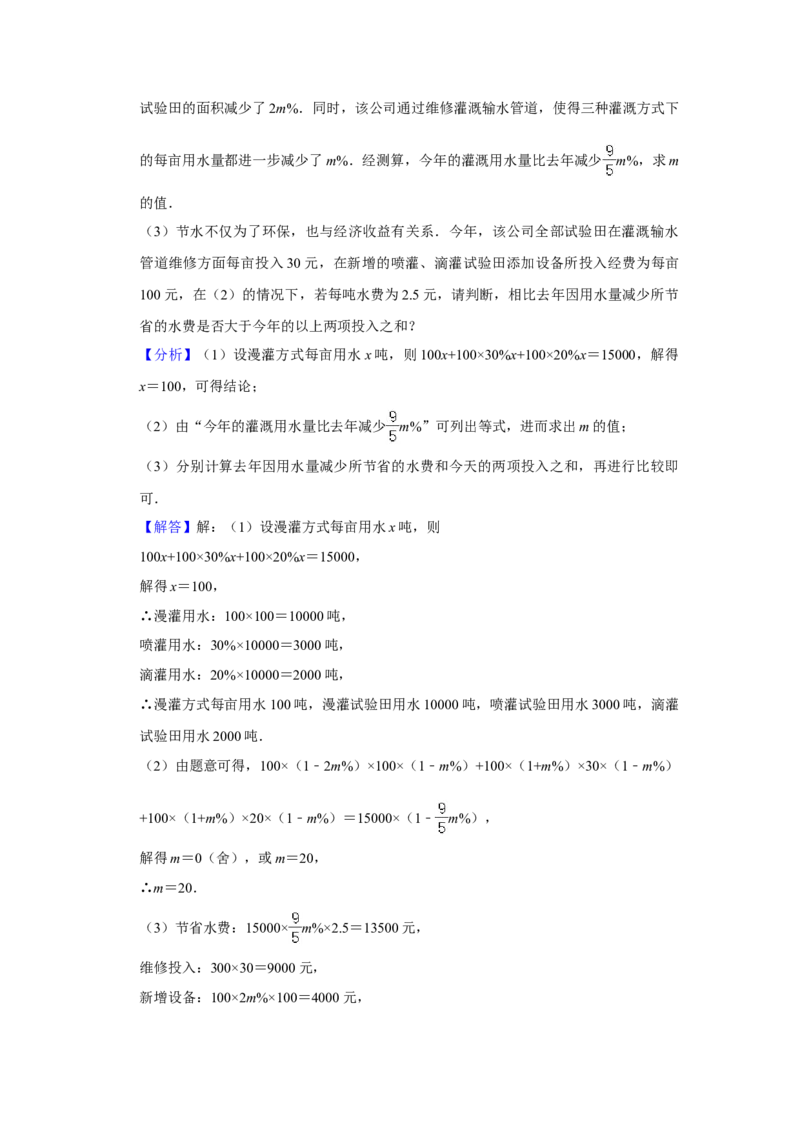
22.(10分)随着农业技术的现代化,节水型灌溉得到逐步推广.喷灌和滴灌是比漫灌更
节水的灌溉方式,喷灌和滴灌时每亩用水量分别是漫灌时的30%和20%.去年,新丰收
公司用各100亩的三块试验田分别采用喷灌、滴灌和漫灌的灌溉方式,共用水15000吨.
(1)请问用漫灌方式每亩用水多少吨?去年每块试验田各用水多少吨?
(2)今年该公司加大对农业灌溉的投入,喷灌和滴灌试验田的面积都增加了m%,漫灌
试验田的面积减少了2m%.同时,该公司通过维修灌溉输水管道,使得三种灌溉方式下
的每亩用水量都进一步减少了m%.经测算,今年的灌溉用水量比去年减少 m%,求m
的值.
(3)节水不仅为了环保,也与经济收益有关系.今年,该公司全部试验田在灌溉输水
管道维修方面每亩投入30元,在新增的喷灌、滴灌试验田添加设备所投入经费为每亩
100元,在(2)的情况下,若每吨水费为2.5元,请判断,相比去年因用水量减少所节
省的水费是否大于今年的以上两项投入之和?
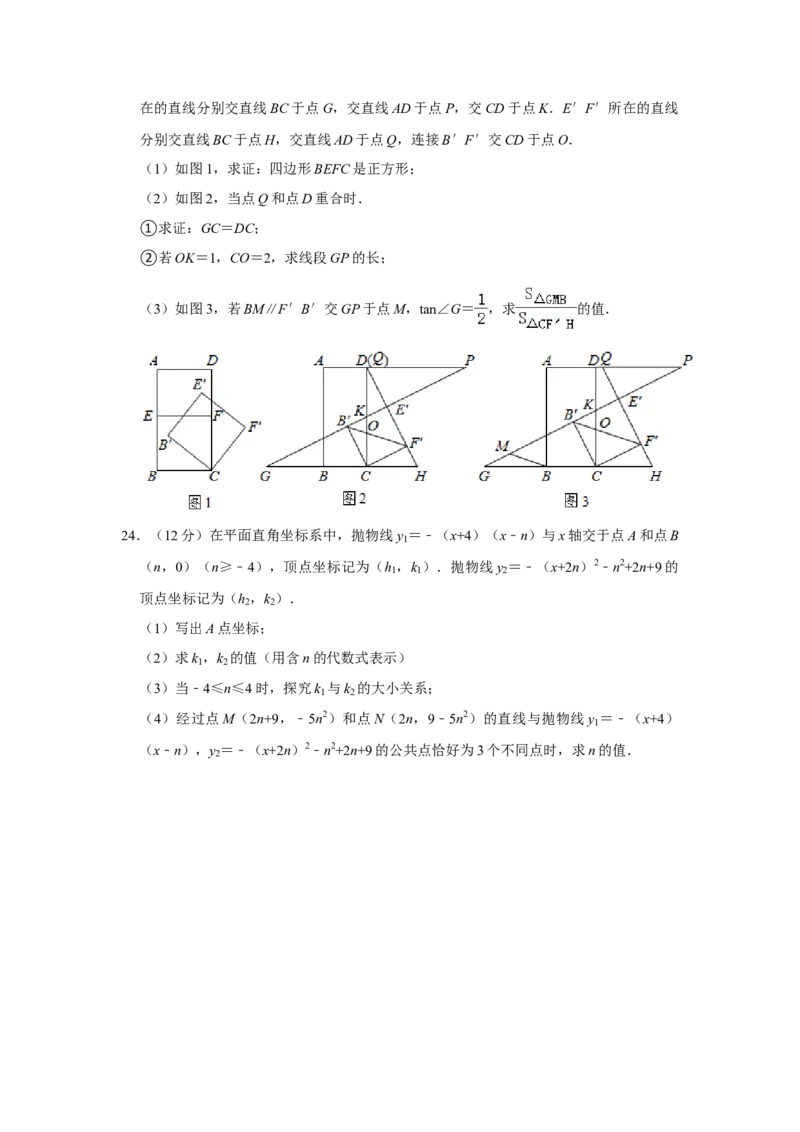
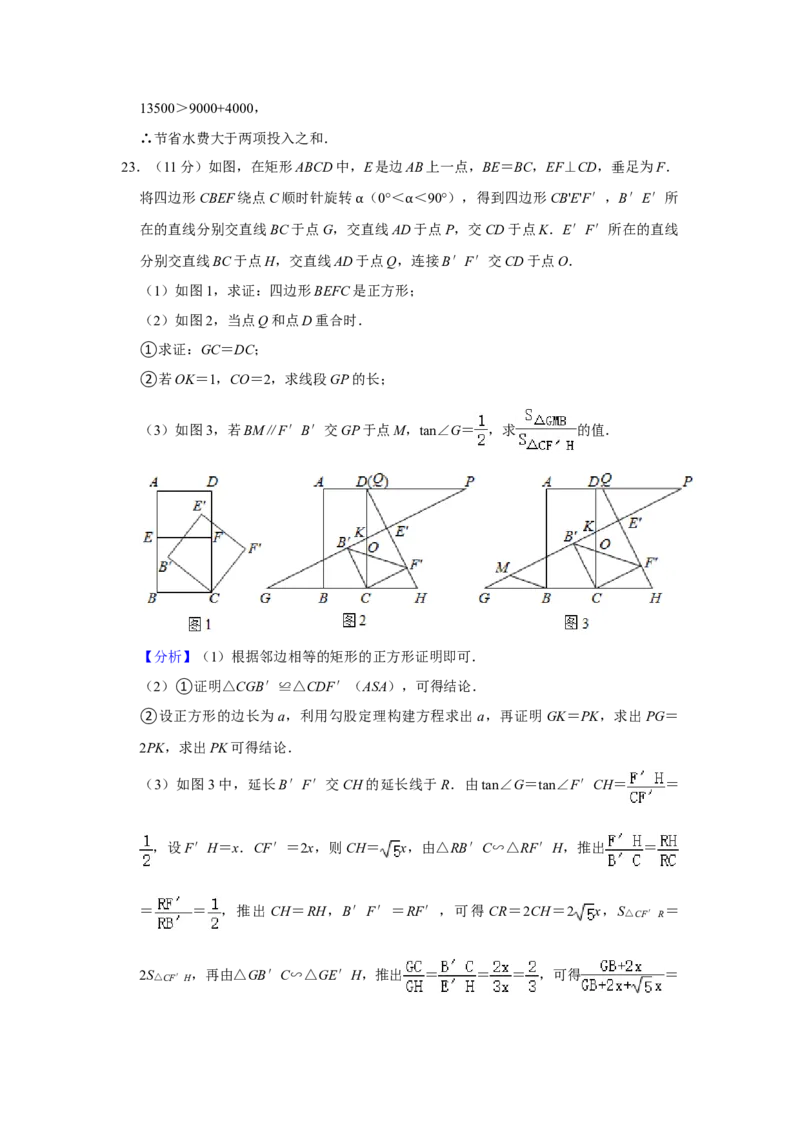
23.(11分)如图,在矩形ABCD中,E是边AB上一点,BE=BC,EF⊥CD,垂足为F.
将四边形CBEF绕点C顺时针旋转 (0°< <90°),得到四边形CB'E'F′,B′E′所
α α在的直线分别交直线BC于点G,交直线AD于点P,交CD于点K.E′F′所在的直线
分别交直线BC于点H,交直线AD于点Q,连接B′F′交CD于点O.
(1)如图1,求证:四边形BEFC是正方形;
(2)如图2,当点Q和点D重合时.
①求证:GC=DC;
②若OK=1,CO=2,求线段GP的长;
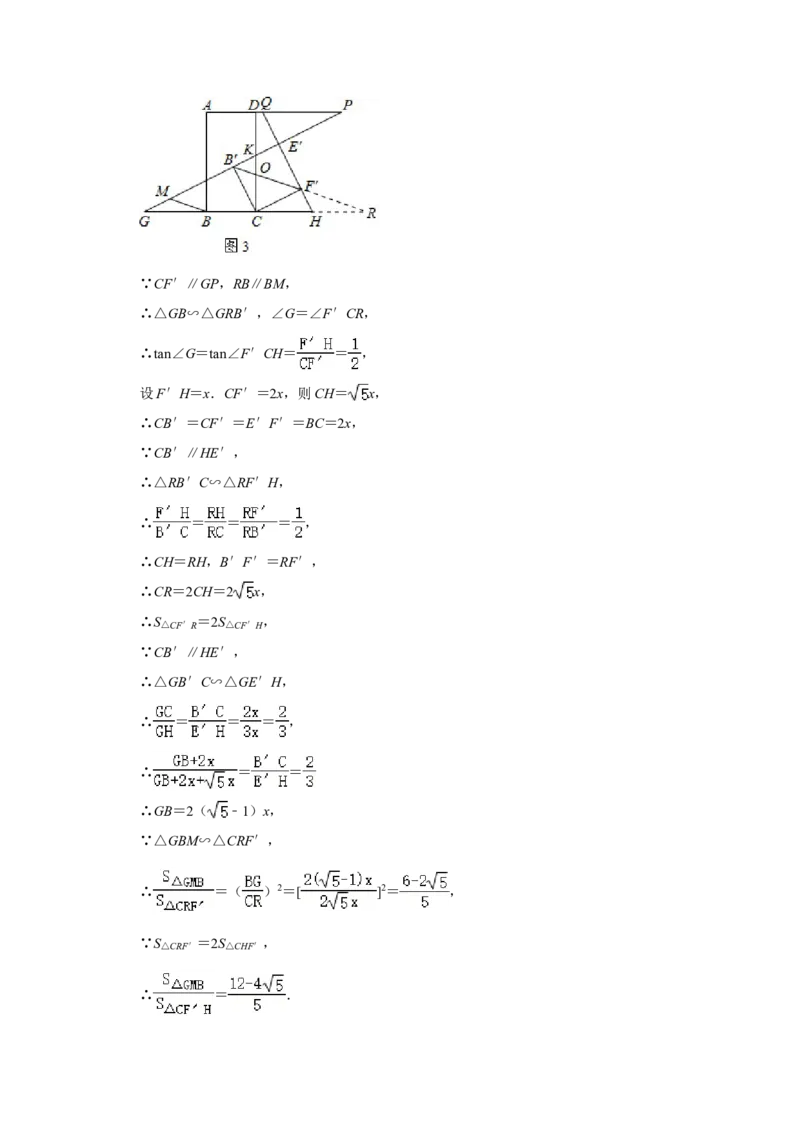
(3)如图3,若BM∥F′B′交GP于点M,tan∠G= ,求 的值.
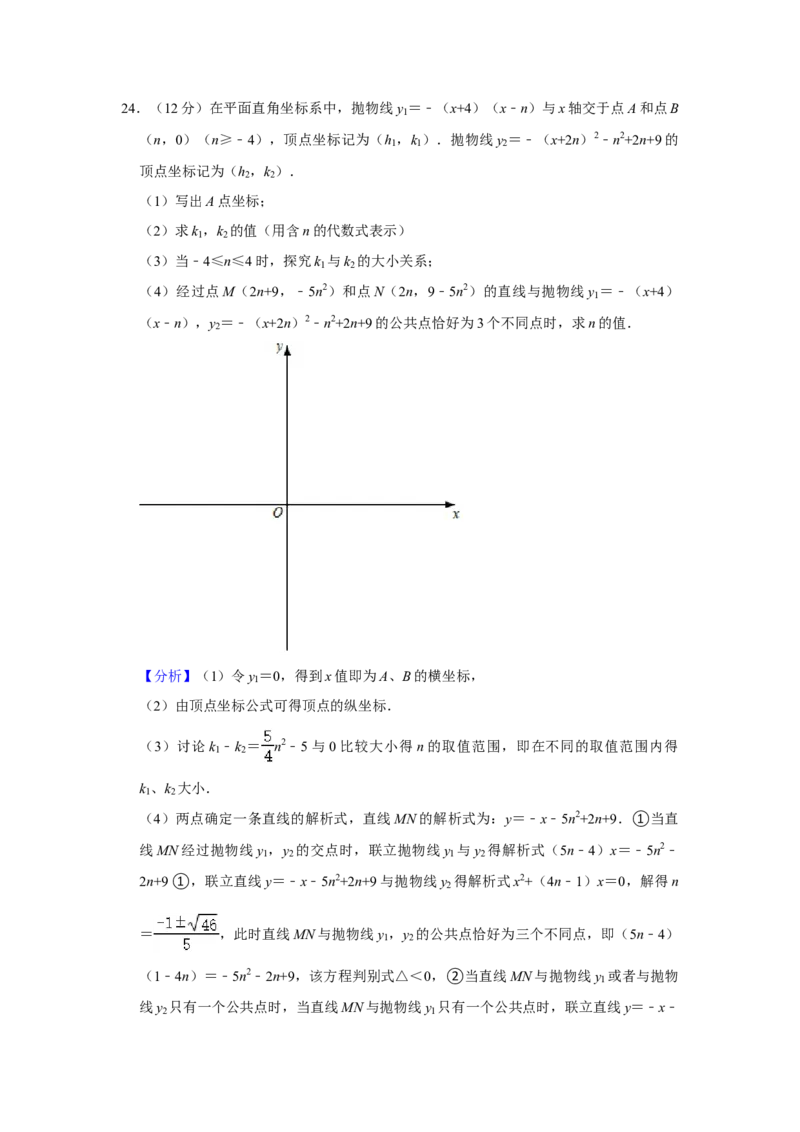
24.(12分)在平面直角坐标系中,抛物线y =﹣(x+4)(x﹣n)与x轴交于点A和点B
1
(n,0)(n≥﹣4),顶点坐标记为(h ,k ).抛物线y =﹣(x+2n)2﹣n2+2n+9的
1 1 2
顶点坐标记为(h ,k ).
2 2
(1)写出A点坐标;
(2)求k ,k 的值(用含n的代数式表示)
1 2
(3)当﹣4≤n≤4时,探究k 与k 的大小关系;
1 2
(4)经过点M(2n+9,﹣5n2)和点N(2n,9﹣5n2)的直线与抛物线y =﹣(x+4)
1
(x﹣n),y =﹣(x+2n)2﹣n2+2n+9的公共点恰好为3个不同点时,求n的值.
22021年湖北省宜昌市中考数学试卷
参考答案与试题解析
一、选择题(下列各小题中,只有一个选项是符合题目要求的,请在答题卡上指定的位置
填涂符合要求的选项前面的字母代号,每小题3分,计33分)
1.﹣2021的倒数是( )
A.2021 B.﹣2021 C. D.﹣
【分析】根据乘积是1的两个数互为倒数判断即可.
【解答】解:﹣2021的倒数是 .
故选:D.
2.下列四幅图案是四所大学校徽的主体标识,其中是中心对称图形的是( )
A. B.
C. D.
【分析】把一个图形绕某一点旋转180°,如果旋转后的图形能够与原来的图形重合,那
么这个图形就叫做中心对称图形.据此判断即可.
【解答】解:A.不是中心对称图形,故本选项不合题意;
B.不是中心对称图形,故本选项不合题意;
C.是中心对称图形,故本选项符合题意;
D.不是中心对称图形,故本选项不合题意.
故选:C.
3.2021年5月15日07时18分,“天问一号”火星探测器成功登陆火星表面,开启了中
国人自主探测火星之旅.地球与火星的最近距离约为5460万公里.“5460万”用科学记数法表示为( )
A.5.46×102 B.5.46×103 C.5.46×106 D.5.46×107
【分析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的
值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相
同.当原数绝对值≥10时,n是正数;当原数的绝对值<1时,n是负数.
【解答】解:5460万=54600000=5.46×107,
故选:D.
4.如图,将一副三角尺按图中所示位置摆放,点F在AC上,其中∠ACB=90°,∠ABC=
60°,∠EFD=90°,∠DEF=45°,AB∥DE,则∠AFD的度数是( )
A.15° B.30° C.45° D.60°
【分析】利用三角形的内角和定理可得∠A=30°,∠D=45°,由平行线的性质定理可得
∠1=∠D=45°,利用三角形外角的性质可得结果.
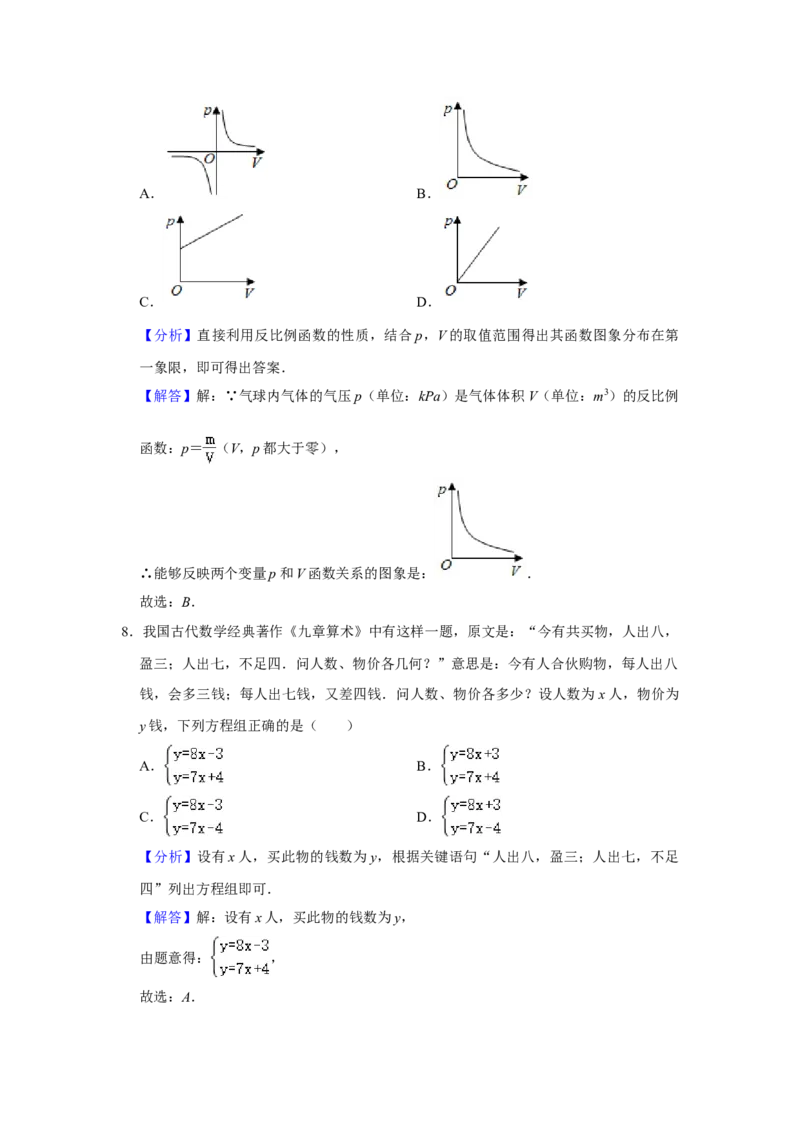
【解答】解:如图,
∵∠ACB=90°,∠ABC=60°,
∴∠A=180°﹣∠ACB﹣∠ABC=180°﹣90°﹣60°=30°,
∵∠EFD=90°,∠DEF=45°,
∴∠D=180°﹣∠EFD﹣∠DEF=180°﹣90°﹣45°=45°,
∵AB∥DE,∴∠1=∠D=45°,
∴∠AFD=∠1﹣∠A=45°﹣30°=15°,
故选:A.
5.下列运算正确的是( )
A.x3+x3=x6 B.2x3﹣x3=x3 C.(x3)2=x5 D.x3•x3=x9
【分析】分别根据合并同类项法则,幂的乘方运算法则以及同底数幂的乘法法则逐一判
断即可;合并同类项的法则:把同类项的系数相加,所得结果作为系数,字母和字母的
指数不变;幂的乘方,底数不变,指数相乘;同底数幂相乘,底数不变,指数相加.
【解答】解:A.x3+x3=2x3,故本选项不合题意;
B.2x3﹣x3=x3,故本选项符合题意;
C.(x3)2=x6,故本选项不合题意;
D.x3•x3=x6,故本选项不合题意;
故选:B.
6.在六张卡片上分别写有6,﹣ ,3.1415, ,0, 六个数,从中随机抽取一张,卡
π
片上的数为无理数的概率是( )
A. B. C. D.
【分析】先找出无理数,再利用概率公式求解即可求得答案.
【解答】解:∵六张卡片上分别写有6,﹣ ,3.1415, ,0, 六个数,无理数的
π
是 , ,
π
∴从中任意抽取一张卡片上的数为无理数的概率是: = .
故选:C.
7.某气球内充满了一定质量 m的气体,当温度不变时,气球内气体的气压 p(单位:
kPa)是气体体积V(单位:m3)的反比例函数:p= ,能够反映两个变量p和V函数
关系的图象是( )A. B.
C. D.
【分析】直接利用反比例函数的性质,结合p,V的取值范围得出其函数图象分布在第
一象限,即可得出答案.
【解答】解:∵气球内气体的气压p(单位:kPa)是气体体积V(单位:m3)的反比例
函数:p= (V,p都大于零),
∴能够反映两个变量p和V函数关系的图象是: .
故选:B.
8.我国古代数学经典著作《九章算术》中有这样一题,原文是:“今有共买物,人出八,
盈三;人出七,不足四.问人数、物价各几何?”意思是:今有人合伙购物,每人出八
钱,会多三钱;每人出七钱,又差四钱.问人数、物价各多少?设人数为x人,物价为
y钱,下列方程组正确的是( )
A. B.
C. D.
【分析】设有x人,买此物的钱数为y,根据关键语句“人出八,盈三;人出七,不足
四”列出方程组即可.
【解答】解:设有x人,买此物的钱数为y,
由题意得: ,
故选:A.9.如图,△ABC的顶点是正方形网格的格点,则cos∠ABC的值为( )
A. B. C. D.
【分析】由图可知,可把∠ABC放在Rt△ABD中,利用勾股定理可求出斜边AB的长,
再利用余弦的定义可得cos∠ABC= = = .
【解答】解:法一、如图,
在Rt△ABD中,∠ADB=90°,AD=BD=3,
∴AB= = =3 ,
∴cos∠ABC= = = .
故选:B.
法二、在Rt△ABD中,∠ADB=90°,AD=BD=3,
∴∠ABD=∠BAD=45°,
∴cos∠ABC=cos45°= .
故选:B.
10.如图,C,D是 O上直径AB两侧的两点,设∠ABC=25°,则∠BDC=( )
⊙A.85° B.75° C.70° D.65°
【分析】连接OC,根据圆周角定理可得∠AOC的度数,再根据平角的性质可得∠BOC
的度数,再根据圆周角定理即可求出∠BDC的度数.
【解答】解:连接OC,如图,
∵∠ABC=25°,
∴∠AOC=2∠ABC=2×25°=50°,
∴∠BOC=180°﹣∠AOC=180°﹣50°=30°,
∴ .
故选:D.
11.从前,古希腊一位庄园主把一块边长为 a米(a>6)的正方形土地租给租户张老汉,
第二年,他对张老汉说:“我把这块地的一边增加6米,相邻的另一边减少6米,变成
矩形土地继续租给你,租金不变,你也没有吃亏,你看如何?”如果这样,你觉得张老
汉的租地面积会( )
A.没有变化 B.变大了 C.变小了 D.无法确定
【分析】矩形的长为(a+6)米,矩形的宽为(a﹣6)米,矩形的面积为(a+6)(a﹣
6),根据平方差公式即可得出答案.
【解答】解:矩形的面积为(a+6)(a﹣6)=a2﹣36,
∴矩形的面积比正方形的面积a2小了36平方米,
故选:C.
二、填空题(将答案写在答题卡上指定的位置.每小题3分,计12分.)
12.用正负数表示气温的变化量,上升为正,下降为负.登山队攀登一座山峰,每登高
1km气温的变化量为﹣6℃,攀登2km后,气温下降 1 2 ℃.
【分析】根据每登高1km气温的变化量为﹣6℃,可以得到登2km后,气温下降的度数.
【解答】解:由题意可得,
2÷1×(﹣6)
=2×(﹣6)=﹣12(℃),
即气温下降12℃,
故答案为:12.
13.如图,在平面直角坐标系中,将点A(﹣1,2)向右平移2个单位长度得到点B,则点
B关于x轴的对称点C的坐标是 ( 1 ,﹣ 2 ) .
【分析】直接利用平移的性质得出B点坐标,再利用关于x轴对称点的坐标特点:横坐
标不变,纵坐标互为相反数,即可得出答案.
【解答】解:∵将点A(﹣1,2)向右平移2个单位长度得到点B,
∴B(1,2),
则点B关于x轴的对称点C的坐标是(1,﹣2).
故答案为:(1,﹣2).
14.社团课上,同学们进行了“摸球游戏”:在一个不透明的盒子里装有几十个除颜色不
同外其余均相同的黑、白两种球,将盒子里面的球搅匀后从中随机摸出一个球记下颜色,
再把它放回盒子中,不断重复上述过程.整理数据后,制作了“摸出黑球的频率”与
“摸球的总次数”的关系图象如图所示,经分析可以推断盒子里个数比较多的是 白
球 .(填“黑球”或“白球”)
【分析】根据频率估计概率得出摸到黑球的近似概率,再得出摸到白球的概率,即可推
断出是白球多还是黑球多.
【解答】解:由图可知,摸出黑球的概率约为0.2,∴摸出白球的概率约为0.8,
∴白球的个数比较多,
故答案为白球.
15.“莱洛三角形”是工业生产中加工零件时广泛使用的一种图形.如图,以边长为 2厘
米的等边三角形ABC的三个顶点为圆心,以边长为半径画弧,三段圆弧围成的图形就
是“莱洛三角形”,该“莱洛三角形”的面积为 ( 2 ﹣ 2 ) 平方厘米.(圆周
率用 表示) π
π
【分析】图中三角形的面积是由三块相同的扇形叠加而成,其面积等于三块扇形的面积
相加,再减去两个等边三角形的面积,分别求出即可.
【解答】解:过A作AD⊥BC于D,
∵AB=AC=BC=2厘米,∠BAC=∠ABC=∠ACB=60°,
∵AD⊥BC,
∴BD=CD=1厘米,AD= BD= 厘米,
∴△ABC的面积为 BC•AD= (厘米2),
S扇形BAC = = (厘米2),
π
∴莱洛三角形的面积S=3× ﹣2× =(2 ﹣2 )厘米2,
π π
故答案为:(2 ﹣2 ).
π
三、解答题(将解答过程写在答题卡上指定的位置,本大题共有9小题,计75分.)
16.(6分)先化简,再求值: ÷ ﹣ ,从1,2,3这三个数中选择一个你认为适合的x代入求值.
【分析】根据分式的除法和减法可以化简题目中的式子,然后从 1,2,3这三个数中选
择一个使得原分式有意义的值代入化简后的式子即可解答本题.
【解答】解: ÷ ﹣
= •(x+1)﹣
=
= ,
∵(x+1)(x﹣1)≠0,
∴x≠1,﹣1,
∴x=2或3,
当x=2时,原式= =1.
17.(6分)解不等式组 .
【分析】先求出每个不等式的解集,再求出不等式组的解集即可.
【解答】解: ,
解不等式①得:x≤1,
解不等式②得:x≤5,
∴不等式组解集为x≤1.
18.(7分)如图,在△ABC中,∠B=40°,∠C=50°.
(1)通过观察尺规作图的痕迹,可以发现直线DF是线段AB的 垂直平分线 ,射
线AE是∠DAC的 角平分线 ;
(2)在(1)所作的图中,求∠DAE的度数.【分析】(1)根据作图痕迹判断即可.
(2)想办法求出∠CAD,可得结论.
【解答】解:(1)通过观察尺规作图的痕迹,可以发现直线DF是线段AB的垂直平分
线,射线AE是∠DAC的 角平分线.
故答案为:垂直平分线,角平分线.
(2)∵DF垂直平分线段AB,
∴DA=DB,
∴∠BAD=B=40°,
∵∠B=40°,∠C=50°,
∴∠BAC=90°,
∴∠CAD=50°,
∵AE平分∠CAD,
∴∠DAE= ∠CAD=25°.
19.(7分)国家规定“中小学生每天在校体育活动时间不低于 1h”.为此,某市就“每
天在校体育活动时间”的问题随机调查了辖区内部分初中学生,根据调查结果绘制成的
统计图(部分)如图所示,其中分组情况是:
A组:t<0.5h
B组:0.5h≤t<1h
C组:1h≤t<1.5h
D组:t≥1.5h
请根据上述信息解答下列问题:
(1)本次调查的人数是 40 0 人;(2)请根据题中的信息补全频数分布直方图;
(3)D组对应扇形的圆心角为 3 6 °;
(4)本次调查数据的中位数落在 C 组内;
(5)若该市辖区约有80000名初中学生,请估计其中达到国家规定体育活动时间的学
生人数约有多少.
【分析】(1)根据A组的人数和百分比即可求出总人数;
(2)根据总人数和条形统计图即可求出C组人数;
(3)先算出D组所占的百分比,再求出对应的圆心角;
(4)根据第200个和第201个数据所在的组即可求出中位数所在的组;
(5)根据优秀人数的百分比即可估算出全市优秀的人数.
【解答】解:(1)∵A组有40人,占10%,
∴总人数为 (人),
故答案为400;
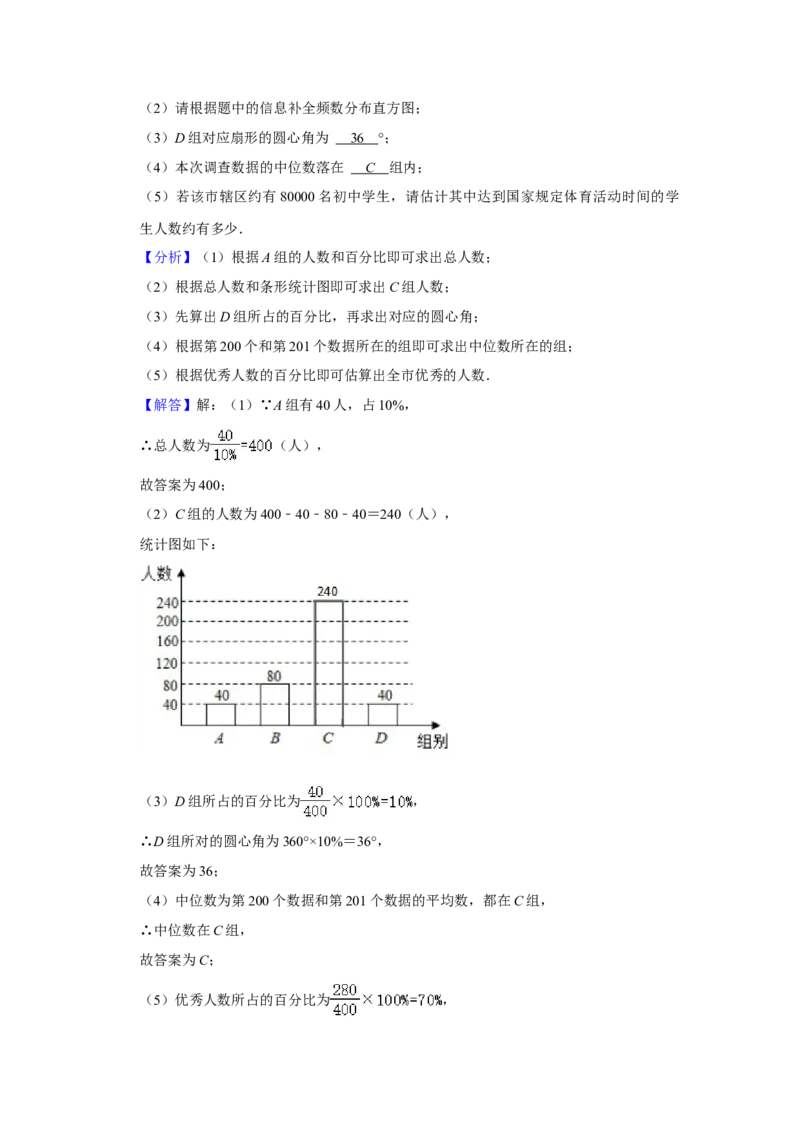
(2)C组的人数为400﹣40﹣80﹣40=240(人),
统计图如下:
(3)D组所占的百分比为 ,
∴D组所对的圆心角为360°×10%=36°,
故答案为36;
(4)中位数为第200个数据和第201个数据的平均数,都在C组,
∴中位数在C组,
故答案为C;
(5)优秀人数所占的百分比为 ,∴全市优秀人数大约为80000×70%=56000(人).
20.(8分)甲超市在端午节这天进行苹果优惠促销活动,苹果的标价为10元/kg,如果一
次购买4kg以上的苹果,超过4kg的部分按标价6折售卖.
x(单位:kg)表示购买苹果的重量,y(单位:元)表示付款金额.
(1)文文购买3kg苹果需付款 3 0 元;购买5kg苹果需付款 4 6 元;
(2)求付款金额y关于购买苹果的重量x的函数解析式;
(3)当天,隔壁的乙超市也在进行苹果优惠促销活动,同样的苹果的标价也为10元/
kg,且全部按标价的8折售卖,文文如果要购买10kg苹果,请问她在哪个超市购买更划
算?
【分析】(1)根据题意直接写出购买3kg和5kg苹果所需付款;
(2)分0<x≤4和x>4两种情况写出函数解析式即可;
(3)通过两种付款比较那个超市便宜即可.
【解答】解:(1)由题意可知:文文购买3kg苹果,不优惠,
∴文文购买3kg苹果需付款:3×10=30(元),
购买5kg苹果,4kg不优惠,1kg优惠,
∴购买5kg苹果需付款:4×10+1×10×0.6=46(元),
故答案为:30,46;
(2)由题意得:
当0<x≤4时,y=4x,
当x>4时,y=4×10+(x﹣4)×10×0.6=6x+16,
∴付款金额y关于购买苹果的重量x的函数解析式为:y= ;
(3)文文在甲超市购买10kg苹果需付费:6×10+16=76(元),
文文在乙超市购买10kg苹果需付费:10×10×0.8=80(元),
∴文文应该在甲超市购买更划算.
21.(8分)如图,在菱形ABCD中,O是对角线BD上一点(BO>DO),OE⊥AB,垂
足为E,以OE为半径的 O分别交DC于点H,交EO的延长线于点F,EF与DC交于
点G. ⊙
(1)求证:BC是 O的切线;
(2)若G是OF的⊙中点,OG=2,DG=1.
①求 的长;②求AD的长.
【分析】(1)过点O作OM⊥BC于点M,证明OM=OE即可;
(2)①先求出∠HOE=120°,再求出OH=4,代入弧长公式即可;
②过A作AN⊥BD,由△DOG∽△DAN,对应边成比例求出AD的长.
【解答】解:(1)证明:如图1,过点O作OM⊥BC于点M,
∵BD是菱形ABCD的对角线,
∴∠ABD=∠CBD,
∵OM⊥BC,OE⊥AB,
∴OE=OM,
∴BC是 O的切线.
⊙
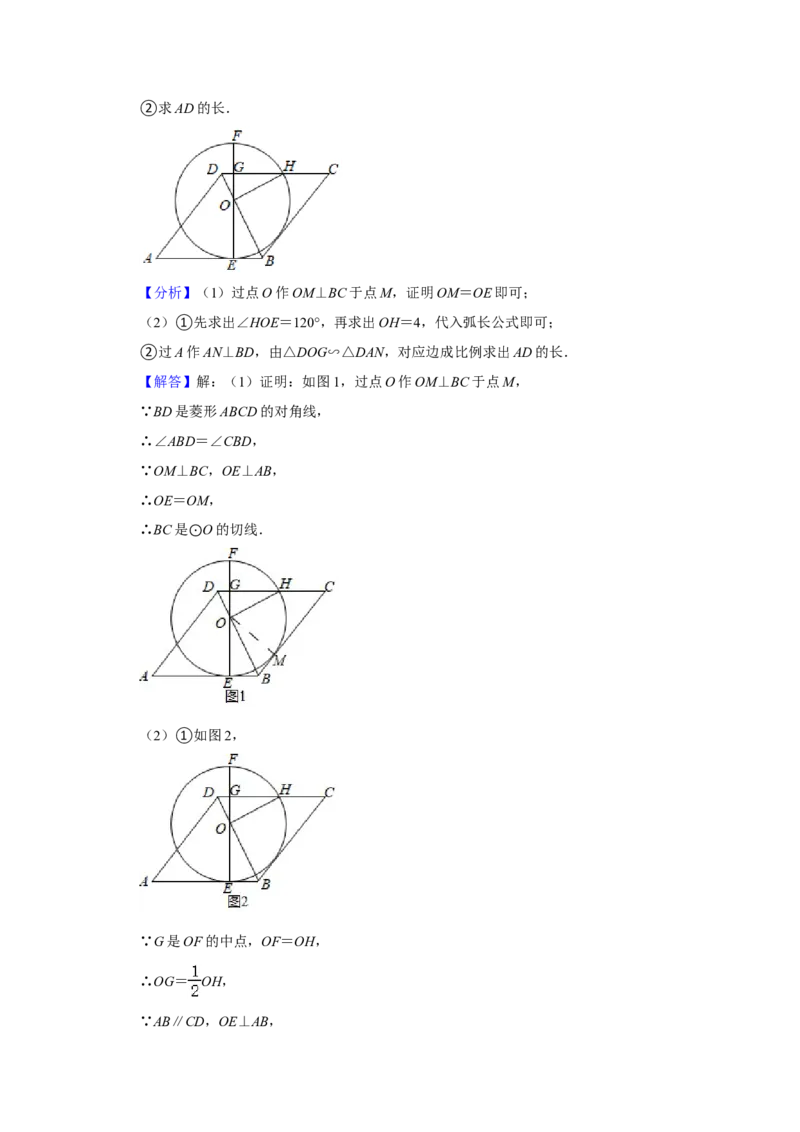
(2)①如图2,
∵G是OF的中点,OF=OH,
∴OG= OH,
∵AB∥CD,OE⊥AB,∴OF⊥CD,
∴∠OGH=90°,
∴sin∠GHO= ,
∴∠GHO=30°,
∴∠GOH=60°,
∴∠HOE=120°,
∵OG=2,
∴OH=4,
∴由弧长公式得到 的长: = .
②如图3,过A作AN⊥BD于点N,
∵DG=1,OG=2,OE=OH=4,
∴OD= ,OB=2 ,DN= ,
∴△DOG∽△DAN,
∴ ,
∴ ,
∴AD= .
22.(10分)随着农业技术的现代化,节水型灌溉得到逐步推广.喷灌和滴灌是比漫灌更
节水的灌溉方式,喷灌和滴灌时每亩用水量分别是漫灌时的30%和20%.去年,新丰收
公司用各100亩的三块试验田分别采用喷灌、滴灌和漫灌的灌溉方式,共用水15000吨.
(1)请问用漫灌方式每亩用水多少吨?去年每块试验田各用水多少吨?
(2)今年该公司加大对农业灌溉的投入,喷灌和滴灌试验田的面积都增加了m%,漫灌试验田的面积减少了2m%.同时,该公司通过维修灌溉输水管道,使得三种灌溉方式下
的每亩用水量都进一步减少了m%.经测算,今年的灌溉用水量比去年减少 m%,求m
的值.
(3)节水不仅为了环保,也与经济收益有关系.今年,该公司全部试验田在灌溉输水
管道维修方面每亩投入30元,在新增的喷灌、滴灌试验田添加设备所投入经费为每亩
100元,在(2)的情况下,若每吨水费为2.5元,请判断,相比去年因用水量减少所节
省的水费是否大于今年的以上两项投入之和?
【分析】(1)设漫灌方式每亩用水x吨,则100x+100×30%x+100×20%x=15000,解得
x=100,可得结论;
(2)由“今年的灌溉用水量比去年减少 m%”可列出等式,进而求出m的值;
(3)分别计算去年因用水量减少所节省的水费和今天的两项投入之和,再进行比较即
可.
【解答】解:(1)设漫灌方式每亩用水x吨,则
100x+100×30%x+100×20%x=15000,
解得x=100,
∴漫灌用水:100×100=10000吨,
喷灌用水:30%×10000=3000吨,
滴灌用水:20%×10000=2000吨,
∴漫灌方式每亩用水100吨,漫灌试验田用水10000吨,喷灌试验田用水3000吨,滴灌
试验田用水2000吨.
(2)由题意可得,100×(1﹣2m%)×100×(1﹣m%)+100×(1+m%)×30×(1﹣m%)
+100×(1+m%)×20×(1﹣m%)=15000×(1﹣ m%),
解得m=0(舍),或m=20,
∴m=20.
(3)节省水费:15000× m%×2.5=13500元,
维修投入:300×30=9000元,
新增设备:100×2m%×100=4000元,13500>9000+4000,
∴节省水费大于两项投入之和.
23.(11分)如图,在矩形ABCD中,E是边AB上一点,BE=BC,EF⊥CD,垂足为F.
将四边形CBEF绕点C顺时针旋转 (0°< <90°),得到四边形CB'E'F′,B′E′所
在的直线分别交直线BC于点G,交α直线ADα于点P,交CD于点K.E′F′所在的直线
分别交直线BC于点H,交直线AD于点Q,连接B′F′交CD于点O.
(1)如图1,求证:四边形BEFC是正方形;
(2)如图2,当点Q和点D重合时.
①求证:GC=DC;
②若OK=1,CO=2,求线段GP的长;
(3)如图3,若BM∥F′B′交GP于点M,tan∠G= ,求 的值.
【分析】(1)根据邻边相等的矩形的正方形证明即可.
(2)①证明△CGB′≌△CDF′(ASA),可得结论.
②设正方形的边长为a,利用勾股定理构建方程求出a,再证明GK=PK,求出PG=
2PK,求出PK可得结论.
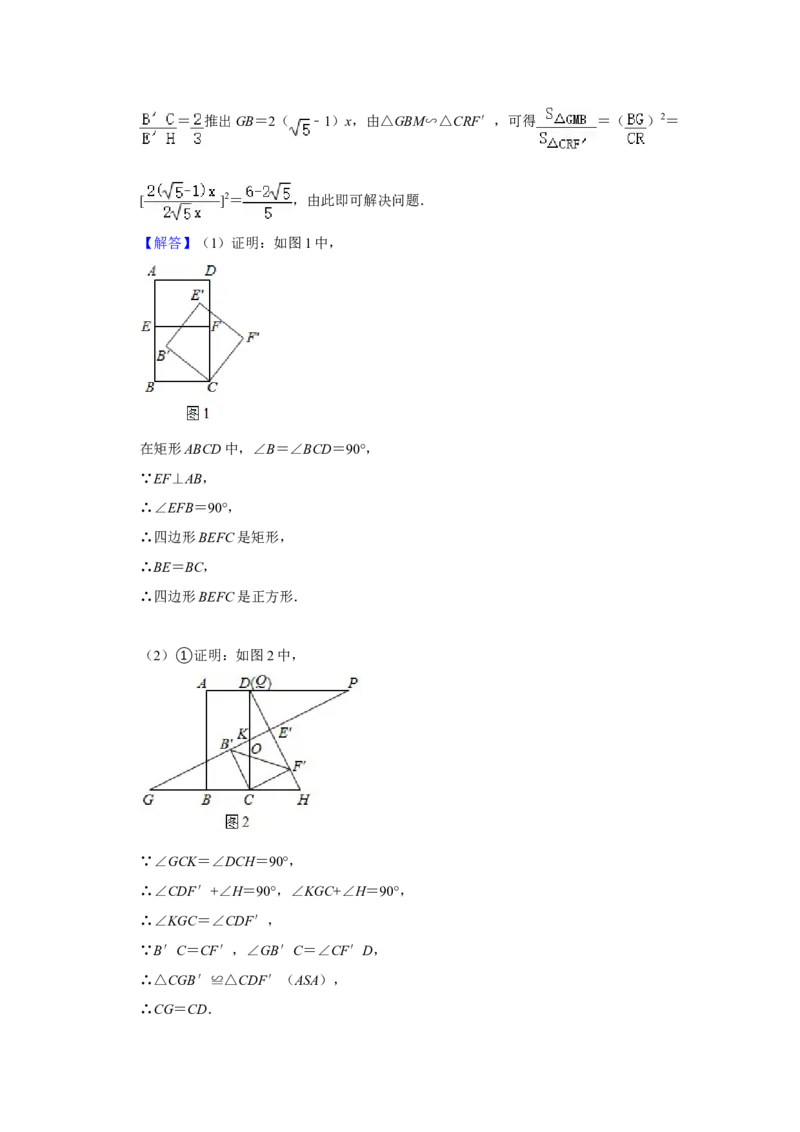
(3)如图3中,延长B′F′交CH的延长线于R.由tan∠G=tan∠F′CH= =
,设F′H=x.CF′=2x,则CH= x,由△RB′C∽△RF′H,推出 =
= = ,推出 CH=RH,B′F′=RF′,可得 CR=2CH=2 x,S△CF′R =
2S△CF′H ,再由△GB′C∽△GE′H,推出 = = = ,可得 == 推出GB=2( ﹣1)x,由△GBM∽△CRF′,可得 =( )2=
[ ]2= ,由此即可解决问题.
【解答】(1)证明:如图1中,
在矩形ABCD中,∠B=∠BCD=90°,
∵EF⊥AB,
∴∠EFB=90°,
∴四边形BEFC是矩形,
∴BE=BC,
∴四边形BEFC是正方形.
(2)①证明:如图2中,
∵∠GCK=∠DCH=90°,
∴∠CDF′+∠H=90°,∠KGC+∠H=90°,
∴∠KGC=∠CDF′,
∵B′C=CF′,∠GB′C=∠CF′D,
∴△CGB′≌△CDF′(ASA),
∴CG=CD.②解:设正方形的边长为a,
∵KB′∥CF′,
∴△B′KO∽△F′CO,
∴ = = ,
∴B′K= B′C= a,
在Rt△B′KC中,B′K2+B′C2=CK2,
∴a2+( a)2=32,
∴a= ,
由 = ,可得B′K=KE′= a,
∵KE′∥CF′
∴△DKE′∽△DCF′,
∴ = = = ,
∴DE′=E′F′=a,
∴PE′=2a,
∴PK= a,
∵DK=KC,∠P=∠G,∠DKP=∠GKC,
∴△PKD≌△GKC(AAS),
∴GK=PK,
∴PG=2PK=5a,
∴PG=5a=6 .
(3)解:如图3中,延长B′F′交CH的延长线于R.∵CF′∥GP,RB∥BM,
∴△GB∽△GRB′,∠G=∠F′CR,
∴tan∠G=tan∠F′CH= = ,
设F′H=x.CF′=2x,则CH= x,
∴CB′=CF′=E′F′=BC=2x,
∵CB′∥HE′,
∴△RB′C∽△RF′H,
∴ = = = ,
∴CH=RH,B′F′=RF′,
∴CR=2CH=2 x,
∴S△CF′R =2S△CF′H ,
∵CB′∥HE′,
∴△GB′C∽△GE′H,
∴ = = = ,
∴ = =
∴GB=2( ﹣1)x,
∵△GBM∽△CRF′,
∴ =( )2=[ ]2= ,
∵S△CRF′ =2S△CHF′ ,
∴ = .24.(12分)在平面直角坐标系中,抛物线y =﹣(x+4)(x﹣n)与x轴交于点A和点B
1
(n,0)(n≥﹣4),顶点坐标记为(h ,k ).抛物线y =﹣(x+2n)2﹣n2+2n+9的
1 1 2
顶点坐标记为(h ,k ).
2 2
(1)写出A点坐标;
(2)求k ,k 的值(用含n的代数式表示)
1 2
(3)当﹣4≤n≤4时,探究k 与k 的大小关系;
1 2
(4)经过点M(2n+9,﹣5n2)和点N(2n,9﹣5n2)的直线与抛物线y =﹣(x+4)
1
(x﹣n),y =﹣(x+2n)2﹣n2+2n+9的公共点恰好为3个不同点时,求n的值.
2
【分析】(1)令y =0,得到x值即为A、B的横坐标,
1
(2)由顶点坐标公式可得顶点的纵坐标.
(3)讨论k ﹣k = n2﹣5与0比较大小得n的取值范围,即在不同的取值范围内得
1 2
k 、k 大小.
1 2
(4)两点确定一条直线的解析式,直线MN的解析式为:y=﹣x﹣5n2+2n+9.①当直
线MN经过抛物线y ,y 的交点时,联立抛物线y 与y 得解析式(5n﹣4)x=﹣5n2﹣
1 2 1 2
2n+9①,联立直线y=﹣x﹣5n2+2n+9与抛物线y 得解析式x2+(4n﹣1)x=0,解得n
2
= ,此时直线MN与抛物线y ,y 的公共点恰好为三个不同点,即(5n﹣4)
1 2
(1﹣4n)=﹣5n2﹣2n+9,该方程判别式△<0,②当直线MN与抛物线y 或者与抛物
1
线y 只有一个公共点时,当直线MN与抛物线y 只有一个公共点时,联立直线y=﹣x﹣
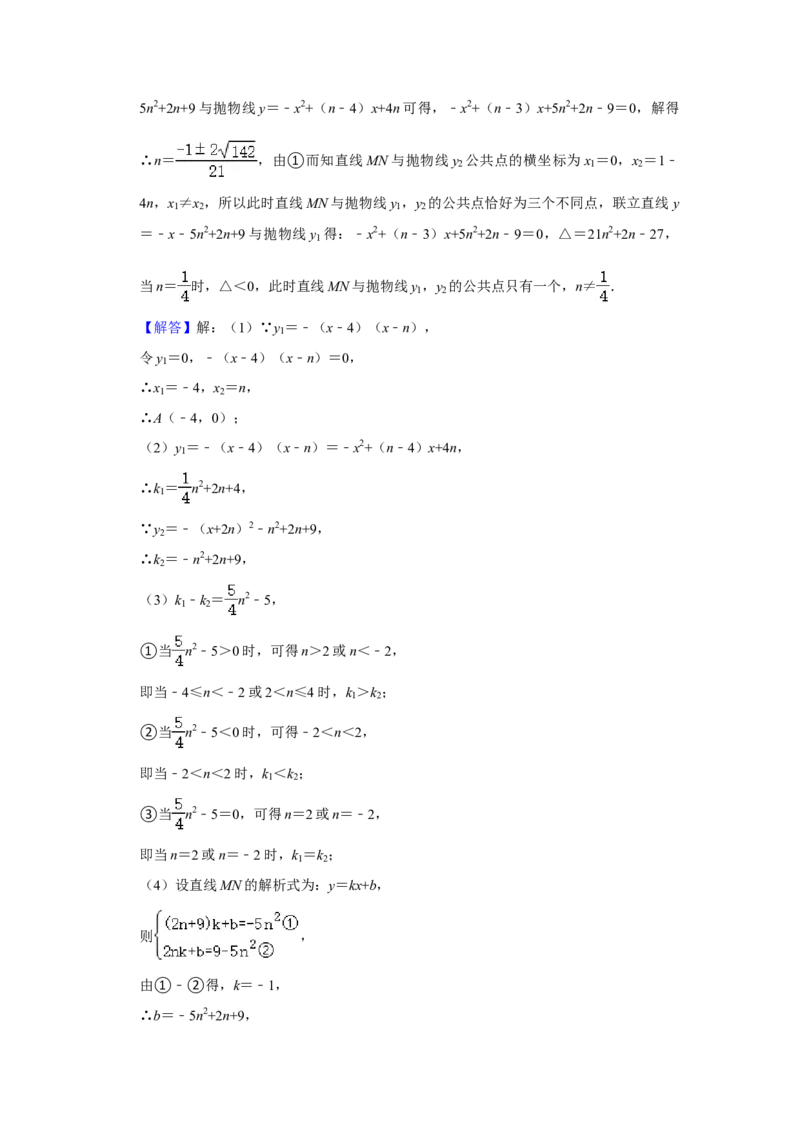
2 15n2+2n+9与抛物线y=﹣x2+(n﹣4)x+4n可得,﹣x2+(n﹣3)x+5n2+2n﹣9=0,解得
∴n= ,由①而知直线MN与抛物线y 公共点的横坐标为x =0,x =1﹣
2 1 2
4n,x ≠x ,所以此时直线MN与抛物线y ,y 的公共点恰好为三个不同点,联立直线y
1 2 1 2
=﹣x﹣5n2+2n+9与抛物线y 得:﹣x2+(n﹣3)x+5n2+2n﹣9=0,△=21n2+2n﹣27,
1
当n= 时,△<0,此时直线MN与抛物线y ,y 的公共点只有一个,n≠ .
1 2
【解答】解:(1)∵y =﹣(x﹣4)(x﹣n),
1
令y =0,﹣(x﹣4)(x﹣n)=0,
1
∴x =﹣4,x =n,
1 2
∴A(﹣4,0);
(2)y =﹣(x﹣4)(x﹣n)=﹣x2+(n﹣4)x+4n,
1
∴k = n2+2n+4,
1
∵y =﹣(x+2n)2﹣n2+2n+9,
2
∴k =﹣n2+2n+9,
2
(3)k ﹣k = n2﹣5,
1 2
①当 n2﹣5>0时,可得n>2或n<﹣2,
即当﹣4≤n<﹣2或2<n≤4时,k >k ;
1 2
②当 n2﹣5<0时,可得﹣2<n<2,
即当﹣2<n<2时,k <k ;
1 2
③当 n2﹣5=0,可得n=2或n=﹣2,
即当n=2或n=﹣2时,k =k ;
1 2
(4)设直线MN的解析式为:y=kx+b,
则 ,
由①﹣②得,k=﹣1,
∴b=﹣5n2+2n+9,直线MN的解析式为:y=﹣x﹣5n2+2n+9.
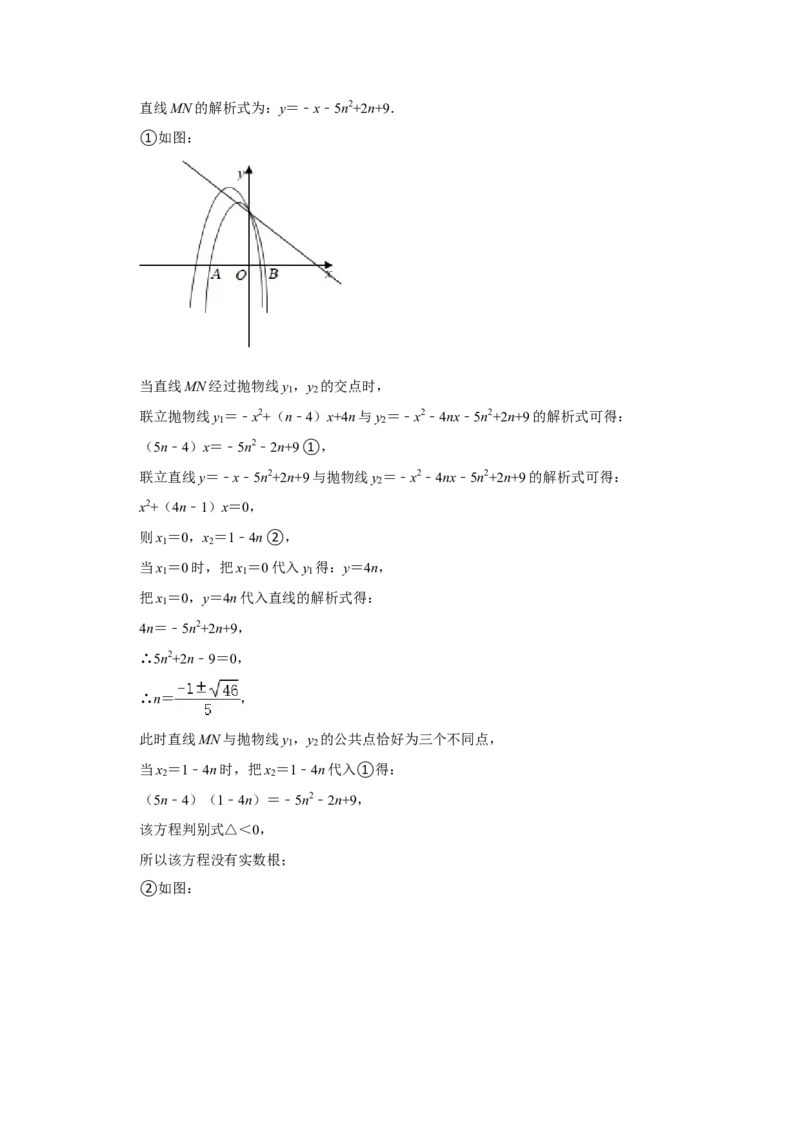
①如图:
当直线MN经过抛物线y ,y 的交点时,
1 2
联立抛物线y =﹣x2+(n﹣4)x+4n与y =﹣x2﹣4nx﹣5n2+2n+9的解析式可得:
1 2
(5n﹣4)x=﹣5n2﹣2n+9①,
联立直线y=﹣x﹣5n2+2n+9与抛物线y =﹣x2﹣4nx﹣5n2+2n+9的解析式可得:
2
x2+(4n﹣1)x=0,
则x =0,x =1﹣4n②,
1 2
当x =0时,把x =0代入y 得:y=4n,
1 1 1
把x =0,y=4n代入直线的解析式得:
1
4n=﹣5n2+2n+9,
∴5n2+2n﹣9=0,
∴n= ,
此时直线MN与抛物线y ,y 的公共点恰好为三个不同点,
1 2
当x =1﹣4n时,把x =1﹣4n代入①得:
2 2
(5n﹣4)(1﹣4n)=﹣5n2﹣2n+9,
该方程判别式△<0,
所以该方程没有实数根;
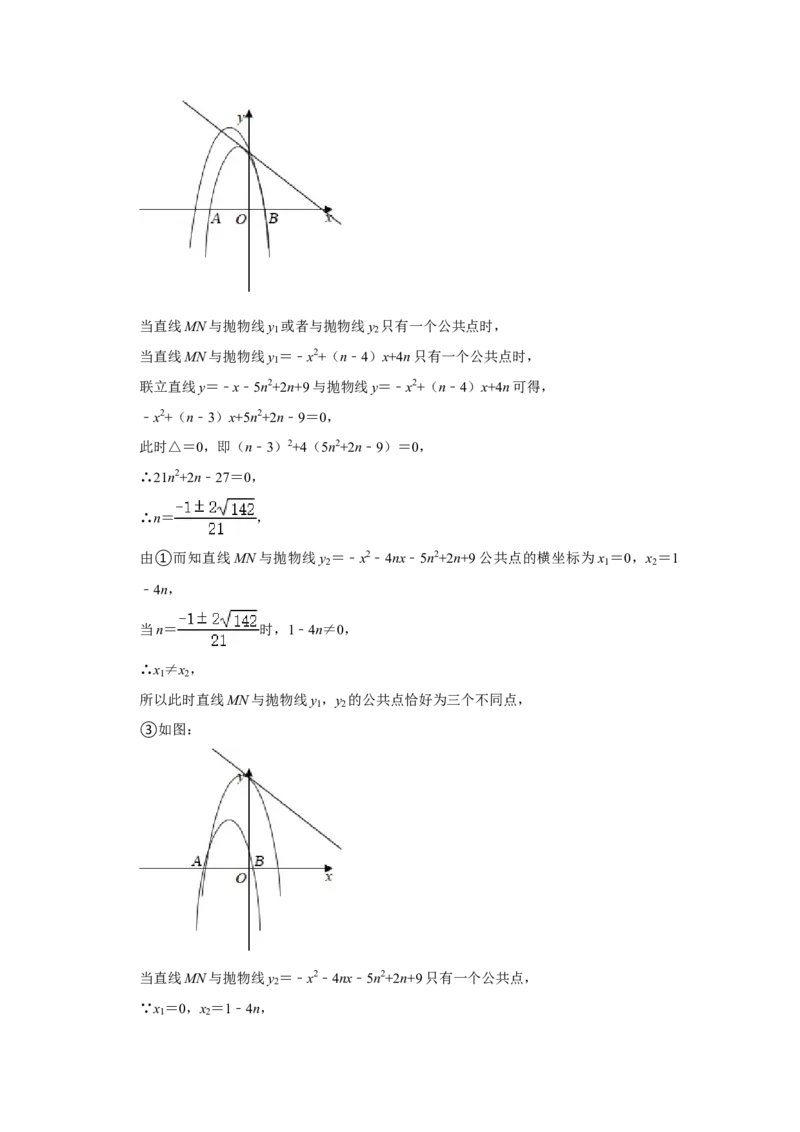
②如图:当直线MN与抛物线y 或者与抛物线y 只有一个公共点时,
1 2
当直线MN与抛物线y =﹣x2+(n﹣4)x+4n只有一个公共点时,
1
联立直线y=﹣x﹣5n2+2n+9与抛物线y=﹣x2+(n﹣4)x+4n可得,
﹣x2+(n﹣3)x+5n2+2n﹣9=0,
此时△=0,即(n﹣3)2+4(5n2+2n﹣9)=0,
∴21n2+2n﹣27=0,
∴n= ,
由①而知直线MN与抛物线y =﹣x2﹣4nx﹣5n2+2n+9公共点的横坐标为x =0,x =1
2 1 2
﹣4n,
当n= 时,1﹣4n≠0,
∴x ≠x ,
1 2
所以此时直线MN与抛物线y ,y 的公共点恰好为三个不同点,
1 2
③如图:
当直线MN与抛物线y =﹣x2﹣4nx﹣5n2+2n+9只有一个公共点,
2
∵x =0,x =1﹣4n,
1 2∴n= ,
联立直线y=﹣x﹣5n2+2n+9与抛物线y =﹣x2+(n﹣4)x+4n,
1
﹣x2+(n﹣3)x+5n2+2n﹣9=0,
△=(n﹣3)2+4(5n2+2n﹣9)=21n2+2n﹣27,
当n= 时,△<0,
此时直线MN与抛物线y ,y 的公共点只有一个,
1 2
∴n≠ ,
综上所述:n = ,n = ,n = ,n =﹣2﹣ .
1 2 3 4