文档内容
2021年湖南省怀化市中考数学试卷
一、选择题(每小题4分,共40分;每小题的四个选项中只有一项是正确的,请将正确选
项的代号填涂在答题卡的相应位置上)
1.(4分)数轴上表示数5的点和原点的距离是( )
A. B.5 C.﹣5 D.﹣
2.(4分)到2020年底,我国完成了“脱贫攻坚”任务,有约9980万的贫困人口实现了
脱贫.将数据9980万用科学记数法表示是( )
A.9.98×103 B.9.98×105 C.9.98×106 D.9.98×107
3.(4分)以下说法错误的是( )
A.多边形的内角大于任何一个外角
B.任意多边形的外角和是360°
C.正六边形是中心对称图形
D.圆内接四边形的对角互补
4.(4分)对于一元二次方程2x2﹣3x+4=0,则它根的情况为( )
A.没有实数根 B.两根之和是3
C.两根之积是﹣2 D.有两个不相等的实数根
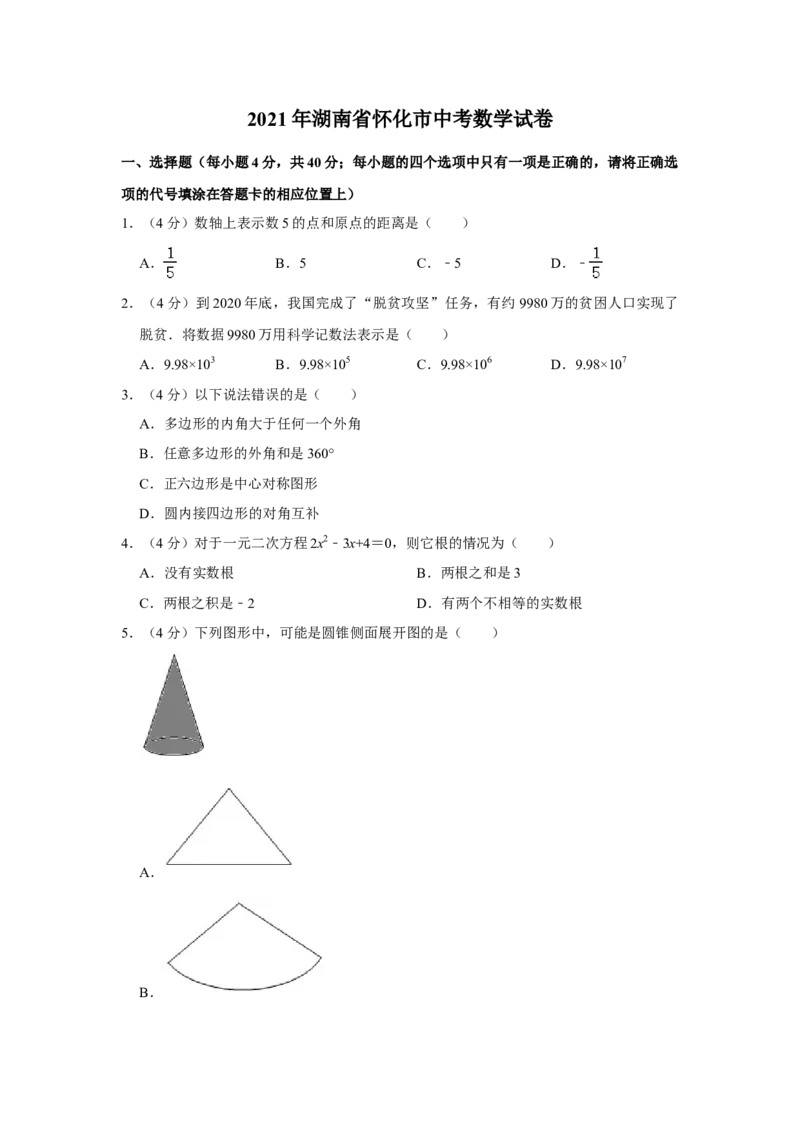
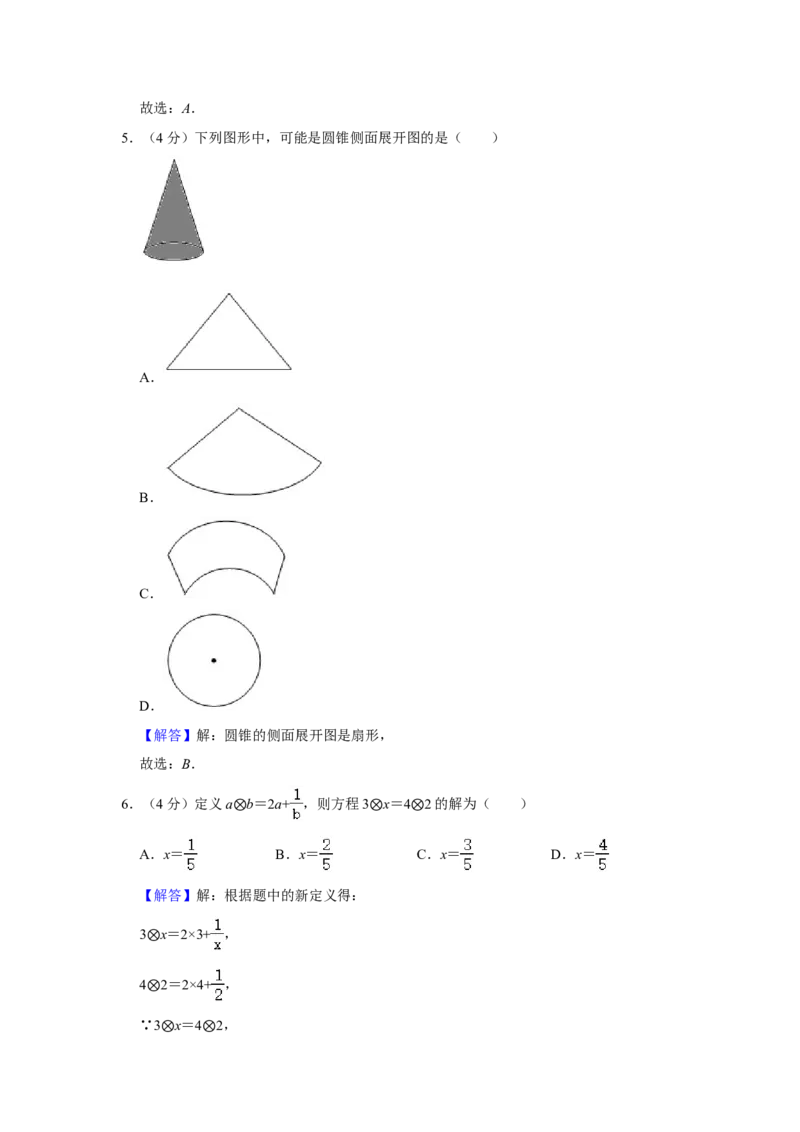
5.(4分)下列图形中,可能是圆锥侧面展开图的是( )
A.
B.C.
D.
6.(4分)定义a b=2a+ ,则方程3 x=4 2的解为( )
⊗ ⊗ ⊗
A.x= B.x= C.x= D.x=
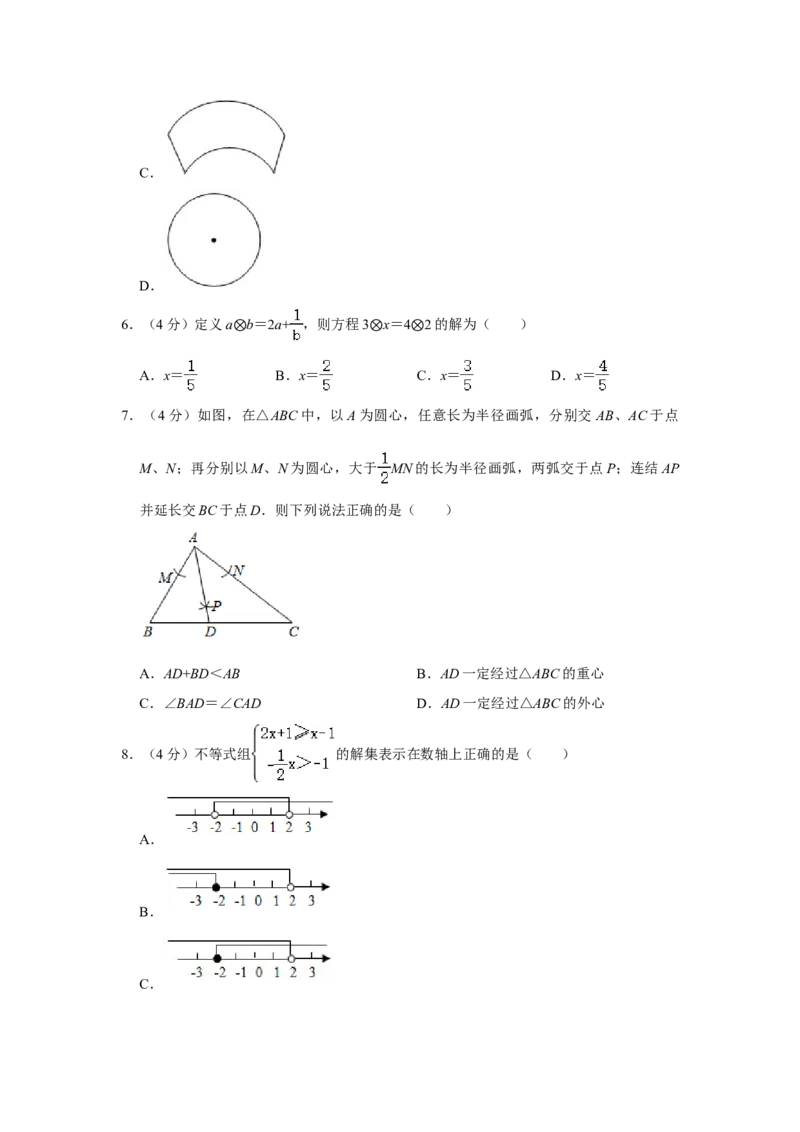
7.(4分)如图,在△ABC中,以A为圆心,任意长为半径画弧,分别交 AB、AC于点
M、N;再分别以M、N为圆心,大于 MN的长为半径画弧,两弧交于点P;连结AP
并延长交BC于点D.则下列说法正确的是( )
A.AD+BD<AB B.AD一定经过△ABC的重心
C.∠BAD=∠CAD D.AD一定经过△ABC的外心
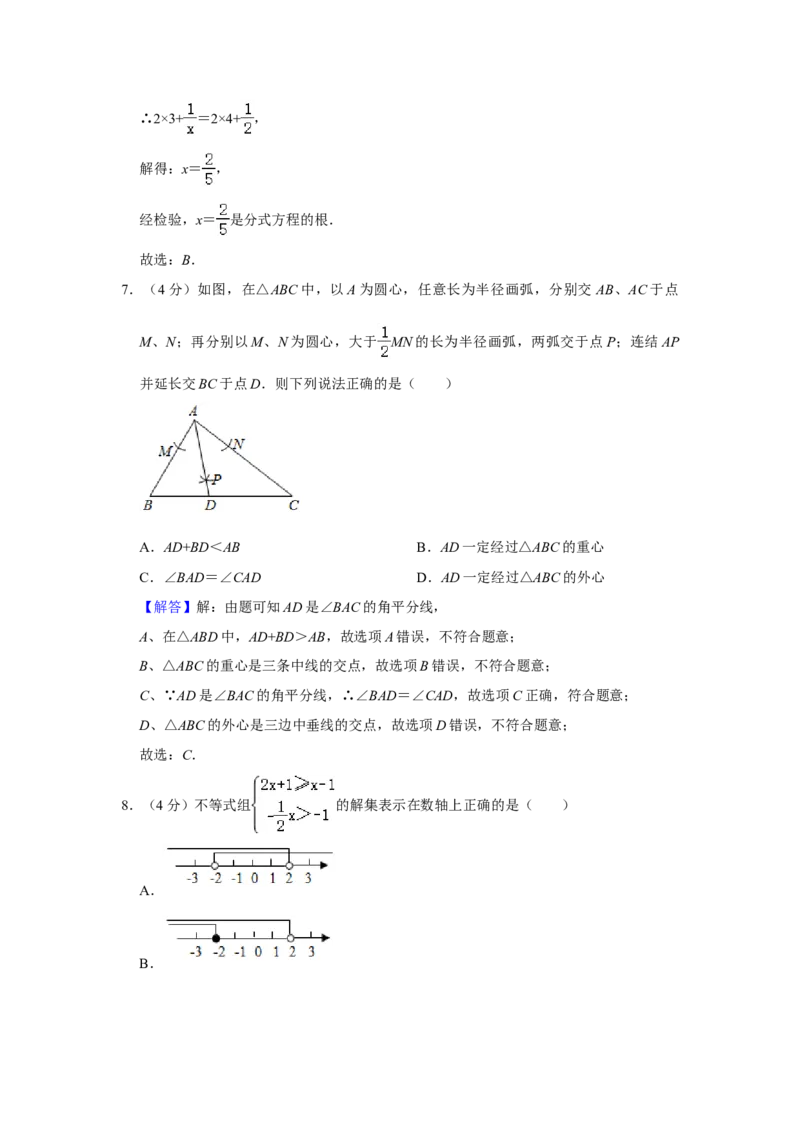
8.(4分)不等式组 的解集表示在数轴上正确的是( )
A.
B.
C.D.
9.(4分)“成语”是中华文化的瑰宝,是中华文化的微缩景观.下列成语:①“水中捞
月”,②“守株待兔”,③“百步穿杨”,④“瓮中捉鳖”描述的事件是不可能事件
的是( )
A.① B.② C.③ D.④
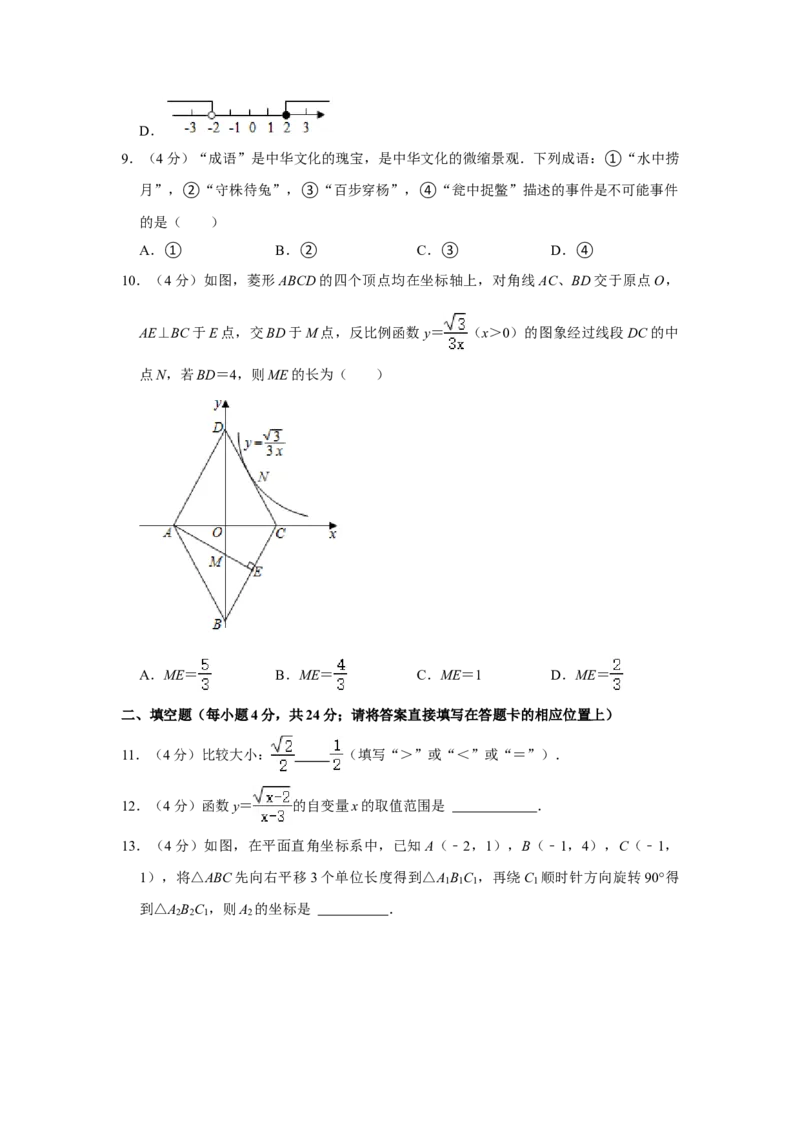
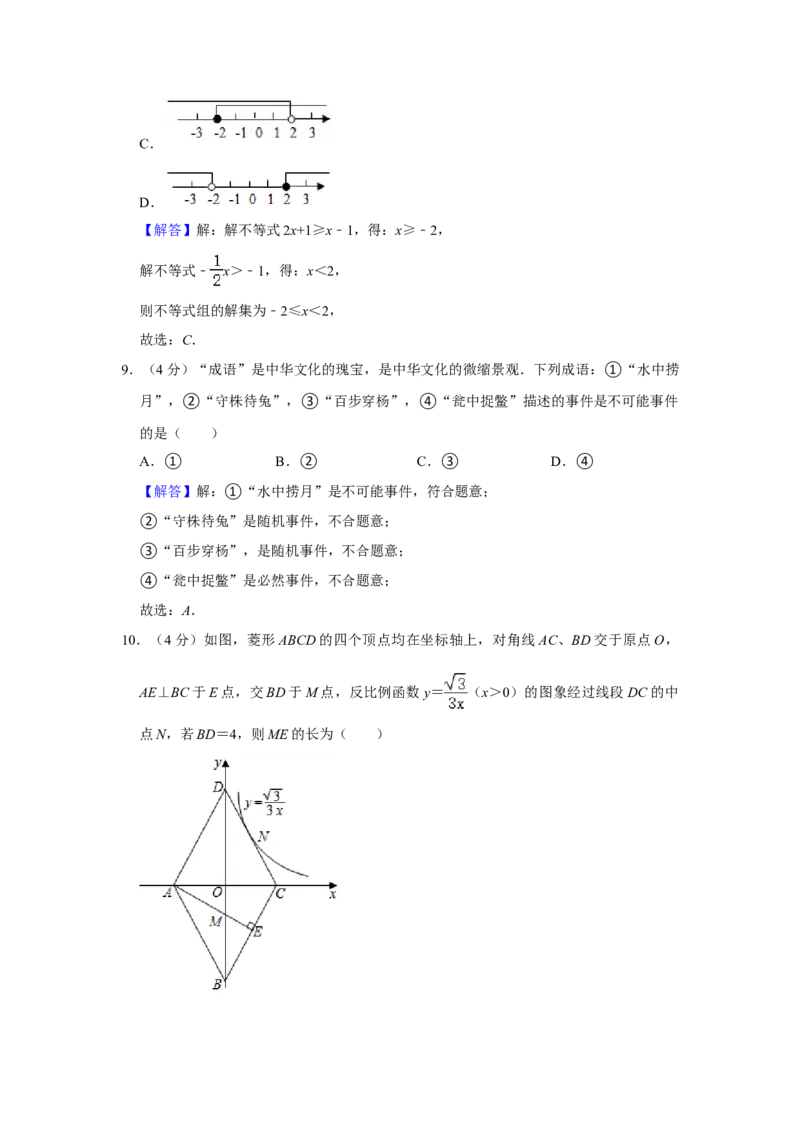
10.(4分)如图,菱形ABCD的四个顶点均在坐标轴上,对角线AC、BD交于原点O,
AE⊥BC于E点,交BD于M点,反比例函数y= (x>0)的图象经过线段DC的中
点N,若BD=4,则ME的长为( )
A.ME= B.ME= C.ME=1 D.ME=
二、填空题(每小题4分,共24分;请将答案直接填写在答题卡的相应位置上)
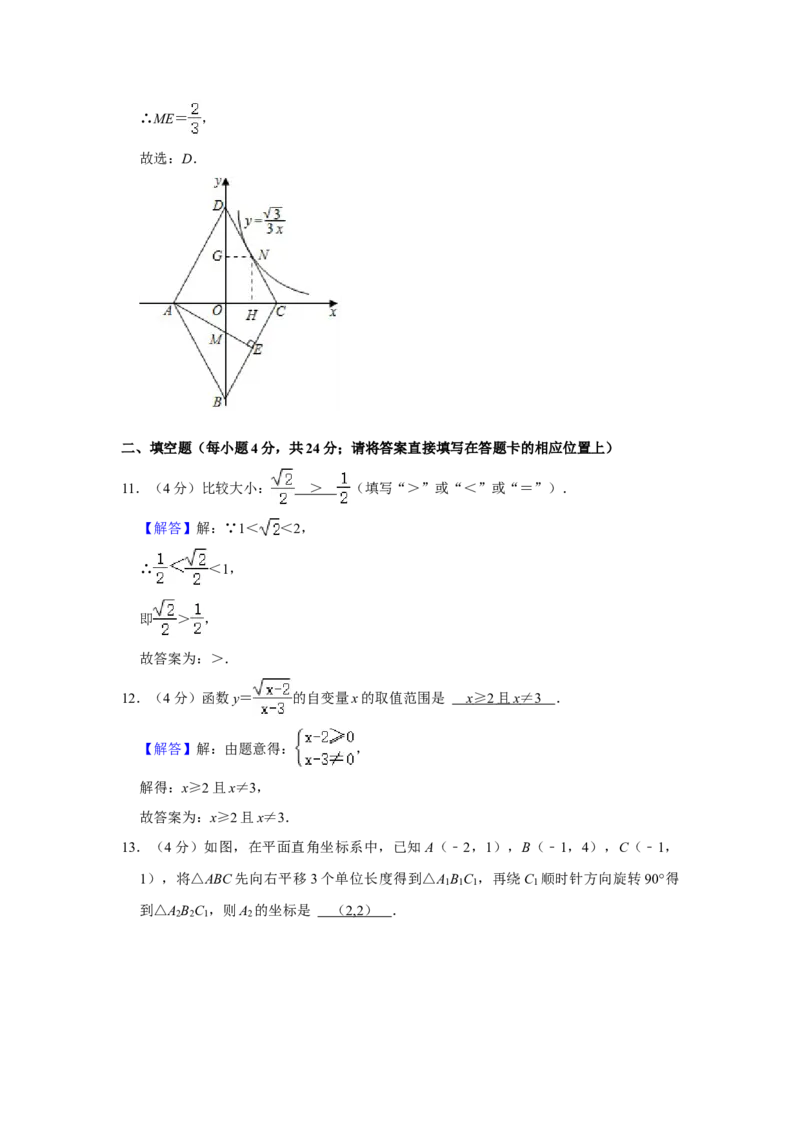
11.(4分)比较大小: (填写“>”或“<”或“=”).
12.(4分)函数y= 的自变量x的取值范围是 .
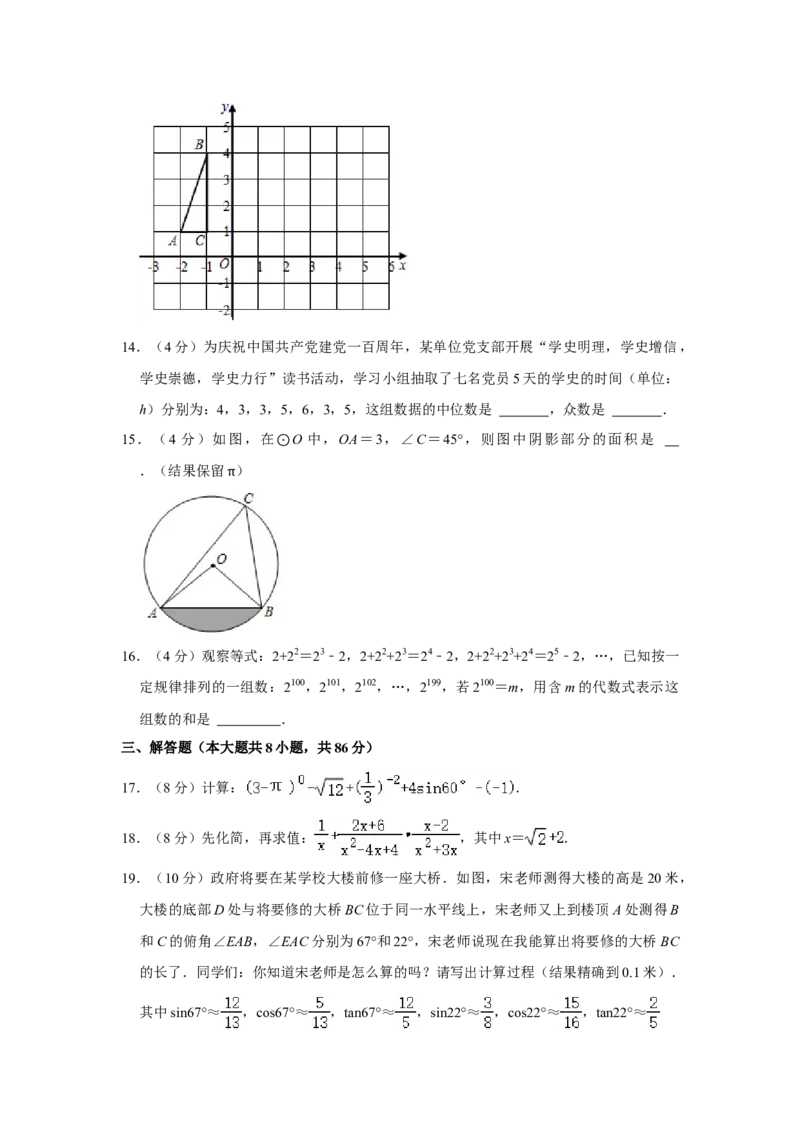
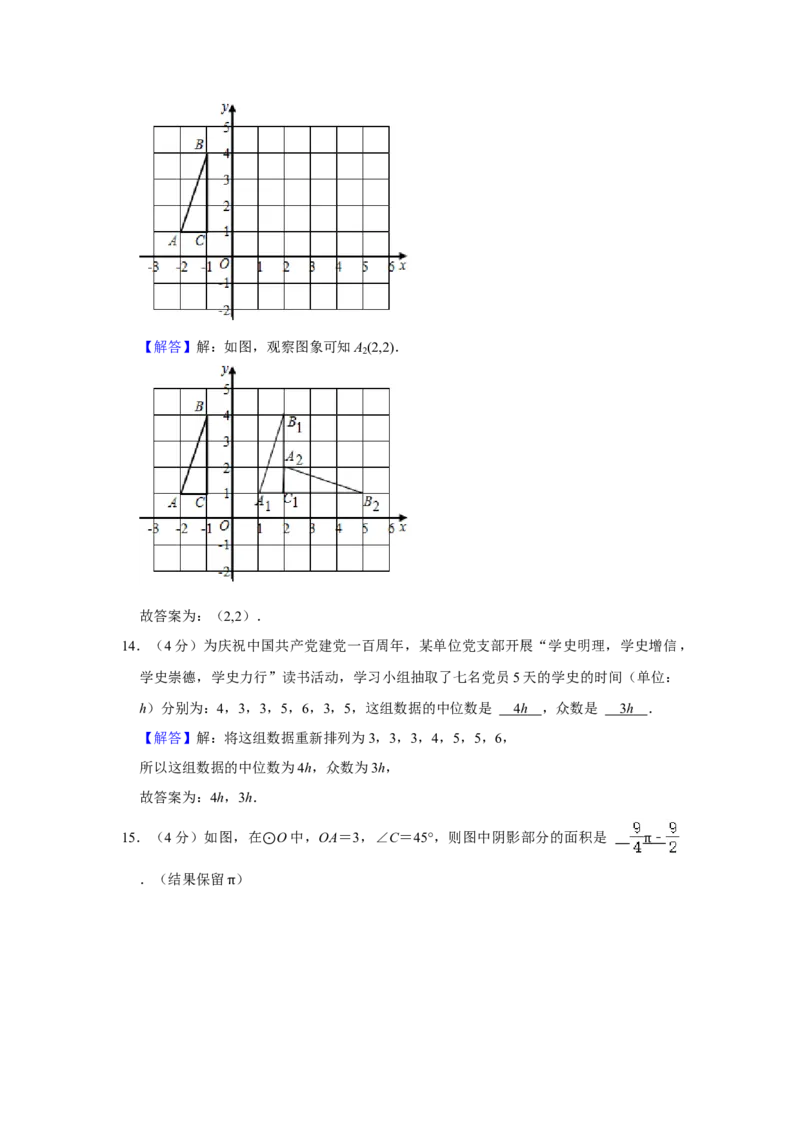
13.(4分)如图,在平面直角坐标系中,已知A(﹣2,1),B(﹣1,4),C(﹣1,
1),将△ABC先向右平移3个单位长度得到△A B C ,再绕C 顺时针方向旋转90°得
1 1 1 1
到△A B C ,则A 的坐标是 .
2 2 1 214.(4分)为庆祝中国共产党建党一百周年,某单位党支部开展“学史明理,学史增信,
学史崇德,学史力行”读书活动,学习小组抽取了七名党员5天的学史的时间(单位:
h)分别为:4,3,3,5,6,3,5,这组数据的中位数是 ,众数是 .
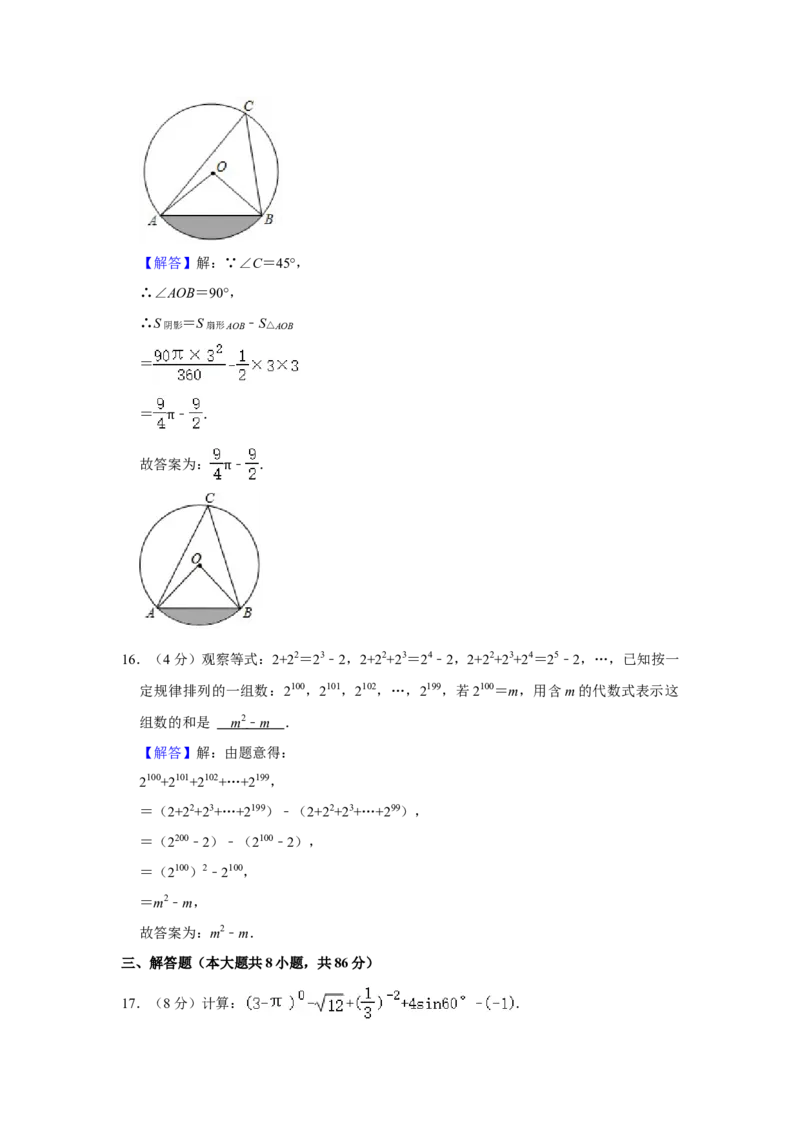
15.(4 分)如图,在 O 中,OA=3,∠C=45°,则图中阴影部分的面积是
.(结果保留 ) ⊙
π
16.(4分)观察等式:2+22=23﹣2,2+22+23=24﹣2,2+22+23+24=25﹣2,…,已知按一
定规律排列的一组数:2100,2101,2102,…,2199,若2100=m,用含m的代数式表示这
组数的和是 .
三、解答题(本大题共8小题,共86分)
17.(8分)计算: .
18.(8分)先化简,再求值: ,其中x= .
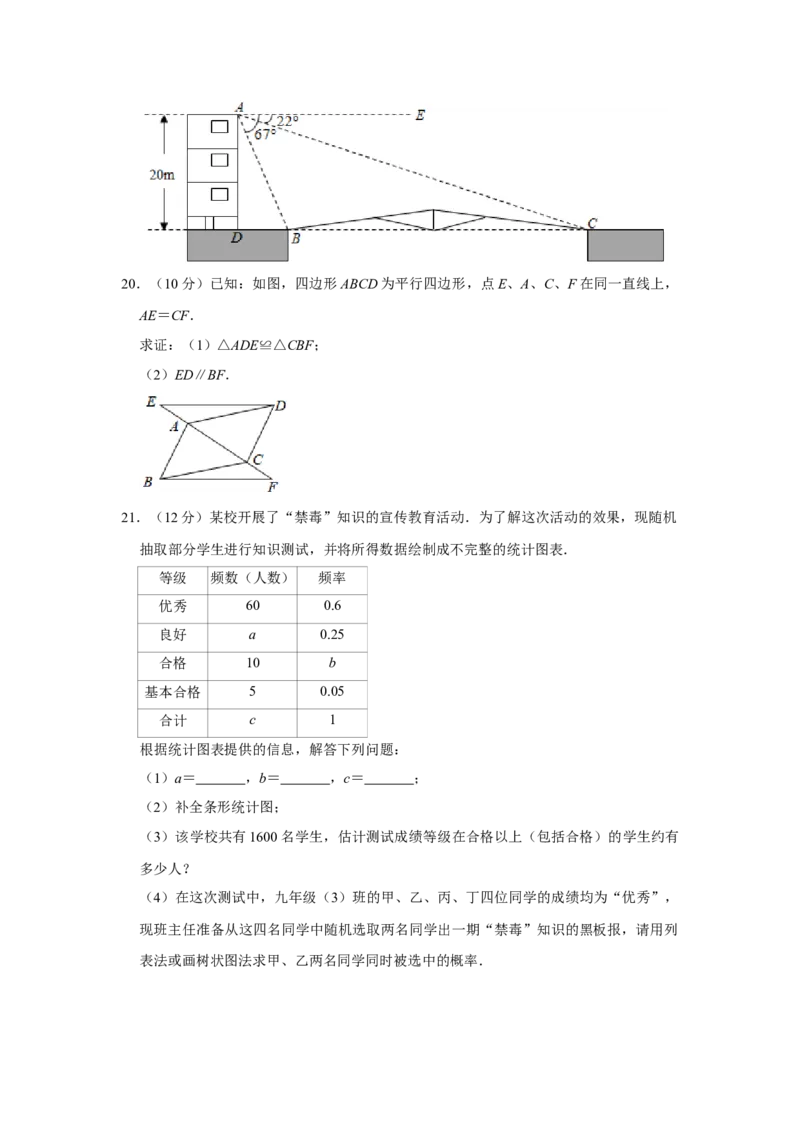
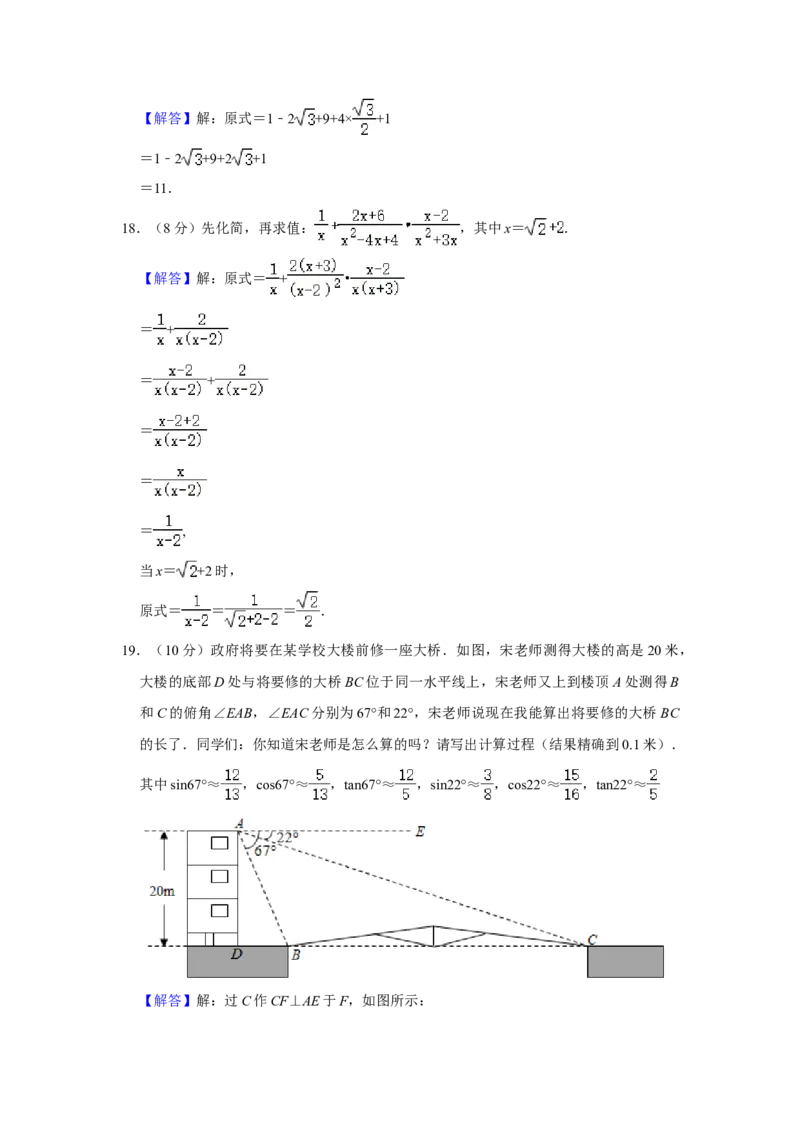
19.(10分)政府将要在某学校大楼前修一座大桥.如图,宋老师测得大楼的高是20米,
大楼的底部D处与将要修的大桥BC位于同一水平线上,宋老师又上到楼顶A处测得B
和C的俯角∠EAB,∠EAC分别为67°和22°,宋老师说现在我能算出将要修的大桥BC
的长了.同学们:你知道宋老师是怎么算的吗?请写出计算过程(结果精确到0.1米).
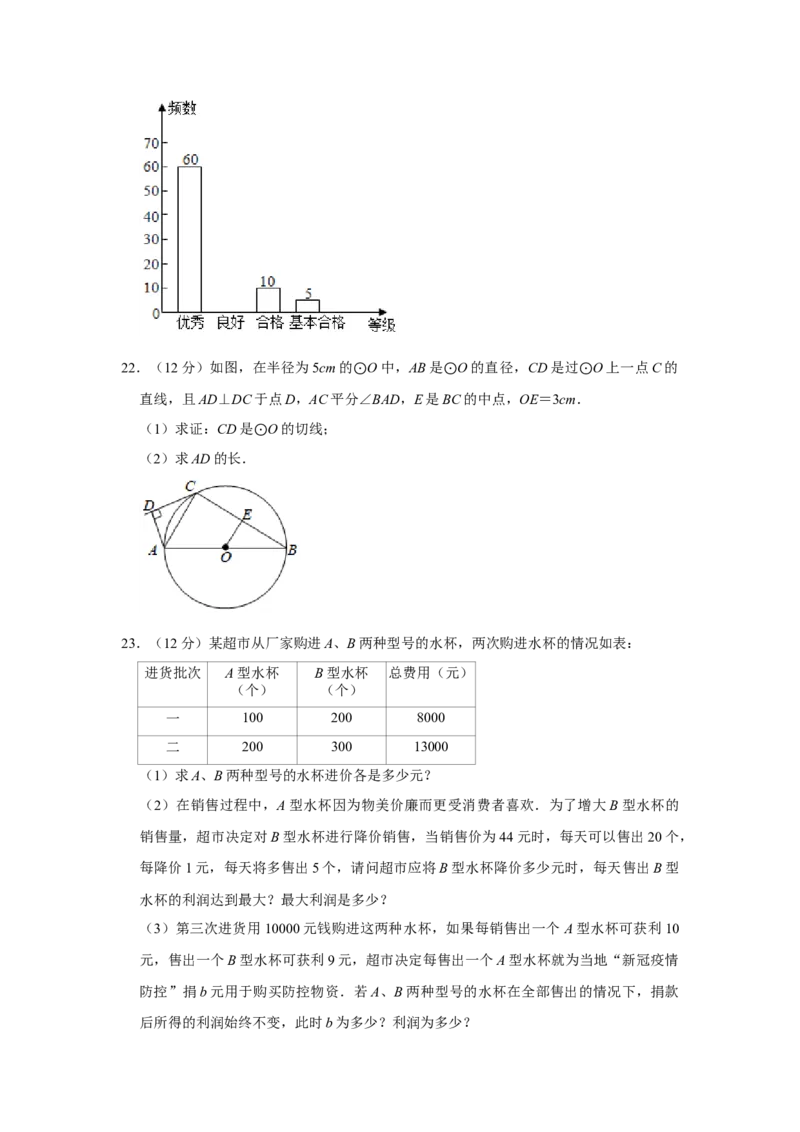
其中sin67°≈ ,cos67°≈ ,tan67°≈ ,sin22°≈ ,cos22°≈ ,tan22°≈20.(10分)已知:如图,四边形ABCD为平行四边形,点E、A、C、F在同一直线上,
AE=CF.
求证:(1)△ADE≌△CBF;
(2)ED∥BF.
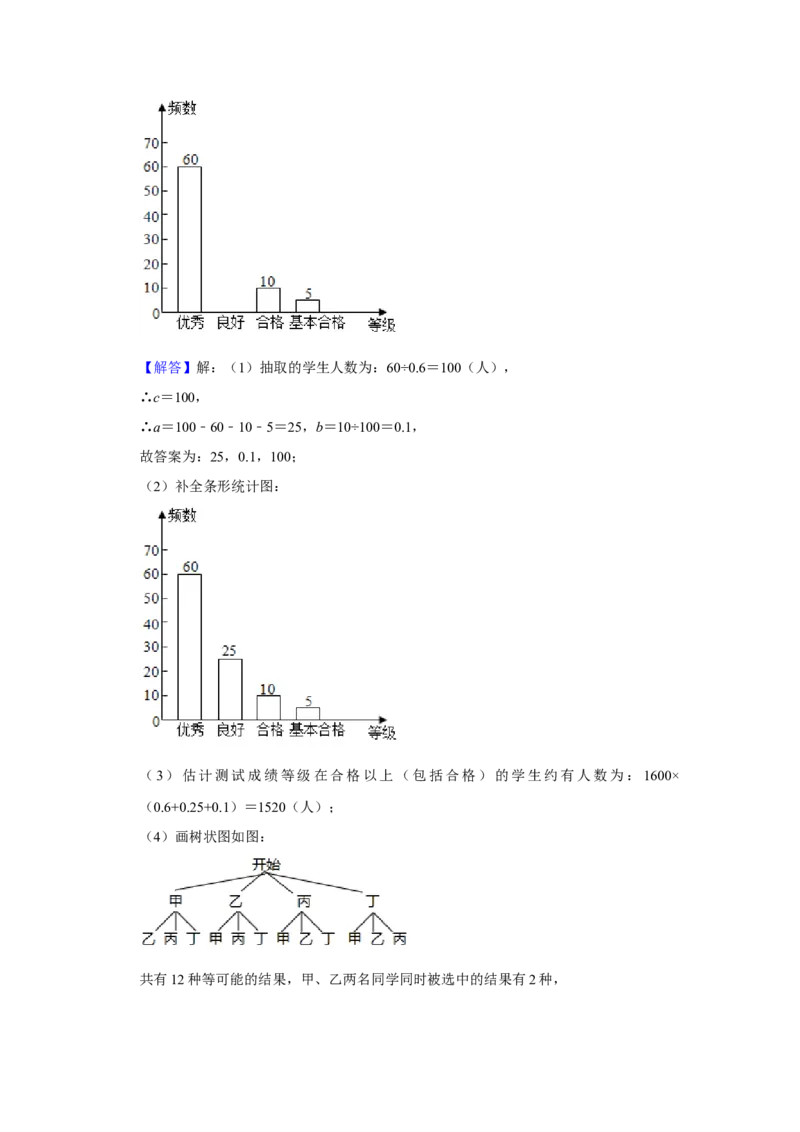
21.(12分)某校开展了“禁毒”知识的宣传教育活动.为了解这次活动的效果,现随机
抽取部分学生进行知识测试,并将所得数据绘制成不完整的统计图表.
等级 频数(人数) 频率
优秀 60 0.6
良好 a 0.25
合格 10 b
基本合格 5 0.05
合计 c 1
根据统计图表提供的信息,解答下列问题:
(1)a= ,b= ,c= ;
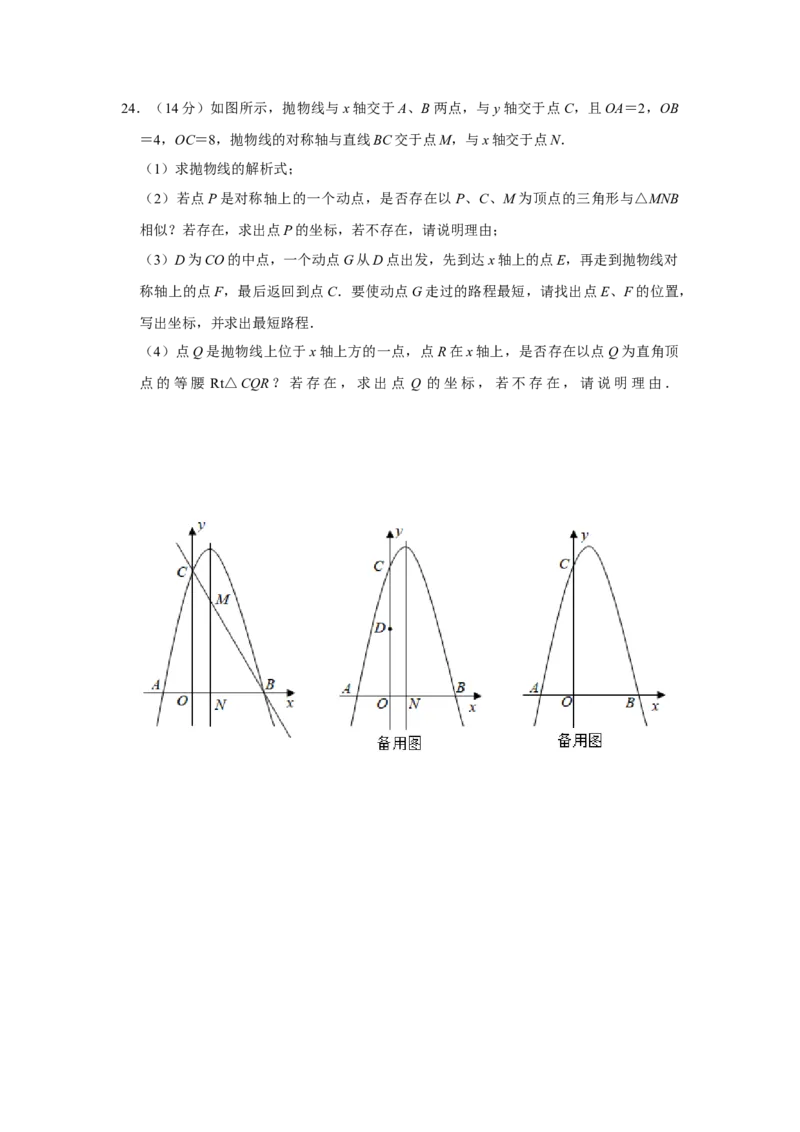
(2)补全条形统计图;
(3)该学校共有1600名学生,估计测试成绩等级在合格以上(包括合格)的学生约有
多少人?
(4)在这次测试中,九年级(3)班的甲、乙、丙、丁四位同学的成绩均为“优秀”,
现班主任准备从这四名同学中随机选取两名同学出一期“禁毒”知识的黑板报,请用列
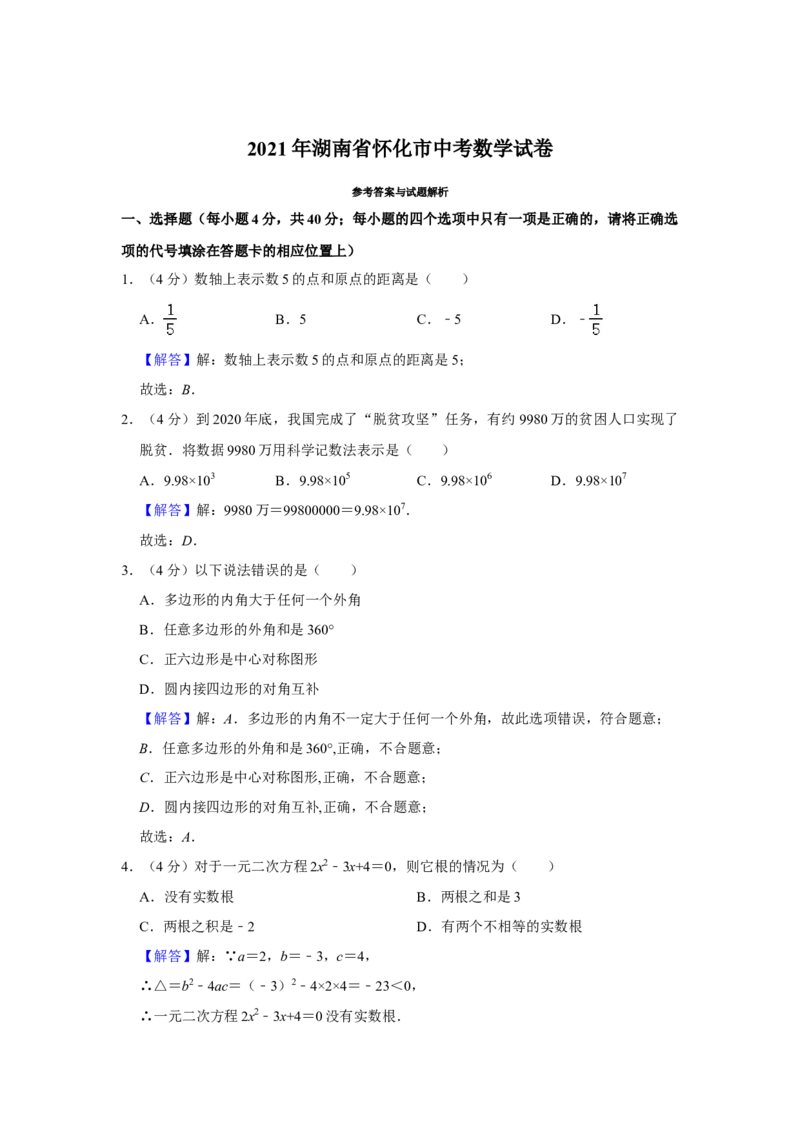
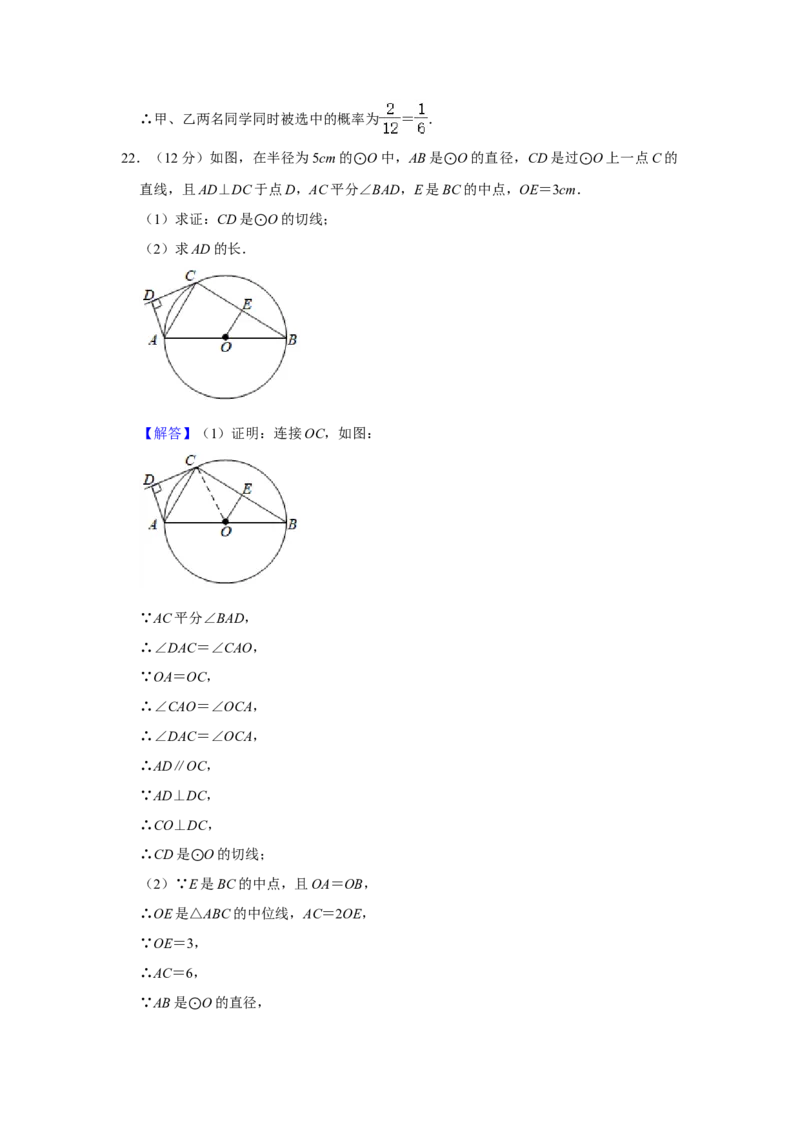
表法或画树状图法求甲、乙两名同学同时被选中的概率.22.(12分)如图,在半径为5cm的 O中,AB是 O的直径,CD是过 O上一点C的
直线,且AD⊥DC于点D,AC平分⊙∠BAD,E是B⊙C的中点,OE=3cm.⊙
(1)求证:CD是 O的切线;
(2)求AD的长.⊙
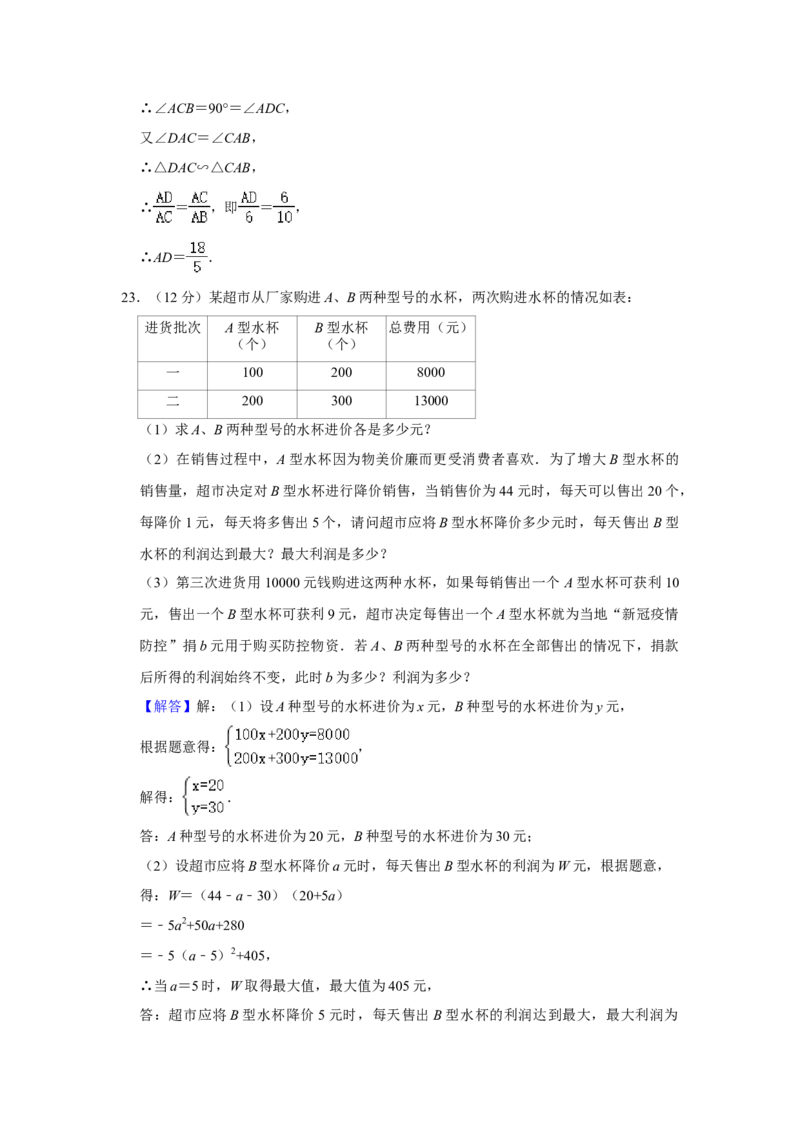
23.(12分)某超市从厂家购进A、B两种型号的水杯,两次购进水杯的情况如表:
进货批次 A型水杯 B型水杯 总费用(元)
(个) (个)
一 100 200 8000
二 200 300 13000
(1)求A、B两种型号的水杯进价各是多少元?
(2)在销售过程中,A型水杯因为物美价廉而更受消费者喜欢.为了增大B型水杯的
销售量,超市决定对B型水杯进行降价销售,当销售价为44元时,每天可以售出20个,
每降价1元,每天将多售出5个,请问超市应将B型水杯降价多少元时,每天售出B型
水杯的利润达到最大?最大利润是多少?
(3)第三次进货用10000元钱购进这两种水杯,如果每销售出一个 A型水杯可获利10
元,售出一个B型水杯可获利9元,超市决定每售出一个A型水杯就为当地“新冠疫情
防控”捐b元用于购买防控物资.若A、B两种型号的水杯在全部售出的情况下,捐款
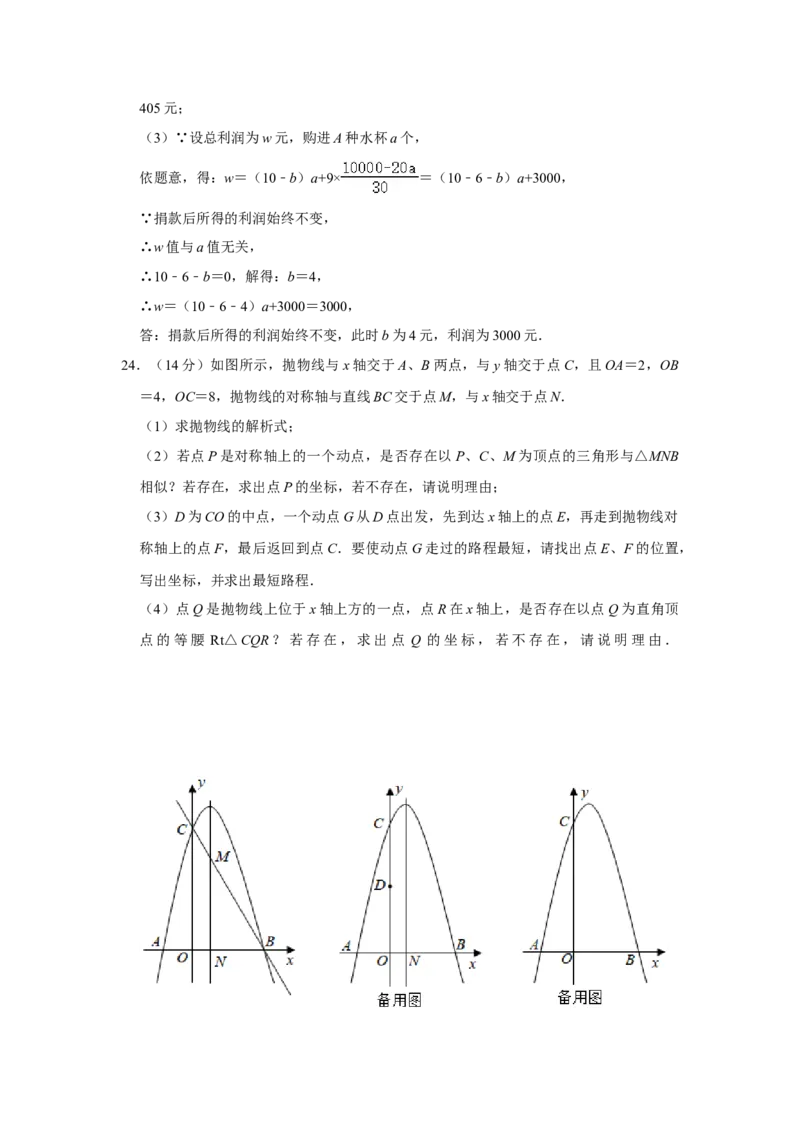
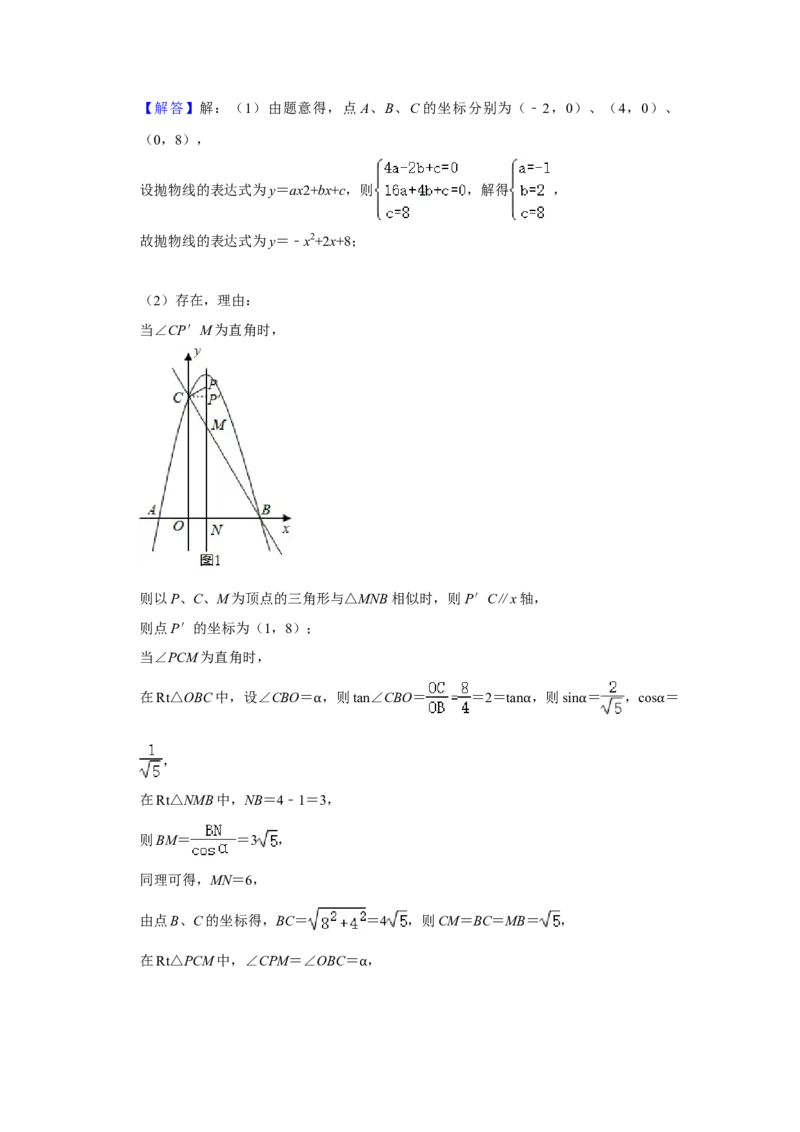
后所得的利润始终不变,此时b为多少?利润为多少?24.(14分)如图所示,抛物线与x轴交于A、B两点,与y轴交于点C,且OA=2,OB
=4,OC=8,抛物线的对称轴与直线BC交于点M,与x轴交于点N.
(1)求抛物线的解析式;
(2)若点P是对称轴上的一个动点,是否存在以P、C、M为顶点的三角形与△MNB
相似?若存在,求出点P的坐标,若不存在,请说明理由;
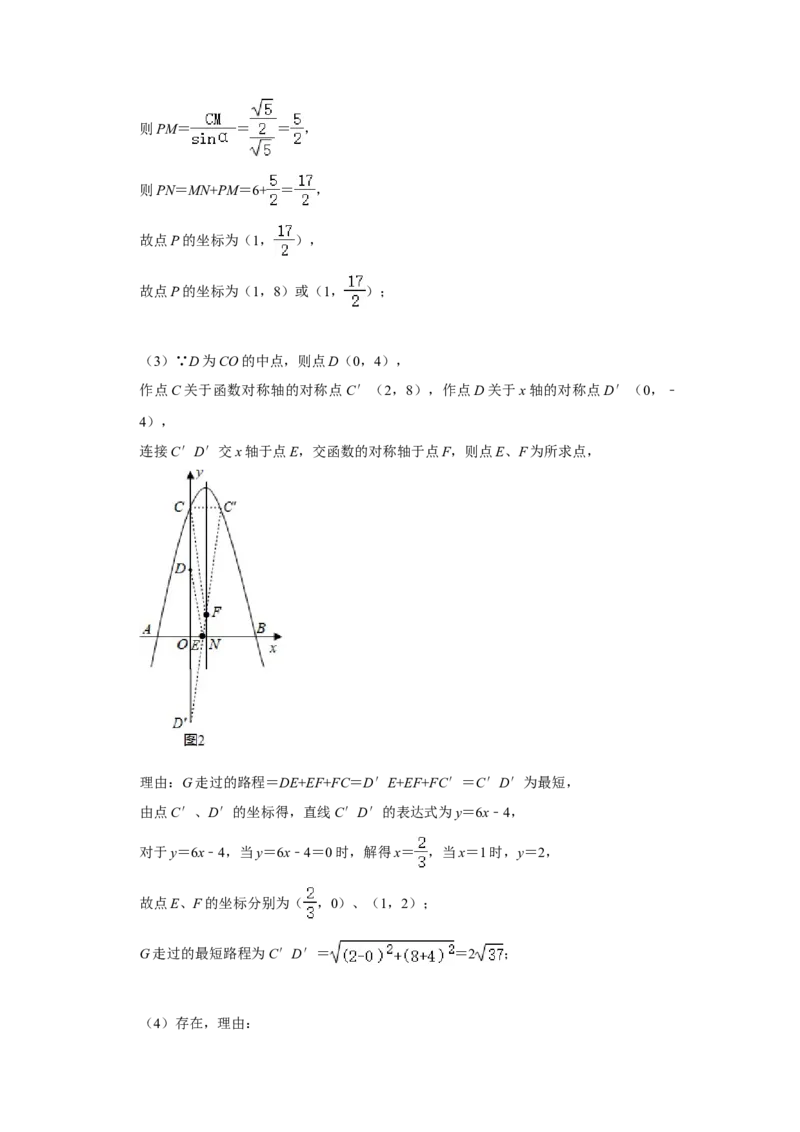
(3)D为CO的中点,一个动点G从D点出发,先到达x轴上的点E,再走到抛物线对
称轴上的点F,最后返回到点C.要使动点G走过的路程最短,请找出点E、F的位置,
写出坐标,并求出最短路程.
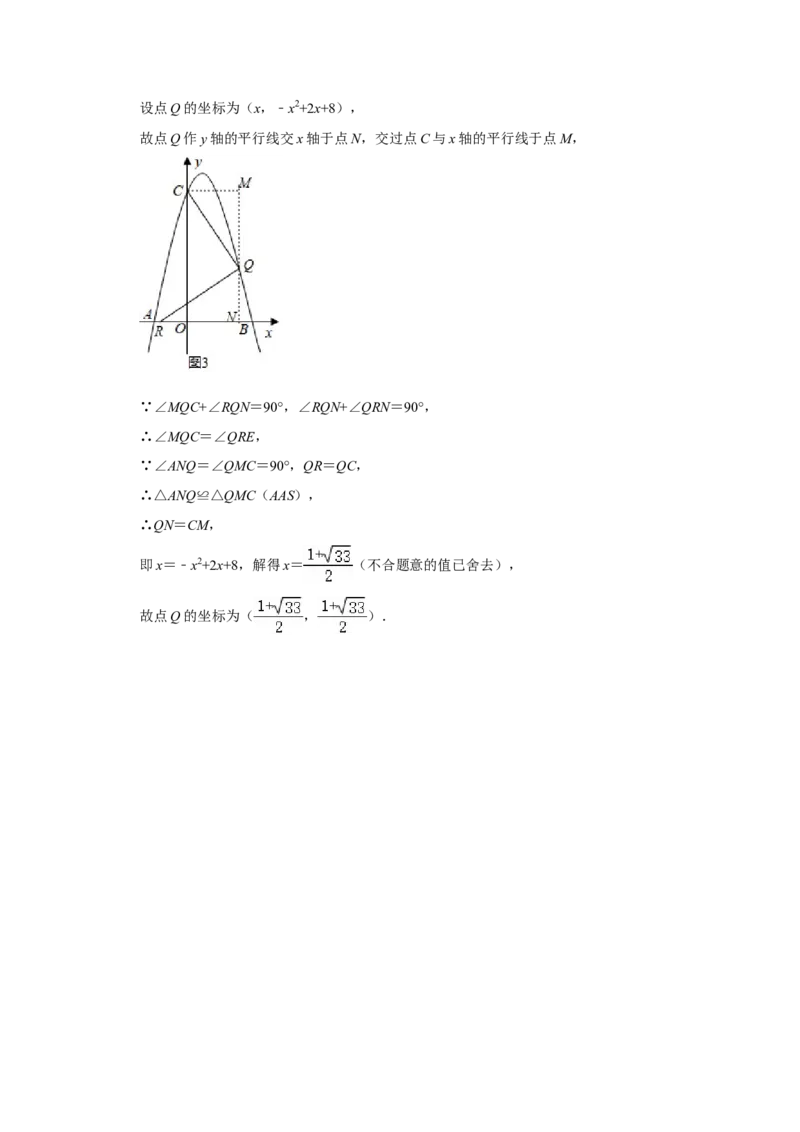
(4)点Q是抛物线上位于x轴上方的一点,点R在x轴上,是否存在以点Q为直角顶
点的等腰 Rt△CQR?若存在,求出点 Q 的坐标,若不存在,请说明理由.2021年湖南省怀化市中考数学试卷
参考答案与试题解析
一、选择题(每小题4分,共40分;每小题的四个选项中只有一项是正确的,请将正确选
项的代号填涂在答题卡的相应位置上)
1.(4分)数轴上表示数5的点和原点的距离是( )
A. B.5 C.﹣5 D.﹣
【解答】解:数轴上表示数5的点和原点的距离是5;
故选:B.
2.(4分)到2020年底,我国完成了“脱贫攻坚”任务,有约9980万的贫困人口实现了
脱贫.将数据9980万用科学记数法表示是( )
A.9.98×103 B.9.98×105 C.9.98×106 D.9.98×107
【解答】解:9980万=99800000=9.98×107.
故选:D.
3.(4分)以下说法错误的是( )
A.多边形的内角大于任何一个外角
B.任意多边形的外角和是360°
C.正六边形是中心对称图形
D.圆内接四边形的对角互补
【解答】解:A.多边形的内角不一定大于任何一个外角,故此选项错误,符合题意;
B.任意多边形的外角和是360°,正确,不合题意;
C.正六边形是中心对称图形,正确,不合题意;
D.圆内接四边形的对角互补,正确,不合题意;
故选:A.
4.(4分)对于一元二次方程2x2﹣3x+4=0,则它根的情况为( )
A.没有实数根 B.两根之和是3
C.两根之积是﹣2 D.有两个不相等的实数根
【解答】解:∵a=2,b=﹣3,c=4,
∴△=b2﹣4ac=(﹣3)2﹣4×2×4=﹣23<0,
∴一元二次方程2x2﹣3x+4=0没有实数根.故选:A.
5.(4分)下列图形中,可能是圆锥侧面展开图的是( )
A.
B.
C.
D.
【解答】解:圆锥的侧面展开图是扇形,
故选:B.
6.(4分)定义a b=2a+ ,则方程3 x=4 2的解为( )
⊗ ⊗ ⊗
A.x= B.x= C.x= D.x=
【解答】解:根据题中的新定义得:
3 x=2×3+ ,
⊗
4 2=2×4+ ,
⊗
∵3 x=4 2,
⊗ ⊗∴2×3+ =2×4+ ,
解得:x= ,
经检验,x= 是分式方程的根.
故选:B.
7.(4分)如图,在△ABC中,以A为圆心,任意长为半径画弧,分别交 AB、AC于点
M、N;再分别以M、N为圆心,大于 MN的长为半径画弧,两弧交于点P;连结AP
并延长交BC于点D.则下列说法正确的是( )
A.AD+BD<AB B.AD一定经过△ABC的重心
C.∠BAD=∠CAD D.AD一定经过△ABC的外心
【解答】解:由题可知AD是∠BAC的角平分线,
A、在△ABD中,AD+BD>AB,故选项A错误,不符合题意;
B、△ABC的重心是三条中线的交点,故选项B错误,不符合题意;
C、∵AD是∠BAC的角平分线,∴∠BAD=∠CAD,故选项C正确,符合题意;
D、△ABC的外心是三边中垂线的交点,故选项D错误,不符合题意;
故选:C.
8.(4分)不等式组 的解集表示在数轴上正确的是( )
A.
B.C.
D.
【解答】解:解不等式2x+1≥x﹣1,得:x≥﹣2,
解不等式﹣ x>﹣1,得:x<2,
则不等式组的解集为﹣2≤x<2,
故选:C.
9.(4分)“成语”是中华文化的瑰宝,是中华文化的微缩景观.下列成语:①“水中捞
月”,②“守株待兔”,③“百步穿杨”,④“瓮中捉鳖”描述的事件是不可能事件
的是( )
A.① B.② C.③ D.④
【解答】解:①“水中捞月”是不可能事件,符合题意;
②“守株待兔”是随机事件,不合题意;
③“百步穿杨”,是随机事件,不合题意;
④“瓮中捉鳖”是必然事件,不合题意;
故选:A.
10.(4分)如图,菱形ABCD的四个顶点均在坐标轴上,对角线AC、BD交于原点O,
AE⊥BC于E点,交BD于M点,反比例函数y= (x>0)的图象经过线段DC的中
点N,若BD=4,则ME的长为( )A.ME= B.ME= C.ME=1 D.ME=
【解答】解:过N作y轴和x轴的垂线NG,NH,
设N(b,a),
∵反比例函数y= (x>0)的图象经过点N,
∴ab= ,
∵四边形ABCD是菱形,
∴BD⊥AC,DO= BD=2,
∵NH⊥x轴,NG⊥y轴,
∴四边形NGOH是矩形,
∴NG∥x轴,NH∥y轴,
∵N为CD的中点,
∴DO•CO=2a•2b=4ab= ,
∴CO= ,
∴tan∠CDO= = .
∴∠CDO=30°,
∴∠DCO=60°,
∵四边形ABCD是菱形,
∴∠ADC=∠ABC=2∠CDO=60°,∠ACB=∠DCO=60°,
∴△ABC是等边三角形,
∵AE⊥BC,BO⊥AC,
∴AE=BO=2,∠BAE=30°=∠ABO,
∴AM=BM,
∴OM=EM,
∵∠MBE=30°,
∴BM=2EM=2OM,
∴3EM=OB=2,∴ME= ,
故选:D.
二、填空题(每小题4分,共24分;请将答案直接填写在答题卡的相应位置上)
11.(4分)比较大小: > (填写“>”或“<”或“=”).
【解答】解:∵1< <2,
∴ <1,
即 > ,
故答案为:>.
12.(4分)函数y= 的自变量x的取值范围是 x ≥ 2 且 x ≠ 3 .
【解答】解:由题意得: ,
解得:x≥2且x≠3,
故答案为:x≥2且x≠3.
13.(4分)如图,在平面直角坐标系中,已知A(﹣2,1),B(﹣1,4),C(﹣1,
1),将△ABC先向右平移3个单位长度得到△A B C ,再绕C 顺时针方向旋转90°得
1 1 1 1
到△A B C ,则A 的坐标是 ( 2, 2 ) .
2 2 1 2【解答】解:如图,观察图象可知A (2,2).
2
故答案为:(2,2).
14.(4分)为庆祝中国共产党建党一百周年,某单位党支部开展“学史明理,学史增信,
学史崇德,学史力行”读书活动,学习小组抽取了七名党员5天的学史的时间(单位:
h)分别为:4,3,3,5,6,3,5,这组数据的中位数是 4 h ,众数是 3 h .
【解答】解:将这组数据重新排列为3,3,3,4,5,5,6,
所以这组数据的中位数为4h,众数为3h,
故答案为:4h,3h.
15.(4分)如图,在 O中,OA=3,∠C=45°,则图中阴影部分的面积是 ﹣
⊙ π
.(结果保留 )
π【解答】解:∵∠C=45°,
∴∠AOB=90°,
∴S阴影 =S扇形AOB ﹣S△AOB
=
= ﹣ .
π
故答案为: ﹣ .
π
16.(4分)观察等式:2+22=23﹣2,2+22+23=24﹣2,2+22+23+24=25﹣2,…,已知按一
定规律排列的一组数:2100,2101,2102,…,2199,若2100=m,用含m的代数式表示这
组数的和是 m 2 ﹣ m .
【解答】解:由题意得:
2100+2101+2102+…+2199,
=(2+22+23+…+2199)﹣(2+22+23+…+299),
=(2200﹣2)﹣(2100﹣2),
=(2100)2﹣2100,
=m2﹣m,
故答案为:m2﹣m.
三、解答题(本大题共8小题,共86分)
17.(8分)计算: .【解答】解:原式=1﹣2 +9+4× +1
=1﹣2 +9+2 +1
=11.
18.(8分)先化简,再求值: ,其中x= .
【解答】解:原式= + •
= +
= +
=
=
= ,
当x= +2时,
原式= = = .
19.(10分)政府将要在某学校大楼前修一座大桥.如图,宋老师测得大楼的高是20米,
大楼的底部D处与将要修的大桥BC位于同一水平线上,宋老师又上到楼顶A处测得B
和C的俯角∠EAB,∠EAC分别为67°和22°,宋老师说现在我能算出将要修的大桥BC
的长了.同学们:你知道宋老师是怎么算的吗?请写出计算过程(结果精确到0.1米).
其中sin67°≈ ,cos67°≈ ,tan67°≈ ,sin22°≈ ,cos22°≈ ,tan22°≈
【解答】解:过C作CF⊥AE于F,如图所示:则FC=AD=20米,AF=DC,
在Rt△ACF中,∠EAC=22°,
∵tan∠EAC= =tan22°≈ ,
∴DC=AF≈ FC=50(米),
在Rt△ABD中,∠ABD=∠EAB=67°,
∵tan∠ABD= =tan22°≈ ,
∴BD≈ AD= (米),
∴BC=DC﹣BD=50﹣ ≈41.7(米),
即大桥BC的长约为41.7米.
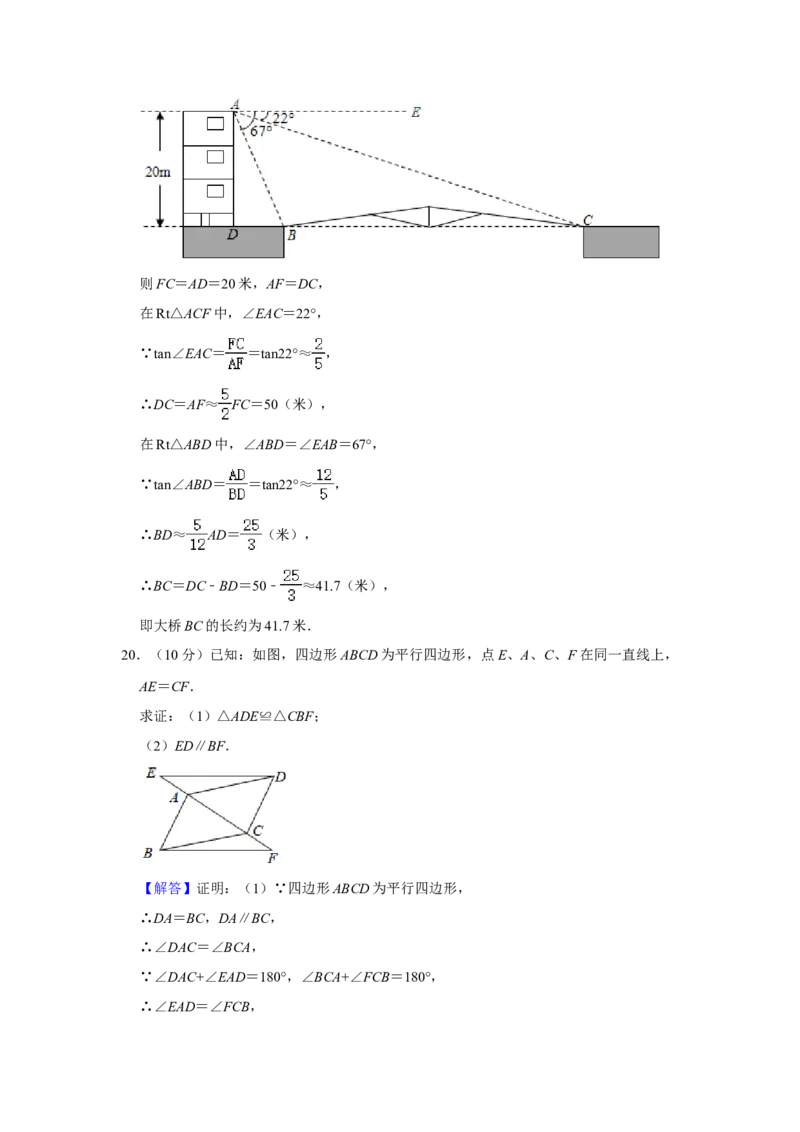
20.(10分)已知:如图,四边形ABCD为平行四边形,点E、A、C、F在同一直线上,
AE=CF.
求证:(1)△ADE≌△CBF;
(2)ED∥BF.
【解答】证明:(1)∵四边形ABCD为平行四边形,
∴DA=BC,DA∥BC,
∴∠DAC=∠BCA,
∵∠DAC+∠EAD=180°,∠BCA+∠FCB=180°,
∴∠EAD=∠FCB,在△ADE和△CBF中,
,
∴△ADE≌△CBF(SAS);
(2)由(1)知,△ADE≌△CBF,
∴∠E=∠F,
∴ED∥BF.
21.(12分)某校开展了“禁毒”知识的宣传教育活动.为了解这次活动的效果,现随机
抽取部分学生进行知识测试,并将所得数据绘制成不完整的统计图表.
等级 频数(人数) 频率
优秀 60 0.6
良好 a 0.25
合格 10 b
基本合格 5 0.05
合计 c 1
根据统计图表提供的信息,解答下列问题:
(1)a= 2 5 ,b= 0. 1 ,c= 10 0 ;
(2)补全条形统计图;
(3)该学校共有1600名学生,估计测试成绩等级在合格以上(包括合格)的学生约有
多少人?
(4)在这次测试中,九年级(3)班的甲、乙、丙、丁四位同学的成绩均为“优秀”,
现班主任准备从这四名同学中随机选取两名同学出一期“禁毒”知识的黑板报,请用列
表法或画树状图法求甲、乙两名同学同时被选中的概率.【解答】解:(1)抽取的学生人数为:60÷0.6=100(人),
∴c=100,
∴a=100﹣60﹣10﹣5=25,b=10÷100=0.1,
故答案为:25,0.1,100;
(2)补全条形统计图:
(3)估计测试成绩等级在合格以上(包括合格)的学生约有人数为:1600×
(0.6+0.25+0.1)=1520(人);
(4)画树状图如图:
共有12种等可能的结果,甲、乙两名同学同时被选中的结果有2种,∴甲、乙两名同学同时被选中的概率为 = .
22.(12分)如图,在半径为5cm的 O中,AB是 O的直径,CD是过 O上一点C的
直线,且AD⊥DC于点D,AC平分⊙∠BAD,E是B⊙C的中点,OE=3cm.⊙
(1)求证:CD是 O的切线;
(2)求AD的长.⊙
【解答】(1)证明:连接OC,如图:
∵AC平分∠BAD,
∴∠DAC=∠CAO,
∵OA=OC,
∴∠CAO=∠OCA,
∴∠DAC=∠OCA,
∴AD∥OC,
∵AD⊥DC,
∴CO⊥DC,
∴CD是 O的切线;
(2)∵E⊙是BC的中点,且OA=OB,
∴OE是△ABC的中位线,AC=2OE,
∵OE=3,
∴AC=6,
∵AB是 O的直径,
⊙∴∠ACB=90°=∠ADC,
又∠DAC=∠CAB,
∴△DAC∽△CAB,
∴ = ,即 = ,
∴AD= .
23.(12分)某超市从厂家购进A、B两种型号的水杯,两次购进水杯的情况如表:
进货批次 A型水杯 B型水杯 总费用(元)
(个) (个)
一 100 200 8000
二 200 300 13000
(1)求A、B两种型号的水杯进价各是多少元?
(2)在销售过程中,A型水杯因为物美价廉而更受消费者喜欢.为了增大B型水杯的
销售量,超市决定对B型水杯进行降价销售,当销售价为44元时,每天可以售出20个,
每降价1元,每天将多售出5个,请问超市应将B型水杯降价多少元时,每天售出B型
水杯的利润达到最大?最大利润是多少?
(3)第三次进货用10000元钱购进这两种水杯,如果每销售出一个 A型水杯可获利10
元,售出一个B型水杯可获利9元,超市决定每售出一个A型水杯就为当地“新冠疫情
防控”捐b元用于购买防控物资.若A、B两种型号的水杯在全部售出的情况下,捐款
后所得的利润始终不变,此时b为多少?利润为多少?
【解答】解:(1)设A种型号的水杯进价为x元,B种型号的水杯进价为y元,
根据题意得: ,
解得: .
答:A种型号的水杯进价为20元,B种型号的水杯进价为30元;
(2)设超市应将B型水杯降价a元时,每天售出B型水杯的利润为W元,根据题意,
得:W=(44﹣a﹣30)(20+5a)
=﹣5a2+50a+280
=﹣5(a﹣5)2+405,
∴当a=5时,W取得最大值,最大值为405元,
答:超市应将B型水杯降价5元时,每天售出B型水杯的利润达到最大,最大利润为405元;
(3)∵设总利润为w元,购进A种水杯a个,
依题意,得:w=(10﹣b)a+9× =(10﹣6﹣b)a+3000,
∵捐款后所得的利润始终不变,
∴w值与a值无关,
∴10﹣6﹣b=0,解得:b=4,
∴w=(10﹣6﹣4)a+3000=3000,
答:捐款后所得的利润始终不变,此时b为4元,利润为3000元.
24.(14分)如图所示,抛物线与x轴交于A、B两点,与y轴交于点C,且OA=2,OB
=4,OC=8,抛物线的对称轴与直线BC交于点M,与x轴交于点N.
(1)求抛物线的解析式;
(2)若点P是对称轴上的一个动点,是否存在以P、C、M为顶点的三角形与△MNB
相似?若存在,求出点P的坐标,若不存在,请说明理由;
(3)D为CO的中点,一个动点G从D点出发,先到达x轴上的点E,再走到抛物线对
称轴上的点F,最后返回到点C.要使动点G走过的路程最短,请找出点E、F的位置,
写出坐标,并求出最短路程.
(4)点Q是抛物线上位于x轴上方的一点,点R在x轴上,是否存在以点Q为直角顶
点的等腰 Rt△CQR?若存在,求出点 Q 的坐标,若不存在,请说明理由.【解答】解:(1)由题意得,点A、B、C的坐标分别为(﹣2,0)、(4,0)、
(0,8),
设抛物线的表达式为y=ax2+bx+c,则 ,解得 ,
故抛物线的表达式为y=﹣x2+2x+8;
(2)存在,理由:
当∠CP′M为直角时,
则以P、C、M为顶点的三角形与△MNB相似时,则P′C∥x轴,
则点P′的坐标为(1,8);
当∠PCM为直角时,
在Rt△OBC中,设∠CBO= ,则tan∠CBO= =2=tan ,则sin = ,cos =
α α α α
,
在Rt△NMB中,NB=4﹣1=3,
则BM= =3 ,
同理可得,MN=6,
由点B、C的坐标得,BC= =4 ,则CM=BC=MB= ,
在Rt△PCM中,∠CPM=∠OBC= ,
α则PM= = = ,
则PN=MN+PM=6+ = ,
故点P的坐标为(1, ),
故点P的坐标为(1,8)或(1, );
(3)∵D为CO的中点,则点D(0,4),
作点C关于函数对称轴的对称点C′(2,8),作点D关于x轴的对称点D′(0,﹣
4),
连接C′D′交x轴于点E,交函数的对称轴于点F,则点E、F为所求点,
理由:G走过的路程=DE+EF+FC=D′E+EF+FC′=C′D′为最短,
由点C′、D′的坐标得,直线C′D′的表达式为y=6x﹣4,
对于y=6x﹣4,当y=6x﹣4=0时,解得x= ,当x=1时,y=2,
故点E、F的坐标分别为( ,0)、(1,2);
G走过的最短路程为C′D′= =2 ;
(4)存在,理由:设点Q的坐标为(x,﹣x2+2x+8),
故点Q作y轴的平行线交x轴于点N,交过点C与x轴的平行线于点M,
∵∠MQC+∠RQN=90°,∠RQN+∠QRN=90°,
∴∠MQC=∠QRE,
∵∠ANQ=∠QMC=90°,QR=QC,
∴△ANQ≌△QMC(AAS),
∴QN=CM,
即x=﹣x2+2x+8,解得x= (不合题意的值已舍去),
故点Q的坐标为( , ).
声明:试题解析著作权属菁优网所有,未经书面同意,不得复制发布
日期:2021/6/25 7:42:57;用户:柯瑞;邮箱:ainixiaoke00@163.com;学号:500557