文档内容
【淘宝:中小学教辅资源店 微信:mlxt2022】
宜宾市2022年初中学业水平考试暨高中阶段学校招生考试
数学
一、选择题:本大题共12个小题,每小题4分,共48分.在每小题给出的四个选项中,
只有一项是符合题目要求的,请将正确选项填涂在答题卡对应题目上.
1.4的平方根是( )
A.2 B. C. D.16
2.如图是由5个相同的正方体搭成的几何体,从正面看,所看到的图形是( )
A. B. C. D.
3.下列计算不正确的是( )
A. B. C. D.
4.某校在中国共产主义青年团成立100周年之际,举行了歌咏比赛,七位评委对某个选手
的打分分别为:91,88,95,93,97,95,94.这组数据的众数和中位数分别是( )
A.94,94 B.95,95 C.94,95 D.95,94
5.如图,在 中, ,D是BC上的点, 交AC于点E,
交AB于点F,那么四边形AEDF的周长是( )
A.5 B.10 C.15 D.20
6.2020年12月17日,我国嫦娥五号返回器携带着月球样本玄武岩成功着陆地球.2021
年10月19日,中国科学院发布了一项研究成果:中国科学家测定,嫦娥五号带回的玄武
岩形成的年龄为 亿年.用科学记数法表示此玄武岩形成的年龄最小的为(
)(单位:年)
A. B. C. D.
7.某家具厂要在开学前赶制540套桌凳,为了尽快完成任务,厂领导合理调配,加强第一
线人力,使每天完成的桌凳比原计划多2套,结果提前3天完成任务.问原计划每天完成
多少套桌凳?设原计划每天完成x套桌凳,则所列方程正确的是( )
A. B. C. D.【淘宝:中小学教辅资源店 微信:mlxt2022】
8.若关于x的一元二次方程 有两个不相等的实数根,则a的取值范围是(
)
A. B. 且 C. 且 D.
9.如图,在矩形纸片ABCD中, , ,将 沿BD折叠到 位置,
DE交AB于点F,则 的值为( )
A. B. C. D.
10.已知m、n是一元二次方程 的两个根,则 的值为
( )
A.0 B.-10 C.3 D.10
11.已知抛物线 的图象与x轴交于点 、 ,若以AB为直
径的圆与在x轴下方的抛物线有交点,则a的取值范围是( )
A. B. C. D.
12.如图, 和 都是等腰直角三角形, ,点D是BC
边上的动点(不与点B、C重合),DE与AC交于点F,连结CE.下列结论:①
;② ;③若 ,则 ;④在 内存在唯
一一点P,使得 的值最小,若点D在AP的延长线上,且AP的长为2,则
.其中含所有正确结论的选项是( )
A.①②④ B.①②③ C.①③④ D.①②③④
二、填空题:本大题共6个小题,每小题4分,共24分.请把答案直接填在答题卡对应题
中横线上.
13.分解因式: ______.【淘宝:中小学教辅资源店 微信:mlxt2022】
14.不等式组 的解集为______.
15.如图, 中,点E、F分别在边AB、AC上, .若 , ,
,则 ______.
16.《数学九章》是中国南宋时期杰出数学家秦九韶的著作,书中提出了已知三角形三边
a、b、c求面积的公式,其求法是:“以小斜幂并大斜幂减中斜幂,余半之,自乘于上,
以小斜幂乘大斜幂减上,余四约之,为实.一为从隅,开平方得积.”若把以上这段文字
写成公式,即为 .现有周长为18的三角形的三边满足
,则用以上给出的公式求得这个三角形的面积为______.
17.我国古代数学家赵爽的“弦图”是由四个全等的直角三角形和一个小正方形拼成的一
个大正方形(如图所示).若直角三角形的内切圆半径为3,小正方形的面积为49,则大
正方形的面积为______.
18.如图, 是边长为10的等边三角形,反比例函数 的图象与边
MN、OM分别交于点A、B(点B不与点M重合).若 于点B,则k的值为
______.
三、解答题:本大题共7个小题,共78分.解答应写出文字说明、证明过程或演算步骤.【淘宝:中小学教辅资源店 微信:mlxt2022】
19.(本题满分10分)
计算:
(1) ;
(2) .
20.(本题满分10分)
已知:如图,点A、D、C、F在同一直线上, , , .
求证: .
21.(本题满分10分)
在4月23日世界读书日来临之际,为了解某校九年级(1)班同学们的阅读爱好,要求所
有同学从4类书籍中(A:文学类;B:科幻类;C:军事类;D:其他类),选择一类自
己最喜欢的书籍进行统计.根据统计结果,绘制了如图所示的两幅不完整的统计图.根据
图中信息回答问题:
(1)求九年级(1)班的人数并补全条形统计图;
(2)在扇形统计图中,求m的值;
(3)如果选择C类书籍的同学中有2名女同学,其余为男同学,现要在选择C类书籍的同
学中选取两名同学去参加读书交流活动,请你用画树状图或列表的方法求出恰好是一男一
女同学去参加读书交流活动的概率.
22.(本题满分10分)
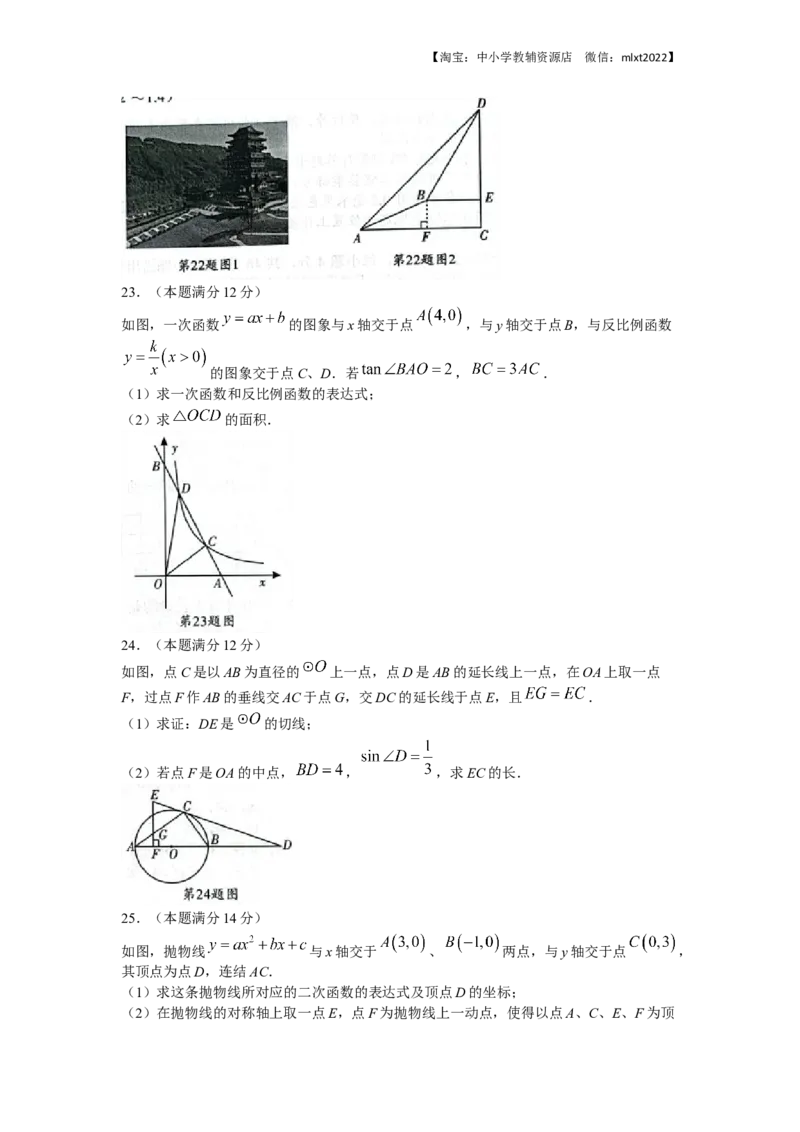
宜宾东楼始建于唐代,重建于宜宾建城2200周年之际的2018年,新建成的东楼(如图1)
成为长江首城会客厅、旅游休闲目的地、文化地标打卡地.某数学小组为测量东楼的高度,
在梯步A处(如图2)测得楼顶D的仰角为45°,沿坡比为7:24的斜坡AB前行25米到达
平台B处,测得楼顶D的仰角为60°,求东楼的高度DE.(结果精确到1米.参考数据:
, )【淘宝:中小学教辅资源店 微信:mlxt2022】
23.(本题满分12分)
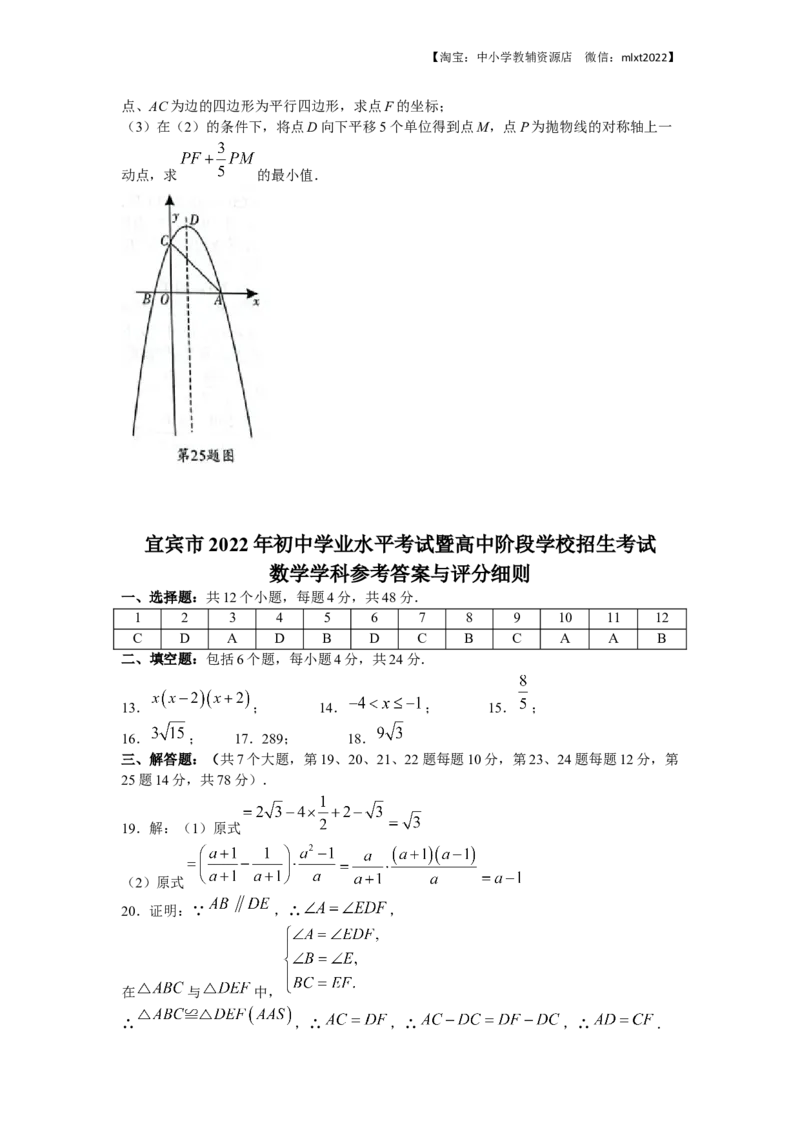
如图,一次函数 的图象与x轴交于点 ,与y轴交于点B,与反比例函数
的图象交于点C、D.若 , .
(1)求一次函数和反比例函数的表达式;
(2)求 的面积.
24.(本题满分12分)
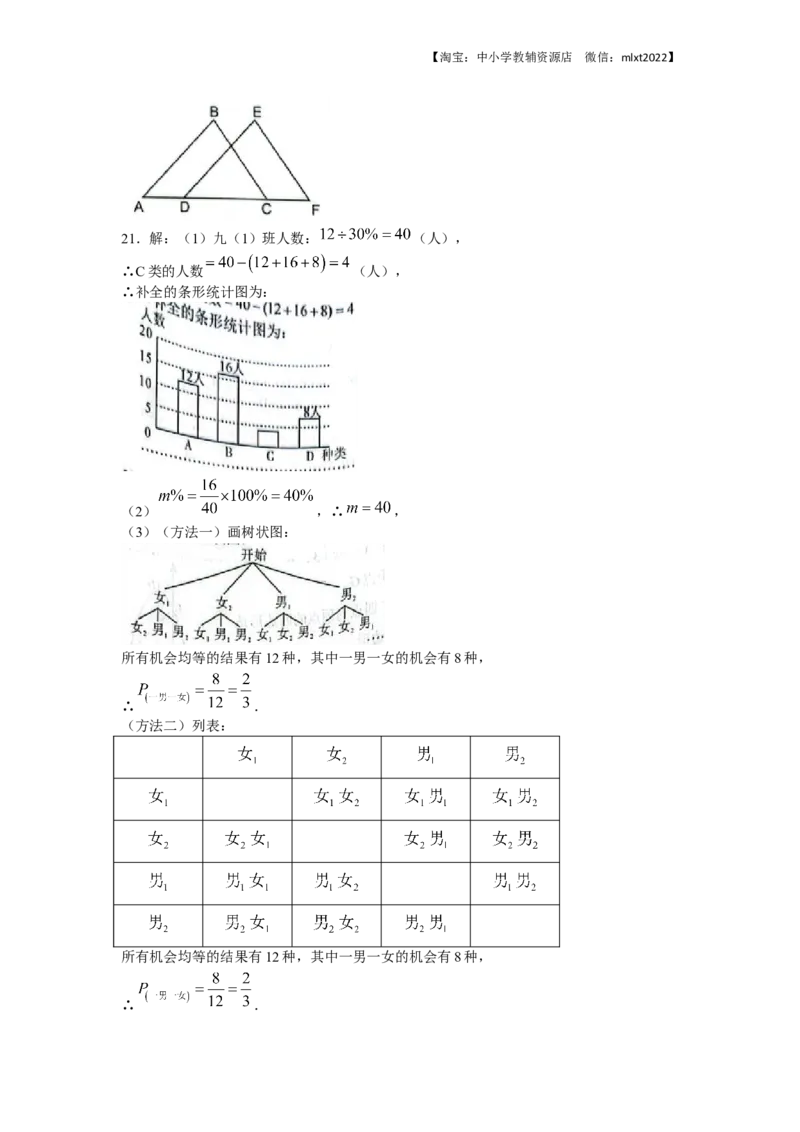
如图,点C是以AB为直径的 上一点,点D是AB的延长线上一点,在OA上取一点
F,过点F作AB的垂线交AC于点G,交DC的延长线于点E,且 .
(1)求证:DE是 的切线;
(2)若点F是OA的中点, , ,求EC的长.
25.(本题满分14分)
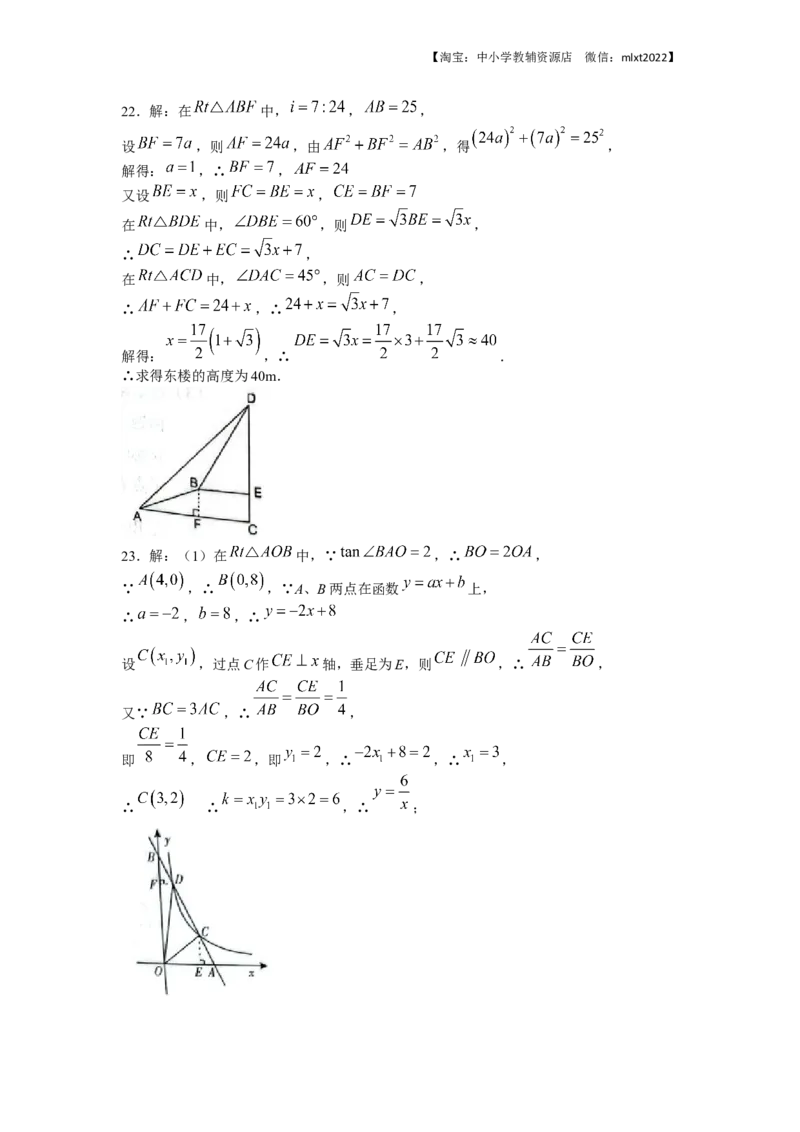
如图,抛物线 与x轴交于 、 两点,与y轴交于点 ,
其顶点为点D,连结AC.
(1)求这条抛物线所对应的二次函数的表达式及顶点D的坐标;
(2)在抛物线的对称轴上取一点E,点F为抛物线上一动点,使得以点A、C、E、F为顶【淘宝:中小学教辅资源店 微信:mlxt2022】
点、AC为边的四边形为平行四边形,求点F的坐标;
(3)在(2)的条件下,将点D向下平移5个单位得到点M,点P为抛物线的对称轴上一
动点,求 的最小值.
宜宾市2022年初中学业水平考试暨高中阶段学校招生考试
数学学科参考答案与评分细则
一、选择题:共12个小题,每题4分,共48分.
1 2 3 4 5 6 7 8 9 10 11 12
C D A D B D C B C A A B
二、填空题:包括6个题,每小题4分,共24分.
13. ; 14. ; 15. ;
16. ; 17.289; 18.
三、解答题:(共7个大题,第19、20、21、22题每题10分,第23、24题每题12分,第
25题14分,共78分).
19.解:(1)原式
(2)原式
20.证明:∵ ,∴ ,
在 与 中,
∴ ,∴ ,∴ ,∴ .【淘宝:中小学教辅资源店 微信:mlxt2022】
21.解:(1)九(1)班人数: (人),
∴C类的人数 (人),
∴补全的条形统计图为:
(2) ,∴ ,
(3)(方法一)画树状图:
所有机会均等的结果有12种,其中一男一女的机会有8种,
∴ .
(方法二)列表:
所有机会均等的结果有12种,其中一男一女的机会有8种,
∴ .【淘宝:中小学教辅资源店 微信:mlxt2022】
22.解:在 中, , ,
设 ,则 ,由 ,得 ,
解得: ,∴ ,
又设 ,则 ,
在 中, ,则 ,
∴ ,
在 中, ,则 ,
∴ ,∴ ,
解得: ,∴ .
∴求得东楼的高度为40m.
23.解:(1)在 中,∵ ,∴ ,
∵ ,∴ ,∵A、B两点在函数 上,
∴ , ,∴
设 ,过点C作 轴,垂足为E,则 ,∴ ,
又∵ ,∴ ,
即 , ,即 ,∴ ,∴ ,
∴ ∴ ,∴ ;【淘宝:中小学教辅资源店 微信:mlxt2022】
(2)解方程组 ,得 ,
∴ ,
过D作 轴,垂足为点
∵
∴
.
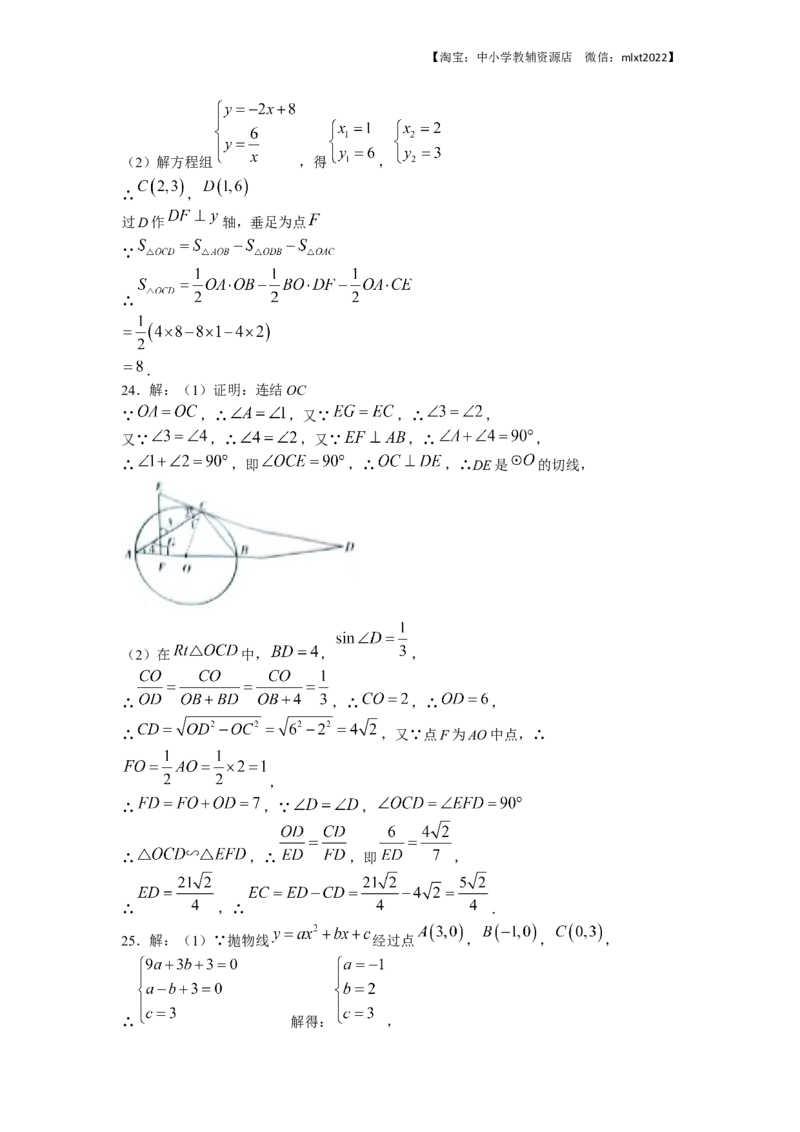
24.解:(1)证明:连结OC
∵ ,∴ ,又∵ ,∴ ,
又∵ ,∴ ,又∵ ,∴ ,
∴ ,即 ,∴ ,∴DE是 的切线,
(2)在 中, , ,
∴ ,∴ ,∴ ,
∴ ,又∵点F为AO中点,∴
,
∴ ,∵ ,
∴ ,∴ ,即 ,
∴ ,∴ .
25.解:(1)∵抛物线 经过点 , , ,
∴ 解得: ,【淘宝:中小学教辅资源店 微信:mlxt2022】
∴抛物线的解析式为: ,
∵ , ,
∴顶点D的坐标为 ;
(2)设直线AC的解析式为: ,
把点 , 代入得: , ,
∴直线AC解析式为: ,过点F作 于点G,
∵以A、C、E、F四点为顶点的四边形是以AC为边的平行四边形,∴ ,
又∵ ∴
∴ ∴ ,
设F点的坐标为 ,
则G点的坐标为 ,
∴ ,∴ 或 ,当 时,
∴
当 时,
∴ ∴ 或 ;
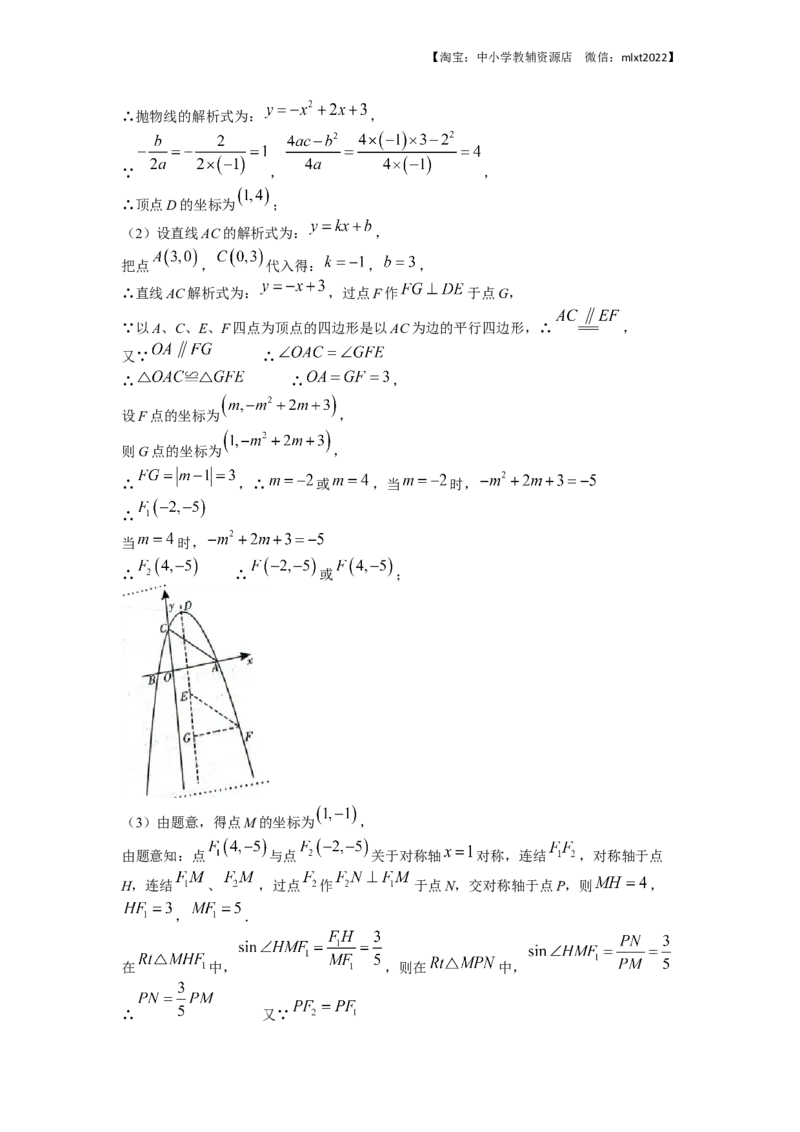
(3)由题意,得点M的坐标为 ,
由题意知:点 与点 关于对称轴 对称,连结 ,对称轴于点
H,连结 、 ,过点 作 于点N,交对称轴于点P,则 ,
, .
在 中, ,则在 中,
∴ 又∵【淘宝:中小学教辅资源店 微信:mlxt2022】
∴ 为最小值,又∵ ,
∴ ,∴求得 的最小值为 .