青海省百所名校2024届高三下学期二模考试理科数学试卷(1)_2024年4月_024月合集_2024届青海省金太阳（同心圆）高三下学期4月联考

高三数学试卷（理科） 考生注意： 1.本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分，共 150 分。考试时间 120 分钟。 2.请将各题答案填写在答题卡上 3.本试卷主要考试内容：高考全部内容。 第Ⅰ卷 一、选择题：本大题共 12 小题，每小题 5 分，共 60 分，在每小题给出的四个选项中，只有 一项是符合题目要求的 1.已知集合A1,2,3，B  x|x2 2x20  ，则AI B（ ） A.1 B.1,2 C.1,2,3 D. 2.复数z 2i43i的虚部为（ ） A.6 B.-6 C.8 D.-8 3  3.已知为锐角，sin ，则cos （ ） 5 2 10 3 10 5 2 5 A. B. C. D. 10 10 5 5 4.若圆M：(x 2)2  y2 m2（m0）与双曲线C：x2  y2 1的渐近线相切，则m （ ） A.1 B.2 C. 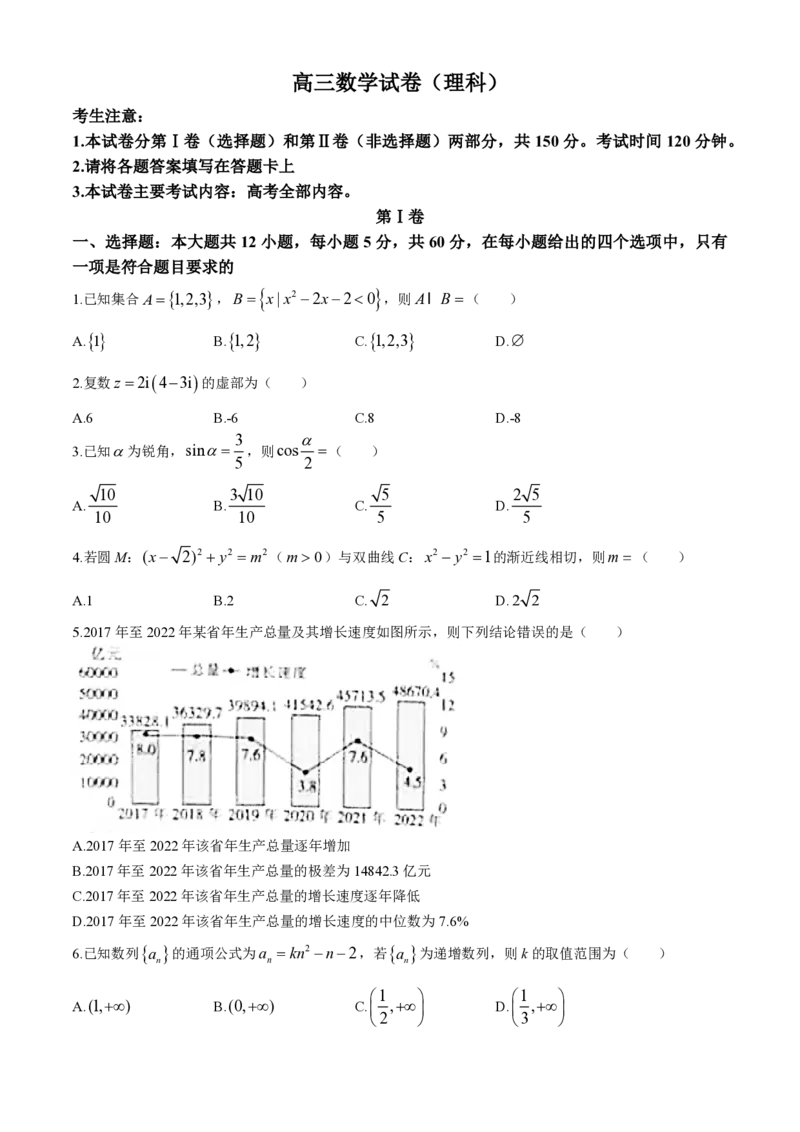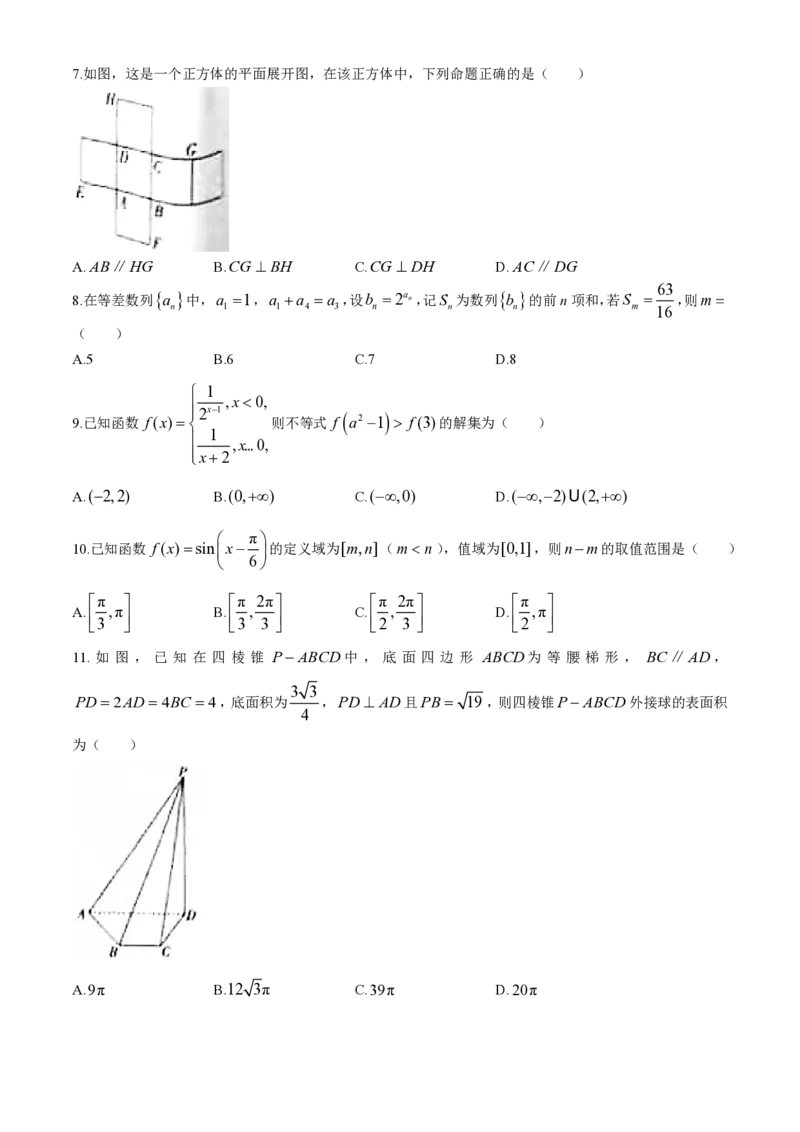2 D.2 2 5.2017年至2022年某省年生产总量及其增长速度如图所示，则下列结论错误的是（ ） A.2017年至2022年该省年生产总量逐年增加 B.2017年至2022年该省年生产总量的极差为14842.3亿元 C.2017年至2022年该省年生产总量的增长速度逐年降低 D.2017年至2022年该省年生产总量的增长速度的中位数为7.6% 6.已知数列a 的通项公式为a kn2 n2，若a 为递增数列，则k的取值范围为（ ） n n n 1  1  A.(1,) B.(0,) C. ,  D. ,  2  3  学科网（北京）股份有限公司7.如图，这是一个正方体的平面展开图，在该正方体中，下列命题正确的是（ ） A.AB∥HG B.CG  BH C.CG  DH D.AC∥DG 63 8.在等差数列a 中，a 1，a a a ，设b 2a n，记S 为数列b 的前n项和，若S  ，则m  n 1 1 4 3 n n n m 16 （ ） A.5 B.6 C.7 D.8  1 ,x0,  9.已知函数 f(x)   2x1 则不等式 f  a2 1   f(3)的解集为（ ） 1  ,x…0, x2 A.(2,2) B.(0,) C.(,0) D.(,2)U(2,)  π 10.已知函数 f(x)sin  x 的定义域为[m,n]（m  n），值域为[0,1]，则nm的取值范围是（ ）  6 π  π 2π π 2π π  A. ,π B. , C. , D. 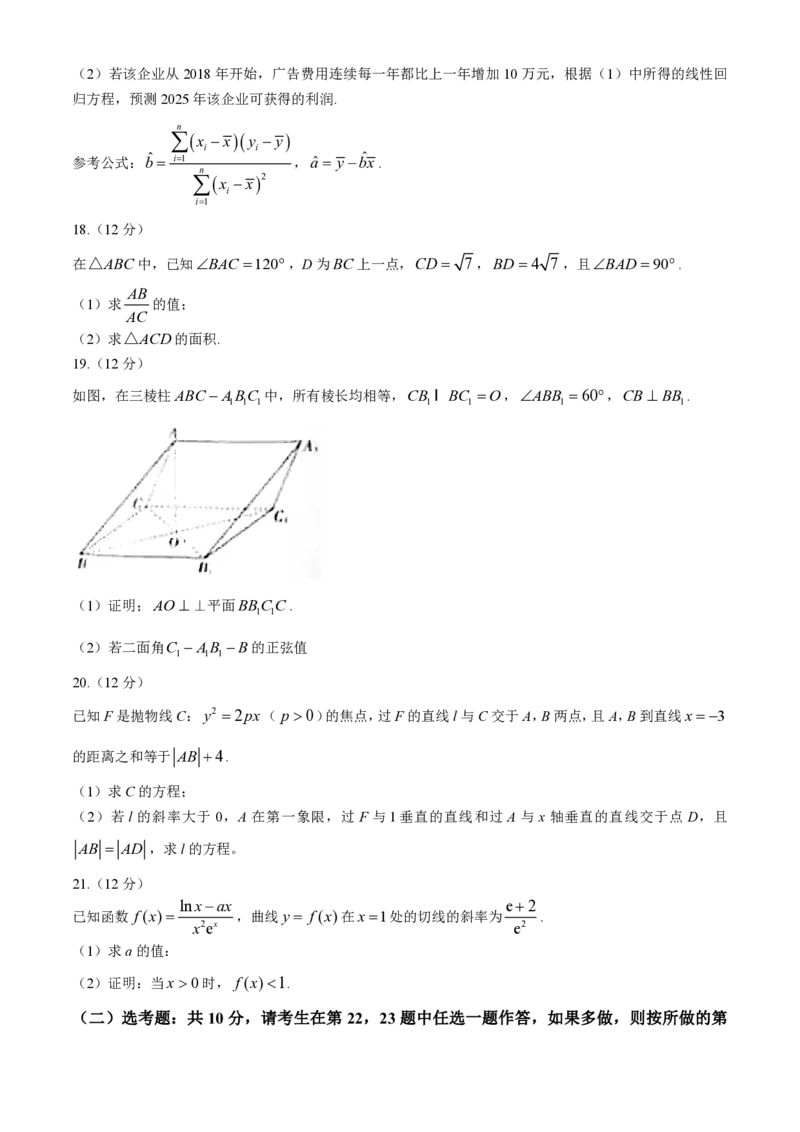,π         3  3 3  2 3  2  11. 如 图 ， 已 知 在 四 棱 锥 PABCD中 ， 底 面 四 边 形 ABCD为 等 腰 梯 形 ， BC∥AD， 3 3 PD2AD4BC 4，底面积为 ，PD AD且PB 19，则四棱锥PABCD外接球的表面积 4 为（ ） A.9π B.12 3π C.39π D.20π 学科网（北京）股份有限公司12. 已知定义在 R上的函数 f(x)，其导数为 f(x)，且满足 f(x y) f(x) f(y)xy(x y)， 2 f(1) ， f(1)0，给出下列四个结论： 3 ① f(x)为奇函数；② f(10)99；③ f(3)3：④ f(x)在(0,1)上单调递减. 其中所有正确结论的序号为（ ） A.①② B.①③ C.②③④ D.①②④ 第Ⅱ卷 二、填空题：本大题共 4小题，每小题 5分，共 20分.把答案填在答题卡中的横线上. x y…2,  13.若x，y满足约束条件x y„ 2,则z  yx的最大值为_____________.  y„ 2,  14.青团是江南人家在清明节吃的一道传统点心，某企业设计了一款青团礼盒，该礼盒刚好可以装3个青团， 如图所示.若将豆沙馅、莲蓉馅、芝麻馅的青团各1个，随机放入该礼盒中，则豆沙馅和莲蓉馅的青团相邻 的概率为_____________. x2 y2 15.已知椭圆C：  1（a b0）的左、右焦点分别为F ，F ，上顶点为A，过F 作AF 的垂线， a2 b2 1 2 1 1 3a 与y轴交于点P，若 PF  ，则椭圆C的离心率为____________. 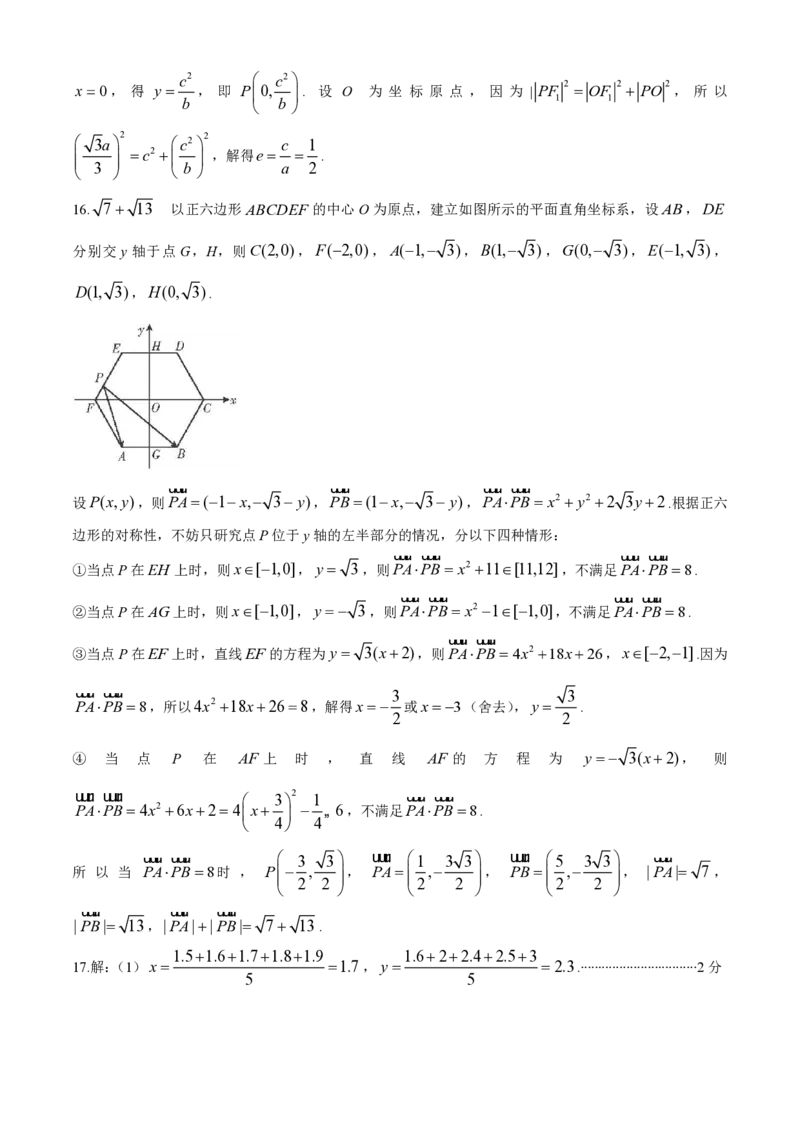1 3 uuur uuur uuur uuur 16.已知P是正六边形ABCDEF 边上任意一点，且AB2，PAPB8，则|PA||PB|__________. 三、解答题：共 70分.解答应写出文字说明、证明过程或演算步骤，第 17~21题为必考题，每 个试题考生都必须作答.第 22、23题为选考题，考生根据要求作答。 （一）必考题：共 60分. 17.（12分） 某企业近年来的广告费用x（百万元）与所获得的利润y（千万元）的数据如下表所示，已知y与x之间具 有线性相关关系. 年份 2018 2019 2020 2021 2022 广告费用x/百万元 1.5 1.6 1.7 1.8 1.9 利润y/千万元 1.6 2 2.4 2.5 3 （1）求y关于x的线性回归方程： 学科网（北京）股份有限公司（2）若该企业从2018年开始，广告费用连续每一年都比上一年增加10万元，根据（1）中所得的线性回 归方程，预测2025年该企业可获得的利润. n x xy  y i i 参考公式：b ˆ  i1 ，aˆ  yb ˆ x. n x x2 i i1 18.（12分） 在△ABC中，已知BAC 120，D为BC上一点，CD 7，BD4 7 ，且BAD90. AB （1）求 的值； AC （2）求△ACD的面积. 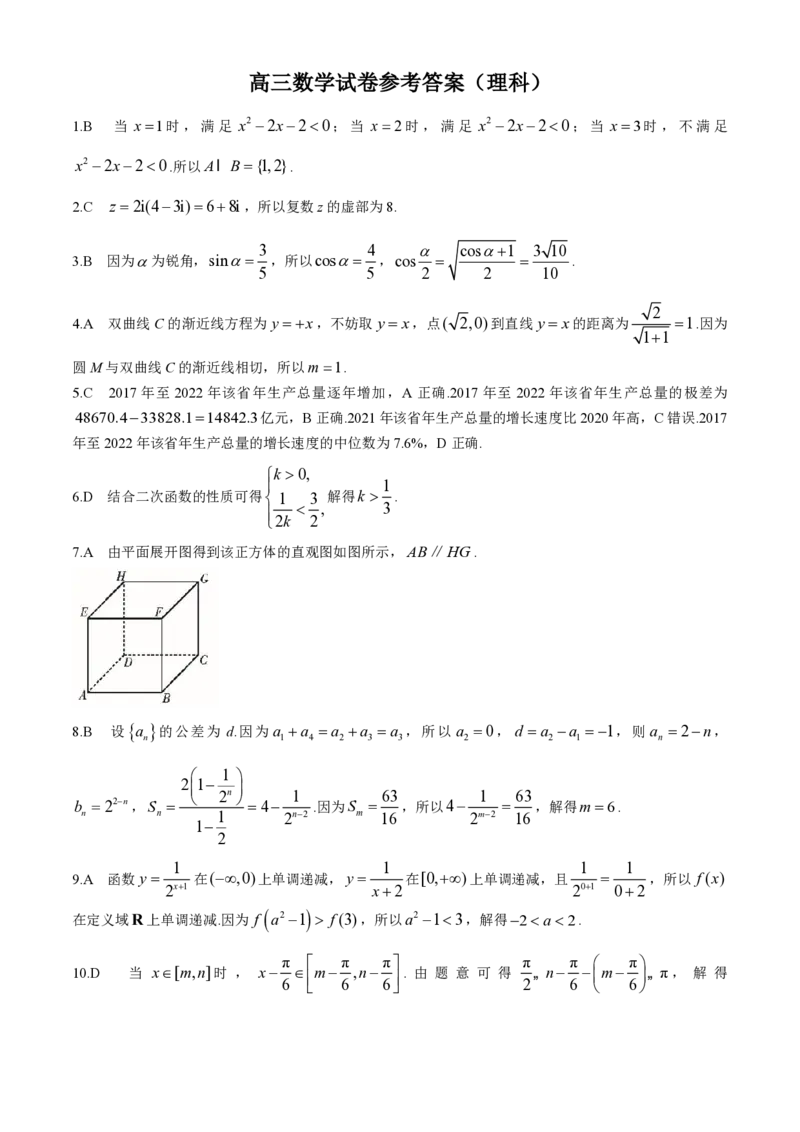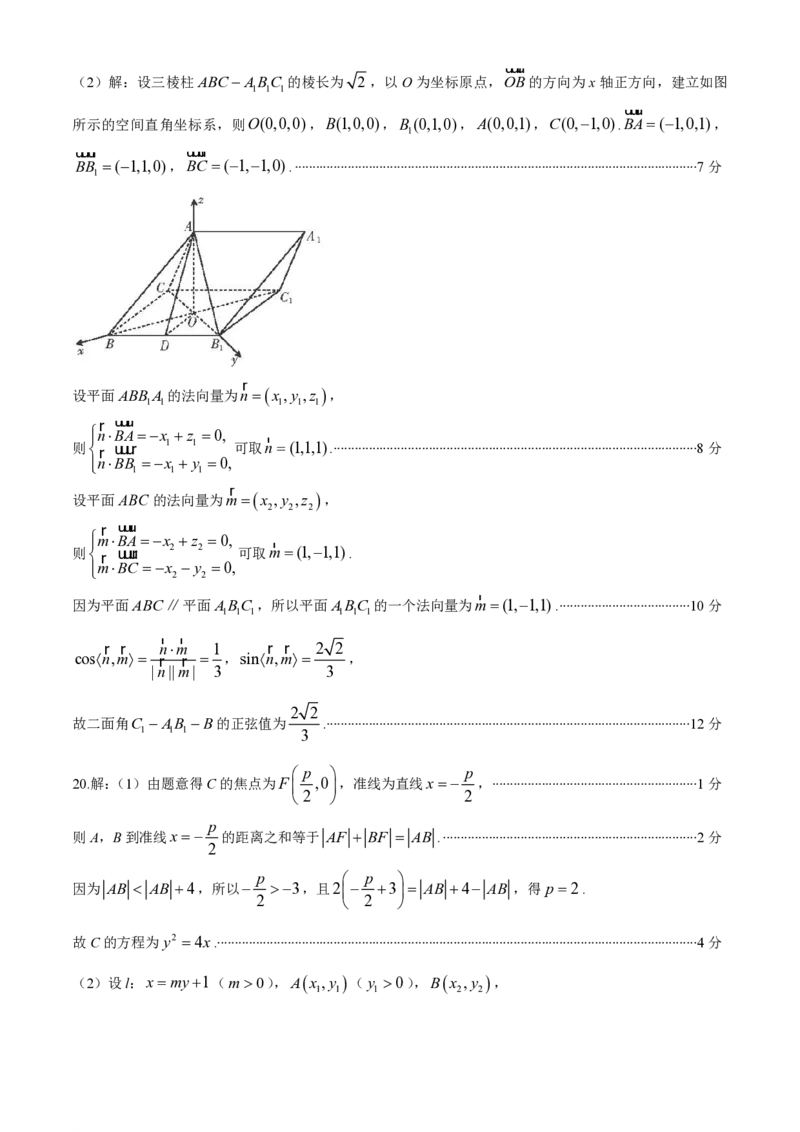19.（12分） 如图，在三棱柱ABCABC 中，所有棱长均相等，CB I BC O，ABB 60，CB BB . 1 1 1 1 1 1 1 （1）证明；AO⊥平面BBCC. 1 1 （2）若二面角C AB B的正弦值 1 1 1 20.（12分） 已知F是抛物线C：y2 2px（ p0）的焦点，过F的直线l与C交于A，B两点，且A，B到直线x3 的距离之和等于 AB 4. （1）求C的方程； （2）若 l 的斜率大于 0，A 在第一象限，过 F 与 l 垂直的直线和过 A 与 x 轴垂直的直线交于点 D，且 AB  AD ，求l的方程。 21.（12分） lnxax e2 已知函数 f(x) ，曲线y  f(x)在x1处的切线的斜率为 . x2ex e2 （1）求a的值： （2）证明：当x 0时， f(x)1. （二）选考题：共 10 分，请考生在第 22，23 题中任选一题作答，如果多做，则按所做的第 学科网（北京）股份有限公司一题计分. 22.［选修4-4：坐标系与参数方程］（10分） xcos2t xcos4t 在直角坐标系xOy中，曲线C 的参数方程为 （t为参数），曲线C 的参数方程为 1 y sint 2 y sint （t为参数）. （1）写出C 及C 的普通方程； 1 2 （2）以坐标原点O为极点，x轴正半轴为极轴建立极坐标系，求C 与C 交点的极坐标. 1 2 23.［选修4-5；不等式选讲］（10分） 1 1 1 已知a，b，c均为正实数，且   1，证明： a b1 c2 （1）abc…6； （2）若b2c，则a2 9c2…18. 学科网（北京）股份有限公司高三数学试卷参考答案（理科） 1.B 当 x1时，满足 x2 2x20；当 x  2时，满足 x2 2x20；当 x3时，不满足 x2 2x20.所以AI B{1,2}. 2.C z 2i(43i)68i，所以复数z的虚部为8. 3 4  cos1 3 10 3.B 因为为锐角，sin ，所以cos ，cos   . 5 5 2 2 10 2 4.A 双曲线C的渐近线方程为 y x，不妨取 yx，点( 2,0)到直线 yx的距离为 1.因为 11 圆M与双曲线C的渐近线相切，所以m 1. 5.C 2017 年至 2022 年该省年生产总量逐年增加，A 正确.2017 年至 2022 年该省年生产总量的极差为 48670.433828.114842.3亿元，B正确.2021年该省年生产总量的增长速度比2020年高，C错误.2017 年至2022年该省年生产总量的增长速度的中位数为7.6%，D正确. k 0,  1 6.D 结合二次函数的性质可得 1 3 解得k  .  , 3  2k 2 7.A 由平面展开图得到该正方体的直观图如图所示，AB∥HG. 8.B 设a 的公差为 d.因为 a a a a a ，所以 a 0， d a a 1，则 a 2n， n 1 4 2 3 3 2 2 1 n  1  2 1    2n  1 63 1 63 b 22n，S  4 .因为S  ，所以4  ，解得m6. n n 1 2n2 m 16 2m2 16 1 2 1 1 1 1 9.A 函数y  在(,0)上单调递减，y  在[0,)上单调递减，且  ，所以 f(x) 2x1 x2 201 02 在定义域R上单调递减.因为 f  a2 1   f(3)，所以a2 13，解得2a2. π  π π π π  π 10.D 当 x[m,n]时 ， x   m ,n  . 由 题 意 可 得 „ n   m  „ π， 解 得 6  6 6 2 6  6 学科网（北京）股份有限公司π  nm ,π .   2  3 3 3 π 11.D 取AD的中点为F.因为AD2BC 2，面积为 ，所以梯形的高为 ，则BAD ，连接 4 2 3 BF，所以△ABF为等边三角形，点F为梯形ABCD外接圆的圆心.连接BD，在△BCD中，根据余弦定 2π BC2 CD2 BD2 1 理得cos   ，所以BD 3.因为PB 19，PD4，所以PD2 BD2  3 2BCCD 2 PB2，所以PD BD.因为PD AD，所以PD平面ABCD.过AD的中点F作FO∥PD交PA于点 O，则FO 平面 ABCD，且 O 为PA的中点，所以点 O 为Rt△PAD外接圆圆心，所以 O 为四棱锥 1 1 PABCD外 接 球 球 心 ， 所 以 外 接 球 半 径 为 PA PD2  AD2  5， 故 表 面 积 2 2 S 4π( 5)2 20π. 12.D 令x y 0，得 f(0) f(0) f(0)，所以 f(0)0. 令y x，得 f(0) f(x) f(x)0，所以 f(x)为奇函数，故①正确. 2 令y1，得 f(x1) f(x) f(1)x(x1) f(x)x(x1) ， 3 2 2 2 所以 f(2) f(1)12  ， f(3) f(2)23 6，故③错误. 3 3 3 因为 f(x1) f(x)2x1，所以 f(x) f(x1)2x1，…， f(2) f(1)3， 所以 f(x)35L (2x1) x2 1，所以 f(10)99，故②正确. 当x(0,1)时， fx)0，所以 f(x)在(0,1)上单调递减，故④正确. 13.2 由题意，作出可行域（图略），数形结合可得当直线过点(0,2)时，z取得最大值，最大值为2. 2 2 14. 豆沙馅和莲蓉馅的青团相邻，则芝麻馅的青团不能放在中间，其概率为 . 3 3 1 b c c 15. 设F(c,0)，则直线AF 的斜率为 ，直线PF 的斜率为 ，直线PF 的方程为y  (xc).令 2 1 2 c 1 b 1 b 学科网（北京）股份有限公司c2  c2  2 2 2 x 0， 得 y  ， 即 P0, . 设 O 为 坐 标 原 点 ， 因 为 | PF  OF  PO ， 所 以 b  b  1 1 2 2  3a c2  c 1     c2   ，解得e  .  3   b  a 2 16. 7  13 以正六边形ABCDEF 的中心O为原点，建立如图所示的平面直角坐标系，设AB，DE 分别交 y 轴于点 G，H，则C(2,0)，F(2,0)， A(1, 3)，B(1, 3)，G(0, 3)，E(1, 3)， D(1, 3)，H(0, 3). uuur uuur uuur uuur 设P(x,y)，则PA(1x, 3 y)，PB(1x, 3 y)，PAPB x2  y2 2 3y2.根据正六 边形的对称性，不妨只研究点P位于y轴的左半部分的情况，分以下四种情形： uuur uuur uuur uuur ①当点P在EH 上时，则x[1,0]，y  3，则PAPB x2 11[11,12]，不满足PAPB8. uuur uuur uuur uuur ②当点P在AG上时，则x[1,0]，y  3，则PAPB x2 1[1,0]，不满足PAPB8. uuur uuur ③当点P在EF上时，直线EF的方程为y  3(x2)，则PAPB4x2 18x26，x[2,1].因为 uuur uuur 3 3 PAPB8，所以4x2 18x268，解得x 或x3（舍去），y  . 2 2 ④ 当 点 P 在 AF 上 时 ， 直 线 AF 的 方 程 为 y  3(x2)， 则 uuur uuur  3 2 1 uuur uuur PAPB4x2 6x24  x   „ 6，不满足PAPB8.  4 4 uuur uuur  3 3 uuur 1 3 3 uuur 5 3 3 uuur 所 以 当 PAPB8时 ， P , ， PA , ， PB , ， |PA| 7，       2 2 2 2 2 2       uuur uuur uuur |PB| 13，|PA||PB| 7  13. 1.51.61.71.81.9 1.622.42.53 17.解：（1）x 1.7，y  2.3.∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙2分 5 5 学科网（北京）股份有限公司5 x2 1.52 1.62 1.72 1.82 1.92 14.55，∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙4分 i i1 5 x y 1.51.61.621.72.41.82.51.9319.88，∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙6分 i i i1 5 x y 5xy i i 19.8851.72.3 b ˆ  i1  3.3，∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙7分 5 14.5551.72 x2 5x2 i i1 ˆ aˆ  ybx2.33.31.73.31.∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙8分 故所求的线性回归方程为yˆ 3.3x3.31.∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙9分 （2）由题可知，到2025年时广告费用为2.2百万元，故可预测该公司所获得的利润约为3.32.23.31 3.95（千万元）.∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙12分 AC CD 18.解：（1）在△ACD中，  ，所以AC 2 7sinADC 2 7sinADB.3分 sinADC sinCAD AB 在△ABD中，BAD90，sinADB ，所以AB4 7sinADB.∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙6分 BD AB 4 7sinADB 故  2.∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙8分 AC 2 7sinADB （2）在△ABC中，由余弦定理可得BC2  AC2  AB2 2ACABcosBAC， 解得AB2AC 10，∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙10分 则AD BD2 AB2 2 3.∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙11分 1 5 3 故△ACD的面积为 ACADsinCAD .∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙12分 2 2 19.（1）证明：设D为BB 的中点，连接AD，OD，AB . 1 1 在△ABB 中，因为BB  BC CC  BC，CB BB ，所以四边形BBCC是正方形. 1 1 1 1 1 1 1 1 因为CB I BC O，所以△OBB 是等腰直角三角形，OD BB . 1 1 1 1 因为ADI OD D，所以BB 平面AOD.∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙4分 1 因为AO平面AOD，所以BB  AO. 1 在△ACB 中，AC  AB ，O为BC的中点，所以AO BC. 1 1 1 1 因为BCI BB  B ，所以AO平面BBCC.∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙6分 1 1 1 1 1 学科网（北京）股份有限公司uuur （2）解：设三棱柱ABCABC 的棱长为 2 ，以O为坐标原点，OB的方向为x轴正方向，建立如图 1 1 1 uuur 所示的空间直角坐标系，则O(0,0,0)，B(1,0,0)，B (0,1,0)，A(0,0,1)，C(0,1,0).BA(1,0,1)， 1 uuur uuur BB (1,1,0)，BC (1,1,0).∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙7分 1 r 设平面ABB A 的法向量为n x ,y ,z ， 1 1 1 1 1 uuur r  nBAx z 0, r 则r uuur 1 1 可取n (1,1,1).∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙8分  nBB x  y 0, 1 1 1 r 设平面ABC 的法向量为mx ,y ,z ， 2 2 2 uuur r  mBAx z 0, r 则r uuur 2 2 可取m(1,1,1).  mBC x  y 0, 2 2 r 因为平面ABC∥平面ABC ，所以平面ABC 的一个法向量为m(1,1,1).∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙10分 1 1 1 1 1 1 r r r r nm 1 r r 2 2 cosn,m  r r  ，sinn,m  ， |n||m| 3 3 2 2 故二面角C AB B的正弦值为 .∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙12分 1 1 1 3  p  p 20.解：（1）由题意得C的焦点为F  ,0 ，准线为直线x ，∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙1分  2  2 p 则A，B到准线x 的距离之和等于 AF  BF  AB .∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙2分 2 p  p  因为 AB  AB 4，所以 3，且2   3   AB 4 AB ，得 p2. 2  2  故C的方程为y2 4x.∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙4分 （2）设l：xmy1（m0），Ax ,y （y 0），Bx ,y ， 1 1 1 2 2 学科网（北京）股份有限公司y2 4x, y  y 4m, 由 得y2 4my40，则 1 2 ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙6分 xmy1,  y y 4, 1 2 所以 AB  x x 2my  y 44  m2 1  .∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙7分 1 2 1 2 t 1 设Dx ,t，由k k 1，得k   m，即t mx 1m2y ，∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙9分 1 DF AB DF x 1 k 1 1 1 AB 所以 AD  y m2y   m2 1  y .∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙10分 1 1 1 由 AB 4  m2 1   AD   m2 1  y ，得 y 4，代入 y2 4my40，得1616m40，即 1 1 3 m . 4 故l的方程为4x3y40.∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙12分 1 a  x2ex   2xex x2ex (lnxax)    x  21.（1）解： f(x) ，  x2ex2 (1a)e(2ee)(a) e2ae e2 1 f(1)   ，解得a .∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙4分 e2 e2 e2 e x lnx 1 lnx e （2）证明：结合（1）可得 1，即证xex   .∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙6分 x2ex e x 1 设函数g(x) xex  ，g(x)(x1)ex. e 当x 0时，g(x)0，g(x)在(0,)上单调递增， 1 g(x) g(0) .∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙8分 e lnx 1lnx 设函数h(x) ，h(x) . x x 当x(0,e)时，h(x)0，当x(e,)时，h(x)0， 所以h(x)在(0,e)上单调递增，在(e,)上单调递减， 1 h(x)„ h(e) .∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙11分 e 1 所以g(x) …h(x)， f(x)1得证.∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙12分 e 22.解：（1）xcos2t 12sin2t 12y2，即x2y2 10. cos2t[1,1]，所以x[1,1]，所以C 的普通方程为2y2 x10（1„ x„ 1）.∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙2分 1 学科网（北京）股份有限公司xcos4t 2cos22t12  12sin2t 2 12  12y22 1，即8y4 8y2 x10. 因为cos4t[1,1]，所以x[1,1]，所以C 的普通方程为8y4 8y2 x10（1„ x„ 1）.∙∙∙∙∙∙∙∙5分 2  1  1 x , x , 2y2 x10,   2   2 x1, （2）联立 解得 或 或 ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙8分 8y4 8y2 x10,  3  3 y 0. y  y   2  2  1 3  1 3 C 与C 交点的直角坐标为 , ， , ，(1,0).∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙9分 1 2  2 2   2 2       2π  4π C 与C 交点的极坐标为 1, ， 1, ，(1,0).∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙10分 1 2  3   3  注：第（1）问，C 的普通方程中x的范围写成x… 1，C 的普通方程中x的范围写成x„ 1不扣分；若C 1 2 1 及C 的普通方程没有给出x的范围，则扣1分. 2  4π  2π 第（2）问答案，交点的极坐标写成其他形式，只要符合题意，不扣分，如极坐标 1, 写成 1, .  3   3  1 1 1  23.证明：（1）abc[a(b1)(c2)]     3 a b1 c2  a b1 a c2 b1 c2   3       3 ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙3分  b1 a c2 a c2 b1 …322236，当且仅当a b1c23，即a3，b  2，c 1时，等号成立∙∙∙∙∙∙∙∙∙∙∙∙5分 （2）因为b2c，由（1）得a2cca3c…6，所以(a3c)2…36.∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙7分 因为a2 9c2…2a3c，所以2  a2 9c2 …a2 9c2 2a3c(a3c)2…36， 所以a2 9c2…18.∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙10分 学科网（北京）股份有限公司