文档内容
2023 年高考考前押题密卷(全国乙卷)
文科数学
(考试时间:120分钟 试卷满分:150分)
注意事项:
1.本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。答卷前,考生务必将自己的姓名、准考
证号填写在答题卡上。
2.回答第Ⅰ卷时,选出每小题答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑。如需改动,
用橡皮擦干净后,再选涂其他答案标号。写在本试卷上无效。
3.回答第Ⅱ卷时,将答案写在答题卡上。写在本试卷上无效。
4.考试结束后,将本试卷和答题卡一并交回。
第Ⅰ卷
一、选择题:本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一个选项是符合题
目要求的.
1.已知集合 , ,则 ( )
A. B.
C. D.
【答案】D
【详解】由题意可得:
故选:D
2.已知复数 满足 ,给出下列四个命题其中正确的是( )
A. B. 的虚部为 C. D.
【答案】B
【详解】∵ ,∴ ,故z的虚部为 ,
1
学科网(北京)股份有限公司则 , , ,所以B正确,A,C,D不正确.
故选:B.
3.已知命题p: , ;命题q:直线 : 与 : 相互垂直的充要条件为
,则下列命题中为真命题的是( )
A. B. C. D.
【答案】B
【详解】令 ,则 ,所以p为真命题;
若 与 相互垂直,则 ,解得 ,故q为假命题,
所以只有 为真命题.
故选:B.
4.函数 的最小正周期是( )
A. B. C. D.
【答案】C
【详解】因为 , 的最小正周期 ,
所以函数 的最小正周期是 .
故选:C.
5.设实数 , 满足约束条件 则目标函数 的取值范围是( )
A. B. C. D.
【答案】D
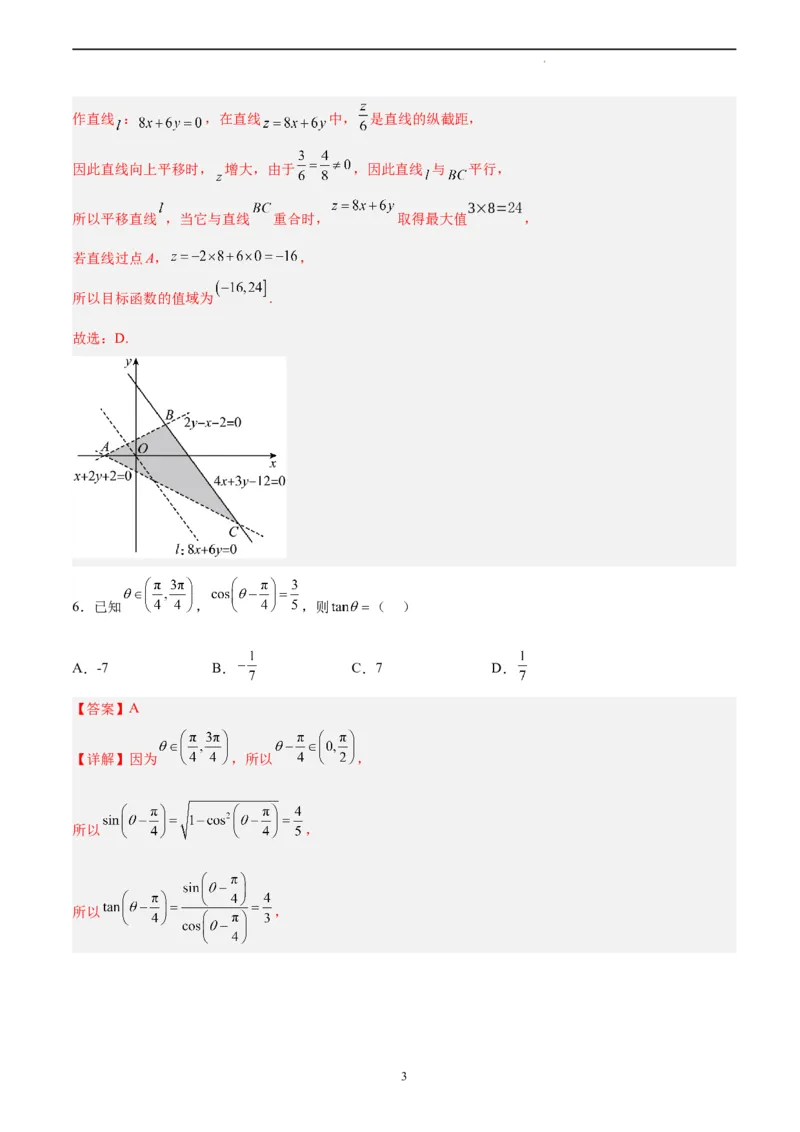
【详解】作出可行域,如图 内部(含线段 不包含顶点的部分),
2
学科网(北京)股份有限公司作直线 : ,在直线 中, 是直线的纵截距,
因此直线向上平移时, 增大,由于 ,因此直线 与 平行,
3×8=24
所以平移直线 ,当它与直线 重合时, 取得最大值 ,
若直线过点A, ,
所以目标函数的值域为 .
故选:D.
6.已知 , ,则 ( )
A.-7 B. C.7 D.
【答案】A
【详解】因为 ,所以 ,
所以 ,
所以 ,
3
学科网(北京)股份有限公司所以 .
故选:A.
7.《易经》是中国传统文化中的精髓,如图是易经八卦图(含乾、坤,巽、震、坎、离、艮、兑八卦),
每一卦由三根线组成( 表示一根阳线, 表示一根阴线),从八卦中任取两卦,这两卦
的六根线中恰有5根阳线和1根阴线的概率为( )
A. B. C. D.
【答案】B
【详解】从八卦中任取两卦,共有 种情况,
其中这两卦的六根线中恰有5根阳线和1根阴线,则必有一卦为乾,另一卦从兑、离、巽中选出一卦,故共
有 ,
故这两卦的六根线中恰有5根阳线和1根阴线的概率为 .
故选:B
8.已知函数 (a,b为常数,其中 且 )的图象如图所示,则下列结论正确的是
( )
4
学科网(北京)股份有限公司A. , B. ,
C. , D. ,
【答案】D
【详解】解:由图象可得函数在定义域上单调递增,
所以 ,排除A,C;
又因为函数过点 ,
所以 ,解得 .
故选:D
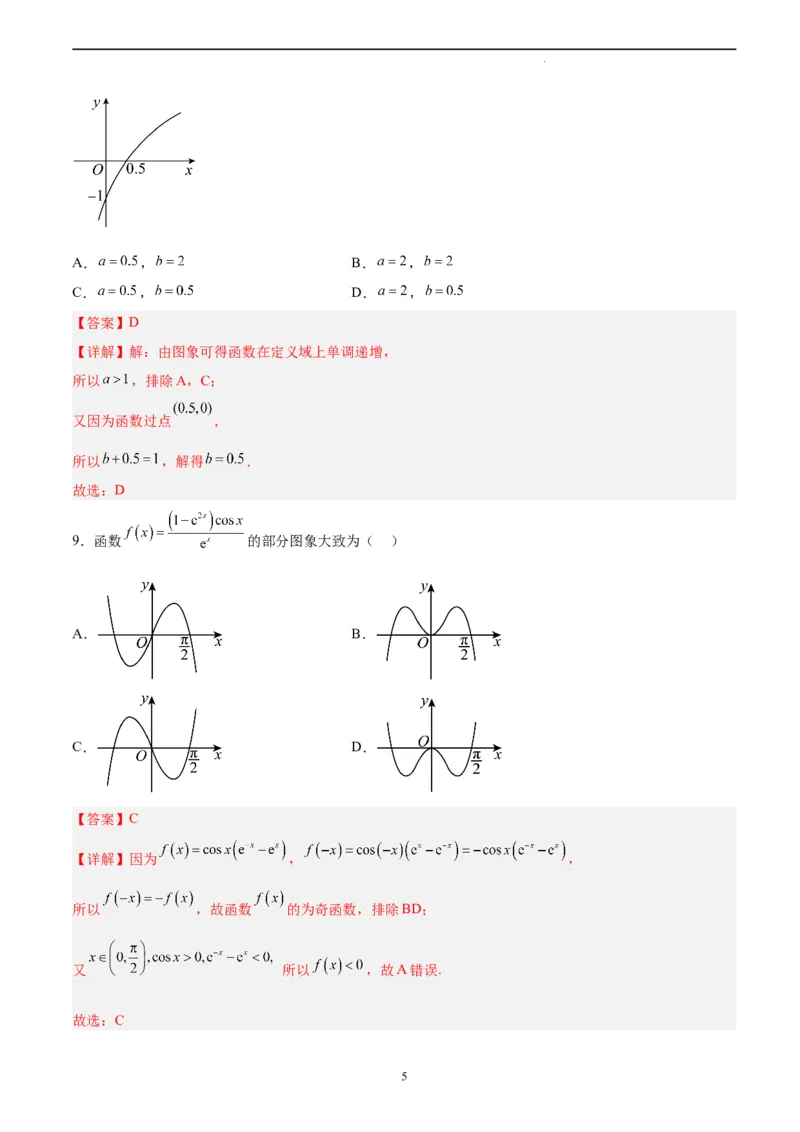
9.函数 的部分图象大致为( )
A. B.
C. D.
【答案】C
【详解】因为 , ,
所以 ,故函数 的为奇函数,排除BD;
又 所以 ,故A错误.
故选:C
5
学科网(北京)股份有限公司10.在《九章算术》中,将四个面都是直角三角形的四面体称为鳖臑.在鳖臑 中 平面BCD,
,且 ,则鳖臑 外接球的表面积为( )
A. B. C. D.
【答案】C
【详解】
如图,取 的中点为 ,连接 ,
因为 平面BCD, 平面 ,故 ,
同理 .
因为 的中点为 ,故 .
而 , 平面 ,故 平面 ,
而 平面 ,故 ,
故 ,所以 为三棱锥 外接球的球心,
又 ,故 ,所以 ,
故三棱锥 外接球半径为 ,故其外接球的表面积为 .
故选:C.
11.已知 , 是椭圆 的上、下顶点, 为 的一个焦点,若 的面积为 ,则
的长轴长为( )
A.3 B.6 C.9 D.18
【答案】B
【详解】由题可知 ,则 ,所以 ,所以 ,
故 的长轴长为 .
6
学科网(北京)股份有限公司故选:B
12.函数 的定义域为 ,满足 ,且当 时, .若对任意
,都有 ,则 的最大值是( )
A. B. C. D.
【答案】A
【详解】因 ,又当 时, ,
当 , ,时, ,
则 ,
,
当 , ,时, ,
则 ,
,
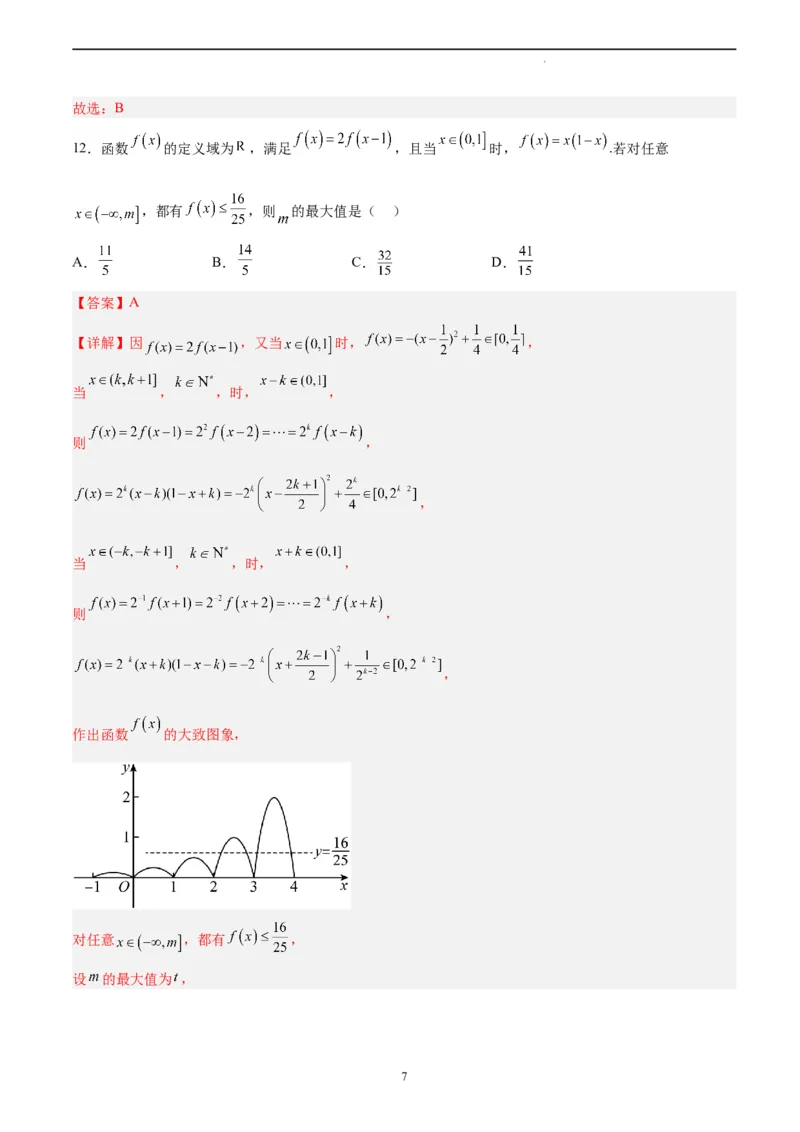
作出函数 的大致图象,
对任意 ,都有 ,
设 的最大值为 ,
7
学科网(北京)股份有限公司则 ,且
所以 ,解得
所以m的最大值为 .
故选:A.
第Ⅱ卷
二、填空题:本题共4小题,每小题5分,共20分.
13.已知向量 ,且 ,则 ___________.
【答案】
【详解】由题设 ,且 ,
所以 ,则 .
故答案为: 微信搜索“高中试卷君”公众号 领取押题卷联考卷
14.点 到抛物线 的准线的距离为6,那么抛物线的标准方程是______.
【答案】 或 .
【详解】将 化为 ,
当 时,准线 ,由已知得 ,所以 ,所以 ;
当 时,准线 ,由已知得 ,所以 或 (舍),
所以抛物线方程为 或 .
故答案为: 或 .
8
学科网(北京)股份有限公司15.在△ABC中,角A,B,C所对的边分别为a,b,c,其中 ,且满足 ,
,则边a等于________.
【答案】
【详解】由 ,显然 ,则 ,
又 ,则 ,
由 ,
又 ,则 ,整理得 ,
又 ,则 ,所以 ,得 ,
又由正弦定理有 ,则 .
故答案为: . 微信搜索“高中试卷君”公众号 领取押题卷联考卷
16.如图是正方体的平面展开图,则在这个正方体中,异面直线AB与CD的夹角为__________.
【答案】
9
学科网(北京)股份有限公司【详解】
如图所示,把展开图恢复到原正方体.
连接AE,BE.由正方体可得 且 ,
∴四边形ADCE是平行四边形,∴AE DC.
∴ 或其补角是异面直线AB与CD所成的角.
由正方体可得: ,∴ 是等边三角形,∴ .
∴异面直线AB与CD所成的角是60°.
故答案为:60°
三、解答题:共70分.解答应写出文字说明、证明过程或演算步骤.第 17~21题为必考题,每个试题考生
都必须作答.第22、23题为选考题,考生根据要求作答.
17.某校随机抽出30名女教师和20名男教师参加学校组织的“纪念中国人民抗日战争暨世界反法西斯战争
胜利75周年”知识竞赛(满分100分),若分数为80分及以上的为优秀,50~80分之间的为非优秀,统计
并得到如下列联表:
女教
男教师 总计
师
优秀 20 6 26
非优秀 10 14 24
总计 30 20 50
(1)男、女教师中成绩为优秀的频率分别是多少?
(2)判断是否有99%的把握认为这次竞赛成绩是否优秀与性别有关?
附: ,其中 .
0.050 0.010 0.001
10
学科网(北京)股份有限公司3.841 6.635 10.828
【详解】(1)由题意可得:男教师中成绩为优秀的频率是 ,女教师中成绩为优秀的频率是 .
(2) ,
故没有 的把握认为这次竞赛成绩是否优秀与性别有关.
18.如图,在底面为矩形的四棱锥 中, 底面ABCD.
(1)证明:平面 平面PCD.
(2)若 , ,E在棱AD上,且 ,求四棱锥 的体积.
【详解】(1)证明:由四边形ABCD为矩形,得 .
因为 底面ABCD, 平面ABCD,所以 .
因为 , 平面PAD,所以 平面PAD.
因为 平面PCD,所以平面 平面PCD.
(2)因为 , ,所以 ,
因为直角梯形ABCE的面积 .
所以 .
19.数列 满足 .
(1)求证: 是等比数列;
(2)若 ,求 的前 项和为 .
11
学科网(北京)股份有限公司【详解】(1)
所以数列 是以2为首项,2为公比的等比数列.
(2)由(1)可得, ,所以 ,
设 设其前 项和为 ,
则 ①
②
减②得
所以
所以
20.已知双曲线 的离心率等于2,点 到直线 的距离等于1.
(1)求 的标准方程;
(2)设 为 在第一象限的一个点, , 为 的焦点,如果线段 , , 的长度构成等差数列,
求点 的坐标.
【详解】(1)因为点 到直线 的距离等于1,所以 ,解得 .
12
学科网(北京)股份有限公司又 ,所以 ,所以 ,故 的标准方程为 .
(2)设点 坐标为 ,由 为 在第一象限的一个点,得 且 ;
又 , , 构成等差数列,所以 .
由 得 .
又 ,所以 ,即 ,所以 ,
代入 得 ,所以点 坐标为 .
21.已知函数 , .
(1)若 ,求函数 的最小值及取得最小值时的 值;
(2)求证: ;
(3)若函数 对 恒成立,求实数a的取值范围.
【详解】(1)解:当 时, ,定义域为 ,
所以 ,令 得 ,
所以,当 时, , 单调递减;当 时, , 单调递增,
所以,函数 在 处取得最小值, .
(2)解:由(1)知,当 时, ,即 ,
所以,要证 成立,只需证 ,
令 ,则 ,
13
学科网(北京)股份有限公司所以,当 时, 恒成立,
所以,函数 为单调递增函数,
所以, ,即 ,
所以 ,
所以 成立
(3)解:因为函数 对 恒成立
所以 对 恒成立,
令 ,则 ,
当 时, , 在 上单调递增,
所以,由 可得 ,即满足 对 恒成立;
当 时,则 , , 在 上单调递增,
因为当 趋近于 时, 趋近于负无穷,不成立,故不满足题意;
当 时,令 得
令 , 恒成立,故 在 上单调递增,
因为当 趋近于正无穷时, 趋近于正无穷,当 趋近于 时, 趋近于负无穷,
所以 ,使得 , ,
所以,当 时, , 单调递减,当 时, , 单调递增,
所以,只需 即可;
14
学科网(北京)股份有限公司所以, , ,
因为 ,所以 ,
所以 ,解得 ,
所以, ,
综上,实数a的取值范围为
22.在直角坐标系 中,曲线M的方程为 ,曲线N的方程为 ,以坐标原点O为极点,
x轴的正半轴为极轴,建立极坐标系.
(1)求曲线M,N的极坐标方程;
(2)若射线 与曲线M交于点A(异于极点),与曲线N交于点B,且 ,
求 .
【详解】(1)解:由 ,可得 ,即 ,
又由 ,可得 ,
所以曲线M的极坐标方程为 .
由 ,可得 ,即 ,
即曲线N的极坐标方程为 .
(2)解:将 代入 ,可得 ,
将 代入 ,可得 ,
15
学科网(北京)股份有限公司则 ,
因为 ,所以 ,
又因为 ,所以 .
23.已知函数 .
(1)若 ,解不等式 ;
(2)若 ,求a的取值范围.
【详解】(1)若 ,可知 ,
当 时,不等式 转化为 ,
解得 ,
当 时,不等式 转化为 ,不等式恒成立,
当 时,不等式 转化为 ,
解得 ,
综上,不等式 的解集为 ;
(2)若 ,则 ,
因为 ,
当且仅当 时,等号成立,
故 ,
即 或 ,
16
学科网(北京)股份有限公司解得 或 ,
则a的取值范围为 .
17
学科网(北京)股份有限公司18
学科网(北京)股份有限公司