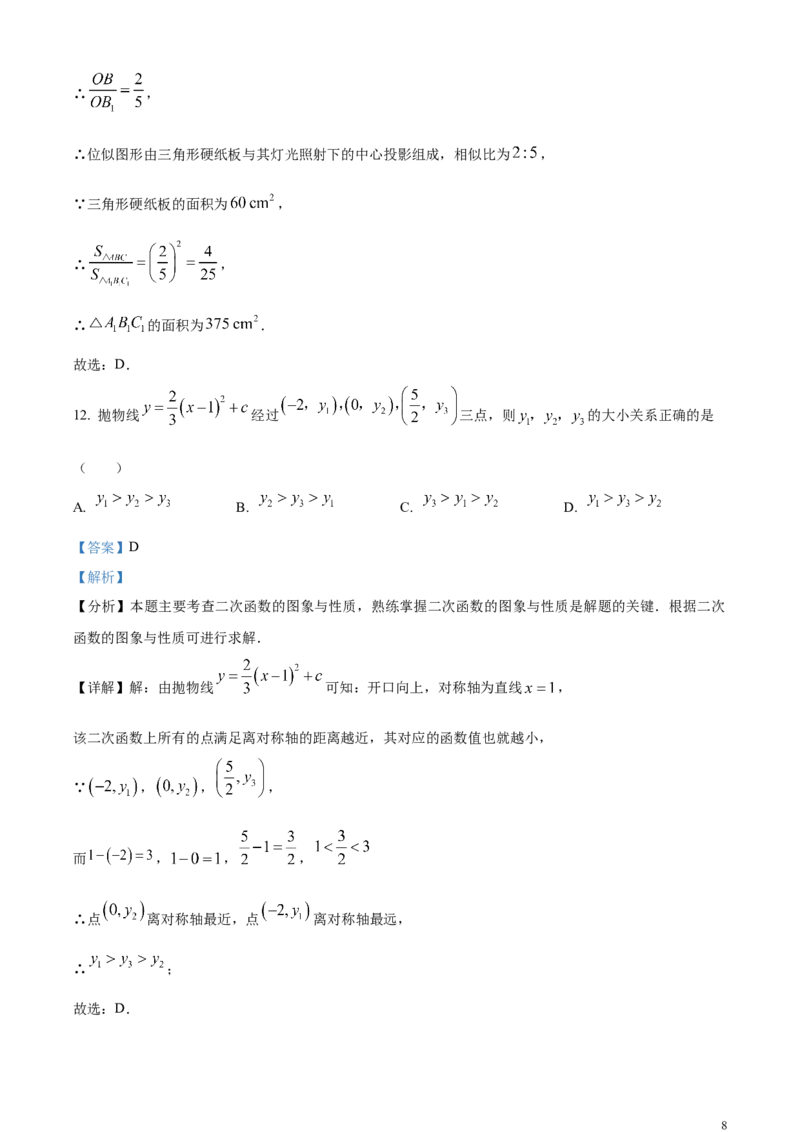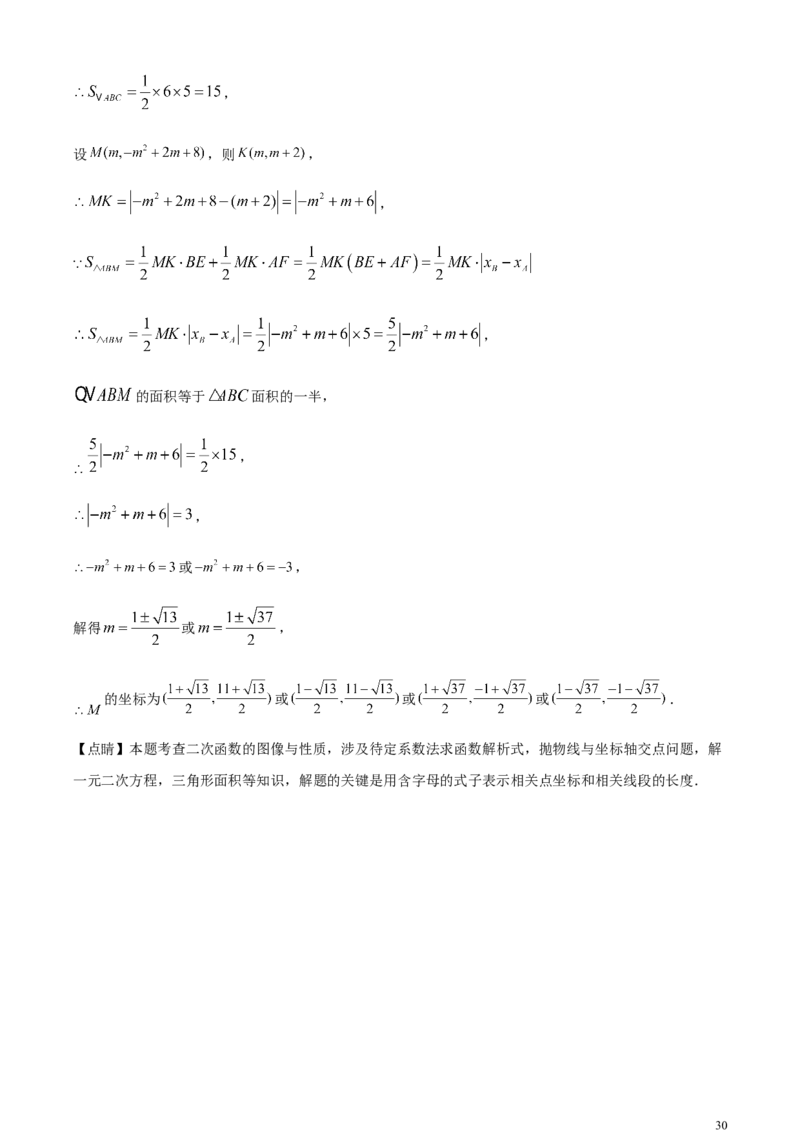文档内容
凉山州 2024 年初中学业水平暨高中阶段学校招生考试试题
数学
注意事项:
1.答题前,考生务必将自己的姓名、座位号、准考证号用 0.5毫米的黑色墨迹签字在答题卡
上,并在答题卡背面上方填涂座位号,同时检查条形码粘贴是否正确.
2.选择题使用2B铅笔涂在答题卡对应题目标号的位置上;非选择题用 0.5毫米黑色字笔书
写在答题卡对应题目标号的答题区域内,超出答题区域书写的答案无效;在草稿纸卷上答题
无效.
3.考试结束后,由监考教师将试题卷,答题卡,草稿纸一并收回.
本试卷共6页,分为A卷(100分),B卷(50分),全卷满分150分,考试时间12(A卷
又分为第Ⅰ卷和第Ⅱ卷.
A卷(共100分)
第Ⅰ卷选择题(共48分)
一、选择题(共12小题,每小题4分,共48分)在每小题给出的四个选项中只有一项的,
请把正确选项的字母序号填涂在答题卡上对应的位置.
1. 下列各数中: ,负数有( )
.
A 1个 B. 2个 C. 3个 D. 4个
【答案】C
【解析】
【分析】本题考查了对正数和负数定义的理解,难度不大,注意0既不是正数也不是负数.
根据正数和负数的定义判断即可,注意:0既不是负数也不是正数.
【详解】解: ,是正数;
,是负数;
,是负数;
0既不是正数,也不是负数;
,是负数;
,是正数;
负数有 , , ,共3个.
故选:C.
2. 如图,由3个相同的小正方体搭成的几何体的俯视图是( )
1A. B. C. D.
【答案】B
【解析】
【分析】本题考查了简单组合体的三视图,俯视图是从物体的上面看得到的视图.
找到从上面看所得到的图形即可.
【详解】解:从上面可看,是一行两个相邻的正方形.
故选:B.
3. 下列运算正确的是( )
A. B.
C. D.
【答案】A
【解析】
【分析】本题考查了整式的运算,根据合并同类项法则、积的乘方、同底数幂的除法和乘法分别计算即可
判断求解,掌握整式的运算法则是解题的关键.
【详解】解: 、 ,该选项正确,符合题意;
、 ,该选项错误,不合题意;
、 ,该选项错误,不合题意;
、 ,该选项错误,不合题意;
故选: .
4. 一副直角三角板按如图所示的方式摆放,点 在 的延长线上,当 时, 的度数为(
2)
A. B. C. D.
【答案】B
【解析】
【分析】本题考查平行线的性质,三角形的外角的性质,掌握平行线的性质,是解题的关键.证明
,再利用 ,进行求解即可.
【详解】解:由题意,得: ,
∵ ,
∴ ,
∴ ;
故选B.
5. 点 关于原点对称的点是 ,则 的值是( )
A. B. C. D.
【答案】A
【解析】
【分析】本题考查了关于原点对称的点的坐标特征,代数式求值,根据关于原点对称的点,横纵坐标互为
相反数可得 , ,再代入代数式计算即可求解,掌握关于原点对称的点的坐标特征是解题的关
键.
【详解】解:∵点 关于原点对称的点是 ,
∴ , ,
∴ ,
故选: .
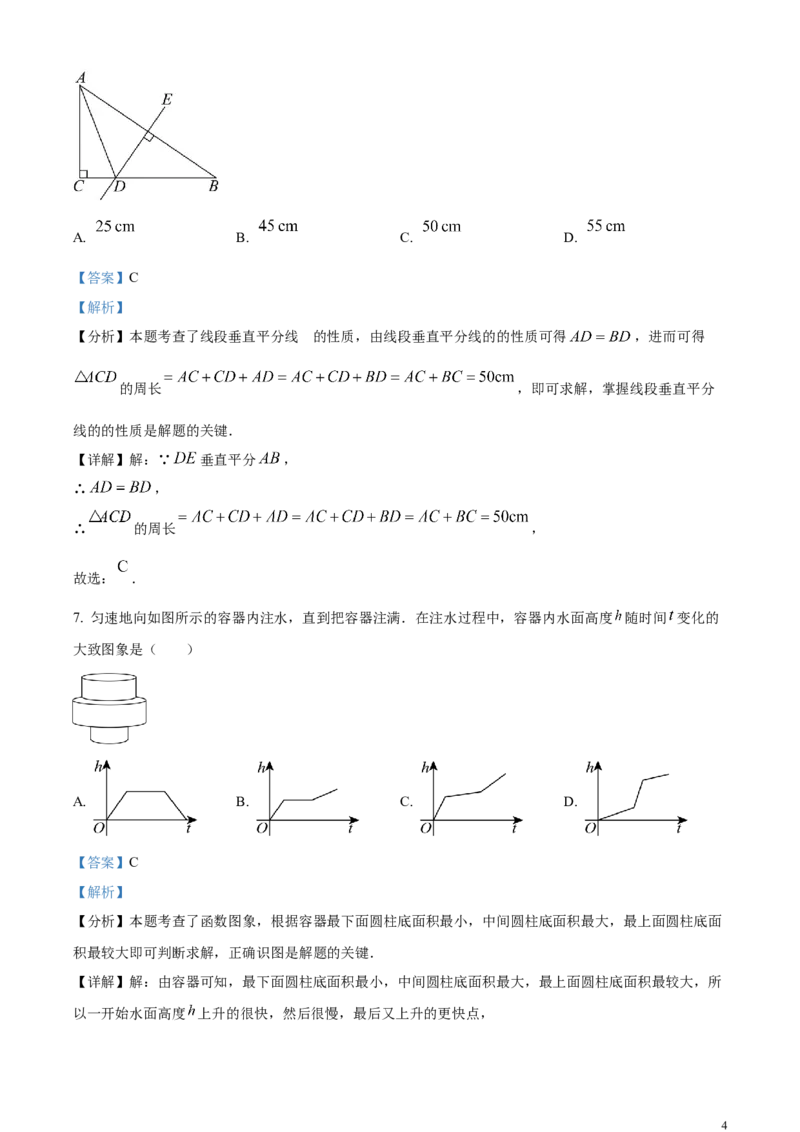
6. 如图,在 中, 垂直平分 交 于点 ,若 的周长为 ,
则 ( )
3A. B. C. D.
【答案】C
【解析】
【分析】本题考查了线段垂直平分线 的的性质,由线段垂直平分线的的性质可得 ,进而可得
的周长 ,即可求解,掌握线段垂直平分
线的的性质是解题的关键.
【详解】解:∵ 垂直平分 ,
∴ ,
∴ 的周长 ,
故选: .
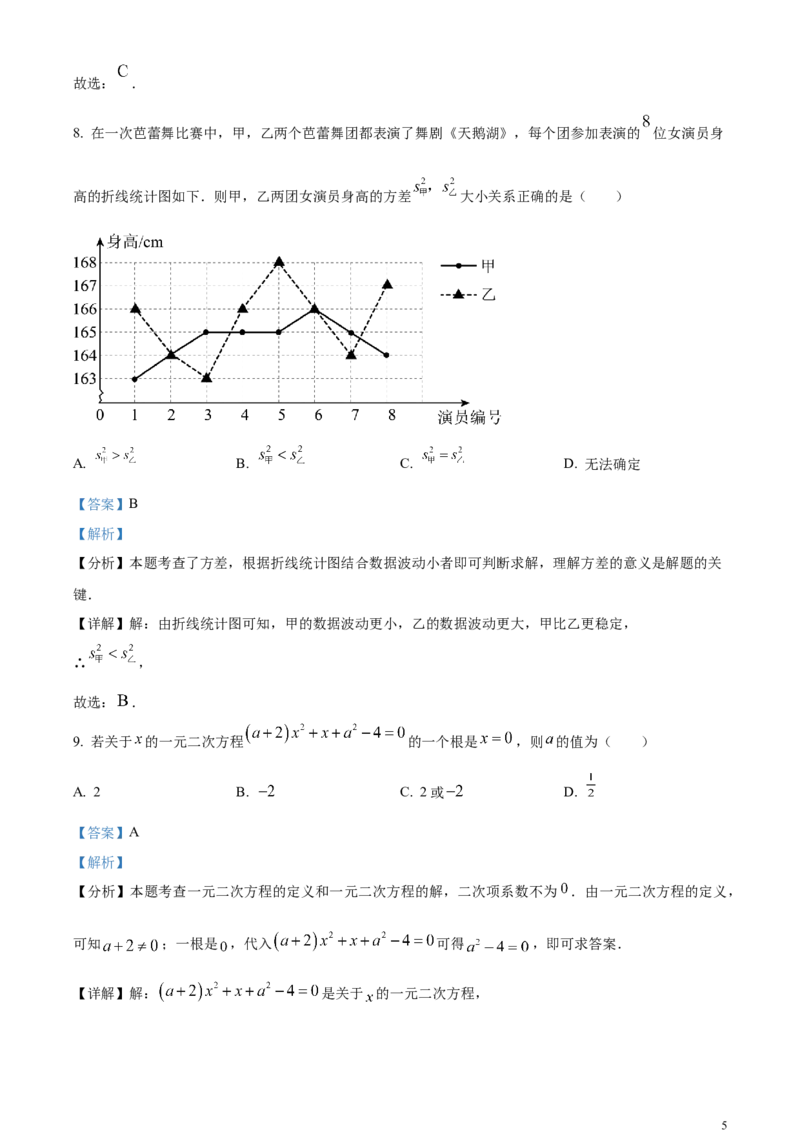
7. 匀速地向如图所示的容器内注水,直到把容器注满.在注水过程中,容器内水面高度 随时间 变化的
大致图象是( )
A. B. C. D.
【答案】C
【解析】
【分析】本题考查了函数图象,根据容器最下面圆柱底面积最小,中间圆柱底面积最大,最上面圆柱底面
积最较大即可判断求解,正确识图是解题的关键.
【详解】解:由容器可知,最下面圆柱底面积最小,中间圆柱底面积最大,最上面圆柱底面积最较大,所
以一开始水面高度 上升的很快,然后很慢,最后又上升的更快点,
4故选: .
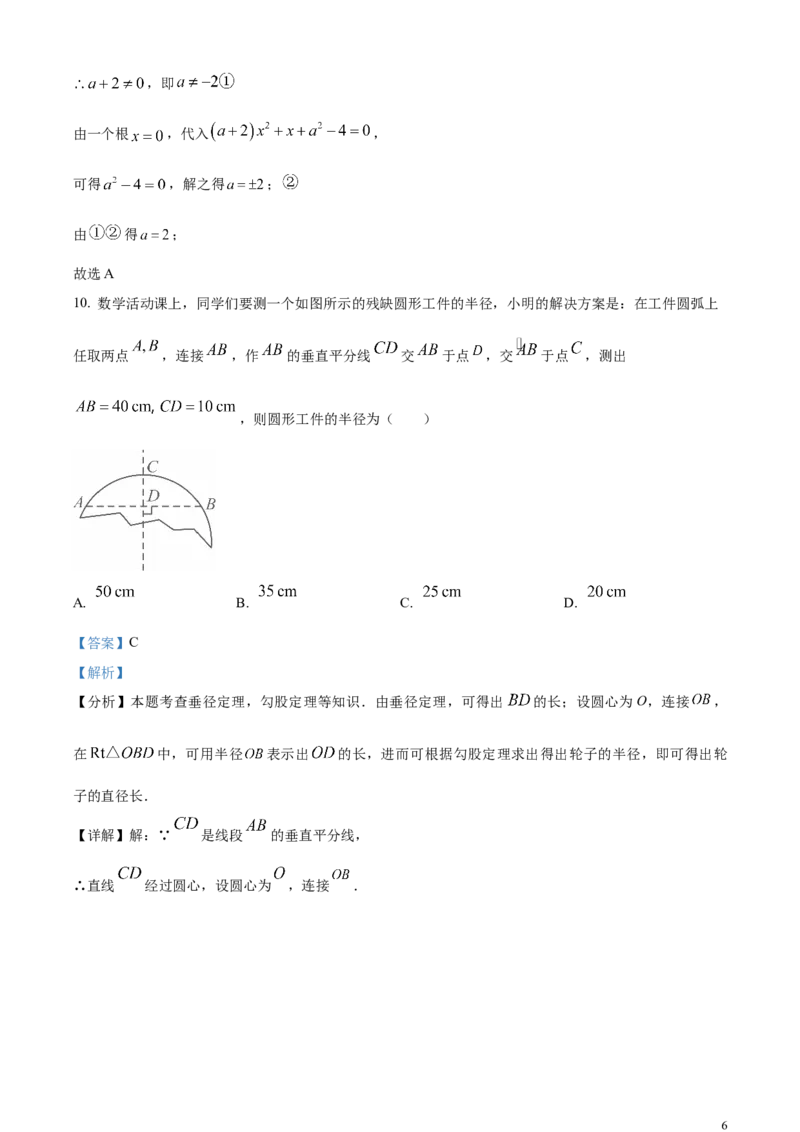
8. 在一次芭蕾舞比赛中,甲,乙两个芭蕾舞团都表演了舞剧《天鹅湖》,每个团参加表演的 位女演员身
高的折线统计图如下.则甲,乙两团女演员身高的方差 大小关系正确的是( )
A. B. C. D. 无法确定
【答案】B
【解析】
【分析】本题考查了方差,根据折线统计图结合数据波动小者即可判断求解,理解方差的意义是解题的关
键.
【详解】解:由折线统计图可知,甲的数据波动更小,乙的数据波动更大,甲比乙更稳定,
∴ ,
故选: .
9. 若关于 的一元二次方程 的一个根是 ,则 的值为( )
A. 2 B. C. 2或 D.
【答案】A
【解析】
【分析】本题考查一元二次方程的定义和一元二次方程的解,二次项系数不为 .由一元二次方程的定义,
可知 ;一根是 ,代入 可得 ,即可求答案.
【详解】解: 是关于 的一元二次方程,
5,即
由一个根 ,代入 ,
可得 ,解之得 ;
由 得 ;
故选A
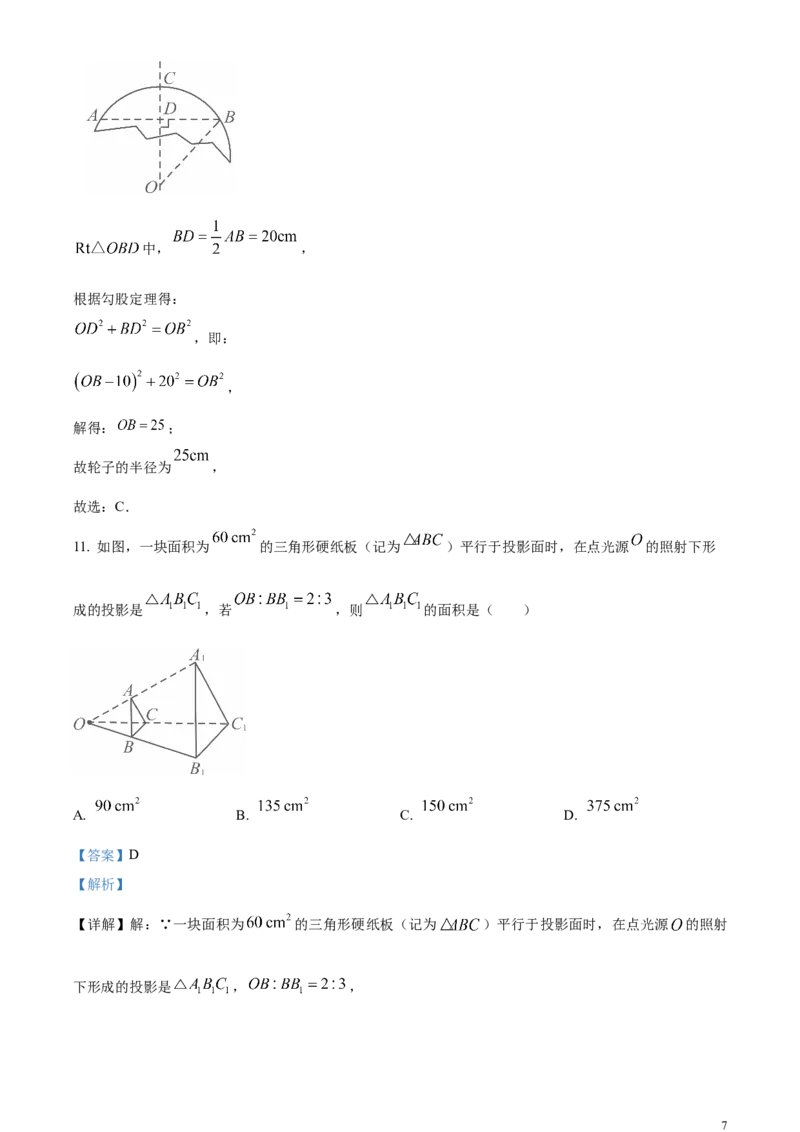
10. 数学活动课上,同学们要测一个如图所示的残缺圆形工件的半径,小明的解决方案是:在工件圆弧上
任取两点 ,连接 ,作 的垂直平分线 交 于点 ,交 于点 ,测出
,则圆形工件的半径为( )
A. B. C. D.
【答案】C
【解析】
【分析】本题考查垂径定理,勾股定理等知识.由垂径定理,可得出 的长;设圆心为O,连接 ,
在 中,可用半径 表示出 的长,进而可根据勾股定理求出得出轮子的半径,即可得出轮
子的直径长.
【详解】解:∵ 是线段 的垂直平分线,
∴直线 经过圆心,设圆心为 ,连接 .
6中, ,
根据勾股定理得:
,即:
,
解得: ;
故轮子的半径为 ,
故选:C.
11. 如图,一块面积为 的三角形硬纸板(记为 )平行于投影面时,在点光源 的照射下形
成的投影是 ,若 ,则 的面积是( )
A. B. C. D.
【答案】D
【解析】
【详解】解:∵一块面积为 的三角形硬纸板(记为 )平行于投影面时,在点光源 的照射
下形成的投影是 , ,
7∴ ,
∴位似图形由三角形硬纸板与其灯光照射下的中心投影组成,相似比为 ,
∵三角形硬纸板的面积为 ,
∴ ,
∴ 的面积为 .
故选:D.
12. 抛物线 经过 三点,则 的大小关系正确的是
( )
A. B. C. D.
【答案】D
【解析】
【分析】本题主要考查二次函数的图象与性质,熟练掌握二次函数的图象与性质是解题的关键.根据二次
函数的图象与性质可进行求解.
【详解】解:由抛物线 可知:开口向上,对称轴为直线 ,
该二次函数上所有的点满足离对称轴的距离越近,其对应的函数值也就越小,
∵ , , ,
而 , , ,
∴点 离对称轴最近,点 离对称轴最远,
∴ ;
故选:D.
8第Ⅱ卷非选择题(共52分)
二、填空题(共5小题,每小题4分,共20分)
13. 已知 ,且 ,则 ______.
【答案】
【解析】
【分析】本题考查了因式分解的应用,先把 的左边分解因式,再把 代入即可求出
的值.
【详解】解:∵ ,
∴ ,
∵ ,
∴ .
故答案为: .
14. 方程 的解是_______
【答案】x=9
【解析】
【分析】观察可得最简公分母是x(x-3),方程两边乘最简公分母,可以把分式方程转化为整式方程求解.
【详解】解:方程的两边同乘x(x-3),得
3x-9=2x,
解得x=9.
检验:把x=9代入x(x-3)=54≠0.
∴原方程的解为:x=9.
故答案为:x=9.
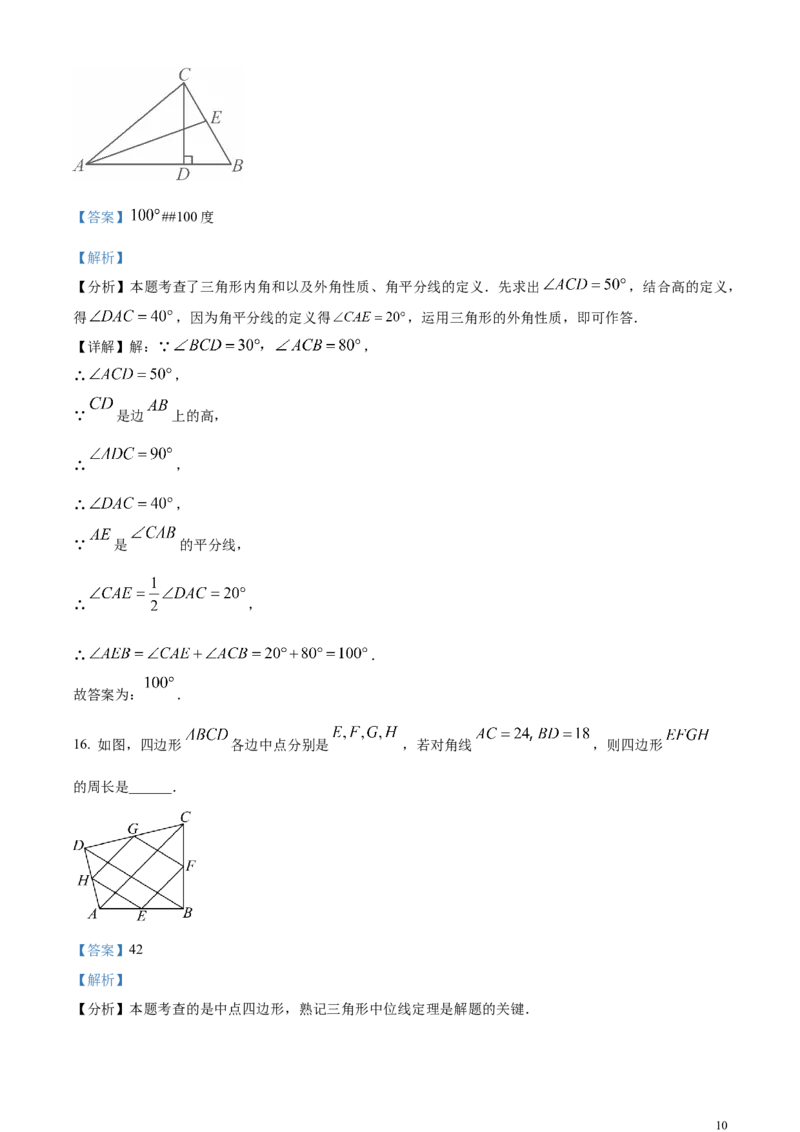
15. 如图, 中, 是边 上的高, 是 的平分线,
则 的度数是______.
9【答案】 ##100度
【解析】
【分析】本题考查了三角形内角和以及外角性质、角平分线的定义.先求出 ,结合高的定义,
得 ,因为角平分线的定义得 ,运用三角形的外角性质,即可作答.
【详解】解:∵ ,
∴ ,
∵ 是边 上的高,
∴ ,
∴ ,
∵ 是 的平分线,
∴ ,
∴ .
故答案为: .
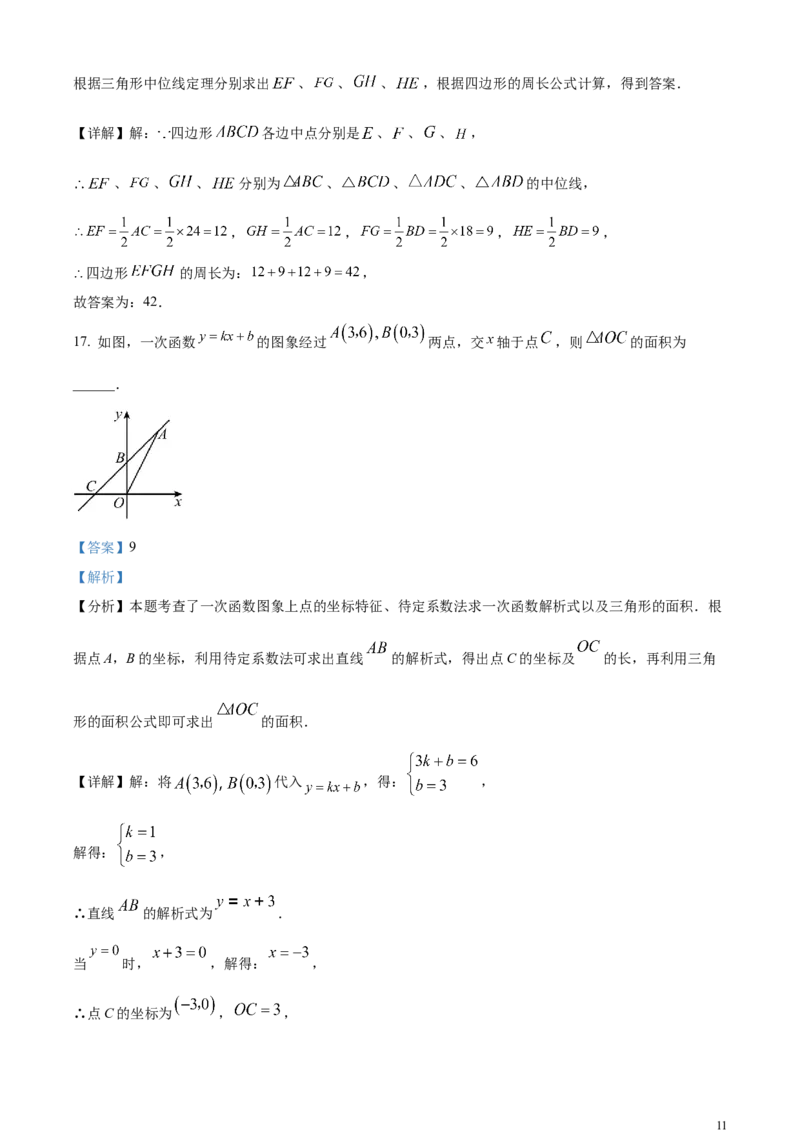
16. 如图,四边形 各边中点分别是 ,若对角线 ,则四边形
的周长是______.
【答案】42
【解析】
【分析】本题考查的是中点四边形,熟记三角形中位线定理是解题的关键.
10根据三角形中位线定理分别求出 、 、 、 ,根据四边形的周长公式计算,得到答案.
【详解】解: 四边形 各边中点分别是 、 、 、 ,
、 、 、 分别为 、 、 、 的中位线,
, , , ,
四边形 的周长为: ,
故答案为:42.
17. 如图,一次函数 的图象经过 两点,交 轴于点 ,则 的面积为
______.
【答案】9
【解析】
【分析】本题考查了一次函数图象上点的坐标特征、待定系数法求一次函数解析式以及三角形的面积.根
据点A,B的坐标,利用待定系数法可求出直线 的解析式,得出点C的坐标及 的长,再利用三角
形的面积公式即可求出 的面积.
【详解】解:将 代入 ,得: ,
解得: ,
∴直线 的解析式为 .
当 时, ,解得: ,
∴点C的坐标为 , ,
11∴ .
故答案为:9.
三、解答题(共5小题,共32分)解答应写出文字说明,证明过程或演算步骤.
18. 计算: .
【答案】2
【解析】
【分析】本题考查了实数的混合运算.分别进行零指数幂、负整数指数幂、二次根式及绝对值的运算,然
后代入特殊角的三角函数值代入运算即可.
【详解】解:
.
19. 求不等式 的整数解.
【答案】
【解析】
【分析】本题考查了解一元一次不等式组,熟练掌握知识点是解题的关键.
先将 变形为 ,再解每一个不等式,取解集的公共部分作为不等式组的解集,
再找出其中的整数解即可.
【详解】解:由题意得 ,
12解①得: ,
解②得: ,
∴该不等式组的解集为: ,
∴整数解为:
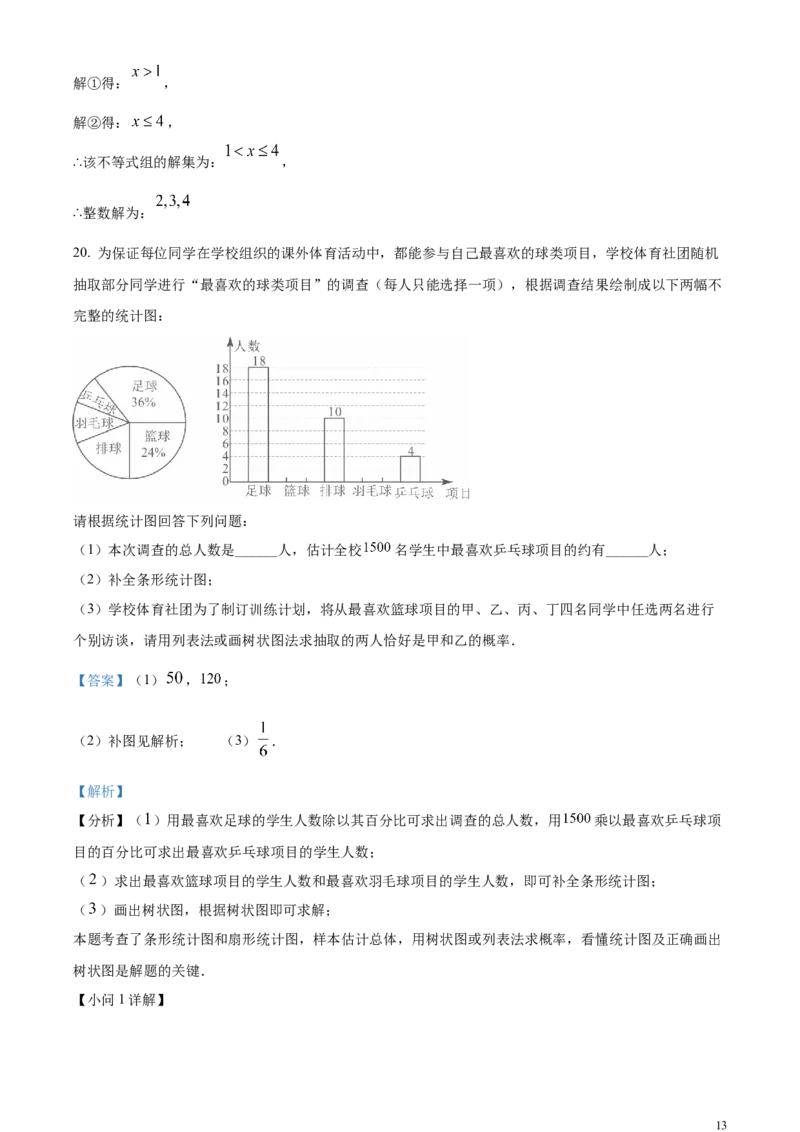
20. 为保证每位同学在学校组织的课外体育活动中,都能参与自己最喜欢的球类项目,学校体育社团随机
抽取部分同学进行“最喜欢的球类项目”的调查(每人只能选择一项),根据调查结果绘制成以下两幅不
完整的统计图:
请根据统计图回答下列问题:
(1)本次调查的总人数是______人,估计全校 名学生中最喜欢乒乓球项目的约有______人;
(2)补全条形统计图;
(3)学校体育社团为了制订训练计划,将从最喜欢篮球项目的甲、乙、丙、丁四名同学中任选两名进行
个别访谈,请用列表法或画树状图法求抽取的两人恰好是甲和乙的概率.
【答案】(1) , ;
(2)补图见解析; (3) .
【解析】
【分析】( )用最喜欢足球的学生人数除以其百分比可求出调查的总人数,用 乘以最喜欢乒乓球项
目的百分比可求出最喜欢乒乓球项目的学生人数;
( )求出最喜欢篮球项目的学生人数和最喜欢羽毛球项目的学生人数,即可补全条形统计图;
( )画出树状图,根据树状图即可求解;
本题考查了条形统计图和扇形统计图,样本估计总体,用树状图或列表法求概率,看懂统计图及正确画出
树状图是解题的关键.
【小问1详解】
13解:本次调查的总人数是 人,
估计全校 名学生中最喜欢乒乓球项目的约有 人,
故答案为: , ;
【小问2详解】
解:最喜欢篮球项目的学生有 人,
∴最喜欢羽毛球项目的学生有 人,
∴补全条形统计图如下:
【小问3详解】
解:画树状图如下:
由树状图可知,共有 种等结果,其中抽取的两人恰好是甲和乙的结果有 种,
∴抽取的两人恰好是甲和乙的概率为 .
21. 为建设全域旅游西昌,加快旅游产业发展. 年 月 日位于西昌主城区东部的历史风貌核心区
唐园正式开园,坐落于唐园内的怀远塔乃唐园至高点,为七层密檐式八角砖混结构阁楼式塔楼,建筑面积
为 平方米,塔顶金碧辉煌,为“火珠垂莲”窣( )堵坡造型.某校为了让学生进一步了解怀远
塔,组织九年级( )班学生利用综合实践课测量怀远塔的高度.小江同学站在如图所示的怀远塔前的平
地上 点处,测得塔顶 的仰角为 ,眼睛 距离地面 ,向塔前行 ,到达点 处,测得塔顶
14的仰角为 ,求塔高 .(参考数据: ,结果精确到 )
【答案】 .
【解析】
【分析】本题考查了解直角三角形的应用 仰角俯角问题,设 ,解直角三角形得到
, ,再根据 可得 ,解方程求
出 即可求解,正确解直角三角形是解题的关键.
【详解】解:由题意可得, , , , ,
设 ,
在 中, ,
在 中, ,
∵ ,
∴ ,
解得 ,
∴ ,
15答:塔高 为 .
22. 如图,正比例函数 与反比例函数 的图象交于点 .
(1)求反比例函数的解析式;
(2)把直线 向上平移3个单位长度与 的图象交于点 ,连接 ,求
的面积.
【答案】(1)
(2)6
【解析】
【分析】本题考查了一次函数与反比例函数的交点问题,待定系数法求函数解析式,一次函数的平移等知
识,熟练掌握函数的平移法则是关键.
(1)待定系数法求出反比例函数解析式即可;
(2)先得到平移后直线解析式,联立方程组求出点 坐标,根据平行线间的距离可得 ,代
入数据计算即可.
【小问1详解】
解: 点 在正比例函数图象上,
,解得 ,
,
在反比例函数图象上,
16,
反比例函数解析式为 .
【小问2详解】
解:把直线 向上平移3个单位得到解析式为 ,
令 ,则 ,
∴记直线与 轴交点坐标为 ,连接 ,
联立方程组 ,
解得 , (舍去),
,
由题意得: ,
∴ 同底等高,
.
B卷(共50分)
四、填空题(共2小题,每小题5分,共10分)
23. 已知 ,则 的值为______.
17【答案】
【解析】
【分析】本题考查了解一元二次方程,熟练掌握解一元二次方程的方法是解题的关键.
将 代入 ,转化为解一元二次方程, ,要进行舍解.
【详解】解:∵ ,
∴ ,
将 代入
得, ,
即: ,
,
∴ 或 ,
∵ ,
∴ 舍,
∴ ,
故答案为:3.
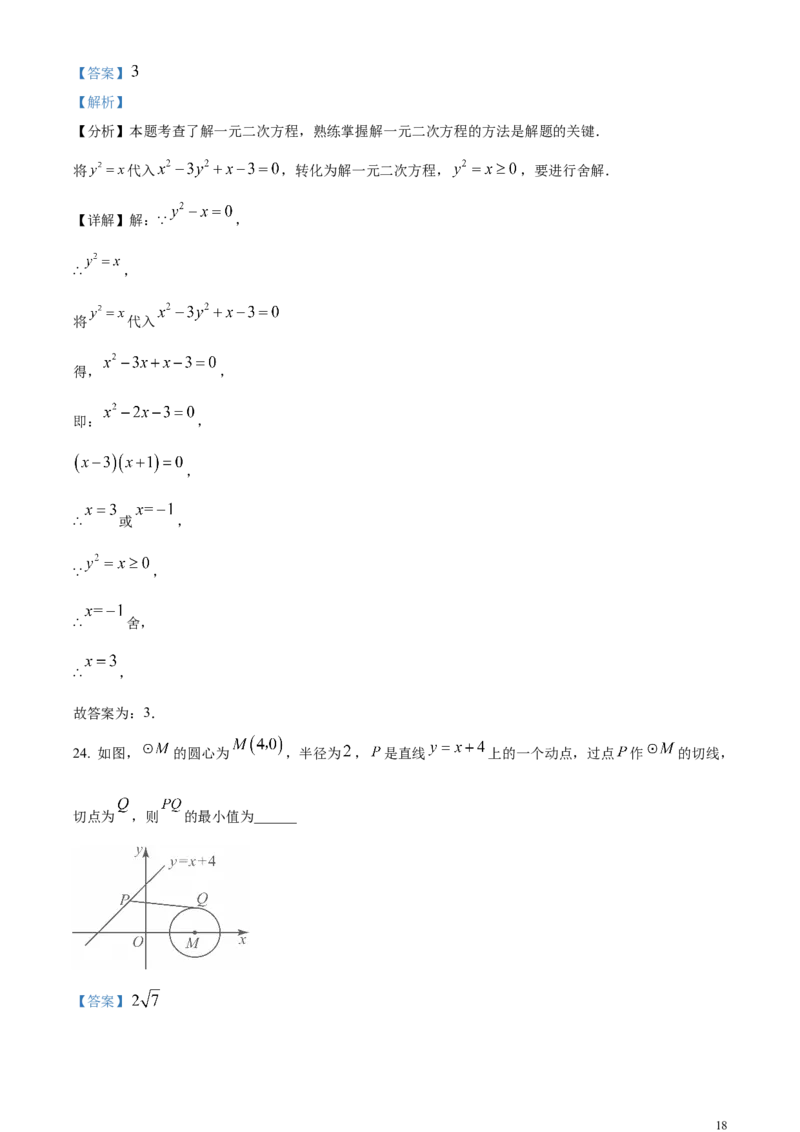
24. 如图, 的圆心为 ,半径为 , 是直线 上的一个动点,过点 作 的切线,
切点为 ,则 的最小值为______
【答案】
18【解析】
【详解】解:记直线 与x,y轴分别交于点A,K,连接 ,
当 , ,当 ,即 ,
解得: ,
而
∴ ,
∴ 均是等腰直角三角形,
∴ ,
∴ ,
∵ 与 相切,
∴ ,
∴ ,
∵ ,
∴当 最小时即 最小,
∴当 时,取得最小值,
即点P与点K重合,此时 最小值为 ,
在 中,由勾股定理得: ,
19∴ ,
∴ 最小值为 .
【点睛】本题考查了圆的切线的性质,勾股定理,一次函数与坐标轴的交点问题,垂线段最短,正确添加
辅助线是解题的关键.
五、解答题(共4小题,共40分)
25. 阅读下面材料,并解决相关问题:
下图是一个三角点阵,从上向下数有无数多行,其中第一行有1个点,第二行有2个点……第 行有 个
点……
容易发现,三角点阵中前4行的点数之和为10.
的
(1)探索:三角点阵中前8行 点数之和为_____,前15行的点数之和为______,那么,前 行的点数之
和为______
的
(2)体验:三角点阵中前 行 点数之和______(填“能”或“不能”)为500.
(3)运用:某广场要摆放若干种造型的盆景,其中一种造型要用420盆同样规格的花,按照第一排2盆,
第二排4盆,第三排6盆……第 排 盆的规律摆放而成,则一共能摆放多少排?
【答案】(1)36;120;
(2)不能 (3)一共能摆放20排.
【解析】
【分析】本题考查了一元二次方程的应用,找准等量关系,正确列出一元二次方程是解题的关键.
(1)根据图形,总结规律,列式计算即可求解;
(2)根据前n行的点数和是500,即可得出关于n的一元二次方程,解之即可判断;
(2)先得到前n行的点数和是 ,再根据题意得出关于n的一元二次方程,解之即可得出n的值.
【小问1详解】
20解:三角点阵中前8行的点数之和为 ,
前15行的点数之和为 ,
那么,前 行的点数之和为 ;
故答案为:36;120; ;
【小问2详解】
解:不能,
理由如下:
由题意得 ,
得 ,
,
∴此方程无正整数解,
所以三角点阵中前n行的点数和不能是500;
故答案为:不能;
【小问3详解】
解:同理,前 行的点数之和为 ,
由题意得 ,
得 ,即 ,
解得 或 (舍去),
∴一共能摆放20排.
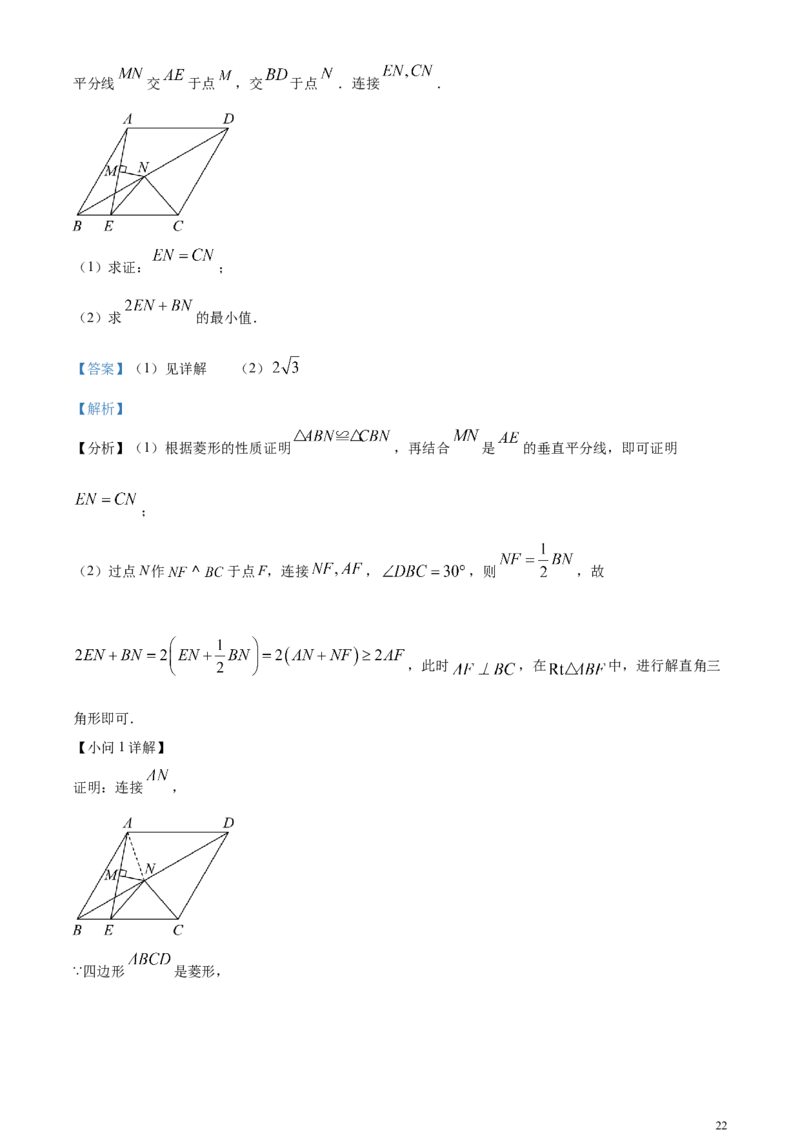
26. 如图,在菱形 中, , 是 边上一个动点,连接 , 的垂直
21平分线 交 于点 ,交 于点 .连接 .
(1)求证: ;
(2)求 的最小值.
【答案】(1)见详解 (2)
【解析】
【分析】(1)根据菱形的性质证明 ,再结合 是 的垂直平分线,即可证明
;
(2)过点N作 于点F,连接 , ,则 ,故
,此时 ,在 中,进行解直角三
角形即可.
【小问1详解】
证明:连接 ,
∵四边形 是菱形,
22∴ , ,
∵ ,
∴ ,
∴ ,
∵ 是 的垂直平分线,
∴ ,
∴ ;
【小问2详解】
解:过点N作 于点F,连接 ,
∵ ,
∴ ,
∵ ,
∴ ,
当点A、N、F三点共线时,取得最小值,如图:
即 ,
23∴在 中, ,
∴ 的最小值为 .
【点睛】本题考查了菱形的性质,垂直平分线的性质,全等三角形的判定与性质,垂线段最短,解直角三
角形,正确添加辅助线是解决本题的关键.
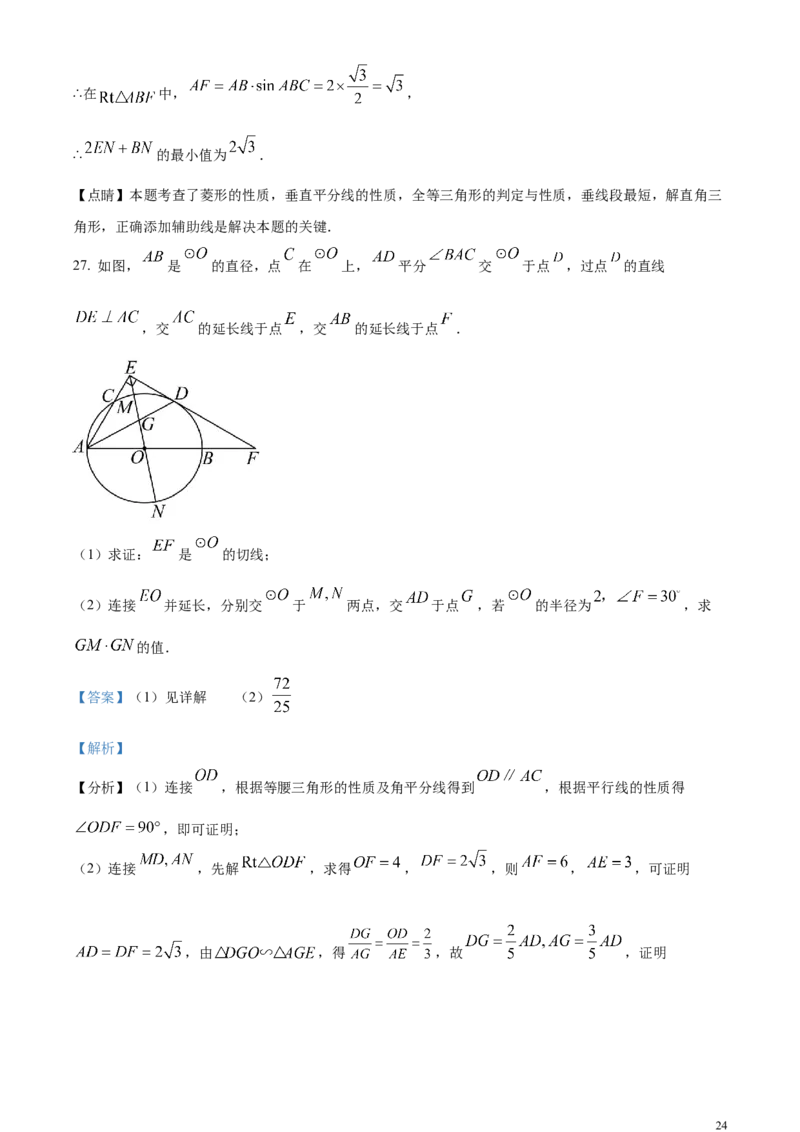
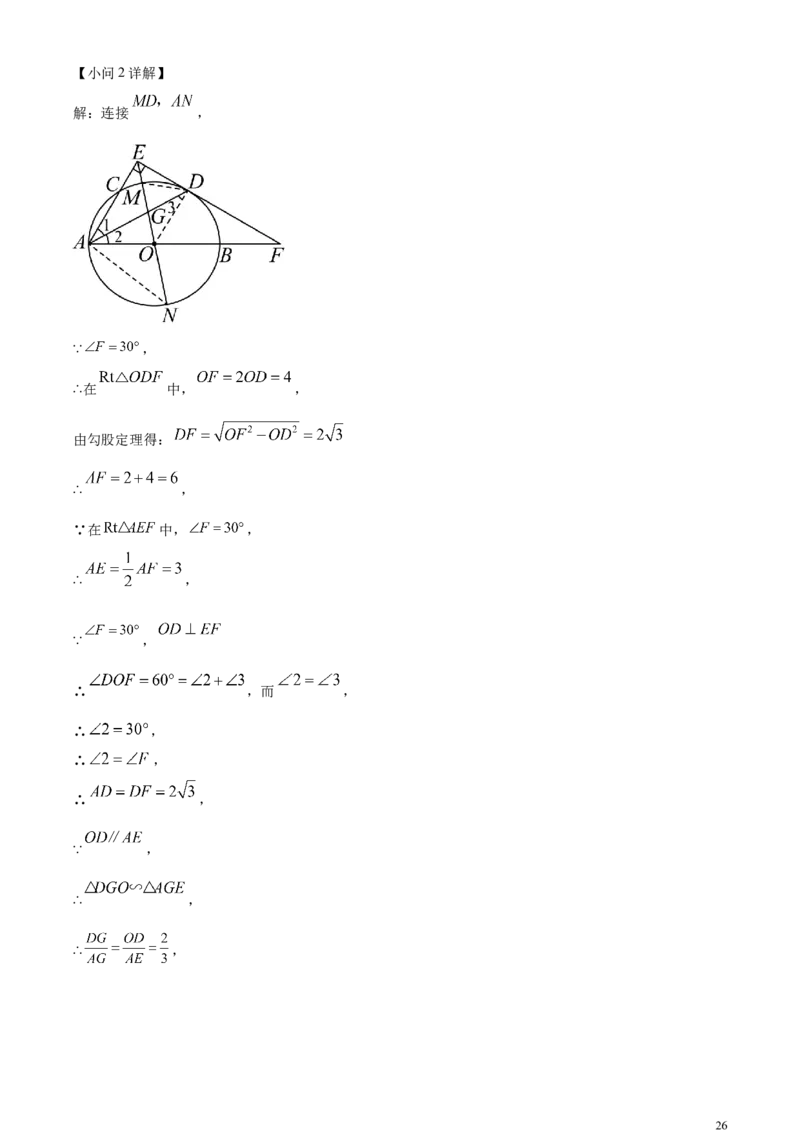
27. 如图, 是 的直径,点 在 上, 平分 交 于点 ,过点 的直线
,交 的延长线于点 ,交 的延长线于点 .
(1)求证: 是 的切线;
(2)连接 并延长,分别交 于 两点,交 于点 ,若 的半径为 ,求
的值.
【答案】(1)见详解 (2)
【解析】
【分析】(1)连接 ,根据等腰三角形的性质及角平分线得到 ,根据平行线的性质得
,即可证明;
(2)连接 ,先解 ,求得 , ,则 , ,可证明
,由 ,得 ,故 ,证明
24,即可得到 .
【小问1详解】
解:连接 ,
∵ ,
∴ ,
∵ 平分 ,
∴ ,
∴ ,
∴ ,
∴
∵ ,
∴ ,
∴ ,
即 ,
∵ 是 的半径
∴ 是 的切线;
25【小问2详解】
解:连接 ,
∵ ,
∴在 中, ,
由勾股定理得:
∴ ,
∵在 中, ,
∴ ,
∵ ,
∴ ,而 ,
∴ ,
∴ ,
∴ ,
∵ ,
∴ ,
∴ ,
26∴ ,
∵ ,
∴ ,
∵ ,
∴ ,
∴ ,
∴ .
【点睛】本题考查了圆的切线的判定,相似三角形的判定与性质,勾股定理, 的直角三角形的性质,
等腰三角形的性质,正确添加辅助线是解题的关键.
28. 如图,抛物线 与直线 相交于 两点,与 轴相交于另一点
.
(1)求抛物线的解析式;
(2)点 是直线 上方抛物线上的一个动点(不与 重合),过点 作直线 轴于点 ,交
直线 于点 ,当 时,求 点坐标;
(3)抛物线上是否存在点 使 的面积等于 面积的一半?若存在,请直接写出点 的坐标;
若不存在,请说明理由.
【答案】(1)抛物线的解析式为
27(2) 的坐标为
(3) 的坐标为 或 或 或
【解析】
【分析】(1)把 代入 求出 ,再用待定系数法可得抛物线 的解析式为
;
(2)设 ,则 , ,由 ,可得 ,解
出 的值可得 的坐标为 ;
(3)过 作 轴交直线 于 ,求出 ,知 ,故 ,设
, 则 , 可 得 ,
,根据 的面积等于 面积的
一半,有 ,可得 ,即 或 ,解出
的值可得答案.
【小问1详解】
解:把 代入 得: ,
,
把 , 代入 得:
,
28解得 ,
抛物线的解析式为 ;
【小问2详解】
解:设 ,则 , ,
,
,
解得 或 (此时 不在直线 上方,舍去);
的坐标为 ;
【小问3详解】
解:抛物线上存在点 ,使 的面积等于 面积的一半,理由如下:
过 作 轴交直线 于 ,过点B作 ,延长 交x轴于点F,如图:
在 中,令 得 ,
解得 或 ,
, ,
,
,
29,
设 ,则 ,
,
∵
,
的面积等于 面积的一半,
,
,
或 ,
解得 或 ,
的坐标为 或 或 或 .
【点睛】本题考查二次函数的图像与性质,涉及待定系数法求函数解析式,抛物线与坐标轴交点问题,解
一元二次方程,三角形面积等知识,解题的关键是用含字母的式子表示相关点坐标和相关线段的长度.
30