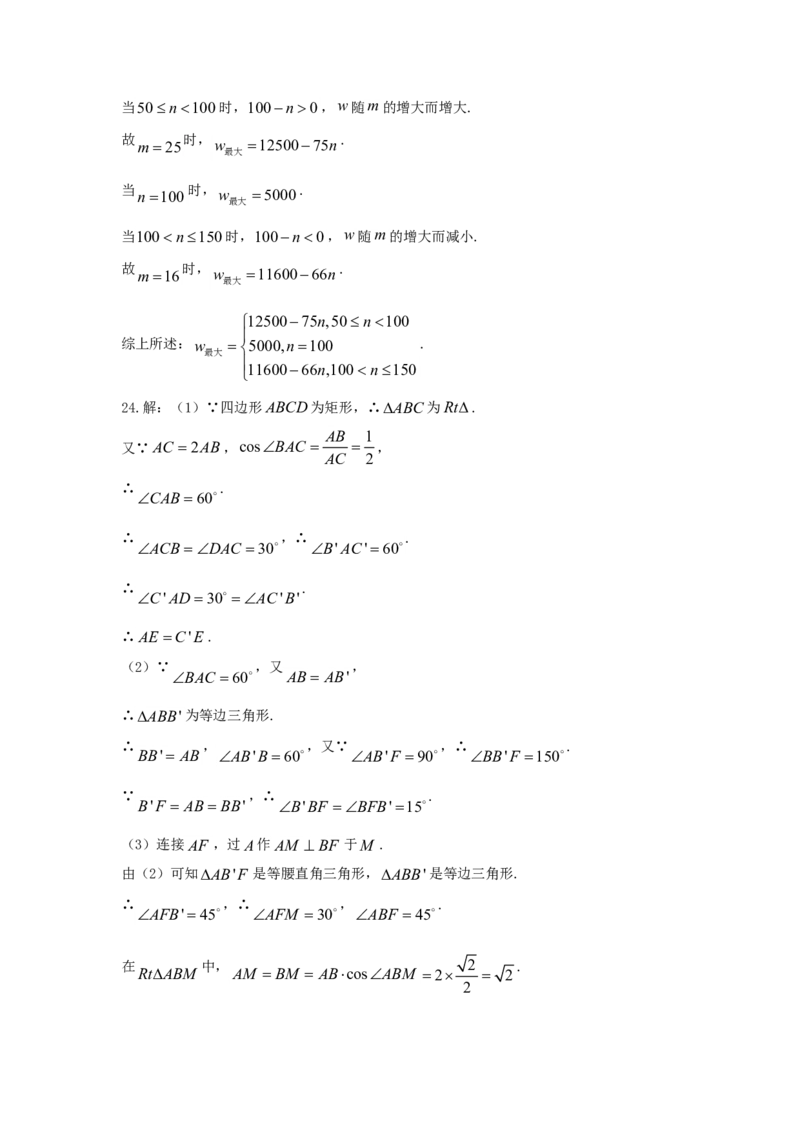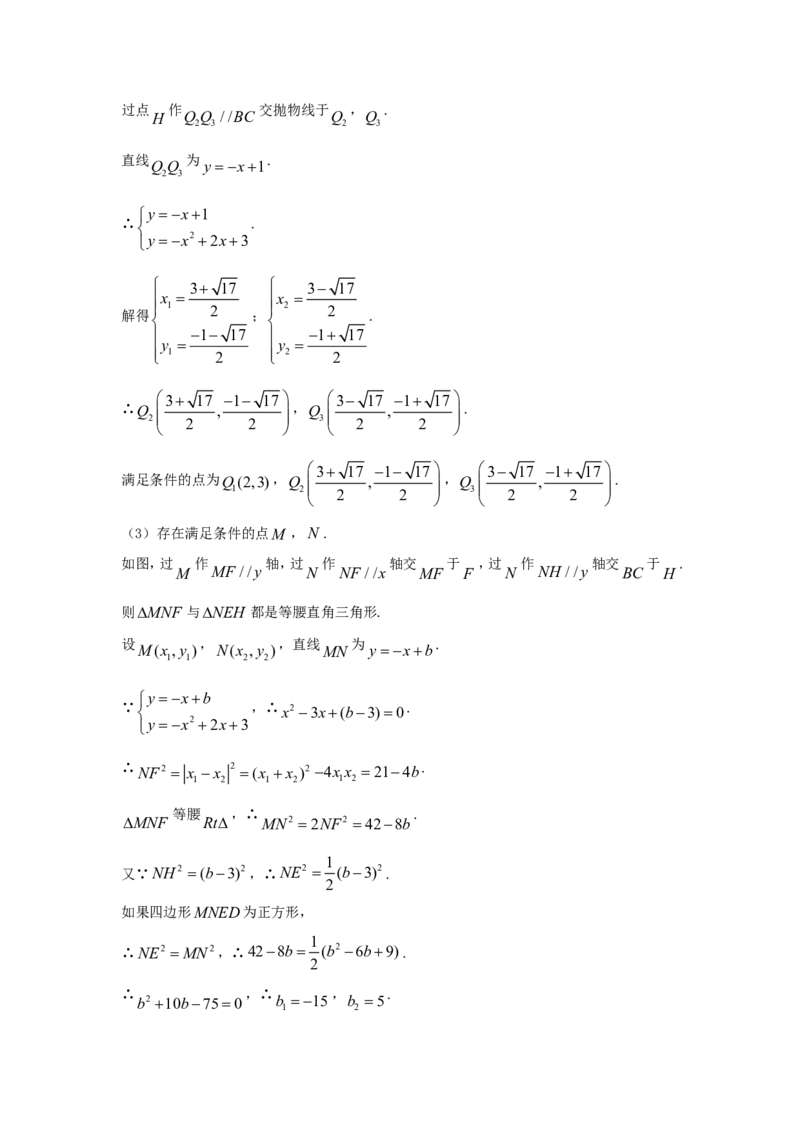四川省南充市2018年中考数学真题试题（含答案）_中考真题_2.数学中考真题2015-2024年_2018年全国中考数学258份

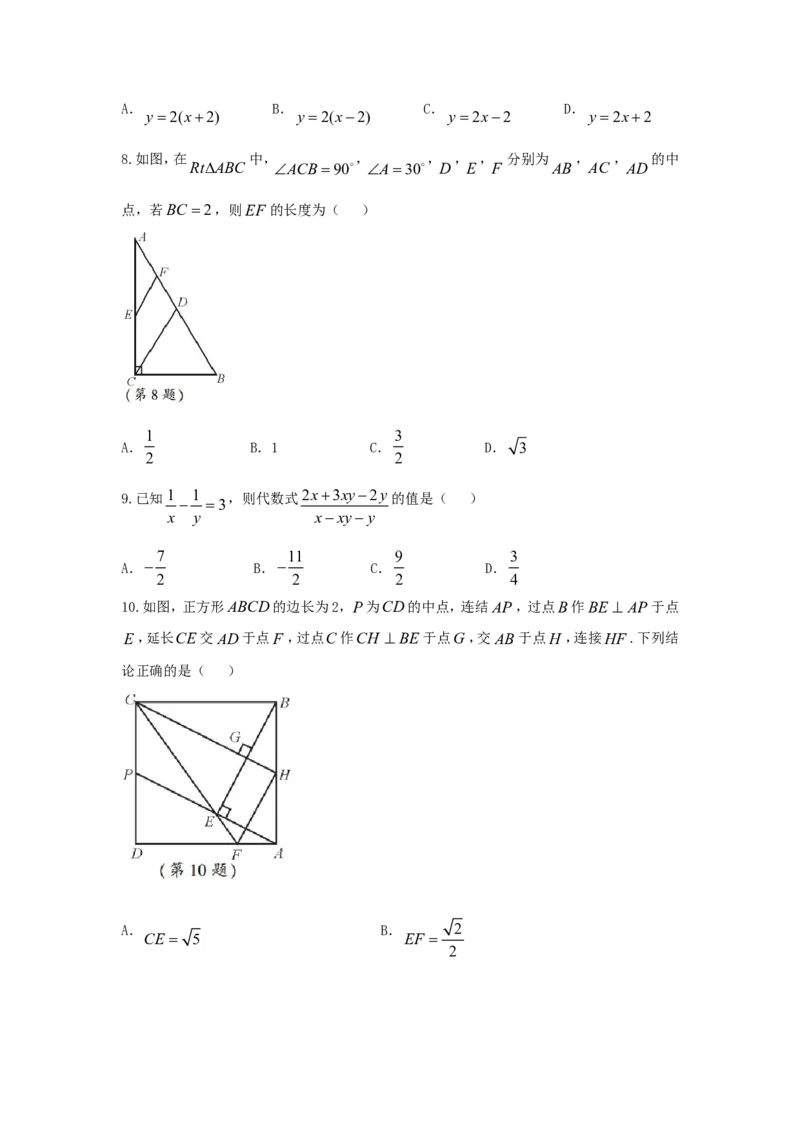
四川省南充市2018年中考数学真题试题（含答案） 一、选择题（本大题共10个小题，每小题3分，共30分） 1.下列实数中，最小的数是（ ） A． B．0 C．1 D．  2 3 8 2.下列图形中，既是轴对称图形又是中心对称图形的是（ ） A．扇形 B．正五边形 C．菱形 D．平行四边形 3.下列说法正确的是（ ） A．调查某班学生的身高情况，适宜采用全面调查 B．篮球队员在罚球线上投篮两次都未投中，这是不可能事件 C．天气预报说明天的降水概率为95%，意味着明天一定下雨 D．小南抛掷两次硬币都是正面向上，说明抛掷硬币正面向上的概率是1 4.下列计算正确的是（ ） A． B． a4ba2ba2b (ab)2 a2 b2 C． D． a2a3 a6 3a2 2a2 a2 5.如图， 是 的直径， 是 上的一点， ，则 的度数是（ ） BC O A O OAC 32 B A． B． C． D． 58 60 64 68 6.不等式x12x1的解集在数轴上表示为（ ） A． B． C． D． 7.直线 向下平移2个单位长度得到的直线是（ ） y 2xA． B． C． D． y 2(x2) y 2(x2) y 2x2 y 2x2 8.如图，在 中， ， ， ， ， 分别为 ， ， 的中 RtABC ACB90 A30 D E F AB AC AD 点，若BC 2，则EF 的长度为（ ） 1 3 A． B．1 C． D． 3 2 2 1 1 2x3xy2y 9.已知 ，则代数式 的值是（ ）  3 x y xxy y 7 11 9 3 A． B． C． D． 2 2 2 4 10.如图，正方形ABCD的边长为2，P为CD的中点，连结AP，过点B作BE  AP于点 E，延长CE交AD于点F ，过点C作CH  BE 于点G ，交AB于点H ，连接HF .下列结 论正确的是（ ） A． B． 2 CE  5 EF  2C． 5 D． cosCEP  HF2  EFCF 5 二、填空题（本大题共6个小题，每小题3分，共18分） 11.某地某天的最高气温是 ，最低气温是 ，则该地当天的温差为 ． 6C 4C C 12.甲、乙两名同学的5次射击训练成绩（单位：环）如下表. 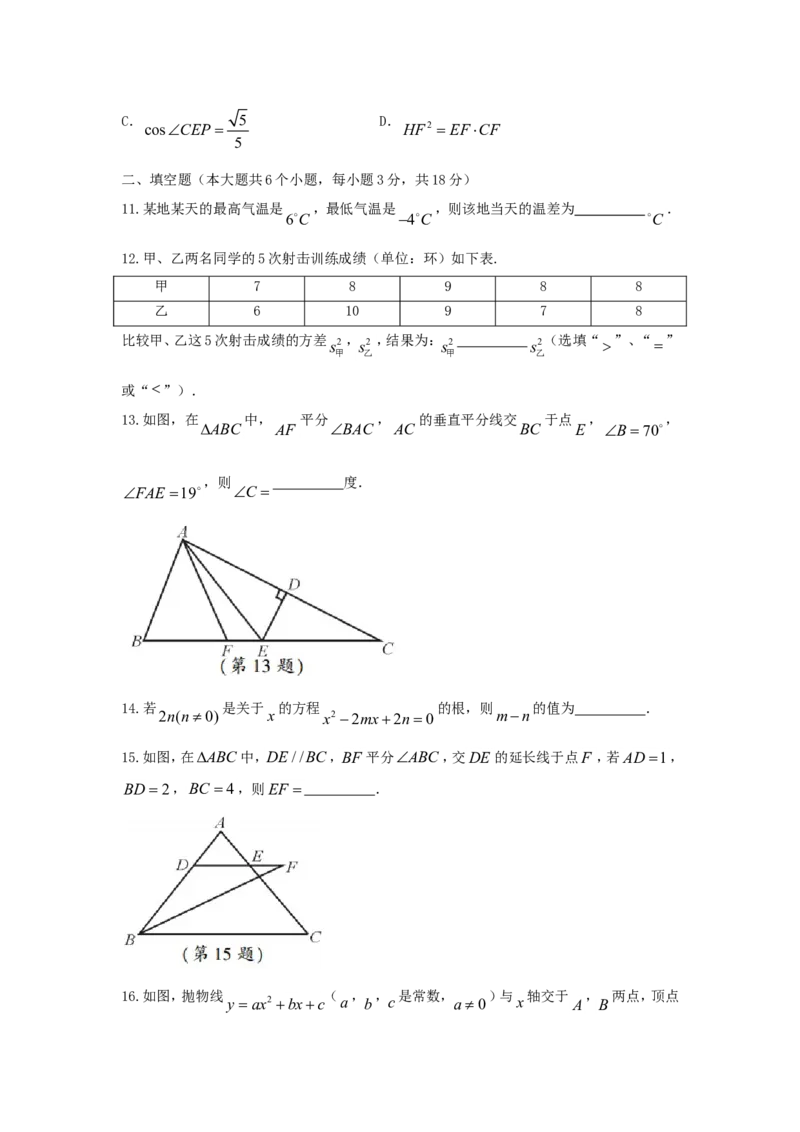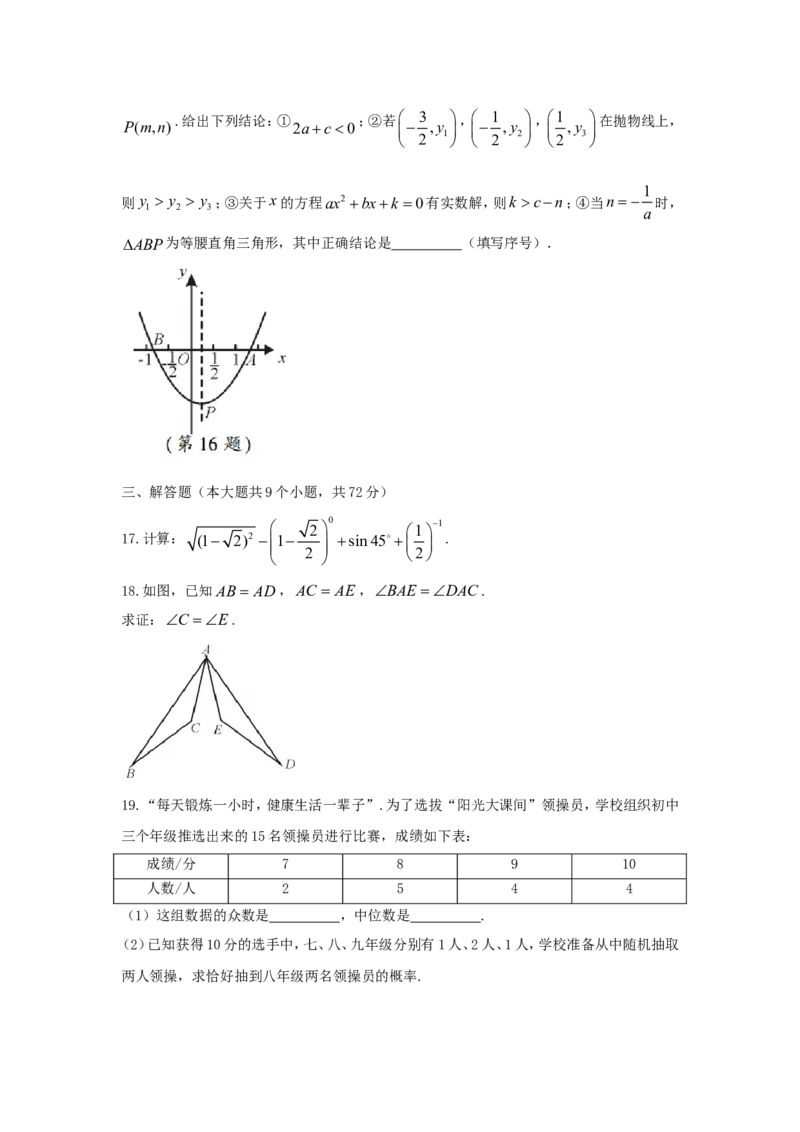甲 7 8 9 8 8 乙 6 10 9 7 8 比较甲、乙这5次射击成绩的方差 ， ，结果为： （选填“ ”、“ ” s2 s2 s2 s2   甲 乙 甲 乙 或“”）． 13.如图，在 中， 平分 ， 的垂直平分线交 于点 ， ， ABC AF BAC AC BC E B70 ，则 度． FAE 19 C  14.若 是关于 的方程 的根，则 的值为 ． 2n(n0) x x2 2mx2n0 mn 15.如图，在ABC中，DE//BC，BF 平分ABC，交DE 的延长线于点F ，若AD1， BD2，BC 4，则EF  ． 16.如图，抛物线 （ ， ， 是常数， ）与 轴交于 ， 两点，顶点 y ax2 bxc a b c a0 x A B.给出下列结论：① ；②若 3 ， 1 ，1 在抛物线上， P(m,n) 2ac0   ,y    ,y   ,y   2 1   2 2  2 3  1 则y  y  y ；③关于x的方程ax2 bxk 0有实数解，则k cn；④当n 时， 1 2 3 a ABP为等腰直角三角形，其中正确结论是 （填写序号）． 三、解答题（本大题共9个小题，共72分）  2  0 1 1 17.计算： (1 2)2   1   sin45   .  2  2 18.如图，已知AB AD，AC  AE，BAE DAC. 求证：C E . 19.“每天锻炼一小时，健康生活一辈子”.为了选拔“阳光大课间”领操员，学校组织初中 三个年级推选出来的15名领操员进行比赛，成绩如下表： 成绩/分 7 8 9 10 人数/人 2 5 4 4 （1）这组数据的众数是 ，中位数是 . （2）已知获得10分的选手中，七、八、九年级分别有1人、2人、1人，学校准备从中随机抽取 两人领操，求恰好抽到八年级两名领操员的概率.20.已知关于 的一元二次方程 . x x2 (2m2)x(m2 2m)0 （1）求证：方程有两个不相等的实数根. （2）如果方程的两实数根为 ， ，且 ，求 的值. x x x2 x 2 10 m 1 2 1 2 m 1 21.如图，直线y kxb(k 0)与双曲线y  (m0)交于点A( ,2)，B(n,1). x 2 （1）求直线与双曲线的解析式； （2）点 在 轴上，如果 ，求点 的坐标. P x S 3 P ABP 22.如图，C是O上一点，点P在直径AB的延长线上，O的半径为3，PB2， PC 4. （1）求证：PC是O的切线. （2）求tanCAB的值. 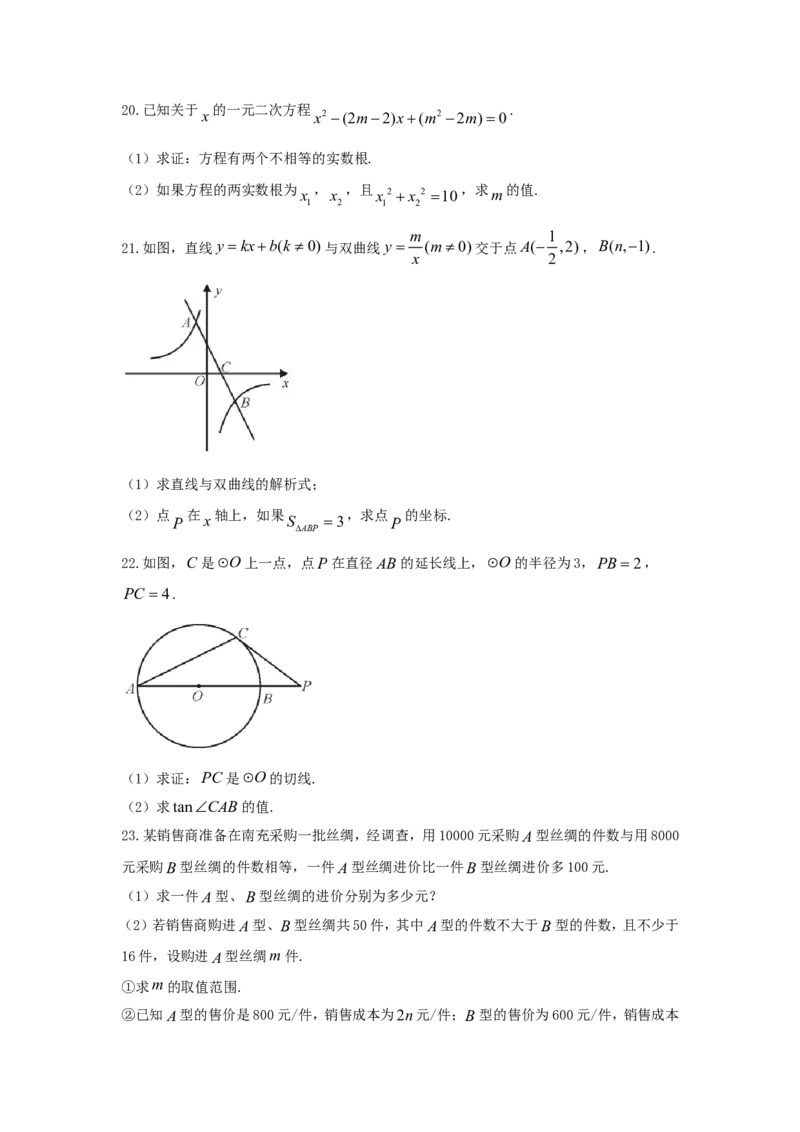23.某销售商准备在南充采购一批丝绸，经调查，用10000元采购A型丝绸的件数与用8000 元采购B型丝绸的件数相等，一件A型丝绸进价比一件B型丝绸进价多100元. （1）求一件A型、B型丝绸的进价分别为多少元？ （2）若销售商购进A型、B型丝绸共50件，其中A型的件数不大于B型的件数，且不少于 16件，设购进A型丝绸m件. ①求m的取值范围. ②已知A型的售价是800元/件，销售成本为2n元/件；B型的售价为600元/件，销售成本为n元/件.如果50n150，求销售这批丝绸的最大利润w（元）与n（元）的函数关系式 （每件销售利润=售价-进价-销售成本）. 24.如图，矩形ABCD中，AC 2AB，将矩形ABCD绕点A旋转得到矩形AB'C'D'，使 点B的对应点B'落在AC 上，B'C'交AD于点E，在B'C'上取点F ，使B'F  AB. （1）求证：AE C'E . （2）求FBB'的度数. （3）已知AB2，求BF 的长. 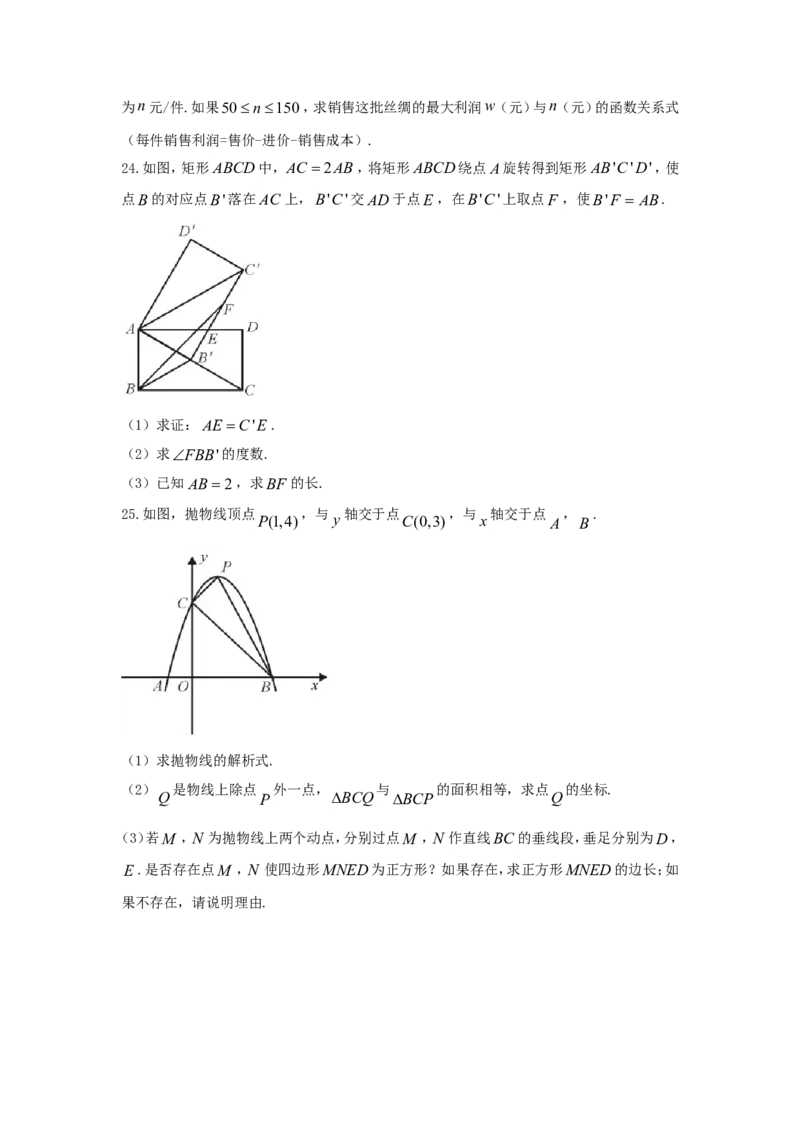25.如图，抛物线顶点 ，与 轴交于点 ，与 轴交于点 ， . P(1,4) y C(0,3) x A B （1）求抛物线的解析式. （2） 是物线上除点 外一点， 与 的面积相等，求点 的坐标. Q P BCQ BCP Q （3）若M ，N 为抛物线上两个动点，分别过点M ，N 作直线BC的垂线段，垂足分别为D， E.是否存在点M ，N 使四边形MNED为正方形？如果存在，求正方形MNED的边长；如 果不存在，请说明理由.南充市二〇一八年初中学业水平考试 数学参考答案 一、选择题 1-5: ACADA 6-10: BCBDD 二、填空题 1 2 11. 10 12.  13. 24 14. 15. 16. ②④ 2 3 三、解答题 17.解：原式 2 3 .  211 2  2 2 2 18.证明：∵BAE DAC，∴BAECAE DACCAE. ∴BAC DAE. 在ABC与ADE中， AB AD  BAC DAE，∴ABC ADE(SAS).  AC  AE  ∴C E . 19.解：（1）8；9. （2）设获得10分的四名选手分别为七、八 、八 、九，列举抽取两名领操员所能产生的全部 1 2 结果，它们是： 七八 ，七八 ，七九，八 八 ，八 九，八 九. 1 2 1 2 1 2 所有可能出现的结果有6种，它们出现的可能性相等，其中恰好抽到八年级两名领操员的结 果有1种. 1 所以，恰好抽到八年级两名领操员的概率为P . 6 20.解：（1）根据题意，得 ， [(2m2)]2 4(m2 2m)40∴方程有两个不相等的实数根. （2）由一元二次方程根与系数的关系，得 ， . x x 2m2 x x m2 2m 1 2 1 2 ∵ ，∴ . x2 x 2 10 (x x )2 2x x 10 1 2 1 2 1 2 ∴ . (2m2)2 2(m2 2m)10 化简，得 ，解得 ， . m2 2m30 m 3 m 1 1 2 ∴m的值为3或-1. 1 m 21.解：（1）∵A( ,2)在y  上， 2 x m 2 1 ∴ 1 ，∴m1.∴y  .  x 2 ∴ . B(1,1) 又∵ 过两点 ， ， y kxb A B  1 ∴ kb2 ，  2  kb1 k 2 解得 .∴ .  y 2x1 b1 1 （2）y 2x1与x轴交点C( ,0)， 2 1 1 S S S  2CP 1CP3， ABP ACP BCP 2 2 解得CP2. 5 3 ∴P( ,0)或( ,0). 2 2 22.解：（1）证明：连接OC . ∵O的半径为3，∴OC OB3. 又∵BP2，∴OP5.在 中， ， OCP OC2 PC2 32 42 52 OP2 ∴ 为直角三角形， . OCP OCP90 ∴OC  PC ，故PC为O的切线. （2）过 作 于点 ， . C CDOP D ODC OCP90 ∵CODPOC，∴OCDOPC . ∴OC OP PC ，∴ ，∴ OC2 9 ， 4 5 ，∴ 12.   OC2 ODOP OD   CD OD OC CD OP 5 DC 3 5 24 又∵ADOAOD ， 5 CD 1 ∴在RtCAD中，tanCAB  . AD 2 23.解：（1）设 型进价为 元，则 型进价为 元，根据题意得： A x B (x100) 10000 8000  . x x100 解得x500. 经检验，x500是原方程的解. ∴B型进价为400元. 答：A、B两型的进价分别为500元、400元. m16 （2）①∵ ，解得 .  16m25 m50m ② w(8005002n)m (600400n)(50m) . (100n)m(1000050n)当50n100时，100n0，w随m的增大而增大. 故 时， . m25 w 1250075n 最大 当 时， . n100 w 5000 最大 当100n150时，100n0，w随m的增大而减小. 故 时， . m16 w 1160066n 最大 1250075n,50n100  综上所述：w 5000,n100 . 最大  1160066n,100n150  24.解：（1）∵四边形ABCD为矩形，∴ABC为Rt. AB 1 又∵AC 2AB，cosBAC   ， AC 2 ∴ . CAB60 ∴ ，∴ . ACBDAC 30 B'AC'60 ∴ . C'AD30 AC'B' ∴AE C'E . （2）∵ ，又 ， BAC 60 AB AB' ∴ABB'为等边三角形. ∴ ， ，又∵ ，∴ . BB' AB AB'B60 AB'F 90 BB'F 150 ∵ ，∴ . B'F  AB  BB' B'BF BFB'15 （3）连接AF ，过A作AM  BF 于M . 由（2）可知AB'F 是等腰直角三角形，ABB'是等边三角形. ∴ ，∴ ， . AFB'45 AFM 30 ABF 45 在 中， 2 . RtABM AM  BM  ABcosABM 2  2 2AM 2 MF    6 在 中， . RtAMF tanAFM 3 3 ∴ . BF  2 6 25.解：（1）设抛物线解析式为： . y a(x1)2 4(a 0) ∵过 ，∴ ，∴ . (0,3) a43 a1 ∴ . y (x1)2 4x2 2x3 （2） ， .直线 为 . B(3,0) C(0,3) BC y x3 ∵ ，∴ . S S PQ//BC PBC QBC ①过 作 交抛物线于 ， P PQ//BC Q 又∵ ，∴直线 为 . P(1,4) PQ y x5 y x5 .  y x2 2x3 x 1 x 2 解得  1 ；  2 .∴Q (2,3).  y 4  y 3 1 1 2 ②设抛物线的对称轴交 于点 ，交 轴于点 . ，∴ . BC G x H G(1,2) PG GH 2过点 作 交抛物线于 ， . H Q Q //BC Q Q 2 3 2 3 直线 为 . Q Q y x1 2 3 y x1 ∴ .  y x2 2x3  3 17  3 17 x  x   1 2  2 2 解得 ； .    1 17  1 17 y  y    1 2   2 2 3 17 1 17  3 17 1 17  ∴Q  ,  ，Q  ,  . 2 2 2  3 2 2      3 17 1 17  3 17 1 17  满足条件的点为Q (2,3)，Q  ,  ，Q  ,  . 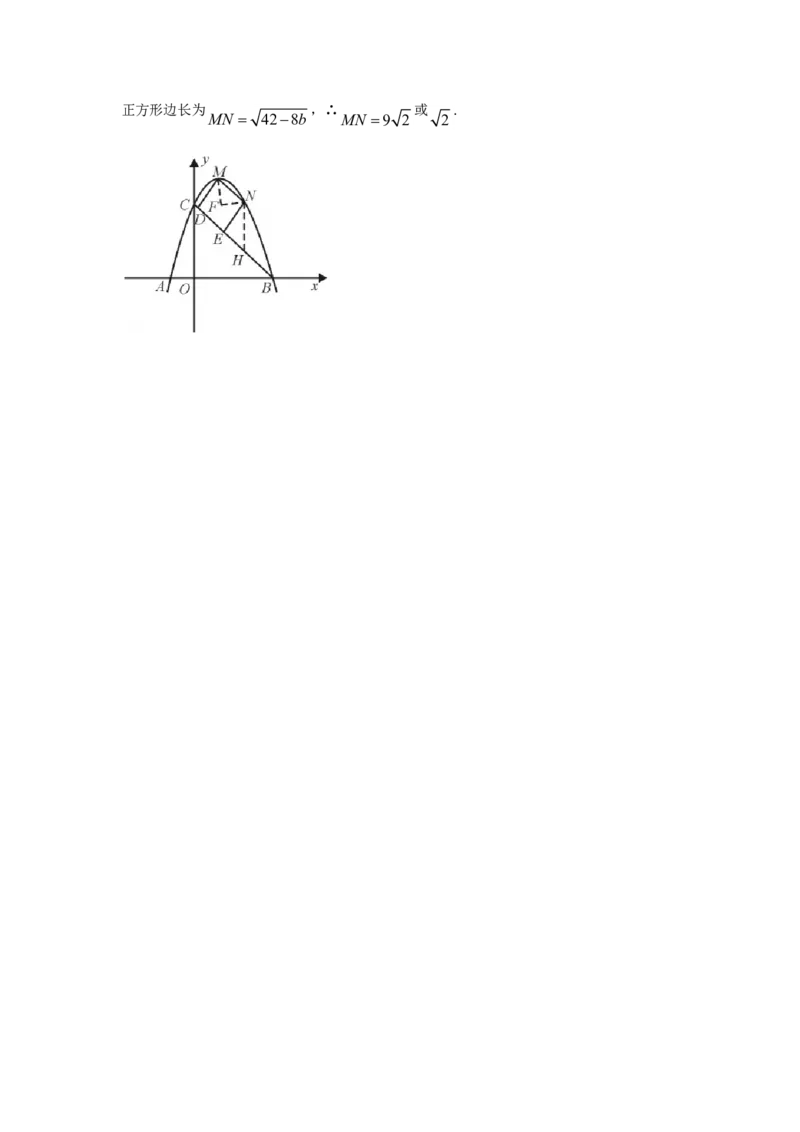1 2 2 2  3 2 2      （3）存在满足条件的点M ，N . 如图，过 作 轴，过 作 轴交 于 ，过 作 轴交 于 . M MF //y N NF //x MF F N NH //y BC H 则MNF 与NEH 都是等腰直角三角形. 设 ， ，直线 为 . M(x ,y ) N(x ,y ) MN y xb 1 1 2 2 y xb ∵  ，∴ x2 3x(b3)0 . y x2 2x3 ∴ NF2  x x 2 (x x )2 4x x 214b. 1 2 1 2 1 2 等腰 ，∴ . MNF Rt MN2 2NF2 428b 1 又∵NH2 (b3)2，∴NE2  (b3)2. 2 如果四边形MNED为正方形， 1 ∴NE2 MN2，∴428b (b2 6b9). 2 ∴ ，∴ ， . b2 10b750 b 15 b 5 1 2正方形边长为 ，∴ 或 . MN  428b MN 9 2 2