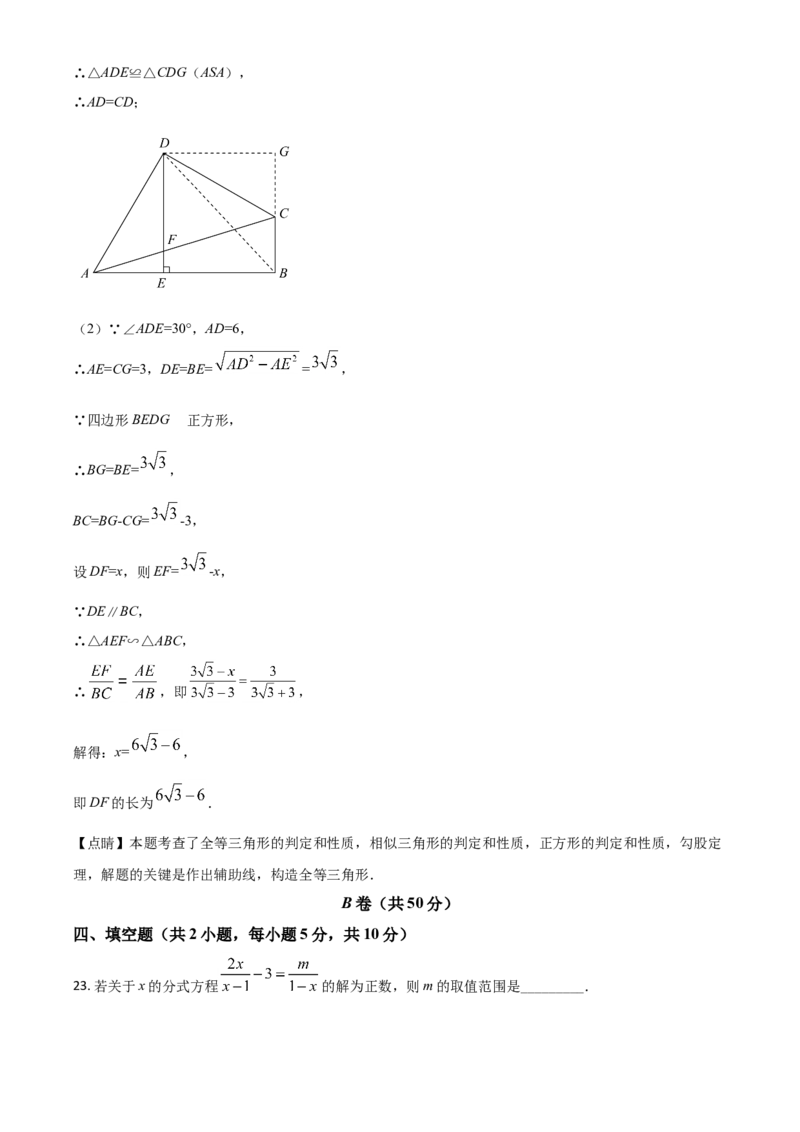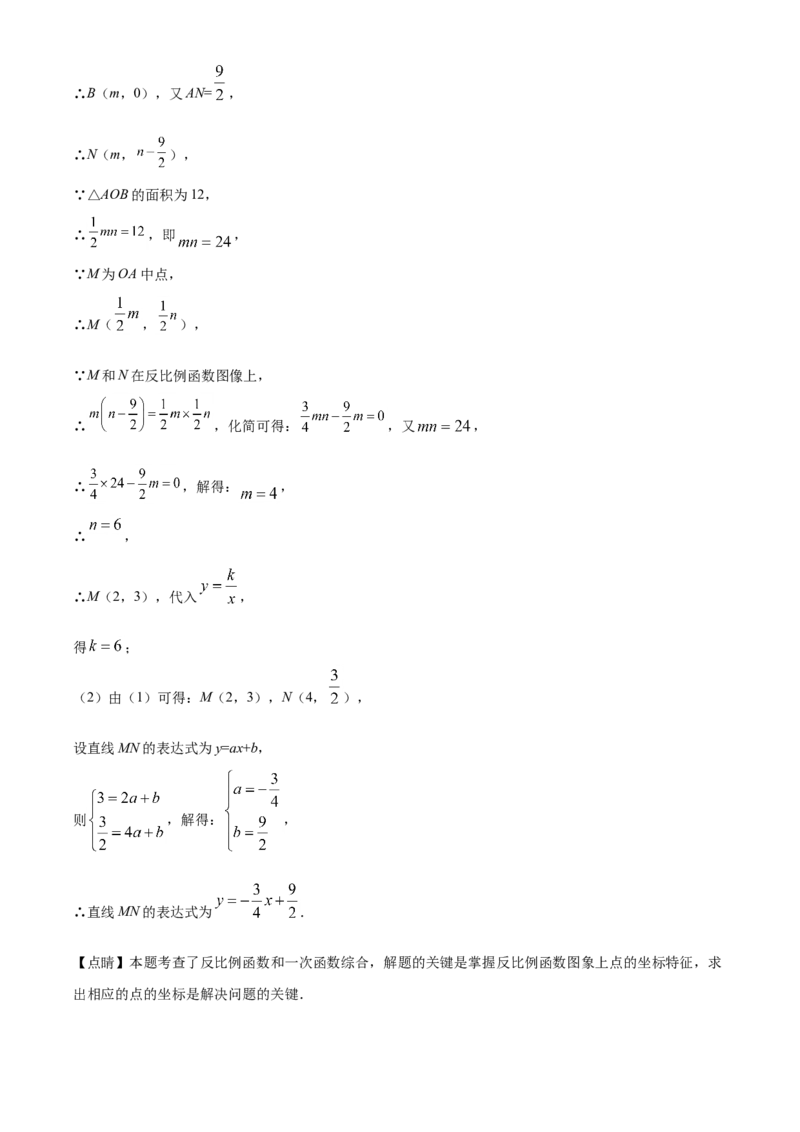文档内容
四川省凉山州 2021 年中考数学试题
A卷(共100分)
第I卷(选择题 共48分)
一、选择题(共12个小题,每小题4分,共48分)在每小题给出的四个选项中只有一项是
正确的,请把正确选项的字母填涂在答题卡上相应的位置.
1. ( )
A. 2021 B. -2021 C. D.
【答案】A
【解析】
【分析】根据绝对值解答即可.
【详解】解: 的绝对值是2021,
故选:A.
【点睛】此题主要考查了绝对值,利用绝对值解答是解题关键.
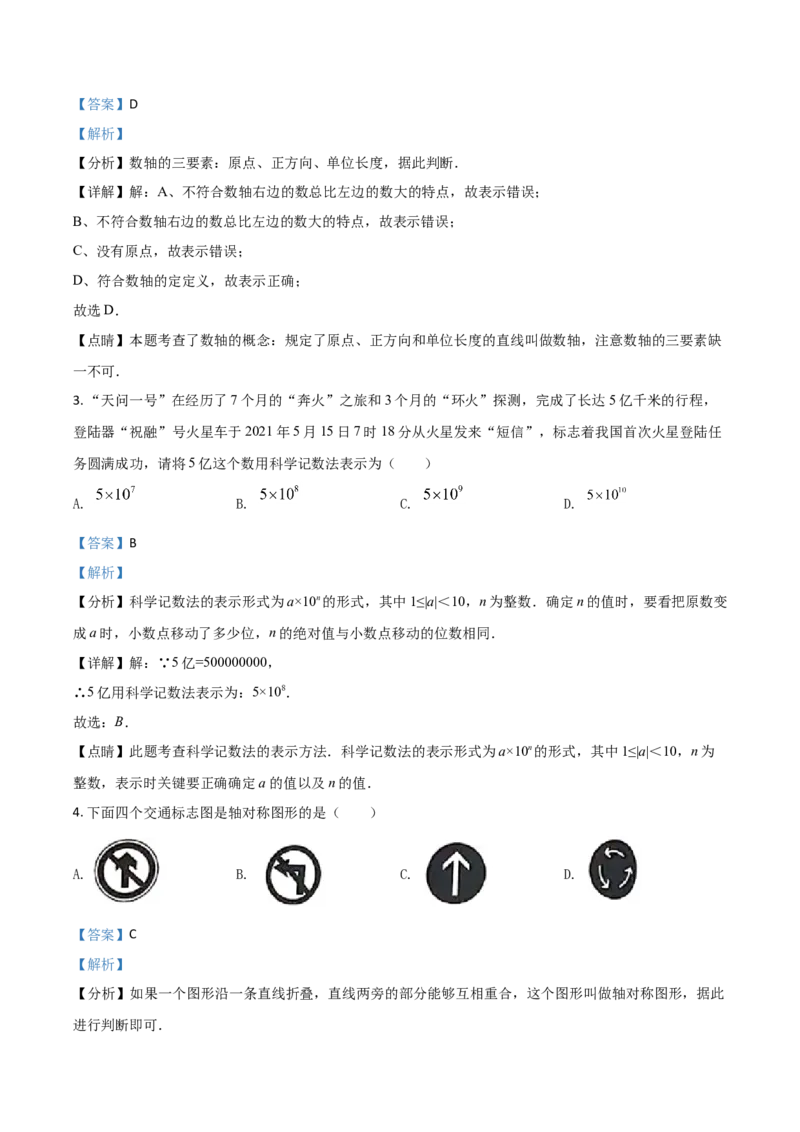
2. 下列数轴表示正确的是( )
A.
B.
C.
D.【答案】D
【解析】
【分析】数轴的三要素:原点、正方向、单位长度,据此判断.
【详解】解:A、不符合数轴右边的数总比左边的数大的特点,故表示错误;
B、不符合数轴右边的数总比左边的数大的特点,故表示错误;
C、没有原点,故表示错误;
D、符合数轴的定定义,故表示正确;
故选D.
【点睛】本题考查了数轴的概念:规定了原点、正方向和单位长度的直线叫做数轴,注意数轴的三要素缺
一不可.
3. “天问一号”在经历了7个月的“奔火”之旅和3个月的“环火”探测,完成了长达5亿千米的行程,
登陆器“祝融”号火星车于2021年5月15日7时18分从火星发来“短信”,标志着我国首次火星登陆任
务圆满成功,请将5亿这个数用科学记数法表示为( )
A. B. C. D.
【答案】B
【解析】
【分析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变
成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.
【详解】解:∵5亿=500000000,
∴5亿用科学记数法表示为:5×108.
故选:B.
【点睛】此题考查科学记数法的表示方法.科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为
整数,表示时关键要正确确定a的值以及n的值.
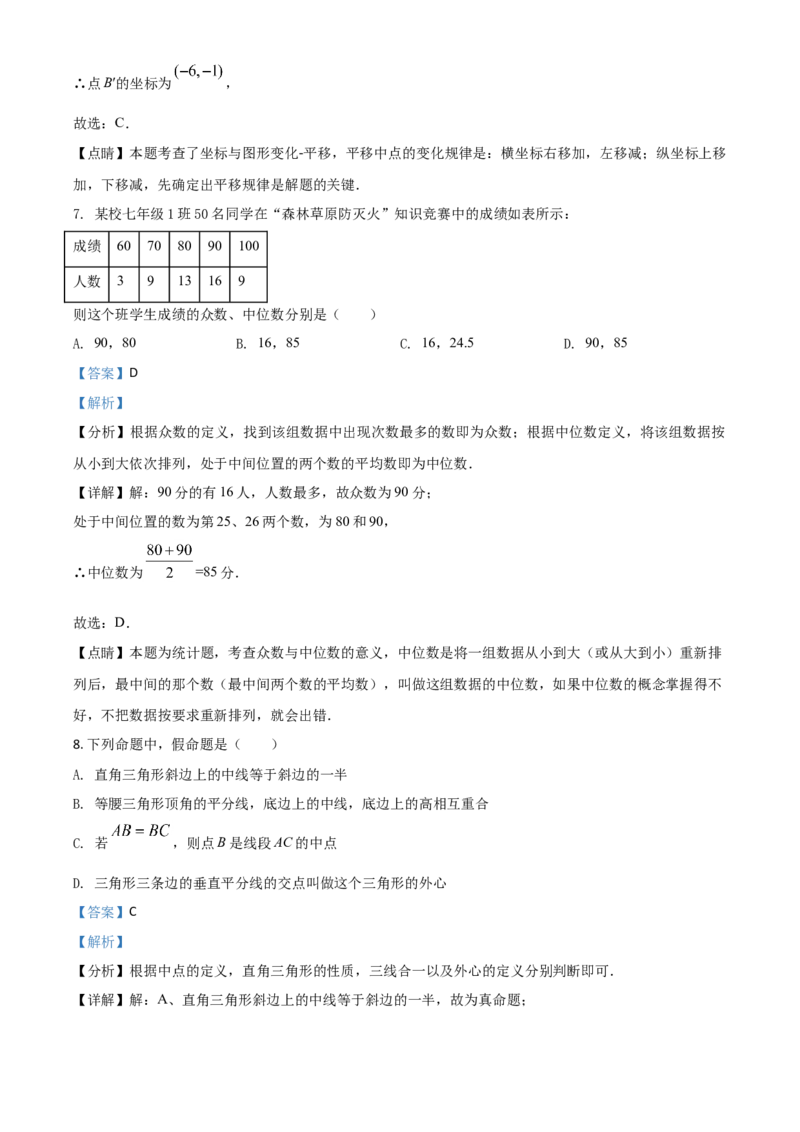
4. 下面四个交通标志图是轴对称图形的是( )
A. B. C. D.
【答案】C
【解析】
【分析】如果一个图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形叫做轴对称图形,据此
进行判断即可.【详解】解:A、不是轴对称图形,故不合题意;
B、不是轴对称图形,故不合题意;
C、是轴对称图形,故符合题意;
D、不是轴对称图形,故不合题意;
故选C.
【点睛】本题考查了轴对称图形,判断轴对称图形的关键是寻找对称轴,图形两部分沿对称轴折叠后可重
合.
5. 的平方根是( )
A. B. 3 C. D. 9
【答案】A
【解析】
【分析】求出81的算术平方根,找出结果的平方根即可.
【详解】解:∵ =9,
∴ 的平方根是±3.
故选:A.
【点睛】此题考查了平方根,以及算术平方根,熟练掌握各自的定义是解本题的关键.
6. 在平面直角坐标系中,将线段AB平移后得到线段 ,点 的对应点 的坐标为 ,则
点 的对应点 的坐标为( )
A. B. C. D.
【答案】C
【解析】
【分析】根据点A到A′确定出平移规律,再根据平移规律列式计算即可得到点B′的坐标.
【详解】解:∵ , ,
∴平移规律为横坐标减4,纵坐标减4,
∵ ,∴点B′的坐标为 ,
故选:C.
【点睛】本题考查了坐标与图形变化-平移,平移中点的变化规律是:横坐标右移加,左移减;纵坐标上移
加,下移减,先确定出平移规律是解题的关键.
7. 某校七年级1班50名同学在“森林草原防灭火”知识竞赛中的成绩如表所示:
成绩 60 70 80 90 100
人数 3 9 13 16 9
则这个班学生成绩的众数、中位数分别是( )
A. 90,80 B. 16,85 C. 16,24.5 D. 90,85
【答案】D
【解析】
【分析】根据众数的定义,找到该组数据中出现次数最多的数即为众数;根据中位数定义,将该组数据按
从小到大依次排列,处于中间位置的两个数的平均数即为中位数.
【详解】解:90分的有16人,人数最多,故众数为90分;
处于中间位置的数为第25、26两个数,为80和90,
∴中位数为 =85分.
故选:D.
【点睛】本题为统计题,考查众数与中位数的意义,中位数是将一组数据从小到大(或从大到小)重新排
列后,最中间的那个数(最中间两个数的平均数),叫做这组数据的中位数,如果中位数的概念掌握得不
好,不把数据按要求重新排列,就会出错.
8. 下列命题中,假命题是( )
A. 直角三角形斜边上的中线等于斜边的一半
B. 等腰三角形顶角的平分线,底边上的中线,底边上的高相互重合
C. 若 ,则点B是线段AC的中点
D. 三角形三条边的垂直平分线的交点叫做这个三角形的外心
【答案】C
【解析】
【分析】根据中点的定义,直角三角形的性质,三线合一以及外心的定义分别判断即可.
【详解】解:A、直角三角形斜边上的中线等于斜边的一半,故为真命题;B、等腰三角形顶角的平分线,底边上的中线,底边上的高相互重合,故为真命题;
的
C、若在同一条直线上AB=BC,则点B是线段AC 中点,故为假命题;
的
D、三角形三条边 垂直平分线的交点叫做这个三角形的外心,故为真命题;
故选C.
【点睛】本题考查了中点的定义,直角三角形的性质,三线合一以及外心的性质,属于基础知识,要熟练
掌握.
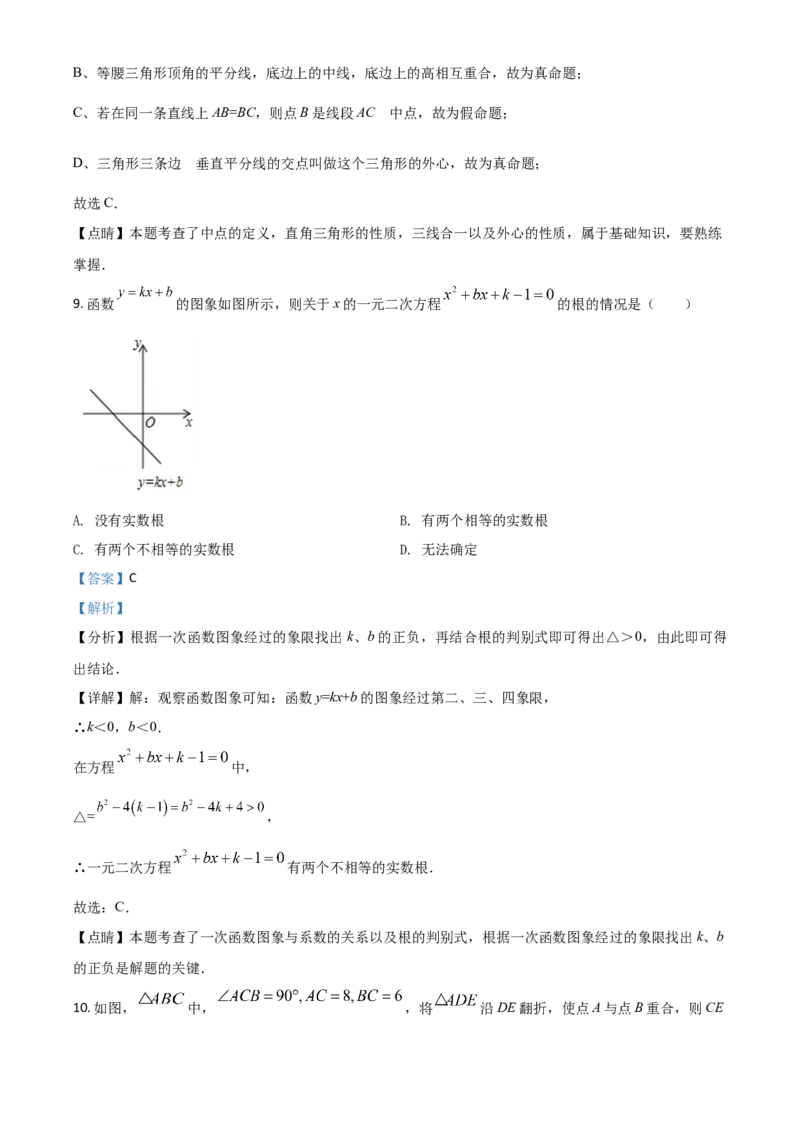
9. 函数 的图象如图所示,则关于x的一元二次方程 的根的情况是( )
A. 没有实数根 B. 有两个相等的实数根
C. 有两个不相等的实数根 D. 无法确定
【答案】C
【解析】
【分析】根据一次函数图象经过的象限找出k、b的正负,再结合根的判别式即可得出△>0,由此即可得
出结论.
【详解】解:观察函数图象可知:函数y=kx+b的图象经过第二、三、四象限,
∴k<0,b<0.
在方程 中,
△= ,
∴一元二次方程 有两个不相等的实数根.
故选:C.
【点睛】本题考查了一次函数图象与系数的关系以及根的判别式,根据一次函数图象经过的象限找出k、b
的正负是解题的关键.
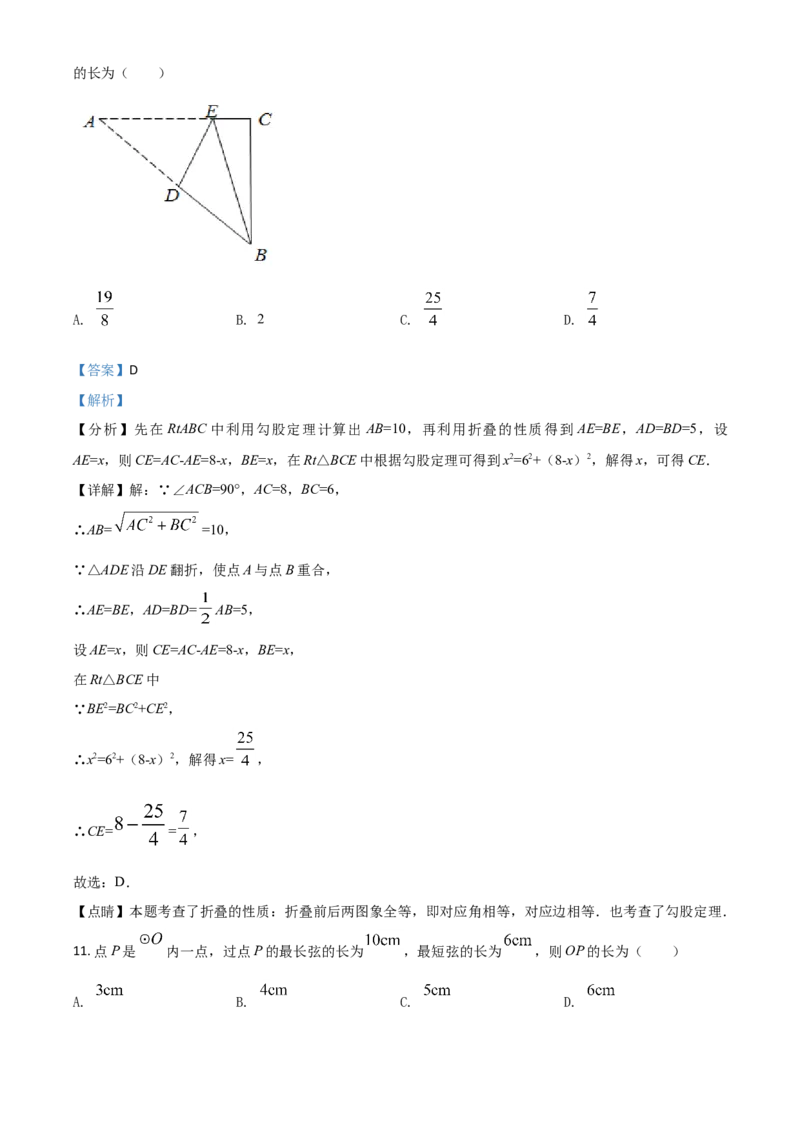
10. 如图, 中, ,将 沿DE翻折,使点A与点B重合,则CE的长为( )
A. B. 2 C. D.
【答案】D
【解析】
【分析】先在 RtABC中利用勾股定理计算出 AB=10,再利用折叠的性质得到 AE=BE,AD=BD=5,设
AE=x,则CE=AC-AE=8-x,BE=x,在Rt△BCE中根据勾股定理可得到x2=62+(8-x)2,解得x,可得CE.
【详解】解:∵∠ACB=90°,AC=8,BC=6,
∴AB= =10,
∵△ADE沿DE翻折,使点A与点B重合,
∴AE=BE,AD=BD= AB=5,
设AE=x,则CE=AC-AE=8-x,BE=x,
在Rt△BCE中
∵BE2=BC2+CE2,
∴x2=62+(8-x)2,解得x= ,
∴CE= = ,
故选:D.
【点睛】本题考查了折叠的性质:折叠前后两图象全等,即对应角相等,对应边相等.也考查了勾股定理.
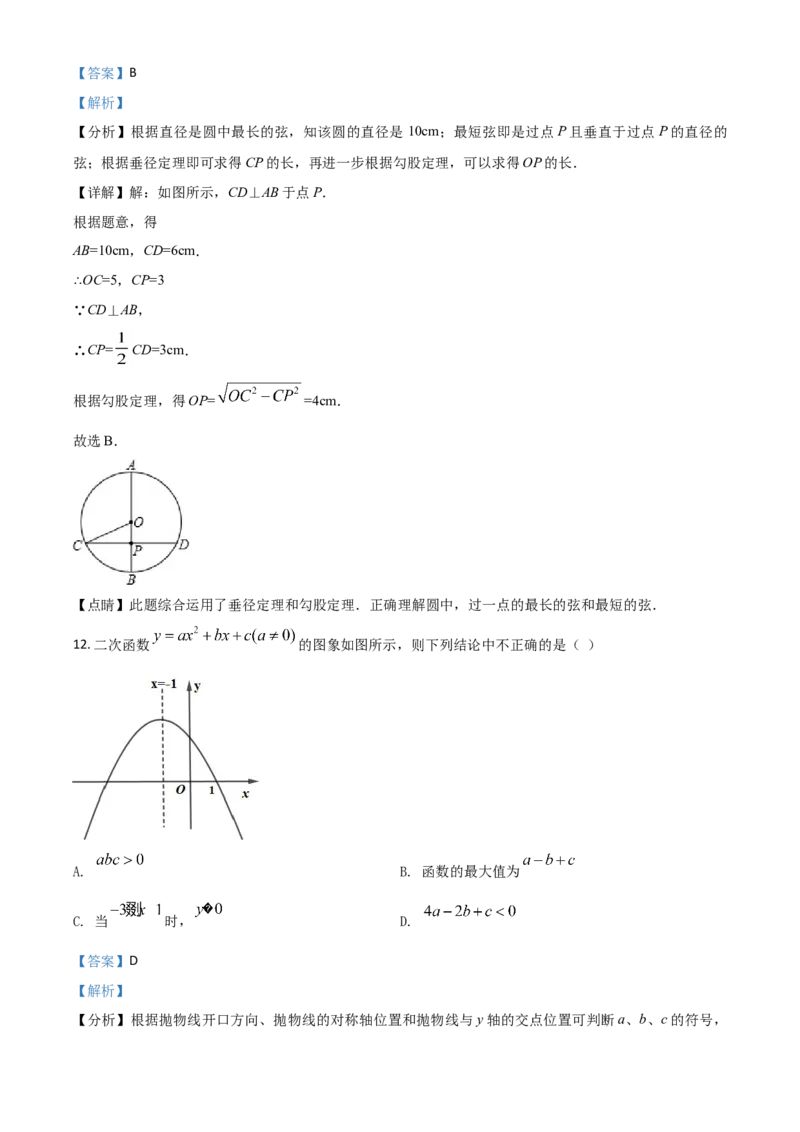
11. 点P是 内一点,过点P的最长弦的长为 ,最短弦的长为 ,则OP的长为( )
A. B. C. D.【答案】B
【解析】
【分析】根据直径是圆中最长的弦,知该圆的直径是10cm;最短弦即是过点P且垂直于过点P的直径的
弦;根据垂径定理即可求得CP的长,再进一步根据勾股定理,可以求得OP的长.
【详解】解:如图所示,CD⊥AB于点P.
根据题意,得
AB=10cm,CD=6cm.
∴OC=5,CP=3
∵CD⊥AB,
∴CP= CD=3cm.
根据勾股定理,得OP= =4cm.
故选B.
【点睛】此题综合运用了垂径定理和勾股定理.正确理解圆中,过一点的最长的弦和最短的弦.
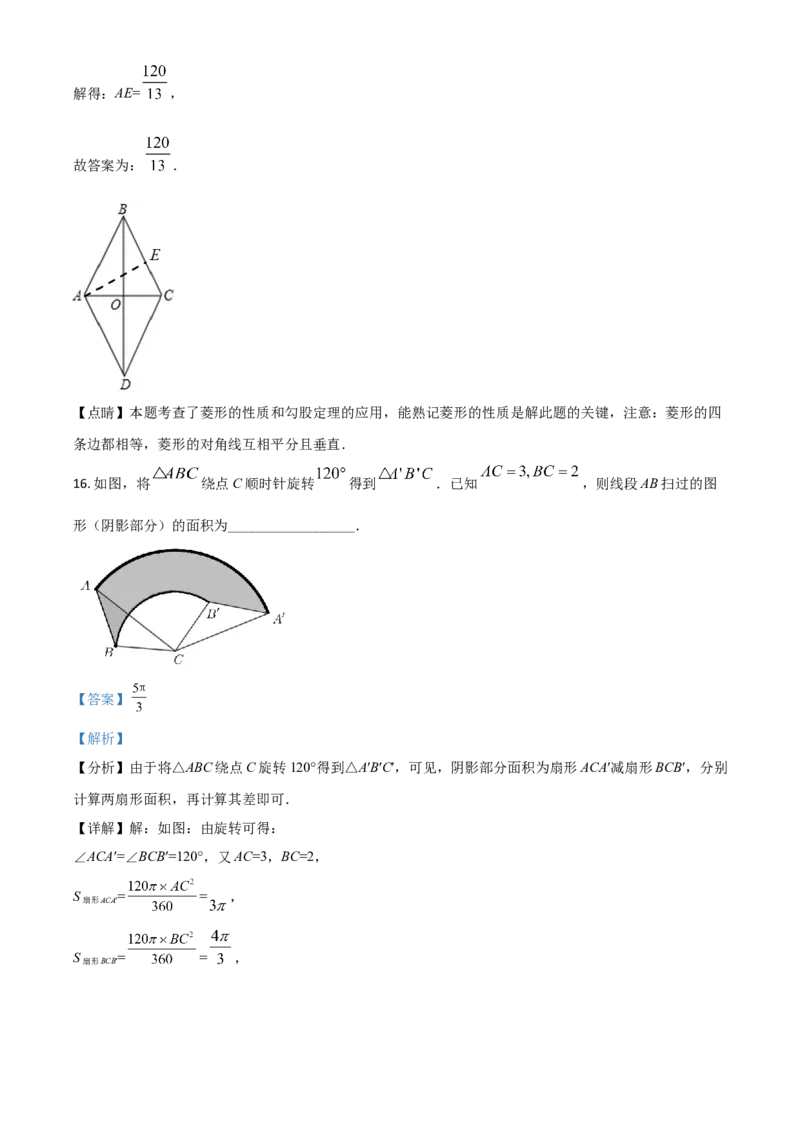
12. 二次函数 的图象如图所示,则下列结论中不正确的是( )
A. B. 函数的最大值为
C. 当 时, D.
【答案】D
【解析】
【分析】根据抛物线开口方向、抛物线的对称轴位置和抛物线与y轴的交点位置可判断a、b、c的符号,利用抛物线的对称性可得到抛物线与x轴的另一个交点坐标为(-3,0),从而分别判断各选项.
【详解】解:∵抛物线开口向下,
∴a<0,
∵抛物线的对称轴为直线x=-1,
∴ ,即b=2a,则b<0,
∵抛物线与y轴交于正半轴,
∴c>0,
则abc>0,故A正确;
当x=-1时,y取最大值为 ,故B正确;
由于开口向上,对称轴为直线x=-1,
则点(1,0)关于直线x=-1对称的点为(-3,0),
即抛物线与x轴交于(1,0),(-3,0),
∴当 时, ,故C正确;
由图像可知:当x=-2时,y>0,
即 ,故D错误;
故选D.
【点睛】本题考查了二次函数与系数的关系:对于二次函数y=ax2+bx+c(a≠0),二次项系数a决定抛物线
的开口方向和大小:当a>0时,抛物线向上开口;抛物线向下开口;一次项系数b和二次项系数a共同决
定对称轴的位置:当a与b同号时(即ab>0),对称轴在y轴左; 当a与b异号时(即ab<0),对称轴
在y轴右.常数项c决定抛物线与y轴交点:抛物线与y轴交于(0,c).
第II卷(非选择题 共52分)
二、填空题(共5个小题,每小题4分,共20分)
13. 函数 中,自变量x的取值范围是______________.
【答案】x≥-3且x≠0
【解析】
【分析】根据二次根式的性质和分式的意义,被开方数大于等于0,分母不等于0列不等式组求解.
【详解】解:根据题意得:x+3≥0且x≠0,
解得x≥-3且x≠0.故答案为:x≥-3且x≠0.
【点睛】本题考查了函数自变量的取值范围.考查的知识点为:分式有意义,分母不为0,二次根式有意
义,被开方数是非负数.
14. 已知 是方程 的解,则a的值为______________.
【答案】-1
【解析】
【分析】根据方程解的定义,将x=1,y=3代入方程 ,即可求得a的值.
【详解】解:根据题意,将x=1,y=3代入方程 ,
得: ,
解得:a=-1,
故答案为:-1.
【点睛】本题考查了二元一次方程的解,要求理解什么是二元一次方程的解,并会把x,y的值代入原方程
验证二元一次方程的解.
15. 菱形 中,对角线 ,则菱形的高等于___________.
【答案】
【解析】
【分析】过A作AE⊥BC,垂足为E,根据菱形的性质求出菱形边长,再利用菱形的面积公式得到方程,
解之可得AE.
【详解】解:如图,过A作AE⊥BC,垂足为E,即AE为菱形ABCD的高,
∵菱形ABCD中,AC=10,BD=24,
∴OB= BD=12,OA= AC=5,
在Rt△ABO中,AB=BC= =13,
∵S = ,
菱形ABCD
∴ ,解得:AE= ,
故答案为: .
【点睛】本题考查了菱形的性质和勾股定理的应用,能熟记菱形的性质是解此题的关键,注意:菱形的四
条边都相等,菱形的对角线互相平分且垂直.
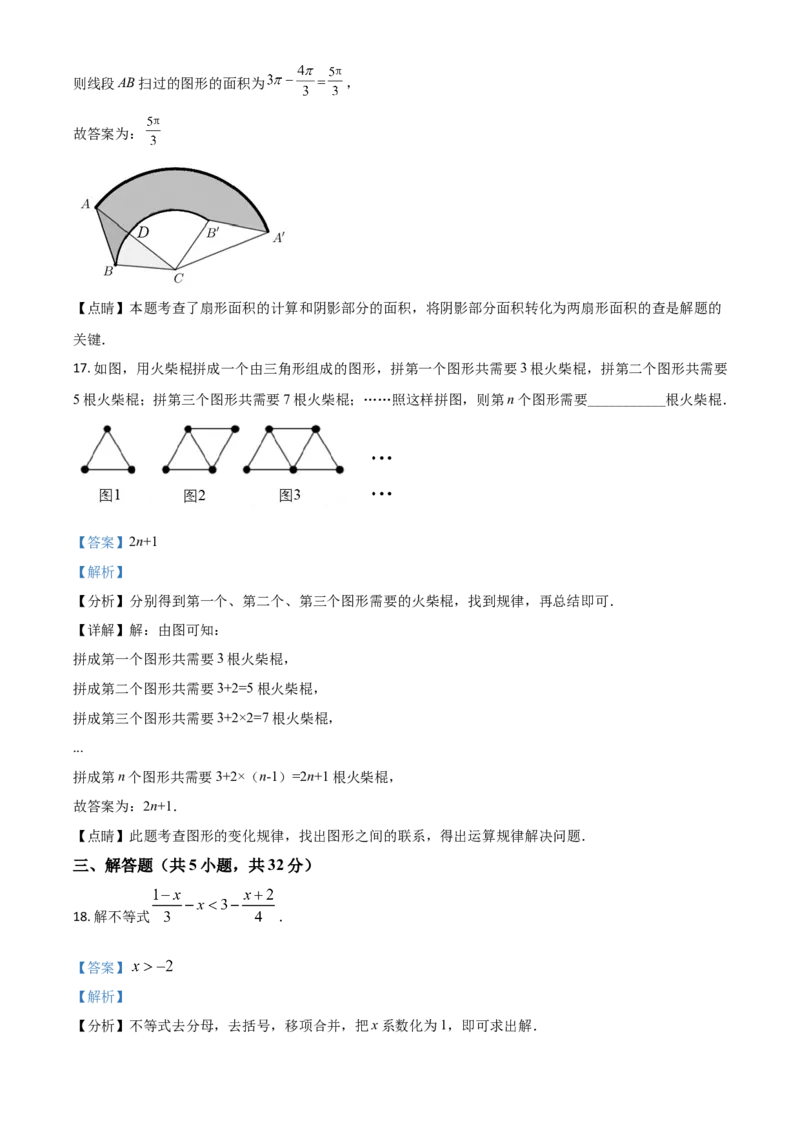
16. 如图,将 绕点C顺时针旋转 得到 .已知 ,则线段AB扫过的图
形(阴影部分)的面积为__________________.
【答案】
【解析】
【分析】由于将△ABC绕点C旋转120°得到△A′B′C′,可见,阴影部分面积为扇形ACA′减扇形BCB′,分别
计算两扇形面积,再计算其差即可.
【详解】解:如图:由旋转可得:
∠ACA′=∠BCB′=120°,又AC=3,BC=2,
S = = ,
扇形ACA′
S = = ,
扇形BCB′则线段AB扫过的图形的面积为 = ,
故答案为:
【点睛】本题考查了扇形面积的计算和阴影部分的面积,将阴影部分面积转化为两扇形面积的查是解题的
关键.
17. 如图,用火柴棍拼成一个由三角形组成的图形,拼第一个图形共需要3根火柴棍,拼第二个图形共需要
5根火柴棍;拼第三个图形共需要7根火柴棍;……照这样拼图,则第n个图形需要___________根火柴棍.
【答案】2n+1
【解析】
【分析】分别得到第一个、第二个、第三个图形需要的火柴棍,找到规律,再总结即可.
【详解】解:由图可知:
拼成第一个图形共需要3根火柴棍,
拼成第二个图形共需要3+2=5根火柴棍,
拼成第三个图形共需要3+2×2=7根火柴棍,
...
拼成第n个图形共需要3+2×(n-1)=2n+1根火柴棍,
故答案为:2n+1.
【点睛】此题考查图形的变化规律,找出图形之间的联系,得出运算规律解决问题.
三、解答题(共5小题,共32分)
18. 解不等式 .
【答案】
【解析】
【分析】不等式去分母,去括号,移项合并,把x系数化为1,即可求出解.【详解】解: ,
去分母,得 ,
去括号,得 ,
移项,得 ,
合并同类项,得 ,
系数化成1,得 .
【点睛】本题考查了解一元一次不等式,解此题的关键点是能正确根据不等式的性质进行变形,注意:移
项要变号.
19. 已知 ,求 的值.
【答案】-4
【解析】
【分析】根据已知求出xy=-2,再将所求式子变形为 ,代入计算即可.
【详解】解:∵ ,
∴ ,
∴ ,
∴ .
【点睛】本题考查了代数式求值,解题的关键是掌握分式的运算法则和因式分解的应用.
20. 随着手机的日益普及,学生使用手机给学校管理和学生发展带来诸多不利影响,为了保护学生视力,
防止学生沉迷网络和游戏,让学生在学校专心学习,促进学生身心健康发展,教育部办公厅于2021年1月
15日颁发了《教育部办公厅关于加强中小学生手机管理工作的通知》,为贯彻《通知》精神、某学校团委
组织了“我与手机说再见”为主题的演讲比赛,根据参赛同学的得分情况绘制了如图所示的两幅不完整的
统计图.(其中A表示“一等奖”,B表示“二等奖”,C表示“三等奖”,D表示“优秀奖”)请你根据统计图中所提供的信息解答下列问题:
(1)获奖总人数为______人, _______;
(2)请将条形统计图补充完整;
(3)学校将从获得一等奖的4名同学(其中有一名男生,三名女生)中随机抽取两名参加全市的比赛,请
利用树状图或列表法求抽取同学中恰有一名男生和一名女生的概率.
【答案】(1)40,30;(2)见解析;(3)
【解析】
【分析】(1)用B等级的人数除以对应百分比可得获奖总人数,再减去A、B、D的人数可得C等级的人
数,除以获奖总人数可得对应百分比,即可得到m值;
(2)求出C等级的人数,即可补全统计图;
(3)画树状图展示所有12种等可能的结果,找出抽出的恰好是一名男生和一名女生的结果数,然后根据
概率公式求解.
【详解】解:(1)8÷20%=40人,
(40-4-8-16)÷40×100%=30%,
则m=30;
(2)40-4-8-16=12人,
补全统计图如下:(3)如图,
共有12种情况,恰好选中1名男生和1名女生的有6种,
所以恰好选中1名男生和1名女生的概率是 .
【点睛】本题考查了扇形统计图,条形统计图,列表法或树状图法求概率等知识点,能正确画出条形统计
图和树状图是解此题的关键.
21. 王刚同学在学习了解直角三角形及其应用的知识后,尝试利用所学知识测量河对岸大树AB的高度,他
在点C处测得大树顶端A的仰角为 ,再从C点出发沿斜坡走 米到达斜坡上D点,在点D处测得
树顶端A的仰角为 ,若斜坡CF的坡比为 (点 在同一水平线上).
(1)求王刚同学从点C到点D的过程中上升的高度;
(2)求大树AB的高度(结果保留根号).【答案】(1)2米;(2) 米
【解析】
【分析】(1)作DH⊥CE于H,解Rt△CDH,即可求出DH;
(2)延长AD交CE于点G,解Rt△GDH、Rt△CDH,求出GH、CH,得到GC,再说明AB=BC,在
△ABG中,利用正切的定义求出AB即可.
【详解】解:(1)过D作DH⊥CE于H,如图所示:
在Rt△CDH中, ,
∴CH=3DH,
∵CH2+DH2=CD2,
∴(3DH)2+DH2=( )2,
解得:DH=2或-2(舍),
∴王刚同学从点C到点D的过程中上升的高度为2米;
(2)延长AD交CE于点G,设AB=x米,
由题意得,∠AGC=30°,
∴GH= = = ,
∵CH=3DH=6,
∴GC=GH+CH= +6,
在Rt△BAC中,∠ACB=45°,
∴AB=BC,
∴tan∠AGB= ,
解得:AB= ,
即大树AB的高度为 米.【点睛】本题考查的是解直角三角形的应用-仰角俯角问题,掌握锐角三角函数的定义、仰角俯角的概念是
解题的关键.
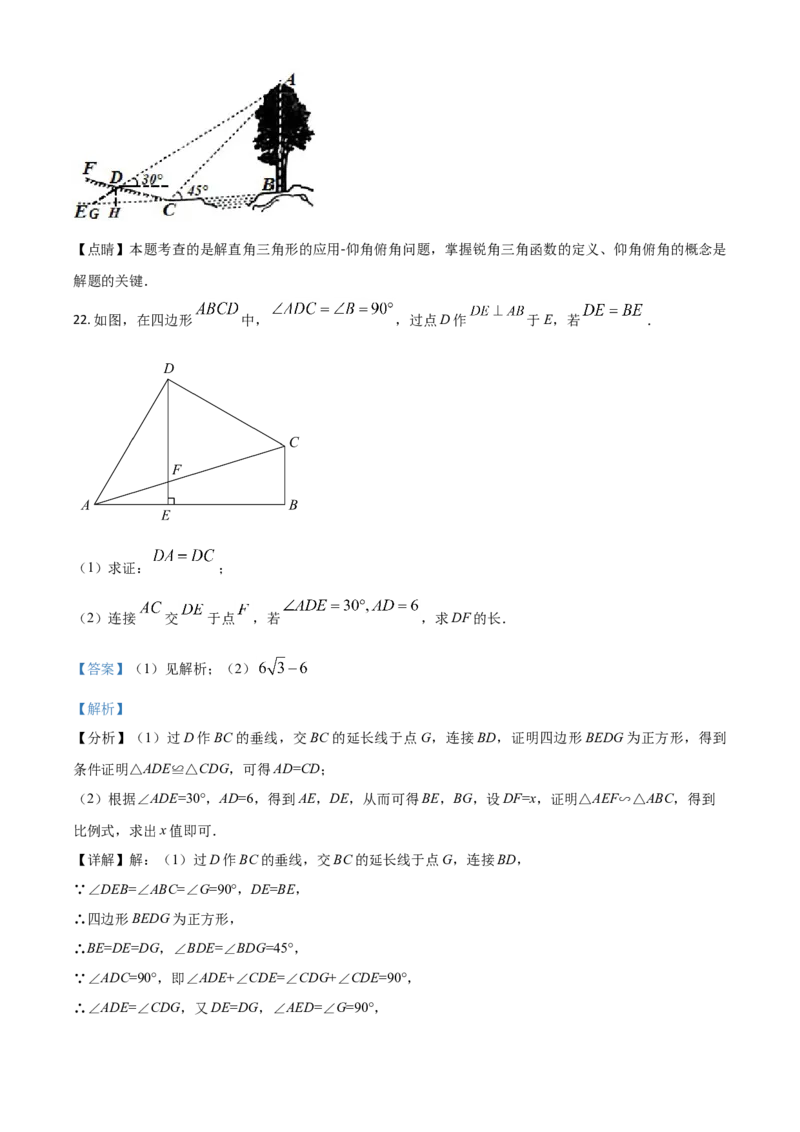
22. 如图,在四边形 中, ,过点D作 于E,若 .
(1)求证: ;
(2)连接 交 于点 ,若 ,求DF的长.
【答案】(1)见解析;(2)
【解析】
【分析】(1)过D作BC的垂线,交BC的延长线于点G,连接BD,证明四边形BEDG为正方形,得到
条件证明△ADE≌△CDG,可得AD=CD;
(2)根据∠ADE=30°,AD=6,得到AE,DE,从而可得BE,BG,设DF=x,证明△AEF∽△ABC,得到
比例式,求出x值即可.
【详解】解:(1)过D作BC的垂线,交BC的延长线于点G,连接BD,
∵∠DEB=∠ABC=∠G=90°,DE=BE,
∴四边形BEDG为正方形,
∴BE=DE=DG,∠BDE=∠BDG=45°,
∵∠ADC=90°,即∠ADE+∠CDE=∠CDG+∠CDE=90°,
∴∠ADE=∠CDG,又DE=DG,∠AED=∠G=90°,∴△ADE≌△CDG(ASA),
∴AD=CD;
(2)∵∠ADE=30°,AD=6,
∴AE=CG=3,DE=BE= = ,
为
∵四边形BEDG 正方形,
∴BG=BE= ,
BC=BG-CG= -3,
设DF=x,则EF= -x,
∵DE∥BC,
∴△AEF∽△ABC,
∴ ,即 ,
解得:x= ,
即DF的长为 .
【点睛】本题考查了全等三角形的判定和性质,相似三角形的判定和性质,正方形的判定和性质,勾股定
理,解题的关键是作出辅助线,构造全等三角形.
B卷(共50分)
四、填空题(共2小题,每小题5分,共10分)
23. 若关于x的分式方程 的解为正数,则m的取值范围是_________.【答案】m>-3且m≠-2
【解析】
【分析】先利用m表示出x的值,再由x为正数求出m的取值范围即可.
【详解】解:方程两边同时乘以x-1得, ,
解得 ,
∵x为正数,
∴m+3>0,解得m>-3.
∵x≠1,
∴m+3≠1,即m≠-2.
∴m的取值范围是m>-3且m≠-2.
故答案为:m>-3且m≠-2.
【点睛】本题考查的是分式方程的解,熟知求出使分式方程中令等号左右两边相等且分母不等于0的未知
数的值,这个值叫方程的解是解答此题的关键.
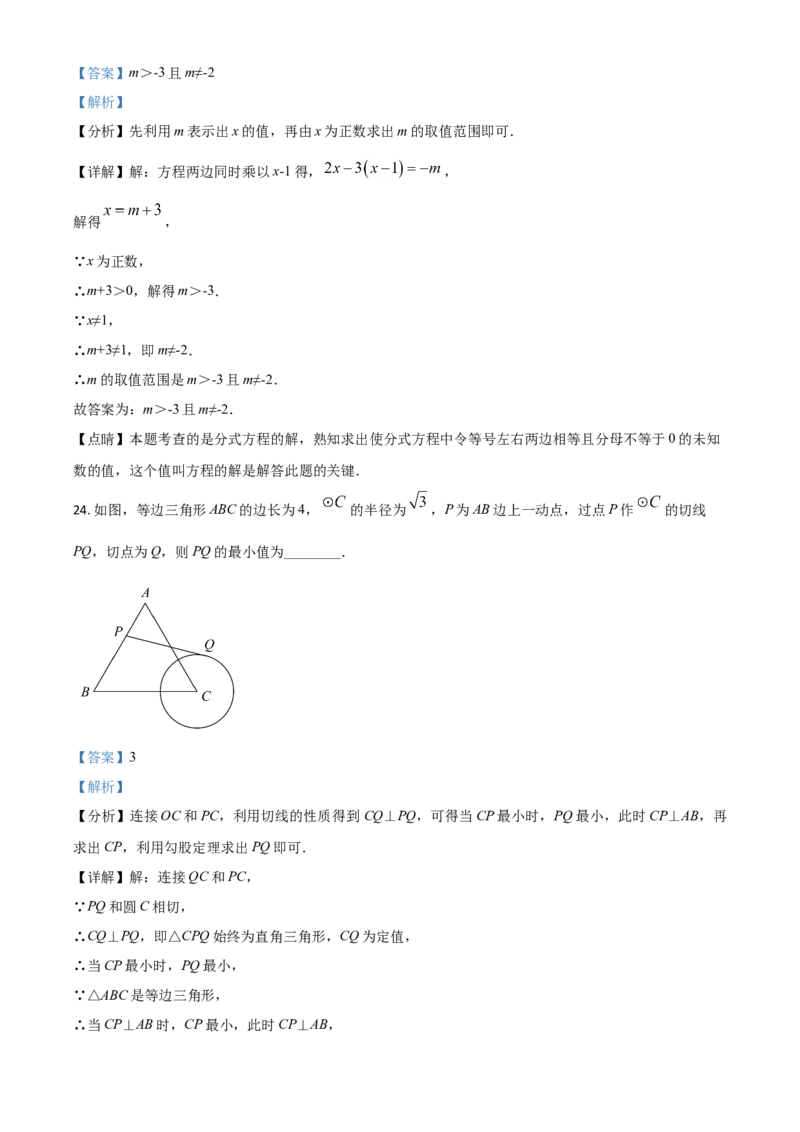
24. 如图,等边三角形ABC的边长为4, 的半径为 ,P为AB边上一动点,过点P作 的切线
PQ,切点为Q,则PQ的最小值为________.
【答案】3
【解析】
【分析】连接OC和PC,利用切线的性质得到CQ⊥PQ,可得当CP最小时,PQ最小,此时CP⊥AB,再
求出CP,利用勾股定理求出PQ即可.
【详解】解:连接QC和PC,
∵PQ和圆C相切,
∴CQ⊥PQ,即△CPQ始终为直角三角形,CQ为定值,
∴当CP最小时,PQ最小,
∵△ABC是等边三角形,
∴当CP⊥AB时,CP最小,此时CP⊥AB,∵AB=BC=AC=4,
∴AP=BP=2,
∴CP= = ,
∵圆C的半径CQ= ,
∴PQ= =3,
故答案为:3.
【点睛】本题考查了切线的性质,等边三角形的性质,以及勾股定理.此题难度适中,注意掌握辅助线的
作法,注意得到当PC⊥AB时,线段PQ最短是关键.
五、解答题(共4小题,共40分)
25. 阅读以下材料,苏格兰数学家纳皮尔(J.Npler,1550-1617年)是对数的创始人,他发明对数是在指
数书写方式之前,直到18世纪瑞士数学家欧拉(Evler.1707-1783年)才发现指数与对数之间的联系.
对数的定义:一般地.若 ( 且 ),那么x叫做以a为底N的对数,
记作 ,比如指数式 可以转化为对数式 ,对数式 可以转化为指数
式 .我们根据对数的定义可得到对数的一个性质:
,理由如下:
设 ,则 .
.由对数的定义得
又.
根据上述材料,结合你所学的知识,解答下列问题:
(1)填空:① ___________;② _______,③ ________;
(2)求证: ;
(3)拓展运用:计算 .
【答案】(1)5,3,0;(2)见解析;(3)2
【解析】
【分析】(1)直接根据定义计算即可;
(2)结合题干中的过程,同理根据同底数幂的除法即可证明;
(3)根据公式:log (M•N)=log M+log N和log =log M-log N的逆用,将所求式子表示为:
a a a a a a
,计算可得结论.
【详解】解:(1)①∵ ,∴ 5,
②∵ ,∴ 3,
③∵ ,∴ 0;
(2)设log M=m,log N=n,
a a
∴ , ,
∴ ,
∴ ,
∴ ;
(3)=
=
=2.
【点睛】本题考查整式的混合运算、对数与指数之间的关系与相互转化的关系,解题的关键是明确新定义,
明白指数与对数之间的关系与相互转化关系.
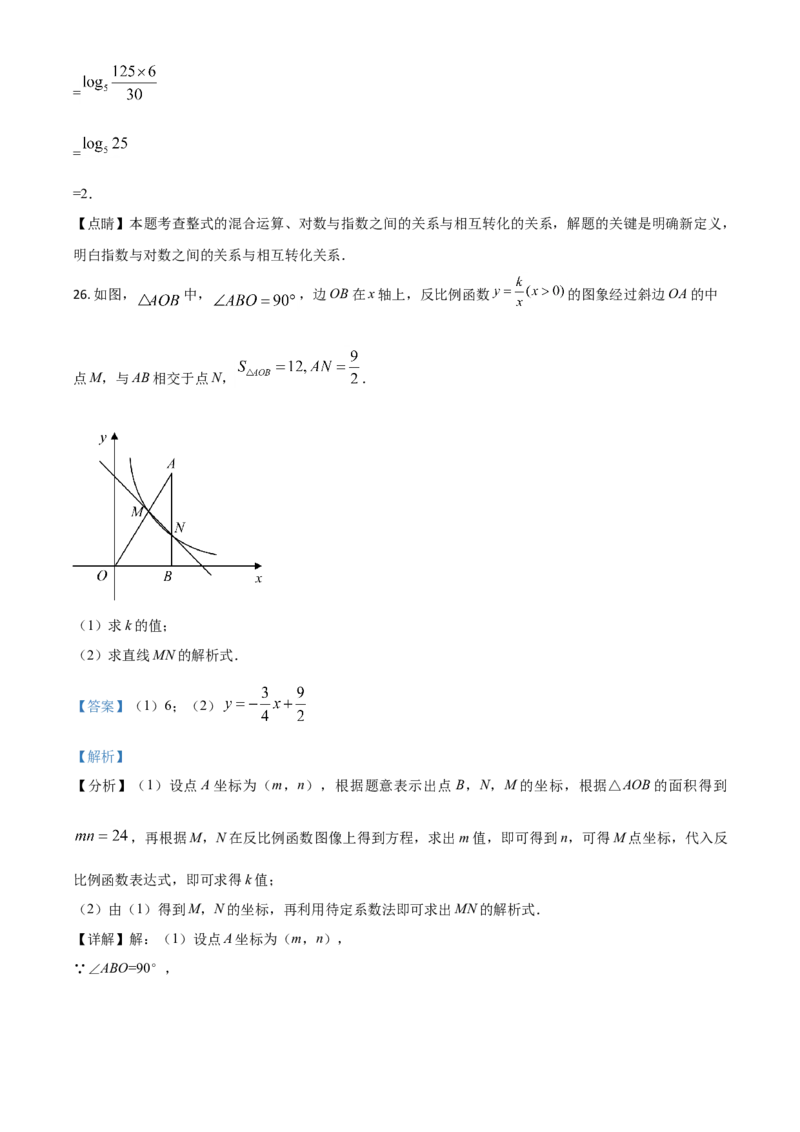
26. 如图, 中, ,边OB在x轴上,反比例函数 的图象经过斜边OA的中
点M,与AB相交于点N, .
(1)求k的值;
(2)求直线MN的解析式.
【答案】(1)6;(2)
【解析】
【分析】(1)设点A坐标为(m,n),根据题意表示出点B,N,M的坐标,根据△AOB的面积得到
,再根据M,N在反比例函数图像上得到方程,求出m值,即可得到n,可得M点坐标,代入反
比例函数表达式,即可求得k值;
(2)由(1)得到M,N的坐标,再利用待定系数法即可求出MN的解析式.
【详解】解:(1)设点A坐标为(m,n),
∵∠ABO=90°,∴B(m,0),又AN= ,
∴N(m, ),
∵△AOB的面积为12,
∴ ,即 ,
∵M为OA中点,
∴M( , ),
∵M和N在反比例函数图像上,
∴ ,化简可得: ,又 ,
∴ ,解得: ,
∴ ,
∴M(2,3),代入 ,
得 ;
(2)由(1)可得:M(2,3),N(4, ),
设直线MN的表达式为y=ax+b,
则 ,解得: ,
∴直线MN的表达式为 .
【点睛】本题考查了反比例函数和一次函数综合,解题的关键是掌握反比例函数图象上点的坐标特征,求
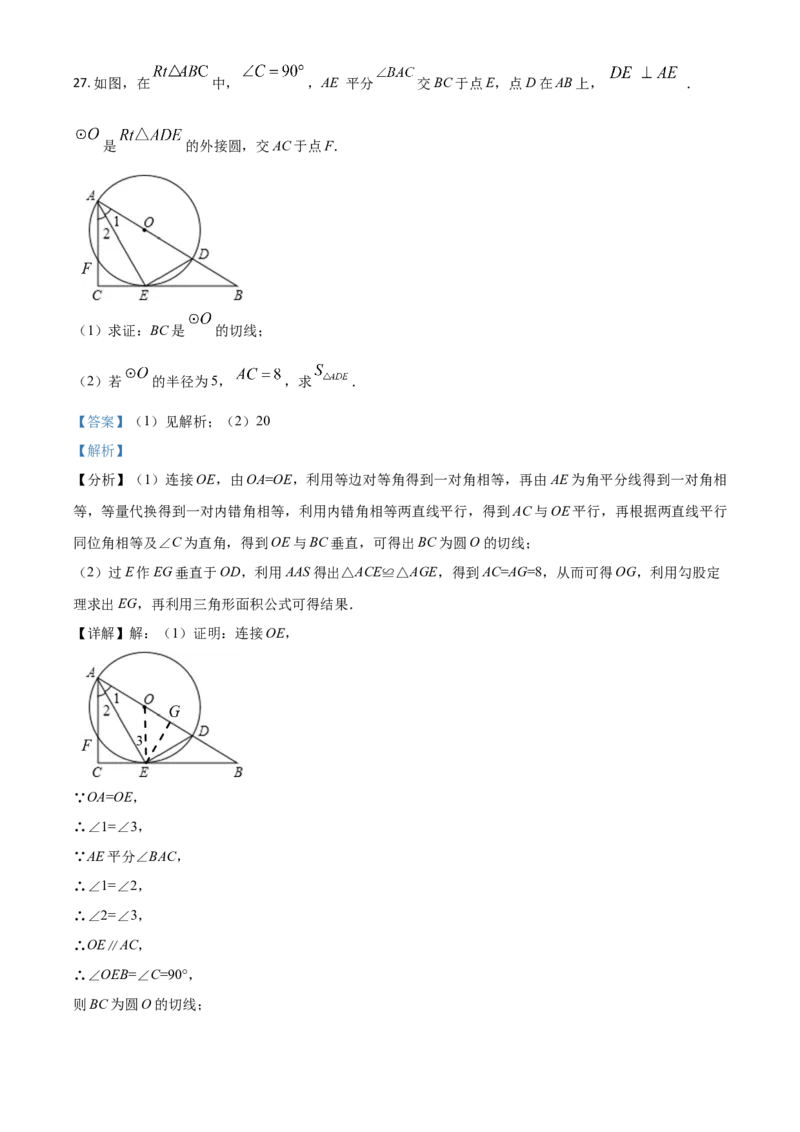
出相应的点的坐标是解决问题的关键.27. 如图,在 中, ,AE 平分 交BC于点E,点D在AB上, .
是 的外接圆,交AC于点F.
(1)求证:BC是 的切线;
(2)若 的半径为5, ,求 .
【答案】(1)见解析;(2)20
【解析】
【分析】(1)连接OE,由OA=OE,利用等边对等角得到一对角相等,再由AE为角平分线得到一对角相
等,等量代换得到一对内错角相等,利用内错角相等两直线平行,得到AC与OE平行,再根据两直线平行
同位角相等及∠C为直角,得到OE与BC垂直,可得出BC为圆O的切线;
(2)过E作EG垂直于OD,利用AAS得出△ACE≌△AGE,得到AC=AG=8,从而可得OG,利用勾股定
理求出EG,再利用三角形面积公式可得结果.
【详解】解:(1)证明:连接OE,
∵OA=OE,
∴∠1=∠3,
∵AE平分∠BAC,
∴∠1=∠2,
∴∠2=∠3,
∴OE∥AC,
∴∠OEB=∠C=90°,
则BC为圆O的切线;(2)过E作EG⊥AB于点G,
在△ACE和△AGE中,
,
∴△ACE≌△AGE(AAS),
∴AC=AG=8,
∵圆O的半径为5,
∴AD=OA+OD=10,
∴OG=3,
∴EG= =4,
∴△ADE的面积= =20.
【点睛】此题考查了切线的判定,涉及的知识有:全等三角形的判定与性质,勾股定理,平行线的判定与
性质,切线的判定方法有两种:有点连接证垂直;无点作垂线,证明垂线段等于半径.
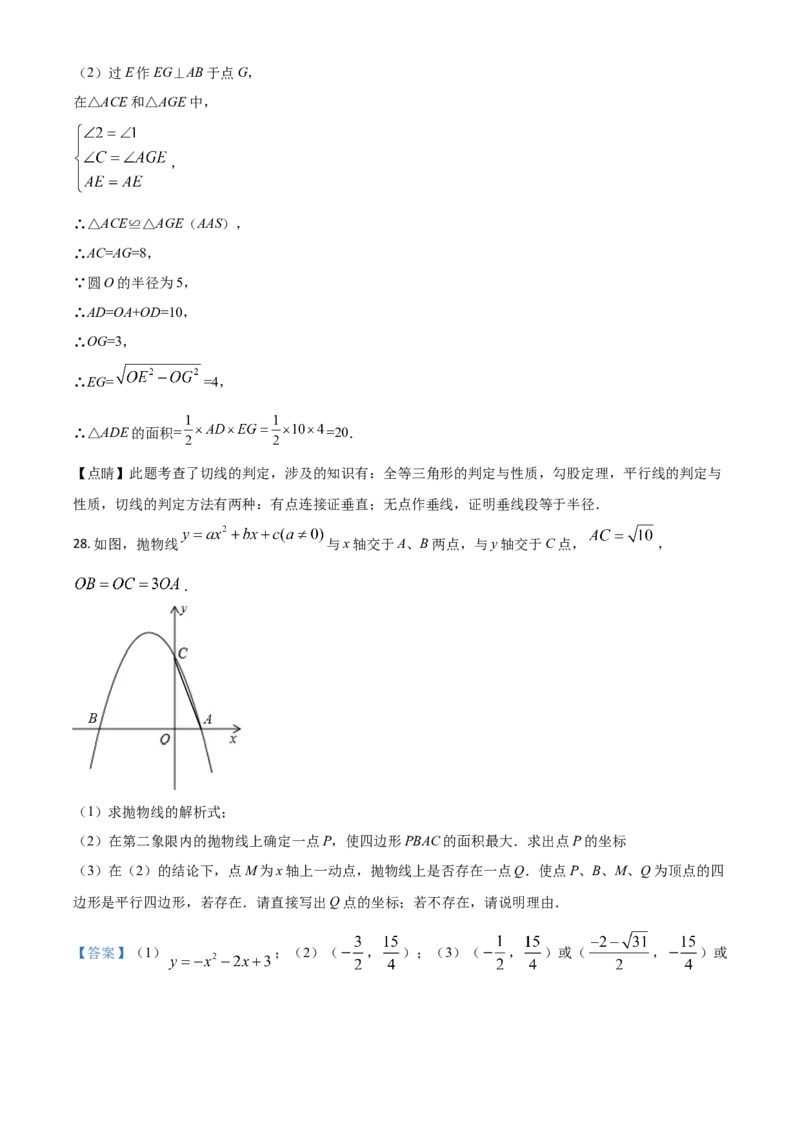
28. 如图,抛物线 与x轴交于A、B两点,与y轴交于C点, ,
.
(1)求抛物线的解析式;
(2)在第二象限内的抛物线上确定一点P,使四边形PBAC的面积最大.求出点P的坐标
(3)在(2)的结论下,点M为x轴上一动点,抛物线上是否存在一点Q.使点P、B、M、Q为顶点的四
边形是平行四边形,若存在.请直接写出Q点的坐标;若不存在,请说明理由.
【答案】(1) ;(2)( , );(3)( , )或( , )或( , )
【解析】
【分析】(1)根据OB=OC=3OA,AC= ,利用勾股定理求出OA,可得OB和OC,得到A,B,C的
坐标,利用待定系数法求出抛物线的解析式;
(2)判断出四边形BACP的面积最大时,△BPC的最大面积,过点P作y轴的平行线交BC于点H,求出
直线BC的表达式,设点P(x,-x2-2x+3),利用三角形面积公式S = ,即可求出S 面积
△BPC △BPC
最小时点P的坐标;
(3)分类讨论,一是当BP为平行四边形对角线时,二是当BP为平行四边形一边时,利用平移规律即可
求出点Q的坐标.
【详解】解:(1)∵OB=OC=3OA,AC= ,
∴ ,即 ,
解得:OA=1,OC=OB=3,
∴A(1,0),B(-3,0),C(0,3),代入 中,
则 ,解得: ,
∴抛物线的解析式为 ;
(2)如图,四边形PBAC的面积=△BCA的面积+△PBC的面积,
而△ABC的面积是定值,故四边形PBAC的面积最大,只需要△BPC的最大面积即可,
过点P作y轴的平行线交BC于点H,
∵B(-3,0),C(0,3),设直线BC的表达式为y=mx+n,
则 ,解得: ,
∴直线BC的表达式为y=x+3,
设点P(x,-x2-2x+3),则点H(x,x+3),S = = = ,
△BPC
∵ ,故S有最大值,即四边形PBAC的面积有最大值,
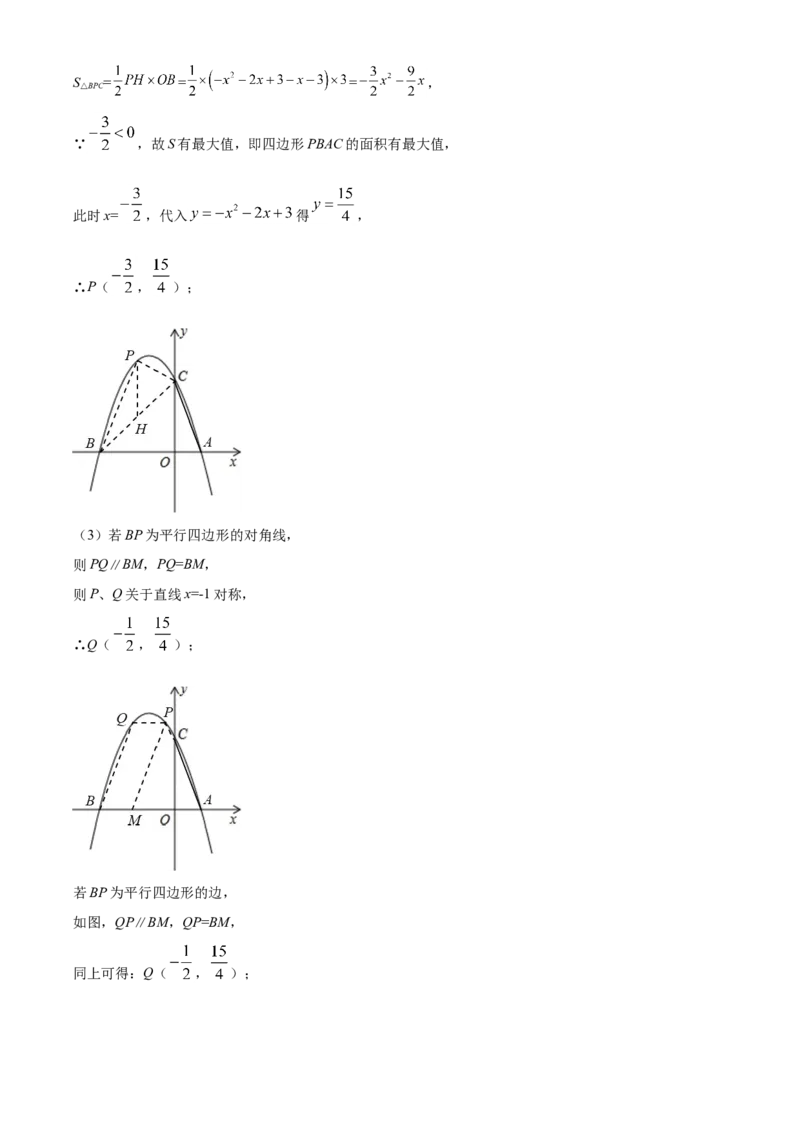
此时x= ,代入 得 ,
∴P( , );
(3)若BP为平行四边形的对角线,
则PQ∥BM,PQ=BM,
则P、Q关于直线x=-1对称,
∴Q( , );
若BP为平行四边形的边,
如图,QP∥BM,QP=BM,
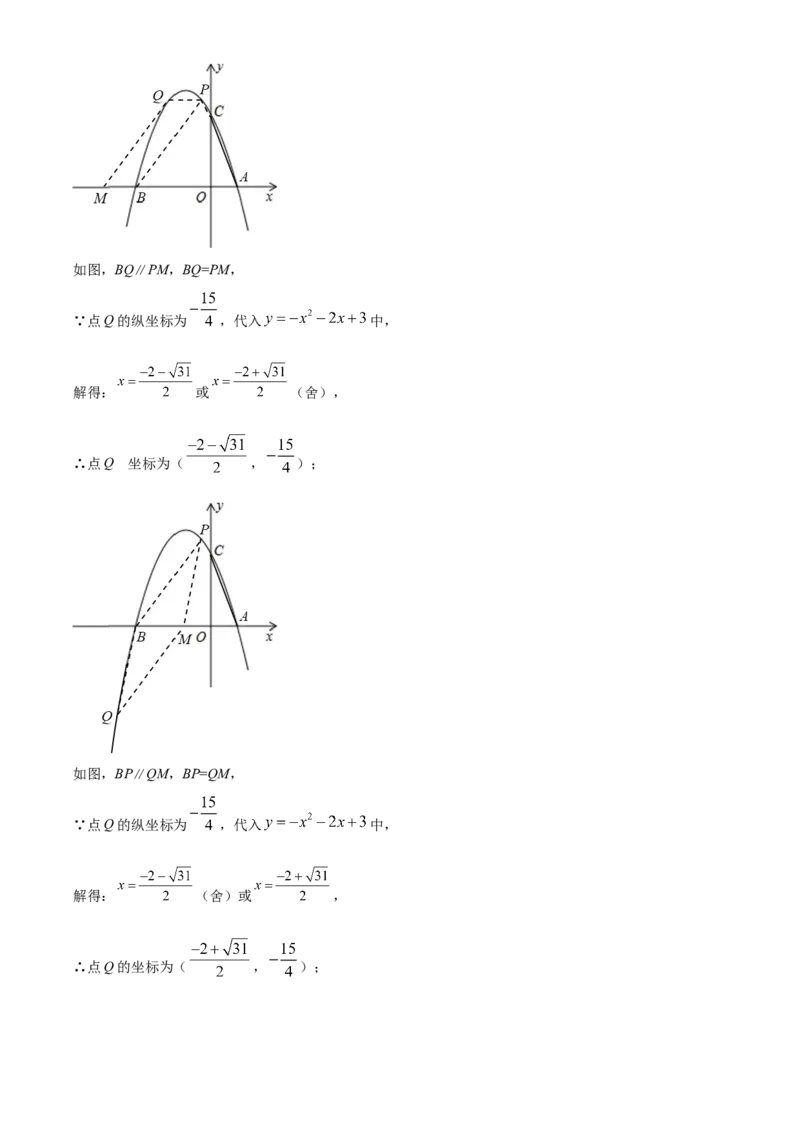
同上可得:Q( , );如图,BQ∥PM,BQ=PM,
∵点Q的纵坐标为 ,代入 中,
解得: 或 (舍),
∴点Q 的坐标为( , );
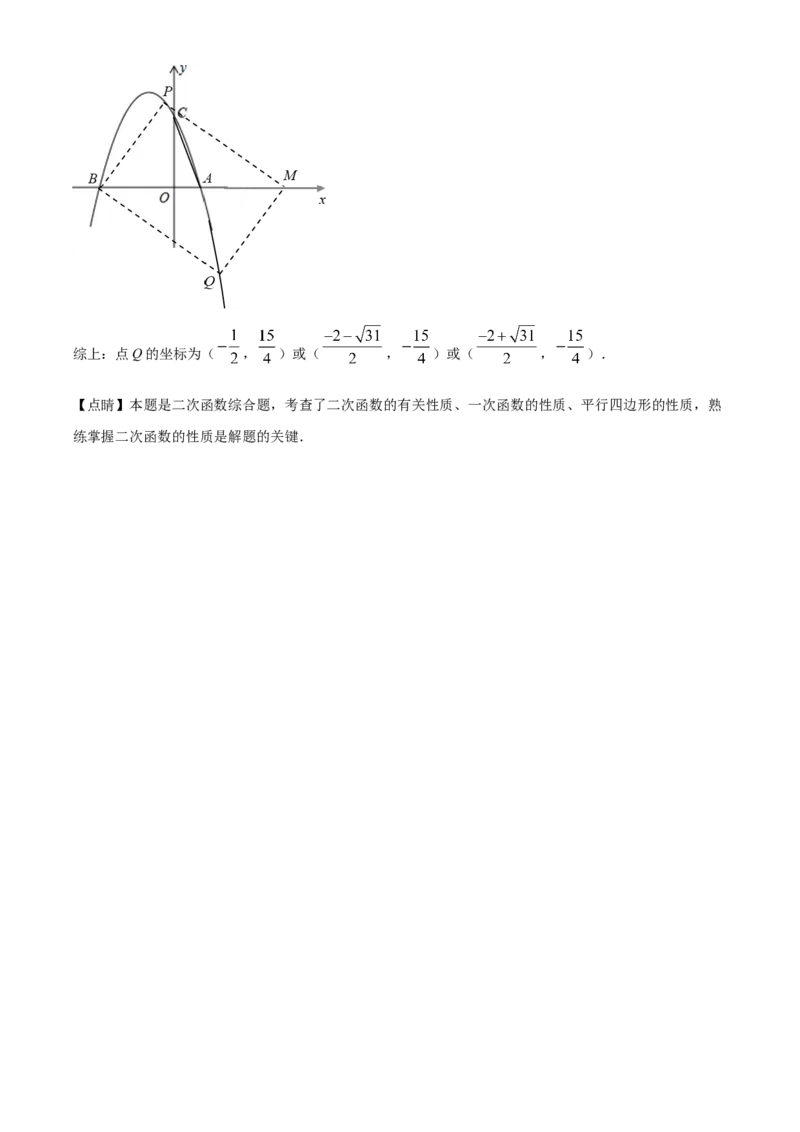
如图,BP∥QM,BP=QM,
∵点Q的纵坐标为 ,代入 中,
解得: (舍)或 ,
∴点Q的坐标为( , );综上:点Q的坐标为( , )或( , )或( , ).
【点睛】本题是二次函数综合题,考查了二次函数的有关性质、一次函数的性质、平行四边形的性质,熟
练掌握二次函数的性质是解题的关键.