文档内容
2023 年高考考前押题密卷(全国乙卷理)
数学·参考答案
1 2 3 4 5 6 7 8 9 10 11 12
B D C B C B C B B D A C
13.8
14.
15.
16. /
17.(12分)
【详解】(1)因为 ,
所以 ,又 ,
所以 ,
∴数列 是首项为 ,公比为 的等比数列.…………………………………………4分
(2)由(1)知, ,∴ ,
∵ ,∴ ,
∴
……………………………………6分
令
……………………………………8分
1
学科网(北京)股份有限公司两式相减 ,
所以
所以 ,……………………………………10分
又 ,
∴ ……………………………………12分
18.(12分)微信搜索“高中试卷君”公众号 领取押题卷联考卷
【详解】(1)证明:在四棱锥 中, ,
又平面 底面 ,且平面 底面 底面
所以 平面 ,
因为 平面 ,所以 ,
又 ,且 底面 底面 ,
所以 底面 ,
因为 平面 ,
所以 .……………………………………4分
(2)不妨令 ,设 ,
作 ,垂足为 ,因为 ,所以 ,
又 ,所以 ,
由(1)知 底面 ,所以 ,
分别以直线 为 轴, 轴, 轴建系如图,……………………………………6分
2
学科网(北京)股份有限公司则 ,
,……………………………………7
分
设平面 的一个法向量为 ,
则 即 令 ,则 ,
可得平面 的一个法向量为 ,……………………………………9分
设直线 与平面 所成角为 ,
则 ,
,
解得 ,
所以平面 的一个法向量为 ,
设平面 的法向量为 ,
则 即 令 ,则 1,
可得平面 的一个法向量为 ,……………………………………11分
设平面 与平面 所成锐二面角为 ,
则
所以平面 与平面 所成锐二面角的余弦值为 .……………………………………12分
19.(12分)微信搜索“高中试卷君”公众号 领取押题卷联考卷
3
学科网(北京)股份有限公司【详解】(1)记“甲取红球”为事件 ,“甲取黄球”为事件 ,“甲取蓝球”为事件 ,“乙
取红球”为事件 ,“乙取红球”为事件 ,“乙取红球”为事件 ,
……………………………………1分
则由已知可得, , , , , , .
……………………………………3分
由已知,乙胜可以用事件 来表示,
根据独立事件以及互斥事件可知, .
……………………………………5分
(2)由题意知, , , .
用随机变量 来表示乙得分,则 可取 ,
则 , , ,
……………………………………7分
所以 .
所以 .……………………………………9分
因为 ,所以 ,且 , , ,
所以 ,……………………………………11分
当且仅当 , , 时,等号成立.
所以,乙得分均值的最大值为 ,此时 , , .……………………………………12分
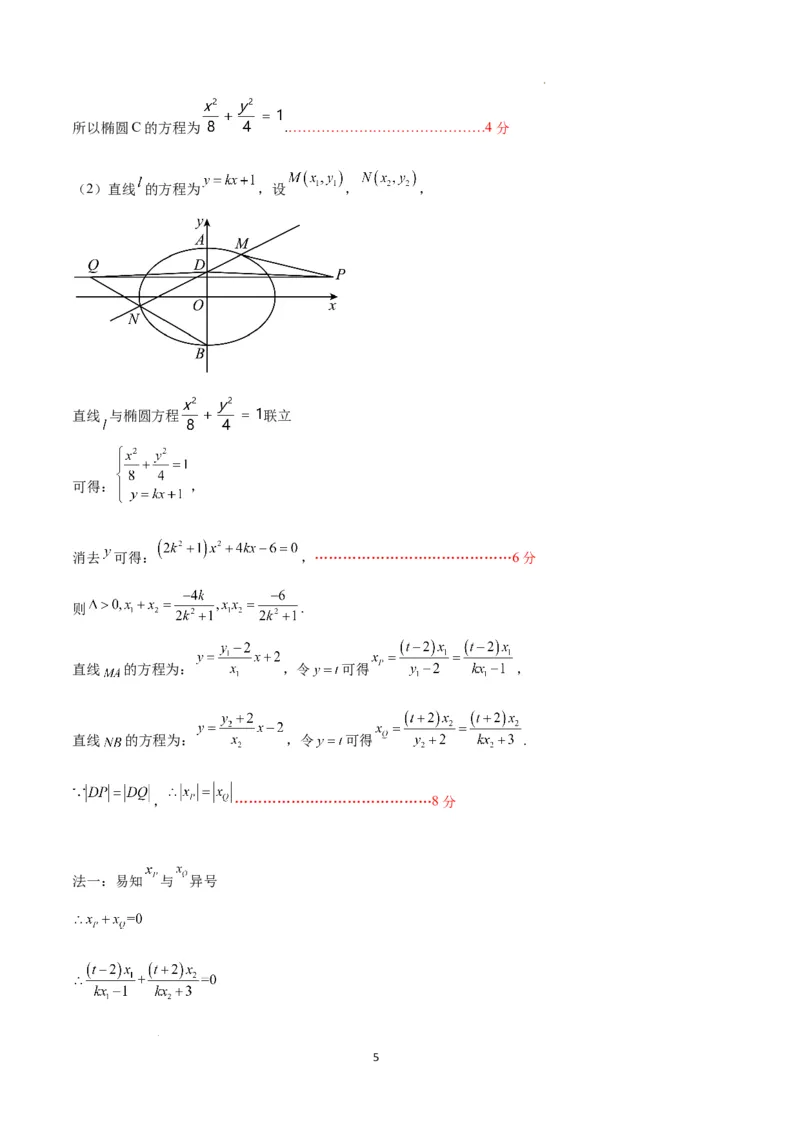
20.(12分)
【详解】(1)由题意可知:
4
学科网(北京)股份有限公司所以椭圆C的方程为 .……………………………………4分
(2)直线 的方程为 ,设 , ,
直线 与椭圆方程 联立
可得: ,
消去 可得: ,……………………………………6分
则 .
直线 的方程为: ,令 可得 ,
直线 的方程为: ,令 可得 .
, ……………………………………8分
法一:易知 与 异号
5
学科网(北京)股份有限公司……………………………………12分
法二:
……………………………………12分
21.(12分)微信搜索“高中试卷君”公众号 领取押题卷联考卷
6
学科网(北京)股份有限公司【详解】(1)解:函数 ,则 ,
因为 在点 处的切线斜率为 ,
所以 ,解得 .……………………………………3分
(2)由(1)知: ,
当 时,令 ,得 ,令 ,得 ,
所以 在 上单调递减,在 上单调递增.……………………………………7分
(3) ,
令 ,则 ,……………………………………8分
因为 ,所以 ,
则 在 上单调递增,又 ,所以 恒成立,即 ;
……………………………………10分
令 , , 时, , 时, ,所以
在 上单调递增,在 上单调递减, , 恒成立,即
,
所以 ,得证.……………………………………12分
22.[选修4-4:坐标系与参数方程](10分)
【详解】(1)因为 ,
7
学科网(北京)股份有限公司所以 ,
所以 ,
整理得 ,
曲线C的直角坐标方程为 ,
所以 其中 为参数.
则对应的参数方程为 其中 为参数.……………………………………5分
(2)由(1)参数方程可设 ,
则由 ,
得 其中 为参数.
对应的直角坐标方程为 ,
圆心 到l距离 ,则 与l相离.……………………………………10分
23.[选修4-5:不等式选讲](10分)
【详解】(1) ,
当 时, ,得 ,故 ;
当 时, ,得 ,故 ;
8
学科网(北京)股份有限公司当 时,由 ,得 ,此时无解.
综上所述:原不等式的解集是 .……………………………………5分
(2) ,故 , , ,则 ,
,
,故 , ,
,故m的最大值为2.……………………………………10分
9
学科网(北京)股份有限公司10
学科网(北京)股份有限公司