文档内容
2023 年高考考前押题密卷(全国乙卷理)
数学
(考试时间:120分钟 试卷满分:150分)
注意事项:
1.本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。答卷前,考生务必将自己的姓名、准考
证号填写在答题卡上。
2.回答第Ⅰ卷时,选出每小题答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑。如需改动,
用橡皮擦干净后,再选涂其他答案标号。写在本试卷上无效。
3.回答第Ⅱ卷时,将答案写在答题卡上。写在本试卷上无效。
4.考试结束后,将本试卷和答题卡一并交回。
第Ⅰ卷
一、选择题:本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一个选项是符合题
目要求的.
1.已知集合 ,集合 ,则 ( )
A. B. C. D.
【答案】B
【详解】解 可得, ,所以 .
又 ,所以 .
所以 .
故选:B.
2.若复数 ,则 ( )
A.25 B.20 C.10 D.5
【答案】D
【详解】因为 ,所以 ,
1
学科网(北京)股份有限公司故选:D.
3.已知定义在 上的函数 满足 , 为奇函数,则 ( )
A.0 B.1 C.2 D.3
【答案】C
【详解】因为 ,所以 ,所以 的周期为6,
又 为奇函数,所以 ,所以 ,
令 ,得 ,所以 ,
所以 ,
故选:C.
4.从甲,乙等五名同学中随机选3人参加社区服务工作,则甲,乙中至少有一人入选的概率为( )
A. B. C. D.
【答案】B
【详解】从甲,乙等五名同学中随机选3人的方法数为 ,甲乙两人都没入选只有一种方法,概率为
,
因此甲、乙中至少有一人入选的概率为 .
故选:B.
5.党的二十大报告提出了要全面推进乡村振兴,其中人才振兴是乡村振兴的关键.如图反映了某县2017-
2022这六年间引入高科技人才数量的占比情况.已知2017、2018、2020、2021这四年引入高科技人才的数
量逐年成递增的等差数列,且这四年引入高科技人才的数量占六年引入高科技人才的数量和的一半,2018
年与2019年引入人才的数量相同,2019、2021、2022这三年引入高科技人才的数量成公比为2的等比数列,
则2022年引入高科技人才的数量占比为( ).
2
学科网(北京)股份有限公司A.30% B.35% C.40% D.45%
【答案】C
【详解】由题可设2017、2018、2020、2021这四年引入高科技人才的数量占比为m, , ,
,
则2019年引入高科技人才的数量占比为 ,2022年引入高科技人才的数量占比为 ,
依题意有 ,且 ,
解得 ,
所以2022年引入高科技人才的数量占比为 .
故选:C.
6.若函数 在 上为增函数,则实数 的取值范围为( )
A. B. C. D.
【答案】B
【详解】
,
令 ,
得 ,∴函数 在 , 单调递增,
3
学科网(北京)股份有限公司由题知 在 上单调递增,∵ ,
∴ ,解得 .
故选:B.
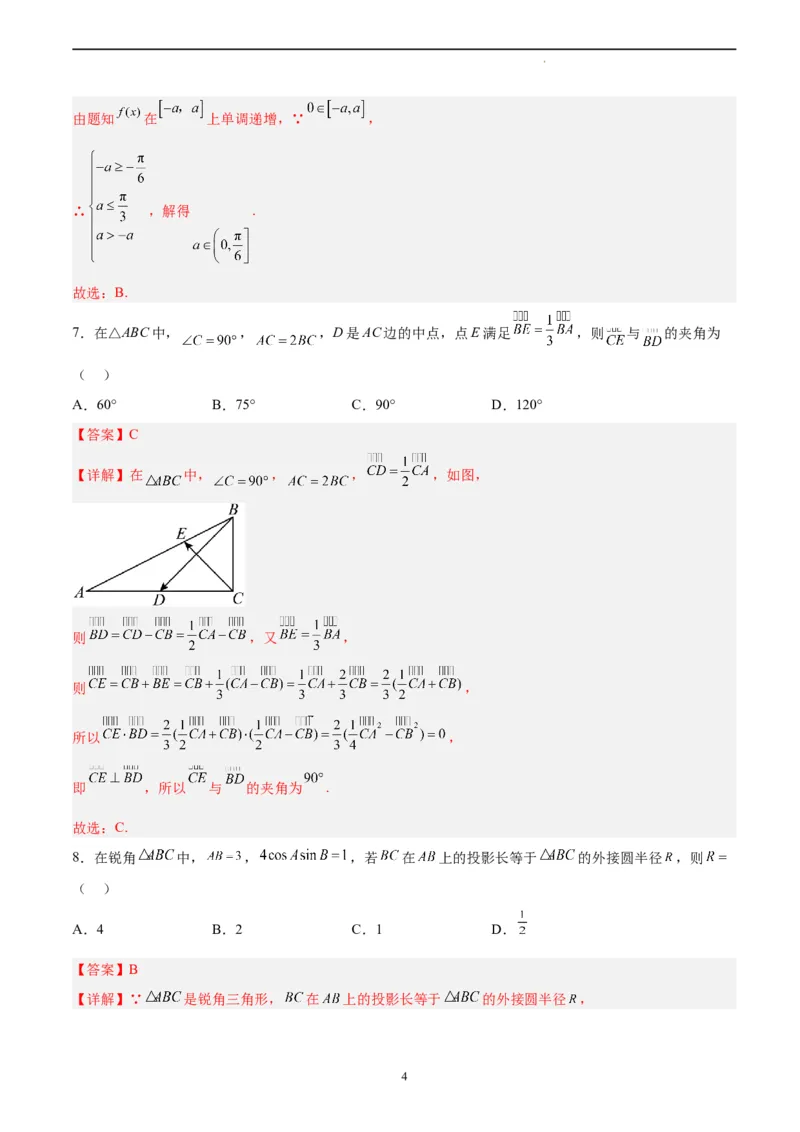
7.在△ABC中, , ,D是AC边的中点,点E满足 ,则 与 的夹角为
( )
A.60° B.75° C.90° D.120°
【答案】C
【详解】在 中, , , ,如图,
则 ,又 ,
则 ,
所以 ,
即 ,所以 与 的夹角为 .
故选:C.
8.在锐角 中, , ,若 在 上的投影长等于 的外接圆半径 ,则
( )
A.4 B.2 C.1 D.
【答案】B
【详解】∵ 是锐角三角形, 在 上的投影长等于 的外接圆半径 ,
4
学科网(北京)股份有限公司,
又 , , ,
,
两式相加得: ,即 ,
,即 ,
又 , , .
故选:B.
9.黄地绿彩云龙纹盘是收藏于中国国家博物馆的一件明代国宝级瓷器.该龙纹盘敞口,弧壁,广底,圈足.器
内施白釉,外壁以黄釉为地,刻云龙纹并填绿彩,美不胜收.黄地绿彩云龙纹盘可近似看作是圆台和圆柱的
组合体,其口径22.5cm,足径14.4cm,高3.8cm,其中底部圆柱高0.8cm,则黄地绿彩云龙纹盘的侧面积约
为( )(附:圆台的侧面积 , , 为两底面半径, 为母线长,其中 的值取3,
)
A. B. C. D.
【答案】B
【详解】设该圆台的母线长为 ,两底面圆半径分别为 , (其中 ),
则 , , ,
所以 ,
故圆台部分的侧面积为 ,
圆柱部分的侧面积为 ,
5
学科网(北京)股份有限公司故该黄地绿彩云龙纹盘的侧面积约为 .
故选:B.
10.已知双曲线C: (a>0,b>0)的离心率为 ,左,右焦点分别为 , 关于C的一条渐
近线的对称点为P.若 ,则 的面积为( )
A.2 B. C.3 D.4
【答案】D
【详解】
设 与渐近线 交于 ,则 , , ,
所以 , ,
由 分别是 与 的中点,知 且 ,即 ,
由 得 ,所以 ,
故选:D
11.已知直线 与 相交于点 ,线段 是圆 的一
条动弦,且 ,则 的最小值为( )
A. B. C. D.
【答案】A
6
学科网(北京)股份有限公司【详解】由圆的方程知:圆心 ,半径 ;
由 得: , 恒过定点 ;
由 得: , 恒过定点 ;
由直线 方程可知: , ,即 ,
设 ,则 , ,
,整理可得: ,
即点 的轨迹是以 为圆心, 为半径的圆,
又直线 斜率存在, 点轨迹不包含 ;
若点 为弦 的中点,则 ,位置关系如图:
连接 ,
由 知: ,
则 ,
(当
在 处取等号),微信搜索“高中试卷君”公众号 领取押题卷联考卷
7
学科网(北京)股份有限公司即 的最小值为 .
故选:A.
12.已知 , , ,则( )
A. B.
C. D.
【答案】C
【详解】设 ,求导 ,所以当 时, , 单调递增,
故 ,即 ,所以 ;
设 ,求导 ,所以当 时, , 单调递增,
,所以 ,故 .
故选:C
第Ⅱ卷
二、填空题:本题共4小题,每小题5分,共20分.
13.某班有48名学生,一次考试的数学成绩X(单位:分)服从正态分布 ,且成绩在 上的
学生人数为16,则成绩在90分以上的学生人数为____________.
【答案】8
【详解】由X(单位:分)服从正态分布 ,知正态密度曲线的对称轴为 ,成绩在 上
的学生人数为16,
由对称性知成绩在80分上的学生人数为24人,所以90分以上的学生人数为 .
故答案为:8
14.已知向量 , ,其中 , ,若 ,则 的最小值为_______.
【答案】 微信搜索“高中试卷君”公众号 领取押题卷联考卷
8
学科网(北京)股份有限公司【详解】 , , ,
,即 ,
由 , ,则 ,
当且仅当 ,即 时等号成立,
故 的最小值为 .
故答案为:
15.已知抛物线 的焦点为F,准线为l,过F且斜率为 的直线与C交于A,B两点,D
为AB的中点,且 于点M,AB的垂直平分线交x轴于点N,四边形DMFN的面积为 ,则
______.
【答案】
【详解】由题意可知, ,直线 的方程为 .
设 ,由 ,得 .
所以 ,所以 .
由 ,得 .
如图所示,作 轴于点 ,则 .
9
学科网(北京)股份有限公司因为 ,故 ,
,又 ,故 .
又 ,得四边形 为平行四边形.
所以其面积为 ,解得 .
故答案为:
16.如图,已知 , 是相互垂直的两条异面直线,直线 与 , 均相互垂直,且 ,动点 ,
分别位于直线 , 上,若直线 与 所成的角 ,三棱锥 的体积的最大值为________.
【答案】 /
【详解】因为直线 三条直线两两垂直,
如图,将图形还原为长方体 ,
10
学科网(北京)股份有限公司因为 ,所以 即为直线 与 所成的角的平面角,
则 ,
因为 平面 , 平面 ,所以 ,
在 中,由 ,得 ,
所以 ,
,
当且仅当 时,取等号,
所以三棱锥 的体积的最大值为 .
故答案为: .
三、解答题:共70分.解答应写出文字说明、证明过程或演算步骤.第 17~21题为必考题,每个试题考生
都必须作答.第22、23题为选考题,考生根据要求作答.
17.已知数列 满足
(1)求证:数列 是等比数列;
(2)设 ,求 的前 项和
11
学科网(北京)股份有限公司【详解】(1)因为 ,
所以 ,又 ,
所以 ,
∴数列 是首项为 ,公比为 的等比数列.
(2)由(1)知, ,∴ ,
∵ ,∴ ,
∴
令
两式相减 ,
所以
所以 ,
又 ,
∴
18.如图,在四棱锥 中,底面 是直角梯形, ,且平面
底面
12
学科网(北京)股份有限公司(1)求证: ;
(2)若 ,且直线 与平面 所成角的正弦值为 .求平面 与平面 所成锐二
面角的余弦值.
【详解】(1)证明:在四棱锥 中, ,
又平面 底面 ,且平面 底面 底面
所以 平面 ,
因为 平面 ,所以 ,
又 ,且 底面 底面 ,
所以 底面 ,
因为 平面 ,
所以 .
(2)不妨令 ,设 ,
作 ,垂足为 ,因为 ,所以 ,
又 ,所以 ,
由(1)知 底面 ,所以 ,
分别以直线 为 轴, 轴, 轴建系如图,
13
学科网(北京)股份有限公司则 ,
,
设平面 的一个法向量为 ,
则 即 令 ,则 ,
可得平面 的一个法向量为 ,
设直线 与平面 所成角为 ,
则 ,
,
解得 ,
所以平面 的一个法向量为 ,
设平面 的法向量为 ,
则 即 令 ,则 1,
可得平面 的一个法向量为 ,
设平面 与平面 所成锐二面角为 ,
14
学科网(北京)股份有限公司则
所以平面 与平面 所成锐二面角的余弦值为 .
19.甲、乙两人各有一只箱子.甲的箱子里放有大小形状完全相同的3个红球、2个黄球和1个蓝球.乙的箱子
里放有大小形状完全相同的x个红球、y个黄球和z个蓝球, .现两人各从自己的箱子
里任取一球,规定同色时乙胜,异色时甲胜.
(1)当 , , 时,求乙胜的概率;
(2)若规定:当乙取红球、黄球和蓝球获胜的得分分别是1分、2分和3分,否则得零分.求乙得分均值的最大
值,并求此时x,y,z的值.
【详解】(1)记“甲取红球”为事件 ,“甲取黄球”为事件 ,“甲取蓝球”为事件 ,“乙取红球”
为事件 ,“乙取红球”为事件 ,“乙取红球”为事件 ,
则由已知可得, , , , , , .
由已知,乙胜可以用事件 来表示,
根据独立事件以及互斥事件可知, .
(2)由题意知, , , .
用随机变量 来表示乙得分,则 可取 ,
则 , , ,
所以 .
所以 .
因为 ,所以 ,且 , , ,
15
学科网(北京)股份有限公司所以 ,
当且仅当 , , 时,等号成立.
所以,乙得分均值的最大值为 ,此时 , , .
20.已知椭圆 过点 和 ,且 .
(1)求椭圆 的方程;
(2)过点 斜率为 的直线 交椭圆 于 ,直线 分别交直线 于点 .若
,求 的值.
【详解】(1)由题意可知:
所以椭圆C的方程为 .
(2)直线 的方程为 ,设 , ,
直线 与椭圆方程 联立可得: ,消去 可得: ,
则 .
直线 的方程为: ,令 可得 ,
16
学科网(北京)股份有限公司直线 的方程为: ,令 可得 .
,
法一:易知 与 异号
法二:
17
学科网(北京)股份有限公司21.设函数 .
(1)若 在点 处的切线斜率为 ,求a的值;
(2)当 时,求 的单调区间;
(3)若 ,求证:在 时, .
【详解】(1)解:函数 ,则 ,
因为 在点 处的切线斜率为 ,
所以 ,解得 .
(2)由(1)知: ,
当 时,令 ,得 ,令 ,得 ,
所以 在 上单调递减,在 上单调递增.
(3) ,
令 ,则 ,
18
学科网(北京)股份有限公司因为 ,所以 ,
则 在 上单调递增,又 ,所以 恒成立,即 ;
令 , , 时, , 时, ,所以 在
上单调递增,在 上单调递减, , 恒成立,即 ,
所以 ,得证.
(二)选考题:共10分.请考生在第22、23题中任选一题作答.如果多做,则按所做的第一题计分.
22.[选修4-4:坐标系与参数方程](10分)
在直角坐标系 中,以坐标原点为极点,x轴正半轴为极轴建立极坐标系.曲线C的极坐标方程为
,直线l的普通方程为 .
(1)将C的极坐标方程化为参数方程;
(2)设点A的直角坐标为 ,M为C上的动点,点P满足 ,写出P的轨迹 的参数方程并判
断 与l的位置关系.
【详解】(1)因为 ,
所以 ,
所以 ,
整理得 ,
曲线C的直角坐标方程为 ,
所以 其中 为参数.
19
学科网(北京)股份有限公司则对应的参数方程为 其中 为参数.
(2)由(1)参数方程可设 ,
则由 ,
得 其中 为参数.
对应的直角坐标方程为 ,
圆心 到l距离 ,则 与l相离.
23.[选修4-5:不等式选讲](10分)微信搜索“高中试卷君”公众号 领取押题卷联考卷
已知
(1)求不等式 的解集;
(2)若 ,且 , 恒成立,求m的最大值.
【详解】(1) ,
当 时, ,得 ,故 ;
当 时, ,得 ,故 ;
当 时,由 ,得 ,此时无解.
综上所述:原不等式的解集是 .
(2) ,故 , , ,则 ,
20
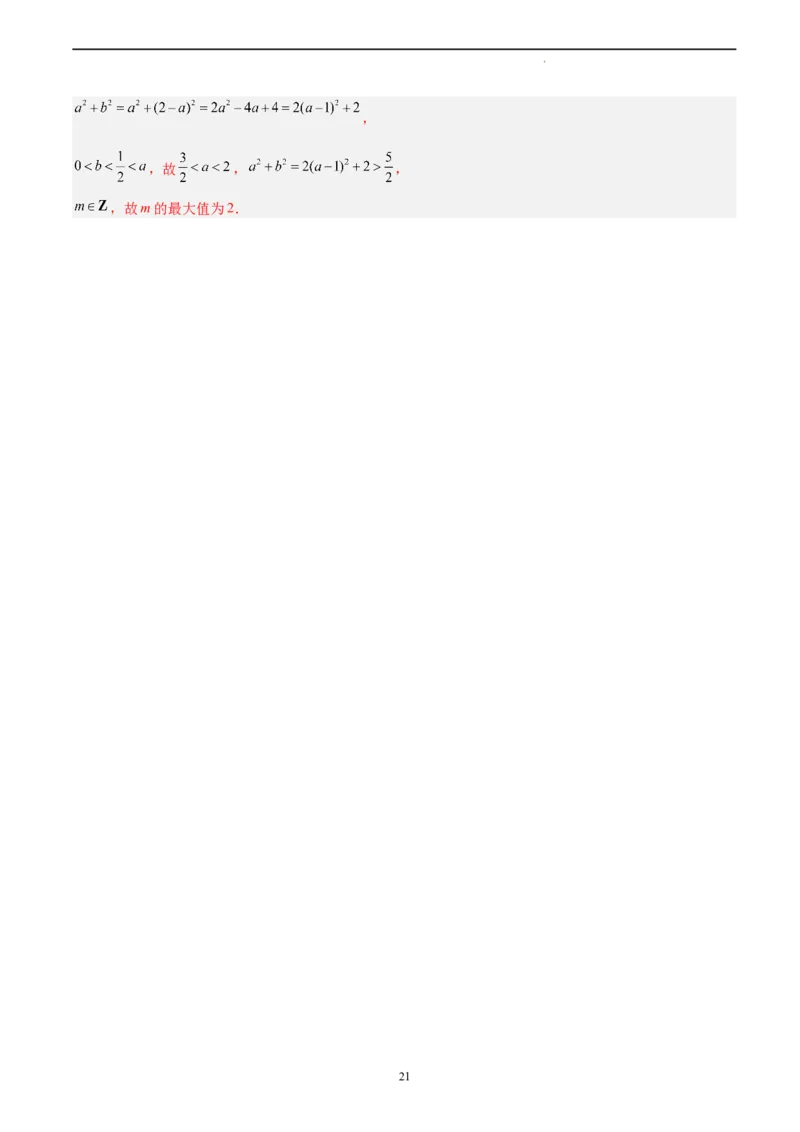
学科网(北京)股份有限公司,
,故 , ,
,故m的最大值为2.
21
学科网(北京)股份有限公司22
学科网(北京)股份有限公司