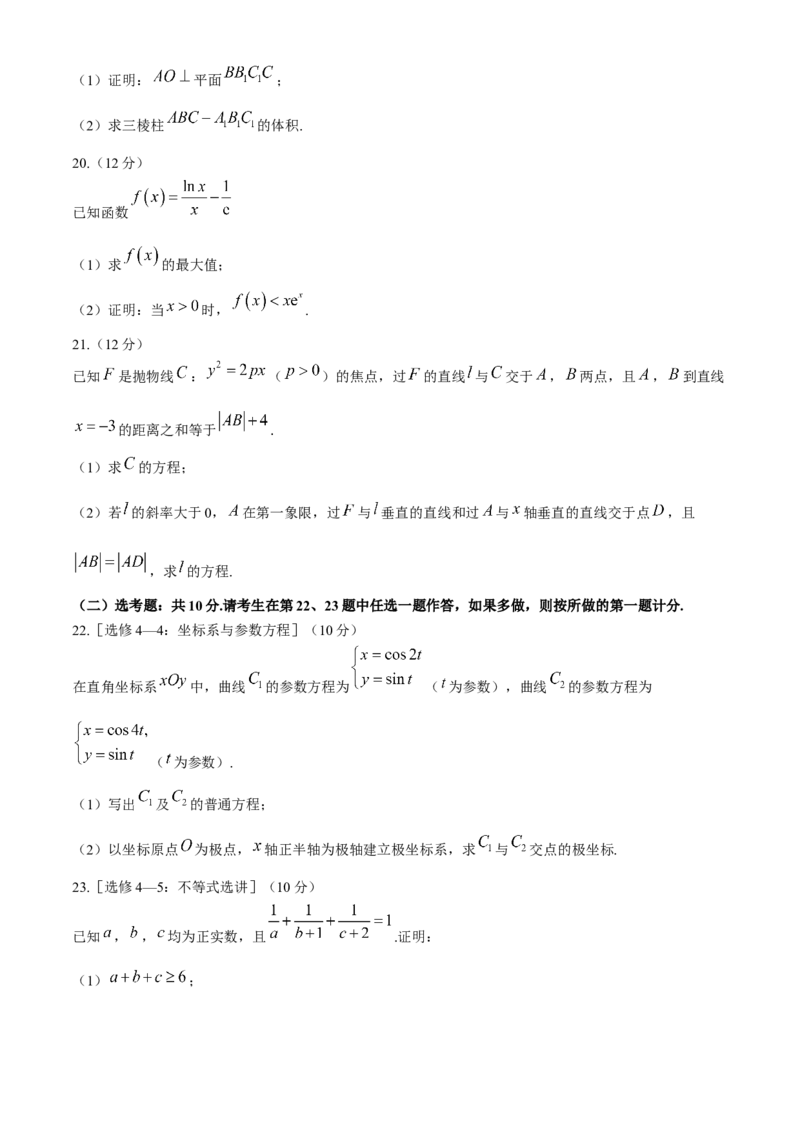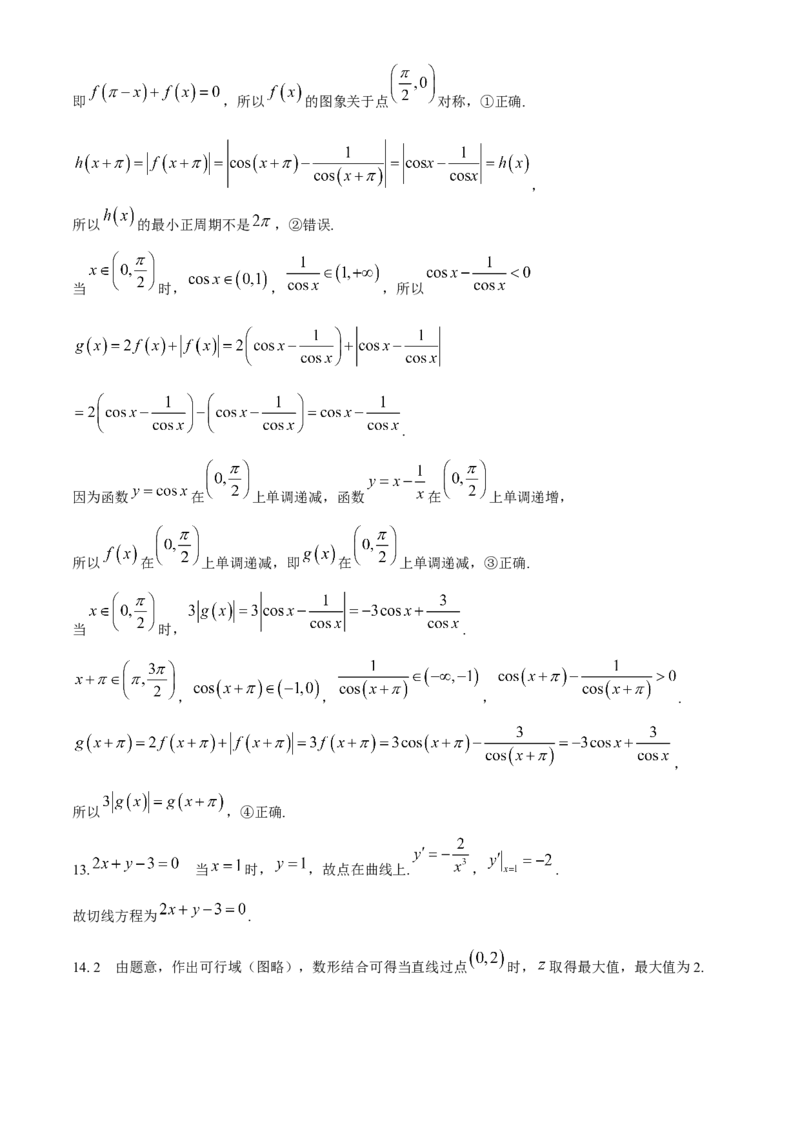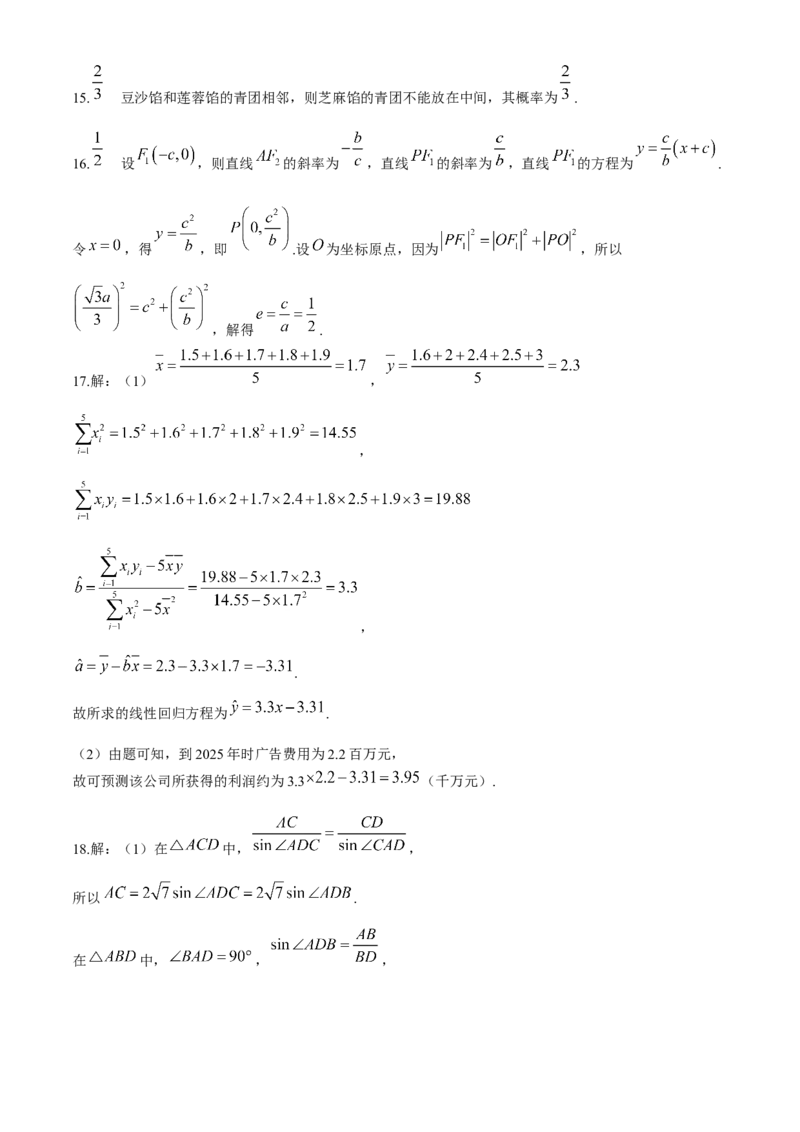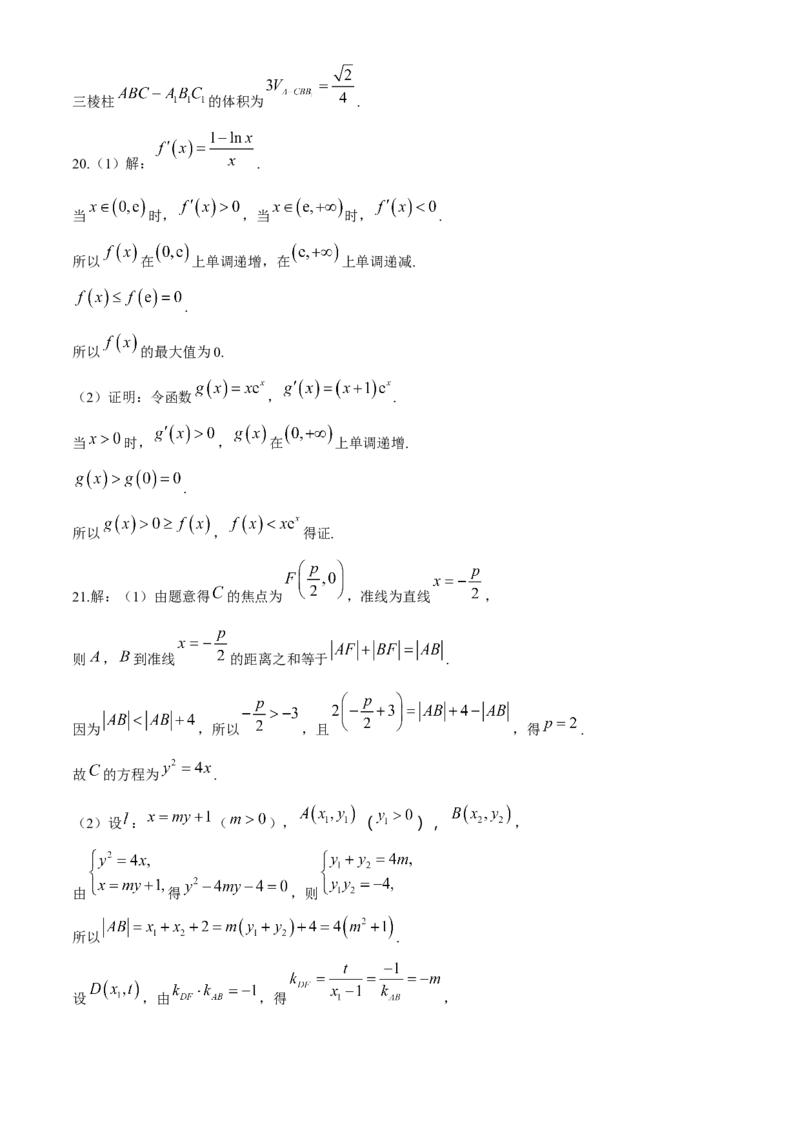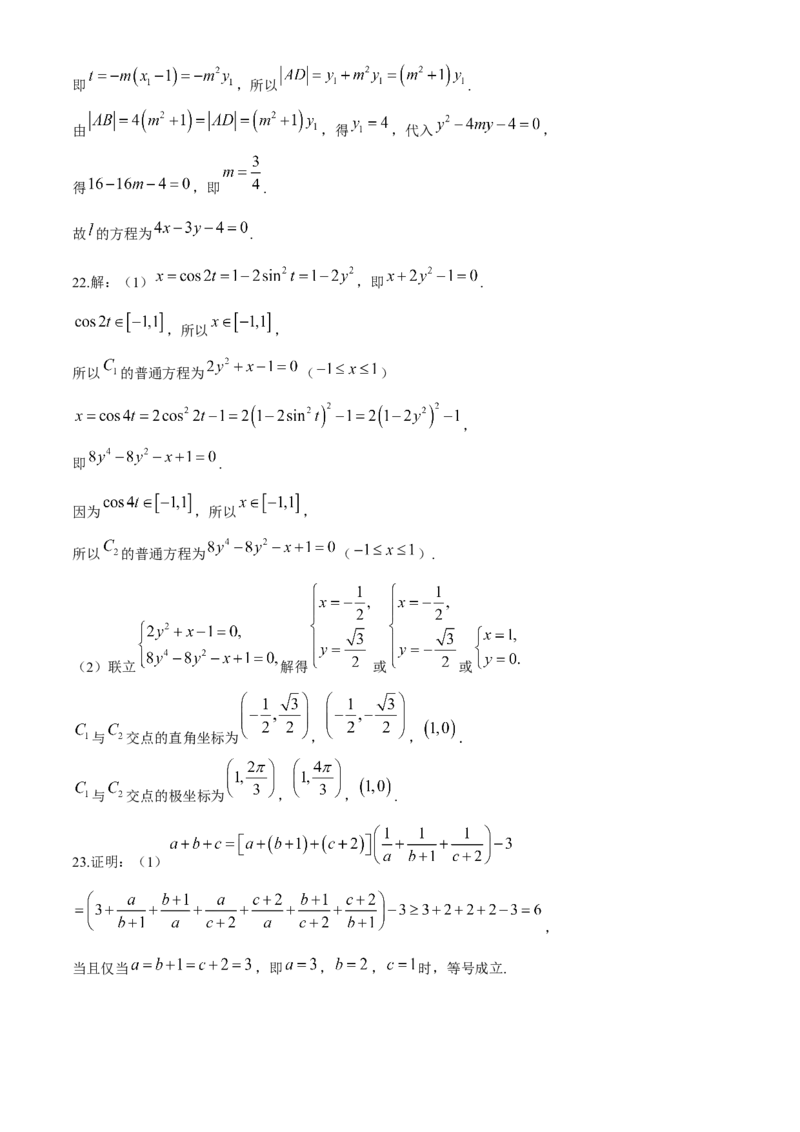文档内容
高三数学试卷(文科)
考生注意:
1.本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共150分,考试时间120分钟.
2.请将各题答案填写在答题卡上.
3.本试卷主要考试内容:高考全部内容.
第Ⅰ卷
一、选择题:本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有
一项是符合题目要求的.
1.设集合 , ,则 ( )
A. B. C. D.
2.复数 的虚部为( )
A.6 B C.8 D.
3.已知 为锐角, ,则 ( )
A. B. C. D.
4.若圆 : ( )与双曲线 : 的渐近线相切,则 ( )
A.1 B.2 C. D.
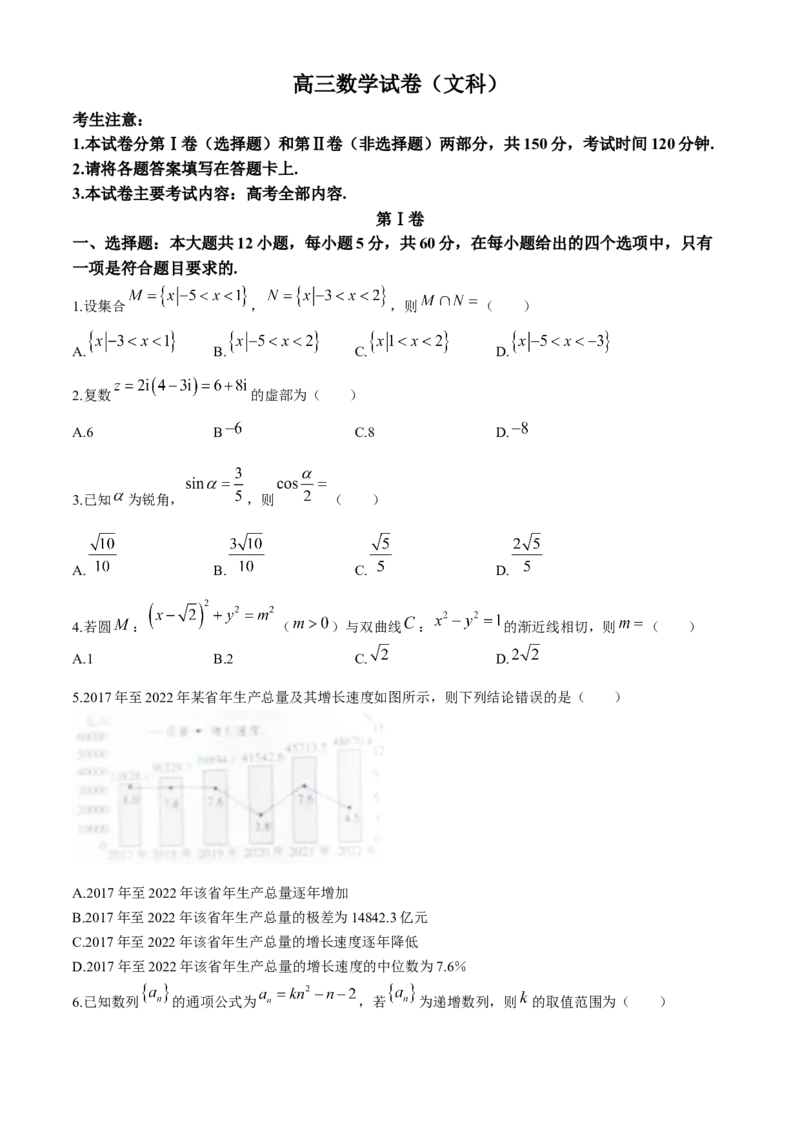
5.2017年至2022年某省年生产总量及其增长速度如图所示,则下列结论错误的是( )
A.2017年至2022年该省年生产总量逐年增加
B.2017年至2022年该省年生产总量的极差为14842.3亿元
C.2017年至2022年该省年生产总量的增长速度逐年降低
D.2017年至2022年该省年生产总量的增长速度的中位数为7.6%
6.已知数列 的通项公式为 ,若 为递增数列,则 的取值范围为( )
学科网(北京)股份有限公司A. B. C. D.
7.如图,这是一个正方体的平面展开图,在该正方体中,下列命题正确的是( )
A. B. C. D.
8.在等差数列 中, , ,设 ,记 为数列 的前 项和,
若 ,则 ( )
A.5 B.6 C.7 D.8
9.已知函数 则不等式 的解集为( )
A. B. C. D.
10.如图,在 中, 是 的中点, 是 的中点,过点 作直线分别交 , 于点 ,
,且 , ,则 的最小值为( )
A.1 B.2 C.4 D.
学科网(北京)股份有限公司11.将一个母线长为 ,底面半径为 的圆锥木头加工打磨成一个球状零件,则能制作的最大零件的
表面积为( )
A. B. C. D.
12.已知函数 ,现给出下列四个结论:
① 的图象关于点 对称;
②函数 的最小正周期为 ;
③函数 在 上单调递减;
④对于函数 , , .
其中所有正确结论的序号为( )
A.①② B.①③ C.①③④ D.②③④
第Ⅱ卷
二、填空题:本大题共4小题,每小题5分,共20分,把答案填在答题卡中的横线上.
13.曲线 在点 处的切线方程为______.
14.若 , 满足约束条件 ,则 的最大值为______.
15.青团是江南人家在清明节吃的一道传统点心,某企业设计了一款青团礼盒,该礼盒刚好可以装3个青团,
如图所示.若将豆沙馅、莲蓉馅、芝麻馅的青团各1个,随机放入该礼盒中,则豆沙馅和莲蓉馅的青团相邻
的概率为______.
学科网(北京)股份有限公司16.已知椭圆 : ( )的左、右焦点分别为 , ,上顶点为 ,过 作 的垂
线,与 轴交于点 ,若 ,则椭圆 的离心率为______.
三、解答题:共70分,解答应写出文字说明、证明过程或演算步骤,第17~21题为必考题,
每个试题考生都必须作答,第22.23题为选考题,考生根据要求作答.
(一)必考题:共60分.
17.(12分)
某企业近年来的广告费用 (百万元)与所获得的利润 (千万元)的数据如下表所示,已知 与 之间
具有线性相关关系
年份 2018 2019 2020 2021 2022
广告费用 /百万元 1.5 1.6 1.7 1.8 1.9
利润 /千万元 1.6 2 2.4 2.5 3
(1)求 关于 的线性回归方程;
(2)若该企业从2018年开始,广告费用连续每一年都比上一年增加10万元,根据(1)中所得的线性回
归方程,预测2025年该企业可获得的利润.
参考公式: ,
18.(12分)
在 中,已知 , 为 上一点, , ,且 .
(1)求 的值;
(2) 的面积.
19.(12分)
如图,在三棱柱 中,所有棱长均为1, , , .
学科网(北京)股份有限公司(1)证明: 平面 ;
(2)求三棱柱 的体积.
20.(12分)
已知函数
(1)求 的最大值;
(2)证明:当 时, .
21.(12分)
已知 是抛物线 : ( )的焦点,过 的直线 与 交于 , 两点,且 , 到直线
的距离之和等于 .
(1)求 的方程;
(2)若 的斜率大于0, 在第一象限,过 与 垂直的直线和过 与 轴垂直的直线交于点 ,且
,求 的方程.
(二)选考题:共10分.请考生在第22、23题中任选一题作答,如果多做,则按所做的第一题计分.
22.[选修4—4:坐标系与参数方程](10分)
在直角坐标系 中,曲线 的参数方程为 ( 为参数),曲线 的参数方程为
( 为参数).
(1)写出 及 的普通方程;
(2)以坐标原点 为极点, 轴正半轴为极轴建立极坐标系,求 与 交点的极坐标.
23.[选修4—5:不等式选讲](10分)
已知 , , 均为正实数,且 .证明:
(1) ;
学科网(北京)股份有限公司(2)若 ,则 .
学科网(北京)股份有限公司高三数学试卷参考答案(文科)
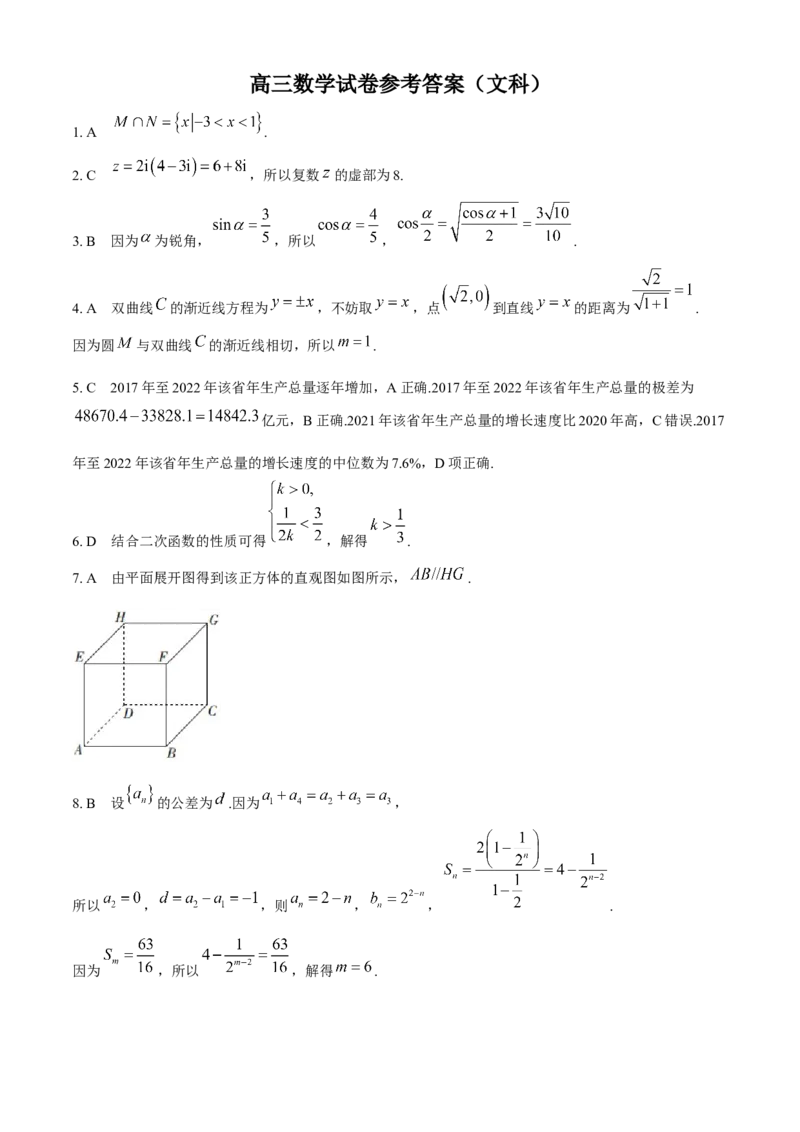
1. A .
2. C ,所以复数 的虚部为8.
3. B 因为 为锐角, ,所以 , .
4. A 双曲线 的渐近线方程为 ,不妨取 ,点 到直线 的距离为 .
因为圆 与双曲线 的渐近线相切,所以 .
5. C 2017年至2022年该省年生产总量逐年增加,A正确.2017年至2022年该省年生产总量的极差为
亿元,B正确.2021年该省年生产总量的增长速度比2020年高,C错误.2017
年至2022年该省年生产总量的增长速度的中位数为7.6%,D项正确.
6. D 结合二次函数的性质可得 ,解得 .
7. A 由平面展开图得到该正方体的直观图如图所示, .
8. B 设 的公差为 .因为 ,
所以 , ,则 , , .
因为 ,所以 ,解得 .
学科网(北京)股份有限公司9. A 函数 在 上单调递减, 在 上单调递减,且 ,
所以 在定义域 上单调递减.因为 ,所以 ,解得 .
10. A 因为 是 的中点,且 , ,
所以 .因为 , , 三点共线,
所以 ,即 ,
所以 ,
当且仅当 时,等号成立.
11. A 能制作的最大零件即为圆锥的内切球,如图,圆锥 内切球的半径等于 内切圆的半径,
设 内切圆的半径为 ,由 ,
得 ,则 ,
所以能制作的最大零件的表面积为 .
12. C ,
学科网(北京)股份有限公司即 ,所以 的图象关于点 对称,①正确.
,
所以 的最小正周期不是 ,②错误.
当 时, , ,所以
.
因为函数 在 上单调递减,函数 在 上单调递增,
所以 在 上单调递减,即 在 上单调递减,③正确.
当 时, .
, , , .
,
所以 ,④正确.
13. 当 时, ,故点在曲线上. , .
故切线方程为 .
14. 2 由题意,作出可行域(图略),数形结合可得当直线过点 时, 取得最大值,最大值为2.
学科网(北京)股份有限公司15. 豆沙馅和莲蓉馅的青团相邻,则芝麻馅的青团不能放在中间,其概率为 .
16. 设 ,则直线 的斜率为 ,直线 的斜率为 ,直线 的方程为 .
令 ,得 ,即 .设 为坐标原点,因为 ,所以
,解得 .
17.解:(1) ,
,
,
.
故所求的线性回归方程为 .
(2)由题可知,到2025年时广告费用为2.2百万元,
故可预测该公司所获得的利润约为3.3 (千万元).
18.解:(1)在 中, ,
所以 .
在 中, , ,
学科网(北京)股份有限公司所以 .故 .
(2)在 中,由余弦定理可得 ,
解得 ,
则 .
故 的面积为 .
19.(1)证明:设 为 的中点,连接 , , .
在 中,因为 , ,
所以 是等边三角形,所以 是正方形.
因为 , ,所以四边形 是正方形.
因为 ,所以 是等腰直角三角形, .
因为 ,所以 平面 .
因为 平面 ,所以 .
在 中, , 为 的中点,所以 .
因为 ,所以 平面 .
(2)解: .
学科网(北京)股份有限公司三棱柱 的体积为 .
20.(1)解: .
当 时, ,当 时, .
所以 在 上单调递增,在 上单调递减.
.
所以 的最大值为0.
(2)证明:令函数 , .
当 时, , 在 上单调递增.
.
所以 , 得证.
21.解:(1)由题意得 的焦点为 ,准线为直线 ,
则 , 到准线 的距离之和等于 .
因为 ,所以 ,且 ,得 .
故 的方程为 .
(2)设 : ( ), ( ), ,
由 得 ,则
所以 .
设 ,由 ,得 ,
学科网(北京)股份有限公司即 ,所以 .
由 ,得 ,代入 ,
得 ,即 .
故 的方程为 .
22.解:(1) ,即 .
,所以 ,
所以 的普通方程为 ( )
,
即 .
因为 ,所以 ,
所以 的普通方程为 ( ).
(2)联立 解得 或 或
与 交点的直角坐标为 , , .
与 交点的极坐标为 , , .
23.证明:(1)
,
当且仅当 ,即 , , 时,等号成立.
学科网(北京)股份有限公司(2)因为 ,由(1)得 ,所以 .
因为 ,所以 ,
所以 .
学科网(北京)股份有限公司