鞍山市普通高中2023-2024学年度高三第二次质量监测数学_2024年4月_01按日期_3号_2024届辽宁省鞍山市高三下学期第二次质量监测

鞍山市普通高中 2023—2024 学年度高三第二次质量监测 数学试题卷 注意事项： 1．答题前，考生先将自己的姓名、准考证号码填写清楚，将条形码准确粘贴在条形码区域内。 2．选择题必须使用 2B 铅笔填涂；非选择题必须使用 0.5 毫米黑色字迹的签字笔书写，字体工 整、笔迹清楚。 3．请按照题号顺序在答题卡各题目的答题区域内作答，超出答题区域书写的答案无效；在草稿 纸、试题卷上答题无效。 4．作图可先使用铅笔画出，确定后必须用黑色字迹的签字笔描黑。 5．保持卡面清洁，不要折叠、不要弄破、弄皱。不准使用涂改液、修正带、刮纸刀。 考试时间：120 分钟 满分：150 分 一、单项选择题：本题共 8 小题，每小题 5 分，共 40 分。在每小题给出的四个选项中，只有 一项是符合题目要求的。 2mi 1．已知复数z 为纯虚数，则实数m的值为（ ） 2i A．1 B．4 C．1 D．4 2．已知直线l: x y2 0，点C在圆 x1 2  y2 2 上运动，那么点C到直线l的距离的最大值为（ ） 3 5 3 2 A． 2 1 B． 2 C． 2 D． 2 2 2 2          3．已知非零向量a，b满足 a 2 b ，向量a在向量b方向上的投影向量是 2b，则a与b夹角的余弦值 为（ ） 2 2 2 2 A． B． C． D． 3 6 2 3 4．设l，m是两条不同的直线，，是两个不同的平面，若l，∥ ，则“ml”是“m”的（ ） A．充分不必要条件 B．必要不充分条件 C．充要条件 D．既不充分也不必要条件 5．在某次美术专业测试中，若甲、乙、丙三人获得优秀等级的概率分别是0.6，0.8和0.5，且三人的测试结 果相互独立，则测试结束后，在甲、乙、丙三人中恰有两人没达优秀等级的前提条件下，乙没有达优秀等级的 概率为（ ） 1 5 5 17 A． B． C． D． 26 13 8 29 n n 1 1  5  1  5  6．数列 a n  的通项公式为a n  5      2       2      ，则a 5 （ ）   3 A． 5 B．27 5 C．5 D．8 5 7．校数学兴趣社团对“学生性别和选学生物学是否有关”作了尝试性调查．其中被调查的男女生人数相同．男 4 3 生选学生物学的人数占男生人数的 ，女生选学生物学的人数占女生人数 ．若有90% 的把握认为选学生物 5 5 学和性别有关，则调查人数中男生不可能有（ ）人． A．20 B．30 C．35 D．40 附表： P K2 k 0.100 0.050 0.010 0.005 0.001   k 2.706 3.841 6.635 7.879 10.828 2 nadbc 其中，K2  ． abcdacbd 8．已知，均为锐角，sin3sincos ，则tan取得最大值时，tan 的值为（ ） A． 2 B． 3 C．1 D．2 二、多项选择题：本题共 3 小题，每小题 6 分，共 18 分。在每小题给出的选项中，有多项符 合题目要求。全部选对的得 6 分，部分选对的得部分分，有选错的得 0 分。  π  9．已知 fx sin x  在 0,π 上是单调函数，则下列结论中正确的有（ ）  6  1 A．当0时，的取值范围是0 3 1 B．当0 时，的取值范围是 0 3 2 C．当0时，的取值范围是0 3 2 D．当0 时，的取值范围是 0 3 10．如图，正方体 ABCDABCD 的棱长为2，E，F ，G ，H 分别是棱 AA ，AD ，BC ，CC 的 1 1 1 1 1 1 1 1 1 1  中点，点M 满足HM HG，其中 0,1 ，则下列结论正确的是（ ） A．过M ，E，F 三点的平面截正方体所得截面图形有可能为正六边形 B．三棱锥 A MEF 的体积为定值 1 1 C．当 时， AC∥ 平面MEF 2 D．当1 时，三棱锥 A MEF 外接球的表面积为6π 1 11．在平面直角坐标系中，定义dA,B  x x  y  y 为点 Ax, y 到点Bx , y  的“折线距离”．点 1 2 1 2 1 1 2 2 O是坐标原点，点Q在直线2x y2 5 0上，点P在圆x2  y2 1 上，点R在抛物线 y2 4x上．下 列结论中正确的结论为（ ） A．dO,Q 的最小值为2 B．dO,P 的最大值为 2 5 1 C．dP,Q 的最小值为 D．dR,Q 的最小值为 5  2 4 三、填空题：本题共 3 小题，每小题 5 分，共 15 分。 12．已知圆锥的底面半径为2，母线与底面所成的角为60，则该圆锥的表面积为______． 13． fx  x2ex的极大值为______． x2 y2 14．已知双曲线C:  1a0,b0 的右焦点为F ，左、右顶点分别为 A，A ，PF  x轴于点F ， a2 b2 1 2   且PF 2QF ．当AQA 最大时，点P恰好在双曲线C上，则双曲线C的离心率为______． 1 2 四、解答题：本题共 5 小题，共 77 分。解答应写出文字说明、证明过程或演算步骤。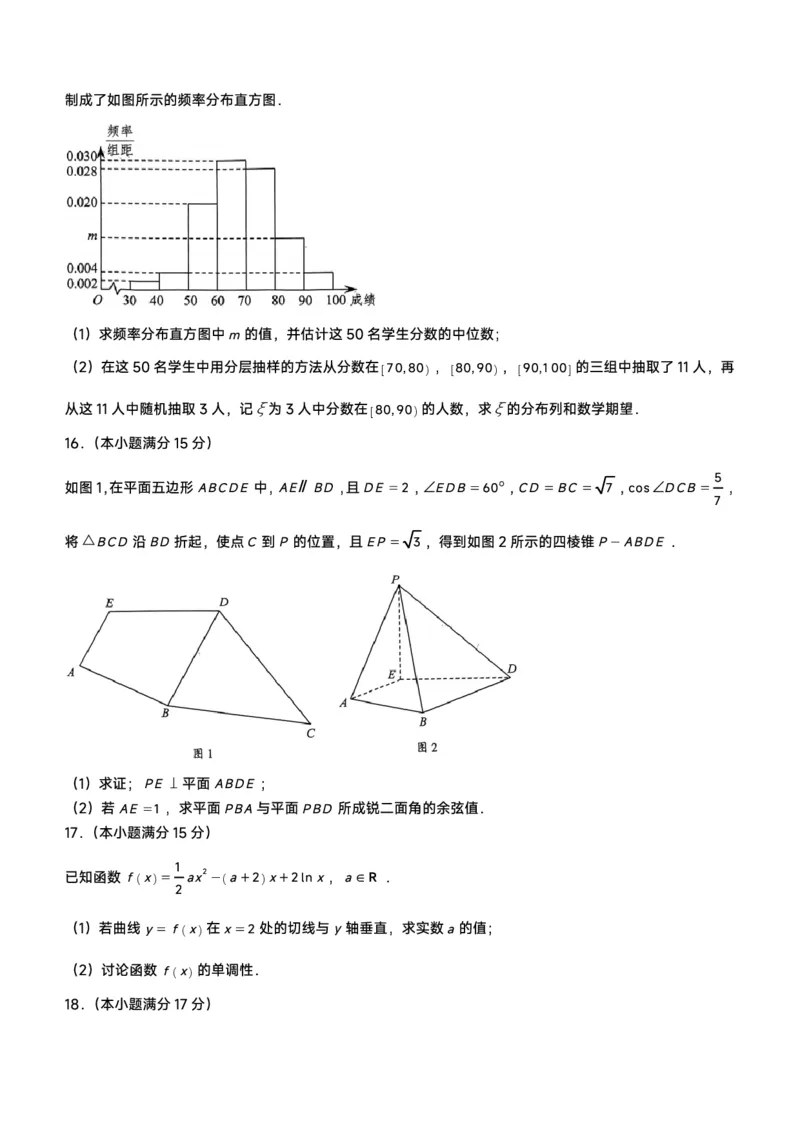 15．（本小题满分12分） 鞍山市普通高中某次高三质量监测考试后，将化学成绩按赋分规则转换为等级分数（赋分后学生的分数全部介 于30至100之间）．某校为做好本次考试的评价工作，从本校学生中随机抽取了50名学生的化学等级分数， 经统计，将分数按照 30,40 ， 40,50 ， 50,60 ， 60,70 ， 70,80 ， 80,90 ， 90,100 分成7组，制成了如图所示的频率分布直方图． （1）求频率分布直方图中m的值，并估计这50名学生分数的中位数； （2）在这50名学生中用分层抽样的方法从分数在 70,80 ， 80,90 ， 90,100 的三组中抽取了11人，再 从这11人中随机抽取3人，记为3人中分数在 80,90 的人数，求的分布列和数学期望． 16．（本小题满分15分） 5 如图1，在平面五边形 ABCDE中，AE ∥ BD，且DE 2 ，EDB60，CD BC 7 ，cosDCB ， 7 将△BCD沿BD折起，使点C到P的位置，且EP 3 ，得到如图2所示的四棱锥PABDE ． （1）求证；PE 平面 ABDE； （2）若 AE 1 ，求平面PBA与平面PBD所成锐二面角的余弦值． 17．（本小题满分15分） 1 已知函数 fx  ax2 a2x2ln x，aR ． 2 （1）若曲线 y fx 在x2 处的切线与 y轴垂直，求实数a的值； （2）讨论函数 fx 的单调性． 18．（本小题满分17分）x2 y2 焦点在x轴上的椭圆  1 的左顶点为M ， Ax, y ，Bx , y  ，Cx, y  为椭圆上不同三点， 4 b2 1 1 2 2 3 3   1 且当OBOC时，直线MB和直线MC的斜率之积为 ． 4 （1）求b的值； （2）若△OAB的面积为1，求x2 x2 和 y2  y2的值； 1 2 1 2 （3）在（2）的条件下，设 AB的中点为D，求 OD  AB 的最大值． 19．（本小题满分17分） 设数列 a  的前n项和为S ，已知2S a 2n1 1  nN*  ，且a 5． n n n n1 2 a  （1）证明： n 1为等比数列，并求数列 a  的通项公式； 2n  n （2）设b log  a 2n  ，若对于任意的nN* ，不等式b 1 n  a 2n  60恒成立，求实数 n 3 n n n 的取值范围； （3）高斯是德国著名数学家，近代数学的奠基者之一，享有“数学王子”的称号，用他名字定义的函数称为高 a 2n 斯函数 fx  x ，其中 x 表示不超过x的最大整数，如 2.3 2 ，  1.9 2，设c   n  ，数 n  4  列 c 的前n项和为T ，求T 除以16的余数． n n 2024