文档内容
更多全科试卷,请关注公众号:高中试卷君
2024 届高三二轮复习“8+3+3”小题强化训练(11)
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有
一项是符合题目要求的.
1.用分层抽样的方法从某社区的500名男居民和700名女居民中选取12人参与社区服务满意度调
研,则女居民比男居民多选取( )
A. 8人 B. 6人 C. 4人 D. 2人
【答案】D
【解析】由题可知,男居民选取 人,女居民选取 人,
则女居民比男居民多选取2人.
故选:D.
2.若复数 满足 ,则在复平面内 对应的点位于( )
A. 第一象限 B. 第二象限
C. 第三象限 D. 第四象限
【答案】A
【解析】由 ,对应点为 在第一象限.
故选:A
3.从6名女生3名男生中选出2名女生1名男生,则不同的选取方法种数为( )
A. 33 B. 45 C. 84 D. 90
【答案】B
【解析】 .
故选:B
4.已知向量 与 是非零向量,且满足 在 上的投影向量为 , ,则 与 的夹
角为( )
A. B. C. D.
【答案】A
【解析】设 与 的夹角为 ,
在 上的投影向量为
所以 ,
所以 ,
所以 为钝角,且 .
故选:A
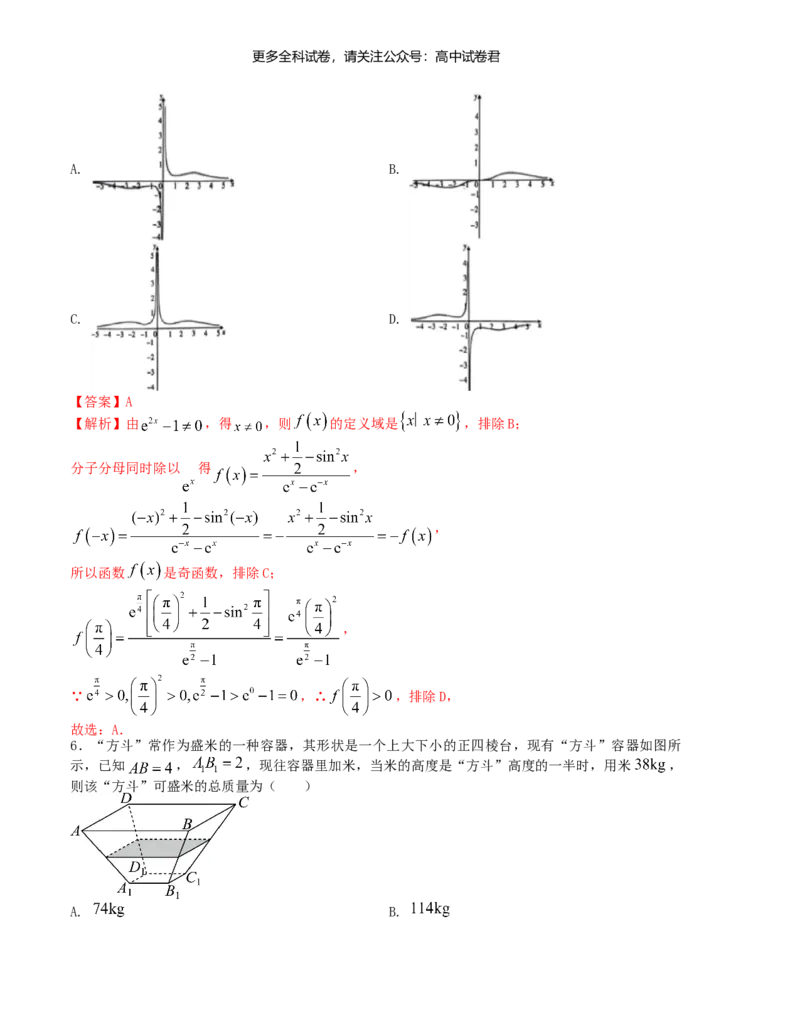
5.函数 的部分图像大致为( )更多全科试卷,请关注公众号:高中试卷君
A. B.
C. D.
【答案】A
【解析】由 ,得 ,则 的定义域是 ,排除B;
分子分母同时除以 得 ,
,
所以函数 是奇函数,排除C;
,
∵ ,∴ ,排除D,
故选:A.
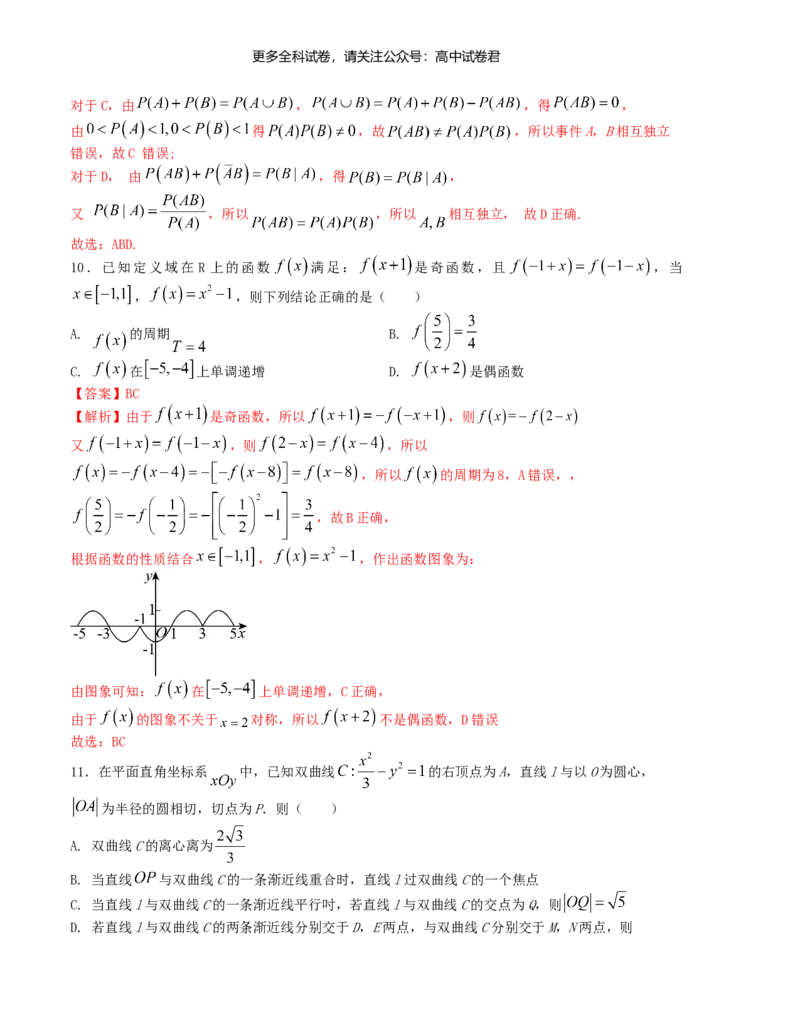
6.“方斗”常作为盛米的一种容器,其形状是一个上大下小的正四棱台,现有“方斗”容器如图所
示,已知 , ,现往容器里加米,当米的高度是“方斗”高度的一半时,用米 ,
则该“方斗”可盛米的总质量为( )
A. B.更多全科试卷,请关注公众号:高中试卷君
C. D.
【答案】D
【解析】设线段 、 、 、 的中点分别为 、 、 、 ,如下图所示:
易知四边形 为等腰梯形,因为线段 、 的中点分别为 、 ,
则 ,
设棱台 的高为 ,体积为 ,
则棱台 的高为 ,设其体积为 ,
则 ,则 ,
所以, ,所以,该“方斗”可盛米的总质量为 .
故选:D.
7.定义:满足 为常数, )的数列 称为二阶等比数列, 为二阶公
比.已知二阶等比数列 的二阶公比为 ,则使得 成立的最小正整数
为( )
A. 7 B. 8 C. 9 D. 10
【答案】B
【解析】由题意知二阶等比数列 二阶公比为 ,则 ,
的
故 ,
将以上各式累乘得: ,
故 ,令 ,由于 ,
故 ,即 ,
又 的值随n的增大而增大,且 ,
当 时, ,更多全科试卷,请关注公众号:高中试卷君
当 时, ,
故n的最小值为8,
故选:B
8.已知函数 在区间 上 最小值恰为 ,则所有满足条
的
件的 的积属于区间( )
A. B. C. D.
【答案】C
【解析】当 时 ,因为此时 的最小值为 ,
.
所以 ,即
若 ,此时 能取到最小值 ,即 ,
代入可得 ,满足要求;
若 取不到最小值 ,则需满足 ,即 ,
在 上单调递减,所以存在唯一 符合题意;
所以 或者 ,所以所有满足条件的 的积属于区间 ,
故选:C
二、选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合
题目要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.
9.已知 分别为随机事件 的对立事件,满足 ,则下列叙述可以说
明事件A,B为相互独立事件的是( )
A. B.
C. D.
【答案】ABD
【解析】对于A,由 , 得 即 ,所以 相互独
立, 故A正确;
对于B,由 , 得 ,
又 ,所以 ,
得 即 ,所以 相互独立,
所以 相互独立,故B正确;更多全科试卷,请关注公众号:高中试卷君
对于C,由 , ,得 ,
由 得 ,故 ,所以事件A,B相互独立
错误,故C 错误;
对于D, 由 ,得 ,
又 ,所以 ,所以 相互独立, 故D正确.
故选:ABD.
10.已知定义域在 R 上的函数 满足: 是奇函数,且 ,当
, ,则下列结论正确的是( )
A. 的周期 B.
C. 在 上单调递增 D. 是偶函数
【答案】BC
【解析】由于 是奇函数,所以 ,则
又 ,则 ,所以
,所以 的周期为8,A错误,,
,故B正确,
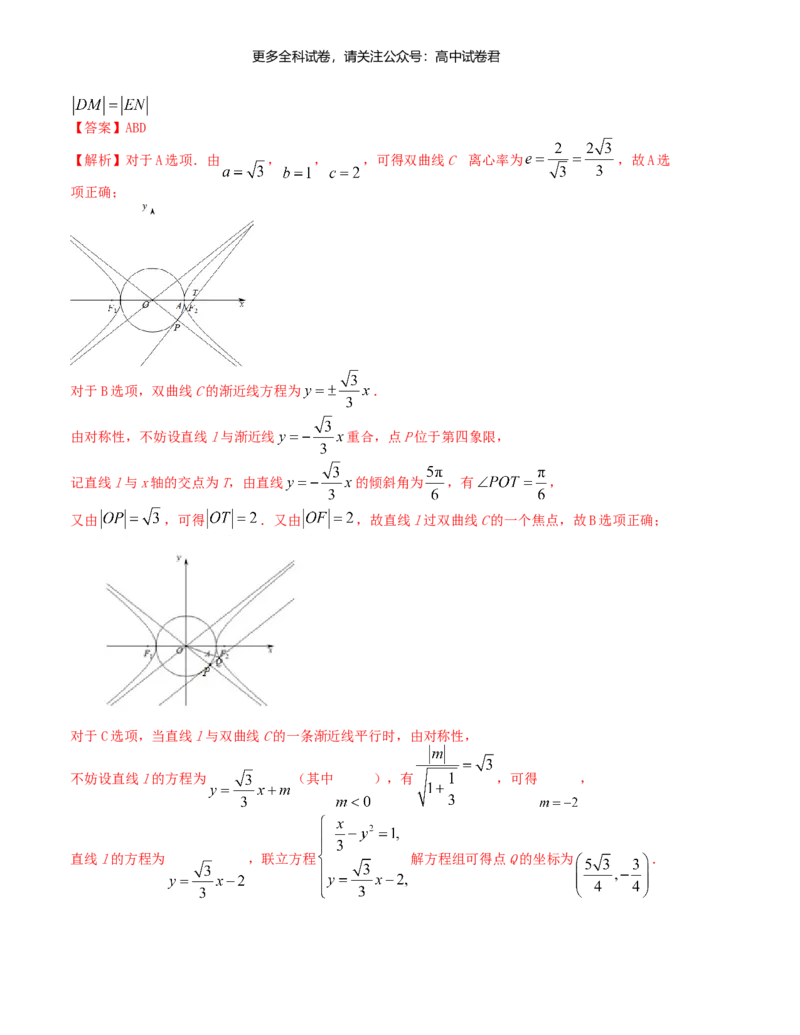
根据函数的性质结合 , ,作出函数图象为:
由图象可知: 在 上单调递增,C正确,
由于 的图象不关于 对称,所以 不是偶函数,D错误
故选:BC
11.在平面直角坐标系 中,已知双曲线 的右顶点为A,直线l与以O为圆心,
为半径的圆相切,切点为P.则( )
A. 双曲线C的离心离为
B. 当直线 与双曲线C的一条渐近线重合时,直线l过双曲线C的一个焦点
C. 当直线l与双曲线C的一条渐近线平行吋,若直线l与双曲线C的交点为Q,则
D. 若直线l与双曲线C的两条渐近线分别交于D,E两点,与双曲线C分别交于M,N两点,则更多全科试卷,请关注公众号:高中试卷君
【答案】ABD
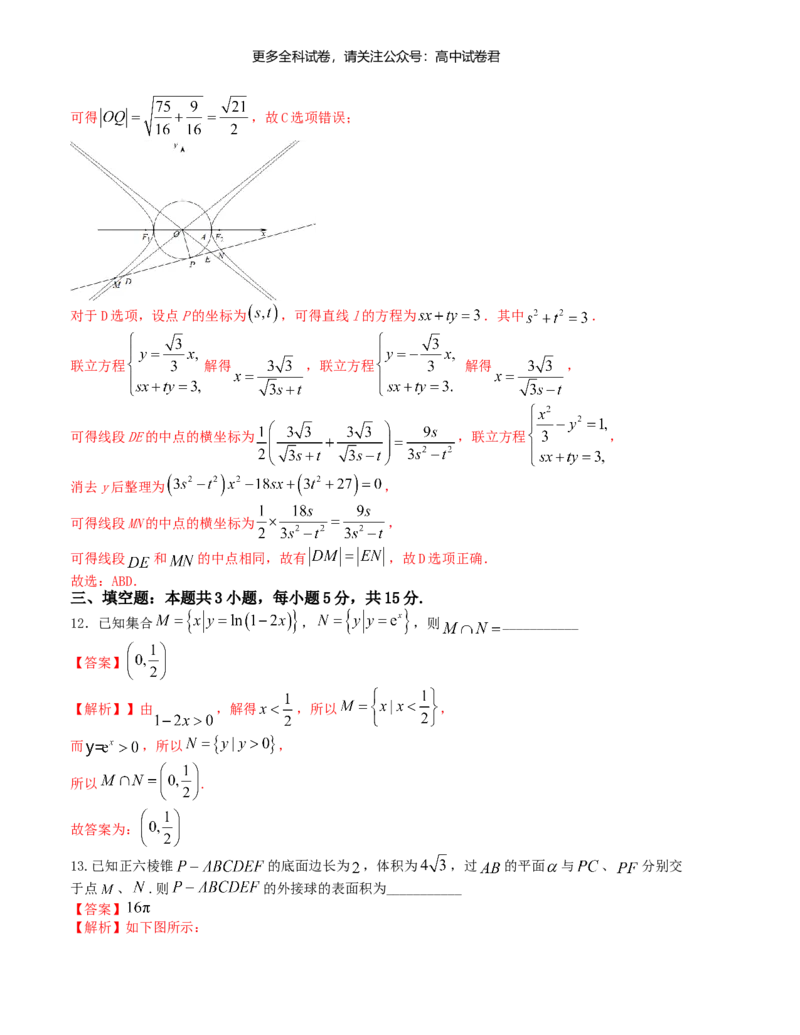
【解析】对于A选项.由 , , ,可得双曲线C 离心率为 ,故A选
的
项正确;
对于B选项,双曲线C的渐近线方程为 .
由对称性,不妨设直线l与渐近线 重合,点P位于第四象限,
记直线l与x轴的交点为T,由直线 的倾斜角为 ,有 ,
又由 ,可得 .又由 ,故直线l过双曲线C的一个焦点,故B选项正确;
对于C选项,当直线l与双曲线C的一条渐近线平行时,由对称性,
不妨设直线l的方程为 (其中 ),有 ,可得 ,
直线l的方程为 ,联立方程 解方程组可得点Q的坐标为 .更多全科试卷,请关注公众号:高中试卷君
可得 ,故C选项错误;
对于D选项,设点P的坐标为 ,可得直线l的方程为 .其中 .
联立方程 解得 ,联立方程 解得 ,
可得线段DE的中点的横坐标为 ,联立方程 ,
消去y后整理为 ,
可得线段MN的中点的横坐标为 ,
可得线段 和 的中点相同,故有 ,故D选项正确.
故选:ABD.
三、填空题:本题共3小题,每小题5分,共15分.
12.已知集合 , ,则 ___________
【答案】
【解析】】由 ,解得 ,所以 ,
而 ,所以 ,
所以 .
故答案为:
13.已知正六棱锥 的底面边长为 ,体积为 ,过 的平面 与 、 分别交
于点 、 .则 的外接球的表面积为___________
【答案】
【解析】如下图所示:更多全科试卷,请关注公众号:高中试卷君
记正六边形 的中心为点 ,由正棱锥的几何性质可得 底面 ,
易知 是边长为 的等边三角形,
则 ,
,
所以, ,故 ,
故 为正六棱锥 外接球球心,且该球的半径为 ,
因此, 的外接球的表面积为 .
故答案为:
14.已知椭圆 的右焦点为 ,过点 的直线与圆 相切于点 且与
椭圆相交于 、 两点,若 、 恰为线段 的三等分点,则椭圆的离心率为___________
【答案】
【解析】不妨设切点 在第一象限,点 在第一象限,记椭圆的左焦点为 ,连接 、 ,
由圆的几何性质可知 ,
易知 、 分别为 、 的中点,则 ,且 ,
所以, ,由椭圆的定义可得 ,
由勾股定理可得 ,即 ,更多全科试卷,请关注公众号:高中试卷君
整理可得 ,可得 ,
因此,该椭圆的离心率为 ,
故答案为: