文档内容
内蒙古包头市2018年中考数学真题试题
一、选择题:本大题共有12小题,每小题3分,共36分.每小题只有一个正确选项
1.(3.00分)计算﹣ ﹣|﹣3|的结果是( )
A.﹣1 B.﹣5 C.1 D.5
2.(3.00分)如图,是由几个大小相同的小立方块所搭几何体的俯视图,其中小正方形中的
数字表示在该位置的小立方块的个数,则这个几何体的主视图是( )
A. B. C. D.
3.(3.00分)函数y= 中,自变量x的取值范围是( )
A.x≠1 B.x>0 C.x≥1 D.x>1
4.(3.00分)下列事件中,属于不可能事件的是( )
A.某个数的绝对值大于0
B.某个数的相反数等于它本身
C.任意一个五边形的外角和等于540°
D.长分别为3,4,6的三条线段能围成一个三角形
5.(3.00分)如果2xa+1y与x2yb﹣1是同类项,那么 的值是( )
A. B. C.1 D.3
6.(3.00分)一组数据1,3,4,4,4,5,5,6的众数和方差分别是( )
A.4,1 B.4,2 C.5,1 D.5,2
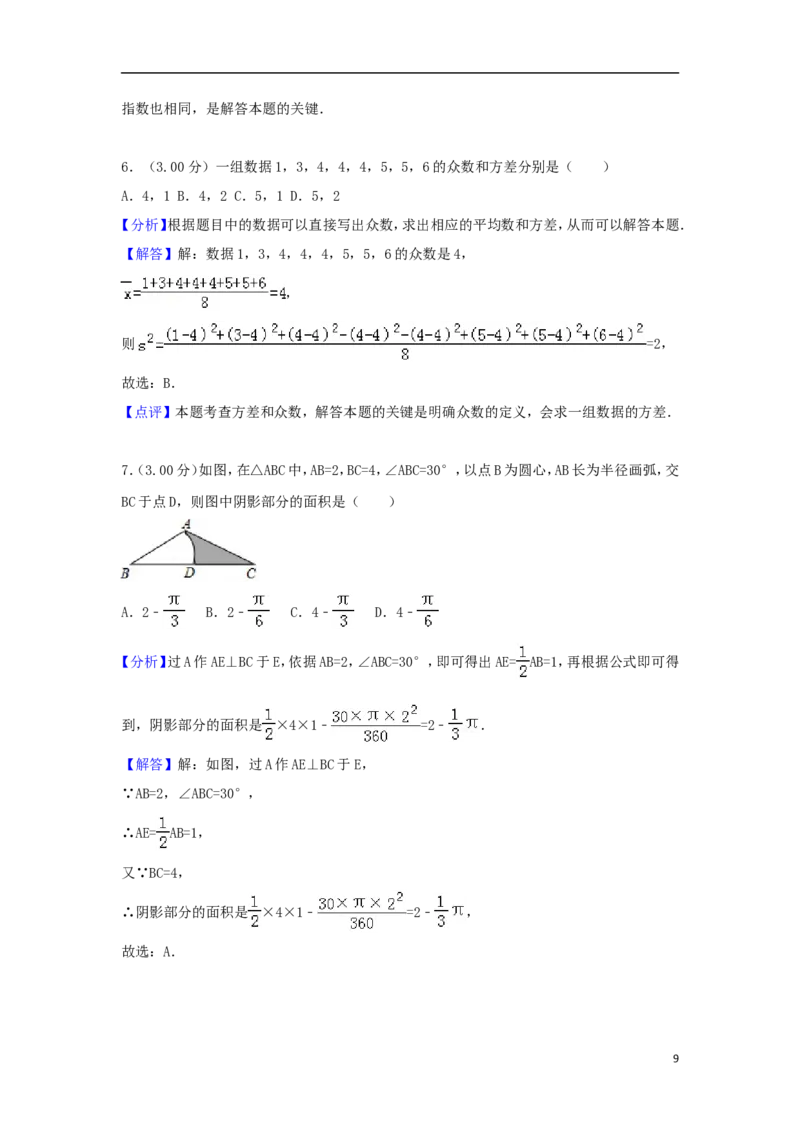
7.(3.00分)如图,在△ABC中,AB=2,BC=4,∠ABC=30°,以点B为圆心,AB长为半径画弧,交
BC于点D,则图中阴影部分的面积是( )
A.2﹣ B.2﹣ C.4﹣ D.4﹣
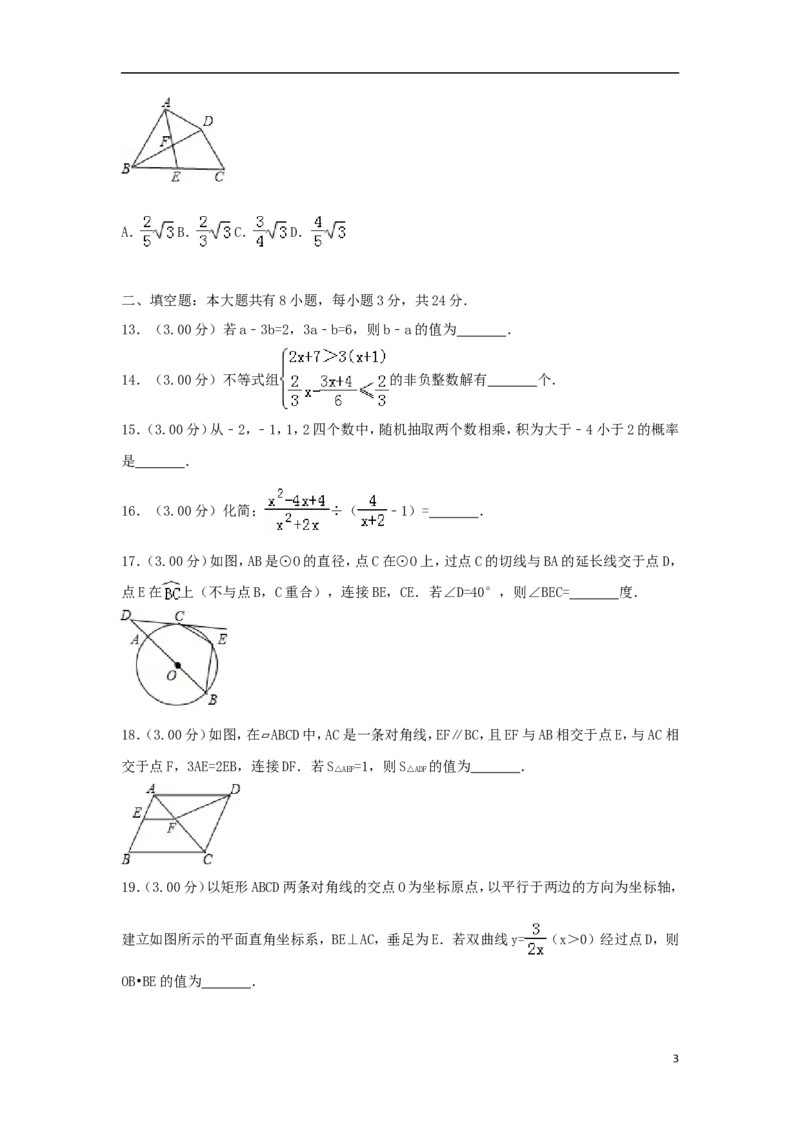
18.(3.00分)如图,在△ABC中,AB=AC,△ADE的顶点D,E分别在BC,AC上,且∠DAE=90°,
AD=AE.若∠C+∠BAC=145°,则∠EDC的度数为( )
A.17.5° B.12.5° C.12° D.10°
9.(3.00分)已知关于x的一元二次方程x2+2x+m﹣2=0有两个实数根,m为正整数,且该方程
的根都是整数,则符合条件的所有正整数m的和为( )
A.6 B.5 C.4 D.3
10.(3.00分)已知下列命题:
①若a3>b3,则a2>b2;
②若点A(x,y)和点B(x,y)在二次函数y=x2﹣2x﹣1的图象上,且满足x<x<1,则y>
1 1 2 2 1 2 1
y>﹣2;
2
③在同一平面内,a,b,c是直线,且a∥b,b⊥c,则a∥c;
④周长相等的所有等腰直角三角形全等.
其中真命题的个数是( )
A.4个 B.3个 C.2个 D.1个
11.(3.00分)如图,在平面直角坐标系中,直线l:y=﹣ x+1与x轴,y轴分别交于点A和
1
点B,直线l:y=kx(k≠0)与直线l 在第一象限交于点C.若∠BOC=∠BCO,则k的值为( )
2 1
A. B. C. D.2
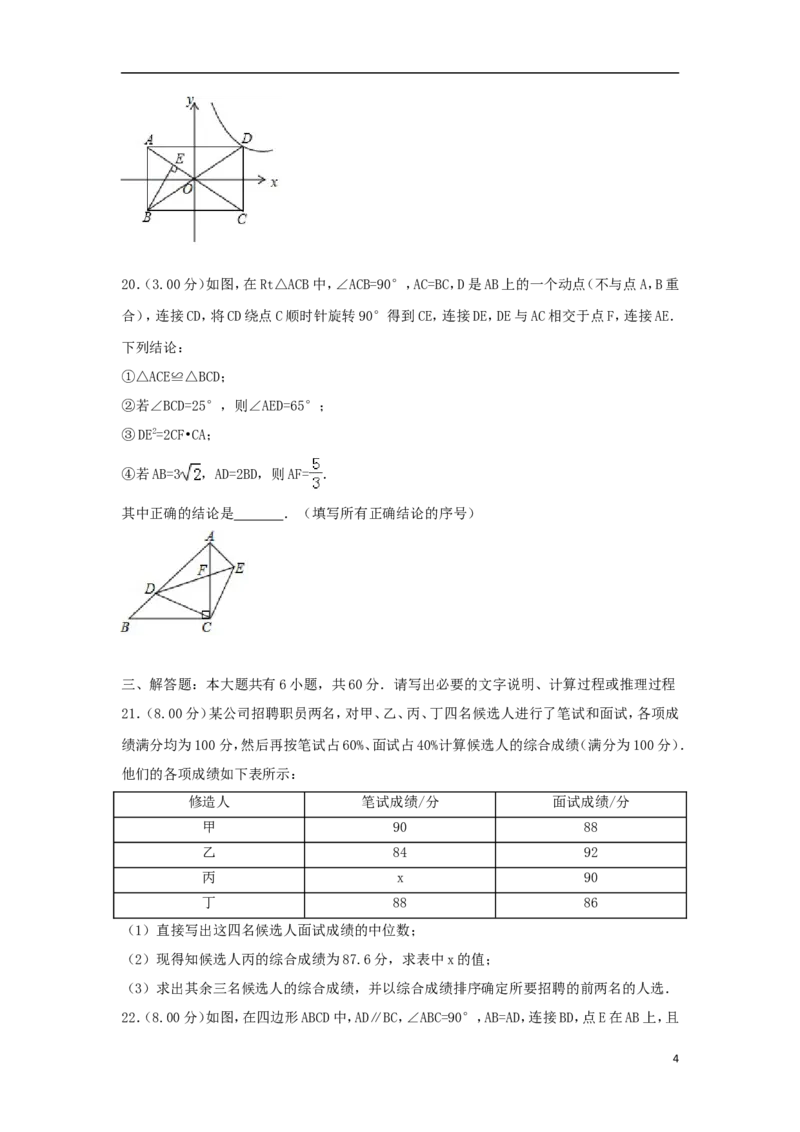
12.(3.00分)如图,在四边形ABCD中,BD平分∠ABC,∠BAD=∠BDC=90°,E为BC的中点,AE
与BD相交于点F.若BC=4,∠CBD=30°,则DF的长为( )
2A. B. C. D.
二、填空题:本大题共有8小题,每小题3分,共24分.
13.(3.00分)若a﹣3b=2,3a﹣b=6,则b﹣a的值为 .
14.(3.00分)不等式组 的非负整数解有 个.
15.(3.00分)从﹣2,﹣1,1,2四个数中,随机抽取两个数相乘,积为大于﹣4小于2的概率
是 .
16.(3.00分)化简; ÷( ﹣1)= .
17.(3.00分)如图,AB是⊙O的直径,点C在⊙O上,过点C的切线与BA的延长线交于点D,
点E在 上(不与点B,C重合),连接BE,CE.若∠D=40°,则∠BEC= 度.
18.(3.00分)如图,在 ABCD中,AC是一条对角线,EF∥BC,且EF与AB相交于点E,与AC相
▱
交于点F,3AE=2EB,连接DF.若S =1,则S 的值为 .
△AEF △ADF
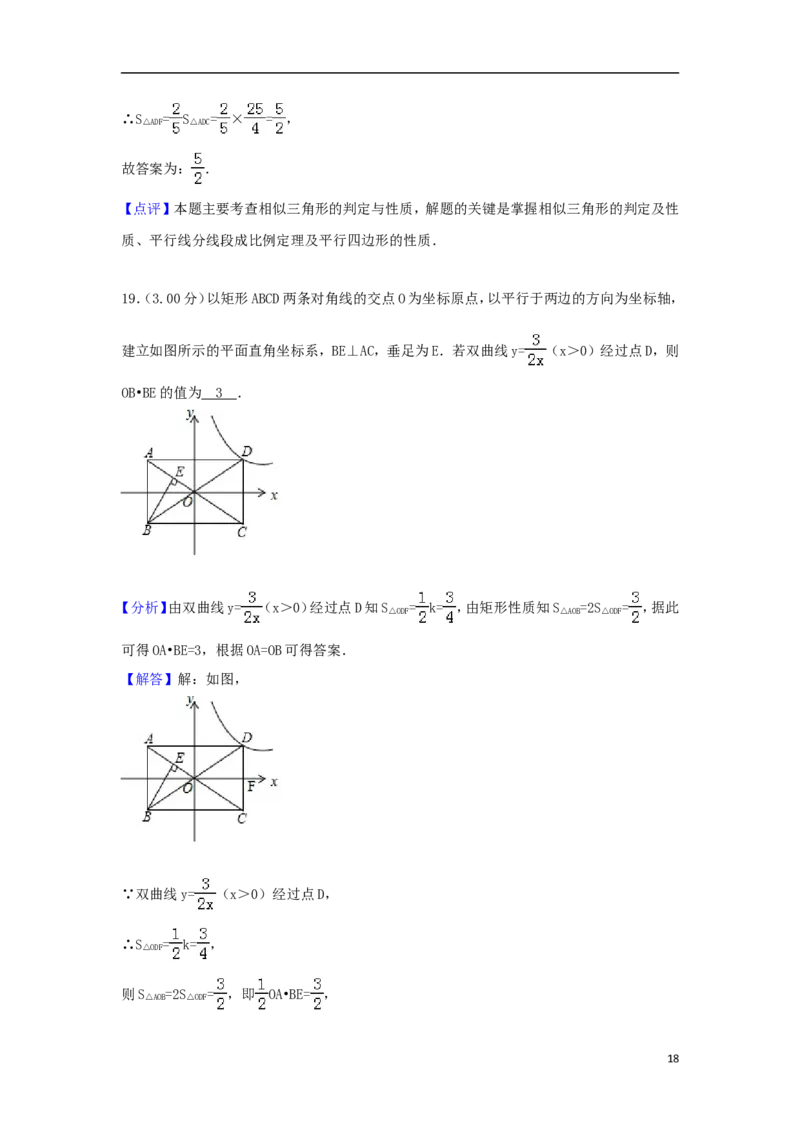
19.(3.00分)以矩形ABCD两条对角线的交点O为坐标原点,以平行于两边的方向为坐标轴,
建立如图所示的平面直角坐标系,BE⊥AC,垂足为E.若双曲线y= (x>0)经过点D,则
OB•BE的值为 .
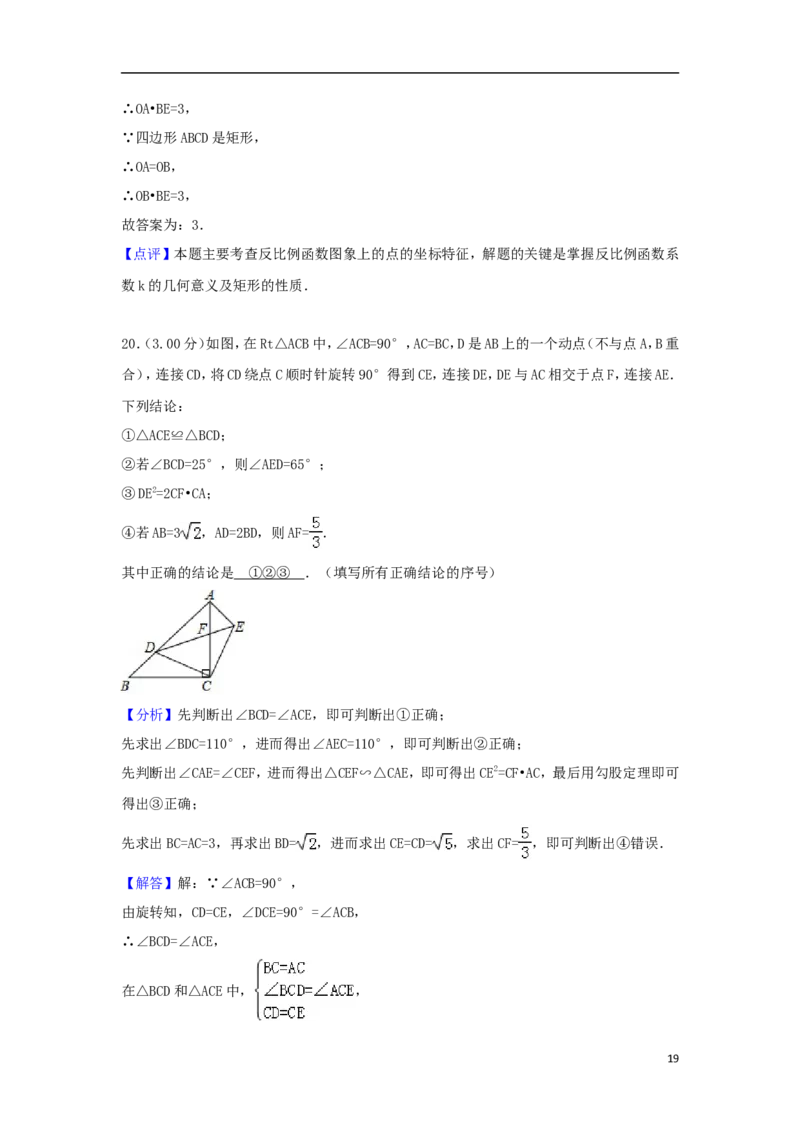
320.(3.00分)如图,在Rt△ACB中,∠ACB=90°,AC=BC,D是AB上的一个动点(不与点A,B重
合),连接CD,将CD绕点C顺时针旋转90°得到CE,连接DE,DE与AC相交于点F,连接AE.
下列结论:
①△ACE≌△BCD;
②若∠BCD=25°,则∠AED=65°;
③DE2=2CF•CA;
④若AB=3 ,AD=2BD,则AF= .
其中正确的结论是 .(填写所有正确结论的序号)
三、解答题:本大题共有6小题,共60分.请写出必要的文字说明、计算过程或推理过程
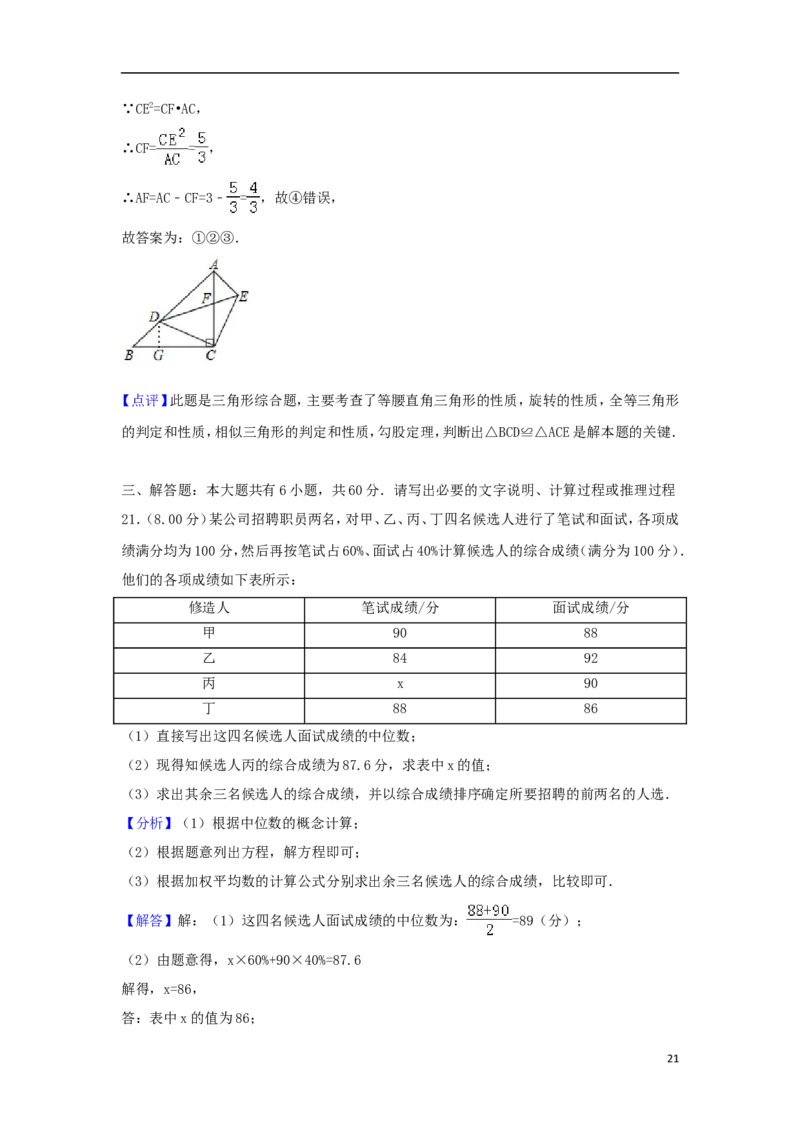
21.(8.00分)某公司招聘职员两名,对甲、乙、丙、丁四名候选人进行了笔试和面试,各项成
绩满分均为100分,然后再按笔试占60%、面试占40%计算候选人的综合成绩(满分为100分).
他们的各项成绩如下表所示:
修造人 笔试成绩/分 面试成绩/分
甲 90 88
乙 84 92
丙 x 90
丁 88 86
(1)直接写出这四名候选人面试成绩的中位数;
(2)现得知候选人丙的综合成绩为87.6分,求表中x的值;
(3)求出其余三名候选人的综合成绩,并以综合成绩排序确定所要招聘的前两名的人选.
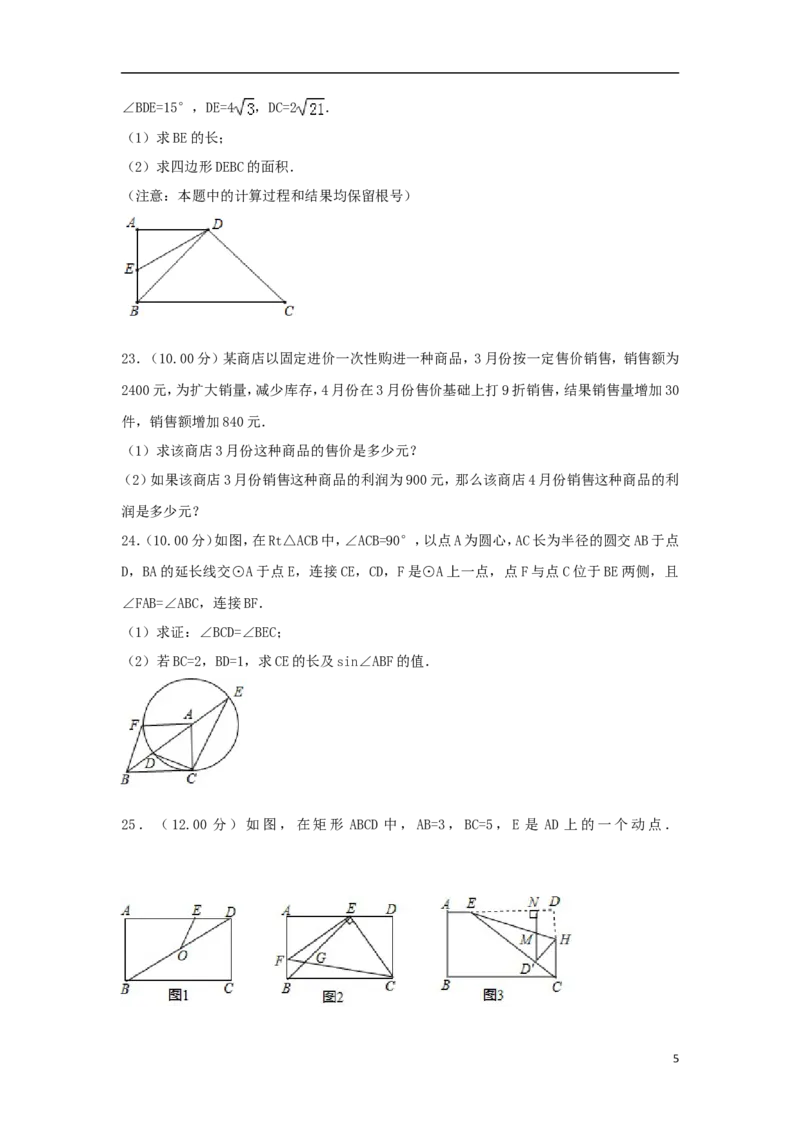
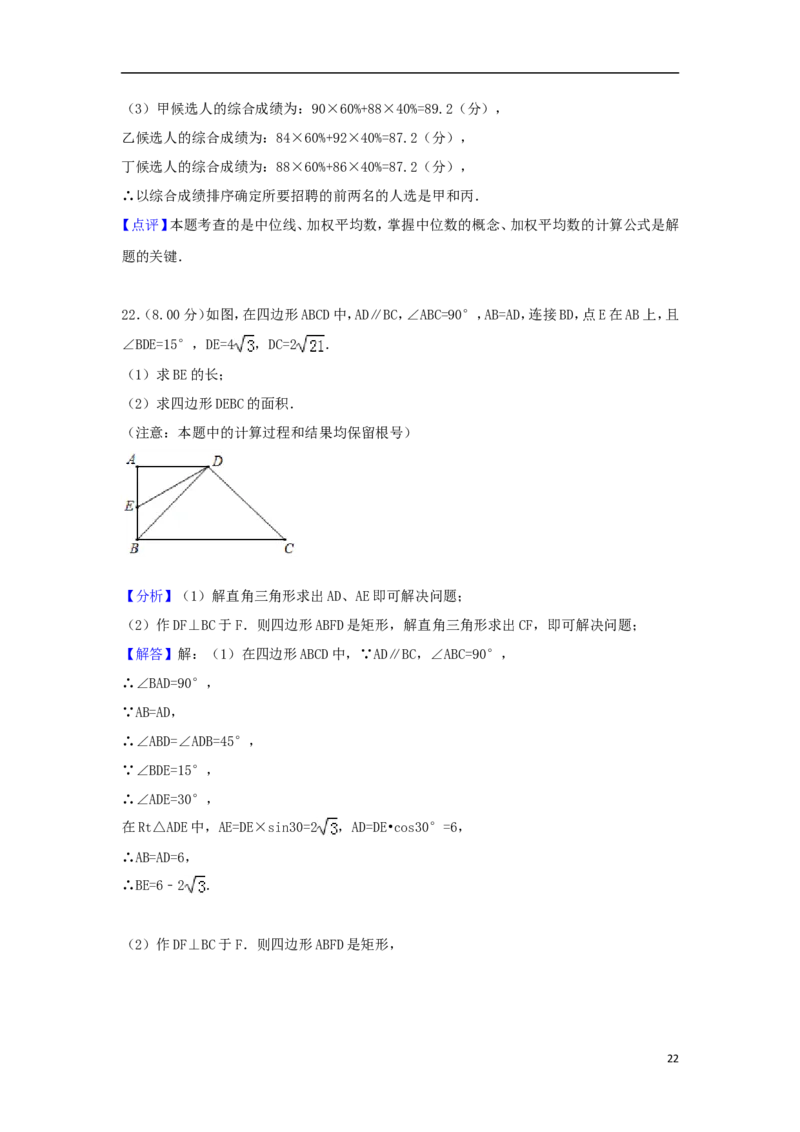
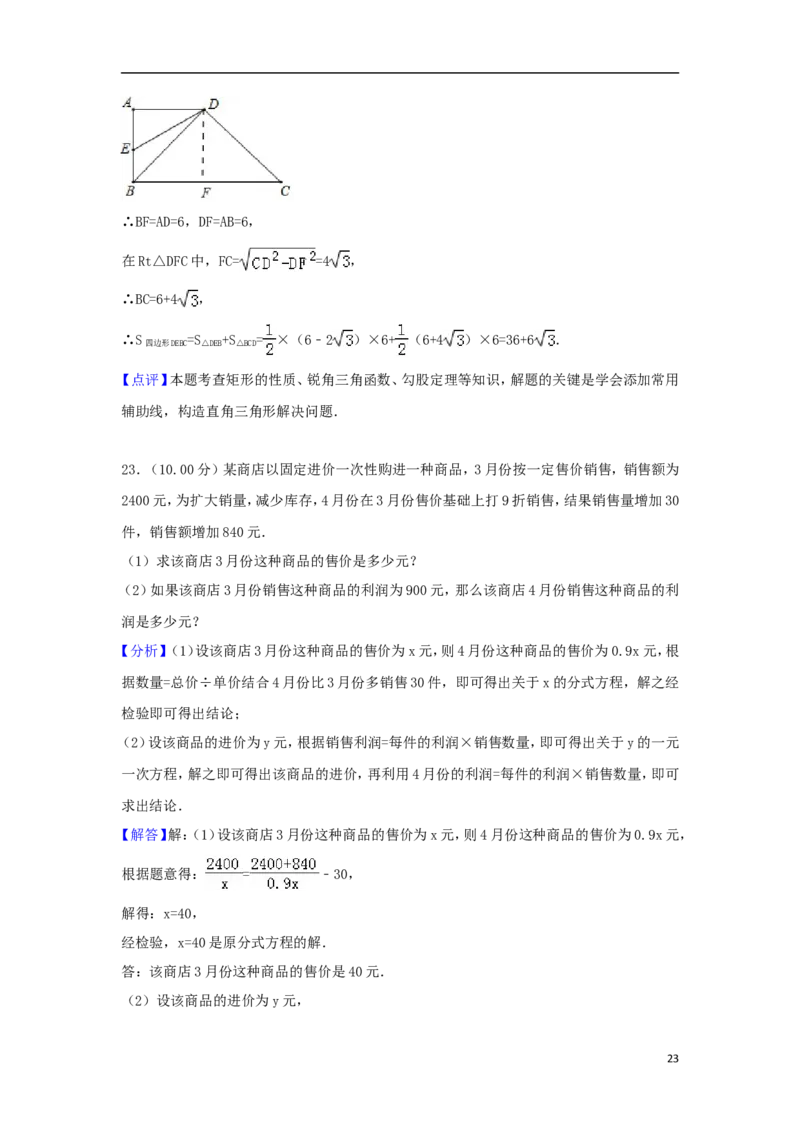
22.(8.00分)如图,在四边形ABCD中,AD∥BC,∠ABC=90°,AB=AD,连接BD,点E在AB上,且
4∠BDE=15°,DE=4 ,DC=2 .
(1)求BE的长;
(2)求四边形DEBC的面积.
(注意:本题中的计算过程和结果均保留根号)
23.(10.00分)某商店以固定进价一次性购进一种商品,3月份按一定售价销售,销售额为
2400元,为扩大销量,减少库存,4月份在3月份售价基础上打9折销售,结果销售量增加30
件,销售额增加840元.
(1)求该商店3月份这种商品的售价是多少元?
(2)如果该商店3月份销售这种商品的利润为900元,那么该商店4月份销售这种商品的利
润是多少元?
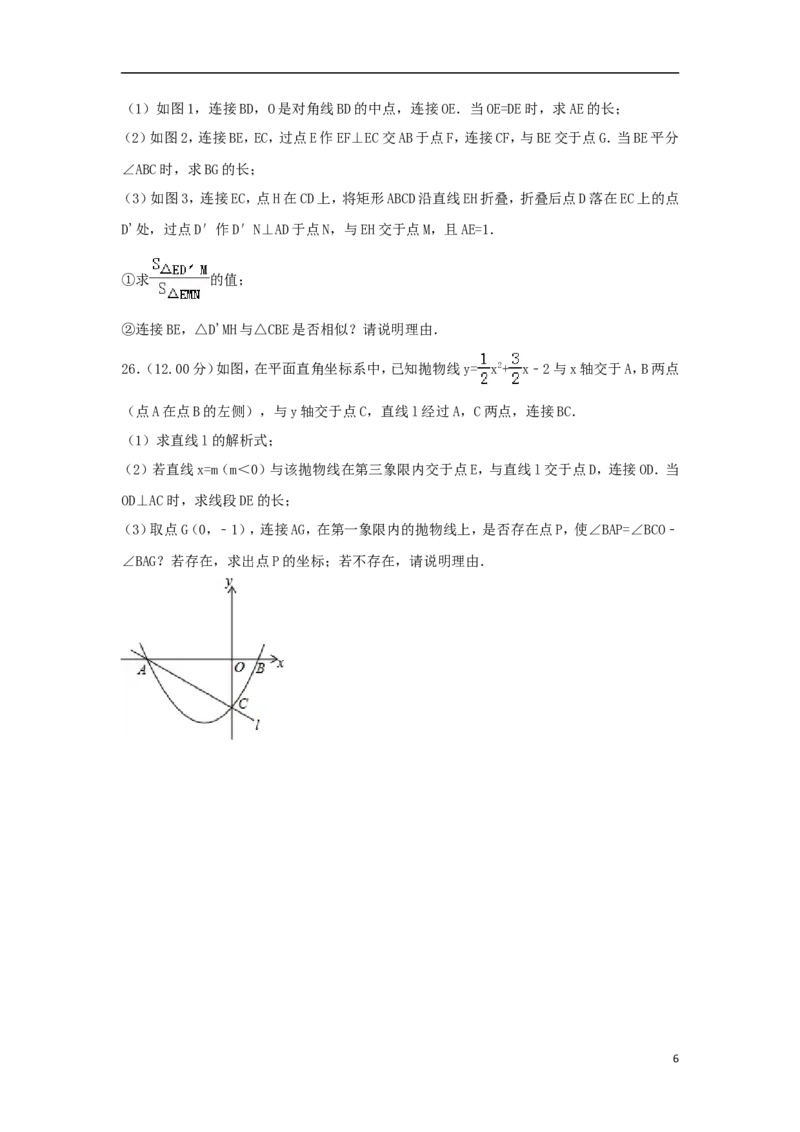
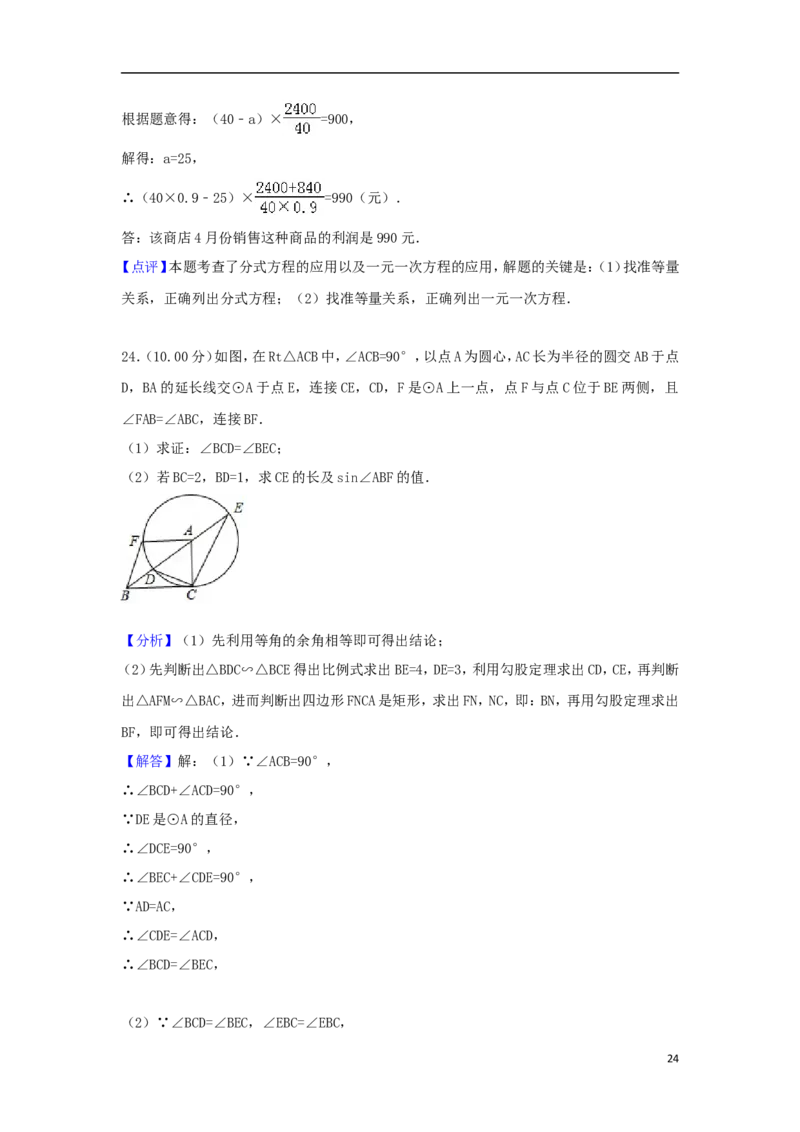
24.(10.00分)如图,在Rt△ACB中,∠ACB=90°,以点A为圆心,AC长为半径的圆交AB于点
D,BA的延长线交⊙A于点E,连接CE,CD,F是⊙A上一点,点F与点C位于BE两侧,且
∠FAB=∠ABC,连接BF.
(1)求证:∠BCD=∠BEC;
(2)若BC=2,BD=1,求CE的长及sin∠ABF的值.
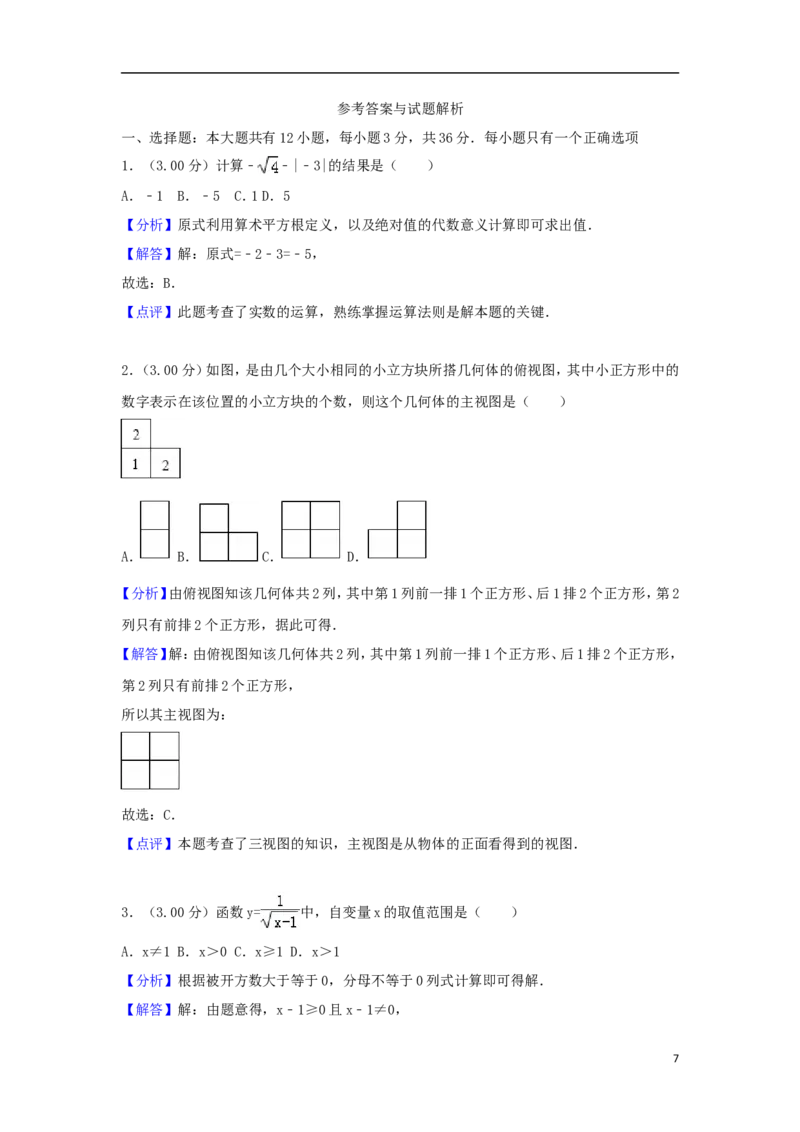
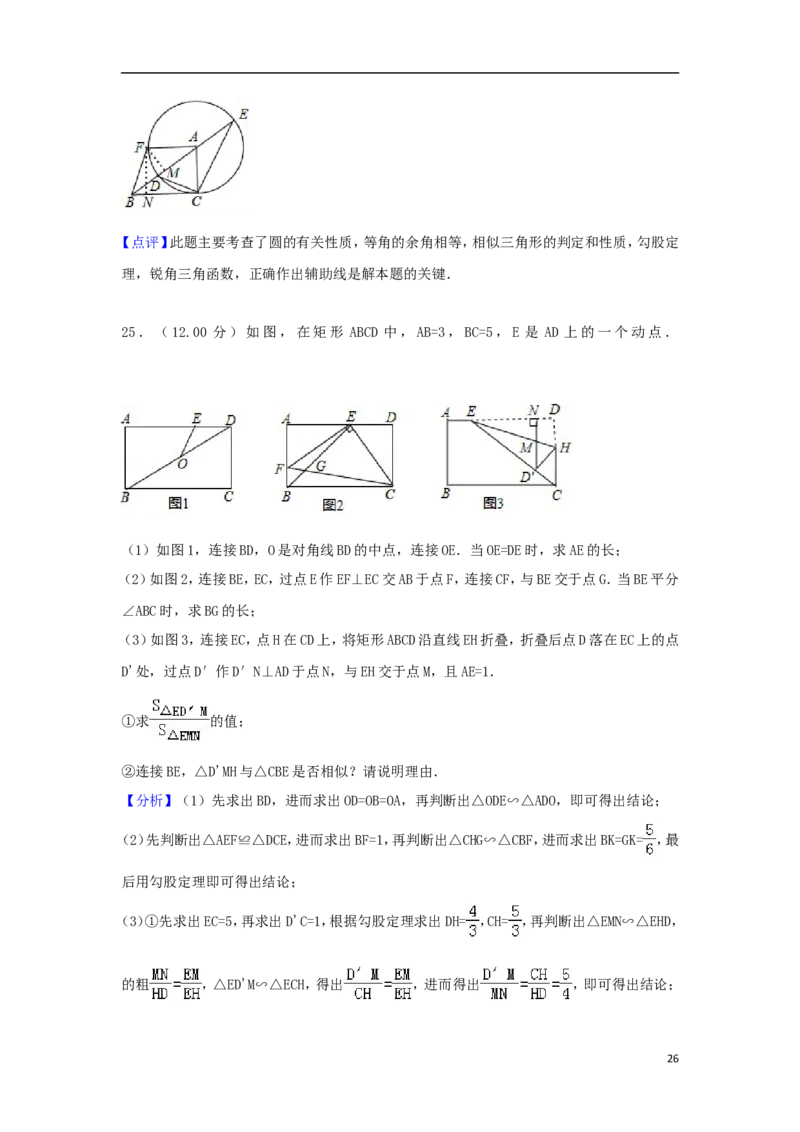
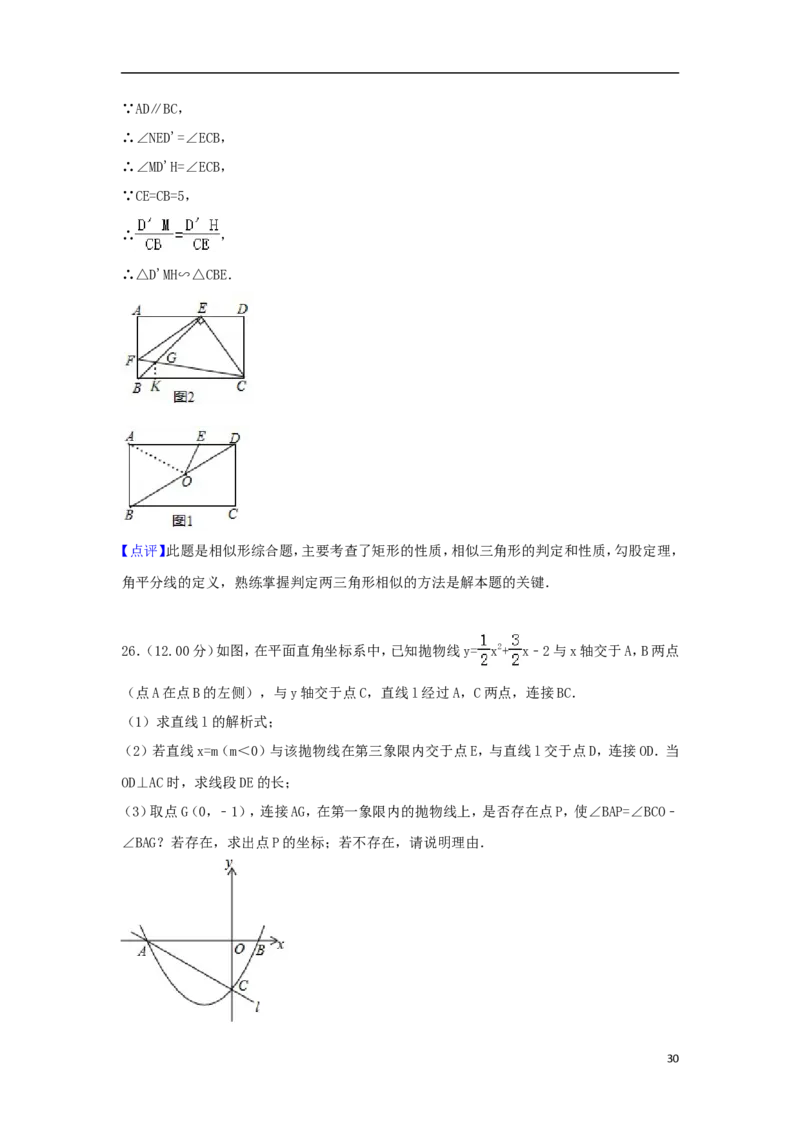
25.(12.00 分)如图,在矩形 ABCD 中,AB=3,BC=5,E 是 AD 上的一个动点.
5(1)如图1,连接BD,O是对角线BD的中点,连接OE.当OE=DE时,求AE的长;
(2)如图2,连接BE,EC,过点E作EF⊥EC交AB于点F,连接CF,与BE交于点G.当BE平分
∠ABC时,求BG的长;
(3)如图3,连接EC,点H在CD上,将矩形ABCD沿直线EH折叠,折叠后点D落在EC上的点
D'处,过点D′作D′N⊥AD于点N,与EH交于点M,且AE=1.
①求 的值;
②连接BE,△D'MH与△CBE是否相似?请说明理由.
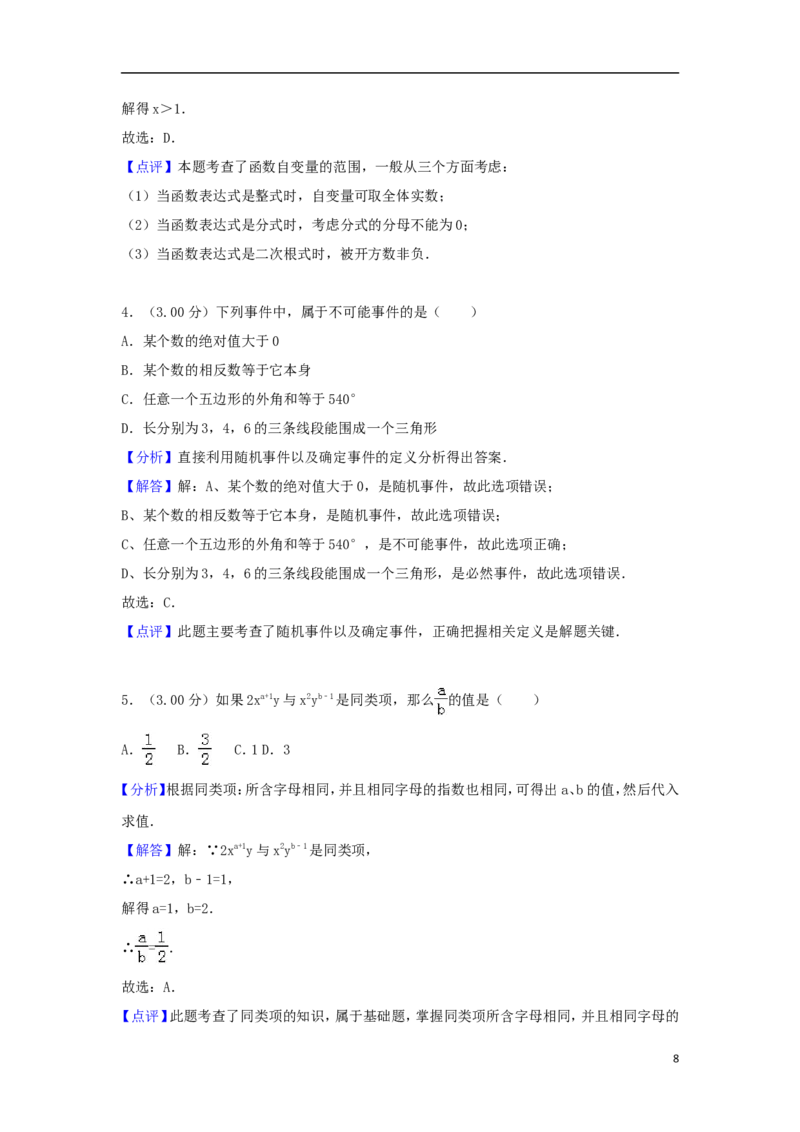
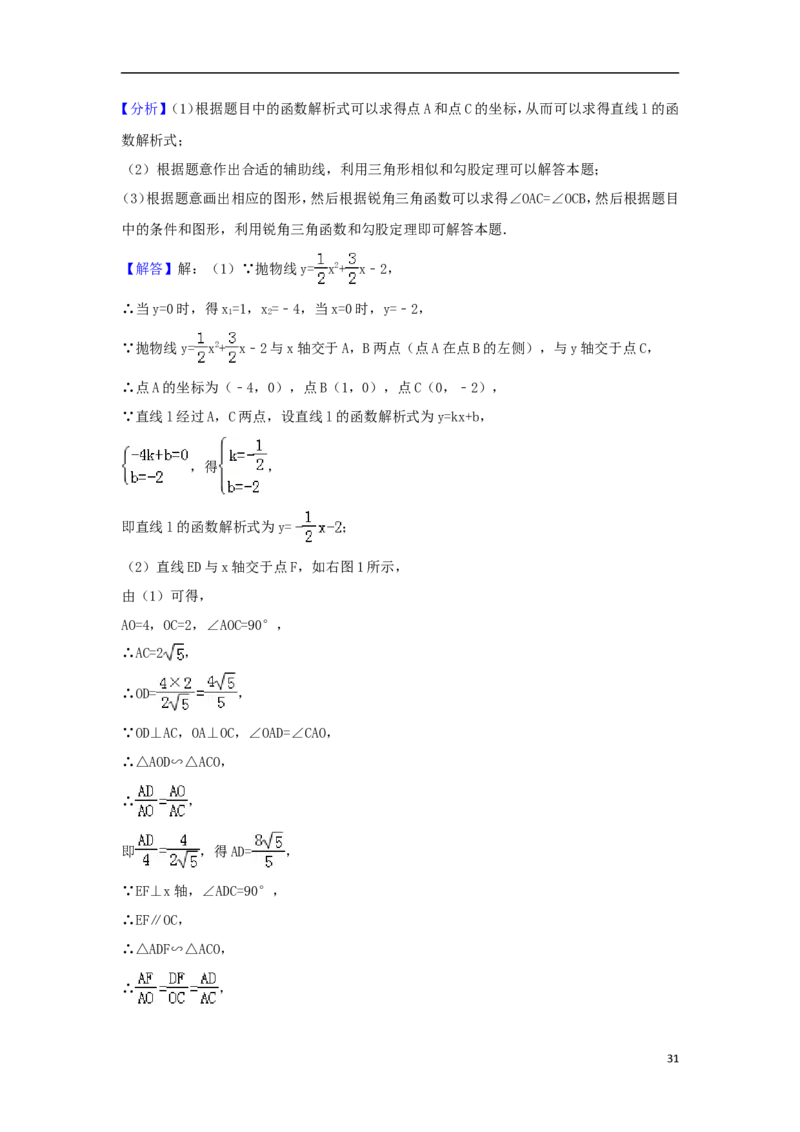
26.(12.00分)如图,在平面直角坐标系中,已知抛物线y= x2+ x﹣2与x轴交于A,B两点
(点A在点B的左侧),与y轴交于点C,直线l经过A,C两点,连接BC.
(1)求直线l的解析式;
(2)若直线x=m(m<0)与该抛物线在第三象限内交于点E,与直线l交于点D,连接OD.当
OD⊥AC时,求线段DE的长;
(3)取点G(0,﹣1),连接AG,在第一象限内的抛物线上,是否存在点P,使∠BAP=∠BCO﹣
∠BAG?若存在,求出点P的坐标;若不存在,请说明理由.
6参考答案与试题解析
一、选择题:本大题共有12小题,每小题3分,共36分.每小题只有一个正确选项
1.(3.00分)计算﹣ ﹣|﹣3|的结果是( )
A.﹣1 B.﹣5 C.1 D.5
【分析】原式利用算术平方根定义,以及绝对值的代数意义计算即可求出值.
【解答】解:原式=﹣2﹣3=﹣5,
故选:B.
【点评】此题考查了实数的运算,熟练掌握运算法则是解本题的关键.
2.(3.00分)如图,是由几个大小相同的小立方块所搭几何体的俯视图,其中小正方形中的
数字表示在该位置的小立方块的个数,则这个几何体的主视图是( )
A. B. C. D.
【分析】由俯视图知该几何体共2列,其中第1列前一排1个正方形、后1排2个正方形,第2
列只有前排2个正方形,据此可得.
【解答】解:由俯视图知该几何体共2列,其中第1列前一排1个正方形、后1排2个正方形,
第2列只有前排2个正方形,
所以其主视图为:
故选:C.
【点评】本题考查了三视图的知识,主视图是从物体的正面看得到的视图.
3.(3.00分)函数y= 中,自变量x的取值范围是( )
A.x≠1 B.x>0 C.x≥1 D.x>1
【分析】根据被开方数大于等于0,分母不等于0列式计算即可得解.
【解答】解:由题意得,x﹣1≥0且x﹣1≠0,
7解得x>1.
故选:D.
【点评】本题考查了函数自变量的范围,一般从三个方面考虑:
(1)当函数表达式是整式时,自变量可取全体实数;
(2)当函数表达式是分式时,考虑分式的分母不能为0;
(3)当函数表达式是二次根式时,被开方数非负.
4.(3.00分)下列事件中,属于不可能事件的是( )
A.某个数的绝对值大于0
B.某个数的相反数等于它本身
C.任意一个五边形的外角和等于540°
D.长分别为3,4,6的三条线段能围成一个三角形
【分析】直接利用随机事件以及确定事件的定义分析得出答案.
【解答】解:A、某个数的绝对值大于0,是随机事件,故此选项错误;
B、某个数的相反数等于它本身,是随机事件,故此选项错误;
C、任意一个五边形的外角和等于540°,是不可能事件,故此选项正确;
D、长分别为3,4,6的三条线段能围成一个三角形,是必然事件,故此选项错误.
故选:C.
【点评】此题主要考查了随机事件以及确定事件,正确把握相关定义是解题关键.
5.(3.00分)如果2xa+1y与x2yb﹣1是同类项,那么 的值是( )
A. B. C.1 D.3
【分析】根据同类项:所含字母相同,并且相同字母的指数也相同,可得出a、b的值,然后代入
求值.
【解答】解:∵2xa+1y与x2yb﹣1是同类项,
∴a+1=2,b﹣1=1,
解得a=1,b=2.
∴ = .
故选:A.
【点评】此题考查了同类项的知识,属于基础题,掌握同类项所含字母相同,并且相同字母的
8指数也相同,是解答本题的关键.
6.(3.00分)一组数据1,3,4,4,4,5,5,6的众数和方差分别是( )
A.4,1 B.4,2 C.5,1 D.5,2
【分析】根据题目中的数据可以直接写出众数,求出相应的平均数和方差,从而可以解答本题.
【解答】解:数据1,3,4,4,4,5,5,6的众数是4,
,
则 =2,
故选:B.
【点评】本题考查方差和众数,解答本题的关键是明确众数的定义,会求一组数据的方差.
7.(3.00分)如图,在△ABC中,AB=2,BC=4,∠ABC=30°,以点B为圆心,AB长为半径画弧,交
BC于点D,则图中阴影部分的面积是( )
A.2﹣ B.2﹣ C.4﹣ D.4﹣
【分析】过A作AE⊥BC于E,依据AB=2,∠ABC=30°,即可得出AE= AB=1,再根据公式即可得
到,阴影部分的面积是 ×4×1﹣ =2﹣ .
【解答】解:如图,过A作AE⊥BC于E,
∵AB=2,∠ABC=30°,
∴AE= AB=1,
又∵BC=4,
∴阴影部分的面积是 ×4×1﹣ =2﹣ ,
故选:A.
9【点评】本题主要考查了扇形面积的计算,求阴影面积的主要思路是将不规则图形面积转化
为规则图形的面积,常用的方法:①直接用公式法;②和差法;③割补法.
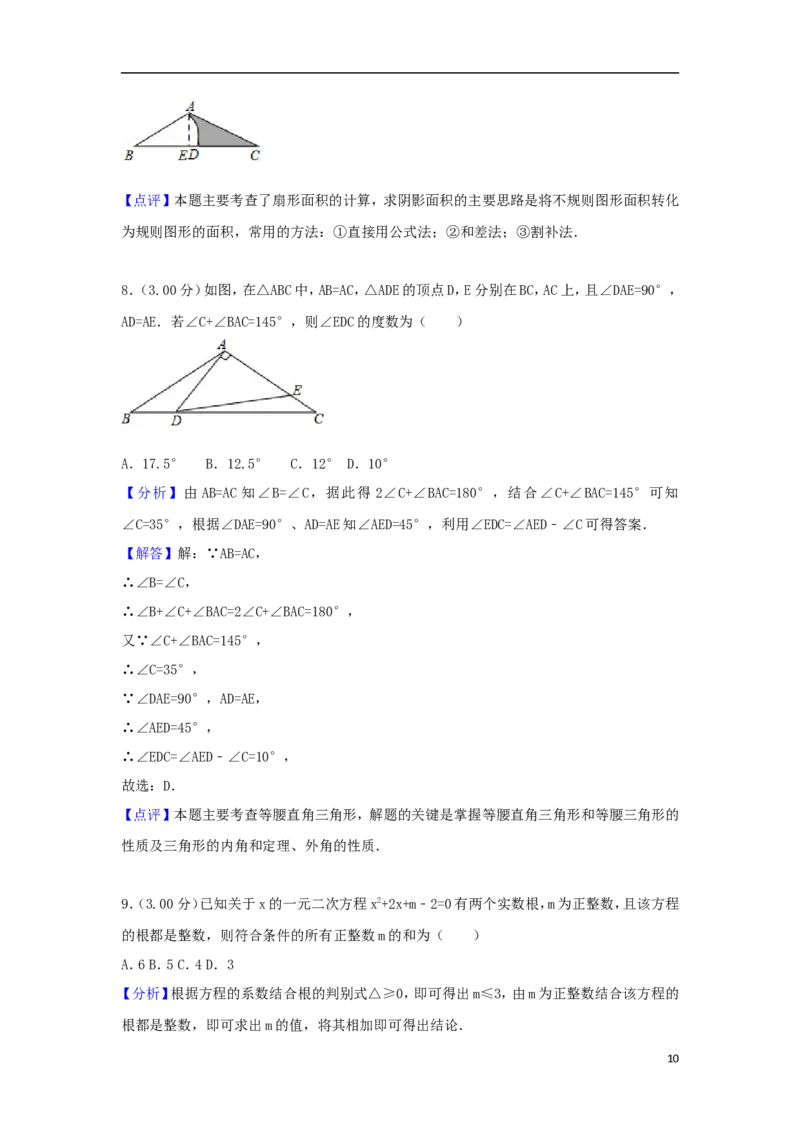
8.(3.00分)如图,在△ABC中,AB=AC,△ADE的顶点D,E分别在BC,AC上,且∠DAE=90°,
AD=AE.若∠C+∠BAC=145°,则∠EDC的度数为( )
A.17.5° B.12.5° C.12° D.10°
【分析】由 AB=AC 知∠B=∠C,据此得 2∠C+∠BAC=180°,结合∠C+∠BAC=145°可知
∠C=35°,根据∠DAE=90°、AD=AE知∠AED=45°,利用∠EDC=∠AED﹣∠C可得答案.
【解答】解:∵AB=AC,
∴∠B=∠C,
∴∠B+∠C+∠BAC=2∠C+∠BAC=180°,
又∵∠C+∠BAC=145°,
∴∠C=35°,
∵∠DAE=90°,AD=AE,
∴∠AED=45°,
∴∠EDC=∠AED﹣∠C=10°,
故选:D.
【点评】本题主要考查等腰直角三角形,解题的关键是掌握等腰直角三角形和等腰三角形的
性质及三角形的内角和定理、外角的性质.
9.(3.00分)已知关于x的一元二次方程x2+2x+m﹣2=0有两个实数根,m为正整数,且该方程
的根都是整数,则符合条件的所有正整数m的和为( )
A.6 B.5 C.4 D.3
【分析】根据方程的系数结合根的判别式△≥0,即可得出m≤3,由m为正整数结合该方程的
根都是整数,即可求出m的值,将其相加即可得出结论.
10【解答】解:∵a=1,b=2,c=m﹣2,关于x的一元二次方程x2+2x+m﹣2=0有实数根
∴△=b2﹣4ac=22﹣4(m﹣2)=12﹣4m≥0,
∴m≤3.
∵m为正整数,且该方程的根都是整数,
∴m=2或3.
∴2+3=5.
故选:B.
【点评】本题考查了根的判别式以及一元二次方程的整数解,牢记“当△≥0时,方程有实数
根”是解题的关键.
10.(3.00分)已知下列命题:
①若a3>b3,则a2>b2;
②若点A(x,y)和点B(x,y)在二次函数y=x2﹣2x﹣1的图象上,且满足x<x<1,则y>
1 1 2 2 1 2 1
y>﹣2;
2
③在同一平面内,a,b,c是直线,且a∥b,b⊥c,则a∥c;
④周长相等的所有等腰直角三角形全等.
其中真命题的个数是( )
A.4个 B.3个 C.2个 D.1个
【分析】依据a,b的符号以及绝对值,即可得到a2>b2不一定成立;依据二次函数y=x2﹣2x﹣
1图象的顶点坐标以及对称轴的位置,即可得y>y>﹣2;依据a∥b,b⊥c,即可得到a∥c;
1 2
依据周长相等的所有等腰直角三角形的边长对应相等,即可得到它们全等.
【解答】解:①若a3>b3,则a2>b2不一定成立,故错误;
②若点A(x,y)和点B(x,y)在二次函数y=x2﹣2x﹣1的图象上,且满足x<x<1,则y>
1 1 2 2 1 2 1
y>﹣2,故正确;
2
③在同一平面内,a,b,c是直线,且a∥b,b⊥c,则a⊥c,故错误;
④周长相等的所有等腰直角三角形全等,故正确.
故选:C.
【点评】本题主要考查了命题与定理,任何一个命题非真即假.要说明一个命题的正确性,一
般需要推理、论证,而判断一个命题是假命题,只需举出一个反例即可.
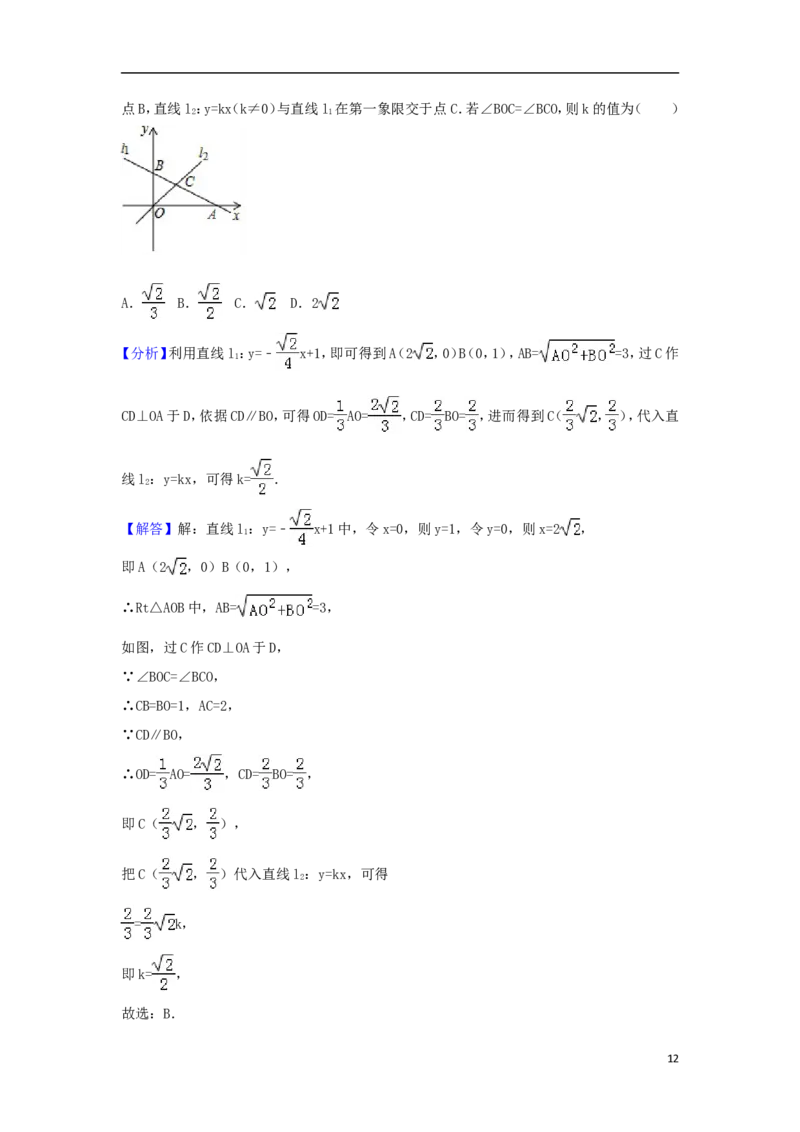
11.(3.00分)如图,在平面直角坐标系中,直线l:y=﹣ x+1与x轴,y轴分别交于点A和
1
11点B,直线l:y=kx(k≠0)与直线l 在第一象限交于点C.若∠BOC=∠BCO,则k的值为( )
2 1
A. B. C. D.2
【分析】利用直线l:y=﹣ x+1,即可得到A(2 ,0)B(0,1),AB= =3,过C作
1
CD⊥OA于D,依据CD∥BO,可得OD= AO= ,CD= BO= ,进而得到C( , ),代入直
线l:y=kx,可得k= .
2
【解答】解:直线l:y=﹣ x+1中,令x=0,则y=1,令y=0,则x=2 ,
1
即A(2 ,0)B(0,1),
∴Rt△AOB中,AB= =3,
如图,过C作CD⊥OA于D,
∵∠BOC=∠BCO,
∴CB=BO=1,AC=2,
∵CD∥BO,
∴OD= AO= ,CD= BO= ,
即C( , ),
把C( , )代入直线l:y=kx,可得
2
= k,
即k= ,
故选:B.
12【点评】本题主要考查了两直线相交或平行问题,两条直线的交点坐标,就是由这两条直线相
对应的一次函数表达式所组成的二元一次方程组的解.
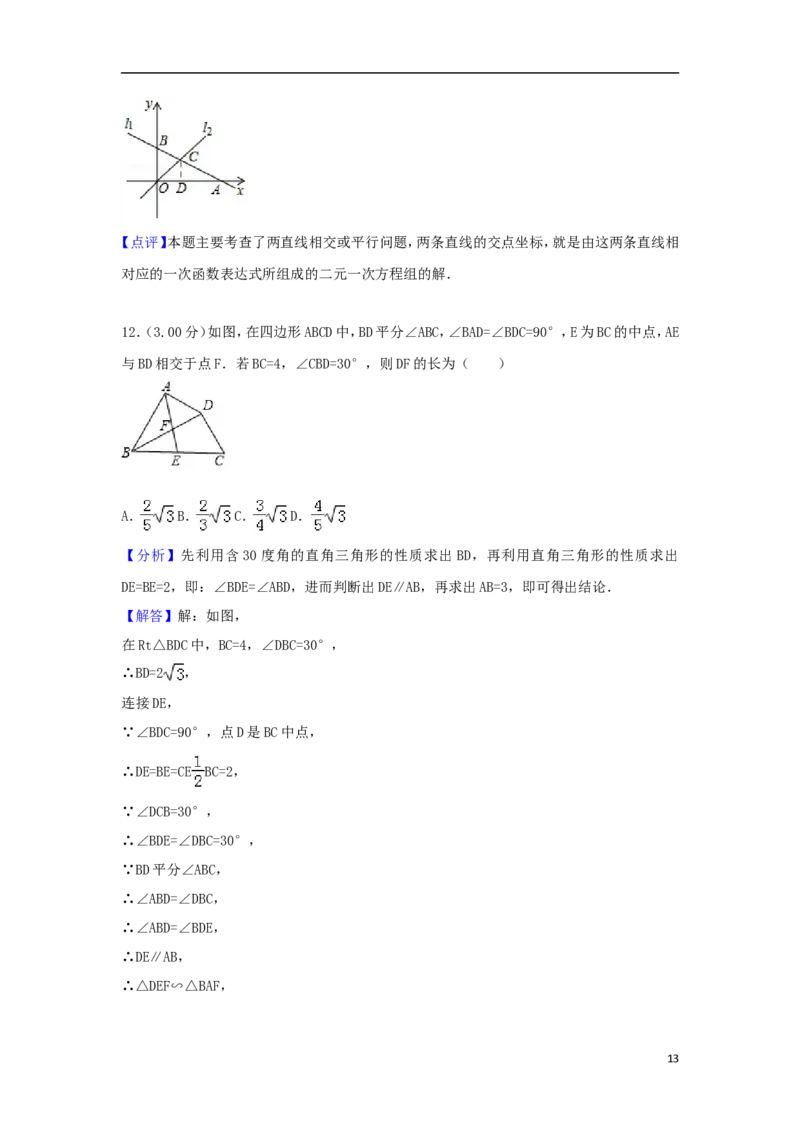
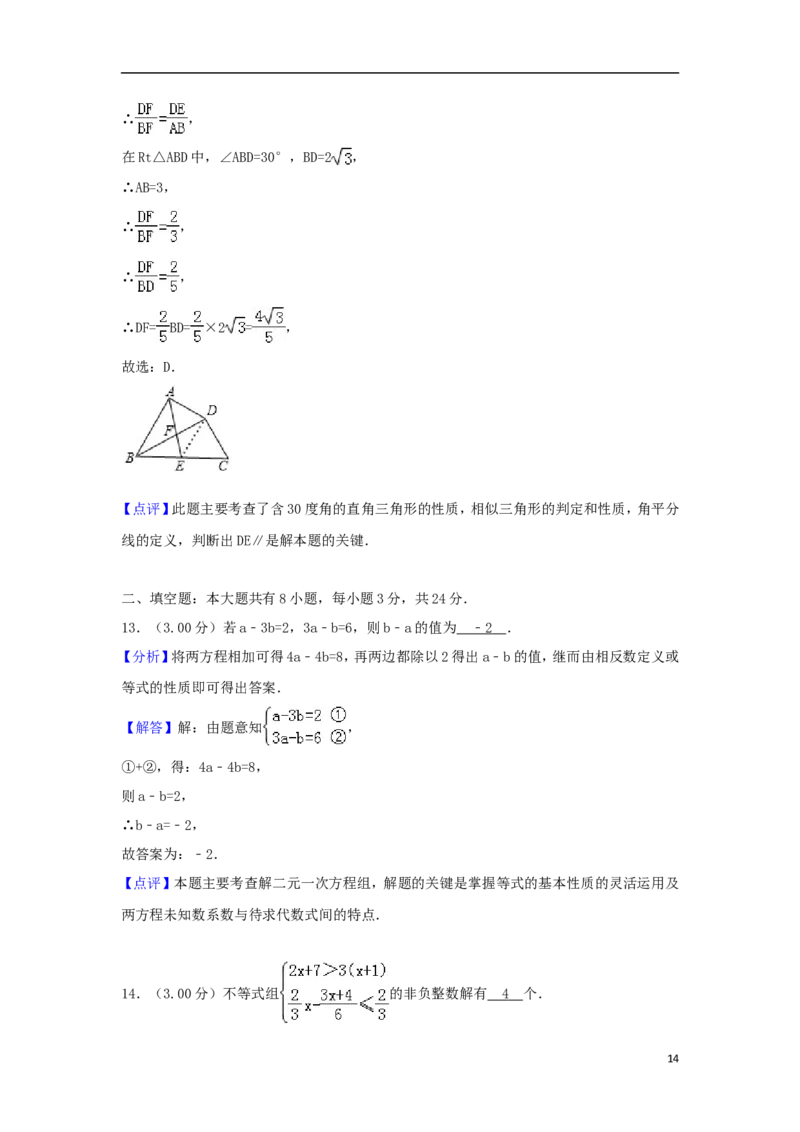
12.(3.00分)如图,在四边形ABCD中,BD平分∠ABC,∠BAD=∠BDC=90°,E为BC的中点,AE
与BD相交于点F.若BC=4,∠CBD=30°,则DF的长为( )
A. B. C. D.
【分析】先利用含30度角的直角三角形的性质求出BD,再利用直角三角形的性质求出
DE=BE=2,即:∠BDE=∠ABD,进而判断出DE∥AB,再求出AB=3,即可得出结论.
【解答】解:如图,
在Rt△BDC中,BC=4,∠DBC=30°,
∴BD=2 ,
连接DE,
∵∠BDC=90°,点D是BC中点,
∴DE=BE=CE BC=2,
∵∠DCB=30°,
∴∠BDE=∠DBC=30°,
∵BD平分∠ABC,
∴∠ABD=∠DBC,
∴∠ABD=∠BDE,
∴DE∥AB,
∴△DEF∽△BAF,
13∴ ,
在Rt△ABD中,∠ABD=30°,BD=2 ,
∴AB=3,
∴ ,
∴ ,
∴DF= BD= ×2 = ,
故选:D.
【点评】此题主要考查了含30度角的直角三角形的性质,相似三角形的判定和性质,角平分
线的定义,判断出DE∥是解本题的关键.
二、填空题:本大题共有8小题,每小题3分,共24分.
13.(3.00分)若a﹣3b=2,3a﹣b=6,则b﹣a的值为 ﹣ 2 .
【分析】将两方程相加可得4a﹣4b=8,再两边都除以2得出a﹣b的值,继而由相反数定义或
等式的性质即可得出答案.
【解答】解:由题意知 ,
①+②,得:4a﹣4b=8,
则a﹣b=2,
∴b﹣a=﹣2,
故答案为:﹣2.
【点评】本题主要考查解二元一次方程组,解题的关键是掌握等式的基本性质的灵活运用及
两方程未知数系数与待求代数式间的特点.
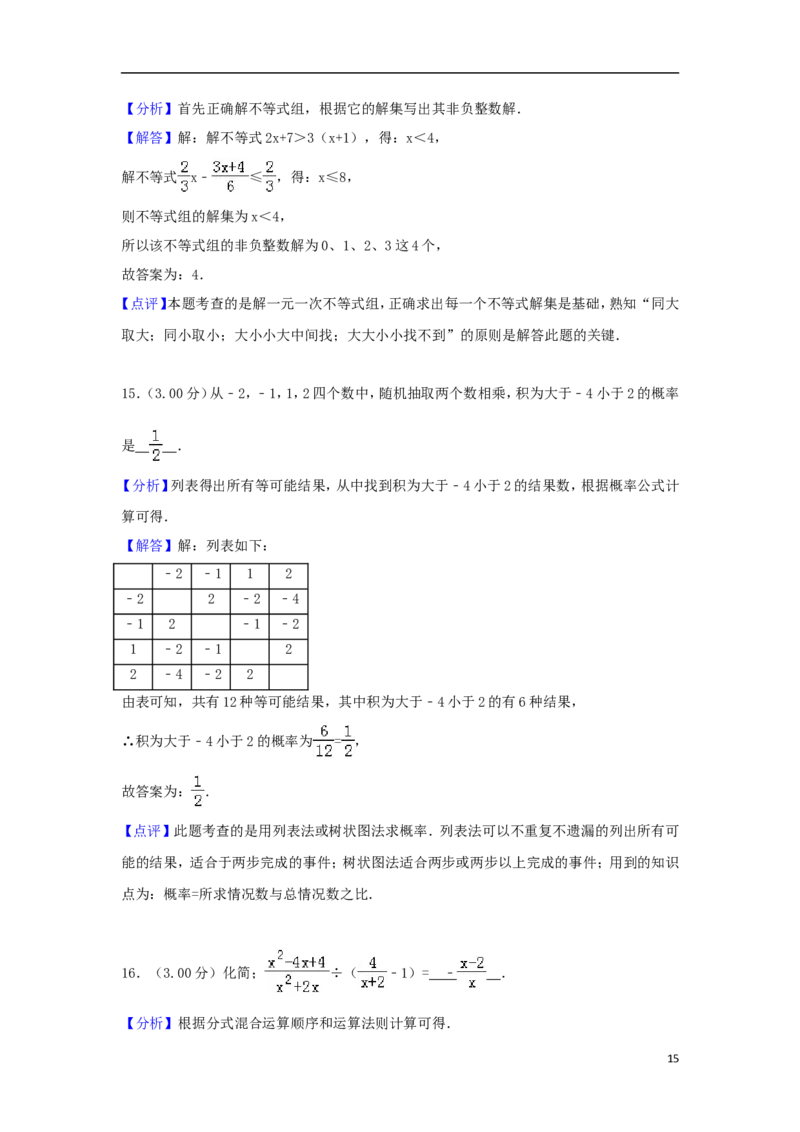
14.(3.00分)不等式组 的非负整数解有 4 个.
14【分析】首先正确解不等式组,根据它的解集写出其非负整数解.
【解答】解:解不等式2x+7>3(x+1),得:x<4,
解不等式 x﹣ ≤ ,得:x≤8,
则不等式组的解集为x<4,
所以该不等式组的非负整数解为0、1、2、3这4个,
故答案为:4.
【点评】本题考查的是解一元一次不等式组,正确求出每一个不等式解集是基础,熟知“同大
取大;同小取小;大小小大中间找;大大小小找不到”的原则是解答此题的关键.
15.(3.00分)从﹣2,﹣1,1,2四个数中,随机抽取两个数相乘,积为大于﹣4小于2的概率
是 .
【分析】列表得出所有等可能结果,从中找到积为大于﹣4小于2的结果数,根据概率公式计
算可得.
【解答】解:列表如下:
﹣2 ﹣1 1 2
﹣2 2 ﹣2 ﹣4
﹣1 2 ﹣1 ﹣2
1 ﹣2 ﹣1 2
2 ﹣4 ﹣2 2
由表可知,共有12种等可能结果,其中积为大于﹣4小于2的有6种结果,
∴积为大于﹣4小于2的概率为 = ,
故答案为: .
【点评】此题考查的是用列表法或树状图法求概率.列表法可以不重复不遗漏的列出所有可
能的结果,适合于两步完成的事件;树状图法适合两步或两步以上完成的事件;用到的知识
点为:概率=所求情况数与总情况数之比.
16.(3.00分)化简; ÷( ﹣1)= ﹣ .
【分析】根据分式混合运算顺序和运算法则计算可得.
15【解答】解:原式= ÷( ﹣ )
= ÷
= •
=﹣ ,
故答案为:﹣ .
【点评】本题主要考查分式的混合运算,解题的关键是掌握分式混合运算顺序和运算法则.
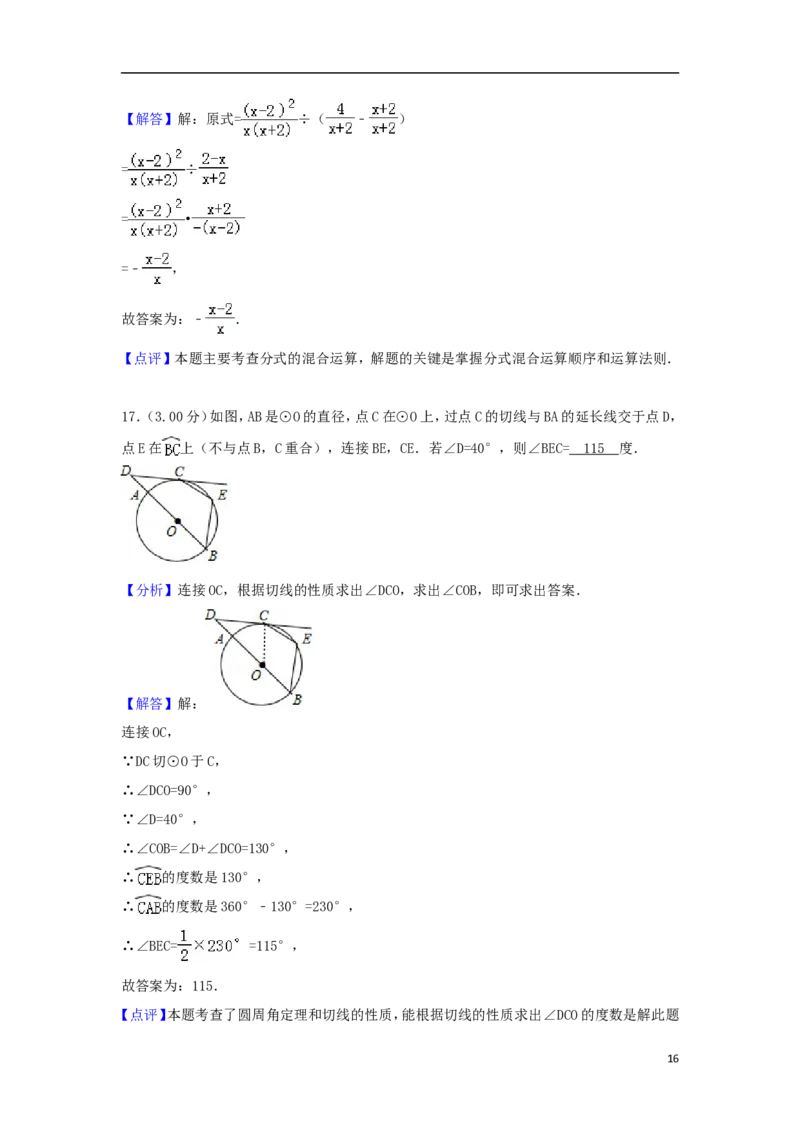
17.(3.00分)如图,AB是⊙O的直径,点C在⊙O上,过点C的切线与BA的延长线交于点D,
点E在 上(不与点B,C重合),连接BE,CE.若∠D=40°,则∠BEC= 11 5 度.
【分析】连接OC,根据切线的性质求出∠DCO,求出∠COB,即可求出答案.
【解答】解:
连接OC,
∵DC切⊙O于C,
∴∠DCO=90°,
∵∠D=40°,
∴∠COB=∠D+∠DCO=130°,
∴ 的度数是130°,
∴ 的度数是360°﹣130°=230°,
∴∠BEC= =115°,
故答案为:115.
【点评】本题考查了圆周角定理和切线的性质,能根据切线的性质求出∠DCO的度数是解此题
16的关键.
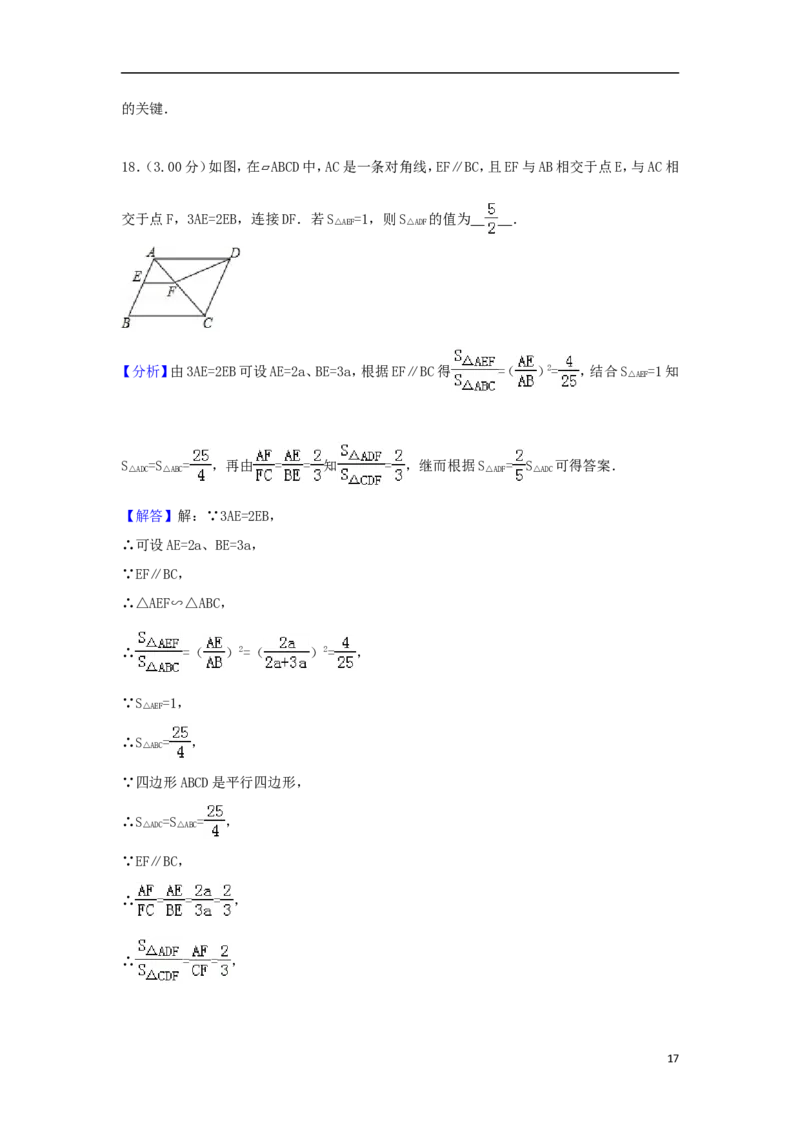
18.(3.00分)如图,在 ABCD中,AC是一条对角线,EF∥BC,且EF与AB相交于点E,与AC相
▱
交于点F,3AE=2EB,连接DF.若S =1,则S 的值为 .
△AEF △ADF
【分析】由3AE=2EB可设AE=2a、BE=3a,根据EF∥BC得 =( )2= ,结合S =1知
△AEF
S =S = ,再由 = = 知 = ,继而根据S = S 可得答案.
△ADC △ABC △ADF △ADC
【解答】解:∵3AE=2EB,
∴可设AE=2a、BE=3a,
∵EF∥BC,
∴△AEF∽△ABC,
∴ =( )2=( )2= ,
∵S =1,
△AEF
∴S = ,
△ABC
∵四边形ABCD是平行四边形,
∴S =S = ,
△ADC △ABC
∵EF∥BC,
∴ = = = ,
∴ = = ,
17∴S = S = × = ,
△ADF △ADC
故答案为: .
【点评】本题主要考查相似三角形的判定与性质,解题的关键是掌握相似三角形的判定及性
质、平行线分线段成比例定理及平行四边形的性质.
19.(3.00分)以矩形ABCD两条对角线的交点O为坐标原点,以平行于两边的方向为坐标轴,
建立如图所示的平面直角坐标系,BE⊥AC,垂足为E.若双曲线y= (x>0)经过点D,则
OB•BE的值为 3 .
【分析】由双曲线y= (x>0)经过点D知S = k= ,由矩形性质知S =2S = ,据此
△ODF △AOB △ODF
可得OA•BE=3,根据OA=OB可得答案.
【解答】解:如图,
∵双曲线y= (x>0)经过点D,
∴S = k= ,
△ODF
则S =2S = ,即 OA•BE= ,
△AOB △ODF
18∴OA•BE=3,
∵四边形ABCD是矩形,
∴OA=OB,
∴OB•BE=3,
故答案为:3.
【点评】本题主要考查反比例函数图象上的点的坐标特征,解题的关键是掌握反比例函数系
数k的几何意义及矩形的性质.
20.(3.00分)如图,在Rt△ACB中,∠ACB=90°,AC=BC,D是AB上的一个动点(不与点A,B重
合),连接CD,将CD绕点C顺时针旋转90°得到CE,连接DE,DE与AC相交于点F,连接AE.
下列结论:
①△ACE≌△BCD;
②若∠BCD=25°,则∠AED=65°;
③DE2=2CF•CA;
④若AB=3 ,AD=2BD,则AF= .
其中正确的结论是 ①②③ .(填写所有正确结论的序号)
【分析】先判断出∠BCD=∠ACE,即可判断出①正确;
先求出∠BDC=110°,进而得出∠AEC=110°,即可判断出②正确;
先判断出∠CAE=∠CEF,进而得出△CEF∽△CAE,即可得出CE2=CF•AC,最后用勾股定理即可
得出③正确;
先求出BC=AC=3,再求出BD= ,进而求出CE=CD= ,求出CF= ,即可判断出④错误.
【解答】解:∵∠ACB=90°,
由旋转知,CD=CE,∠DCE=90°=∠ACB,
∴∠BCD=∠ACE,
在△BCD和△ACE中, ,
19∴△BCD≌△ACE,故①正确;
∵∠ACB=90°,BC=AC,
∴∠B=45°
∵∠BCD=25°,
∴∠BDC=180°﹣45°﹣25°=110°,
∵△BCD≌△ACE,
∴∠AEC=∠BDC=110°,
∵∠DCE=90°,CD=CE,
∴∠CED=45°,
则∠AED=∠AEC﹣∠CED=65°,故②正确;
∵△BCD≌△ACE,
∴∠CAE=∠CBD=45°=∠CEF,
∵∠ECF=∠ACE,
∴△CEF∽△CAE,
∴ ,
∴CE2=CF•AC,
在等腰直角三角形CDE中,DE2=2CE2=2CF•AC,故③正确;
如图,过点D作DG⊥BC于G,
∵AB=3 ,
∴AC=BC=3,
∵AD=2BD,
∴BD= AB= ,
∴DG=BG=1,
∴CG=BC﹣BG=3﹣1=2,
在Rt△CDG中,根据勾股定理得,CD= = ,
∵△BCD≌△ACE,
∴CE= ,
20∵CE2=CF•AC,
∴CF= = ,
∴AF=AC﹣CF=3﹣ = ,故④错误,
故答案为:①②③.
【点评】此题是三角形综合题,主要考查了等腰直角三角形的性质,旋转的性质,全等三角形
的判定和性质,相似三角形的判定和性质,勾股定理,判断出△BCD≌△ACE是解本题的关键.
三、解答题:本大题共有6小题,共60分.请写出必要的文字说明、计算过程或推理过程
21.(8.00分)某公司招聘职员两名,对甲、乙、丙、丁四名候选人进行了笔试和面试,各项成
绩满分均为100分,然后再按笔试占60%、面试占40%计算候选人的综合成绩(满分为100分).
他们的各项成绩如下表所示:
修造人 笔试成绩/分 面试成绩/分
甲 90 88
乙 84 92
丙 x 90
丁 88 86
(1)直接写出这四名候选人面试成绩的中位数;
(2)现得知候选人丙的综合成绩为87.6分,求表中x的值;
(3)求出其余三名候选人的综合成绩,并以综合成绩排序确定所要招聘的前两名的人选.
【分析】(1)根据中位数的概念计算;
(2)根据题意列出方程,解方程即可;
(3)根据加权平均数的计算公式分别求出余三名候选人的综合成绩,比较即可.
【解答】解:(1)这四名候选人面试成绩的中位数为: =89(分);
(2)由题意得,x×60%+90×40%=87.6
解得,x=86,
答:表中x的值为86;
21(3)甲候选人的综合成绩为:90×60%+88×40%=89.2(分),
乙候选人的综合成绩为:84×60%+92×40%=87.2(分),
丁候选人的综合成绩为:88×60%+86×40%=87.2(分),
∴以综合成绩排序确定所要招聘的前两名的人选是甲和丙.
【点评】本题考查的是中位线、加权平均数,掌握中位数的概念、加权平均数的计算公式是解
题的关键.
22.(8.00分)如图,在四边形ABCD中,AD∥BC,∠ABC=90°,AB=AD,连接BD,点E在AB上,且
∠BDE=15°,DE=4 ,DC=2 .
(1)求BE的长;
(2)求四边形DEBC的面积.
(注意:本题中的计算过程和结果均保留根号)
【分析】(1)解直角三角形求出AD、AE即可解决问题;
(2)作DF⊥BC于F.则四边形ABFD是矩形,解直角三角形求出CF,即可解决问题;
【解答】解:(1)在四边形ABCD中,∵AD∥BC,∠ABC=90°,
∴∠BAD=90°,
∵AB=AD,
∴∠ABD=∠ADB=45°,
∵∠BDE=15°,
∴∠ADE=30°,
在Rt△ADE中,AE=DE×sin30=2 ,AD=DE•cos30°=6,
∴AB=AD=6,
∴BE=6﹣2 .
(2)作DF⊥BC于F.则四边形ABFD是矩形,
22∴BF=AD=6,DF=AB=6,
在Rt△DFC中,FC= =4 ,
∴BC=6+4 ,
∴S =S +S = ×(6﹣2 )×6+ (6+4 )×6=36+6 .
四边形DEBC △DEB △BCD
【点评】本题考查矩形的性质、锐角三角函数、勾股定理等知识,解题的关键是学会添加常用
辅助线,构造直角三角形解决问题.
23.(10.00分)某商店以固定进价一次性购进一种商品,3月份按一定售价销售,销售额为
2400元,为扩大销量,减少库存,4月份在3月份售价基础上打9折销售,结果销售量增加30
件,销售额增加840元.
(1)求该商店3月份这种商品的售价是多少元?
(2)如果该商店3月份销售这种商品的利润为900元,那么该商店4月份销售这种商品的利
润是多少元?
【分析】(1)设该商店3月份这种商品的售价为x元,则4月份这种商品的售价为0.9x元,根
据数量=总价÷单价结合4月份比3月份多销售30件,即可得出关于x的分式方程,解之经
检验即可得出结论;
(2)设该商品的进价为y元,根据销售利润=每件的利润×销售数量,即可得出关于y的一元
一次方程,解之即可得出该商品的进价,再利用4月份的利润=每件的利润×销售数量,即可
求出结论.
【解答】解:(1)设该商店3月份这种商品的售价为x元,则4月份这种商品的售价为0.9x元,
根据题意得: = ﹣30,
解得:x=40,
经检验,x=40是原分式方程的解.
答:该商店3月份这种商品的售价是40元.
(2)设该商品的进价为y元,
23根据题意得:(40﹣a)× =900,
解得:a=25,
∴(40×0.9﹣25)× =990(元).
答:该商店4月份销售这种商品的利润是990元.
【点评】本题考查了分式方程的应用以及一元一次方程的应用,解题的关键是:(1)找准等量
关系,正确列出分式方程;(2)找准等量关系,正确列出一元一次方程.
24.(10.00分)如图,在Rt△ACB中,∠ACB=90°,以点A为圆心,AC长为半径的圆交AB于点
D,BA的延长线交⊙A于点E,连接CE,CD,F是⊙A上一点,点F与点C位于BE两侧,且
∠FAB=∠ABC,连接BF.
(1)求证:∠BCD=∠BEC;
(2)若BC=2,BD=1,求CE的长及sin∠ABF的值.
【分析】(1)先利用等角的余角相等即可得出结论;
(2)先判断出△BDC∽△BCE得出比例式求出BE=4,DE=3,利用勾股定理求出CD,CE,再判断
出△AFM∽△BAC,进而判断出四边形FNCA是矩形,求出FN,NC,即:BN,再用勾股定理求出
BF,即可得出结论.
【解答】解:(1)∵∠ACB=90°,
∴∠BCD+∠ACD=90°,
∵DE是⊙A的直径,
∴∠DCE=90°,
∴∠BEC+∠CDE=90°,
∵AD=AC,
∴∠CDE=∠ACD,
∴∠BCD=∠BEC,
(2)∵∠BCD=∠BEC,∠EBC=∠EBC,
24∴△BDC∽△BCE,
∴ ,
∵BC=2,BD=1,
∴BE=4,EC=2CD,
∴DE=BE﹣BD=3,
在Rt△DCE中,DE2=CD2+CE2=9,
∴CD= ,CE= ,
过点F作FM⊥AB于M,
∵∠FAB=∠ABC,∠FMA=∠ACB=90°,
∴△AFM∽△BAC,
∴ ,
∵DE=3,
∴AD=AF=AC= ,AB= ,
∴FM= ,
过点F作FN⊥BC于N,
∴∠FNC=90°,
∵∠FAB=∠ABC,
∴FA∥BC,
∴∠FAC=∠ACB=90°,
∴四边形FNCA是矩形,
∴FN=AC= ,NC=AF= ,
∴BN= ,
在Rt△FBN中,BF= ,
在Rt△FBM中,sin∠ABF= .
25【点评】此题主要考查了圆的有关性质,等角的余角相等,相似三角形的判定和性质,勾股定
理,锐角三角函数,正确作出辅助线是解本题的关键.
25.(12.00 分)如图,在矩形 ABCD 中,AB=3,BC=5,E 是 AD 上的一个动点.
(1)如图1,连接BD,O是对角线BD的中点,连接OE.当OE=DE时,求AE的长;
(2)如图2,连接BE,EC,过点E作EF⊥EC交AB于点F,连接CF,与BE交于点G.当BE平分
∠ABC时,求BG的长;
(3)如图3,连接EC,点H在CD上,将矩形ABCD沿直线EH折叠,折叠后点D落在EC上的点
D'处,过点D′作D′N⊥AD于点N,与EH交于点M,且AE=1.
①求 的值;
②连接BE,△D'MH与△CBE是否相似?请说明理由.
【分析】(1)先求出BD,进而求出OD=OB=OA,再判断出△ODE∽△ADO,即可得出结论;
(2)先判断出△AEF≌△DCE,进而求出BF=1,再判断出△CHG∽△CBF,进而求出BK=GK= ,最
后用勾股定理即可得出结论;
(3)①先求出EC=5,再求出D'C=1,根据勾股定理求出DH= ,CH= ,再判断出△EMN∽△EHD,
的粗 ,△ED'M∽△ECH,得出 ,进而得出 ,即可得出结论;
26②先判断出∠MD'H=∠NED',进而判断出∠MD'H=∠ECB,即可得出 ,即可.
【解答】解:(1)如图1,连接OA,在矩形ABCD中,CD=AB=3,AD=BC=5,∠BAD=90°
在Rt△ABD中,根据勾股定理得,BD= ,
∵O是BD中点,
∴OD=OB=OA= ,
∴∠OAD=∠ODA,
∵OE=DE,
∴∠EOD=∠ODE,
∴∠EOD=∠ODE=∠OAD,
∴△ODE∽△ADO,
∴ ,∴
DO2=DE•DA,
∴设AE=x,
∴DE=5﹣x,
∴( )2=5(5﹣x),
∴x= ,
即:AE= ;
(2)如图2,在矩形ABCD中,
∵BE平分∠ABC,
∴∠ABE=∠EBC=45°,
∵AD∥BC,
∴∠AEB=∠EBC,
∴∠ABE=∠AEB,
∴AE=AB=3,
∴AE=CD=3,
∵EF⊥EC,
∴∠FEC=90°,
27∴∠AEF+∠CED=90°,
∵∠A=90°,
∴∠AEF+∠AFE=90°,
∴∠CED=∠AFE,
∵∠D=∠A=90°,
∴△AEF≌△DCE,
∴AF=DE=2,
∴BF=AB﹣AF=1,
过点G作GK⊥BC于K,
∴∠EBC=∠BGK=45°,
∴BK=GK,∠ABC=∠GKC=90°,
∵∠KCG=∠BCF,
∴△CHG∽△CBF,
∴ ,
设BK=GK=y,
∴CK=5﹣y,
∴y= ,
∴BK=GK= ,
在Rt△GKB中,BG= ;
(3)①在矩形ABCD中,∠D=90°,
∵AE=1,AD=5,
∴DE=4,
∵DC=3,
∴EC=5,
由折叠知,ED'=ED=4,D'H=DH,∠ED'H=∠D=90°,
∴D'C=1,
设D'H=DH=z,
∴HC=3﹣z,
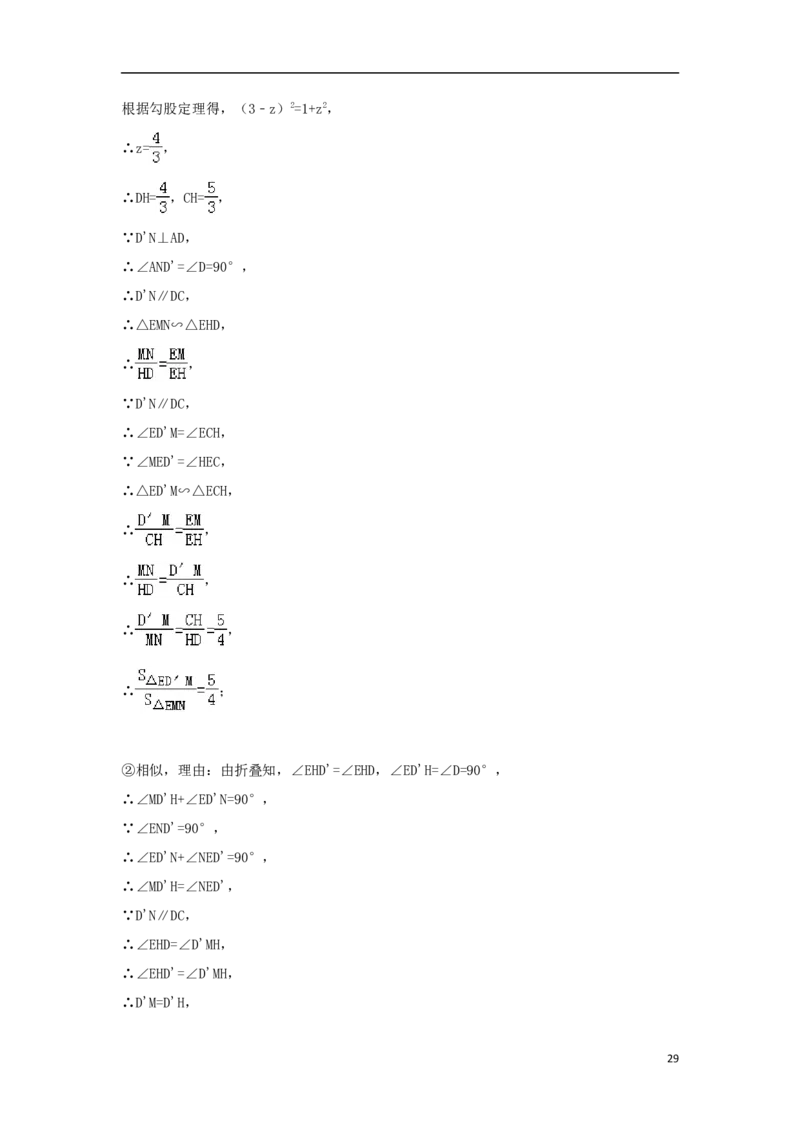
28根据勾股定理得,(3﹣z)2=1+z2,
∴z= ,
∴DH= ,CH= ,
∵D'N⊥AD,
∴∠AND'=∠D=90°,
∴D'N∥DC,
∴△EMN∽△EHD,
∴ ,
∵D'N∥DC,
∴∠ED'M=∠ECH,
∵∠MED'=∠HEC,
∴△ED'M∽△ECH,
∴ ,
∴ ,
∴ ,
∴ ;
②相似,理由:由折叠知,∠EHD'=∠EHD,∠ED'H=∠D=90°,
∴∠MD'H+∠ED'N=90°,
∵∠END'=90°,
∴∠ED'N+∠NED'=90°,
∴∠MD'H=∠NED',
∵D'N∥DC,
∴∠EHD=∠D'MH,
∴∠EHD'=∠D'MH,
∴D'M=D'H,
29∵AD∥BC,
∴∠NED'=∠ECB,
∴∠MD'H=∠ECB,
∵CE=CB=5,
∴ ,
∴△D'MH∽△CBE.
【点评】此题是相似形综合题,主要考查了矩形的性质,相似三角形的判定和性质,勾股定理,
角平分线的定义,熟练掌握判定两三角形相似的方法是解本题的关键.
26.(12.00分)如图,在平面直角坐标系中,已知抛物线y= x2+ x﹣2与x轴交于A,B两点
(点A在点B的左侧),与y轴交于点C,直线l经过A,C两点,连接BC.
(1)求直线l的解析式;
(2)若直线x=m(m<0)与该抛物线在第三象限内交于点E,与直线l交于点D,连接OD.当
OD⊥AC时,求线段DE的长;
(3)取点G(0,﹣1),连接AG,在第一象限内的抛物线上,是否存在点P,使∠BAP=∠BCO﹣
∠BAG?若存在,求出点P的坐标;若不存在,请说明理由.
30【分析】(1)根据题目中的函数解析式可以求得点A和点C的坐标,从而可以求得直线l的函
数解析式;
(2)根据题意作出合适的辅助线,利用三角形相似和勾股定理可以解答本题;
(3)根据题意画出相应的图形,然后根据锐角三角函数可以求得∠OAC=∠OCB,然后根据题目
中的条件和图形,利用锐角三角函数和勾股定理即可解答本题.
【解答】解:(1)∵抛物线y= x2+ x﹣2,
∴当y=0时,得x=1,x=﹣4,当x=0时,y=﹣2,
1 2
∵抛物线y= x2+ x﹣2与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C,
∴点A的坐标为(﹣4,0),点B(1,0),点C(0,﹣2),
∵直线l经过A,C两点,设直线l的函数解析式为y=kx+b,
,得 ,
即直线l的函数解析式为y= ;
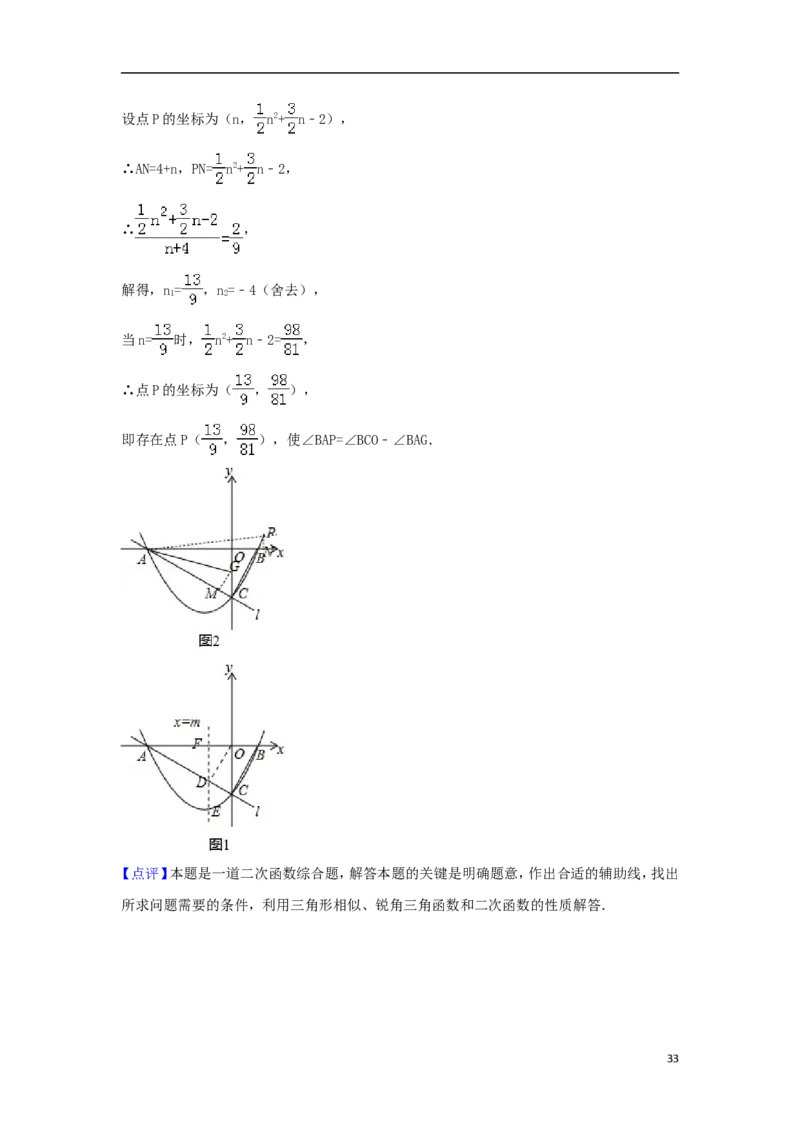
(2)直线ED与x轴交于点F,如右图1所示,
由(1)可得,
AO=4,OC=2,∠AOC=90°,
∴AC=2 ,
∴OD= ,
∵OD⊥AC,OA⊥OC,∠OAD=∠CAO,
∴△AOD∽△ACO,
∴ ,
即 ,得AD= ,
∵EF⊥x轴,∠ADC=90°,
∴EF∥OC,
∴△ADF∽△ACO,
∴ ,
31解得,AF= ,DF= ,
∴OF=4﹣ = ,
∴m=﹣ ,
当m=﹣ 时,y= ×( )2+ ×(﹣ )﹣2=﹣ ,
∴EF= ,
∴DE=EF﹣FD= ;
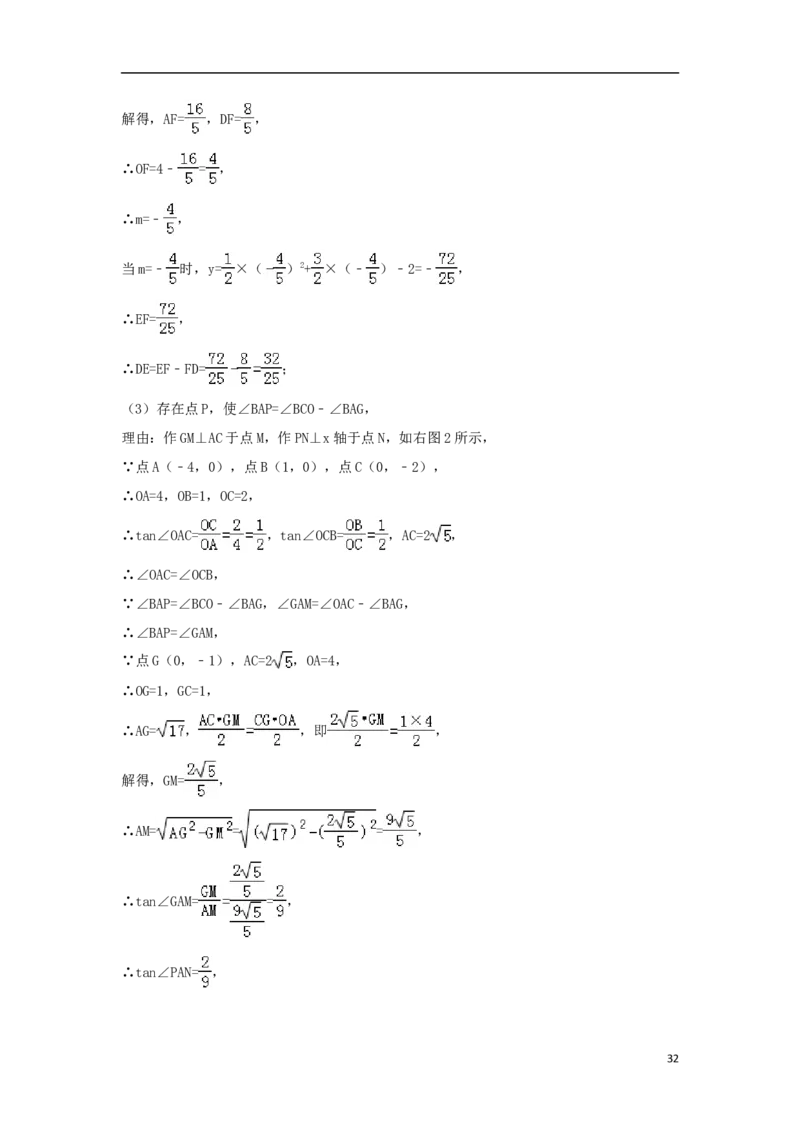
(3)存在点P,使∠BAP=∠BCO﹣∠BAG,
理由:作GM⊥AC于点M,作PN⊥x轴于点N,如右图2所示,
∵点A(﹣4,0),点B(1,0),点C(0,﹣2),
∴OA=4,OB=1,OC=2,
∴tan∠OAC= ,tan∠OCB= ,AC=2 ,
∴∠OAC=∠OCB,
∵∠BAP=∠BCO﹣∠BAG,∠GAM=∠OAC﹣∠BAG,
∴∠BAP=∠GAM,
∵点G(0,﹣1),AC=2 ,OA=4,
∴OG=1,GC=1,
∴AG= , ,即 ,
解得,GM= ,
∴AM= = = ,
∴tan∠GAM= = ,
∴tan∠PAN= ,
32设点P的坐标为(n, n2+ n﹣2),
∴AN=4+n,PN= n2+ n﹣2,
∴ ,
解得,n= ,n=﹣4(舍去),
1 2
当n= 时, n2+ n﹣2= ,
∴点P的坐标为( , ),
即存在点P( , ),使∠BAP=∠BCO﹣∠BAG.
【点评】本题是一道二次函数综合题,解答本题的关键是明确题意,作出合适的辅助线,找出
所求问题需要的条件,利用三角形相似、锐角三角函数和二次函数的性质解答.
33