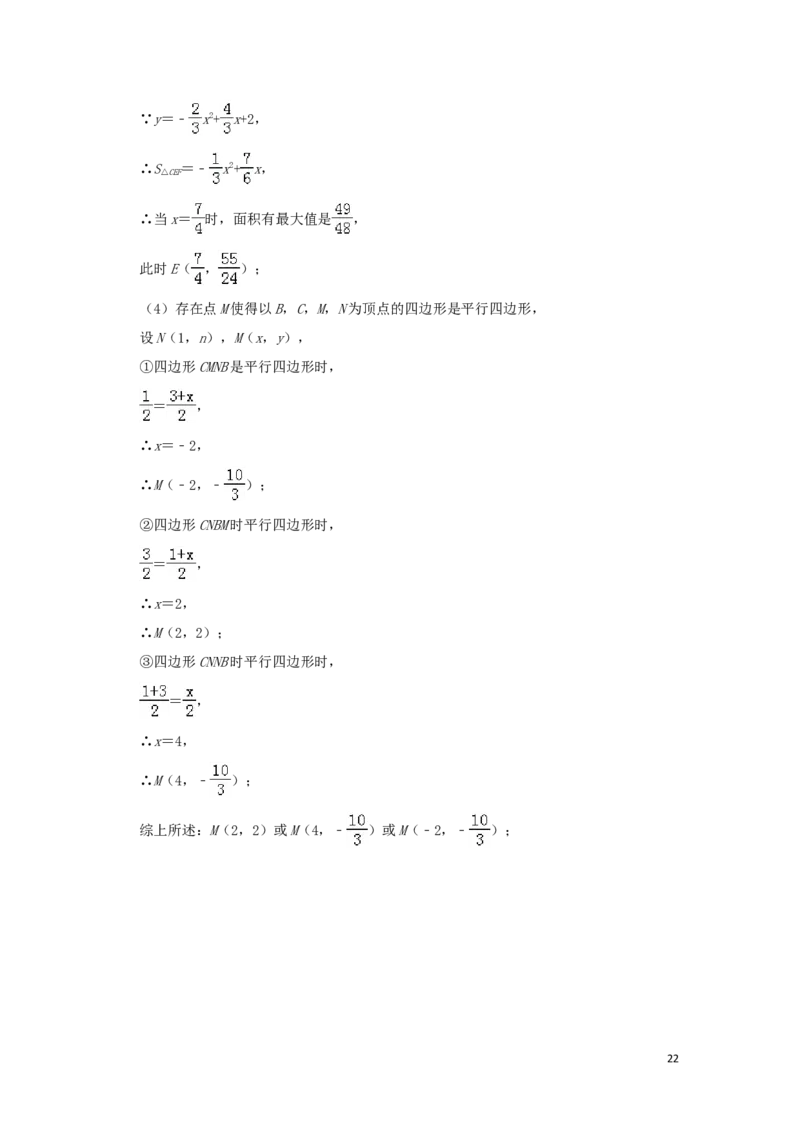文档内容
2019年内蒙古包头市中考数学试卷
一、选择题:本大题共12小题,每小题3分,共36分.
1.(3分)计算|﹣ |+( )﹣1的结果是( )
A.0 B. C. D.6
2.(3分)实数a,b在数轴上的对应点的位置如图所示.下列结论正确的是( )
A.a>b B.a>﹣b C.﹣a>b D.﹣a<b
3.(3分)一组数据2,3,5,x,7,4,6,9的众数是4,则这组数据的中位数是( )
A.4 B. C.5 D.
4.(3分)一个圆柱的三视图如图所示,若其俯视图为圆,则这个圆柱的体积为( )
A.24 B.24π C.96 D.96π
5.(3分)在函数y= ﹣ 中,自变量x的取值范围是( )
A.x>﹣1 B.x≥﹣1 C.x>﹣1且x≠2 D.x≥﹣1且x≠2
6.(3分)下列说法正确的是( )
A.立方根等于它本身的数一定是1和0
B.顺次连接菱形四边中点得到的四边形是矩形
C.在函数y=kx+b(k≠0)中,y的值随着x值的增大而增大
D.如果两个圆周角相等,那么它们所对的弧长一定相等
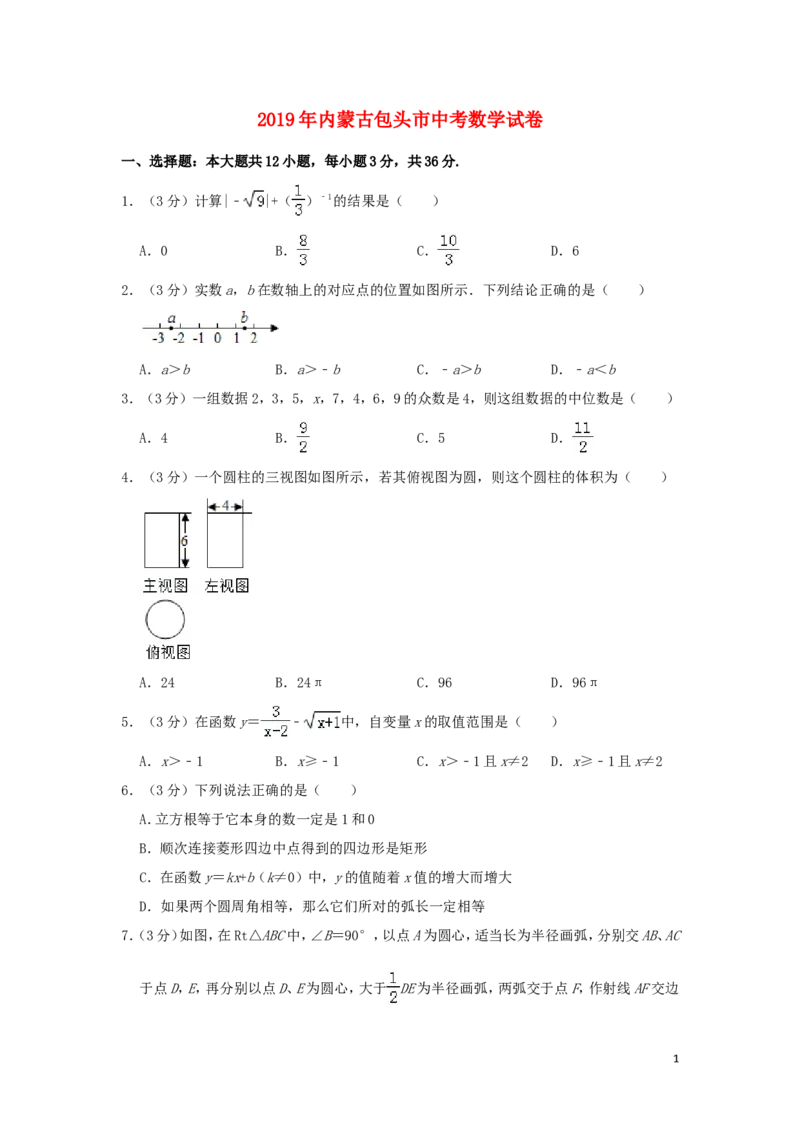
7.(3分)如图,在Rt△ABC中,∠B=90°,以点A为圆心,适当长为半径画弧,分别交AB、AC
于点D,E,再分别以点D、E为圆心,大于 DE为半径画弧,两弧交于点F,作射线AF交边
1BC于点G,若BG=1,AC=4,则△ACG的面积是( )
A.1 B. C.2 D.
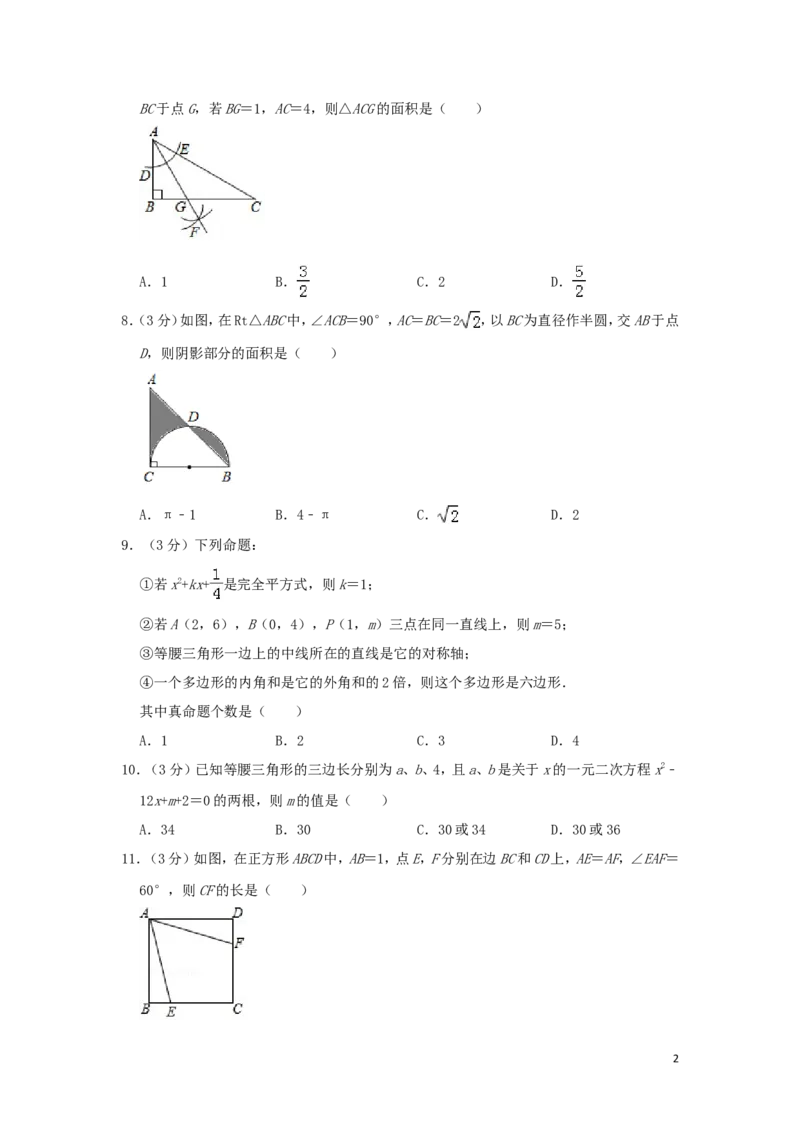
8.(3分)如图,在Rt△ABC中,∠ACB=90°,AC=BC=2 ,以BC为直径作半圆,交AB于点
D,则阴影部分的面积是( )
A.π﹣1 B.4﹣π C. D.2
9.(3分)下列命题:
①若x2+kx+ 是完全平方式,则k=1;
②若A(2,6),B(0,4),P(1,m)三点在同一直线上,则m=5;
③等腰三角形一边上的中线所在的直线是它的对称轴;
④一个多边形的内角和是它的外角和的2倍,则这个多边形是六边形.
其中真命题个数是( )
A.1 B.2 C.3 D.4
10.(3分)已知等腰三角形的三边长分别为a、b、4,且a、b是关于x的一元二次方程x2﹣
12x+m+2=0的两根,则m的值是( )
A.34 B.30 C.30或34 D.30或36
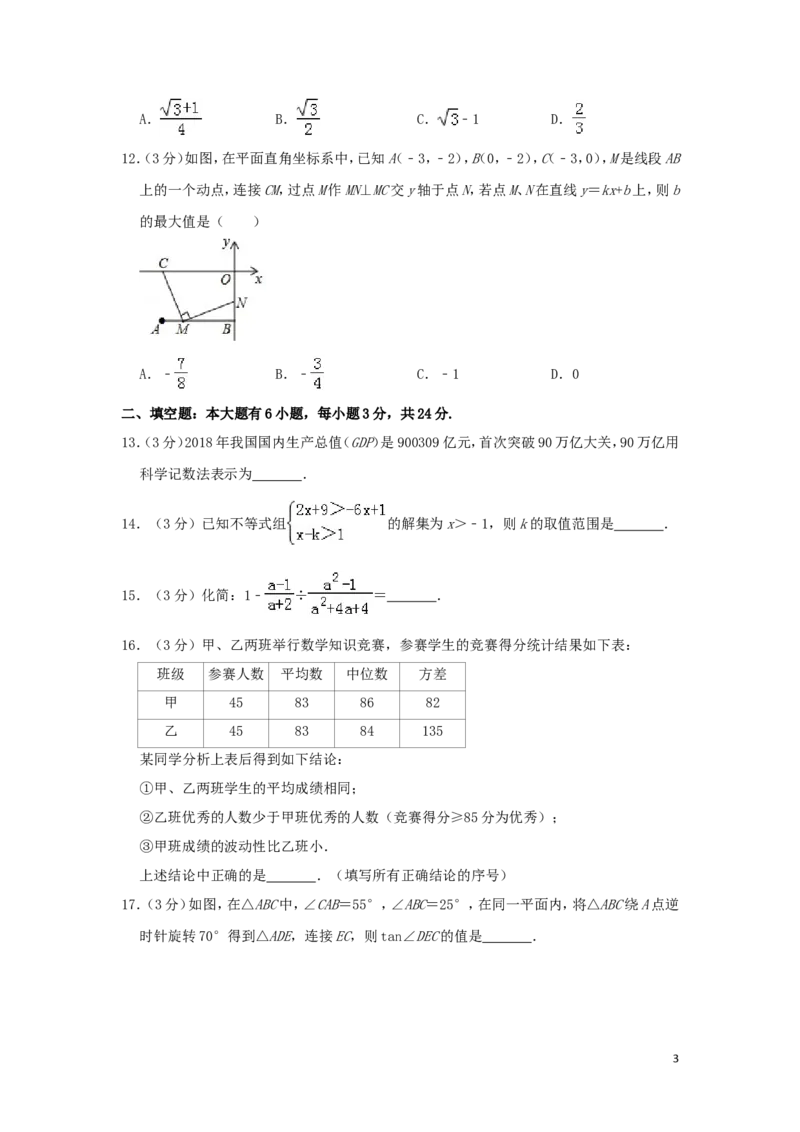
11.(3分)如图,在正方形ABCD中,AB=1,点E,F分别在边BC和CD上,AE=AF,∠EAF=
60°,则CF的长是( )
2A. B. C. ﹣1 D.
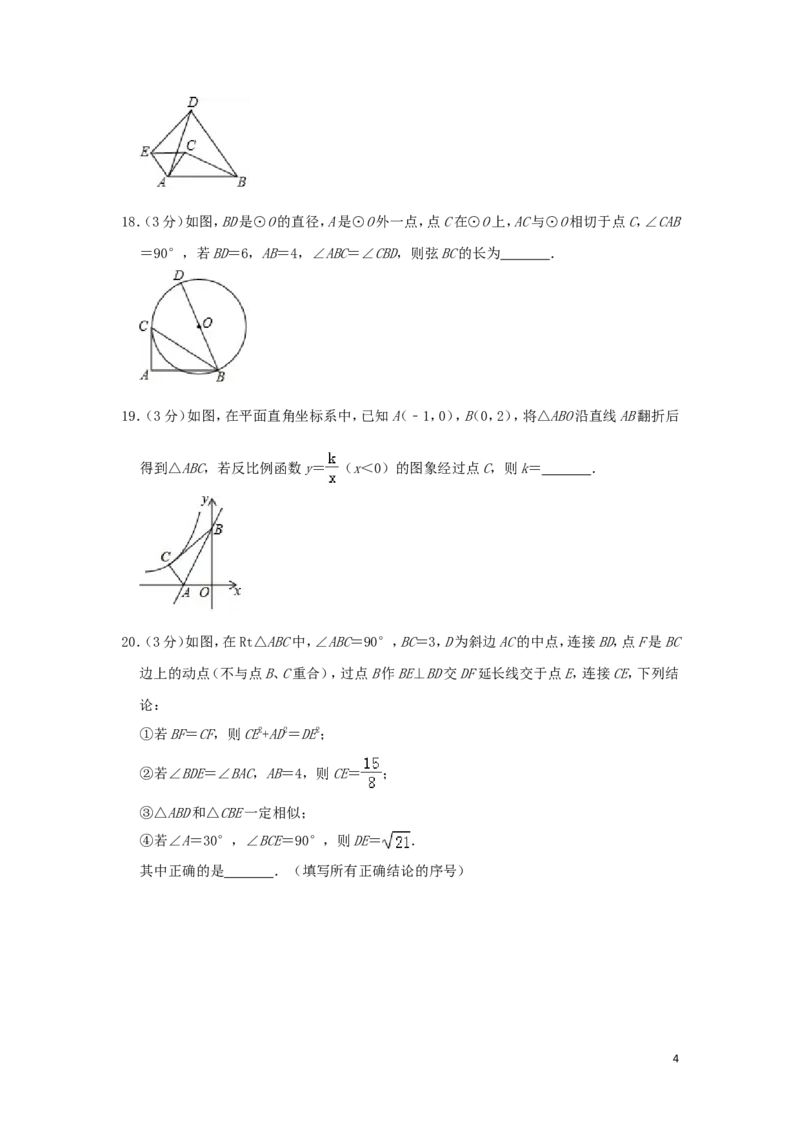
12.(3分)如图,在平面直角坐标系中,已知A(﹣3,﹣2),B(0,﹣2),C(﹣3,0),M是线段AB
上的一个动点,连接CM,过点M作MN⊥MC交y轴于点N,若点M、N在直线y=kx+b上,则b
的最大值是( )
A.﹣ B.﹣ C.﹣1 D.0
二、填空题:本大题有6小题,每小题3分,共24分.
13.(3分)2018年我国国内生产总值(GDP)是900309亿元,首次突破90万亿大关,90万亿用
科学记数法表示为 .
14.(3分)已知不等式组 的解集为x>﹣1,则k的取值范围是 .
15.(3分)化简:1﹣ ÷ = .
16.(3分)甲、乙两班举行数学知识竞赛,参赛学生的竞赛得分统计结果如下表:
班级 参赛人数 平均数 中位数 方差
甲 45 83 86 82
乙 45 83 84 135
某同学分析上表后得到如下结论:
①甲、乙两班学生的平均成绩相同;
②乙班优秀的人数少于甲班优秀的人数(竞赛得分≥85分为优秀);
③甲班成绩的波动性比乙班小.
上述结论中正确的是 .(填写所有正确结论的序号)
17.(3分)如图,在△ABC中,∠CAB=55°,∠ABC=25°,在同一平面内,将△ABC绕A点逆
时针旋转70°得到△ADE,连接EC,则tan∠DEC的值是 .
318.(3分)如图,BD是⊙O的直径,A是⊙O外一点,点C在⊙O上,AC与⊙O相切于点C,∠CAB
=90°,若BD=6,AB=4,∠ABC=∠CBD,则弦BC的长为 .
19.(3分)如图,在平面直角坐标系中,已知A(﹣1,0),B(0,2),将△ABO沿直线AB翻折后
得到△ABC,若反比例函数y= (x<0)的图象经过点C,则k= .
20.(3分)如图,在Rt△ABC中,∠ABC=90°,BC=3,D为斜边AC的中点,连接BD,点F是BC
边上的动点(不与点B、C重合),过点B作BE⊥BD交DF延长线交于点E,连接CE,下列结
论:
①若BF=CF,则CE2+AD2=DE2;
②若∠BDE=∠BAC,AB=4,则CE= ;
③△ABD和△CBE一定相似;
④若∠A=30°,∠BCE=90°,则DE= .
其中正确的是 .(填写所有正确结论的序号)
4三、解答题:本大题共有6小题,共60分.
21.(8分)某校为了解九年级学生的体育达标情况,随机抽取50名九年级学生进行体育达标
项目测试,测试成绩如下表,请根据表中的信息,解答下列问题:
测试成绩(分) 23 25 26 28 30
人数(人) 4 18 15 8 5
(1)该校九年级有450名学生,估计体育测试成绩为25分的学生人数;
(2)该校体育老师要对本次抽测成绩为23分的甲、乙、丙、丁4名学生进行分组强化训练,
要求两人一组,求甲和乙恰好分在同一组的概率.(用列表或树状图方法解答)
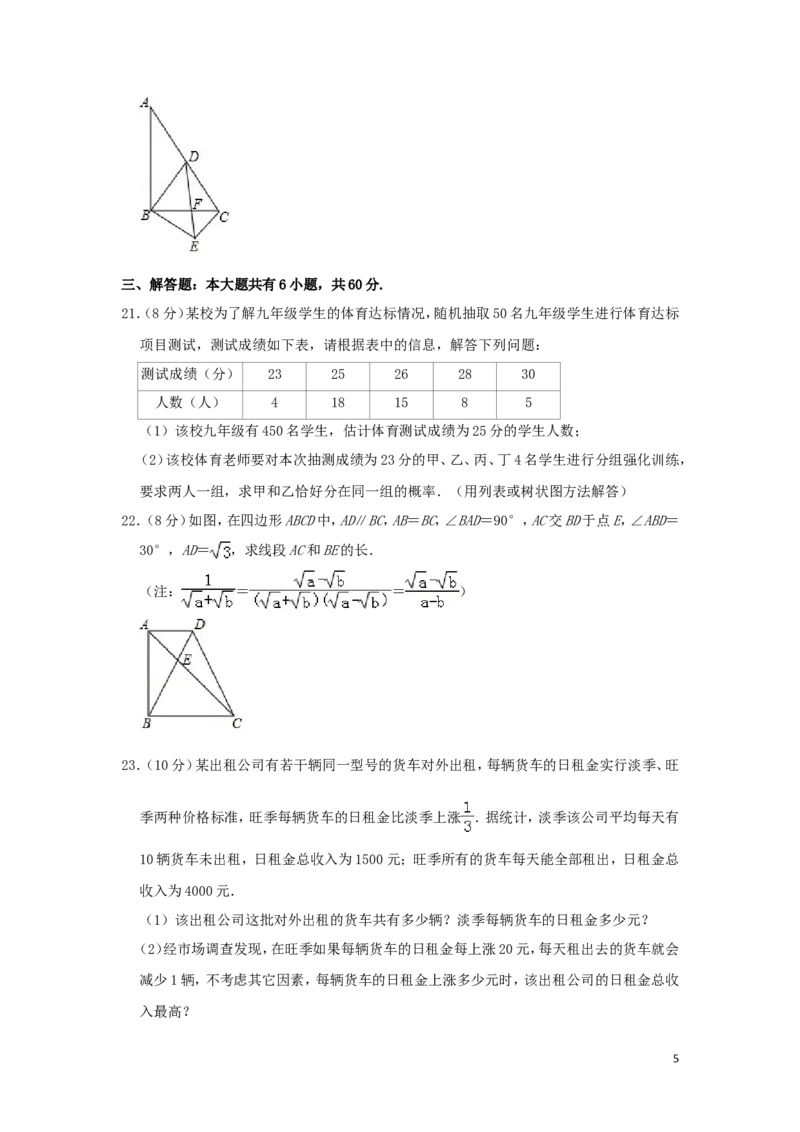
22.(8分)如图,在四边形ABCD中,AD∥BC,AB=BC,∠BAD=90°,AC交BD于点E,∠ABD=
30°,AD= ,求线段AC和BE的长.
(注: = = )
23.(10分)某出租公司有若干辆同一型号的货车对外出租,每辆货车的日租金实行淡季、旺
季两种价格标准,旺季每辆货车的日租金比淡季上涨 .据统计,淡季该公司平均每天有
10辆货车未出租,日租金总收入为1500元;旺季所有的货车每天能全部租出,日租金总
收入为4000元.
(1)该出租公司这批对外出租的货车共有多少辆?淡季每辆货车的日租金多少元?
(2)经市场调查发现,在旺季如果每辆货车的日租金每上涨20元,每天租出去的货车就会
减少1辆,不考虑其它因素,每辆货车的日租金上涨多少元时,该出租公司的日租金总收
入最高?
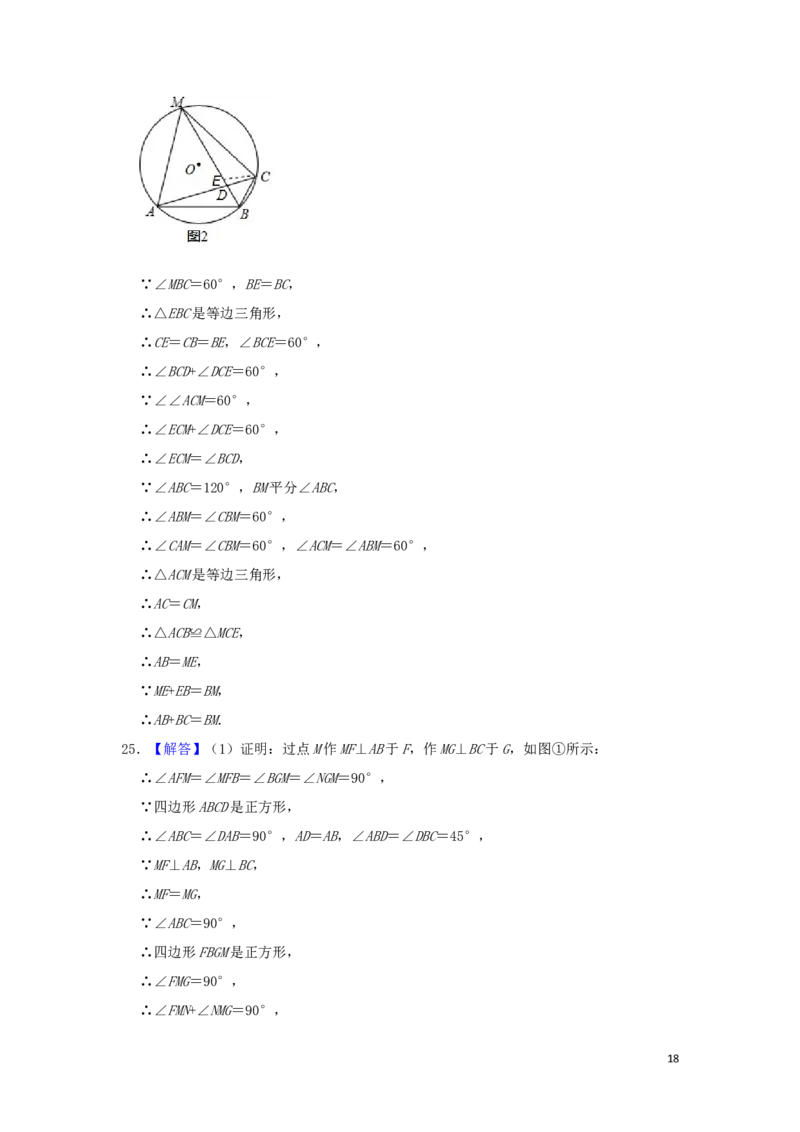
524.(10分)如图,在⊙O中,B是⊙O上的一点,∠ABC=120°,弦AC=2 ,弦BM平分∠ABC
交AC于点D,连接MA,MC.
(1)求⊙O半径的长;
(2)求证:AB+BC=BM.
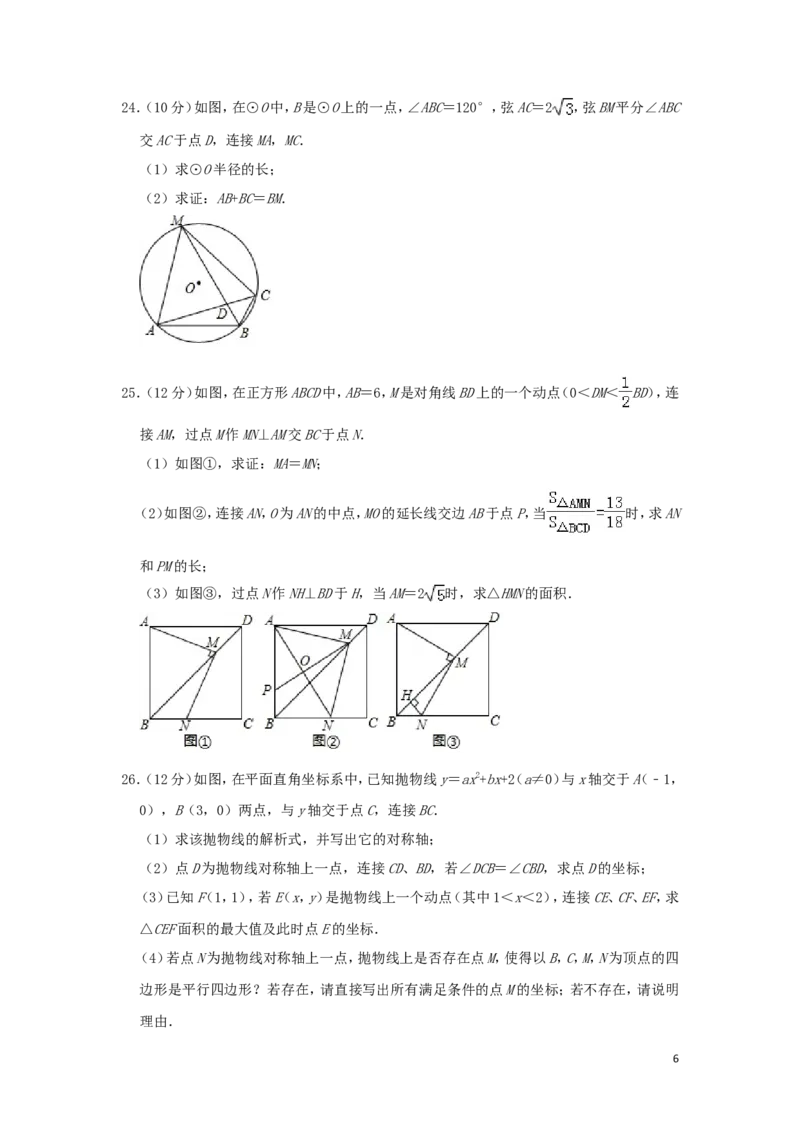
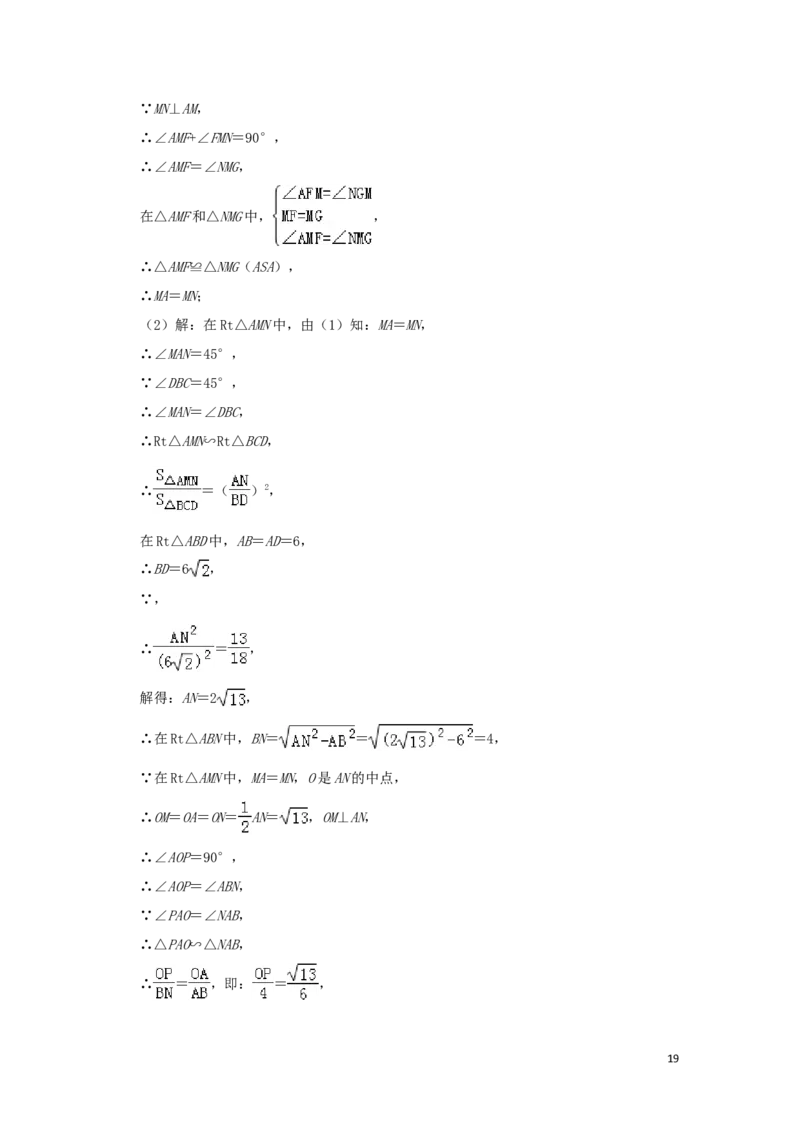
25.(12分)如图,在正方形ABCD中,AB=6,M是对角线BD上的一个动点(0<DM< BD),连
接AM,过点M作MN⊥AM交BC于点N.
(1)如图①,求证:MA=MN;
(2)如图②,连接AN,O为AN的中点,MO的延长线交边AB于点P,当 时,求AN
和PM的长;
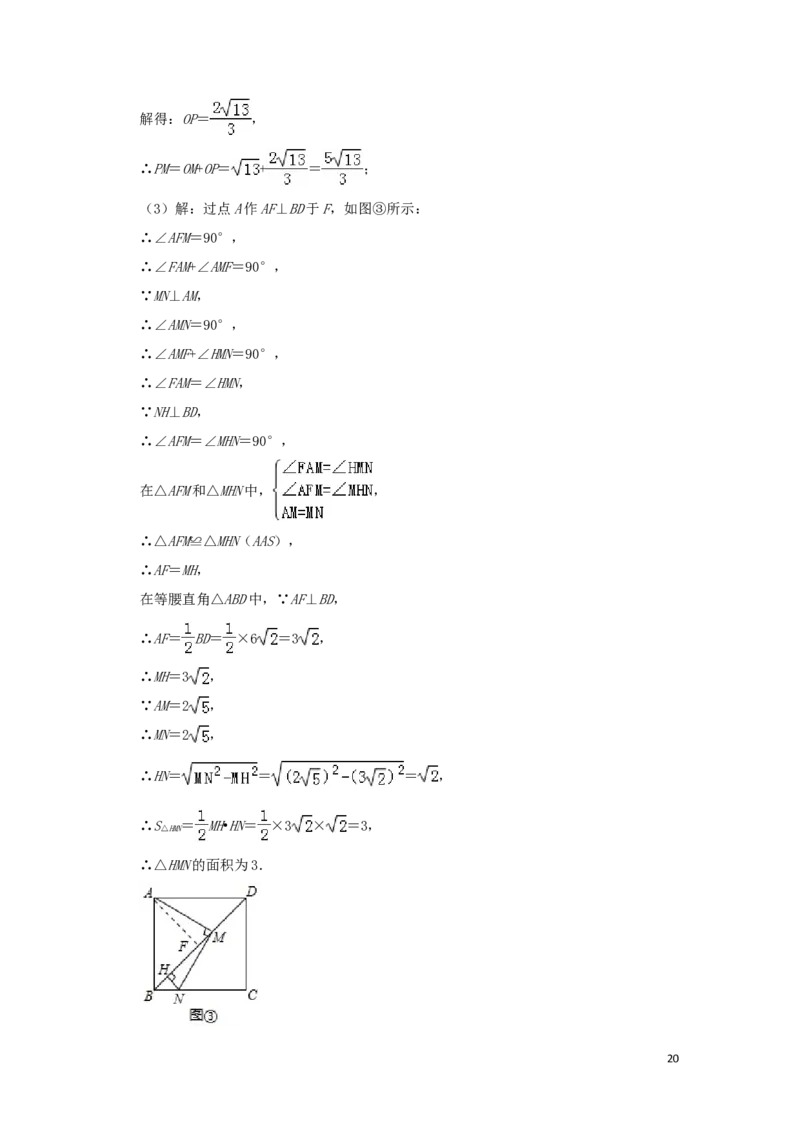
(3)如图③,过点N作NH⊥BD于H,当AM=2 时,求△HMN的面积.
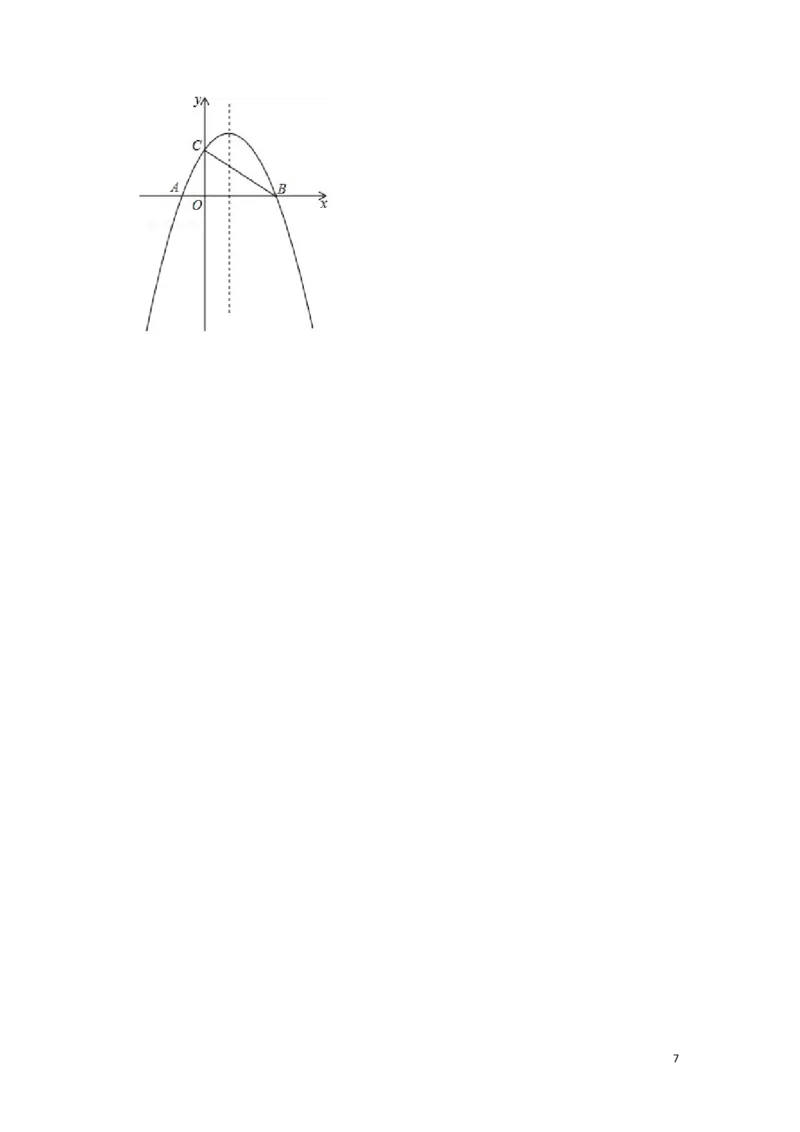
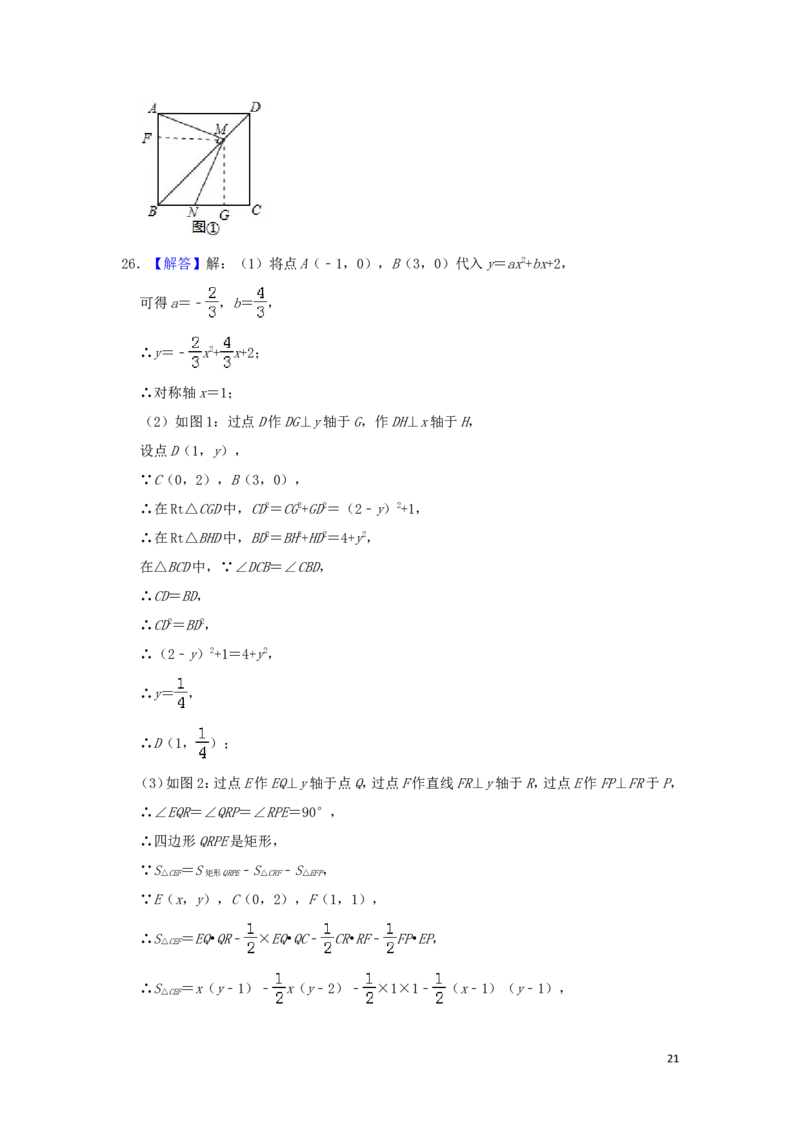
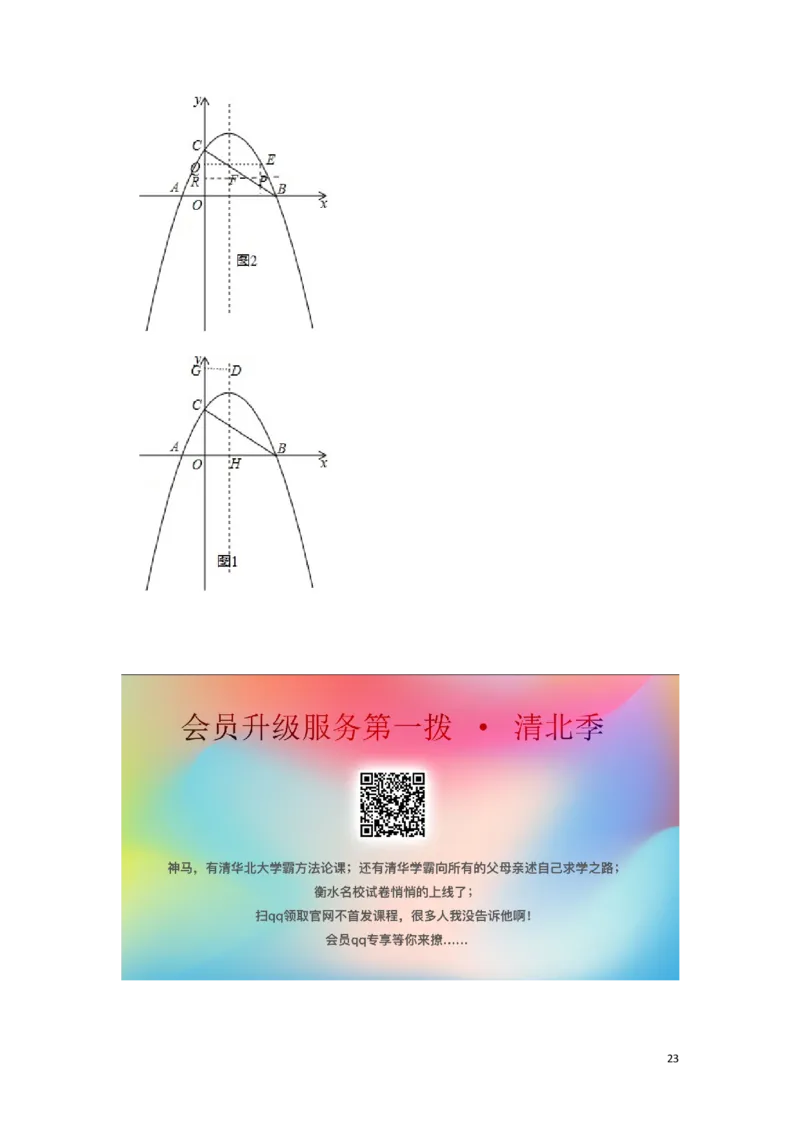
26.(12分)如图,在平面直角坐标系中,已知抛物线y=ax2+bx+2(a≠0)与x轴交于A(﹣1,
0),B(3,0)两点,与y轴交于点C,连接BC.
(1)求该抛物线的解析式,并写出它的对称轴;
(2)点D为抛物线对称轴上一点,连接CD、BD,若∠DCB=∠CBD,求点D的坐标;
(3)已知F(1,1),若E(x,y)是抛物线上一个动点(其中1<x<2),连接CE、CF、EF,求
△CEF面积的最大值及此时点E的坐标.
(4)若点N为抛物线对称轴上一点,抛物线上是否存在点M,使得以B,C,M,N为顶点的四
边形是平行四边形?若存在,请直接写出所有满足条件的点M的坐标;若不存在,请说明
理由.
672019年内蒙古包头市中考数学试卷
参考答案与试题解析
一、选择题:本大题共12小题,每小题3分,共36分.
1.【解答】解:原式=3+3=6.
故选:D.
2.【解答】解:∵﹣3<a<﹣2,1<b<2,∴答案A错误;
∵a<0<b,且|a|>|b|,∴a+b<0,∴a<﹣b,∴答案B错误;
∴﹣a>b,故选项C正确,选项D错误.
故选:C.
3.【解答】解:∵这组数据的众数4,
∴x=4,
将数据从小到大排列为:2,3,4,4,5,6,7,9
则中位数为:4.5.
故选:B.
4.【解答】解:由三视图可知圆柱的底面直径为4,高为6,
∴底面半径为2,
∴V=πr2h=22×6•π=24π,
故选:B.
5.【解答】解:根据题意得,
,
解得,x≥﹣1,且x≠2.
故选:D.
6.【解答】解:A、立方根等于它本身的数一定是±1和0,故错误;
B、顺次连接菱形四边中点得到的四边形是矩形,故正确;
C、在函数y=kx+b(k≠0)中,当k>0时,y的值随着x值的增大而增大,故错误;
D、在同圆或等圆中,如果两个圆周角相等,那么它们所对的弧长一定相等,故错误.
故选:B.
7.【解答】解:由作法得AG平分∠BAC,
∴G点到AC的距离等于BG的长,即G点到AC的距离为1,
所以△ACG的面积= ×4×1=2.
8故选:C.
8.【解答】解:连接CD,
∵BC是半圆的直径,
∴CD⊥AB,
∵在Rt△ABC中,∠ACB=90°,AC=BC=2 ,
∴△ACB是等腰直角三角形,
∴CD=BD,
∴阴影部分的面积= ×2 2 =2,
故选:D.
9.【解答】解:若x2+kx+ 是完全平方式,则k=±1,所以①错误;
若A(2,6),B(0,4),P(1,m)三点在同一直线上,而直线AB的解析式为y=x+4,则x=1
时,m=5,所以②正确;
等腰三角形底边上的中线所在的直线是它的对称轴,所以③错误;
一个多边形的内角和是它的外角和的2倍,则这个多边形是六边形,所以④正确.
故选:B.
10.【解答】解:当a=4时,b<8,
∵a、b是关于x的一元二次方程x2﹣12x+m+2=0的两根,
∴4+b=12,
∴b=8不符合;
当b=4时,a<8,
∵a、b是关于x的一元二次方程x2﹣12x+m+2=0的两根,
∴4+a=12,
∴a=8不符合;
当a=b时,
∵a、b是关于x的一元二次方程x2﹣12x+m+2=0的两根,
∴12=2a=2b,
9∴a=b=6,
∴m+2=36,
∴m=34;
故选:A.
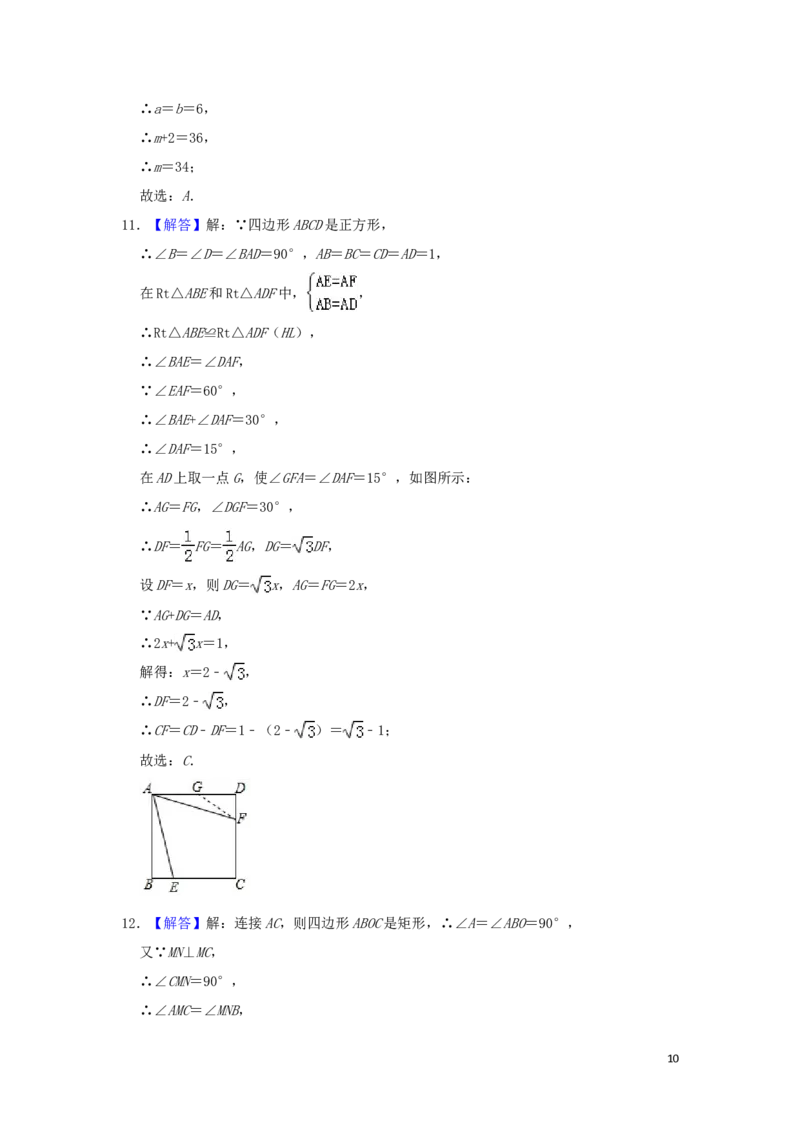
11.【解答】解:∵四边形ABCD是正方形,
∴∠B=∠D=∠BAD=90°,AB=BC=CD=AD=1,
在Rt△ABE和Rt△ADF中, ,
∴Rt△ABE≌Rt△ADF(HL),
∴∠BAE=∠DAF,
∵∠EAF=60°,
∴∠BAE+∠DAF=30°,
∴∠DAF=15°,
在AD上取一点G,使∠GFA=∠DAF=15°,如图所示:
∴AG=FG,∠DGF=30°,
∴DF= FG= AG,DG= DF,
设DF=x,则DG= x,AG=FG=2x,
∵AG+DG=AD,
∴2x+ x=1,
解得:x=2﹣ ,
∴DF=2﹣ ,
∴CF=CD﹣DF=1﹣(2﹣ )= ﹣1;
故选:C.
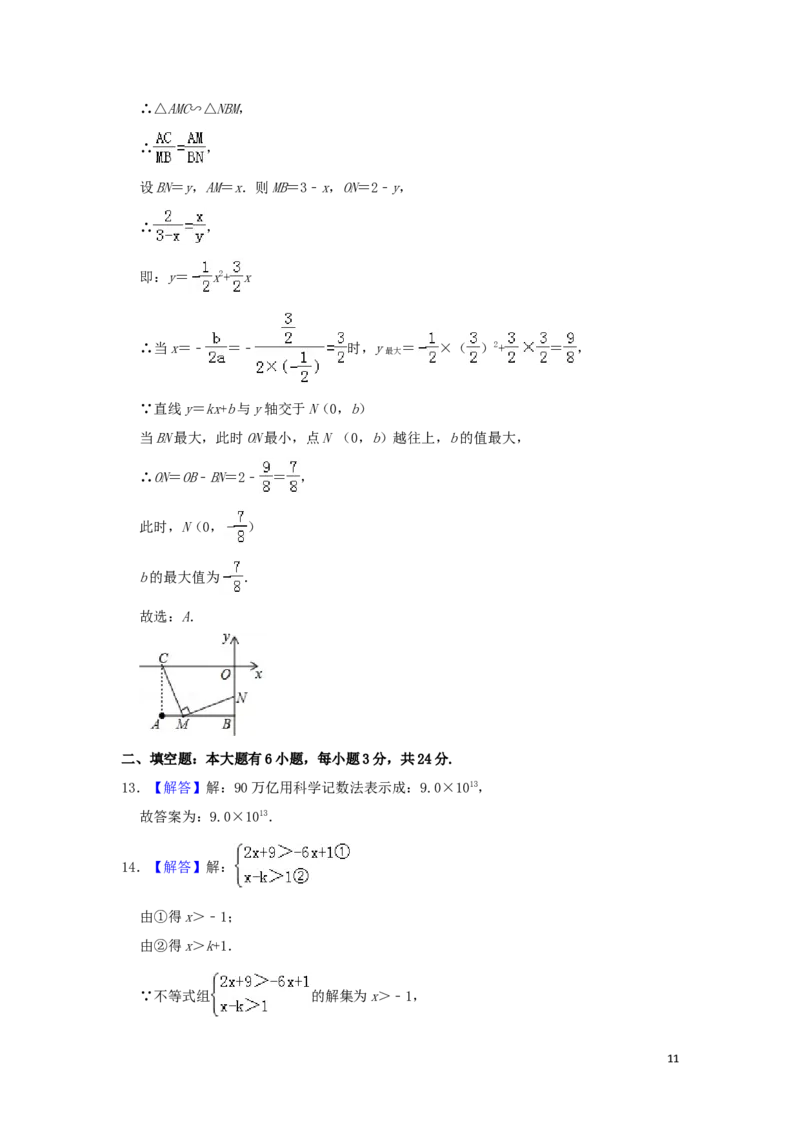
12.【解答】解:连接AC,则四边形ABOC是矩形,∴∠A=∠ABO=90°,
又∵MN⊥MC,
∴∠CMN=90°,
∴∠AMC=∠MNB,
10∴△AMC∽△NBM,
∴ ,
设BN=y,AM=x.则MB=3﹣x,ON=2﹣y,
∴ ,
即:y= x2+ x
∴当x=﹣ =﹣ 时,y = ×( )2+ = ,
最大
∵直线y=kx+b与y轴交于N(0,b)
当BN最大,此时ON最小,点N (0,b)越往上,b的值最大,
∴ON=OB﹣BN=2﹣ = ,
此时,N(0, )
b的最大值为 .
故选:A.
二、填空题:本大题有6小题,每小题3分,共24分.
13.【解答】解:90万亿用科学记数法表示成:9.0×1013,
故答案为:9.0×1013.
14.【解答】解:
由①得x>﹣1;
由②得x>k+1.
∵不等式组 的解集为x>﹣1,
11∴k+1≤﹣1,
解得k≤﹣2.
故答案为k≤﹣2.
15.【解答】解:1﹣ ÷ =1﹣ • =1﹣ =﹣ ,
故答案为:﹣ .
16.【解答】解:由表格可知,甲、乙两班学生的成绩平均成绩相同;
根据中位数可以确定,乙班优秀的人数少于甲班优秀的人数;
根据方差可知,甲班成绩的波动性比乙班小.
故①②③正确,
故答案为:①②③.
17.【解答】解:由旋转的性质可知:AE=AC,∠CAE=70°,
∴∠ACE=∠AEC=55°,
又∵∠AED=∠ACB,∠CAB=55°,∠ABC=25°,
∴∠ACB=∠AED=100°,
∴∠DEC=100°﹣55°=45°,
∴tan∠DEC=tan45°=1,
故答案为:1
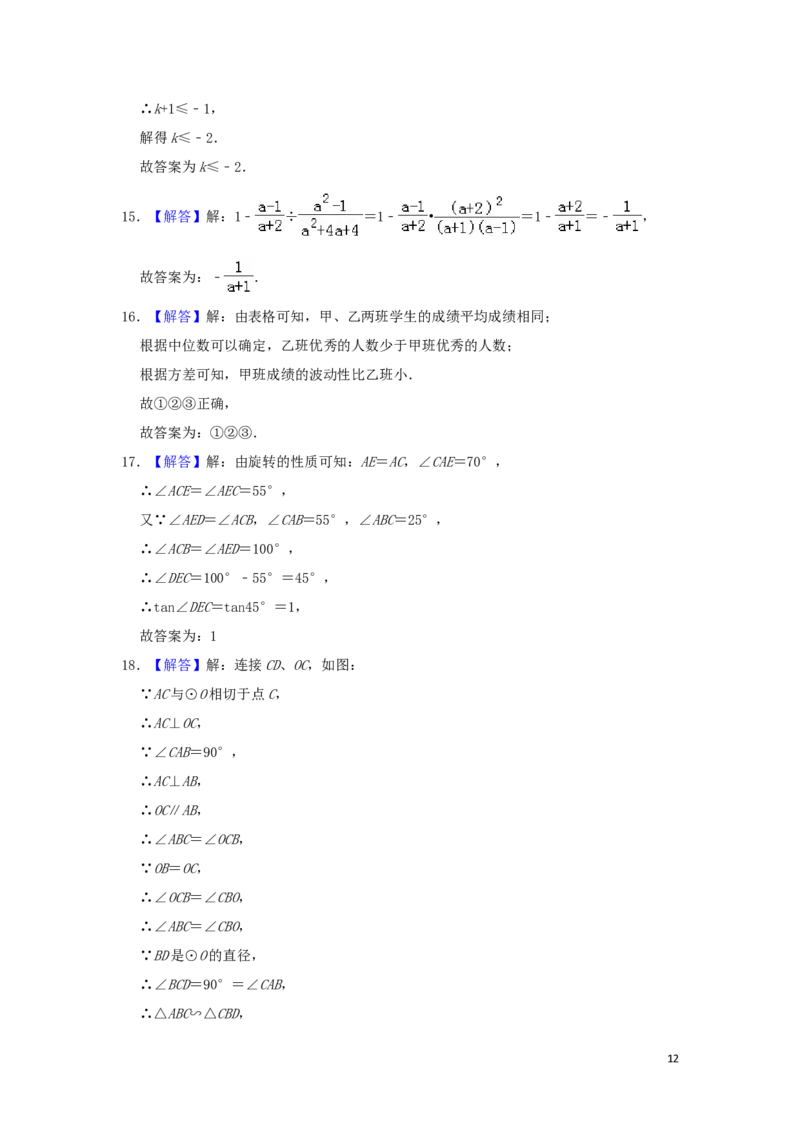
18.【解答】解:连接CD、OC,如图:
∵AC与⊙O相切于点C,
∴AC⊥OC,
∵∠CAB=90°,
∴AC⊥AB,
∴OC∥AB,
∴∠ABC=∠OCB,
∵OB=OC,
∴∠OCB=∠CBO,
∴∠ABC=∠CBO,
∵BD是⊙O的直径,
∴∠BCD=90°=∠CAB,
∴△ABC∽△CBD,
12∴ = ,
∴BC2=AB×BD=4×6=24,
∴BC= =2 ;
故答案为:2 .
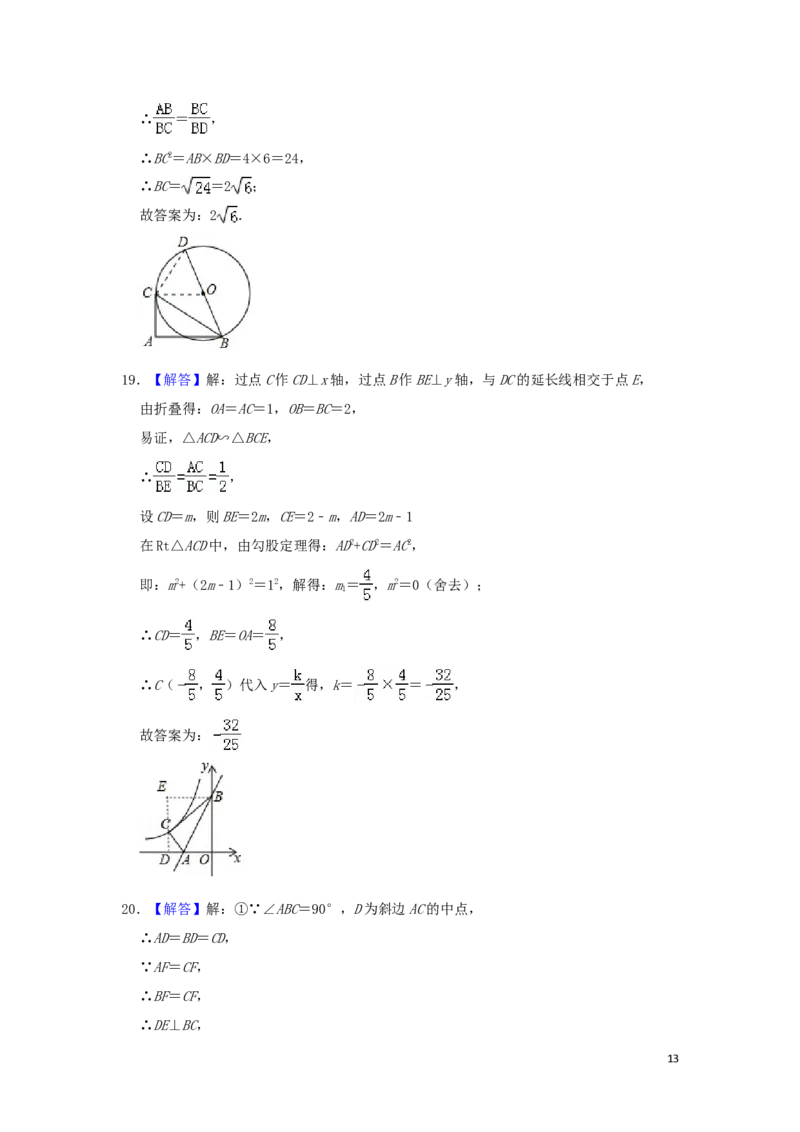
19.【解答】解:过点C作CD⊥x轴,过点B作BE⊥y轴,与DC的延长线相交于点E,
由折叠得:OA=AC=1,OB=BC=2,
易证,△ACD∽△BCE,
∴ ,
设CD=m,则BE=2m,CE=2﹣m,AD=2m﹣1
在Rt△ACD中,由勾股定理得:AD2+CD2=AC2,
即:m2+(2m﹣1)2=12,解得:m= ,m2=0(舍去);
1
∴CD= ,BE=OA= ,
∴C( , )代入y= 得,k= = ,
故答案为:
20.【解答】解:①∵∠ABC=90°,D为斜边AC的中点,
∴AD=BD=CD,
∵AF=CF,
∴BF=CF,
∴DE⊥BC,
13∴BE=CE,∵
∵BE⊥BD,
∴BD2+BE2=DE2,
∴CE2+AD2=DE2,
故①正确;
②∵AB=4,BC=3,
∴AC= ,
∴ ,
∵∠A=∠BDE,∠ABC=∠DBE=90°,
∴△ABC∽△DBE,
∴ ,
即 .
∴BE= ,
∵AD=BD,
∴∠A=∠ABD,
∵∠A=∠BDE,∠BDC=∠A+∠ABD,
∴∠A=∠CDE,
∴DE∥AB,
∴DE⊥BC,
∵BD=CD,
∴DE垂直平分BC,
∴BE=CE,
∴CE= ,
故②正确;
③∵∠ABC=∠DBE=90°,
∴∠ABD=∠CBE,
14∵ ,
但随着F点运动,BE的长度会改变,而BC=3,
∴ 或 不一定等于 ,
∴△ABD和△CBE不一定相似,
故③错误;
④∵∠A=30°,BC=3,
∴∠A=∠ABD=∠CBE=30°,AC=2BC=6,
∴BD= ,
∵BC=3,∠BCE=90°,
∴BE= ,
∵∴ ,
故④正确;
故答案为:①②④.
三、解答题:本大题共有6小题,共60分.
21.【解答】解:(1)450× =162(人),
答:该校九年级有450名学生,估计体育测试成绩为25分的学生人数为162人;
(2)画树状图如图:
共有12个等可能的结果,甲和乙恰好分在同一组的结果有2个,
∴甲和乙恰好分在同一组的概率为 = .
22.【解答】解:在Rt△ABD中
∵∠BAD=90°,∠ABD=30°,AD= ,
∴tan∠ABD= ,
15∴ = ,
∴AB=3,
∵AD∥BC,
∴∠BAD+∠ABC=180°,
∴∠ABC=90°,
在Rt△ABC中,∵AB=BC=3,
∴AC= =3 ,
∵AD∥BC,
∴△ADE∽△CBE,
∴ = ,
∴ = ,
设DE= x,则BE=3x,
∴BD=DE+BE=( +3)x,
∴ = ,
∵在Rt△ABD中,∠ABD=30°,
∴BD=2AD=2 ,
∴DE=2 × ,
∴DE=3﹣ ,
∴BE= (3﹣ )=3 ﹣3.
23.【解答】解:(1)该出租公司这批对外出租的货车共有x辆,
根据题意得, ,
解得:x=20,
16经检验:x=20是分式方程的根,
∴1500÷(20﹣10)=150(元),
答:该出租公司这批对外出租的货车共有20辆,淡季每辆货车的日租金150元;
(2)设每辆货车的日租金上涨a元时,该出租公司的日租金总收入为W元,
根据题意得,W=[a+150×(1+ )]×(20﹣ ),
∴W=﹣ a2+10a+4000=﹣ (a﹣100)2+4500,
∵﹣ <0,
∴当a=100时,W有最大值,
答:每辆货车的日租金上涨100元时,该出租公司的日租金总收入最高.
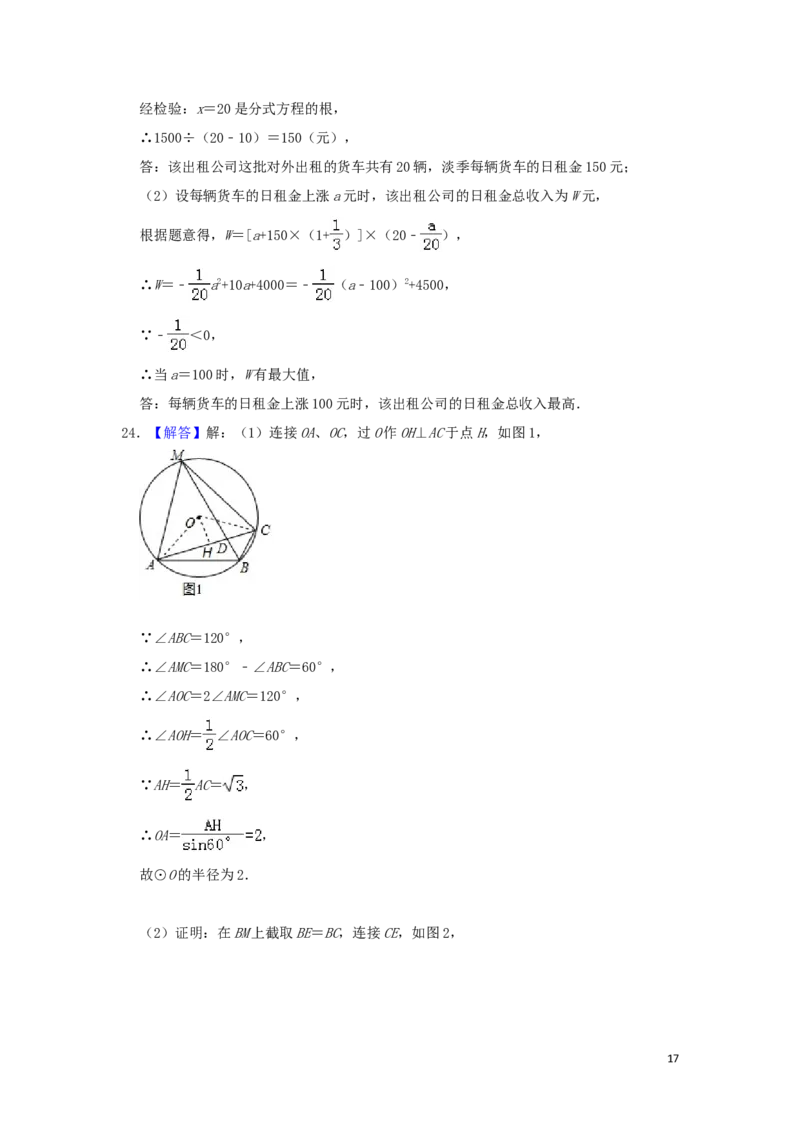
24.【解答】解:(1)连接OA、OC,过O作OH⊥AC于点H,如图1,
∵∠ABC=120°,
∴∠AMC=180°﹣∠ABC=60°,
∴∠AOC=2∠AMC=120°,
∴∠AOH= ∠AOC=60°,
∵AH= AC= ,
∴OA= ,
故⊙O的半径为2.
(2)证明:在BM上截取BE=BC,连接CE,如图2,
17∵∠MBC=60°,BE=BC,
∴△EBC是等边三角形,
∴CE=CB=BE,∠BCE=60°,
∴∠BCD+∠DCE=60°,
∵∠∠ACM=60°,
∴∠ECM+∠DCE=60°,
∴∠ECM=∠BCD,
∵∠ABC=120°,BM平分∠ABC,
∴∠ABM=∠CBM=60°,
∴∠CAM=∠CBM=60°,∠ACM=∠ABM=60°,
∴△ACM是等边三角形,
∴AC=CM,
∴△ACB≌△MCE,
∴AB=ME,
∵ME+EB=BM,
∴AB+BC=BM.
25.【解答】(1)证明:过点M作MF⊥AB于F,作MG⊥BC于G,如图①所示:
∴∠AFM=∠MFB=∠BGM=∠NGM=90°,
∵四边形ABCD是正方形,
∴∠ABC=∠DAB=90°,AD=AB,∠ABD=∠DBC=45°,
∵MF⊥AB,MG⊥BC,
∴MF=MG,
∵∠ABC=90°,
∴四边形FBGM是正方形,
∴∠FMG=90°,
∴∠FMN+∠NMG=90°,
18∵MN⊥AM,
∴∠AMF+∠FMN=90°,
∴∠AMF=∠NMG,
在△AMF和△NMG中, ,
∴△AMF≌△NMG(ASA),
∴MA=MN;
(2)解:在Rt△AMN中,由(1)知:MA=MN,
∴∠MAN=45°,
∵∠DBC=45°,
∴∠MAN=∠DBC,
∴Rt△AMN∽Rt△BCD,
∴ =( )2,
在Rt△ABD中,AB=AD=6,
∴BD=6 ,
∵,
∴ = ,
解得:AN=2 ,
∴在Rt△ABN中,BN= = =4,
∵在Rt△AMN中,MA=MN,O是AN的中点,
∴OM=OA=ON= AN= ,OM⊥AN,
∴∠AOP=90°,
∴∠AOP=∠ABN,
∵∠PAO=∠NAB,
∴△PAO∽△NAB,
∴ = ,即: = ,
19解得:OP= ,
∴PM=OM+OP= + = ;
(3)解:过点A作AF⊥BD于F,如图③所示:
∴∠AFM=90°,
∴∠FAM+∠AMF=90°,
∵MN⊥AM,
∴∠AMN=90°,
∴∠AMF+∠HMN=90°,
∴∠FAM=∠HMN,
∵NH⊥BD,
∴∠AFM=∠MHN=90°,
在△AFM和△MHN中, ,
∴△AFM≌△MHN(AAS),
∴AF=MH,
在等腰直角△ABD中,∵AF⊥BD,
∴AF= BD= ×6 =3 ,
∴MH=3 ,
∵AM=2 ,
∴MN=2 ,
∴HN= = = ,
∴S = MH•HN= ×3 × =3,
△HMN
∴△HMN的面积为3.
2026.【解答】解:(1)将点A(﹣1,0),B(3,0)代入y=ax2+bx+2,
可得a=﹣ ,b= ,
∴y=﹣ x2+ x+2;
∴对称轴x=1;
(2)如图1:过点D作DG⊥y轴于G,作DH⊥x轴于H,
设点D(1,y),
∵C(0,2),B(3,0),
∴在Rt△CGD中,CD2=CG2+GD2=(2﹣y)2+1,
∴在Rt△BHD中,BD2=BH2+HD2=4+y2,
在△BCD中,∵∠DCB=∠CBD,
∴CD=BD,
∴CD2=BD2,
∴(2﹣y)2+1=4+y2,
∴y= ,
∴D(1, );
(3)如图2:过点E作EQ⊥y轴于点Q,过点F作直线FR⊥y轴于R,过点E作FP⊥FR于P,
∴∠EQR=∠QRP=∠RPE=90°,
∴四边形QRPE是矩形,
∵S =S ﹣S ﹣S ,
△CEF 矩形QRPE △CRF △EFP
∵E(x,y),C(0,2),F(1,1),
∴S =EQ•QR﹣ ×EQ•QC﹣ CR•RF﹣ FP•EP,
△CEF
∴S =x(y﹣1)﹣ x(y﹣2)﹣ ×1×1﹣ (x﹣1)(y﹣1),
△CEF
21∵y=﹣ x2+ x+2,
∴S =﹣ x2+ x,
△CEF
∴当x= 时,面积有最大值是 ,
此时E( , );
(4)存在点M使得以B,C,M,N为顶点的四边形是平行四边形,
设N(1,n),M(x,y),
①四边形CMNB是平行四边形时,
= ,
∴x=﹣2,
∴M(﹣2,﹣ );
②四边形CNBM时平行四边形时,
= ,
∴x=2,
∴M(2,2);
③四边形CNNB时平行四边形时,
= ,
∴x=4,
∴M(4,﹣ );
综上所述:M(2,2)或M(4,﹣ )或M(﹣2,﹣ );
2223