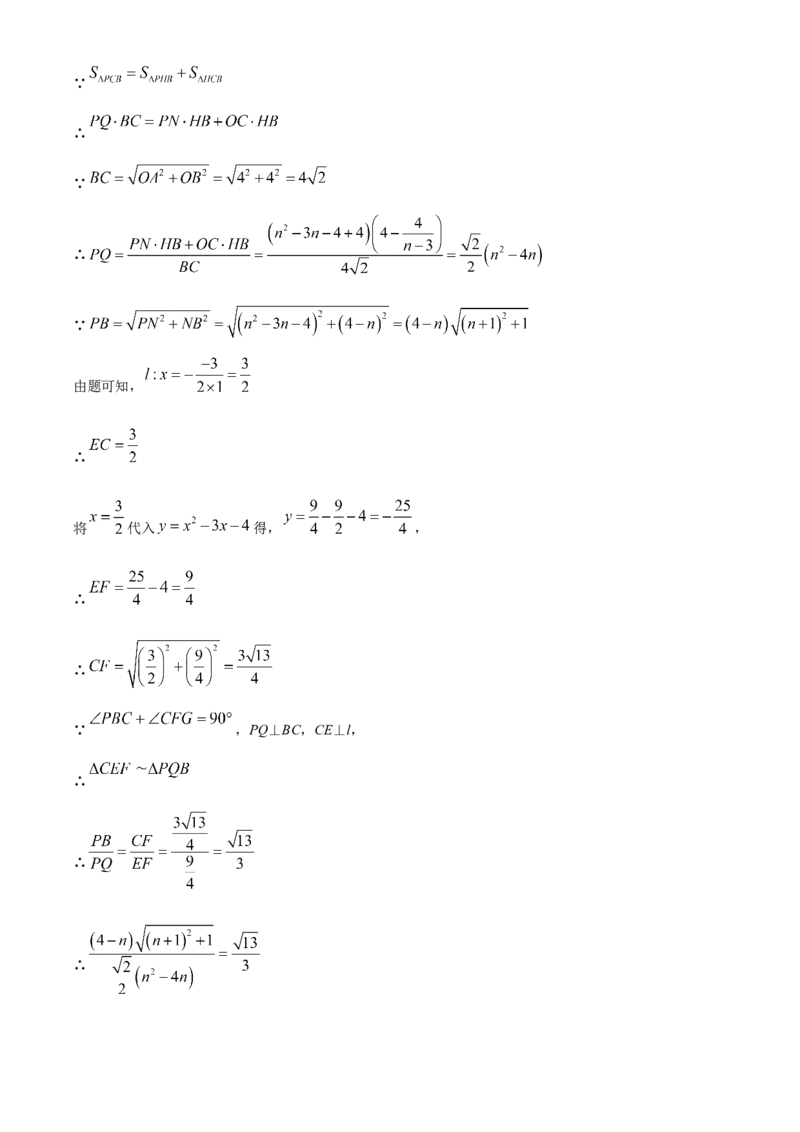文档内容
数学试卷
(本试卷共26道题 满分150分 考试时间120分钟)
注意:所有试题必须在答题卡上作答,在本试卷上作答无效。
第一部分 选择题(共30分)
一、选择题(本题包括10小题,每小题3分,共30分。在每小题给出的四个选项中,只有
一项符合题目要求)
1. 的倒数是( )
A. B. C. D. 6
【答案】A
【解析】
【分析】根据互为倒数两个数的乘积等于1进行解答即可得.
【详解】解: 的倒数是 .
故选A.
【点睛】本题考查了倒数的定义,熟练掌握倒数的定义是解题的关键.
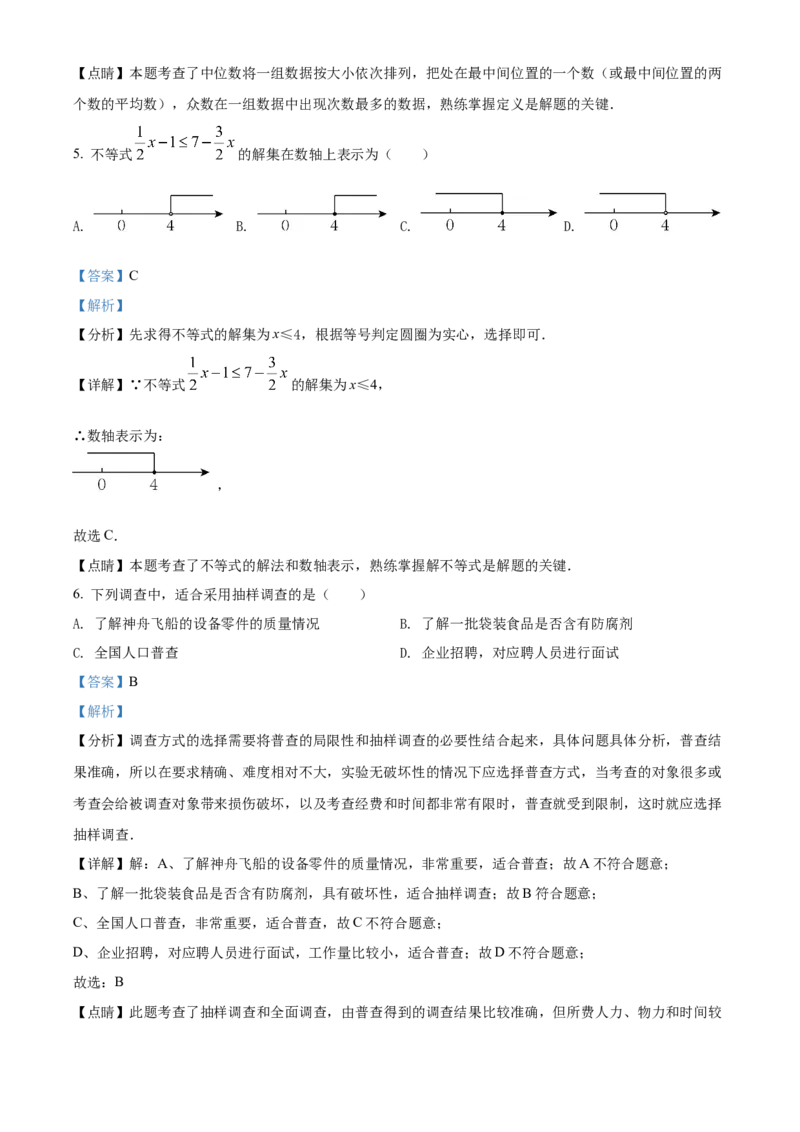
2. 如图是某几何体的三视图,该几何体是( )
A. B. C. D.
【答案】C
【解析】
【分析】由主视图和左视图确定是柱体,锥体还是球体,再由俯视图确定具体形状.
【详解】解:主视图和左视图都是等腰三角形,那么此几何体为锥体,由俯视图为圆,可得此几何体是圆
锥.
故选:C.【点睛】本题考查了由三视图判断几何体,主视图和左视图的大致轮廓为三角形的几何体为锥体.
3. 下列运算正确的是( )
A. B. C. D.
【答案】B
【解析】
【分析】由同底数幂乘法、积的乘方、负整数指数幂的乘法、合并同类项,分别进行判断,即可得到答案.
【详解】解: ,故A错误;
,故B正确;
,故C错误;
不能合并,不D错误;
故选:B.
【点睛】本题考查了同底数幂乘法、积的乘方、负整数指数幂的乘法、合并同类项,解题的关键是掌握运
算法则,正确的进行判断.
4. 某校开展安全知识竞赛,进入决赛的学生有20名,他们的决赛成绩如下表所示:
10
决赛成绩/分 99 98 97
0
人数 3 7 6 4
则这20名学生决赛成绩的中位数和众数分别是( )
A. 98,98 B. 98.99 C. 98.5,98 D. 98.5,99
【答案】D
【解析】
【分析】根据众数,中位数的定义计算选择即可.
【详解】∵99出现的次数最多,7次,
∴众数为99;
∵中位数是第10个,11个数据的平均数即 ,
故选D.【点睛】本题考查了中位数将一组数据按大小依次排列,把处在最中间位置的一个数(或最中间位置的两
个数的平均数),众数在一组数据中出现次数最多的数据,熟练掌握定义是解题的关键.
5. 不等式 的解集在数轴上表示为( )
A. B. C. D.
【答案】C
【解析】
【分析】先求得不等式的解集为x≤4,根据等号判定圆圈为实心,选择即可.
【详解】∵不等式 的解集为x≤4,
∴数轴表示为:
,
故选C.
【点睛】本题考查了不等式的解法和数轴表示,熟练掌握解不等式是解题的关键.
6. 下列调查中,适合采用抽样调查的是( )
A. 了解神舟飞船的设备零件的质量情况 B. 了解一批袋装食品是否含有防腐剂
C. 全国人口普查 D. 企业招聘,对应聘人员进行面试
【答案】B
【解析】
【分析】调查方式的选择需要将普查的局限性和抽样调查的必要性结合起来,具体问题具体分析,普查结
果准确,所以在要求精确、难度相对不大,实验无破坏性的情况下应选择普查方式,当考查的对象很多或
考查会给被调查对象带来损伤破坏,以及考查经费和时间都非常有限时,普查就受到限制,这时就应选择
抽样调查.
【详解】解:A、了解神舟飞船的设备零件的质量情况,非常重要,适合普查;故A不符合题意;
B、了解一批袋装食品是否含有防腐剂,具有破坏性,适合抽样调查;故B符合题意;
C、全国人口普查,非常重要,适合普查,故C不符合题意;
D、企业招聘,对应聘人员进行面试,工作量比较小,适合普查;故D不符合题意;
故选:B
【点睛】此题考查了抽样调查和全面调查,由普查得到的调查结果比较准确,但所费人力、物力和时间较多,而抽样调查得到的调查结果比较近似.
7. 下列命题不正确的是( )
A. 经过直线外一点,有且只有一条直线与这条直线平行
B. 负数的立方根是负数
C. 对角线互相垂直的四边形是菱形
D. 五边形的外角和是
【答案】C
【解析】
【分析】由平行线公理、立方根的定义、菱形的判定定理、多边形的外角和,分别进行判断,即可得到答
案.
【详解】解:A、经过直线外一点,有且只有一条直线与这条直线平行;故A正确;
B、负数的立方根是负数;故B正确;
C、对角线互相垂直的平行四边形是菱形,故C错误;
D、五边形的外角和是 ,故D正确;
故选:C
【点睛】本题考查了判断命题的真假,以及考查了平行线公理、立方根的定义、菱形的判定定理、多边形
的外角和,解题的关键是掌握所学的知识,正确的进行判断.
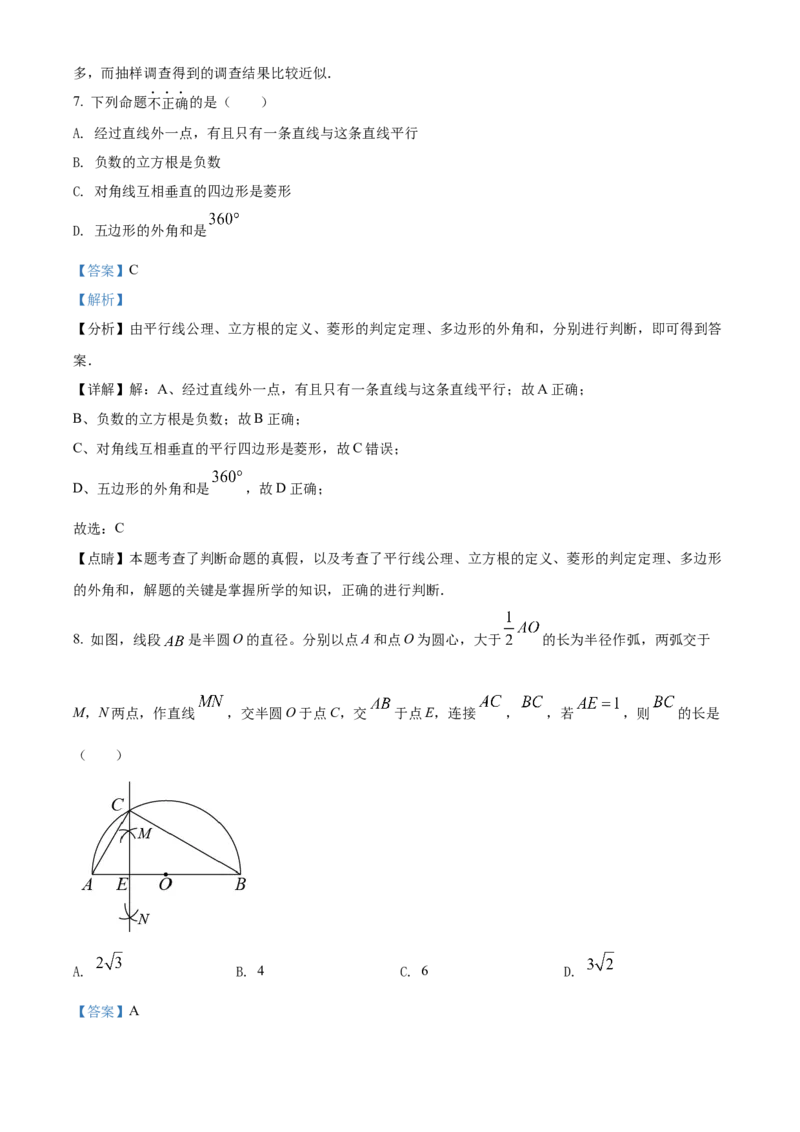
8. 如图,线段 是半圆O的直径。分别以点A和点O为圆心,大于 的长为半径作弧,两弧交于
M,N两点,作直线 ,交半圆O于点C,交 于点E,连接 , ,若 ,则 的长是
( )
A. B. 4 C. 6 D.
【答案】A【解析】
【分析】根据作图知CE垂直平分AC,即可得 , ,根据圆的半径得 ,
,根据圆周角的推论得 ,根据勾股定理即可得 .
【详解】解:根据作图知CE垂直平分AC,
∴ , ,
∴ ,
∴ ,
即 ,
∵线段AB是半圆O的直径,
∴ ,
在 中,根据勾股定理得,
,
故选A.
【点睛】本题考查了圆,勾股定理,圆周角推论,解题的关键是掌握这些知识点.
9. 《九章算术》是中国传统数学重要的著作,奠定了中国传统数学的基本框架,其中《盈不足》卷记载了
一道有趣的数学问题:“今有共买物,人出八,赢三;人出七,不足四,问人数、物价各几何?”译文:
“今有人合伙购物,每人出8钱,会多出3钱;每人出7钱,又差4钱,问人数,物价各多少?”设人数
为x人,物价为y钱,根据题意,下面所列方程组正确的是( )
A. B. C. D.
【答案】B【解析】
【分析】根据译文可知“人数×8-3=钱数和人数×7+4=钱数”即可列出方程组.
【详解】解:由题意可得, ,
故选:B.
【点睛】本题考查列二元一次方程组.解题的关键是明确题意,找出等量关系,列出相应的方程.
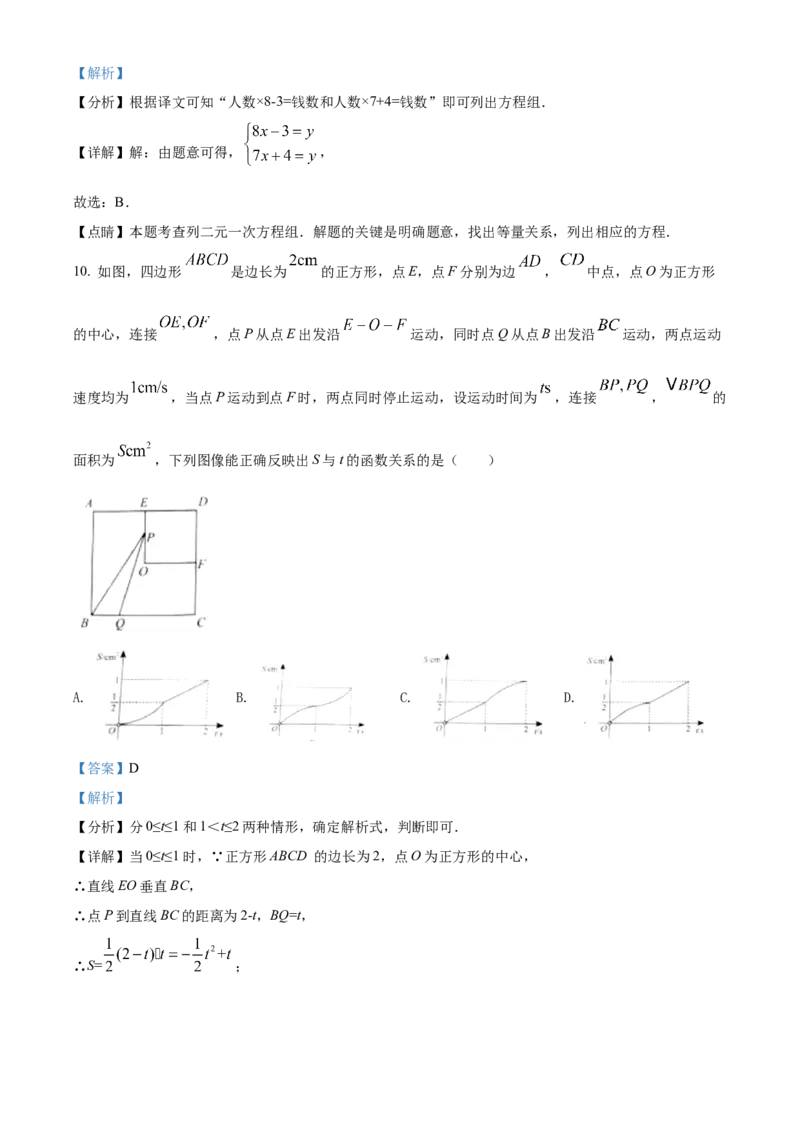
10. 如图,四边形 是边长为 的正方形,点E,点F分别为边 , 中点,点O为正方形
的中心,连接 ,点P从点E出发沿 运动,同时点Q从点B出发沿 运动,两点运动
速度均为 ,当点P运动到点F时,两点同时停止运动,设运动时间为 ,连接 , 的
面积为 ,下列图像能正确反映出S与t的函数关系的是( )
A. B. C. D.
【答案】D
【解析】
【分析】分0≤t≤1和1<t≤2两种情形,确定解析式,判断即可.
【详解】当0≤t≤1时,∵正方形ABCD 的边长为2,点O为正方形的中心,
∴直线EO垂直BC,
∴点P到直线BC的距离为2-t,BQ=t,
∴S= ;当1<t≤2时,∵正方形ABCD 的边长为2,点F分别为边 , 中点,点O为正方形的中心,
∴直线OF∥BC,
∴点P到直线BC的距离为1,BQ=t,
∴S= ;
故选D.
【点睛】本题考查了正方形的性质,二次函数的解析式,一次函数解析式,正确确定面积,从而确定解析
式是解题的关键.
第二部分 非选择题(共120分)
二、填空题(本题包括8小题,每小题3分,共24分)
11. 目前,我国基本医疗保险覆盖已超过13.5亿人,数据13.5亿用科学记数法表示为____________.
【答案】
【解析】
【分析】用移动小数点的方法确定a值,根据整数位数减一原则确定n值,最后写成 的形式即可.
【详解】∵13.5亿= ,
故答案为: .
【点睛】本题考查了科学记数法表示大数,熟练掌握把小数点点在左边第一个非零数字的后面确定a,运
用整数位数减去1确定n值是解题的关键.
12. 分解因式: ____________.
【答案】
【解析】
【分析】先提取公因数y,再利用完全平方公式进行二次分解.完全平方公式:(a±b)2=a2±2ab+b2.
【详解】解: ;
故答案为:
【点睛】本题考查了提公因式法分解因式和利用完全平方公式分解因式,难点在于需要进行二次分解因式.
13. 点 在一次函数 的图像上,当 时, ,则a的取值范围是____________.
【答案】a<2
【解析】
【分析】根据一次函数的性质,建立不等式计算即可.
【详解】∵当 时, ,
∴a-2<0,
∴a<2,
故答案为:a<2.
【点睛】本题考查了一次函数的性质,熟练掌握性质是解题的关键.
14. 若关于x的方程 有两个不相等的实数根,且 ,则从满足条件的所有整数m中随
机选取一个,恰好是负数的概率是____________.
【答案】
【解析】
【分析】根据题意,由关于x的一元二次方程的根的判别式 ,可计算 ,再结合 可知
,进而推导满足条件的所有整数为-3、-2、-1、0、1、2共计6个,其中负数有3个,由简单概
率的计算公式即可得出结果.
【详解】解:根据题意,关于x的方程 有两个不相等的实数根,
故该一元二次方程的根的判别式 ,即 ,
解得 ,
又∵ ,
∴ ,
∴满足条件的所有整数为-3、-2、-1、0、1、2共计6个,其中负数有-3、-2、-1共计3个,∴满足条件的所有整数m中随机选取一个,恰好是负数的概率是 .
故答案为: .
【点睛】本题主要考查了一元二次方程的根的判别式、简单概率计算等知识,解题关键是读懂题意,综合
运用所学知识解决问题.
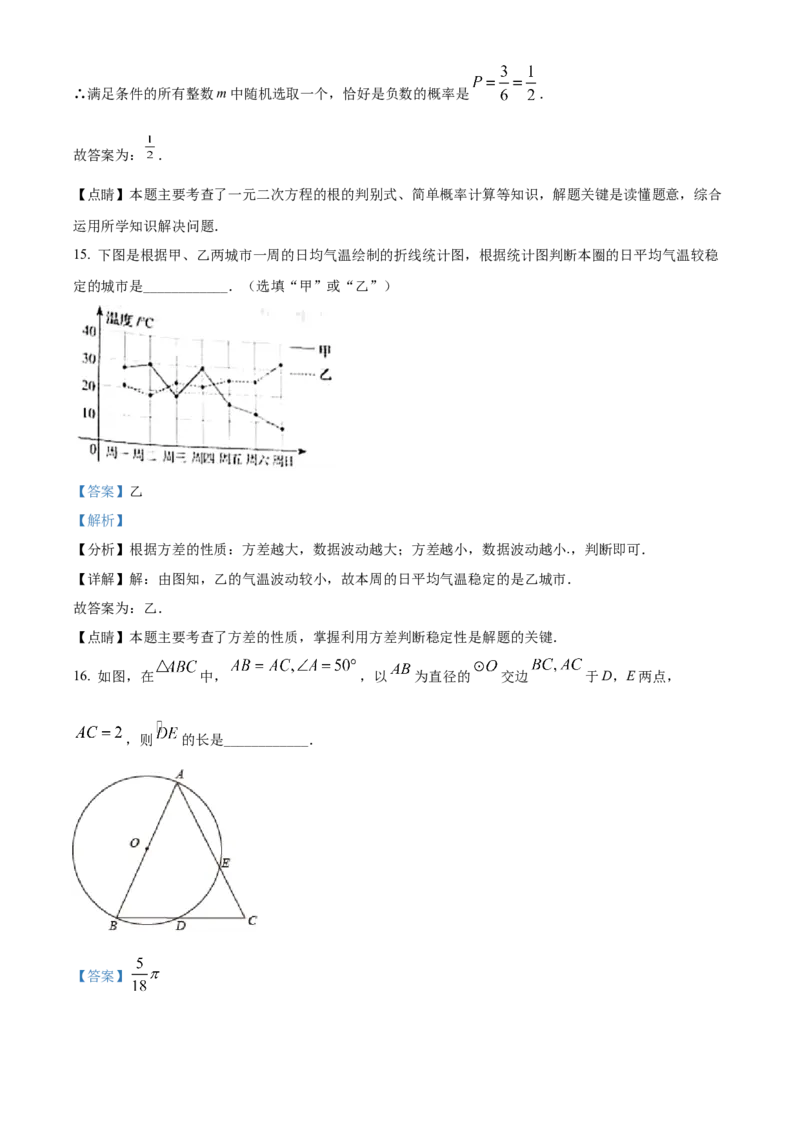
15. 下图是根据甲、乙两城市一周的日均气温绘制的折线统计图,根据统计图判断本圈的日平均气温较稳
定的城市是____________.(选填“甲”或“乙”)
【答案】乙
【解析】
【分析】根据方差的性质:方差越大,数据波动越大;方差越小,数据波动越小.,判断即可.
【详解】解:由图知,乙的气温波动较小,故本周的日平均气温稳定的是乙城市.
故答案为:乙.
【点睛】本题主要考查了方差的性质,掌握利用方差判断稳定性是解题的关键.
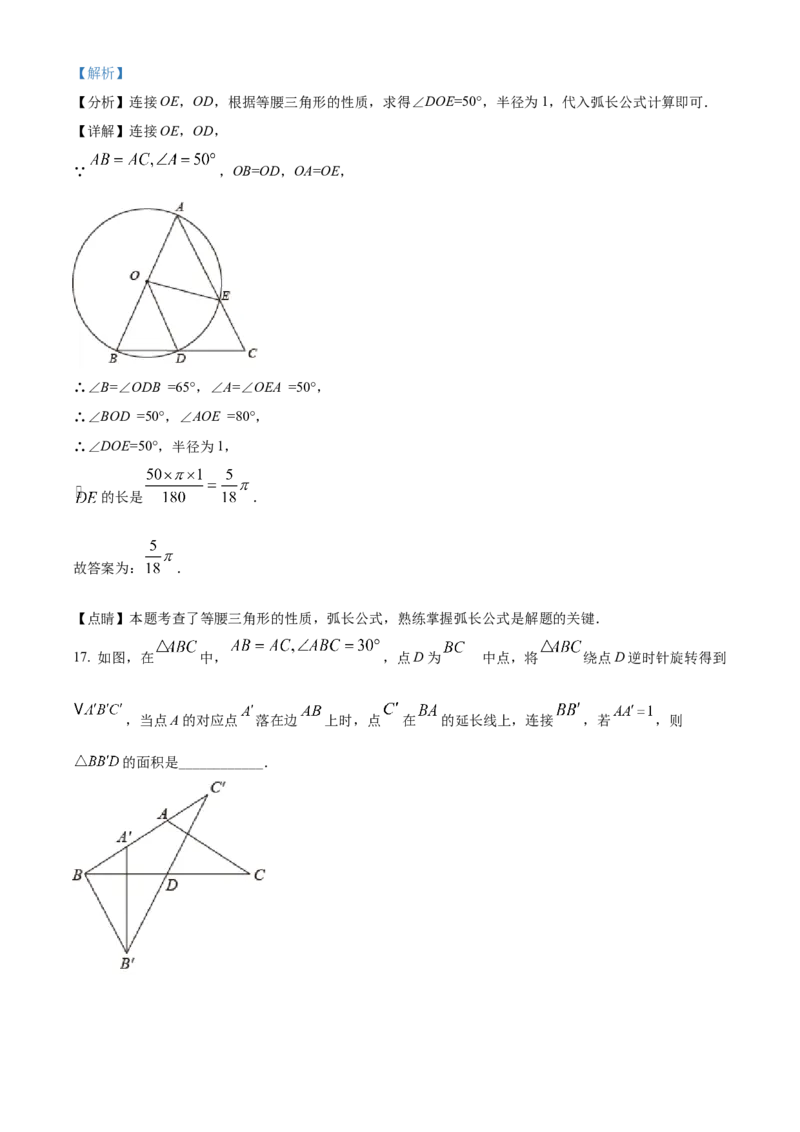
16. 如图,在 中, ,以 为直径的 交边 于D,E两点,
,则 的长是____________.
【答案】【解析】
【分析】连接OE,OD,根据等腰三角形的性质,求得∠DOE=50°,半径为1,代入弧长公式计算即可.
【详解】连接OE,OD,
∵ ,OB=OD,OA=OE,
∴∠B=∠ODB =65°,∠A=∠OEA =50°,
∴∠BOD =50°,∠AOE =80°,
∴∠DOE=50°,半径为1,
的长是 .
故答案为: .
【点睛】本题考查了等腰三角形的性质,弧长公式,熟练掌握弧长公式是解题的关键.
的
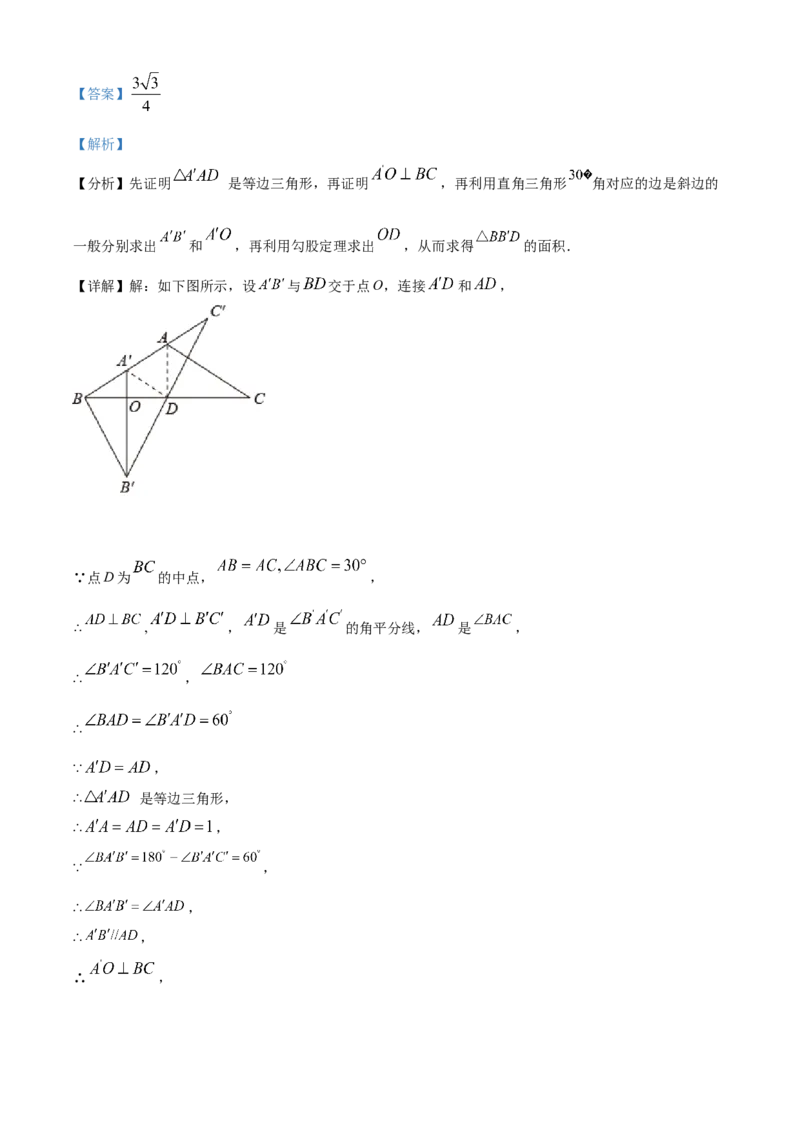
17. 如图,在 中, ,点D为 中点,将 绕点D逆时针旋转得到
,当点A的对应点 落在边 上时,点 在 的延长线上,连接 ,若 ,则
的面积是____________.【答案】
【解析】
【分析】先证明 是等边三角形,再证明 ,再利用直角三角形 角对应的边是斜边的
一般分别求出 和 ,再利用勾股定理求出 ,从而求得 的面积.
【详解】解:如下图所示,设 与 交于点O,连接 和 ,
∵点D为 的中点, ,
∴ , , 是 的角平分线, 是 ,
∴ ,
∴
∵ ,
∴ 是等边三角形,
∴ ,
∵ ,
∴ ,
∴ ,
∴ ,∴ ,
∴
∵
∵ ,
∴
∴ , ,
∴ .
【点睛】本题考查等腰三角形、等边三角形和直角三角形的性质,证明 是等边三角形是解本题的
关键.
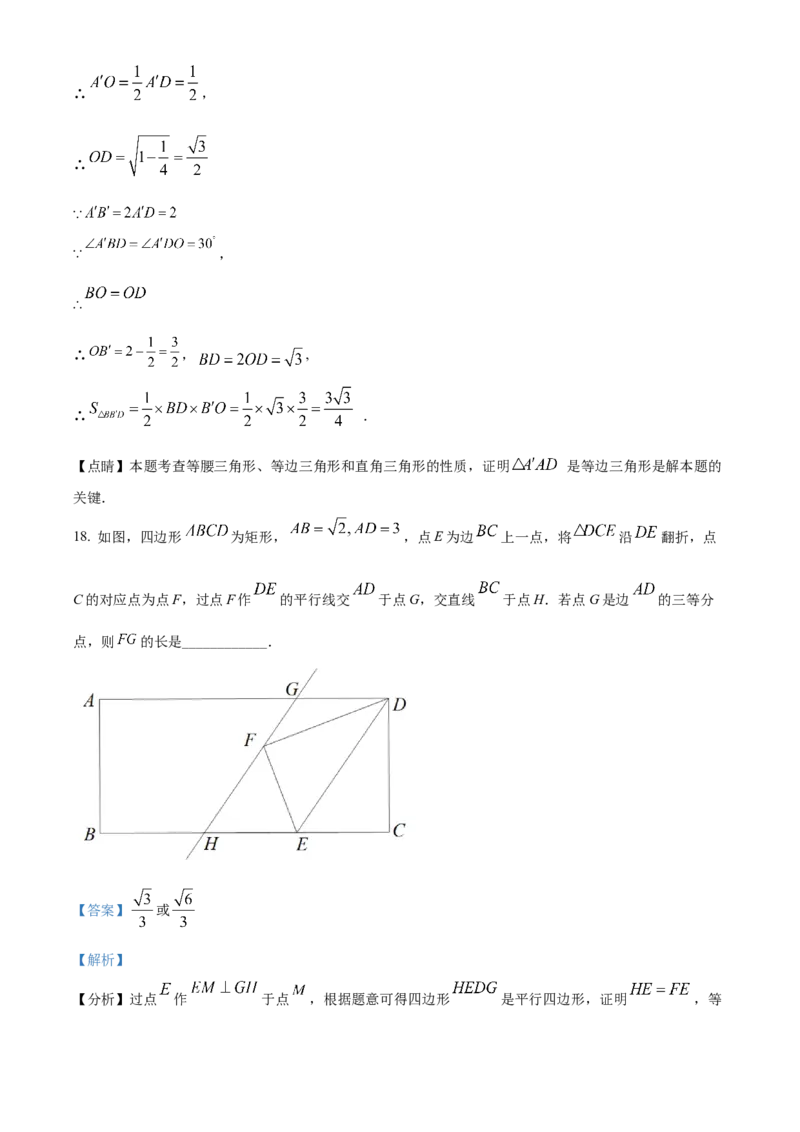
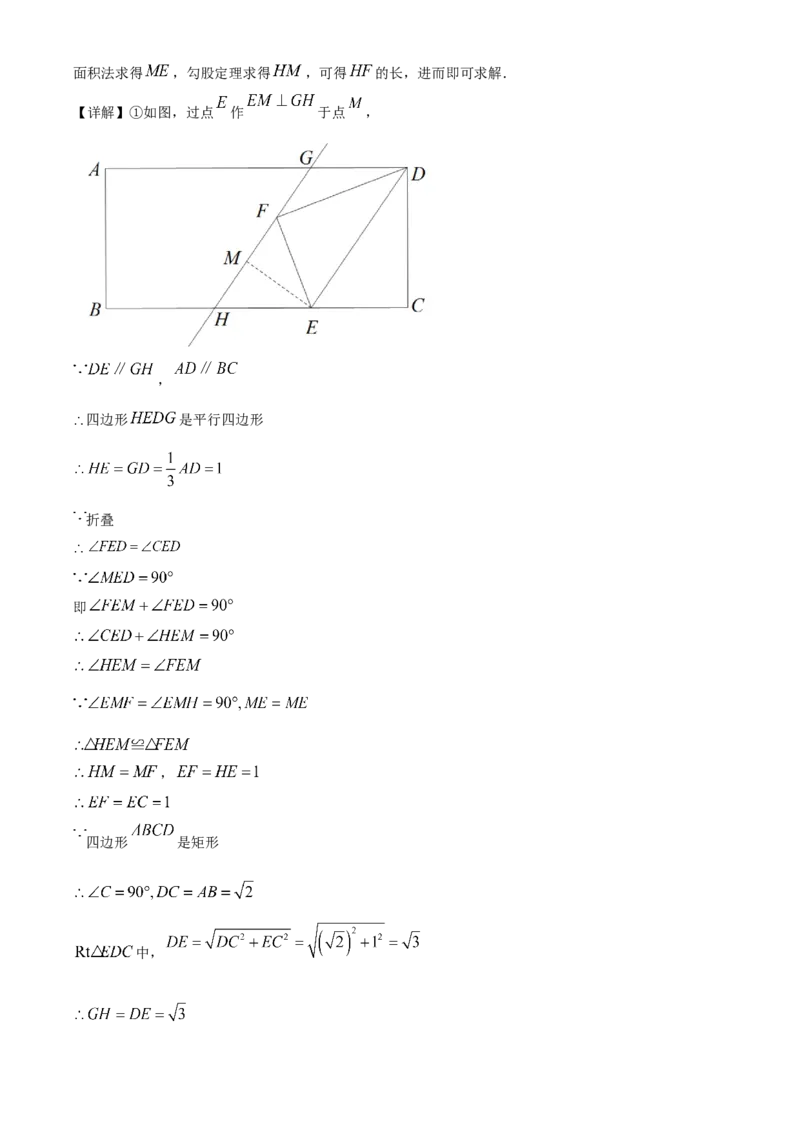
18. 如图,四边形 为矩形, ,点E为边 上一点,将 沿 翻折,点
C的对应点为点F,过点F作 的平行线交 于点G,交直线 于点H.若点G是边 的三等分
点,则 的长是____________.
【答案】 或
【解析】
【分析】过点 作 于点 ,根据题意可得四边形 是平行四边形,证明 ,等面积法求得 ,勾股定理求得 ,可得 的长,进而即可求解.
【详解】①如图,过点 作 于点 ,
,
四边形 是平行四边形
折叠
即
,
四边形 是矩形
中,,
中,
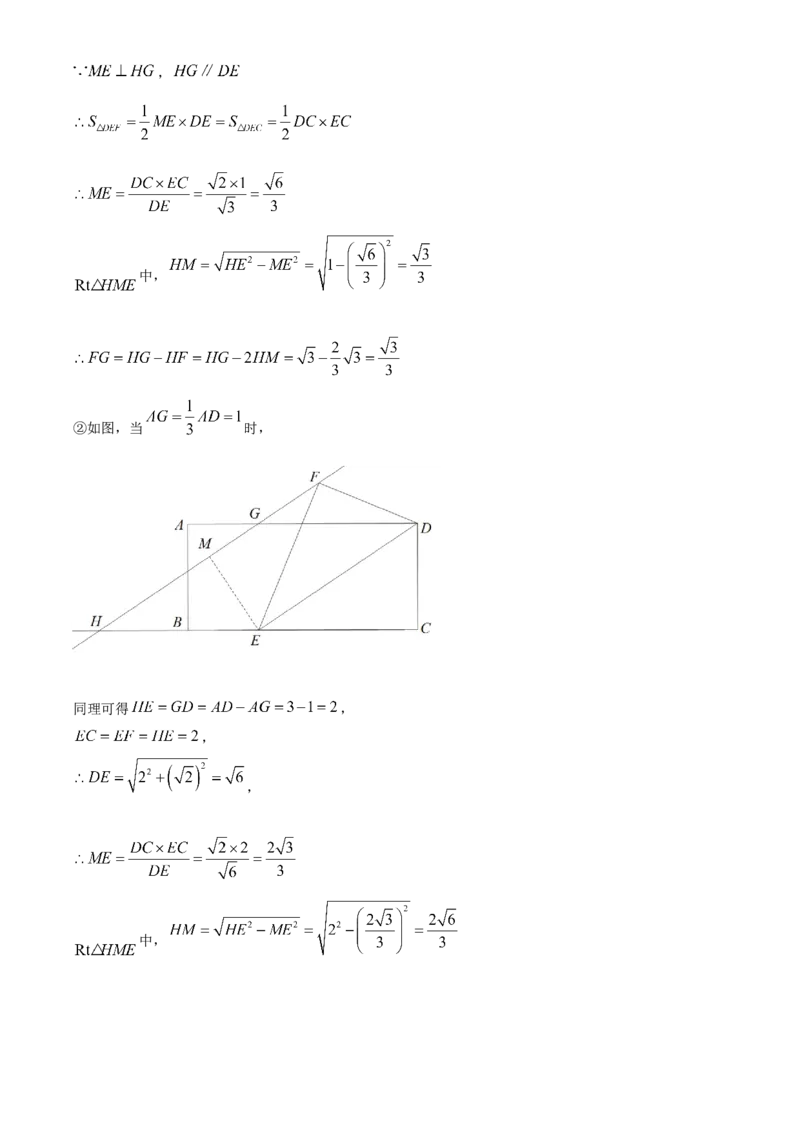
②如图,当 时,
同理可得 ,
,
,
中,故答案为: 或
【点睛】本题考查了勾股定理,折叠,矩形的性质,平行四边形的性质与判定,掌握以上知识,注意分类
讨论是解题的关键.
三、解答题(第19题8分,第20题14分,共22分)
19. 先化简,再求值: ,其中 .
【答案】 ,
【解析】
【分析】根据分式的运算法则“除以一个数等于乘以它的倒数”把除法改写成乘法;利用平方差公式和完全
平方公式将分式的分子分母分别因式分解;约分化简后,求x的值;去掉绝对值符号时注意正负,正数的
绝对值是他本身,负数的绝对值是它的相反数,最后将x的值代入原式.
【详解】解:原式=
=
=
=
=
原式= = =
【点睛】此题考查了分式的混合运算,熟练地掌握分式的混合运算法则和用公式法进行因式分解是解题的
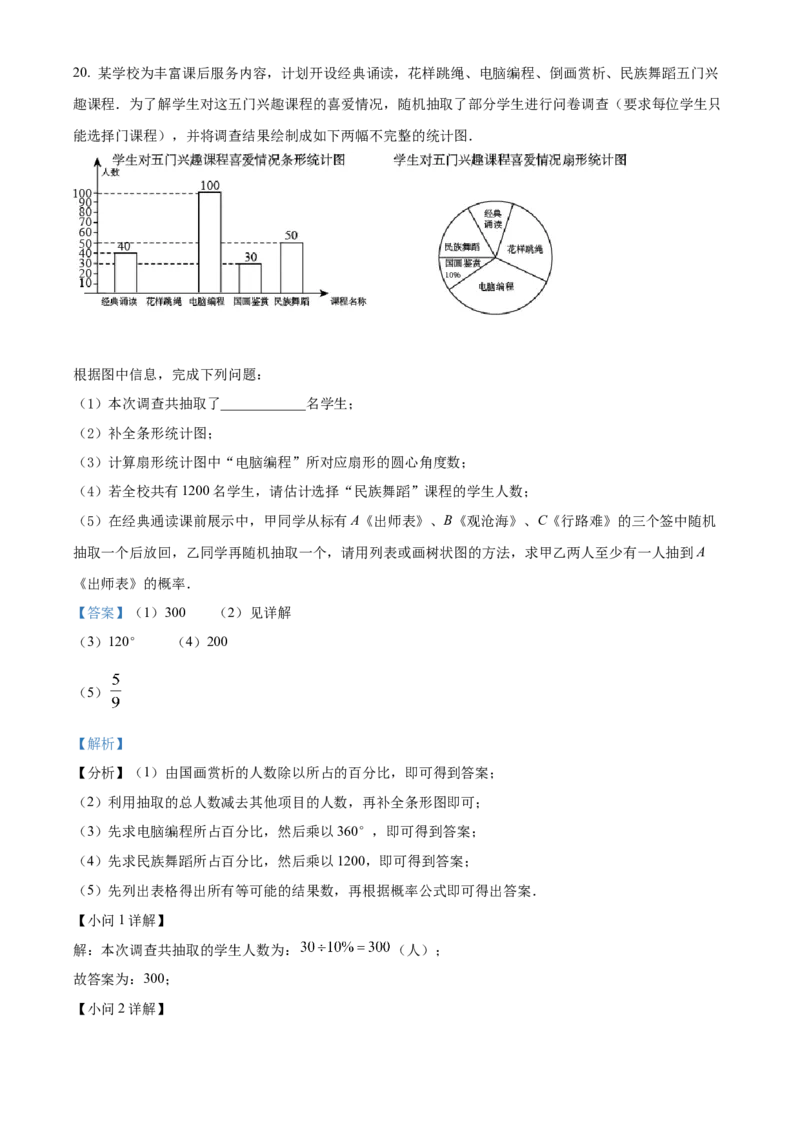
关键.注意最后求值的结果要分母有理化.20. 某学校为丰富课后服务内容,计划开设经典诵读,花样跳绳、电脑编程、倒画赏析、民族舞蹈五门兴
趣课程.为了解学生对这五门兴趣课程的喜爱情况,随机抽取了部分学生进行问卷调查(要求每位学生只
能选择门课程),并将调查结果绘制成如下两幅不完整的统计图.
根据图中信息,完成下列问题:
(1)本次调查共抽取了____________名学生;
(2)补全条形统计图;
(3)计算扇形统计图中“电脑编程”所对应扇形的圆心角度数;
(4)若全校共有1200名学生,请估计选择“民族舞蹈”课程的学生人数;
(5)在经典通读课前展示中,甲同学从标有A《出师表》、B《观沧海》、C《行路难》的三个签中随机
抽取一个后放回,乙同学再随机抽取一个,请用列表或画树状图的方法,求甲乙两人至少有一人抽到A
《出师表》的概率.
【答案】(1)300 (2)见详解
(3)120° (4)200
(5)
【解析】
【分析】(1)由国画赏析的人数除以所占的百分比,即可得到答案;
(2)利用抽取的总人数减去其他项目的人数,再补全条形图即可;
(3)先求电脑编程所占百分比,然后乘以360°,即可得到答案;
(4)先求民族舞蹈所占百分比,然后乘以1200,即可得到答案;
(5)先列出表格得出所有等可能的结果数,再根据概率公式即可得出答案.
【小问1详解】
解:本次调查共抽取的学生人数为: (人);
故答案为:300;
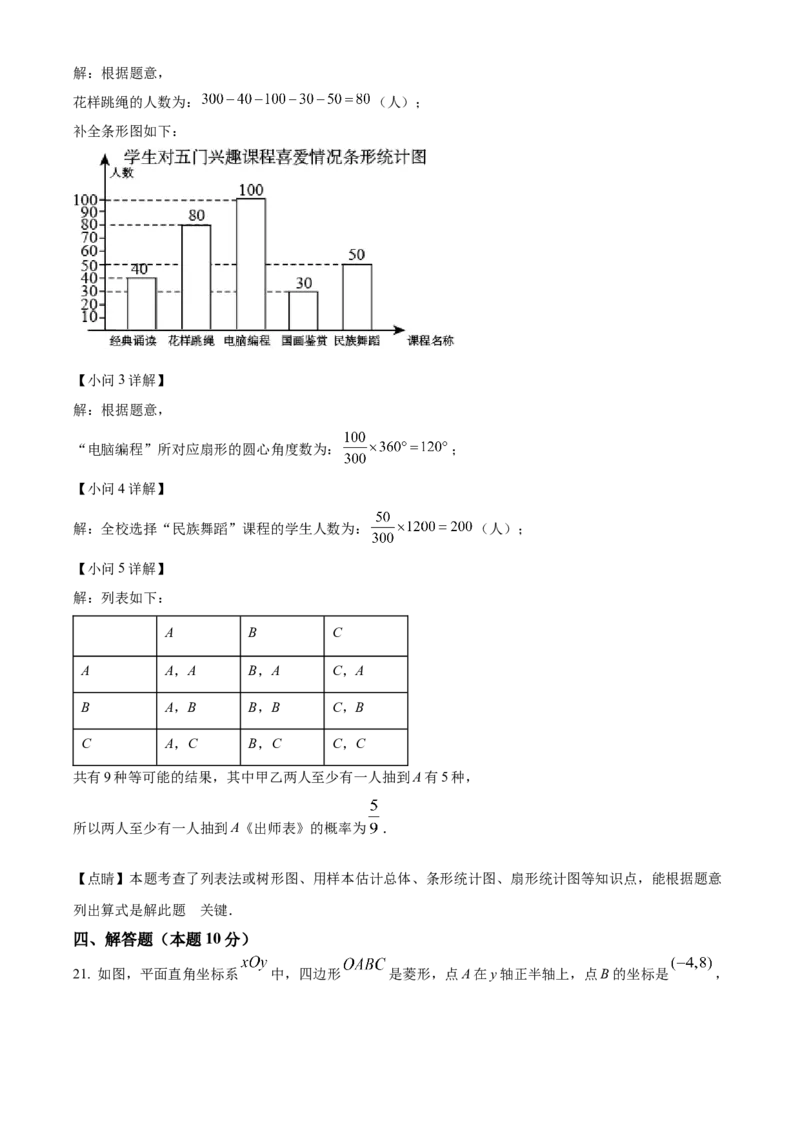
【小问2详解】解:根据题意,
花样跳绳的人数为: (人);
补全条形图如下:
【小问3详解】
解:根据题意,
“电脑编程”所对应扇形的圆心角度数为: ;
【小问4详解】
解:全校选择“民族舞蹈”课程的学生人数为: (人);
【小问5详解】
解:列表如下:
A B C
A A,A B,A C,A
B A,B B,B C,B
C A,C B,C C,C
共有9种等可能的结果,其中甲乙两人至少有一人抽到A有5种,
所以两人至少有一人抽到A《出师表》的概率为 .
【点睛】本题考查了列表法或树形图、用样本估计总体、条形统计图、扇形统计图等知识点,能根据题意
列出算式是解此题 的关键.
四、解答题(本题10分)
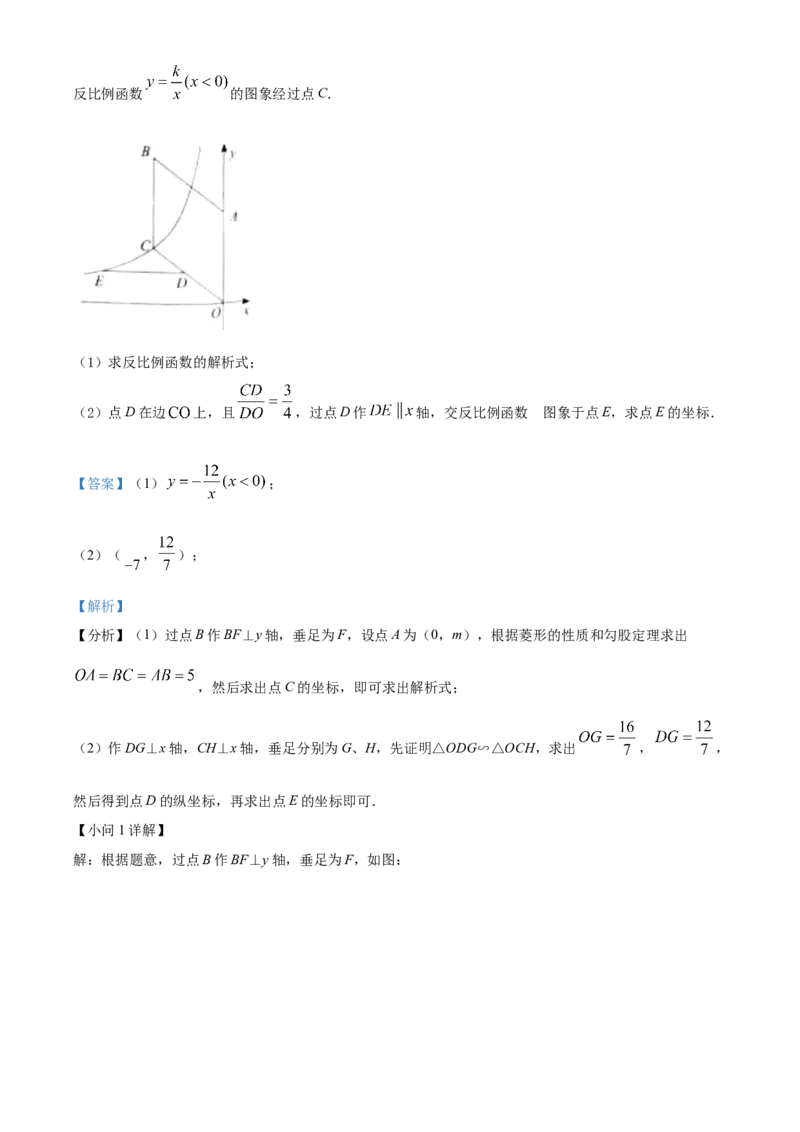
21. 如图,平面直角坐标系 中,四边形 是菱形,点A在y轴正半轴上,点B的坐标是 ,反比例函数 的图象经过点C.
(1)求反比例函数的解析式;
(2)点D在边 上,且 ,过点D作 轴,交反比例函数 图的象于点E,求点E的坐标.
【答案】(1) ;
(2)( , );
【解析】
【分析】(1)过点B作BF⊥y轴,垂足为F,设点A为(0,m),根据菱形的性质和勾股定理求出
,然后求出点C的坐标,即可求出解析式;
(2)作DG⊥x轴,CH⊥x轴,垂足分别为G、H,先证明△ODG∽△OCH,求出 , ,
然后得到点D的纵坐标,再求出点E的坐标即可.
【小问1详解】
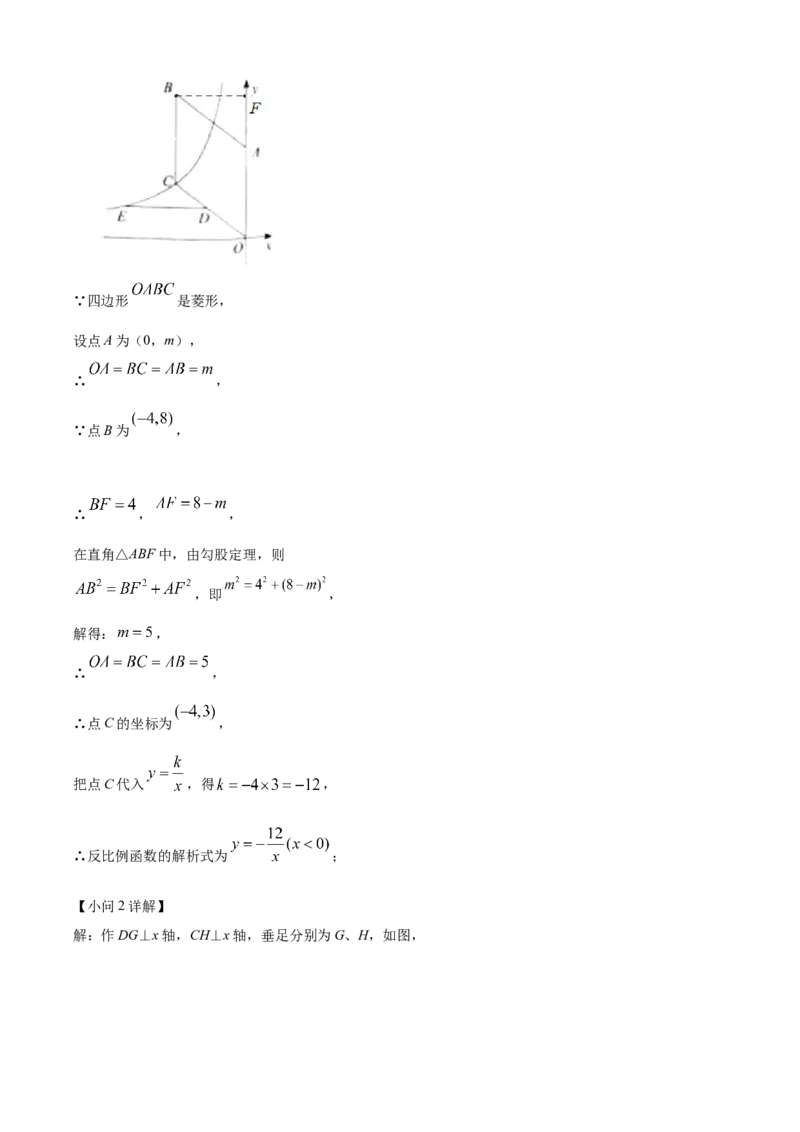
解:根据题意,过点B作BF⊥y轴,垂足为F,如图:∵四边形 是菱形,
设点A为(0,m),
∴ ,
∵点B为 ,
∴ , ,
在直角△ABF中,由勾股定理,则
,即 ,
解得: ,
∴ ,
∴点C的坐标为 ,
把点C代入 ,得 ,
∴反比例函数的解析式为 ;
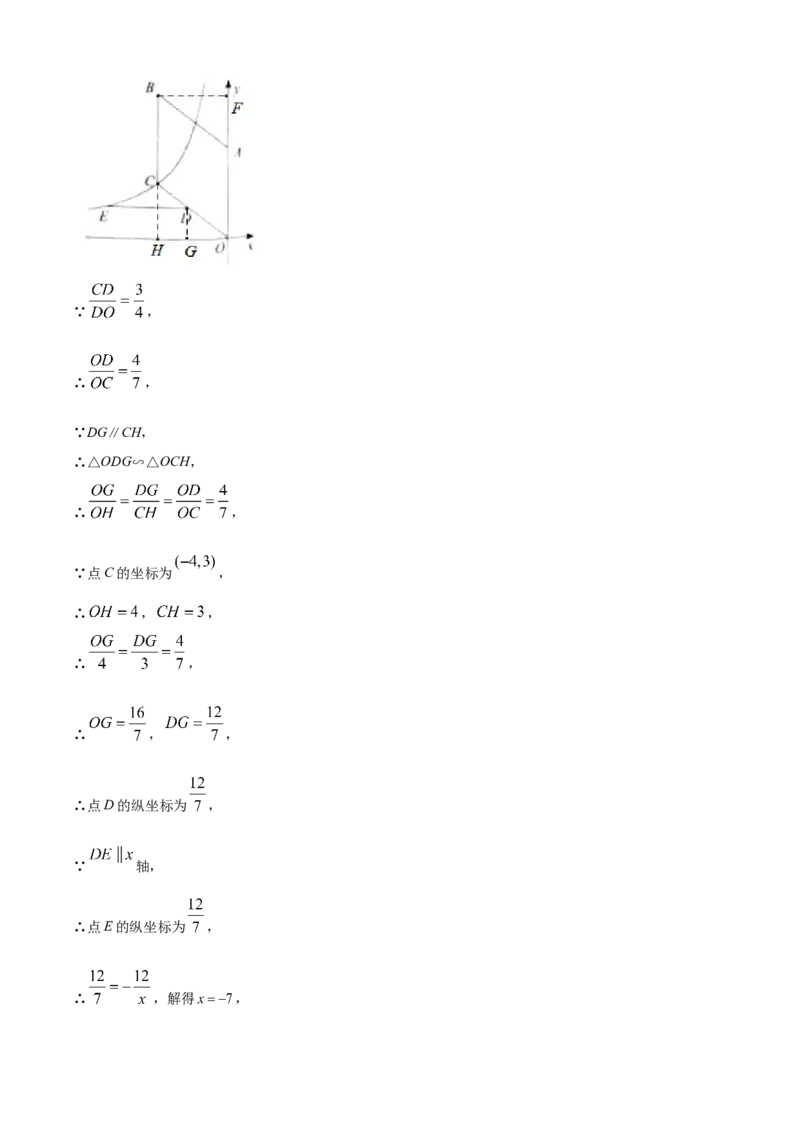
【小问2详解】
解:作DG⊥x轴,CH⊥x轴,垂足分别为G、H,如图,∵ ,
∴ ,
∵DG∥CH,
∴△ODG∽△OCH,
∴ ,
∵点C的坐标为 ,
∴ , ,
∴ ,
∴ , ,
∴点D的纵坐标为 ,
∵ 轴,
∴点E的纵坐标为 ,
∴ ,解得 ,∴点E的坐标为( , );
【点睛】本题考查了菱形的性质,反比例函数的图像和性质,相似三角形的判定和性质,勾股定理等知识,
解题的关键是熟练掌握题意,正确的作出辅助线,从而进行解题.
五、解答题(第22题10分,第23题12分,共22分)
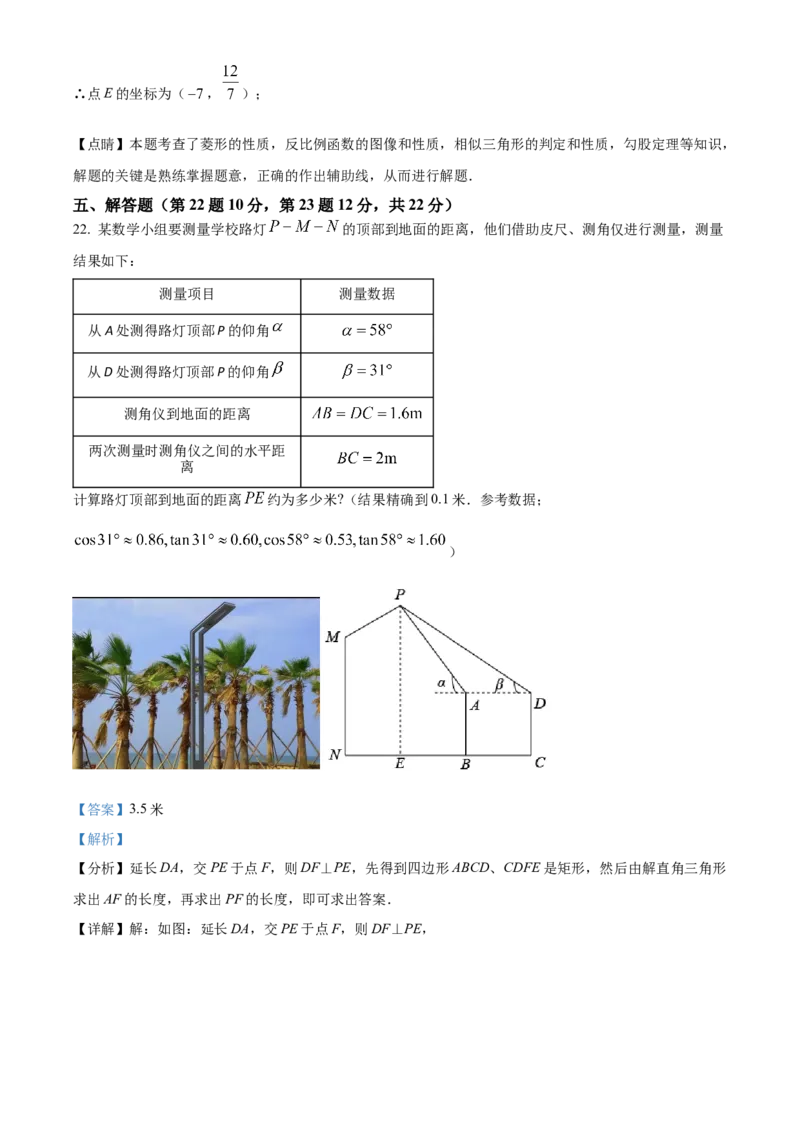
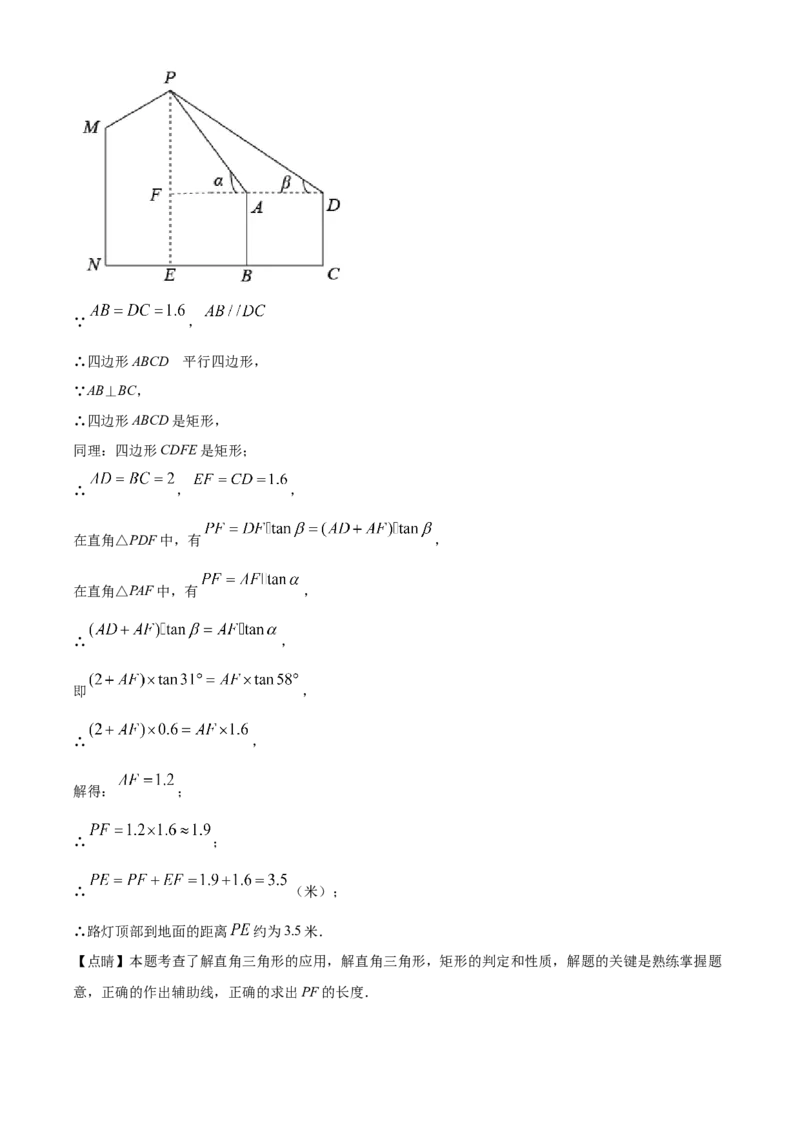
22. 某数学小组要测量学校路灯 的顶部到地面的距离,他们借助皮尺、测角仅进行测量,测量
结果如下:
测量项目 测量数据
从A处测得路灯顶部P的仰角
从D处测得路灯顶部P的仰角
测角仪到地面的距离
两次测量时测角仪之间的水平距
离
计算路灯顶部到地面的距离 约为多少米?(结果精确到0.1米.参考数据;
)
【答案】3.5米
【解析】
【分析】延长DA,交PE于点F,则DF⊥PE,先得到四边形ABCD、CDFE是矩形,然后由解直角三角形
求出AF的长度,再求出PF的长度,即可求出答案.
【详解】解:如图:延长DA,交PE于点F,则DF⊥PE,∵ ,
∴四边形ABCD 是平行四边形,
∵AB⊥BC,
∴四边形ABCD是矩形,
同理:四边形CDFE是矩形;
∴ , ,
在直角△PDF中,有 ,
在直角△PAF中,有 ,
∴ ,
即 ,
∴ ,
解得: ;
∴ ;
∴ (米);
∴路灯顶部到地面的距离 约为3.5米.
【点睛】本题考查了解直角三角形的应用,解直角三角形,矩形的判定和性质,解题的关键是熟练掌握题
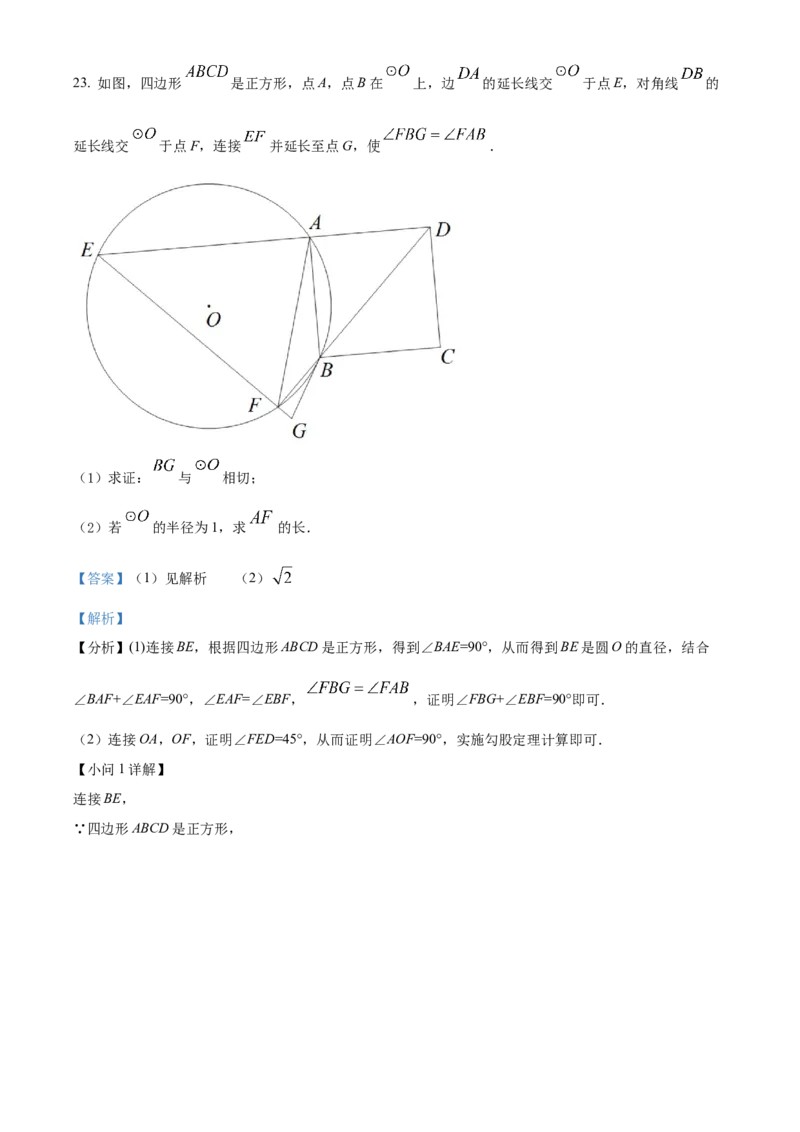
意,正确的作出辅助线,正确的求出PF的长度.23. 如图,四边形 是正方形,点A,点B在 上,边 的延长线交 于点E,对角线 的
延长线交 于点F,连接 并延长至点G,使 .
(1)求证: 与 相切;
(2)若 的半径为1,求 的长.
【答案】(1)见解析 (2)
【解析】
【分析】(1)连接BE,根据四边形ABCD是正方形,得到∠BAE=90°,从而得到BE是圆O的直径,结合
∠BAF+∠EAF=90°,∠EAF=∠EBF, ,证明∠FBG+∠EBF=90°即可.
(2)连接OA,OF,证明∠FED=45°,从而证明∠AOF=90°,实施勾股定理计算即可.
【小问1详解】
连接BE,
∵四边形ABCD是正方形,∴∠BAE=90°,
∴BE是圆O的直径,
∵∠BAF+∠EAF=90°,∠EAF=∠EBF, ,
∴∠FBG+∠EBF=90°,
∴∠OBG=90°,
故BG是圆O的切线.
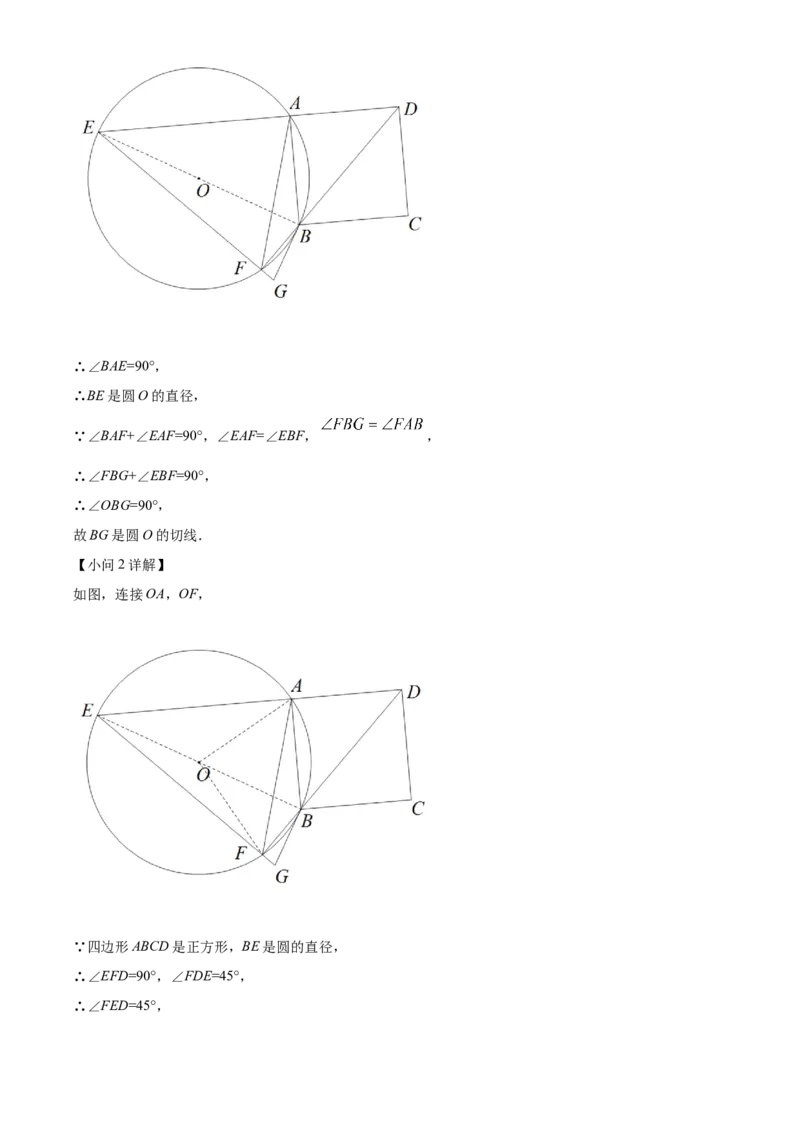
【小问2详解】
如图,连接OA,OF,
∵四边形ABCD是正方形,BE是圆的直径,
∴∠EFD=90°,∠FDE=45°,
∴∠FED=45°,∴∠AOF=90°,
∵OA=OF=1,
∴ ,
∴AF= ,AF=- (舍去).
【点睛】本题考查了圆的切线判定,圆周角定理,勾股定理,熟练掌握切线的判定定理,圆周角定理,勾
股定理是解题的关键.
六、解答题(本题14分)
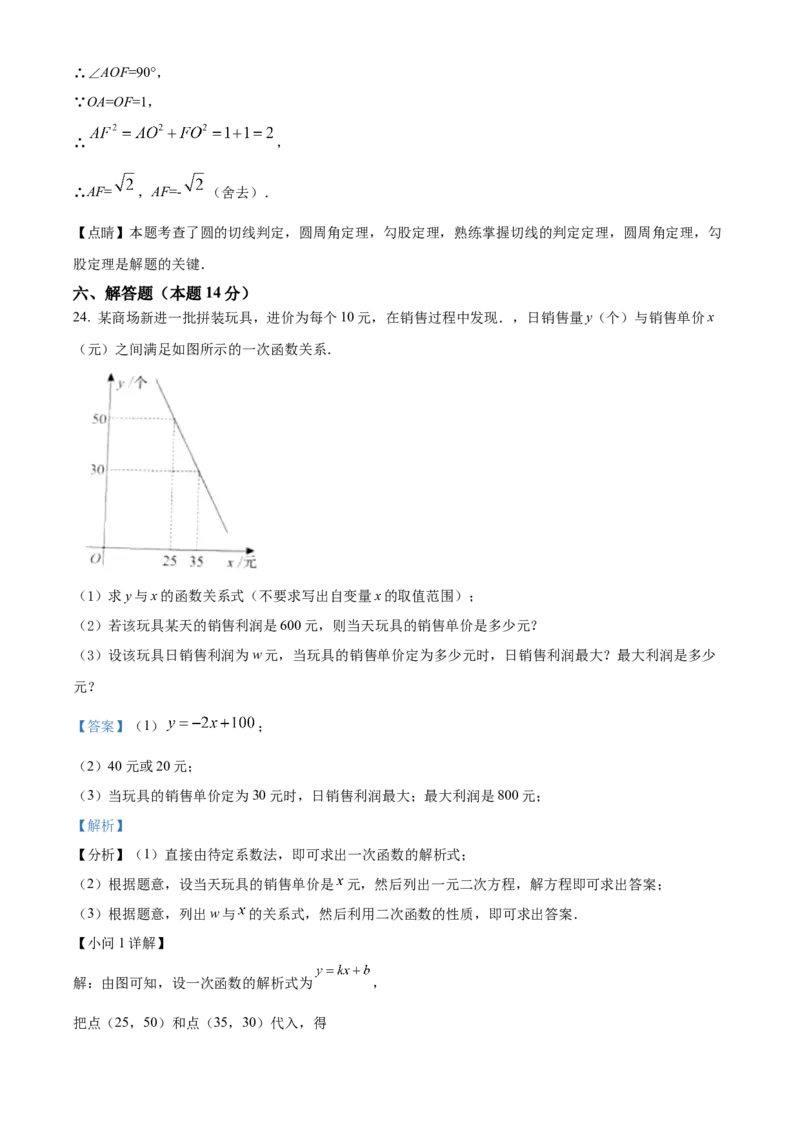
24. 某商场新进一批拼装玩具,进价为每个10元,在销售过程中发现.,日销售量y(个)与销售单价x
(元)之间满足如图所示的一次函数关系.
(1)求y与x的函数关系式(不要求写出自变量x的取值范围);
(2)若该玩具某天的销售利润是600元,则当天玩具的销售单价是多少元?
(3)设该玩具日销售利润为w元,当玩具的销售单价定为多少元时,日销售利润最大?最大利润是多少
元?
【答案】(1) ;
(2)40元或20元;
(3)当玩具的销售单价定为30元时,日销售利润最大;最大利润是800元;
【解析】
【分析】(1)直接由待定系数法,即可求出一次函数的解析式;
(2)根据题意,设当天玩具的销售单价是 元,然后列出一元二次方程,解方程即可求出答案;
(3)根据题意,列出w与 的关系式,然后利用二次函数的性质,即可求出答案.
【小问1详解】
解:由图可知,设一次函数的解析式为 ,
把点(25,50)和点(35,30)代入,得,解得 ,
的
∴一次函数 解析式为 ;
【小问2详解】
解:根据题意,设当天玩具的销售单价是 元,则
,
解得: , ,
∴当天玩具的销售单价是40元或20元;
【小问3详解】
解:根据题意,则
,
整理得: ;
∵ ,
∴当 时, 有最大值,最大值为800;
∴当玩具的销售单价定为30元时,日销售利润最大;最大利润是800元.
【点睛】本题考查了二次函数的性质,二次函数的最值,一次函数的应用,解一元二次方程,解题的关键
是熟练掌握题意,正确的找出题目的关系,从而进行解题.
七、解答题(本题14分)
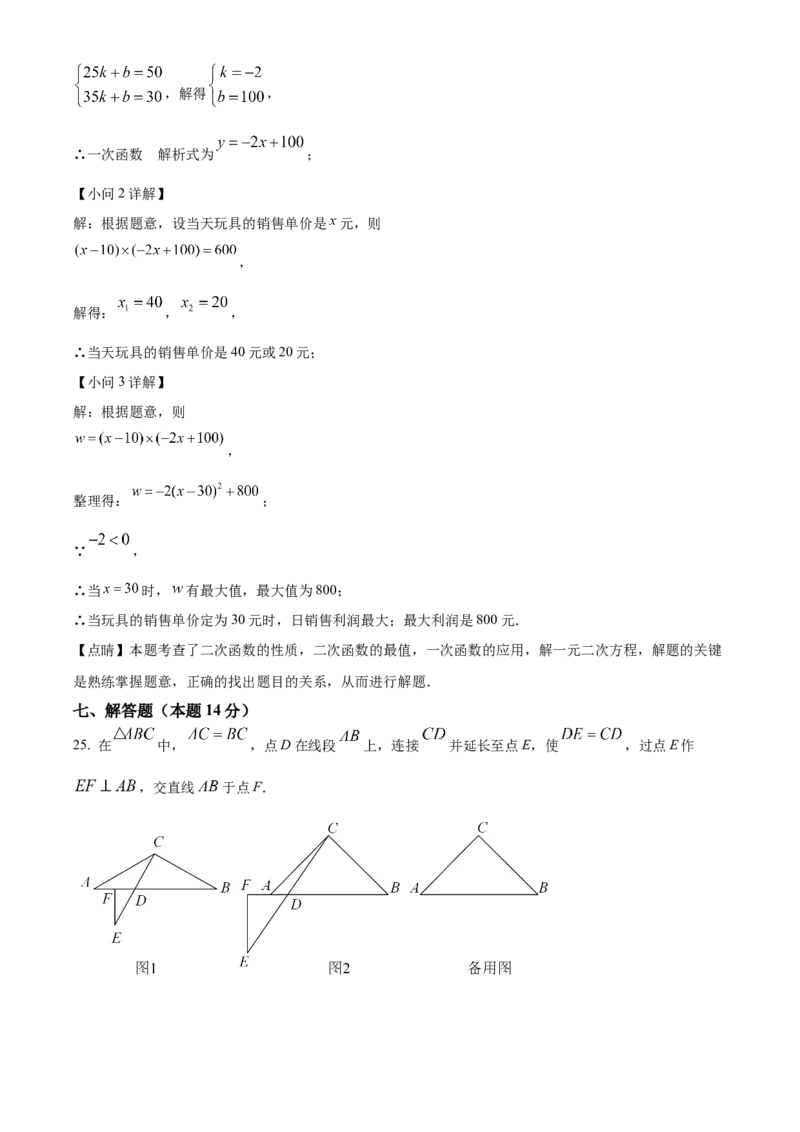
25. 在 中, ,点D在线段 上,连接 并延长至点E,使 ,过点E作
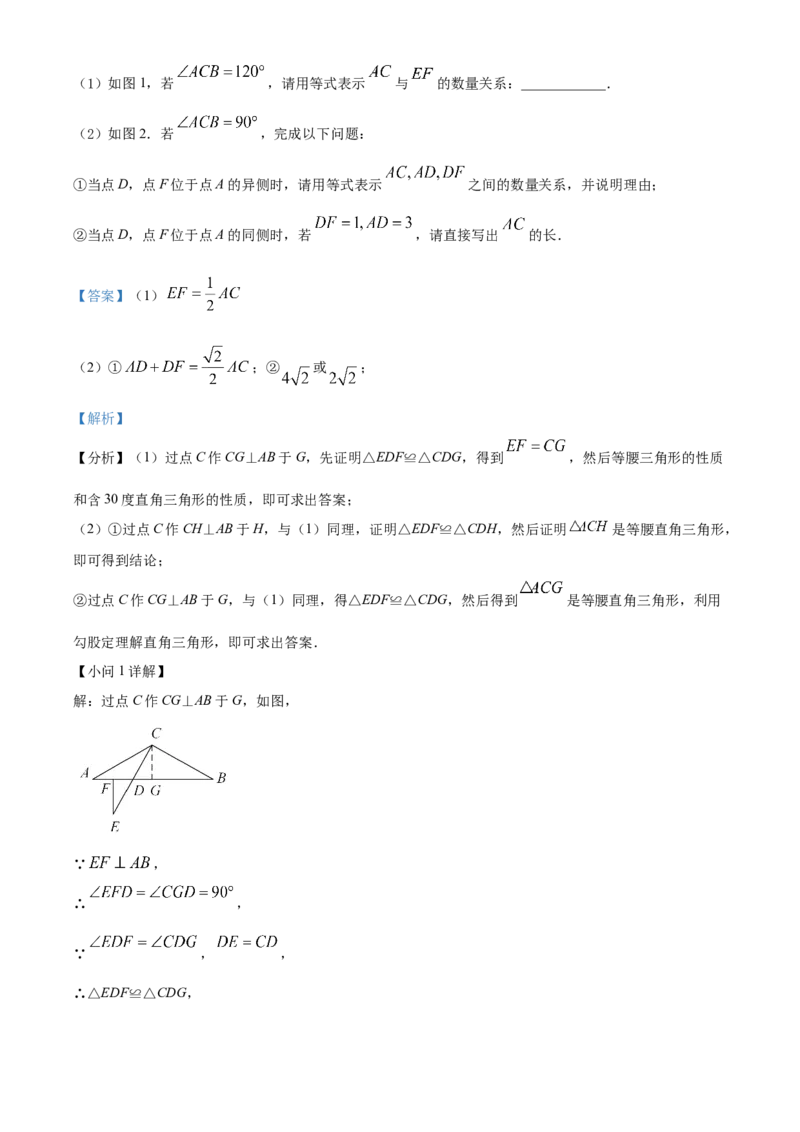
,交直线 于点F.(1)如图1,若 ,请用等式表示 与 的数量关系:____________.
(2)如图2.若 ,完成以下问题:
①当点D,点F位于点A的异侧时,请用等式表示 之间的数量关系,并说明理由;
②当点D,点F位于点A的同侧时,若 ,请直接写出 的长.
【答案】(1)
(2)① ;② 或 ;
【解析】
【分析】(1)过点C作CG⊥AB于G,先证明△EDF≌△CDG,得到 ,然后等腰三角形的性质
和含30度直角三角形的性质,即可求出答案;
(2)①过点C作CH⊥AB于H,与(1)同理,证明△EDF≌△CDH,然后证明 是等腰直角三角形,
即可得到结论;
②过点C作CG⊥AB于G,与(1)同理,得△EDF≌△CDG,然后得到 是等腰直角三角形,利用
勾股定理解直角三角形,即可求出答案.
【小问1详解】
解:过点C作CG⊥AB于G,如图,
∵ ,
∴ ,
∵ , ,
∴△EDF≌△CDG,∴ ;
∵在 中, , ,
∴ ,
∴ ,
∴ ;
故答案为: ;
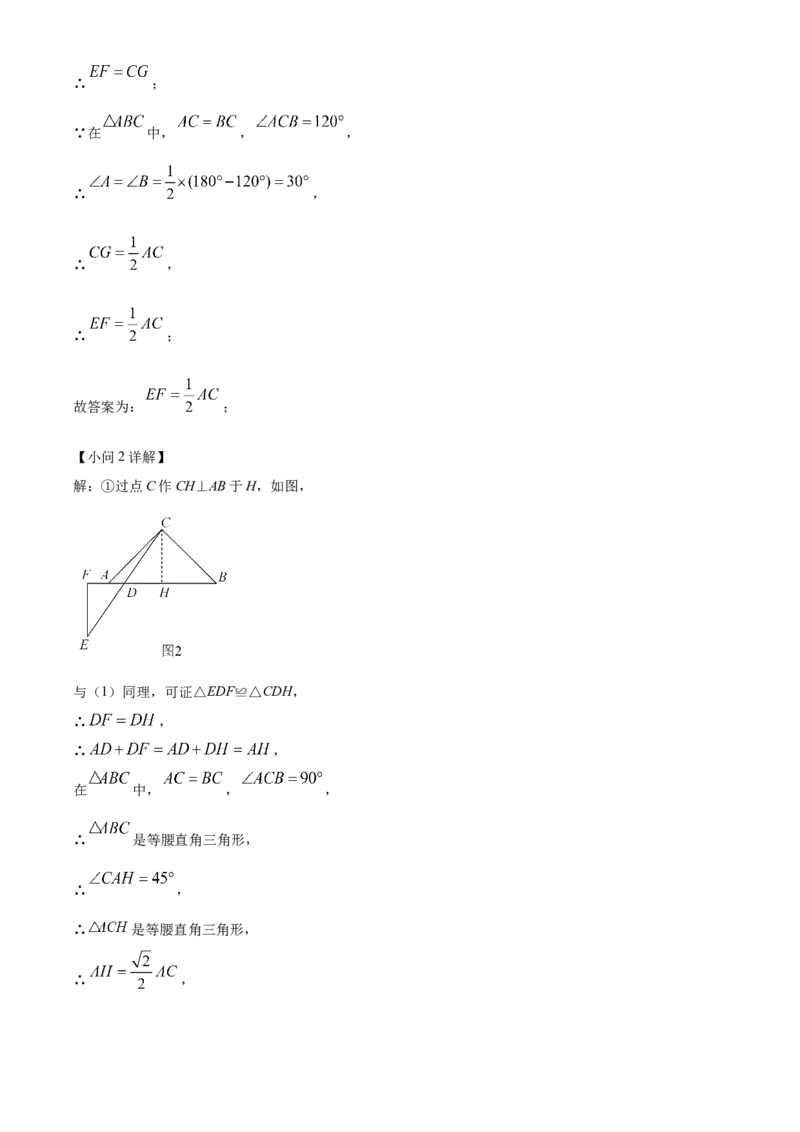
【小问2详解】
解:①过点C作CH⊥AB于H,如图,
与(1)同理,可证△EDF≌△CDH,
∴ ,
∴ ,
在 中, , ,
∴ 是等腰直角三角形,
∴ ,
∴ 是等腰直角三角形,
∴ ,∴ ;
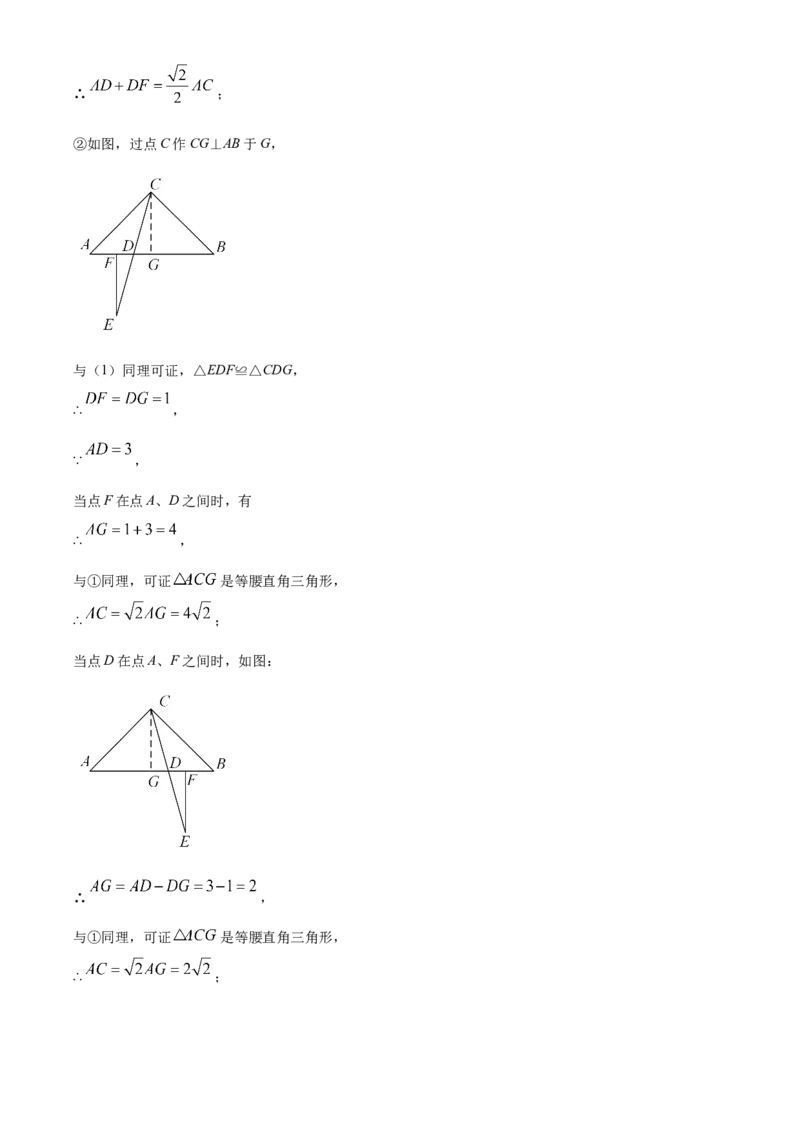
②如图,过点C作CG⊥AB于G,
与(1)同理可证,△EDF≌△CDG,
∴ ,
∵ ,
当点F在点A、D之间时,有
∴ ,
与①同理,可证 是等腰直角三角形,
∴ ;
当点D在点A、F之间时,如图:
∴ ,
与①同理,可证 是等腰直角三角形,
∴ ;综合上述,线段 的长为 或 .
【点睛】本题考查了等腰直角三角形的判定和性质,全等三角形的判定和性质,勾股定理解直角三角形,
三角形的内角和定理,解题的关键是熟练掌握所学的知识,正确的作出辅助线,正确得到三角形全等.
八、解答题(本题14分)
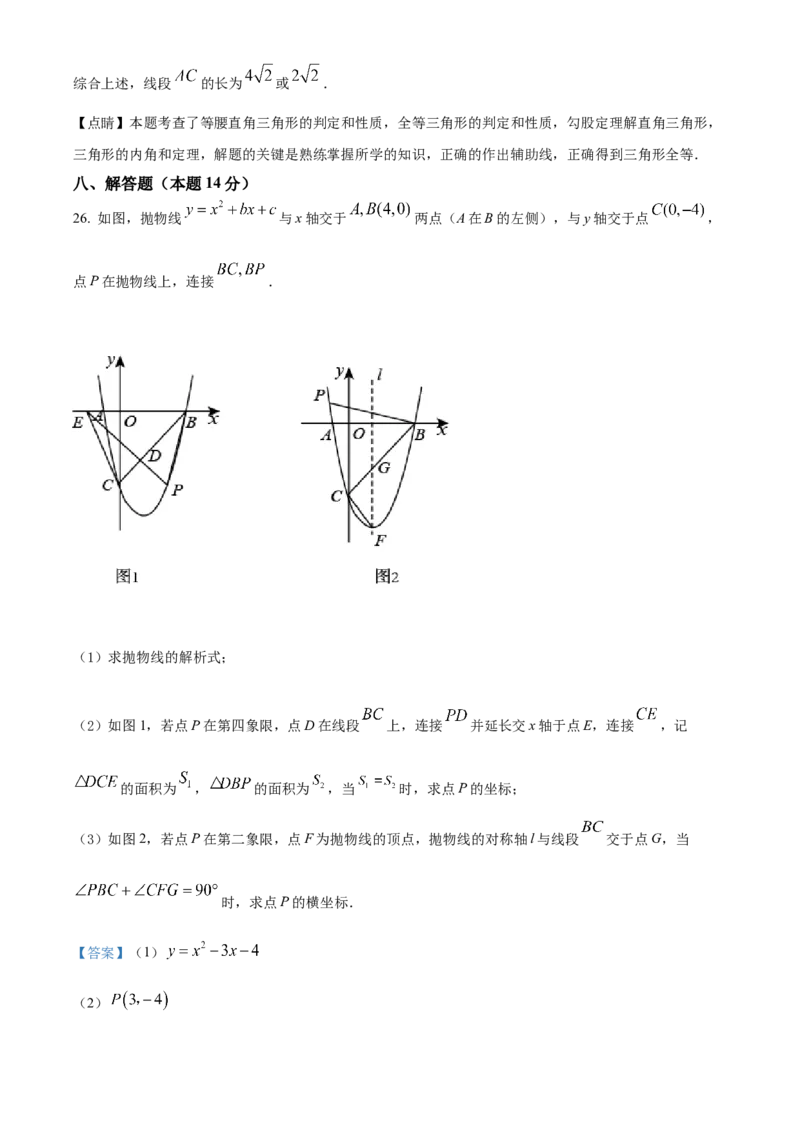
26. 如图,抛物线 与x轴交于 两点(A在B的左侧),与y轴交于点 ,
点P在抛物线上,连接 .
(1)求抛物线的解析式;
(2)如图1,若点P在第四象限,点D在线段 上,连接 并延长交x轴于点E,连接 ,记
的面积为 , 的面积为 ,当 时,求点P的坐标;
(3)如图2,若点P在第二象限,点F为抛物线的顶点,抛物线的对称轴l与线段 交于点G,当
时,求点P的横坐标.
【答案】(1)
(2)(3)点P的横坐标为
【解析】
【分析】(1)将将 、 两点代入 即可求解;
(2)设点 ,由 , 可得 即
可求解;
(3)作CE⊥l,PQ⊥BC,PN⊥x轴,连接PC交x轴于点H,设 ,PC的表达式为:
,由P,C代入 得,PC的表达式,由 可表示
PQ、PB,分别求EF、CF,由 ,PQ⊥BC,CE⊥l,证 即可求解;
【小问1详解】
解:将 、 两点代入 得,
,解得:
∴抛物线的解析式为:
【小问2详解】
由 可得,
设点
则
∵ ,
∴∴
解得: (舍去)
∴
【小问3详解】
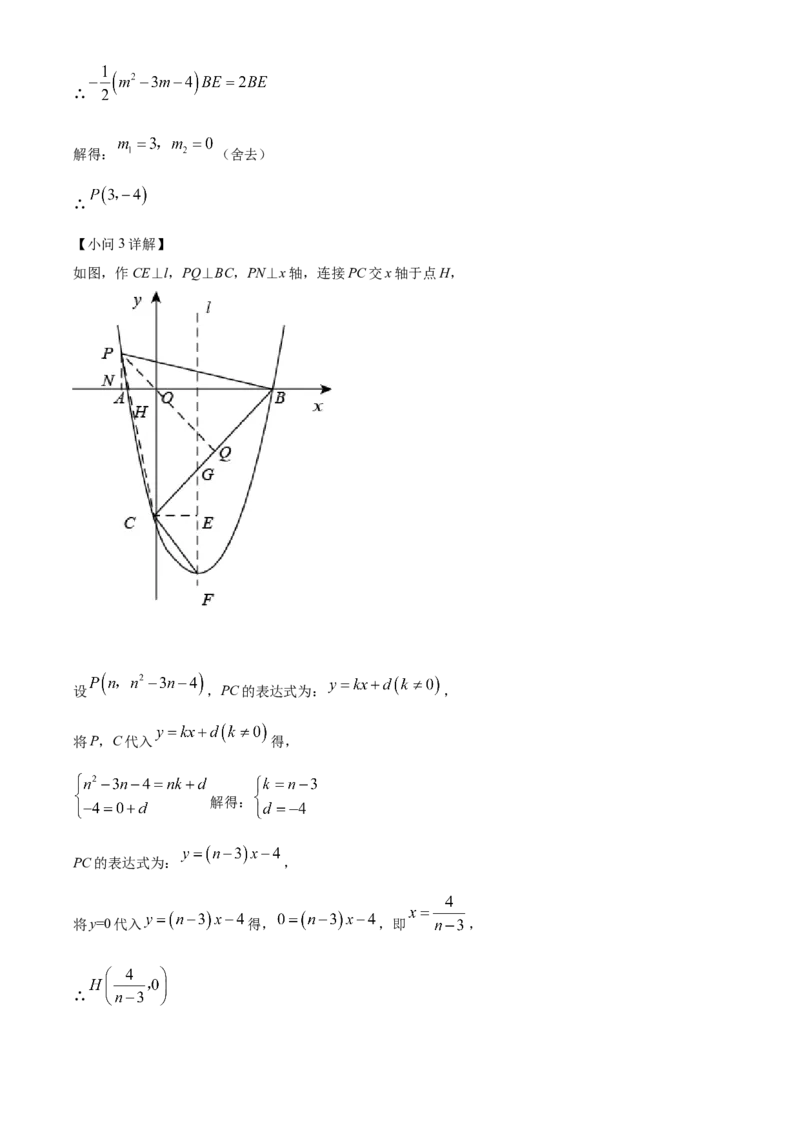
如图,作CE⊥l,PQ⊥BC,PN⊥x轴,连接PC交x轴于点H,
设 ,PC的表达式为: ,
将P,C代入 得,
解得:
PC的表达式为: ,
将y=0代入 得, ,即 ,
∴∵
∴
∵
∴
∵
由题可知,
∴
将 代入 得, ,
∴
∴
∵ ,PQ⊥BC,CE⊥l,
∴
∴
∴解得: (舍去).
【点睛】本题主要考查二次函数的综合应用,一次函数的应用,三角形的相似,勾股定理,掌握相关知识
正确构造辅助线是解题的关键.