文档内容
2022 年辽宁省营口市中考数学真题
第一部分 选择题
一、选择题(下列各题的备选答案中,只有一个是正确的,每小题3分,共30分)
1. 在 ,0, ,2这四个实数中,最大的数是( )
A. 0 B. C. 2 D.
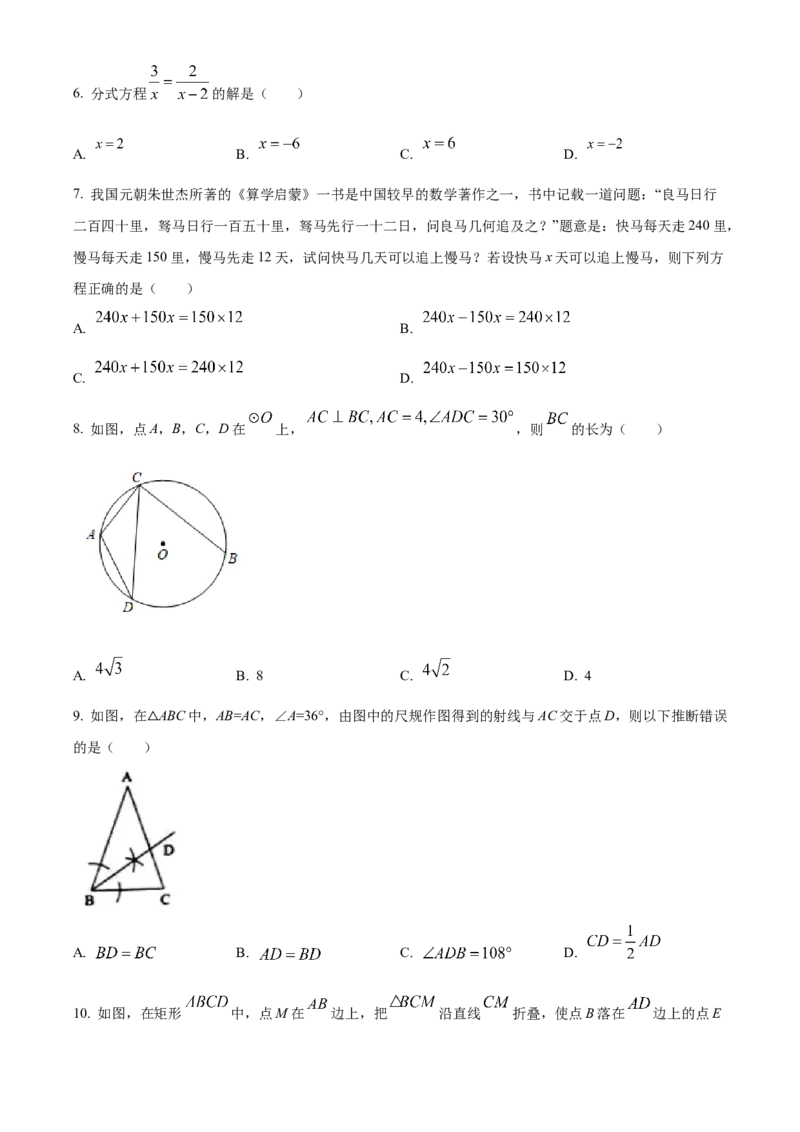
2. 如图是由五个相同的正方体搭成的几何体,这个几何体的左视图是( )
A. B. C. D.
3. 下列计算正确的是( )
A. B. C. D.
4. 如图,直线 的顶点B,C分别在 上,若 ,则 的大小为
( )
A. B. C. D.
的
5. 关于x 一元二次方程 有两个实数根,则实数m的取值范围为( )
A. B. C. D.6. 分式方程 的解是( )
A. B. C. D.
7. 我国元朝朱世杰所著的《算学启蒙》一书是中国较早的数学著作之一,书中记载一道问题:“良马日行
二百四十里,驽马日行一百五十里,驽马先行一十二日,问良马几何追及之?”题意是:快马每天走240里,
慢马每天走150里,慢马先走12天,试问快马几天可以追上慢马?若设快马x天可以追上慢马,则下列方
程正确的是( )
A. B.
C. D.
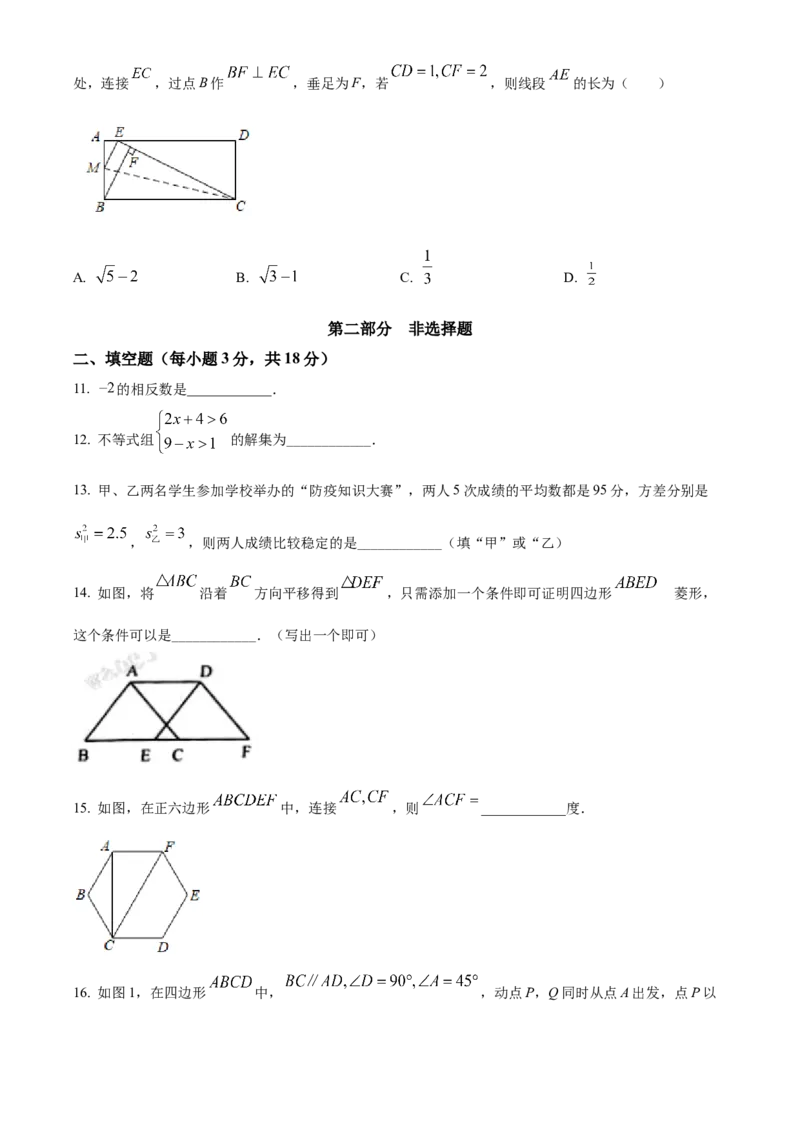
8. 如图,点A,B,C,D在 上, ,则 的长为( )
A. B. 8 C. D. 4
9. 如图,在 ABC中,AB=AC,∠A=36°,由图中的尺规作图得到的射线与AC交于点D,则以下推断错误
的是( )△
A. B. C. D.
10. 如图,在矩形 中,点M在 边上,把 沿直线 折叠,使点B落在 边上的点E处,连接 ,过点B作 ,垂足为F,若 ,则线段 的长为( )
A. B. C. D.
第二部分 非选择题
二、填空题(每小题3分,共18分)
11. 的相反数是____________.
12. 不等式组 的解集为____________.
13. 甲、乙两名学生参加学校举办的“防疫知识大赛”,两人5次成绩的平均数都是95分,方差分别是
, ,则两人成绩比较稳定的是____________(填“甲”或“乙)
是
14. 如图,将 沿着 方向平移得到 ,只需添加一个条件即可证明四边形 菱形,
这个条件可以是____________.(写出一个即可)
15. 如图,在正六边形 中,连接 ,则 ____________度.
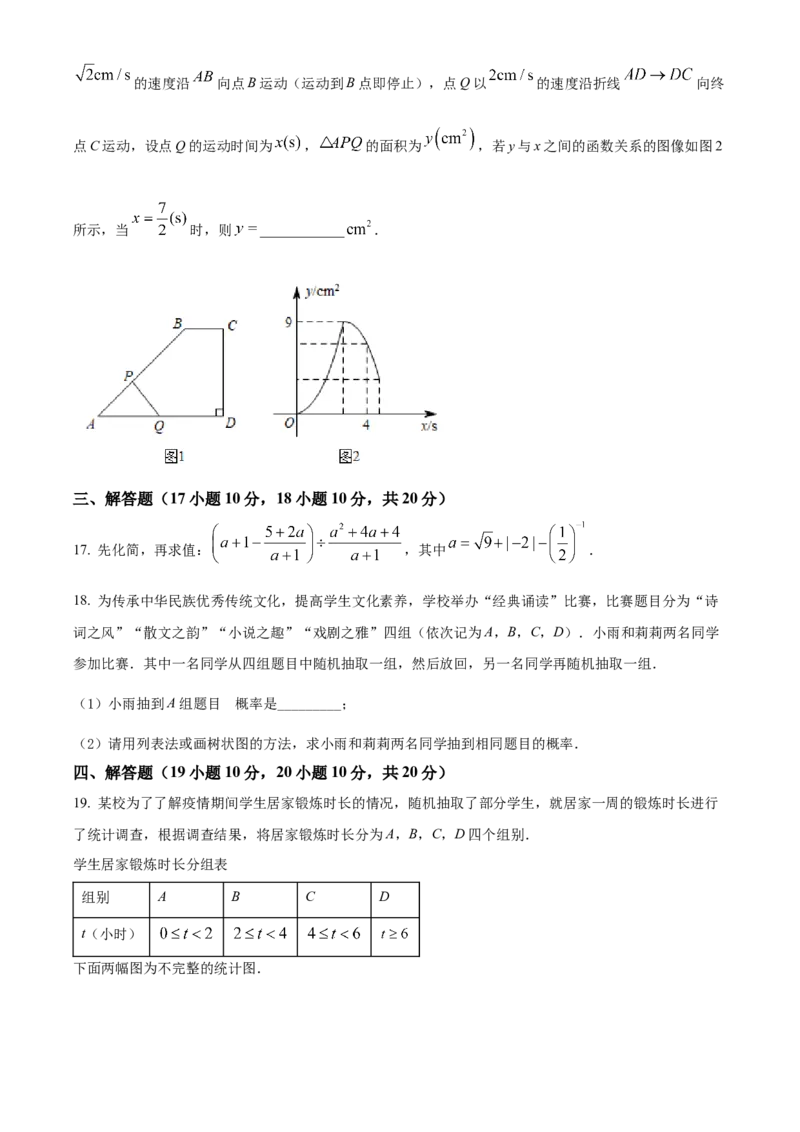
16. 如图1,在四边形 中, ,动点P,Q同时从点A出发,点P以的速度沿 向点B运动(运动到B点即停止),点Q以 的速度沿折线 向终
点C运动,设点Q的运动时间为 , 的面积为 ,若y与x之间的函数关系的图像如图2
所示,当 时,则 ____________ .
三、解答题(17小题10分,18小题10分,共20分)
17. 先化简,再求值: ,其中 .
18. 为传承中华民族优秀传统文化,提高学生文化素养,学校举办“经典诵读”比赛,比赛题目分为“诗
词之风”“散文之韵”“小说之趣”“戏剧之雅”四组(依次记为A,B,C,D).小雨和莉莉两名同学
参加比赛.其中一名同学从四组题目中随机抽取一组,然后放回,另一名同学再随机抽取一组.
的
(1)小雨抽到A组题目 概率是_________;
(2)请用列表法或画树状图的方法,求小雨和莉莉两名同学抽到相同题目的概率.
四、解答题(19小题10分,20小题10分,共20分)
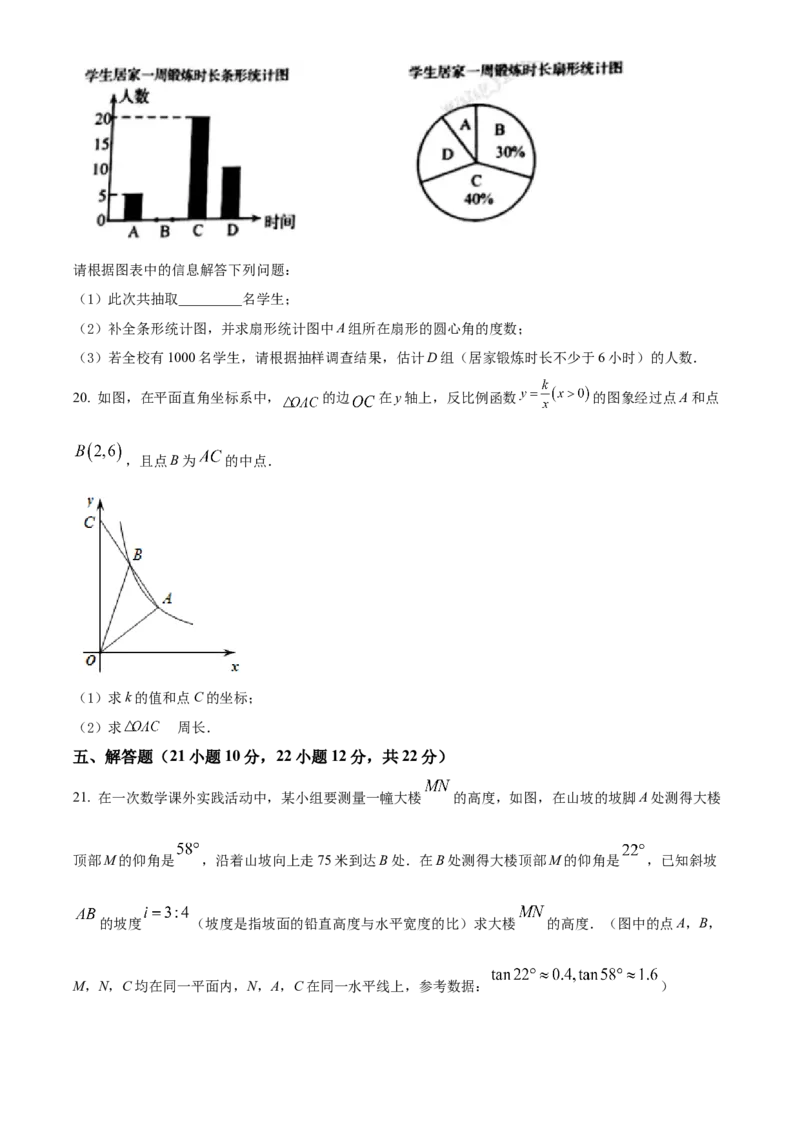
19. 某校为了了解疫情期间学生居家锻炼时长的情况,随机抽取了部分学生,就居家一周的锻炼时长进行
了统计调查,根据调查结果,将居家锻炼时长分为A,B,C,D四个组别.
学生居家锻炼时长分组表
组别 A B C D
t(小时)
下面两幅图为不完整的统计图.请根据图表中的信息解答下列问题:
(1)此次共抽取_________名学生;
(2)补全条形统计图,并求扇形统计图中A组所在扇形的圆心角的度数;
(3)若全校有1000名学生,请根据抽样调查结果,估计D组(居家锻炼时长不少于6小时)的人数.
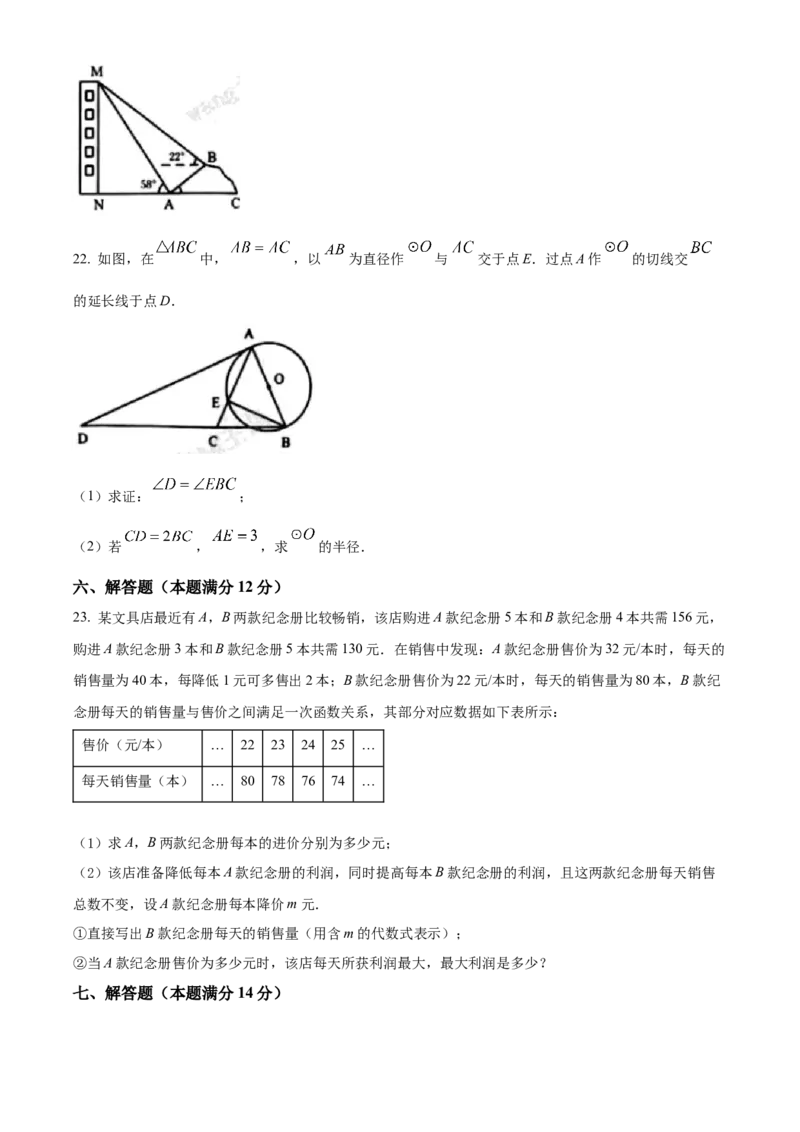
20. 如图,在平面直角坐标系中, 的边 在y轴上,反比例函数 的图象经过点A和点
,且点B为 的中点.
(1)求k的值和点C的坐标;
(2)求 的周长.
五、解答题(21小题10分,22小题12分,共22分)
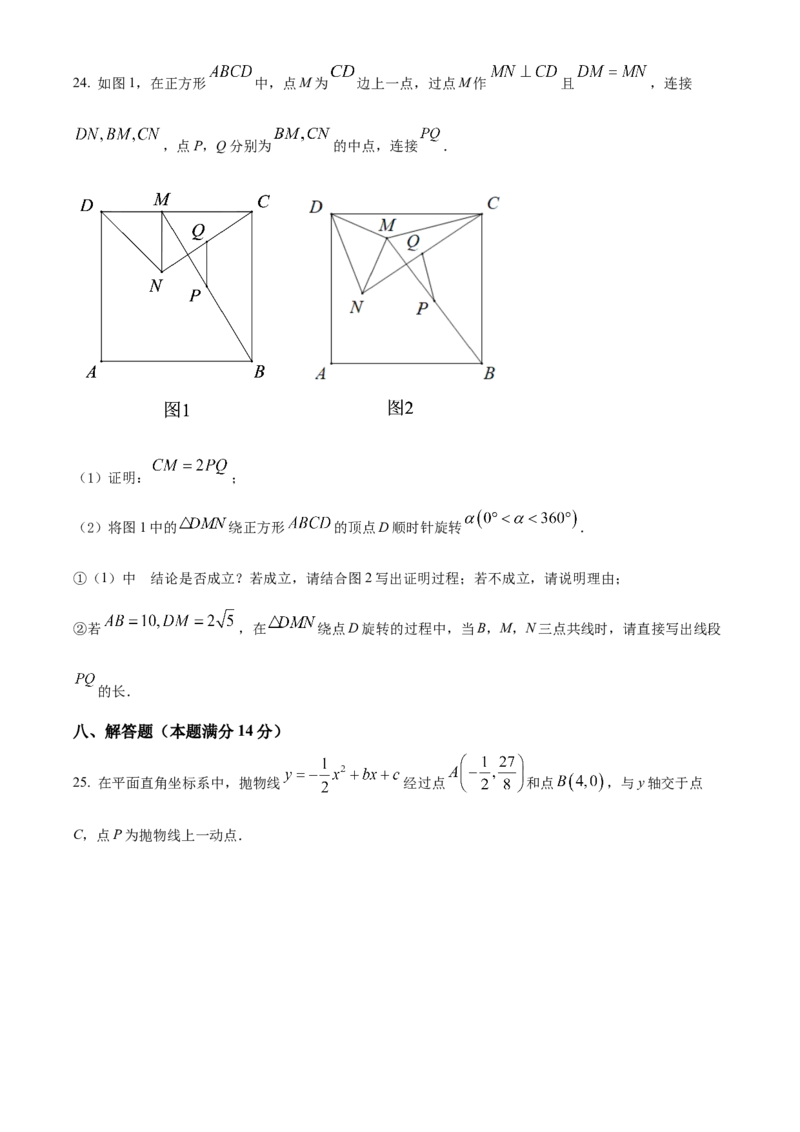
21. 在一次数学课外实践活动中,某小组要测量一幢大楼 的高度,如图,在山坡的坡脚A处测得大楼
顶部M的仰角是 ,沿着山坡向上走75米到达B处.在B处测得大楼顶部M的仰角是 ,已知斜坡
的坡度 (坡度是指坡面的铅直高度与水平宽度的比)求大楼 的高度.(图中的点A,B,
M,N,C均在同一平面内,N,A,C在同一水平线上,参考数据: )22. 如图,在 中, ,以 为直径作 与 交于点E.过点A作 的切线交
的延长线于点D.
(1)求证: ;
(2)若 , ,求 的半径.
六、解答题(本题满分12分)
23. 某文具店最近有A,B两款纪念册比较畅销,该店购进A款纪念册5本和B款纪念册4本共需156元,
购进A款纪念册3本和B款纪念册5本共需130元.在销售中发现:A款纪念册售价为32元/本时,每天的
销售量为40本,每降低1元可多售出2本;B款纪念册售价为22元/本时,每天的销售量为80本,B款纪
念册每天的销售量与售价之间满足一次函数关系,其部分对应数据如下表所示:
售价(元/本) … 22 23 24 25 …
每天销售量(本) … 80 78 76 74 …
(1)求A,B两款纪念册每本的进价分别为多少元;
(2)该店准备降低每本A款纪念册的利润,同时提高每本B款纪念册的利润,且这两款纪念册每天销售
总数不变,设A款纪念册每本降价m元.
①直接写出B款纪念册每天的销售量(用含m的代数式表示);
②当A款纪念册售价为多少元时,该店每天所获利润最大,最大利润是多少?
七、解答题(本题满分14分)24. 如图1,在正方形 中,点M为 边上一点,过点M作 且 ,连接
,点P,Q分别为 的中点,连接 .
(1)证明: ;
(2)将图1中的 绕正方形 的顶点D顺时针旋转 .
的
①(1)中 结论是否成立?若成立,请结合图2写出证明过程;若不成立,请说明理由;
②若 ,在 绕点D旋转的过程中,当B,M,N三点共线时,请直接写出线段
的长.
八、解答题(本题满分14分)
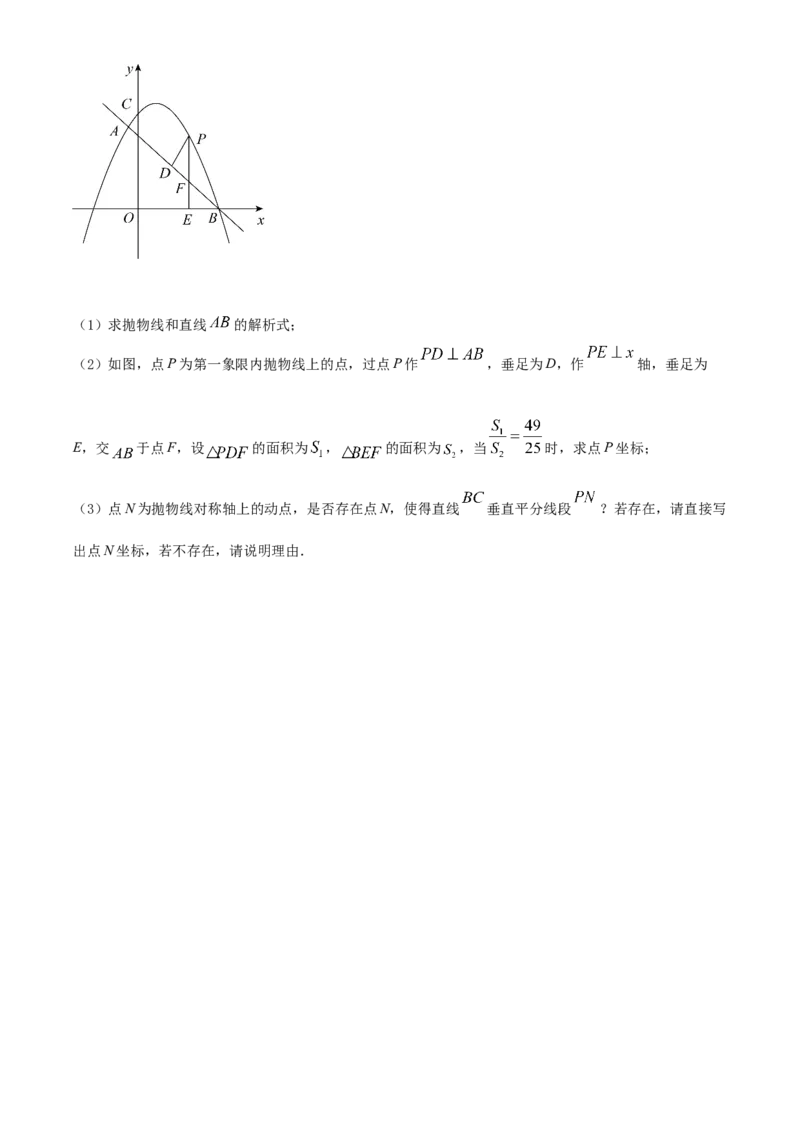
25. 在平面直角坐标系中,抛物线 经过点 和点 ,与y轴交于点
C,点P为抛物线上一动点.(1)求抛物线和直线 的解析式;
(2)如图,点P为第一象限内抛物线上的点,过点P作 ,垂足为D,作 轴,垂足为
E,交 于点F,设 的面积为 , 的面积为 ,当 时,求点P坐标;
(3)点N为抛物线对称轴上的动点,是否存在点N,使得直线 垂直平分线段 ?若存在,请直接写
出点N坐标,若不存在,请说明理由.