文档内容
2023年陕西省中考数学试卷(副卷)
一、选择题(共8小题,每小题3分,计24分.每小题只有一个选项是符合题意的)
1.(3分)计算:|﹣17|=( )
1 1
A.17 B.﹣17 C. D.-
17 17
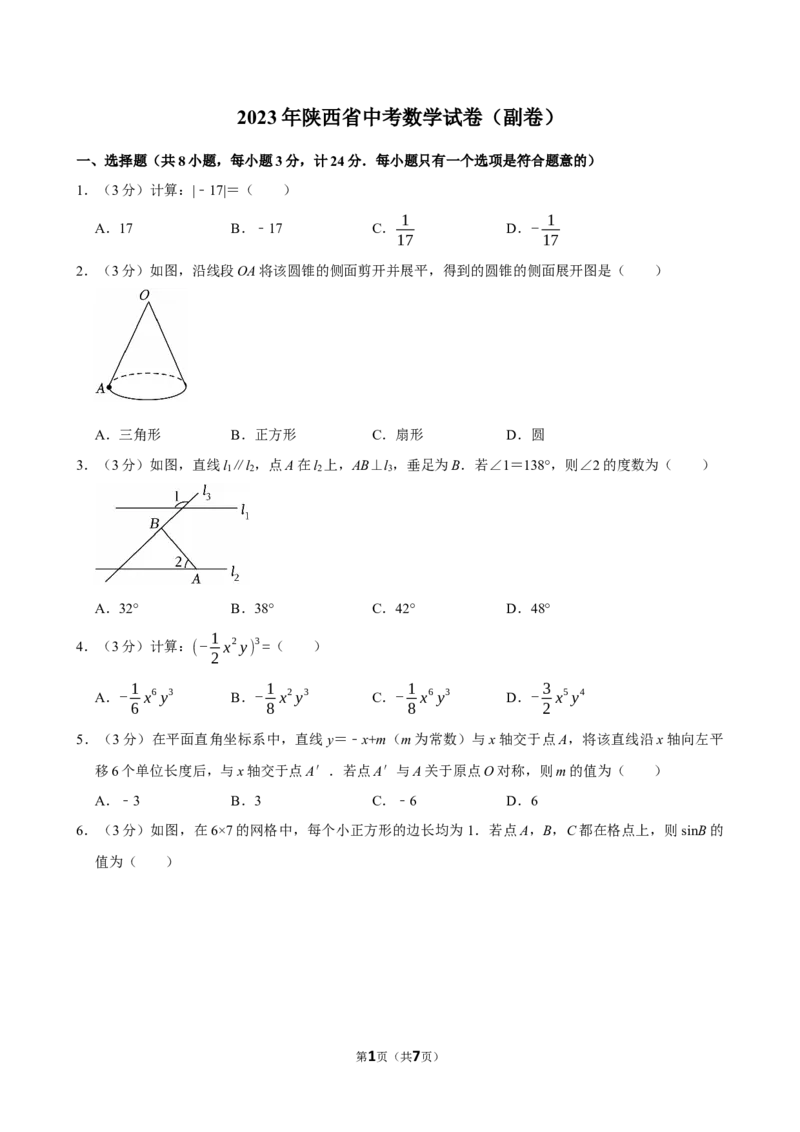
2.(3分)如图,沿线段OA将该圆锥的侧面剪开并展平,得到的圆锥的侧面展开图是( )
A.三角形 B.正方形 C.扇形 D.圆
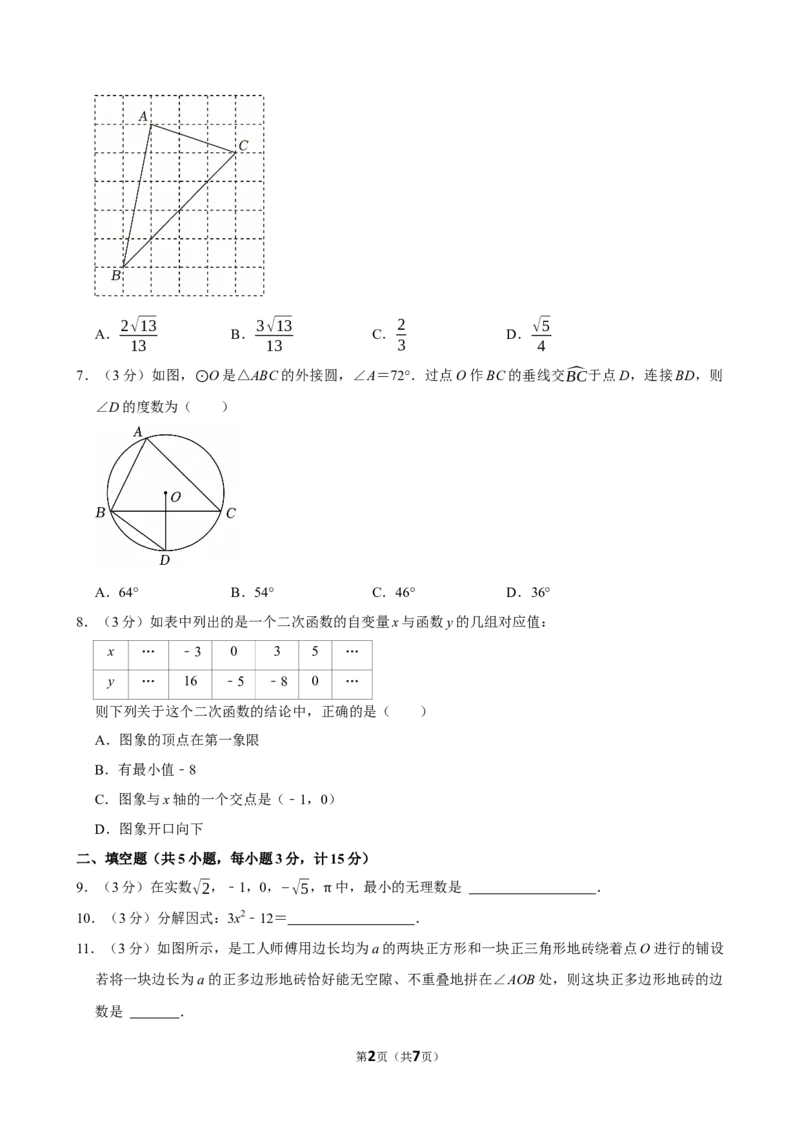
3.(3分)如图,直线l ∥l ,点A在l 上,AB⊥l ,垂足为B.若∠1=138°,则∠2的度数为( )
1 2 2 3
A.32° B.38° C.42° D.48°
1
4.(3分)计算:(- x2y) 3=( )
2
1 1 1 3
A.- x6 y3 B.- x2y3 C.- x6 y3 D.- x5y4
6 8 8 2
5.(3分)在平面直角坐标系中,直线y=﹣x+m(m为常数)与x轴交于点A,将该直线沿x轴向左平
移6个单位长度后,与x轴交于点A′.若点A′与A关于原点O对称,则m的值为( )
A.﹣3 B.3 C.﹣6 D.6
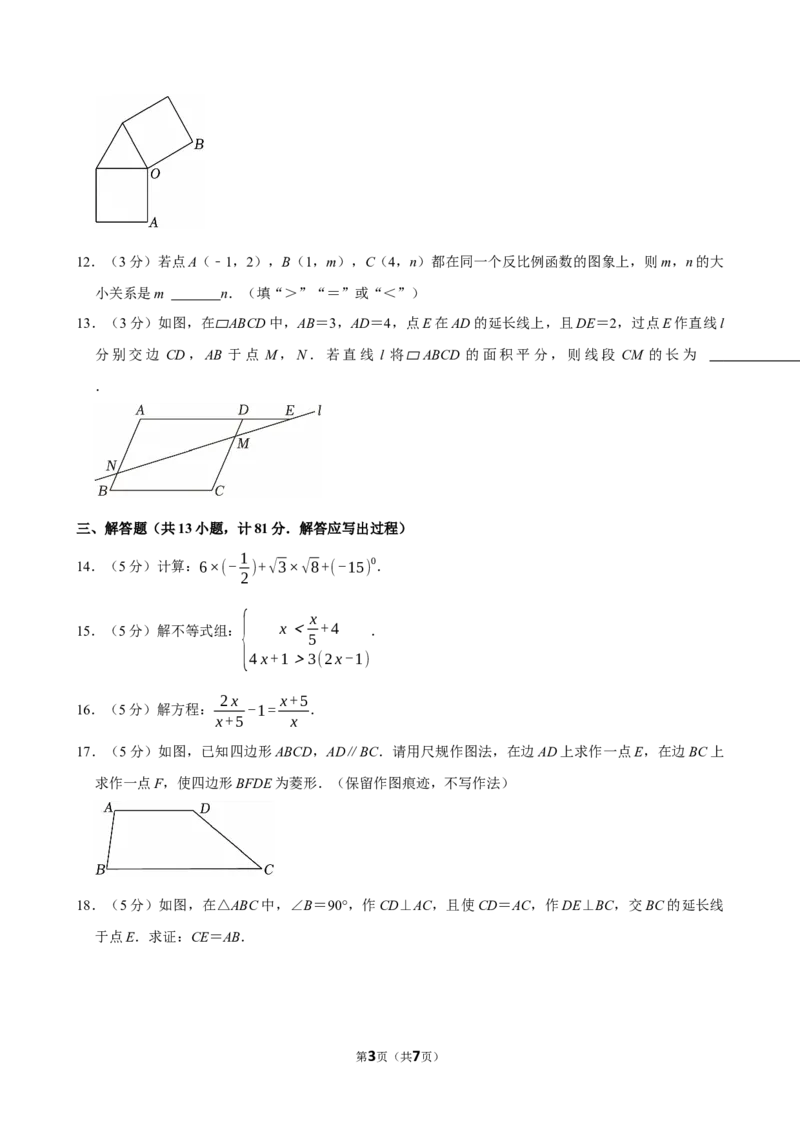
6.(3分)如图,在6×7的网格中,每个小正方形的边长均为1.若点A,B,C都在格点上,则sinB的
值为( )
第1页(共7页)2√13 3√13 2 √5
A. B. C. D.
13 13 3 4
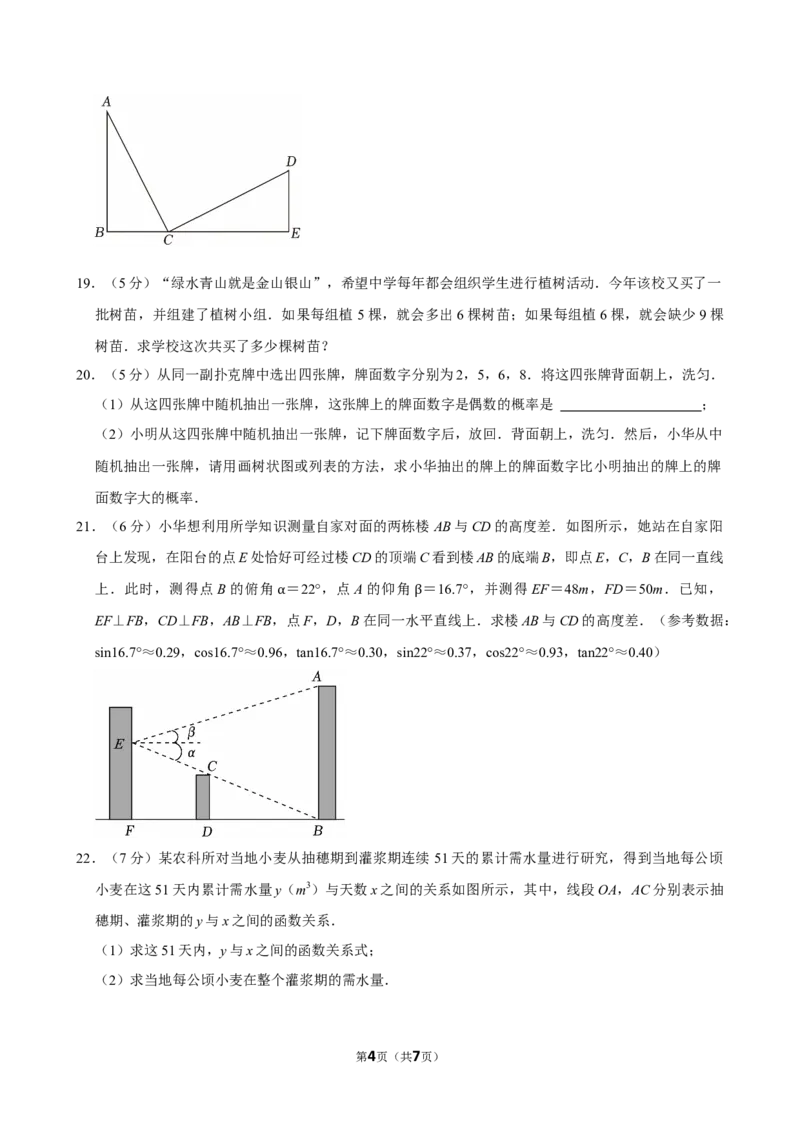
7.(3分)如图, O是△ABC的外接圆,∠A=72°.过点O作BC的垂线交^BC于点D,连接BD,则
∠D的度数为( ⊙ )
A.64° B.54° C.46° D.36°
8.(3分)如表中列出的是一个二次函数的自变量x与函数y的几组对应值:
x … ﹣3 0 3 5 …
y … 16 ﹣5 ﹣8 0 …
则下列关于这个二次函数的结论中,正确的是( )
A.图象的顶点在第一象限
B.有最小值﹣8
C.图象与x轴的一个交点是(﹣1,0)
D.图象开口向下
二、填空题(共5小题,每小题3分,计15分)
9.(3分)在实数√2,﹣1,0,-√5, 中,最小的无理数是 .
10.(3分)分解因式:3x2﹣12= π .
11.(3分)如图所示,是工人师傅用边长均为a的两块正方形和一块正三角形地砖绕着点O进行的铺设
若将一块边长为a的正多边形地砖恰好能无空隙、不重叠地拼在∠AOB处,则这块正多边形地砖的边
数是 .
第2页(共7页)12.(3分)若点A(﹣1,2),B(1,m),C(4,n)都在同一个反比例函数的图象上,则m,n的大
小关系是m n.(填“>”“=”或“<”)
13.(3分)如图,在 ABCD中,AB=3,AD=4,点E在AD的延长线上,且DE=2,过点E作直线l
分别交边 CD,AB▱于点 M,N.若直线 l 将 ABCD 的面积平分,则线段 CM 的长为
. ▱
三、解答题(共13小题,计81分.解答应写出过程)
1
14.(5分)计算:6×(- )+√3×√8+(-15) 0.
2
{ x
15.(5分)解不等式组: x< +4 .
5
4x+1>3(2x-1)
2x x+5
16.(5分)解方程: -1= .
x+5 x
17.(5分)如图,已知四边形ABCD,AD∥BC.请用尺规作图法,在边AD上求作一点E,在边BC上
求作一点F,使四边形BFDE为菱形.(保留作图痕迹,不写作法)
18.(5分)如图,在△ABC中,∠B=90°,作CD⊥AC,且使CD=AC,作DE⊥BC,交BC的延长线
于点E.求证:CE=AB.
第3页(共7页)19.(5分)“绿水青山就是金山银山”,希望中学每年都会组织学生进行植树活动.今年该校又买了一
批树苗,并组建了植树小组.如果每组植 5棵,就会多出6棵树苗;如果每组植6棵,就会缺少9棵
树苗.求学校这次共买了多少棵树苗?
20.(5分)从同一副扑克牌中选出四张牌,牌面数字分别为2,5,6,8.将这四张牌背面朝上,洗匀.
(1)从这四张牌中随机抽出一张牌,这张牌上的牌面数字是偶数的概率是 ;
(2)小明从这四张牌中随机抽出一张牌,记下牌面数字后,放回.背面朝上,洗匀.然后,小华从中
随机抽出一张牌,请用画树状图或列表的方法,求小华抽出的牌上的牌面数字比小明抽出的牌上的牌
面数字大的概率.
21.(6分)小华想利用所学知识测量自家对面的两栋楼 AB与CD的高度差.如图所示,她站在自家阳
台上发现,在阳台的点E处恰好可经过楼CD的顶端C看到楼AB的底端B,即点E,C,B在同一直线
上.此时,测得点 B的俯角 =22°,点A的仰角 =16.7°,并测得EF=48m,FD=50m.已知,
EF⊥FB,CD⊥FB,AB⊥FB,α点F,D,B在同一水β平直线上.求楼AB与CD的高度差.(参考数据:
sin16.7°≈0.29,cos16.7°≈0.96,tan16.7°≈0.30,sin22°≈0.37,cos22°≈0.93,tan22°≈0.40)
22.(7分)某农科所对当地小麦从抽穗期到灌浆期连续 51天的累计需水量进行研究,得到当地每公顷
小麦在这51天内累计需水量y(m3)与天数x之间的关系如图所示,其中,线段OA,AC分别表示抽
穗期、灌浆期的y与x之间的函数关系.
(1)求这51天内,y与x之间的函数关系式;
(2)求当地每公顷小麦在整个灌浆期的需水量.
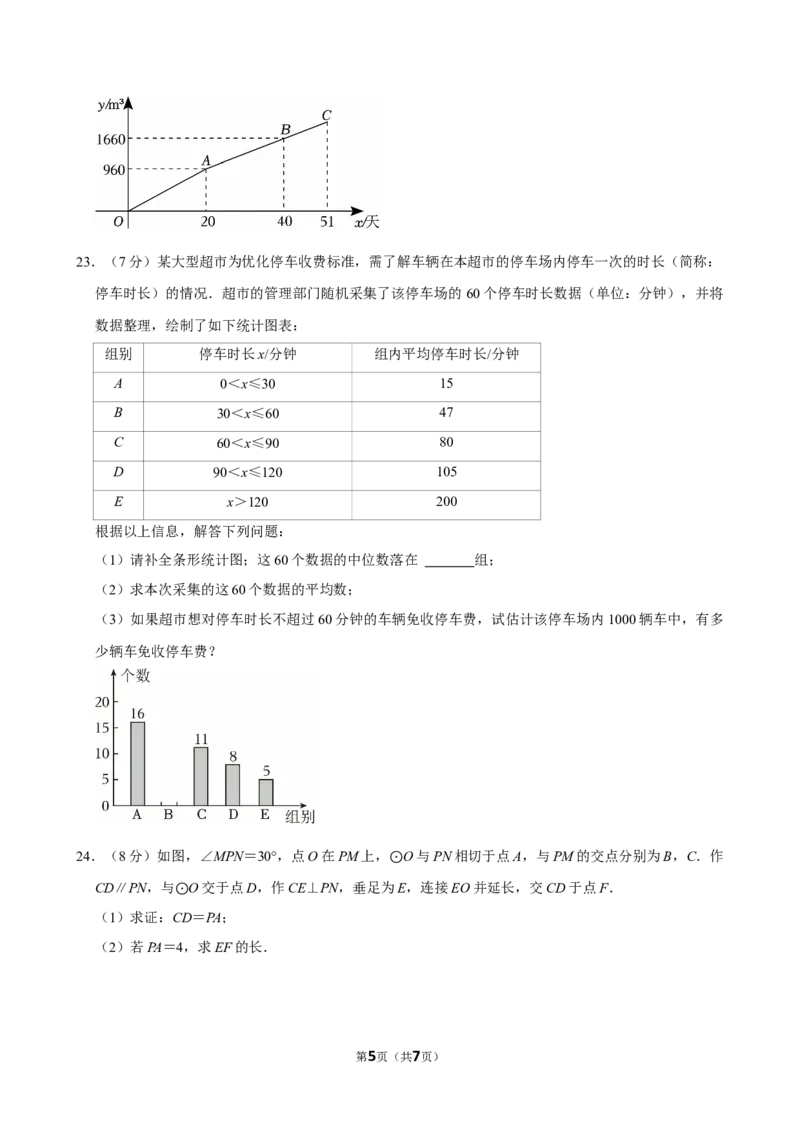
第4页(共7页)23.(7分)某大型超市为优化停车收费标准,需了解车辆在本超市的停车场内停车一次的时长(简称:
停车时长)的情况.超市的管理部门随机采集了该停车场的 60个停车时长数据(单位:分钟),并将
数据整理,绘制了如下统计图表:
组别 停车时长x/分钟 组内平均停车时长/分钟
A 0<x≤30 15
B 30<x≤60 47
C 60<x≤90 80
D 90<x≤120 105
E x>120 200
根据以上信息,解答下列问题:
(1)请补全条形统计图;这60个数据的中位数落在 组;
(2)求本次采集的这60个数据的平均数;
(3)如果超市想对停车时长不超过60分钟的车辆免收停车费,试估计该停车场内1000辆车中,有多
少辆车免收停车费?
24.(8分)如图,∠MPN=30°,点O在PM上, O与PN相切于点A,与PM的交点分别为B,C.作
CD∥PN,与 O交于点D,作CE⊥PN,垂足为⊙E,连接EO并延长,交CD于点F.
(1)求证:C⊙D=PA;
(2)若PA=4,求EF的长.
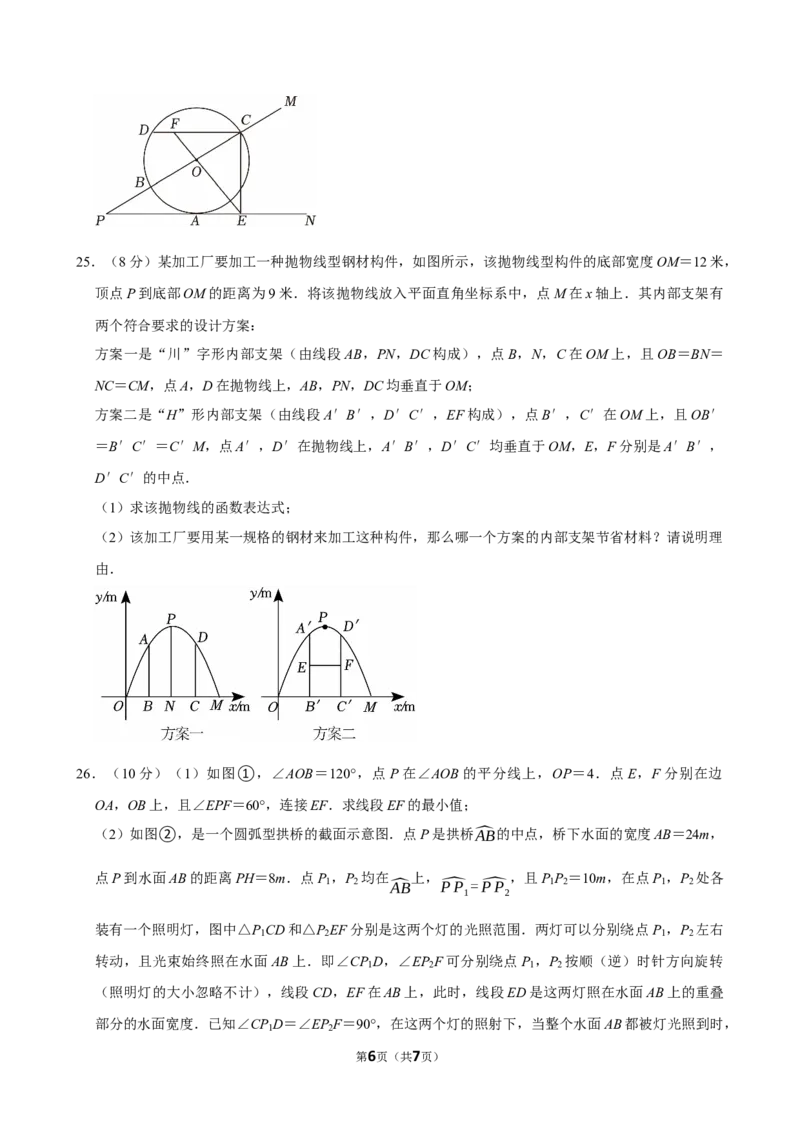
第5页(共7页)25.(8分)某加工厂要加工一种抛物线型钢材构件,如图所示,该抛物线型构件的底部宽度OM=12米,
顶点P到底部OM的距离为9米.将该抛物线放入平面直角坐标系中,点M在x轴上.其内部支架有
两个符合要求的设计方案:
方案一是“川”字形内部支架(由线段AB,PN,DC构成),点B,N,C在OM上,且OB=BN=
NC=CM,点A,D在抛物线上,AB,PN,DC均垂直于OM;
方案二是“H”形内部支架(由线段A′B′,D′C′,EF构成),点B′,C′在OM上,且OB′
=B′C′=C′M,点A′,D′在抛物线上,A′B′,D′C′均垂直于OM,E,F分别是A′B′,
D′C′的中点.
(1)求该抛物线的函数表达式;
(2)该加工厂要用某一规格的钢材来加工这种构件,那么哪一个方案的内部支架节省材料?请说明理
由.
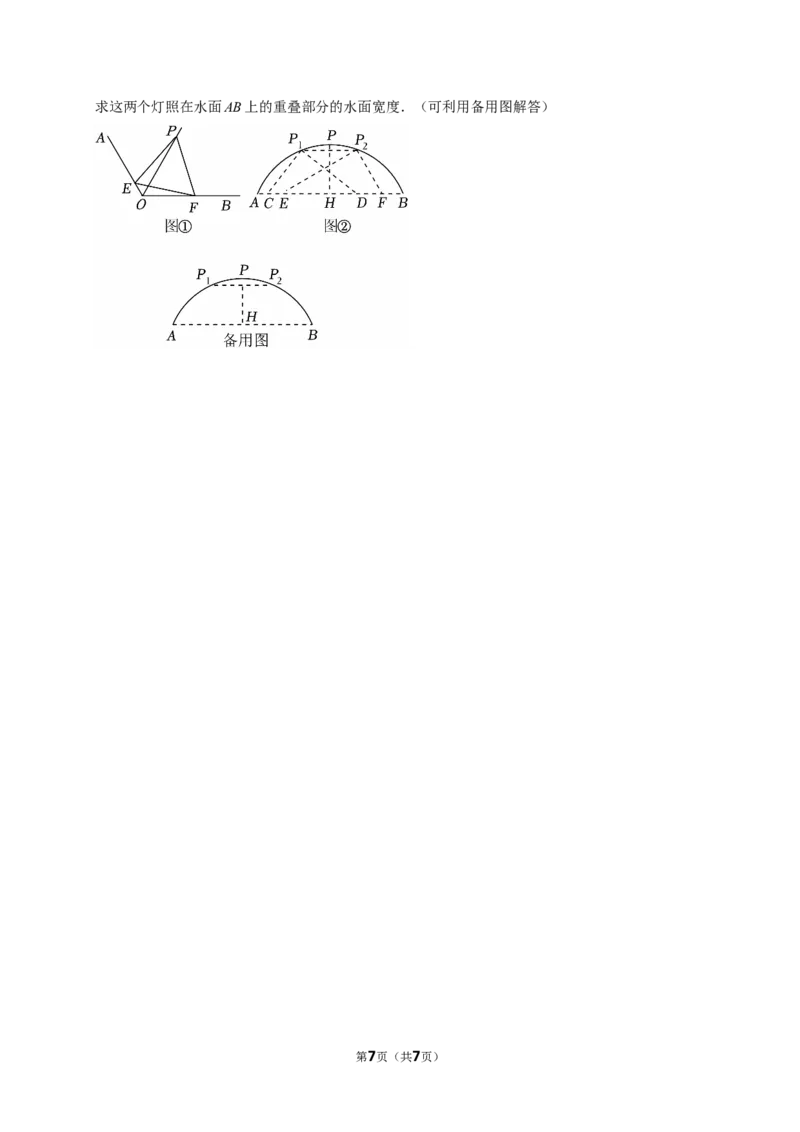
26.(10分)(1)如图①,∠AOB=120°,点P在∠AOB的平分线上,OP=4.点E,F分别在边
OA,OB上,且∠EPF=60°,连接EF.求线段EF的最小值;
(2)如图②,是一个圆弧型拱桥的截面示意图.点P是拱桥^AB的中点,桥下水面的宽度AB=24m,
点P到水面AB的距离PH=8m.点P ,P 均在 上, ,且P P =10m,在点P ,P 处各
1 2 ^AB ^PP =^PP 1 2 1 2
1 2
装有一个照明灯,图中△P CD和△P EF分别是这两个灯的光照范围.两灯可以分别绕点P ,P 左右
1 2 1 2
转动,且光束始终照在水面AB上.即∠CP D,∠EP F可分别绕点P ,P 按顺(逆)时针方向旋转
1 2 1 2
(照明灯的大小忽略不计),线段CD,EF在AB上,此时,线段ED是这两灯照在水面AB上的重叠
部分的水面宽度.已知∠CP D=∠EP F=90°,在这两个灯的照射下,当整个水面AB都被灯光照到时,
1 2
第6页(共7页)求这两个灯照在水面AB上的重叠部分的水面宽度.(可利用备用图解答)
声明:试题解析著作权属菁优网所有,未经书面同意,不得复制发布日期:2025/1/12 22:00:39;用户:庞俊梅;邮箱:18715777852;学号:54801
第7页(共7页)