文档内容
2024年湖北省中考数学试卷
一、选择题(共10题,每题3分,共30分,在每题给出的四个选项中,只有一项符合题目要求)
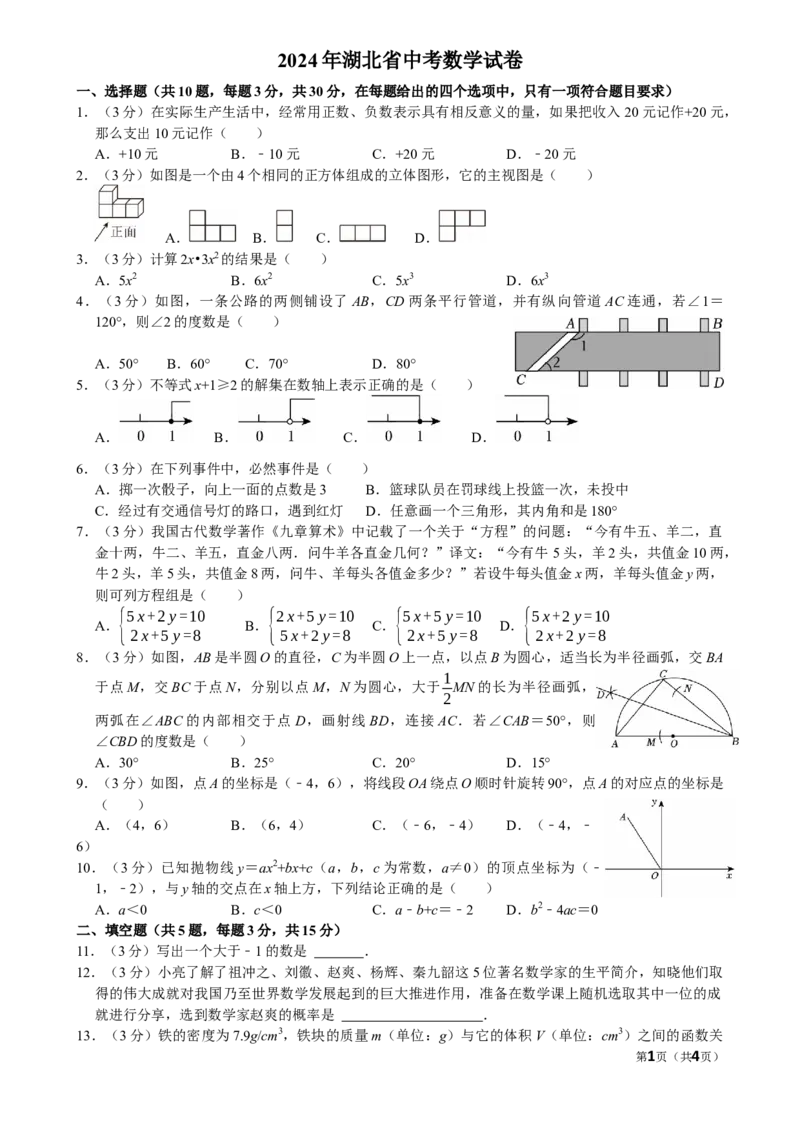
1.(3分)在实际生产生活中,经常用正数、负数表示具有相反意义的量,如果把收入 20元记作+20元,
那么支出10元记作( )
A.+10元 B.﹣10元 C.+20元 D.﹣20元
2.(3分)如图是一个由4个相同的正方体组成的立体图形,它的主视图是( )
A. B. C. D.
3.(3分)计算2x•3x2的结果是( )
A.5x2 B.6x2 C.5x3 D.6x3
4.(3分)如图,一条公路的两侧铺设了 AB,CD两条平行管道,并有纵向管道 AC连通,若∠1=
120°,则∠2的度数是( )
A.50° B.60° C.70° D.80°
5.(3分)不等式x+1≥2的解集在数轴上表示正确的是( )
A. B. C. D.
6.(3分)在下列事件中,必然事件是( )
A.掷一次骰子,向上一面的点数是3 B.篮球队员在罚球线上投篮一次,未投中
C.经过有交通信号灯的路口,遇到红灯 D.任意画一个三角形,其内角和是180°
7.(3分)我国古代数学著作《九章算术》中记载了一个关于“方程”的问题:“今有牛五、羊二,直
金十两,牛二、羊五,直金八两.问牛羊各直金几何?”译文:“今有牛 5头,羊2头,共值金10两,
牛2头,羊5头,共值金8两,问牛、羊每头各值金多少?”若设牛每头值金x两,羊每头值金y两,
则可列方程组是( )
{5x+2y=10 {2x+5 y=10 {5x+5 y=10 {5x+2y=10
A. B. C. D.
2x+5 y=8 5x+2y=8 2x+5 y=8 2x+2y=8
8.(3分)如图,AB是半圆O的直径,C为半圆O上一点,以点B为圆心,适当长为半径画弧,交BA
1
于点M,交BC于点N,分别以点M,N为圆心,大于 MN的长为半径画弧,
2
两弧在∠ABC的内部相交于点 D,画射线BD,连接AC.若∠CAB=50°,则
∠CBD的度数是( )
A.30° B.25° C.20° D.15°
9.(3分)如图,点A的坐标是(﹣4,6),将线段OA绕点O顺时针旋转90°,点A的对应点的坐标是
( )
A.(4,6) B.(6,4) C.(﹣6,﹣4) D.(﹣4,﹣
6)
10.(3分)已知抛物线y=ax2+bx+c(a,b,c为常数,a≠0)的顶点坐标为(﹣
1,﹣2),与y轴的交点在x轴上方,下列结论正确的是( )
A.a<0 B.c<0 C.a﹣b+c=﹣2 D.b2﹣4ac=0
二、填空题(共5题,每题3分,共15分)
11.(3分)写出一个大于﹣1的数是 .
12.(3分)小亮了解了祖冲之、刘徽、赵爽、杨辉、秦九韶这5位著名数学家的生平简介,知晓他们取
得的伟大成就对我国乃至世界数学发展起到的巨大推进作用,准备在数学课上随机选取其中一位的成
就进行分享,选到数学家赵爽的概率是 .
13.(3分)铁的密度为7.9g/cm3,铁块的质量m(单位:g)与它的体积V(单位:cm3)之间的函数关
第1页(共4页)系式为m=7.9V,当V=10cm3时,m= g.
m 1
14.(3分)计算 + 的结果是 .
m+1 m+1
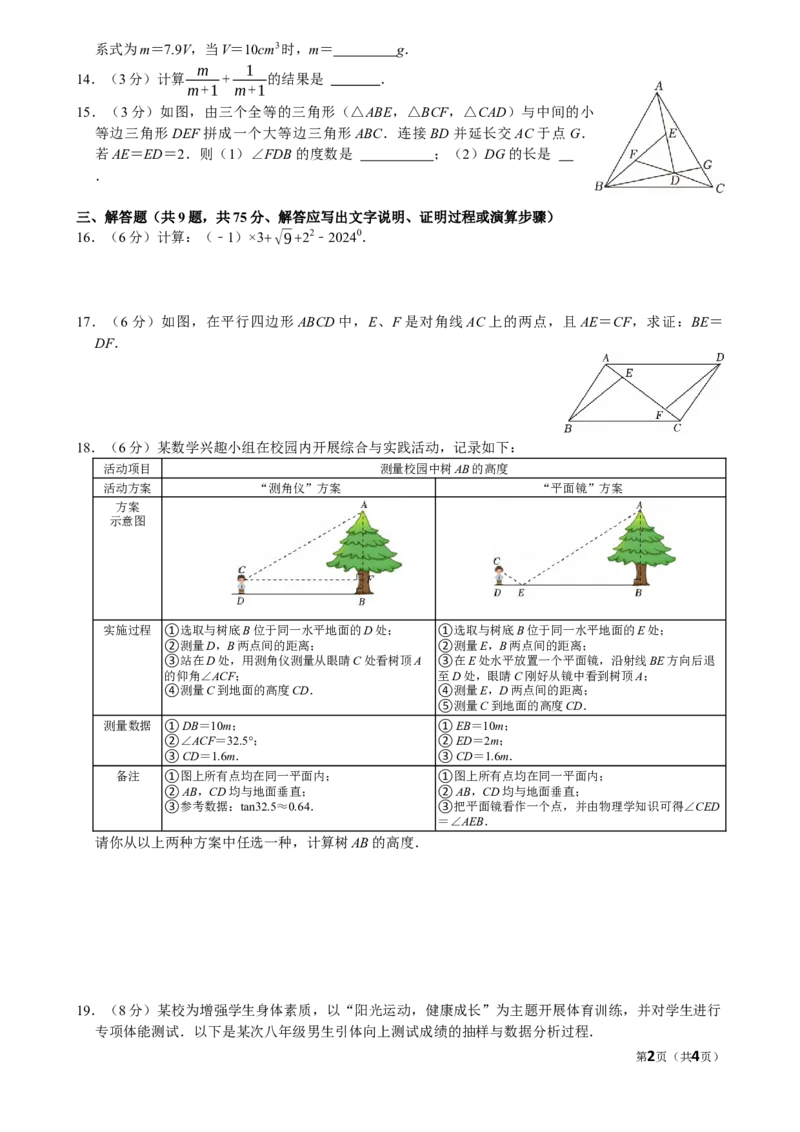
15.(3分)如图,由三个全等的三角形(△ABE,△BCF,△CAD)与中间的小
等边三角形DEF拼成一个大等边三角形ABC.连接BD并延长交AC于点G.
若AE=ED=2.则(1)∠FDB的度数是 ;(2)DG的长是
.
三、解答题(共9题,共75分、解答应写出文字说明、证明过程或演算步骤)
16.(6分)计算:(﹣1)×3+√9+22﹣20240.
17.(6分)如图,在平行四边形ABCD中,E、F是对角线AC上的两点,且AE=CF,求证:BE=
DF.
18.(6分)某数学兴趣小组在校园内开展综合与实践活动,记录如下:
活动项目 测量校园中树AB的高度
活动方案 “测角仪”方案 “平面镜”方案
方案
示意图
实施过程 ①选取与树底B位于同一水平地面的D处; ①选取与树底B位于同一水平地面的E处;
②测量D,B两点间的距离; ②测量E,B两点间的距离;
③站在D处,用测角仪测量从眼睛C处看树顶A ③在E处水平放置一个平面镜,沿射线BE方向后退
的仰角∠ACF; 至D处,眼睛C刚好从镜中看到树顶A;
④测量C到地面的高度CD. ④测量E,D两点间的距离;
⑤测量C到地面的高度CD.
测量数据 ①DB=10m; ①EB=10m;
②∠ACF=32.5°; ②ED=2m;
③CD=1.6m. ③CD=1.6m.
备注 ①图上所有点均在同一平面内; ①图上所有点均在同一平面内;
②AB,CD均与地面垂直; ②AB,CD均与地面垂直;
③参考数据:tan32.5≈0.64. ③把平面镜看作一个点,并由物理学知识可得∠CED
=∠AEB.
请你从以上两种方案中任选一种,计算树AB的高度.
19.(8分)某校为增强学生身体素质,以“阳光运动,健康成长”为主题开展体育训练,并对学生进行
专项体能测试.以下是某次八年级男生引体向上测试成绩的抽样与数据分析过程.
第2页(共4页)【收集数据】随机抽取若干名男生的测试成绩.
【整理数据】将抽取的成绩进行整理,用x(引体向上个数)表示成绩,分成四组:
A组(0≤x<5),B组(5≤x<10),C组(10≤x<14),D组(x≥14).
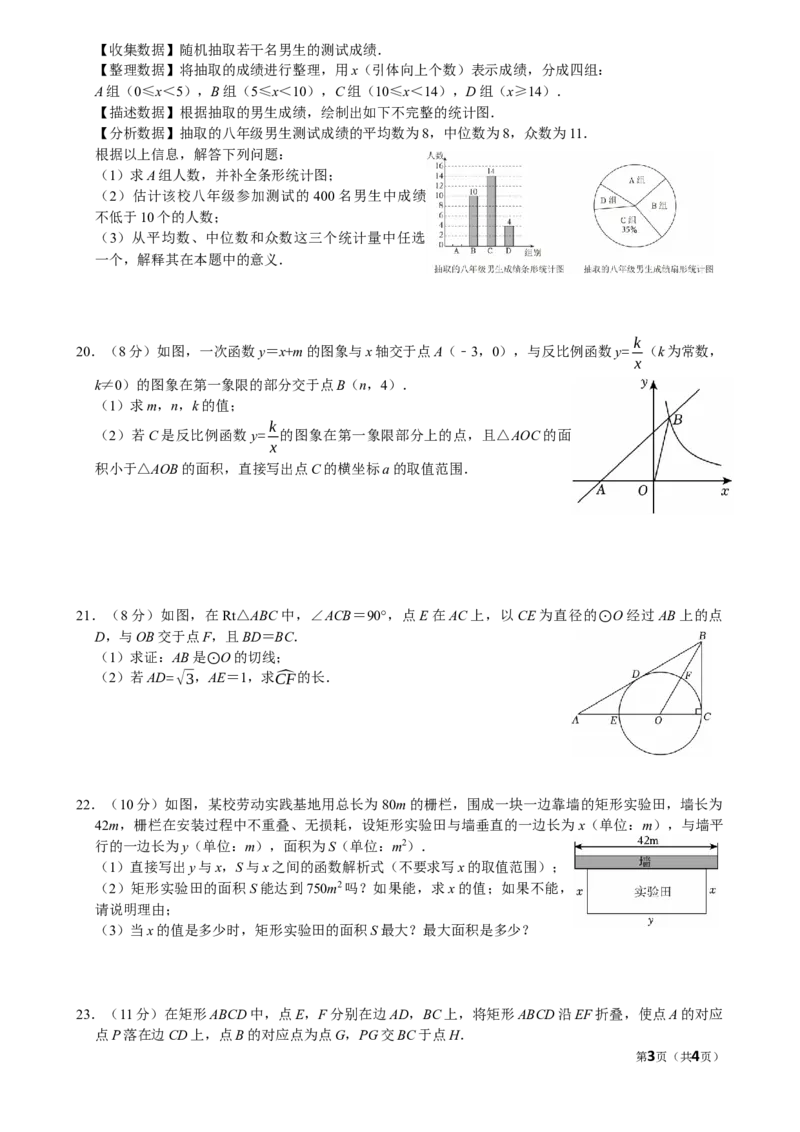
【描述数据】根据抽取的男生成绩,绘制出如下不完整的统计图.
【分析数据】抽取的八年级男生测试成绩的平均数为8,中位数为8,众数为11.
根据以上信息,解答下列问题:
(1)求A组人数,并补全条形统计图;
(2)估计该校八年级参加测试的400名男生中成绩
不低于10个的人数;
(3)从平均数、中位数和众数这三个统计量中任选
一个,解释其在本题中的意义.
k
20.(8分)如图,一次函数y=x+m的图象与x轴交于点A(﹣3,0),与反比例函数y= (k为常数,
x
k≠0)的图象在第一象限的部分交于点B(n,4).
(1)求m,n,k的值;
k
(2)若C是反比例函数y= 的图象在第一象限部分上的点,且△AOC的面
x
积小于△AOB的面积,直接写出点C的横坐标a的取值范围.
21.(8分)如图,在Rt△ABC中,∠ACB=90°,点E在AC上,以CE为直径的 O经过AB上的点
D,与OB交于点F,且BD=BC.
⊙
(1)求证:AB是 O的切线;
(2)若AD=√3,AE=1,求C^F的长.
⊙
22.(10分)如图,某校劳动实践基地用总长为80m的栅栏,围成一块一边靠墙的矩形实验田,墙长为
42m,栅栏在安装过程中不重叠、无损耗,设矩形实验田与墙垂直的一边长为 x(单位:m),与墙平
行的一边长为y(单位:m),面积为S(单位:m2).
(1)直接写出y与x,S与x之间的函数解析式(不要求写x的取值范围);
(2)矩形实验田的面积S能达到750m2吗?如果能,求x的值;如果不能,
请说明理由;
(3)当x的值是多少时,矩形实验田的面积S最大?最大面积是多少?
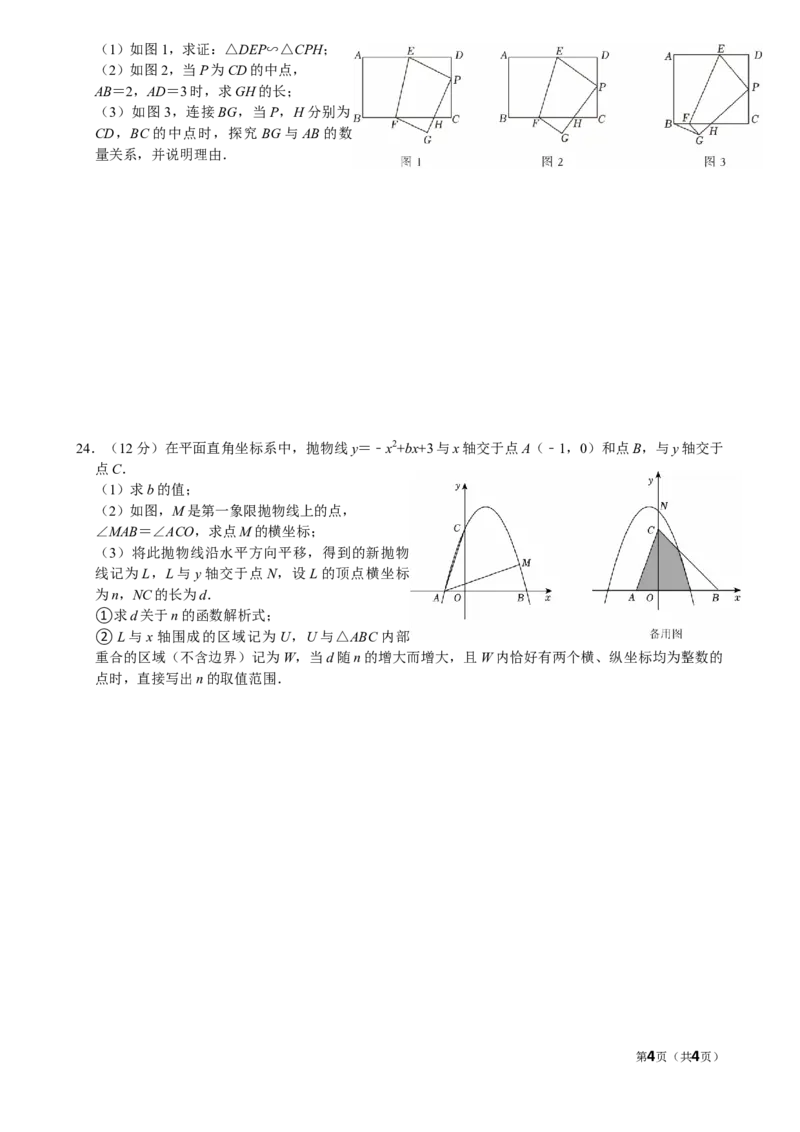
23.(11分)在矩形ABCD中,点E,F分别在边AD,BC上,将矩形ABCD沿EF折叠,使点A的对应
点P落在边CD上,点B的对应点为点G,PG交BC于点H.
第3页(共4页)(1)如图1,求证:△DEP∽△CPH;
(2)如图2,当P为CD的中点,
AB=2,AD=3时,求GH的长;
(3)如图3,连接BG,当P,H分别为
CD,BC的中点时,探究 BG与AB的数
量关系,并说明理由.
24.(12分)在平面直角坐标系中,抛物线y=﹣x2+bx+3与x轴交于点A(﹣1,0)和点B,与y轴交于
点C.
(1)求b的值;
(2)如图,M是第一象限抛物线上的点,
∠MAB=∠ACO,求点M的横坐标;
(3)将此抛物线沿水平方向平移,得到的新抛物
线记为L,L与y轴交于点N,设L的顶点横坐标
为n,NC的长为d.
①求d关于n的函数解析式;
②L与x轴围成的区域记为 U,U与△ABC内部
重合的区域(不含边界)记为W,当d随n的增大而增大,且W内恰好有两个横、纵坐标均为整数的
点时,直接写出n的取值范围.
第4页(共4页)