文档内容
2024年湖北省中考数学试卷
参考答案与试题解析
题号 1 2 3 4 5 6 7 8 9 10
答案 B A D B A D A C B C
一、选择题(共10题,每题3分,共30分,在每题给出的四个选项中,只有一项符合题目要求)
1.(3分)在实际生产生活中,经常用正数、负数表示具有相反意义的量,如果把收入 20元记作+20元,
那么支出10元记作( )
A.+10元 B.﹣10元 C.+20元 D.﹣20元
【分析】在一对具有相反意义的量中,先规定其中一个为正,则另一个就用负表示.
【解答】解:“正”和“负”相对,所以,在生产生活中,正数和负数都有现实意义.例如收 20元记
作+20元,则支出10元记作﹣10元.
故选:B.
2.(3分)如图是一个由4个相同的正方体组成的立体图形,它的主视图是( )
A. B. C. D.
【分析】找到从正面看所得到的图形即可,注意所有的看到的棱都应表现在主视图中.
【解答】解:从正面看有两层,底层4个正方形,上层左边个正方形.
故选:A.
3.(3分)计算2x•3x2的结果是( )
A.5x2 B.6x2 C.5x3 D.6x3
【分析】根据单项式乘单项式法则计算即可.
【解答】解:2x•3x2=6x3.
故选:D.
4.(3分)如图,一条公路的两侧铺设了 AB,CD两条平行管道,并有纵向管道 AC连通,若∠1=
120°,则∠2的度数是( )
A.50° B.60° C.70° D.80°
【分析】根据两直线平行,同旁内角互补进行计算,即可解答.
【解答】解:∵AB∥CD,
∴∠1+∠2=180°,
∵∠1=120°,
∴∠2=180°﹣∠1=60°,
故选:B.
5.(3分)不等式x+1≥2的解集在数轴上表示正确的是( )
A. B.
第1页(共15页)C. D.
【分析】求出不等式的解集,再在数轴上表示出来即可.
【解答】解:∵x+1≥2,
∴x≥1,
在数轴上表示为:
.
故选:A.
6.(3分)在下列事件中,必然事件是( )
A.掷一次骰子,向上一面的点数是3
B.篮球队员在罚球线上投篮一次,未投中
C.经过有交通信号灯的路口,遇到红灯
D.任意画一个三角形,其内角和是180°
【分析】根据必然事件、随机事件的意义进行判断即可.
【解答】解:A.掷一次骰子,向上一面的点数是3,是随机事件,不符合题意;
B.篮球队员在罚球线上投篮一次,未投中,是随机事件,不符合题意;
C.经过有交通信号灯的路口,遇到红灯,是随机事件,不符合题意;
D.任意画一个三角形,其内角和是180°,是必然事件,符合题意.
故选:D.
7.(3分)我国古代数学著作《九章算术》中记载了一个关于“方程”的问题:“今有牛五、羊二,直
金十两,牛二、羊五,直金八两.问牛羊各直金几何?”译文:“今有牛 5头,羊2头,共值金10两,
牛2头,羊5头,共值金8两,问牛、羊每头各值金多少?”若设牛每头值金x两,羊每头值金y两,
则可列方程组是( )
{5x+2y=10 {2x+5 y=10
A. B.
2x+5 y=8 5x+2y=8
{5x+5 y=10 {5x+2y=10
C. D.
2x+5 y=8 2x+2y=8
【分析】因为每头牛值金x两,每头羊值金y两,根据“牛5头,羊2头,共值金10两;牛2头,羊5
头,共值金8两”,即可得出关于x、y的二元一次方程组,此题得解.
{5x+2y=10
【解答】解:根据题意得: .
2x+5 y=8
故选:A.
8.(3分)如图,AB是半圆O的直径,C为半圆O上一点,以点B为圆心,适当长为半径画弧,交BA
1
于点M,交BC于点N,分别以点M,N为圆心,大于 MN的长为半径画弧,两弧在∠ABC的内部相
2
交于点D,画射线BD,连接AC.若∠CAB=50°,则∠CBD的度数是( )
A.30° B.25° C.20° D.15°
【分析】由圆周角定理得到∠ACB=90°,由直角三角形的性质得到∠ABC=40°,根据角平分线的定义
即可求得答案.
第2页(共15页)【解答】解:∵AB是半圆O的直径,
∴∠ACB=90°,
∵∠CAB=50°,
∴∠ABC=90°﹣50°=40°,
由题意得,BD为∠ABC的平分线,
1
∴∠CBD=∠ABD= ∠ABC=20°.
2
故选:C.
9.(3分)如图,点A的坐标是(﹣4,6),将线段OA绕点O顺时针旋转90°,点A的对应点的坐标是
( )
A.(4,6) B.(6,4) C.(﹣6,﹣4) D.(﹣4,﹣6)
【分析】根据题意画出旋转后的图形,再结合全等三角形的判定与性质即可解决问题.
【解答】解:如图所示,
分别过点A和点B作x轴的垂线,垂足分别为M和N,
由旋转可知,
OA=OB,∠AOB=90°,
∴∠AOM+∠BON=∠A+∠AOM=90°,
∴∠A=∠BON.
在△AOM和△OBN中,
{
∠A=∠BON
∠AMO=∠ONB,
OA=OB
∴△AOM≌△OBN(AAS),
∴BN=MO,ON=AM.
∵点A的坐标为(﹣4,6),
∴BN=MO=4,ON=AM=6,
∴点B的坐标为(6,4).
故选:B.
10.(3分)已知抛物线y=ax2+bx+c(a,b,c为常数,a≠0)的顶点坐标为(﹣1,﹣2),与y轴的交
点在x轴上方,下列结论正确的是( )
A.a<0 B.c<0 C.a﹣b+c=﹣2 D.b2﹣4ac=0
【分析】依据题意,由抛物线顶点为(﹣1,﹣2),故可设抛物线为y=a(x+1)2﹣2,从而y=a
(x2+2x+1)﹣2=ax2+2ax+a﹣2,则b=2a,c=a﹣2,结合抛物线与y轴的交点在x轴上方,可得c=
a﹣2>0,则a>2>0,故可判断A、B;又抛物线的顶点为(﹣1,﹣2),从而当x=﹣1时,y=a﹣
第3页(共15页)b+c=﹣2,故可判断C;又b=2a,c=a﹣2,可得b2﹣4ac=4a2﹣4a(a﹣2)=8a>0,故可判断D.
【解答】解:由题意,∵抛物线顶点为(﹣1,﹣2),
∴可设抛物线为y=a(x+1)2﹣2.
∴y=a(x2+2x+1)﹣2=ax2+2ax+a﹣2.
又抛物线为y=ax2+bx+c,
∴b=2a,c=a﹣2.
∵抛物线与y轴的交点在x轴上方,
∴c=a﹣2>0.
∴a>2>0,故A、B均不正确.
又抛物线的顶点为(﹣1,﹣2),
∴当x=﹣1时,y=a﹣b+c=﹣2,故C正确.
由b=2a,c=a﹣2,
∴b2﹣4ac=4a2﹣4a(a﹣2)=8a>0,故D错误.
故选:C.
二、填空题(共5题,每题3分,共15分)
11.(3分)写出一个大于﹣1的数是 0 .
【分析】根据正数都大于0,负数都小于0,正数大于一切负数即可写出答案,答案不唯一.
【解答】解:比﹣1大的数如:0,
故答案为:0(答案不唯一).
12.(3分)小亮了解了祖冲之、刘徽、赵爽、杨辉、秦九韶这5位著名数学家的生平简介,知晓他们取
得的伟大成就对我国乃至世界数学发展起到的巨大推进作用,准备在数学课上随机选取其中一位的成
1
就进行分享,选到数学家赵爽的概率是 .
5
【分析】根据概率公式计算即可.
【解答】解:因为总共有5人,
1
所以从中任选一个,恰好是赵爽是概率是 .
5
1
故答案为: .
5
13.(3分)铁的密度为7.9g/cm3,铁块的质量m(单位:g)与它的体积V(单位:cm3)之间的函数关
系式为m=7.9V,当V=10cm3时,m= 7 9 g.
【分析】将V=10代入m=7.9V,求出对应m的值即可.
【解答】解:当V=10时,m=7.9×10=79.
故答案为:79.
m 1
14.(3分)计算 + 的结果是 1 .
m+1 m+1
【分析】利用分式的加减法则计算即可.
m+1
【解答】解:原式= = 1,
m+1
故答案为:1.
15.(3分)如图,由三个全等的三角形(△ABE,△BCF,△CAD)与中间的小等边三角形DEF拼成一
个大等边三角形ABC.连接BD并延长交AC于点G.若AE=ED=2.则(1)∠FDB的度数是 30 °
4
;(2)DG的长是 √3 .
5
第4页(共15页)【分析】(1)利用三角形相似及AE=DE可得BF=DF,再利用三角形的外角性质结合可求得∠DBF
=30°;
(2)作 CH⊥BG 交 BG 的延长线于点 H,利用直角三角形的性质求得 CH=1,FH=√3,证明
△ADG∽△CHG,利用相似三角形的性质列式计算即可求解.
【解答】解:∵△ABE≌△BCF≌△CAD(已知),
∴AD=BE=CF,AE=BF=DC,
∵AE=ED=2,
∴AD=BE=4,
∵△DEF为等边三角形,
∴EF=DF=DE=2,∠EFD=∠EDF=60°,
∴BF=DF=DC=2,
1
∴∠FDB=∠FBD= ∠EFD=30°,∠ADB=∠EDF+∠FDB=90°,
2
如图,过点C作CH⊥BG的延长线于点H,
∵∠CDH=30°,
1
∴CH=CD×sin30°=2× =1,
2
√3
DH=CD×cos30°=2× =√3,
2
∵∠ADG=∠CHG,∠AGD=∠CGH,
∴△ADG∽△CHG,
DG AD 4
∴ = = ,
HG CH 1
4 4
∴DG= DH= √3.
5 5
三、解答题(共9题,共75分、解答应写出文字说明、证明过程或演算步骤)
16.(6分)计算:(﹣1)×3+√9+22﹣20240.
【分析】直接利用零指数幂的性质以及算术平方根、有理数的混合运算法则分别计算,进而得出答案.
【解答】解:原式=﹣3+3+4﹣1
=3.
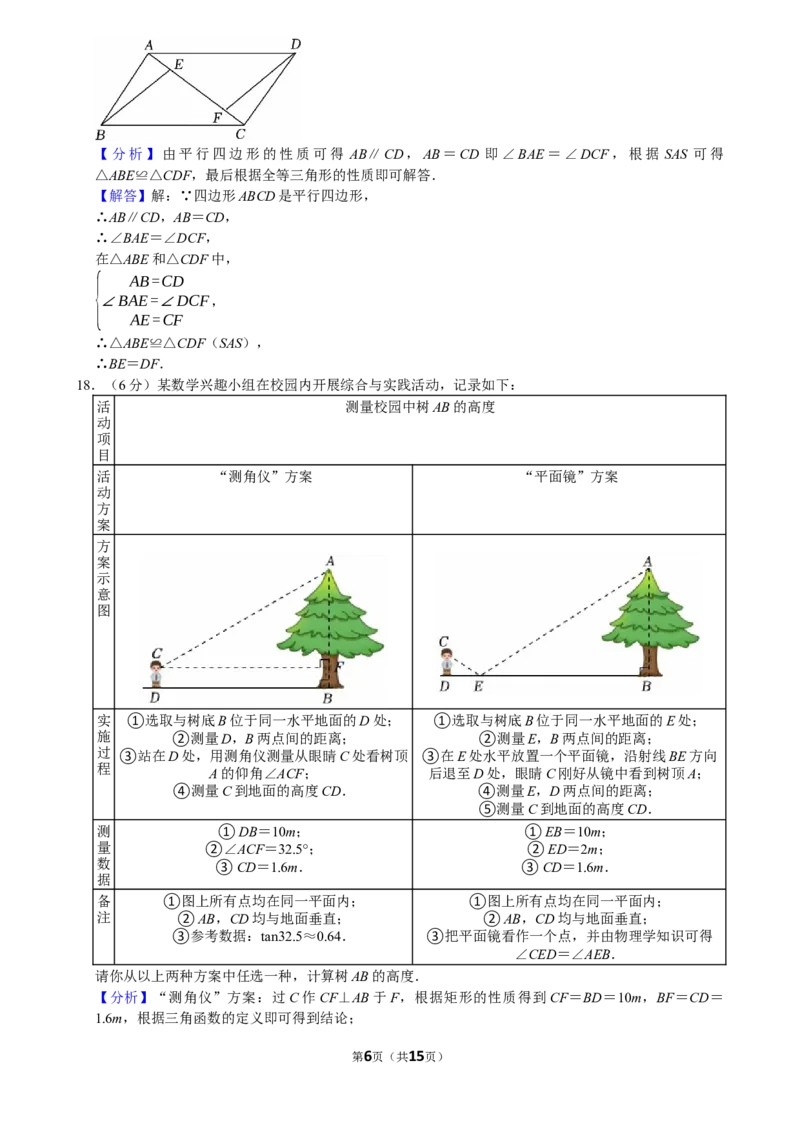
17.(6分)如图,在平行四边形ABCD中,E、F是对角线AC上的两点,且AE=CF,求证:BE=
DF.
第5页(共15页)【分析】由平行四边形的性质可得 AB∥CD,AB=CD 即∠BAE=∠DCF,根据 SAS 可得
△ABE≌△CDF,最后根据全等三角形的性质即可解答.
【解答】解:∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,
∴∠BAE=∠DCF,
在△ABE和△CDF中,
{
AB=CD
∠BAE=∠DCF,
AE=CF
∴△ABE≌△CDF(SAS),
∴BE=DF.
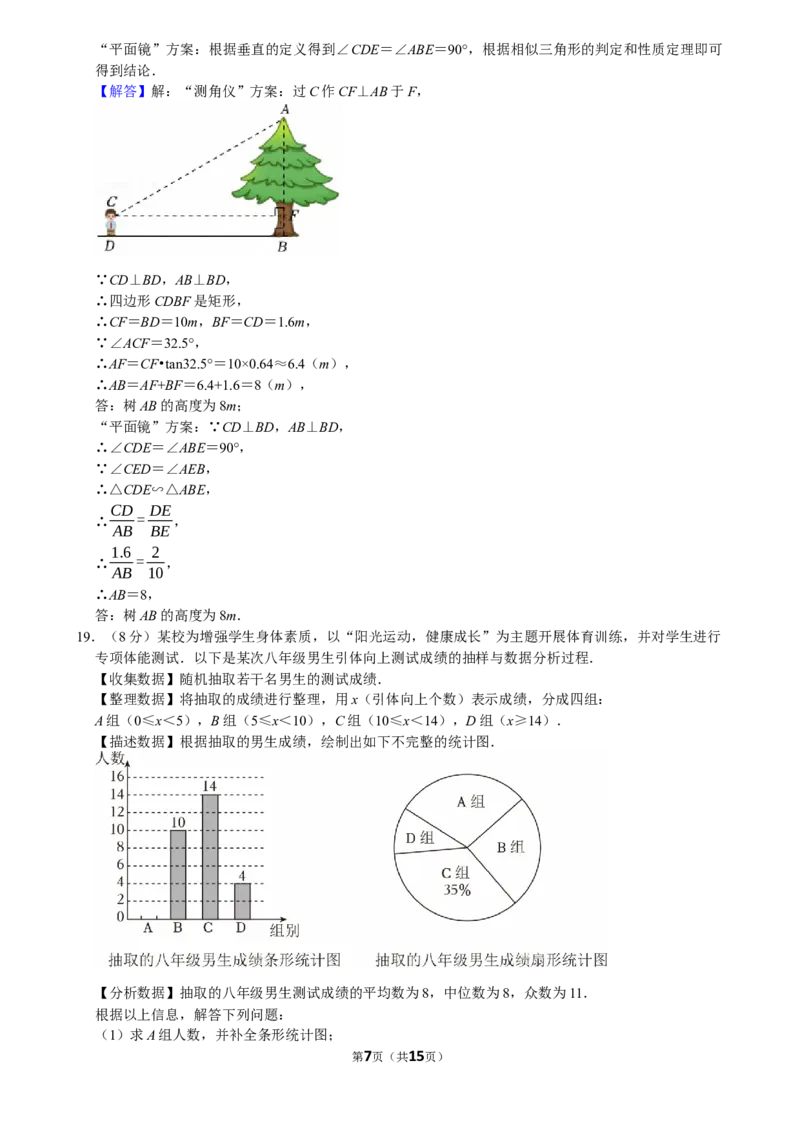
18.(6分)某数学兴趣小组在校园内开展综合与实践活动,记录如下:
活 测量校园中树AB的高度
动
项
目
活 “测角仪”方案 “平面镜”方案
动
方
案
方
案
示
意
图
实 ①选取与树底B位于同一水平地面的D处; ①选取与树底B位于同一水平地面的E处;
施 ②测量D,B两点间的距离; ②测量E,B两点间的距离;
过 ③站在D处,用测角仪测量从眼睛C处看树顶 ③在E处水平放置一个平面镜,沿射线BE方向
程
A的仰角∠ACF; 后退至D处,眼睛C刚好从镜中看到树顶A;
④测量C到地面的高度CD. ④测量E,D两点间的距离;
⑤测量C到地面的高度CD.
测 ①DB=10m; ①EB=10m;
量 ②∠ACF=32.5°; ②ED=2m;
数 ③CD=1.6m. ③CD=1.6m.
据
备 ①图上所有点均在同一平面内; ①图上所有点均在同一平面内;
注 ②AB,CD均与地面垂直; ②AB,CD均与地面垂直;
③参考数据:tan32.5≈0.64. ③把平面镜看作一个点,并由物理学知识可得
∠CED=∠AEB.
请你从以上两种方案中任选一种,计算树AB的高度.
【分析】“测角仪”方案:过C作CF⊥AB于F,根据矩形的性质得到CF=BD=10m,BF=CD=
1.6m,根据三角函数的定义即可得到结论;
第6页(共15页)“平面镜”方案:根据垂直的定义得到∠CDE=∠ABE=90°,根据相似三角形的判定和性质定理即可
得到结论.
【解答】解:“测角仪”方案:过C作CF⊥AB于F,
∵CD⊥BD,AB⊥BD,
∴四边形CDBF是矩形,
∴CF=BD=10m,BF=CD=1.6m,
∵∠ACF=32.5°,
∴AF=CF•tan32.5°=10×0.64≈6.4(m),
∴AB=AF+BF=6.4+1.6=8(m),
答:树AB的高度为8m;
“平面镜”方案:∵CD⊥BD,AB⊥BD,
∴∠CDE=∠ABE=90°,
∵∠CED=∠AEB,
∴△CDE∽△ABE,
CD DE
∴ = ,
AB BE
1.6 2
∴ = ,
AB 10
∴AB=8,
答:树AB的高度为8m.
19.(8分)某校为增强学生身体素质,以“阳光运动,健康成长”为主题开展体育训练,并对学生进行
专项体能测试.以下是某次八年级男生引体向上测试成绩的抽样与数据分析过程.
【收集数据】随机抽取若干名男生的测试成绩.
【整理数据】将抽取的成绩进行整理,用x(引体向上个数)表示成绩,分成四组:
A组(0≤x<5),B组(5≤x<10),C组(10≤x<14),D组(x≥14).
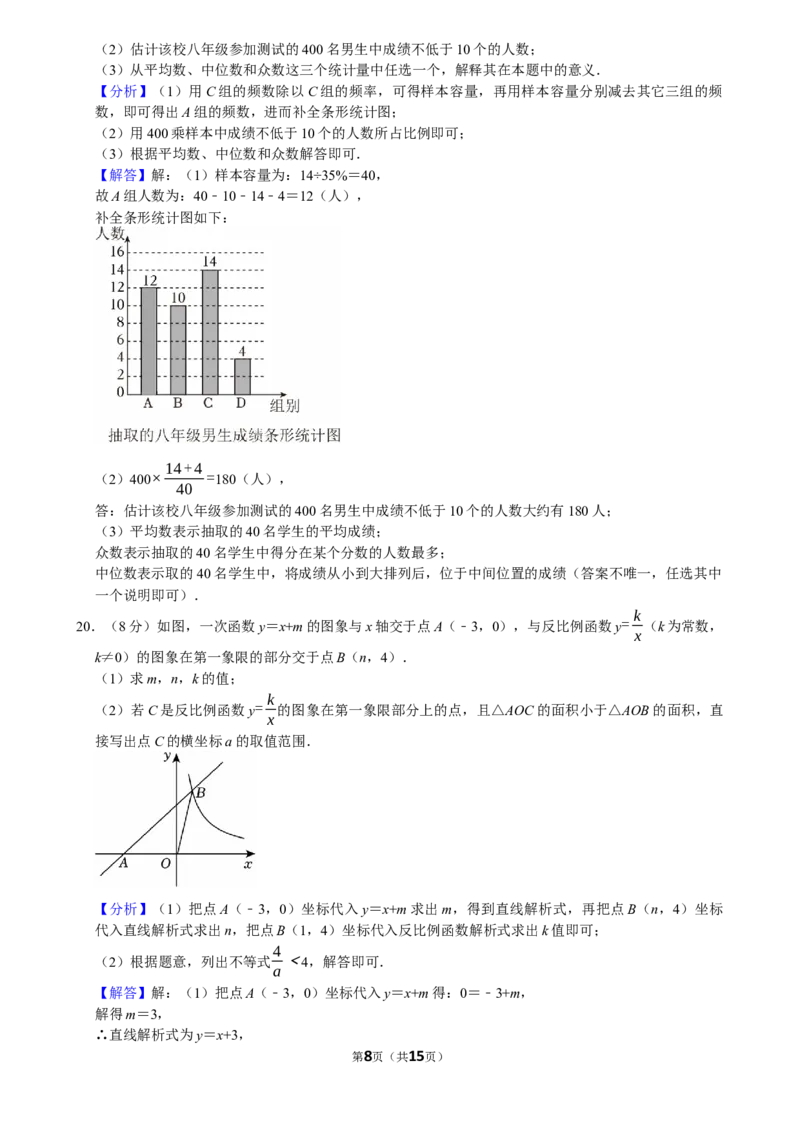
【描述数据】根据抽取的男生成绩,绘制出如下不完整的统计图.
【分析数据】抽取的八年级男生测试成绩的平均数为8,中位数为8,众数为11.
根据以上信息,解答下列问题:
(1)求A组人数,并补全条形统计图;
第7页(共15页)(2)估计该校八年级参加测试的400名男生中成绩不低于10个的人数;
(3)从平均数、中位数和众数这三个统计量中任选一个,解释其在本题中的意义.
【分析】(1)用C组的频数除以C组的频率,可得样本容量,再用样本容量分别减去其它三组的频
数,即可得出A组的频数,进而补全条形统计图;
(2)用400乘样本中成绩不低于10个的人数所占比例即可;
(3)根据平均数、中位数和众数解答即可.
【解答】解:(1)样本容量为:14÷35%=40,
故A组人数为:40﹣10﹣14﹣4=12(人),
补全条形统计图如下:
14+4
(2)400× =180(人),
40
答:估计该校八年级参加测试的400名男生中成绩不低于10个的人数大约有180人;
(3)平均数表示抽取的40名学生的平均成绩;
众数表示抽取的40名学生中得分在某个分数的人数最多;
中位数表示取的40名学生中,将成绩从小到大排列后,位于中间位置的成绩(答案不唯一,任选其中
一个说明即可).
k
20.(8分)如图,一次函数y=x+m的图象与x轴交于点A(﹣3,0),与反比例函数y= (k为常数,
x
k≠0)的图象在第一象限的部分交于点B(n,4).
(1)求m,n,k的值;
k
(2)若C是反比例函数y= 的图象在第一象限部分上的点,且△AOC的面积小于△AOB的面积,直
x
接写出点C的横坐标a的取值范围.
【分析】(1)把点A(﹣3,0)坐标代入y=x+m求出m,得到直线解析式,再把点B(n,4)坐标
代入直线解析式求出n,把点B(1,4)坐标代入反比例函数解析式求出k值即可;
4
(2)根据题意,列出不等式 <4,解答即可.
a
【解答】解:(1)把点A(﹣3,0)坐标代入y=x+m得:0=﹣3+m,
解得m=3,
∴直线解析式为y=x+3,
第8页(共15页)把点B(n,4)坐标代入直线解析式得4=n+3,
解得n=1,
k
把点B(1,4)坐标代入反比例函数解析式得:4= ,
1
解得k=4,
4
∴反比例函数解析式为y= ,
x
(2)∵△AOC的面积小于△AOB的面积,
∴y <y ,即y <4,
C B C
∵点C在反比例函数图象上,且在第一象限,
4
∴ <4,
a
∴a>1.
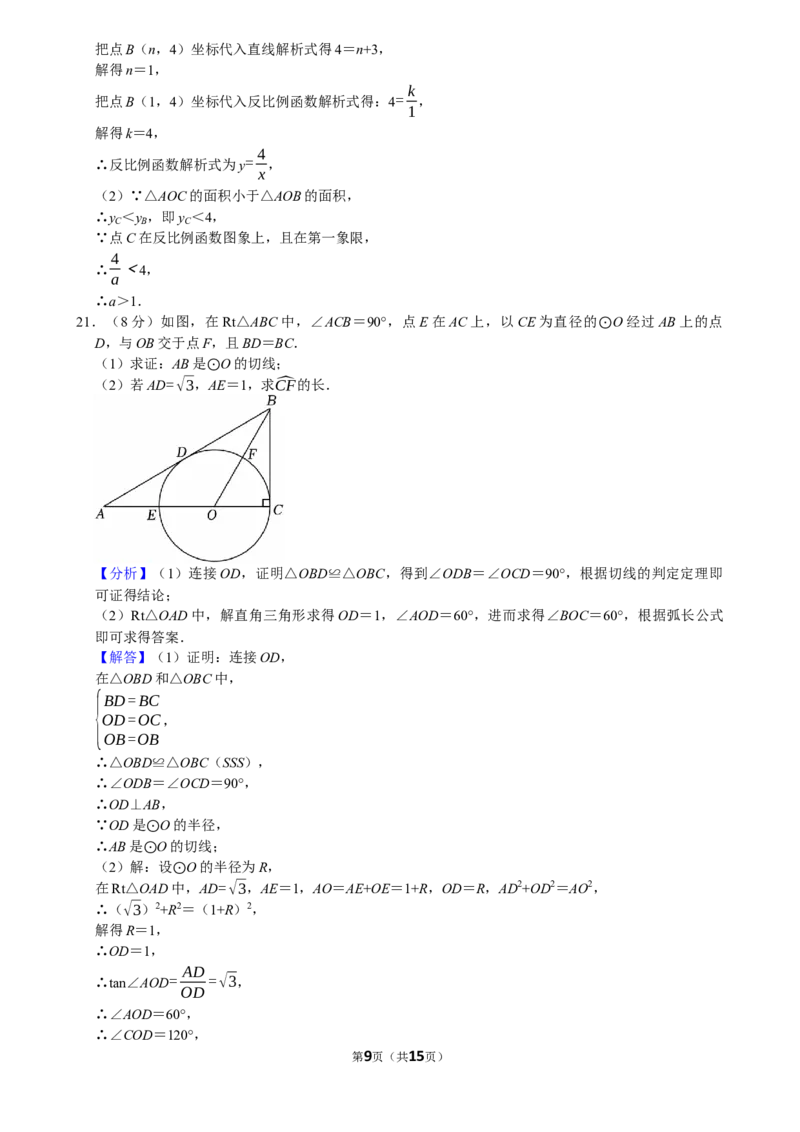
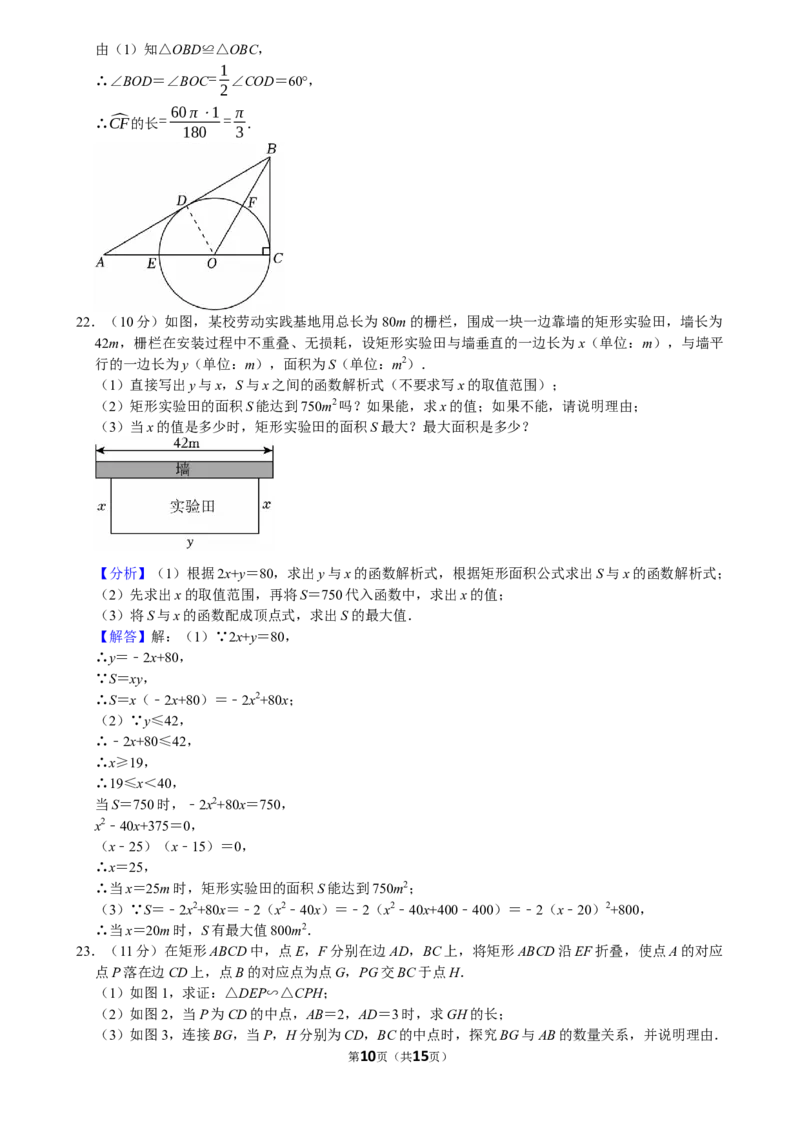
21.(8分)如图,在Rt△ABC中,∠ACB=90°,点E在AC上,以CE为直径的 O经过AB上的点
D,与OB交于点F,且BD=BC.
⊙
(1)求证:AB是 O的切线;
(2)若AD=√3,AE=1,求C^F的长.
⊙
【分析】(1)连接OD,证明△OBD≌△OBC,得到∠ODB=∠OCD=90°,根据切线的判定定理即
可证得结论;
(2)Rt△OAD中,解直角三角形求得OD=1,∠AOD=60°,进而求得∠BOC=60°,根据弧长公式
即可求得答案.
【解答】(1)证明:连接OD,
在△OBD和△OBC中,
{BD=BC
OD=OC,
OB=OB
∴△OBD≌△OBC(SSS),
∴∠ODB=∠OCD=90°,
∴OD⊥AB,
∵OD是 O的半径,
∴AB是 O的切线;
⊙
(2)解:设 O的半径为R,
⊙
在Rt△OAD中,AD=√3,AE=1,AO=AE+OE=1+R,OD=R,AD2+OD2=AO2,
⊙
∴(√3)2+R2=(1+R)2,
解得R=1,
∴OD=1,
AD
∴tan∠AOD= =√3,
OD
∴∠AOD=60°,
∴∠COD=120°,
第9页(共15页)由(1)知△OBD≌△OBC,
1
∴∠BOD=∠BOC= ∠COD=60°,
2
60π⋅1 π
∴C^F的长= = .
180 3
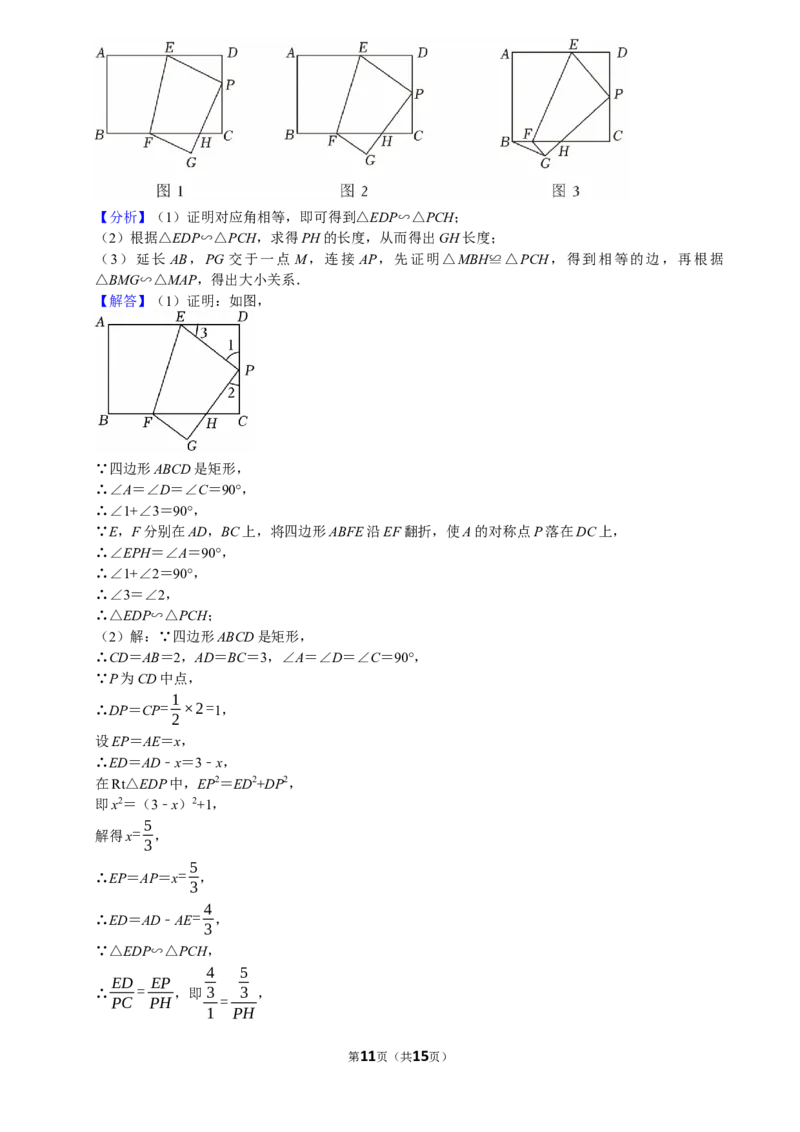
22.(10分)如图,某校劳动实践基地用总长为80m的栅栏,围成一块一边靠墙的矩形实验田,墙长为
42m,栅栏在安装过程中不重叠、无损耗,设矩形实验田与墙垂直的一边长为 x(单位:m),与墙平
行的一边长为y(单位:m),面积为S(单位:m2).
(1)直接写出y与x,S与x之间的函数解析式(不要求写x的取值范围);
(2)矩形实验田的面积S能达到750m2吗?如果能,求x的值;如果不能,请说明理由;
(3)当x的值是多少时,矩形实验田的面积S最大?最大面积是多少?
【分析】(1)根据2x+y=80,求出y与x的函数解析式,根据矩形面积公式求出S与x的函数解析式;
(2)先求出x的取值范围,再将S=750代入函数中,求出x的值;
(3)将S与x的函数配成顶点式,求出S的最大值.
【解答】解:(1)∵2x+y=80,
∴y=﹣2x+80,
∵S=xy,
∴S=x(﹣2x+80)=﹣2x2+80x;
(2)∵y≤42,
∴﹣2x+80≤42,
∴x≥19,
∴19≤x<40,
当S=750时,﹣2x2+80x=750,
x2﹣40x+375=0,
(x﹣25)(x﹣15)=0,
∴x=25,
∴当x=25m时,矩形实验田的面积S能达到750m2;
(3)∵S=﹣2x2+80x=﹣2(x2﹣40x)=﹣2(x2﹣40x+400﹣400)=﹣2(x﹣20)2+800,
∴当x=20m时,S有最大值800m2.
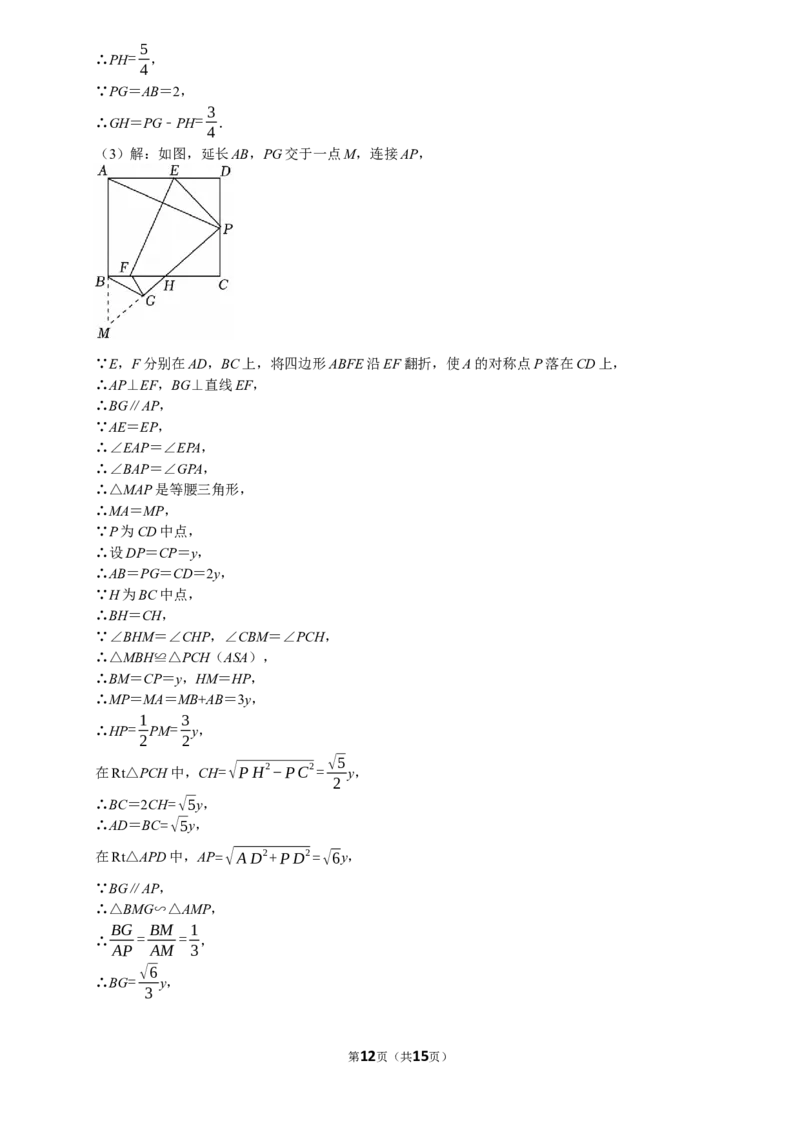
23.(11分)在矩形ABCD中,点E,F分别在边AD,BC上,将矩形ABCD沿EF折叠,使点A的对应
点P落在边CD上,点B的对应点为点G,PG交BC于点H.
(1)如图1,求证:△DEP∽△CPH;
(2)如图2,当P为CD的中点,AB=2,AD=3时,求GH的长;
(3)如图3,连接BG,当P,H分别为CD,BC的中点时,探究BG与AB的数量关系,并说明理由.
第10页(共15页)【分析】(1)证明对应角相等,即可得到△EDP∽△PCH;
(2)根据△EDP∽△PCH,求得PH的长度,从而得出GH长度;
(3)延长 AB,PG 交于一点 M,连接 AP,先证明△MBH≌△PCH,得到相等的边,再根据
△BMG∽△MAP,得出大小关系.
【解答】(1)证明:如图,
∵四边形ABCD是矩形,
∴∠A=∠D=∠C=90°,
∴∠1+∠3=90°,
∵E,F分别在AD,BC上,将四边形ABFE沿EF翻折,使A的对称点P落在DC上,
∴∠EPH=∠A=90°,
∴∠1+∠2=90°,
∴∠3=∠2,
∴△EDP∽△PCH;
(2)解:∵四边形ABCD是矩形,
∴CD=AB=2,AD=BC=3,∠A=∠D=∠C=90°,
∵P为CD中点,
1
∴DP=CP= ×2=1,
2
设EP=AE=x,
∴ED=AD﹣x=3﹣x,
在Rt△EDP中,EP2=ED2+DP2,
即x2=(3﹣x)2+1,
5
解得x= ,
3
5
∴EP=AP=x= ,
3
4
∴ED=AD﹣AE= ,
3
∵△EDP∽△PCH,
4 5
ED EP
∴ = ,即3 3 ,
PC PH =
1 PH
第11页(共15页)5
∴PH= ,
4
∵PG=AB=2,
3
∴GH=PG﹣PH= .
4
(3)解:如图,延长AB,PG交于一点M,连接AP,
∵E,F分别在AD,BC上,将四边形ABFE沿EF翻折,使A的对称点P落在CD上,
∴AP⊥EF,BG⊥直线EF,
∴BG∥AP,
∵AE=EP,
∴∠EAP=∠EPA,
∴∠BAP=∠GPA,
∴△MAP是等腰三角形,
∴MA=MP,
∵P为CD中点,
∴设DP=CP=y,
∴AB=PG=CD=2y,
∵H为BC中点,
∴BH=CH,
∵∠BHM=∠CHP,∠CBM=∠PCH,
∴△MBH≌△PCH(ASA),
∴BM=CP=y,HM=HP,
∴MP=MA=MB+AB=3y,
1 3
∴HP= PM= y,
2 2
√5
在Rt△PCH中,CH=√PH2−PC2= y,
2
∴BC=2CH=√5y,
∴AD=BC=√5y,
在Rt△APD中,AP=√AD2+PD2=√6y,
∵BG∥AP,
∴△BMG∽△AMP,
BG BM 1
∴ = = ,
AP AM 3
√6
∴BG= y,
3
第12页(共15页)AB 2y
= =√6
∴BG √6 ,
y
3
∴AB=√6BG.
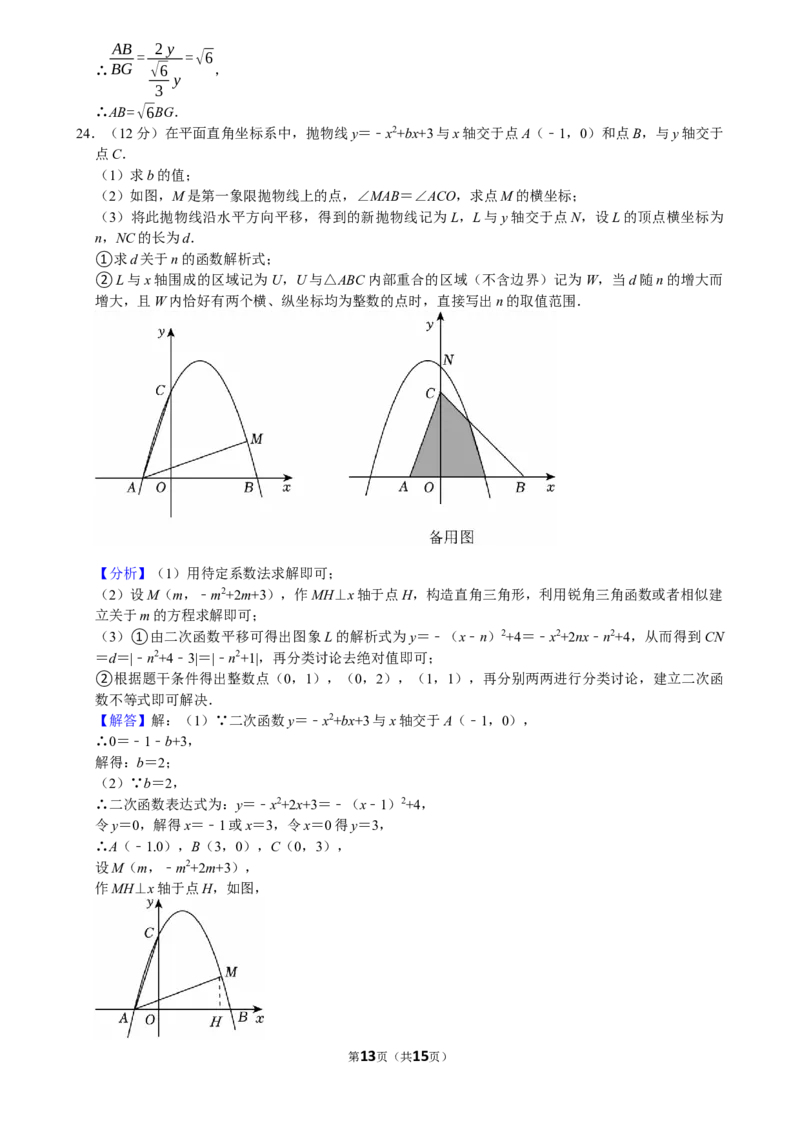
24.(12分)在平面直角坐标系中,抛物线y=﹣x2+bx+3与x轴交于点A(﹣1,0)和点B,与y轴交于
点C.
(1)求b的值;
(2)如图,M是第一象限抛物线上的点,∠MAB=∠ACO,求点M的横坐标;
(3)将此抛物线沿水平方向平移,得到的新抛物线记为L,L与y轴交于点N,设L的顶点横坐标为
n,NC的长为d.
①求d关于n的函数解析式;
②L与x轴围成的区域记为U,U与△ABC内部重合的区域(不含边界)记为W,当d随n的增大而
增大,且W内恰好有两个横、纵坐标均为整数的点时,直接写出n的取值范围.
【分析】(1)用待定系数法求解即可;
(2)设M(m,﹣m2+2m+3),作MH⊥x轴于点H,构造直角三角形,利用锐角三角函数或者相似建
立关于m的方程求解即可;
(3)①由二次函数平移可得出图象L的解析式为y=﹣(x﹣n)2+4=﹣x2+2nx﹣n2+4,从而得到CN
=d=|﹣n2+4﹣3|=|﹣n2+1|,再分类讨论去绝对值即可;
②根据题干条件得出整数点(0,1),(0,2),(1,1),再分别两两进行分类讨论,建立二次函
数不等式即可解决.
【解答】解:(1)∵二次函数y=﹣x2+bx+3与x轴交于A(﹣1,0),
∴0=﹣1﹣b+3,
解得:b=2;
(2)∵b=2,
∴二次函数表达式为:y=﹣x2+2x+3=﹣(x﹣1)2+4,
令y=0,解得x=﹣1或x=3,令x=0得y=3,
∴A(﹣1.0),B(3,0),C(0,3),
设M(m,﹣m2+2m+3),
作MH⊥x轴于点H,如图,
第13页(共15页)∵∠MAB=∠ACO,
MH OA
∴tan∠MAB=tan∠ACO,即 = ,
AH OC
−m2+2m+3 1
∴ =
m+1 3
8
解得m= 或m=﹣1(舍去),
3
8
∴M的横坐标为 ;
3
(3)①∵将二次函数沿水平方向平移,
∴纵坐标不变为4,
∴图象L的解析式为y=﹣(x﹣n)2+4=﹣x2+2nx﹣n2+4,
∴N(0,﹣n2+4),
∴d=CN=|﹣n2+4﹣3|=|﹣n2+1|,
{n2−1 (n≥1或n≤−1)
∴d= ;
−n2+1 (−1<n<1)
{n2−1 (n≥1或n≤−1)
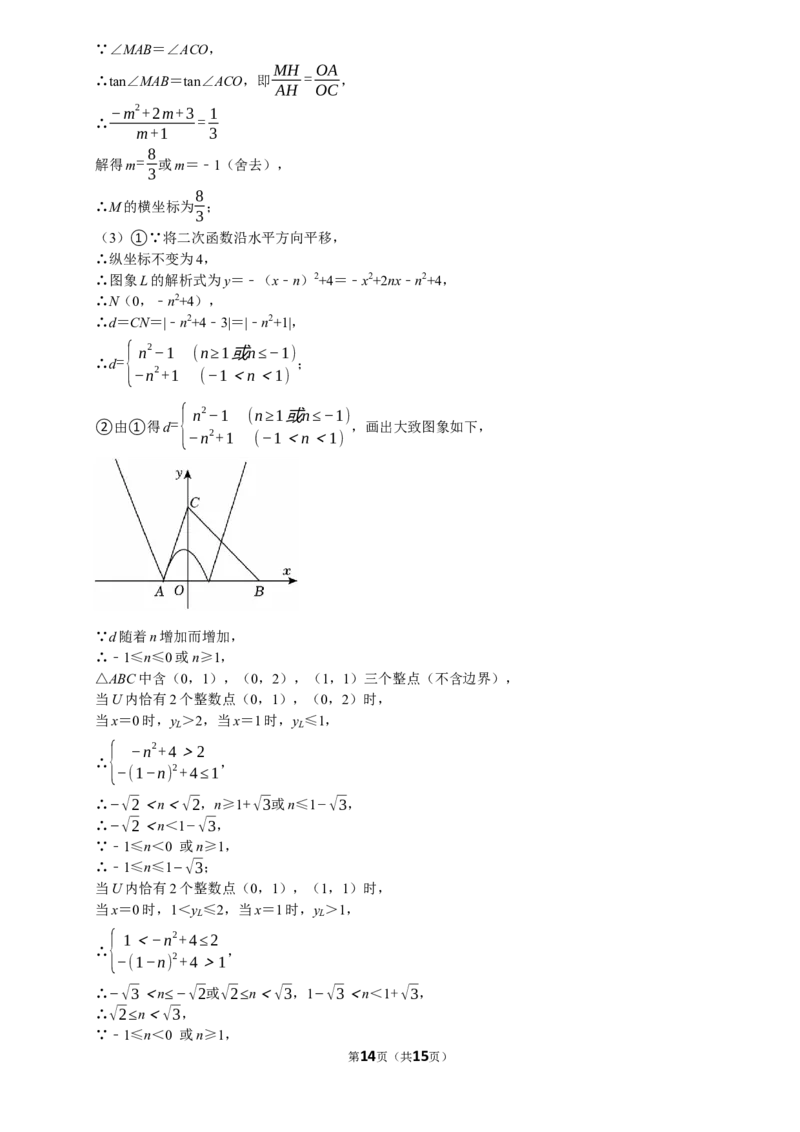
②由①得d= ,画出大致图象如下,
−n2+1 (−1<n<1)
∵d随着n增加而增加,
∴﹣1≤n≤0或n≥1,
△ABC中含(0,1),(0,2),(1,1)三个整点(不含边界),
当U内恰有2个整数点(0,1),(0,2)时,
当x=0时,y >2,当x=1时,y ≤1,
L L
{ −n2+4>2
∴ ,
−(1−n) 2+4≤1
∴−√2<n<√2,n≥1+√3或n≤1−√3,
∴−√2<n<1−√3,
∵﹣1≤n<0 或n≥1,
∴﹣1≤n≤1−√3;
当U内恰有2个整数点(0,1),(1,1)时,
当x=0时,1<y ≤2,当x=1时,y >1,
L L
{ 1<−n2+4≤2
∴ ,
−(1−n) 2+4>1
∴−√3<n≤−√2或√2≤n<√3,1−√3<n<1+√3,
∴√2≤n<√3,
∵﹣1≤n<0 或n≥1,
第14页(共15页)∴√2≤n<√3;
当U内恰有2个整数点(0,2),(1,1)时,此种情况不存在,舍去.
综上所述,n的取值范围为﹣1≤n≤1−√3或√2≤n<√3.
声明:试题解析著作权属菁优网所有,未经书面同意,不得复制发布日期:2025/1/11 21:38:44;用户:庞俊梅;邮箱:18715777852;学号:54801167
第15页(共15页)