文档内容
2023 年高考考前押题密卷(上海卷)
数学·参考答案
1. (4分)
2.2 (4分)
3. (4分)
4. (4分)
5. 或 (4分)
6. (4分)
7.8 (4分)
8. (4分)
9.100 (5分)
10. (5分)
11. (5分)
12. (5分)
13 14 15 16
D D C B
每小题 (5分)
17.解:(1)在 中, ,O为AC的中点.
则中线 ,且 ;
同理在 中有 ,则 ; ...............2分
因为 ,O为AC的中点.
所以 且 ;
在 中有 ,则 , ...............4分
因为 , 平面ABC,
1
学科网(北京)股份有限公司所以 ⊥平面ABC. ...............6分
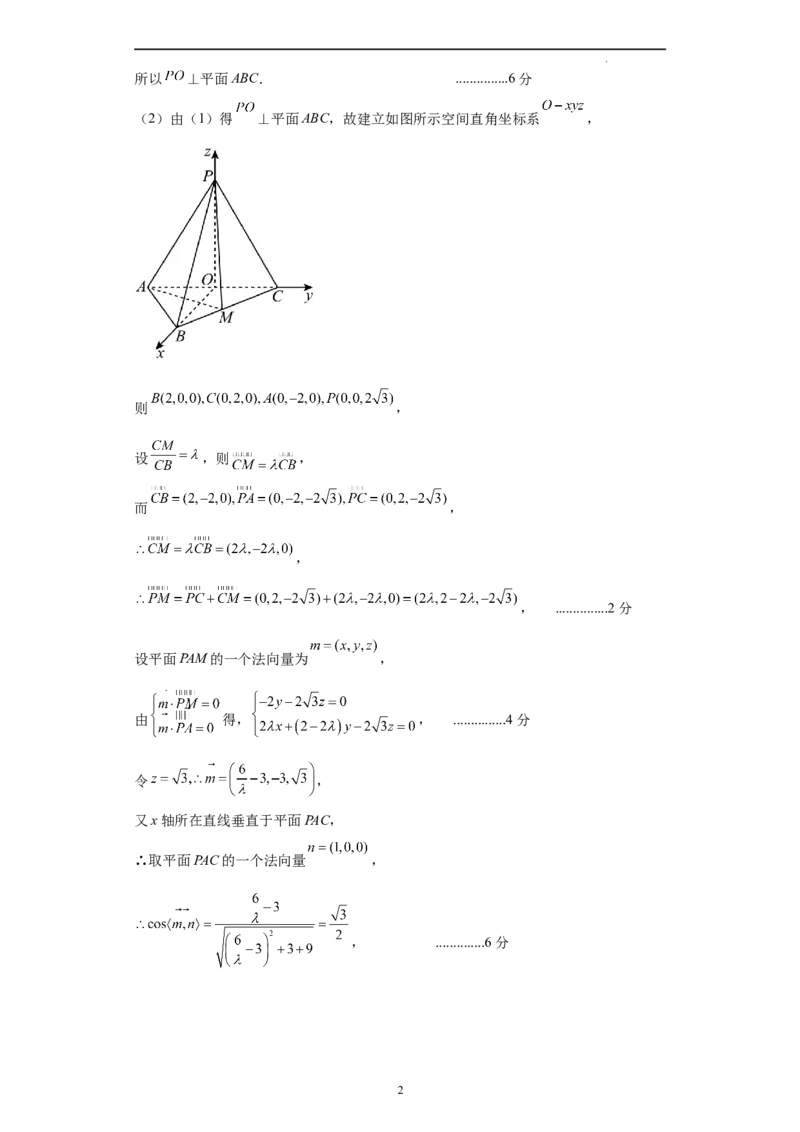
(2)由(1)得 ⊥平面ABC,故建立如图所示空间直角坐标系 ,
则 ,
设 ,则 ,
而 ,
,
, ...............2分
设平面PAM的一个法向量为 ,
由 得, , ...............4分
令 ,
又x轴所在直线垂直于平面PAC,
∴取平面PAC的一个法向量 ,
, ..............6分
2
学科网(北京)股份有限公司平方得 ,令 ,
,
. ...............8分
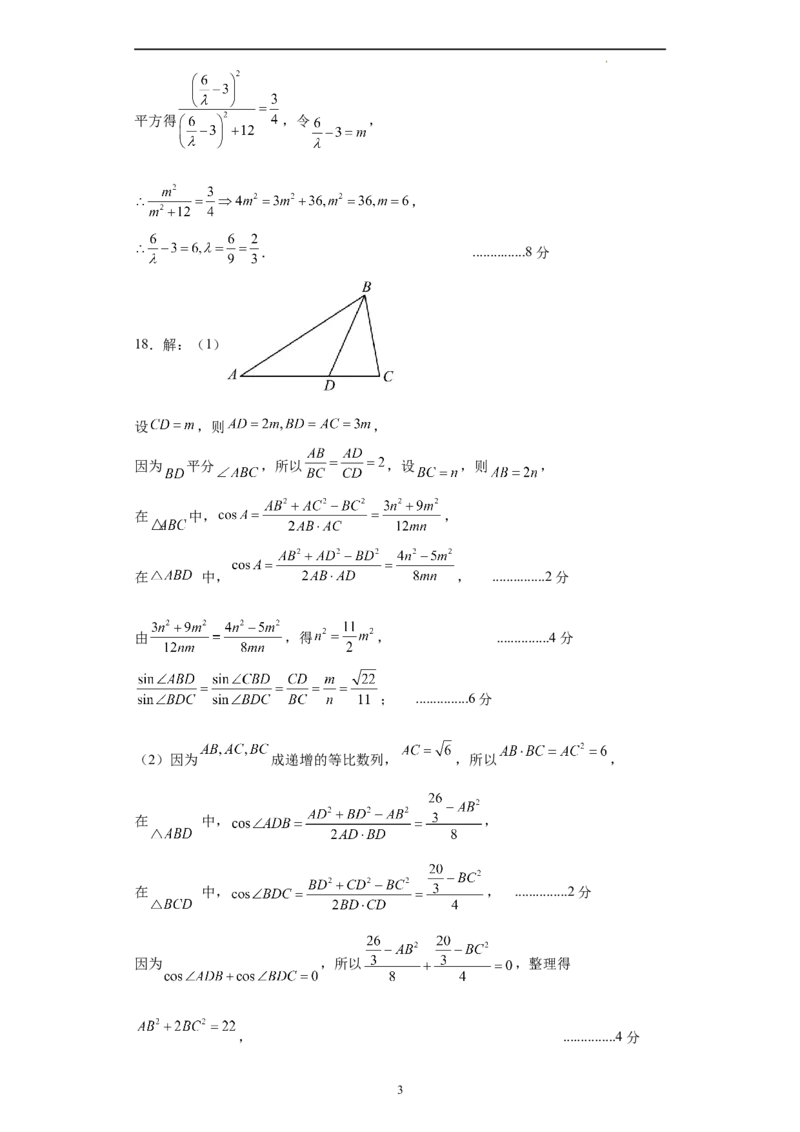
18.解:(1)
设 ,则 ,
因为 平分 ,所以 ,设 ,则 ,
在 中, ,
在 中, , ...............2分
由 ,得 , ...............4分
; ...............6分
(2)因为 成递增的等比数列, ,所以 ,
在 中, ,
在 中, , ...............2分
因为 ,所以 ,整理得
, ...............4分
3
学科网(北京)股份有限公司又 ,所以 ,解得 或 , ...............6分
若 ,则 ,不符合题意,
若 ,则 ,符合题意,此时 ,
则 的面积 . ...............8分
19.解:(1)依题意 的可能取值为 、 ,
则 , , ...............4分
所以 的分布列为
. ..............6分
(2)当一天的进货量为 (单位:盒), 为正整数且 时利润 的可能
取值为 或 , ...............2分
且 , , ...............4分
所以 , ...............6分
显然 随着 的增大而减少,所以当 时 的期望达到最大值,
. ...............8分
20.解:(1)由于椭圆的一个顶点与两焦点构成等边三角形,且 ,
所以 ,解得 , ...............3分
4
学科网(北京)股份有限公司所以椭圆方程为 . ...............4分
(2)由(1)得 ,由于 在椭圆内,
所以,过 且与坐标轴不平行的直线 与椭圆必有两个交点,
设此时直线 的方程为 ,
由 消去 并化简得 ,...............1分
设 ,则 , ...............2分
设 ,
所以
,
所以 ,所以 ,
所以点 是左焦点 的配对点. ...............6分
(3)依题意,点 有配对点 ,
设直线 的方程为 ,由于 ,
所以 必须在 之间,而 在椭圆上,结合椭圆的对称性以及直线 与坐标轴不
5
学科网(北京)股份有限公司平行, 微信搜索“高中试卷君”公众号 领取押题卷联考卷
可知 的取值范围是 .
此时 在椭圆的内部,直线 必与椭圆有两个交点, ..............2分
由 消去 并化简得 ,
设 ,则 ,
由于 ,所以 ,
即
,
所以 . ..............6分
21.解:(1)∵ ,则 ,
若 是增函数,则 ,
且 ,可得 ,
故原题意等价于 对 恒成立, ..............2分
6
学科网(北京)股份有限公司构建 ,则 ,
令 ,解得 ;令 ,解得 ;
则 在 上递增,在 递减,故 ,
∴ 的取值范围为 . ..............4分
(2)(i)由(1)可知:当 时, 单调递增,
∵ ,则 ,即 ,
整理得 , ...........2分
构建 ,则 ,
令 ,解得 ;令 ,解得 ;
则 在 上递减,在 递增,
故 ,即 ,当且仅当 时等号成立, ..........4分
令 ,可得 ,
故 ; ..............6分
(ii)∵ ,则 ,
可知 有两个不同实数根 ,由(1)知 ,
可得 ,
同理可得 , ...........2分
构建 ,则 ,
7
学科网(北京)股份有限公司当 时, ;当 时, ;当 时, ;
且 ,故 对 恒成立,
故 在 上单调递减, . .........4分
∵ ,则 ,即 ,
且 ,则 ,故 ,
可得 ; 微信搜索“高中试卷君”公众号 领取押题卷联考卷
又∵ ,由(i)可得 ,即 ,
则 ,
且 ,则 ,
可得 ;
综上所述: .
可得 ,则
故 . ...........8分
8
学科网(北京)股份有限公司9
学科网(北京)股份有限公司