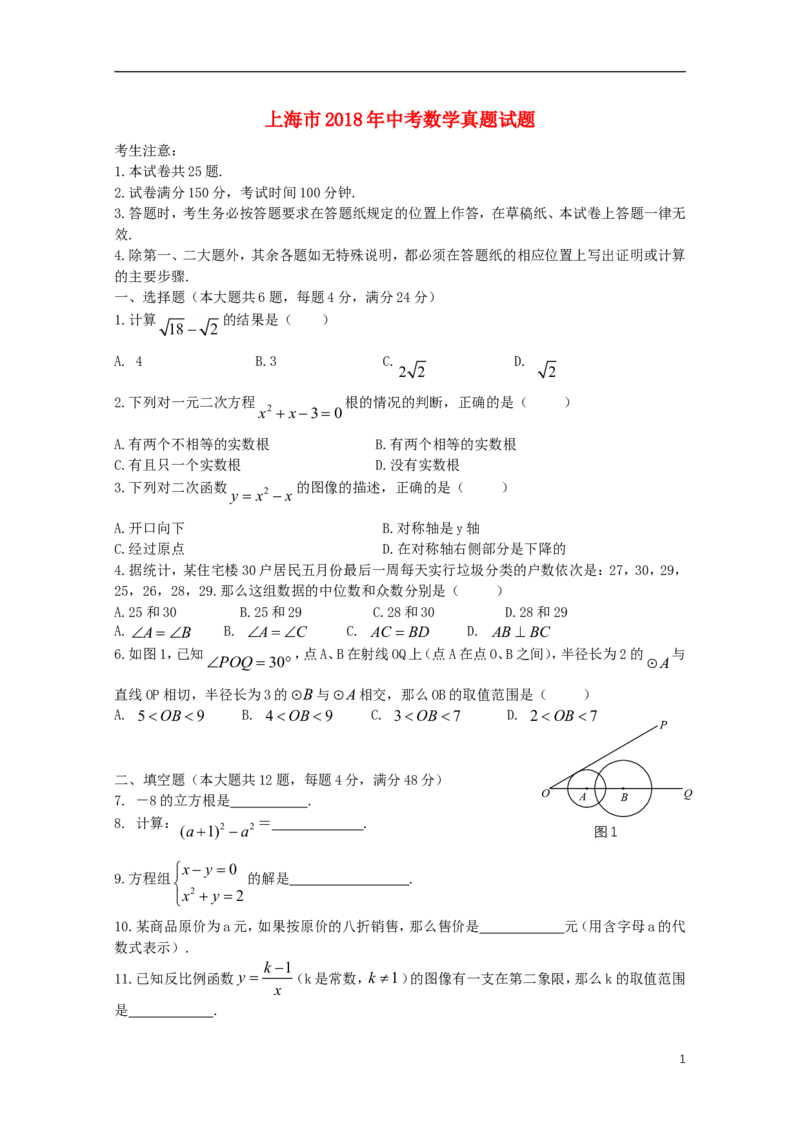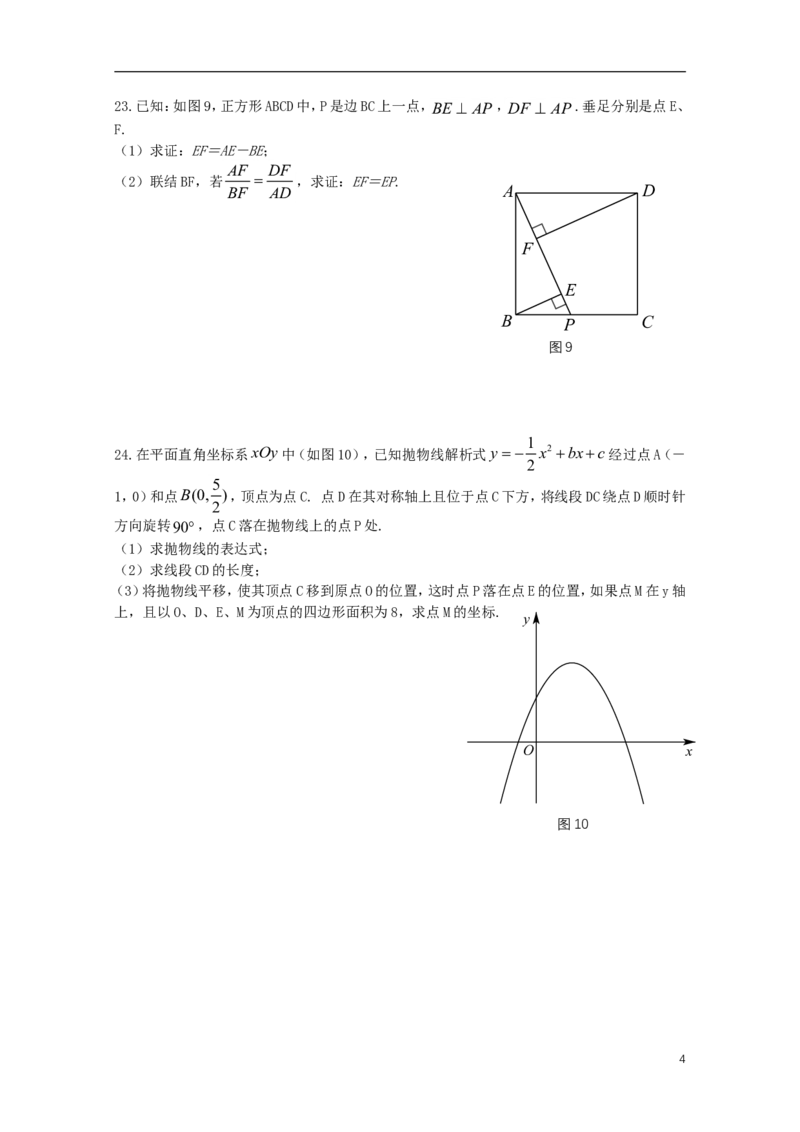上海市2018年中考数学真题试题（含扫描答案）_中考真题_2.数学中考真题2015-2024年_2018年全国中考数学258份

上海市2018年中考数学真题试题 考生注意： 1.本试卷共25题. 2.试卷满分150分，考试时间100分钟. 3.答题时，考生务必按答题要求在答题纸规定的位置上作答，在草稿纸、本试卷上答题一律无 效. 4.除第一、二大题外，其余各题如无特殊说明，都必须在答题纸的相应位置上写出证明或计算 的主要步骤. 一、选择题（本大题共6题，每题4分，满分24分） 1.计算 的结果是（ ） 18 2 A. 4 B.3 C. D. 2 2 2 2.下列对一元二次方程 根的情况的判断，正确的是（ ） x2 x30 A.有两个不相等的实数根 B.有两个相等的实数根 C.有且只一个实数根 D.没有实数根 3.下列对二次函数 的图像的描述，正确的是（ ） y  x2 x A.开口向下 B.对称轴是y轴 C.经过原点 D.在对称轴右侧部分是下降的 4.据统计，某住宅楼30户居民五月份最后一周每天实行垃圾分类的户数依次是：27，30，29， 25，26，28，29.那么这组数据的中位数和众数分别是（ ） A.25和30 B.25和29 C.28和30 D.28和29 A.AB B. AC C. AC  BD D. AB BC 6.如图1，已知 ，点A、B在射线OQ上（点A在点O、B之间），半径长为2的 与 POQ30 A 直线OP相切，半径长为3的B与A相交，那么OB的取值范围是（ ） A. 5OB9 B. 4OB9 C. 3OB7 D. 2OB7 P 二、填空题（本大题共12题，每题4分，满分48分） 7. －8的立方根是 . O A B Q 8. 计算： ＝ . (a1)2 a2 图1 x y 0 9.方程组 的解是 .  x2  y 2 10.某商品原价为a元，如果按原价的八折销售，那么售价是 元（用含字母a的代 数式表示）. k1 11.已知反比例函数y  （k是常数，k 1）的图像有一支在第二象限，那么k的取值范围 x 是 . 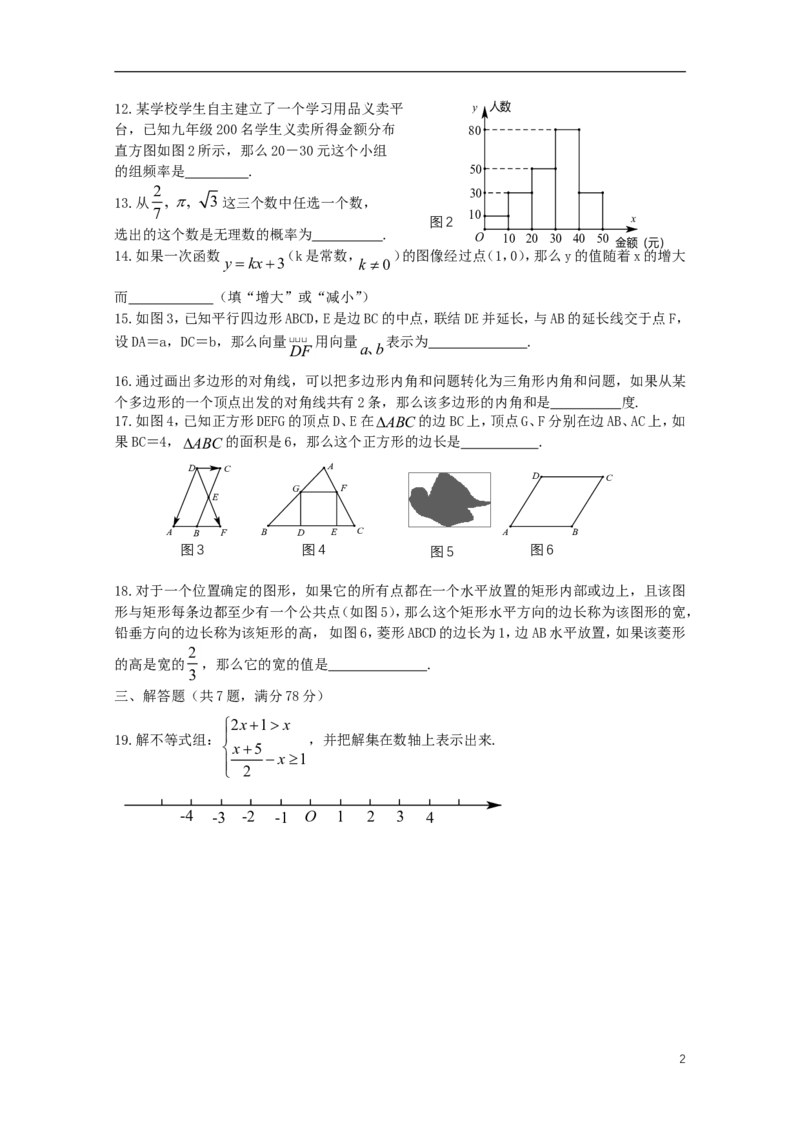112.某学校学生自主建立了一个学习用品义卖平 y 人数 台，已知九年级200名学生义卖所得金额分布 80 直方图如图2所示，那么20－30元这个小组 的组频率是 . 50 2 30 13.从 , , 3 这三个数中任选一个数， 7 10 图2 x 选出的这个数是无理数的概率为 . O 10 20 30 40 50 金额（元） 14.如果一次函数 （k是常数， ）的图像经过点（1，0），那么y的值随着x的增大 y kx3 k 0 而 （填“增大”或“减小”） 15.如图3，已知平行四边形ABCD，E是边BC的中点，联结DE并延长，与AB的延长线交于点F， 设DA＝a，DC＝b，那么向量(cid:3) 用向量 (cid:3)(cid:3) 表示为 . DF a、b 16.通过画出多边形的对角线，可以把多边形内角和问题转化为三角形内角和问题，如果从某 个多边形的一个顶点出发的对角线共有2条，那么该多边形的内角和是 度. 17.如图4，已知正方形DEFG的顶点D、E在ABC的边BC上，顶点G、F分别在边AB、AC上，如 果BC＝4，ABC的面积是6，那么这个正方形的边长是 . D C A D C G F E A B F B D E C A B 图3 图4 图5 图6 18.对于一个位置确定的图形，如果它的所有点都在一个水平放置的矩形内部或边上，且该图 形与矩形每条边都至少有一个公共点（如图5），那么这个矩形水平方向的边长称为该图形的宽， 铅垂方向的边长称为该矩形的高， 如图6，菱形ABCD的边长为1，边AB水平放置，如果该菱形 2 的高是宽的 ，那么它的宽的值是 . 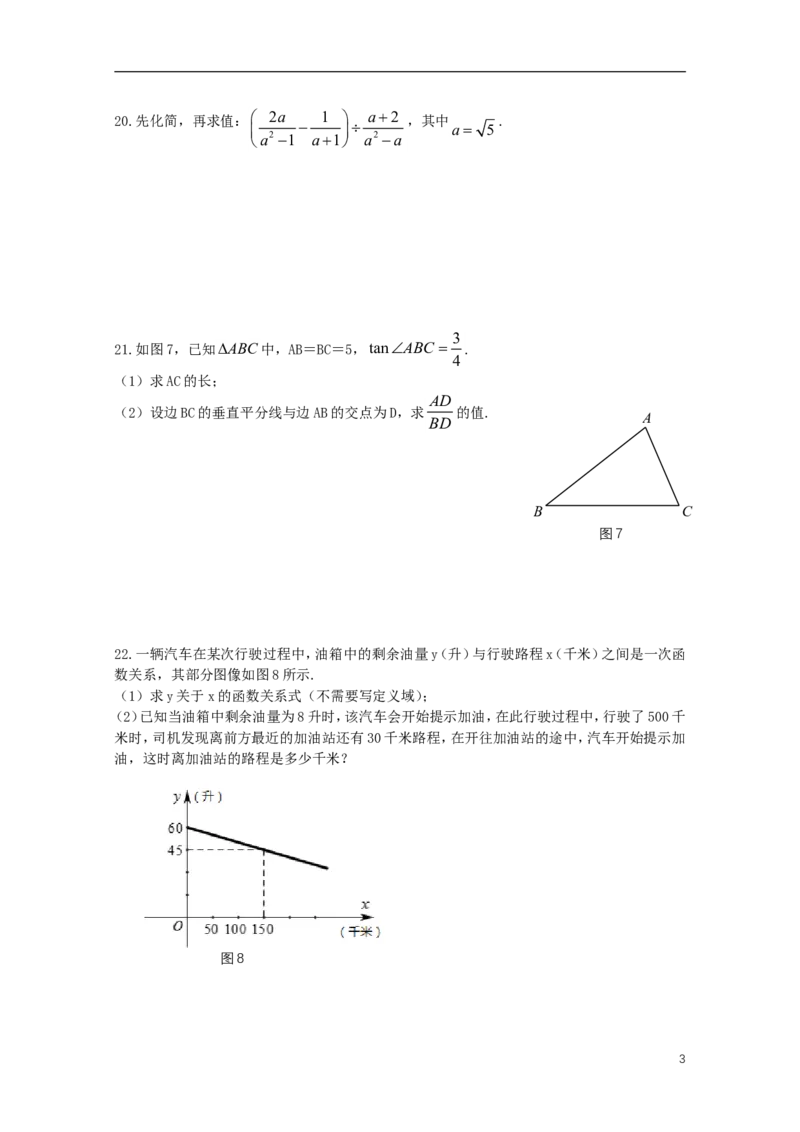3 三、解答题（共7题，满分78分） 2x1 x 19.解不等式组： ，并把解集在数轴上表示出来. x5 x1   2 -4 -3 -2 -1 O 1 2 3 4 220.先化简，再求值： 2a 1  a2 ，其中 .     a 5 a2 1 a1 a2 a 3 21.如图7，已知ABC中，AB＝BC＝5，tanABC  . 4 （1）求AC的长； AD （2）设边BC的垂直平分线与边AB的交点为D，求 的值. A BD B C 图7 22.一辆汽车在某次行驶过程中，油箱中的剩余油量y（升）与行驶路程x（千米）之间是一次函 数关系，其部分图像如图8所示. （1）求y关于x的函数关系式（不需要写定义域）； （2）已知当油箱中剩余油量为8升时，该汽车会开始提示加油，在此行驶过程中，行驶了500千 米时，司机发现离前方最近的加油站还有30千米路程，在开往加油站的途中，汽车开始提示加 油，这时离加油站的路程是多少千米？ 图8 323.已知：如图9，正方形ABCD中，P是边BC上一点，BE  AP，DF  AP.垂足分别是点E、 F. （1）求证：EF＝AE－BE； AF DF （2）联结BF，若  ，求证：EF＝EP. 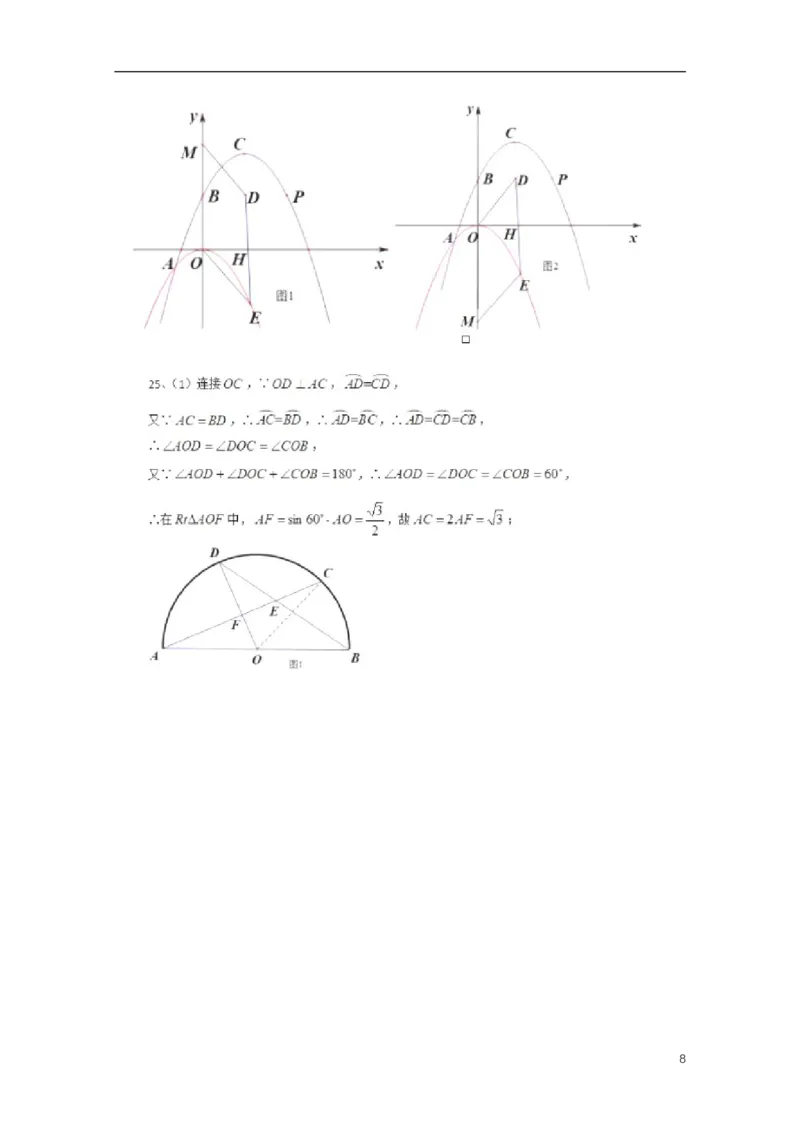BF AD A D F E B P C 图9 1 24.在平面直角坐标系xOy中（如图10），已知抛物线解析式y  x2 bxc经过点A（－ 2 5 1，0）和点B(0, )，顶点为点C. 点D在其对称轴上且位于点C下方，将线段DC绕点D顺时针 2 方向旋转90，点C落在抛物线上的点P处. （1）求抛物线的表达式； （2）求线段CD的长度； （3）将抛物线平移，使其顶点C移到原点O的位置，这时点P落在点E的位置，如果点M在y轴 上，且以O、D、E、M为顶点的四边形面积为8，求点M的坐标. 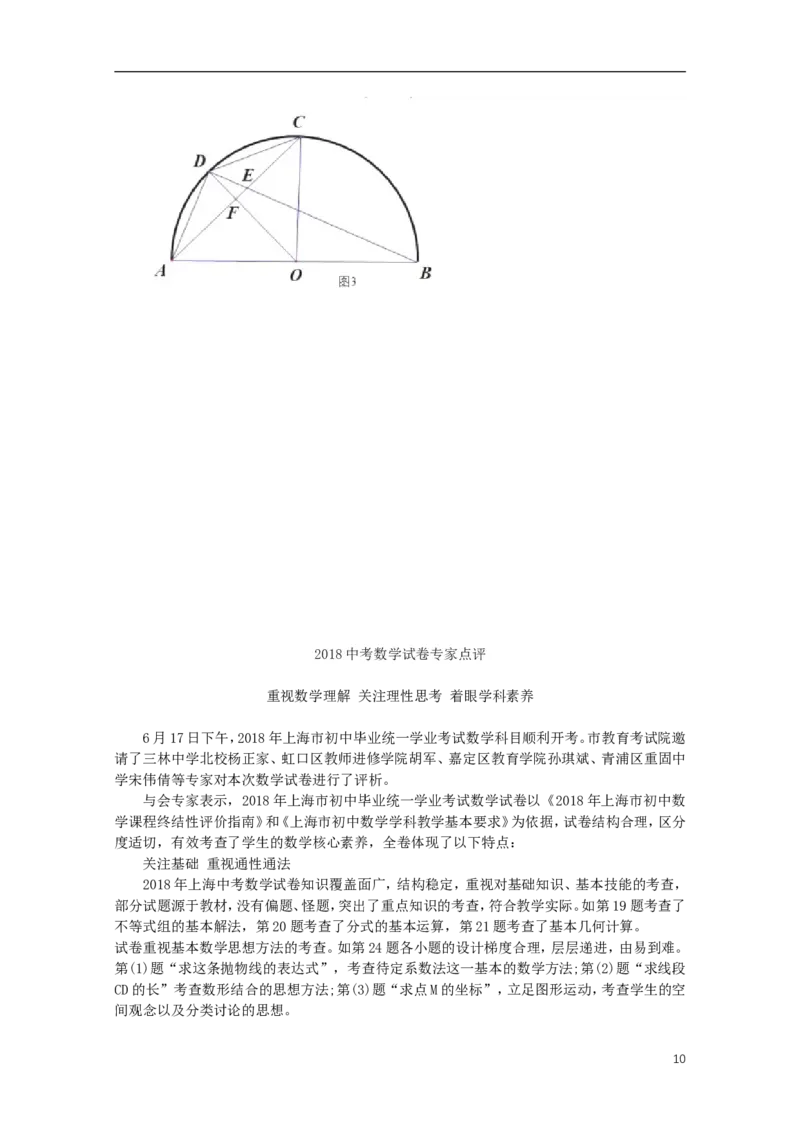y O x 图10 425. 已知O的直径AB＝2，弦AC与弦BD交于点E，且OD AC，垂足为点F. （1）如图11，如果AC＝BD，求弦AC的长； （2）如图12，如果E为弦BD的中点，求ABD的余切值； （3）联结BC、CD、DA，如果BC是O的内接正n边形的一边，CD是O的内接正(n+4)边形的一 边，求ACD的面积. D D C C E E F F A O B A O B A O B 图11 图12 备用图 5参考答案 67892018中考数学试卷专家点评 重视数学理解 关注理性思考 着眼学科素养 6月17日下午，2018年上海市初中毕业统一学业考试数学科目顺利开考。市教育考试院邀 请了三林中学北校杨正家、虹口区教师进修学院胡军、嘉定区教育学院孙琪斌、青浦区重固中 学宋伟倩等专家对本次数学试卷进行了评析。 与会专家表示，2018年上海市初中毕业统一学业考试数学试卷以《2018年上海市初中数 学课程终结性评价指南》和《上海市初中数学学科教学基本要求》为依据，试卷结构合理，区分 度适切，有效考查了学生的数学核心素养，全卷体现了以下特点： 关注基础 重视通性通法 2018年上海中考数学试卷知识覆盖面广，结构稳定，重视对基础知识、基本技能的考查， 部分试题源于教材，没有偏题、怪题，突出了重点知识的考查，符合教学实际。如第19题考查了 不等式组的基本解法，第20题考查了分式的基本运算，第21题考查了基本几何计算。 试卷重视基本数学思想方法的考查。如第24题各小题的设计梯度合理，层层递进，由易到难。 第(1)题“求这条抛物线的表达式”，考查待定系数法这一基本的数学方法;第(2)题“求线段 CD的长”考查数形结合的思想方法;第(3)题“求点M的坐标”，立足图形运动，考查学生的空 间观念以及分类讨论的思想。 10联系实际 突出数学应用 试卷注重数学知识与现实生活的联系，考查学生在实际生活中分析问题、解决问题的能力 如选择题第4题以居民垃圾分类为素材，要求学生找出相关数据中的中位数和众数;第12题以 某校学生自主建立学习用品义卖平台为素材，要求学生根据义卖所得金额的频数分布直方图， 求“20-30元这个小组的组频率”;第22题用汽车在行驶过程中油箱用油量和行驶路程之间 的函数关系来求解相关问题等，这些试题的背景取材来自现实生活，渗透环保意识，弘扬助人 精神，富有亲切感，让学生在解题的同时，感受数学在生活中的广泛运用，体现了学科育人价值 关注理解 凸显理性思考 试卷注重阅读理解能力、探究性学习能力，引导学生抓住数学本质、数学规律来解决问题。 如第25题中，“求弦AC的长”对同圆或等圆中的弦、弧、圆心角三者之间关系的理解是问题 解决的关键;“求∠ABD的余切值”需要学生联系基本图形，将所求的余切值转换为相关线段 之间的关系，考查了知识间的联系和转换;“求△ACD的面积”需要学生理解正多边形的相关 概念，通过数形结合建立方程，运用代数方法解决几何问题。这类试题较好体现了对数学理性 思考的关注。 引导教学 着眼核心能力 试卷着眼于学生数学核心能力的培育，如数学表达、运算求解、推理论证、空间想象、数据 处理等能力均在试卷中有所体现，对课堂教学起到了较好的引导作用，引导课堂教学关注思维 过程与方法，用数学的方式观察、思考、表达、解决所面对的问题。如第23题是一道几何证明题， 改编自教材，考查逻辑推理能力，培养思维和表达的严密性。 11