数学（二）-2024年高考考前20天终极冲刺攻略_2024高考押题卷_62024学科网全系列_21学科网高考考前终极攻略_数学-2024年高考考前20天终极冲刺攻略

学科网（北京）股份有限公司目 录 contents （二） 三角恒等变换（选填题）……………………………………………………03 平面向量（选填题）…………………………………………………………18 指对数运算及比较大小（选填题）…………………………………………37 三角函数（选填题） ………………………………………………………50 集合（选填题）………………………………………………………………70 学科网（北京）股份有限公司三角恒等变换（选填题） 年份 题号 知识点 考点 2021年I 6 三角恒等变换 已知条件求值问题 卷 2021年II 无 卷 2022年I 无 卷 ①三角函数和差、半角正余弦公式 2022年II ②三角函数和差、半角正切公式 6 三角函数化简 卷 ③三角函数辅助角公式 ④三角函数万能公式 ①三角函数和差、半角正余弦公式 2023年新 ②三角函数和差、半角正切公式 8 三角恒等变换 高考1 ③三角函数辅助角公式 ④三角函数万能公式 ①三角函数和差、半角正余弦公式 2023 年 新 ②三角函数和差、半角正切公式 高考2 7 三角函数的诱导公式 ③三角函数辅助角公式 ④三角函数万能公式 近三年，三角恒等变换在选填中占据一个位置，考查的考点一般来说是： 1、已知条件求值问题（①“给角求值”②“给值求值”③“给值求角”） 2、求非特殊角三角函数值运算（①整体换元利用恒等变形公式计算其结果②对偶式处理③记住一些特殊角 的三角函数值） 3 原创精品资源学科网独家享有版权，侵权必究！ 学科网（北京）股份有限公司3、正余弦三角函数值加减问题（①三角函数和差、半角正余弦公式②三角函数和差、半角正切公式③ 三 角函数辅助角公式④三角函数三剑客） 4、 tan与齐次式互换（掌握五类变形的标准） 题干的设置一般来说在上述的四项考点中选其一项。三角恒等变换需要认真分类，熟练掌握各类题的 技巧，即目测题后瞬间就能想到对应的做题方案，便可轻松搞定。 三角恒等变换在2024新高考新题型中的考查形式依然以选择或者填空为主，以考查齐次化和已知条件 求值问题为主，三角恒等变换在选填中难度中等，考生可适当留意常见的变换并分类，每一类总结出一个 固定模板，以便此类题在高考出现时考生能做到心中有数，快速解答. 一、已知条件求值问题 Ⅰ诱导公式的秒记 奇变偶不变，符号看象限  ①奇变偶不变关键要看所加弧度是 的奇数倍还是偶数倍 2 若是奇数倍则sin cos互变，若是偶数倍，则sin cos不变  3 3  例如：sin  ∵ 是 的3倍，3属于奇数，故先变为cos  2  2 2 ②符号看象限首先将永远看成300，其次利用sin看上下，cos看左右进行秒杀 上个例题中变成cos后，然后判断符号，2700 300 3000，所以位于第四象限，利用sin看上下， 所以原式为负，化简结果为cos  例如：cos    ∵是 的2倍，2属于偶数，故先变为cos，然后判断符号， 2 1800 300 2100，所以位于第三象限，利用cos看左右，所以原式为负，化简结果为cos. 4 原创精品资源学科网独家享有版权，侵权必究！ 学科网（北京）股份有限公司Ⅱ诱导公式的延伸 结论Ⅰ：sinn    1nsin nZ   推导如下 ①当n2k kZ 时， 由诱导公式有sin2k  sin  12k sin kZ   ②当n2k1kZ 时，由诱导公式有 sin 2k1   sin2k  sin   sin  12k1sin kZ 结论Ⅱ：cosn    1ncos nZ   推导如下 ①当n2k kZ 时， 由诱导公式有cos2k  cos  12k cos kZ   ②当n2k1kZ 时，由诱导公式有 cos 2k1   cos2k  cos   cos  12k1cos kZ 结论Ⅲ：sinn    1n1sin nZ   ①当n2k kZ 时， 由诱导公式有sin2k  sin  12k1sin kZ   ②当n2k1kZ 时，由诱导公式有 sin 2k1   sin2k  sin   sin  12k sin kZ 结论Ⅳ：cosn    1ncos nZ   推导如下 ①当n2k kZ 时， 由诱导公式有cos2k  cos  12k cos kZ   ②当n2k1kZ 时，由诱导公式有 cos 2k1   cos2k  cos   cos  12k1cos kZ Ⅲ诱导公式的妙用 5 原创精品资源学科网独家享有版权，侵权必究！ 学科网（北京）股份有限公司技巧总结 题中出现同名三角函数相加且首尾互余或互补时，则采用倒序相加的思想处理此类问题  2 n2  n1    模型：cos cos   cos cos n为大于2的奇数 …① n n n n n1  n2  2    cos cos   cos cos n为大于2的奇数 …② n n n n  n1    n2  2   由①+②得cos cos cos cos   n为大于2的奇数  n n  n n  由诱导公式可得每一组都为0 Ⅳ诱导公式的超级应用 技巧总结 针对已知条件求值问题，则遵循以下步骤（万能） 第一步：将目标角和已知角全拿出来 第二步：通过加减乘消去或x 第三步：用已知角代替目标角 第四步：利用诱导公式或三角恒等变换处理 二、求非特殊角三角函数值运算问题 Ⅰ三角函数非特殊角选择问题 技巧总结 记住常见数据：sin60 0.1,sin120 0.2,sin180 0.3,sin240 0.4,sin300 0.5 sin370 0.6,sin440 0.7,sin530 0.8,sin640 0.9,sin900 1.0 sin750 0.96，sin450 0.71 Ⅱ三角函数非特殊角填空问题 技巧总结 一些非特殊角的三角恒等变形求值填空题，由于最后得出的是一个具体的数值，故将其设为一个元t，再利 用恒等变形公式计算其结果 Ⅲ针对非特殊角三角函数值运算有两种思路 思路1：采用对偶式处理 步骤如下： 第一步：令原式为x，对偶式为 y 6 原创精品资源学科网独家享有版权，侵权必究！ 学科网（北京）股份有限公司第二步：两式相加x y ?，两式相减x y ? 第三步：解二元一次方程组，求解x 思路2：若原式拥有两个角的运算，可借助三角形处理 步骤如下： 第一步：构造△ABC,A?、B?、C ?外接圆直径2R1 第二步：应用正弦定理求出a ?、b?、c? 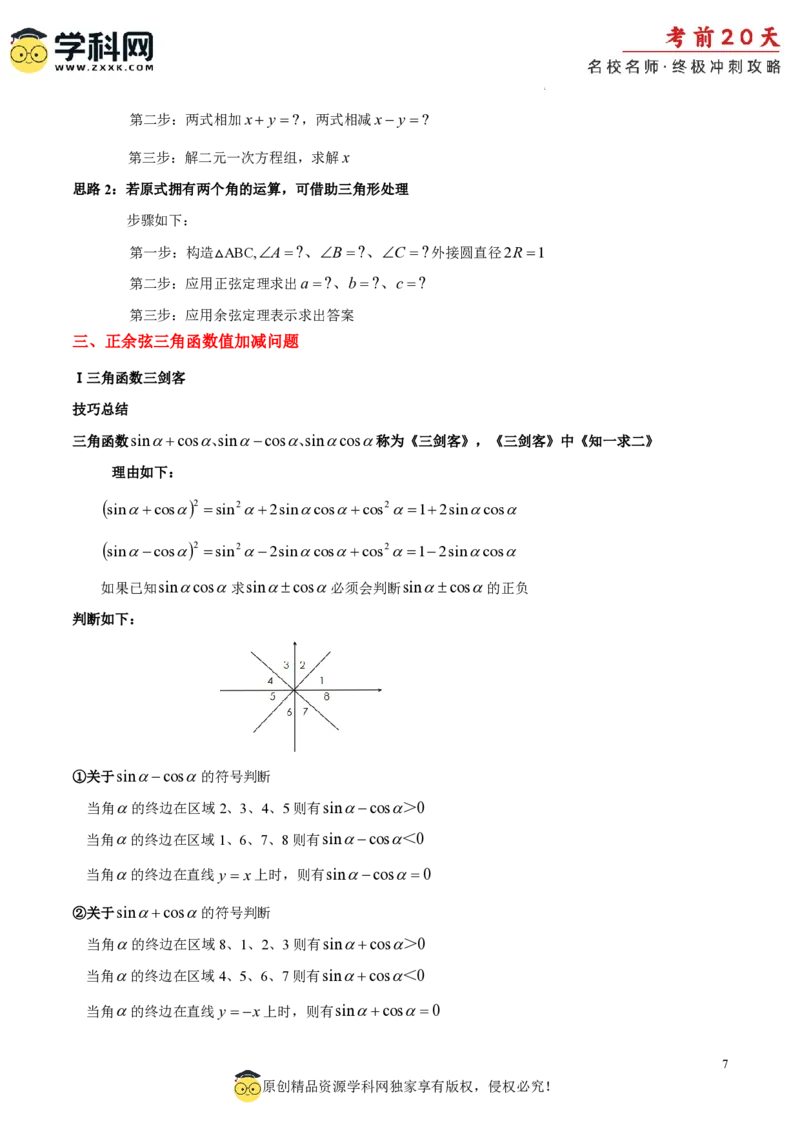第三步：应用余弦定理表示求出答案 三、正余弦三角函数值加减问题 Ⅰ三角函数三剑客 技巧总结 三角函数sincos、sincos、sincos称为《三剑客》，《三剑客》中《知一求二》 理由如下： sincos 2 sin22sincoscos212sincos sincos 2 sin22sincoscos212sincos 如果已知sincos求sincos必须会判断sincos的正负 判断如下： ①关于sincos的符号判断 当角的终边在区域2、3、4、5则有sincos＞0 当角的终边在区域1、6、7、8则有sincos＜0 当角的终边在直线y  x上时，则有sincos0 ②关于sincos的符号判断 当角的终边在区域8、1、2、3则有sincos＞0 当角的终边在区域4、5、6、7则有sincos＜0 当角的终边在直线y x上时，则有sincos0 7 原创精品资源学科网独家享有版权，侵权必究！ 学科网（北京）股份有限公司③关于sintan的符号判断 当角的终边在区域1、2、5、6则有sintan＞0,sintan＜0 当角的终边在区域3、4、7、8则有sintan＜0,sintan＞0 当角的终边在x轴上时，则有sintan0   结论：④若 f   sincos 2sin 则  4   Ⅰ当角在终边在区域1、2内时， f    1, 2     Ⅱ当角在终边在区域3、8内时， f  0,1     Ⅲ当角在终边在区域4、7内时， f  1,0   Ⅳ当角在终边在区域5、6内时， f     2,1   ⑤若 f   sincos 2sin 则  4   Ⅰ当角在终边在区域3、4内时， f    1, 2     Ⅱ当角在终边在区域2、5内时， f  0,1     Ⅲ当角在终边在区域1、6内时， f  1,0   Ⅳ当角在终边在区域7、8内时， f     2,1 结论1：出现asinbcos A形式则采用对偶式处理 asinbcos A   1   acosbsin B   2  12  22  asinbcos 2  acosbsin 2  A2 B2 a2 b2  A2 B2  B2 a2 b2 A2 然后利用二元一次方程组快速求解sin、cos a 特殊情况：asinbcos a2 b2 则tan b 结论2：速记一些常见的勾股数，然后利用直角三角形处理      3,4,5，5,12,13，7,24,25，8,15,17，1,1，2，1，3,2 1,2，5 1,3，10   1,7,5 2 8 原创精品资源学科网独家享有版权，侵权必究！ 学科网（北京）股份有限公司Ⅱ三角函数和差、半角正余弦公式 技巧总结 ①两角和与差的正弦公式 口诀：正余余正，符号相同   sin sincoscossin   sin sincoscossin   sin sincoscossin2sincos故：sin22sincos ②两角和与差的余弦公式 口诀：余余正正，符号相反   cos coscossinsin   cos coscossinsin cos    coscossinsincos2sin22cos2112sin2 Ⅲ三角函数和差、半角正切公式 技巧总结 tantan tantan     ①tan  ②tan  1tantan 1tantan    ③tantantan 1tantan    ④tantantan 1tantan tantan tantan ⑤1tantan ⑥1tantan     tan tan     ⑦tantantantantan tan  只要k ,kZ 都有tantan 3tantan 3 3  只要k ,kZ 都有 3tantan  tantan1 6  只要k ,kZ 都有tantantantan1 4 ⑧△ABC中，tanAtanBtanC tanAtanBtanC（正切恒等式） Ⅳ三角函数辅助角公式 技巧总结 9 原创精品资源学科网独家享有版权，侵权必究！ 学科网（北京）股份有限公司形如：asinbcos 第一步：asinbcos a2 b2 sin     a2 b2 cos    第二步：等号左侧若是加号，则等号右侧也为加号，等号左侧若是减号，等号右侧也为减号.   第三步：的求算，只需在第一象限标明点 a,b 寻找夹角即可达到秒杀的境界. 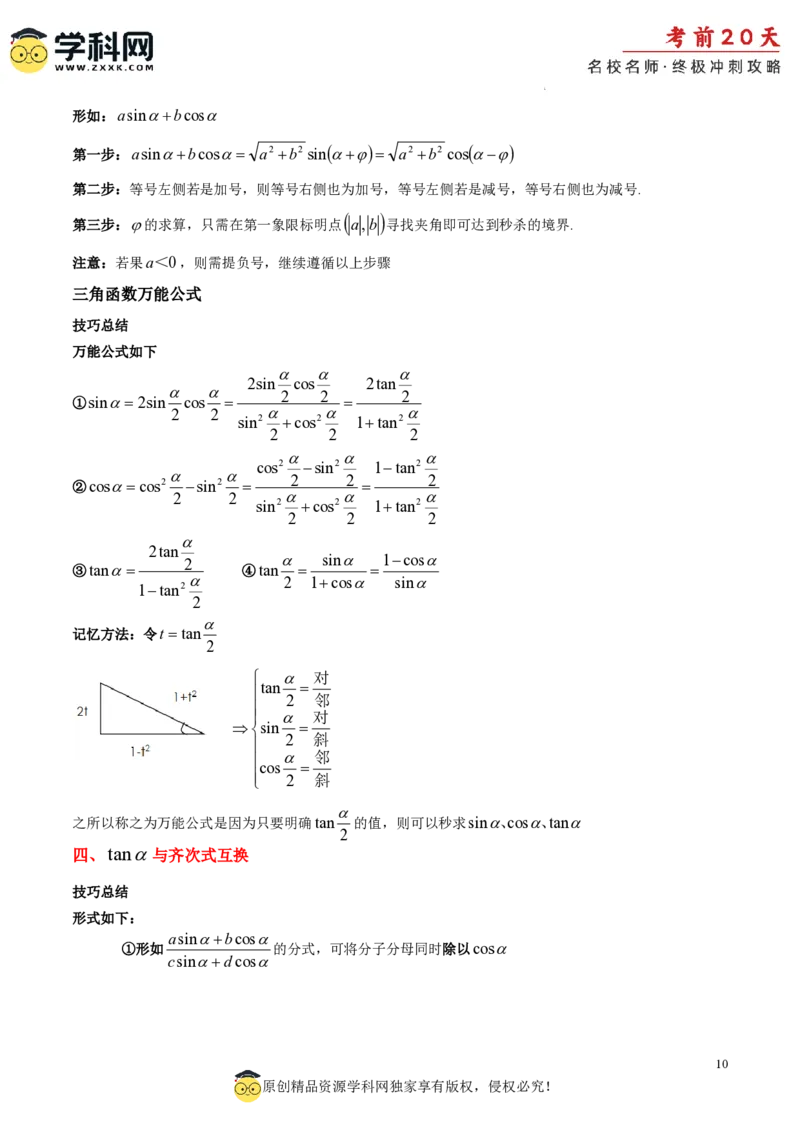注意：若果a＜0，则需提负号，继续遵循以上步骤 三角函数万能公式 技巧总结 万能公式如下    2sin cos 2tan   2 2 2 ①sin2sin cos   2 2    sin2 cos2 1tan2 2 2 2    cos2 sin2 1tan2   2 2 2 ②coscos2 sin2   2 2    sin2 cos2 1tan2 2 2 2  2tan 2  sin 1cos ③tan ④tan    2 1cos sin 1tan2 2  记忆方法：令t tan 2   对 tan   2 邻    对 sin  2 斜    邻 cos    2 斜  之所以称之为万能公式是因为只要明确tan 的值，则可以秒求sin、cos、tan 2 四、tan与齐次式互换 技巧总结 形式如下： asinbcos ①形如 的分式，可将分子分母同时除以cos csindcos 10 原创精品资源学科网独家享有版权，侵权必究！ 学科网（北京）股份有限公司asin bcos  cos cos atanb 得：  csin dcos ctand  cos cos asin2bsincosccos2 ②形如 的分式，可将分子分母同时除以cos2 dsin2esincos f cos2 asin2 bsincos ccos2   asin2bsincosccos2 cos2 cos2 cos2 得：  dsin2esincos f cos2 dsin2 esincos f cos2   cos2 cos2 cos2 atan2btanc  dtan2etan f ③形如asin2bsincosccos2的式子，可将其看成分母为1的分式 asin2bsincosccos2 asin2bsincosccos2 即：  1 sin2cos2 可将分子分母同时除以cos2 asin2 bsincos ccos2   asin2bsincosccos2 cos2 cos2 cos2 即：  sin2cos2 sin2 cos2  cos2 cos2 atan2btanc  tan21 ④形如asinbcos A  asinbcos 2  A2 a2sin22absincosb2cos2 A2 a2sin22absincosb2cos2   A2 1 a2sin22absincosb2cos2   A2 sin2cos2 a2 tan22abtanb2   A2求tan即可 tan21 ⑤形如acos2bsin2acos22bsincos转化为形式③ 11 原创精品资源学科网独家享有版权，侵权必究！ 学科网（北京）股份有限公司1 1 典例1【2023新高考1卷】已知sin ,cossin ，则cos22（ ）． 3 6 7 1 1 7 A. B. C.  D.  9 9 9 9 【答案】B 1 1 1 【解析】因为sin()sincoscossin ，而cossin ，因此sincos ， 3 6 2 2 则sin()sincoscossin ， 3 2 1 所以cos(22)cos2()12sin2()12( )2  . 3 9 故选：B 1 5  典例2【2023新高考全国Ⅱ卷】 已知为锐角，cos ，则sin （ ）． 4 2 3 5 1 5 3 5 1 5 A. B. C. D. 8 8 4 4 【答案】D  1 5 【解析】因为cos12sin2  ，而为锐角， 2 4  2  51 解得：sin  3 5 51．   2 8 16 4 故选：D．   典例3【2022新高考全国II卷】若sin()cos()2 2cos    sin，则（ ）  4 A. tan1 B. tan1 C. tan1 D. tan1 【答案】C 12 原创精品资源学科网独家享有版权，侵权必究！ 学科网（北京）股份有限公司【解析】[方法一]：直接法 由已知得：sincoscossincoscossinsin2cossinsin, 即：sincoscossincoscossinsin0， 即：sincos0 所以tan1 故选：C [方法二]：特殊值排除法  解法一:设β=0则sinα +cosα =0，取= ，排除A, B； 2  再取α=0则sinβ +cosβ= 2sinβ，取β= ，排除D；选C. 4 [方法三]：三角恒等变换   sin()cos() 2sin（ ）= 2sin（[  ）] 4 4     2sin（ ）cos 2co（s  ）sin2 2co（s  ）sin 4 4 4   所以 2sin（ ）cos 2co（s  ）sin 4 4    sin（ ）cosco（s  ）sin=0即sin（ ）=0 4 4 4    2 2 sin（ ）=sin（）cos co（s ）sin = sin（） co（s ）=0 4 4 4 2 2 sin（）=co（s ）即tan(）=-1, 故选：C.   典例4【2021新高考全国Ⅰ卷】 下列区间中，函数 f x7sin  x 单调递增的区间是（ ）  6    π   3 3  A.  0,  B.  ,π  C.  ,  D.  ,2  2  2   2   2  【答案】A 13 原创精品资源学科网独家享有版权，侵权必究！ 学科网（北京）股份有限公司   【解析】因为函数y sinx的单调递增区间为 2k ,2k  kZ ，  2 2       对于函数 f x7sin  x ，由2k  x 2k kZ，  6  2 6 2  2 解得2k  x2k kZ， 3 3   2 取k 0，可得函数 f x 的一个单调递增区间为  , ，  3 3      2     2 则 0,     , ， ,     , ，A选项满足条件，B不满足条件；  2  3 3   2   3 3  5 8 取k1，可得函数 f x 的一个单调递增区间为 , ，  3 3   3   2  3 5 8 3  5 8  ,     , 且 ,    , ， ,2    , ，CD选项均不满足条件.  2   3 3   2   3 3   2   3 3  故选：A. π sin1sin2 预测1（2024·宁夏银川·模拟预测）若tan( )2，则 （ ） 4 cossin 3 3 6 6 A．- B． C． D． 5 5 5 5 1 预测2（2024·浙江·模拟预测）已知coscoscoscos ，则 3 sinsinsinsin（ ） 1 1 1 1 A． B． C． D． 6 3 6 3  π π   π 预测3（2024·山西·模拟预测）已知sinsin cossin ，则tan2 （ ）  6 3   4 3 A． 3 B． C．2 3 D．2 3 3 r r r r 预测4（2024·贵州遵义·模拟预测）已知向量a(4,2)，b (2cos,2sin)，当ab取得最大值时tan 14 原创精品资源学科网独家享有版权，侵权必究！ 学科网（北京）股份有限公司（ ） 1 1 1 1 A． B． C． D． 2 3 4 5 1 预测5（2024·青海西宁·模拟预测）已知tantan5,coscos ,则sin（ ） 6 1 1 5 4 A． B． C． D． 6 5 6 5  π 3 2π π  π 押题1已知sin     ，则sin （ ）  6 3  3 3  3 3 6 3 6 6 3 A． B． C． D． 6 6 3 3  π 3 5  3π 押题2已知x  0,  ,sinxcosx ，则tanx （ ）  4 5  4  A．3 B．3 C． 5 D．2 1  3π  π 押题3已知cosx ,xπ, ，则cosx （ ） 5  2   3 6 21 6 21 6 21 2 6 3 A． B． C． D． 10 10 10 10 π  π  押题4若 ,π，且5cos2 2sin ，则tan（ ） 2  4  4 3 1 A． B． C． D．1 3 4 3 π π 1 押题5已知,满足tan( )3,tan( ) ，则tan(2)（ ） 6 12 2 1 1 3 2 A． B． C． D． 3 3 4 3 名校预测 预测1：答案A π tan1 【详解】tan( ) 2，解得tan3， 4 1tan 15 原创精品资源学科网独家享有版权，侵权必究！ 学科网（北京）股份有限公司sin1sin2 sincossin2 sincossin 所以   cossin cossin cos2sin2 tan1tan 313 3    . 1tan2 19 5 故选：A. 预测2：答案B 【详解】因为coscoscossinsin， 又coscoscossinsin， 所以coscossinsincoscossinsin， 1 因为coscoscoscos ， 3 1 则sinsinsinsincoscoscoscos . 3 故选：B. 预测3：答案C  π π  【详解】由sinsin cossin ，  6 3  3 1 3 1 得 sin2 sincos cos2 sincos， 2 2 2 2 3 3 1 即  cos2sin2  sincos，所以 cos2 sin2， 2 2 2 所以tan2 3，  π 31 所以tan2  2 3.  4 1 31 故选：C. 预测4：答案A r r 2 5 5 【详解】ab 4sin8cos4 5sin()，其中sin ，cos ， 5 5  r r 故当2k (kZ)时，ab取得最大值4 5， 2    sin2k  sin  2  cos 1 此时tan    ， cos    sin 2 cos2k   2  16 原创精品资源学科网独家享有版权，侵权必究！ 学科网（北京）股份有限公司故选：A. 预测5：答案C sincoscossin 【详解】因为tantan 5, coscos 1 又coscos , 6 5 所以sincoscossinsin5coscos , 6 故选C. 名师押题 押题1：答案B 2π π π π π  π 3  π 6 【详解】由  可得   ，又sin  ，则cos  ， 3 3 2 6 2  6 3  6 3  π  π π  π π  π π 3 3 6 1 3 6 故sin sin  sin cos cos sin      故选：B．  3  6 6  6 6  6 6 3 2 3 2 6 押题2：答案A 3 5  π 3 5  π 3 10 【详解】因为sinxcosx ，所以 2sinx  ，所以sinx  ， 5  4 5  4 10  π π π π  π  π 10 又x  0,  ，所以x   ,  ，所以cosx  1sin2 x   ，  4 4 4 2  4  4 10  π  3π  π   π 所以tanx 3，故tanx tan x π  tanx 3.  4  4   4   4 故选：A 押题3：答案A 1  3π  1 2 2 6 【详解】Qcosx ，xπ, ，sinx 1cos2x  1   ， 5  2   5 5  π π π 1 1  2 6 3 6 21 cos  x 3   cosxcos 3 sinxsin 3  5  2     5     2  10 ， 故选：A． 押题4：答案A 17 原创精品资源学科网独家享有版权，侵权必究！ 学科网（北京）股份有限公司【详解】由5cos2 2sin   π   得5  cos2sin2   2    2 cos 2 sin    ， 4   2 2  即5cossincossincossin， π  因为 ,π，所以cossin0， 2  1 所以cossin ，结合cos2sin21，且cos0,sin0， 5 3 4 sin 4 得cos ,sin ，所以tan  . 5 5 cos 3 故选：A. 押题5：答案B π 2tan( ) π 1 π π 12 4 【详解】由tan( ) ，得tan( 2)tan2( )  ， 12 2 6 12 π 3 1tan2( ) 12 π π 4 tan( )tan( 2) 3 π π 6 6 3 1 所以tan(2)tan[( )( 2)]   . 6 6 π π 4 3 1tan( )tan( 2) 13 6 6 3 故选：B 平面向量（选填题） 年份 题号 知识点 考点 2021年I 10 坐标向量 坐标向量与三角函数的综合 卷 2021年II 15 平面向量 平面向量数量积 卷 2022年I 3 平面向量 用基底表示某向量 卷 18 原创精品资源学科网独家享有版权，侵权必究！ 学科网（北京）股份有限公司2022年II 平面向量数量积 4 坐标向量 卷 2023年新 3 坐标向量 平面向量数量积 高考1 16 平面向量 平面向量与双曲线综合 2023 年新 高考2 13 平面向量 平面向量数量积 近三年，平面向量在选填中占据一个位置，考查的考点一般来说是： 1、平面向量的基础知识及共线定理（①平面向量的四则运算②平面向量共线定理） 2、平面向量极化恒等式及等和线（①极化恒等式②等和线定理） 3、平面向量建系法及对角线向量定理（①平面向量建系法.②对角线向量定理③平面向量奔驰定理及向量四 心④平面向量的基本运算及基底） 题干的设置一般来说在上述的三项考点中选其一项。平面向量题目中若表示向量则最好采用建系的思 想，平面向量题目中若表示求向量积最值问题则最好采用极化恒等的思想，另外考生们要想灵活应用小技 巧则需在有限的时间内多推导几遍，考场中便可轻松搞定。 从近三年的全国卷的考查情况来看，本节是高考的热点，其中平面向量数量积定值和向量积最值考查 比较频繁平面向量三类题目比重相当，新高考主要以基向量表示平面向量及向量积最值的形式考查，因小 结论偏多，考生需多推导一遍，试题灵活，下面为考生已总结.. 一、平面向量的基础知识及共线定理 平面向量的四则运算 技巧总结 ①向量加法与减法的法则： 平行四边形法则：以同一点O为起点的两个已知向量a，b为邻边作▱OACB，则以O为起点的对角线OC 就是a与b的和. 19 原创精品资源学科网独家享有版权，侵权必究！ 学科网（北京）股份有限公司图形表示： uuur uuur uuur uuur uuur uuur 字母表示：OAOB=OC ，OAOBBA uuur uuur uuur uuur 坐标表示：记OAx , y ，OBx , y 则OAOBx y , x y  1 1 2 2 1 1 2 2 uuur uuur OBOAx x , y y 2 1 2 1 三角形法则：如果把两个向量的起点放在一起，那么这两个向量的差是以减向量的终点为起点，被减向量 的终点为终点的向量. 图形表示： uuur uuur uuur 字母表示：OA ABOB uuur uuur uuur uuur 坐标表示：记OAx , y ，OBx , y 则OAOBx y , x y  1 1 2 2 1 1 2 2 uuur uuur OBOAx x , y y 2 1 2 1 ②向量数乘的定义   实数与向量a的积是一个向量，这种运算叫做向量的数乘，记作a 图形表示：    字母表示：ABma mR r    坐标表示：记a=(x, y)， 则ma  mx,my ③两个向量的数量积 图形表示： r r r r r r 字母表示：ababcos a,b r r uurr 坐标表示：记a(x ,y)，b(x ,y )，则ab xx  y y 1 1 2 2 1 2 1 2 注意：     1、向量b 与非零向量a共线的充要条件是有且只有一个实数，使得b a .     2、设a  x ,y ,b  x ,y ,a∥b， x y x y 0， 1 1 2 2 1 2 2 1 r r a⊥b ab0 x x y y 0. 1 2 2 1 20 原创精品资源学科网独家享有版权，侵权必究！ 学科网（北京）股份有限公司 r x x  y y 3、两个向量a，b 的夹角公式：cos 1 2 1 2 . x2  y 2  x 2  y 2 1 1 2 2 平面向量共线定理 技巧总结 uuur uuur uuur 定理1：已知PC PAPB，若1，则A、B、C三点共线；反之亦然 平面向量共线定理证明 若点 A、B、C互不重合，P是 A、B、C三点所在平面上的任意一点，且满足PC  xPA yPB，则 A、B、C三点共线 x y 1. 证明:(1)由x y 1 A、B、C三点共线.由x y 1得 PC  xPA yPB xPA(1x)PB PCPB x(PAPB) BC  xBA. 即BC，BA共线，故A、B、C三点共线. (2)由A、B、C三点共线 x y 1. 由A、B、C三点共线得BC，BA共线，即存在实数x使得BC BA.   故BPPC BPPA  PC PA  1  PB.令x,y 1，则有x y 1. 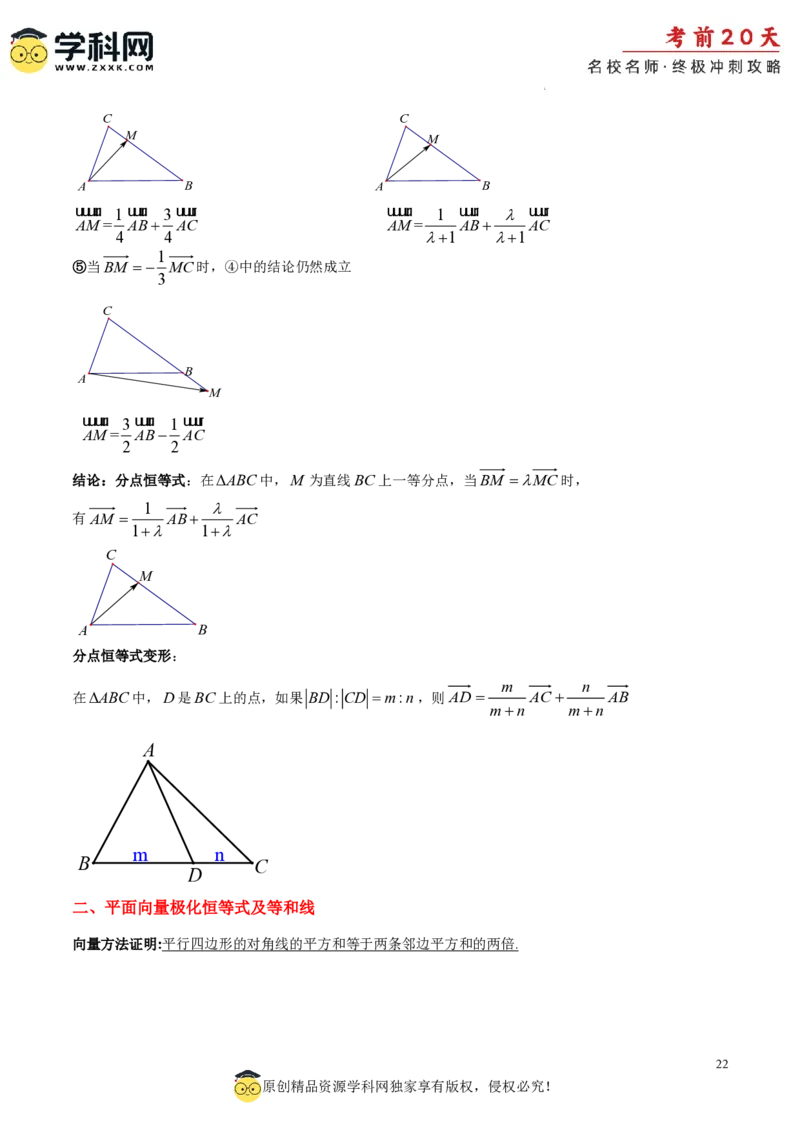推广1：分点恒等式 ①当M 为BC中点时； ②当BM 2MC ； C C M M A B A B uuuur uuur uuur uuuur uuur uuur 1 1 1 2 AM= AB AC AM= AB AC 2 2 3 3 ③当BM 3MC时； ④当BM MC时， 21 原创精品资源学科网独家享有版权，侵权必究！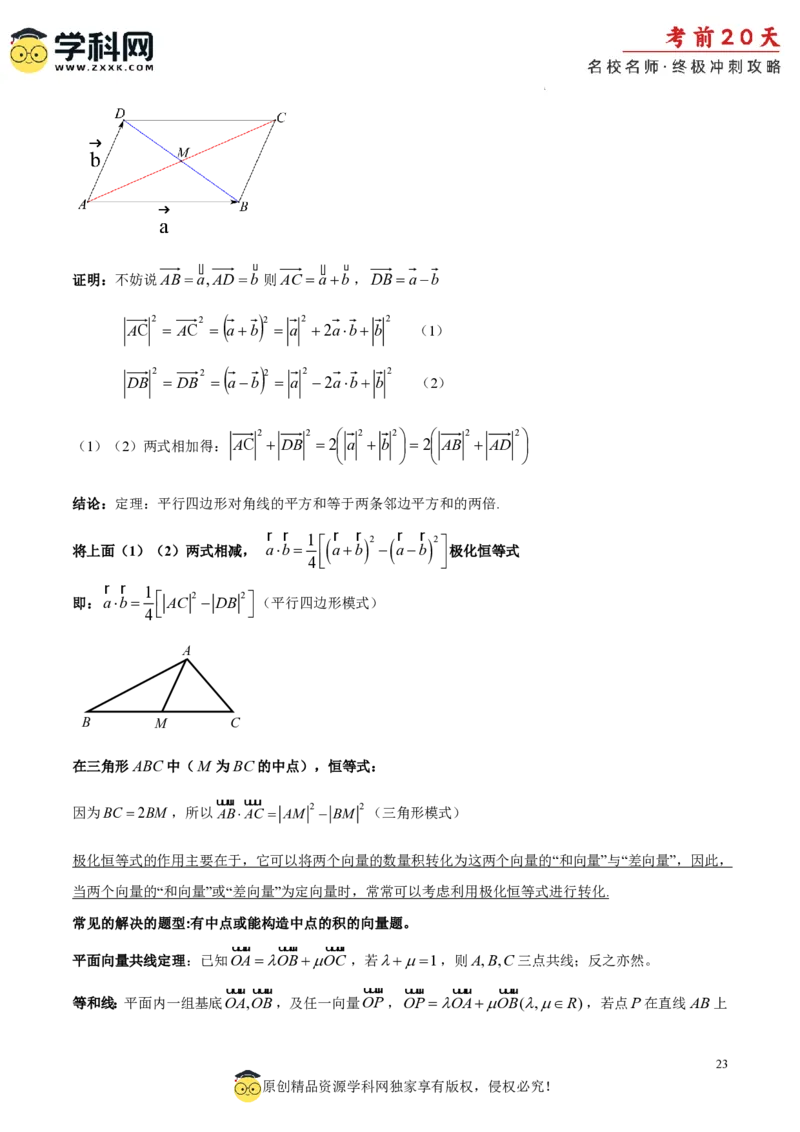 学科网（北京）股份有限公司C C M M A B A B uuuur uuur uuur uuuur uuur uuur 1 3 1  AM= AB AC AM= AB AC 4 4 1 1 1 ⑤当BM  MC时，④中的结论仍然成立 3 C B A M uuuur uuur uuur 3 1 AM= AB AC 2 2 结论：分点恒等式：在ABC中，M 为直线BC上一等分点，当BM MC时， 1  有AM  AB AC 1 1 C M A B 分点恒等式变形： m n 在ABC中，D是BC上的点，如果 BD : CD m:n，则AD  AC AB mn mn A m n B C D 二、平面向量极化恒等式及等和线 向量方法证明:平行四边形的对角线的平方和等于两条邻边平方和的两倍. 22 原创精品资源学科网独家享有版权，侵权必究！ 学科网（北京）股份有限公司    证明：不妨说ABa,ADb 则AC ab ，DBab 2 2   2 2 2 AC  AC  ab  a 2ab b （1） 2 2   2 2 2 DB  DB  ab  a 2ab b （2） 2 2  2 2  2 2 （1）（2）两式相加得： AC  DB 2 a  b 2 AB  AD      结论：定理：平行四边形对角线的平方和等于两条邻边平方和的两倍. r r r r r r 1 2  2 将上面（1）（2）两式相减， ab ab  ab 极化恒等式 4  r r 1 即：ab  AC 2  DB 2 （平行四边形模式） 4  A B M C 在三角形ABC中（M 为BC的中点），恒等式： uuur uuur 因为BC 2BM ，所以ABAC  AM 2  BM 2（三角形模式） 极化恒等式的作用主要在于，它可以将两个向量的数量积转化为这两个向量的“和向量”与“差向量”，因此， 当两个向量的“和向量”或“差向量”为定向量时，常常可以考虑利用极化恒等式进行转化. 常见的解决的题型:有中点或能构造中点的积的向量题。 uuur uuur uuur 平面向量共线定理：已知OAOBOC ，若1，则A,B,C三点共线；反之亦然。 uuur uuur uuur uuur uuur uuur 等和线：平面内一组基底OA,OB，及任一向量OP，OPOAOB(,R)，若点P在直线AB上 23 原创精品资源学科网独家享有版权，侵权必究！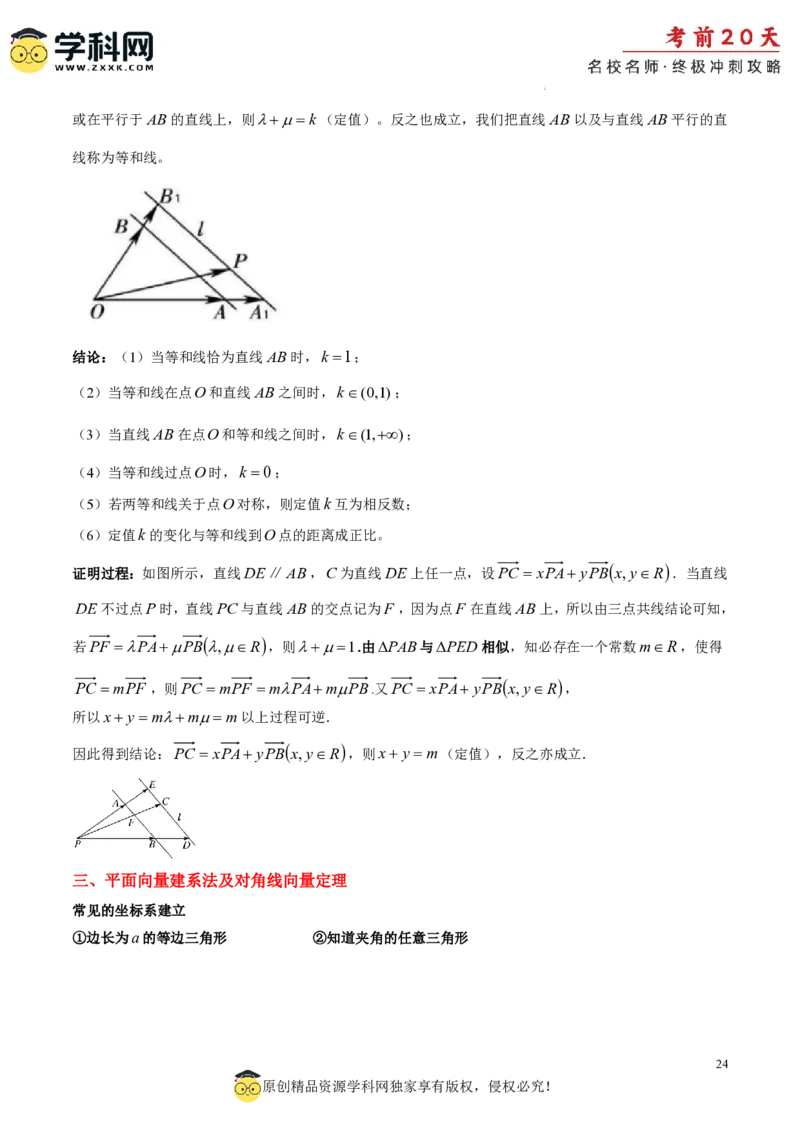 学科网（北京）股份有限公司或在平行于AB的直线上，则k（定值）。反之也成立，我们把直线AB以及与直线AB平行的直 线称为等和线。 结论：（1）当等和线恰为直线AB时，k 1； （2）当等和线在点O和直线AB之间时，k(0,1)； （3）当直线AB在点O和等和线之间时，k(1,)； （4）当等和线过点O时，k 0； （5）若两等和线关于点O对称，则定值k互为相反数； （6）定值k的变化与等和线到O点的距离成正比。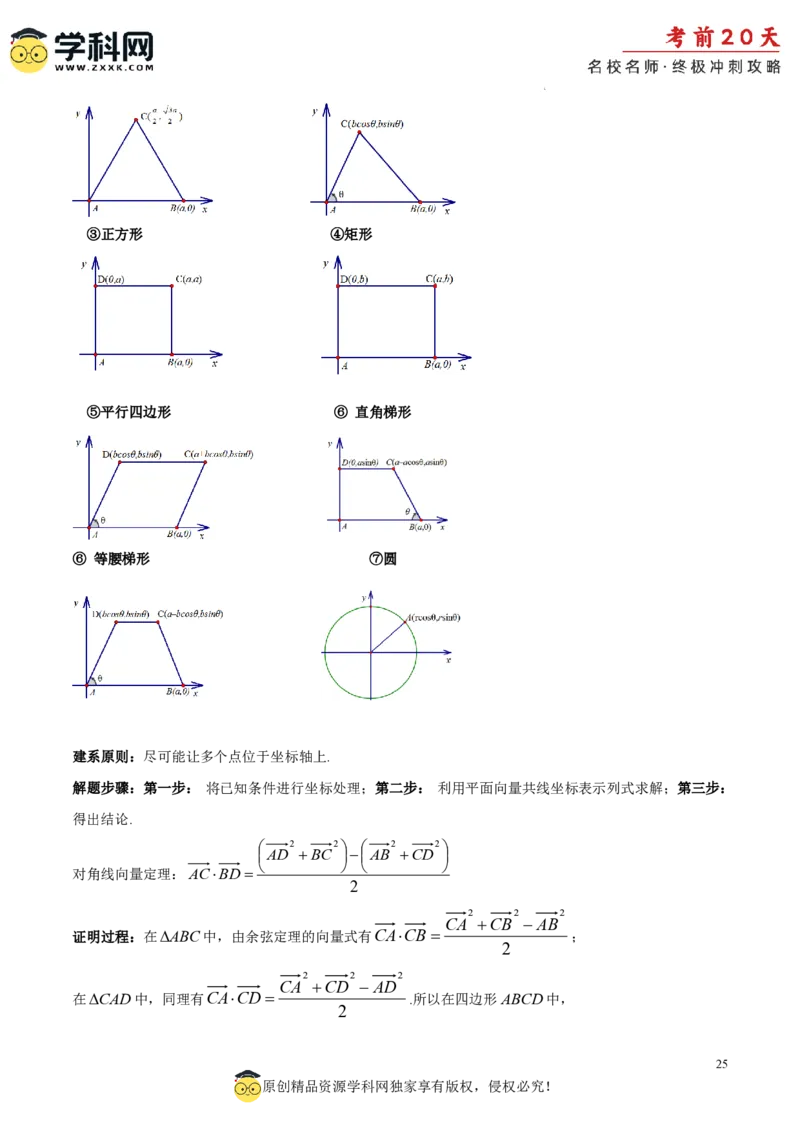 证明过程：如图所示，直线DE∥AB，C为直线DE上任一点，设PC  xPA yPB  x,yR  ．当直线 DE不过点P时，直线PC与直线AB的交点记为F ，因为点F 在直线AB上，所以由三点共线结论可知，   若PF PAPB,R ，则1.由PAB与PED相似，知必存在一个常数mR，使得   PC mPF ，则PC mPF mPAmPB.又PC  xPA yPB x,yR ， 所以x y mmm以上过程可逆． 因此得到结论：PC  xPA yPB  x,yR  ，则x y m（定值），反之亦成立． 三、平面向量建系法及对角线向量定理 常见的坐标系建立 ①边长为a的等边三角形 ②知道夹角的任意三角形 24 原创精品资源学科网独家享有版权，侵权必究！ 学科网（北京）股份有限公司③正方形 ④矩形 ⑤平行四边形 ⑥ 直角梯形 ⑥ 等腰梯形 ⑦圆 建系原则：尽可能让多个点位于坐标轴上. 解题步骤：第一步： 将已知条件进行坐标处理；第二步： 利用平面向量共线坐标表示列式求解；第三步： 得出结论.  2 2  2 2 AD BC AB CD      对角线向量定理：ACBD 2 2 2 2 CA CB  AB 证明过程：在ABC中，由余弦定理的向量式有CACB  ； 2 2 2 2 CA CD  AD 在CAD中，同理有CACD  .所以在四边形ABCD中， 2 25 原创精品资源学科网独家享有版权，侵权必究！ 学科网（北京）股份有限公司 2 2  2 2 AD BC AB CD        ACBD AC CDCB  2  2 2  2 2 AD BC AB CD      即ACBD ，表明四边形的两条对角线对应向量的数量积可用四条边的长 2 度表示。 2 2 2 2 结论1：当AC  BD时，有AD BC  AB CD . 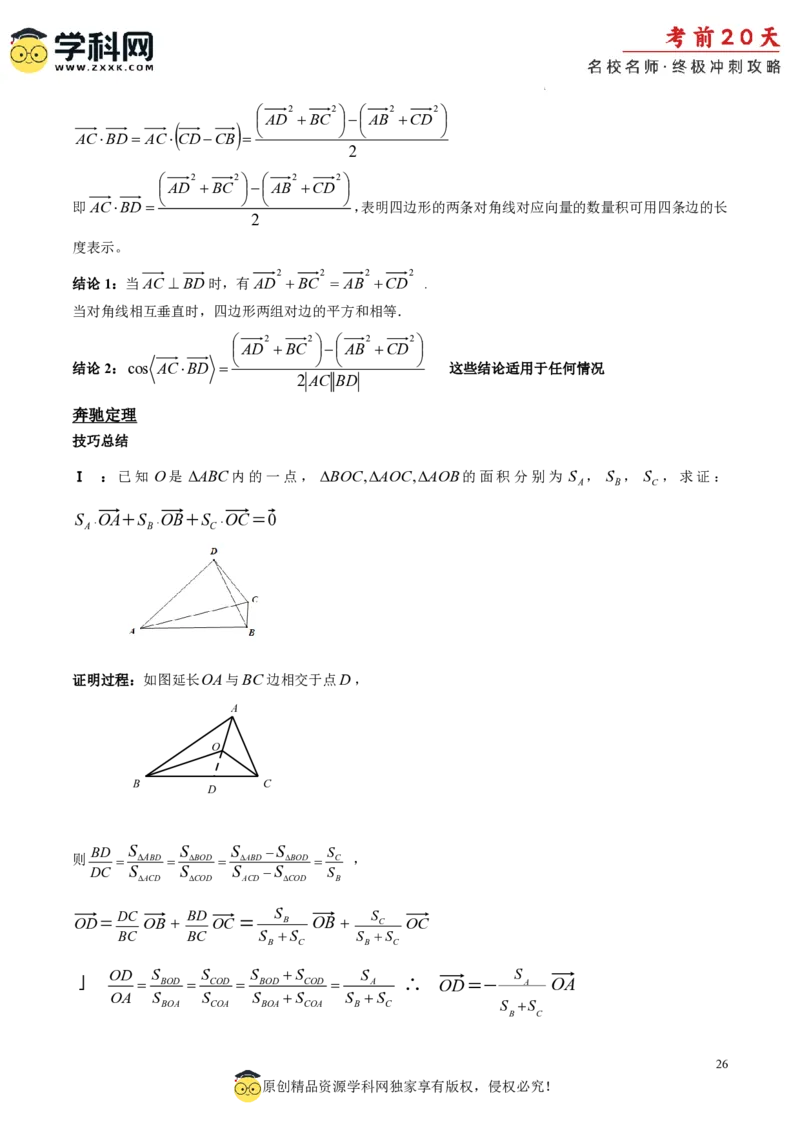当对角线相互垂直时，四边形两组对边的平方和相等．  2 2  2 2 AD BC AB CD      结论2：cos ACBD  这些结论适用于任何情况 2AC BD 奔驰定理 技巧总结 Ⅰ ：已知 O是 ABC内的一点， BOC,AOC,AOB的面积分别为 S ， S ， S ，求证： A B C S A OAS B OBS C OC 0 证明过程：如图延长OA与BC边相交于点D， A O B C D BD S S S S S 则  ABD  BOD  ABD BOD  C ， DC S S S S S ACD COD ACD COD B OD DC OB  BD OC  S B OB  S C OC BC BC S S S S B C B C  OD  S BOD  S COD  S BOD S COD  S A  OD S A OA OA S S S S S S BOA COA BOA COA B C S S B C 26 原创精品资源学科网独家享有版权，侵权必究！ 学科网（北京）股份有限公司  S A OA  S B OB  S C OC S S S S S S B C B C B C S OA  S OB  S OC  0 A  B  C  推论：已知P为ABC内一点，   且xPA yPBzPC 0, x,y,zR,xyz 0,x yz 0 ．则有 ①S :S :S  x : y : z ． PBC PAC PAB S x S y S z ② PBC  , PAC  , PAB  ． S x yz S x yz S x yz ABC ABC ABC Ⅱ：奔驰定理在三角形四心中的具体形式： （1）O是ABC的重心 S :S :S 1:1:1OAOBOC 0. A B C （2）O是ABC的内 S :S :S a:b:c aOAbOBcOC 0. A B C （3）O是ABC的外心  S :S :S sin2A:sin2B:sin2C sin2AOAsin2BOBsin2COC 0. A B C （4）O是ABC的垂心 S :S :S tanA:tanB:tanC  tanAOAtanBOBtanCOC 0. A B C 四心的概念介绍 （1）重心——中线的交点：重心将中线长度分成2：1； （2）垂心——高线的交点：高线与对应边垂直； （3）内心——角平分线的交点（内切圆的圆心）：角平分线上的任意点到角两边的距离相等； （4）外心——中垂线的交点（外接圆的圆心）：外心到三角形各顶点的距离相等。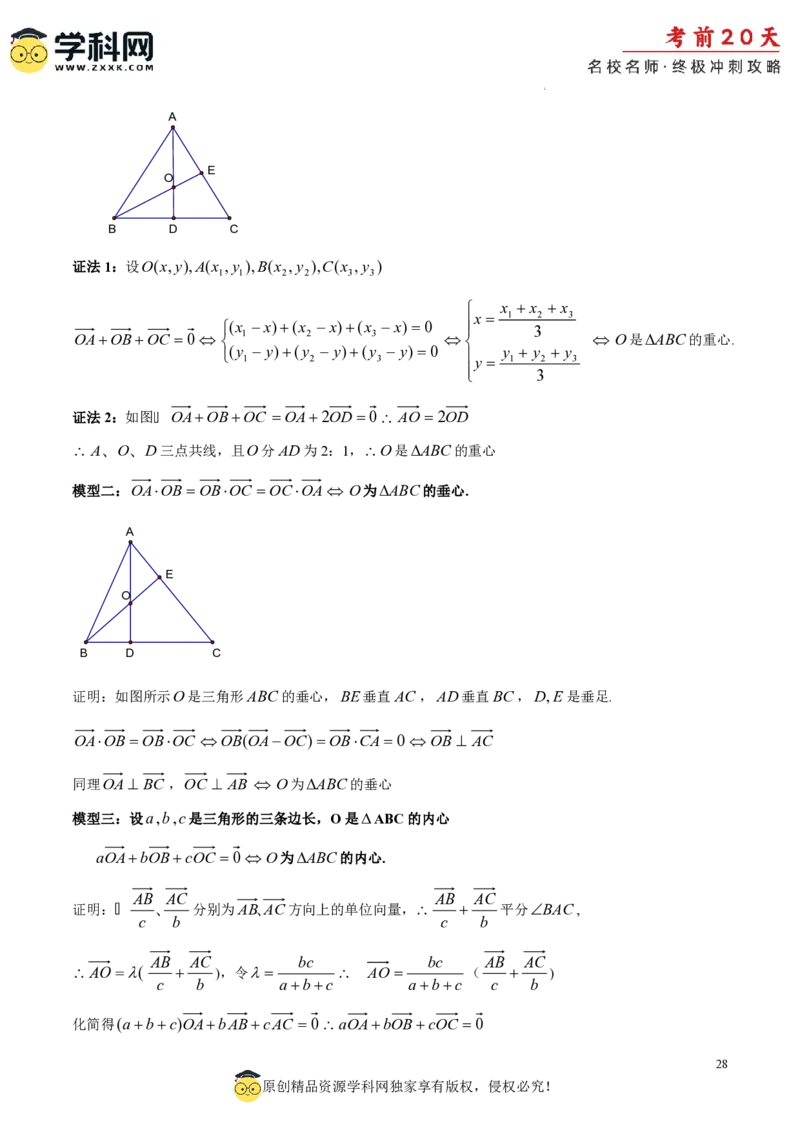 模型总结： 模型一：OAOBOC 0 O是ABC的重心. 27 原创精品资源学科网独家享有版权，侵权必究！ 学科网（北京）股份有限公司A E O B D C 证法1：设O(x,y),A(x ,y ),B(x ,y ),C(x ,y ) 1 1 2 2 3 3  x  x  x x  1 2 3 (x x)(x x)(x x) 0   3 OAOBOC 0  1 2 3    O是ABC的重心. (y  y)(y  y)(y  y) 0 y  y  y  1 2 3  y  1 2 3   3 证法2：如图 OAOBOC OA2OD 0 AO  2OD  A、O、D三点共线，且O分AD为2：1，O是ABC的重心 模型二：OAOB OBOC OCOA O为ABC的垂心. A E O B D C 证明：如图所示O是三角形ABC的垂心，BE垂直AC，AD垂直BC，D,E是垂足. OAOB OBOC  OB(OAOC) OBCA0  OB  AC 同理OA BC ，OC  AB  O为ABC的垂心 模型三：设a,b,c是三角形的三条边长，O是ABC的内心 aOAbOBcOC 0 O为ABC的内心. AB AC AB AC 证明： 、 分别为AB、AC方向上的单位向量，  平分BAC, c b c b AB AC bc bc AB AC AO (  )，令  AO  （  ) c b abc abc c b 化简得(abc)OAbABcAC 0aOAbOBcOC 0 28 原创精品资源学科网独家享有版权，侵权必究！ 学科网（北京）股份有限公司模型四： OA  OB  OC  O为ABC的外心。（证明略） 模型五：变形四心 变形1：O是平面上一定点，A、B、C是平面上不共线的三个点，动点P满足OP OA(AB AC)，    0, ，则点P的轨迹一定通过ABC的重心 证明：ABC，D、E分别为边BC、AC 的中点.  AB AC  2ADOP OA2AD OP OA APAP  2ADAP//AD 点P的轨迹一定通过ABC的重心. 变 形 2 ： O是 平 面 上 一 定 点 ， A、B、C是 平 面 上 不 共 线 的 三 个 点 ， 动 点 P满 足 AB AC OP OA(  )，  0,  ，则点P的轨迹一定通过ABC的内心 AB AC AB AC 证明： 、 分别为AB、AC方向上的单位向量， AB AC AB AC   平分BAC,点P的轨迹一定通过ABC的内心. AB AC 变 形 3 ： O是 平 面 上 一 定 点 ， A、B、C是 平 面 上 不 共 线 的 三 个 点 ， 动 点 P满 足 AB AC OP  OA(  ) ，  0,  ，则点P的轨迹一定通过ABC的垂心 AB cosB AC cosC 证明：AD垂直BC，BE垂直AC，D,E 是垂足. AB AC ABBC ACBC (  )BC =  AB cosB AC cosC AB cosB AC cosC  AB BC cosB AC BC cosC =  = BC + BC =0 AB cosB AC cosC 点P的轨迹一定通过ABC的垂心. 变形4：O是ABC所在平面内一点，动点P满足 29 原创精品资源学科网独家享有版权，侵权必究！ 学科网（北京）股份有限公司   AB AC    OPOA  ， 0, ，则动点P的轨迹一定通过ABC的重心    AB sinB AC sinC   AB AC AB AC   证明：    ，h为BC边上的高∴AP  AB AC . AB sinB AC sinC h h h 变形 5 ：已知 O是平面上的一定点， A，B，C是平面上不共线的三个点，动点 P满足 uuur uuur uuur uuur uuur   OBOC AB AC OP  uuur  uuur  ，(0，)，则动点P的轨迹一定通过△ABC的外心。 2  AB cosB AC cosC   uuur uuur uuur OBOC 证明：取BC中点M, 则 =OD， 2 uuur uuur uuur uuur  AB AC  uuur OPOD uuur  uuur  ,移项后同乘BC  AB cosB AC cosC   uuur uuur uuur uuur uuur uuur uuur   uuur uuur   AB AC ABBC ACBC DP uuur  uuur  DPBC  uuur  uuur   AB cosB AC cosC  AB cosB AC cosC     uuur uuur  uuur uuur  uuur uuur DPBC   BC  BC 0，即DP BC uuur uuur uuur uuur uuur uuur 变形 6：若H 为△ABC所在平面内一点，且 HA 2  BC 2  HB 2  CA 2  HC 2  AB 2 则点H 是△ABC的垂心 uuur uuur uuur uuur uuur uuur uuur uuur uuur uuur 2 2 2 2 2  2 2  2 证明： HA  BC  HB  CA  HA  BH HC = HB  CH HA uuur uuur uuur uuur uuur uuur uuur uuur uuur uuur uuur uuur 得HAHB HCHA HACB0,即HACB，同理可得HB AC,HC  BC 典例1【2021新高考1卷】已知O为坐标原点，点Pcos,sin ，P cos,sin ， 1 2 P  cos,sin ，A(1,0)，则（ ） 3 uuur uuur uuur uuur A. OP  OP B. AP  AP 1 2 1 2 30 原创精品资源学科网独家享有版权，侵权必究！ 学科网（北京）股份有限公司uuur uuur uuur uuur uuur uuur uuur uuur C. OAOP OPOP D. OAOP OP OP 3 1 2 1 2 3 【答案】AC uuur uuur uuur 【解析】A：OP (cos,sin)，OP (cos,sin)，所以|OP | cos2sin21， 1 2 1 uuur uuur uuur |OP | (cos)2 (sin)2 1，故|OP ||OP |，正确； 2 1 2 uuur uuur B：AP (cos1,sin)，AP (cos1,sin)，所以 1 2 uuur   | AP | (cos1)2 sin2 cos22cos1sin2 2(1cos)  4sin2 2|sin | 1 2 2 uuur  uuur uuur ，同理|AP | (cos1)2sin22|sin |，故| AP |,| AP |不一定相等，错误； 2 2 1 2 uuur uuur C：由题意得：OAOP 1cos()0sin()cos()， 3 uuur uuur OPOP coscossin(sin)cos()，正确； 1 2 uuur uuur D：由题意得：OAOP 1cos0sincos， 1 uuur uuur OP OP coscos()(sin)sin() 2 3 uuur uuur uuur uuur cos  βαβ cosα2β ，故一般来说OAOP OP OP 故错误； 1 2 3 故选：AC r r r r r r r 典例2【2021新高考全国Ⅱ卷】 已知向量abc0， a 1， b  c 2， r r r r r r abbcca _______． 9 【答案】 2 r r r r r r r r r r r r r r r r r r  2 2 2 2     【解析】由已知可得 abc a b c 2 abbcca 92 abbcca 0， r r r r r r 9 因此，abbcca  . 2 9 故答案为： . 2 uuur r uuur r uuur 典例3【2022新高考全国Ⅰ卷】在VABC中，点D在边AB上，BD 2DA．记CAm，CDn，则CB （ ） 31 原创精品资源学科网独家享有版权，侵权必究！ 学科网（北京）股份有限公司r r r r r r r r A. 3m2n B. 2m3n C. 3m2n D. 2m3n 【答案】B uuur uuur uuur uuur uuur uuur   【解析】因为点D在边AB上，BD 2DA，所以BD2DA，即CDCB2 CACD ， uuur uuur uuur r ur r r 所以CB 3CD2CA3n2m 2m3n． 故选：B． r r r r r r r r r 典例4【2022新高考全国Ⅱ卷】 已知向量a (3,4),b(1,0),c atb，若a,c b,c ，则t （ ） A. 6 B. 5 C. 5 D. 6 【答案】C r r r r 93t16 3t 【解析】解：c 3t,4 ,cos a,c cos b,c ,即 r  r ,解得t 5, 5c c 故选：C r r r r r r     典例5【2023新高考全国Ⅰ卷】 已知向量a 1,1,b1,1，若 ab  ab ，则（ ） A. 1 B. 1 C. 1 D. 1 【答案】D r r r r r r 【解析】因为a 1,1,b1,1，所以ab1,1，ab1,1， r r r r r r r r         由 ab  ab 可得， ab  ab 0， 即 11110，整理得：1． 故选：D． r r 预测1（2024·广东佛山·模拟预测）已知a与b为两个不共线的单位向量，则（ ） r r r r r r     A． ab //a B．a ab 32 原创精品资源学科网独家享有版权，侵权必究！ 学科网（北京）股份有限公司r r π r r r π r r r π r r π C．若 a,b  ，则 ab,b  D．若 ab,a  ，则 a,b  3 3 4 2 r r r r 3π  预测2（2024·安徽池州·模拟预测）已知向量a1,1,b2,4，若a与b的夹角为，则cos   2  （ ） 10 10 3 10 3 10 A． B． C． D． 10 10 10 10 r r r r r r r 3 r r r r r 预测3（2024·广西·模拟预测）已知向量a,b,c满足 a 1,b  3，ab= , ac,bc 30o，则 c 的最 2 大值等于（ ） A．2 7 B． 7 C．2 D． 2 r r r r r r r 预测4（2024·河南信阳·模拟预测）已知e为单位向量，向量a满足ae 2， ae 1，则 a 的最大值为 （ ） A．4 B．2 C． 5 D．5 预测5（2024·宁夏固原·模拟预测）已知向量a r 1,1,b r 0,t，若a r   a r 2b r  ，则b r （ ） 2 A． B．1 C． 2 D．2 2 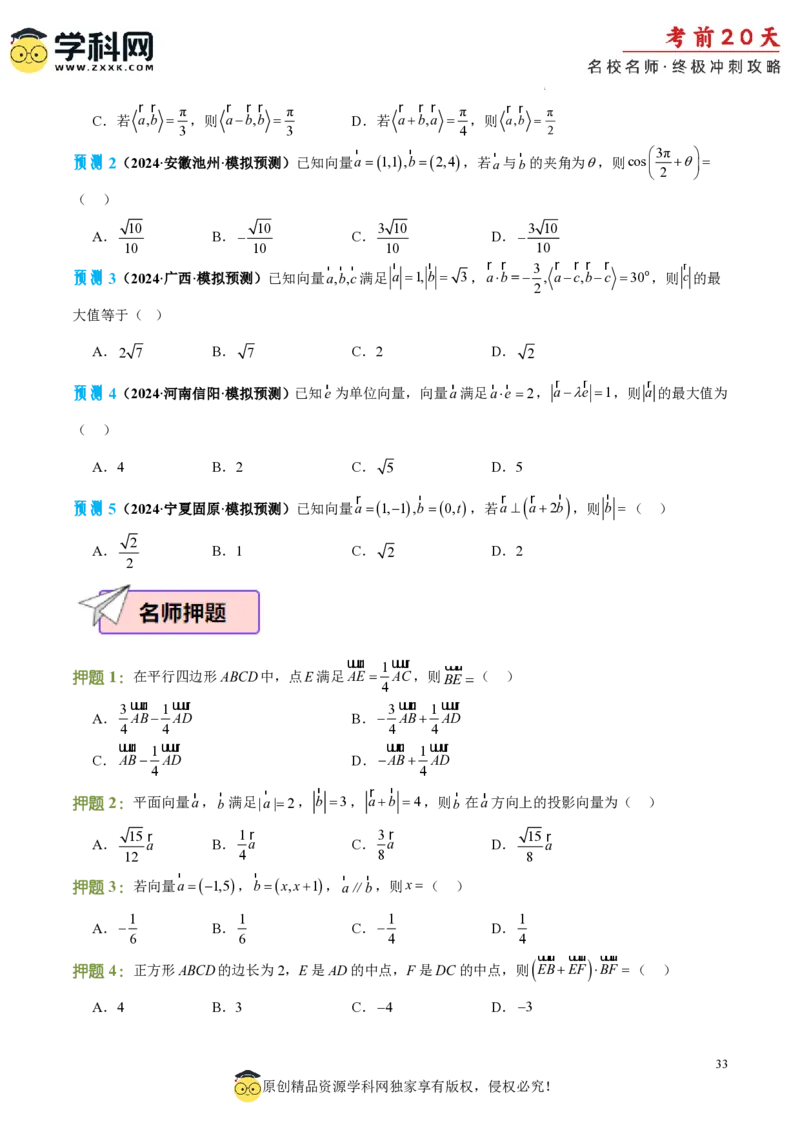uuur 1uuur uuur 押题1：在平行四边形ABCD中，点E满足AE AC，则BE（ ） 4 3uuur 1uuur 3uuur 1uuur A． AB AD B． AB AD 4 4 4 4 uuur 1uuur uuur 1uuur C．AB AD D．AB AD 4 4 r r r r r r r r 押题2：平面向量a，b 满足|a|2， b 3， ab 4，则b 在a方向上的投影向量为（ ） 15 r 1 r 3r 15 r A． a B． a C． a D． a 12 4 8 8 r r r r 押题3：若向量a1,5，bx,x1，a∥b，则x（ ） 1 1 1 1 A． B． C． D． 6 6 4 4 uuur uuur uuur   押题4：正方形ABCD的边长为2，E是AD的中点，F是DC的中点，则 EBEF BF （ ） A．4 B．3 C．4 D．3 33 原创精品资源学科网独家享有版权，侵权必究！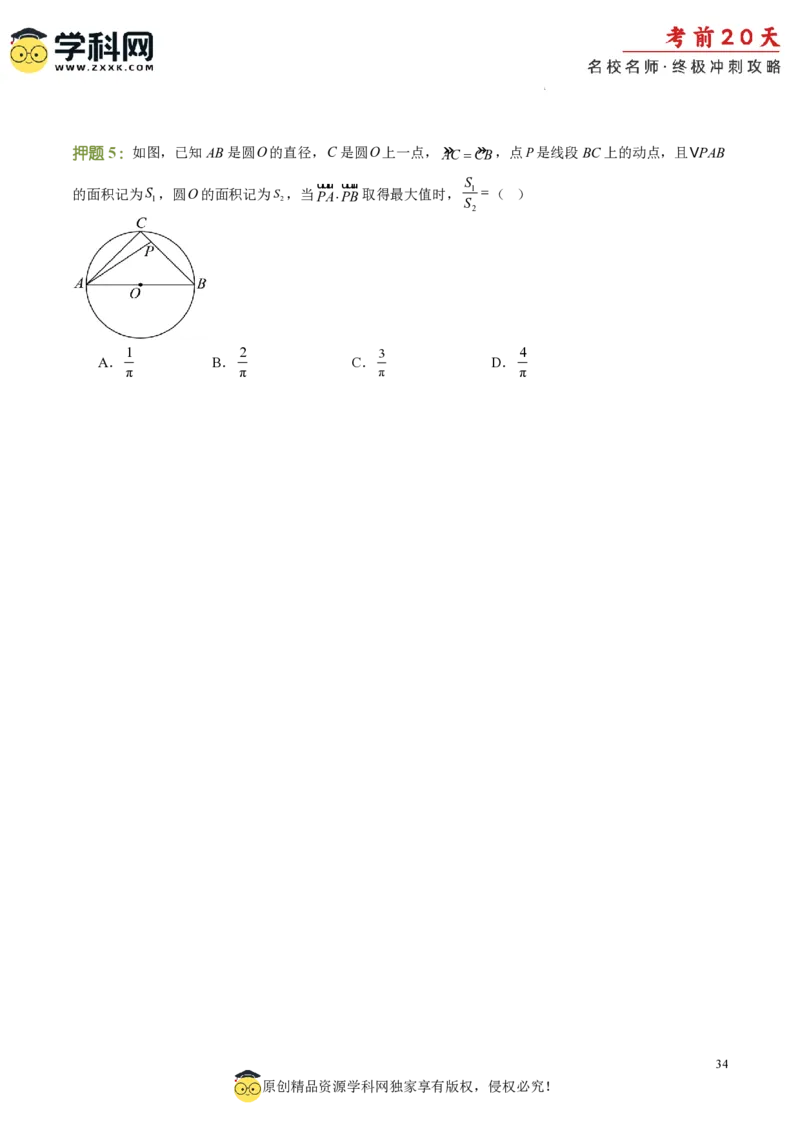 学科网（北京）股份有限公司押题5：如图，已知AB是圆O的直径，C是圆O上一点，» AC C » B，点P是线段BC上的动点，且VPAB uuur uuur S 的面积记为S ，圆O的面积记为S ，当PAPB取得最大值时， 1 （ ） 1 2 S 2 1 2 3 4 A． B． C． D． π π π π 34 原创精品资源学科网独家享有版权，侵权必究！ 学科网（北京）股份有限公司名校预测 预测1：答案 D r r r r r r r r 【详解】选项A：若  ab  //a，则a  ab  ，即1ab， r r 与a与b为两个不共线的单位向量矛盾，故选项A说法错误； r r 选项B：设a与b的夹角为，则0π，cos1， r r r r r r r r r    2 2 所以a ab  a ab a  a b cos1cos0，故选项B 说法错误； r r π r r r r π 1 选项C：若 a,b  ，则ab a b cos  ， 3 3 2  r r  r r r  r 2 1 r r 2 r 2 r r r 2 r r 所以 ab bab b  ， ab  a 2ab b 1，即 ab 1， 2 r r r   r r r ab b 1 所以cos ab,b  r r r  ， ab b 2 r r r r r r 2π 又0 ab,b π，所以 ab,b  ，故选项C说法错误； 3 r r r r r r r r r r r r r r r r    2 2  2  2 选项D：因为a ab  a ab1ab， ab  a 2ab b 22ab， r r r   r r r r r ab a 1ab 2 r r r r 所以cos ab,a  r r r  r r  ，化简得1ab 1ab， ab a 22ab 2 r r r r r r 设a与b的夹角为，则0π，cos1，所以ab a b cos1， r r r r r r π 所以 1ab 1，即ab0，所以 a,b  ，故选项D说法正确； 2 故选：D 预测2：答案A r r ab 1214 3 【详解】由题意得cos r r   ,0,π ， a b 2 2242 10 2 3π   3  10 所以cos sin 1    ．  2   10 10 故选：A 预测3：答案A 35 原创精品资源学科网独家享有版权，侵权必究！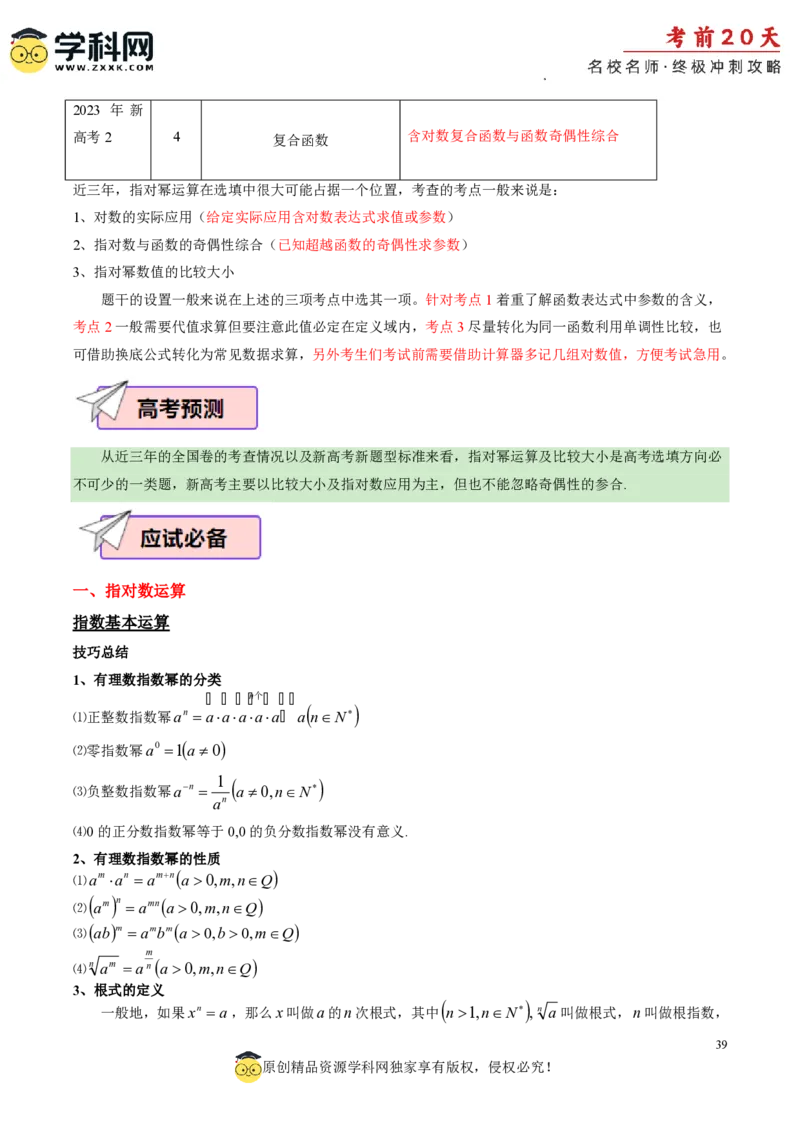 学科网（北京）股份有限公司uuur r uuur r uuur r 【详解】设OAa,OBb,OC c， r r r r r r 3 ab 3 因为 a 1,b  3，ab ，所以cosAOB r r  AOB150， 2 a b 2 r r r r 又ac,bc 30o，所以cosACB30，所以点A,O,B,C共圆， r 要使 c 的最大，即OC 为直径， 在VAOB中，由余弦定理可得AB2 OA2OB22OAOBcosAOB7 AB 7， AB 又由正弦定理2R 2 7， sinAOB r 即 c 的最大值等于2 7， 故选：A. 预测4：答案C r r 【详解】因为 ae 1， r r r r r r r r r 所以 ae2 ae2  a22aee2  a242 1 r r 所以 a2 24122 5 5，所以 a  5. 故选：C 预测5：答案B r r 【详解】由题意知，abt， r r r r r r r r r r r r r 由a(a2b)，得a(a2b)a22ab 22ab 0，解得ab1， r 因此t 1，解得t 1，即b(0,1)， r 所以|b|1. 故选：B 名师押题 押题1：答案B 【详解】因为ABCD为平行四边形， uuur 1uuur 1 uuur uuur  则由AE AC  ABAD ， 4 4 uuur uuur uuur 1 uuur uuur  uuur 3uuur 1uuur ∴BE AEAB ABAD AB AB AD. 4 4 4 36 原创精品资源学科网独家享有版权，侵权必究！ 学科网（北京）股份有限公司故选：B. 押题2：答案C r r r r r r r r r r r r 3 【详解】由 ab  (ab)2  |a|2 2ab+|b|2  132ab 4可得ab ， 2 r r r r r 3 而b r 在a r 方向上的投影向量为|b|co r sb,a a r  a r b a r  2 a r  3 a r . |a| |a|2 4 8 故选：C. 押题3：答案A r r 1 【详解】因为a // b ，所以x15x0，解得x . 6 故选：A 押题4：答案D uuur uuur uuur uuur uuur uuur uuur uuur uuur      【详解】 EBEF BF  EAABEDDF · BCCF  1uuur uuur 1uuur 1uuur  uuur 1uuur   ADAB AD AB·AD AB  2 2 2  2  3uuur  uuur 1uuur   AB·AD AB 2  2  3uuur uuur 3uuur 1uuur  ABAD AB AB 2 2 2 3 0 22 3. 4 故选：D. 故选：ABD 押题5：答案A 【详解】由题意可知：OCAB，以O为坐标原点建立平面直角坐标系， 37 原创精品资源学科网独家享有版权，侵权必究！ 学科网（北京）股份有限公司不妨设OC 2，则A2,0,B2,0,C0,2， 可知直线BC对应的一次函数解析式为y2x，可设Pa,2a,0a2， uuur uuur 可得PA2a,a2,PB2a,a2， uuur uuur 则PAPB2a2aa22 2a122，且0a2， 因为y2a12 2开口向上，对称轴为a1， uuur uuur 且0a2，可知当a0时，即点P与点C重合时，PAPB取到最大值， 1 S 4 1 此时S  244，且S 4π，所以 1   . 1 2 2 S 4π π 2 故选：A. 指对幂运算及比较大小（选填题） 年份 题号 知识点 考点 2021年I 13 指对幂 指数与函数奇偶性综合 卷 2021年II 7 指对幂 指对幂数值的比较大小 卷 2022年I 7 指对幂 指对幂数值的比较大小 卷 2022年II 无 卷 2023年新 4 复合函数 指数的运算及函数单调性求参 高考1 38 原创精品资源学科网独家享有版权，侵权必究！ 学科网（北京）股份有限公司2023 年 新 高考2 4 复合函数 含对数复合函数与函数奇偶性综合 近三年，指对幂运算在选填中很大可能占据一个位置，考查的考点一般来说是： 1、对数的实际应用（给定实际应用含对数表达式求值或参数） 2、指对数与函数的奇偶性综合（已知超越函数的奇偶性求参数） 3、指对幂数值的比较大小 题干的设置一般来说在上述的三项考点中选其一项。针对考点1着重了解函数表达式中参数的含义， 考点2一般需要代值求算但要注意此值必定在定义域内，考点3尽量转化为同一函数利用单调性比较，也 可借助换底公式转化为常见数据求算，另外考生们考试前需要借助计算器多记几组对数值，方便考试急用。 从近三年的全国卷的考查情况以及新高考新题型标准来看，指对幂运算及比较大小是高考选填方向必 不可少的一类题，新高考主要以比较大小及指对数应用为主，但也不能忽略奇偶性的参合. 一、指对数运算 指数基本运算 技巧总结 1、有理数指数幂的分类    n个     ⑴正整数指数幂an aaaaa a nN ⑵零指数幂a0 1  a0  1   ⑶负整数指数幂an  a 0,nN an ⑷0的正分数指数幂等于0,0的负分数指数幂没有意义. 2、有理数指数幂的性质 ⑴aman amn a 0,m,nQ  ⑵  am n amn a0,m,nQ  ⑶ abm ambma0,b0,mQ m ⑷n am an  a 0,m,nQ  3、根式的定义   一般地，如果xn a，那么x叫做a的n次根式，其中 n1,nN , n a 叫做根式，n叫做根指数， 39 原创精品资源学科网独家享有版权，侵权必究！ 学科网（北京）股份有限公司a叫做开方数. 4、对于根式n a ，要注意以下几点 ⑴nN且n1；  a,a0 ⑵当n为奇数时，n an a；当n为偶数时，n an  a  ； a,a0 ⑶负数没有偶次方根； ⑷0的任何次方根都是0 5、多重根号问题，首先先写成指数形式  3 7 7  1 1  a a2  a4 a8 1 1  a2  a1  a1 a2 a a a  ， a2  a2  a  1 1 1 7 1 1 1 1    a2 a4 a8 a8  a4 a8 a8 a2 6、指数的逆运算过程 1 1 1 -  3 - 3 27 - 3  3 3 3 3 1 2 3           8  8   2  2 3 指数特殊运算 技巧总结 形如xx1 a，求下列各种形式的值的思路． 2  1 1  1 1  （1） x2 x  2 ；根据x2 x 2   xx12计算即可；   （2）x2 x2；根据  xx12  x2 x2 2计算即可； （3） x2 x2 ．由于xx1   xx12   xx12 4，进而根据x2 x2   xx1 xx1 即可求解. （4）x1x1；根据xx1   xx12   xx12 4计算即可 （5）x3 x3根据  x2 x2 x+x1  x3 x3+xx1计算即可 （6）x3 x3根据  x2 x2 xx1  x3 x3 xx1计算即可 对数基本运算 技巧总结 1、对数运算法则 M    ①外和内乘：log MN log M log N ②外差内除：log  log M log N a a a a  N  a a n ③提公次方法：log bn  log bm,nR ④特殊对数：log 10 am m a a ⑤指中有对，没心没肺，真数为几，直接取几：alog a b b,log ab b a 2、对数的定义 40 原创精品资源学科网独家享有版权，侵权必究！ 学科网（北京）股份有限公司一般地，如果ax  N  a 0,a 1  ，那么数x叫做以a为底N 的对数，记xlog N ,其中a叫做对数的底 a   数，N 叫做对数的真数 N 0 3、换底公式 log b 1 ①常用换底log b m ②倒数原理log b a log a a log a m b lgb lgc lgc ③约分技巧log blog c   log c④具体数字归一处理：lg2lg51 a b lga lgb lga a 二、指对幂比较大小 指对数大小比较问题 技巧总结 指对数大小比较问题已经成为高考的重难点问题，我们这里介绍五大核心思想. 核心思想一：同步《升降》次法 log blog bn a am 形如：log 3log 32 log 33 log 34 log 31 2 22 23 24 21 注意：一般情况下以2,3为底的对数比较大小，底数真数次方一起同升同降. 口诀：2,3为底眼睛亮，底真次方同升降. 核心思想二：先分离常数再比大小 当底数与真数出现倍数关系，必须先将对数分离常数后作比较.   ①log pm log plog mlog p1 m m m m   ②log pmn log plog mn log pn m m m m 口诀：底真出现倍数时，分离常数用起来 核心思想三：利用糖水变甜不等式比较大小 当对数比较大小形式中出现底数与真数成等差数列时，可以采用糖水不等式放缩处理. bm b am a 形如：a b0,m0则存在  ，或  am a bm b 模型演练：①比较log 3与log 4的大小 2 3 3 ln3ln 根据糖水不等式log 3 ln3  ln3m m0 ，令mln 3 ，即 ln3  2 2 ln2 ln2m 2 ln2 3 ln2ln 2 9 ln ln4 2  log 4故log 3log 4 ln3 ln3 3 2 3 ②比较log 3与log 5的大小 4 6 41 原创精品资源学科网独家享有版权，侵权必究！ 学科网（北京）股份有限公司6 ln3ln 根据糖水不等式log 3 ln3  ln3m m0 ，令mln 6 ，即 ln3  4 4 ln4 ln4m 4 ln4 6 ln4ln 4 18 ln ln5 4  log 5故log 3log 5 ln6 ln6 6 4 6 口诀：底大真小底大者大，底小真大底小者大. 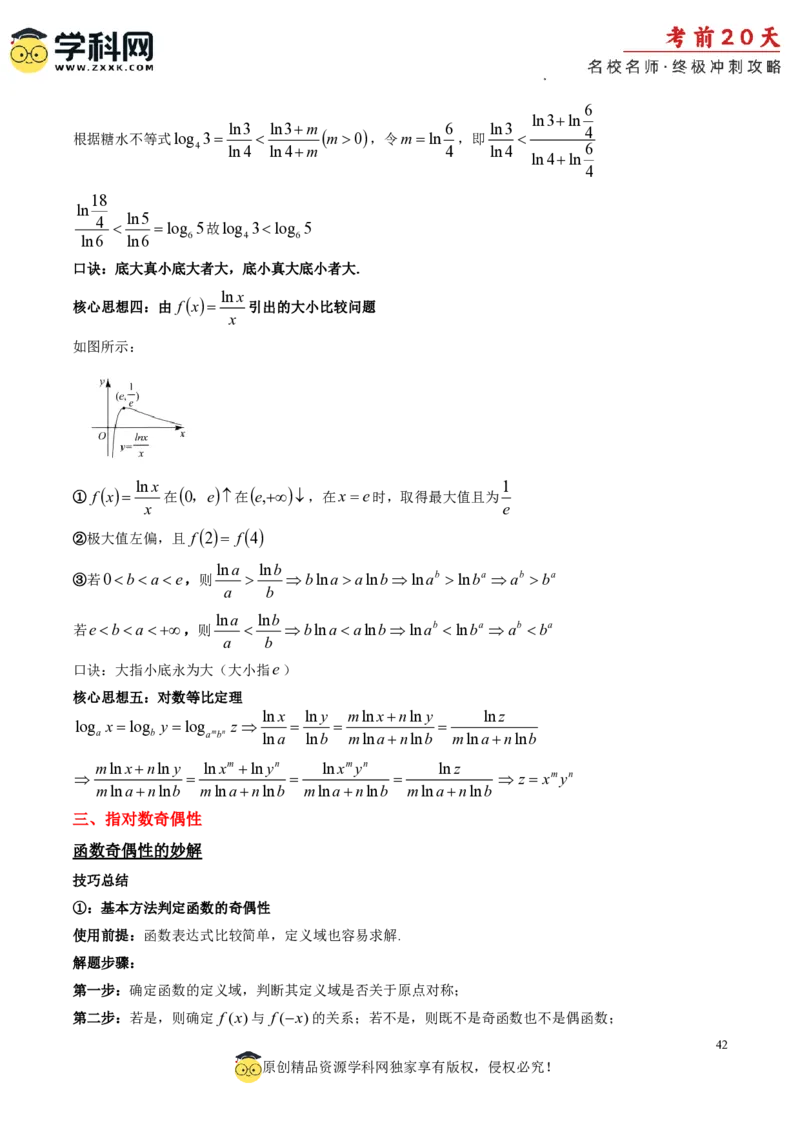lnx 核心思想四：由 fx  引出的大小比较问题 x 如图所示： lnx 1 ① fx  在  0，e  在  e,  ，在xe时，取得最大值且为 x e     ②极大值左偏，且 f 2  f 4 lna lnb ③若0bae，则  blna alnblnab lnba ab ba a b lna lnb 若eba，则  blnaalnblnab lnba ab ba a b 口诀：大指小底永为大（大小指e） 核心思想五：对数等比定理 lnx ln y mlnxnln y lnz log xlog y log z    a b ambn lna lnb mlnanlnb mlnanlnb mlnxnln y lnxm ln yn lnxmyn lnz      z  xmyn mlnanlnb mlnanlnb mlnanlnb mlnanlnb 三、指对数奇偶性 函数奇偶性的妙解 技巧总结 ①：基本方法判定函数的奇偶性 使用前提：函数表达式比较简单，定义域也容易求解. 解题步骤： 第一步：确定函数的定义域，判断其定义域是否关于原点对称； 第二步：若是，则确定 f(x)与 f(x)的关系；若不是，则既不是奇函数也不是偶函数； 42 原创精品资源学科网独家享有版权，侵权必究！ 学科网（北京）股份有限公司第三步: 得出结论. 利用函数的奇偶性求函数的解析式 使用前提：已知函数在给定的某个区间上的解析式，求其在对称区间(或对称区间的子区间)上的解析式. 解题步骤： 第一步：首先设出所求区间的自变量x； 第二步：运用已知条件将其转化为已知区间满足的x的取值范围； 第三步：利用已知解析式确定所求区间相应的函数的表达式. 分段函数的奇偶性 使用前提：所给函数的解析式为分段函数，需要判定函数的奇偶性 秒杀：口诀：奇函数定奇变偶、偶函数定偶变奇，奇双负，偶单负.           定义在 , 上任意的函数 f x 都可以唯一表示成一个奇函数g x 和一个偶函数h x 之和，当 f x 以分段函数形式出现奇偶性时，则函数一定满足：         Ⅰ：奇函数 f x f x  g x h x         Ⅱ：偶函数 f x  f x g x h x   若 f x 不容易拆分出奇函数和偶函数之和时，则直接采用         Ⅰ：奇函数 f x f x Ⅱ：偶函数 f x  f x 解题步骤： 解题模板1：利用传统的方法分类讨论确定函数的奇偶性 第一步：确定函数的定义域，判断其定义域是否关于原点对称； 第二步：若是，则确定 f x与 f x的关系；若不是，则既不是奇函数也不是偶函数； 第三步：得出结论. 解题模板2： 第一步： 确定函数的定义域 第二步： 写出 f x形式的分段函数 第三步： 确定函数的奇偶性 常见基本函数的奇偶性：   (1)一次函数y kxb k 0 ，当b0时，是奇函数，当b0时，是非奇非偶函数. (2)二次函数y ax2 bxc  a0  ，当b0时，是偶函数；当b0时，是非奇非偶函数. k (3)反比例函数y  k 0,x0是奇函数. x (4)指数函数y ax(a0且a 1)是非奇非偶函数 (5)对数函数y log x(a0且a 1，x0)是非奇非偶函数. a 43 原创精品资源学科网独家享有版权，侵权必究！ 学科网（北京）股份有限公司   (6) 三角函数 y sinx  xR  是奇函数， y cosx  xR  是偶函数， y tanx  xk ,kZ 是奇  2  函数.   (7)常值函数 f x a，当a0时，是偶函数，当a0时，既是奇函数又是偶函数. 特殊函数的奇偶性： 奇函数：两指两对 ax 1 2m ax 1 2m ⑴ f  x  m m  x0  ， f  x  m m  mR       ax 1  ax 1  ax 1  ax 1 ⑵函数 f  x    ax ax    ax  1    a2x 1      ax   ax  xm  2m   xm  2m  ⑶ fx log  log 1 ， fx log  log 1  a  xm a  xm a xm a  xm ⑷函数 f  x  log    mx 2 1mx  ，函数 f  x  log    mx 2 1mx  a  a  ax  ax a2x  1   ⑸函数 f x   ax ax a2x 1      f x  f x 0 考点：形如①已知 f  x  奇函数，则  0   0  M 最大值 m 最小值 0      f x  f x 2a ②已知 f  x  奇函数a，则  0   0  M 最大值 m 最小值 2a 偶函数： ⑴函数 f  x    ax ax  ⑵函数 fx log  amx 1   mx a 2   ⑶函数 f x 类型的一切函数. 典例1【2023新高考1卷】设函数 f x2xxa 在区间 0,1 上单调递减，则a的取值范围是（ ） A. ,2 B. 2,0 C. 0,2 D. 2, 【答案】D 44 原创精品资源学科网独家享有版权，侵权必究！ 学科网（北京）股份有限公司【解析】函数y 2x在R上单调递增，而函数 f x2xxa 在区间 0,1 上单调递减， a a2 a 则有函数y  x(xa)(x )2  在区间 0,1 上单调递减，因此 1，解得a2， 2 4 2 所以a的取值范围是 2, . 故选：D 2x1 典例2【2023新高考全国Ⅱ卷】 若 f xxaln 为偶函数，则a （ ）． 2x1 1 A. 1 B. 0 C. D. 1 2 【答案】B 1 【解析】因为 f(x) 为偶函数，则 f(1) f(1)，(1a)ln (1a)ln3，解得a0， 3 2x1 1 1 当a0时， f x xln ， 2x12x10，解得x 或x ， 2x1 2 2  1 1 则其定义域为x x 或x ，关于原点对称.  2 2 2x1 2x1 2x1 1 2x1 f xxln xln xln    xln  f x， 2x1 2x1 2x1 2x1 故此时 f x 为偶函数. 故选：B. 1 典例3【2022新高考全国Ⅰ卷】设a0.1e0.1,b ，cln0.9，则（ ） 9 A. abc B. cba C. c