文档内容
2024年高考押题预测卷【全国卷02】
理科数学·全解全析
第一部分(选择题 共60分)
一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题
目要求的.
1.已知集合 , ,则 ( )
A. B. C. D.
【详解】由 ,解得 或 ,
所以 ,则 ,
由 ,即 ,所以 ,解得 ,
所以 ,
所以 .
故选:C
2.已知复数 ,则 的虚部为( )
A. B. C.1 D.
【详解】因为 ,又 , , ,
所以 ,
所以 ,所以 的虚部为 .
1
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司故选:A
3.设 , 是两条不同的直线, , 是两个不同的平面,若 , ,则“ ”是“ ”
的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
【详解】若 , , ,则 与 的位置关系不能确定;
若 ,因为 ,所以 ,又 ,所以 成立.
所以“ ”是“ ”的必要不充分条件.
故选:B
4.已知函数 的图象如图所示,则函数 的解析式可能为( )
A. B.
C. D.
【详解】对于A,函数 的定义域为R,而题设函数的图象中在自变量为0时无意义,
不符合题意,排除;
对于B,当 时, ,不符合图象,排除.
对于C,当 时, ,不符合图象,排除;
故选:D
5.已知平面向量 满足 ,则 与 的夹角为( )
A. B. C. D.
2
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司【详解】由题意知平面向量 满足 ,
故 ,所以 ,
所以 ,所以 ,
则 , ,故 ,
故选:B.
6.已知 在R上单调递增,且为奇函数.若正实数a,b满足 ,则 的最小值
为( )
A. B. C. D.
【详解】由于 为奇函数,所以 ,
由 得 ,
由于 所以 ,
当且仅当 时取等号,故 的最小值为 ,
故选:A
7.2024年3月16日下午3点,在贵州省黔东南苗族侗族自治州榕江县“村超”足球场,伴随平地村足球
队在对阵口寨村足球队中踢出的第一脚球,2024年第二届贵州“村超”总决赛阶段的比赛正式拉开帷幕.
某校足球社的五位同学准备前往村超球队所在村寨调研,将在第一天前往平地村、口寨村、忠诚村,已知
每个村至少有一位同学前往,五位同学都会进行选择并且每位同学只能选择其中一个村,若学生甲和学生
乙必须选同一个村,则不同的选法种数是( )
A.18 B.36 C.54 D.72
【详解】若五位同学最终选择为 ,先选择一位同学和学生甲和学生乙组成3人小组,
3
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司剩余两人各去一个村,进行全排列,此时有 种选择,
若五位同学最终选择为 ,将除了甲乙外的三位同学分为两组,再进行全排列,
此时有 种选择,
综上,共有 种选择.
故选:B
8.已知 ,则 ( )
A. B.
C. D.
【详解】解:因为 ,
所以 ,
两式相加得: ,即 ,
化简得 ,
所以 ,
故选:A
9.已知 ,则 的大小关系是( )
A. B. C. D.
【详解】对 ,因为 ,则 ,即函数 在 单调递减,
且 时, ,则 ,即 ,所以 ,
因为 且 ,所以 ,
又 ,所以 .
4
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司故选:C
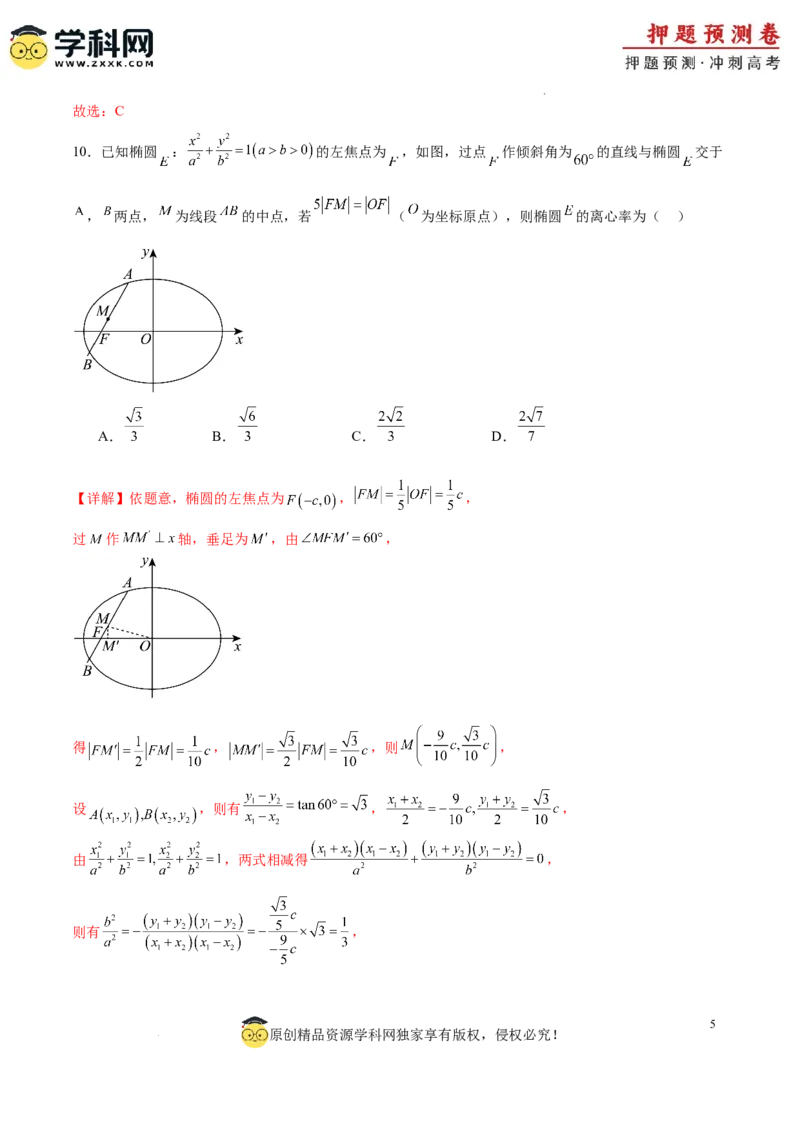
10.已知椭圆 : 的左焦点为 ,如图,过点 作倾斜角为 的直线与椭圆 交于
, 两点, 为线段 的中点,若 ( 为坐标原点),则椭圆 的离心率为( )
A. B. C. D.
【详解】依题意,椭圆的左焦点为 , ,
过 作 轴,垂足为 ,由 ,
得 , ,则 ,
设 ,则有 , ,
由 ,两式相减得 ,
则有 ,
5
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司所以 .
故选:B.
11.在棱长为1的正方体 中, 分别为 的中点,点 在正方体的表面上运动,
且满足 ,则下列说法正确的是( )
A.点 可以是棱 的中点 B.线段 的最大值为
C.点 的轨迹是正方形 D.点 轨迹的长度为
【详解】
在正方体 中,以点 为坐标原点,分别以 、 、 方向为 轴、 轴、 轴正方
向,建立空间直角坐标系,
因为该正方体的棱长为 , 分别为 的中点,
则 , , , ,
6
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司所以 ,设 ,则 ,
因为 ,
所以 , ,当 时, ;当 时, ;
取 , , , ,
连接 , , , ,则 , ,
所以四边形 为矩形,
则 , ,即 , ,
又 ,且 平面 , 平面 ,
所以 平面 ,
又 , ,所以 为 中点,则 平面 ,
所以,为使 ,必有点 平面 ,又点 在正方体的表面上运动,
所以点 的轨迹为四边形 ,
因此点 不可能是棱 的中点,即A错;
又 , ,所以 ,则点 的轨迹不是正方形;
且矩形 的周长为 ,故C错,D正确;
因为点 为 中点,则点 为矩形 的对角线交点,所以点 到点 和点 的距离相等,且最大,
所以线段 的最大值为 ,故B错.
故选:D.
【点睛】关键点点睛:求解本题的关键在于建立适当的空间直角坐标系,利用空间向量的方法,由
,求出动点轨迹图形,即可求解.
12.若函数 有两个不同的极值点 ,且 恒成立,则实数
7
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司的取值范围为( )
A. B. C. D.
【详解】依题意得 ,
若函数 有两个不同的极值点 ,
则方程 有两个不相等的正实数根 ,
可得 ,解得 ,
因为 ,
可得
.
设 ,则 ,
则 单调递减, ,可知 .
所以实数 的取值范围是 .
故选:B.
第二部分(非选择题 共90分)
二、填空题:本大题共4小题,每小题5分,共20分
13.若数列 满足 , ,则 .
【详解】因为数列 满足 , ,
8
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司所以 ,
,
,
……
,
以上各式相加得 ,
所以 .
【点睛】本题主要考查求数列的通项公式,熟记累加法即可,属于常考题型.
14.已知函数 ,其中 为常数,且 ,将函数 的图象向左平移 个单位
所得的图象对应的函数 在 取得极大值,则 的值为 .
【详解】由题意可知 ,
因为 在 取得极大值,所以 在 取得最大值,
所以 , ,即 ,
又因为 ,所以,当且仅当 时, 满足条件,所以 ,
故答案为: .
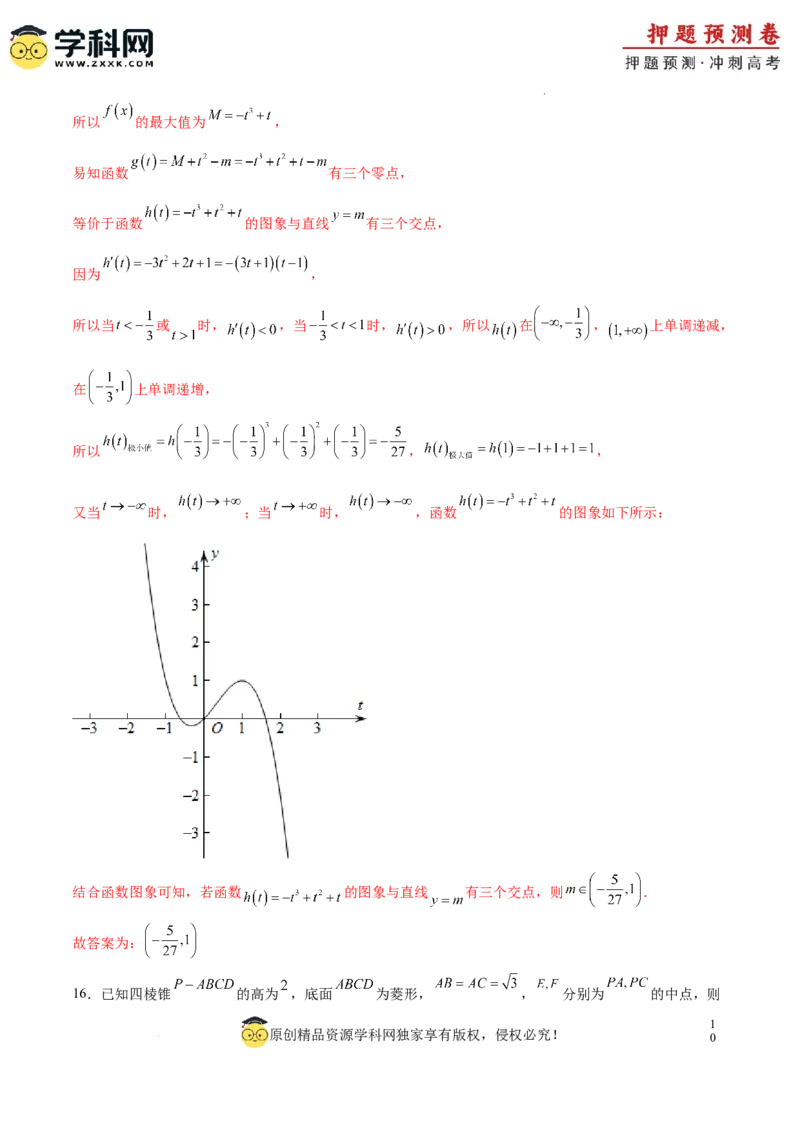
15.已知函数 的最大值为 ,若函数 有三个零点,则实数 的
取值范围是 .
【详解】解:因为 ,
9
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司所以 的最大值为 ,
易知函数 有三个零点,
等价于函数 的图象与直线 有三个交点,
因为 ,
所以当 或 时, ,当 时, ,所以 在 , 上单调递减,
在 上单调递增,
所以 , ,
又当 时, ;当 时, ,函数 的图象如下所示:
结合函数图象可知,若函数 的图象与直线 有三个交点,则 .
故答案为:
16.已知四棱锥 的高为 ,底面 为菱形, , 分别为 的中点,则
1
原创精品资源学科网独家享有版权,侵权必究!
0
学科网(北京)股份有限公司四面体 的体积为 ;三棱锥 的外接球的表面积的最小值为 .
【详解】如图,设 ,连接 ,
,
易知 分别为 中点, ,
所以 ,
,
四边形 是菱形, ,
为全等的正三角形,
,
;
因为 是边长为 的正三角形,记其中心为 ,
则 的外接圆的半径为 ,
设三棱锥 的外接球的半径为 ,球心为 ,则 底面
过 作 底面 交于 ,则 ,
1
原创精品资源学科网独家享有版权,侵权必究!
1
学科网(北京)股份有限公司结合图象可知 ,其中 , ,
因为 到平面 的距离为2,即 ,所以 ,
易知关于 的函数 在 上单调递增,
所以当且仅当 时, 取得最小值,
此时, 三点共线,由 ,解得 ,
所以棱锥 的外接球的表面积的最小值为 .
故答案为: ; .
三、解答题:本大题共70分.解答应写出文字说明、证明过程或演算步骤.第17~21题为必考题,每个试
题考生都必须作答.第22、23题为选考题,考生根据要求作答.
(一)必考题:共60分.
17.已知 的内角 的对边分别为 .
(1)求 的值;
(2)若 的面积为 ,且 ,求 的周长.
【详解】(1)解:因为 ,由正弦定理得 ,.....................................1分
可得 ,
即 ,......................................................................3分
因为 ,可得 ,所以 ,即 ,
所以 ...........................................................................................................................6分
(2)解:由(1)知 ,
1
原创精品资源学科网独家享有版权,侵权必究!
2
学科网(北京)股份有限公司因为若 的面积为 ,可得 ,即 ,解得 ,...................8分
又因为 ,
由余弦定理得 ,
整理得 ,解得 ,..........................................................................................................................10分
所以 ,
所以 的周长为 ............................................................................................................12分
18.某校高三年级进行班级数学文化知识竞赛,每班选三人组成代表队,其中1班和2班进入最终的决赛.
决赛第一轮要求两个班级的代表队队员每人回答一道必答题,答对则为本班得1分,答错或不答都得0分.
已知1班的三名队员答对的概率分别为 、 、 , 班的三名队员答对的概率都是 ,每名队员回答正
确与否相互之间没有影响.用 、 分别表示1班和2班的总得分.
(1)求随机变量 、 的数学期望 ;
(2)若 ,求2班比1班得分高的概率.
【详解】(1)依题意可得 的可能取值为 、 、 、 ,
所以 ,
,
,
,
所以随机变量 的分布列为
1
原创精品资源学科网独家享有版权,侵权必究!
3
学科网(北京)股份有限公司0 1 2 3
..............................................................................................................................................................................3分
所以 .............................................................................................4分
又 班的总得分 满足 ,则 ............................................................................6分
(2)设“ ”为事件 ,“ 班比 班得分高”为事件 ,..........................................................7分
则
,..........................................................................................................................................................9分
,
所以 ,.................................................................................................11分
所以 班比 班得分高的概率为 .............................................................................................................12分
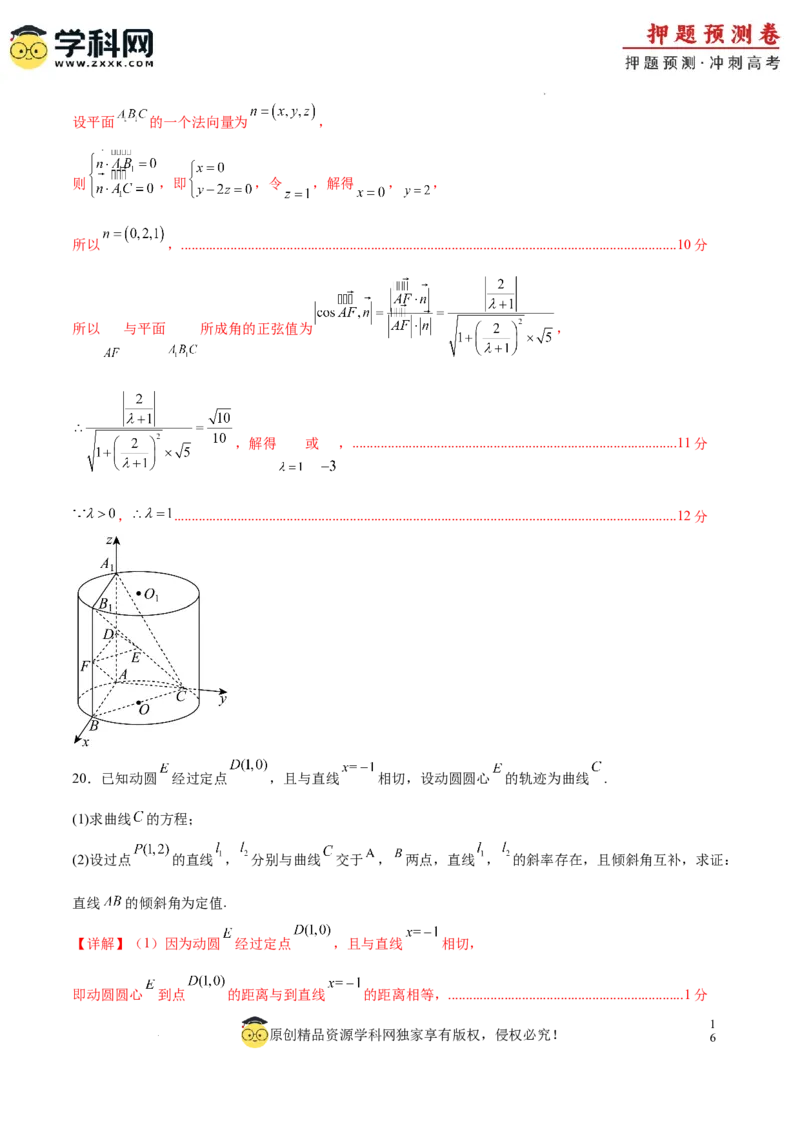
19.如图,在圆柱 中,一平面沿竖直方向截圆柱得到截面矩形 ,其中 , 为圆柱 的
母线,点 在底面圆周上,且 过底面圆心 ,点D,E分别满足 ,过 的平面
与 交于点 ,且 .
1
原创精品资源学科网独家享有版权,侵权必究!
4
学科网(北京)股份有限公司(1)当 时,证明:平面 平面 ;
(2)若 与平面 所成角的正弦值为 ,求 的值.
【详解】(1)当 时,得 ,又 , ,
所以 , ,.............................................................................................................................2分
平面 , 平面 , 平面 ,
同理得 平面 ,..................................................................................................................................4分
因为 是平面 内两条相交直线,
所以平面 平面 ...............................................................................................................................5分
(2)因为 , 为圆柱 的母线,所以 垂直平面 ,又点C在底面圆周上,且 过底面圆
心O,
所以 ,所以 两两互相垂直.以点 为坐标原点, 分别为 轴,建立如图
空间直角坐标系,..............................................................................................................................................6分
设 ,则 , , , , ,
所以 , , , ,........................................................7分
因为 ,所以 ,则
,.....................................................................................8分
1
原创精品资源学科网独家享有版权,侵权必究!
5
学科网(北京)股份有限公司设平面 的一个法向量为 ,
则 ,即 ,令 ,解得 , ,
所以 ,.............................................................................................................................................10分
所以 与平面 所成角的正弦值为 ,
,解得 或 ,............................................................................................11分
, ...............................................................................................................................................12分
20.已知动圆 经过定点 ,且与直线 相切,设动圆圆心 的轨迹为曲线 .
(1)求曲线 的方程;
(2)设过点 的直线 , 分别与曲线 交于 , 两点,直线 , 的斜率存在,且倾斜角互补,求证:
直线 的倾斜角为定值.
【详解】(1)因为动圆 经过定点 ,且与直线 相切,
即动圆圆心 到点 的距离与到直线 的距离相等,...................................................................1分
1
原创精品资源学科网独家享有版权,侵权必究!
6
学科网(北京)股份有限公司又点 不在直线 上,
由抛物线的定义可知动圆圆心 是以 为焦点,直线 为准线的抛物线,...............................3分
所以动圆圆心 的轨迹为 ....................................................................................................................4分
(2)依题意设直线 方程为 ,
直线 , 的斜率存在,且倾斜角互补,
的方程为 .
联立方程组 ,消元得 ,
,.........................................................................................6分
因为此方程的一个根为 ,设 , ,
则 ,同理可得 ,................................................................................8分
, .
.
,...........................................................................................................................................10分
设直线 的倾斜角为 ,则 ,又 ,所以 ,......................................................11分
直线 的斜率为定值 ,倾斜角为定值 .......................................................................................12分
1
原创精品资源学科网独家享有版权,侵权必究!
7
学科网(北京)股份有限公司21.已知函数 .
(1)若函数 在 处的切线与坐标轴围成的三角形的面积为 ,求 的值;
(2)若函数 的最小值为 ,求 的值.
【详解】(1)因为 ,所以 ,
则 ,又 ,
所以函数 在 处的切线方程为 ..........................................................2分
由题意,显然 ,令 得 ,令 得 ,
所以函数 在 处的切线与坐标轴围成的三角形的面积为 ,
所以 ,解得 或 ..........................................................................................................4分
(2)由(1)知 ,令 ,
所以 ,当 时, 在 上单调递减,
当 时, , 在 上单调递增................................................................................6分
因为 ,所以当 时, ,
又
1
原创精品资源学科网独家享有版权,侵权必究!
8
学科网(北京)股份有限公司所以 在 上必存在唯一零点 ,使得 .....................................................................8分
当 时, ,即 在 上单调递减,
当 时, ,即 在 上单调递增.
所以 在 处取得最小值,
即 ,且 ,即 ,
所以 ................................................................10分
设 ,所以 ,
当 时, 单调递增, ,
当 时, , 单调递减, ,
又 ,所以函数 在 上存在唯一的 ,使得 成立,
所以 ,所以 ,即 .........................................................................................12分
(二)选考题:共10分.请考生在22、23题中任选一题作答,如果多做,则按所做的第一题计分.
选修4-4:坐标系与参数方程
22.已知在平面直角坐标系 中,以坐标原点O为极点,x轴的非负半轴为极轴建立极坐标系,曲线
的极坐标方程为 ;在平面直角坐标系 中,曲线 的参数方程为 ( 为参
数),点 的极坐标为 且点 在曲线 上.
(1)求曲线 的普通方程以及曲线 的极坐标方程;
1
原创精品资源学科网独家享有版权,侵权必究!
9
学科网(北京)股份有限公司(2)已知直线 与曲线 分别交于 , 两点,其中 , 异于原点 ,求 的面积.
【详解】(1)因为曲线 的极坐标方程为 ,所以 ,
由 ,得曲线 的直角坐标方程为 ;
由曲线 的参数方程为 ( 为参数),又 ,
得 ,..........................................................................................................................................2分
因为 ,所以 ,即 ,
即曲线 的极坐标方程为 .
又点 在曲线 上,所以 ,解得 ,
所以曲线 的极坐标方程为 ;.................................................................................................4分
(2)因为点 ,则 ,即点 的直角坐标为 ,.................................5分
由(1)得曲线 的直角坐标方程为 ,
联立 ,解得 或 ,所以 ,
联立 ,解得 或 ,所以 ,............................................................8分
2
原创精品资源学科网独家享有版权,侵权必究!
0
学科网(北京)股份有限公司则 ,
点 到直线 的距离 ,.................................................................9分
所以 .........................................................................................................................10分
选修4-5:不等式选讲
23.已知函数 .
(1)当 时,求不等式 的解集;
(2)若 恒成立,求 的取值范围.
【详解】(1)当 时, 可化为 ......................................................................1分
当 时, ,解得 ;
当 时, ,解得 ;
当 时, ,解得 ................................................................................................4分
故当 时,不等式 的解集为 .......................................................................................5分
(2)因为 ,
所以 等价于 ........................................................................................7分
因为 ,当且仅当 时取等号,....................................8分
2
原创精品资源学科网独家享有版权,侵权必究!
1
学科网(北京)股份有限公司所以 的最小值为 ,所以 ,
解得 或 ,
故 的取值范围是 ..............................................................................................................10分
2
原创精品资源学科网独家享有版权,侵权必究!
2
学科网(北京)股份有限公司