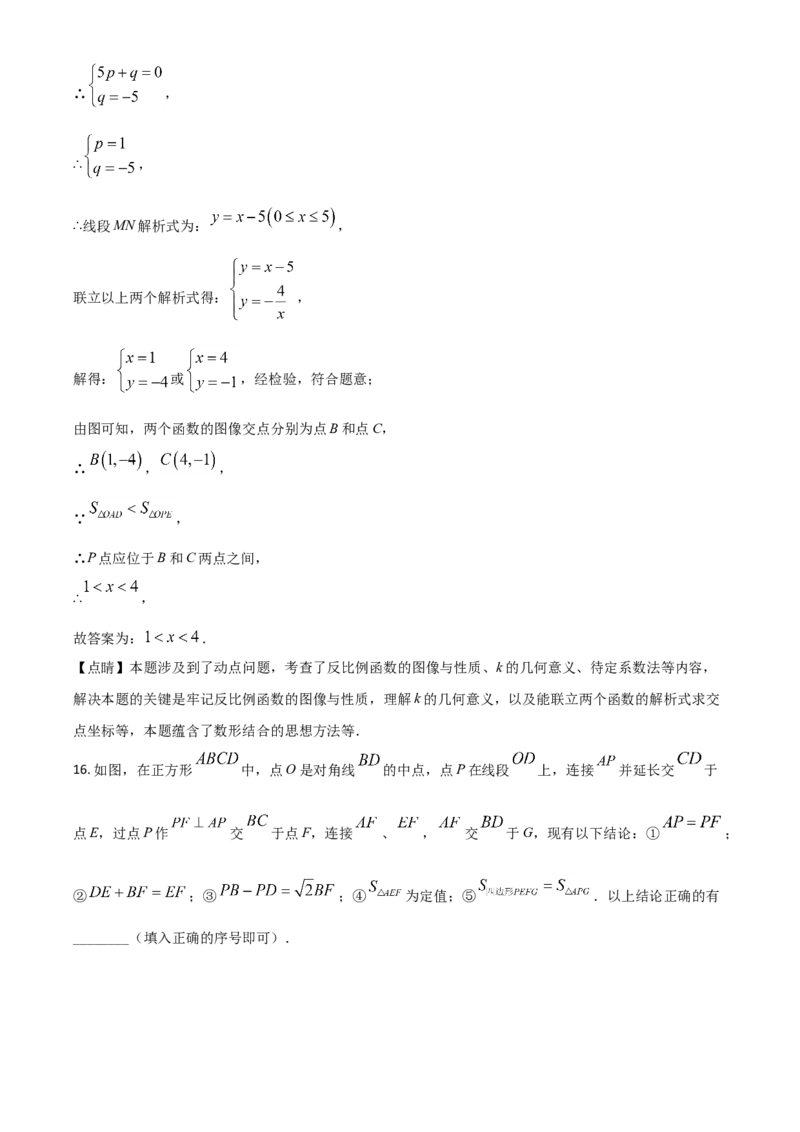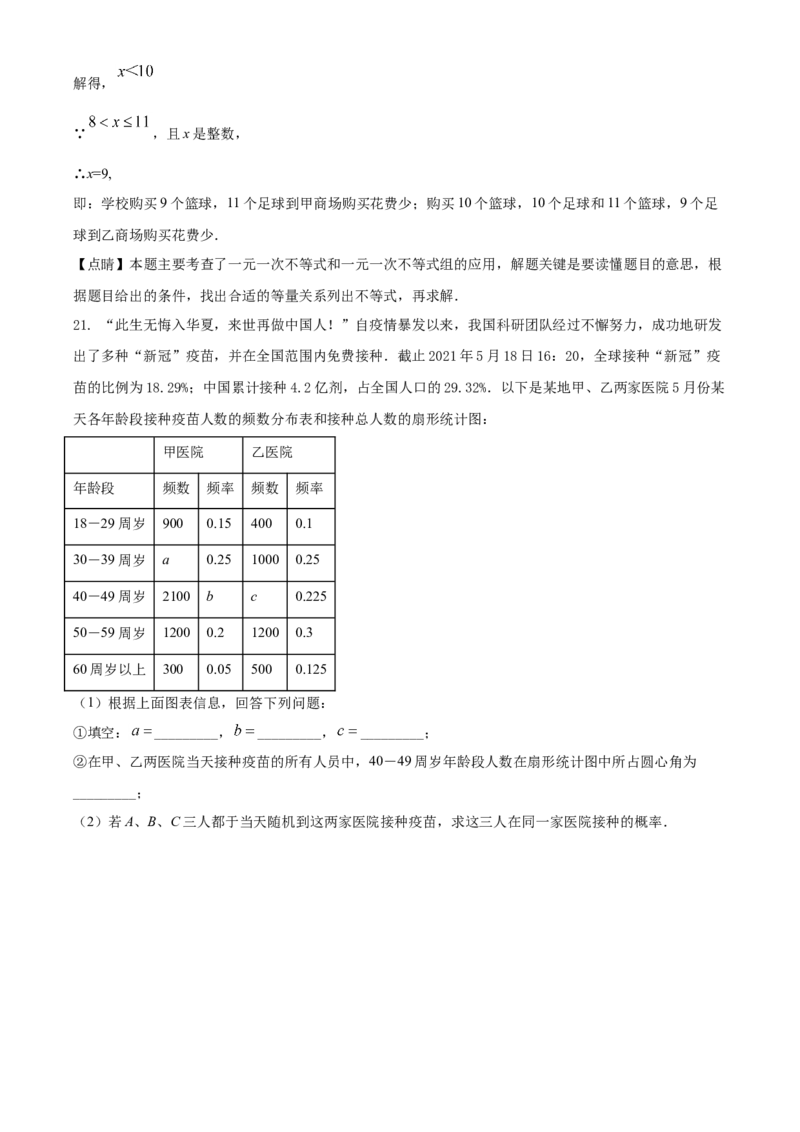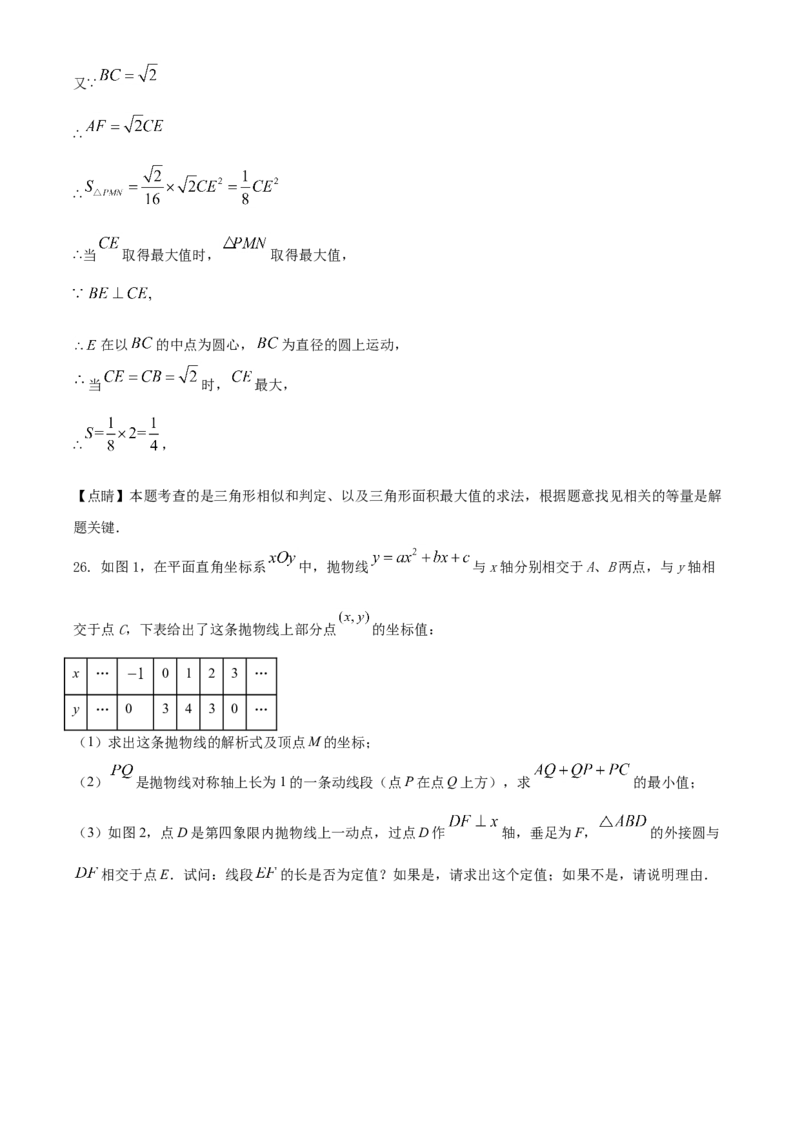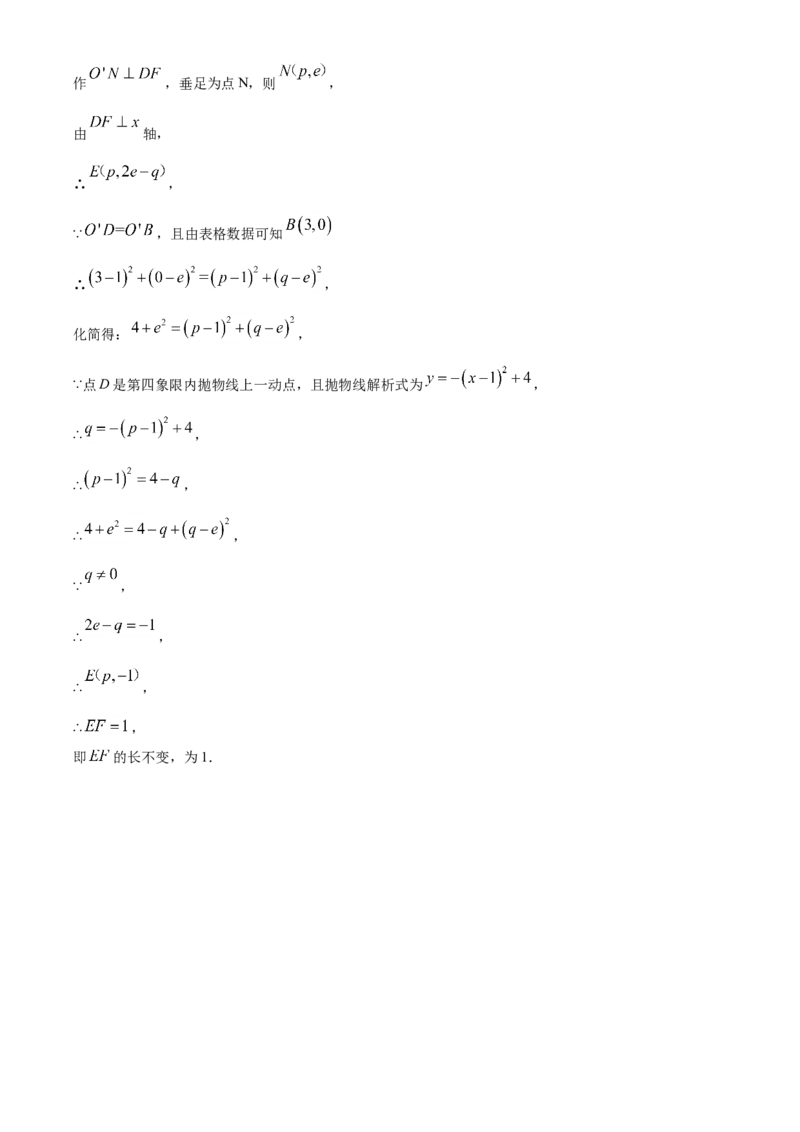文档内容
四川省广元市 2021 中考数学试题
一、选择题.(每小题给出的四个选项中,只有一个是符合题意的.每小题3分,共30分)
1. 计算 的最后结果是( )
A. 1 B. C. 5 D.
【答案】C
【解析】
【分析】先计算绝对值,再将减法转化为加法运算即可得到最后结果.
【详解】解:原式 ,
故选:C.
【点睛】本题考查了绝对值化简和有理数的加减法运算,解决本题的关键是牢记绝对值定义与有理数运算
法则,本题较基础,考查了学生对概念的理解与应用.
2. 下列图形均表示医疗或救援的标识,其中既是轴对称图形又是中心对称图形的是( )
A. B.
C. D.
【答案】C
【解析】
【分析】根据轴对称及中心对称图形的定义逐一判断即可得答案.
【详解】A.是轴对称图形,但不是中心对称图形,故该选项不符合题意,
B.是轴对称图形,但不是中心对称图形,故该选项不符合题意,
C.是轴对称图形,又是中心对称图形,故该选项符合题意,D.既不是轴对称图形,又不是中心对称图形,故该选项不符合题意,
故选:C.
【点睛】本题考查轴对称图形及中心对称图形的概念,轴对称图形的关键是寻找对称轴,图形两部分沿对
称轴折叠后能完全重合;中心对称图形的关键是寻找对称中心,图形绕对称中心旋转180°后,两部分能
够完全重合;熟练掌握定义是解题关键.
3. 下列运算正确的是( )
A. B.
C. D.
【答案】B
【解析】
【分析】分别根据完全平方公式、平方差公式、单项式乘以多项式法则、多项式乘以多项式法则进行计算
即可判断求解.
【详解】解:A. ,原选项计算错误,不合题意;
B. ,原选项计算正确,符合题意;
C. ,原选项计算错误,不合题意;
D. ,原选项计算错误,不合题意.
故选:B
【点睛】本题考查了整式的乘法运算,乘法公式等知识,熟知乘法公式和整式的乘法法则是解题关键.
的
4. 一组数据:1,2,2,3,若添加一个数据3,则不发生变化 统计量是( )
A. 平均数 B. 中位数 C. 众数 D. 方差
【答案】B
【解析】
【分析】依据平均数、中位数、众数、方差的定义和公式求解即可.
【详解】解:A、原来数据的平均数是 2,添加数字3后平均数为 ,所
以平均数发生了变化,故A不符合题意;B、原来数据的中位数是2,添加数字3后中位数仍为2,故B与要求相符;
C、原来数据的众数是2,添加数字3后众数为2和 3,故C与要求不符;
D、原来数据的方差= ,
添加数字3后的方差= ,故方差发生了变化,
故选项D不符合题意.
故选:B.
【点睛】本题主要考查的是众数、中位数、方差、平均数,熟练掌握相关概念和公式是解题的关键.
5. 下列命题中,真命题是( )
A.
B. 对角线互相垂直的四边形是菱形
C. 顺次连接矩形各边中点的四边形是正方形
D. 已知抛物线 ,当 时,
【答案】D
【解析】
【分析】根据零次幂、菱形的判定、正方形的判定及二次函数的图象与性质可直接进行排除选项.
【详解】解:A、 ,错误,故不符合题意;
B、对角线互相垂直且平分的四边形是菱形,错误,故不符合题意;
C、顺次连接矩形各边中点的四边形是菱形,错误,故不符合题意;
D、由抛物线 可得与x轴的交点坐标为 ,开口向上,然后可得当
时, ,正确,故符合题意;
故选D.
【点睛】本题主要考查零次幂、菱形的判定、正方形的判定及二次函数的图象与性质,熟练掌握零次幂、
菱形的判定、正方形的判定及二次函数的图象与性质是解题的关键.
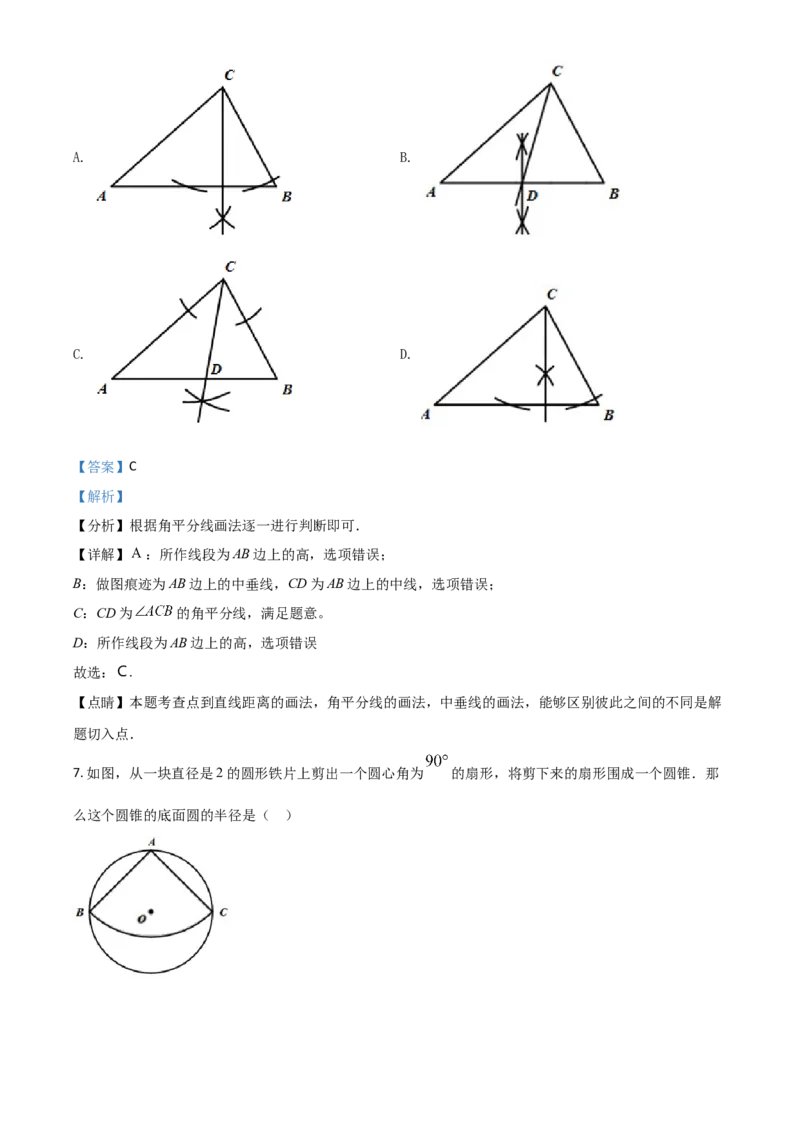
6. 观察下列作图痕迹,所作线段 为 的角平分线的是( )A. B.
C. D.
【答案】C
【解析】
【分析】根据角平分线画法逐一进行判断即可.
【详解】 :所作线段为AB边上的高,选项错误;
B:做图痕迹为AB边上的中垂线,CD为AB边上的中线,选项错误;
C:CD为 的角平分线,满足题意。
D:所作线段为AB边上的高,选项错误
故选:C.
【点睛】本题考查点到直线距离的画法,角平分线的画法,中垂线的画法,能够区别彼此之间的不同是解
题切入点.
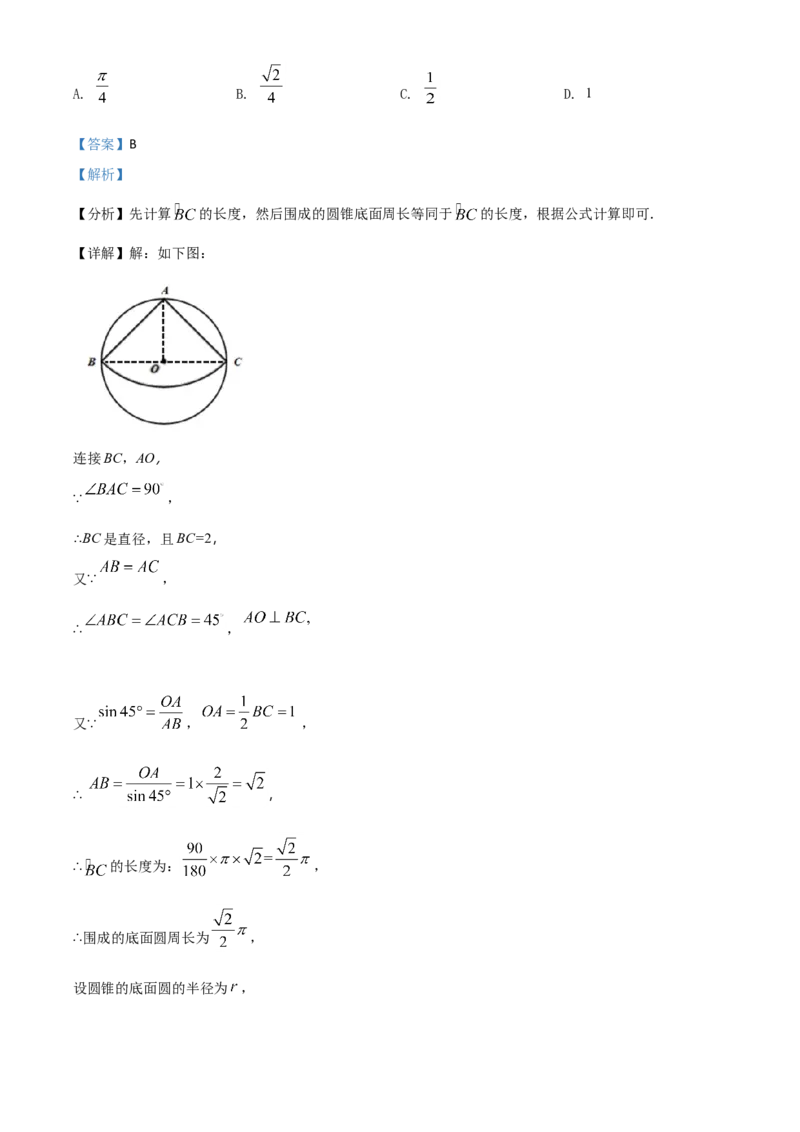
7. 如图,从一块直径是2的圆形铁片上剪出一个圆心角为 的扇形,将剪下来的扇形围成一个圆锥.那
么这个圆锥的底面圆的半径是( )A. B. C. D. 1
【答案】B
【解析】
【分析】先计算 的长度,然后围成的圆锥底面周长等同于 的长度,根据公式计算即可.
【详解】解:如下图:
连接BC,AO,
∵ ,
∴BC是直径,且BC=2,
又∵ ,
∴ ,
又∵ , ,
∴ ,
∴ 的长度为: ,
∴围成的底面圆周长为 ,
设圆锥的底面圆的半径为 ,则: ,
∴ .
故选:
【点睛】本题考查扇形弧长的计算,圆锥底面半径的计算,解直角三角形等相关知识点,根据条件计算出
扇形的半径是解题的关键.
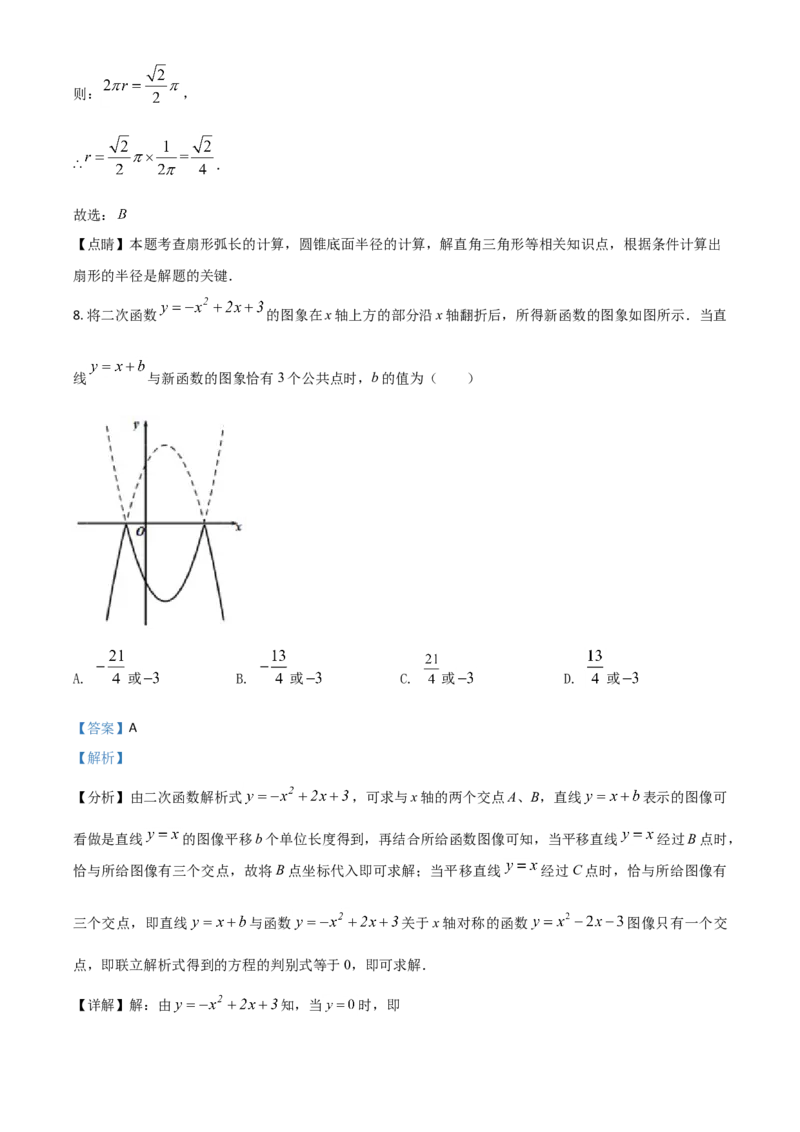
8. 将二次函数 的图象在x轴上方的部分沿x轴翻折后,所得新函数的图象如图所示.当直
线 与新函数的图象恰有3个公共点时,b的值为( )
A. 或 B. 或 C. 或 D. 或
【答案】A
【解析】
【分析】由二次函数解析式 ,可求与x轴的两个交点A、B,直线 表示的图像可
看做是直线 的图像平移b个单位长度得到,再结合所给函数图像可知,当平移直线 经过B点时,
恰与所给图像有三个交点,故将B点坐标代入即可求解;当平移直线 经过C点时,恰与所给图像有
三个交点,即直线 与函数 关于x轴对称的函数 图像只有一个交
点,即联立解析式得到的方程的判别式等于0,即可求解.
【详解】解:由 知,当 时,即解得:
作函数 的图像并平移至过点B时,恰与所给图像有三个交点,此时有:
平移图像至过点C时,恰与所给图像有三个交点,即当 时,只有一个交点
当 的函数图像由 的图像关于x轴对称得到
当 时对应的解析式为
即 ,整理得:
综上所述 或
故答案是:A.
【点睛】本题主要考察二次函数翻折变化、交点个数问题、函数图像平移的性质、二次函数与一元二次方
程的关系等知识,属于函数综合题,中等难度.解题的关键是数形结合思想的运用,从而找到满足题意的
条件.
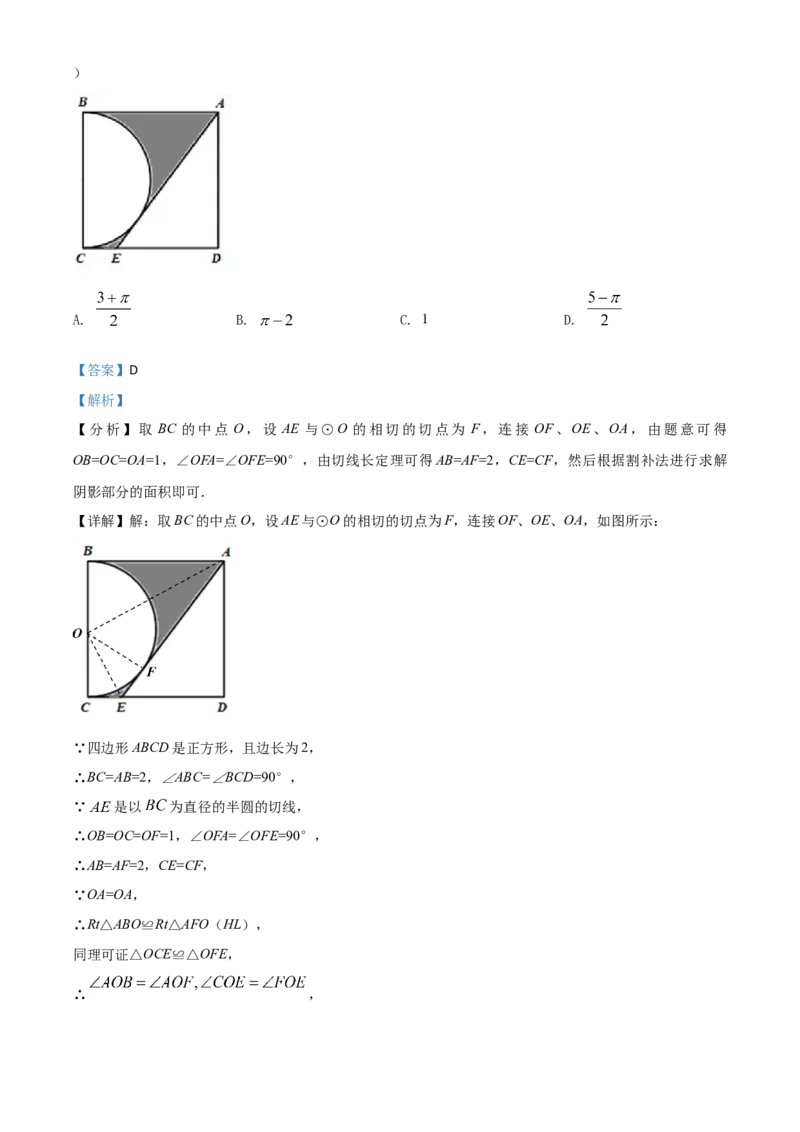
9. 如图,在边长为2的正方形 中, 是以 为直径的半圆的切线,则图中阴影部分的面积为()
A. B. C. 1 D.
【答案】D
【解析】
【分析】取 BC 的中点 O,设 AE 与⊙O 的相切的切点为 F,连接 OF、OE、OA,由题意可得
OB=OC=OA=1,∠OFA=∠OFE=90°,由切线长定理可得AB=AF=2,CE=CF,然后根据割补法进行求解
阴影部分的面积即可.
【详解】解:取BC的中点O,设AE与⊙O的相切的切点为F,连接OF、OE、OA,如图所示:
∵四边形ABCD是正方形,且边长为2,
∴BC=AB=2,∠ABC=∠BCD=90°,
∵ 是以 为直径的半圆的切线,
∴OB=OC=OF=1,∠OFA=∠OFE=90°,
∴AB=AF=2,CE=CF,
∵OA=OA,
∴Rt△ABO≌Rt△AFO(HL),
同理可证△OCE≌△OFE,
∴ ,∴ ,
∴ ,
∴ ,
∴ ,
∴ ,
∴ ;
故选D.
【点睛】本题主要考查切线 的性质定理、切线长定理、正方形的性质及相似三角形的性质与判定,熟练掌
握切线的性质定理、切线长定理、正方形的性质及相似三角形的性质与判定是解题的关键.
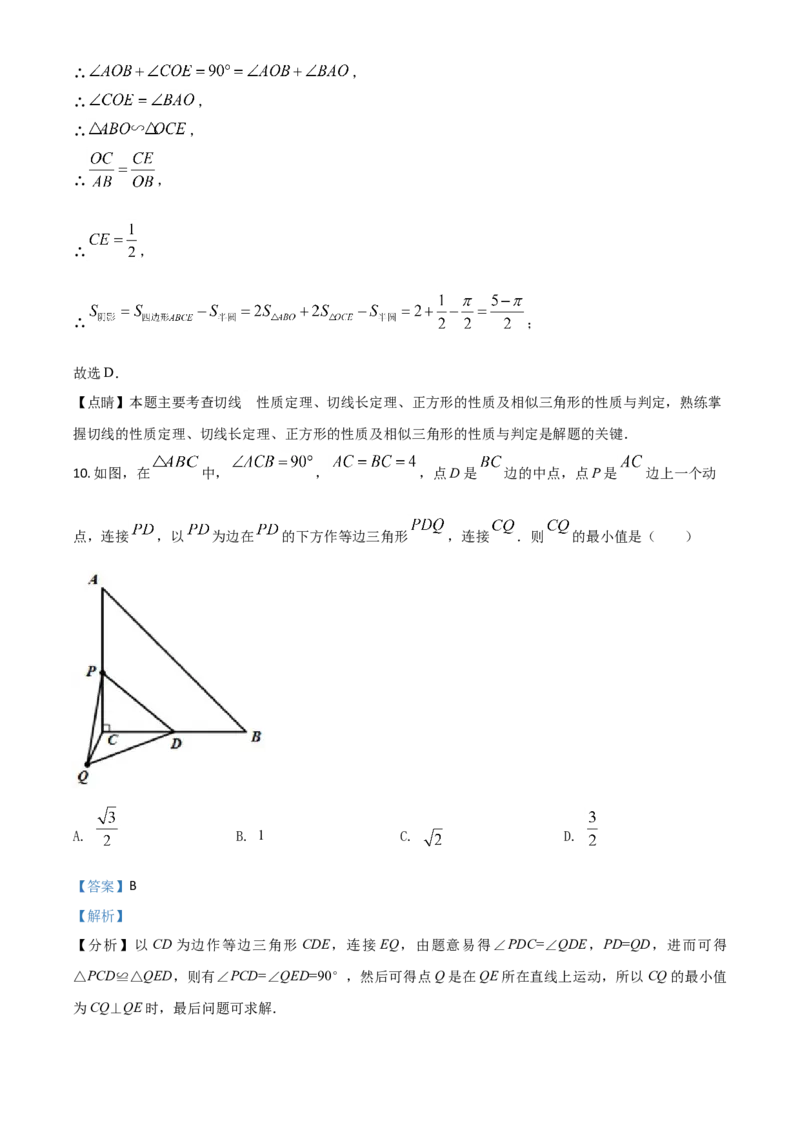
10. 如图,在 中, , ,点D是 边的中点,点P是 边上一个动
点,连接 ,以 为边在 的下方作等边三角形 ,连接 .则 的最小值是( )
A. B. 1 C. D.
【答案】B
【解析】
【分析】以CD为边作等边三角形 CDE,连接 EQ,由题意易得∠PDC=∠QDE,PD=QD,进而可得
△PCD≌△QED,则有∠PCD=∠QED=90°,然后可得点Q是在QE所在直线上运动,所以CQ的最小值
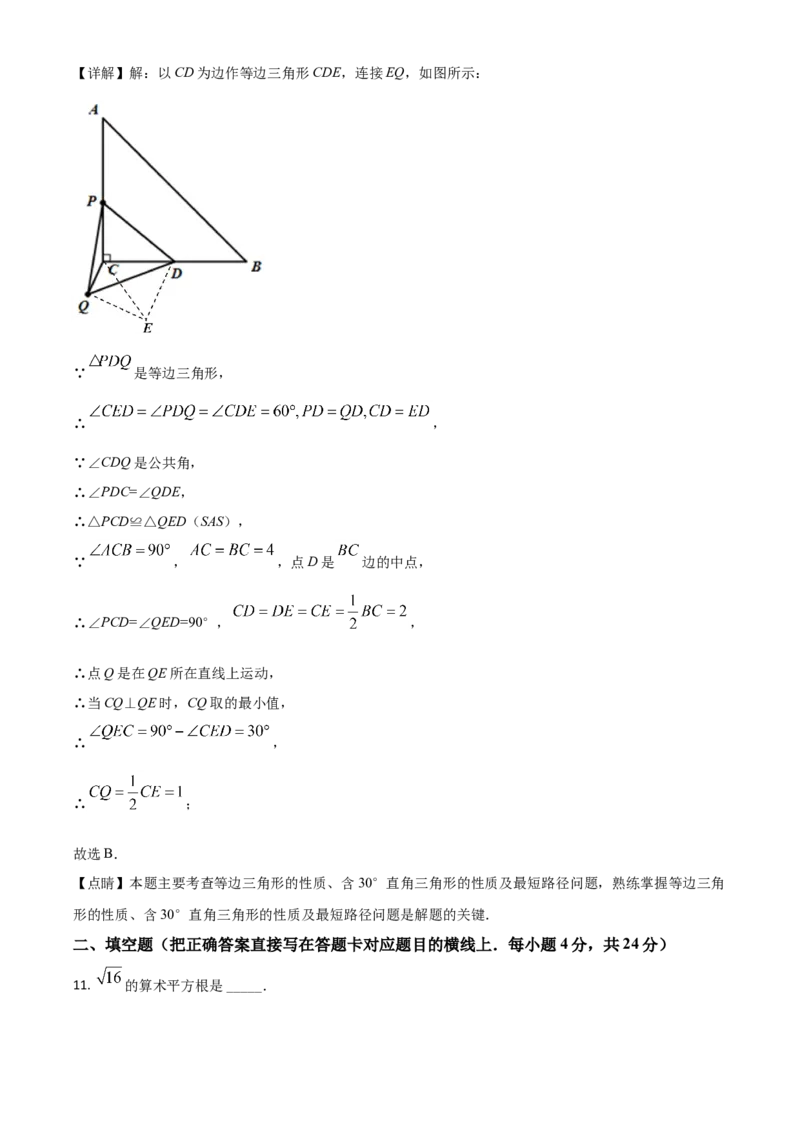
为CQ⊥QE时,最后问题可求解.【详解】解:以CD为边作等边三角形CDE,连接EQ,如图所示:
∵ 是等边三角形,
∴ ,
∵∠CDQ是公共角,
∴∠PDC=∠QDE,
∴△PCD≌△QED(SAS),
∵ , ,点D是 边的中点,
∴∠PCD=∠QED=90°, ,
∴点Q是在QE所在直线上运动,
∴当CQ⊥QE时,CQ取的最小值,
∴ ,
∴ ;
故选B.
【点睛】本题主要考查等边三角形的性质、含30°直角三角形的性质及最短路径问题,熟练掌握等边三角
形的性质、含30°直角三角形的性质及最短路径问题是解题的关键.
二、填空题(把正确答案直接写在答题卡对应题目的横线上.每小题4分,共24分)
11. 的算术平方根是 _____.【答案】2
【解析】
【详解】∵ , 的算术平方根是2,
∴ 的算术平方根是2.
【点睛】这里需注意: 的算术平方根和 的算术平方根是完全不一样的;因此求一个式子的平方根、
立方根和算术平方根时,通常需先将式子化简,然后再去求,避免出错.
12. 中国杂交水稻之父、中国工程院院士、共和国勋章获得者袁隆平于2021年5月22日因病去世,享年91
岁,袁隆平的去世是中国乃至全世界的重大损失.袁隆平一生致力于水稻杂交技术研究,为提高我国水稻
亩产量做出了巨大贡献.截至2012年,“种三产四”丰产工程项目累计示范推广面积达2000多万亩,增
产20多亿公斤.将20亿这个数据用科学记数法表示为________.
【答案】
【解析】
【分析】科学记数法要求,小数点在第一个不为零的整数后面,其他数为小数,小数点移动位数等于幂的
指数,向左移动,指数为正,向右移动,指数为负.
【详解】
故答案为: .
【点睛】本题考查科学记数法,根据相关原则进行计算是解题关键点.
13. 如图,实数 , ,m在数轴上所对应的点分别为A,B,C,点B关于原点O的对称点为D.若
m为整数,则m的值为________.
【答案】-3
【解析】
【分析】先求出D点表示的数,再得到m的取值范围,最后在范围内找整数解即可.
【详解】解:∵点B关于原点O的对称点为D,点B表示的数为 ,∴点D表示的数为 ,
∵A点表示 ,C点位于A、D两点之间,
∴ ,
∵m为整数,
∴ ;
故答案为: .
【点睛】本题考查了数轴上点的特征,涉及到相反数的性质、对无理数进行估值、确定不等式组的整数解
等问题,解决本题的关键是牢记相关概念和性质,本题蕴含了数形结合的思想方法.
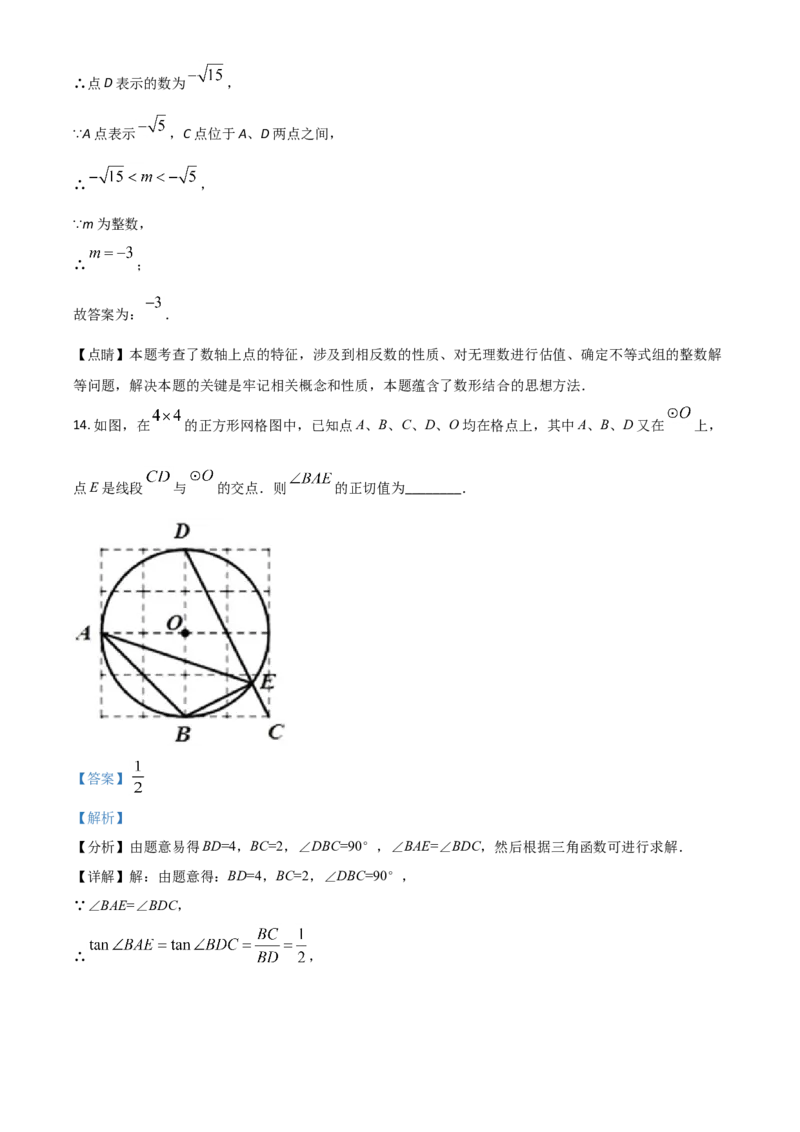
14. 如图,在 的正方形网格图中,已知点A、B、C、D、O均在格点上,其中A、B、D又在 上,
点E是线段 与 的交点.则 的正切值为________.
【答案】
【解析】
【分析】由题意易得BD=4,BC=2,∠DBC=90°,∠BAE=∠BDC,然后根据三角函数可进行求解.
【详解】解:由题意得:BD=4,BC=2,∠DBC=90°,
∵∠BAE=∠BDC,
∴ ,故答案为 .
【点睛】本题主要考查三角函数及圆周角定理,熟练掌握三角函数及圆周角定理是解题的关键.
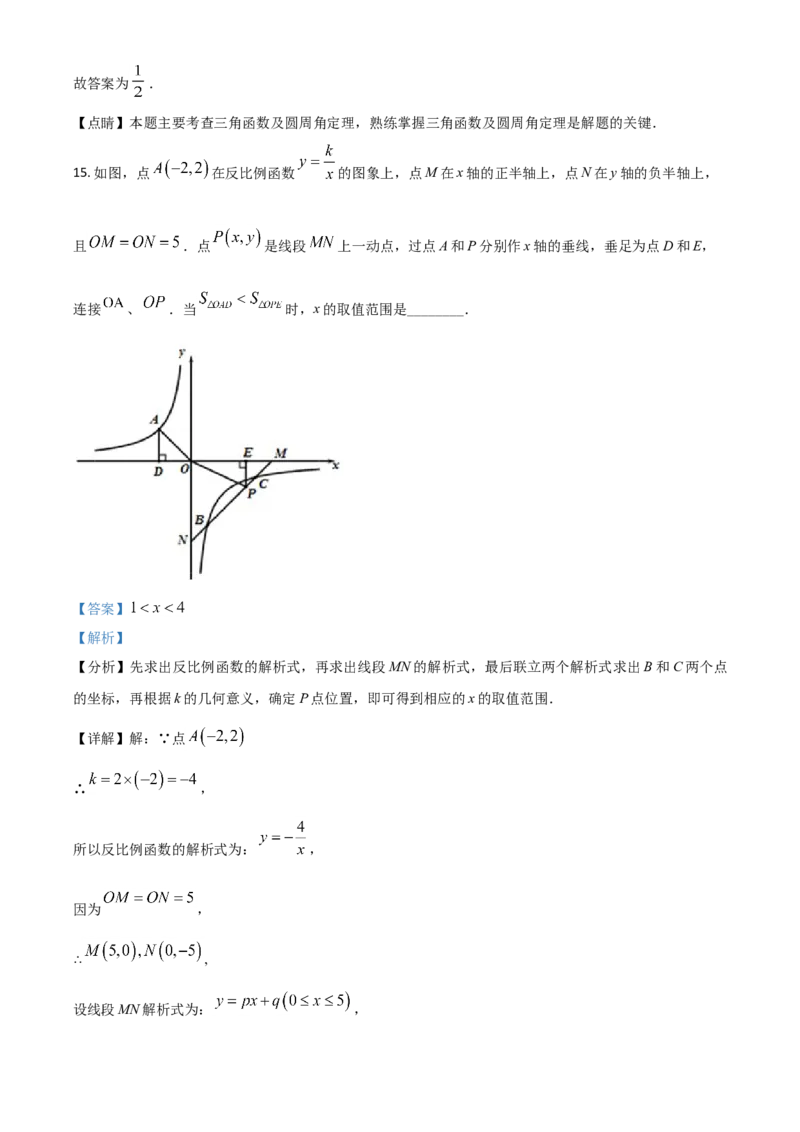
15. 如图,点 在反比例函数 的图象上,点M在x轴的正半轴上,点N在y轴的负半轴上,
且 .点 是线段 上一动点,过点A和P分别作x轴的垂线,垂足为点D和E,
连接 、 .当 时,x的取值范围是________.
【答案】
【解析】
【分析】先求出反比例函数的解析式,再求出线段MN的解析式,最后联立两个解析式求出B和C两个点
的坐标,再根据k的几何意义,确定P点位置,即可得到相应的x的取值范围.
【详解】解:∵点
∴ ,
所以反比例函数的解析式为: ,
因为 ,
∴ ,
设线段MN解析式为: ,∴ ,
∴ ,
∴线段MN解析式为: ,
联立以上两个解析式得: ,
解得: 或 ,经检验,符合题意;
由图可知,两个函数的图像交点分别为点B和点C,
∴ , ,
∵ ,
∴P点应位于B和C两点之间,
∴ ,
故答案为: .
【点睛】本题涉及到了动点问题,考查了反比例函数的图像与性质、k的几何意义、待定系数法等内容,
解决本题的关键是牢记反比例函数的图像与性质,理解k的几何意义,以及能联立两个函数的解析式求交
点坐标等,本题蕴含了数形结合的思想方法等.
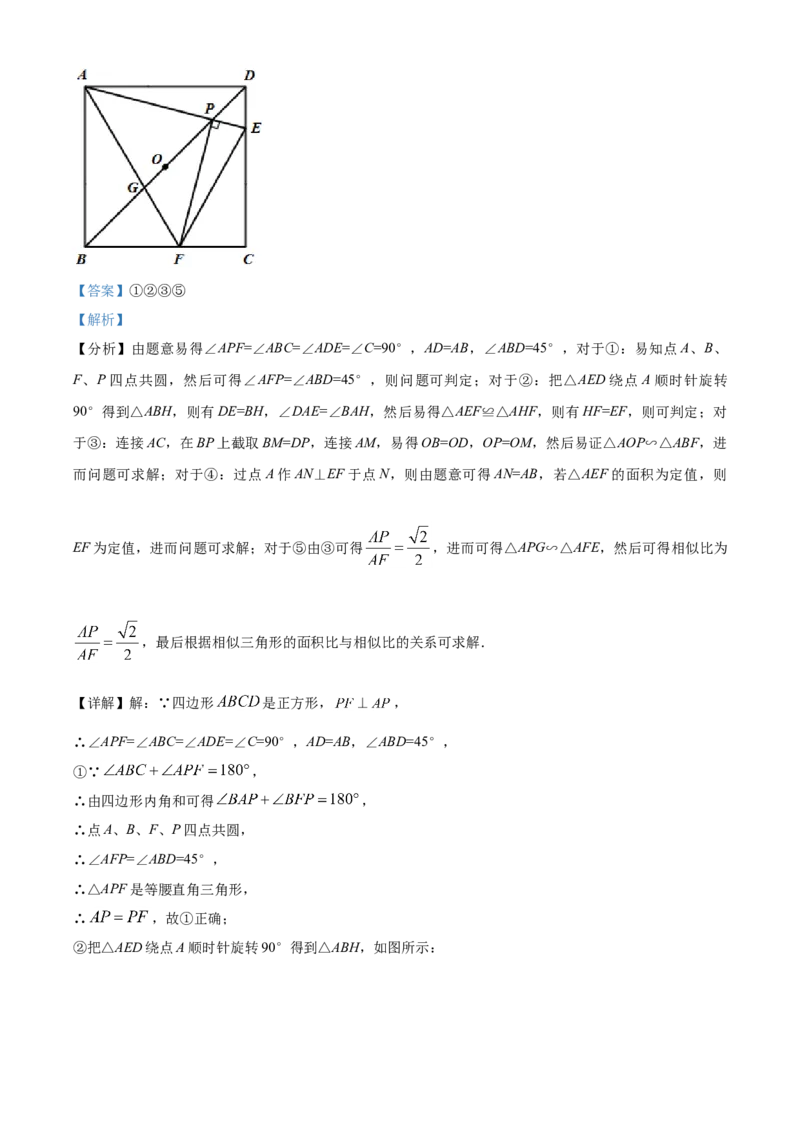
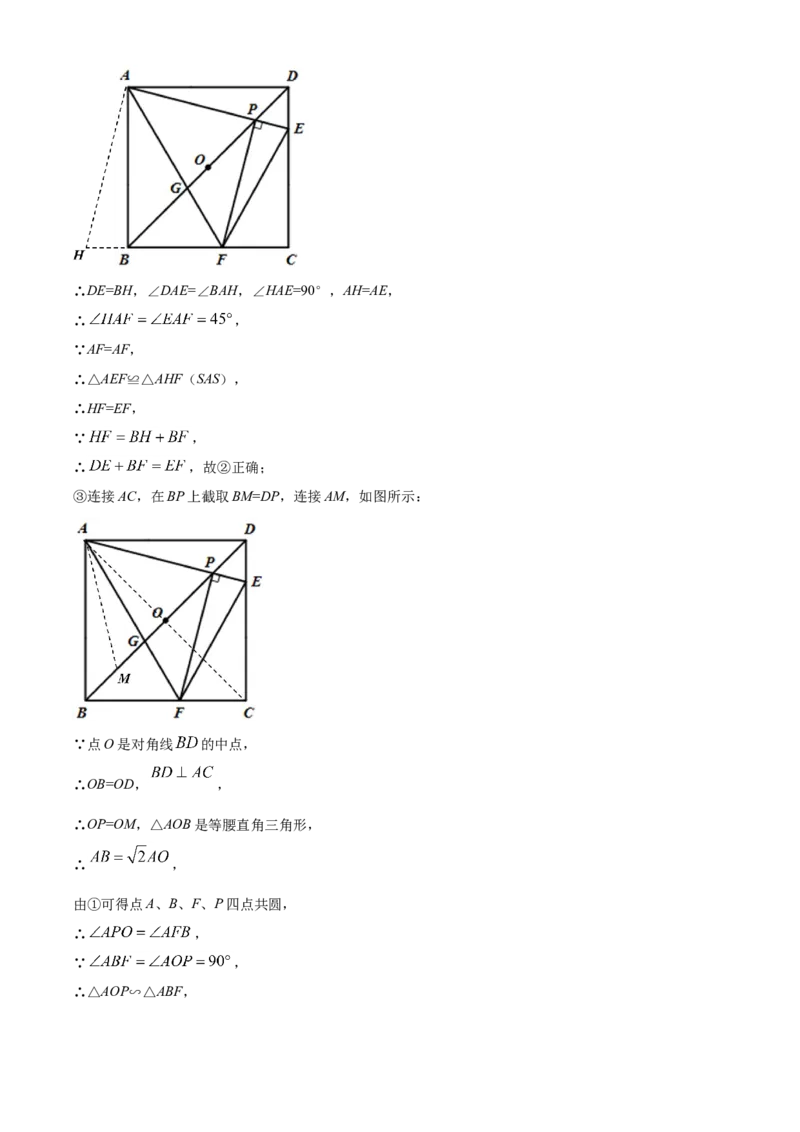
16. 如图,在正方形 中,点O是对角线 的中点,点P在线段 上,连接 并延长交 于
点E,过点P作 交 于点F,连接 、 , 交 于G,现有以下结论:① ;
② ;③ ;④ 为定值;⑤ .以上结论正确的有
________(填入正确的序号即可).【答案】①②③⑤
【解析】
【分析】由题意易得∠APF=∠ABC=∠ADE=∠C=90°,AD=AB,∠ABD=45°,对于①:易知点A、B、
F、P四点共圆,然后可得∠AFP=∠ABD=45°,则问题可判定;对于②:把△AED绕点A顺时针旋转
90°得到△ABH,则有DE=BH,∠DAE=∠BAH,然后易得△AEF≌△AHF,则有HF=EF,则可判定;对
于③:连接AC,在BP上截取BM=DP,连接AM,易得OB=OD,OP=OM,然后易证△AOP∽△ABF,进
而问题可求解;对于④:过点A作AN⊥EF于点N,则由题意可得AN=AB,若△AEF的面积为定值,则
EF为定值,进而问题可求解;对于⑤由③可得 ,进而可得△APG∽△AFE,然后可得相似比为
,最后根据相似三角形的面积比与相似比的关系可求解.
【详解】解:∵四边形 是正方形, ,
∴∠APF=∠ABC=∠ADE=∠C=90°,AD=AB,∠ABD=45°,
①∵ ,
∴由四边形内角和可得 ,
∴点A、B、F、P四点共圆,
∴∠AFP=∠ABD=45°,
∴△APF是等腰直角三角形,
∴ ,故①正确;
②把△AED绕点A顺时针旋转90°得到△ABH,如图所示:∴DE=BH,∠DAE=∠BAH,∠HAE=90°,AH=AE,
∴ ,
∵AF=AF,
∴△AEF≌△AHF(SAS),
∴HF=EF,
∵ ,
∴ ,故②正确;
③连接AC,在BP上截取BM=DP,连接AM,如图所示:
∵点O是对角线 的中点,
∴OB=OD, ,
∴OP=OM,△AOB是等腰直角三角形,
∴ ,
由①可得点A、B、F、P四点共圆,
∴ ,
∵ ,
∴△AOP∽△ABF,∴ ,
∴ ,
∵ ,
∴ ,故③正确;
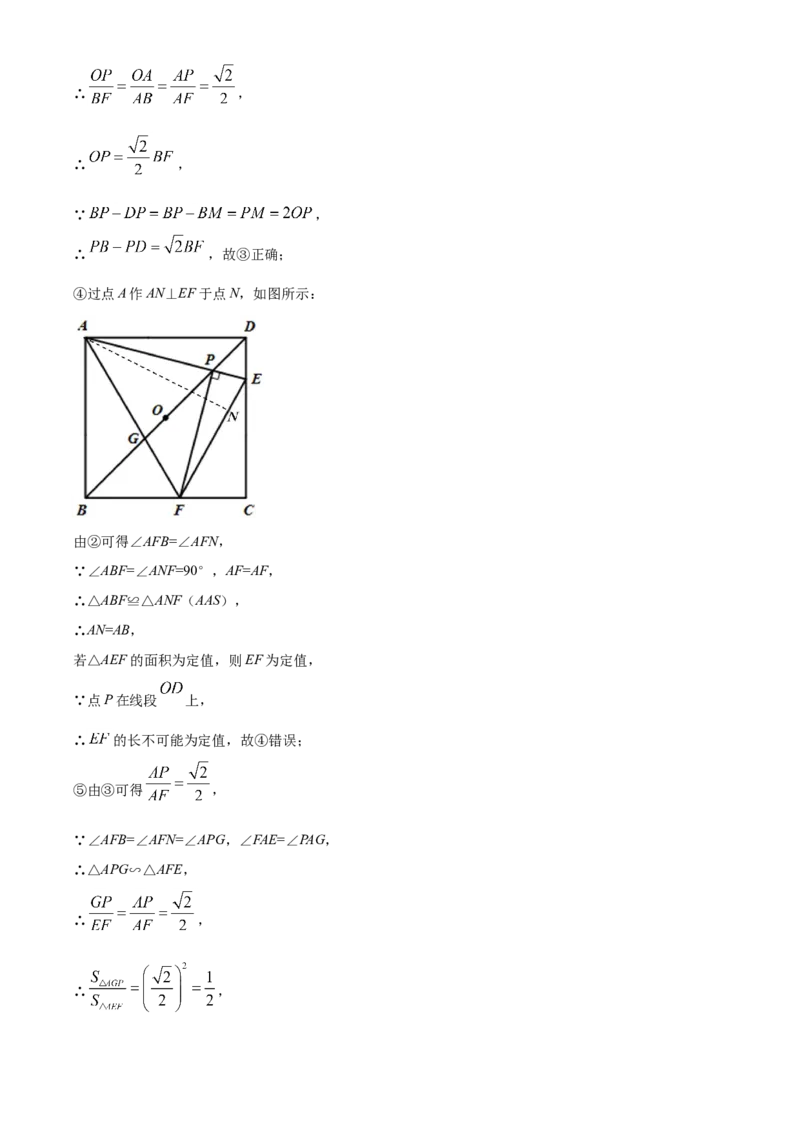
④过点A作AN⊥EF于点N,如图所示:
由②可得∠AFB=∠AFN,
∵∠ABF=∠ANF=90°,AF=AF,
∴△ABF≌△ANF(AAS),
∴AN=AB,
若△AEF的面积为定值,则EF为定值,
∵点P在线段 上,
∴ 的长不可能为定值,故④错误;
⑤由③可得 ,
∵∠AFB=∠AFN=∠APG,∠FAE=∠PAG,
∴△APG∽△AFE,
∴ ,
∴ ,∴ ,
∴ ,故⑤正确;
综上所述:以上结论正确的有①②③⑤;
故答案为①②③⑤.
【点睛】本题主要考查正方形的性质、旋转的性质、圆的基本性质及相似三角形的性质与判定,熟练掌握
正方形的性质、旋转的性质、圆的基本性质及相似三角形的性质与判定是解题的关键.
三、解答题(96分)要求写出必要的解答步骤或证明过程
17. 解方程: .
【答案】
【解析】
【分析】根据整式方程的计算过程,去分母、去括号、移项、合并同类项、系数化为1,就可以得到结果.
【详解】解:去分母得: ,
去括号得: ,
移项并合并同类项得: ,
系数化为1得: ,
故答案为: .
【点睛】本题考查整式方程的计算,注意每个步骤的要求是解题的关键.
18. 先化简,再求值: .其中 , .
【答案】 ,
【解析】
【分析】先算括号内的,再进行分式的除法运算进行化简,然后再代值求解即可.
【详解】解:原式= ,把 , 代入得:原式= .
【点睛】本题主要考查分式的化简求值及二次根式的运算,熟练掌握分式的化简求值及二次根式的运算是
解题的关键.
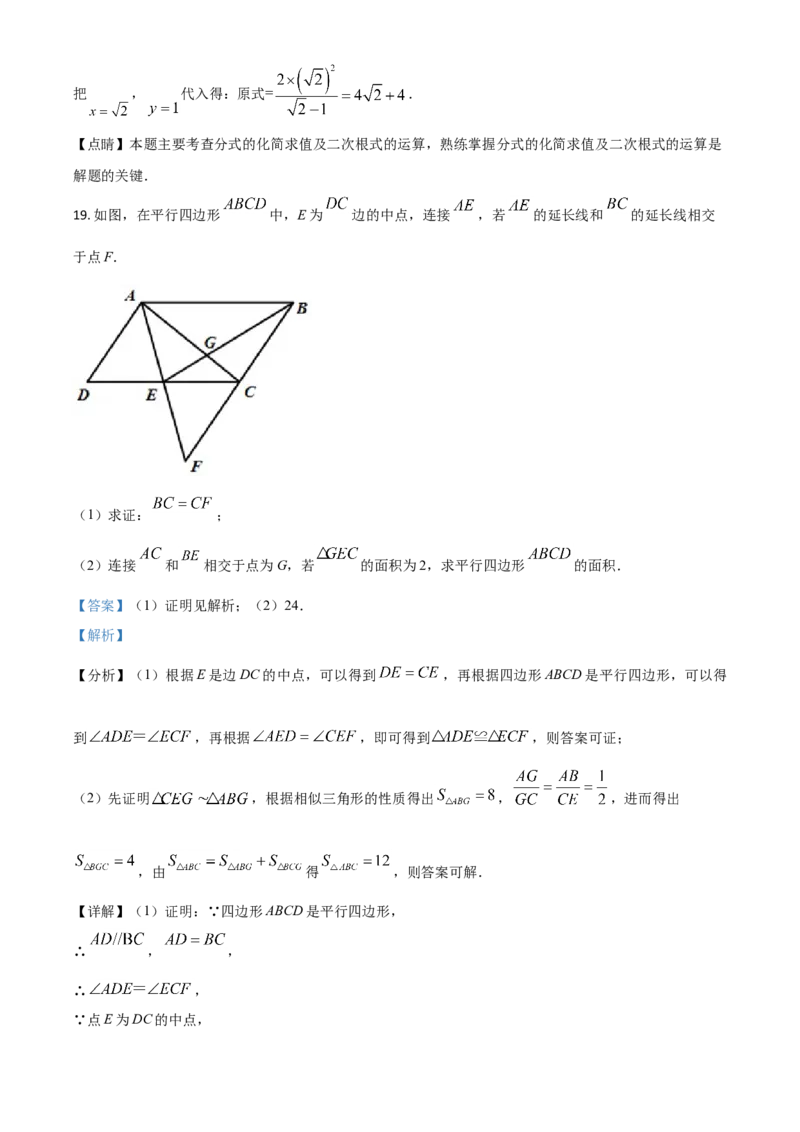
19. 如图,在平行四边形 中,E为 边的中点,连接 ,若 的延长线和 的延长线相交
于点F.
(1)求证: ;
(2)连接 和 相交于点为G,若 的面积为2,求平行四边形 的面积.
【答案】(1)证明见解析;(2)24.
【解析】
【分析】(1)根据E是边DC的中点,可以得到 ,再根据四边形ABCD是平行四边形,可以得
到 ,再根据 ,即可得到 ,则答案可证;
(2)先证明 ,根据相似三角形的性质得出 , ,进而得出
,由 得 ,则答案可解.
【详解】(1)证明:∵四边形ABCD是平行四边形,
∴ , ,
∴ ,
∵点E为DC的中点,∴ ,
在 和 中
∴ ,
∴ ,
∴ ;
(2)∵四边形ABCD是平行四边形,点E为DC的中点,
∴ , ,
∴ , ,
∴ ,
∵ 的面积为2,
∴ ,即 ,
∵
∴ ,
∴ ,
∴ ,
∴ .
【点睛】本题考查平行四边形的性质、全等三角形的判定与性质,相似三角形的判定和性质,解答本题的
关键是明确题意,利用数形结合的思想解答.
20. 为增强学生体质,丰富学生课余活动,学校决定添置一批篮球和足球.甲、乙两家商场以相同的价格
出售同种品牌的篮球和足球,已知篮球价格为200元/个,足球价格为150元/个.(1)若学校计划用不超过3550元的总费用购买这款篮球和足球共20个,且购买篮球的数量多于购买足球
数量的 .学校有哪几种购买方案?
(2)若甲、乙两商场各自推出不同的优惠方案:甲商场累计购物超过500元后,超出500元的部分按90%
收费;乙商场累计购物超过2000元后,超出2000元的部分按80%收费.若学校按(1)中的方案购买,学
校到哪家商场购买花费少?
【答案】(1)有三种方案,为:①购买9个篮球,11个足球;②10个篮球,10个足球;③11个篮球,9
个足球;(2)学校购买9个篮球,11个足球到甲商场购买花费少;购买10个篮球,10个足球和11个篮
球,9个足球到乙商场购买花费少.
【解析】
【分析】(1)设学校购买篮球x个,购买足球(20-x)个,根据“学校计划用不超过3550元 的总费用购
买”和“购买篮球的数量多于购买足球数量的 ”列出不等式组,求解即可;
(2)设学校购买篮球x个,购买足球(20-x)个,分别计算出在甲,乙两商场的费用列出不等式求解即可.
【详解】解:(1)设学校购买篮球x个,购买足球(20-x)个,根据题意得,
解得,
∵x是整数,
∴x=9,10或11
∴20-x=12,10或9
故有三种方案,为:①购买9个篮球,11个足球;②10个篮球,10个足球;③11个篮球,9个足球;
(2)设学校购买篮球x个,购买足球(20-x)个,
在甲商场花费: 元;
在乙商场花费: 元;
∴要使学校到甲商场花费最少,则有:解得,
∵ ,且x是整数,
∴x=9,
即:学校购买9个篮球,11个足球到甲商场购买花费少;购买10个篮球,10个足球和11个篮球,9个足
球到乙商场购买花费少.
【点睛】本题主要考查了一元一次不等式和一元一次不等式组的应用,解题关键是要读懂题目的意思,根
据题目给出的条件,找出合适的等量关系列出不等式,再求解.
21. “此生无悔入华夏,来世再做中国人!”自疫情暴发以来,我国科研团队经过不懈努力,成功地研发
出了多种“新冠”疫苗,并在全国范围内免费接种.截止2021年5月18日16:20,全球接种“新冠”疫
苗的比例为18.29%;中国累计接种4.2亿剂,占全国人口的29.32%.以下是某地甲、乙两家医院5月份某
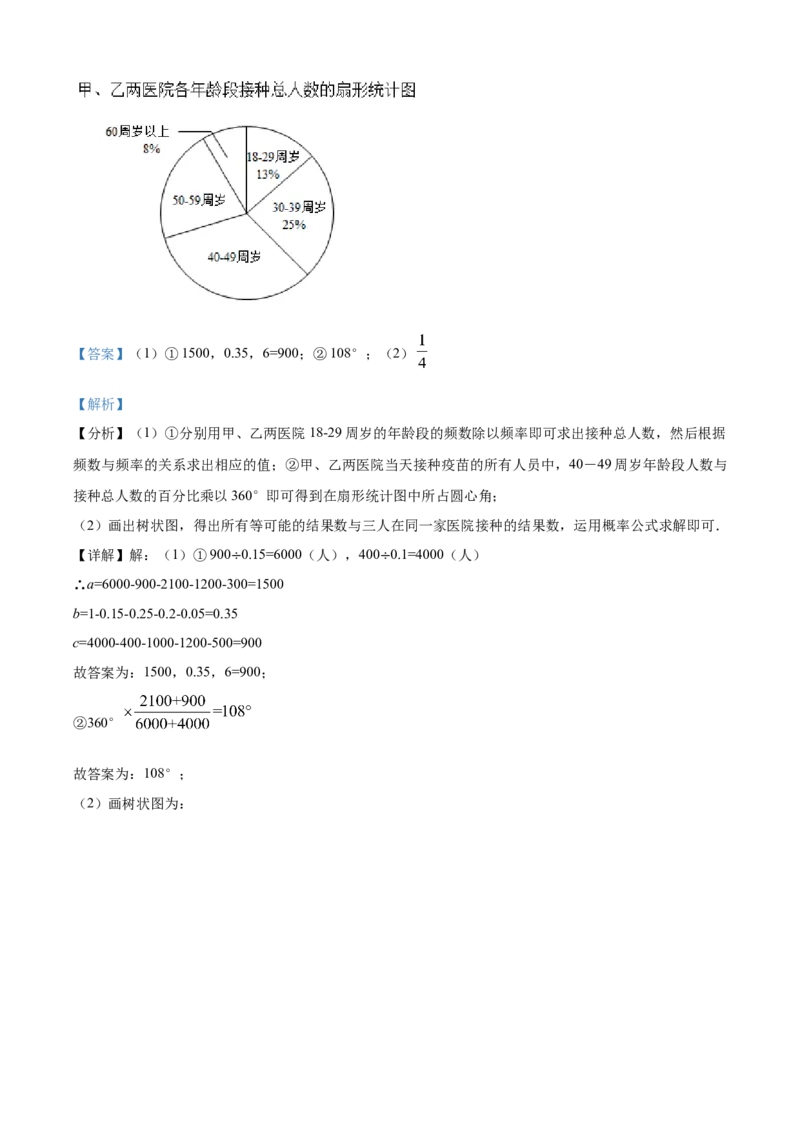
天各年龄段接种疫苗人数的频数分布表和接种总人数的扇形统计图:
甲医院 乙医院
年龄段 频数 频率 频数 频率
18-29周岁 900 0.15 400 0.1
30-39周岁 a 0.25 1000 0.25
40-49周岁 2100 b c 0.225
50-59周岁 1200 0.2 1200 0.3
60周岁以上 300 0.05 500 0.125
(1)根据上面图表信息,回答下列问题:
①填空: _________, _________, _________;
②在甲、乙两医院当天接种疫苗的所有人员中,40-49周岁年龄段人数在扇形统计图中所占圆心角为
_________;
(2)若A、B、C三人都于当天随机到这两家医院接种疫苗,求这三人在同一家医院接种的概率.【答案】(1)①1500,0.35,6=900;②108°;(2)
【解析】
【分析】(1)①分别用甲、乙两医院18-29周岁的年龄段的频数除以频率即可求出接种总人数,然后根据
频数与频率的关系求出相应的值;②甲、乙两医院当天接种疫苗的所有人员中,40-49周岁年龄段人数与
接种总人数的百分比乘以360°即可得到在扇形统计图中所占圆心角;
(2)画出树状图,得出所有等可能的结果数与三人在同一家医院接种的结果数,运用概率公式求解即可.
【详解】解:(1)①900 0.15=6000(人),400 0.1=4000(人)
∴a=6000-900-2100-1200-3÷00=1500 ÷
b=1-0.15-0.25-0.2-0.05=0.35
c=4000-400-1000-1200-500=900
故答案为:1500,0.35,6=900;
②360°
故答案为:108°;
(2)画树状图为:∴所有等可能的结果共有8种情况,而同在一所医院接种的有2种结果数,
∴三人在同一家医院接种的概率 .
【点睛】此题考查了条形统计图,扇形统计图以及概率的计算,读懂统计图,从不同的统计图中得到必要
的信息是解决问题的关键.当有两个元素时,可用树形图列举,也可以列表列举.
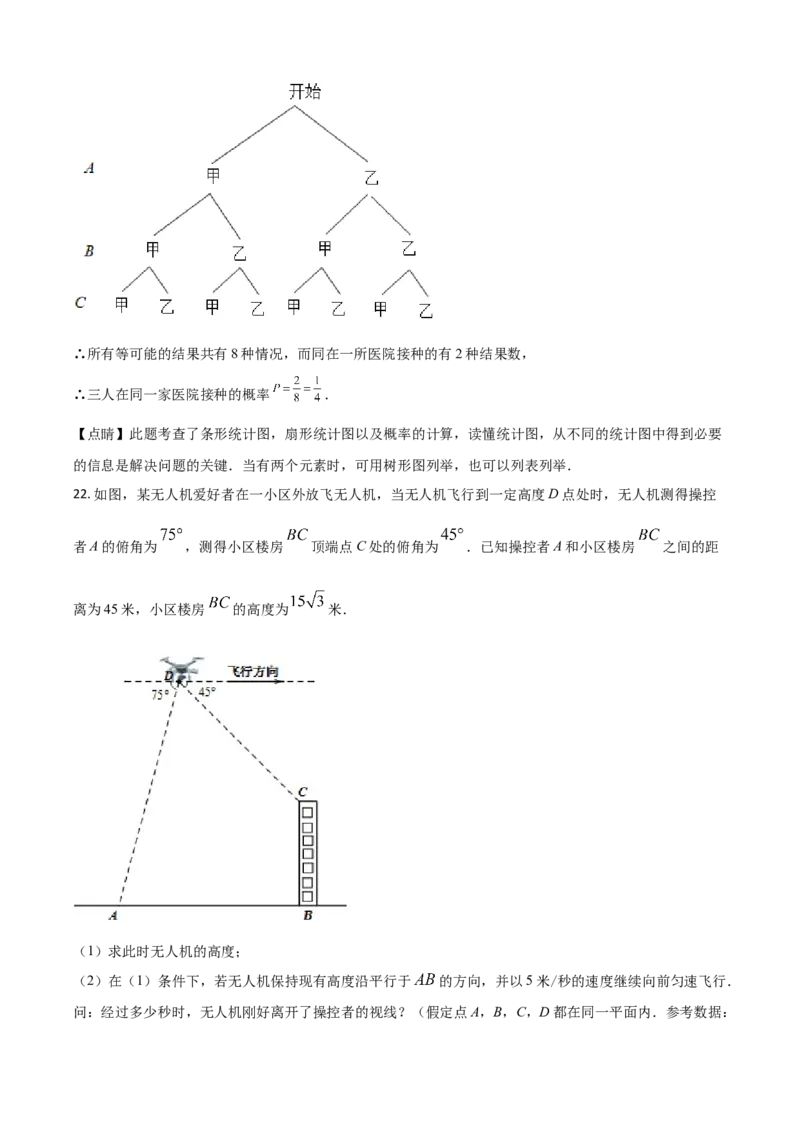
22. 如图,某无人机爱好者在一小区外放飞无人机,当无人机飞行到一定高度D点处时,无人机测得操控
者A的俯角为 ,测得小区楼房 顶端点C处的俯角为 .已知操控者A和小区楼房 之间的距
离为45米,小区楼房 的高度为 米.
(1)求此时无人机的高度;
(2)在(1)条件下,若无人机保持现有高度沿平行于 的方向,并以5米/秒的速度继续向前匀速飞行.
问:经过多少秒时,无人机刚好离开了操控者的视线?(假定点A,B,C,D都在同一平面内.参考数据:, .计算结果保留根号)
【答案】(1) 米;(2) 秒
【解析】
【分析】(1)通过作辅助线构造直角三角形,解直角三角形即可求出DE的值,进而得到DH的值;
(2)先利用特殊角的三角函数值求出∠BAC的度数,接着求出∠GFA的度数,作辅助线构造直角三角形
求出DG和GF,进而得到DF的值,最后除以无人机速度即可.
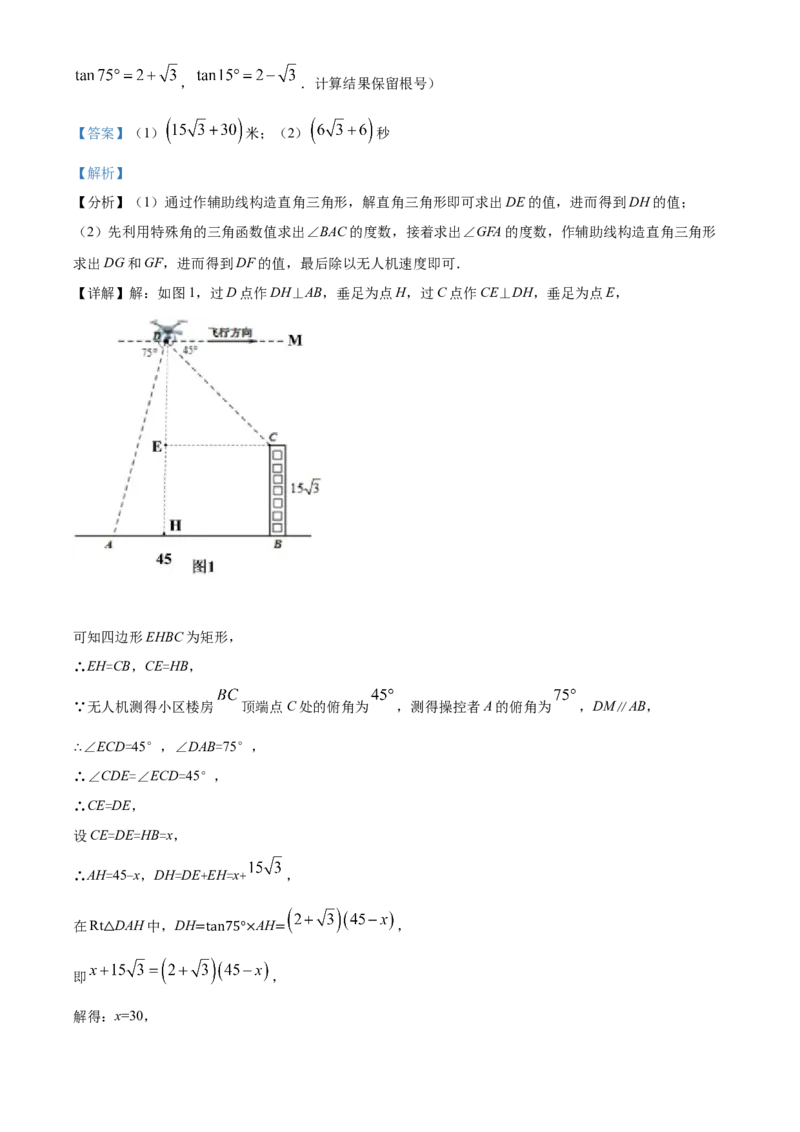
【详解】解:如图1,过D点作DH⊥AB,垂足为点H,过C点作CE⊥DH,垂足为点E,
可知四边形EHBC为矩形,
∴EH=CB,CE=HB,
∵无人机测得小区楼房 顶端点C处的俯角为 ,测得操控者A的俯角为 ,DM∥AB,
∴∠ECD=45°,∠DAB=75°,
∴∠CDE=∠ECD=45°,
∴CE=DE,
设CE=DE=HB=x,
∴AH=45-x,DH=DE+EH=x+ ,
在Rt DAH中,DH AH ,
△ =tan75°× =
即 ,
解得:x=30,∴DH=
∴此时无人机的高度为 米;
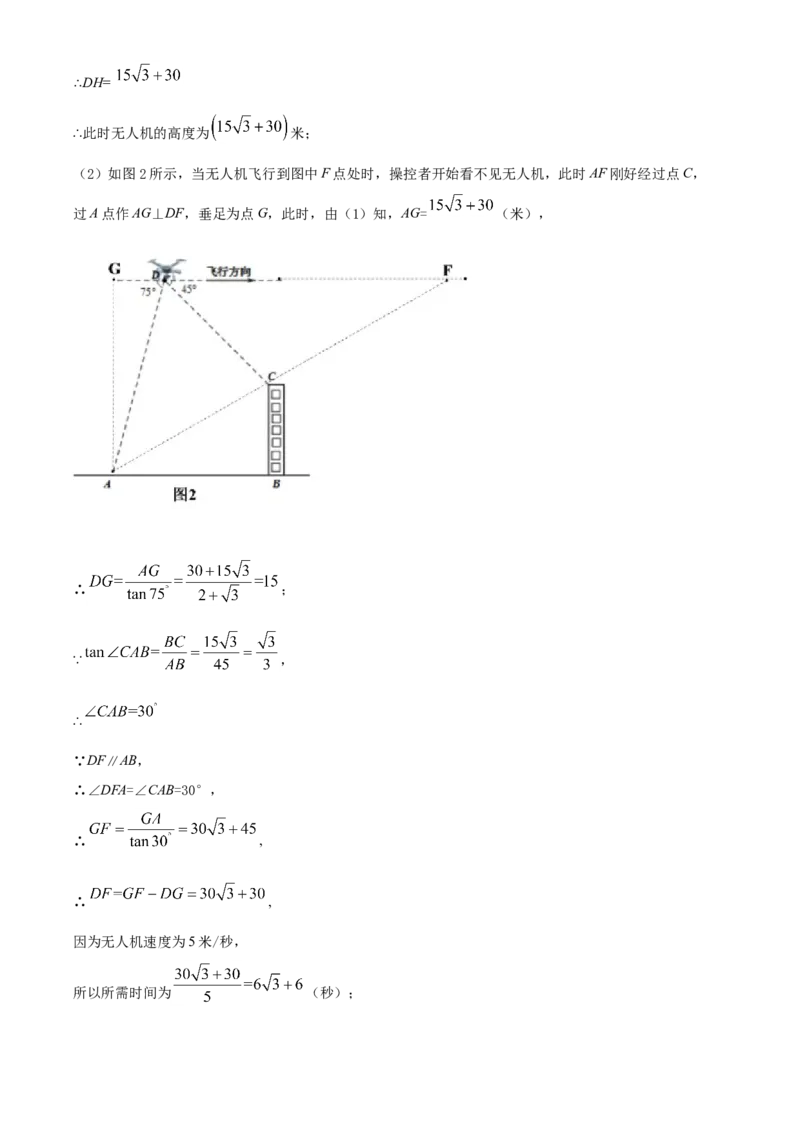
(2)如图2所示,当无人机飞行到图中F点处时,操控者开始看不见无人机,此时AF刚好经过点C,
过A点作AG⊥DF,垂足为点G,此时,由(1)知,AG= (米),
∴ ;
∵ ,
∴
∵DF∥AB,
∴∠DFA=∠CAB=30°,
∴ ,
∴ ,
因为无人机速度为5米/秒,
所以所需时间为 (秒);所以经过 秒时,无人机刚好离开了操控者的视线.
【点睛】本题综合考查了解直角三角形的应用,涉及到了等腰直角三角形的性质、矩形的判定与性质、特
殊角的三角函数值、解直角三角形等知识,解决本题的关键是读懂题意,能从题意与图形中找出隐含条件,
能构造直角三角形求解等,本题蕴含了数形结合的思想方法等.
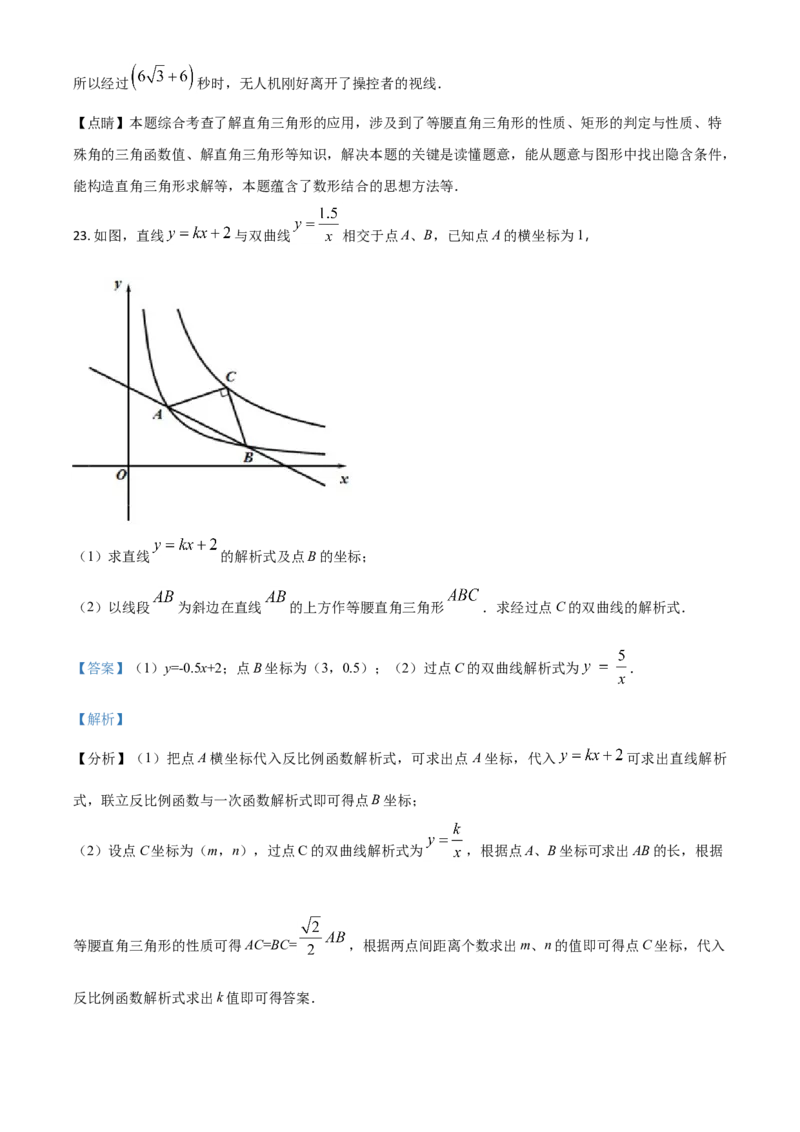
23. 如图,直线 与双曲线 相交于点A、B,已知点A的横坐标为1,
(1)求直线 的解析式及点B的坐标;
(2)以线段 为斜边在直线 的上方作等腰直角三角形 .求经过点C的双曲线的解析式.
【答案】(1)y=-0.5x+2;点B坐标为(3,0.5);(2)过点C的双曲线解析式为 .
【解析】
【分析】(1)把点A横坐标代入反比例函数解析式,可求出点 A坐标,代入 可求出直线解析
式,联立反比例函数与一次函数解析式即可得点B坐标;
(2)设点C坐标为(m,n),过点C的双曲线解析式为 ,根据点A、B坐标可求出AB的长,根据
等腰直角三角形的性质可得AC=BC= ,根据两点间距离个数求出m、n的值即可得点C坐标,代入
反比例函数解析式求出k值即可得答案.【详解】(1)∵点A在双曲线 上,点A 的横坐标为1,
∴当x=1时,y=1.5,
∴点A坐标为(1,1.5),
∵直线 与双曲线 相交于点A、B,
∴k+2=1.5,
解得:k=-0.5,
∴直线 的解析式为y=-0.5x+2,
联立反比例函数与一次函数解析式得 ,
解得: , (舍去),
∴点B坐标为(3,0.5).
(2)设点C坐标为(m,n),过点C的双曲线解析式为 ,
∵A(1,1.5),B(3,0.5),
∴AB= = ,
∵△ABC是等腰直角三角形,
∴AC=BC= = ,
∴ ,
整理得: ,
∴ ,解得: ,
∴ 或0(舍去),
∴点C坐标为( ,2),
把点C坐标代入双曲线解析式得: ,
解得: ,
∴过点C的双曲线解析式为 .
【点睛】本题考查反比例函数与一次函数综合,熟练掌握反比例函数图象上的点的坐标特征是解题关键.
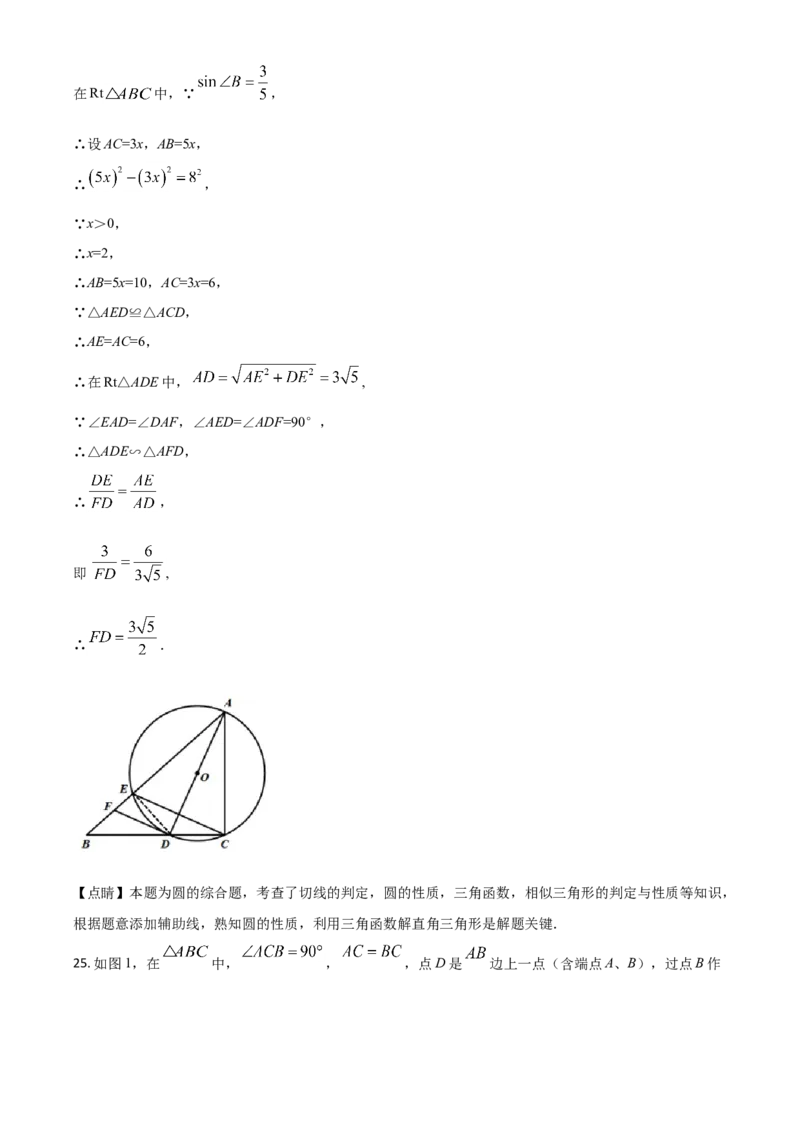
24. 如图,在Rt 中, , 是 的平分线,以 为直径的 交 边于点
E,连接 ,过点D作 ,交 于点F.
(1)求证: 是 的切线;
(2)若 , ,求线段 的长.
【答案】(1)证明见详解;(2) .
【解析】
【分析】(1)先根据圆周角定理、角平分线定义、平行线性质证明∠EAD=∠FDE,再根据AD为 直
径,得到∠ADE+∠DAE=90°,进而得到AD⊥FD,问题得证;(2)先求出DE=3,证明△AED≌△ACD,得到DE=DC=3,BC=BD+CD=8,解Rt 中求出AC=6,
进而得到AE=6,求出 ,证明△ADE∽△AFD,得到 ,即可求出 .
【详解】解:(1)证明:连接DE,
∵
∴∠CAD=∠CED,
∵ 是 的平分线,
∴∠CAD=∠EAD,
∴∠CED=∠EAD,
∵ ,
∴∠CED=∠FDE,
∴∠EAD=∠FDE,
∵AD为 直径,
∴∠AED=∠ACD=90°,
∴∠ADE+∠DAE=90°,
∴∠ADE+∠FDE=90°,
即AD⊥FD,
又∵ 为 直径,
∴ 是 的切线;
(2)∵∠AED=90°,
∴∠BED=90°,
∴ ,
∵∠AED=∠ACD,∠DAE=∠DAC,AD=AD,
∴△AED≌△ACD,
∴DE=DC=3,
∴BC=BD+CD=8,在Rt 中,∵ ,
∴设AC=3x,AB=5x,
∴ ,
∵x>0,
∴x=2,
∴AB=5x=10,AC=3x=6,
∵△AED≌△ACD,
∴AE=AC=6,
∴在Rt△ADE中, ,
∵∠EAD=∠DAF,∠AED=∠ADF=90°,
∴△ADE∽△AFD,
∴ ,
即 ,
∴ .
【点睛】本题为圆的综合题,考查了切线的判定,圆的性质,三角函数,相似三角形的判定与性质等知识,
根据题意添加辅助线,熟知圆的性质,利用三角函数解直角三角形是解题关键.
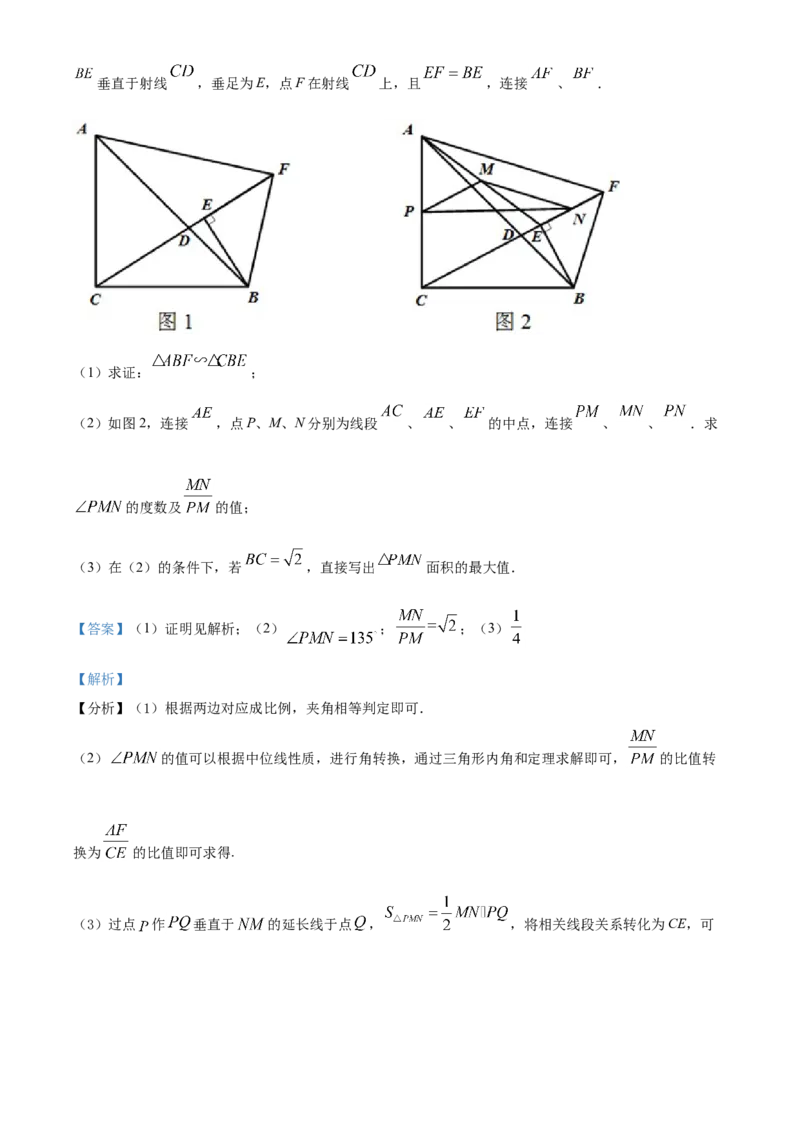
25. 如图1,在 中, , ,点D是 边上一点(含端点A、B),过点B作垂直于射线 ,垂足为E,点F在射线 上,且 ,连接 、 .
(1)求证: ;
(2)如图2,连接 ,点P、M、N分别为线段 、 、 的中点,连接 、 、 .求
的度数及 的值;
(3)在(2)的条件下,若 ,直接写出 面积的最大值.
【答案】(1)证明见解析;(2) ; ;(3)
【解析】
【分析】(1)根据两边对应成比例,夹角相等判定即可.
(2) 的值可以根据中位线性质,进行角转换,通过三角形内角和定理求解即可, 的比值转
换为 的比值即可求得.
(3)过点 作 垂直于 的延长线于点 , ,将相关线段关系转化为CE,可得关系 ,观察图象,当 时,可得最大值.
【详解】(1)证明:∵ ,
∴ ,
∵ 垂直于射线 ,
∴
又∵
∴ ,
∵
即:
又∵
∴
(2)解:∵点P、M、N分别为线段 、 、 的中点
∴ , ,
∴ ,
∴
又∵
∴
又∵
∴∴
又∵
∴
又∵
又∵
∴
∴
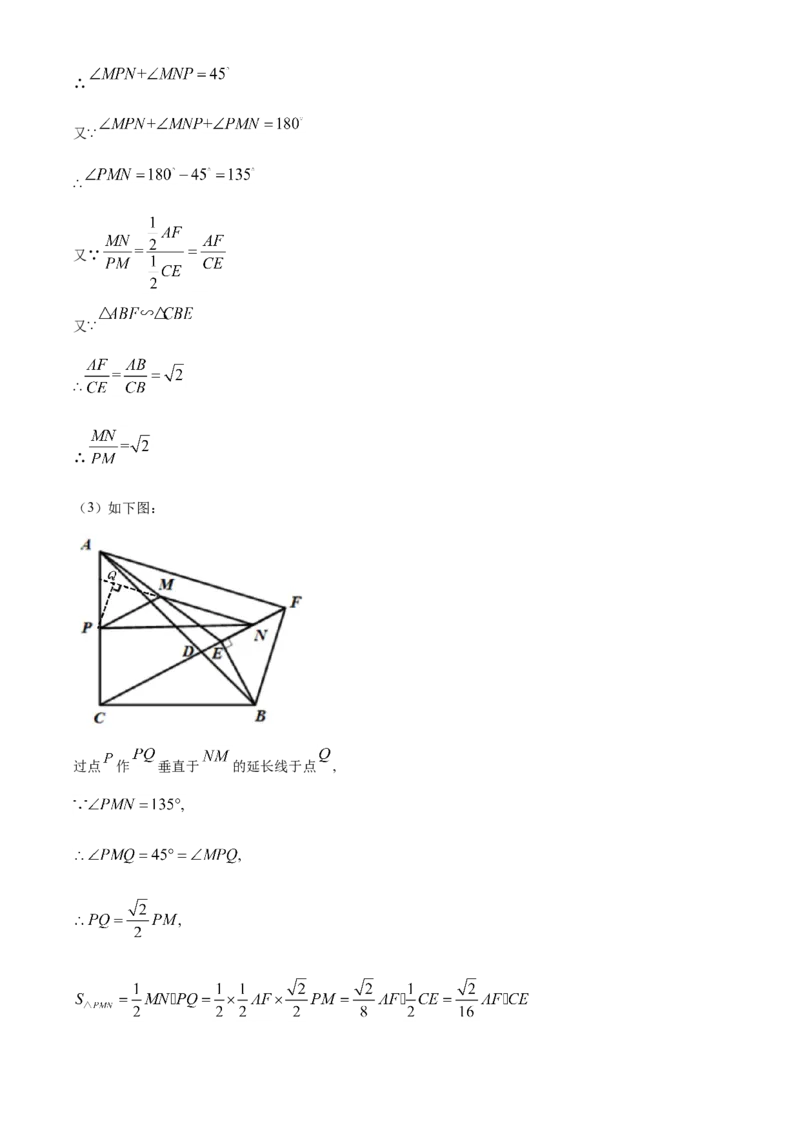
(3)如下图:
过点 作 垂直于 的延长线于点 ,又∵
∴
∴
∴当 取得最大值时, 取得最大值,
在以 的中点为圆心, 为直径的圆上运动,
当 时, 最大,
∴ ,
【点睛】本题考查的是三角形相似和判定、以及三角形面积最大值的求法,根据题意找见相关的等量是解
题关键.
26. 如图1,在平面直角坐标系 中,抛物线 与x轴分别相交于A、B两点,与y轴相
交于点C,下表给出了这条抛物线上部分点 的坐标值:
x … 0 1 2 3 …
y … 0 3 4 3 0 …
(1)求出这条抛物线的解析式及顶点M的坐标;
(2) 是抛物线对称轴上长为1的一条动线段(点P在点Q上方),求 的最小值;
(3)如图2,点D是第四象限内抛物线上一动点,过点D作 轴,垂足为F, 的外接圆与
相交于点E.试问:线段 的长是否为定值?如果是,请求出这个定值;如果不是,请说明理由.【答案】(1) ; ;(2) ;(3)是,1.
【解析】
【分析】(1)依据表格数据,设出抛物线的顶点式,利用待定系数法求解即可;
的
(2)利用平移和找对称点 方式,将 的长转化为 ,再利用两点之间线段最
短确定 的最小值等于CE的长,加1后即能确定 的最小值;
(3)设出圆心和D点的坐标,接着表示出E点的坐标,利用圆心到B点的距离等于圆心到D点的距离,
求出q和e的关系,得到E点的纵坐标,进而确定EF的长为定值.
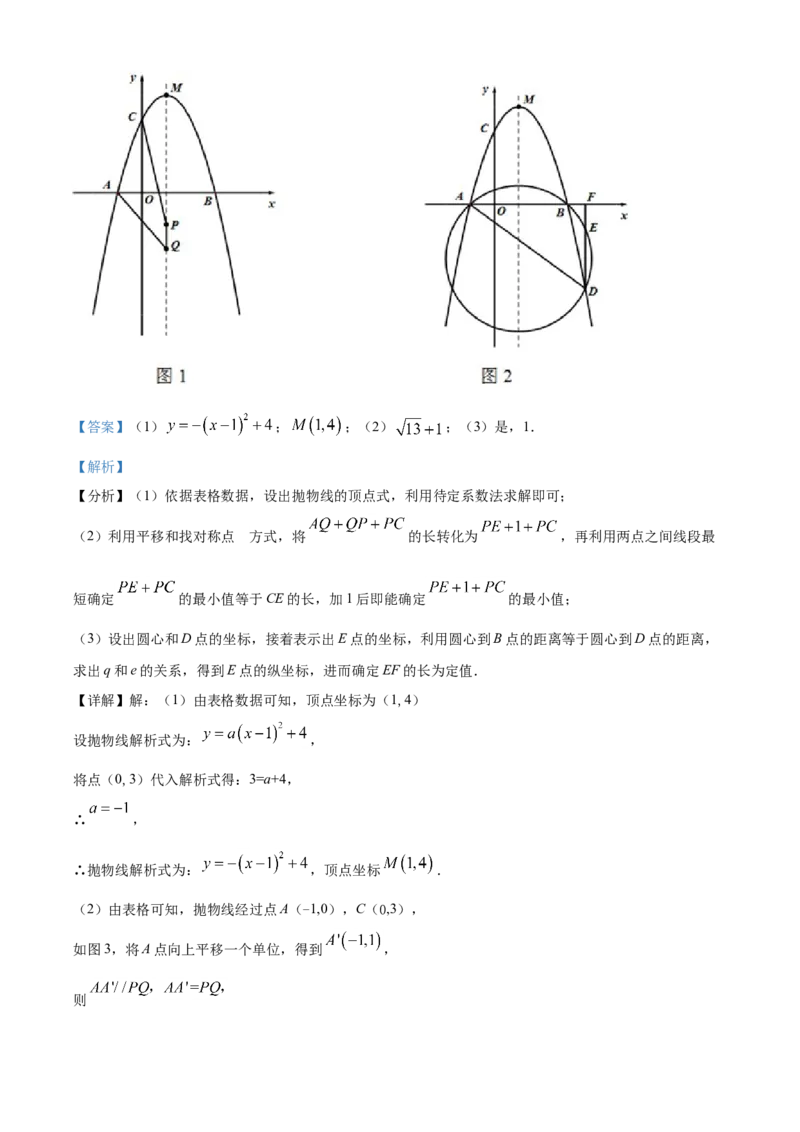
【详解】解:(1)由表格数据可知,顶点坐标为(1,4)
设抛物线解析式为: ,
将点(0,3)代入解析式得:3=a+4,
∴ ,
∴抛物线解析式为: ,顶点坐标 .
(2)由表格可知,抛物线经过点A(-1,0),C(0,3),
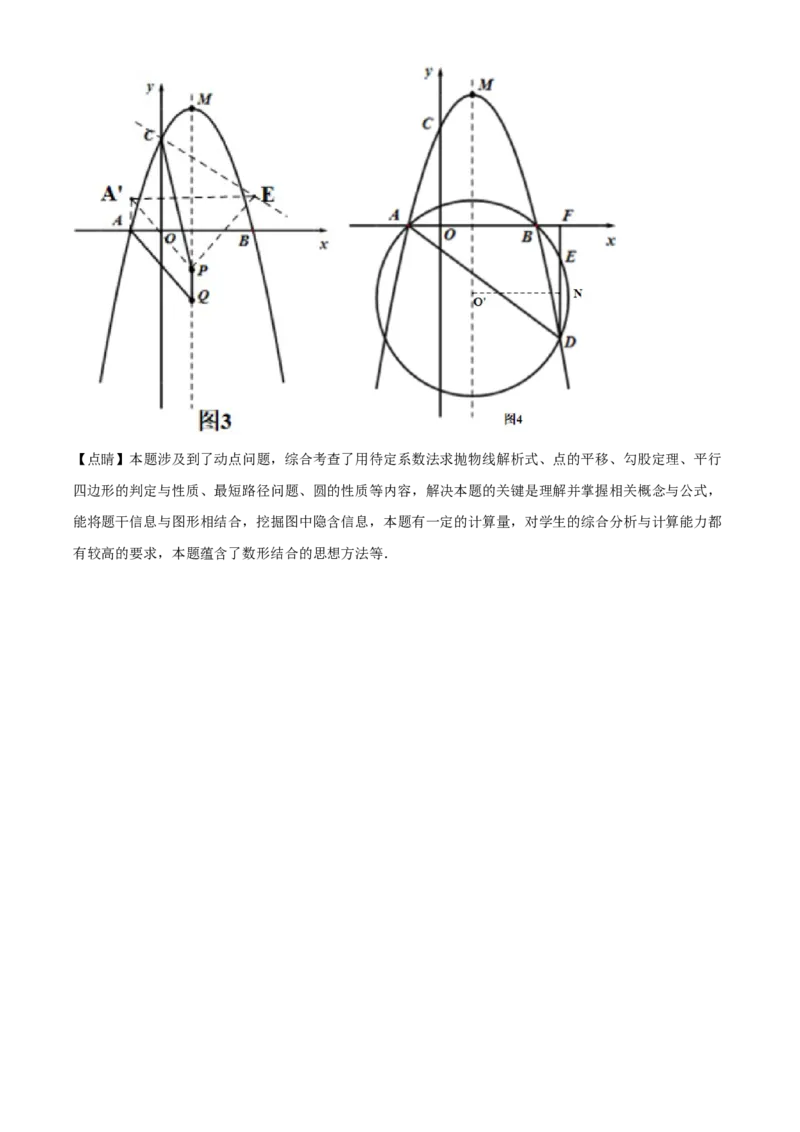
如图3,将A点向上平移一个单位,得到 ,
则∴四边形 是平行四边形,
∴ ,
作 关于MQ的对称点E,则
∴ ,
∴ ,
当P、E、C三点共线时, 最短,
设直线CE的解析式为: ,
将C、E两点坐标代入解析式可得: ,
∴ ,
∴直线CE的解析式为: ,
令 ,则 ,
∴当 时,P、E、C三点共线,此时 最短,
∴ 的最小值为 .
(3)是;
理由:设 ,
因为A、B两点关于直线x=1对称,
所以圆心位于该直线上,
所以可设 的外接圆的圆心为 ,作 ,垂足为点N,则 ,
由 轴,
∴ ,
∵ ,且由表格数据可知
∴ ,
化简得: ,
∵点D是第四象限内抛物线上一动点,且抛物线解析式为 ,
∴ ,
∴ ,
∴ ,
∵ ,
∴ ,
∴ ,
∴ ,
即 的长不变,为1.【点睛】本题涉及到了动点问题,综合考查了用待定系数法求抛物线解析式、点的平移、勾股定理、平行
四边形的判定与性质、最短路径问题、圆的性质等内容,解决本题的关键是理解并掌握相关概念与公式,
能将题干信息与图形相结合,挖掘图中隐含信息,本题有一定的计算量,对学生的综合分析与计算能力都
有较高的要求,本题蕴含了数形结合的思想方法等.