数学（全国卷理科02）（参考答案）_2024高考押题卷_62024学科网全系列_24学科网高考押题预测卷_2024年高考数学押题预测卷_数学（全国卷理科02）-2024年高考押题预测卷

2024年高考押题预测卷【全国卷02】 理科数学·全解全析 第一部分（选择题 共60分） 一、选择题：本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题 目要求的． 1 2 3 4 5 6 7 8 9 10 11 12 C A B D B A B A C B D B 二、填空题：本大题共4小题，每小题5分，共20分 13． 14． 15． 16． ； . 三、解答题：本大题共70分．解答应写出文字说明、证明过程或演算步骤．第17~21题为必考题，每个试 题考生都必须作答．第22、23题为选考题，考生根据要求作答． （一）必考题：共60分． cosC cosA cosC cosA 17.【详解】（1）解：因为  ，由正弦定理得  ，................................1分 c 4ba sinC 4sinBsinA 可得4sinBcosCsinAcosC cosAsinC， 4sinBcosC sinAcosCcosAsinC sin(AC)sinB 即 ，......................................................................3分 1 因为 ，可得 ，所以 ，即cosC  ， B(0,π) sinB0 4cosC 1 4 15 所以sinC  1cos2C  ...........................................................................................................................6分 4 15 sinC （2）解：由（1）知 4 ， 15 1 15 1 15 15 absinC  ab  因为若ABC的面积为 2 ，可得2 2 ，即2 4 2 ，解得ab4，...................8分 2 6 又因为ab c， 3 1 原创精品资源学科网独家享有版权，侵权必究！ 学科网（北京）股份有限公司1 5 2 6 由余弦定理得c2 a2b22abcosC (ab)22ab2ab (ab)2 ab( c)210， 4 2 3 c2 6 c 6 整理得 ，解得 ，...........................................................................................................................10分 2 6 所以ab  6 4， 3 ABC abc4 6 所以 的周长为 ............................................................................................................12分  0 1 2 3 18.【详解】（1）依题意可得 的可能取值为 、 、 、 ，  3 2 1 1 P01 1 1  所以  4 3 2 24， 3 2 1  3 2  1  3 2 1 1 P1 1 1 1  1 1 1   4 3 2  4 3  2  4 3 2 4 ， 3 2  1 3  2 1  3 2 1 11 P2  1  1  1    4 3  2 4  3 2  4 3 2 24 ， 3 2 1 1 P3    ， 4 3 2 4 所以随机变量的分布列为  0 1 2 3 1 1 11 1 P 24 4 24 4 ..............................................................................................................................................................................3分 1 1 11 1 23 所以E0 1 2 3  ．............................................................................................4分 24 4 24 4 12  2 2 B3,  E3 2 又2班的总得分满足  3，则 3 ．...........................................................................6分 2 A 2 1 B （2）设“ ”为事件 ，“ 班比 班得分高”为事件 ，..........................................................7分 2 原创精品资源学科网独家享有版权，侵权必究！ 学科网（北京）股份有限公司1 2 2  2 1 2  2 2 11  2 3 PA C2  1  C1 1   C31  则 24 3 3  3 4 3 3  3 24 3  3 59  ，..........................................................................................................................................................9分 2427 1 2 2  2 1 PAB C2  1  24 3 3  3 54， PAB 1 2427 12 PB A    所以 PA 54 59 59 ，.................................................................................................11分 12 所以 班比 班得分高的概率为 ．............................................................................................................12分 2 1 59 uuuur uuur uuuur uuur uuur uuur 2 BF 2FB AD2DA BE2EC 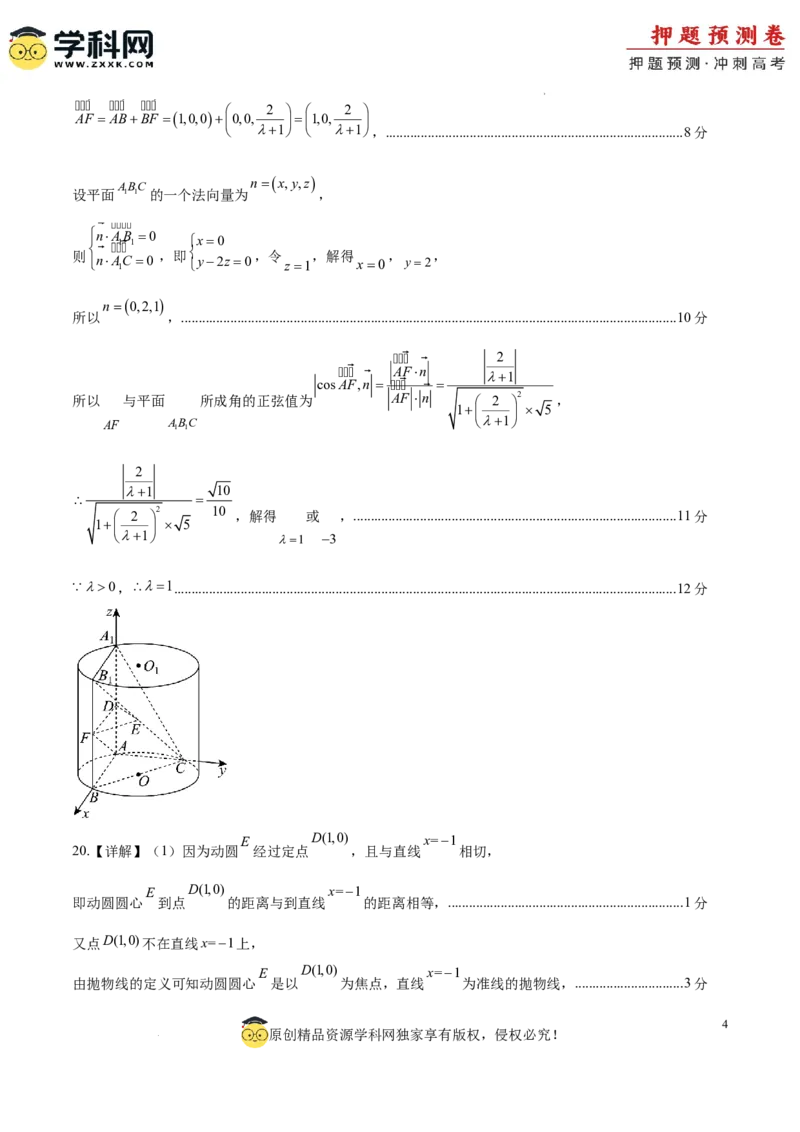19.【详解】（1）当 时，得 1 ，又 1 ， 1 ， 所以DF//AB，EF//BC，.............................................................................................................................2分  DF 平面ABC，AB平面ABC，DF//平面ABC， 同理得EF//平面ABC，..................................................................................................................................4分 因为EF,DE是平面DEF 内两条相交直线， 所以平面DEF//平面ABC...............................................................................................................................5分 AA BB OO AA ABC BC 1 1 1 1 （2）因为 ， 为圆柱 的母线，所以 垂直平面 ，又点C在底面圆周上，且 过底面圆 心O， ABAC AB,AC,AA 1 A AB,AC,AA 1 x,y,z 所以 ，所以 两两互相垂直.以点 为坐标原点， 分别为 轴，建立如 图空间直角坐标系，..........................................................................................................................................6分 A0,0,0 B1,0,0 C0,1,0 A 0,0,2 B 1,0,2 设 AC 1 ，则 ， ， ， 1 ， 1 ， (cid:3) (cid:3) (cid:3) (cid:3) AB1,0,0 BB 0,0,2 AB 1,0,0 AC 0,1,2 所以 ， 1 ， 1 1 ， 1 ，........................................................7分 因为  B  1  F (cid:3)   F (cid:3) B  0，所以  B  F (cid:3)   1 1  B  B (cid:3) 1     0,0,  2 1    ，则 3 原创精品资源学科网独家享有版权，侵权必究！ 学科网（北京）股份有限公司(cid:3) (cid:3) (cid:3)  2   2  AF  ABBF 1,0,00,0, 1,0,   1  1，.....................................................................................8分 (cid:3) nx,y,z ABC 设平面 1 1 的一个法向量为 ， (cid:3) (cid:3) 则    n (cid:3)   A  1(cid:3) B 1 0 ，即   x0 ，令 ，解得 ， ， nA 1 C 0 y2z0 z1 x0 y2 (cid:3) n0,2,1 所以 ，.............................................................................................................................................10分 (cid:3) (cid:3) 2 (cid:3) (cid:3) AFn 1 cosAF,n  (cid:3) (cid:3)  所以 与平面 所成角的正弦值为 AF n  2  2 ， 1   5 AF ABC 1 1 1 2 1 10    2  2 10 ，解得 或 ，............................................................................................11分 1   5 1 1 3 0，1...............................................................................................................................................12分 E D(1,0) x=1 20.【详解】（1）因为动圆 经过定点 ，且与直线 相切， E D(1,0) x=1 即动圆圆心 到点 的距离与到直线 的距离相等，...................................................................1分 又点D(1,0)不在直线x=1上， E D(1,0) x=1 由抛物线的定义可知动圆圆心 是以 为焦点，直线 为准线的抛物线，...............................3分 4 原创精品资源学科网独家享有版权，侵权必究！ 学科网（北京）股份有限公司E y2 4x 所以动圆圆心 的轨迹为 ....................................................................................................................4分 l yk(x1)2 k 0 （2）依题意设直线 1方程为 ， l l  直线 1， 2的斜率存在，且倾斜角互补， l yk(x1)2 2 的方程为 ． yk(x1)2  联立方程组y2 4x ，消元得k2x2(2k24k4)x(k2)2 0， Δ  2k24k4 2 4k2k22 16k12 0 ，.........................................................................................6分 Ax,y  Bx ,y  因为此方程的一个根为 1 ，设 1 1 ， 2 2 ， (k2)2 k24k4 k24k4 则x   ，同理可得x  ，................................................................................8分 1 k2 k2 2 k2 2k28 8k 8 x x  ， x x   ． 1 2 k2 1 2 k2 k 2k28 8 y 1 y 2 [k(x 1 1)2][k(x 2 1)2]k(x 1 x 2 )2k k 2k k ． y y k  1 2 1 AB x x ，..........................................................................................................................................10分 1 2 3π 设直线 的倾斜角为 ，则 ，又0,π，所以  ，......................................................11分 AB  tan1 4 3π 直线 的斜率为定值 ，倾斜角为定值 ．......................................................................................12分  AB 1 4 5 原创精品资源学科网独家享有版权，侵权必究！ 学科网（北京）股份有限公司f xxex2ax(a0) fxx1ex 2a 21.【详解】（1）因为 ，所以 ， f12e2a f 1e2a 则 ，又 ， f x ye2a2e2ax1 x1 所以函数 在 处的切线方程为 ．.........................................................2分 e x 由题意，显然 ，令 得 ，令 得 ， ae x0 ye y0 2e2a 1 e e S   e  所以函数 f x 在x1处的切线与坐标轴围成的三角形的面积为 2 2e2a 2， e 3e 所以 2e2a e，解得a 或 a ．.........................................................................................................4分 2 2 fxx1ex 2a gx fxx1ex2a(a0) （2）由（1）知 ，令 ， gxx2ex x<2 gx0,gx ,2 所以 ，当 时， 在 上单调递减， gx0 gx 2, x2 当 时， ， 在 上单调递增．..............................................................................6分 gxx1ex2a0 a0 x2 因为 ，所以当 时， ， g2a2a1e2a 2a2a12a10, 又 gx 2, x gx 0 所以 在 上必存在唯一零点 0，使得 0 ．....................................................................8分 xx gx0 fx0, f x ,x  当 0时， ，即 在 0 上单调递减， xx gx0 fx0, f x x , 当 0时， ，即 在 0 上单调递增． f x xx 所以 在 0处取得最小值， f(x)  f x x ex0 2ax fx 0 2ax 1ex0 即 min 0 0 0，且 0 ，即 0 ， f(x) x ex0 2ax x ex0 x 1ex0 x x2ex0 e 所以 min 0 0 0 0 0 0 ．...............................................................10分 6 原创精品资源学科网独家享有版权，侵权必究！ 学科网（北京）股份有限公司hxx2ex(x2) hxxx2ex 设 ，所以 ， 4 e3 当 x2,0时， hx0,hx单调递增，hxh2 e2  e2 e， x0, hx0 hx hxh00 当 时， ， 单调递减， ， h1e hx 2, x1 x2ex e 又 ，所以函数 在 上存在唯一的 ，使得 成立， 所以 x 0 1 ，所以 2ax 0 1ex0 2e ，即 ae ．........................................................................................12分 （二）选考题：共10分．请考生在22、23题中任选一题作答，如果多做，则按所做的第一题计分． 选修4-4：坐标系与参数方程 22.【详解】（1）因为曲线 的极坐标方程为 ，所以 ， 由 ，得曲线 的直角坐标方程为 ； 由曲线 的参数方程为 （ 为参数），又 ， 得 ，..........................................................................................................................................2分 因为 ，所以 ，即 ， 即曲线 的极坐标方程为 . 又点 在曲线 上，所以 ，解得 ， 所以曲线 的极坐标方程为 ；.................................................................................................4分 （2）因为点 ，则 ，即点 的直角坐标为 ，.................................5分 7 原创精品资源学科网独家享有版权，侵权必究！ 学科网（北京）股份有限公司由（1）得曲线 的直角坐标方程为 ， 联立 ，解得 或 ，所以 ， 联立 ，解得 或 ，所以 ，...........................................................8分 则 ， 点 到直线 的距离 ，................................................................9分 所以 .........................................................................................................................10分 选修4-5：不等式选讲 23.【详解】（1）当 时， 可化为 .................................................................1分 当 时， ，解得 ； 当 时， ，解得 ； 当 时， ，解得 ................................................................................................4分 故当 时，不等式 的解集为 .......................................................................................5分 （2）因为 ， 8 原创精品资源学科网独家享有版权，侵权必究！ 学科网（北京）股份有限公司所以 等价于 ........................................................................................7分 因为 ，当且仅当 时取等号，....................................8分 所以 的最小值为 ，所以 ， 解得 或 ， 故 的取值范围是 ..............................................................................................................10分 9 原创精品资源学科网独家享有版权，侵权必究！ 学科网（北京）股份有限公司