文档内容
2024年高考押题预测卷01
数学·全解全析
一、单选题
1.已知集合 , , ,则实数 的值为( )
A.2 B. 或2 C.1或2 D.0或2
【答案】A
【解析】由 ,得 ,即 ,此时 ,
由 ,得 ,而 ,所以 .故选:A
2.双曲线 的渐近线方程为 ,则 ( )
A. B. C. D.2
【答案】D
【解析】由题意可得 ,又 ,故 .故选:D.
3.已知 , ,若 ,则 ( )
A. B. C.1 D.
【答案】C
【解析】 ,由 得 ,解得 .故选:C.
4.已知 是奇函数,则 ( )
A. B.0 C.1 D.2
【答案】B
【解析】易知 ,且定义域为R,若其为奇函数,
则 ,故 ,经检验成立.故选:B
5.某小组两名男生和两名女生邀请一名老师排成一排合影留念,要求两名男生不相邻,两名女生也不相
邻,老师不站在两端,则不同的排法共有( )
A.8种 B.16种 C.24种 D.32种
1
原创精品资源学科网独家享有版权,侵权必究!
学学学科科科网网网(((北北北京京京)))股股股份份份有有有限限限公公公司司司【答案】D
【解析】当老师从左到右排在第二或第四位时,共有 种排法,
当老师从左到右排在第三位时,共有 种排法,
于是共有 种排法.故选:D.
6.记数列 的前 项和为 ,已知 , 为等差数列,若 ,则 ( )
A. B. C.2 D.
【答案】B
【解析】 ,故 ,
所以数列 是首项为2,公差为1的等差数列,
所以 ,故 ,
所以当 时, ,所以 ,故选:B.
7.已知 的内角A, , 对边分别为 , , ,满足 ,若 ,
则 面积的最大值为( )
A. B. C. D.
【答案】C
【解析】由 ,
由正弦定理得 ,
又 ,且 ,
所以 ,故 ,
又 ,所以 ,
由 ,即 ,得 ,
2
原创精品资源学科网独家享有版权,侵权必究!
学学学科科科网网网(((北北北京京京)))股股股份份份有有有限限限公公公司司司面积的最大值为 ,故选:C.
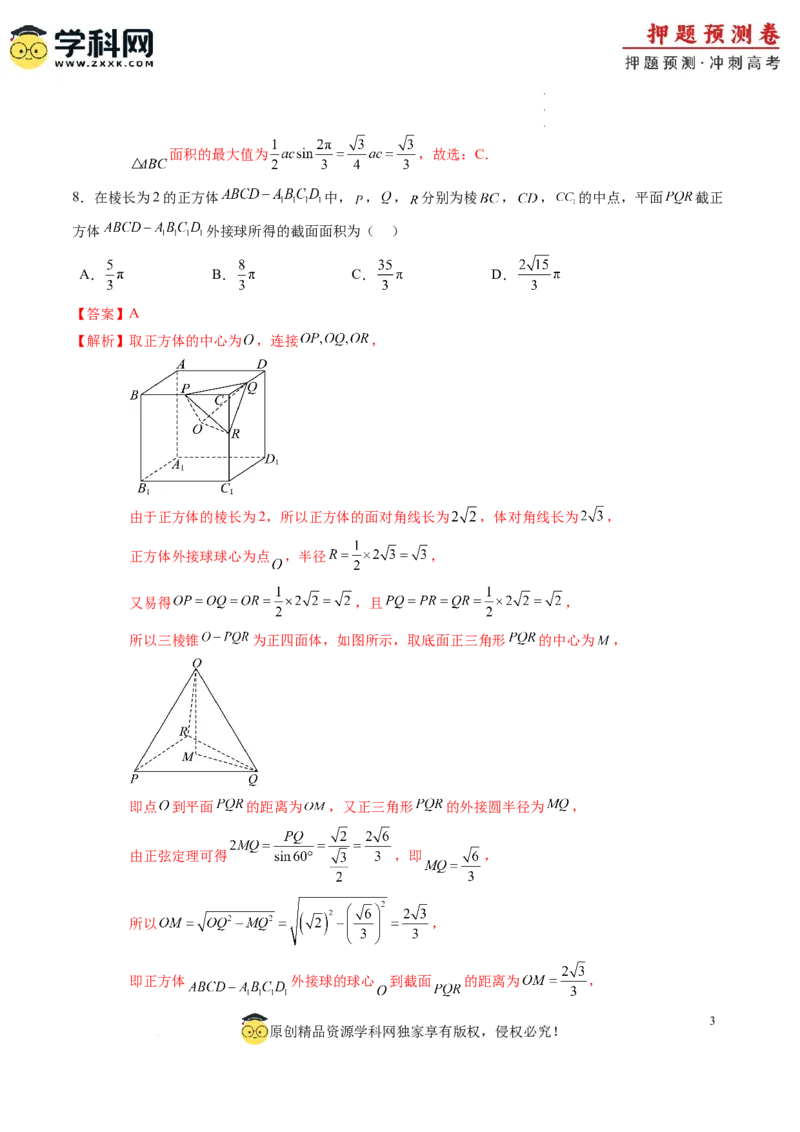
8.在棱长为2的正方体 中, , , 分别为棱 , , 的中点,平面 截正
方体 外接球所得的截面面积为( )
A. B. C. D.
【答案】A
【解析】取正方体的中心为 ,连接 ,
由于正方体的棱长为2,所以正方体的面对角线长为 ,体对角线长为 ,
正方体外接球球心为点 ,半径 ,
又易得 ,且 ,
所以三棱锥 为正四面体,如图所示,取底面正三角形 的中心为 ,
即点 到平面 的距离为 ,又正三角形 的外接圆半径为 ,
由正弦定理可得 ,即 ,
所以 ,
即正方体 外接球的球心 到截面 的距离为 ,
3
原创精品资源学科网独家享有版权,侵权必究!
学学学科科科网网网(((北北北京京京)))股股股份份份有有有限限限公公公司司司所以截面 被球 所截圆的半径 ,
则截面圆的面积为 .故选:A.
二、选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求.全部
选对的得6分,部分选对的得部分分,有选错的得0分.
9.已知i是虚数单位,下列说法正确的是( )
A.已知 ,若 ,则
B.复数 满足 ,则
C.复数z满足 ,则z在复平面内对应的点的轨迹为一条直线
D.复数z满足 ,则
【答案】BCD
【解析】对A,虚数不能比较大小,可知A错误;
对B,根据共轭复数的定义知,当 时, ,则 ,故B正确;
对C,因为复数z满足 ,
则复数 在复平面上对应的点到 两点间的距离相等,
则复数 在复平面上对应的点为两点构成线段的中垂线,
即 在复平面内对应的点的轨迹为一条直线,故C正确;
因为 ,则 ,
又 ,故D正确,故选:BCD.
10.已知函数 , , 为 的两个相邻的对称中心,则
( )
A. 的最小正周期为
B. 的最大值为1
4
原创精品资源学科网独家享有版权,侵权必究!
学学学科科科网网网(((北北北京京京)))股股股份份份有有有限限限公公公司司司C.直线 是曲线 的一条对称轴
D.将 的图象向右平移 个单位长度,所得图象关于原点对称
【答案】AC
【解析】依题意, ,所以 , ,A选项正确;
由 ,即 ,又 ,得 ,
所以 的对称中心为 ,所以 ,
的最大值为2,B选项错误;
当 时, , 是正弦曲线的一条对称轴,
所以直线 是曲线 的一条对称轴,C选项正确;
将 的图象向右平移 个单位长度所得函数为 ,
图象关于 对称,D选项错误.故选:AC.
11.已知函数 的定义域和值域均为 ,对于任意非零实数 ,函数 满足:
,且 在 上单调递减, ,则下列结论错误的是
( )
A. B.
C. 在定义域内单调递减 D. 为奇函数
【答案】BC
【解析】对于 ,令 ,则 ,
因 ,故得 ,故A正确;
对于 由 ,
令 ,则 ,
5
原创精品资源学科网独家享有版权,侵权必究!
学学学科科科网网网(((北北北京京京)))股股股份份份有有有限限限公公公司司司则 ,即 ,
故 是以 为首项,2为公比的等比数列,
于是 ,故B错误;
对于 ,由题意,函数 的定义域为 ,关于原点对称,
令 ,则 ①,
把 都取成 ,可得 ②,
将②式代入①式,可得 ,
化简可得 即 为奇函数,故D正确;
对于C, 在 上单调递减,函数为奇函数,可得 在 上单调递减,
但是不能判断 在定义域上的单调性,例如 ,故C错误.故选:BC.
第二部分(非选择题 共92分)
三、填空题:本题共3小题,每小题5分,共15分。
12. 的展开式中 的系数为 .
【答案】40
【解析】因为 ,
又 展开式的通项为 ( 且 ),
所以 的展开式中含 的项为 ,
故展开式中 的系数为 .
13.已知抛物线 的焦点分别为 ,点 分别在( 上,且线段 平行于x
轴.若 是等腰三角形,则 .
6
原创精品资源学科网独家享有版权,侵权必究!
学学学科科科网网网(((北北北京京京)))股股股份份份有有有限限限公公公司司司【答案】
【解析】设 , , .
不妨设 ,然后分三种情况讨论:
若 ,则有 ,解得 ,此时 ;
若 ,则 ,解得 ,这不可能;
若 ,则 ,这同样不可能.
综上, .
14.已知 为实数,若不等式 对任意 恒成立,则 的最
大值是 .
【答案】6
【解析】因为 ,所以 ,
则不等式 等价于 ,
等价于 ,令 ,则 ,
从而 ,令 ,由对勾函数的性质知 ,
因为 ,即 ,所以 ,
7
原创精品资源学科网独家享有版权,侵权必究!
学学学科科科网网网(((北北北京京京)))股股股份份份有有有限限限公公公司司司令 ,则 ,解得 ,
所以 ,
当且仅当 即 时取等号,
故 的最大值是6.
四、解答题:本题共5小题,共77分。解答应写出文字说明、证明过程或演算步棸。
15.(13分)不透明的袋子中装有3个黑球,2个红球,1个白球,从中任意取出2个球,再放入1个红球
和1个白球.
(1)求取球放球结束后袋子里白球的个数为2的概率;
(2)设取球放球结束后袋子里红球的个数为随机变量 ,求 的分布列以及数学期望.
【答案】(1) ;(2)分布列见解析,
【解析】(1)设事件A为“取球放球结束后袋子里白球的个数为2”,
设事件 为“取出2个黑球”,则 ,
事件 为“取出2个红球”,则 ,
事件 为“取出1个红球1个黑球”,则 ,
因为事件B,C,D互斥,且 ,则 ,
所以取球放球结束后袋子里白球的个数为2的概率为 .
(2)由题意可知:随机变量 的可能取值为1,2,3,则有:
, , ,
所以X的分布列为:
X 1 2 3
P
所以 .
8
原创精品资源学科网独家享有版权,侵权必究!
学学学科科科网网网(((北北北京京京)))股股股份份份有有有限限限公公公司司司16.(15分)已知函数 .
(1)当 时,求曲线 在点 处的切线方程;
(2)当 时,若函数 有最小值2,求 的值.
【答案】(1) ;(2)
【解析】(1)当 时, 的定义域为 ,
则 ,则 ,
由于函数 在点 处切线方程为 ,即 .
(2) 的定义域为 ,
,
当 时,令 ,解得: ;令 ,解得: ,
所以 在 上单调递减,在 上单调递增,
所以, ,即
则令 ,设 ,
令 ,解得: ;令 ,解得: ,
所以 在 上单调递增,在 上单调递减,
所以 ,
所以 ,解得: .
17.(15分)如图,在四棱锥 中,底面 是边长为 的正方形.
9
原创精品资源学科网独家享有版权,侵权必究!
学学学科科科网网网(((北北北京京京)))股股股份份份有有有限限限公公公司司司(1)若直线 是平面 和平面 的交线,证明: ;
(2)若四棱锥 的体积为 ,二面角 和二面角 都是 ,求直线 与平面
所成角的正弦值.
【答案】(1)证明见解析;(2)
【解析】(1)∵正方形 , ,
平面 , 平面 , 平面 ,
又 平面 ,直线 是平面 和平面 的交线, ;
(2)如图,过点 作平面 的垂线,垂足为 ,过点 作 ,垂足为 ,连接 ,
因为二面角 和二面角 都是 ,
可知点 在正方形 内,
四棱锥 的体积为 ,即 ,可得 ,
因为 平面 , 平面 ,所以 ,
因为 , , 平面 ,
所以 平面 ,所以 为二面角 的平面角,
可得 ,可得 ,同理可得点 到 的距离为 ,
以 为坐标原点,向量 ,与平面 垂直的方向分别为 轴
建立如图所示的空间直角坐标系,
则 ,
可得 .
设平面 的法向量为
有 取 ,可得
所以 , ,
1
原创精品资源学科网独家享有版权,侵权必究!
0
学学学科科科网网网(((北北北京京京)))股股股份份份有有有限限限公公公司司司所以 ,
所以直线 与平面 所成角的正弦值为 .
18.(17分)已知椭圆 的左、右焦点分别为 ,上、下顶点分别为 ,且
, 的面积为 .
(1)求 的方程;
(2)已知 为直线 上任一点,设直线 与 的另一个公共点分别为 .问:直线 是否
过一定点?若过定点,求出该定点的坐标;若不过定点,试说明理由.
【答案】(1) ;(2)过定点
【解析】(1)因 ,则由 可得 ,即 ,①
又 的面积为 ,② ,③
由①②③联立,可解得 ,
故 的方程为 .
(2)如图,
依题意,直线 的斜率一定存在,不妨设 , ,则 ,
将其与椭圆方程 联立,消去 ,整理得: ,
则点 的横坐标为 ,
1
原创精品资源学科网独家享有版权,侵权必究!
1
学学学科科科网网网(((北北北京京京)))股股股份份份有有有限限限公公公司司司代入直线方程,求得 ;
同理,直线 的斜率一定存在,则 ,
将其与椭圆方程 联立,消去 ,整理得: ,
则点 的横坐标为 ,代入直线方程,求得 ;
则直线 的方程为: ,
整理得: ,
化简为 ,
展开得: ,
移项合并得 ,故直线 一定经过点 .
19.(17分)已知数列 为有穷正整数数列.若数列A满足如下两个性质,则称数列A为m的k
减数列:
① ;
②对于 ,使得 的正整数对 有k个.
(1)写出所有4的1减数列;
(2)若存在m的6减数列,证明: ;
(3)若存在2024的k减数列,求k的最大值.
【答案】(1)数列 和数列3,1;(2)证明见解析;(3) 的最大值为512072
【解析】(1)由题意得 ,则 或 ,
故所有4的1减数列有数列 和数列3,1.
(2)因为对于 ,使得 的正整数对 有 个,
且存在 的6减数列,所以 ,得 .
①当 时,因为存在 的6减数列,
1
原创精品资源学科网独家享有版权,侵权必究!
2
学学学科科科网网网(((北北北京京京)))股股股份份份有有有限限限公公公司司司所以数列中各项均不相同,所以 .
②当 时,因为存在 的6减数列,
所以数列各项中必有不同的项,所以 .
若 ,满足要求的数列中有四项为1,一项为2,
所以 ,不符合题意,所以 .
③当 时,因为存在 的6减数列,
所以数列各项中必有不同的项,所以 .
综上所述,若存在 的6减数列,则 .
(3)若数列中的每一项都相等,则 ,
若 ,所以数列 存在大于1的项,
若末项 ,将 拆分成 个1后 变大,
所以此时 不是最大值,所以 .
当 时,若 ,交换 的顺序后 变为 ,
所以此时 不是最大值,所以 .
若 ,所以 ,
所以将 改为 ,并在数列末尾添加一项1,所以 变大,
所以此时 不是最大值,所以 .
若数列A中存在相邻的两项 ,设此时 中有 项为2,
将 改为2,并在数列末尾添加 项1后, 的值至少变为 ,
所以此时 不是最大值,
所以数列 的各项只能为2或1,所以数列 为 的形式.
设其中有 项为2,有 项为1,
因为存在2024的 减数列,所以 ,
所以 ,
所以,当且仅当 时, 取最大值为512072.
所以,若存在2024的 减数列, 的最大值为512072.
1
原创精品资源学科网独家享有版权,侵权必究!
3
学学学科科科网网网(((北北北京京京)))股股股份份份有有有限限限公公公司司司