文档内容
2019年内蒙古通辽市中考数学试卷
一、选择题(本题包括10小题,每小题3分,共30分,每小题只有一个正确答案,请在答题卡
上将代表正确答案的字母用2B铅笔涂黑)
1.(3分)﹣的相反数是( )
A.2019 B.﹣ C.﹣2019 D.
2.(3分) 的平方根是( )
A.±4 B.4 C.±2 D.+2
3.(3分)2018年12月,在国家发展改革委发布《关于全力做好2019年春运工作的意见》中
预测,2019年春运全国民航旅客发送量将达到7300万人次,比上一年增长12%,其中7300
万用科学记数法表示为( )
A.73×106 B.7.3×103 C.7.3×107 D.0.73×108
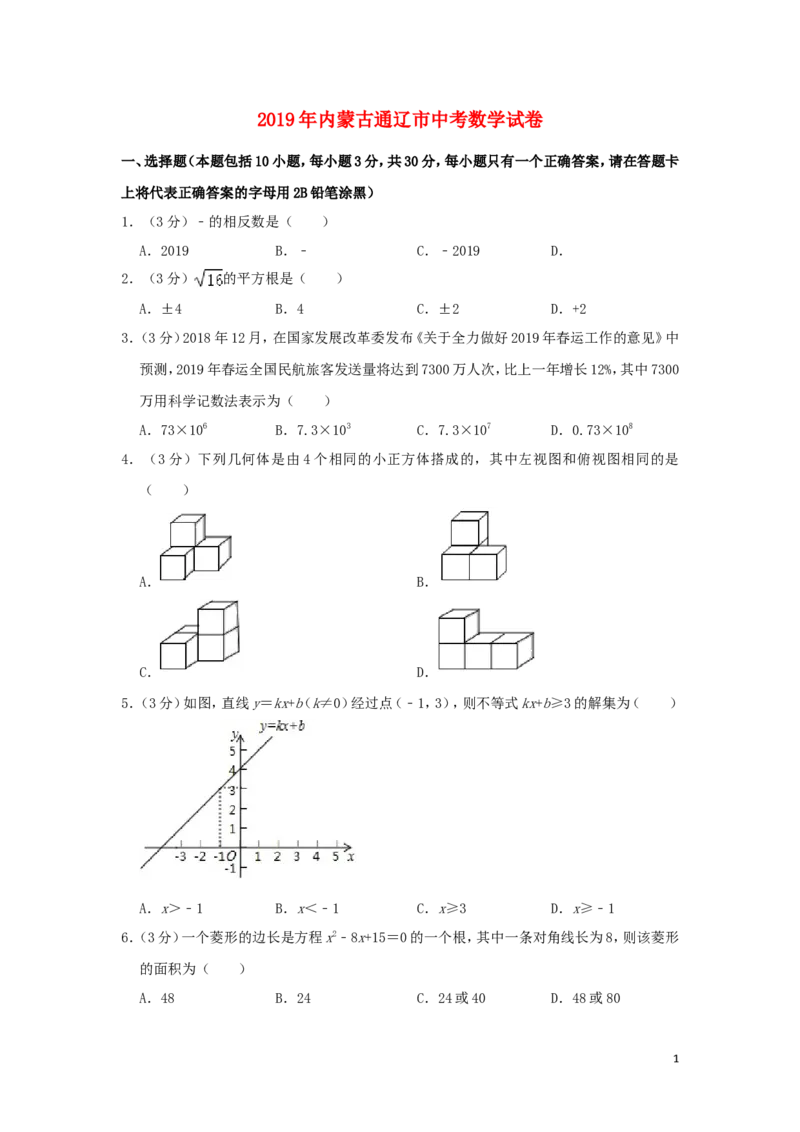
4.(3分)下列几何体是由4个相同的小正方体搭成的,其中左视图和俯视图相同的是
( )
A. B.
C. D.
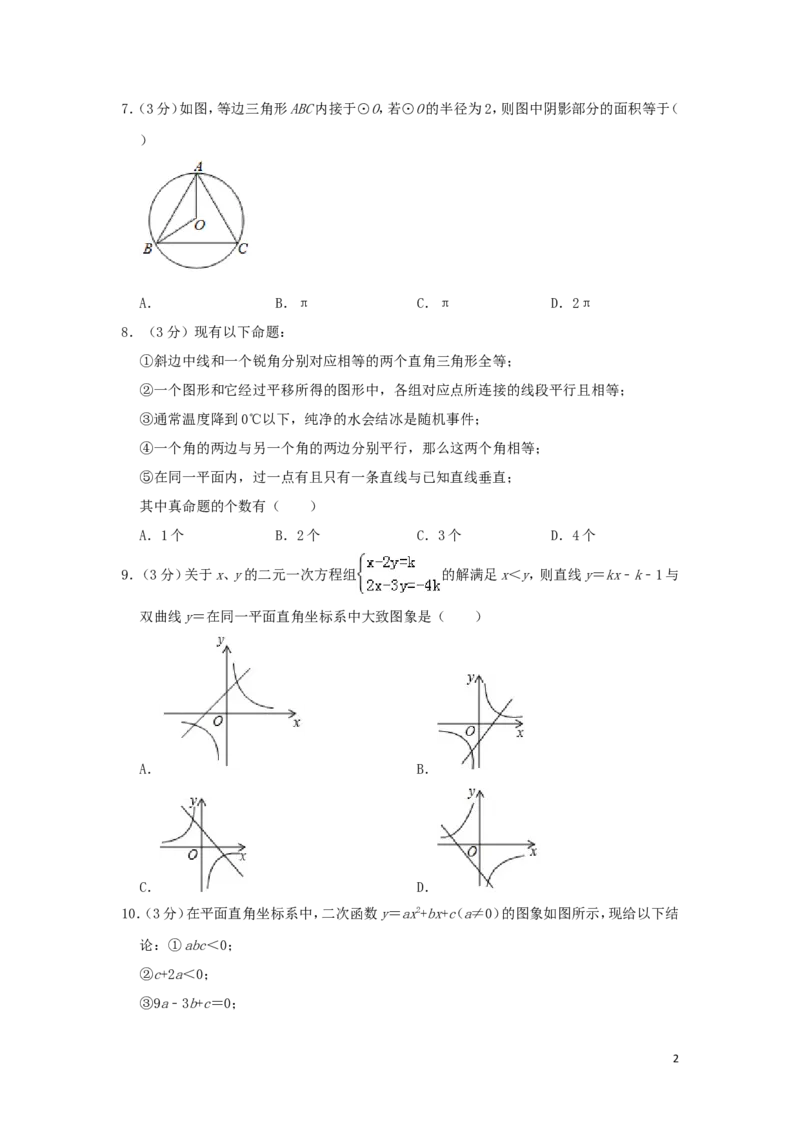
5.(3分)如图,直线y=kx+b(k≠0)经过点(﹣1,3),则不等式kx+b≥3的解集为( )
A.x>﹣1 B.x<﹣1 C.x≥3 D.x≥﹣1
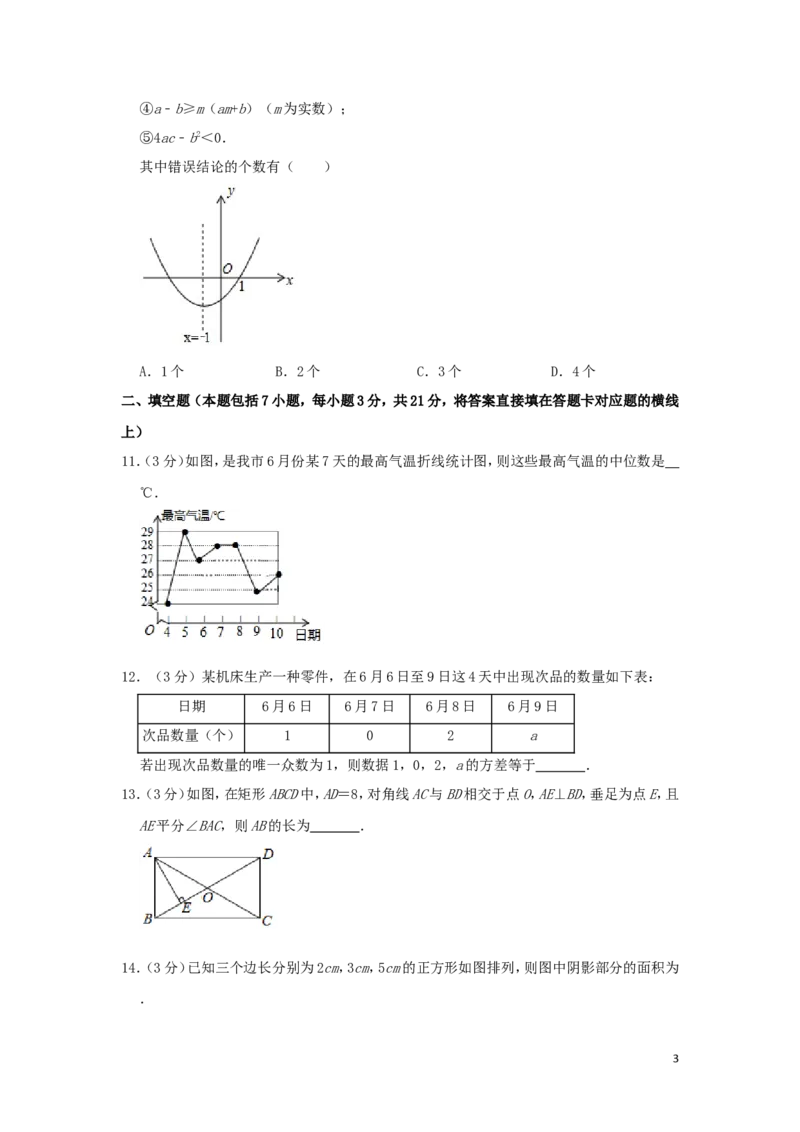
6.(3分)一个菱形的边长是方程x2﹣8x+15=0的一个根,其中一条对角线长为8,则该菱形
的面积为( )
A.48 B.24 C.24或40 D.48或80
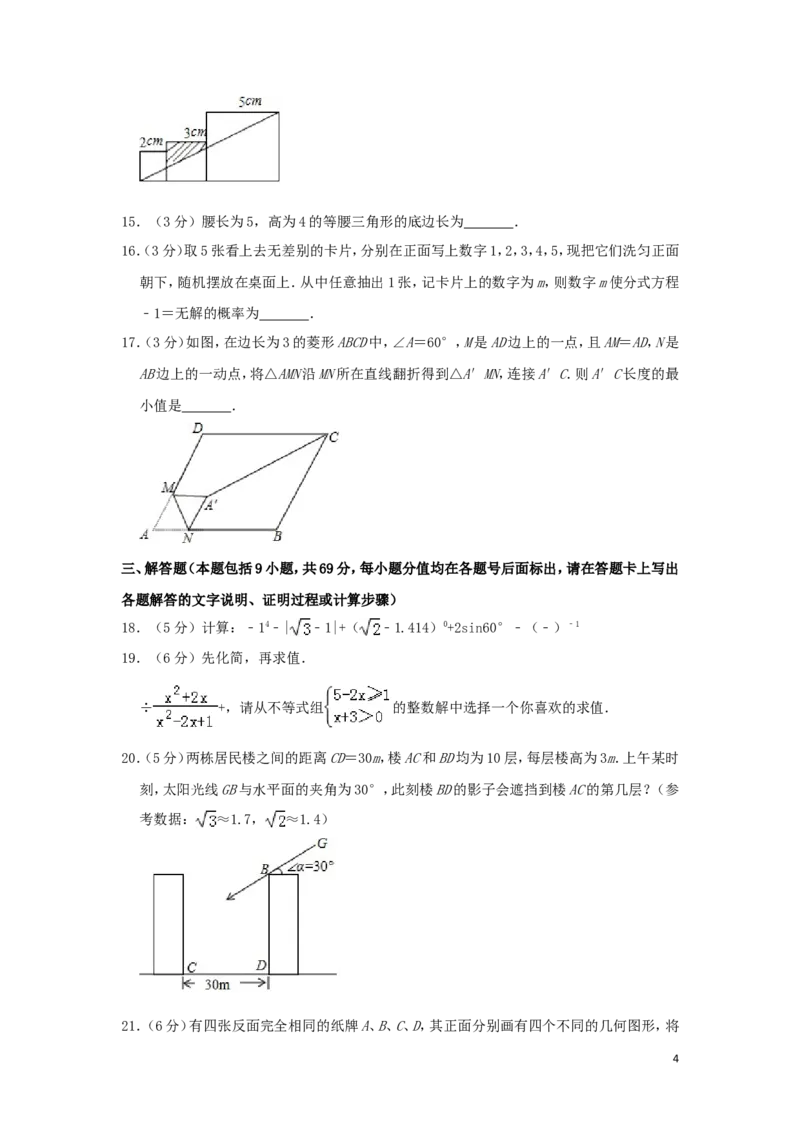
17.(3分)如图,等边三角形ABC内接于⊙O,若⊙O的半径为2,则图中阴影部分的面积等于(
)
A. B.π C.π D.2π
8.(3分)现有以下命题:
①斜边中线和一个锐角分别对应相等的两个直角三角形全等;
②一个图形和它经过平移所得的图形中,各组对应点所连接的线段平行且相等;
③通常温度降到0℃以下,纯净的水会结冰是随机事件;
④一个角的两边与另一个角的两边分别平行,那么这两个角相等;
⑤在同一平面内,过一点有且只有一条直线与已知直线垂直;
其中真命题的个数有( )
A.1个 B.2个 C.3个 D.4个
9.(3分)关于x、y的二元一次方程组 的解满足x<y,则直线y=kx﹣k﹣1与
双曲线y=在同一平面直角坐标系中大致图象是( )
A. B.
C. D.
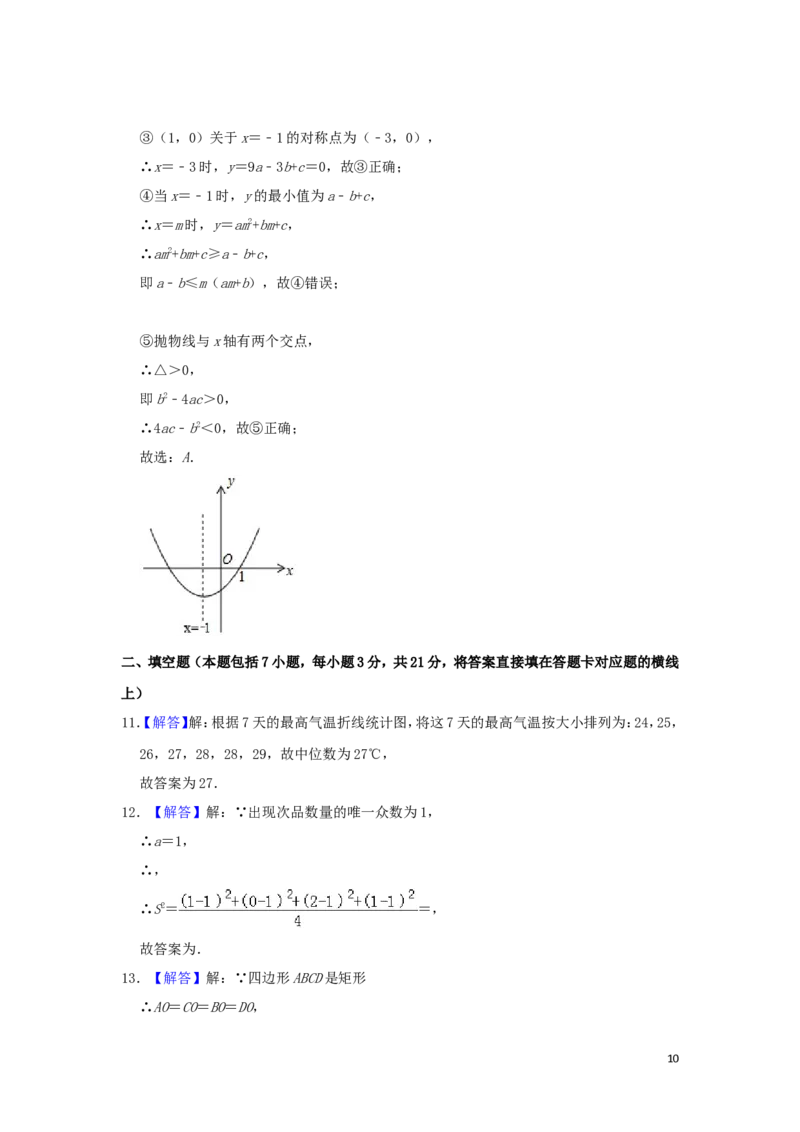
10.(3分)在平面直角坐标系中,二次函数y=ax2+bx+c(a≠0)的图象如图所示,现给以下结
论:①abc<0;
②c+2a<0;
③9a﹣3b+c=0;
2④a﹣b≥m(am+b)(m为实数);
⑤4ac﹣b2<0.
其中错误结论的个数有( )
A.1个 B.2个 C.3个 D.4个
二、填空题(本题包括7小题,每小题3分,共21分,将答案直接填在答题卡对应题的横线
上)
11.(3分)如图,是我市6月份某7天的最高气温折线统计图,则这些最高气温的中位数是
℃.
12.(3分)某机床生产一种零件,在6月6日至9日这4天中出现次品的数量如下表:
日期 6月6日 6月7日 6月8日 6月9日
次品数量(个) 1 0 2 a
若出现次品数量的唯一众数为1,则数据1,0,2,a的方差等于 .
13.(3分)如图,在矩形ABCD中,AD=8,对角线AC与BD相交于点O,AE⊥BD,垂足为点E,且
AE平分∠BAC,则AB的长为 .
14.(3分)已知三个边长分别为2cm,3cm,5cm的正方形如图排列,则图中阴影部分的面积为
.
315.(3分)腰长为5,高为4的等腰三角形的底边长为 .
16.(3分)取5张看上去无差别的卡片,分别在正面写上数字1,2,3,4,5,现把它们洗匀正面
朝下,随机摆放在桌面上.从中任意抽出1张,记卡片上的数字为m,则数字m使分式方程
﹣1=无解的概率为 .
17.(3分)如图,在边长为3的菱形ABCD中,∠A=60°,M是AD边上的一点,且AM=AD,N是
AB边上的一动点,将△AMN沿MN所在直线翻折得到△A′MN,连接A′C.则A′C长度的最
小值是 .
三、解答题(本题包括9小题,共69分,每小题分值均在各题号后面标出,请在答题卡上写出
各题解答的文字说明、证明过程或计算步骤)
18.(5分)计算:﹣14﹣| ﹣1|+( ﹣1.414)0+2sin60°﹣(﹣)﹣1
19.(6分)先化简,再求值.
÷ +,请从不等式组 的整数解中选择一个你喜欢的求值.
20.(5分)两栋居民楼之间的距离CD=30m,楼AC和BD均为10层,每层楼高为3m.上午某时
刻,太阳光线GB与水平面的夹角为30°,此刻楼BD的影子会遮挡到楼AC的第几层?(参
考数据: ≈1.7, ≈1.4)
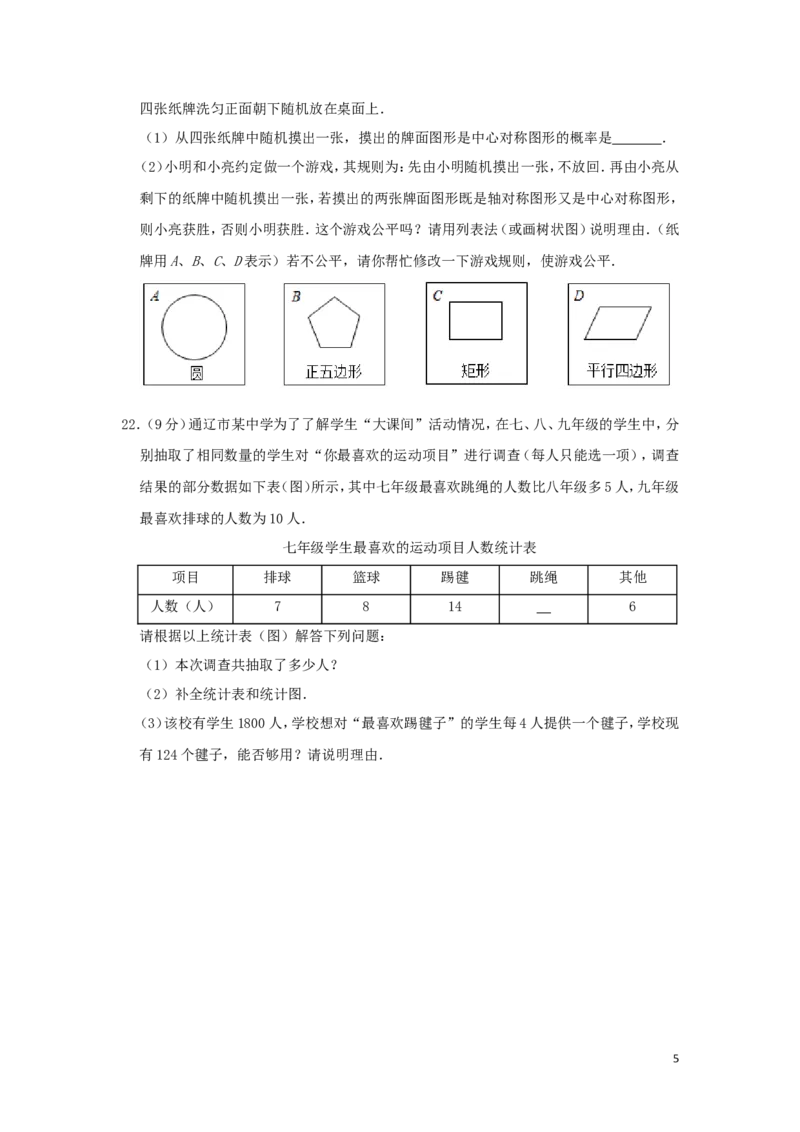
21.(6分)有四张反面完全相同的纸牌A、B、C、D,其正面分别画有四个不同的几何图形,将
4四张纸牌洗匀正面朝下随机放在桌面上.
(1)从四张纸牌中随机摸出一张,摸出的牌面图形是中心对称图形的概率是 .
(2)小明和小亮约定做一个游戏,其规则为:先由小明随机摸出一张,不放回.再由小亮从
剩下的纸牌中随机摸出一张,若摸出的两张牌面图形既是轴对称图形又是中心对称图形,
则小亮获胜,否则小明获胜.这个游戏公平吗?请用列表法(或画树状图)说明理由.(纸
牌用A、B、C、D表示)若不公平,请你帮忙修改一下游戏规则,使游戏公平.
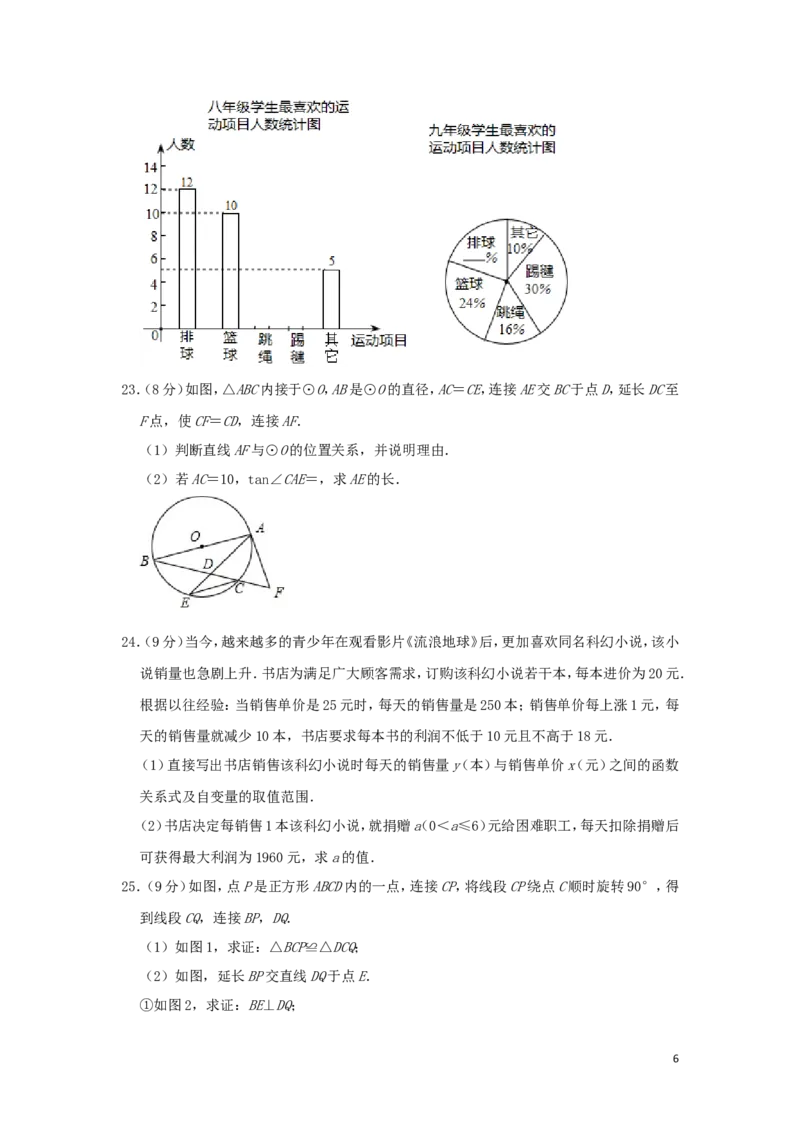
22.(9分)通辽市某中学为了了解学生“大课间”活动情况,在七、八、九年级的学生中,分
别抽取了相同数量的学生对“你最喜欢的运动项目”进行调查(每人只能选一项),调查
结果的部分数据如下表(图)所示,其中七年级最喜欢跳绳的人数比八年级多5人,九年级
最喜欢排球的人数为10人.
七年级学生最喜欢的运动项目人数统计表
项目 排球 篮球 踢毽 跳绳 其他
人数(人) 7 8 14 6
请根据以上统计表(图)解答下列问题:
(1)本次调查共抽取了多少人?
(2)补全统计表和统计图.
(3)该校有学生1800人,学校想对“最喜欢踢毽子”的学生每4人提供一个毽子,学校现
有124个毽子,能否够用?请说明理由.
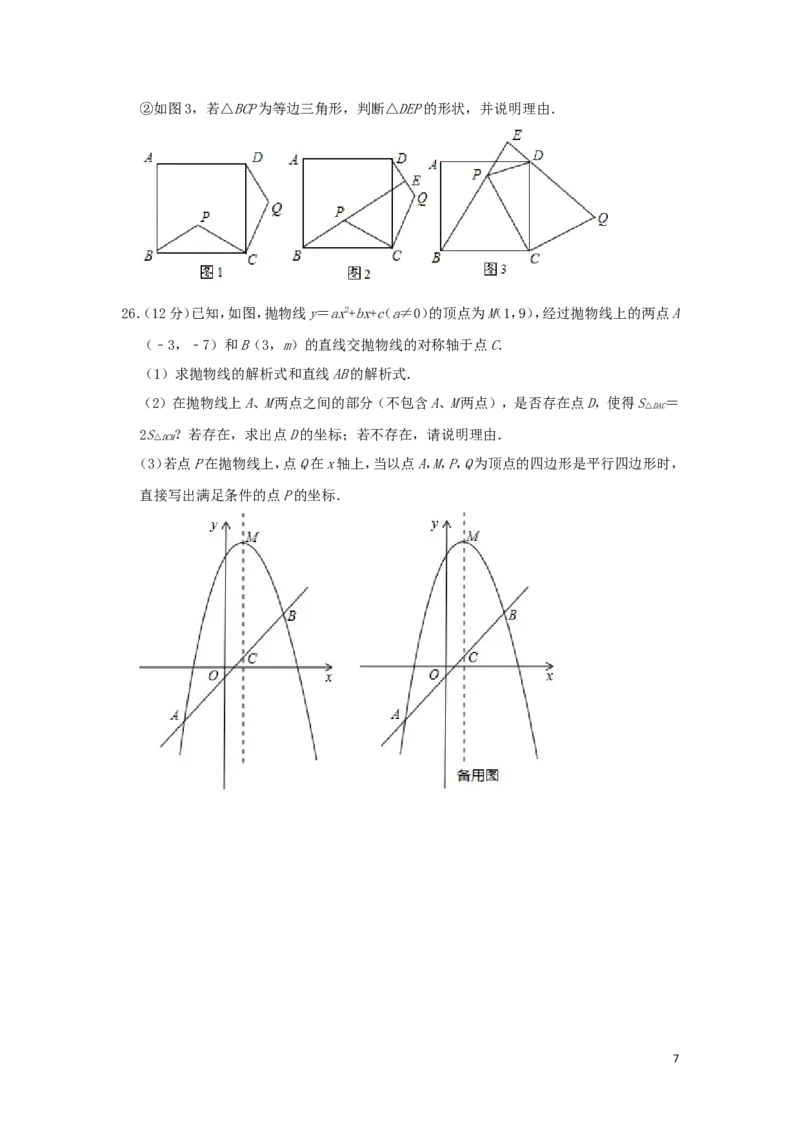
523.(8分)如图,△ABC内接于⊙O,AB是⊙O的直径,AC=CE,连接AE交BC于点D,延长DC至
F点,使CF=CD,连接AF.
(1)判断直线AF与⊙O的位置关系,并说明理由.
(2)若AC=10,tan∠CAE=,求AE的长.
24.(9分)当今,越来越多的青少年在观看影片《流浪地球》后,更加喜欢同名科幻小说,该小
说销量也急剧上升.书店为满足广大顾客需求,订购该科幻小说若干本,每本进价为20元.
根据以往经验:当销售单价是25元时,每天的销售量是250本;销售单价每上涨1元,每
天的销售量就减少10本,书店要求每本书的利润不低于10元且不高于18元.
(1)直接写出书店销售该科幻小说时每天的销售量y(本)与销售单价x(元)之间的函数
关系式及自变量的取值范围.
(2)书店决定每销售1本该科幻小说,就捐赠a(0<a≤6)元给困难职工,每天扣除捐赠后
可获得最大利润为1960元,求a的值.
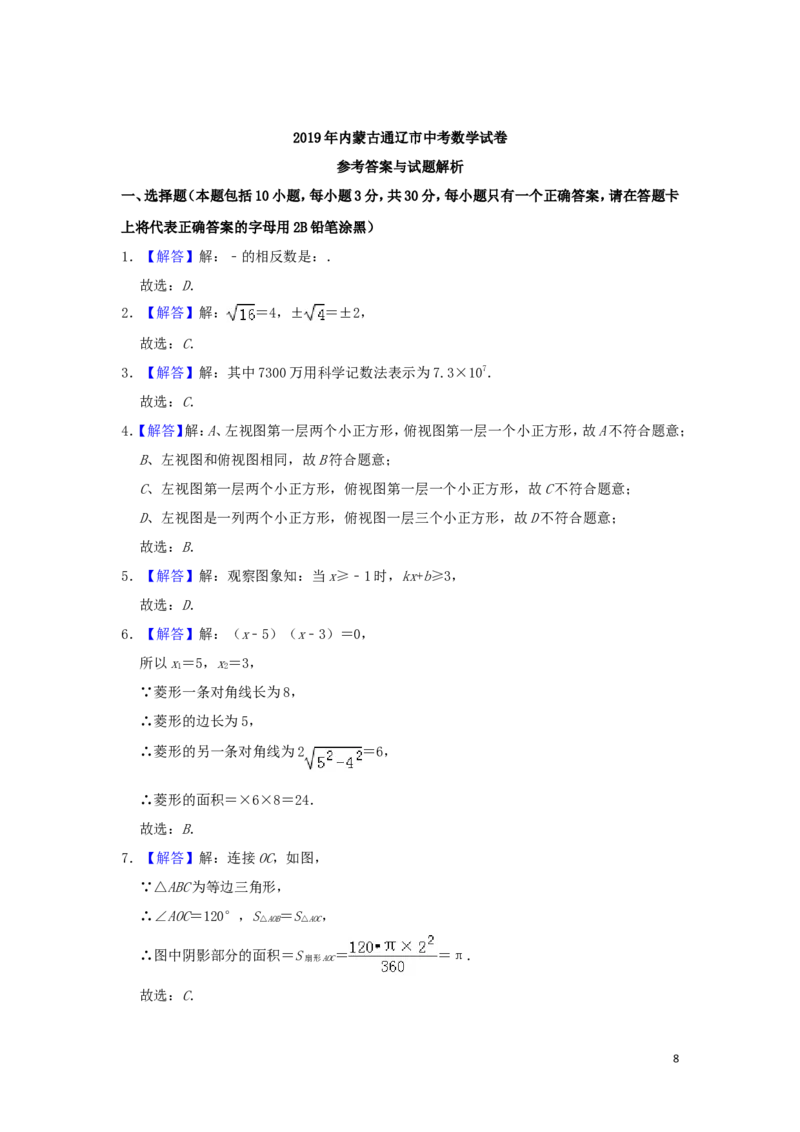
25.(9分)如图,点P是正方形ABCD内的一点,连接CP,将线段CP绕点C顺时旋转90°,得
到线段CQ,连接BP,DQ.
(1)如图1,求证:△BCP≌△DCQ;
(2)如图,延长BP交直线DQ于点E.
①如图2,求证:BE⊥DQ;
6②如图3,若△BCP为等边三角形,判断△DEP的形状,并说明理由.
26.(12分)已知,如图,抛物线y=ax2+bx+c(a≠0)的顶点为M(1,9),经过抛物线上的两点A
(﹣3,﹣7)和B(3,m)的直线交抛物线的对称轴于点C.
(1)求抛物线的解析式和直线AB的解析式.
(2)在抛物线上A、M两点之间的部分(不包含A、M两点),是否存在点D,使得S =
△DAC
2S ?若存在,求出点D的坐标;若不存在,请说明理由.
△DCM
(3)若点P在抛物线上,点Q在x轴上,当以点A,M,P,Q为顶点的四边形是平行四边形时,
直接写出满足条件的点P的坐标.
72019年内蒙古通辽市中考数学试卷
参考答案与试题解析
一、选择题(本题包括10小题,每小题3分,共30分,每小题只有一个正确答案,请在答题卡
上将代表正确答案的字母用2B铅笔涂黑)
1.【解答】解:﹣的相反数是:.
故选:D.
2.【解答】解: =4,± =±2,
故选:C.
3.【解答】解:其中7300万用科学记数法表示为7.3×107.
故选:C.
4.【解答】解:A、左视图第一层两个小正方形,俯视图第一层一个小正方形,故A不符合题意;
B、左视图和俯视图相同,故B符合题意;
C、左视图第一层两个小正方形,俯视图第一层一个小正方形,故C不符合题意;
D、左视图是一列两个小正方形,俯视图一层三个小正方形,故D不符合题意;
故选:B.
5.【解答】解:观察图象知:当x≥﹣1时,kx+b≥3,
故选:D.
6.【解答】解:(x﹣5)(x﹣3)=0,
所以x=5,x=3,
1 2
∵菱形一条对角线长为8,
∴菱形的边长为5,
∴菱形的另一条对角线为2 =6,
∴菱形的面积=×6×8=24.
故选:B.
7.【解答】解:连接OC,如图,
∵△ABC为等边三角形,
∴∠AOC=120°,S =S ,
△AOB △AOC
∴图中阴影部分的面积=S = =π.
扇形AOC
故选:C.
88.【解答】解:①斜边中线和一个锐角分别对应相等的两个直角三角形全等,正确,是真命题;
②一个图形和它经过平移所得的图形中,各组对应点所连接的线段平行且相等或在同一
直线上,错误,是假命题;
③通常温度降到0℃以下,纯净的水会结冰是必然事件,故错误,是假命题;
④一个角的两边与另一个角的两边分别平行,那么这两个角相等或互补,故错误,是假命
题;
⑤在同一平面内,过一点有且只有一条直线与已知直线垂直,正确,是真命题;
真命题有2个,
故选:B.
9.【解答】解:二元一次方程组 中第二个方程减去第一个方程得:x﹣y=﹣5k,
∵关于x、y的二元一次方程组 的解满足x<y,
∴x﹣y<0,
∴﹣5k<0,
即:k>0,
∴y=kx﹣k﹣1经过一三四象限,双曲线y=的两个分支位于一三象限,B选项符合,
故选:B.
10.【解答】解:①由抛物线可知:a>0,c<0,
对称轴x=﹣<0,
∴b>0,
∴abc<0,故①正确;
②由对称轴可知:﹣=﹣1,
∴b=2a,
∵x=1时,y=a+b+c=0,
∴c+3a=0,
∴c+2a=﹣3a+2a=﹣a<0,故②正确;
9③(1,0)关于x=﹣1的对称点为(﹣3,0),
∴x=﹣3时,y=9a﹣3b+c=0,故③正确;
④当x=﹣1时,y的最小值为a﹣b+c,
∴x=m时,y=am2+bm+c,
∴am2+bm+c≥a﹣b+c,
即a﹣b≤m(am+b),故④错误;
⑤抛物线与x轴有两个交点,
∴△>0,
即b2﹣4ac>0,
∴4ac﹣b2<0,故⑤正确;
故选:A.
二、填空题(本题包括7小题,每小题3分,共21分,将答案直接填在答题卡对应题的横线
上)
11.【解答】解:根据7天的最高气温折线统计图,将这7天的最高气温按大小排列为:24,25,
26,27,28,28,29,故中位数为27℃,
故答案为27.
12.【解答】解:∵出现次品数量的唯一众数为1,
∴a=1,
∴,
∴S2= =,
故答案为.
13.【解答】解:∵四边形ABCD是矩形
∴AO=CO=BO=DO,
10∵AE平分∠BAO
∴∠BAE=∠EAO,且AE=AE,∠AEB=∠AEO,
∴△ABE≌△AOE(ASA)
∴AO=AB,且AO=OB
∴AO=AB=BO=DO,
∴BD=2AB,
∵AD2+AB2=BD2,
∴64+AB2=4AB2,
∴AB=
故答案为:.
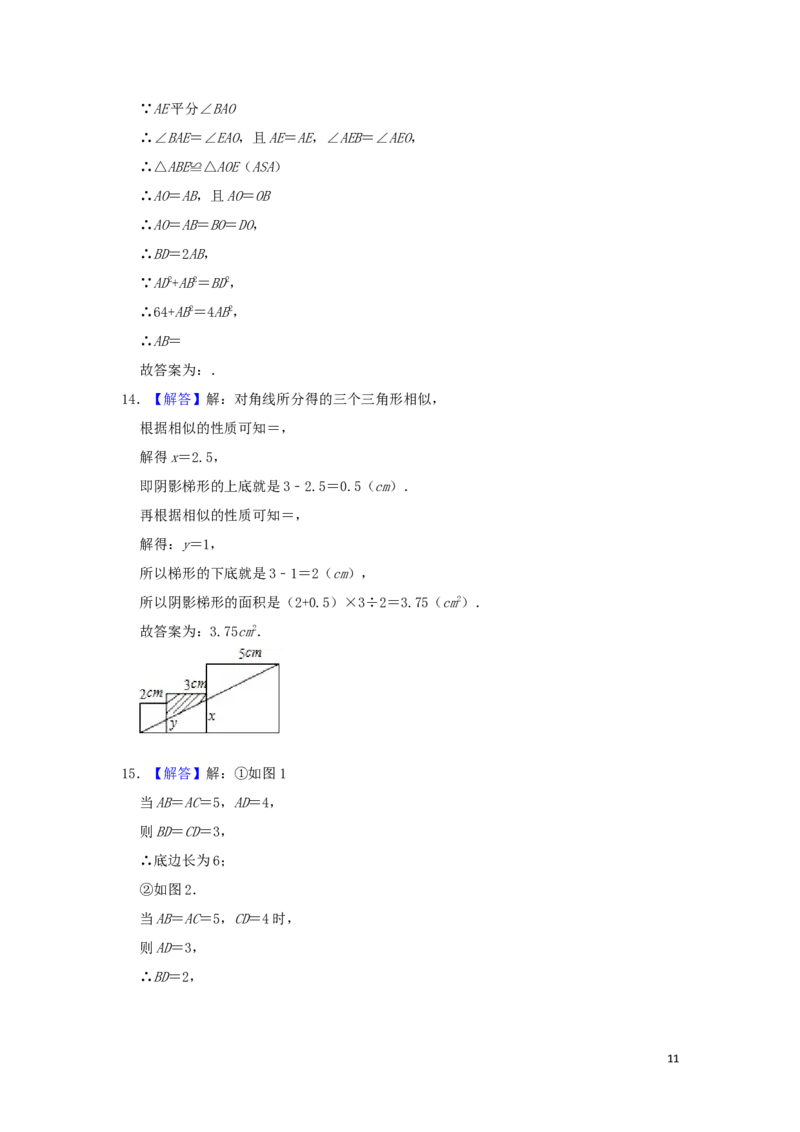
14.【解答】解:对角线所分得的三个三角形相似,
根据相似的性质可知=,
解得x=2.5,
即阴影梯形的上底就是3﹣2.5=0.5(cm).
再根据相似的性质可知=,
解得:y=1,
所以梯形的下底就是3﹣1=2(cm),
所以阴影梯形的面积是(2+0.5)×3÷2=3.75(cm2).
故答案为:3.75cm2.
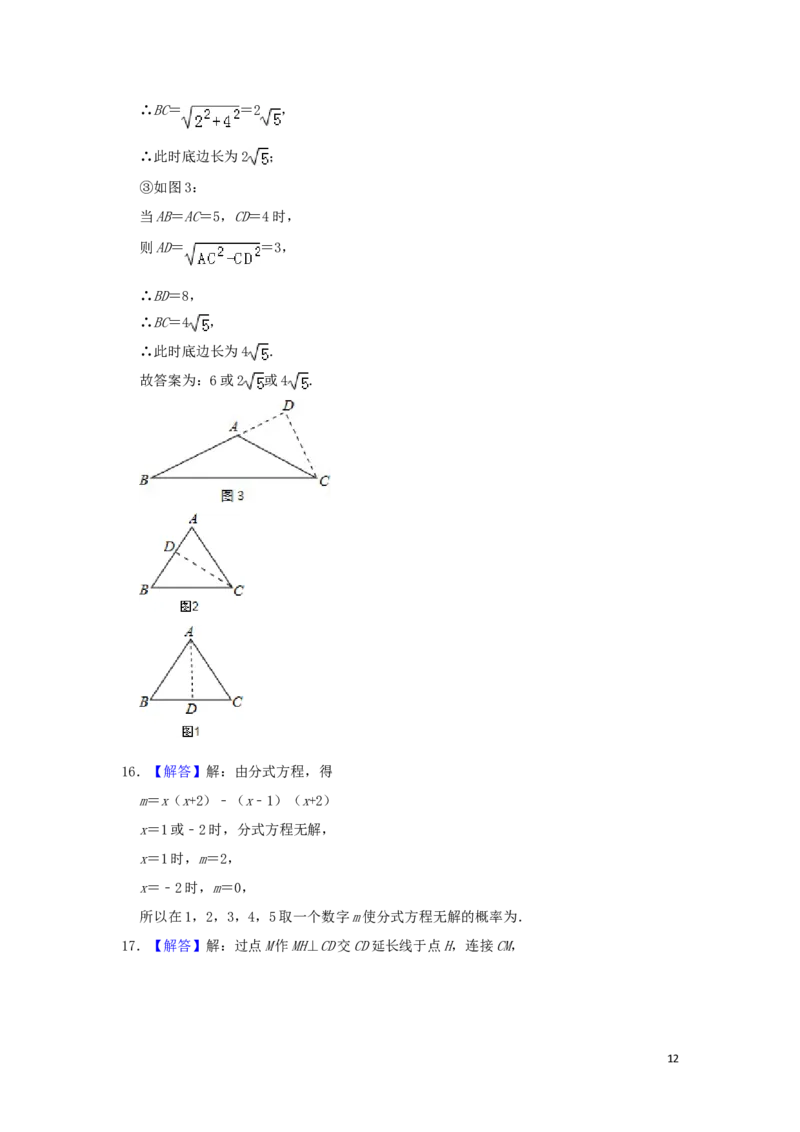
15.【解答】解:①如图1
当AB=AC=5,AD=4,
则BD=CD=3,
∴底边长为6;
②如图2.
当AB=AC=5,CD=4时,
则AD=3,
∴BD=2,
11∴BC= =2 ,
∴此时底边长为2 ;
③如图3:
当AB=AC=5,CD=4时,
则AD= =3,
∴BD=8,
∴BC=4 ,
∴此时底边长为4 .
故答案为:6或2 或4 .
16.【解答】解:由分式方程,得
m=x(x+2)﹣(x﹣1)(x+2)
x=1或﹣2时,分式方程无解,
x=1时,m=2,
x=﹣2时,m=0,
所以在1,2,3,4,5取一个数字m使分式方程无解的概率为.
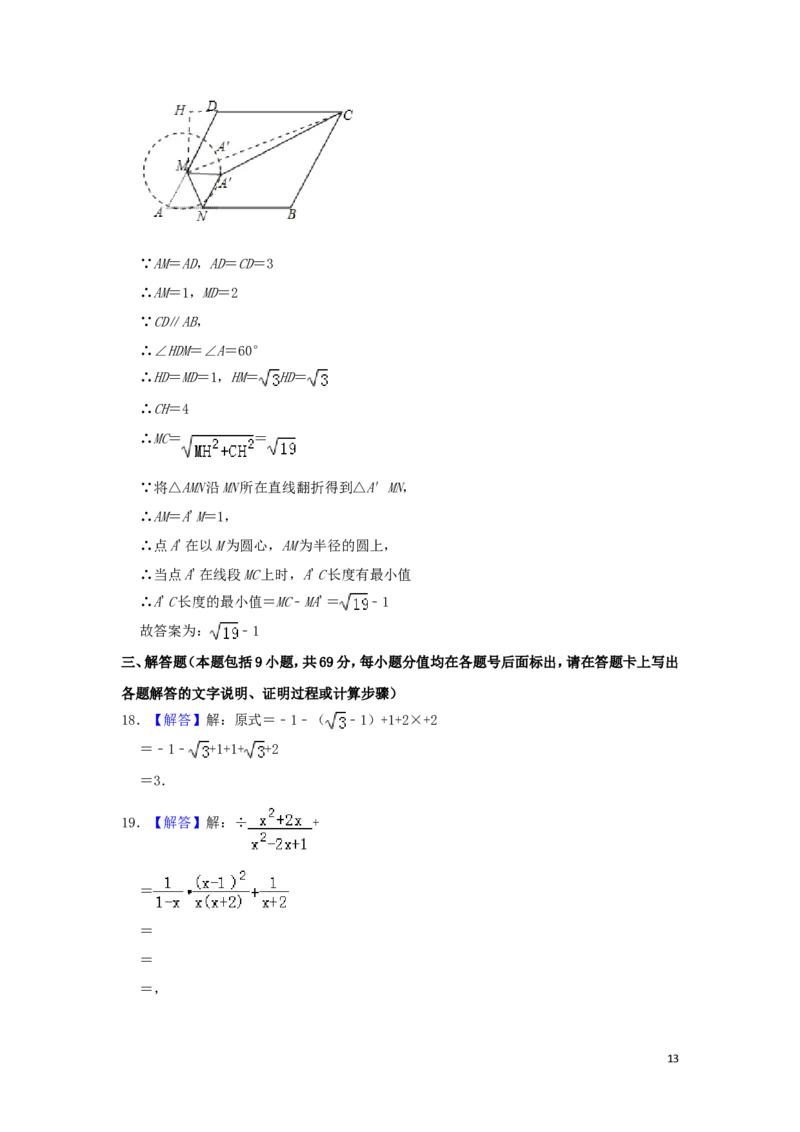
17.【解答】解:过点M作MH⊥CD交CD延长线于点H,连接CM,
12∵AM=AD,AD=CD=3
∴AM=1,MD=2
∵CD∥AB,
∴∠HDM=∠A=60°
∴HD=MD=1,HM= HD=
∴CH=4
∴MC= =
∵将△AMN沿MN所在直线翻折得到△A′MN,
∴AM=A'M=1,
∴点A'在以M为圆心,AM为半径的圆上,
∴当点A'在线段MC上时,A'C长度有最小值
∴A'C长度的最小值=MC﹣MA'= ﹣1
故答案为: ﹣1
三、解答题(本题包括9小题,共69分,每小题分值均在各题号后面标出,请在答题卡上写出
各题解答的文字说明、证明过程或计算步骤)
18.【解答】解:原式=﹣1﹣( ﹣1)+1+2×+2
=﹣1﹣ +1+1+ +2
=3.
19.【解答】解:÷ +
=
=
=
=,
13由不等式组 ,得﹣3<x≤2,
∴当x=2时,原式=.
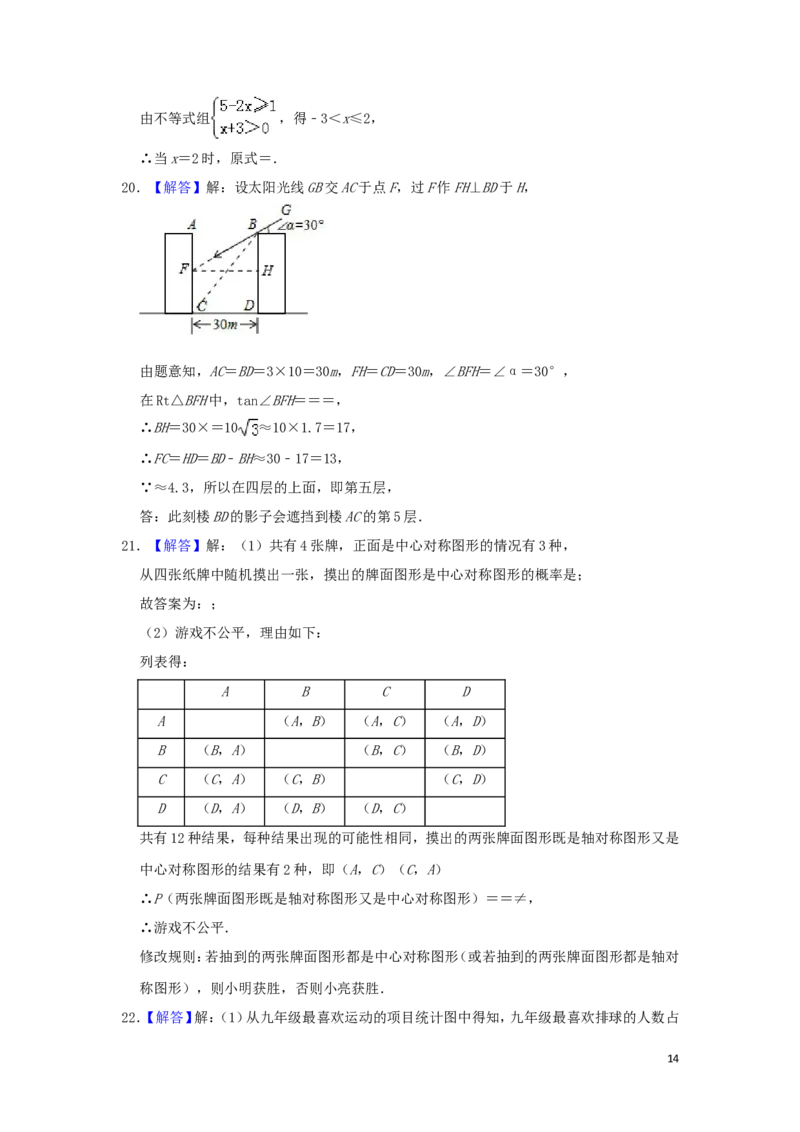
20.【解答】解:设太阳光线GB交AC于点F,过F作FH⊥BD于H,
由题意知,AC=BD=3×10=30m,FH=CD=30m,∠BFH=∠α=30°,
在Rt△BFH中,tan∠BFH===,
∴BH=30×=10 ≈10×1.7=17,
∴FC=HD=BD﹣BH≈30﹣17=13,
∵≈4.3,所以在四层的上面,即第五层,
答:此刻楼BD的影子会遮挡到楼AC的第5层.
21.【解答】解:(1)共有4张牌,正面是中心对称图形的情况有3种,
从四张纸牌中随机摸出一张,摸出的牌面图形是中心对称图形的概率是;
故答案为:;
(2)游戏不公平,理由如下:
列表得:
A B C D
A (A,B) (A,C) (A,D)
B (B,A) (B,C) (B,D)
C (C,A) (C,B) (C,D)
D (D,A) (D,B) (D,C)
共有12种结果,每种结果出现的可能性相同,摸出的两张牌面图形既是轴对称图形又是
中心对称图形的结果有2种,即(A,C)(C,A)
∴P(两张牌面图形既是轴对称图形又是中心对称图形)==≠,
∴游戏不公平.
修改规则:若抽到的两张牌面图形都是中心对称图形(或若抽到的两张牌面图形都是轴对
称图形),则小明获胜,否则小亮获胜.
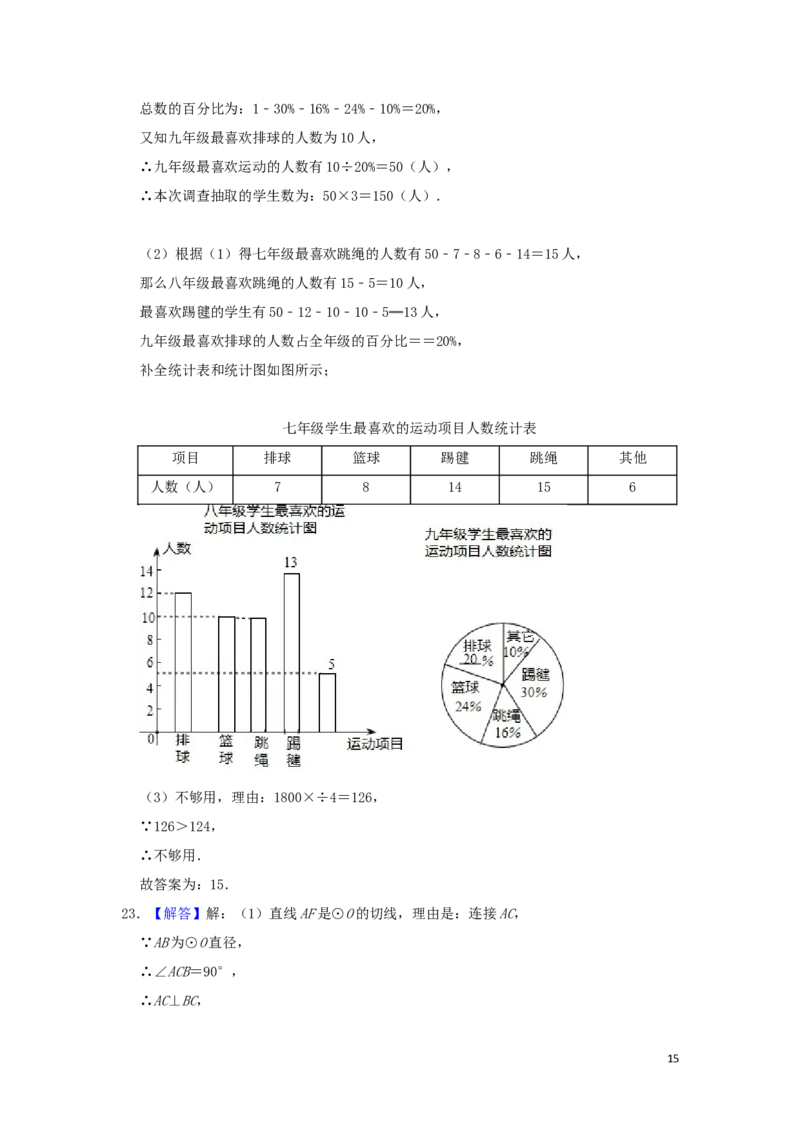
22.【解答】解:(1)从九年级最喜欢运动的项目统计图中得知,九年级最喜欢排球的人数占
14总数的百分比为:1﹣30%﹣16%﹣24%﹣10%=20%,
又知九年级最喜欢排球的人数为10人,
∴九年级最喜欢运动的人数有10÷20%=50(人),
∴本次调查抽取的学生数为:50×3=150(人).
(2)根据(1)得七年级最喜欢跳绳的人数有50﹣7﹣8﹣6﹣14=15人,
那么八年级最喜欢跳绳的人数有15﹣5=10人,
最喜欢踢毽的学生有50﹣12﹣10﹣10﹣5═13人,
九年级最喜欢排球的人数占全年级的百分比==20%,
补全统计表和统计图如图所示;
七年级学生最喜欢的运动项目人数统计表
项目 排球 篮球 踢毽 跳绳 其他
人数(人) 7 8 14 15 6
(3)不够用,理由:1800×÷4=126,
∵126>124,
∴不够用.
故答案为:15.
23.【解答】解:(1)直线AF是⊙O的切线,理由是:连接AC,
∵AB为⊙O直径,
∴∠ACB=90°,
∴AC⊥BC,
15∵CF=CD,
∴∠CAF=∠EAC,
∵AC=CE,
∴∠E=∠EAC,
∵∠B=∠E,
∴∠B=∠FAC,
∵∠B+∠BAC=90°,
∴∠FAC+∠BAC=90°,
∴OA⊥AF,
又∵点A在⊙O上,
∴直线AF是⊙O的切线;
(2)过点C作CM⊥AE,
∵tan∠CAE=,
∴=,
∵AC=10,
∴设CM=3x,则AM=4x,
在Rt△ACM中,根据勾股定理,CM2+AM2=AC2,
∴(3x)2+(4x)2=100,
解得x=2,
∴AM=8,
∵AC=CE,
∴AE=2AE=2×8=16.
24.【解答】解:(1)根据题意得,y=250﹣10(x﹣25)=﹣10x+500(30≤x≤38);
(2)设每天扣除捐赠后可获得利润为w元.
w=(x﹣20﹣a)(﹣10x+500)=﹣10x2+(10a+700)x﹣500a﹣10000(30≤x≤38)
对称轴为x=35+a,且0<a≤6,则30a≤38,
16则当x=35+a时,w取得最大值,
∴(35+a﹣20﹣a)[﹣10x(35+a)+500]=1960
∴a=2,a=58(不合题意舍去),
1 2
∴a=2.
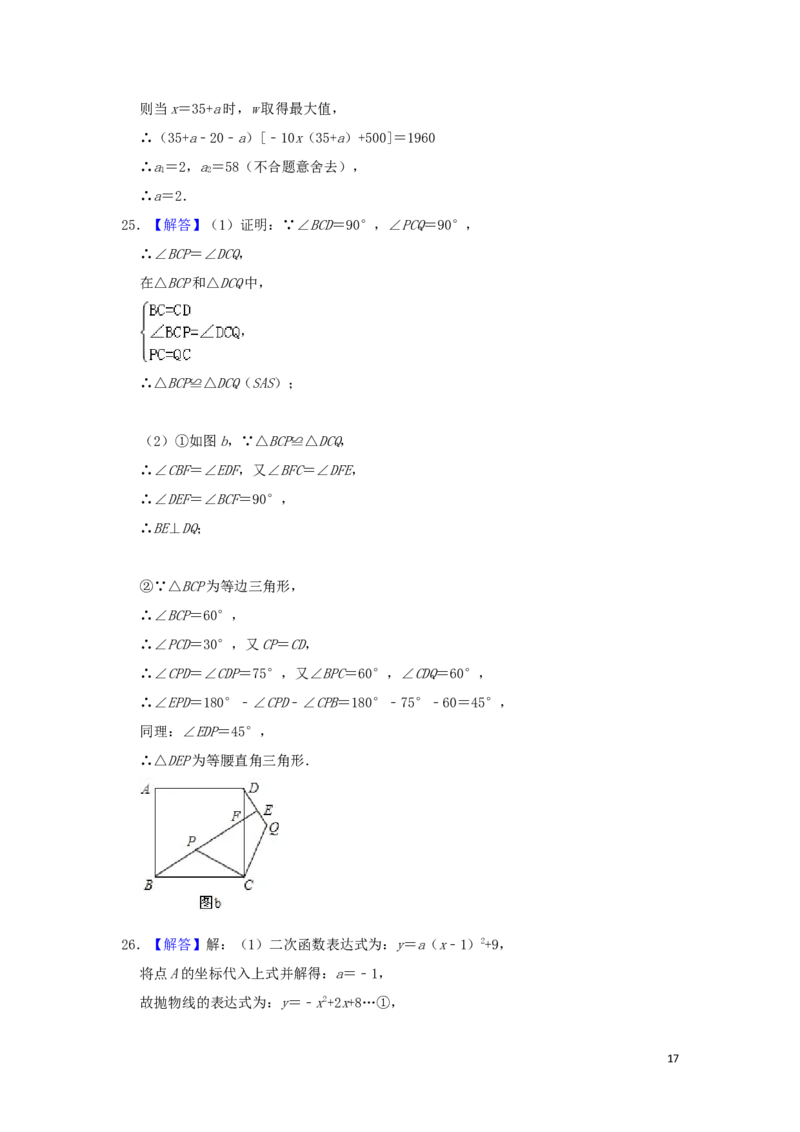
25.【解答】(1)证明:∵∠BCD=90°,∠PCQ=90°,
∴∠BCP=∠DCQ,
在△BCP和△DCQ中,
,
∴△BCP≌△DCQ(SAS);
(2)①如图b,∵△BCP≌△DCQ,
∴∠CBF=∠EDF,又∠BFC=∠DFE,
∴∠DEF=∠BCF=90°,
∴BE⊥DQ;
②∵△BCP为等边三角形,
∴∠BCP=60°,
∴∠PCD=30°,又CP=CD,
∴∠CPD=∠CDP=75°,又∠BPC=60°,∠CDQ=60°,
∴∠EPD=180°﹣∠CPD﹣∠CPB=180°﹣75°﹣60=45°,
同理:∠EDP=45°,
∴△DEP为等腰直角三角形.
26.【解答】解:(1)二次函数表达式为:y=a(x﹣1)2+9,
将点A的坐标代入上式并解得:a=﹣1,
故抛物线的表达式为:y=﹣x2+2x+8…①,
17则点B(3,5),
将点A、B的坐标代入一次函数表达式并解得:
直线AB的表达式为:y=2x﹣1;
(2)存在,理由:
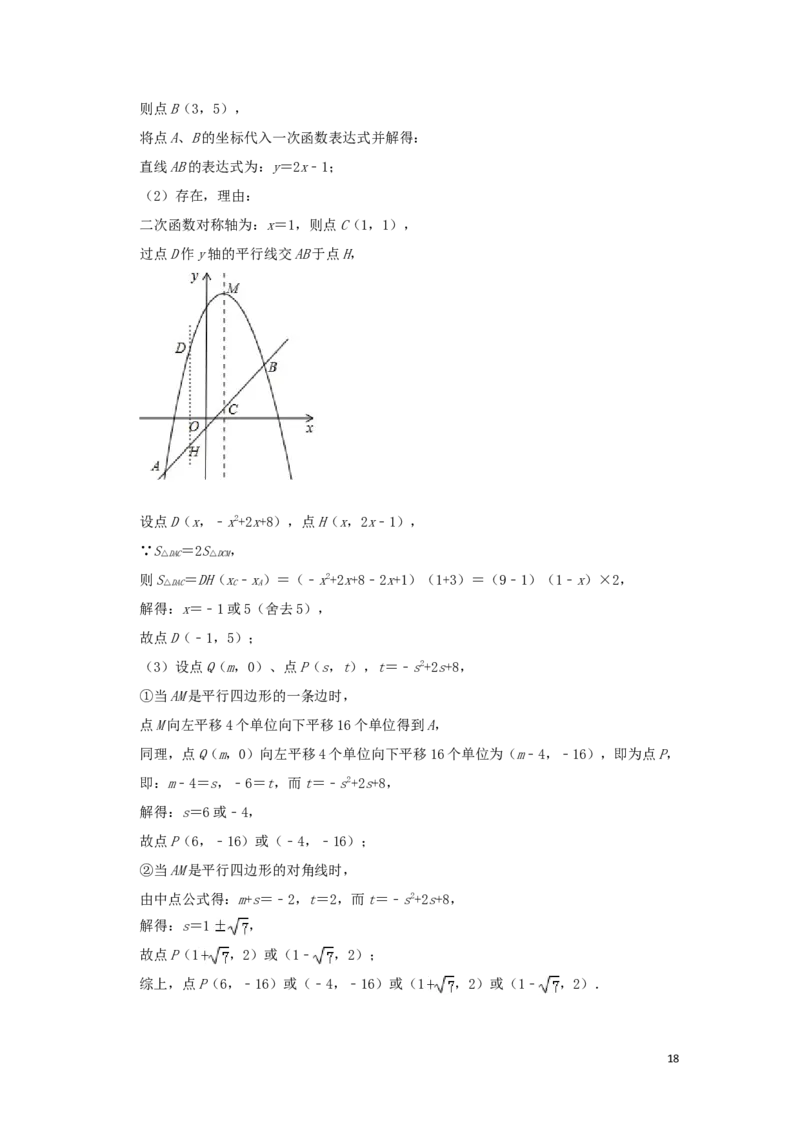
二次函数对称轴为:x=1,则点C(1,1),
过点D作y轴的平行线交AB于点H,
设点D(x,﹣x2+2x+8),点H(x,2x﹣1),
∵S =2S ,
△DAC △DCM
则S =DH(x﹣x)=(﹣x2+2x+8﹣2x+1)(1+3)=(9﹣1)(1﹣x)×2,
△DAC C A
解得:x=﹣1或5(舍去5),
故点D(﹣1,5);
(3)设点Q(m,0)、点P(s,t),t=﹣s2+2s+8,
①当AM是平行四边形的一条边时,
点M向左平移4个单位向下平移16个单位得到A,
同理,点Q(m,0)向左平移4个单位向下平移16个单位为(m﹣4,﹣16),即为点P,
即:m﹣4=s,﹣6=t,而t=﹣s2+2s+8,
解得:s=6或﹣4,
故点P(6,﹣16)或(﹣4,﹣16);
②当AM是平行四边形的对角线时,
由中点公式得:m+s=﹣2,t=2,而t=﹣s2+2s+8,
解得:s=1 ,
故点P(1 ,2)或(1﹣ ,2);
综上,点P(6,﹣16)或(﹣4,﹣16)或(1 ,2)或(1﹣ ,2).
1819