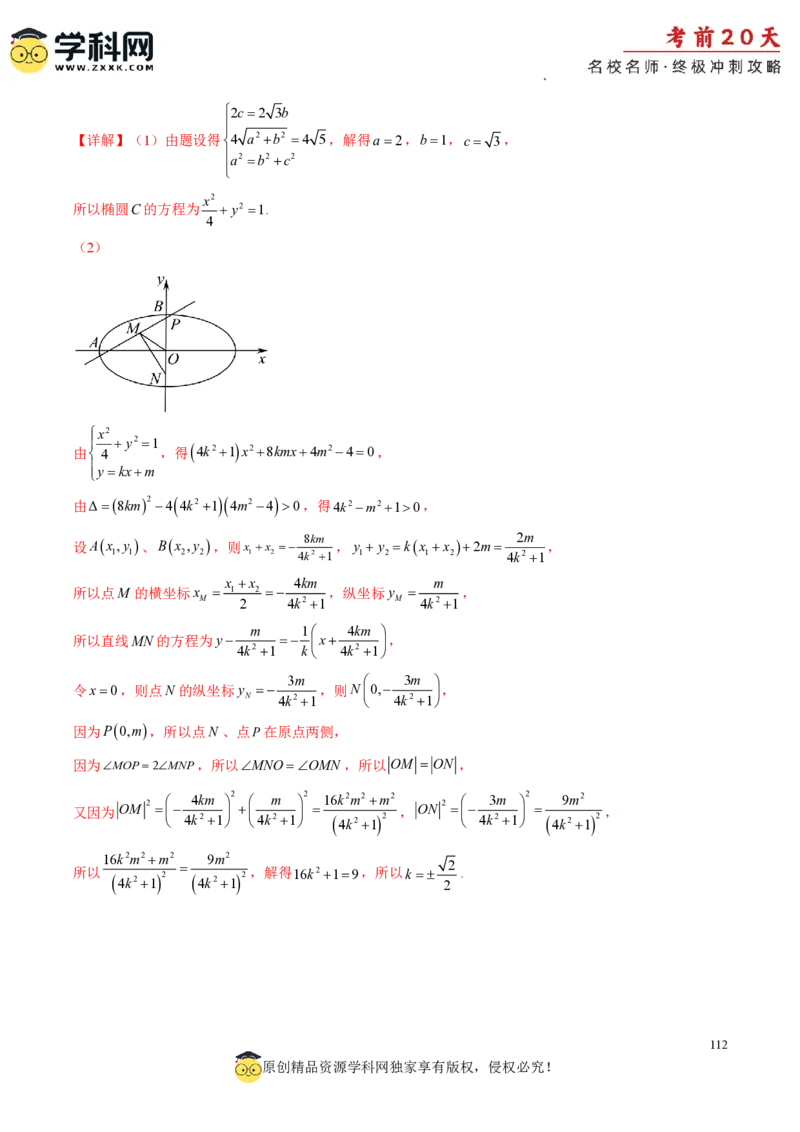
文档内容
学学学科科科网网网(((北北北京京京)))股股股份份份有有有限限限公公公司司司contents
目 录
(四)
解三角形(解答题)………………………………………………………………03
空间立体几何(解答题)…………………………………………………………23
函数与导数(解答题)……………………………………………………………53
圆锥曲线(解答题) ……………………………………………………………77
新定义(解答题)…………………………………………………………………112
学学学科科科网网网(((北北北京京京)))股股股份份份有有有限限限公公公司司司解三角形(解答题)
年份 题号 知识点 考点
①正余弦定理
2021年I卷 19 解三角形
②三角形内部一条线的处理技巧
①正余弦定理
2021年II卷 18 解三角形 ②三角形的面积问题
③根据三角形形状求参数
①正余弦定理
2022年I卷 18 解三角形
②三角形边长关系求最值
①正余弦定理
2022年II卷 18 解三角形
②三角形的面积问题
①正余弦定理
2023年新高考1 17 解三角形
②三角形求高的处理技巧
①正余弦定理
2023年新高考2 17 解三角形
②三角形中线的处理技巧
近三年,解三角形在解答题中占据一个位置,考查的考点一般来说是:
1、三角形题干条件的化解2、三角形的面积定值与最值(①全部转化为边,利用基本不等式求最值与范围②
全部转化为角,利用三角函数求最值与范围)3、三角形周长(长度)定值与最值(①全部转化为边,利用
基本不等式求最值与范围②全部转化为角,利用三角函数求最值与范围)
题干的设置一般来说在上述的三项考点中选其一项。解三角形的三类需要认真分析,每一类题型都有
它独特的处理办法,找准精髓便可轻松搞定。
解三角形在2024新高考新题型中的考查形式依然以解答题为主,以考查基本概念和核心方法为主,大
概率考察三角形内部一条线,考生可适当留意常见的内部中线、角平分线、任意一条线 现象并分类,每一
类总结出一个固定模板,以便此类题在高考出现时考生能做到心中有数,快速解答.
3
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司一、正余弦定理基础问题
《正弦定理》
a b c
①正弦定理: 2R
sin A sinB sinC
sin A a sinB b sinC c
②变形: , ,
sinB b sinC c sin A a
③变形:a:b:csin A:sinB:sinC
abc a b c
④变形:
sin AsinBsinC sin A sinB sinC
⑤变形:asinBbsin A,asinC csin A,bsinC csinB
《余弦定理》
①余弦定理:b2 c2 a2 2bccosA,a2 c2 b2 2accosB,a2 b2 c2 2abcosC
b2 c2 a2 a2 c2 b2 a2 b2 c2
②变形:cosA ,cosB ,cosC
2bc 2ac 2ab
核心问题:什么情况下角化边?什么情况下边化角?
⑴当每一项都有边且次数一样时,采用边化角
⑵当每一项都有角《sin》且次数一样时,采用角化边
⑶当每一项都是边时,直接采用边处理问题
⑷当每一项都有角《sin》及边且次数一样时,采用角化边或变化角均可
二:三角形面积公式
1 1 1
①S absinC,S acsinB,S bcsin A
ABC 2 ABC 2 ABC 2
1 1
②S rabc rl其中r,l分别为ABC内切圆半径及ABC的周长
ABC 2 2
推导:将ABC分为三个分别以ABC的边长为底,内切圆与边相交的半径为高的三角形,利用等面积法
即可得到上述公式
abc
③S 2R2sin AsinBsinC (R为ABC外接圆的半径)
ABC 4R
1 sinBsinC
推导:将a 2Rsin A代入S a2 可得S 2R2sin AsinBsinC
ABC 2 sin A ABC
将a 2Rsin A,b2RsinB,c2RsinC 代入S 2R2sin AsinBsinC
ABC
4
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司abc
可得S
ABC 4R
1 sinBsinC 1 sin AsinC 1 sin AsinB
④S a2 ,S b2 ,S c2
ABC 2 sin A ABC 2 sinB ABC 2 sinC
1
⑤海伦公式S p pa pb pc (其中 p abc )
ABC 2
a2 b2 c2
推导:根据余弦定理的推论cosC
2ab
2
1 1 1 a2 b2 c2
S absinC ab 1cos2C ab 1
ABC 2 2 2 2ab
1 2ab2 a2 b2 c2 2 1 abcbcacababc
4 4
1
令 p abc ,整理得S p pa pb pc
2 ABC
三:三角形中面积最值求算
技巧总结
正规方法:面积公式+基本不等式
1
S absinC c2
① 2 a2 b2 2abcosCc2 2abab
21cosC
a2 b2 c2 2abcosC
1
S acsinB b2
② 2 a2 c2 2accosBb2 2acac
21cosB
a2 c2 b2 2accosB
1
S bcsin A a2
③ 2 b2 c2 2bccosAa2 2bcbc
21cosA
b2 c2 a2 2bccosA
三角形中面积取值范围求算
技巧总结
思路1:如果题干已知一个角,则利用面积公式转化为三角函数求最值(注意角的范围)
思路2:如果题干未知角,则利用面积公式转化为二次函数求最值(注意单一边的范围)
求单一边范围用到的工具
①两边之和大于第三边,两边之差小于第三边
②若为锐角三角形,则两边平方之和大于第三边平方
若为钝角三角形,则两边平方之和小于第三边平方
③若为锐角三角形,则可利用图象破解或cos>0,cos>0建立不等式
5
原创精品资源学科网独家享有版权,侵权必究!
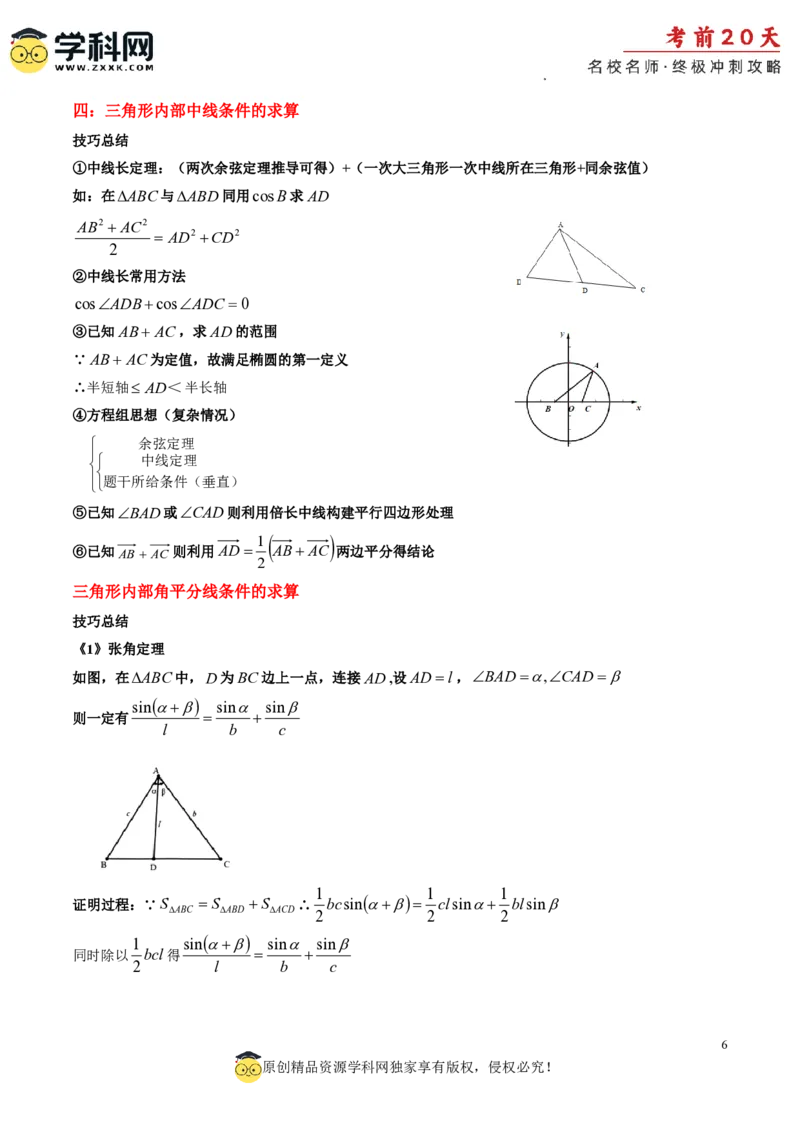
学科网(北京)股份有限公司四:三角形内部中线条件的求算
技巧总结
①中线长定理:(两次余弦定理推导可得)+(一次大三角形一次中线所在三角形+同余弦值)
如:在ABC与ABD同用cosB求AD
AB2 AC2
AD2 CD2
2
②中线长常用方法
cosADBcosADC 0
③已知AB AC,求AD的范围
∵AB AC为定值,故满足椭圆的第一定义
∴半短轴 AD<半长轴
④方程组思想(复杂情况)
余弦定理
中线定理
题干所给条件(垂直)
⑤已知BAD或CAD则利用倍长中线构建平行四边形处理
1
⑥已知AB AC 则利用AD AB AC 两边平分得结论
2
三角形内部角平分线条件的求算
技巧总结
《1》张角定理
如图,在ABC中,D为BC边上一点,连接AD,设ADl,BAD,CAD
sin sin sin
则一定有
l b c
1 1 1
证明过程:∵S S S ∴ bcsin clsin blsin
ABC ABD ACD 2 2 2
1 sin sin sin
同时除以 bcl得
2 l b c
6
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司典例1【2023新高考1卷】已知在VABC中,AB 3C,2sinACsinB.
(1)求sinA;
(2)设AB5,求AB边上的高.
3 10
【答案】(1) (2)6
10
【解析】【1】Q AB3C,
π
πC 3C ,即C ,
4
又2sin(AC)sinBsin(AC),
2sin AcosC2cosAsinC sin AcosCcosAsinC,
sin AcosC 3cosAsinC,
sin A3cosA,
π
即tanA3,所以0 A ,
2
3 3 10
sin A .
10 10
1 10
【2】由(1)知,cosA ,
10 10
2 3 10 10 2 5
由sinB sin(AC) sinAcosCcosAsinC ( ) ,
2 10 10 5
2 5
5
c b 5
由正弦定理, ,可得b 2 10 ,
sinC sinB 2
2
1 1
ABh ABACsin A,
2 2
3 10
hbsinA2 10 6.
10
典例2【2023新高考全国Ⅱ卷】 记VABC的内角A,B,C的对边分别为a,b,c,已知VABC的面积为 3,
D为BC中点,且AD1.
π
(1)若ADC ,求tanB;
3
7
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司(2)若b2 c2 8,求b,c.
3
【答案】(1) ; (2)bc2.
5
【解析】【1】
π
方法1:在VABC中,因为D为BC中点,ADC ,AD1,
3
1 1 1 3 3 1 3
则S ADDCsinADC 1 a a S ,解得a 4,
VADC 2 2 2 2 8 2 VABC 2
2π
在△ABD中,ADB ,由余弦定理得c2 BD2 AD2 2BDADcosADB,
3
1 741 5 7
即c2 41221( )7,解得c 7,则cosB ,
2 2 72 14
5 7 21
sinB 1cos2 B 1( )2 ,
14 14
sinB 3
所以tanB .
cosB 5
π
方法2:在VABC中,因为D为BC中点,ADC ,AD1,
3
1 1 1 3 3 1 3
则S ADDCsinADC 1 a a S ,解得a 4,
VADC 2 2 2 2 8 2 VABC 2
在VACD中,由余弦定理得b2 CD2 AD2 2CDADcosADC ,
即b2 41221 1 3,解得b 3,有AC2 AD2 4CD2,则CAD π ,
2 2
π 3 3 5
C ,过A作AE BC于E,于是CE ACcosC ,AE ACsinC ,BE ,
6 2 2 2
AE 3
所以tanB .
BE 5
【2】
8
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司 1 1
c2 a2 12 a1cos(πADC)
4 2
方法1:在△ABD与VACD中,由余弦定理得 ,
1 1
b2 a2 12 a1cosADC
4 2
1
整理得 a2 2b2 c2,而b2 c2 8,则a2 3,
2
1 3 π
又S 31sinADC ,解得sinADC 1,而0ADC π,于是ADC ,
VADC 2 2 2
所以bc AD2 CD2 2.
uuur uuur uuur uuur uuur uuur
方法2:在VABC中,因为D为BC中点,则2AD AB AC,又CB ABAC ,
uuur uuur uuur uuur uuur uuur
于是4AD 2 CB 2 (AB AC)2 (ABAC)2 2(b2 c2)16,即4a2 16,解得a2 3,
1 3 π
又S 31sinADC ,解得sinADC 1,而0ADC π,于是ADC ,
VADC 2 2 2
所以bc AD2 CD2 2.
典例3【2022新高考全国Ⅰ卷】记VABC的内角A,B,C的对边分别为a,b,c,已知
cosA sin2B
.
1sinA 1cos2B
2
(1)若C ,求B;
3
a2 b2
(2)求 的最小值.
c2
π
【答案】(1) ; (2)4 25.
6
【解析】【1】
cosA sin2B 2sinBcosB sinB
因为 ,即
1sinA 1cos2B 2cos2 B cosB
1
sinBcosAcosBsinAsinBcosABcosC ,
2
π π
而0 B ,所以B ;
2 6
【2】
π π
由(1)知,sinBcosC 0,所以 C π,0 B ,
2 2
9
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司 π
而sinBcosC sin C ,
2
π π 3
所以C B,即有A 2B,所以B 0, ,C ,
2 2 4 2 4
a2 b2 sin2 Asin2 B cos22B1cos2 B
所以
c2 sin2C cos2 B
2cos2 B1 2 1cos2 B 2
4cos2 B 52 854 25 .
cos2 B cos2 B
2 a2 b2
当且仅当cos2 B 时取等号,所以 的最小值为4 25.
2 c2
典例4【2022新高考全国Ⅱ卷】 记VABC的内角A,B,C的对边分别为a,b,c,分别以a,b,c为边长
3 1
的三个正三角形的面积依次为S ,S ,S ,已知S S S ,sinB .
1 2 3 1 2 3 2 3
(1)求VABC的面积;
2
(2)若sinAsinC ,求b.
3
2 1
【答案】(1) (2)
8 2
【解析】【1】
1 3 3 3 3 3 3 3 3
由题意得S a2 a2,S b2,S c2,则S S S a2 b2 c2 ,
1 2 2 4 2 4 3 4 1 2 3 4 4 4 2
a2 c2 b2
即a2 c2 b2 2,由余弦定理得cosB ,整理得accosB1,则cosB0,又
2ac
1
sinB ,
3
1 2 2 2 1 3 2 1 2
则cosB 1 ,ac ,则S acsinB ;
3 3 cosB 4 VABC 2 8
【2】
3 2
b a c b2 a c ac 4 9 b 3
由正弦定理得: ,则 ,则 ,
sinB sin A sinC sin2B sinA sinC sinAsinC 2 4 sinB 2
3
3 1
b sinB .
2 2
10
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司典例5【2021新高考全国Ⅰ卷】 记VABC是内角A,B,C的对边分别为a,b,c.已知b2 ac,点D
在边AC上,BDsinABC asinC.
(1)证明:BDb;
(2)若AD2DC,求cosABC .
7
【答案】(1)证明见解析;(2)cosABC .
12
【解析】(1)设VABC的外接圆半径为R,由正弦定理,
b c
得sinABC ,sinC ,
2R 2R
b c
因为BDsinABC asinC,所以BD a ,即BDbac.
2R 2R
又因为b2 ac,所以BDb.
(2)[方法一]【最优解】:两次应用余弦定理
a2 b2 c2
因为AD2DC,如图,在VABC中,cosC ,①
2ab
b
a2 ( )2 b2
3
在△BCD中,cosC .②
b
2a
3
b 11
由①②得a2 b2 c2 3 a2 ( )2 b2 ,整理得2a2 b2 c2 0.
3 3
c 3c
又因为b2 ac,所以6a2 11ac3c2 0,解得a 或a ,
3 2
c c2 c 3c
当a ,b2 ac 时,ab c(舍去).
3 3 3 3
3c 3c2
( )2 c2
3c 3c2 2 2 7
当a ,b2 ac 时,cosABC .
2 2 3c 12
2 c
2
11
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司7
所以cosABC .
12
[方法二]:等面积法和三角形相似
2
如图,已知AD2DC,则S S ,
△ABD 3 △ABC
1 2 2 1
即 b2sinADB acsinABC,
2 3 3 2
而b2 ac,即sinADBsinABC,
故有ADBABC,从而ABDC.
b c CA BA
由b2 ac,即 ,即 ,即VACB∽VABD,
a b CB BD
2b
AD AB
故 ,即 3 c ,
AB AC
c b
2
又b2 ac,所以c a,
3
c2 a2 b2 7
则cosABC .
2ac 12
[方法三]:正弦定理、余弦定理相结合
2 1
由(1)知BDb AC,再由AD2DC得AD b,CD b.
3 3
AD BD
在VADB中,由正弦定理得 .
sinABD sinA
2
b 2
又ABDC,所以 3 b ,化简得sinC sinA.
3
sinC sin A
2 2
在VABC中,由正弦定理知c a,又由b2 ac,所以b2 a2.
3 3
12
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司4 2
a2 a2 a2
a2 c2 b2 9 3 7
在VABC中,由余弦定理,得cosABC .
2ac 2 12
2 a2
3
7
故cosABC .
12
[方法四]:构造辅助线利用相似的性质
如图,作DE∥AB,交BC于点E,则△DEC∽△ABC.
c a 2a
由AD2DC,得DE ,EC ,BE .
3 3 3
2a c
( )2 ( )2 b2
3 3
在VBED中,cosBED .
2a c
2
3 3
a2 c2 b2
在VABC中cosABC .
2ac
因为cosABC cosBED,
2a c
( )2 ( )2 b2
a2 c2 b2
3 3
所以 ,
2ac 2a c
2
3 3
整理得6a2 11b2 3c2 0.
又因为b2 ac,所以6a2 11ac3c2 0,
c 3
即a 或a c.
3 2
下同解法1.
[方法五]:平面向量基本定理
uuur uuur
因为AD2DC,所以AD2DC.
uuur uuur uuur 2 uuur 1 uuur
以向量BA,BC为基底,有BD BC BA.
3 3
13
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司uuur uuur uuur uuur uuur
2 4 2 4 1 2
所以BD BC BABC BA ,
9 9 9
4 4 1
即b2 a2 accosABC c2,
9 9 9
又因为b2 ac,所以9ac4a2 4accosABCc2.③
由余弦定理得b2 a2 c2 2accosABC,
所以aca2 c2 2accosABC ④
联立③④,得6a2 11ac3c2 0.
3 1
所以a c或a c.
2 3
下同解法1.
[方法六]:建系求解
以D为坐标原点,AC所在直线为x轴,过点D垂直于AC的直线为y轴,
DC 长为单位长度建立直角坐标系,
如图所示,则D0,0,A2,0,C1,0
.
由(1)知,BDb AC 3,所以点B在以D为圆心,3为半径的圆上运动.
设Bx,y3 x3 ,则x2 y2 9.⑤
由b2 ac知, BA BC AC 2 ,
即 (x2)2 y2 (x1)2 y2 9.⑥
7 7 95
联立⑤⑥解得x 或x 3(舍去),y2 ,
4 2 16
3 6
代入⑥式得a |BC| ,c|BA| 6,b3,
2
a2 c2 b2 7
由余弦定理得cosABC .
2ac 12
14
原创精品资源学科网独家享有版权,侵权必究!
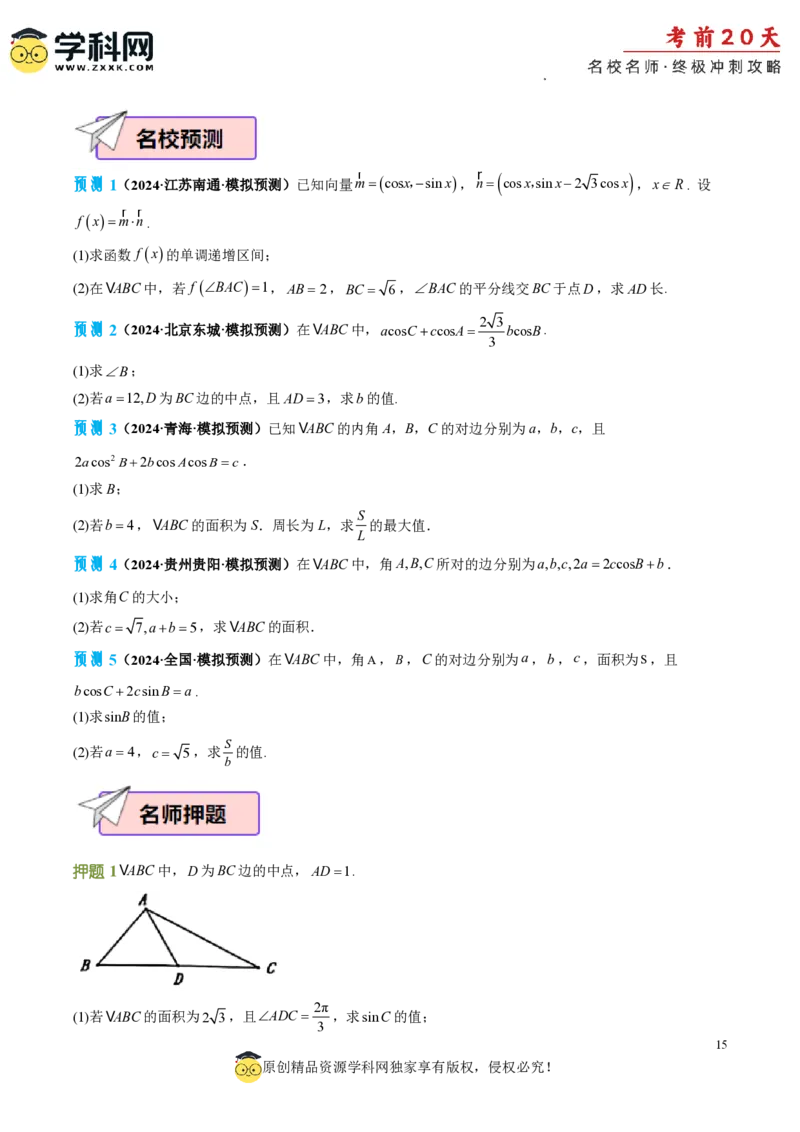
学科网(北京)股份有限公司预测1(2024·江苏南通·模拟预测)已知向量m r cosx,sinx,n r cosx,sinx2 3cosx ,xR. 设
r r
f xmn.
(1)求函数 f x的单调递增区间;
(2)在VABC中,若 f BAC1,AB2,BC 6,BAC的平分线交BC于点D,求AD长.
2 3
预测2(2024·北京东城·模拟预测)在VABC中,acosCccosA bcosB.
3
(1)求B;
(2)若a12,D为BC边的中点,且AD3,求b的值.
预测3(2024·青海·模拟预测)已知VABC的内角A,B,C的对边分别为a,b,c,且
2acos2B2bcosAcosBc.
(1)求B;
S
(2)若b4,VABC的面积为S.周长为L,求 的最大值.
L
预测4(2024·贵州贵阳·模拟预测)在VABC中,角A,B,C所对的边分别为a,b,c,2a2ccosBb.
(1)求角C的大小;
(2)若c 7,ab5,求VABC的面积.
预测5(2024·全国·模拟预测)在VABC中,角A,B,C的对边分别为a,b,c,面积为S,且
bcosC2csinBa.
(1)求sinB的值;
S
(2)若a4,c 5,求 的值.
b
押题1VABC中,D为BC边的中点,AD1.
2π
(1)若VABC的面积为2 3,且ADC ,求sinC的值;
3
15
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司(2)若BC 4,求cosBAC的取值范围.
押题2已知平面四边形ABCD中,AC 180o,BC 3.
(1)若AB6,AD3,CD4,求BD;
9 3
(2)若ABC 120o,VABC的面积为 ,求四边形ABCD周长的取值范围.
2
3 3
押题3记VABC的内角A,B,C的对边分别为a,b,c,若abcabc3,且VABC的面积为 .
4
(1)求角C;
uuur uuur
(2)若AD2DB,求CD 的最小值.
1 3
押题4已知函数 f x sin2x sin2x0的最小正周期为4π.
2 2
(1)求 f x在0,π上的单调递增区间;
(2)在锐角三角形ABC中,内角A,B,C的对边分别为a,b,c,且2accosBbcosC,求 f A的取值范围.
押题5已知△ABC为钝角三角形,它的三个内角A、B、C所对的边分别为a、b、c,且
π π
sin2C sin2Bsin( B)cos( B),ac,bc.
3 6
(1)求tan(AB)的值;
(2)若△ABC的面积为12 3,求c的最小值.
名校预测
预测1:答案(1)(k ,k ),kZ;(2)AD2.
3 6
【详解】(1) f(x)cos2xsinx(sinx2 3cosx)cos2xsin2x2 3sinxcosx
3 1
3sin2xcos2x2( sin2x cos2x)2sin(2x )
2 2 6
令2k 2x 2k ,kZ,
2 6 2
则k xk ,kZ,
3 6
所以函数的单调增区间为(k ,k ),kZ;
3 6
(2)由题意得:2sin(2BAC )1,
6
16
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司 13
因为0BAC,所以 2BAC ,
6 6 6
5
即2BAC ,所以BAC ,
6 6 3
在VABC中,由余弦定理得:BC2 AB2AC22ABACcosBAC,
即64AC22AC,解得AC 31,
因为BAC的平分线交BC于点D,所以S S S ,
△BAD △CAD △ABC
1 1 1
所以 ABADsin ACADsin ACABsin ,
2 6 2 6 2 3
1 31 3( 31)
所以 AD AD ,解得AD2.
2 4 2
π
预测2:答案(1) ;(2)3 7.
6
2 3
【详解】(1)解:因为acosCccosA bcosB,
3
2 3
由正弦定理可得sinAcosCsinCcosA sinBcosB,
3
2 3 2 3
即sin(AC) sinBcosB,sin(πB)sinB sinBcosB,
3 3
2 3
又因为sinB0,所以1 cosB,
3
3 π
解得cosB ,又因为B(0,π),所以B ;
2 6
(2)解:因为D为BC边的中点,a12,所以BDCD6,
设BAD,
BD AD
在△ABD中,由正弦定理可得 ,
sin sinB
6 3
6 π
即sin 1 ,解得sin1,又因为(0,π),所以 ,
2
2
在Rt△ABD中,AB BD2AD2 6232 3 3,
π
在VABC中,AB3 3,BC 12,B ,
6
3
由余弦定理可得:AC2 AB2BC22ABACcosB144272123 3 63,
2
17
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司所以AC 3 7,即b3 7.
π 3
预测3:答案(1) (2)
3 3
【详解】(1)由正弦定理可得,2sinAcos2B2sinBcosAcosBsinC,
所以2sinAcos2B2sinBcosAcosBsinAcosBcosAsinB,
所以sinAcosB(2cosB1)cosAsinB(2cosB1)0,
即(2cosB1)sin(AB)0,
1
由0 ABπ,可知sin(AB)0,所以2cosB10,即cosB ,
2
π
由0Bπ,知B .
3
(2)由余弦定理,得b2 a2c22accosB,即16a2c2ac,
1
所以16ac23ac,即ac ac216,
3
因为S 1 acsinB 3 ac,Labc,所以 S 3ac
3
ac216
,
2 4 L 4ac4 12ac4
S 3 ac2
所以 ac4,又ac (当且仅当ac时取等号),
L 12 4
ac2
所以16ac23ac (当且仅当ac4时取等号),
4
所以ac8(当且仅当ac4时取等号),
S 3 3 3
所以 ac4 84 (当且仅当ac4时取等号),
L 12 12 3
S 3
即 的最大值为 .
L 3
π 3 3
预测4:答案(1)C ;(2) .
3 2
【详解】(1)在VABC中,由2a2ccosBb及正弦定理得:2sinA2sinCcosBsinB,
而sinAsin[π(BC)]sin(BC),则2sin(BC)2sinBcosC2cosBsinC 2sinCcosBsinB,
1
于是2sinBcosCsinB,又B0,π,即sinB0,则cosC ,又C0,π,
2
π
所以C .
3
π
(2)由(1)知,C ,由余弦定理c2 a2b22abcosC,
3
得7a2b2ab(ab)23ab253ab,解得ab6,
18
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司1 3 3 3
所以VABC的面积S absinC ab .
△ABC 2 4 2
5 2 5
预测5:答案(1)sinB (2)
5 5
【详解】(1)由bcosC2csinBa及正弦定理,得sinBcosC2sinCsinBsinA.
又ABCπ,所以sinBcosC2sinCsinBsinBCsinBcosCcosBsinC,
即2sinCsinBcosBsinC.
因为B,C0,π,所以sinC 0,所以cosB2sinB0.
5
又sin2Bcos2B1,所以sinB .
5
2 5
(2)由(1)得cosB 1sin2B ,又a4,c 5,
5
2 5
所以由余弦定理可得b2 a2c22accosB16524 5 5,解得b 5.
5
1 1 5 S 2 2 5
所以S acsinB 4 5 2,所以 .
2 2 5 b 5 5
名师押题
7 3
押题1:答案(1) (2)1,
14 5
1
【详解】(1)因为D为BC边的中点,所以S = S = 3,
VADC 2 VABC
1 1 2π
又S = AD×DCsinÐADC= 3,即 1DCsin 3,解得DC 4,
VADC 2 2 3
在△ADC中由余弦定理AC2 AD2DC22ADDCcosADC,
1
即AC2 1242214 21,所以AC 21,
2
21 1
AC AD 7
在△ADC中由正弦定理 ,即 3 sinC ,解得sinC .
sinADC sinC 14
2
(2)设ADC ,0,π,
在VADB中由余弦定理AB2 AD2BD22ADBDcosADB,
即AB2 1222212cosπ54cos,
在△ADC中由余弦定理AC2 AD2DC22ADDCcosADC,
即AC2 1222212cos54cos,
AB2AC2BC2 54cos54cos16 3
在VABC中由余弦定理cosBAC ,
2ABAC 2 54cos 54cos 2516cos2
19
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司因为0,π,所以cos20,1,则2516cos29,25,
1 1 1
所以 2516cos23,5,所以
, ,
2516cos2 5 3
3 3 3
所以 1, ,即cosBAC1, .
2516cos2 5 5
押题2:答案(1) 33(2) 3 79,6 79
3262BD2
【详解】(1)在△ABD中,由余弦定理得cosA ,
236
3242BD2
在△BCD中,由余弦定理得cosC ,
234
因为AC 180,所以cosAcosC0,
3262BD2 3242BD2
即 0,
236 234
解得BD 33.
1 3 9 3
(2)由已知S 3AB ,得AB6,
△ABC 2 2 2
在VABC中,ABC 120o,由余弦定理得
AC2 3262236cos120 63,则AC 3 7,
设ADx,CD y,(x,0,y0),在VACD中,由余弦定理得
3 7 2 x2y22xycos60 xy23xy,
则xy2 633xy633 xy 2 ,得 xy2 63,
2 4
所以xy6 7,当且仅当x y3 7时取等号,又xy AC 3 7,
所以四边形ABCD周长的取值范围为 3 79,6 79.
2π 6
押题3:答案(1) (2)
3 3
【详解】(1)Qabcabc3,3(ab)2c2 a2b2c22ab
20
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司3
结合余弦定理得32abcosC2ab2ab1cosC,ab ,
21cosC
1 3 3 sinC
QS absinC , 3,
VABC 2 4 1cosC
C C
2sin cos
2 2 C C π C π 2π
即 tan 3,又Q 0, , ,故C ;
cos2 C 2 2 2 2 3 3
2
2π 3
(2)由(1)知:C ,ab 3,
3 21cosC
uuur uuur uuur 1uuur 2uuur
QAD2DB,CD CA CB,
3 3
C uu D ur 2 1 C uu A ur 2 C uu B ur 2 1 b2 4 a2 4 abcosC 1 b2 4 a2 2 ,
3 3 9 9 9 9 9 3
1 4 2 1 4 2 2 2 2
又 b2 a2 2 b2 a2 2 ,
9 9 3 9 9 3 3 3 3
2 6
当且仅当b2a 6时,CD长取最小值,此时CD ,
3 3
6
CD长的最小值为 .
3
2π 2 2 6
押题4:答案(1) 0, ;(2) , .
3 2 4
1 3
【详解】(1) f x sin2x sin2x
2 2
1 1cos2x 3
sin2x
2 2 2
3 1 π
sin2x cos2xsin2x .
2 2 6
2π 1
因为T 4π,所以 ,
2 4
1 π
故 f xsin x .
2 6
π 1 π π 4π 2π
由 2kπ x 2kπ,kZ,解得4kπ x4kπ ,kZ,
2 2 6 2 3 3
21
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司4π 2π
当k 0时, x ,又x0,π,
3 3
2π
所以 f x在0,π上的单调递增区间为 0, .
3
(2)由2accosBbcosC,
得(2sinAsinC)cosBsinBcosC,
所以2sinAcosBsinBcosCcosBsinC sinBCsinA.
因为sinA0,所以cosB 1 ,又B0,π,所以B π ,
2 3
π
0 A
2 π π π A π 5π
又三角形为锐角三角形,则 ,则 A ,所以 ,
2π π 6 2 4 2 6 12
0 A
3 2
A π 5π π π π π π π 2 6
又 f Asin ,sin sin sin cos cos sin ,
2 6 12 4 6 4 6 4 6 4
2 A π 2 6
则 sin ,
2 2 6 4
2 2 6
所以 f A的取值范围为 , .
2 4
押题5:答案(1) 3(2)12
π π 1 π π
【详解】(1)因为sin2C sin2Bsin( B)cos( B)sin2B
sin 2Bsin
3 6 2 2 6
sin2B
1
cos2B
1
sin2B
1
12sin2B
1
3
,
2 2 2 4 4
3
因为sinC 0,所以sinC ,
2
由△ABC为钝角三角形且ac,bc知,C为钝角,
1
所以cosC ,即tanC 3,
2
所以tan(AB)tanπCtanC 3.
1 3
(2)因为S absinC ab12 3,所以ab48,
△ABC 2 4
由余弦定理,c2 a2b22abcosC a2b2ab3ab144,
当且仅当ab4 3时,等号成立,
此时c2的最小值为144,所以c的最小值为12.
22
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司空间立体几何(解答题)
年份 题号 知识点 考点
①证明线线垂直
2021年I
20 空间立体几何 ②二面角的考察
卷
③立体几何的体积求算
2021年II ①证明面面垂直
19 空间立体几何
卷 ②二面角的考察
2022年I ①点面距离求算
19 空间立体几何
卷 ②二面角的考察
2022年II ①证明线面平行
20 空间立体几何
卷 ②二面角的考察
2023年新 ①证明线面平行
18 空间立体几何
高考1 ②二面角的考察
2023 年新
①证明线线垂直
高考2 20 空间立体几何
②二面角的考察
近三年,空间立体几何在解答题中占据一个位置,考查的考点一般来说是:
1、线面及面面平行(①中位线型②平行四边形型③等比例成线段)
2、线面及面面垂直(①线面垂直推导线线垂直②勾股定理)
3、点面距离体积及线面角二面角(①几何法.②向量法;法向量的秒算)
题干的设置一般来说在上述的三项考点中选其两项。空间立体几何题目中首先确定空间几何体底面图
形形状,想方设法先建立好横纵系,而竖轴随便建立,然后根据题干条件表明坐标,另外考生们要想灵活
应用空间向量小技巧则需在有限的时间内多推导几遍,考场中便可轻松搞定。
23
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司从近三年的全国卷的考查情况来看,本节是高考的热点,其中立体几何的棱长有参数,问题中已知线
面角或其它条件先求出参数,再求二面角。此类题计算比较频繁.空间立体几何中求点面距离时空间向量与
等体积法都很方便,考生需要多练习多应用.
一、法向量的求算
技巧总结《三种方法》
方法1、眼神法:给定一个几何体中,若所求平面的法向量直接可以从图中看出,则此平面垂线的方向向量
即为平面的法向量.
方法2、待定系数法:步骤如下:
①设出平面的法向量为n x,y,z .
②找出(求出)平面内的两个不共线的向量
a
a ,b,c
,b
a ,b ,c
.
1 1 1 2 2 2
n a 0
③根据法向量的定义建立关于x,y,z的方程组
n b 0
④解方程组,取其中的一个解,即得法向量.
n a 0
注意:在利用上述步骤求解平面的法向量时,方程组 有无数多个解,只需给x,y,z中的一个变
n b 0
量赋于一个值,即可确定平面的一个法向量;赋的值不同,所求平面的法向量就不同,但它们是共线向
量.
二:空间直角坐标系的构建策略
技巧总结
①:利用共顶点的互相垂直的三条棱,构建空间直角坐标系
②:利用线面垂直关系,构建空间直角坐标系
③:利用面面垂直关系,构建空间直角坐标系
④:利用正棱锥的中心与高所在的直线,构建空间直角坐标系
⑤:利用底面正三角形,构建空间直角坐标系
⑥:利用底面正方形的中心,构建空间直角坐标系
三:空间斜坐标系的构建策略
24
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司技巧总结
空间向量基本定理,空间中任意一个向量都可以由三个不共面向量表示,即a xe ye ze ,我们
1 2 3
记向量a x,y,z b xe ye ze 我们记向量b x,y,z
1 1 1 2 1 3 1 1 1
利用空间斜坐标系步骤如下
第一步:快速表示单位向量e、e、e
1 2 3
第二步:设、、为单位基向量两两之间的夹角,
1 2 3
即e e cos、e e cos、e e cos
1 2 1 2 3 2 1 3 3
第三步:计算模长及数量积(其它运算与直角坐标系的算法都一样)
a xe ye ze 2 x2 y2 z2 2xycos2yzcos 2xzcos
1 2 3 1 2 3
ab xe ye ze xe ye ze
1 2 3 1 1 1 2 1 3
xx yy zz xy yx cos zy yz cos xz zx cos
1 1 1 1 1 1 1 1 2 1 1 3
四:坐标处理距离问题
技巧总结
2
2 PP a
结论1:《点线距离》d PP 1 《异面直线求距离问题》
1
a
推导过程:已知直线l的方向向量是a,点Pl,P l,则直线PP与直线l夹角为θ,则
1 1
2
2
PP a
d PP sin PP 1cos2 PP 1
1 1 1 a
PP n
结论2:《点面距离》d 1
n
提示:P、P分别是平面外及平面上的两点,n是平面的法向量
1
PP n
结论3:《线面距离》d 1
n
提示:P、P分别是直线上及平面上的任意两点,n是平面的法向量
1
PP n
结论4:《面面距离》d 1
n
提示:P、P分别是平面1及平面2的任意两点,n是平面2的法向量
1
结论5:《点点距离》d x x 2 y y 2 z z 2
1 2 1 2 1 2
提示:A x ,y ,z 与B x ,y ,z ,AB的距离为d
1 1 1 2 2 2
五:坐标处理角度问题
25
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司技巧总结:
ab
结论1:异面直线所成角cos 0,
a b 2
①能建空间直角坐标系时,写出相关各点的坐标,然后利用结论求解
ab
cos a,b
②不能建空间直角坐标系时,取基底的思想,在由公式 求出
a b
关键是求出ab 及 a 与 b
ABn
结论2:线面角 cossin 0,
AB n 2
提示:是线AB与平面法向量的夹角,是线AB与平面的夹角
n n
cos 1 2 0,
结论3:二面角的平面角
n n
1 2
提示:是二面角的夹角,具体cos取正取负完全用眼神法观察,若为锐角则取正,若为钝角则
取负.
备注:若AB线上存在一点P,则必须写成APAB,从而求出点P的坐标,从而参与计算
特别注意:空间点不容易表示出来时直接设空间点的坐标,然后利用距离列三个方程求解.
六:处理线与面各种平行关系
技巧总结
线面平行:关键点①必须将刻度尺与所证线重合,然后平移落在所证平面且留下痕迹
②眼神法:观察采用哪一种技巧(五种方法)(记住六大图像)
方法一:中位线型:
如图⑴,在底面为平行四边形的四棱锥PABCD中,点E是PD的中点.求证:PB//平面AEC.
分析:
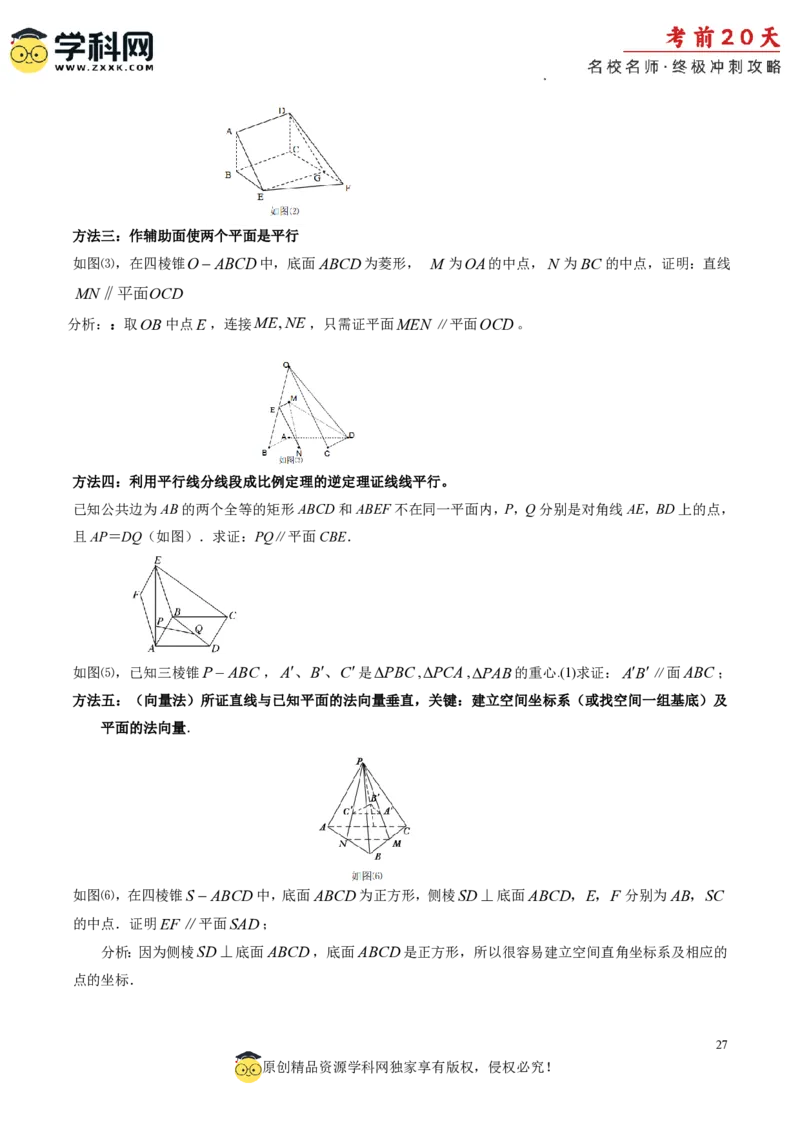
方法二:构造平行四边形
如图⑵, 平行四边形ABCD和梯形BEFC所在平面相交,BE//CF ,求证:AE//平面DCF.
分析:过点E作EG//AD交FC于G, DG就是平面AEGD
与平面DCF的交线,那么只要证明AE//DG即可。
26
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司方法三:作辅助面使两个平面是平行
如图⑶,在四棱锥OABCD中,底面ABCD为菱形, M 为OA的中点,N 为BC的中点,证明:直线
MN‖平面OCD
分析::取OB中点E,连接ME,NE,只需证平面MEN ∥平面OCD。
方法四:利用平行线分线段成比例定理的逆定理证线线平行。
已知公共边为AB的两个全等的矩形ABCD和ABEF不在同一平面内,P,Q分别是对角线AE,BD上的点,
且AP=DQ(如图).求证:PQ∥平面CBE.
如图⑸,已知三棱锥P ABC ,A、B、C是PBC,PCA,PAB的重心.(1)求证:AB∥面ABC;
方法五:(向量法)所证直线与已知平面的法向量垂直,关键:建立空间坐标系(或找空间一组基底)及
平面的法向量.
如图⑹,在四棱锥SABCD中,底面ABCD为正方形,侧棱SD⊥底面ABCD,E,F 分别为AB,SC
的中点.证明EF∥平面SAD;
分析:因为侧棱SD⊥底面ABCD,底面ABCD是正方形,所以很容易建立空间直角坐标系及相应的
点的坐标.
27
原创精品资源学科网独家享有版权,侵权必究!
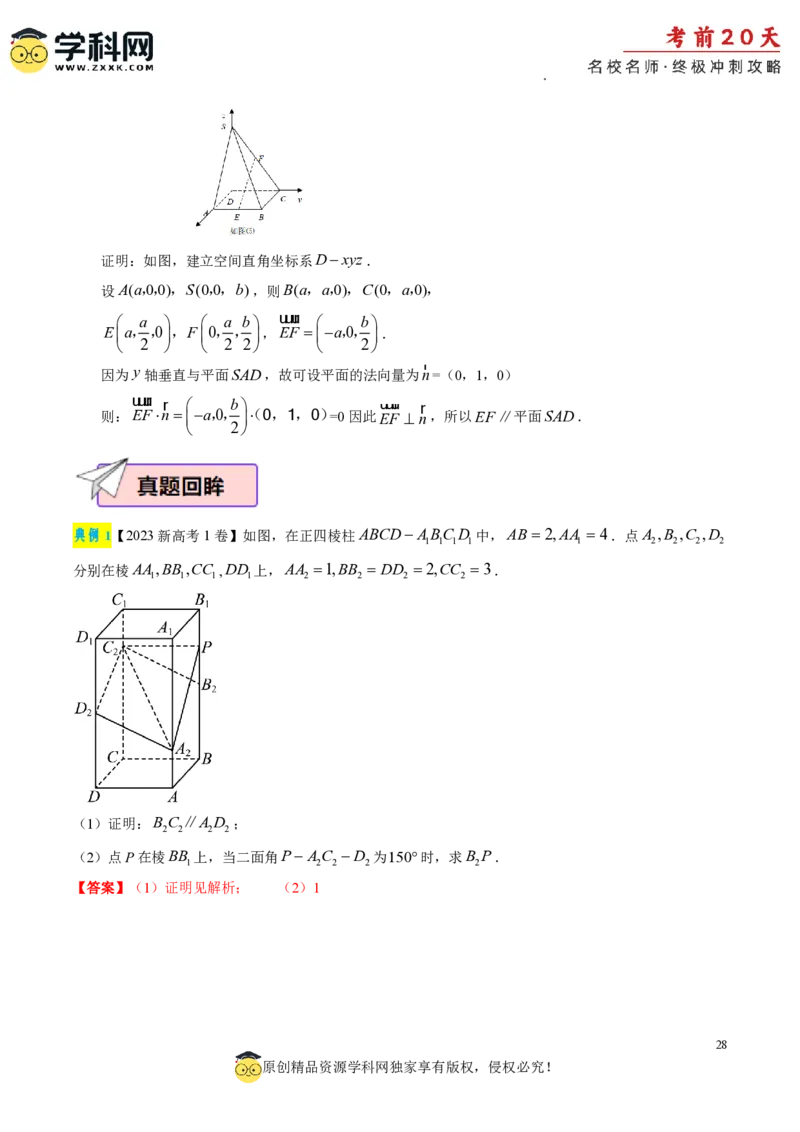
学科网(北京)股份有限公司证明:如图,建立空间直角坐标系Dxyz.
设A(a,0,0),S(0,0,b),则B(a,a,0),C(0,a,0),
uuur
a a b b
E a,,0 ,F 0,, ,EF a,0, .
2 2 2 2
r
因为 y轴垂直与平面SAD,故可设平面的法向量为n=(0,1,0)
uuur r b uuur r
则:EFn a,0, ( 0,1,0)=0因此EF n,所以EF∥平面SAD.
2
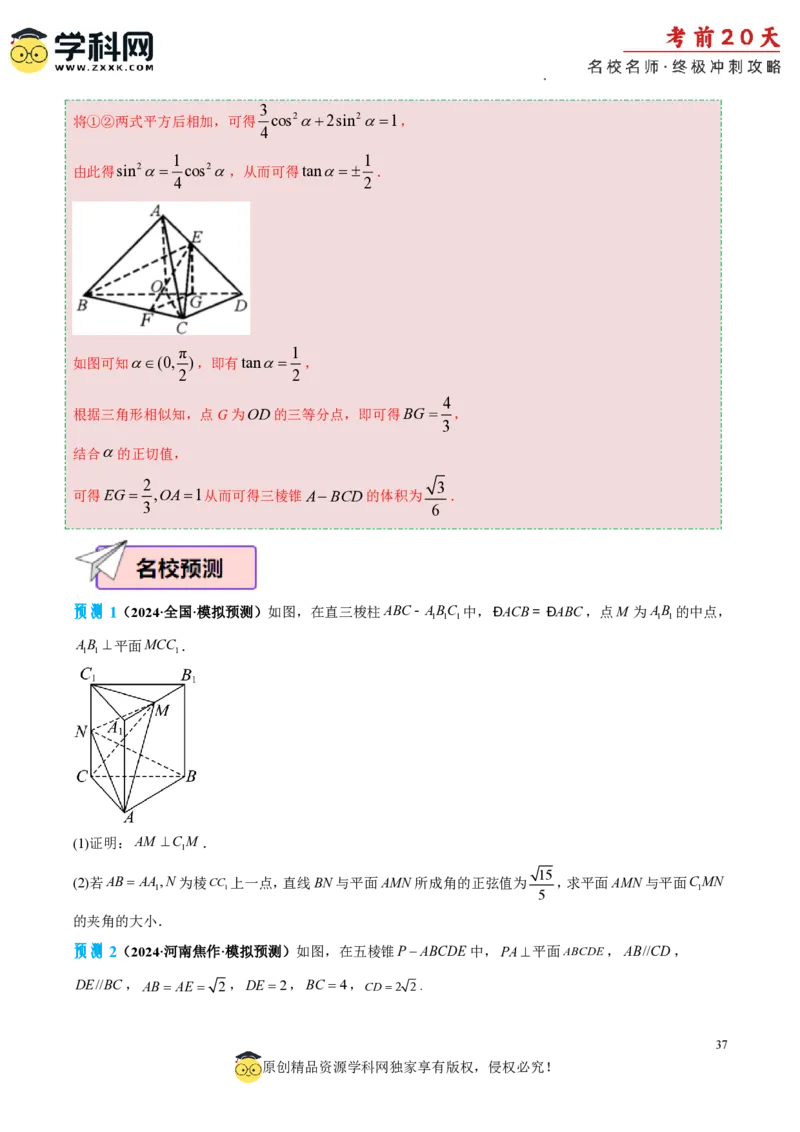
典例1【2023新高考1卷】如图,在正四棱柱ABCDABC D 中,AB 2,AA 4.点A ,B ,C ,D
1 1 1 1 1 2 2 2 2
分别在棱AA,BB,CC ,DD 上,AA 1,BB DD 2,CC 3.
1 1 1 1 2 2 2 2
(1)证明:B C ∥A D ;
2 2 2 2
(2)点P在棱BB 上,当二面角P AC D 为150时,求B P.
1 2 2 2 2
【答案】(1)证明见解析; (2)1
28
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司【解析】【1】
以C为坐标原点,CD,CB,CC 所在直线为x,y,z轴建立空间直角坐标系,如图,
1
则C(0,0,0),C (0,0,3),B (0,2,2),D (2,0,2),A (2,2,1),
2 2 2 2
uuuuur uuuuur
B C (0,2,1),A D (0,2,1),
2 2 2 2
uuuuur uuuuur
B C ∥A D ,
2 2 2 2
又B C,A D 不在同一条直线上,
2 2 2 2
B C ∥A D .
2 2 2 2
【2】
设P(0,2,)(04),
uuuuur uuuur uuuuur
则AC (2,2,2),PC (0,2,3),D C =(2,0,1),
2 2 2 2 2
r
设平面PAC 的法向量n(x,y,z),
2 2
uuuuur
r
nAC 2x2y2z 0
则r
uu2uur2
,
nPC 2y(3)z 0
2
令 z 2,得y 3,x1,
r
n(1,3,2),
ur
设平面AC D 的法向量m(a,b,c),
2 2 2
uuuuur
r
mAC 2a2b2c0
则r
uu2uuu2r
,
mD C 2ac0
2 2
令 a 1,得b1,c 2,
ur
m(1,1,2),
29
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司r ur
r ur nm
6 3
cos n,m r ur cos150 ,
n m 6 4(1)2 (3)2 2
化简可得,2 430,
解得1或3,
P(0,2,1)或P(0,2,3),
B P1.
2
典例2【2023新高考全国Ⅱ卷】 如图,三棱锥ABCD中,DA DB DC,BDCD,
ADBADC 60o,E为BC的中点.
(1)证明:BC DA;
uuur uuur
(2)点F满足EF DA,求二面角DABF 的正弦值.
3
【答案】(1)证明见解析; (2) .
3
【解析】【1】连接AE,DE,因为E为BC中点,DB DC,所以DE BC ①,
因为DA DB DC,ADBADC 60o,所以VACD与△ABD均为等边三角形,
AC AB,从而AE BC②,由①②,AEI DE E,AE,DE 平面ADE ,
所以,BC平面ADE ,而AD平面ADE ,所以BC DA.
【2】不妨设DA DB DC 2,QBDCD,BC 2 2,DE AE 2.
AE2 DE2 4 AD2,AE DE,又Q AE BC,DEI BC E,DE,BC 平面
BCDAE 平面BCD.
以点E为原点,ED,EB,EA所在直线分别为x,y,z轴,建立空间直角坐标系,如图所示:
30
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司设D( 2,0,0),A(0,0, 2),B(0, 2,0),E(0,0,0),
ur uur
设平面DAB与平面ABF 的一个法向量分别为n x ,y ,z ,n x ,y ,z ,
1 1 1 1 2 2 2 2
uuur
二面角DABF 平面角为,而AB 0, 2, 2 ,
uuur uuur uuur
因为EF DA 2,0, 2 ,所以F 2,0, 2 ,即有AF 2,0,0 ,
2x 2z 0 ur
1 1 ,取x 1,所以n (1,1,1);
1 1
2y 2z 0
1 1
2y 2z 0 uur
2 2 ,取y 1,所以n (0,1,1),
2 2
2x 0
2
ur uur
n n
1 2 2 6 6 3
所以, cos ur uur ,从而sin 1 .
n n 3 2 3 9 3
1 2
3
所以二面角DABF 的正弦值为 .
3
典例3【2022新高考全国Ⅰ卷】如图,直三棱柱ABC- ABC 的体积为4,VABC 的面积为2 2.
1 1 1 1
(1)求A到平面ABC的距离;
1
(2)设D为AC的中点,AA AB,平面ABC 平面ABB A ,求二面角ABDC的正弦值.
1 1 1 1 1
3
【答案】(1) 2 (2)
2
【解析】【1】在直三棱柱ABC- ABC 中,设点A到平面ABC的距离为h,
1 1 1 1
1 2 2 1 1 4
则V S h hV S AA V ,
AA 1 BC 3 VA 1 BC 3 A 1 ABC 3 VABC 1 3 ABCA 1 B 1 C 1 3
解得h 2,
31
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司所以点A到平面ABC的距离为 2 ;
1
【2】取AB的中点E,连接AE,如图,因为AA AB,所以AE AB,
1 1 1
又平面ABC 平面ABB A ,平面ABC平面ABB A AB,
1 1 1 1 1 1 1
且AE 平面ABB A ,所以AE 平面ABC,
1 1 1
在直三棱柱ABC- ABC 中,BB 平面ABC,
1 1 1 1
由BC平面ABC,BC平面ABC可得AE BC,BB BC ,
1 1
又AE,BB 平面ABB A 且相交,所以BC平面ABB A ,
1 1 1 1 1
所以BC,BA,BB 两两垂直,以B为原点,建立空间直角坐标系,如图,
1
由(1)得AE 2,所以AA AB2,AB2 2,所以BC 2,
1 1
则A0,2,0,A 0,2,2,B0,0,0,C2,0,0 ,所以AC的中点D1,1,1
,
1 1
uuur uuur uuur
则BD1,1,1,BA0,2,0,BC 2,0,0
,
uuuv
v
ur mBD x yz 0
设平面ABD的一个法向量mx,y,z,则v uuuv ,
mBA2y 0
ur
可取m1,0,1,
r uuuv
r nBDabc0
设平面BDC的一个法向量na,b,c,则r uuuv ,
nBC 2a0
r
可取n0,1,1,
32
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司ur r
ur r
mn 1 1
则 cos m,n ur r ,
m n 2 2 2
2
1 3
所以二面角ABDC的正弦值为 1 .
2 2
典例4【2022新高考全国Ⅱ卷】 如图,PO是三棱锥PABC 的高,PA PB,ABAC,E是PB的
中点.
(1)证明:OE//平面PAC ;
(2)若ABO CBO 30,PO3,PA5,求二面角CAEB的正弦值.
11
【答案】(1)证明见解析 (2)
13
【解析】【1】证明:连接BO并延长交AC于点D,连接OA、PD,
因为PO是三棱锥PABC 的高,所以PO平面ABC,AO,BO平面ABC,
所以PO AO、PO BO,
又PA PB,所以△POA△POB,即OAOB,所以OABOBA,
又ABAC,即BAC 90,所以OABOAD90,OBAODA90,
所以ODAOAD
所以AO DO,即AO DOOB,所以O为BD的中点,又E为PB的中点,所以OE//PD,
又OE 平面PAC ,PD平面PAC ,
所以OE//平面PAC
【2】解:过点A作Az//OP,如图建立空间直角坐标系,
因为PO3,AP5,所以OA AP2 PO2 4,
33
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司又OBAOBC 30,所以BD2OA8,则AD4,AB4 3,
所以AC 12,所以O 2 3,2,0 ,B 4 3,0,0 ,P 2 3,2,3 ,C0,12,0,
3
所以E 3 3,1, ,
2
uuur 3 uuur uuur
则AE 3 3,1, ,AB 4 3,0,0 ,AC 0,12,0,
2
v uuuv 3
r nAE 3 3x y z 0
设平面AEB的法向量为nx,y,z,则 2 ,令z 2,则y=3,x0,
uuuv
v
nAB4 3x0
r
所以n0,3,2;
v uuuv 3
ur mAE 3 3ab c0
设平面AEC的法向量为ma,b,c,则 2 ,
uuuv
v
mAC 12b0
ur
令a 3,则c6,b0,所以m 3,0,6 ;
r ur
r ur
nm 12 4 3
所以 cos n,m r ur .
n m 13 39 13
r ur
4 3
设二面角CAEB的大小为,则 cos cos n,m = ,
13
11 11
所以sin 1cos2 ,即二面角CAEB的正弦值为 .
13 13
典例5【2021新高考全国Ⅰ卷】 如图,在三棱锥ABCD中,平面ABD平面BCD,AB AD,O
为BD的中点.
34
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司(1)证明:OACD;
(2)若VOCD是边长为1的等边三角形,点E在棱AD上,DE 2EA,且二面角EBCD的大小为
45,求三棱锥ABCD的体积.
3
【答案】(1)证明见解析;(2) .
6
【解析】【详解】(1)因为AB AD,O是BD中点,所以OA BD,
因为OA平面ABD,平面ABD平面BCD,
且平面ABD平面BCD BD,所以OA平面BCD.
因为CD平面BCD,所以OACD.
(2)[方法一]:通性通法—坐标法
如图所示,以O为坐标原点,OA为z轴,OD为y轴,垂直OD且过O的直线为x轴,建立空间直角
坐标系Oxyz,
3 1 1 2
则C( , ,0),D(0,1,0),B(0,1,0),设A(0,0,m),E(0, , m),
2 2 3 3
uuur 4 2 uuur 3 3
所以EB(0, , m),BC ( , ,0),
3 3 2 2
r
设n x,y,z 为平面EBC 的法向量,
uuur
r
EBn 0 r 2
则由uuur
r
可求得平面EBC 的一个法向量为n ( 3,1, ).
BCn 0 m
uuur
又平面BCD的一个法向量为OA0,0,m,
35
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司r uuur 2 2
所以cos n,OA ,解得m 1.
4 2
m 4
m2
3 1 1 3 3
又点C到平面ABD的距离为 ,所以V V 21 ,
2 ABCD CABD 3 2 2 6
3
所以三棱锥ABCD的体积为 .
6
[方法二]【最优解】:作出二面角的平面角
如图所示,作EG BD,垂足为点G.
作GF BC,垂足为点F,连结EF ,则OA∥EG.
因为OA平面BCD,所以EG 平面BCD,
EFG为二面角EBCD的平面角.
因为EFG45,所以EG FG.
由已知得OB OD 1,故OB OC 1.
又OBC OCB30,所以BC 3.
2 4 2 2 2
因为GD ,GB ,FG CD ,EG ,OA1,
3 3 3 3 3
1 1 1 1 3 3
V S OA 2S OA 2( 11)1 .
ABCD 3 VBCD 3 VBOC 3 2 2 6
[方法三]:三面角公式
考虑三面角BEDC,记EBD为,EBC为,DBC 30,
记二面角EBCD为.据题意,得45.
对使用三面角的余弦公式,可得coscoscos30,
3
化简可得cos cos.①
2
sin
使用三面角的正弦公式,可得sin ,化简可得sin 2sin.②
sin
36
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司3
将①②两式平方后相加,可得 cos22sin21,
4
1 1
由此得sin2 cos2,从而可得tan .
4 2
π 1
如图可知(0, ),即有tan ,
2 2
4
根据三角形相似知,点G为OD的三等分点,即可得BG ,
3
结合的正切值,
2 3
可得EG ,OA1从而可得三棱锥ABCD的体积为 .
3 6
预测1(2024·全国·模拟预测)如图,在直三梭柱ABC- ABC 中,ÐACB= ÐABC,点M 为AB 的中点,
1 1 1 1 1
AB 平面MCC .
1 1 1
(1)证明:AM CM .
1
15
(2)若AB AA,N为棱CC 上一点,直线BN与平面AMN所成角的正弦值为 ,求平面AMN与平面CMN
1 1 1
5
的夹角的大小.
预测2(2024·河南焦作·模拟预测)如图,在五棱锥PABCDE中,PA平面ABCDE,AB//CD,
DE//BC,AB AE 2,DE2,BC 4,CD2 2.
37
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司(1)证明:CDPE;
(2)若点P与直线CD上一点Q的最小距离为3,求平面PBE与平面PCD夹角的余弦值.
预测3(2024·重庆·模拟预测)如图,ACDE为菱形,AC BC 2,ACB120,平面ACDE平面ABC,
点F在AB上,且AF 2FB,M,N分别在直线CD,AB上.
(1)求证:CF 平面ACDE;
(2)把与两条异面直线都垂直且相交的直线叫做这两条异面直线的公垂线,若EAC 60,MN为直线CD,AB
AN
的公垂线,求 的值;
AF
21
(3)记直线BE与平面ABC所成角为,若tan ,求平面BCD与平面CFD所成角余弦值的范围.
7
预测4(2024·广东韶关·模拟预测)如图,圆柱OO 内有一个直三棱柱ABC- ABC ,三棱柱的底面三角形
1 1 1 1
内接于圆柱底面,已知圆柱OO 的轴截面是边长为6的正方形,AB AC 30,点P在线段OO 上运动.
1 1
(1)证明:BC PA;
1
(2)当PA PB时,求BC与平面APB所成角的正弦值.
1 1
预测5(2024·山西朔州·模拟预测)如图,在四棱锥PABCD中,底面ABCD是边长为1的正方形,
PA2,E,F 分别为PB,PD上的点,PBPD 5,PD平面ABF .
38
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司(1)若EF PB,求PE的长;
(2)若E为PB的中点,求平面PEC与平面AEF夹角的余弦值.
π
押题1:如图,在三棱台ABC- ABC 中,AC 3,AC AA AB2,AB 3,AAC BAC ,
1 1 1 1 1 1 1 1 3
AO AC,垂足为O,连接BO.
1
(1)证明:平面ACC A 平面AOB;
1 1 1
(2)求直线BB与平面ACC A 所成角的正弦值.
1 1 1
押题2:如图所示,三棱柱ABC- ABC 所有棱长都为2,BBC=60o,O为BC中点,D为AC与AC 交
1 1 1 1 1 1
点.
(1)证明:CD//平面AOB ;
1
(2)证明:平面BCD平面ABC ;
1 1
2 13
(3)若直线DB 与平面AOB 所成角的正弦值为 ,求二面角A CB C 的平面角的余弦值.
1 1 1 1 1
13
39
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司押题3:如图,在圆台OO中,AABB 为轴截面,AB2AB 4,AAB60o,C为下底面圆周上一点,F
1 1 1 1 1 1
为下底面圆O内一点,AE垂直下底面圆O于点E,COF EFO.
1
(1)求证:平面OOC//平面AEF;
1 1
(2)若△EFO为等边三角形,求平面AEF和平面AOC的交线l与平面ACF所成角的正弦值.
1 1 1
押题4:如图,在三棱柱ABC- ABC 中,AA AB ,ABBC,四边形BCCB 是菱形.
1 1 1 1 1 1 1 1
(1)证明:AC BC;
1 1
3
(2)若ABBC BC,求二面角BAC C的正弦值.
3 1 1
押题5:如图所示,在四棱锥PABCD中,PA平面ABCD,AD∥BC,ADCD,且
PC BC 2 AD 2CD 2 2, PA 2.
(1)求三棱锥BACP的体积;
(2)求证:ABPC.
名校预测
预测1:答案(1)证明见解析;(2)30.
【详解】(1)证明:因为AB 平面MCC ,CM 平面MCC ,所以AB CM ,
1 1 1 1 1 1 1 1
40
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司由直三棱柱的性质,可得AA 平面ABC ,CM 平面ABC ,所以AA CM ,
1 1 1 1 1 1 1 1 1 1
又因为AA I AB A,AA 平面ABBA ,AB 平面ABBA ,
1 1 1 1 1 1 1 1 1 1 1
所以CM 平面ABBA
1 1 1
因为AM 平面ABBA ,所以AM CM .
1 1 1
(2)解:在底面三角形ABC中,ÐACB= ÐABC,则AC AB,即AC AB ,
1 1 1 1
由(1)知AB CM ,且点M 为AB 的中点,所以AC BC ,
1 1 1 1 1 1 1 1 1
所以△ABC 为等边三角形,
1 1 1
取AB的中点D,连接CD,MD,则CDAB,MDAB,CDMD,
以D为原点,分别以DB,DC,DM 所在直线为x轴、y轴、z轴建立空间直角坐标系,
如图所示,不妨取AB2,则A1,0,0,B1,0,0,M0,0,2,
uuuur uuur uuur
设N 0, 3,m 0m2,则AM 1,0,2,AN 1, 3,m ,BN 1, 3,m ,
uuuur r
r AMnx2z0
设平面AMN的法向量为nx,y,z,则uuur
r
,
ANnx 3ymz0
2m r 2m
取z1,则x2,y ,所以n 2, ,1 ,
3 3
设直线BN 与平面AMN所成的角为,
uuur r 22mm 15
可得sin cosBN,n ,
2m2 5
4m2 5
3
4 15
即 m24m19 5 ,整理得m44m323m216m40,
4m2
3
则m1 m33m220m4 0,
令 f mm33m220m40m2,则 fm3m26m20,
因为3643202040,所以 fm0,所以 f m在0,2上单调递增,
r 3
又 f m f 04,所以m1,此时n2, ,1,
3
因为AB 平面MCC ,所以AB平面MCC ,即AB平面CMN ,
1 1 1 1 1
uuur
所以平面CMN 的法向量可取AB2,0,0,
1
41
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司r uuur
r uuur nAB 4 4 3
cosn,AB r uuur
所以 n AB 1 16 2 ,
4 12 2
3 3
故平面AMN与平面CMN 的夹角为30.
1
5
预测2:答案(1)证明见解析(2)
6
【详解】(1)证明:如图,延长BA交DE的延长线于点F ,
因为AB//CD,DE//BC,所以四边形FBCD为平行四边形.
因为BF CD2 2,所以AB AF AE 2,
所以BEEF.
易知BC DF 4,则EF DE2,
故AE2 AF2 EF2,所以AEBF .
又AB//CD,所以CD AE.
又PA平面ABCDE,CD平面ABCDE,所以PACD.
又PAI AE A,PA,AE平面PAE,
所以CD平面PAE,又PE平面PAE,所以CDPE.
(2)当PQ取最小值时,PQCD,由(1)知PACD,
因为PAI PQP,PA,PQ平面PAQ,所以CD平面PAQ.
又AQ平面PAQ,所以CD AQ,从而A,E,Q三点共线,即线段AE,CD的延长线交于点Q.
连接BD,PQ.
由(1)知A,E分别是BF,DF的中点,所以BD//AE,所以BDAB.
又AB//DQ,所以四边形ABDQ是矩形,
所以AQBD BC2CD2 2 2,又PQ2 PA2AQ2 9,故PA1.
42
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司以A为坐标原点,AB,AE,AP所在直线分别为x轴、y轴、z轴,建立如图所示的空间直角坐标系,
则A(0,0,0),P(0,0,1),B( 2,0,0),E(0, 2,0),C(3 2,2 2,0),D( 2,2 2,0),
uuur uuur uuur uuur
所以BP( 2,0,1),BE( 2, 2,0),DP( 2,2 2,1),DC (2 2,0,0).
r
设平面PBE的法向量为m(x,y,z),
r uuur
mBP0, 2xz0,
则r uuur 即
mBE0, 2x 2y0.
r
令x1,得y1,z 2 ,则平面PBE的一个法向量为m(1,1, 2).
r
设平面PCD的法向量为nx,y,z,
r uuur
nDP0, 2x2 2yz0,
则r uuur 即
nDC 0, 2 2x0.
r
令y1,得x0,z2 2,则平面PCD的一个法向量为n(0,1,2 2).
设平面PBE与平面PCD的夹角为,
r r
r r |mn| 5 5
则cos|cosm,n| r r ,
|m||n| 23 6
5
故平面PBE与平面PCD夹角的余弦值为 .
6
AN 9 5 2 2 5
预测3:答案(1)证明见解析(2) (3) ,
AF 13 8 5
【详解】(1)AB2 AC2BC22ACBCcosACB12,AB2 3,AF 2FB,
4 3 uuur 1uuur 2uuur uuur 2 1uuur 2 4uuur 2 4uuur uuur 4
所以AF ,CF CA CB,CF CA CB CACB ,
3 3 3 9 9 9 3
4 16
AC2CF2 4 AF2,则CF AC,
3 3
又因为平面ACDE平面ABC,平面ACDEI 平面ABC AC,CF 面ABC,
故CF 平面ACDE;
(2)以C为原点,CA的方向为x轴正方向,建立如图所示空间直角坐标系Cxyz,
由EAC 60,可得DCA120,DC2,
所以C0,0,0,D 1,0, 3 ,A2,0,0,F 0, 2 3 ,0
3
uuur 2 3 uuur
所以AF 2, ,0,CD 1,0, 3 ,
3
uuur uuur 2 3 2 3
设AN AF 2, ,0,则N22, ,0,
3 3
43
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司uuuur uuur uuuur 2 3
设CM CD,则M ,0, 3 ,MN 22, , 3,
3
uuuur uuur
2230
MNCD0
由题知,uuuur uuur 4 ,
MNAF 0 442 0
3
9 2 AN 9
解得 , ,故 ;
13 13 AF 13
(3)B 1, 3,0 ,设EAC,
uuur
则E22cos,0,2sin,BE 32cos, 3,2sin ,
r
可取平面ABC的法向量n0,0,1,
r uuur
r uuur nBE 2sin sin
则sincosn,BE r uuur ,
n BE 32cos2 34sin2 43cos
43cossin2
cos ,
43cos
sin 21
则tan ,
43cossin2 7
2 1
整理得10cos29cos20,故cos , ,
5 2
uuur 2 uuur uuur
CF 0, ,0 ,CD2cos,0,2sin,CB 1, 3,0 ,
3
ur uuur 2xcos2zsin0
ur n CD0
记平面CDF的法向量为n x,y,z,则有ur1 uuur 2 ,
1 n CF 0 y0
1 3
ur
可得n sin,0,cos,
1
uur uuur
uur n CD0 2acos2csin0
记平面CBD的法向量为n a,b,c,则有uu2r uuur ,
2 n CB0 a 3b0
2
uur
可得n 3sin,sin, 3cos ,
2
记平面BCD与平面CFD所成角为,
ur uur 3 2 1
则cos cosn,n ,cos , ,
1 2 3sin2 5 2
3 21 15 4 6
所以sin2 , , 3sin2
,
,
4 25
2 5
44
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司3 5 2 2 5
故cos , .
3sin2 8 5
11
预测4:答案(1)证明见解析.(2) .
11
【详解】(1)
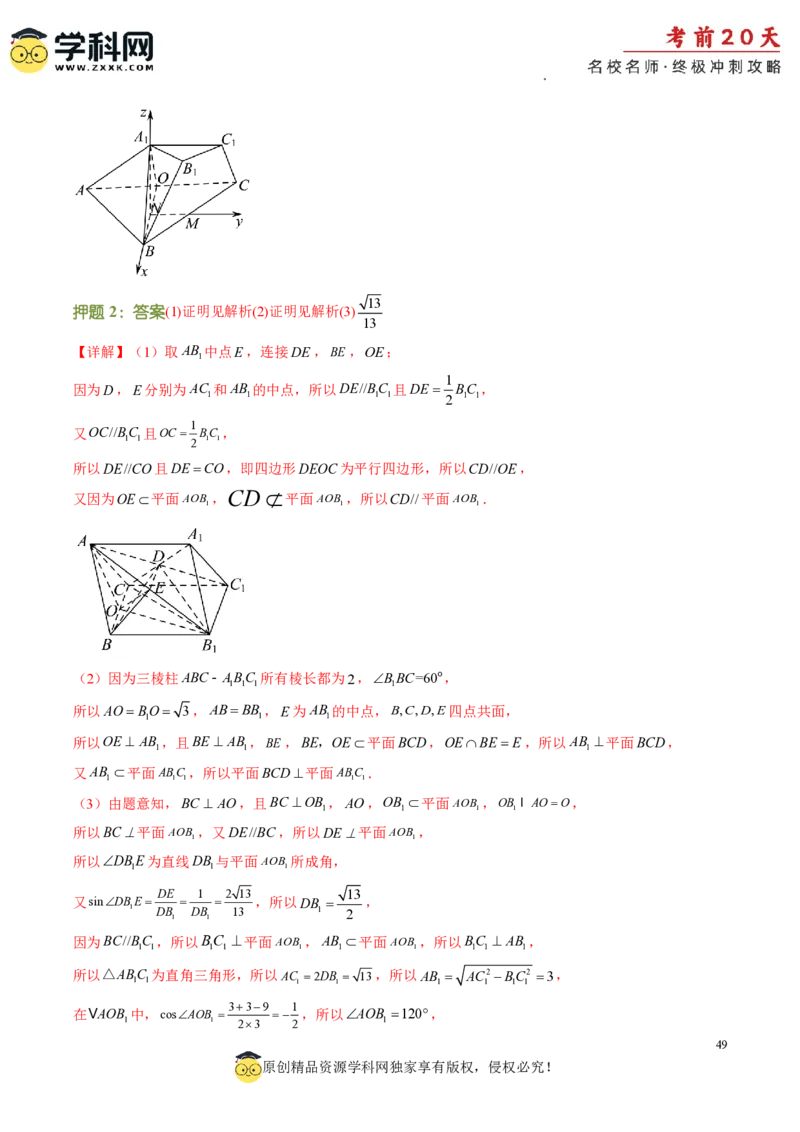
连接AO并延长,交BC于M ,交圆柱侧面于N ,
QAO BC ,OO 为圆柱的高,
1 1 1 1 1
AO、BC、OO 两两垂直,以O 为原点,过点O 做BC 平行线为x轴,以AO 为y轴,以OO为z轴,建
1 1 1 1 1 1 1 1 1 1 1 1
立如图所示空间直角坐标系O xyz,
1
OO AA AN 6,AB AC 30,
1 1
在VABC中,由射影定理得AC2 AMAN 30 AM 5 ,
OM AM AO2,
2
从而CM BM 30 52 5,
uuur
A 0,3,0,B 5,2,6 ,C 5,2,6 ,BC 2 5,0,0 ,
1
uuur
设P0,0,,AP0,3,,
1
uuur uuur
APBC 0,BC PA .
1 1
uuur
(2)由(1)可得,BP 5,2,6 ,
uuur uuur
AP BP , 9 5462 ,得3,即点P是线段OO的中点,
1 1
45
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司uuur uuur
AP0,3,3,BP 5,2,3 ,
1
r
设平面APB的一个法向量为nx,y,z,
1
3y3z0 r 5
则 ,取y1,得n ,1,1,
52y3z0 5
r
设BC的一个方向向量为m1,0,0,于是得:
5
r r 5 11
cosn,m ,
2 11
5
121
5
r r 11
设BC与平面APB所成角为,则sin cosn,m ,
1
11
11
所以BC与平面APB所成角的正弦值为 .
1
11
16 5 2 105
预测5:答案(1) (2)
25 35
【详解】(1)因为PD平面ABF ,AB,AF 平面ABF ,故PD AB,PD AF ,
而底面ABCD是正方形,故ABAD,
因PDI ADD,PD,AD平面PAD,故AB平面PAD,
而PA平面PAD,故AB AP,
又PA2,AD1,PD 5,故PD2 PA2AD2,故PA AD,
故分别以直线AB,AD,AP为x,y,z轴建立如图所示的空间直角坐标系,
uuur
则A0,0,0,B1,0,0,C1,1,0,D0,1,0,P0,0,2,故PD0,1,2,
uuur uuur
设PF PD0,1,20,,2,故F0,,22,
uuur
故AF 0,,22,
uuur uuur 4 4 2
由PDAF 440,故= ,故F0, , ,
5 5 5
uuur
PB1,0,2,
uuur uuur
设PEuPBu1,0,2u,0,2u,故Eu,0,22u,
uuur 4 8
故EF u, ,2u ,
5 5
uuur uuur 16 16
因PBEF ,故PBEF0,所以u4u 0,故u ,
5 25
46
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司uuur 16 uuur 16 16 5
故 PE PB 5 .
25 25 25
1 uuur 1 uuur
(2)因为E为PB的中点,故E ,0,1,故PE ,0,1,PC 1,1,2,
2 2
r
设平面PEC的法向量为nx,y,z,
r uuur 1
nPE0 xz0
则r uuur ,故2 ,取x2,则z1,y=0,
nPC 0 xy2z0
r
故n2,0,1,
4 2 uuur 4 2 uuur 1
由(1)可得F0, , ,故AF 0, , ,而AE ,0,1,
5 5 5 5 2
r
设平面AEF的法向量为ma,b,c,
r uuur
1
ac0
nAE0 2
则r uuur ,故 ,取a4,则c2,b1,
nAF 0 4 b 2 c0
5 5
r
故m4,1,2,
r r
r r mn 6 2 105
故cos m,n r r .
m n 21 5 35
2 105
故平面PEC与平面AEF夹角的余弦值为 .
35
名师押题
3
押题1:答案(1)见解析(2)
10
π
【详解】(1)因为AA AB2,AAC BAC ,AO AO,
1 1 3
所以VAAOVBAO,AO AC,所以BOAC,
1 1
因为AOBOO,AO,BO平面AOB,
1 1 1
47
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司所以AC平面AOB,又因为AC平面ACC A ,
1 1 1
所以平面ACC A 平面AOB;
1 1 1
π
(2)因为AA2,AAC ,AO AC,所以AO1,AO AA2AO2 3,
1 1 3 1 1 1
同理可得:BO 3,所以△AOB是等边三角形,
1
取BO的中点N ,连接AN ,所以AN OB,
1 1
由(1)知,AC平面AOB,AC平面ABC,所以平面ABC平面AOB,
1 1
平面ABC平面AOBOB,OB平面ABC,所以AN 平面ABC,
1 1
取BC的中点M ,连接MN,则MN BO,
所以以N 为坐标原点,建立如图所示的空间直角坐标系,
3 3 3 3 3
则N0,0,0,O 2 ,0,0 ,B 2 ,0,0 ,C 2 ,2,0 ,A 1 0,0, 2 ,A 2 ,1,0 ,
因为 u A uu B ur 2u A u B ur ,设B x,y,z,所以 u A uu B ur x,y,z 3 , 2u A u B ur 2 3,1,0 ,
1 1 3 1 1 1 2 3 3
2 3 2 3 2 3 2 3
所以x ,y ,z ,所以B , , ,
3 3 2
1
3 3 2
uuur 3 2 3 uuur uuur 3 3
可得BB , , ,OA0,1,0,OA ,0, .
1 6 3 2 1 2 2
ur uuur
n OAb0
ur 1
设平面ACC 1 A 1 的法向量为n 1 a,b,c,则ur uuur 3 3 ,
n OA a c0
1 1 2 2
ur
取a 3,可得b0,c1,所以n 3,0,1 ,
1
设直线BB与平面ACC A 所成角的为,
1 1 1
ur uuur
ur uuur n BB 1 1 3
1 1
sin cos n,BB ur uuur
所以 1 1 n BB 100 10 10,
1 1 2 2
36 6
3
故直线BB与平面ACC A 所成角的正弦值为 .
1 1 1 10
48
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司13
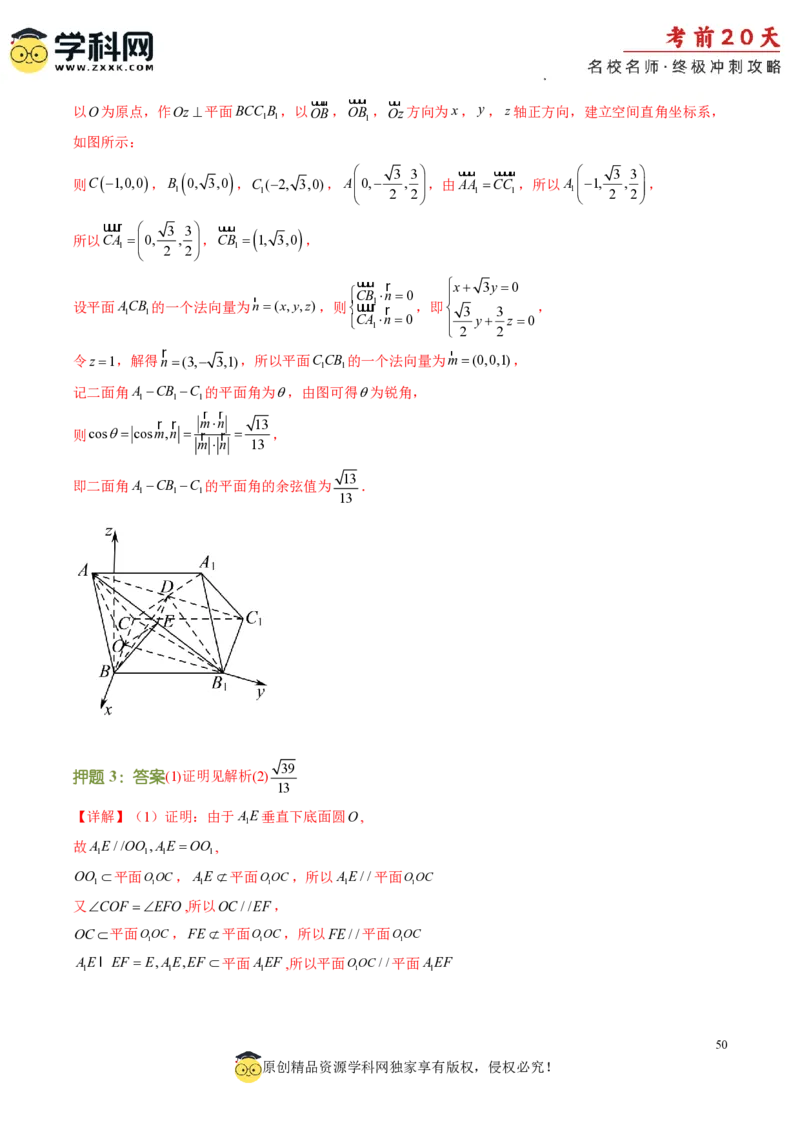
押题2:答案(1)证明见解析(2)证明见解析(3)
13
【详解】(1)取AB 中点E,连接DE,BE,OE;
1
1
因为D,E分别为AC 和AB 的中点,所以DE//BC 且DE BC ,
1 1 1 1 2 1 1
1
又OC//BC 且OC BC ,
1 1 2 1 1
所以DE//CO且DECO,即四边形DEOC为平行四边形,所以CD//OE,
CD
又因为OE平面AOB , 平面AOB ,所以CD//平面AOB .
1 1 1
(2)因为三棱柱ABC- ABC 所有棱长都为2,BBC=60o,
1 1 1 1
所以AOBO 3,ABBB ,E为AB 的中点,B,C,D,E四点共面,
1 1 1
所以OE AB ,且BE AB ,BE,BE,OE平面BCD,OEBEE,所以AB 平面BCD,
1 1 1
又AB 平面ABC ,所以平面BCD平面ABC .
1 1 1 1 1
(3)由题意知,BC AO,且BC OB ,AO,OB 平面AOB ,OB I AOO,
1 1 1 1
所以BC平面AOB ,又DE//BC,所以DE平面AOB ,
1 1
所以DBE为直线DB 与平面AOB 所成角,
1 1 1
DE 1 2 13 13
又sinDBE ,所以DB ,
1 DB DB 13 1 2
1 1
因为BC//BC ,所以BC 平面AOB ,AB 平面AOB ,所以BC AB ,
1 1 1 1 1 1 1 1 1 1
所以△ABC 为直角三角形,所以AC 2DB 13,所以AB AC2BC2 3,
1 1 1 1 1 1 1 1
339 1
在VAOB 中,cosAOB ,所以AOB 120,
1 1 23 2 1
49
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司uuur uuur uur
以O为原点,作Oz平面BCCB ,以OB,OB ,Oz方向为x,y,z轴正方向,建立空间直角坐标系,
1 1 1
如图所示:
则C1,0,0,B 0, 3,0 ,C (2, 3,0),A 0, 3 , 3 ,由 u A u A ur C uu C uur ,所以A 1, 3 , 3 ,
1 1 2 2 1 1 1 2 2
uuur 3 3 uuur
所以CA 0, , ,CB 1, 3,0 ,
1 2 2 1
uuur r x 3y0
r CB n0
设平面A 1 CB 1 的一个法向量为n(x,y,z),则uuur1 r ,即 3 3 ,
CA n0 y z0
1 2 2
r r
令z1,解得n(3, 3,1),所以平面CCB 的一个法向量为m(0,0,1),
1 1
记二面角A CB C 的平面角为,由图可得为锐角,
1 1 1
r r
r r mn 13
则cos cosm,n r r ,
m n 13
13
即二面角A CB C 的平面角的余弦值为 .
1 1 1
13
39
押题3:答案(1)证明见解析(2)
13
【详解】(1)证明:由于AE垂直下底面圆O,
1
故AE//OO,AEOO ,
1 1 1 1
OO 平面OOC,AE平面OOC,所以AE//平面OOC
1 1 1 1 1 1
又COF EFO,所以OC//EF,
OC平面OOC,FE平面OOC,所以FE//平面OOC
1 1 1
AEI EF E,AE,EF 平面AEF,所以平面OOC//平面AEF
1 1 1 1 1
50
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司1
(2)由题意可得四边形AABB 为等腰梯形,且AB2AB 4,AAB60o,故AE ABAB 1,
1 1 1 1 1 2 1 1
AE 3,
1
π
由于△EFO为等边三角形,COF EFO ,AEEOOF EF 1,
3
π
又OC//EF,C在圆O上,所以CAOACOEFA ,CACB,
6
故OF AC,F为AC中点,
过A作AM //EF 交圆O 于点M ,又 OC//EF,故AM //OC,
1 1 1 1
则AM 为平面AEF和平面AOC的交线,
1 1 1
建立如图所示的空间直角坐标系系,
C0,0,0,B2,0,0,A 0,2 3,0 ,F 0, 3,0 ,E 1 , 3 3 ,0 ,A 1 , 3 3 , 3 ,
2 2
1
2 2
uuur uuur 1 3 3
则CF 0, 3,0 ,CA , , 3,
1 2 2
uuur r 1 3 3
r CA m x y 3z0
设平面ACF的法向量为mx,y,z,则 1 2 2 ,
1 uuur r
CFm 3y0,
r
取x2 3,则m 2 3,0,1 ,
uuur 1 3
FE , ,0,
2 2
uuur r
uuur r FEm 3 39
所以cosFE,m uuur r ,
FE m 13 13
39
故AM 与平面ACF所成角的正弦值为
1 1
13
51
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司42
押题4:答案(1)证明见解析(2)
7
【详解】(1)三棱柱ABC- ABC 中,由AA AB 可得ABBB ,
1 1 1 1 1 1 1
因ABBC,且BB I BC B,BB,BC面BBCC,则AB平面BBCC,
1 1 1 1 1 1
因BC平面BBCC,则ABBC,又四边形BCCB 是菱形,则BC BC,
1 1 1 1 1 1 1 1
由ABI BC B,AB,BC 面ABC ,故得 BC面ABC ,因AC 面ABC ,故AC BC.
1 1 1 1 1 1 1 1 1
(2)
3 4412 1
因BB BC BC,不妨设BC2 3,则BB BC 2,由余弦定理,cosBBC ,故得:
1 3 1 1 1 1 222 2
BBC 120,
1
uuur uuur
分别取BA,BC为x,y轴的正方向建立如图所示的空间直角坐标系.( z轴为与平面ABC垂直向上的方向),
uuur uuuur
则有B0,0,0,C 0,1, 3 ,C0,2,0,A2,0,0,BA2,0,0,BC (0,1, 3),
1 1
uuur r
ur BAm2x0 ur
设平面BAC
1
的法向量为m(x,y,z),则uuuur
r
,故可取m(0, 3,1);
BC m y 3z0
1
uuuur uuuur
又因AC 2,1, 3 ,CC 0,1, 3 ,
1 1
uuuur r
r AC n2xy 3z0 r
设平面AC 1 C的法向量为n(x,y,z),则 1uuuur r ,故可取n( 3, 3,1).
CCn y 3z0
1
r r 13 7
设二面角BAC C的平面角为,则 coscosm,n ,因q[0,π],故
1 2 7 7
42
sin 1cos2 .
7
52
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司42
故二面角BAC C的正弦值为 .
1
7
4
押题5:答案(1) (2)证明见解析
3
【详解】(1)在底面ABCD中,AD//BC,ADCD,且 BC 2 AD 2CD 2 2,
所以 AB AC 2, BC 2 2,则 AB2 AC2 BC2,所以ABAC,
1 1 4
故V V 222 .
BACP PABC 3 2 3
(2)由(1)知ABAC,又PA平面ABCD,AP平面ABCD,则ABPA,
且ACPA A,AC,PA平面PAC,
∴AB平面PAC,而PC平面PAC,所以ABPC.
函数与导数(解答题)
年份 题号 知识点 考点
①求不含参单调性
2021年I
22 函数与导数 ②函数求最值解决不等
卷
式问题
2021年II ①求含参单调性
22 函数与导数
卷 ②函数求最值解决不等式问题
2022年I 22 函数与导数 ①利用函数最值求参数
53
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司卷 ②函数零点问题
2022年II ①求不含参单调性
22 函数与导数
卷 ②函数求最值解决参数范围问题
2023年新 ①求含参单调性
19 函数与导数
高考1 ②函数求最值解决不等式问题
2023 年新
①函数求最值解决不等式问题
高考2 22 函数与导数
②函数求极值解决参数范围问题
近三年,导数在解答题中占据一个位置,考查的考点一般来说是:
1、含参与不含参讨论单调性(①含参一次模型②含参二次模型③含参类一次模型④含参类二次模型)
2、能成立与恒成立问题(①能参变分离模型②不能参变分离模型)
3、切线问题、极值点偏移、隐零点问题(①含参与不含参的切线问题及过与在的区别②极值点固定问题的
考察③隐零点问题的巧用)
题干的设置一般来说在上述的三项考点中选其一项或两项。无论是简单导数还是复杂导数,考生都应
掌握两大固定模板(切线及单调性),另外考生们需要多掌握含参问题的转化,尽可能变为能成立与恒成
立问题。
从近三年的全国卷的考查情况以及新高考新题型标准来看,导数是高考解答题必不可少的一类题,类
型1:含参求单调性,类型2:能成立与恒成立求参数问题,类型3:求含参最值与极值各项技巧,导数小
结论偏多,试题大概率位于第一道解答题偏于简单,此类题目多研究即可拿分.
一、指对混合问题(同构)
在解决指数函数与对数函数的混合不等式恒成立求参数范围或证明指对不等式时,如果使用参变分离、隐
零点代换等方法,都避免不了复杂计算,有时效果也不一定好,而使用同构法会达到意想不到的效果.
如何构造同构函数呢?一般情况下含ex和lnx的函数,主要是统一化为左边或化为右边构造同构式.同构式
需要构造这样一个母函数,这个函数既能满足指数与对数互化,又能满足单调性和最值易求等特点,因此
常见的同构形式大多为yxlnx,yxex,或其同族函数.经过同构变形,再结合复合函数的单调性,可以
快速解决证明不等式、恒成立求参数的取值范围等问题.
构造同构函数通常有三种基本模式:
(1)积型
54
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司三种同构方式
aea blnb
同左:aea lnbelnbL (f x)xex
同右:ealnea blnbL (f x)xlnx
取对:alnalnblnlnbL (f x)xlnx
(2)商型
ea b三种同构方式
a
ea elnb ex
同左: L (f x)
a nb x
ea b x
同右: L (f x)
lnea lnb lnx
取对:alnalnblnlnbL (f x)xlnx
(3)和差型
二种同构方式
ea ablnb
同左:ea aelnblnbL (f x)exx
同右:ea lnea blnbL (f x)xlnx
其中xelnx lnex在变形构造同构式中起着重要作用.
二:恒成立与存在性问题
专题阐述:无论是不等式的证明、解不等式,还是不等式的恒成立问题、有解问题、无解问题,构造函数,运用
函数的思想,利用导数研究函数的性质(单调性和最值),达到解题的目的,是一成不变的思路,合理构思,善于从
不同角度分析问题是解题的法宝.
考法一: 不等式恒成立问题
不等式恒成立问题常见处理方法:① 分离参数a f x恒成立(a f x 可)或a f x恒成立
max
(a f x 即可);② 数形结合(y f x图象在ygx 上方即可);③ 最值法:讨论最值 f x 0
min min
或 f x 0恒成立;④ 讨论参数.
max
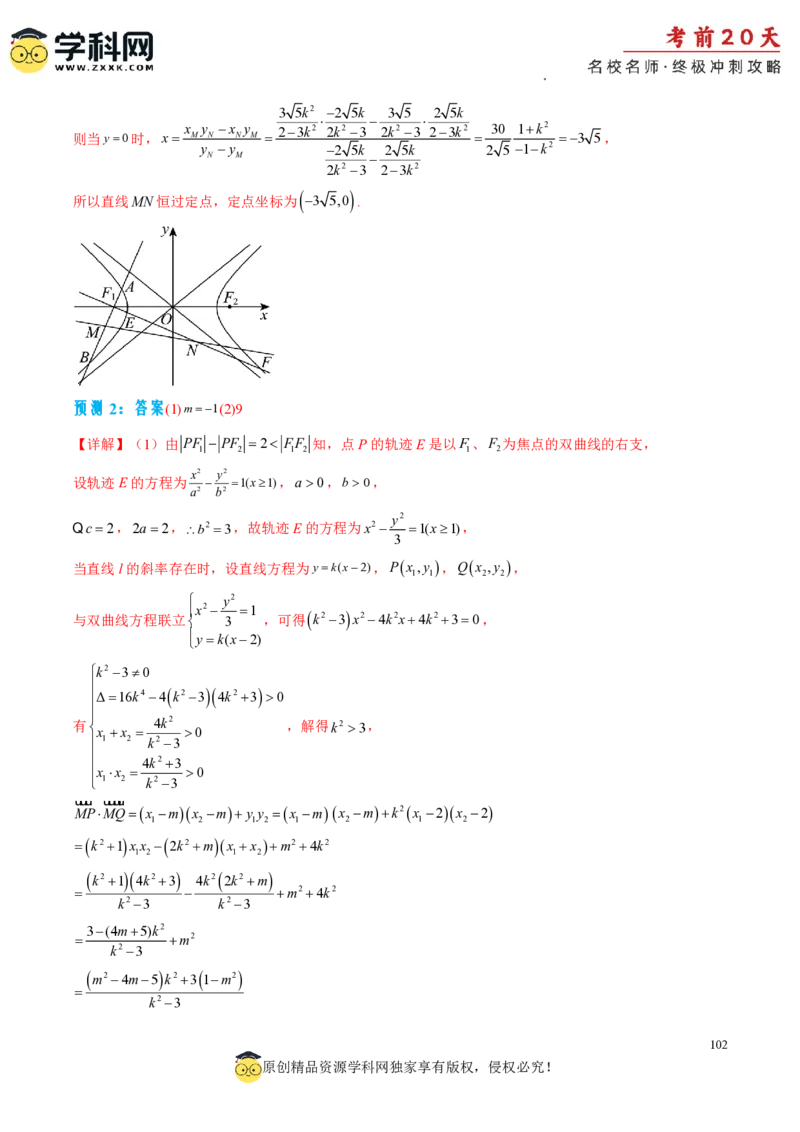
考法二:不等式(方程)有解(能成立)问题
根据导数的方法研究不等式能成立问题,一般可对不等式变形,分离参数,根据分离参数后的结果,构造
函数,由导数的方法求出函数的最值,进而可求出结果;有时也可根据不等式,直接构造函数,根据导数
的方法,利用分类讨论求函数的最值,即可得出结果.
三:极值点偏移问题
专题阐述:极值点偏移问题大体可分为加法型、减法型、乘积型、平方型及商型5个类型,考查学生化归
与转化思想,逻辑思维能力、运算求解能力,是历年高考中题的一个难点.
55
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司处理极值点偏移问题中的类似于x x a(x,x 为 f x0的两根)的问题的基本步骤如下:
1 2 1 2
①求导确定 f x的单调性,得到x,x 的范围;
1 2
②构造函数Fx f x f ax,求导后可得Fx恒正或恒负;
③得到 f x 与 f ax 的大小关系后,将 f x 置换为 f x ;
1 1 1 2
④根据x与ax 所处的范围,结合 f x的单调性,可得到x与ax 的大小关系,由此证得结论.
2 1 2 1
由此,其它类型可模仿上面步骤进行变形及构造.
四:双变量问题
专题阐述:双变量问题主要表现为双变量不等式问题,一般包括中点型、极值和差商积问题、剪刀模型及
主元法.
破解双变量不等式的方法:
一是转化,即由已知条件入手,寻找双参数满足的关系式,并把含双变量的不等式转化为含单变量的不等
式;
二是巧构函数,再借用导数,判断函数的单调性,从而求其最值;
三是回归双变量的不等式的证明,把所求的最值应用到双变量不等式,即可证得结果.
五:凹凸反转问题
专题阐述: 很多时候,我们需要证明函数 f(x)0,但不代表就要证明 f(x) 0,因为大多数情况下, f '(x)
min
的零点是解不出来的.当然,导函数的零点如果解不出来,可以用设隐零点的方法,但是隐零点也不是万能
的方法,如果隐零点不行可尝试用凹凸反转.
f(x)0g(x)h(x),如果能够证明g(x) h(x) ,则g(x)h(x)显然成立,很明显,g(x)是凹函数,
min max
h(x)是凸函数,因为这两个函数的凹凸性刚好相反,所以称为凹凸反转.凹凸反转与隐零点都是用来处理导
函数零点不可求的问题的,两种方法互为补充.
六:隐零点设而不求
专题阐述:隐零点是用导数判断函数单调性和求最值常规方法的补充,而求最值和判断单调性是所有导数
大题共有的解题基础,因此这部分内容是导数的基本功,如果尝试在导数压轴大题上争取更高的分数,则
隐零点问题必须熟练掌握.
隐零点问题的出题特征较为明显,在参数范围的题目中所求的参数经常为整数,因为利用此类方法求出的
最值通常是一个范围,当然也不排除有些题目设计较为巧妙,在求最值时的未知零点可以约分成一个具体
的数字.
56
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司典例1【2023新高考1卷】已知函数 f xa ex a x.
(1)讨论 f x 的单调性;
3
(2)证明:当a0时, f x2lna .
2
【答案】(1)答案见解析 (2)证明见解析
【解析】【1】因为 f(x)a ex a x,定义域为R ,所以 fxaex 1,
当a0时,由于ex 0,则aex 0,故 fxaex 10恒成立,
所以 f x 在R 上单调递减;
当a0时,令 fxaex 10,解得x lna,
当xlna时, fx0,则 f x 在 ,lna 上单调递减;
当x lna时, f¢(x)>0,则 f x 在 lna, 上单调递增;
综上:当a0时, f x 在R 上单调递减;
当a0时, f x 在 ,lna 上单调递减, f x 在 lna, 上单调递增.
【2】方法一:
由(1)得, f x f lnaa elna a lna 1a2 lna,
min
3 3 1
要证 f(x)2lna ,即证1a2 lna 2lna ,即证a2 lna0恒成立,
2 2 2
1 1 2a2 1
令gaa2 lnaa0,则ga2a ,
2 a a
2 2
令ga0,则0a ;令ga0,则a
;
2 2
2 2
所以ga 在0, 上单调递减,在 ,上单调递增,
2 2
2
2 2 1 2
所以ga g ln ln 2 0,则ga0恒成立,
min 2 2 2 2
3
所以当a0时, f(x)2lna 恒成立,证毕.
2
57
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司方法二:
令hxex x1,则hxex 1,
由于yex在R 上单调递增,所以hxex 1在R 上单调递增,
又h0e0 10,
所以当x
0时,hx0;当x0时,hx0;
所以hx
在
,0
上单调递减,在
0,
上单调递增,
故hxh00,则ex
x1,当且仅当x0时,等号成立,
因为 f(x)a ex a xaex a2 xexlna a2 x xlna1a2 x,
当且仅当xlna 0,即x lna时,等号成立,
3 3 1
所以要证 f(x)2lna ,即证xlna1a2 x2lna ,即证a2 lna0,
2 2 2
1 1 2a2 1
令gaa2 lnaa0,则ga2a ,
2 a a
2 2
令ga0,则0a ;令ga0,则a
;
2 2
2 2
所以ga 在0, 上单调递减,在 ,上单调递增,
2 2
2
2 2 1 2
所以ga g ln ln 2 0,则ga0恒成立,
min 2 2 2 2
3
所以当a0时, f(x)2lna 恒成立,证毕.
2
典例2【2023新高考全国Ⅱ卷】 (1)证明:当0 x1时,xx sinx x;
(2)已知函数 f xcosaxln 1x2 ,若x0是 f x 的极大值点,求a的取值范围.
【答案】(1)证明见详解(2) , 2 U 2,
【解析】【详解】(1)构建Fx xsinx,x0,1 ,则Fx1cosx0对x0,1
恒成立,
则Fx
在
0,1 上单调递增,可得Fx F00,
所以xsinx,x0,1
;
构建Gxsinx xx2 x2 xsinx,x0,1 ,
58
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司则Gx2x1cosx,x0,1
,
构建gxGx,x0,1 ,则gx2sinx0对x0,1
恒成立,
则gx
在
0,1 上单调递增,可得gx g00,
即Gx0对x0,1
恒成立,
则Gx
在
0,1 上单调递增,可得GxG00,
所以sinx xx2,x0,1 ;
综上所述:xx sinx x.
(2)令1x2 0,解得1 x1,即函数 f x 的定义域为 1,1 ,
若a0,则 f x1ln 1x2 ,x1,1 ,
因为y lnu在定义域内单调递减,y 1x2在 1,0 上单调递增,在 0,1 上单调递减,
则 f x1ln 1x2 在 1,0 上单调递减,在 0,1 上单调递增,
故x0是 f x 的极小值点,不合题意,所以a0.
当a0时,令b a 0
因为 f xcosaxln 1x2 cos a x ln 1x2 cosbxln 1x2 ,
且 f xcosbxln1x2 cosbxln 1x2 f x ,
所以函数 f x 在定义域内为偶函数,
2x
由题意可得: fxbsinbx ,x1,1,
x2 1
1
(i)当0b2 2时,取mmin ,1,x0,m,则bx0,1 ,
b
2x 2x x b2x2 2b2
由(1)可得 fxbsinbx b2x ,
x2 1 x2 1 1x2
且b2x2 0,2b2 0,1x2 0,
x b2x2 2b2
所以 fx 0,
1x2
即当x0,m0,1 时, f¢(x)>0,则 f x 在 0,m 上单调递增,
结合偶函数的对称性可知: f x 在 m,0 上单调递减,
59
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司所以x0是 f x 的极小值点,不合题意;
1
(ⅱ)当b2 2时,取x 0, 0,1 ,则bx0,1 ,
b
2x 2x x
由(1)可得 fxbsinbx b bxb2x2 b3x3 b2x2 b3x2b2 ,
x2 1 x2 1 1x2
1
构建hxb3x3 b2x2 b3x2b2,x 0, ,
b
1
则hx3b3x2 2b2xb3,x 0, ,
b
1 1
且h0b3 0,h b3 b0,则hx0对x 0, 恒成立,
b b
1 1
可知hx 在 0, 上单调递增,且h02b2 0,h 20,
b b
1 1
所以hx 在 0, 内存在唯一的零点n 0, ,
b b
当x0,n 时,则hx0,且x0,1x2
0,
x
则 fx b3x3 b2x2 b3x2b2 0,
1x2
即当x0,n0,1 时, fx0,则 f x 在 0,n 上单调递减,
结合偶函数的对称性可知: f x 在 n,0 上单调递增,
所以x0是 f x 的极大值点,符合题意;
综上所述:b2 2,即a2 2,解得a 2或a 2,
故a的取值范围为 , 2 U 2, .
典例3【2022新高考全国Ⅰ卷】已知函数 f(x)ex ax和g(x)axlnx有相同的最小值.
(1)求a;
(2)证明:存在直线y b,其与两条曲线y f(x)和y g(x)共有三个不同的交点,并且从左到右的三
个交点的横坐标成等差数列.
【答案】(1)a 1 (2)见解析
60
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司【解析】【1】 f(x)ex ax的定义域为R,而 f(x)ex a,
若a0,则 f(x)0,此时 f(x)无最小值,故a0.
1 ax1
g(x)axlnx的定义域为 0, ,而g(x)a .
x x
当xlna时, f(x)0,故 f(x)在 ,lna 上为减函数,
当xlna时, f(x)0,故 f(x)在 lna, 上为增函数,
故 f(x) f lnaaalna.
min
1 1
当0 x 时,g(x)0,故g(x)在 0, 上为减函数,
a a
1 1
当x 时,g(x)0,故g(x)在 , 上为增函数,
a a
1 1
故g(x) g 1ln .
min a a
因为 f(x)ex ax和g(x)axlnx有相同的最小值,
1 a1
故1ln aalna,整理得到 lna,其中a0,
a 1a
a1 2 1 a2 1
设ga lna,a 0,则ga 0,
1a 1a2 a a1a2
故ga
为
0, 上的减函数,而g10,
1a
故ga0的唯一解为a 1,故 lna的解为a 1.
1a
.
综上,a 1
【2】[方法一]:
1
由(1)可得 f(x)ex x和g(x) xlnx的最小值为1ln11ln 1.
1
当b1时,考虑ex xb的解的个数、xlnxb的解的个数.
设Sxex xb,Sxex 1,
当x
0时,Sx0,当x0时,Sx0,
故Sx
在
,0
上为减函数,在
0,
上为增函数,
所以Sx S01b0,
min
61
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司而Sbeb 0,Sbeb 2b,
设ubeb 2b,其中b1,则ubeb 20,
故ub
在
1, 上为增函数,故ubu1e20,
故Sb0,故Sxex xb有两个不同的零点,即ex xb的解的个数为2.
x1
设Tx xlnxb,Tx ,
x
当0
x1时,Tx0,当x1时,Tx0,
故Tx
在
0,1
上为减函数,在
1,
上为增函数,
所以Tx T11b0,
min
而T eb eb 0,T eb eb 2b0,
Tx xlnxb有两个不同的零点即xlnxb的解的个数为2.
当b1,由(1)讨论可得xlnxb、ex xb仅有一个解,
当b1时,由(1)讨论可得xlnxb、ex xb均无根,
故若存在直线y b与曲线y f x 、y gx 有三个不同的交点,
则b1.
1
设h(x)ex lnx2x,其中x0,故h(x)ex 2,
x
设sxex x1,x0,则sxex 10,
故sx
在
0, 上为增函数,故sxs00即ex
x1,
1
所以h(x) x 1210,所以h(x)在 0, 上为增函数,
x
1 1 2 2
而h(1)e20,h( )ee3 3 e3 0,
e3 e3 e3
1
故hx 0, 上有且只有一个零点x , x 1且:
0 e3 0
当0 x x 时,hx0即ex x xlnx即 f xgx ,
0
当x x 时,hx0即ex x xlnx即 f xgx ,
0
因此若存在直线y b与曲线y f x 、y gx 有三个不同的交点,
62
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司故b f x gx 1,
0 0
此时ex xb有两个不同的根x ,x (x 0 x ),
1 0 1 0
此时xlnxb有两个不同的根x ,x (0 x 1 x ),
0 4 0 4
故ex 1 x b,ex 0 x b,x lnx b0,x lnx b0
1 0 4 4 0 0
所以x blnx 即ex 4 b x 即ex 4 b x bb0,
4 4 4 4
故x b为方程ex xb的解,同理x b也为方程ex xb的解
4 0
又ex 1 x b可化为ex 1 x b即x lnx b0即 x blnx bb0,
1 1 1 1 1 1
故x b为方程xlnxb的解,同理x b也为方程xlnxb的解,
1 0
所以 x ,x x b,x b ,而b1,
1 0 0 4
x x b
故 0 4 即x x 2x .
x x b 1 4 0
1 0
[方法二]:
由(1)知, f(x)ex x,g(x) xlnx,
且 f(x)在(,0)上单调递减,在(0,)上单调递增;
g(x)在(0,1)上单调递减,在(1,)上单调递增,且 f(x) g(x) 1.
min min
①b1时,此时 f(x) g(x) 1b,显然y b与两条曲线y f(x)和y g(x)
min min
共有0个交点,不符合题意;
②b1时,此时 f(x) g(x) 1b,
min min
故y b与两条曲线y f(x)和y g(x)共有2个交点,交点的横坐标分别为0和1;
③b1时,首先,证明y b与曲线y f(x)有2个交点,
即证明F(x) f(x)b有2个零点,F(x) f(x) ex 1,
所以F(x)在(,0)上单调递减,在(0,)上单调递增,
又因为F(b) eb 0,F(0)1b0,F(b) eb 2b 0,
(令t(b)eb 2b,则t(b) eb 2 0,t(b)t(1)e20)
所以F(x) f(x)b在(,0)上存在且只存在1个零点,设为x,在(0,)上存在且只存在1个零点,
1
设为x .
2
其次,证明y b与曲线和y g(x)有2个交点,
63
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司1
即证明G(x) g(x)b有2个零点,G(x) g(x)1 ,
x
所以G(x)(0,1) 上单调递减,在(1,)上单调递增,
又因为G(eb) eb 0,G11b0,G(2b)bln2b 0,
1
(令(b)bln2b,则(b)1 0,(b) (1) 1ln2 0)
b
所以G(x) g(x)b在(0,1)上存在且只存在1个零点,设为x ,在(1,)上存在且只存在1个零点,
3
设为x .
4
再次,证明存在b,使得x x :
2 3
因为F(x )G(x )0,所以bex 2 x x lnx ,
2 3 2 3 3
若x x ,则ex 2 x x lnx ,即ex 2 2x lnx 0,
2 3 2 2 2 2 2
所以只需证明ex 2xlnx 0在(0,1)上有解即可,
即(x) ex 2xlnx在(0,1)上有零点,
1 1 2
因为( )ee3 30,(1)e20,
e3 e3
所以(x) ex 2xlnx在(0,1)上存在零点,取一零点为x ,令x x x 即可,
0 2 3 0
此时取bex 0 x
0
则此时存在直线y b,其与两条曲线y f(x)和y g(x)共有三个不同的交点,
最后证明x x 2x ,即从左到右的三个交点的横坐标成等差数列,
1 4 0
因为F(x ) F(x ) F(x )0G(x )G(x )G(x )
1 2 0 3 0 4
所以F(x )G(x ) F(lnx ),
1 0 0
又因为F(x)在(,0)上单调递减,x 0,0 x 1即lnx 0,所以x lnx ,
1 0 0 1 0
同理,因为F(x )G(ex 0)G(x ),
0 4
又因为G(x)在(1,)上单调递增,x 0即ex 0 1,x 1,所以x ex 0 ,
0 1 4
又因为ex 0 2x lnx 0,所以x x ex 0 lnx 2x ,
0 0 1 4 0 0
即直线y b与两条曲线y f(x)和y g(x)从左到右的三个交点的横坐标成等差数列.
64
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司典例4【2022新高考全国Ⅱ卷】 已知函数 f(x) xeax ex.
(1)当a 1时,讨论 f(x)的单调性;
(2)当x0时, f(x)1,求a的取值范围;
1 1 1
(3)设nN,证明: L ln(n1).
12 1 22 2 n2 n
1
【答案】(1) f x 的减区间为 ,0 ,增区间为 0, . (2)a (3)见解析
2
【解析】【1】当a 1时, f xx1ex,则 fx xex,
当x 0时, fx0,当x0时, f¢(x)>0,
故 f x 的减区间为 ,0 ,增区间为 0, .
【2】设hxxeax ex 1,则h00,
又hx1axeaxex,设gx1axeaxex,
则gx 2aa2x eaxex,
1
若a ,则g02a10,
2
因为gx
为连续不间断函数,
故存在x 0, ,使得x0,x ,总有gx0,
0 0
故gx
在
0,x 为增函数,故gx g00,
0
故hx
在
0,x 为增函数,故hxh00,与题设矛盾.
0
1
若0a ,则hx1axeaxex eaxln1axex,
2
下证:对任意x0,总有ln1x x成立,
65
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司1 x
证明:设Sxln1xx,故Sx 1 0,
1x 1x
故Sx 在 0, 上为减函数,故SxS00即ln1x x成立.
由上述不等式有eaxln1axex eaxaxex e2axex 0,
故hx0总成立,即hx
在
0,
上为减函数,
所以hxh00.
当a0时,有hxeaxexaxeax 1100,
所以hx
在
0, 上为减函数,所以hxh00.
1
综上,a .
2
1
1
【3】取a ,则x0,总有
xe2
x
ex 10
成立,
2
令 1 x,则t 1,t2 ex,x2lnt ,
t e2
1
故2tlnt t2 1即2lntt 对任意的t1恒成立.
t
n1 n1 n
所以对任意的nN*,有2ln ,
n n n1
1
整理得到:lnn1lnn
,
n2n
1 1 1
故 L ln2ln1ln3ln2L lnn1lnn
121 222 n2n
lnn1
,
故不等式成立.
预测1(2024·江苏南通·模拟预测)设函数 f xxalnxxa,aR.
(1)若a0,求函数 f x的单调区间;
(2)若 2 a0,试判断函数 f x在区间 e2,e2 内的极值点的个数,并说明理由;
e2
(3)求证:对任意的正数a,都存在实数t,满足:对任意的xt,ta, f xa1.
x23x2
预测2(2024·辽宁抚顺·模拟预测)设函数 f x ,gxxlnx1.
ex1
66
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司(1)讨论 f x的单调性.
(2)证明:gx0.
(3)当xe1时,证明: f xlnx2.
预测3(2024·湖南·模拟预测)罗尔定理是高等代数中微积分的三大定理之一,它与导数和函数的零点有关,
是由法国数学家米歇尔·罗尔于1691年提出的.它的表达如下:如果函数 f(x)满足在闭区间[a,b]连续,在
开区间(a,b)内可导,且 f(a) f(b),那么在区间(a,b)内至少存在一点m,使得 f(m)0.
(1)运用罗尔定理证明:若函数 f(x)在区间a,b连续,在区间(a,b)上可导,则存在x (a,b),使得
0
f(b) f(a)
f(x ) .
0 ba
1
(2)已知函数 f(x)xlnx,g(x) x2bx1,若对于区间(1,2)内任意两个不相等的实数x,x ,都有
2 1 2
| f(x ) f(x )||g(x )g(x )|成立,求实数b的取值范围.
1 2 1 2
1 1 1 1
(3)证明:当p1,n2时,有 [ ].
np p1 (n1)p1 np1
预测4(2024·安徽·模拟预测)已知函数 f(x)x210x3f(1)lnx.
(1)求函数 f(x)在点(1, f(1))处的切线方程;
(2)求 f(x)的单调区间和极值.
ax1
预测5(2024·重庆·模拟预测)函数 f xlnx .
x1
(1)讨论 f x的单调性;
(2)若函数 f x有两个极值点x,x ,曲线y f x上两点 x,f x , x ,f x 连线斜率记为k,求证:
1 2 1 1 2 2
2a
k ;
a1
(3)盒子中有编号为1~100的100个小球(除编号外无区别),有放回的随机抽取20个小球,记抽取的20
1
个小球编号各不相同的概率为p,求证:p .
e2
押题1:已知函数 f xlnx1,gxex1.
(1)求曲线y f x与ygx的公切线的条数;
(2)若a0,x1,, f x1a2gxa2a1,求a的取值范围.
67
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司1 3
押题2:设函数 f xalnx x1,aR,曲线y f x在点 2,f 2 处的切线与直线5x8y0平
2x 2
行.
(1)求a的值;
(2)求 f x的单调区间和极值.
押题3:已知函数 f xx2alnx1,aR.
(1)当a1时,求曲线y f x在点 1, f 1 处的切线方程;
(2)当a0时,若函数 f x有最小值2,求a的值.
押题4:已知函数 f xex1axaR.
(1)若函数 f x在点 1, f 1 处的切线与直线x2ey10垂直,求a的值;
(2)当x0,2时,讨论函数Fx f xxlnx零点的个数.
押题5:已知函数 f(x)lnxax1,aR.
(1)讨论 f x的单调性;
(2)若x0, f xxe2x2ax恒成立,求实数a的取值范围.
名校预测
预测1:答案(1)减区间(0,1),增区间(1,)(2) f(x)在 e2,e2 内有一个极值点(3)证明见解析
【详解】(1)当a0时, f(x)xlnxx, f(x)lnx,
令 f(x)0,x1,列表分析
x (0,1) 1 (1,)
f(x) 0
f(x) 单调递减 单调递增
故 f(x)的单调递减区间为(0,1),单调递增区间为(1,);
a xlnxa
(2) f xxalnxxa, f(x)lnx ,其中x0,
x x
1
令g(x)xlnxa,g(x)lnx1,令g(x)0,x ,
e
列表分析:
68
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司1 1 1
x (0, ) ( ,)
e e e
g(x) 0
g(x) 单调递减 单调递增
1 1
g(x) g( ) a,
min e e
1 1 a 1
而 f( )ln ae1ae, f(e2)2ae2 (2ae2), f(e2)2 (2e2a),
e e e2 e2
2 1 1 1
若 a0,则 f( )ln ae0, f(e2)(2ae2)0, f(e2) (2e2a)0,
e2 e e e2
因此 f(x)在 e2,e2 上有一个零点,所以 f(x)在 e2,e2 内有一个极值点;
(3)猜想:x(1,1a), f(x)a1恒成立.
证明如下:
1
由(2)得g(x)在( ,)上单调递增,且g(1)a0,g1a1aln1aa.
e
1
因为当x1时,lnx1 (*),
x
1
所以g(1a)(1a)(1 )a0.
a1
故g(x)在(1,1a)上存在唯一的零点,设为x .由
0
x (1,x ) x (x ,1a)
0 0 0
f(x) 0
f(x) 单调递减 单调递增
知,x(1,1a), f xmaxf 1, f 1a ,
又 f(1a)ln(1a)1,而x1时,lnxx1(**),
所以 f(1a)(a1)11a1 f (1).
即x(1,1a), f(x)a1.
所以对任意的正数a,都存在实数t 1,使对任意的x(t,ta),使 f(x)a1.
补充证明(*):
1 1 1 x1
令F(x)lnx 1,x1.F(x) 0,
x x x2 x2
所以F(x)在[1,)上单调递增.
所以x1时,F(x)F10,即lnx1 1 .
x
69
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司补充证明(**)
1
令G(x)lnxx1,x1.G(x) 10,
x
所以G(x)在[1,)上单调递减.
所以x1时,G(x)G10,即lnxx1.
预测2:答案(1)答案见解析(2)证明见解析(3)证明见解析
x23x2 x2x1
【详解】(1)解:由函数 f x ,可得 fx ,
ex1 ex1
令 fx0,解得x 1 5 或x 1 5 .
2 2
1 5 1 5 1 5
当x, 时, fx0;当x , 时, fx0;
2 2 2
1 5
当x ,时, fx0.
2
1 5 1 5 1 5 1 5
故 f x在, 和 ,上单调递减,在 , 上单调递增.
2 2 2 2
x
(2)证明:由函数gxxlnx1的定义域为1,,且gx ,
x1
当x1,0时,gx0,gx单调递减;
当x0,时,gx0,gx单调递增,
所以当x0时,gx的最小值为g00,故gxg00.
(3)证明:当xe1时,lnx21,
x1x2 ex1 elnx2
要证 lnx2,即证 .
ex1 x1 lnx2
ex x1ex
设hx ,则hx ,
x x2
当x1时,hx0,则hx在1,上单调递增,
ex1 elnx2
且hx1 ,hlnx2 ,
x1 lnx2
当xe1时,x11,lnx21,故只需证明x1lnx2.
由(2)知,xlnx1在1,上成立,故x1lnx2,
即 f xlnx2成立.
预测3:答案(1)证明见解析;(2)1ln2b2;(3)证明见解析.
70
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司f(b) f(a)
【详解】(1)令 t,则 f(b)bt f(a)at,
ba
令函数F(x) f(x)tx,则F(a)F(b),F(x) f(x)t,
显然F(x)在a,b上连续,且在(a,b)上可导,由罗尔定理,存在x (a,b),使得F(x )0,
0 0
f(b) f(a)
即 f(x )t0,所以 f(x ) .
0 0 ba
(2)依题意, f(x)lnx1,g(x)xb,
f(x ) f(x ) g(x )g(x )
不妨令x x ,则| 1 2 || 1 2 |恒成立,
1 2 x x x x
1 2 1 2
由(1)得| f(x)||g(x)|,x(1,2),于是lnx1|xb|,即1lnxbxlnx1,
因此xlnx1bxlnx1,令(x)xlnx1(1x2),
x1
求导得(x) 0,函数(x)在(1,2)上单调递增,则0(x)1ln2,
x
而函数yxlnx1在(1,2)上单调递增,其值域为(2,3ln2),
则1ln2b2,所以实数b的取值范围是1ln2b2.
(3)令函数h(x)x1p,x[n1,n],显然函数h(x)在(n1,n)上可导,
h(n1)h(n)
由(1),存在c(n1,n),使得h(c) ,
(n1)n
1 1
又h(x)(1 p)xp,则 h(c)(p1)cp,
(n1)p1 np1
1 1 1 1 1 1
因此 [ ] ,而1n1cn,p1,则cp np,即 ,
p1 (n1)p1 np1 cp cp np
1 1 1 1
所以 [ ].
np p1 (n1)p1 np1
预测4:答案(1)y4x13;
(2)递增区间为(0,2),(3,),递减区间为2,3,极大值1612ln2,极小值2112ln3.
3f(1)
【详解】(1)函数 f(x)x210x3f(1)lnx,求导得 f(x)2x10 ,
x
则 f(1)83f(1),解得 f(1)4,于是 f(x)x210x12lnx, f(1)9,
所以所求切线方程为:y94(x1),即y4x13.
(2)由(1)知,函数 f(x)x210x12lnx,定义域为(0,),
12 2(x2)(x3)
求导得 f(x)2x10 ,
x x
当0x2或x3时, f(x)0,当2x3时, f(x)0,
因此函数 f(x)在(0,2),(3,)上单调递增,在(2,3)上单调递减,
当x2时, f(x)取得极大值 f(2)1612ln2,
71
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司当x3时, f(x)取得极小值 f(3)2112ln3,
所以函数 f(x)的递增区间为(0,2),(3,),递减区间为(2,3),
极大值1612ln2,极小值2112ln3.
预测5:答案(1)答案见解析(2)证明见解析(3)证明见解析
1 ax1ax1 x222ax1
【详解】(1) f x定义域为0,, fx ,
x x12 xx12
对于方程x222ax10,22a244 a22a ,
当0,即0a2时,x222ax10, fx0, f x在0,上单增,
当0,即a0或a2时,方程x222ax10有两不等根,
x a1 a22a ,x a1 a22a,而x x 2a1,xx 1,
1 2 1 2 1 2
所以当a0时,x x 0, f¢(x)>0在0,上恒成立, f x在0,上单增;
1 2
当a2时,0x x ,x0,x 或xx ,时, f¢(x)>0,xx,x 时, fx0,
1 2 1 2 1 2
所以 f x在0,x 和x ,上单增,在x,x 上单减,
1 2 1 2
综上,当a2时, f x在0,上单增;
当a2时, f x在 0,a1 a22a 和 a1 a22a, 上单增,
在 a1 a22a,a1 a22a 上单减;
ax 1 ax 1
lnx 1 lnx 2
(2) f x f x 1 x 1 2 x 1
k 1 2 1 2
x x x x
1 2 1 2
x 2ax x x 2ax x
ln 1 1 2 ln 1 1 2
x x 1x 1 x xx x x 1
2 1 2 2 1 2 1 2
x x x x
1 2 1 2
x
ln 1
x 2a lnx lnx ,
2 1 2 1
x x 12a21 x x
1 2 1 2
2a lnx lnx 1 lnx lnx 2
所以要证k ,即证 1 2 1 1,即证 1 2 ,
a1 x x a1 x x x x
1 2 1 2 1 2
x
2 1 1
x 2x x x x
也即证ln 1 1 2 ln 1 2 0(*)成立.
x x x x x
2 1 2 2 1 1
x
2
x 2t1
设t 1 0,1 ,函数htlnt ,由(1)知ht在0,上单增,且h10,
x t1
2
72
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司所以t0,1时,ht0,所以(*)成立,原不等式得证;
A20 100998281
(3)由题可得p 100 ,
10020 10020
因为998190292 902,988290282 902,…,918990212 902,
9 19
所以p
,
10
2t1
又由(2)知t1,,htlnt 0,
t1
10
2 1
10 10 9 10 2
取t ,有ln ln 0,
9 9 10 9 19
1
9
10 19 10 19
即ln
2,即
e2,
9 9
9 19 1
所以p .
10 e2
名师押题
押题1:答案(1)2条(2)a1
【详解】(1)设 f xlnx1,gxex1的切点分别为 x, f x ,x ,gx ,
1 1 2 2
1
则 fx ,g(x)ex,
x
1 1
故 f xlnx1,gxex1在切点处的切线方程分别为y xx lnx 1 y xlnx ,
x 1 1 x 1
1 1
yex 2 xx ex 2 1 yex 2xx ex 2 ex 2 1
2 2
则需满足;
1
x
ex2
,故ln 1 x ex2 ex2 1 ex2 1 x 10,
ln
1
x x ex2 ex2 1
ex2 2 2
1 2
解得x 0或x 1,
2 2
因此曲线y f x与ygx有两条不同的公切线,
(2)由 f x1a2gxa2a1可得lnx11a2 ex1 a2a1,
即lnx1a2exa对于x1,恒成立,
ln01a2e0a,结合a0,解得a1
设m(x)lnxx1,,
73
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司1
则当x1时m(x) 10,mx单调递减,当0x1时,m(x)0,mx单调递增,
x
故当m(x)m10,故lnxx1,
因此lnx1x,x1,
令Fxxa2exa,x1,则Fx1a2ex,
令Fx1a2ex 0,得x2lna,
当2lna1时,此时a e,Fx1a2ex 0,故Fx在x1上单调递减,
e 2 e2 e 2 e2
所以 FxF11 a2 a a2eae a 2 4 e e 2 4 e e20 ,
e e e e
所以Fxxa2exa0,由于lnx1x进而ln(x1)a2exa0,满足题意,
当2lna1时,此时1a e,
令Fx1a2ex 0,解得1x2lna,Fx单调递增,
令Fx1a2ex 0,解得x2lna,Fx单调递减,
故FxFx F2lna2lna1a,
max
2 a2
令pa2lna1a,则pa 1 ,
a a
2 a2
由于 1a e,所以pa 1 0,
a a
故pa在1a e单调递减,故pa p1,即可pa0,
因此FxFx F2lna2lna1a0Fx0
max
所以Fxxa2exa0,由于lnx1x进而ln(x1)a2exa0,满足题意,
综上可得a1
1 1
押题2:答案(1)a2;(2)递减区间是(0, ),(1,),递增区间是( ,1),极小值22ln3,极大值0.
3 3
1 3 a 1 3
【详解】(1)由函数 f(x)alnx x1,求导得 f(x) ,
2x 2 x 2x2 2
a 1 3 5 7
依题意, f(2) ,解得a2,此时 f(2)2ln2 ,
2 8 2 8 4
显然点(2, f(2))不在直线5x8y0上,符合题意,
所以a2.
1 3 (3x1)(x1)
(2)由(1)知,函数 f(x)2lnx x1的定义域为(0,), f(x) ,
2x 2 2x2
74
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司1 1
当0x 或x1时, f(x)0,当 x1时, f(x)0,
3 3
1 1
即函数 f(x)在(0, ),(1,)上单调递减,在( ,1)上单调递增,
3 3
1 1
当x 时, f(x)取得极小值 f( )22ln3,当x1时, f(x)取得极大值 f(1)0,
3 3
1 1
所以函数 f(x)的递减区间是(0, ),(1,),递增区间是( ,1),极小值22ln3,极大值0.
3 3
押题3:答案(1)yx1(2)a2
【详解】(1)当a1时, f xx2lnx1,y f x的定义域为0,,
1 1
则 fx2x ,则 f12 1, f 11ln112,
x 1
由于函数 f x在点 1, f 1 处切线方程为y2x1,即yx1.
(2) f xx2alnx1,aR的定义域为0,,
a 2x2a
fx2x ,
x x
a a
当a0时,令 f¢(x)>0,解得:x ;令 fx0,解得:0x ,
2 2
a a
所以 f x在0, 上单调递减,在 ,上单调递增,
2 2
a a a a a a
所以, f(x) f aln 12,即 ln 10
min 2 2 2 2 2 2
a
则令t 0,设gtttlnt1,gtlnt,
2
令gt0,解得:t1;令gt0,解得:0t1,
所以gt在0,1上单调递增,在1,上单调递减,
所以gtg11ln110,
a
所以t 1,解得:a2.
2
押题4:答案(1)ae(2)答案见解析
【详解】(1)由题意可知: fxexa,可知 f1ea,
1
且直线x2ey10的斜率为k ,
2e
1
由题意可知:ea 1,解得ae.
2e
75
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司ex 1
(2)由Fx f xxlnx0得a lnx,
x x
ex 1
令gx lnxx0,2,
x x
可知Fx的零点个数即为ya与ygx的交点个数,
x1ex 1 1 x1 ex1
则gx ,
x2 x2 x x2
因为x0,则ex10,
令gx0,解得1 x2;令gx0,解得0x1;
可知gx在0,1内单调递减,在1,2内单调递增,
e21
且x趋近于0时,gx趋近于,g1e1,g2 ln2,
2
e21
当ae1或a ln2时,函数F(x)有一个零点;
2
e21
当e1a ln2时,函数F(x)有两个零点;
2
当ae1时,函数F(x)没有零点.
押题5:答案(1)答案见解析(2) ,2.
1
【详解】(1)函数 f xlnxax1,aR的定义域为0,,且 f(x) a.
x
1
当a0时,x0,, f(x) a0恒成立,此时 f x在区间0,上单调递增;
x
1 1ax 1
当a0时,令 f(x) a 0,解得x ,
x x a
1 1
当x0, 时, fx0, f x在区间0, 上单调递增,
a a
1 1
当x ,时, fx0, f x在区间 ,上单调递减.
a a
综上所述,当a0时, f x在区间0,上单调递增;
76
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司 1 1
当a0时, f x在区间0, 上单调递增,在区间 ,上单调递减.
a a
(2)设gxexx1,则gxex1,
在区间(,0)上,gx0,gx单调递减,在区间0,上,gx0,gx单调递增,
所以gxg0e0010,所以ex x1(当且仅当x0时等号成立).
lnx1
依题意,x0, f xxe2x2ax恒成立,即ae2x 恒成立,
x
lnx1 xe2x(lnx1) e2xlnx(lnx1) 2xlnx1(lnx1)
而e2x 2,
x x x x
当且仅当2xlnx0时等号成立.
1 2
因为函数hx2xlnx在0,上单调递增,h 10,h(1)20,
e e
1
所以存在x ,1,使得2x lnx 0成立.
0 e 0 0
lnx1
所以ae2x
2,即a的取值范围是,2.
x
min
圆锥曲线(解答题)
年份 题号 知识点 考点
77
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司2021年I ①轨迹方程的求算
21 圆锥曲线
卷 ②斜率之和问题
2021年II ①椭圆方程的求算
20 圆锥曲线
卷 ②三点共线及弦长问题
2022年I ①双曲线方程的求算
21 圆锥曲线
卷 ②面积问题
2022年II ①双曲线方程的求算
21 圆锥曲线
卷 ②直线与双曲线综合问题
2023年新 ①轨迹方程的求算
22 圆锥曲线
高考1 ②矩形周长问题
2023 年新 ①轨迹方程的求算
高考2 21 圆锥曲线 ②直线与双曲线定点定
直线问题
近三年,圆锥曲线在解答中占据一个位置,考查的考点一般来说是:
1、阿基米德三角形(①圆锥曲线中的定点、定值、定直线问题 ②阿基米德三角形周长问题③阿基米德三
角形面积问题)
2、齐次化妙解圆锥曲线问题(①圆锥曲线的定义、定值、弦长、面积②圆锥曲线斜率之和或者斜率之积)
3、圆锥曲线之极点与极线(①长度乘积定值②分数和问题)
题干的设置一般来说在上述的三项考点中选其一项或两项。有关圆锥曲线考生需熟记每一种模型,有
关圆锥曲线第二问考生需要多方位掌握,研究每一类结论的来源并数形结合探讨图像,这样方便考生在考
场灵活应对。
从近三年的全国卷的考查情况以及新高考新题型标准来看,圆锥曲线是高考解答题必不可少的一类题,
类型1:轨迹方程的求算,类型2:斜率积和问题。类型3:阿基米德三角形,尤其极点极线熟练掌握,类
型3相对有难度,考生多研究分析.
一、阿基米德三角形
抛物线上一点的切线方程
(1)过抛物线y2 2pxp0上一点Mx ,y 的切线方程为:y y pxx ;
0 0 0 0
(2)过抛物线y2 2pxp0上一点Mx ,y 的切线方程为:y ypxx ;
0 0 0 0
78
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司(3)过抛物线x2 2pyp0上一点Mx ,y 的切线方程为:x x py y ;
0 0 0 0
(4)过抛物线x2 2pyp0上一点Mx ,y 的切线方程为:x xpyy .
0 0 0 0
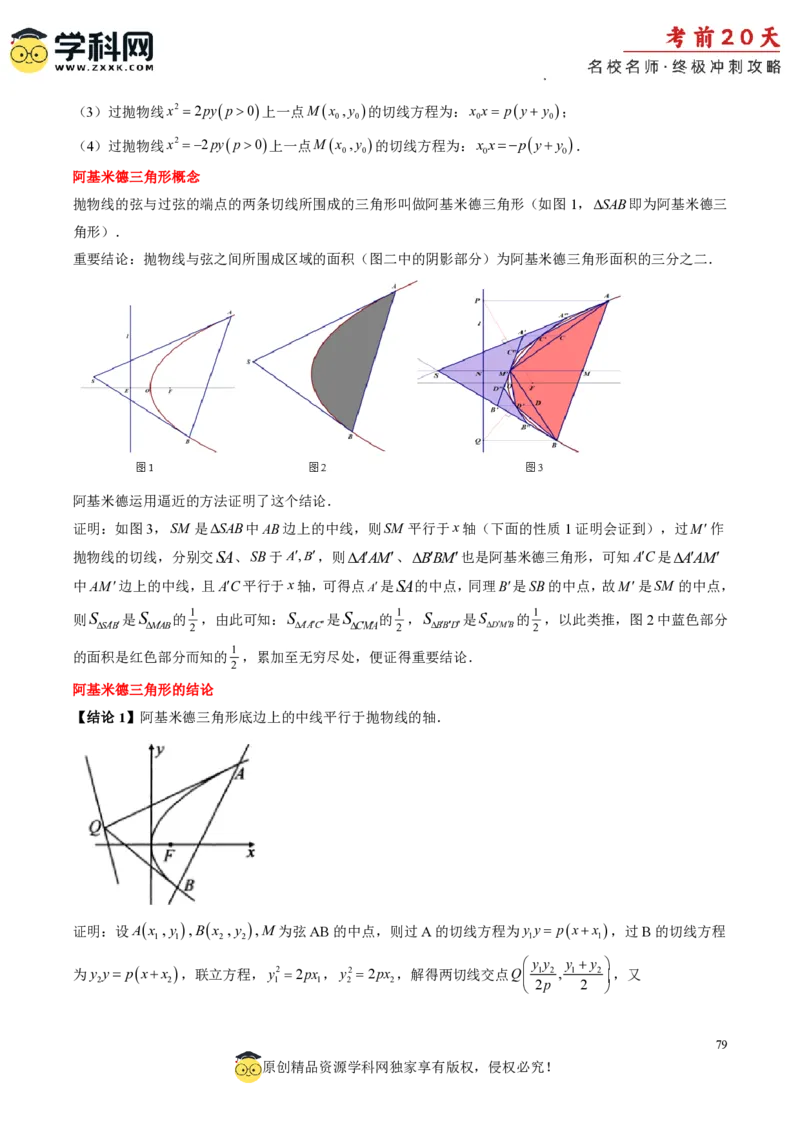
阿基米德三角形概念
抛物线的弦与过弦的端点的两条切线所围成的三角形叫做阿基米德三角形(如图1,SAB即为阿基米德三
角形).
重要结论:抛物线与弦之间所围成区域的面积(图二中的阴影部分)为阿基米德三角形面积的三分之二.
阿基米德运用逼近的方法证明了这个结论.
证明:如图3,SM 是SAB中AB边上的中线,则SM 平行于x轴(下面的性质1证明会证到),过M作
抛物线的切线,分别交SA、SB于A,B,则AAM、BBM也是阿基米德三角形,可知AC是AAM
中AM边上的中线,且AC平行于x轴,可得点A是SA的中点,同理B是SB的中点,故M是SM 的中点,
则S 是S 的 1 ,由此可知:S 是S 的 1 ,S 是S 的 1 ,以此类推,图2中蓝色部分
SAB MAB 2 AAC CMA 2 BBD DMB 2
1
的面积是红色部分而知的 ,累加至无穷尽处,便证得重要结论.
2
阿基米德三角形的结论
【结论1】阿基米德三角形底边上的中线平行于抛物线的轴.
证明:设Ax , y ,Bx , y ,M为弦AB的中点,则过A的切线方程为y y pxx ,过B的切线方程
1 1 2 2 1 1
y y y y
为y y pxx ,联立方程,y2 2px ,y2 2px ,解得两切线交点Q 1 2, 1 2 ,又
2 2 1 1 2 2 2p 2
79
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司x x y y
M
1 2 , 1 2 ,MQ//x轴.
2 2
【结论2】若阿基米德三角形的底边即弦AB过抛物线内的定点C,则另一顶点Q的轨迹为一条直线.
证明:设A(x,y ),B(x ,y ),C(x ,y )为抛物线内的定点,弦AB的过定点C,则过A的切线方程为
1 1 2 2 0 0
y y p(xx ),过B的切线方程为y y p(xx ),则设另一顶点Qx,y,满足yyp(xx)且
1 1 2 2 1 1
y yp(xx ),故弦AB所在的直线方程为yy p(x x),又由于弦AB过抛物线内的定点C(x ,y ),故
2 2 0 0
y yp(xx),即点Q的轨迹方程为直线y y p(xx ) .
0 0 0 0
【结论3】抛物线以C点为中点的弦平行于Q点的轨迹.
证明:由性质2的证明可知:点Q的轨迹方程为直线y y p(xx ) .∵点C为弦AB的中点,故Q的轨迹
0 0
y y x x 2p
方程为 1 2 y p x 1 2 ,斜率k ;而弦AB所在的直线方程为yy p(x x),由性质1的
2 2 y y
1 2
y y y y y y y y 2p
证明可知:y 1 2 ,x 1 2 ,故弦AB所在的直线方程为 1 2 y px 1 2 ,斜率k ,
2 2p 2 2p y y
1 2
又∵直线AB与Q的轨迹方程不重合,故可知两者平行.
【结论4】若直线l与抛物线没有公共点,以l上的点为顶点的阿基米德三角形的底边过定点(若直线l方程
c bp
为:ax+by+c=0,则定点的坐标为C , .
a a
a c
证明:任取直线l:ax+by+c=0上的一点Qx ,y ,则有ax by c0,即y x ┅①,过点Q
0 o 0 0 0 b 0 b
作抛物线y2 2px的两条切线,切点分别为A,B,则又由性质2的证明可知:弦AB所在的直线方程为
a c a c a
y y p(x x),把①式代入可得: x y px x,即 yp x px y,令 y p0
0 0 b 0 b 0 b 0 b b
c c bp
且px y0,可得:弦AB所在的直线过定点C , .
b a a
a3
【结论5】底边为a的阿基米德三角形的面积最大值为 .
8p
证明: AB a,设Q到AB的距离为d,由性质1知:
x x y y y2y 2 2y y (y y )2
d QM 1 2 1 2 1 2 1 2 1 2 (直角边与斜边),
2 2p 4p 4p 4p
设直线AB的方程为 xmyn,则a (1m2)(y y )2 ,
2 1
a2 1 a3
∴(y y )2 a2 d s ad .
1 2 4p 2 8p
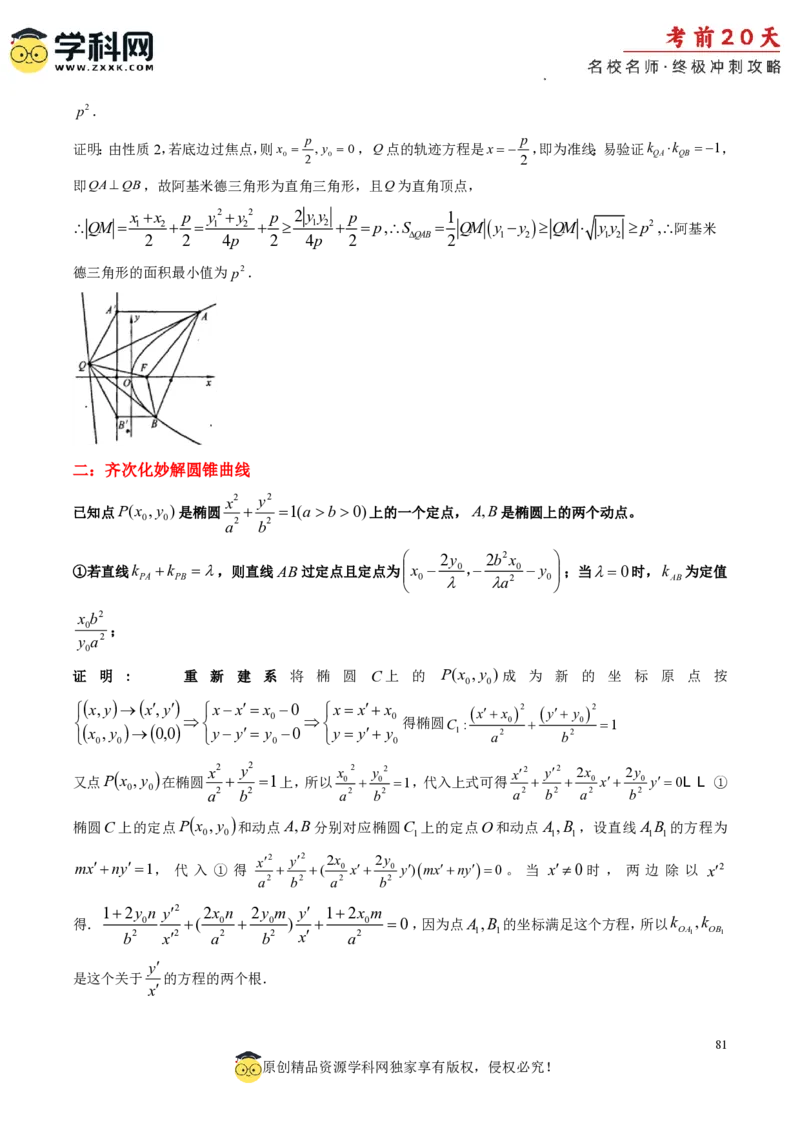
【结论6】若阿基米德三角形的底边过焦点,顶点Q的轨迹为准线,且阿基米德三角形的面积最小值为
80
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司p2.
p p
证明:由性质2,若底边过焦点,则x ,y 0,Q点的轨迹方程是x ,即为准线;易验证k k 1,
0 2 0 2 QA QB
即QAQB,故阿基米德三角形为直角三角形,且Q为直角顶点,
x x p y2y2 p 2 yy p 1
QM 1 2 1 2 1 2 p,S QMy y QM yy p2,阿基米
2 2 4p 2 4p 2 QAB 2 1 2 1 2
德三角形的面积最小值为p2.
二:齐次化妙解圆锥曲线
x2 y2
已知点P(x ,y )是椭圆 1(a b0)上的一个定点,A,B是椭圆上的两个动点。
0 0 a2 b2
2y 2b2x
①若直线k k ,则直线AB过定点且定点为x 0, 0 y ;当0时,k 为定值
PA PB 0 a2 0 AB
x b2
0 ;
y a2
0
证 明 : 重 新 建 系 将 椭 圆 C上 的 P(x ,y )成 为 新 的 坐 标 原 点 按
0 0
x,y x,y xx x 0 x xx xx 2 y y 2
0 0 得椭圆C : 0 0 1
x ,y 0,0 y y y 0 y y y 1 a2 b2
0 0 0 0
x2 y2 x 2 y 2 x2 y2 2x 2y
又点P x ,y 在椭圆 1上,所以 0 0 1,代入上式可得 0 x 0 y0L L ①
0 0 a2 b2 a2 b2 a2 b2 a2 b2
椭圆C上的定点P x ,y 和动点 A,B分别对应椭圆C 上的定点O和动点 A,B ,设直线 AB 的方程为
0 0 1 1 1 1 1
x2 y2 2x 2y
mxny1, 代 入 ① 得 ( 0 x 0 y)mxny0。 当 x0时 , 两 边 除 以 x2
a2 b2 a2 b2
12y n y2 2x n 2y m y 12x m
得. 0 ( 0 0 ) 0 0,因为点A,B 的坐标满足这个方程,所以k ,k
b2 x2 a2 b2 x a2 1 1 OA 1 OB 1
y
是这个关于 的方程的两个根.
x
81
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司2b2x n2a2y m
若k k ,由平移斜率不变可知k k ,故k k 0 0 ,当0
PA PB OA 1 OB 1 OA 1 OB 1 a2 12y n
0
m x b2 x b2
时,所以2b2x n2a2y m0,由此得k 0 。所以AB的斜率为定值 0 ,k 为定值
0 0 A 1 B 1 n y a2 y a2 AB
0 0
x b2
0 ;
y a2
0
2y 2b2x
即2b2x n2a2y ma2 2a2y n 0 m 0 2y n1,由此知点
0 0 0 a2 0
2y 2b2x 2y 2b2x
0, 0 2y 在直线AB :mxny1上,从而直线AB过定点x 0, 0 y .
a2 0 1 1 0 a2 0
a2 b2 a2 b2 b2 y
②若k k ,则直线AB过定点且为 x , y ;当 时,k 为定值 0 ;
PA PB a2 b2 0 a2 b2 0
a2 AB x
0
b2
12x m
b2
证明:若k k ,由平移规律知k k ,所以k k 0 ,若 ,
PA PB OA 1 OB 1 OA 1 OB 1 a2 12y n a2
0
12x m m y b2
则 0 1k 0 ;当 时,即b2 2b2x m a2 2a2y n,
12y n n x a2 0 0
0 0
2b2x 2a2y 2b2x 2a2y
0 m 0 n1,由此知点 0 , 0 在直线AB :mxny1上,从而直线
a2 b2 a2 b2 a2 b2 a2 b2 1 1
a2 b2 a2 b2
AB过定点 x , y .
a2 b2 0 a2 b2 0
x2 y2
Ⅱ:已知点P x , y 是平面内一个定点,椭圆C: 1 a b0 上有两动点A,B
0 0 a2 b2
①若直线k k ,则直线AB过定点.
PA PB
证明:重新建系将椭圆C上的P(x ,y )成为新的坐标原点按
0 0
x,y x,y xx x 0 x xx xx 2 y y 2
0 0 椭圆C : 0 0 1,展开得:
x ,y 0,0 y y y 0 y y y 1 a2 b2
0 0 0 0
x2 y2 2x 2y x2 y2
0 x 0 y 0 0 10.
a2 b2 a2 b2 a2 b2
平面内的定点P x , y 和椭圆C上的动点 A、B分别对应椭圆C 上的定点O和动点 A 、B ,设直线
0 0 1 1 1
AB 的方程为mxny1,代入展开式得
1 1
x2 y2 2x 2y x2 y2
0 x 0 y mxny 0 0 1 mxny2 0(构造齐次式),当x0时,
a2 b2 a2 b2 a2 b2
82
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司两边同时除以x2整理得,
n2x2 ny 12 y2 2mnx22xn 2mny22y m y mx 12 m2y2
0 0 n2 0 0 0 0 2mn 0 0 m20因为点
a2 b2 x2 a2 b2 x a2 b2
y
A、B 的坐标满足这个方程,所以k 和k 是关于 的方程的两根.若k k ,由平移斜率不
1 1 OA 1 OB 1 x PA PB
2mnx2 2x n 2mny2 2y m
0 0 0 0 2mn
a2 b2
变可知k k 所以k k 整理可得到m和n
OA 1 OB 1 OA 1 OB 1 n2x2 ny 1 2
0 0 n2
a2 b2
的关系,从而可知直线AB 过定点,由平移规律可得直线AB过定点.
1 1
②若直线k k ,则直线AB过定点.
PA PB
mx 1 2 m2y2
0 0 m2
a2 b2
证明:若k k ,由平移性质知k k ,所以k k 整理
PA PB OA 1 OB 1 OA 1 OB 1 n2x2 ny 1 2
0 0 n2
a2 b2
可得到m和n的关系,从而可知直线AB 过定点,由平移性质可得直线AB过定点.
1 1
《用齐次化秒解椭圆斜率之和或之积问题,大大的减少了计算量,从而提高准确率》
三:圆锥曲线之极点与极线
从几何角度看极点与极线
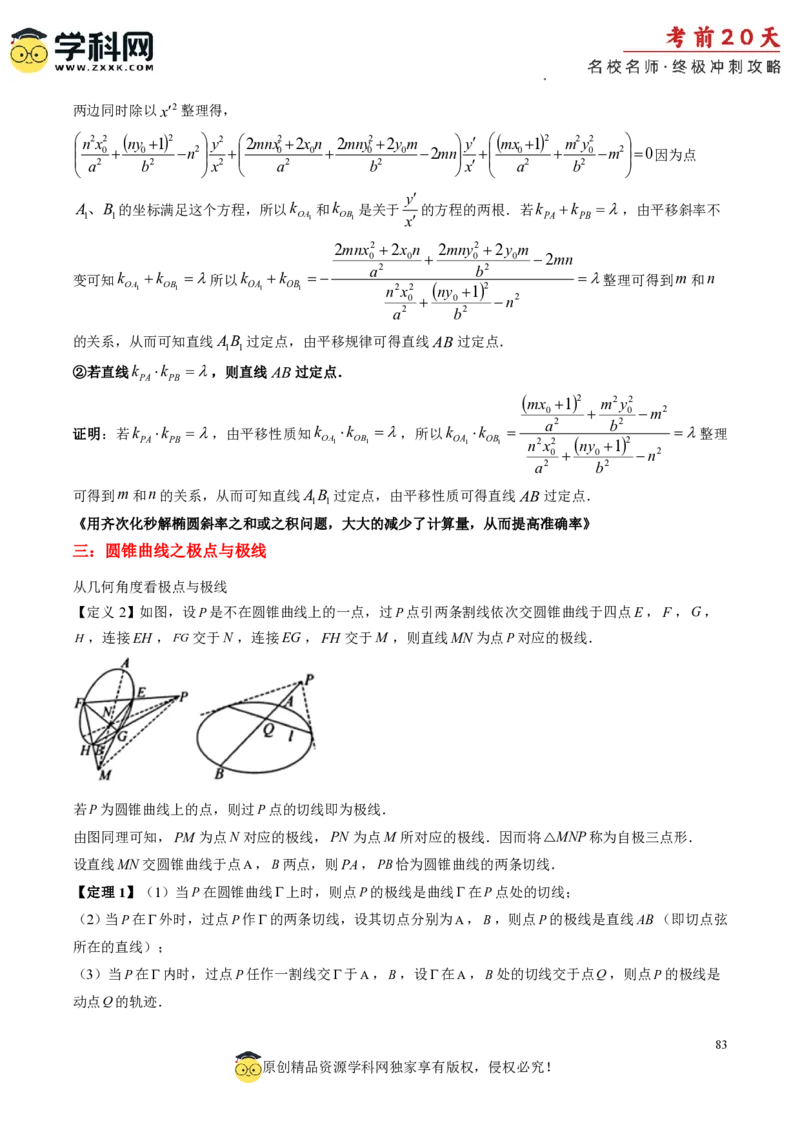
【定义2】如图,设P是不在圆锥曲线上的一点,过P点引两条割线依次交圆锥曲线于四点E,F ,G,
H,连接EH ,FG交于N ,连接EG,FH 交于M ,则直线MN为点P对应的极线.
若P为圆锥曲线上的点,则过P点的切线即为极线.
由图同理可知,PM 为点N 对应的极线,PN 为点M 所对应的极线.因而将△MNP称为自极三点形.
设直线MN交圆锥曲线于点A,B两点,则PA,PB恰为圆锥曲线的两条切线.
【定理1】(1)当P在圆锥曲线上时,则点P的极线是曲线在P点处的切线;
(2)当P在外时,过点P作的两条切线,设其切点分别为A,B,则点P的极线是直线AB(即切点弦
所在的直线);
(3)当P在内时,过点P任作一割线交于A,B,设在A,B处的切线交于点Q,则点P的极线是
动点Q的轨迹.
83
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司定理1给出了极点与极线作法.
PA AQ
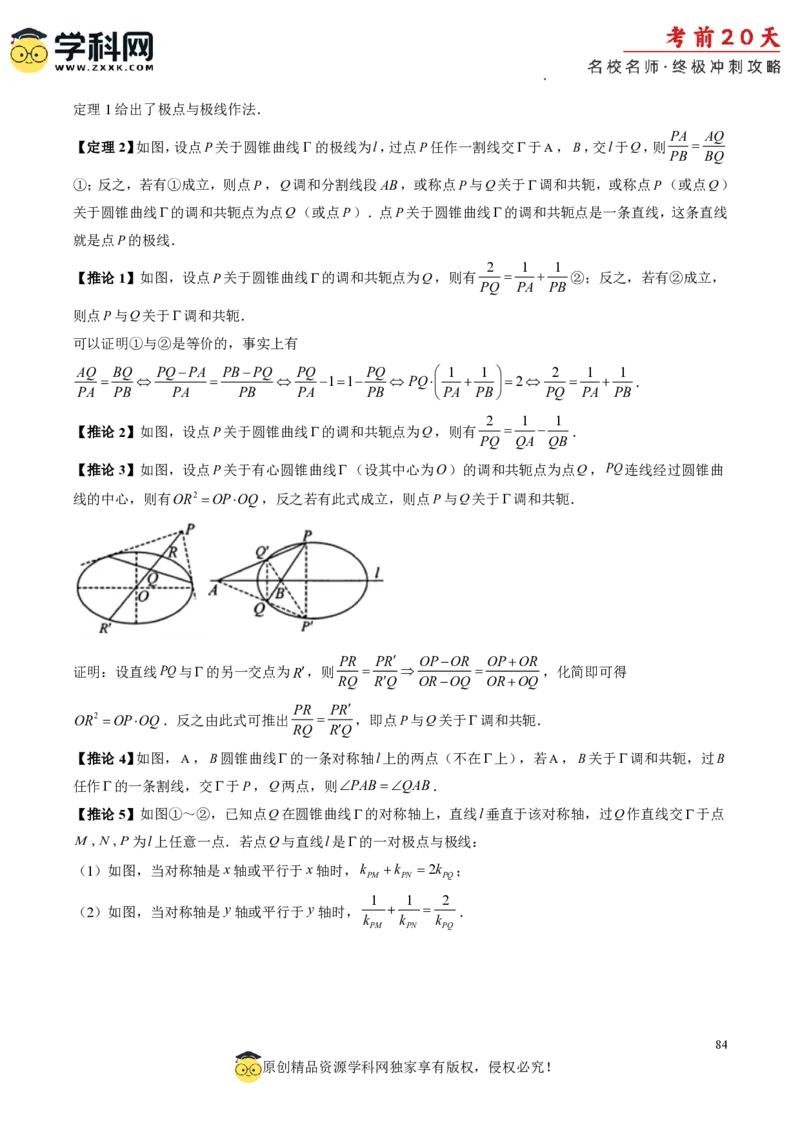
【定理2】如图,设点P关于圆锥曲线Γ的极线为l,过点P任作一割线交于A,B,交l于Q,则
PB BQ
①;反之,若有①成立,则点P,Q调和分割线段AB,或称点P与Q关于调和共轭,或称点P(或点Q)
关于圆锥曲线的调和共轭点为点Q(或点P).点P关于圆锥曲线的调和共轭点是一条直线,这条直线
就是点P的极线.
2 1 1
【推论1】如图,设点P关于圆锥曲线的调和共轭点为Q,则有 ②;反之,若有②成立,
PQ PA PB
则点P与Q关于调和共轭.
可以证明①与②是等价的,事实上有
AQ BQ PQPA PBPQ PQ PQ 1 1 2 1 1
11 PQ 2 .
PA PB PA PB PA PB PA PB PQ PA PB
2 1 1
【推论2】如图,设点P关于圆锥曲线的调和共轭点为Q,则有 .
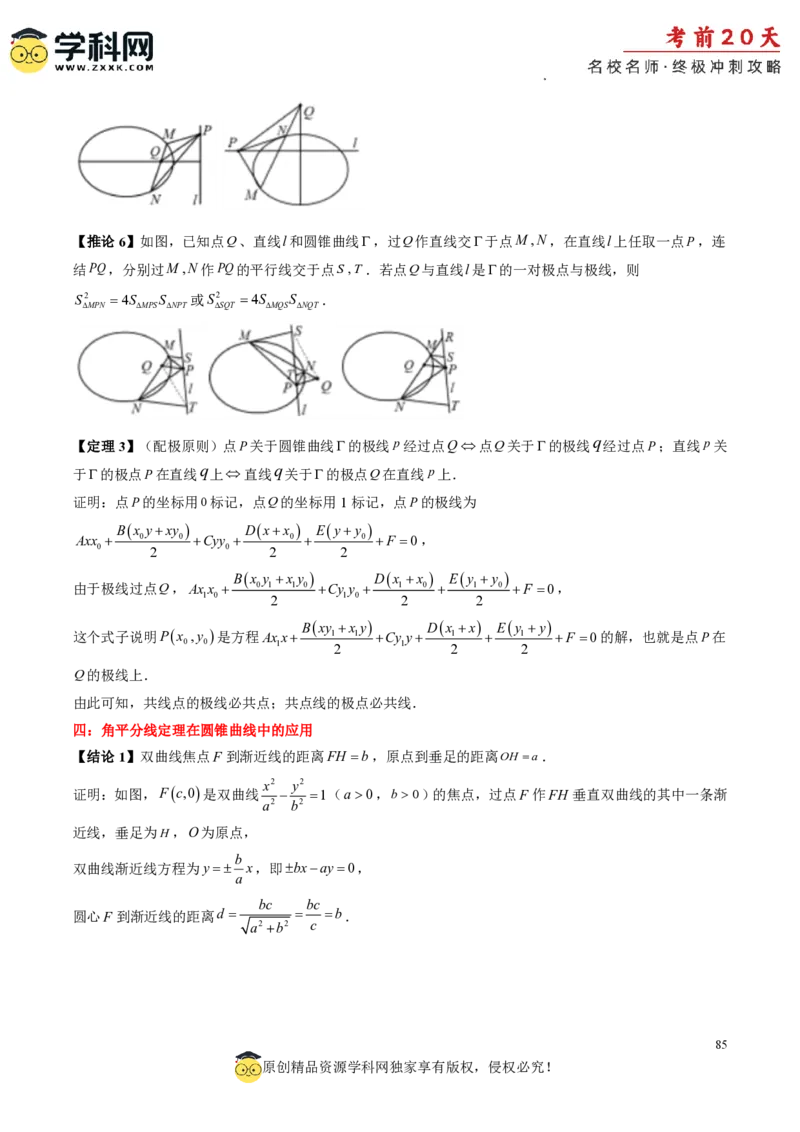
PQ QA QB
【推论3】如图,设点P关于有心圆锥曲线(设其中心为O)的调和共轭点为点Q,PQ连线经过圆锥曲
线的中心,则有OR2 OPOQ,反之若有此式成立,则点P与Q关于调和共轭.
PR PR OPOR OPOR
证明:设直线PQ与的另一交点为R,则 ,化简即可得
RQ RQ OROQ OROQ
PR PR
OR2 OPOQ.反之由此式可推出 ,即点P与Q关于调和共轭.
RQ RQ
【推论4】如图,A,B圆锥曲线的一条对称轴l上的两点(不在上),若A,B关于调和共轭,过B
任作的一条割线,交于P,Q两点,则PABQAB.
【推论5】如图①~②,已知点Q在圆锥曲线的对称轴上,直线l垂直于该对称轴,过Q作直线交于点
M ,N ,P为l上任意一点.若点Q与直线l是的一对极点与极线:
(1)如图,当对称轴是x轴或平行于x轴时,k k 2k ;
PM PN PQ
1 1 2
(2)如图,当对称轴是y轴或平行于y轴时, .
k k k
PM PN PQ
84
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司【推论6】如图,已知点Q、直线l和圆锥曲线,过Q作直线交于点M,N,在直线l上任取一点P,连
结PQ,分别过M,N作PQ的平行线交于点S,T.若点Q与直线l是的一对极点与极线,则
S2 4S S 或S2 4S S .
MPN MPS NPT SQT MQS NQT
【定理3】(配极原则)点P关于圆锥曲线的极线p经过点Q点Q关于的极线 q 经过点P;直线p关
于的极点P在直线 q 上直线 q 关于的极点Q在直线p上.
证明:点P的坐标用0标记,点Q的坐标用1标记,点P的极线为
Bx yxy Dxx Eyy
Axx 0 0 Cyy 0 0 F 0,
0 2 0 2 2
Bx y x y Dx x Ey y
由于极线过点Q,Axx 0 1 1 0 Cy y 1 0 1 0 F 0,
1 0 2 1 0 2 2
Bxy x y Dx x Ey y
这个式子说明Px ,y 是方程Axx 1 1 Cy y 1 1 F 0的解,也就是点P在
0 0 1 2 1 2 2
Q的极线上.
由此可知,共线点的极线必共点;共点线的极点必共线.
四:角平分线定理在圆锥曲线中的应用
【结论1】双曲线焦点F 到渐近线的距离FH b,原点到垂足的距离OH a.
x2 y2
证明:如图,Fc,0是双曲线 1(a0,b 0)的焦点,过点F 作FH 垂直双曲线的其中一条渐
a2 b2
近线,垂足为H,O为原点,
b
双曲线渐近线方程为y x,即bxay0,
a
bc bc
圆心F 到渐近线的距离d b.
a2b2 c
85
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司在双曲线中,两条渐近线与坐标轴的夹角相等,所以经常可以用角平分线化腐朽为神奇.下面先给出三角
形角平分线定理.
【结论2】三角形一个角的平分线分对边所成的两条线段与这个角的两邻边对应成比例.
AB BM
如:在VABC中,AM 平分BAC,则 .
AC CM
1 1
证明:解法1:(面积法)S ABAMsinBAM ,S ACAMsinCAM ,
△ABM 2 △ACM 2
S△ABM :S△ACM AB:AC
又VABM 和△ACM 是等高三角形,面积的比等于底的比,
AB BM
即三角形ABM 面积S:三角形ACM面积S BM :CM , .
AC CM
解法2:(相似)如图,过C作CN//AB交AM 的延长线于N ,则△ABM∽△NCM ,AB/NC BM/CM ,
AB BM
又可证明CAN ANC,AC CN, .
AC CM
解法3:(正弦定理)
AB sinAMB CA sinAMC sinAMB sinAMC AB BM
, ,Q , .
MB sinBAM CM sinCAM sinBAM sinCAM AC CM
1
典例1【2023新高考1卷】在直角坐标系xOy中,点P到x轴的距离等于点P到点 0, 的距离,记动点
2
P的轨迹为W .
(1)求W 的方程;
(2)已知矩形ABCD有三个顶点在W 上,证明:矩形ABCD的周长大于3 3.
1
【答案】(1)y x2 (2)见解析
4
86
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司 1 2 1
【解析】【1】设P(x,y),则 y x2 y ,两边同平方化简得y x2 ,
2 4
1
故W : y x2 .
4
1 1 1
【2】法一:设矩形的三个顶点A a,a2 ,B b,b2 ,C c,c2 在W 上,且abc,易知矩形
4 4 4
四条边所在直线的斜率均存在,且不为0,
1 1
b2 a2
则k k 1,ab0bc,令 4 4 ,
AB BC k abm0
AB ba
1
同理令k bcn0,且mn1,则m ,
BC n
1
设矩形周长为C,由对称性不妨设|m||n|,k k canmn ,
BC AB n
1 1
则 C | AB||BC|(ba) 1m2 (cb) 1n2 (ca) 1n2 n 1n2 , 易 知
2 n
1
n 1n2 0
n
2 2
则令 f(x) x 1 1x2 ,x0, f(x)2 x 1 2x 1 ,
x x x
2
令 f(x)0,解得x ,
2
2
当x0, 时, f(x)0,此时 f(x)单调递减,
2
2
当x ,1, f(x)0,此时 f(x)单调递增,
2
87
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司 2 27
则 f(x) f ,
min 2 4
1 27 3 3
故 C ,即C 3 3.
2 4 2
2
当C 3 3时,n ,m 2 ,且(ba) 1m2 (ba) 1n2 ,即mn时等号成立,矛盾,故
2
C 3 3,
得证.
法二:不妨设A,B,D在W 上,且BA DA,
1
依题意可设A a,a2 ,易知直线BA,DA的斜率均存在且不为0,
4
1
则设BA,DA的斜率分别为k和 ,由对称性,不妨设 k 1,
k
1
直线AB的方程为y k(xa)a2 ,
4
1
y x2
4
则联立 得x2 kxkaa2 0,
1
y k(xa)a2
4
k2 4 kaa2 k2a2 0,则k 2a
则| AB| 1k2 |k2a|,
1 1
同理| AD| 1 2a ,
k2 k
1 1
| AB|| AD| 1k2 |k2a| 1 2a
k2 k
88
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司 1 1
1k23
1k2 k2a 2a 1k2 k
k k k2
(m1)3 1
令k2 m,则m0,1 ,设 f(m) m2 3m 3,
m m
1 (2m1)(m1)2 1
则 f(m)2m3 ,令 f(m)0,解得m ,
m2 m2 2
1
当m 0, 时, f(m)0,此时 f(m)单调递减,
2
1
当m , , f(m)0,此时 f(m)单调递增,
2
1 27
则 f(m) f ,
min 2 4
3 3
| AB|| AD| ,
2
1 1 1
但 1k2 |k2a| 1 2a 1k2 |k2a| 2a ,此处取等条件为k1,与最终取
k2 k k
2 3 3
等时k 不一致,故 AB AD .
2 2
1
法三:为了计算方便,我们将抛物线向下移动 个单位得抛物线W: y x2,
4
矩形ABCD变换为矩形ABCD,则问题等价于矩形ABCD的周长大于3 3.
设
B
t
,t2 ,A
t
,t2 ,C
t
,t2
, 根据对称性不妨设 t 0.
0 0 1 1 2 2 0
则 k t t ,k t t , 由于 AB BC, 则 t t t t 1.
AB 1 0 BC 2 0 1 0 2 0
由于 AB 1t t 2 t t , BC 1t t 2 t t , 且 t 介于 t ,t 之间,
1 0 1 0 2 0 2 0 0 1 2
则 AB BC 1t t 2 t t 1t t 2 t t . 令 t t tan,
1 0 1 0 2 0 2 0 2 0
π
t t cot, 0, ,则t tant ,t cott ,从而
1 0 2 2 0 1 0
AB BC 1cot22t cot 1tan2tan2t
0 0
1 1 sin cos 2t (cossin) sin3cos3
故 AB BC 2t 0
0 sin cos cos2 sin2 sincos sin2cos2
89
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司 π
①当 0, 时,
4
sin3cos3 sin cos 1 2
AB BC 2 2 2 2
sin2cos2 cos2 sin2 sincos sin2
π π
②当 , 时,由于t t t ,从而cott t tant ,
4 2 1 0 2 0 0 0
cot tan
从而 t 又t 0,
2 0 2 0
tan 2t (cossin) sin3cos3
故0t ,由此 AB BC 0
0 2 sincos sin2cos2
sin(cossin)(sincos) sin3cos3 1 cos
sin2cos3 sin2cos2 cos sin2
2 2
sin2sin22cos2 1cos2 1cos2 2cos2
2 2 3 3
1cos2 1cos2 2cos2 3 2 3 2 ,
3
3
3 3 3
当且仅当cos 时等号成立,故 AB BC ,故矩形周长大于3 3.
3 2
.
典例2【2023新高考全国Ⅱ卷】 已知双曲线C的中心为坐标原点,左焦点为 2 5,0 ,离心率为 5.
(1)求C的方程;
(2)记C的左、右顶点分别为A,A ,过点 4,0 的直线与C的左支交于M,N两点,M在第二象限,
1 2
直线MA 与NA 交于点P.证明:点P在定直线上.
1 2
x2 y2
【答案】(1) 1 (2)证明见解析.
4 16
90
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司x2 y2
【解析】【1】设双曲线方程为 1a0,b0,由焦点坐标可知c2 5,
a2 b2
c
则由e 5可得a2,b c2 a2 4,
a
x2 y2
双曲线方程为 1.
4 16
【2】由(1)可得A 2,0,A 2,0 ,设M x ,y ,Nx ,y ,
1 2 1 1 2 2
1 1
显然直线的斜率不为0,所以设直线MN 的方程为xmy4,且 m ,
2 2
与
x2
y2
1联立可得 4m2 1 y2 32my480,且64(4m2 3)0,
4 16
32m 48
则y y ,y y ,
1 2 4m2 1 1 2 4m2 1
y y
直线MA 的方程为y 1 x2 ,直线NA 的方程为y 2 x2 ,
1 x 2 2 x 2
1 2
联立直线MA 与直线NA 的方程可得:
1 2
x2 y x 2 y my 2 my y 2y y 2y
2 1 2 1 1 2 1 2 1
x2 y x 2 y my 6 my y 6y
1 2 1 2 1 2 1
48 32m 16m
m 2 2y 2y
4m2 1 4m2 1 1 4m2 1 1 1
,
48 48m 3
m 6y 6y
4m2 1 1 4m2 1 1
x2 1
由 可得x=1,即x 1,
x2 3 P
据此可得点P在定直线x=1上运动.
x2 y2
典例3【2022新高考全国Ⅰ卷】已知点A(2,1)在双曲线C: 1(a 1)上,直线l交C于P,Q
a2 a2 1
两点,直线AP,AQ的斜率之和为0.
91
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司(1)求l的斜率;
(2)若tanPAQ 2 2 ,求△PAQ的面积.
16 2
【答案】 (1)1; (2) .
9
x2 y2 4 1
【解析】【1】因为点A(2,1)在双曲线C: 1(a 1)上,所以 1,解得a2 2,
a2 a2 1 a2 a21
x2
即双曲线C : y2 1.
2
易知直线l的斜率存在,设l: y kxm,Px ,y ,Qx ,y ,
1 1 2 2
y kxm
联立x2 可得, 12k2 x2 4mkx2m2 20,
y2 1
2
4mk 2m2 2
所以,x x ,x x ,
1 2 2k2 1 1 2 2k2 1
Δ16m2k2 4 2m2 2 2k2 1 0m2 12k2 0且k 2 .
2
y 1 y 1
所以由k k 0可得, 2 1 0,
AP AQ x 2 x 2
2 1
即
x 2kx m1x 2kx m10,
1 2 2 1
即2kx x m12kx x 4m10,
1 2 1 2
2m2 2 4mk
所以2k m12k
4m10,
2k2 1 2k2 1
化简得,8k2 4k44mk10,即 k12k1m0,
所以k 1或m12k,
当m12k时,直线l: y kxmkx21过点A2,1 ,与题意不符,舍去,
故k 1.
【2】[方法一]:【最优解】常规转化
π
不妨设直线PA,AQ的倾斜角为,
,因为k k 0,所以π,由(1)知,
2 AP AQ
x x 2m2 20,
1 2
当P,Q均在双曲线左支时,PAQ2,所以tan22 2,
92
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司2
即 2tan2tan 2 0,解得tan (负值舍去)
2
此时PA与双曲线的渐近线平行,与双曲线左支无交点,舍去;
当P,Q均在双曲线右支时,
因为tanPAQ 2 2 ,所以tan2 2,即tan22 2 ,
即 2tan2tan 2 0,解得tan 2 (负值舍去),
于是,直线PA: y 2x21,直线QA: y 2x21,
y 2x21
3
联立x2 可得, x2 2 24 x104 2 0,
y2 1 2
2
104 2 4 25
因为方程有一个根为2,所以x ,y ,
P 3 P 3
104 2 4 25
同理可得,x ,y .
Q 3 Q 3
5
5 16 21
所以PQ:x y 0, PQ ,点A到直线PQ的距离 3 2 2 ,
3 3 d
2 3
1 16 2 2 16 2
故△PAQ的面积为 .
2 3 3 9
[方法二]:
π PAQ 2
设直线AP的倾斜角为, 0 ,由tanPAQ 2 2 ,得tan ,
2 2 2
y 1
由2PAQ ,得k tan 2 ,即 1 2 ,
AP x 2
1
y 1 x2 104 2 4 2 5
联立 1 2 ,及 1 y2 1得x , y ,
x 2 2 1 1 3 1 3
1
104 2 4 2 5 20 68
同理,x , y ,故x x ,x x
2 3 2 3 1 2 3 1 2 9
而| AP| 3|x 2|,| AQ| 3|x 2|,
1 2
2 2
由tanPAQ 2 2 ,得sinPAQ ,
3
93
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司1 16 2
故S | AP|| AQ|sinPAQ 2|x x 2(x x )4| .
VPAQ 2 1 2 1 2 9
x2 y2
典例4【2022新高考全国Ⅱ卷】 已知双曲线C: 1(a0,b0)的右焦点为F(2,0),渐近线方程为
a2 b2
y 3x.
(1)求C的方程;
(2)过F的直线与C的两条渐近线分别交于A,B两点,点Px ,y ,Qx ,y 在C上,且
1 1 2 2
x x 0,y 0.过P且斜率为 3的直线与过Q且斜率为 3的直线交于点M.从下面①②③中选取两
1 2 1
个作为条件,证明另外一个成立:
①M在AB上;②PQ∥AB;③|MA||MB|.
注:若选择不同的组合分别解答,则按第一个解答计分.
y2
【答案】(1)x2 1 (2)见解析
3
b
【解析】【1】右焦点为F(2,0),∴c2,∵渐近线方程为y 3x,∴ 3,∴b 3a,∴
a
c2 a2 b2 4a2 4,∴a 1,∴b 3.
y2
∴C的方程为:x2 1;
3
【2】由已知得直线PQ的斜率存在且不为零,直线AB的斜率不为零,
若选由①②推③或选由②③推①:由②成立可知直线AB的斜率存在且不为零;
若选①③推②,则M 为线段AB的中点,假若直线AB的斜率不存在,则由双曲线的对称性可知M 在x
轴上,即为焦点F ,此时由对称性可知P、Q关于x轴对称,与从而x x ,已知不符;
1 2
总之,直线AB的斜率存在且不为零.
设直线AB的斜率为k,直线AB方程为y kx2 ,
则条件①M 在AB上,等价于y kx 2ky k2x 2;
0 0 0 0
两渐近线的方程合并为3x2 y2 0,
联立消去y并化简整理得: k23 x24k2x4k2 0
设Ax ,y ,Bx ,y ,线段中点为N x ,y ,则x x 3 x 4 2k2 ,y kx 2 6k ,
3 3 4 4 N N N 2 k23 N N k23
94
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司设Mx ,y ,
0 0
则条件③ AM BM 等价于x x 2 y y 2 x x 2 y y 2 ,
0 3 0 3 0 4 0 4
移项并利用平方差公式整理得:
x x 2x x x y y 2y y y 0,
3 4 0 3 4 3 4 0 3 4
y y
2x
0
x
3
x
4
x
3
x
4
2y
0
y
3
y
4
0,即x
0
x
N
ky
0
y
N
0,
3 4
8k2
即x ky ;
0 0 k23
由题意知直线PM 的斜率为 3, 直线QM 的斜率为 3,
∴由y y 3x x ,y y 3x x ,
1 0 1 0 2 0 2 0
∴y y 3x x 2x ,
1 2 1 2 0
y y 3x x 2x
所以直线PQ的斜率m 1 2 1 2 0 ,
x x x x
1 2 1 2
直线PM :y 3xx y ,即y y 3x 3x,
0 0 0 0
代入双曲线的方程3x2 y2 30,即 3xy 3xy 3中,
得:
y 3x
2
3x
y 3x
3,
0 0 0 0
1 3
解得P的横坐标:x y 3x ,
1 2 3 y 3x 0 0
0 0
1 3
同理:x y 3x ,
2 2 3 y 3x 0 0
0 0
1 3y 3x
∴x x 0 y ,x x 2x 0 x ,
1 2 3 y23x2 0 1 2 0 y23x2 0
0 0 0 0
3x
∴m 0 ,
y
0
∴条件②PQ//AB等价于mk ky 3x ,
0 0
综上所述:条件①M 在AB上,等价于ky k2x 2;
0 0
条件②PQ//AB等价于ky 3x ;
0 0
8k2
条件③ AM BM 等价于x ky ;
0 0 k23
2k2 8k2
选①②推③:由①②解得:x ,x ky 4x ,∴③成立;
0 k23 0 0 0 k23
95
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司2k2 6k2
选①③推②:由①③解得:x ,ky ,
0 k23 0 k23
∴ky 3x ,∴②成立;
0 0
2k2 6k2 6
选②③推①:由②③解得:x ,ky ,∴x 2 ,
0 k23 0 k23 0 k23
∴ky k2x 2,∴①成立.
0 0
典例5【2021新高考全国Ⅰ卷】 在平面直角坐标系xOy中,已知点F 17,0 、
1
F 17,0 ,MF MF 2,点M 的轨迹为C.
2 1 2
(1)求C的方程;
1
(2)设点T 在直线x 上,过T 的两条直线分别交C于A、B两点和P,Q两点,且
2
TA TB TP TQ ,求直线AB的斜率与直线PQ的斜率之和.
y2
【答案】(1)x2 1x1;(2)0.
16
【解析】(1) 因为 MF MF 2 FF 2 17,
1 2 1 2
所以,轨迹C是以点F 、F 为左、右焦点的双曲线的右支,
1 2
x2 y2
设轨迹C的方程为 1a0,b0,则2a2,可得a 1,b 17a2 4,
a2 b2
y2
所以,轨迹C的方程为x2 1x1.
16
(2)[方法一] 【最优解】:直线方程与双曲线方程联立
1
如图所示,设T( ,n),
2
1
设直线AB的方程为ynk (x ),A(x ,y ),B(x ,y ).
1 2 1 1 2 2
96
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司 1
ynk (x )
1 2
联立 ,
y2
x2 1
16
1
化简得(16k2)x2 (k2 2k n)x k2 n2 k n160.
1 1 1 4 1 1
1
k2 n2 k n16
则 k2 2k n 4 1 1 .
x x 1 1 ,x x
1 2 k2 16 1 2 k2 16
1 1
1 1
故|TA| 1k2(x ),|TB| 1k2(x ).
1 1 2 1 2 2
1 1 (n2 12)(1k2)
则|TA||TB|(1k2)(x )(x ) 1 .
1 1 2 2 2 k2 16
1
1 (n2 12)(1k2)
设PQ的方程为ynk (x ),同理|TP||TQ| 2 .
2 2 k2 16
2
1k2 1k2
因为 TA TB TP TQ ,所以 1 2 ,
k2 16 k2 16
1 2
17 17
化简得1 1 ,
k2 16 k2 16
1 2
所以k2 16k2 16,即k2 k2.
1 2 1 2
因为k k ,所以k k 0.
1 2 1 2
[方法二] :参数方程法
1
设T( ,m).设直线AB的倾斜角为,
2 1
1
x tcos
则其参数方程为 2 1,
y mtsin
1
联立直线方程与曲线C的方程16x2 y2 160(x1),
1
可得16( t2cos2tcos)(m2 t2sin22mtsin)160,
4 1 1 1 1
整理得(16cos2sin2)t2 (16cos2msin)t(m2 12)0.
1 1 1 1
设TAt ,TBt ,
1 2
(m2 12) m2 12
由根与系数的关系得|TA||TB|t t .
1 2 16cos2sin2 117cos2
1 1 1
97
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司设直线PQ的倾斜角为,TPt ,TQt ,
2 3 4
m2 12
同理可得|TP||TQ|t t
3 4 117cos2
2
由|TA||TB||TP||TQ|,得cos2 cos2.
1 2
因为 ,所以cos cos.
1 2 1 2
由题意分析知 .所以tantan 0,
1 2 1 2
故直线AB的斜率与直线PQ的斜率之和为0.
[方法三]:利用圆幂定理
因为 TA TB TP TQ ,由圆幂定理知A,B,P,Q四点共圆.
1 1
设T( ,t),直线AB的方程为yt k (x ),
2 1 2
1
直线PQ的方程为yt k (x ),
2 2
k k
则二次曲线(k x y 1 t)(k x y 2 t)0.
1 2 2 2
y2
又由x2 1,得过A,B,P,Q四点的二次曲线系方程为:
16
k k y2
(k x y 1 t)(k x y 2 t)(x2 1)0(0),
1 2 2 2 16
整理可得:
k k
(k k )x2 ( )y2 (k k )xyt(k k )k k x ( 1 2 2t)ym0,
1 2 16 1 2 1 2 1 2 2
k k t
其中m t2 1 2 (k k ) .
4 2 1 2
由于A,B,P,Q四点共圆,则xy项的系数为0,即k k 0.
1 2
x2 y2
预测1(2024·浙江·模拟预测)已知双曲线C: 1a0,b0左右焦点分别为F,F ,点P3,2在
a2 b2 1 2
6
双曲线上且,点P3,2到双曲线两条渐近线的距离乘积为 过,F分别作两条斜率存在且互相垂直的直线l ,l ,
5 1 1 2
已知l 与C双曲线左支交于A,B两点,l 与C左右两支分别交于E,F 两点.
1 2
(1)求双曲线C的方程;
98
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司(2)若线段AB,EF 的中点分别为M ,N ,求证:直线MN恒过定点,并求出该定点坐标.
预测2(2024·全国·模拟预测)已知F(2,0),F (2,0),点P满足 PF PF 2,记点P的轨迹为E.直线l
1 2 1 2
过点F 且与轨迹E交于P、Q两点.
2
(1)无论直线l绕点F 怎样转动,在x轴上总存在定点M(m,0),使MPMQ恒成立,求实数m的值;
2
(2)在(1)的条件下,求VMPQ面积的最小值.
预测3(2024·重庆·模拟预测)已知抛物线C:y2 4x的焦点为F ,P(x ,y )是C上一点, PF 2x .
0 0 0
(1)求△OFP的面积;
(2)设P在第一象限,过点(1,0)的直线交C于A,B两点,直线PA,PB分别与y轴相交于M,N两点,求线段
MN的中点坐标.
x2 y2
预测4(2024·贵州安顺·模拟预测)已知双曲线C: 1(a0,b0)的一条渐近线方程为y 3x,右焦
a2 b2
点F 到渐近线的距离为 3.
(1)求双曲线C的标准方程;
uuuur uuur
(2)过点F 的直线l与双曲线C交于M,N两点,A1,0.求AMAN的值.
预测5(2024·广东韶关·模拟预测)已知椭圆C:
x2
y2
1(ab0)的离心率为 1 ,长轴长为4,A,B是其
a2 b2 2
左、右顶点,F 是其右焦点.
(1)求椭圆C的标准方程;
(2)设Px ,y y 0是椭圆C上一点,PFB的角平分线与直线AP交于点T.
0 0 0
①求点T的轨迹方程;
9
②若△TPF 面积为 ,求x .
4 0
x2 y2
1
押题1:(2024·广东韶关·模拟预测)已知椭圆C: 1(ab0)的离心率为 ,长轴长为4,A,B
a2 b2 2
是其左、右顶点,F 是其右焦点.
(1)求椭圆C的标准方程;
(2)设Px ,y y 0是椭圆C上一点,PFB的角平分线与直线AP交于点T.
0 0 0
①求点T的轨迹方程;
9
②若△TPF 面积为 ,求x .
4 0
99
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司x2 y2
押题2:已知椭圆E: 1(ab0)的左,右焦点分别为F,F ,且F,F 与短轴的一个端点Q构
a2 b2 1 2 1 2
2 3
成一个等腰直角三角形,点P , 在椭圆E,过点F 作互相垂直且与x轴不重合的两直线AB,CD分
2 2 2
别交椭圆E于A,B和点C,D,且点M ,N 分别是弦AB,CD的中点.
(1)求椭圆E的标准方程;
(2)若D0,1,求以CD为直径的圆的方程;
(3)直线MN是否过x轴上的一个定点?若是,求出该定点坐标;若不是,说明理由.
押题3:在平面直角坐标系xOy中,过点F(1,0)的直线l与抛物线C:y2 4x交于M,N两点(M 在第一象
限).
(1)当|MF|3|NF|时,求直线l的方程;
(2)若三角形OMN的外接圆与曲线C交于点D(异于点O,M,N),
(i)证明:△MND的重心的纵坐标为定值,并求出此定值;
(ii)求凸四边形OMDN的面积的取值范围.
x2 y2
押题4:已知椭圆E: 1ab0过点0,1,且焦距为2 3.
a2 b2
(1)求椭圆E的标准方程;
(2)过点S1,0作两条互相垂直的弦AB,CD,设弦AB,CD的中点分别为M,N.
①证明:直线MN必过定点;
②若弦AB,CD的斜率均存在,求VMNS面积的最大值.
x2 y2
押题5:已知椭圆C: 1ab0的焦距是短轴长的 3倍,以椭圆的四个顶点为顶点的四边形周
a2 b2
长为4 5.
(1)求椭圆的方程;
(2)直线ykxmkm0与椭圆C交于A、B两点,与y轴交于点P,线段AB的垂直平分线与AB交于点
M,与y轴交于点N,O为坐标原点,如果MOP2MNP,求k的值.
100
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司名校预测
x2 y2
预测1:答案(1) 1(2)证明见解析, 3 5,0
3 2
b b
【详解】(1)设双曲线C的两渐近线方程分别为y x,y x,
a a
点P3,2到双曲线两渐近线的距离乘积为 3b2a 3b2a 9b24a2 6 ,
c c c2 5
a2b2 c2
9b24a2
6
由题意可得: ,解得a2 3,b2 2,
c2 5
9 4
1
a2 b2
x2 y2
所以双曲线C的方程为 1.
3 2
(2)设直线l 的方程为yk x 5 ,
1
1
由l ,l 互相垂直得l 的方程y x 5 ,
1 2 2 k
yk x 5
联立方程得
x2 y2
,消y得 23k2 x26 5k2x15k260,
1
3 2
x x 3 5k2 2 5k
0成立,所以x 1 2 ,y k x 5 ,
M 2 23k2 M M 23k2
3 5k2 2 5k
所以点M 坐标为 , ,
23k2 23k2
1
y x 5
k x x 3 5 1 2 5k
联立方程得 ,所以x 3 4 ,y x 5 ,
x2 y2 N 2 2k23 N k N 2k23
1
3 2
3 5 2 5k
所以点N 坐标为 , ,
2k23 2k23
根据对称性判断知定点在x轴上,
y y
直线MN的方程为yy N M xx ,
M x x M
N M
101
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司3 5k2 2 5k 3 5 2 5k
x y x y 23k2 2k23 2k23 23k2 30 1k2
则当y0时,x M N N M 3 5,
y y 2 5k 2 5k 2 5 1k2
N M
2k23 23k2
所以直线MN恒过定点,定点坐标为 3 5,0 .
预测2:答案(1)m1(2)9
【详解】(1)由 PF PF 2 FF 知,点P的轨迹E是以F、F 为焦点的双曲线的右支,
1 2 1 2 1 2
x2 y2
设轨迹E的方程为 1(x1),a0,b 0,
a2 b2
y2
Qc2,2a2,b2 3,故轨迹E的方程为x2 1(x1),
3
当直线l的斜率存在时,设直线方程为yk(x2),Px,y ,Qx ,y ,
1 1 2 2
y2
与双曲线方程联立 x2 3 1 ,可得 k23 x24k2x4k230,
yk(x2)
k230
Δ16k44 k23 4k23 0
有
4k2
,解得k2 3,
x x 0
1 2 k23
4k23
x x 0
1 2 k23
uuur uuuur
MPMQx mx my y x m x mk2x 2x 2
1 2 1 2 1 2 1 2
k21 xx 2k2m x x m24k2
1 2 1 2
k21 4k23 4k2 2k2m
m24k2
k23 k23
3(4m5)k2
m2
k23
m24m5 k23 1m2
k23
102
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司uuur uuuur
QMPMQ,MPMQ0,
故得3 1m2 k2 m24m5 0对任意的k2 3恒成立,
1m2 0,
解得m1,
m24m50,
当m1时,MPMQ.
当直线l的斜率不存在时,不妨设P(2,3),则Q(2,3),
3 3
此时有 1,即此时结论也成立,
21 21
综上,当m1时,MPMQ;
6
1k2
(2)由(1)知M(1,0),当直线l的斜率存在时, PQ 1k2 x x 1k2 x x 24xx ,
1 2 1 2 1 2 k23
3|k|
点M到直线PQ的距离为d,则d ,
1k2
9 1k2 k2 1k2 k2
1 9|k| 1k2
S |PQ|d 9 ,
VMPQ 2 k23 k23 k23 2
12 7 1 12 7
令k23t(t0),则S 9 1,Q 0,S 9 19,
VMPQ t2 t t VMPQ t2 t
1
当直线l的斜率不存在时,S 369,
VMPQ 2
综上可知,S 的最小值为9.
VMPQ
预测3:答案(1)1(2)0,1
【详解】(1)根据抛物线的定义知: PF x 12x ,得x 1,则y 2,
0 0 0 0
1 1
所以△OFP的面积为S OF y 121.
2 0 2
(2)设过点1,0的直线方程为xmy1,Ax,y ,Bx ,y ,M0,y ,N0,y ,
1 1 2 2 M N
y2 4x
由 ,得y2 4my40,
xmy1
103
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司由16m2160,得m1或m 1,且y y 4m,y y = 4,
1 2 1 2
y 2
又直线PA的方程为y2 1 x1 ,
x 1
1
y2
1 y
y 2 2x y 2 1 2y
令x0,得y1 1 1 1 1 ,
x 1 x 1 y2 y 2
1 1 1 1 1
4
2y 2y
于是M0, 1 ,同理N0, 2 ,
y 2 y 1
1 2
2y 2y 4y y 4y y 1616m
所以y y 1 2 1 2 1 2 2,
M N y 2 y 2 y y 2y y 4 88m
1 2 1 2 1 2
故线段MN的中点坐标为0,1.
y2
预测4:答案(1)x2 1(2)0
3
x2 y2 b
【详解】(1)解:由双曲线C: 1的渐近线方程为y 3x,可得 3,
a2 b2 a
3c
又由焦点F(c,0)到渐近线的距离为 3,可得d 3,可得c2,
( 3)212
y2
又因为c2 a2 b2,可得a1,b 3,所以双曲线的方程为x2 1.
3
(2)解:由(1)知c2,可得F(2,0),
y2
当直线l的斜率不存在时,即l:x2,将x2代入x2 1,可得y 3或y 3,
1 2
3
不妨设M(2,3),N(2,3),
uuuur uuur
又由A(1,0),可得AM (3,3),AN (3,3),
uuuur uuur
所以AMAN 333(3)0;
当直线l的斜率存在时,即l:yk(x2),
yk(x2)
联立方程组 y2 ,整理得(3k2)x24k2x4k230,
x2 1
3
104
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司设M(x,y ),N(x ,y ),则(4k2)24(3k2)(4k23)0,
1 1 2 2
4k2 4k23
且x x ,xx ,
1 2 k23 1 2 k23
则y y k2(x 2)(x 2)k2xx 2k2(x x )4k2,
1 2 1 2 1 2 1 2
uuuur uuur
且AM (x 1,y ),AN (x 1,y ),
1 1 2 2
uuuur uuur
则AMAN (x 1)(x 1)y y xx (x x )1y y
1 2 1 2 1 2 1 2 1 2
xx (x x )1k2xx 2k2(x x )4k2
1 2 1 2 1 2 1 2
(12k2)xx (k21)(x x )4k21
1 2 1 2
4k23 4k2
(12k2) (k21) 4k21
k23 k23
4k28k44k23k24k434k412k2k23
0,
k23
uuuur uuur
综上可得:AMAN 0.
x2 y2
预测5:答案(1) 1(2)n1x4(y0);n2x 1
0
4 3
c 1
e
a 2 a2
【详解】(1)由题意知, ,解得 ,
2a4 b 3
a2 b2c2
x2 y2
所以椭圆C的标准方程为 1;
4 3
(2)①:由(1)知,A(2,0),B(2,0),F(1,0),P(x ,y ),设BFT ,则PFB2,
0 0
3 1
易知当x 1时,P(1, ),k 1,此时AP:y x1,FT:yx1,
0 2 FT 2
1
y x1 x4
由 2 ,解得 ,即T(4,3);
yx1
y3
y y
当x 1时,k tan2 y 0 , sin2 0 0 ,设直线FT 的斜率为k,
0 FP x 1 PF (x 1)2y2
0 0 0
3
(x 1)23 x2 (x 1)
则 ktan 1cos2 1 1 (x 0 1)2y 0 2 (x 0 1) 0 4 0 0 3(2x 0 ),
sin2 sin2 tan2 y y 2y
0 0 0
3(2x ) y
所以直线FT 方程为y 0 (x1),又直线AT 方程为y 0 (x2),
2y x 2
0 0
105
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司 3(2x )
y 0 (x1)
由 2y 0 ,得 3(2x 0 ) (x1) y 0 (x2),即 3(4x 0 2)2y 0 x 3(4x 0 2)4y 0 ,
y 2y x 2 2(2x )y 2(2x )y
y 0 (x2) 0 0 0 0 0 0
x 2
0
3
123x24(3 x2)
解得x 3(4x 0 2)4y 0 0 4 0 2(123x 0 2) 4,
3(4x2)2y 3 1
0 0 123x22(3 x2) (123x2)
0 4 0 2 0
6y 6y
将x4代入直线AT 方程,得y 0 ,即T(4, 0 ),
x 2 x 2
0 0
6y
又y 0,2x 2,所以 0 0,
0 0 x 2
0
故点T的轨迹方程为x4(y0);
1 1 6y 3 6y
②:由 AF 3,得S S S AF y AF 0 (y 0 ),
VTPF VTAF VPAF 2 0 2 x 2 2 0 x 2
0 0
9 9 3 6y 3 6y
又S ,所以 (y 0 ),得 y 0 ,
VTPF 4 4 2 0 x 2 2 0 x 2
0 0
3(x 2) 3 3(x 2) 3
整理得y 0 ,又y 3 x2 ,所以 0 3 x2 ,
0 82x 0 4 0 82x 4 0
0 0
整理得x310x235x 260,即(x 1)(x29x 26)0,
0 0 0 0 0 0
由2x 2,解得x 1.
0 0
名师押题
押题1:答案(1)y2 2x(2)证明见解析(3)8
【详解】(1)设直线AB的方程为xmy1,
y2 2px
由 ,得y22pmy2p0,
xmy1
设Ax,y ,Bx ,y ,
1 1 2 2
y2 y2 y y 2
则y y 2p,xx 1 2 1 2 1,
1 2 1 2 2p 2p 4p2
uuur uuur
从而OAOBxx y y 12p1,解得p1,
1 2 1 2
所以抛物线C的方程为y2 2x;
(2)要证 AD BG BD AG ,即证DG平分ADB,即证k k 0,
AD BD
106
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司由(1)可知y y 2,y y 2pm2m,
1 2 1 2
y y y y
k k 1 2 1 2
则 AD BD x 1 x 1 y2 y2
1 2 1 1 2 1
2 2
2y y y y 4y y 8m8m
1 2 1 2 1 2 0,
y22 y22 y22 y22
1 2 1 2
故 AD BG BD AG ;
(3)记AM,AN分别与圆G切于点T,F,连接TG,MG,NG,
由题意,得 AT AG2TG2 1 y21 2 y21 1 y2,
2 1 1 2 1
由切线长定理,知 AT AF , NO NF , MO MT ,
1 1 y2
所以S MN y2 1 MN ,
VAMN 2 2 1 4
又S S S S
△AMN △MAG △ANG △MNG
1 1 1
AM 1 AN 1 MN 1
2 2 2
1
MT AT NF AF MO ON
2
1
2 MO 2 NO 2 AT
2
MN AT
1 y2 2y2
MN y2 1 MN ,解得 MN 1 ,
2 1 4 y24
1
1 y4 1 16 1
所以S 1 y24 8 2488,
VAMN 2 y24 2 1 y24 2
1 1
当且仅当y244,即y 2 2时,取等号,
1 1
故VAMN 面积的最小值为8.
107
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司x2 2 1 8 2
押题2:答案(1) y2 1(2)(x )2(y )2 (3)( ,0)
2 3 3 9 3
x2 y2 2 3
【详解】(1)解:因为椭圆E: 1(ab0)经过点P , ,
a2 b2
2 2
且F,F 与短轴的一个端点Q构成一个等腰直角三角形,
1 2
2 3
可得bc,则a2 b2c2 2b2,所以 1,解得a2 2,b2 1,
22b2 b2
x2
所以椭圆E的标准分别为 y2 1.
2
(2)解:由(1)得F(1,0),D(0,1),所以直线CD的方程为xy1,
1
xy1
4 1 4 1
联立方程组x2 ,解得x ,y 或x0,y1,所以C( , ),
y2 1 3 3 3 3
2
2 1 4 2 1 8
则CD的中点为N( , )且CD 2,故以CD为直径的圆的方程为(x )2(y )2 .
3 3 3 3 3 9
1
(3)解:设直线AB的方程为xmy1,且m0,则直线CD的方程为x y1,
m
xmy1
联立方程组x2 ,整理得(m22)y22my10,
y2 1
2
2 1
设A(x,y ),B(x ,y ),则0且y y ,y y ,
1 1 2 2 1 2 m22 1 2 m22
4
所以x x (my 1)(my 1)m(y y )2 ,
1 2 1 2 1 2 m22
2 m
由中点坐标公式得M( , ),
m22 m22
1 2m2 m
将M 的坐标中的用 代换,可得CD的中点为N( , ),
m 2m21 2m21
3m m 3m 2
所以k ,所以直线MN的方程为y (x ),
MN 2(m21) m22 2(m21) m22
m 3 2
即y ( x1),则直线MN过定点( ,0).
m21 2 3
3 2
押题3:答案(1)y 3x 3(2)(i)证明见解析;纵坐标为0;(ii) ,.
2
【详解】(1)解:设直线MN:xmy1,Mx,y ,Nx ,y
1 1 2 2
xmy1
联立 ,消去x,得y24my40,
y2 4x
所以y y 4m,y y 4,
1 2 1 2
108
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司|MF|3|NF|,则y 3y
1 2
y y 2y 4m 1 3
1 2 2 ,则m2 ,又由题意m0,m ,
y y 3y 2 4 3 3
1 2 2
直线的方程是y 3x 3;
(2)(1)方法1:设Mx,y ,Nx ,y ,Dx ,y
1 1 2 2 3 3
因为O,M,D,N四点共圆,设该圆的方程为x2y2dxey0,
x2y2dxey0
联立 ,消去x,得y4(4d 16)y216ey0,
y2 4x
即y y3(4d 16)y16e 0,
所以y ,y ,y 即为关于y的方程y3(4d 16)y16e0的3个根,
1 2 3
则y3(4d 16)y16ey y y y y y ,
1 2 3
因为yy yy yy y3y y y y2y y y y y y yy y y ,
1 2 3 1 2 3 1 2 2 3 1 3 1 2 3
由y2的系数对应相等得,y y y 0,所以VMND的重心的纵坐标为0.
1 2 3
4 4 4 4
方法2:设Mx,y ,Nx ,y ,Dx ,y ,则k ,k ,k ,k ,
1 1 2 2 3 3 OM y ON y MD y y ND y y
1 2 1 3 2 3
因为O,M,D,N四点共圆,所以当M,D在直线异侧时,MON MDN ,
即tanMON tanMDN 0,
k k 4y y
tanMON OM ON 2 1 ,
1k k y y 16
OM ON 1 2
k k 4y y
tanMDN ND MD 1 2 ,
1k k y y y y 16
ND MD 1 3 2 3
化简可得:y y y ;
3 1 2
当M,D在直线同侧时,MON=MDN ,
即tanMON=tanMDN,
k k 4y y
tanMON OM ON 2 1 ,
1k k y y 16
OM ON 1 2
k k 4y y
tanMDN ND MD 1 2 ,
1k k y y y y 16
ND MD 1 3 2 3
化简可得:y y y ;
3 1 2
综上可得VMND的重心的纵坐标为0.
(2)记VOMN,VMND的面积分别为S ,S ,由已知得直线MN的斜率不为0,设直线MN:xmy1,联立
1 2
xmy1
,消去x,得y24my40,所以y y 4m,y y 4,
y2 4x 1 2 1 2
109
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司1 1
所以S OF y y 16m216 2 m21,
1 2 1 2 2
由(1)得,y y y 4m,
3 1 2
所以x 1 y2 1 (4m)2 4m2,即D 4m2,4m ,
3 4 3 4
因为 MN x x 2my y 44m24,
1 2 1 2
8m21
点D到直线MN的距离d ,
m21
1 1
8m21
所以S MN d 4m24 2 m218m21,
2 2 2 m21
所以S S S 2 m212 m218m21 2 m21 1 8m21
1 2
M 在第一象限,即y 0,y 0,y 4m0,
1 2 3
依次连接O,M,D,N构成凸四边形OMDN,所以y y y y ,即y 2y ,
3 1 2 2 1 2
4
又因为y y 4, 2y ,即y2 2,即 2 y 0,
1 2 y 2 2 2
2
4 2 1
所以4m y y y 22 2 2,即m ,即m2 ,
1 2 2 y 4 8
2
所以S 2 m21 1 8m21 16m2 m21,
3 2
设t m21,则t ,
4
令 f(t)16t t21 ,则 f(t)16 t21 16t t21 48t216,
3 2 3 2
因为t ,所以 f(t)48t2160,所以 f(t)在区间 ,上单调递增,所以
4 4
3 2 3 2
f(t) f ,
4 2
3 2
所以S的取值范围为 ,.
2
x2 1
押题4:答案(1) y2 1(2)①证明见解析;②
4 25
【详解】(1)依题意有b1,c 3,解得a2 b2c2 4,
x2
所以椭圆的方程为 y2 1.
4
1
(2)①设l :xmy1m0,Ax,y ,Bx ,y ,则l :x y1m0,
AB 1 1 2 2 CD m
110
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司联立 xmy1 ,故 m24 y22my30,16m2480,y y 2m ,
x24y2 4 1 2 m24
8
x x my y 2
1 2 1 2 m24
4 m 1 4m2 m
故M , ,由 代替m,得N , ,
m24 m24 m 14m2 14m2
4 4m2 4 4
当 ,即m2 1时,l :x ,过点K ,0.
m24 14m2 MN 5 5
当 m2 4 4 1 4m 4m 2 2 ,即m2 1时, K MN 4 m 5m 21 ,l MN :y m2 m 4 4 m 5m 21 x m2 4 4 m2 1,m0 ,
4 m21 4 4m216 4 4
令y0,x
5 m24
m24
5 m24
5
,直线MN恒过点K
5
,0
.
4
当m0,经验证直线MN过点K ,0.
5
4
综上,直线MN恒过点K ,0.
5
1
m
1 1 1 m m 1 m3m 1 m
②S S S KS y y ,
VMNS VMKS VNKS 2 M N 2 5 14m2 m24 2 4m417m24 2 4
4m2 17
m2
1
m
令t m 1 2,,S 1 m 1 t 1 1 ,
m VMNS 2 4 2 4t29 2 9
4m2 17 4t
m2 t
∵S 在t2,上单调递减,
△MNS
1 1 1 1 1
S
∴ VMNS 2 9 2 9 25,当且仅当t2,m1时取等号.
4t 8
t 2
1
故VMNS面积的最大值为 .
25
x2 2
押题5:答案(1) y2 1(2)
4 2
111
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司2c2 3b
【详解】(1)由题设得4 a2b2 4 5,解得a2,b1,c 3,
a2 b2c2
x2
所以椭圆C的方程为 y2 1.
4
(2)
x2
由 4 y2 1 ,得 4k21 x28kmx4m240,
ykxm
由Δ8km2 4 4k21 4m24 0,得4k2m210,
设Ax,y 、Bx ,y ,则x x 8km ,y y kx x 2m 2m ,
1 1 2 2 1 2 4k21 1 2 1 2 4k21
x x 4km m
所以点M 的横坐标x 1 2 ,纵坐标y ,
M 2 4k21 M 4k21
m 1 4km
所以直线MN的方程为y x ,
4k21 k 4k21
3m 3m
令x0,则点N 的纵坐标y ,则N0, ,
N 4k21 4k21
因为P0,m,所以点N 、点P在原点两侧,
因为MOP2MNP,所以MNOOMN,所以OM ON ,
又因为OM 2 4km 2 m 2 16k2m2m2 ,ON 2 3m 2 9m2 ,
4k21 4k21 4k21 2 4k21 4k21 2
16k2m2m2 9m2
2
所以 4k21 2 4k21 2 ,解得16k219,所以k 2 .
112
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司新定义(解答题)
年份 题号 知识点 考点
2021年I
无
卷
2021年II
无
卷
2022年I
无
卷
2022年II
无
卷
2023年新
无
高考1
2023 年新
高考2 无
从新高考新题型标准来看,新定义题型是高考解答题必不可少的一类题,类型1:数列新定义。类型
2:集合新定义。类型3:三角函数新定义,类型4:平面向量新定义,考生需从多方面认识,此类题目相
对有难度,解答此类题目一定要把题干的新定义理解到位.
一、数列新定义破解大招
113
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司高考对数列的考查常常涉及等差数列、等比数列中的一些基本问题,如等差数列、等比数列的通项
公式,求和公式,前n项和S 与通项a 之间的关系,判断等差数列、等比数列的方法等.另外,也要关注新
n n
定义与数列的结合,此类题往往涉及推理与证明的相关知识,对思维的要求较高,所以要注意多角度、全
方位分析题目的条件和结论,拓宽看问题的视野.
新定义题型的特点:通过给出一个新概念,或约定一种新运算,或给出几个新模型来创设全新的问题
情景,要求考生在阅读理解的基础上,依据题目提供的信息,联系所学的知识和方法,实现信息的迁移,
达到灵活解题的目的;遇到新定义问题,应耐心读题,分析新定义的特点,弄清新定义的性质,按新定义
的要求,“照章办事”,逐条分析、验证、运算,使问题得以解决.
二:集合新定义破解大招
解决以集合为背景的新定义问题,要抓住两点:
第一点:紧扣新定义,首先分析新定义的特点,把定义所叙述的问题的本质弄清楚,并能够应用到具体的
解题过程之中,这是新定义型集合问题难点的关键所在;
第二点:用好集合的性质,解题时要善于从试题中发现可以使用集合性质的一些因素,在关键之外用好集
合的运算与性质.
三:三角函数新定义破解大招
与三角函数的新定义有关问题的求解策略:
①通过给出一个新的三角函数的定义,或约定一种新的运算,或给出几个新模型来创设新问题的情景,要
求在阅读理解的基础上,依据题目提供的信息,联系所学的知识和方法,实现信息的迁移,达到灵活解题
的目的;
②遇到新定义问题,应耐心读题,分析新定义的特点,弄清新定义的性质,按新定义的要求,“照章办事”,
逐条分析,运算,验证,使得问题得以解决.
三角函数新定义问题;主要把握住三角函数与其它知识点之间的转换关系即可,熟记三角恒等变换的有关
公式;求取值范围转换为函数问题.
特别注意:新定义“伴随函数”得出函数 f(x)的表达式,然后利用三角函数性质求解.对于函数
f(x)asinxbcosx一般借助辅助角公式进行变形,即 f(x)asinxbcosx a2b2 sin(x),其中
a b
cos ,sin .
a2b2 a2b2
四:平面向量新定义破解大招
平面向量新定义一般与三角恒等变换相结合合,充分理解新定义,且熟练掌握向量和三角函数知识
uuuv
才能解决此类题,特别是求长度,要设出向量,表达出OPsinxsinx,先证明充分性,再
证明必要性
114
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司预测1(2024·海南海口·模拟预测)在计算机科学中,n维数组X x,x ,L ,x ,x 0,1,iN ,n2是
1 2 n i
一种基础而重要的数据结构,它在各种编程语言中被广泛使用.对于n维数组
Aa,a ,L ,a ,Bb,b ,L ,b ,定义A与B的差为ABa b , a b ,L , a b ,A与B之间的距
1 2 n 1 2 n 1 1 2 2 n n
n
离为d(A,B) a b .
i i
i1
(1)若n维数组C 0,0,L ,0,证明:dA,CdB,CdA,B;
(2)证明:对任意的数组A,B,C,有dAC,BCdA,B;
(3)设集合S X X x,x ,L ,x ,x 0,1,iN ,n2 ,PS ,若集合P中有mm2个n维数组,记P
n 1 2 n i n
mn
中所有两元素间的距离的平均值为dP,证明:dP
.
2m1
a b
1 1
r a r b r r r
预测2(2024·全国·模拟预测)设有n维向量a 2 ,b 2 ,称a,bab a b a b 为向量a
1 1 2 2 n n
a b
n n
r r r r r
和b 的内积,当
a,b
0,称向量a和b 正交.设S
n
为全体由1和1构成的n元数组对应的向量的集合.
1
r 2 r r r
(1)若a
3
,写出一个向量b ,使得
a,b
0.
4
(2)令B x r ,y r x r ,y r S .若mB,证明:mn为偶数.
n
r r
(3)若n4, f 4是从S 中选出向量的个数的最大值,且选出的向量均满足a,b0,猜测 f 4的值,并
4
给出一个实例.
预测3(2024·全国·模拟预测)在平面直角坐标系中,两点Px,y ,Qx ,y 的“曼哈顿距离”定义为
1 1 2 2
x x y y ,记为PPQP,如点P1,2,Q2,4的“曼哈顿距离”为5,记为PPQP5.
1 2 1 2
(1)若点P0,2,M 是满足PPQP2的动点Q的集合,求点集M 所占区域的面积;
(2)若动点P在直线yx2上,动点Q在函数yex的图象上,求PPQP的最小值;
(3)设点Pa,b,动点Q在函数y2x2x2,2 的图象上,PPQP的最大值记为Ma,b,求Ma,b的最
小值.
uuv uuuv uuv v
预测4(2024·上海虹口·模拟预测)平面内的“向量列” a ,如果对于任意的正整数n,均有a a d ,
n n1 n
115
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司uv uuv r r
则称此“向量列”为“等差向量列”,d 称为“公差向量”.平面内的“向量列” b ,如果b 0且对于任意的正整
n 1
uuuv uuv
数n,均有b qb (q0),则称此“向量列”为“等比向量列”,常数 q 称为“公比”.
n1 n
uuv uv uv uv uuv uuv
(1)如果“向量列” a 是“等差向量列”,用a 和“公差向量”d 表示a a L a ;
n 1 1 2 n
uuv v uv uuv uuv
(2)已知 a 是“等差向量列”,“公差向量”d (3, 0),a (1, 1),a (x , y ); b 是“等比向量列”,“公
n 1 n n n n
uv uuv uv uv uuv uuv uuv uuv
比”q= 2,b (1, 3),b (m , k ).求a b a b L a b .
1 n n n 1 1 2 2 n n
uuuur
预测5(2024全国·模拟预测)已知O为坐标原点,对于函数 f xasinxbcosx,称向量OM a,b为函
uuuur
数 f x的伴随向量,同时称函数 f x为向量OM 的伴随函数.
π uuuur
(1)设函数gxsinx sinx,试求gx的伴随向量OM ;
3
(2)记向量O uu N ur 1, 3 的伴随函数为 f x,求当 f x 6 且x π , π 时,sinx的值;
5 3 6
uuuur 2 2 π
(3)当向量OM , 时,伴随函数为 f x,函数hx f 2x,求hx在区间
t,t
上最大值与最
2 2 4
小值之差的取值范围.
押题1:超越数得名于欧拉,它的存在是法国数学家刘维尔(Joseph Liouville)最早证明的.一个超越数
不是任何一个如下形式的整系数多项式方程的根:a xna xn1L axa 0(a ,a ,…,a Z,
n n1 1 0 0 1 n
a 0).数学家证明了自然对数的底数e与圆周率π是超越数.回答下列问题:
n
已知函数 f xexb xn(nN*)只有一个正零点.
n n
(1)求数列b 的通项公式;
n
(2)(ⅰ)构造整系数方程a xna 0,证明:若mN,则em为有理数当且仅当m0.
n 0
(ⅱ)数列b 中是否存在不同的三项构成等比数列?若存在,求出这三项的值;否则说明理由.
n
押题2:在n个数码1,2,L ,nnN,n2构成的一个排列 j j L j 中,若一个较大的数码排在一个较小的
1 2 n
数码的前面,则称它们构成逆序(例如 j j ,则 j 与 j 构成逆序),这个排列的所有逆序的总个数称为
2 5 2 5
这个排列的逆序数,记为Tj j L j ,例如,T3122,
1 2 n
(1)计算T(51243);
(2)设数列a 满足a a T51243T3412,a 2,求a 的通项公式;
n n1 n 1 n
1 1 1
(3)设排列 j j L j nN,n2满足 j n1ii1,2,L ,n,b Tj j L j ,S L ,求S ,
1 2 n i n 1 2 n n b b b n
2 3 n1
116
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司押题3:若数列x 满足:存在等差数列c ,使得集合 x c∣nN* 元素的个数为不大于k kN* ,
n n n n
则称数列x 具有Qk性质.
n
(1)已知数列a 满足a 2,a a 2cos nπ sin nπ nN* .求证:数列 a cos nπ 是等差数列,且
n 1 n1 n 2 2 n 2
数列a 有Q3性质;
n
(2)若数列a 有Qk 性质,数列b 有Qk 性质,证明:数列a b 有Qkk 性质;
n 1 n 2 n n 1 2
(3)记T 为数列f 的前n项和,若数列T 具有Qk性质,是否存在mN*,使得数列f 具有Qm性
n n n n
质?说明理由.
押题4:我们知道,二维空间(平面)向量可用二元有序数组a,a 表示;三维空间向盘可用三元有序数
1 2
组a,a ,a 表示.一般地,n维空间向量用n元有序数组a ,a ,L ,a 表示,其中a k 1,2,L ,n称为空间
1 2 3 1 2 n k
向量的第k个分量,k为这个分量的下标.对于nn3维空间向量a ,a ,L ,a ,定义集合
1 2 n
Amk∣a m,k 1,2,L ,n .记Am的元素的个数为 Am (约定空集的元素个数为0).
k
(1)若空间向量a ,a ,a ,a ,a ,a ,a ,a 6,3,2,5,3,7,5,5,求A5及 A5 ;
1 2 3 4 5 6 7 8
1 1 1
(2)对于空间向量a ,a ,L ,a .若 L n,求证:i,j1,2,L ,n,若i j,则a a ;
1 2 n Aa Aa Aa i j
1 2 n
(3)若空间向量a,a ,a ,L ,a 的坐标满足Aa a k,a a 1,当n3时,求证:
1 2 3 n k2 k1 1 2
a2a2L a2 2a a .
1 2 n n1 n
3π π
押题5:若函数 f x满足 f x f x且 f x f xxR,则称函数 f x为“M 函数”.
4 2
4x
(1)试判断 f xsin 是否为“M 函数”,并说明理由;
3
π 3π
(2)函数 f x为“M 函数”,且当x ,π 时, f xsinx,求y f x的解析式,并写出在 0, 上的单
4 2
调递增区间;
π 3kπ
(3)在(2)的条件下,当x , π kN时,关于x的方程 f xa(a为常数)有解,记该方程
2 2
所有解的和为Sk,求S3
.
名校预测
预测1:答案(1)证明见解析(2)证明见解析(3)证明见解析
117
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司【详解】(1)设A与B中对应项中同时为0的有x0 xn个,同时为1的有y0 ynx个,
则对应项不同的为nx y个,所以dA,Bnx y.
所以dA,CdB,C2ynx ynx ydA,B;
(2)设Aa,a ,L ,a ,Bb,b ,L ,b ,C c,c ,L ,c T ,
1 2 n 1 2 n 1 2 n n
因为AC a c , a c ,L , a c ,
1 1 2 2 n n
BC b c ,b c ,L ,b c ,
1 1 2 2 n n
n
所以d(AC,BC) a c b c ,
i i i i
i1
因为c 0,1,i1,2,L ,n.
i
所以当c 0时, a c b c a b ,
i i i i i i i
当c 1时, a c b c 1a 1b a b ,
i i i i i i i i i
n n
所以d(AC,BC) a c b c a b d(A,B);
i i i i i i
i1 i1
m
(3)记集合P中所有两个元素间距离的总和为d P,P ,
i j
i,j1
1 m
则d(P) d P,P .
C2 i j
m i,j1
设集合P中所有元素的第k(k 1,2,L ,n)个位置的数字共有t 个1,mt 个0,
k k
m n
则d P,P t mt ,
i j k k
i,j1 k1
因为t ,mt 0,
k k
t mt 2 m2
所以t mt k k ,
k k 2 4
m n nm2
所以d P,P t mt ,
i j k k 4
i,j1 k1
1 m 2 nm2 mn
所以d(P) d P,P .
C2 i j m(m1) 4 2(m1)
m i,j1
1
r 1
预测2:答案(1)b (答案不唯一)(2)证明见解析(3) f 44,答案见解析.
1
0
118
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司 1
r 1
【详解】(1)由定义,只需满足b 2b 3b 4b 0,不妨取b (答案不唯一).
1 2 3 4 1
0
x y
1 1
r x r y r r
(2)对于mB,i1,2,,n,存在x 2 ,x 1,1,y 2 ,y 1,1,使得x,ym.
i i
x y
n n
1,x y n
当x y 时,xy 1;当x y 时,x y 1.令 i i ,k .
i i i i i i i i i 0,x
i
y
i i1
i
r r n
所以x,yx y knk2kn.
i i
i1
所以mn2knn2k为偶数.
(3)当n4时,可猜测互相正交的4维向量最多有4个,即 f 44.
1 1 1 1
r 1 r 1 r 1 r 1
不妨取a ,a ,a ,a ,
1 1 2 1 3 1 4 1
1 1 1 1
r r r r r r r r r r r r
则有a,a 0,a,a 0,a,a 0,a ,a 0,a ,a 0,a ,a 0.
1 2 1 3 1 4 2 3 2 4 3 4
1 1 1
r r r r 1 1 1
若存在a ,使a,a 0,则a 或 或 .
5 1 5 5 1 1 1
1 1 1
1 1 1
r 1 r r r 1 r r r 1 r r
当a 时,a ,a 4;当a 时,a ,a 4;当a 时,a ,a 4,
5 1 4 5 5 1 2 5 5 1 3 5
1 1 1
故找不到第5个向量与已知的4个向量互相正交.
81
预测3:答案(1)8 (2)3 (3)
16
【详解】(1)设点Qx,y,由PPQ||2,得 x y2 2,
x y 2的图象是以原点为中心,
顺次连接四点2,0,0,2,2,0,0,2所形成的正方形,
将其上移2个单位长度即得 x y2 2的图象,
所以点集M 所占区域是:
以四点2,2,0,4,2,2,0,0为顶点的正方形及其内部,面积为8.
119
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司(2)设Px,x 2,Q x ,ex2 ,则PPQ|| x x x 2ex2 ,
1 1 2 1 2 1
将PPQP看成关于x的函数,则PPQP在x x 或x ex2 2时取得最小值,
1 1 2 1
即PPQ|| ex2 x 2 ,
min 2
令 f xexx2,则 fxex1,
当x,0时, fx0;
当x0,时, fx0,
所以 f x在,0上单调递减,在0,上单调递增,
则 f(x) f 03,此时x 0,
min 2
所以PPQP的最小值为3.
(3)设点Q x,2x2 ,x2,2,则PPQ|| ax b2x2 ,x2,2,
若存在实数a,b,使Ma,bt,
则PPQ|| ax b2x2 t对任意的x2,2成立,
1 1 1
令x ,则 a b t,
4 4 8
令x2,则 a2 b8 t,
1 1
所以:2t a b a2 b8
4 8
1 1 9 63 81
a a2b b8 ,
4 8 4 8 8
81
所以t ,
16
79 79
令a0,b ,则PPQ|| x 2x2 是2,2上的偶函数,
16 16
79 79
当x0,2 时,若2x2 ,即x2 ,
16 32
79 1 2 81 81 1
则PPQ||x 2x2 2x ,当且仅当x 时等号成立;
16 4 16 16 4
79 79 81
若 x2 4,则PPQ||2x2x ,当且仅当x2时等号成立,
32 16 16
79 81
所以存在实数a,b且a0,b ,使得Ma,b的最小值为 .
16 16
uv 1 v
预测4:答案(1)na n(n1)d ;(2)(3n2)2n2.
1 2
120
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司uuv v
【详解】(1)设a x , y ,d d , d .
n n n 1 2
uuuv uuv v x x d
由a a d ,得 n1 n 1 ,所以数列x 是以x 为首项,公差为d 的等差数列;数列y 是以y 首
n1 n y y d n 1 1 n 1
n1 n 2
项,公差为d 的等差数列.
2
uv uuv uuv
a a L a (x x L x , y y L y )
1 2 n 1 2 n 1 2 n
1 1 1
nx nn1d , ny nn1d nx, y nn1d , d
1 2 1 1 2 2 1 1 2 1 2
ur 1 r
na nn1d.
1 2
uuv uuv
(2)设a x , y ,b m , k .
n n n n n n
uuuv uuv
由a a x , y x , y x x , y y 3, 0,从而x x 3,y y 0.数列
n1 n n1 n1 n n n1 n n1 n n1 n n1 n
x 是以1为首项,公差为3的等差数列,从而x 3n2.数列y 是常数列,y 1.
n n n n
uuuv uuv
由b 2b 得m 2m ,k 2k ,又m 1,k 3,数列m 是以1为首项,公比为2的等比数列;
n1 n n1 n n1 n 1 1 n
数列k 是以3为首项,公比为2的等比数列,从而有m 2n1,k 32n1.……10分
n n n
uv uv uuv uuv uuv uuv
a b a b L a b xm x m L x m yk y k L y k
1 1 2 2 n n 1 1 2 2 n n 1 1 2 2 n n
令S xm x m L x m 1142722L 3n22n1………①
n 1 1 2 2 n n
2S 12422723L 3n22n…………②.
n
①-②得,S 13 22223L 2n1 3n22n,得S 53n52n
n n
3
12n
令T yk y k L y k 3 2n1
n 1 1 2 2 n n 12
uv uv uuv uuv uuv uuv
从而a b a b L a b S T 3n22n2
1 1 2 2 n n n n
预测5:答案(1)O uu M uur 3 , 3 (2) 34 3 (3) 2 2 , 2
2 2 10 2
1 3 3 3
uuuur 3 3
【详解】(1)因为g(x) sinx cosxsinx sinx cosx,所以OM , .
2 2 2 2 2 2
π
(2)依题意 f xsinx 3cosx2sinx ,
3
6 π 6 π 3 π π π π π 4
由 f x 得2sinx ,sinx ,x , ,x 0, ,所以cosx ,
5 3 5 3 5 3 6 3 2 3 5
π π 1 π 3 π 34 3
所以sinxsin x sinx cosx .
3 3 2 3 2 3 10
121
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司 π
(3)由题 f x的函数解析式 f xsinx ,所以hxsin2x
4 4
区间
t,t
的长度为 ,函数hxsin2x 的周期为,
4 4 4
若hx的对称轴在区间 t,t π 内,不妨设对称轴x 在 t,t 内,最大值为1,
4 8 4
π π 2
当ht ht即h h0 时,
4 4 2
函数hx在区间 t,t 上的最大值与最小值之差取得最小值为1 2 2 2 ;
4 2 2
2 2
其它的对称轴在 t,t 内时最大值与最小值之均大于 ,
4 2
当t 或t 时,最大值与最小值之差取得最大值1.
8 8
π π 5π π 3π
若hx的对称轴不在区间 t,t 内,不妨设 tt 即 t ,
4 8 4 8 8 8
则hx在区间 t,t 内单调,在两端点处取得最大值与最小值,则最大值与最小值之差为:
4
ht ht sin2t sin2t
4 2 4 4
cos2t sin2t 2sin2t 2sin2t 1, 2 ,
4 4 4 4
2 2
综上,故函数hx在区间
t,t
上的最大值与最小值之差的取值范围为 , 2
4 2
名师押题
押题1:答案(1)b ennn(2)(ⅰ)证明见解析.(ⅱ)答案见解析.
n
【详解】(1)若 f xexb xn只有一个正零点,可得ex b xn,b xnex 1,
n n n n
令g(x)xnex,g(x)nxn1exxnex xn1exnx,
令g(x)0,x(n,),令g(x)0,x(0,n),
故g(x)在(0,n)上单调递增,在(n,)上单调递减,
可得g(x)在xn处取得最大值,且最大值为g(n)xnen,
而当x0时,g(x)0,当x时,g(x)0,
由题意得,当g(x)最大时,符合题意,
故b nnen 1,即b ennn.
n n
(2)(ⅰ)若m0,则em 1为有理数;
122
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司p
若m正整数,假设em为有理数,则em y,p,qZ,q0,
q
则方程qy p0的根中有有理数,
又在方程qxm p0中,发现xe是它的根,
而已知e是超越数,故e不是方程的根,与qy p0矛盾,即em不为有理数;
综上所述:mN,em为有理数当且仅当m0;
(ⅱ)若数列b 中存在不同的三项构成等比数列,则emmmennn elll2 ,
n
可得emn2l mmnnl2l,由方程右边是有理数知左边是有理数,
由上问知当且仅当mn2l时成立,故mmnn l2l lmln,
m n m
则( )m( )n 1,设1 x,则ml(1x),nl(1x),
l l l
则1xm 1xn 1,将ml(1x),nl(1x)代入进行化简,
可得1xl(1x)1xlx 1,故1x1x 1x1x l 1,
故1x1x 1x1x 1,构造函数 f x1xln1x1xln1x,
而 fxln 1x2 0,知 f x在其定义域内单调递减,
又 f 00,故若1x1x 1x1x 1,则有x0,即mmnn l2l成立,
当且仅当mnl时成立.
即数列b 中不存在不同的三项构成等比数列,
n
2n
押题2:答案(1)5(2)a 5n11(3)S
n n n1
【详解】(1)在排列51243中,与5构成逆序的有4个,与1构成逆序的有0个,
与2构成逆序的有0个,与4构成逆序的有1个,与3构成逆序的有0个,
所以T(51243)400105.
(2)由(1)中的方法,同理可得T(3412)4,
又T(51243)5,所以a 5a 4,
n1 n
设a 5a ,得a 5a 4,
n1 n n1 n
所以44,解得1,则a 15a 1,
n1 n
因为a 110,
1
所以数列a 1是首项为1,公比为5的等比数列,
n
所以a 15n1,则a 5n11.
n n
(3)因为 j n1i(i1,2,L ,n),
i
123
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司n1n
所以b Tj j L j n1n2L 10 ,
n 1 2 n 2
1 2 1 1
所以 2 ,
b (n1)n n n1
n1
1 1 1 1 1 1 2n
所以S 21 L 21 .
n 2 2 3 n n1 n1 n1
押题3:答案(1)证明见解析(2)证明见解析(3)存在,且mk2k2,理由见解析
n1π nπ π nπ
【详解】(1)由cos cos sin ,
2 2 2 2
n1π nπ nπ nπ nπ
故a cos a 2cos sin sin a cos 2,
n1 2 n 2 2 2 n 2
n1π nπ
即a cos a cos 2,
n1 2 n 2
π nπ
又a cos a 2,故数列a cos 是以2为首项,2为公差的等差数列,
1 2 1 n 2
nπ nπ
则a cos 2n,即a 2ncos ,
n 2 n 2
nπ nπ
故存在等差数列d 2n,使a d 2ncos 2ncos ,
n n n 2 2
nπ
由cos 1,0,1,故数列a 有Q3性质;
2 n
(2)设对数列a ,存在等差数列e ,使e a s,s ,L ,s ,
n n n n 1 2 k1
对数列b ,存在等差数列 g ,使g b t ,t ,L ,t ,
n n n n 1 2 k2
则对数列a b ,存在等差数列e g ,
n n n n
使a b g e 的值为s t i1,2,3L k , j1,2,3L k ,
n n n n i j 1 2
这样的s t 最多有kk 个,即数列a b 有Qkk 性质;
i j 1 2 n n 1 2
(3)设对数列T ,存在等差数列H ,且其公差为d,使得T H h,h ,L ,h ,
n n n n 1 2 k
当n2时,有 f T T T H T H H H
n n n1 n n n1 n1 n n1
T H T H d ,
n n n1 n1
由T H h,h ,L ,h ,
n n 1 2 k
故当n2时,T H T H d h h di, j1,2,3,L ,k,
n n n1 n1 i j
当i j时,h h d d,当i j时,h h d可能有kk1k2k种,
i j i j
故这样的h h d最多有k2k1个,
i j
124
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司即存在等差数列p :p 0,使 f p nN* f h h d i, j1,2,3,L ,k ,
n n n n 1 i j
f p nN* 的元素个数不超过k2k2个,
n n
故一定存在mk2k2,使得数列f 具有Qm性质.
n
押题4:答案(1)A54,7,8, A5 3;(2)证明见解析(3)证明见解析
【详解】(1)由a ,a ,a ,a ,a ,a ,a ,a 6,3,2,5,3,7,5,5,知a a a 5,
1 2 3 4 5 6 7 8 4 7 8
所以A54,7,8, A5 3;
1
(2)依题意, Aa 1,i1,2,L ,n,则有 1,
i Aa
i
1 1 1
所以 L n,当且仅当 Aa 1i1,2,L ,n时取等号, 又因为
Aa Aa Aa i
1 2 n
1 1 1
L n,所以 Aa 1,i1,2,L ,n,a,a ,L ,a 互不相同,
Aa Aa Aa i 1 2 n
1 2 n
故i,j1,2,L ,n,若i j,则a a ;
i j
(3)由Aa a k,得a a a ,则有a a a ①,
k2 k1 k k2 k1 k1 k k2
由a a 1及①,可得
1 2
a2 aa ,
1 1 2
a2 a a a a a aa ,
2 2 3 1 2 3 1 2
a2 a a a a a a a ,
3 3 4 2 3 4 2 3
......
a2 a a a a a a a .
n1 n1 n n2 n1 n n2 n1
以上各式相加,得a2a2L a2 a a a2 a a a .
1 2 n n1 n n n n1 n
由a a 1及①,当n3时,0a a ,
1 2 n1 n
所以a2a2L a2 a a a a a a 2a a ,
1 2 n n n1 n n n1 n1 n1 n
即a2a2L a2 2a a .
1 2 n n1 n
押题5:答案(1)不是,理由见解析;
3kπ 3kπ π 3kπ π
cosx , x kZ
2 2 2 2 4 π π 3π
(2) f x ,
,
,
π,
;
sin x 3kπ , 3kπ π x 3kπ πkZ 4 2 2
2 2 4 2
125
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司7π,a0
20π,0a 2 或a1
2
(3)S3
2
30π,a
2
2
40π, a1
2
4x
【详解】(1) f xsin 不是为“M 函数”,理由如下:
3
π 4π 2π 4x 4x 4π
因为 f xsin x sin , f xsin sin
2 32 3 3 3 3
π
所以 f x f xxR,
2
4x
因此,函数 f xsin 不是“M 函数”.
3
3π 3π
(2)函数 f x满足 f x f x,令xx 得
4 4
3π 3π 3π
f x
f x f x,
4 4 4
3π 3π
即 f x f x,所以函数 f x为周期函数,且最小正周期为T ,
2 2
因为 f π x f xxR,则 f x的一个对称轴为x π .
2 4
3kπ π 3kπ 3kπ π
①当x , π kZ时,x ,π kZ,
2 4 2 2 4
3kπ 3kπ
则 f x f x sinx kZ;
2 2
3kπ π 3kπ π 3kπ π π
②当x , kZ,则x , kZ,
2 2 2 4 2 2 4
π 3kπ π
则 x
,π
kZ,
2 2 4
π 3kπ π 3kπ 3kπ
所以, f x f x sin x cosx kZ.
2 2 2 2 2
3kπ 3kπ π 3kπ π
cosx , x kZ
2 2 2 2 4
综上所述, f x ,
sin x 3kπ , 3kπ π x 3kπ πkZ
2 2 4 2
3π π π 3π
所以函数 f x在 0, 上的单调递增区间为 , , π, .
2 4 2 2
126
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司 π
(3)由(2)可得函数 f x在 ,π 上的图象如下图所示,
2
π
下面考虑方程 f xa在区间 ,π 的根之和.
2
①当0a 2 或a1时,方程 f xa有两个实数解,其和为 π ;
2 2
②当a 2 时,方程 f xa有三个实数解,其和为 3π ;
2 4
③当 2 a1时,方程 f xa有四个实数解,其和为π.
2
π 3kπ
当x , π kN时,关于x的方程 f xa(a为常数)有解,
2 2
记该方程所有解的和为Sk,
π 3π
所以,当a0时,S3 4 1237π;
2 2
当0a 2 或a1时,S32
π 4 3π 123
20π;
2 4 2
2 π 3π
当a 时,S33
4 123
30π;
2 4 2
2 π 3π
当 a1时,S34
4 123
40π.
2 4 2
7π,a0
20π,0a 2 或a1
2
因此,S3 2 .
30π,a
2
2
40π, a1
2
127
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司