数学（广东专用02，新题型结构）（参考答案）_2024高考押题卷_62024学科网全系列_24学科网高考押题预测卷_2024年高考数学押题预测卷

2024年高考押题预测卷【广东专用02】 数学·参考答案 第一部分（选择题 共58分） 一、选择题：本题共8小题，每小题5分，共40分。在每小题给出的四个选项中，只有一项是符合题目要 求的。 1 2 3 4 5 6 7 8 D C B D B A D C 二、选择题：本题共3小题，每小题6分，共18分．在每小题给出的选项中，有多项符合题目要求．全部 选对的得6分，部分选对的得部分分，有选错的得0分． 9 10 11 BCD BCD CD 第二部分（非选择题 共92分） 三、填空题：本题共3小题，每小题5分，共15分。 13．30 14． 15． 四、解答题：本题共5小题，共77分。解答应写出文字说明、证明过程或演算步棸。 15．（13分） 【解析】（1）由题意可知，点 在线段 的垂直平分线上，所以 ， 又点 是圆 上一动点，所以 ．（2分） ①当 时， ； ②当 时， ， 所以 的轨迹 满足 ，（5分） 根据双曲线定义可知， 点的轨迹 是以 为左､右焦点，实轴长为 的双曲线， 1 原创精品资源学科网独家享有版权，侵权必究！ 学科网（北京）股份有限公司可得 ，所以 的轨迹 的方程为 ．（7分） （2）设 ，所以 ，（8分） 因为直线 的斜率为 ，所以 ，即 ，（10分） 与 联立解得 （舍去）或3．（12分） 所以点 的坐标为 ．（13分） 16．（15分） 【解析】（1）因为 ， ， 所以根据余弦定理可得 ， 代入数值解得 ， 所以 ，所以 .（2分） 又因为 ，M是BC的中点， 所以 ， ， 所以在 中， ， ，（4分） 解得 ， 所以 ，所以 . 因为 ，所以 ， 又 ， ， 平面 ， 平面 ， 所以 平面 ，（5分） 2 原创精品资源学科网独家享有版权，侵权必究！ 学科网（北京）股份有限公司而 平面 ， 所以 . 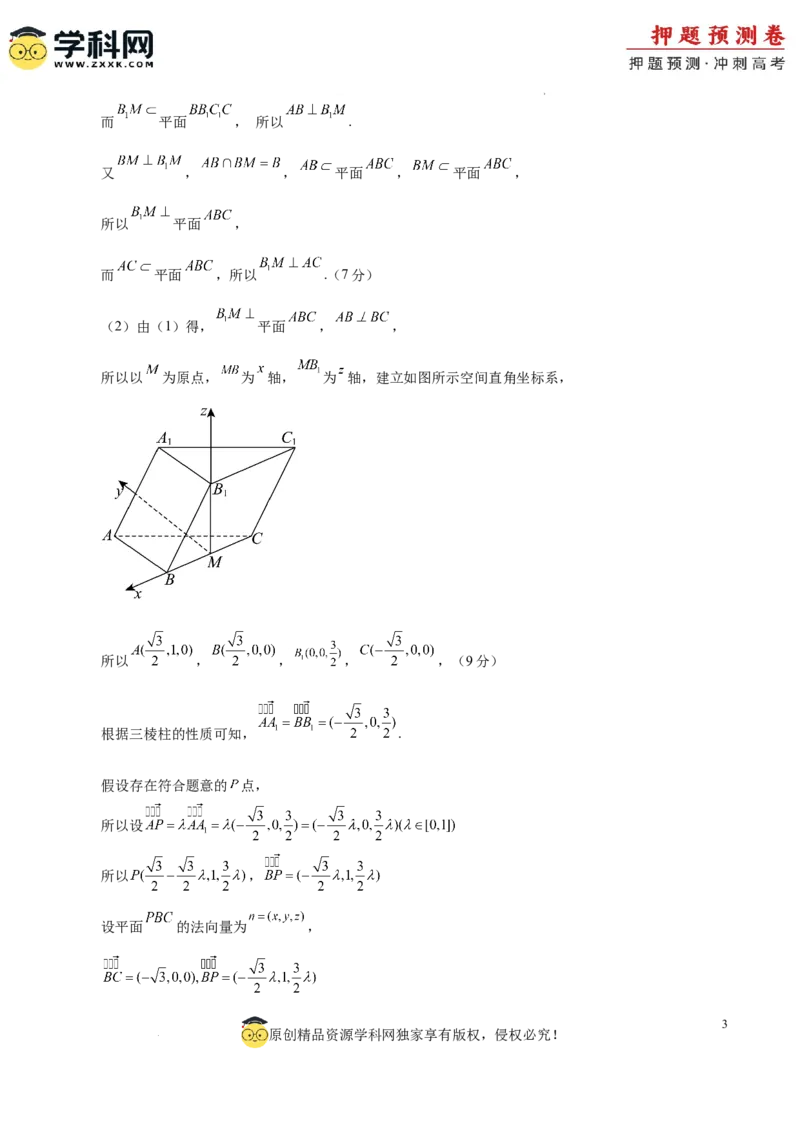又 ， ， 平面 ， 平面 ， 所以 平面 ， 而 平面 ，所以 .（7分） （2）由（1）得， 平面 ， ， 所以以 为原点， 为 轴， 为 轴，建立如图所示空间直角坐标系， 所以 ， ， ， ，（9分） 根据三棱柱的性质可知， . 假设存在符合题意的 点， 所以设 所以 ， 设平面 的法向量为 ， 3 原创精品资源学科网独家享有版权，侵权必究！ 学科网（北京）股份有限公司由 ，得到 ，取 ，所以 ，（12分） 所以平面 的法向量为 而且平面 的法向量为 ， 因为二面角 的正弦值为 ，所以二面角的余弦值为 ，（13分） 所以 ，解得 ， 又因为 ，所以 ， 此时 ，所以 . 综上，在棱 上存在点P，使得二面角 的正弦值为 ， 的长度为 .（15分） 17．（15分） 【解析】（1）由题意可知这2人恰好来自不同年级的概率是 ；（5分） （2）由题意可知 ，（6分） 所以 ， 显然 时， ，即 单调递减； 时， ，即 单调递增； 则 时， 取得最大值，（9分） 由题意可知 的可能取值为 ，（10分） 4 原创精品资源学科网独家享有版权，侵权必究！ 学科网（北京）股份有限公司则 ， ， ， ，（13分） 则其分布列为： X 0 1 2 3 P 所以 .（15分） 18．（17分） 【解析】（1）对 求导得 .（1分） 当 时，对 有 ，故 在 上单调递增； 当 时，有 ，而当 时， ，故当 时 ，当 时 ，从而 在 上单调递 5 原创精品资源学科网独家享有版权，侵权必究！ 学科网（北京）股份有限公司增，在 上单调递减.（5分） 综上，当 时， 在 上单调递增； 当 时， 在 上单调递增，在 上单调递减.（6分） （2）若 ，由于 ，故存在正数 使得 ，条件满足； 若 ，则由（1）的结论，知 在 上单调递增，在 上单调递减，从而此时对任 意的 都有 ，条件不满足. 综上， 的取值范围是 .（9分） （3）设 ， ，我们分唯一性和存在性两方面来证明. 唯一性：由 ，知 的导数等于 ，而 ，故 显然恒 为负，从而 在 上单调递减.（10分） 特别地， 在 上单调递减. 这表明，使得 的 至多有一个，从而唯一性得证. 存在性：我们先考虑函数 ，这里 . 由于 ，故当 时 ，当 时 ，从而 在 上单调递减，在 上单调递增，从而对于任意的 6 原创精品资源学科网独家享有版权，侵权必究！ 学科网（北京）股份有限公司，都有 ，即 .（12分） 这就得到，对任意 ，有 . 从而，对任意的 ，都有 ；而对任意的 ，都有 . 然后回到原题，首先我们有 . 同时我们又有 ， ，（15分） 故 . 由零点存在定理，知一定存在 ，使得 . 综合上述的存在性和唯一性两个方面，知存在唯一的 ，使得 .（17 分） 19．（17分） 【解析】（1）因为 关于 单调递增， 所以 ，（2分） ， 7 原创精品资源学科网独家享有版权，侵权必究！ 学科网（北京）股份有限公司于是 ， 的前 项和 ．（5分） （2）由题意可知 ， ， 所以 ，（7分） 因此 ，即 是单调递增数列，且 ， 由“生成数列”的定义可得 ．（9分） （3）若 是等差数列，证明：存在正整数 ，当 时， 是等差数列． 当 是一个常数列，则其公差 必等于0， ， 则 ，因此 是常数列，也即为等差数列；（12分） 当 是一个非常数的等差数列，则其公差 必大于0， ， 所以要么 ，要么 ， 又因为 是由正整数组成的数列，所以 不可能一直递减，（14分） 记 ，则当 时，有 ， 于是当 时， ， 故当 时， ，…，（16分） 因此存在正整数 ，当 时， ，…是等差数列． 综上，命题得证．（17分） 8 原创精品资源学科网独家享有版权，侵权必究！ 学科网（北京）股份有限公司