文档内容
绝密★启用前
2024 年高考押题预测卷【广东专用 03】
数 学
(考试时间:120分钟 试卷满分:150分)
注意事项:
1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑。如需改动,用
橡皮擦干净后,再选涂其他答案标号。回答非选择题时,将答案写在答题卡上。写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
第一部分(选择题 共58分)
一、选择题:本题共8小题,每小题5分,共40分。在每小题给出的四个选项中,只有一项是符合题目要
求的。
1.已知集合 , ,若 ,则满足集合 的个数为( )
A.4 B.6 C.7 D.8
2.若复数 的实部为 ,则点 的轨迹是( )
A.直径为2的圆 B.实轴长为2的双曲线
C.直径为1的圆 D.虚轴长为2的双曲线
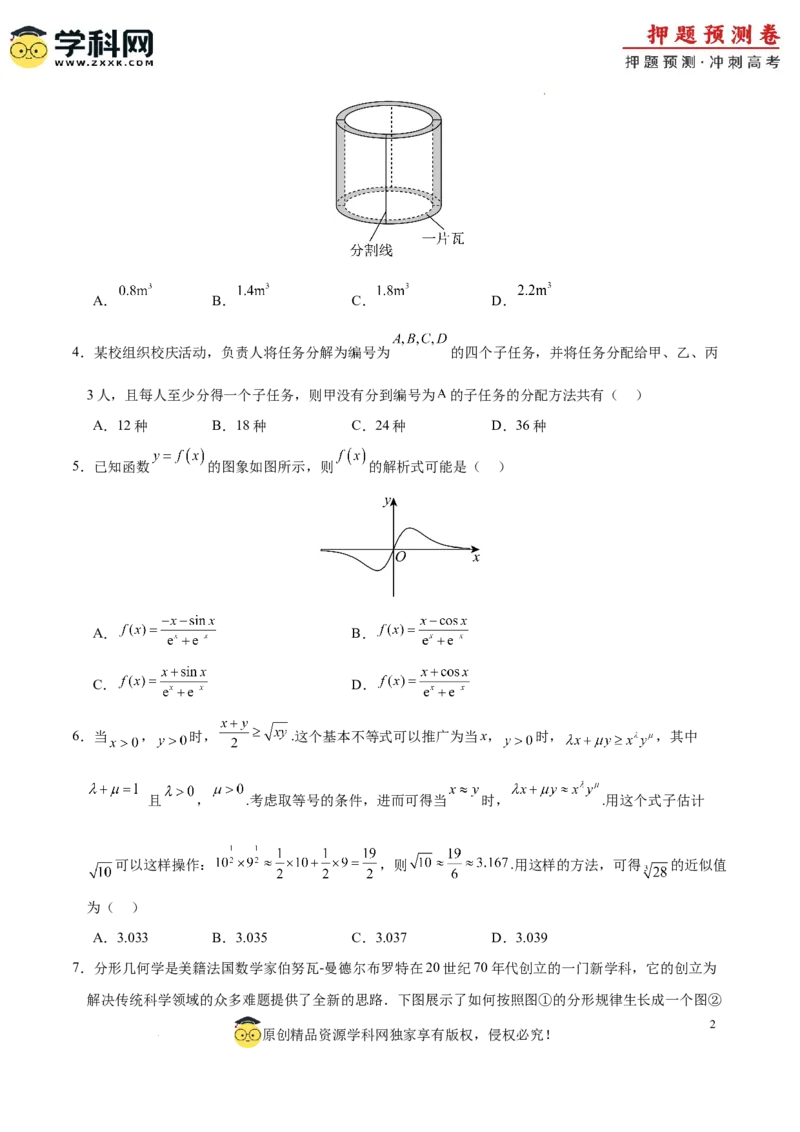
3.《天工开物》是我国明代科学家宋应星所著的一部综合性科学技术著作,书中记载了一种制造瓦片的
方法.某校高一年级计划实践这种方法,为同学们准备了制瓦用的粘土和圆柱形的木质圆桶,圆桶底面外
圆的直径为 ,高为 .首先,在圆桶的外侧面均匀包上一层厚度为 的粘土,然后,沿圆桶
母线方向将粘土层分割成四等份(如图),等粘土干后,即可得到大小相同的四片瓦.每位同学制作四片
瓦,全年级共500人,需要准备的粘土量(不计损耗)与下列哪个数字最接近.(参考数据: )
( )
1
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司A. B. C. D.
4.某校组织校庆活动,负责人将任务分解为编号为 的四个子任务,并将任务分配给甲、乙、丙
3人,且每人至少分得一个子任务,则甲没有分到编号为 的子任务的分配方法共有( )
A.12种 B.18种 C.24种 D.36种
5.已知函数 的图象如图所示,则 的解析式可能是( )
A. B.
C. D.
6.当 , 时, .这个基本不等式可以推广为当x, 时, ,其中
且 , .考虑取等号的条件,进而可得当 时, .用这个式子估计
可以这样操作: ,则 .用这样的方法,可得 的近似值
为( )
A.3.033 B.3.035 C.3.037 D.3.039
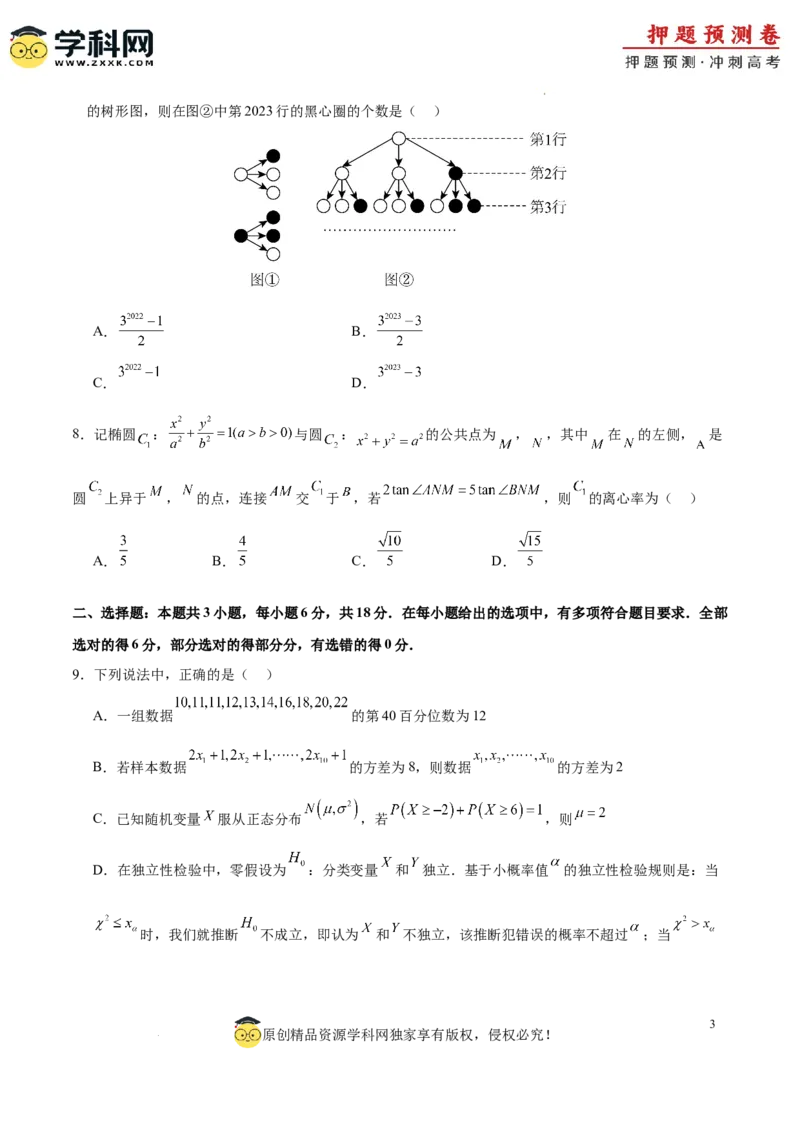
7.分形几何学是美籍法国数学家伯努瓦-曼德尔布罗特在20世纪70年代创立的一门新学科,它的创立为
解决传统科学领域的众多难题提供了全新的思路.下图展示了如何按照图①的分形规律生长成一个图②
2
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司的树形图,则在图②中第2023行的黑心圈的个数是( )
A. B.
C. D.
8.记椭圆 : 与圆 : 的公共点为 , ,其中 在 的左侧, 是
圆 上异于 , 的点,连接 交 于 ,若 ,则 的离心率为( )
A. B. C. D.
二、选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求.全部
选对的得6分,部分选对的得部分分,有选错的得0分.
9.下列说法中,正确的是( )
A.一组数据 的第40百分位数为12
B.若样本数据 的方差为8,则数据 的方差为2
C.已知随机变量 服从正态分布 ,若 ,则
D.在独立性检验中,零假设为 :分类变量 和 独立.基于小概率值 的独立性检验规则是:当
时,我们就推断 不成立,即认为 和 不独立,该推断犯错误的概率不超过 ;当
3
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司时,我们没有充分证据推断 不成立,可以认为 和 独立
10.已知函数 的定义域为 , 不恒为零,且 ,则( )
A.
B. 为偶函数
C. 在 处取得极小值
D.若 ,则
11.如图,平面 , ,M为线段AB的中点,直线MN与平面 的所成角大小为
30°,点P为平面 内的动点,则( )
A.以 为球心,半径为2的球面在平面 上的截痕长为
B.若P到点M和点N的距离相等,则点P的轨迹是一条直线
C.若P到直线MN的距离为1,则 的最大值为
D.满足 的点P的轨迹是椭圆
第二部分(非选择题 共92分)
三、填空题:本题共3小题,每小题5分,共15分。
12.若向量 , , // ,则 .
13.在 中, , , ,点 在线段AB的延长线上,且 ,则
.
14.在平面直角坐标系 中,O为坐标原点,定义 、 两点之间的“直角距离”为
4
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司.已知两定点 , ,则满足 的点M的轨迹所
围成的图形面积为 .
四、解答题:本题共5小题,共77分。解答应写出文字说明、证明过程或演算步棸。
15.(13分)
甲、乙两人进行中国象棋比赛,采用五局三胜制,假设他们没有平局的情况,甲每局赢的概率均为 ,
且每局的胜负相互独立,
(1)求该比赛三局定胜负的概率;
(2)在甲赢第一局的前提下,设该比赛还需要进行的局数为 ,求 的分布列与数学期望.
16.(15分)
如图,在圆台 中, 为轴截面, 为下底面圆周上一点, 为
下底面圆 内一点, 垂直下底面圆 于点 .
(1)求证:平面 平面 ;
(2)若 为等边三角形,求平面 和平面 的交线 与平面 所成角的正弦值.
17.(15分)
在 个数码 构成的一个排列 中,若一个较大的数码排在一个较小的数码
的前面,则称它们构成逆序(例如 ,则 与 构成逆序),这个排列的所有逆序的总个数称为
5
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司这个排列的逆序数,记为 ,例如, ,
(1)计算 ;
(2)设数列 满足 ,求 的通项公式;
(3)设排列 满足 ,
求 ,
18.(17分)
已知双曲线 的焦距为 ,点 在 上.
(1)求 的方程;
(2)直线 与 的右支交于 , 两点,点 与点 关于 轴对称,点 在 轴上的投影为点
.
(ⅰ)求 的取值范围;
(ⅱ)求证:直线 过点 .
6
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司19.(17分)
已知函数 .
(1)当 时,求函数 在 处的切线方程;
(2) 时;
(ⅰ)若 ,求 的取值范围;
(ⅱ)证明: .
7
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司