北京市2019年中考数学真题试题_中考真题_2.数学中考真题2015-2024年_2019年全国中考数学206份

2019年北京市中考数学试卷 一、 选择题（本题共16分，每小题2分） 二、 第1-8题均有四个选项，符合题意的选项只有一个． 1．4月24日是中国航天日，1970年的这一天，我国自行设计、制造的第一颗人造地球卫星 “东方红一号”成功发射，标志着中国从此进入了太空时代，它的运行轨道，距地球最近点 439000米．将439000用科学记数法表示应为 0.439�106 4.39�106 （A） （B） 4.39�105 439�103 （C） （D） 2．下列倡导节约的图案中，是轴对称图形的是 （A） （B） （C） （D） 3．正十边形的外角和为 180 360 720 1440 （A） （B） （C） （D） 4．在数轴上，点A，B在原点O的两侧，分别表示数a，2，将点A向右平移1个单位长度，得 到点C．若CO=BO，则a的值为 （A） -3 （B）-2 （C）-1 （D） 1 5．已知锐角∠AOB 如图， P M （1）在射线OA上取一点C，以点O为圆心，OC长为半径作 ，交射线 A OB于点D，连接CD； C （2）分别以点C，D为圆心，CD长为半径作弧，交 于点M，N； O D B （3）连接OM，MN． N 根据以上作图过程及所作图形，下列结论中错误的是 （A）∠COM=∠COD （B）若OM=MN，则∠AOB=20° Q （C）MN∥CD （D）MN=3CD  2mn 1     m2 n2   mn 1  m2 mn m 6．如果 ，那么代数式 的值为 3 1 （A） （B） （C）1 （D）3 11 1  a b ab 0 a b 7．用三个不等式 ， ， 中的两个不等式作为题设，余下的一个不等式作 为结论组成一个命题，组成真命题的个数为 （A）0 （B）1 （C）2 （D）3 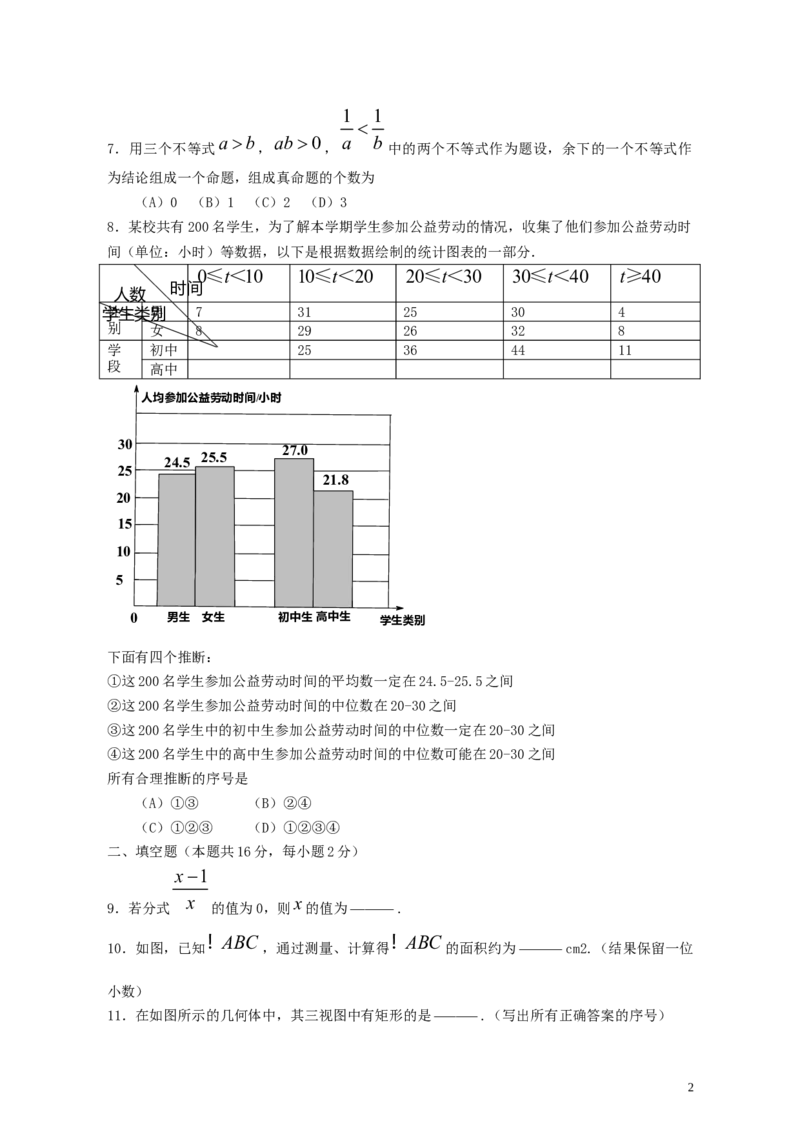8．某校共有200名学生，为了解本学期学生参加公益劳动的情况，收集了他们参加公益劳动时 间（单位：小时）等数据，以下是根据数据绘制的统计图表的一部分． 0≤t＜10 10≤t＜20 20≤t＜30 30≤t＜40 t≥40 时间 人数 学性生类男别 7 31 25 30 4 别 女 8 29 26 32 8 学 初中 25 36 44 11 段 高中 人均参加公益劳动时间/小时 30 27.0 25.5 24.5 25 21.8 20 15 10 5 0 男生 女生 初中生高中生 学生类别 下面有四个推断： ①这200名学生参加公益劳动时间的平均数一定在24.5-25.5之间 ②这200名学生参加公益劳动时间的中位数在20-30之间 ③这200名学生中的初中生参加公益劳动时间的中位数一定在20-30之间 ④这200名学生中的高中生参加公益劳动时间的中位数可能在20-30之间 所有合理推断的序号是 （A）①③ （B）②④ （C）①②③ （D）①②③④ 二、填空题（本题共16分，每小题2分） x1 x x ______ 9．若分式 的值为0，则 的值为 . ! 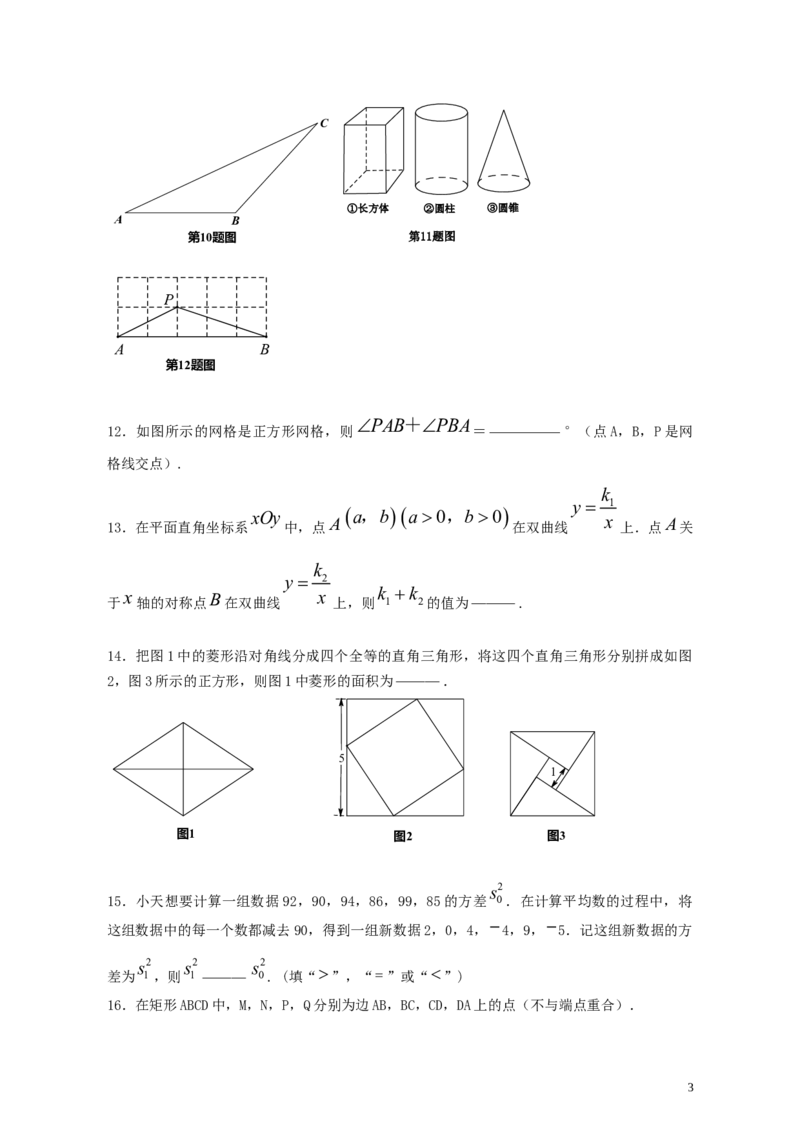ABC ! ABC ______ 10．如图，已知 ，通过测量、计算得 的面积约为 cm2.（结果保留一位 小数） ______ 11．在如图所示的几何体中，其三视图中有矩形的是 .（写出所有正确答案的序号） 2C ①长方体 ②圆柱 ③圆锥 A B 第10题图 第11题图 P A B 第12题图 PAB＋PBA __________ 12．如图所示的网格是正方形网格，则 ＝ °（点A，B，P是网 格线交点）. k y  1 xOy a，b a 0，b 0 A x A 13．在平面直角坐标系 中，点 在双曲线 上．点 关 k y  2 x B x k k ______ 于 轴的对称点 在双曲线 上，则 1 2的值为 . 14．把图1中的菱形沿对角线分成四个全等的直角三角形，将这四个直角三角形分别拼成如图 ______ 2，图3所示的正方形，则图1中菱形的面积为 ． 5 1 图1 图2 图3 s2 15．小天想要计算一组数据92，90，94，86，99，85的方差 0．在计算平均数的过程中，将   这组数据中的每一个数都减去90，得到一组新数据2，0，4， 4，9， 5．记这组新数据的方 s2 s2 s2 差为 1 ，则 1 ______ 0. (填“  ”，“”或“  ”) 16．在矩形ABCD中，M，N，P，Q分别为边AB，BC，CD，DA上的点（不与端点重合）． 3对于任意矩形ABCD，下面四个结论中， ①存在无数个四边形MNPQ是平行四边形； ②存在无数个四边形MNPQ是矩形； ③存在无数个四边形MNPQ是菱形； ④至少存在一个四边形MNPQ是正方形． ______ 所有正确结论的序号是 ． 三、解答题（本题共68分，第17-21题，每小题5分，第22-24题，每小题6分，第25题5分， 第26题6分，第27-28题，每小题7分） 解答应写出文字说明、演算步骤或证明过程． 1  3 40  2sin60 （ ）1 4 17．计算： . 4(x1)  x2,  x7  x. 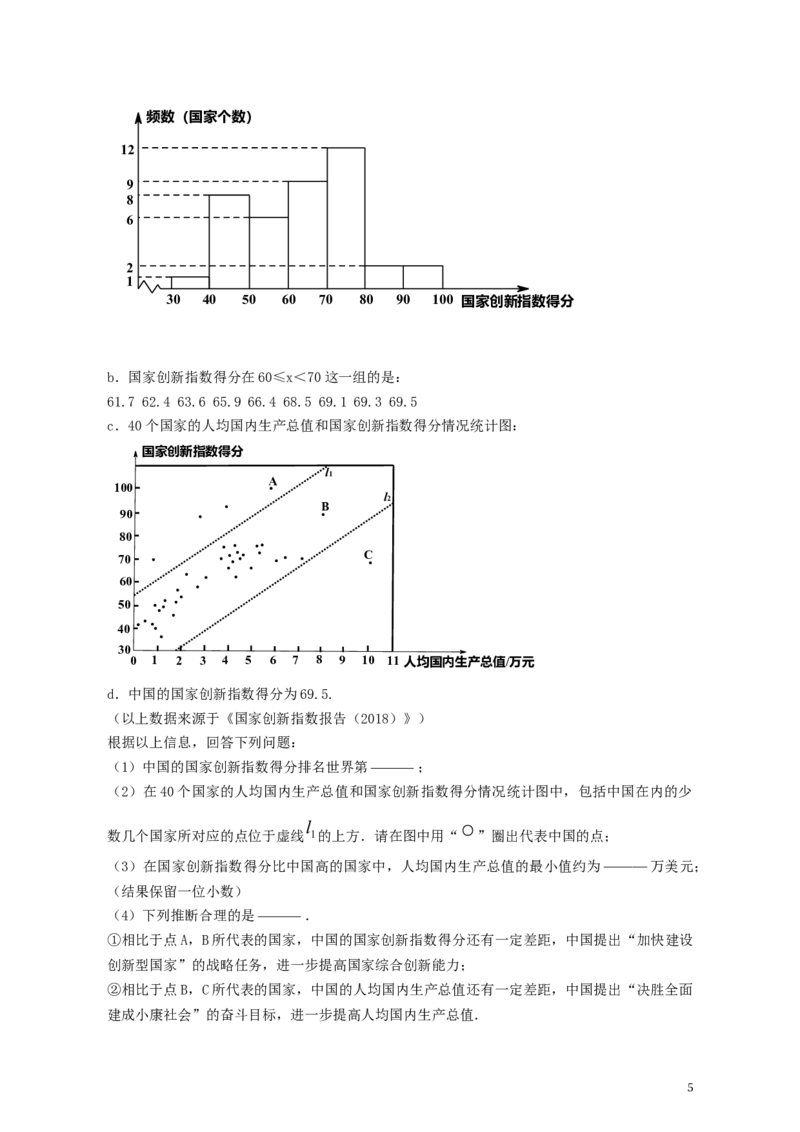  3 18．解不等式组： x2 2x2m1 0 19．关于x的方程 有实数根，且m为正整数，求m的值及此时方程的 根． 20．如图，在菱形ABCD中，AC为对角线，点E，F分别在AB，AD上，BE=DF，连接EF． （1）求证：AC⊥EF； A （2）延长 EF 交 CD 的延长线于点 G，连接 BD 交 AC 于点 O，若 BD=4， E F 1 2 B D tanG= ，求AO的长． C 21．国家创新指数是反映一个国家科学技术和创新竞争力的综合指数．对 国家创新指数得分排名前40的国家的有关数据进行收集、整理、描述和分析．下面给出了部分 信息： a．国家创新指数得分的频数分布直方图（数据分成7组： 30≤x＜40，40≤x＜50，50≤x＜60，60≤x＜70，70≤x＜80，80≤x＜90，90≤x≤100）； 4频数（国家个数） 12 9 8 6 2 1 30 40 50 60 70 80 90 100 国家创新指数得分 b．国家创新指数得分在60≤x＜70这一组的是： 61.7 62.4 63.6 65.9 66.4 68.5 69.1 69.3 69.5 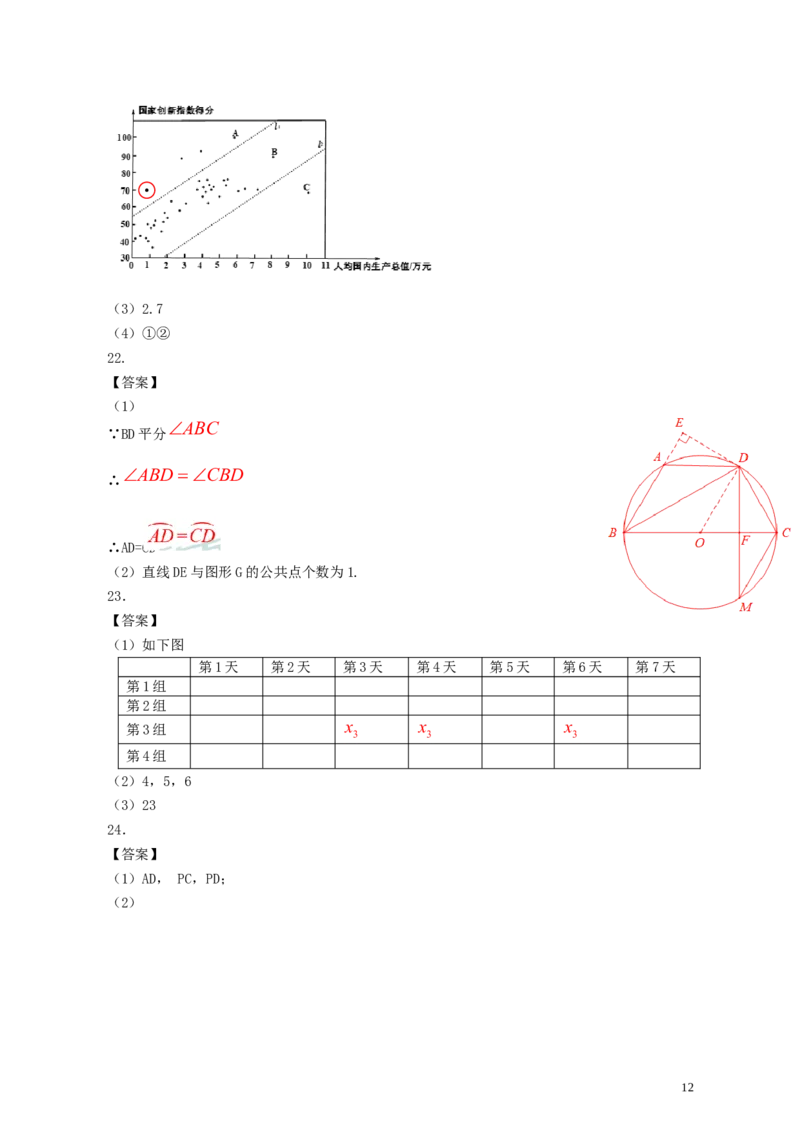c．40个国家的人均国内生产总值和国家创新指数得分情况统计图： 国家创新指数得分 l 1 A 100 l 2 B 90 80 C 70 60 50 40 30 0 1 2 3 4 5 6 7 8 9 10 11 人均国内生产总值/万元 d．中国的国家创新指数得分为69.5. 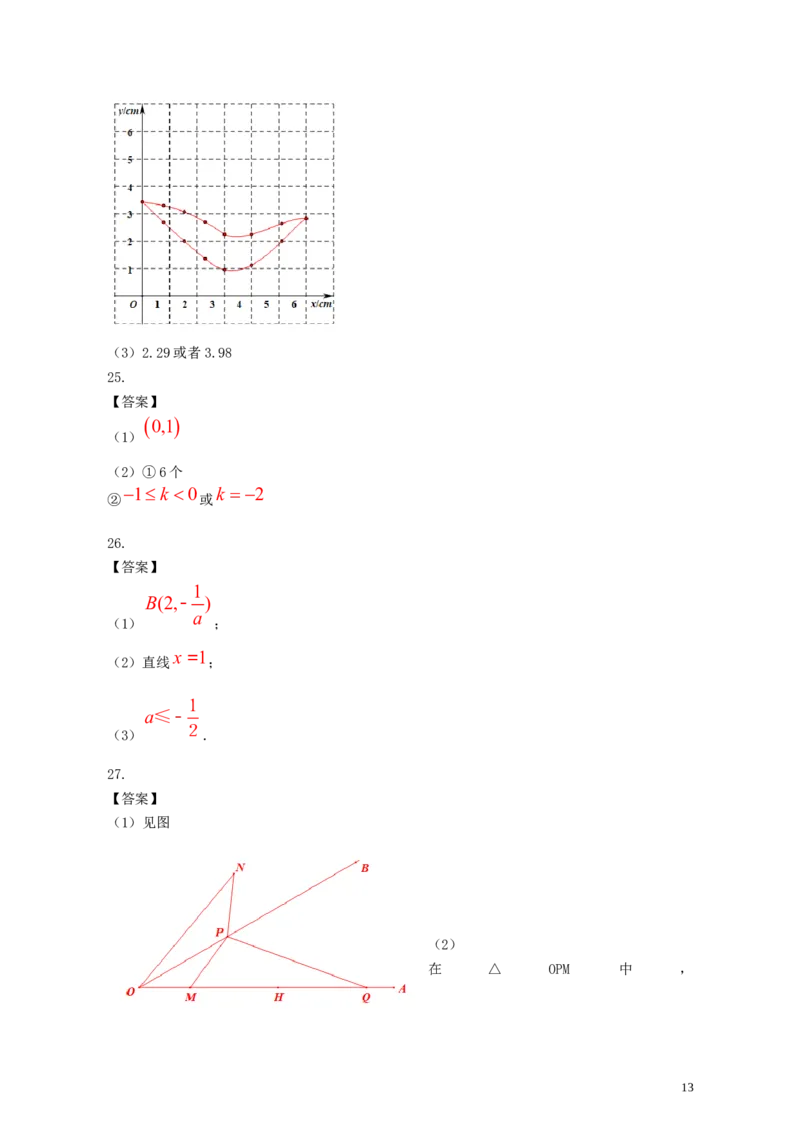（以上数据来源于《国家创新指数报告（2018）》） 根据以上信息，回答下列问题： ______ （1）中国的国家创新指数得分排名世界第 ； （2）在40个国家的人均国内生产总值和国家创新指数得分情况统计图中，包括中国在内的少 l  数几个国家所对应的点位于虚线 1的上方．请在图中用“ ”圈出代表中国的点； ______ （3）在国家创新指数得分比中国高的国家中，人均国内生产总值的最小值约为 万美元； （结果保留一位小数） ______ （4）下列推断合理的是 ． ①相比于点A，B所代表的国家，中国的国家创新指数得分还有一定差距，中国提出“加快建设 创新型国家”的战略任务，进一步提高国家综合创新能力； ②相比于点B，C所代表的国家，中国的人均国内生产总值还有一定差距，中国提出“决胜全面 建成小康社会”的奋斗目标，进一步提高人均国内生产总值． 522．在平面内，给定不在同一直线上的点A，B，C，如图所示．点O到点A，B，C的距离均等于 ABC a（a为常数），到点O的距离等于a的所有点组成图形G， 的平分线交图形G于点D， 连接AD，CD． （1）求证：AD=CD；   （2）过点D作DE BA，垂足为E，作DF BC，垂足为F，延长DF交图形G于点M，连接CM． 若AD=CM，求直线DE与图形G的公共点个数． A B C 23．小云想用7天的时间背诵若干首诗词，背诵计划如下： x ①将诗词分成4组，第i组有 i首，i =1，2，3，4； i+1 i +3 ②对于第i组诗词，第i天背诵第一遍，第（ ）天背诵第二遍，第（ ）天背诵第三遍， i  三遍后完成背诵，其它天无需背诵， 1，2，3，4； 第1天 第2天 第3天 第4天 第5天 第6天 第7天 x x x 第1组 1 1 1 x x x 第2组 2 2 2 第3组 x x x 第4组 4 4 4 ③每天最多背诵14首，最少背诵4首． 解答下列问题： x （1）填入 3补全上表； x 4 x 3 x  4 x _________ （2）若 1 ， 2 ， 3 ，则 4的所有可能取值为 ； ______ （3）7天后，小云背诵的诗词最多为 首． 624．如图，P是 与弦AB所围成的图形的外部的一定点，C是 上一动点，连接PC交弦AB 于点D． C A D P B 小腾根据学习函数的经验，对线段PC，PD，AD的长度之间的关系进行了探究． 下面是小腾的探究过程，请补充完整： （1）对于点C在 上的不同位置，画图、测量，得到了线段 PC，PD，AD的长度的几组值， 如下表： 位置1 位置2 位置3 位置4 位置5 位置6 位置7 位置8 PC/cm 3.44 3.30 3.07 2.70 2.25 2.25 2.64 2.83 PD/cm 3.44 2.69 2.00 1.36 0.96 1.13 2.00 2.83 AD/cm 0.00 0.78 1.54 2.30 3.01 4.00 5.11 6.00 ______ ______ ______ 在PC，PD，AD的长度这三个量中，确定 的长度是自变量， 的长度和 的 长度都是这个自变量的函数； xOy （2）在同一平面直角坐标系 中，画出（1）中所确定的函数的图象； y/cm 6 5 4 3 2 1 O 1 2 3 4 5 6 x/cm 7______ （3）结合函数图象，解决问题：当PC=2PD时，AD的长度约为 cm． xOy y  kx1k  0 y  k x  k 25. 在平面直角坐标系 中，直线l： 与直线 ，直线 分 y  k x  k C 别交于点A，B，直线 与直线 交于点 ． y l （1）求直线 与 轴的交点坐标； AB，BC，CA （2）横、纵坐标都是整数的点叫做整点．记线段 围成的区域（不含边界）为 W ． k  2 W ①当 时，结合函数图象，求区域 内的整点个数； W k ②若区域 内没有整点，直接写出 的取值范围． 1 y =ax2 +bx - xOy y a 26．在平面直角坐标系 中，抛物线 与 轴交于点A，将点A向右平移 2个单位长度，得到点B，点B在抛物线上． a （1）求点B的坐标（用含 的式子表示）； （2）求抛物线的对称轴； 1 1 P( ,- ) Q(2,2) 2 a （3）已知点 ， ．若抛物线与线段PQ恰有一个公共点，结合函数图象，求 a 的取值范围． AOB 30 OH  3 1 27．已知 ，H为射线OA上一定点， ，P为射线OB上一点，M为 8OMP 线段OH上一动点，连接PM，满足 为钝角，以点P为中心，将线段PM顺时针旋转 150 ，得到线段PN，连接ON． （1）依题意补全图1； OMP OPN （2）求证： ； （3）点M关于点H的对称点为Q，连接QP．写出一个OP的值，使得对于任意的点M总有 ON=QP，并证明． B B A O H A O H 图1 备用图 D E ! ABC 28．在△ABC中， ， 分别是 两边的中点，如果 上的所有点都在△ABC的内部 或边上，则称 为△ABC的中内弧．例如，下图中 是△ABC的一条中内弧． A D E B C AB  AC  2 2，D，E AB，AC （1）如图，在 Rt△ABC 中， 分别是 的中点．画出 △ABC的最长的中内弧 ，并直接写出此时 的长； 9A D E B C A0,2，B0,0，C4t,0t 0 （2）在平面直角坐标系中，已知点 ，在△ABC中， D，E AB，AC 分别是 的中点． 1 t  2 P ①若 ，求△ABC的中内弧 所在圆的圆心 的纵坐标的取值范围； P ②若在△ABC中存在一条中内弧 ，使得 所在圆的圆心 在△ABC的内部或边上，直接写 出t的取值范围． 102019年北京市中考数学答案 一. 选择题. 题号 1 2 3 4 5 6 7 8 答案 C C B A D D D C 二. 填空题. 9.1 10. 测量可知 11. ①② 12. 45° 13. 0 14. 12 15. = 16. ①②③ 三. 解答题. 17． 2 3+3 【答案】 18． x 2 【答案】 19. x  x 1 【答案】m=1，此方程的根为 1 2 20. 【答案】 （1）证明：∵四边形ABCD为菱形 ∴AB=AD，AC平分∠BAD ∵BE=DF AB BE  AD DF ∴ ∴AE=AF ∴△AEF是等腰三角形 ∵AC平分∠BAD ∴AC⊥EF （2）AO =1. 21. 【答案】 （1）17 （2） 11（3）2.7 （4）①② 22. 【答案】 （1） ABC ∵BD平分 ABD CBD ∴ ∴AD=CD （2）直线DE与图形G的公共点个数为1. 23． 【答案】 （1）如下图 第1天 第2天 第3天 第4天 第5天 第6天 第7天 第1组 第2组 x x x 第3组 3 3 3 第4组 （2）4，5，6 （3）23 24． 【答案】 （1）AD， PC，PD； （2） 12（3）2.29或者3.98 25. 【答案】 0,1 （1） （2）①6个 1 k 0 k  2 ② 或 26. 【答案】 1 B(2,- ) a （1） ； x =1 （2）直线 ； 1 a≤- ２ （3） ． 27. 【答案】 （1）见图 （2） 在 △ OPM 中 ， 13OMP=180POM OPM 150OPM OPN MPN OPM 150OPM OMP OPN （3）OP=2. 28. 【答案】 （1）如图： A D E nr 1801 l    B C 180 180 （2） 1 y  y 1 P 2 ① P 或 ； 0t  2 ② 1415