文档内容
2024年高考押题预测卷01【新高考卷】
数学·全解全析
一、单选题
1.设集合 ,则 ( )
A. B. C. D.
【答案】B
【详解】 ,得 ,即 ,
,得 ,即 , ,
所以 .
故选:B
2.设数列 的前 项之积为 ,满足 ( ),则 ( )
A. B. C. D.
【答案】C
【详解】因为 ,
所以 ,即 ,所以 ,
所以 ,显然 ,
所以 ,
所以数列 是首项为 ,公差为2的等差数列,
所以 ,
1
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司即 ,所以 .
故选:C.
3.某企业的废水治理小组积极探索改良工艺,致力于使排放的废水中含有的污染物数量逐渐减少.已知
改良工艺前排放的废水中含有的污染物数量为 ,首次改良工艺后排放的废水中含有的污染物数量
为 ,第n次改良工艺后排放的废水中含有的污染物数量 满足函数模型 (
, ),其中 为改良工艺前排放的废水中含有的污染物数量, 为首次改良工艺后排放的废水
中含有的污染物数量,n为改良工艺的次数.假设废水中含有的污染物数量不超过 时符合废水排
放标准,若该企业排放的废水符合排放标准,则改良工艺的次数最少为( )(参考数据: ,
)
A.12 B.13 C.14 D.15
【答案】D
【详解】由题意知 , ,
当 时, ,故 ,解得 ,
所以 .
由 ,得 ,即 ,
得 ,又 ,
所以 ,
故若该企业排放的废水符合排放标准,则改良工艺的次数最少要15次.
故选:D
2
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司4.已知点 在抛物线 上,抛物线 的准线与 轴交于点 ,线段 的中点 也在抛物线
上,抛物线 的焦点为 ,则线段 的长为( )
A.1 B.2 C.3 D.4
【答案】C
【详解】
如图,不妨设点 在第一象限,依题知 是 的中位线,可知 ,过 向准线做垂
线,垂足分别为 ,
同理 是 的中位线, ,由抛物线定义知 ,故得
,
又 ,则 点横坐标是 ,代入 可得其纵坐标为 ,故 .
故选:C.
5.已知 ,则 的大小关系是( )
A. B. C. D.
【答案】B
【详解】对 ,因为 ,则 ,即函数 在 单调递减,
且 时, ,则 ,即 ,所以 ,
因为 且 ,所以 ,
3
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司又 ,所以 .
故选:B
6.设等差数列 的公差为 ,则“ ”是“ 为递增数列”的( )
A.充分不必要条件 B.必要不充分条件
C.充分必要条件 D.既不充分也不必要条件
【答案】A
【详解】由等差数列 的公差为 ,得 ,则 ,
当 时, ,而 ,则 ,因此 , 为递增数列;
当 为递增数列时,则 ,即有 ,整理得 ,不能推出 ,
所以“ ”是“ 为递增数列”的充分不必要条件.
故选:A
7.已知 ,则 ( )
A. B.
C. D.
【答案】A
【详解】解:因为 ,
所以 ,
两式相加得: ,即 ,
化简得 ,
所以 ,
4
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司故选:A
8.已知函数 的导函数 ,若函数 有一极大值点为 ,则实数 的取值
范围为( )
A. B.
C. D.
【答案】D
【详解】由题意 ,令 ,
若 恒成立,易知:当 时 ,当 时 ,
所以 是 的极小值点,不合题意,故 有两个不同零点.
设 的两个零点分别为 ,则 ,
结合三次函数的图象与性质知: ,
在 、 上 , 单调递减,在 、 上 , 单调递增,
是 的极大值点,符合题意,
此时需 ,得 ,所以实数 的取值范围为 .
故选:D.
二、选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求.全部
选对的得6分,部分选对的得部分分,有选错的得0分.
9.已知复数 ,则下列命题一定成立的有( )
A.若 ,则 B.若 ,则
C. D.
5
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司【答案】AC
【分析】根据共轭复数的概念和复数的四则运算,结合复数模的计算及性质,逐项判断即可.
【详解】设 ,则 .
对于A: ,
若 ,则 ,
所以 ,即 ,故A一定成立;
对于B: ,若 ,则 ①,
,同理 ,
若 ,则需满足 且 ,与①式不同,故B不一定成立;
选项C: ,
,
所以 ,故C一定成立;
选项D: ②,
,与②式不同,故D不一定成立.
故选:AC
10.已知 ,下列结论正确的是( )
A.若 的最小正周期为 ,则
B.若 的图象向左平移 个单位长度后得到的图象关于 轴对称,则
6
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司C.若 在 上恰有4个极值点,则 的取值范围为
D.存在 ,使得 在 上单调递减
【答案】ABC
【详解】由 ,
对于A,若 的最小正周期为 ,则 ,故A正确;
对于B,若 的图象向左平移 个单位长度后得 ,其图象关
于纵轴对称,
则有 ,显然 ,故B正确;
对于C, ,
根据题意有 ,故C正确;
对于D, ,
显然 , ,即该区间为包含 的连续区间,
根据正弦函数的单调性可知:该区间不可能单调递减,故D错误.
故选:ABC
11.六氟化硫,化学式为 ,在常压下是一种无色、无臭、无毒、不燃的稳定气体,有良好的绝缘性,
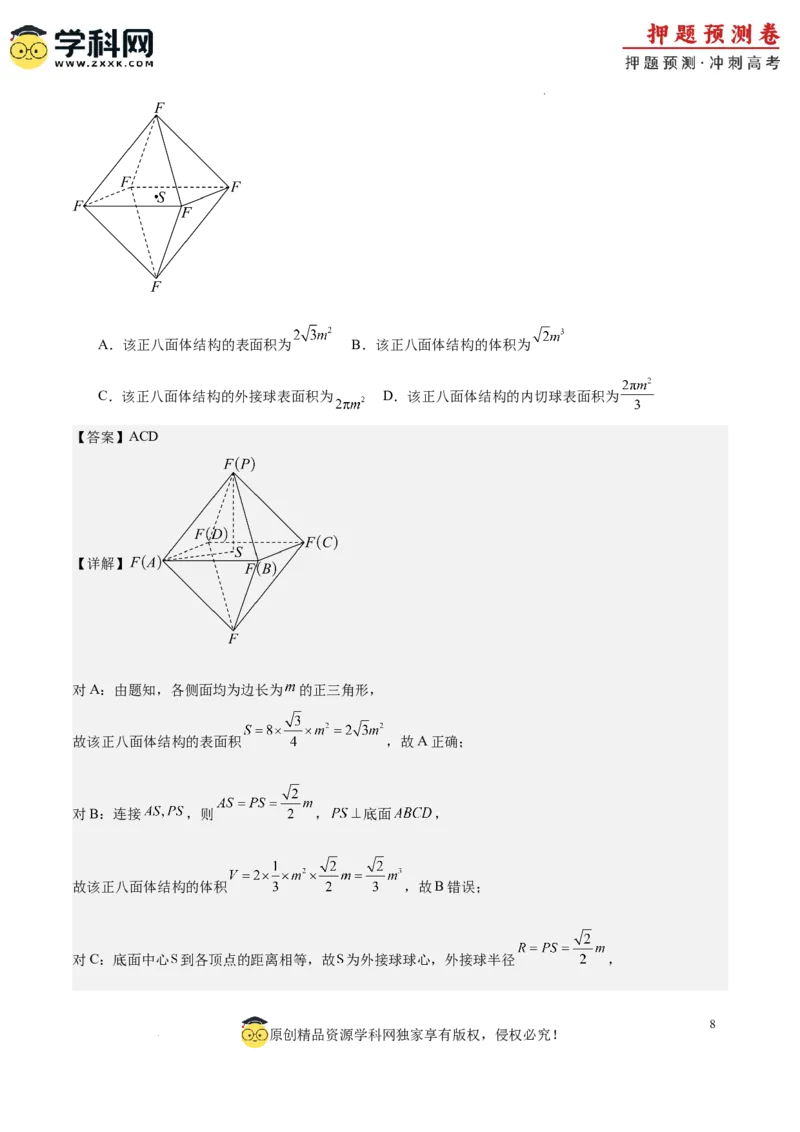
在电器工业方面具有广泛用途.六氟化硫结构为正八面体结构,如图所示,硫原子位于正八面体的中心,
6个氟原子分别位于正八面体的6个顶点,若相邻两个氟原子之间的距离为m,则( )
7
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司A.该正八面体结构的表面积为 B.该正八面体结构的体积为
C.该正八面体结构的外接球表面积为 D.该正八面体结构的内切球表面积为
【答案】ACD
【详解】
对A:由题知,各侧面均为边长为 的正三角形,
故该正八面体结构的表面积 ,故A正确;
对B:连接 ,则 , 底面 ,
故该正八面体结构的体积 ,故B错误;
对C:底面中心 到各顶点的距离相等,故 为外接球球心,外接球半径 ,
8
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司故该正八面体结构的外接球表面积 ,故C正确;
对D:该正八面体结构的内切球半径 ,
故内切球的表面积 ,故D正确;
故选:ACD.
第二部分(非选择题 共92分)
三、填空题:本题共3小题,每小题5分,共15分。
12. 的展开式中 的系数为 .
【答案】
【详解】
二项式 的展开式通项公式为 ,
当 时, ,当 时, ,
因此展开式中含 的项为 ,故所求系数为 .
故答案为:24.
13.已知高为2的圆锥内接于球O,球O的体积为 ,设圆锥顶点为P,平面 为经过圆锥顶点的平面,
且与直线 所成角为 ,设平面 截球O和圆锥所得的截面面积分别为 , ,则 .
【答案】
【详解】令球 半径为 ,则 ,解得 ,由平面 与直线 成 角,
得平面 截球所得小圆半径 ,因此 ,
由球 的内接圆锥高为2,得球心 到此圆锥底面距离 ,则圆锥底面圆半径
9
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司,
令平面 截圆锥所得截面为等腰 ,线段 为圆锥底面圆 的弦,
点 为弦 中点,如图,依题意 , , ,
,显然 ,于是 ,
所以 .
故答案为:
14.已知双曲线 的左右顶点分别为 ,点 是双曲线 上在第一象限内的点,直线
的倾斜角分别为 ,则 ;当 取最小值时, 的面积为
.
【答案】
【详解】设 ,则 ,可得 ,
又因为 分别为双曲线 的左右顶点,可得 ,
所以 ;
1
原创精品资源学科网独家享有版权,侵权必究!
0
学科网(北京)股份有限公司又由 ,所以 ,
当且仅当 时,等号成立,所以 ,解得 ,
所以 ,所以 ,
所以 的面积为 .
故答案为: ; .
四、解答题:本题共5小题,共77分。解答应写出文字说明、证明过程或演算步棸。
15.如图,在平面四边形ABCD中, , .
(1)若 , ,求 的值;
(2)若 , ,求四边形ABCD的面积.
【答案】(1) (2)
【详解】(1)在 中, , ,则 ,
,
在 中,由正弦定理得 ,
.
(2)在 和 中,由余弦定理得
,
1
原创精品资源学科网独家享有版权,侵权必究!
1
学科网(北京)股份有限公司,
得 ,又 ,得 ,
则 , ,
四边形ABCD的面积
.
16.已知函数 .
(1)若 ,求函数 在 上的最大值和最小值;
(2)讨论函数 的单调性.
【答案】(1)最大值为 ,最小值为 ;(2)答案见解析.
【详解】(1)当 时, ,则 ,
令 ,得 或 ,
由于 ,
所以当 , , 在 单调递减,
所以当 , , 在 单调递增,
所以 在 时取到极小值,且 ,
又因为 , ,
综上,函数 在 上的最大值为 ,最小值为 .
(2)因为 ,所以 ,
当 ,即 时, ,
1
原创精品资源学科网独家享有版权,侵权必究!
2
学科网(北京)股份有限公司在 单调递增,
当 ,即 时,
令 ,则 ,
所以当 , , 在 单调递增,
当 , , 在 单调递减,
当 , , 在 单调递增.
综上所述,当 时, 在 单调递增,
当 时, 在 , 单调递增,在 单调递减.
17.2023年12月2日,中央广播电视总台甲辰龙年春晚的主标识正式发布,中央广播电视总台《2024年
春节联欢晚会》以“龙行龘龘,欣欣家国”为主题,创新“思想+艺术+技术”融合传播,与全球华人相
约除夕,共享一台精彩纷呈、情真意切、热气腾腾的文化盛宴.为了解大家对“龘”这个字的认知情况,
某网站进行了调查,并对每一类情况赋予相应的认知度分值,得到如下表格:
A类:不会读不会 B类:会读不会 C类:会读且会写但不理 D类:会读、会写且理
认知情况
写 写 解 解
人数/万人 10 30 5 5
认知度分
50 70 90 100
值
(1)求参与调查的人员认知度分值的平均数与方差;
(2)为了帮助大家记住这个主题,该网站设计了一个有奖游戏,参与者点击游戏按钮,“龙行龘龘,欣欣家
国”这8个字将进行随机排列,若相同的字分别相邻(即龘与龘相邻,欣与欣相邻),则这个参与者可以
获得奖励,已知每个参与者是否获得奖励互不影响,若2人同时参与游戏,求恰好有1人获得奖励的概率;
(3)若从参与调查的人员中按照分层抽样的方法抽取20人进行座谈,再从这20人中随机选取3人赠送小礼
品,这3人中属于D类的人数记为X,求X的分布列及数学期望.
【答案】(1)71,209(2) (3)分布列见解析,
【详解】(1)参与调查的人员认知度分值的平均数为
1
原创精品资源学科网独家享有版权,侵权必究!
3
学科网(北京)股份有限公司,
方差为 .
(2)将这8个字随机排列,不同的排列方法有 种,
相同的字分别相邻的不同情况有 种,
故参与者可以获得奖励的概率 .
若2人同时参与游戏,则恰好有1人获奖的概率为 .
(3)根据分层抽样的规则可知,A类抽取4人,B类抽取12人,C类抽取2人,D类抽取2人,则X的所
有可能取值为0,1,2,则 , , ,
∴X的分布列为
X 0 1 2
P
∴X的数学期望为 .
18.已知四棱柱 如图所示,底面 为平行四边形,其中点 在平面 内的投影
为点 ,且 .
1
原创精品资源学科网独家享有版权,侵权必究!
4
学科网(北京)股份有限公司(1)求证:平面 平面 ;
(2)已知点 在线段 上(不含端点位置),且平面 与平面 的夹角的余弦值为 ,求
的值.
【答案】(1)证明见解析(2)
【详解】(1)不妨设 ,
因为 平面 平面 ,故 ,
在 中, ,
由余弦定理, ,
得 ,故 ,则 ,
因为 平面 ,所以 平面 ,
而 平面 ,所以平面 平面 ;
(2)由(1)知, 两两垂直,
如图所示,以 为坐标原点,建立的空间直角坐标系 ,
则 ,
故 ,
,所以 ,
1
原创精品资源学科网独家享有版权,侵权必究!
5
学科网(北京)股份有限公司设 ,则 ,即 ,
所以 ;
设 为平面 的一个法向量,
则 ,
令 ,则 ,所以 ,
因为 轴 平面 ,则可取 为平面 的一个法向量,
设平面 与平面 的夹角为 ,
则 ,
解得 ,故 .
19.人类对地球形状的认识经历了漫长的历程.古人认为宇宙是“天圆地方”的,以后人们又认为地球是
个圆球.17世纪,牛顿等人根据力学原理提出地球是扁球的理论,这一理论直到1739年才为南美和北欧的
弧度测量所证实.其实,之前中国就曾进行了大规模的弧度测量,发现纬度越高,每度子午线弧长越长的
事实,这同地球两极略扁,赤道隆起的理论相符.地球的形状类似于椭球体,椭球体的表面为椭球面,在
空间直角坐标系下,椭球面 ,这说明椭球完全包含在由平面
所围成的长方体内,其中 按其大小,分别称为椭球的长半轴、中半轴和短半轴.
1
原创精品资源学科网独家享有版权,侵权必究!
6
学科网(北京)股份有限公司某椭球面与坐标面 的截痕是椭圆 .
(1)已知椭圆 在其上一点 处的切线方程为 .过椭圆 的左焦点
作直线 与椭圆 相交于 两点,过点 分别作椭圆的切线,两切线交于点 ,求 面积的最小
值.
(2)我国南北朝时期的伟大科学家祖暅于5世纪末提出了祖暅原理:“幂势既同,则积不容异”.祖暅原理
用现代语言可描述为:夹在两个平行平面之间的两个几何体,被平行于这两个平面的任意平面所截,如果
截得的两个截面的面积总相等,那么这两个几何体的体积相等.当 时,椭球面 围成的椭球是一个旋
转体,类比计算球的体积的方法,运用祖暅原理求该椭球的体积.
【答案】(1) (2)
【详解】(1)椭圆 的标准方程为 ,则 .
当直线 的倾斜角为 时, 分别为椭圆的左、右顶点,此时两切线平行无交点,不符合题意,
所以直线 的倾斜角不为 ,
设直线 ,
由 ,得 ,
则 ,
所以
1
原创精品资源学科网独家享有版权,侵权必究!
7
学科网(北京)股份有限公司,
又椭圆 在点 处的切线方程为 ,在点 处的切线方程为 ,
由 ,得 ,
代入 ,得 ,所以 ,
则点 到直线 的距离 ,
所以 ,
设 ,则 ,
令 ,则 ,所以 在 上单调递增,
所以当 ,即 时, 的面积最小,最小值是 ;
(2)椭圆 的焦点在 轴上,长半轴长为 ,短半轴长为1,
椭球由椭圆 及其内部绕 轴旋转 而成旋转体,
构造一个底面半径为1,高为 的圆柱,在圆柱中挖去一个以圆柱下底面圆心为顶点,
圆柱上底面为底面的圆锥后得到一新几何体,
1
原创精品资源学科网独家享有版权,侵权必究!
8
学科网(北京)股份有限公司当平行于底面的截面与圆锥顶点距离为 时,设小圆锥底面半径为 ,
则 ,即 ,所以新几何体的截面面积为 ,
把 代入 ,得 ,解得 ,
所以半椭球的截面面积为 ,
由祖暅原理,得椭球的体积 .
1
原创精品资源学科网独家享有版权,侵权必究!
9
学科网(北京)股份有限公司