文档内容
2019年四川省广安市中考数学试卷
一、选择题(本大题共10小题,共30.0分)
1. -2019的绝对值是( )
1 1
A. -2019 B. 2019 C. - D.
2019 2019
2. 下列运算正确的是( )
A. a2+a3=a5 B. 3a2 ⋅4a3=12a6C. 5√3-√3=5 D. √2×√3=√6
3. 第二届“一带一路”国际合作高峰论坛于2019年4月25日至27日在北京召开,
“一带一路”建设进行5年多来,中资金融机构为“一带一路”相关国家累计发
放贷款250000000000元,重点支持了基础设施、社会民生等项目.数字
250000000000用科学记数法表示,正确的是( )
A. 0.25×1011 B. 2.5×1011 C. 2.5×1010 D. 25×1010
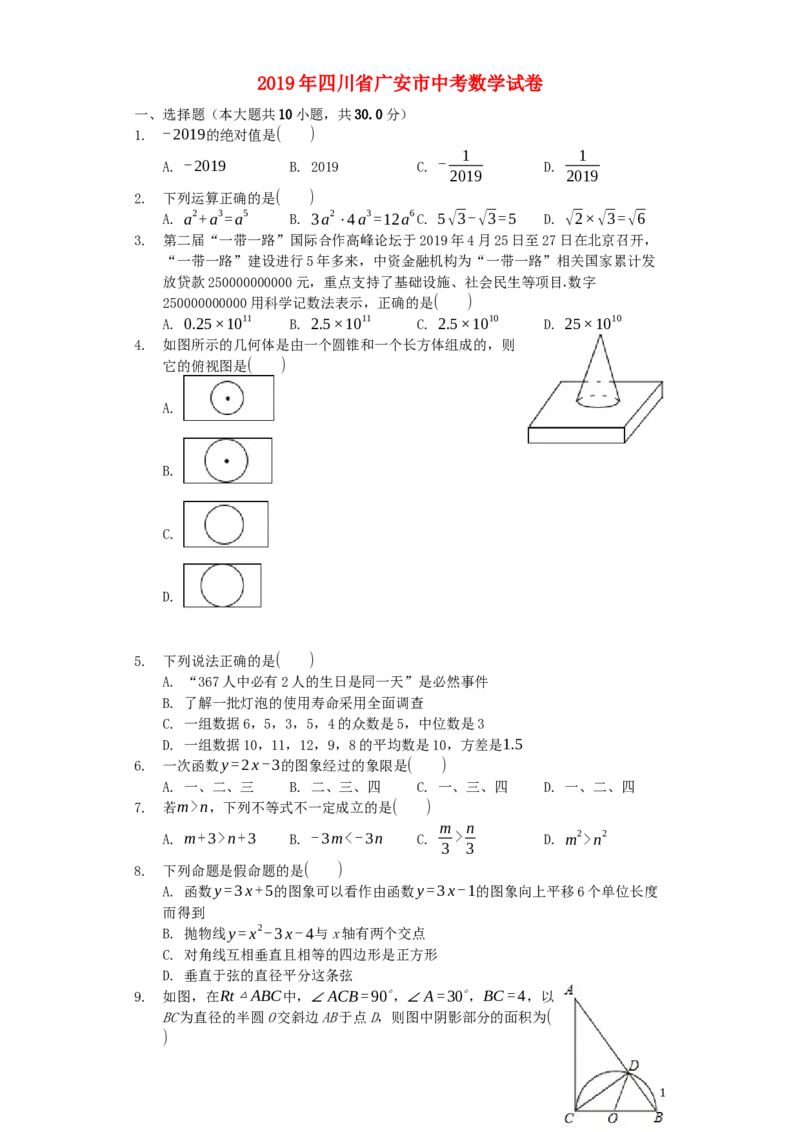
4. 如图所示的几何体是由一个圆锥和一个长方体组成的,则
它的俯视图是( )
A.
B.
C.
D.
5. 下列说法正确的是( )
A. “367人中必有2人的生日是同一天”是必然事件
B. 了解一批灯泡的使用寿命采用全面调查
C. 一组数据6,5,3,5,4的众数是5,中位数是3
D. 一组数据10,11,12,9,8的平均数是10,方差是1.5
6. 一次函数y=2x-3的图象经过的象限是( )
A. 一、二、三 B. 二、三、四 C. 一、三、四 D. 一、二、四
7. 若m>n,下列不等式不一定成立的是( )
m n
A. m+3>n+3 B. -3m<-3n C. > D. m2>n2
3 3
8. 下列命题是假命题的是( )
A. 函数y=3x+5的图象可以看作由函数y=3x-1的图象向上平移6个单位长度
而得到
B. 抛物线y=x2-3x-4与x轴有两个交点
C. 对角线互相垂直且相等的四边形是正方形
D. 垂直于弦的直径平分这条弦
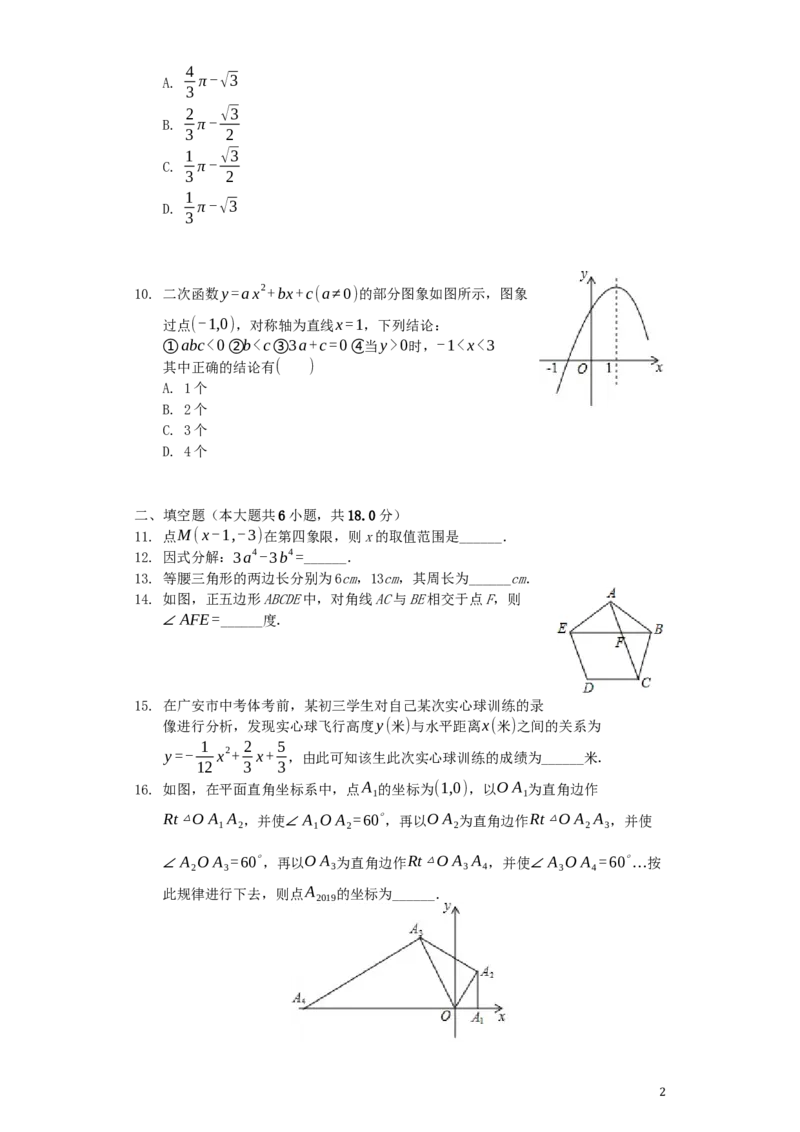
9. 如图,在Rt△ABC中,∠ACB=90∘,∠A=30∘,BC=4,以
BC为直径的半圆O交斜边AB于点D,则图中阴影部分的面积为(
)
14
A. π-√3
3
2 √3
B. π-
3 2
1 √3
C. π-
3 2
1
D. π-√3
3
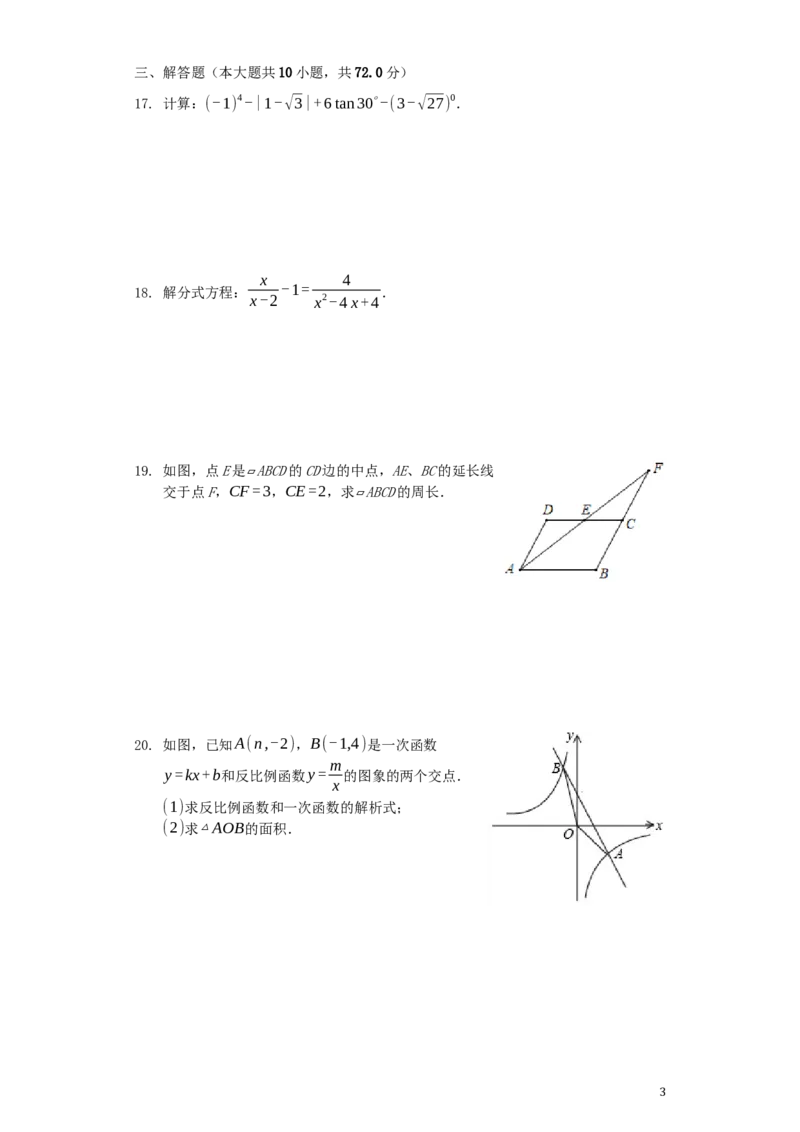
10. 二次函数y=ax2+bx+c(a≠0)的部分图象如图所示,图象
过点(-1,0),对称轴为直线x=1,下列结论:
①abc<0②b0时,-11
12. 3(a2+b2 )(a+b)(a-b)
13. 32
14. 72
15. 10
16. (-22017,22017√3)
√3
17. 解:原式=1-(√3-1)+6× -1
3
=1-√3+1+2√3-1
=1+√3.
x 4
18. 解:
-1=
,
x-2 x2-4x+4
方程两边乘(x-2) 2得:x(x-2)-(x-2) 2=4,
解得:x=4,
检验:当x=4时,(x-2) 2≠0.
所以原方程的解为x=4.
19. 解:∵四边形ABCD是平行四边形,
∴AD//BC,
∴∠DAE=∠F,∠D=∠ECF.
又 ,
∴△ADE≌△FCE(AAS).
∴AD=CF=3,DE=CE=2.
∴DC=4.
∴平行四边形ABCD的周长为2(AD+DC)=14.
m
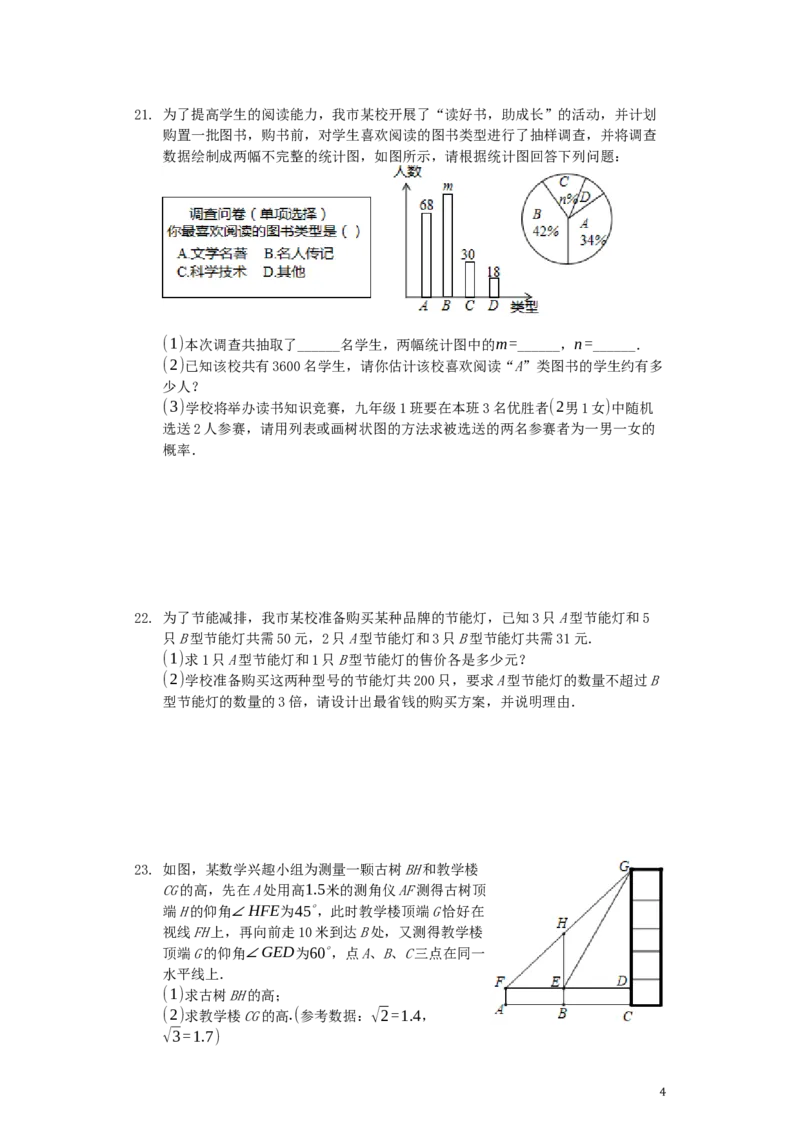
20. 解:(1)∵A(n,-2),B(-1,4)是一次函数y=kx+b的图象与反比例函数y=
x
的图象的两个交点,
m
∴4= ,得m=-4,
-1
4
∴y=- ,
x
4
∴-2=- ,得n=2,
n
∴点A(2,-2),
{ 2k+b=-2 { k=-2
∴ -k+b= 4 ,解得 b= 2 ,
∴一函数解析式为y=-2x+2,
74
即反比例函数解析式为y=- ,一函数解析式为y=-2x+2;
x
(2)设直线与y轴的交点为C,当x=0时,y=-2×0+2=2,
∴点C的坐标是(0,2),
∵点A(2,-2),点B(-1,4),
1 1
∴S =S +S = ×2×2+ ×2×1=3.
△AOB △AOC △BOC 2 2
21. 200 84 15
22. 解:(1)设1只A型节能灯的售价是x元,1只B型节能灯的售价是y元,
{ 3x+5y=50 { x=5
2x+3 y= 31 ,解得, y= 7 ,
答:1只A型节能灯的售价是5元,1只B型节能灯的售价是7元;
(2)设购买A型号的节能灯a只,则购买B型号的节能灯(200-a)只,费用为w元,
w=5a+7(200-a)=-2a+1400,
∵a≤3(200-a),
∴a≤150,
∴当a=150时,w取得最小值,此时w=1100,200-a=50,
答:当购买A型号节能灯150只,B型号节能灯50只时最省钱.
23. 解:(1)在Rt△EFH中,∠HEF=90∘,∠HFE=45∘,
∴HE=EF=10,
∴BH=BE+HE=1.5+10=11.5,
∴古树的高为11.5米;
(2)在Rt△EDG中,∠GED=60∘,
∴DG=DEtan60∘=√3DE,
设DE=x米,则DG=√3x米,
在Rt△GFD中,∠GDF=90∘,∠GFD=45∘,
∴GD=DF=EF+DE,
∴√3x=10+x,
解得:x=5√3+5,
∴CG=DG+DC=√3x+1.5=√3(5√3+5)+1.5=16.5+5√3≈25,
答:教学楼CG的高约为25米.
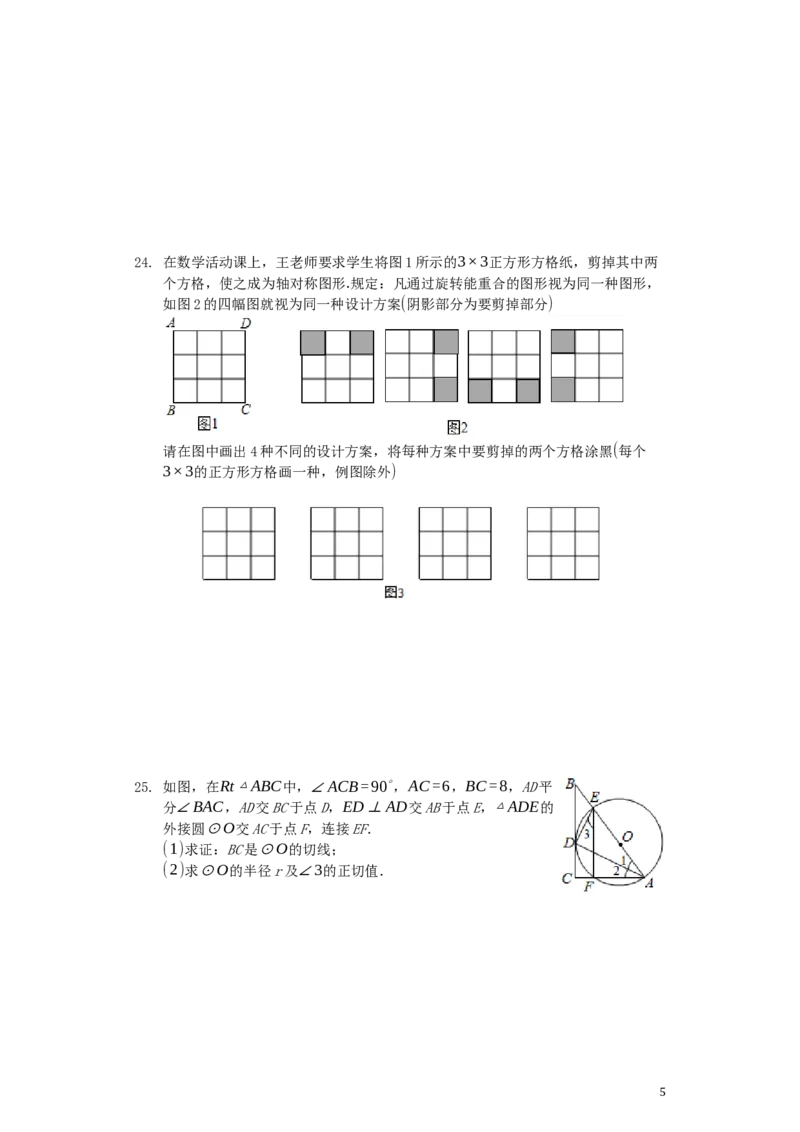
24. 解:如图所示
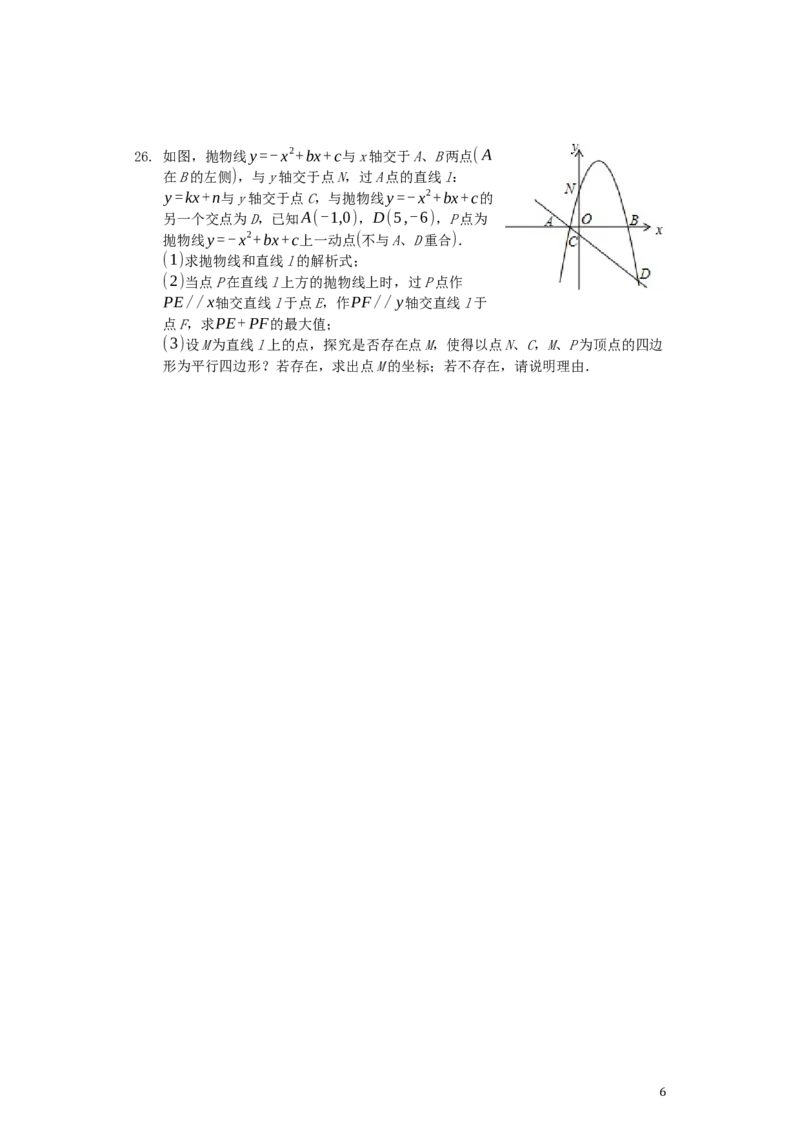
25. (1)证明:∵ED⊥AD,
∴∠EDA=90∘,
∵AE是⊙O的直径,
∴AE的中点是圆心O,
连接OD,则OA=OD,
∴∠1=∠ODA,
∵AD平分∠BAC,
∴∠2=∠1=∠ODA,
∴OD//AC,
∴∠BDO=∠ACB=90∘,
8∴BC是⊙O的切线;
(2)解:在Rt△ABC中,由勾股定理得,AB=√BC2+AB2=√82+62=10,
∵OD//AC,
∴△BDO∽△BCA,
OD OB r 10-r
∴ = ,即 = ,
AC AB 6 10
15
∴r= ,
4
在Rt△BDO中,BD=√OB2-OD2=√(10-r) 2-r2=5,
∴CD=BC-BD=8-5=3,
CD 3 1
在Rt△ACD中,tan∠2= = = ,
AC 6 2
∵∠3=∠2,
1
∴tan∠3=tan∠2= .
2
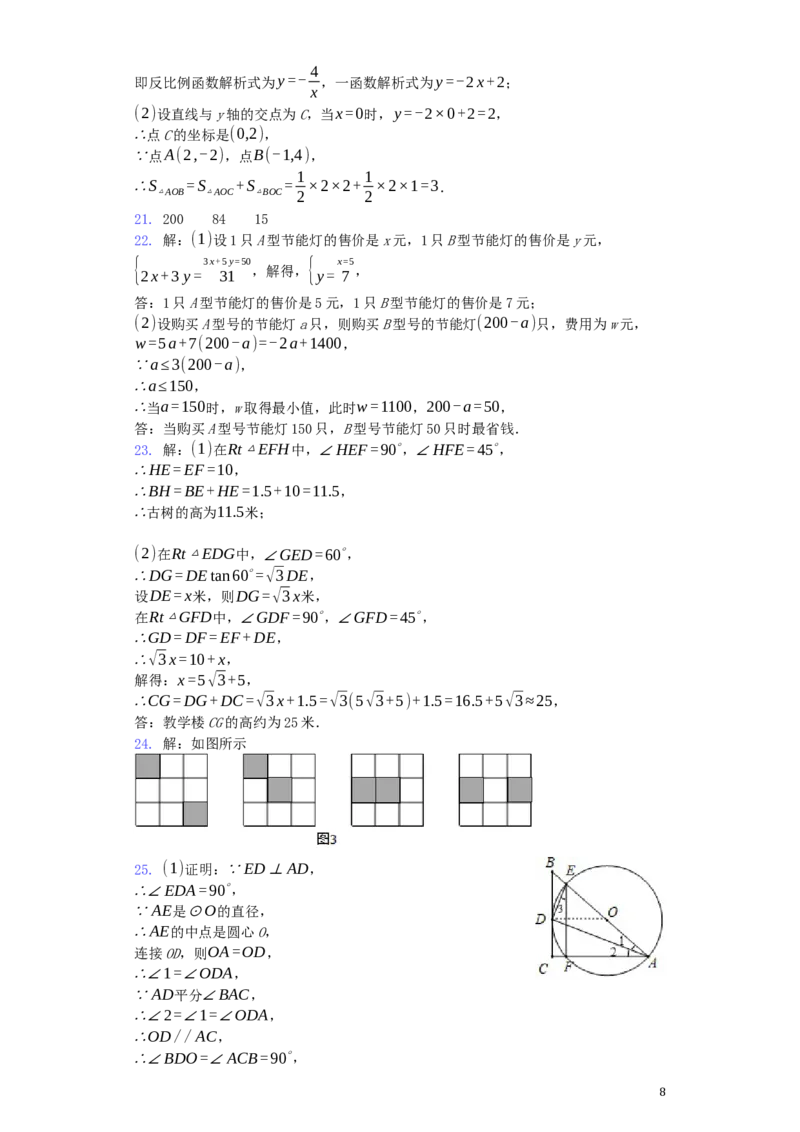
26. 解:(1)将点A、D的坐标代入直线表达式得: { 5k+n=- -k+ 6 n=0 ,解得:
{ k=-1
n=- 1 ,
故直线l的表达式为:y=-x-1,
将点A、D的坐标代入抛物线表达式,
同理可得抛物线的表达式为:y=-x2+3x+4;
(2)直线l的表达式为:y=-x-1,则直线l与x轴的夹角为45∘,
即:则PE=PE,
设点P坐标为(x,-x2+3x+4)、则点F(x,-x-1),
PE+PF=2PF=2(-x2+3x+4+x+1)=-2(x-2) 2+18,
∵-2<0,故PE+PF有最大值,
当x=2时,其最大值为18;
(3)NC=5,
①当NC是平行四边形的一条边时,
设点P坐标为(x,-x2+3x+4)、则点M(x,-x-1),
由题意得:|y - y |=5,即:|-x2+3x+4+x+1|=5,
M P
解得:x=2±√14或0或4(舍去0),
则点P坐标为(2+√14,-3-√14)或(2-√14,-3+√14)或(4,-5);
②当NC是平行四边形的对角线时,
91
则NC的中点坐标为(- ,2),
2
设点P坐标为(m,-m2+3m+4)、则点M(n,-n-1),
N、C,M、P为顶点的四边形为平行四边形,则NC的中点即为PM中点,
1 m+n -m2+3m+4-n-1
即:- = ,2= ,
2 2 2
解得:m=0或-4(舍去0),
故点P(-4,3);
故点P的坐标为:(2+√14,-3-√14)或(2-√14,-3+√14)或(4,-5)或(-4,3).
10