文档内容
【答案】德阳市2018年初中毕业生学业考试与高中阶段学校招生考试
第 I卷 (选择题,共36分)
一、选择题(本大题共12个小题,每小题3分,共36分)
1.如果把收入100元记作+100元,那么支出80元记作
十20 元 及 +100 元 ^80 元 IX ~80 元
解析:考察实数的概念,易选0
2丨下列计算或运算中,正确的是
丄 06^02^ 0^ 及 ( ^ 2)3
^ (口 一 9 IX ^02~62
解析:考查幂运算与整式乘法,易选匸
选项丄06 ^02 ^04
选项 5:考查了立方:(七 2)3^ - 8 。6
选项0 考查了平方差公式: 所以卜一3乂3十…
选项从考查了完全平方差公式:
3|如图,直线…|6, V是截线且交于点儿若21 = 60。,22 = 100。,则乙4二
^^400 5.50。 ^ 600 0.70。
解析:考查三线八角,利用平行转移角,易选2 ^
幺 1=23=60。,之2二之4=100。
7^4+25=180。,
人 25=80。
(第3题图)4 卜列计算或运算中,正确的是
^ 8 ―^8 二 2
^ 6715-2^ = 3745 IX -3^ = 7^
解析:考查二次根式的加减乘除与化简,易选5
选项丄 2^^ 二 2^^ 二 々 X 士 二
选项 5: ^8-^8 ^ 3^2-272=72
选项 0 6^15^273 = ^^=375
2^3
选项从 ~3^3
5^把实数1 12X10^3用小数表示为
10.0612 5.6120 0.0.00612 612000
解析:考查科学计数法,易选匸
6^ 下列说法正确的是
儿 “明天降雨的概率为50^”,意味着明天一定有半天都在降雨
凡了解全国快递包裹产生的包装垃圾数量适合采用全面调查(普查〕方式
匕 掷一枚质地均匀的骰子,骰子停止转动后,6点朝上是必然事件
IX —组数据的方差越大,则这组数据的波动也越大
解析:考查方差、事件、概率统计,易选01.受央视《朗读者》节目的启发的影响,某校七年级2班近期准备组织一次朗诵活动,语文老
师调查了全班学生平均每天的阅读事件,统计结果如下表所示,则在本次调查中,全班学生
平均每天阅读时间的中位数和众数分别是
每天阅读时间(小吋〉 0.5 1 1.5 2
人数 8 19 10 3
克 2,1 召. 1,1.5 匕 1,2 IX 1’ 1
解析:考查中位数和众数,易选
8丨如图是一个几何体的三视图,根据图中数据计算这个几何体
的表面积是
丄 16冗 1271
俯视阁
10^ IX 4^
(第8题阁)
解析:考査三视图与圆锥计算.根据左视图可知,底面圆半径为2,因此底面圆面积为4疋;又因
为侧面扇形半径为6,因此侧面扇形面积为1/7^1x2x24x6=12;^ 因此,表面积为:4冗十12冗
二16:,易选丄
9丨已知圆内接正三角形的面积为巧,则该圆的内接正六边形的边心距是
克2 凡1 匕 6 0 . 4
解析:如图.设的边长为由正三角形的面积公式得由120。的等腰三角形三边比例1: 1:名 知 尺 亨 ,
10.如图,将边长为巧的正方形绕点5 逆时针旋转30。,那么图中阴影部分的面积为
儿 3 ^3 ^ 3-^3 0 3 - 1
^ 01
【解析】:易证:幺1=22=23=^4=30。 人沿兵1
^ ^ 5^8!^ 31^8X10
人5明影二5正方形一 5匕腹0 〉:3 ―力
故选
(第10题阁)
11.如果关于X的不等式组丨2""—丨》6的整数解仅有广2、厂3,那么适合这个不等式组的整数〜
|3卜 4 0
办组成的有序数对(^ 办)共有
丄3个 及4个
【解析】:由不等式得:|么
又‘.‘整数解仅有1=2、^3
又 6为整数
二『3或4,6=9或10或 11
人 (山 共 有 6种12.如图,四边形』0研是平行四边形,点5 为0五的中点,延长7 0 至点(^,使内9=306,连接
35、3(7、5(7,则 在 中
丄 6:2:1 5.3:2;! ^6:3:2 ^4:3:2
【解析】:如图,设乂5 4 0厂相交于点仏
日、丁 謝 腿 80 1
易址:---二----二^二一
爾 篇 ^ 2
设 31801^3 则 5^40^25
2
足 8
01^1=00
人 5^400=5^40^=25,8^20^=8^803^8
(第12题阁)
人 5^80 : 8^00 : 5^500=3 : 2 : 1
故选5
二、填空题〔每小题3分,共 15分)
13.分解因式:2 ^ 2十4 ^ 十2尤二 2々 十 。2
解析:2吓2十4印十2尤
^ IV (灾2十二少‘ +丄)
二2尤(少’ + ”2
14.己知一组数据10,15,10,X,18,20的平均数为15,则这组数据的方差为〒.
解:(⑴+匕+⑴十.丫十巧+ 二^)) ^
6 一
人广17
52 15)2 十如―15)2 十叫―15)2 十07一15)2 十【18一15】2 十⑶-叫 2]
6
6
4415.如下表,从左到右在每个小格子中都填入一个整数,使得其中任意三个相邻格子中所填整数
之和都相等,则第2018个格子的数为 -1
解:由题意得3+口十厶二口十厶十;:可得17 = 3
同 理 可 得 格 子 中 的 数 每 3个数字形成一个循环
易得2018+3 = 672…2,得第2018个格子的数为-1
16.如图,点 乃 为 的 25边上的中点,点 五为 的 中 点,八20匸为正三角形,给出下列
结论,① ② 如 乂 如 乏 ,③幺叹0=21^8,④若义0 2,点尸是25上一动点 ’点尸到
4
^\5匚边的距离分别为九必,则42十如的最小值是其中正确的结论是 ①③④ (填
写正确结论的番号)
解析:①由题可得,2五
是正三角形
:^00^600 ,(^ 丄20
人2和幺1^8=30。
在沁厶5匚五中,25=30。,。於⑶
②V之5=30。
③在正厶25匚中,由三线合一可得,幺五6^=30。
人 ^^00=^008
④如图’ 必
在 中 :42十也1:碰
易证四边形^为矩形
要使42十也2最小,只需厦最小即⑶ 最小,当⑶丄仙时
即尸与五重合时,42十^22最小.
易得:“2=3
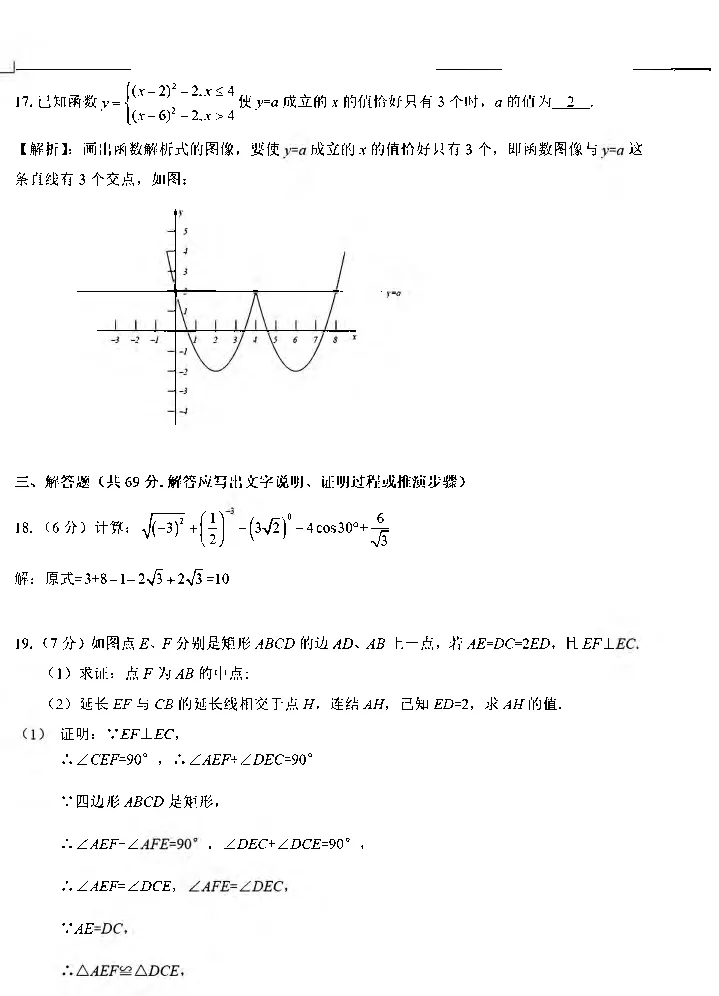
必2最小值为317.己知函数 ‘户 ] [( ^ 卜 — 6 2 ) ) 2 ,2 - — 2 2 ’ ’ ; 。 ^4 4 ^ 1 1=0成立的X的值恰好只有3个时,^的 信 为 2 ^
【解析】:画出函数解析式的图像,要使成立的^的值恰好只有3个,即函数图像与这
条直线有3个交点,如图:
三、解答题(共69分.解答应写出文字说明、证明过程或推演步骤)
18. “ 分)计算:^ 7 十〔去) -(3V^)。-4^0530。+全
解:原式^3+8-1-24 + 24=10
19. (了分)如图点五、尸分别是矩形乂召⑶的边20、2 5 匕一点,若池:1^:2五0,且斤丄
(丄)求证:点尸为25的中点;
(之)延长砂'与⑶的延长线相交于点丑,连结…7,己知瓜5=2,求七/的值.
证明:‘/五厂丄及:,
二乂五厂:90。,人乙4五巧幺1)5090。
V 四边形25^0是矩形,
人幺2五 巧 之 ,^ 0^^00^900 ,
二乙力五1^幺IX:五,
‘:尬二五 只,
0=4
V处 4 0 他 2肌
人25=22厂,
人尸为2 5的中点^
(之) 解:由 ^ ) 知 厂 5,且乂五//忍片,
人幺厂5/7=2凡4^=90。, “ 五厂:21^'拙 ,
人 厶 '爸厶5/7凡
V五0=2,且处:2五0 ,
人处:4’
人册:仙:狀:4,
二 他 :仙2 十5片2 46+16=32,
:遍 :4^2
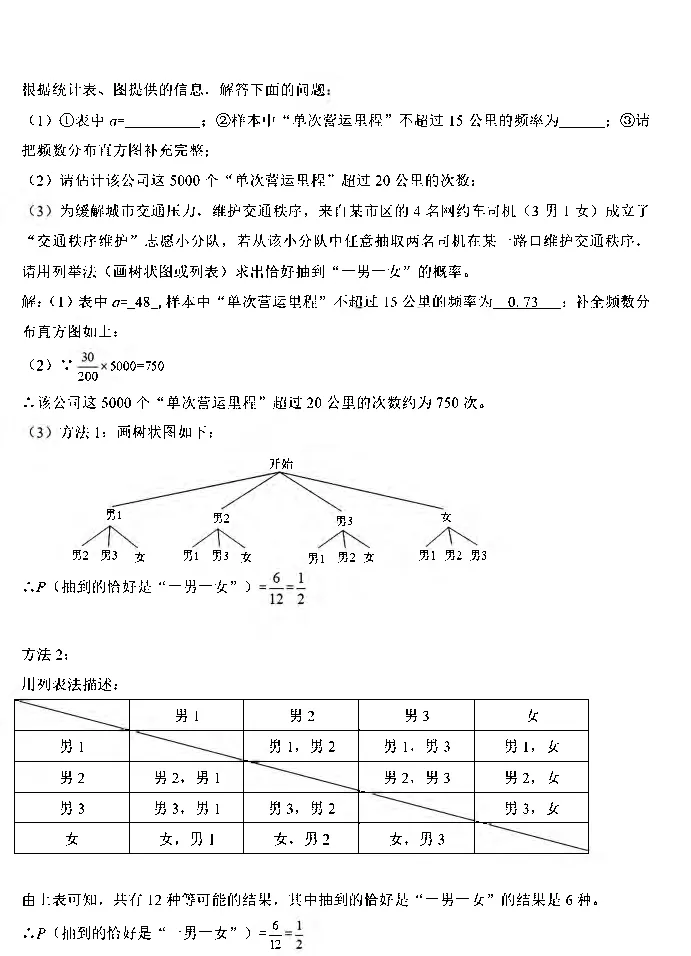
20^〈11分)某网络约车公司近期推出了” 520专享”服务计划,即要求公司员工做到” 5 星级服
务、2分钟响应、0客户投诉”,为进一步提升服务品质,公司监管部门决定了解“单次营运里
程”的分布情况。老王收集了本公司的5000个 “单次营运里程”数据,这些里程数据均不超过
25 (公里〕,他从中随机抽取了 200个数据作为一个样本,整理、统计结果如下表,并绘制了不
完整的频数分布直方图。
频数(次)
组別 巾次营运1程“X” (公甩) 频数
,
80
笫一组 72 70
8
第二组 5〈610 0 :
笫三组 10〈说 5 26 1
^|
笫四组 15〈成 20 24
笫五组 20〈\^25 30 第根据统计表、图提供的信息,解答下面的问题
(丄)①表中0: ;②样本中“单次营运里程”不超过15公 里 的 频 率 为 ;③请
把频数分布直方图补充完整;
(之)请估计该公司这5000个 “单次营运里程”超过20公里的次数;
为缓解城市交通压力,维护交通秩序,来自某市区的4名网约车司机〔3男1女)成立了
“交通秩序维护”志愿小分队,若从该小分队中任意抽取两名司机在某一路口维护交通秩序,
请用列举法(画树状图或列表)求出恰好抽到“一男一女”的概率。
解:(丨)表中0148—,样本中“单次营运里程”不轺过15公里的频率为0.73 :补全频数分
布直方图如上:
⑵ V 5000=750
200
人该公司这5000个 “单次营运里程”超过20公里的次数约为750次。
方法1:画树状图如下:
开始
男1 男2 男3 女
男2 男3 女 男1 男3 女 男1 男2 女 男1 男2 男3
“? ^抽到的恰好是“一男一女”〉
方法2:
用列表法描述:
男1 男2 男3 女
男1 男1,男2 男1,男3 男1,女
男2 男2,男1 男2,男3 男2,女
男3 男3,男1 男3,男2 男3,女
女 女,男1 女,男2 女,男3
由上表可知,共有12种等可能的结果,其中抽到的恰好是“一男一女”的结果是6种。
人尸〔抽到的恰好是“一男一女”〉^&21.〔10分)如图,在平面直角坐标系中,直线.VI:匕+/^认矣0)与双曲线只二〗。弇0〉交于2 、5
(丄)求直线和双曲线的解析式;
(之)把直线》沿X轴负方向平移2个单位后得到直线;^3,直线V 与双曲线”交于0、五两点,
当片〉”时,求X的取值范围.
解:⑴ 7 5 〔-1’ -4〕
又V 点8在双曲线上,即“ -!) X “ ) 二4’
又^ 点2 在双曲线上,即2川二4,即〃1=2, 2 (之口),
V; 3 〔-1, 在直线义产匕十6上,
解得
[-4 : -是屮厶,^ 〔办二 -2,
二直线和双曲线的解析式分别为:^产2^2和
(之)V 直线》是直线》沿^轴负方向平移2个单位得到,
人灾3二2 (^) -2二2枓2, (第21题丨冬丨)
:一1
解方程组: 得, 或
IV ^ 2-^ + 2
二一1
人点乃(“ ),五(-之’ -2〕’
人当72〉73时,X的取值范围是:文〈-2或
11.〔10分)为配合“一带一路”国家倡议,某铁路货运集装箱物流园区正式启动了 2期扩建工
程.一项地基基础加固处理工程由2、8 两个工程公司承担建设,己知2 工程公司单独建设完成
此项工程需要180天^2 工程公司单独施工45天后,8 工程公司参与合作,两工程公司又共同施
丁.54天后完成了此项工程^
求5 工程公司单独建设完成此项工程需要多少天?
(之)由于受工程建设工期的限制,物流园区管委会决定将此项工程划包成两部分,要求两工程
公司同时开工,2 工程公司建设其中一部分用了川天完成,8 I:程公司建设另一部分用了 ”天
完成,其中川,”均为正整数,且…〈46,”〈92,求 丄 5 两个工程公司各施工建设了多少天?
解:(丨)设5 工程公司单独建设完成这项工程需要X天,由题意得:解之得:^ 120,
经检验^120是原方程的解且符合题意.
答:8 1:程公司单独建设需要120天完成^
0 V」工程公司建设其中一部分用了川天完成,8 工程公司建设另一部分用了 ”天完成,
人川X 丄十”父― 即77=120—一坩
180 120 3
1)1〈 46
又7川〈46,?7〈92,:^\
120— 一
2 …〈92,解得 42〈川〈46,
、 3
?川为正整数,
人"厂43,44,45;
而『120-|川也为正整数,
1/1=45,11=90:
答:2 工程公司施工建设了 45天,8 I:程公司施工建设了 90天.
23^ (“分)如图,在直角三角形250中,24?5二90。,点丑是八25(7的内心,2片的延长线
和三角形256'的外接圆0 相交于点乃,连结155.
求证:011=05;
(之)过点0 作 的 平 行 线 交 2匸、仙 的延长线分别于点五、厂,己知0^=1,圆0 的直径为5,
①求证:^ 为圆0 的切线;② 求 '的长I
(丄)证明:连结尺5,
7 点片为厶25匸的内心,
(第23题阁)丄5(7,3 0 / / ^
人2匸丄五7 ,
人㈨ 丄 ⑶
人砂'是 圆 0的切线
②如图’多 点 乃 作 1)0丄 仙于 点 0,
V 幺凡10二幺以45,
“0五:亂 00=03 ^ ^1)05=900 ,
人 厶 ⑶ 5 竺厶5肌
人別二⑶吐
在衍厶2乃5 中,1)0?丄25,
又幺0 5 0 ^ 4 5 0 ,
人么080吣/\及80,
...081:彳 1=5
1)5=75 ; 00=2 ^ 二五0:2‘
又 V V 为内心,
而 1)0 II從 二厶0厂I?… :’
^ 0厂 00
0厂十1)^1义五
②解法二:
连 接 ⑶ ,
V 』、(^、0 、5 在〇0 上, 二幺五
又^
/.18是直径 二乙450=90。
又V 拉"乂 5
人 2 五^ ^40=90。
人厶及?乃…厶2?凡4
^ 00 01:
''^ 3 ~ ^ 8又7 点孖为内心
人 /1 ^0=^18^0
00=1)8
广0 1
而 25=5,0五:1,即〒 ^ ^ 5
在衍厶五⑶中,由勾股定理:五1 ^0^2-於 :5-1=4 二五0=2
又?况为内心
人处、404
而 1)0//^
二厶070…厶从五
# 0厂 00
即一5 ^ = 1
01^ + 2 4 3
14.〔14分)如图,在等腰直角三角形中,252090。,点2 在.V轴上,点5 在;^轴上,
点匚0 ,0 ,二次函数.1^ | ^ 十虹的图像经过点匸.
(丄)求二次函数的解析式,并 把 解 析 式 化 成 的 形 式 ;
(之)把么250沿X轴正方向平移,当点5 落在抛物线上时,求八25匚扫过区域的面积;
^ ) 在抛物线上是否存在异于点0 的点么使八25户是以25为直角边的等腰直角三角形?如
果存在,请求出所有符合条件的点5 的坐标;如果不存在,请说明理由.
解:(丨)‘/点匸。,0 在二次函数的图像上,
人匕^3 2十3办一~ ,解得办丄,
3 2 6
人二次函数的解析式为:
4 3 6 2
化成义二+ — /,)2十分的开多式为7二全〔义一一'^ ;
0 作⑶丄^丫轴,由丄4化三厶似0 ,可得614=0^1,^03=2^ 即5 〔0,2〕
人当点5 平移到抛物线上的点3 时,V (…,IX
由 2二上"72 — 丄〃7 — ~ ,解得二一3,川2
3 6 2 2
而 35 ^ ^40 ^」22 十 1 二 ^5人^ 8 0 扫过的面积^ 十 \七X七^9.5
(” ①当252户二903时,由丄4化三丄^ 厂,此时点尸1:-1,-0 ,
尤二―1日寸,7 ^ ”2 ―^)^—丄)—^ ^-1,点尸(-】,―丄)在抛物线上;
②当乙45户^903时,同理可求得点尸(-^, IX
^丫 二-2时,” ‘ (―之)2—丄※(―之卜互。 ,此时点户〔-2,1〉在抛物线上.
1 3 6 2
综上所述,符合条件的点户有一个,?(-丨,-1〕