文档内容
方法精讲-资料 2
(笔记)
主讲教师:张小飞
授课时间:2024.05.30
粉笔公考·官方微信方法精讲-资料 2(笔记)
【注意】资料 1课后作业:不仅要会填空,最好能够默写下来。
1.一步除法只截分母,多步除法分子、分母(上下)都截。
2.首位不同,算选项差距大,截2位;首位相同,次位差>首位,算选项差
距大,截2位;除此以外的其他情况都是差距小,都截 3位(首位相同,次位差
≤首位,算选项差距小,截 3位)。
3.分数比较:一大一小直接看,分子大的分数大;同大同小,竖着直接除(直
除);横着看倍数(分子倍数大,由分子决定,分子大的分数值大;分母倍数大,
由分母决定,分母大的分数值小)。
4.同比指和上年同期相比;环比指和上一个统计周期(上一个时期)相比(包
括季度环比、月环比、周环比、日环比等等)。
5.已知现期量和增长量,基期量计算公式为基期量=现期量-增长量;加减法,
估算即可;已知现期量和增长率,基期量计算公式为基期量=现期量/(1+r)。所
1有的除法,都可以截位直除。
6.当|r|小于等于 5%时,基期量计算可化除为乘,公式为现期/(1+r)≈现
期-现期*r。
7.基期和差,很多年之前的题目选项是两正两负,可先用正负和现期坑排除,
再计算。近几年的题目,一般都需要计算,带着分析做,算一个、分析另外一个,
计算和分析相结合。
8.已知增长量和基期量,现期量计算公式为现期量=基期量+增长量;已知增
长率和基期量,现期量计算公式为现期量=基期量*(1+r)。
资料分析 方法精讲 2
学习任务:
1.课程内容:一般增长率、增长量
2.授课时长:3 小时
3.对应讲义:第 132~144页
4.重点内容:
(1)增长率相关术语的联系与区别
(2)一般增长率的题型识别及计算公式
(3)一般增长率的比较技巧
(4)增长量的计算与比较技巧
第三节 一般增长率
第四节 增长量
第三节 一般增长率
基本术语:
增长率
增长率用来表述基期量与现期量变化的相对量。增长率又称增速、增幅或者
增长幅度、增值率等。增长率为负时表示下降,下降率也可直接写成负的增长率。
百分数与百分点
2百分数:用来反映量之间的比例关系。
百分点:用来反映百分数的变化。
增长率与倍数
增长率指比基数多出的比率,倍数指两数的直接比值。
若 A是B的n倍,则 n=r+1(r指A相对于 B的增长率)。
成数与翻番
成数:几成相当于十分之几。
翻番:翻一番为原来的 2倍;翻两番为原来的 4倍;以此类推,翻 n番为原
来的2n倍。
增幅、降幅与变化幅度
增幅一般就是指增长率,有正有负。
降幅指下降的幅度,降幅比较大小时,只比较增长率的绝对值(前提必须为
下降)。
变化幅度指增长或下降的绝对比率,变化幅度比较大小时,用增长率的绝对
值。
前置:基本术语
一、一般增长率计算
二、一般增长率比较
【注意】讲解前先了解跟一般增长率相关的基本统计术语,术语不难,需要
理解。
基本术语
1.增长率
增长率(rate,r)是用来表述基期量与现期量变化的相对量。
基本公式为:r=增长量/基期量
增长率又称增速、增幅或者增长幅度、增值率等。
增长率为负时表示下降,下降率也可直接写成负的增长率。例:下降 7%,
则r=-7%
3【引例】2022年 A省地区生产总值为3000 亿元,2023年为3300 亿元。2023
年的同比增长率为:
【注意】增长率:
1.增长率(rate,r)是用来表述基期量与现期量变化的相对量(比率)。
2.基本公式:r=增长量/基期量。
3.增长率又称增速、增幅或者增长幅度、增值率等(记住“小名”)。
4.增长率本身有正有负,增长率为负时表示下降,下降率也可直接写成负的
增长率。例:下降 7%,则r=-7%,负号不能丢。
5.引例:同比是比上年,2023 年上年是 2022 年,问同比增长率,给现期、
基期,r=(现期量- 基期量)/基期量=(3300-3000)/3000=300/3000=10%。
2.百分数与百分点
百分数:用来反映量之间的比例关系。例如比重、增长率。一般用除法计算
百分点:用来反映百分数的变化。一般用加减法计算。
【引例 1】2022 年 A 省地区生产总值为 3000 亿元,2023 年为 3300 亿元,
其中第一产业为660 亿元。
问:2023年的同比增长率为:
2023 年第一产业占地区生产总值的比重为:
【引例 2】2023 年A省地区生产总值同比增长 10%,2022年同比增长 8%。
问:2023年A 省地区生产总值的同比增长率比 2022年高:
【注意】百分数与百分点:共同点是大小相等,比如从大小上来说 1%=1 个
百分点,但用法不同。
1.百分数:用来反映量之间的比例关系;例如比重(比重=部分/总体,表示
占比关系)、增长率(现期量和基期量相比增长的比率);一般用除法计算。
2.百分点:用来反映百分数的变化(应用比较窄)。一般用加减法计算,百
分点是两个百分数做减法得到(%-%=百分点)。
3.引例 1:2022 年 A 省地区生产总值为 3000 亿元,2023 年为 3300 亿元,
其中第一产业为660 亿元。问:
(1)2023年的同比增长率:r=10%。
4(2)2023 年第一产业占地区生产总值的比重:比重=部分/总体
=660/3300=20%。
4.引例 2:2023 年 A 省地区生产总值同比增长 10%,2022 年同比增长 8%。
问2023 年A省地区生产总值的同比增长率比 2022年高多少?
答:2023 年增长率=10%、2022 年增长率=8%,两个百分数做减法,所求
=10%-8%=2 个百分点。
3.增长率与倍数
增长率指比基期量多出的比率,倍数指两数的直接比值。
130 是100的( )倍
130 比100增长( )%
二者关系:是几倍=r+1
r=是几倍-1
【引例 1】A比 B增长50%,则A是B的( )倍
【引例 2】2023 年是2022年的1.8倍,则 2023年比2022 年增长( )%。
【注意】增长率与倍数:
1.增长率指现期量比基期量多出的比率,倍数指两数的直接比值。
2.例:
(1)130是100 的( )倍。
答:130/100=1.3 倍。
(2)130比100 增长( )%。
答:增长了百分之多少,求增长率,r=(现期- 基期)/基期=(130-100)
/100=30/100=30%。
(3)关联:1.3 和 30%之间刚好差 1,1.3 倍=30%+1,则是几倍=r+1、r=是
几倍-1。
3.二者关系:
(1)是几倍=r+1。
(2)r=是几倍-1。
4.引例 1:A比 B增长50%,则A是B的( )倍。
5答:是几倍=r+1=50%+1=1.5 倍。
5.引例 2:2023 年是2022年的1.8倍,则 2023年比2022 年增长( )%。
答:r=是几倍-1=1.8-1=0.8=80%。
4.成数与翻番
成数:几成相当于十分之几、百分之几十。
翻番:翻一番为原来的 2倍,翻两番为原来的 4倍,以此类推,翻 n番为原
来的2n倍
【引例 1】增长 3 成即为增长( )%;第一产业占 GDP 的两成,则占比为
( )%。
【引例 2】10翻 2番变为( ),翻3番变为( ),翻4番变为( )。
2013 年为200,2023年为1600,则2023 年比2013年翻了( )番。
【注意】成数与翻番:不难,考得不多。
1.成数:几成相当于十分之几、百分之几十。比如女生占全班同学的 5 成,
即占50%。
2.引例 1:增长 3成即为增长30%;第一产业占 GDP的两成,则占比为 20%。
3.翻番:翻一番为原来的 2¹=2倍,翻两番为原来的 2²=4倍,翻三番为原来
的2³=8 倍,以此类推,翻 n番为原来的2n倍。
4.引例 2:
(1)10翻2番变为(10*2²=10*4=40),翻 3番变为(10*2³=10*8=80),翻
4番变为(10*24=10*16=160)。
(2)判断对错:2013年为200,2023年为 1600,则2023年比 2013年翻了
8番。
答:这句话是错的。如果翻了 8 番,要变为 28倍,而 1600/200=8 倍=2³,
是 8 倍=2³=2n,n=3,为翻 3 番。翻番和倍数不同,数据很难达到翻天覆地的变
化,遇到翻番,不可能翻太多番,都是关系到民生的真实数据,翻太多番不现实,
但凡比3番还大的多半是错的,很难出现那么大的变化。
5.增幅、降幅与变化幅度
6增幅:一般就是指增长率,有正有负,计算比较时,带着符号做题。
降幅:指下降的幅度,计算比较时,用绝对值(前提必须为下降)。
变化幅度:指增长或下降的绝对比率,计算比较时,用绝对值。
【注意】增幅、降幅与变化幅度:最容易混的一组。增长率是一个大的概念,
里面有一些小的概念,而增速、增幅、增长速度、增长幅度(“小名”)本身就是
增长率。
1.增幅(广义的概念):一般就是指增长率,有正有负,既可以有正增长、
也可以有负增长。计算、比较大小时,带着符号做题(尤其负号)。
例:A.增长 1%,r=1%;B.下降 2%,r=-2%;C.增长 3%,r=3%;D.下降 4%,
r=-4%。在四个选项中,增长率最大的:不管计算还是比较,带着符号,正数>
负数,所以最大的是 C 项(3%);增长率最小的:两个负数小,-2%>-4%,故增
长率最小的是D项(-4%)。
2.降幅(增长率中的一小类,是狭义的概念):指下降的幅度(增长率为负),
计算、比较时,用绝对值(“降”已经代表是负的,只看幅度本身);前提必须是
下降的,如果是增长的,则压根就不属于降幅的范畴。
例:A.增长 1%,不是降幅(比如问四个男性中最帅的,张老师不能参与比
较,因为张老师不是男性);B.下降 2%,降幅为 2%,不用写负号,“降”就已经
表示了负号;C.增长 3%,不是降幅;D.下降 4%,是降幅,降幅为4%。在四个选
项中,降幅(下降幅度)最大的是D项,降幅(下降幅度)最小的是 B项。
3.变化幅度(狭义的概念):指增长或下降的绝对比率(即增长率的绝对值),
计算、比较时,用绝对值。只要变了即可,不管变大还是变小,变大是正的,变
小是负的。
例:A.增长1%,不管正负,只看绝对值,变化幅度为1%;B.下降 2%,变化
幅度为 2%;C.增长 3%,变化幅度为 3%;D.下降 4%,变化幅度为 4%。在四个选
7项中,变化幅度最大的是 D 项、变化幅度最小的是 A 项。比如 A.增加了 2 元、
B.减少了 3元,变化量最大的是 B项,因为B 项变化了3元、A项只变化了 2元。
一、计算
一、一般增长率计算
题型识别:增长率,增速,增幅;增长/下降+%
考查方式:(1)给百分点:直接加减
【引例 1】2023 年收入同比下降20%,增速比上年提高/扩大/快 5个百分点。
问:2022 年收入的增长率为:
【引例 2】2023 年收入同比下降20%,增速比上年降低/收窄/回落 5个百分
点。问:2022年收入的增长率为:
方法一:按文字理解计算
方法二:高减低加
(给“提高”做减法,给“降低”做加法)
【注意】一般增长率计算:
1.题型识别:直接问增长率、增速、增幅是多少;增长/下降+%(如果只问
“增长/下降”多少,就看单位,单位是“%”,说明是问增长率)。
2.考查方式——给百分点:直接加减。理解不了就记结论。
3.引例 1:2023 年收入同比下降20%,增速比上年提高/扩大/快 5个百分点。
问2022 年收入的增长率为?
答:增速、增幅都是增长率,增长率有正有负,要带着符号做题,“下降20%”
8→2023 年增速=-20%,“比上年提高/扩大/快 5 个百分点”,“提高/扩大/快”是
一个意思,上年是2022 年,问 2022年增长率,2023年比2022年高(2023年大、
2022年小),说明2022 年增长率更小,求一个更小的数,用减法,所求=-20%-5
个百分点=-25%。
4.引例 2:2023 年收入同比下降20%,增速比上年降低/收窄/回落 5个百分
点。问2022年收入的增长率为?
答:2023年增速=-20%,“降低/收窄/回落”是一个意思,都代表“降低”,
2023年增长率比2022 年降低,说明2023年更小、2022年更大,求更大的数据,
用加法,所求=-20%+5 个百分点=-15%。
5.方法:
(1)方法一:按文字理解计算(求的数更小,做减法;求的数更大,做加
法)。
(2)方法二(结论):高减低加(给“提高”→已知比所求的大、所求的更
小→做减法,给“降低”→已知的小、所求的大→做加法)。
①例 1:提高,用减法。
②例 2:降低,用加法。
2022 年,全国软件业利润总额 12648 亿元,同比增长 5.7%,增速较上年同
期回落 1.9 个百分点。软件业务出口额 524.1 亿美元,同比增长 3.0%,增速较
上年同期回落5.8个百分点。其中,软件外包服务出口额同比增长 9.2%。
【例 1】(2024 四川)2021 年,全国软件业利润总额同比增速比软件业务出
口额同比增速:
A.低 1.2个百分点 B.低2.7个百分点
C.高 1.2个百分点 D.高2.7个百分点
【解析】1.问题时间 2021年,增速、增幅都是增长率,求两个增长率的差,
为增长率题型。材料给2022年数据,时间上不要“掉坑”,给一个增长率、百分
点,求增长率,用加减法,结论是“高减低加”。结合材料,“2022 年,全国软
件业利润总额12648 亿元,同比增长5.7%,增速较上年同期回落 1.9 个百分点”,
“回落”即“降低”,高减低加,用加法,2021 年全国软件业利润总额同比增速
9=5.7%+1.9个百分点=7.6%;“软件业务出口额 524.1亿美元,同比增长 3.0%,增
速较上年同期回落 5.8个百分点”,“回落”即“降低”,高减低加,用加法,2021
年软件业务出口额同比增速=3.0%+5.8 个百分点=8.8%,所求=7.6%-8.8%=-1.2
个百分点,前者更小,排除 C、D项;小了 1.2个百分点,对应A项。【选A】
【引例1】2023年收入同比下降20%,降幅比上年提高/扩大/快5个百分点。
问:2022年收入的降幅为:增长率为:
【引例 2】2023 年收入同比下降20%,降幅比上年降低/收窄/回落 5个百分
点。
问:2022年收入的降幅为:增长率为:
出现“降幅”:
1.求降幅:用绝对值高减低加
2.求 r:再加负号
【注意】
1.引例1:2023年收入同比下降20%,降幅比上年提高/扩大/快5个百分点。
问:
(1)2022年收入的降幅为?
答:材料说的是降幅,只能用降幅做计算,“降”已经代表负号,只看幅度,
2023年降幅=20%,用降幅做“高减低加”,得到的也是降幅;2022年降幅=20%-5
个百分点=15%。
(2)增长率为?
答:求增长率,带上负号,为-15%。
102.引例 2:2023 年收入同比下降20%,降幅比上年降低/收窄/回落 5个百分
点。问:
(1)2022年收入的降幅为?
答:2023年降幅=20%,高减低加,2022 年降幅=20%+5个百分点=25%。
(2)增长率为?
答:带上负号,2022年增长率=-25%。
3.出现“降幅”:
(1)求降幅:用绝对值高减低加。
(2)求r:再加负号。
4.到底用降幅还是增长率进行“高减低加”由材料决定,材料给降幅,用降
幅“高减低加”;材料给增速(增长率),用增速“高减低加”。
2020 年全年,汽车产销降幅收窄至 2%以内。汽车产量为 2522.5 万辆,销量
为2531.1万辆,同比分别下降2.0%和1.9%,降幅分别比2020年上半年收窄14.8
和15.0个百分点。2020年全年,新能源汽车销量为136.7万辆,同比增长10.9%。
【例 2】(2021 联考)2020年上半年汽车销量降幅估计在:
A.10 个百分点以内 B.10~12个百分点
C.12~14个百分点 D.15个百分点以上
【解析】2.问降幅,是增长率的一种,选项不严谨,应为百分数,A.10%以
内、B.10%~12%、C.12%~14%、D.15%以上。问题时间 2020 年上半年,材料给
2020 年全年,时间不一样,问“销量”;结合材料,“汽车产量为 2522.5 万辆,
销量为 2531.1 万辆,同比分别下降 2.0%和 1.9%,降幅分别比 2020 年上半年收
窄14.8 和15.0个百分点”,“分别”要按顺序对应,第一个数据都对应“产量”、
第二个数据对应“销量”,给百分点,求百分数,用加减法,高减低加,“收窄”
即“降低”,做加法,说的是“降幅”,要用降幅“高减低加”,2020 年全年降幅
=1.9%,则上半年降幅=1.9%+15 个百分点=16.9%,问降幅,直接选,对应 D 项。
【选D】
【注意】
111.题型:求降幅→r计算。
2.公式:给百分点,直接加减(高减低加)。
3.降幅比 2020 年上半年收窄 15.0 个百分点,可以直接加减,即 2020 年全
年降幅-2020年上半年降幅=-15个百分点。
一、一般增长率计算
题型识别:增长率,增速,增幅;增长/下降+%
考查方式:
(1)给百分点:直接加减
(2)给具体值:r=增长量/基期量=(现期量- 基期量)/基期量=增长量/
(现期量-增长量)
速算技巧:截位直除
【注意】一般增长率计算:
1.题型识别:增长率,增速,增幅;增长/下降+%。
2.考查方式——给具体值(考查多):套公式,r=增长量/基期量(基本公式,
很少直接考)=(现期量- 基期量)/基期量(考查更多)=增长量/(现期量-增
长量)(偶尔考查)。常用的两个公式,要么分子做减法、要么分母做减法,建议
三个公式都记住。
3.速算技巧:截位直除(选项差距大,截两位;选项差距小,截三位)。
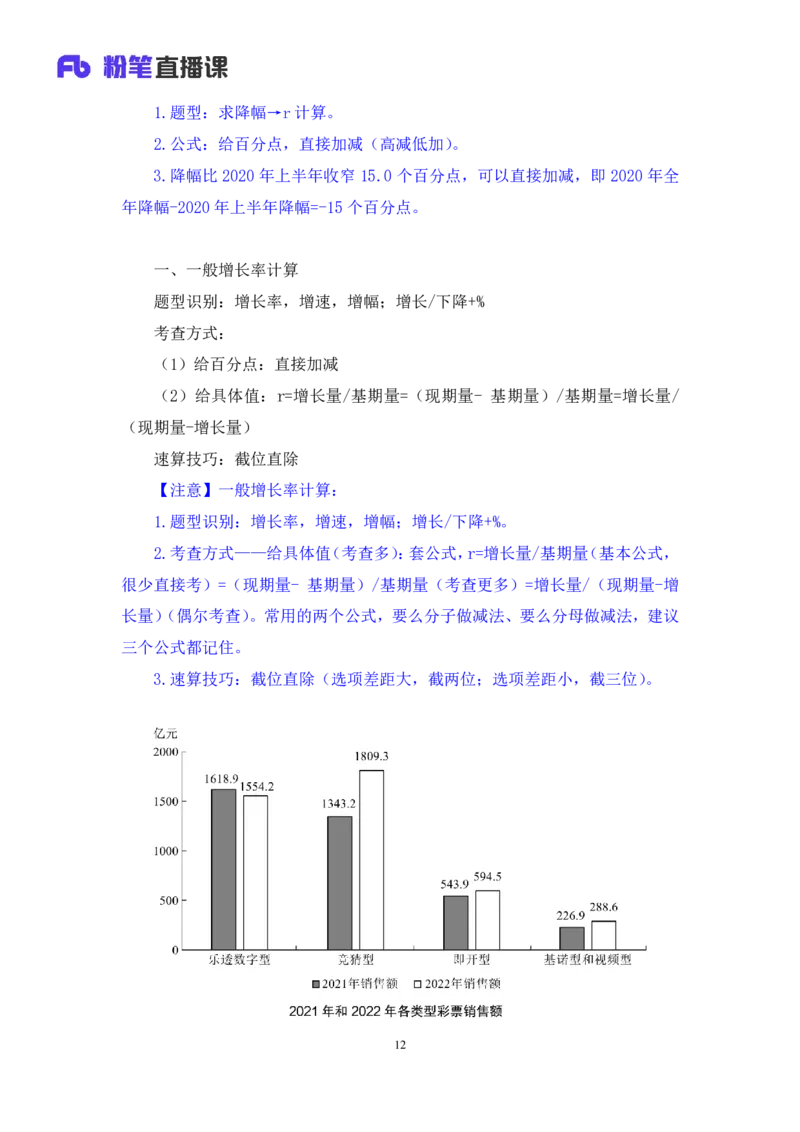
12【例 3】(2023 吉林)2022年,竞猜型彩票销售额同比增长:
A.-34.7% B.-25.7%
C.25.7% D.34.7%
【解析】3.增长+%,求增长率;同比是比上年,即比 2021 年。结合材料,
找“竞猜型彩票”数据,灰色对应2021年数据、白色对应2022年数据,给现期、
基期,r=(现期- 基期)/基期,r≈(1809-1343)/1343=466/1343,结果是正
数,排除A、B项;46/13首位商3+,对应D 项。【选D】
【注意】
1.题型:求同比增长+%→r计算。
2.公式:给现期、基期,r=(现期- 基期)/基期。
3.不建议用“现期/基期-1”计算,比如增加选项 E.14.3%,就非常容易错
选 E 项,因为 1809/1343 首位商 1,但其实要算到第二位,现期/基期-1≈
1809/1343-1=1.3+-1=0.3+,所以不建议先除再减,先减再除会更快。
【例4】(2021江苏)2019年末江苏省金融机构各项存款额度比上年末增长:
A.8.5% B.9.4%
C.10.2% D.10.8%
【解析】4.给2019 年数据,问2019年,增长+%,问增长率;对应材料找各
项存款额度,“绝对值”就是2019年的数据(现期量);增加+单位→增长量,给
现期量、增长量,r=增长量/基期量(2018年)=增长量/(现期-增长量)≈13089/
13(152837-13089),C、D项首位相同(不满足首位不同),次位差 0-0=0<首位1
(不满足次位差>首位),选项差距小,截三位,分母算出前四位,对第四位“四
舍五入”,152837-13089=1398XX,四舍五入保留前三位是 140,原式
=13089/1398XX,截三位转化为 13089/140,首位商不到 1,排除C、D 项;能“瞪”
出来直接选,“瞪”不出来就列竖式,首位商 9有余数,对应B项。【选 B】
【注意】
1.题型:求增长%→r计算。
2.公式:给现期、增长量,r=增长量/(现期-增长量)。
3.A 项是“坑”,用“增长量/现期量”就会错选 A项。
提问方式:哪些指标的增长率>10%(20%、50%)
解题思路:只需要满足现期量>基期量*1.1(1.2、1.5)
推导过程(了解即可)
增长率=(现期量- 基期量)/基期量>10%→现期量- 基期量>基期量*10%
→现期量>基期量+基期量*10%→现期量>基期量*1.1
【注意】
1.提问方式:哪些指标的增长率>10%(20%、50%)。
2.解题思路:只需要满足现期量>基期量*1.1(1.2、1.5)。
3.推导过程(了解即可):增长率=(现期量- 基期量)/基期量>10%→现期
量- 基期量>基期量*10%→现期量>基期量+基期量*10%→现期量>基期量*1.1。
4.如果考查增长率>20%、50%,就将10%换成20%、50%,即将1.1 换为 1.2、
1.5即可。
5.例:假设2023 年数据=1567,2022年数据=1162。
(1)问2023年的同比增长率是否超过10%:r >10%→2022年*1.1<2023
2023年
年,一个数*1.1→错位相加,1162+116.2=1200+(即使进位最多变为 13 开头)
<1567,超过 10%。
(2)问2023年的同比增长率是否超过20%:只需满足“现期量>基期量*1.2”,
错位加两次(两倍),1162+116.2+116.2=1300+(即使进位最多变为 14开头)<
141567,超过 20%。
(3)问2023年的同比增长率是否超过50%:只需满足“现期量>基期量*1.5”,
一个数*1.5→本身+一半,1162+581=1700+>1567,没有超过50%。
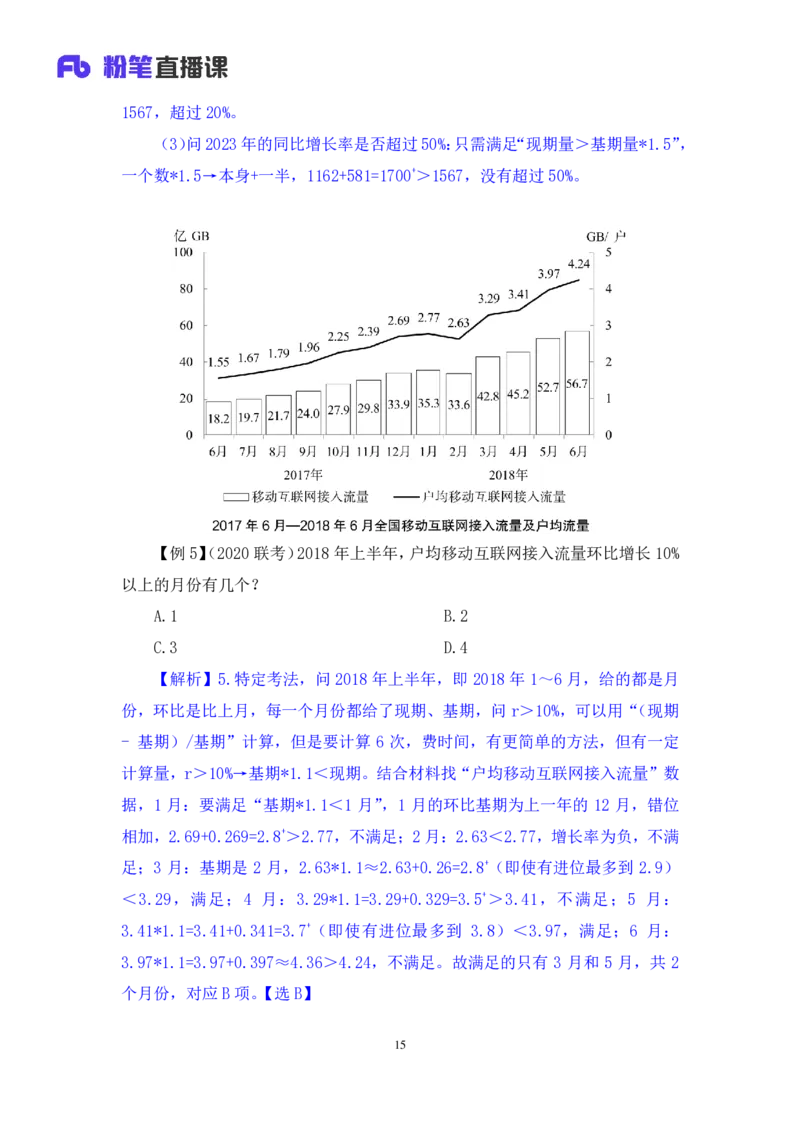
【例 5】(2020联考)2018 年上半年,户均移动互联网接入流量环比增长 10%
以上的月份有几个?
A.1 B.2
C.3 D.4
【解析】5.特定考法,问 2018 年上半年,即 2018 年 1~6 月,给的都是月
份,环比是比上月,每一个月份都给了现期、基期,问 r>10%,可以用“(现期
- 基期)/基期”计算,但是要计算 6 次,费时间,有更简单的方法,但有一定
计算量,r>10%→基期*1.1<现期。结合材料找“户均移动互联网接入流量”数
据,1 月:要满足“基期*1.1<1 月”,1 月的环比基期为上一年的 12 月,错位
相加,2.69+0.269=2.8+>2.77,不满足;2 月:2.63<2.77,增长率为负,不满
足;3 月:基期是 2 月,2.63*1.1≈2.63+0.26=2.8+(即使有进位最多到 2.9)
<3.29,满足;4 月:3.29*1.1=3.29+0.329=3.5+>3.41,不满足;5 月:
3.41*1.1=3.41+0.341=3.7+(即使有进位最多到 3.8)<3.97,满足;6 月:
3.97*1.1=3.97+0.397≈4.36>4.24,不满足。故满足的只有 3 月和 5 月,共 2
个月份,对应B项。【选B】
15【注意】
1.题型:问环比增长 10%以上的有几个→r计算。
2.公式:给现期、基期,基期*1.1<现期。
3.这类题目必然会有计算量,但凡能看出来就不用写,写得越少速度越快。
二、比较
二、一般增长率比较
题型识别:增长率最大/小,增长最快/慢
计算公式:r=增长量/基期量=(现期量- 基期量)/基期量=现期量/基期量
-1
速算技巧:
(1)先看“现期量/基期量”,能出答案则直接选(一般“现期量/基期量”
≥2)
(2)不能,则比较“(现期量- 基期量)/基期量”(一般“现期量/基期量”
<2)
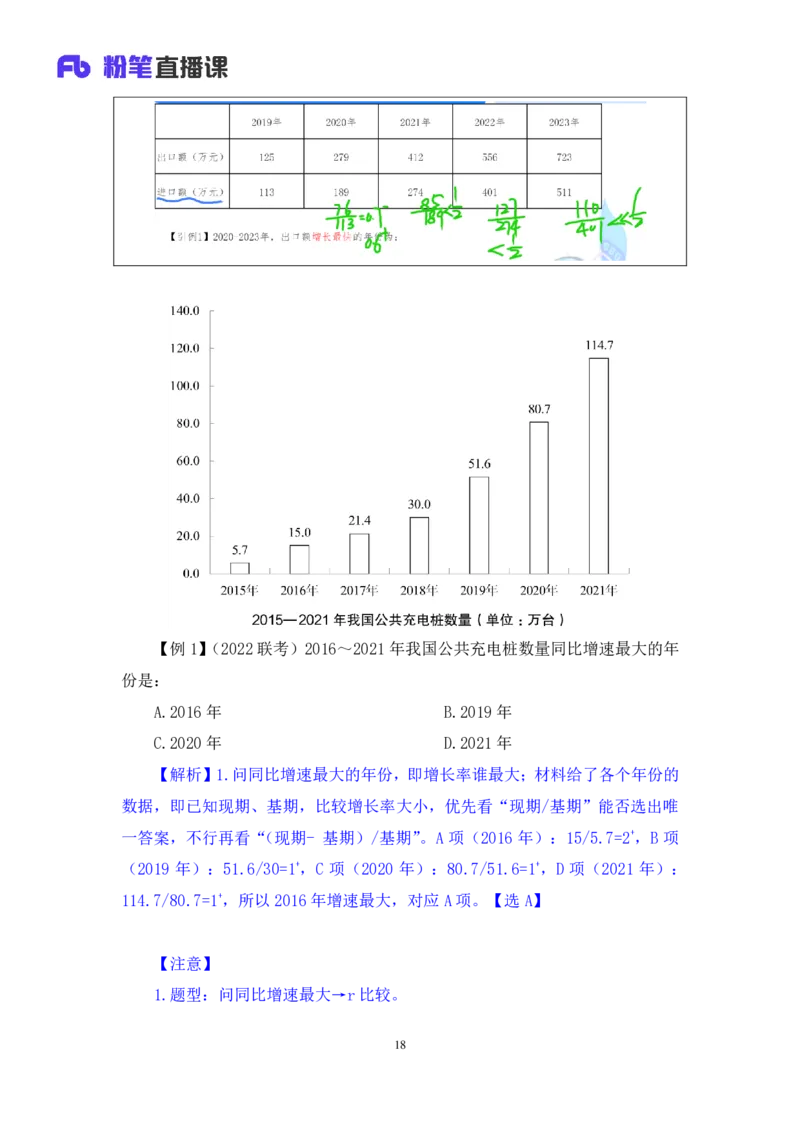
【引例 1】2020~2023年,出口额增长最快的年份为:
16【引例 2】2020~2023年,进口额增长最快的年份为:
【注意】一般增长率比较:
1.题型识别:增长率最大/小,增长最快/慢。一般会说速度快、速度慢,增
长的快/慢就是增长的速度快/慢,增长速度就是增长率。
2.计算公式:r=增长量/基期量=(现期量- 基期量)/基期量=现期量/基期
量- 基期量/基期量=现期量/基期量-1。一般都给现期、基期,四个选项都“-1”
或都不“-1”大小关系不变,比如 A.现期=300、基期=100,B.现期=400、基期
=200,r =300/100-1=2,r =400/200-1=1,r >r ;如果只看“现期/基期”,
A项 B项 A项 B项
仍然是 300/100=3>400/200=2,因此都“-1”不影响大小关系。
3.速算技巧:
(1)先看“现期量/基期量”,能出答案则直接选(一般存在某项的“现期
量/基期量”≥2)。
(2)不能,则比较“(现期量- 基期量)/基期量”(一般“现期量/基期量”
<2)。
4.引例:
(1)2020~2023 年,出口额增长最快的年份为?
答:给现期、基期,比较增长率,优先看“现期/基期”,2020年:279/125=2+;
2021 年:412/279=1+;2022 年:556/412=1+;2023 年:723/556=1+,只有 2020
年超过2,2020年增长最快。
(2)2020~2023 年,进口额增长最快的年份为?
答:2020年:189/113=1+;2021年:274/189=1+;2022年:401/274=1+;2023
年:511/401=1+,发现“现期/基期”均为 1+,如果口算能力强,快速估算第二
位(比如1.8>1.1);老师更推荐用基本公式,比较“(现期量- 基期量)/基期
量”,r =(189-113)/113=76/113=0.7-(0.6+);r =(274-189)/189=85/189
2020年 2021年
<1/2;r =(401-274)/274=127/274<1/2;r =110/401<<1/2,故2020
2022年 2023年
年增长率最大。
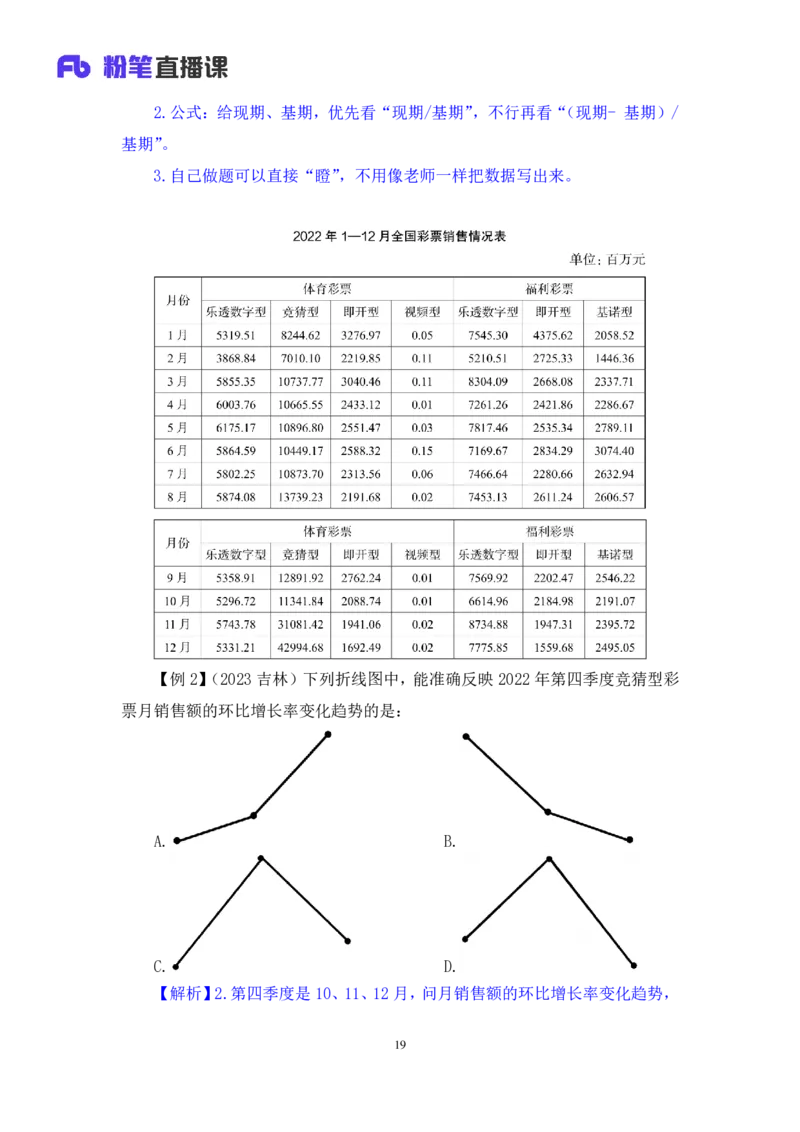
17【例 1】(2022 联考)2016~2021年我国公共充电桩数量同比增速最大的年
份是:
A.2016 年 B.2019年
C.2020 年 D.2021年
【解析】1.问同比增速最大的年份,即增长率谁最大;材料给了各个年份的
数据,即已知现期、基期,比较增长率大小,优先看“现期/基期”能否选出唯
一答案,不行再看“(现期- 基期)/基期”。A 项(2016 年):15/5.7=2+,B 项
(2019 年):51.6/30=1+,C 项(2020 年):80.7/51.6=1+,D 项(2021 年):
114.7/80.7=1+,所以 2016年增速最大,对应 A项。【选A】
【注意】
1.题型:问同比增速最大→r比较。
182.公式:给现期、基期,优先看“现期/基期”,不行再看“(现期- 基期)/
基期”。
3.自己做题可以直接“瞪”,不用像老师一样把数据写出来。
【例 2】(2023 吉林)下列折线图中,能准确反映 2022年第四季度竞猜型彩
票月销售额的环比增长率变化趋势的是:
A. B.
C. D.
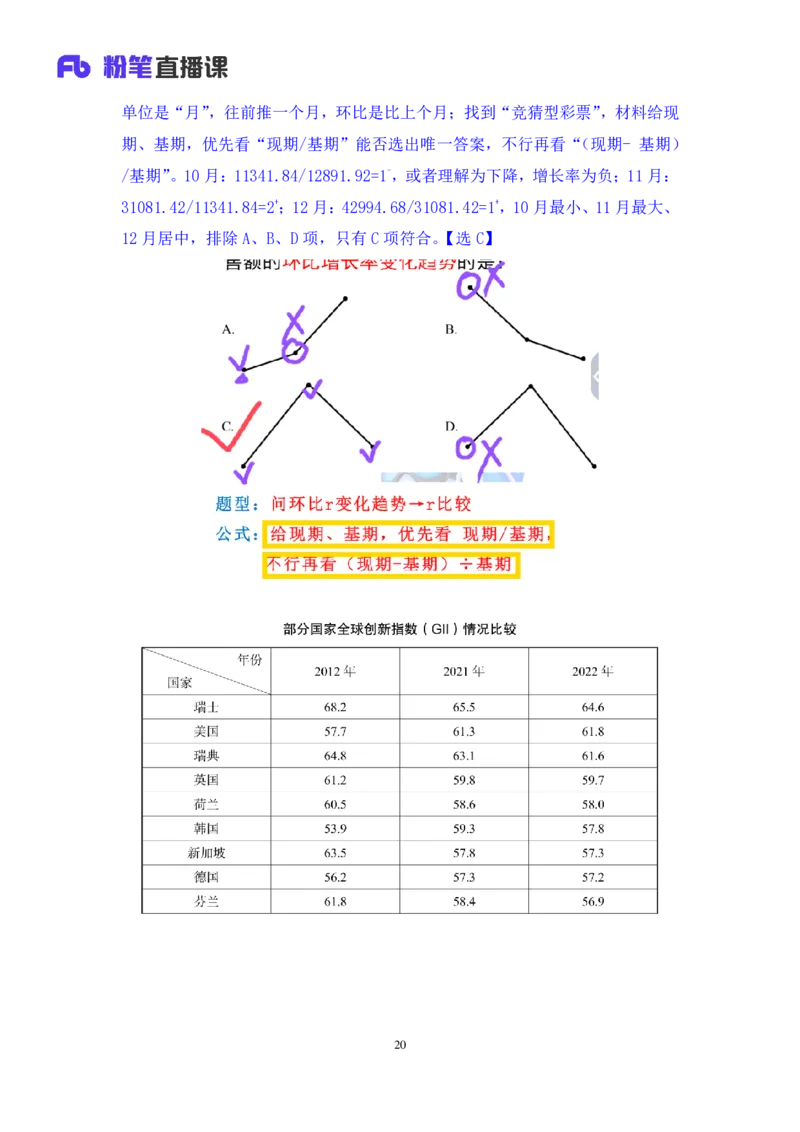
【解析】2.第四季度是 10、11、12月,问月销售额的环比增长率变化趋势,
19单位是“月”,往前推一个月,环比是比上个月;找到“竞猜型彩票”,材料给现
期、基期,优先看“现期/基期”能否选出唯一答案,不行再看“(现期- 基期)
/基期”。10月:11341.84/12891.92=1-,或者理解为下降,增长率为负;11月:
31081.42/11341.84=2+;12月:42994.68/31081.42=1+,10月最小、11月最大、
12月居中,排除A、B、D项,只有C项符合。【选C】
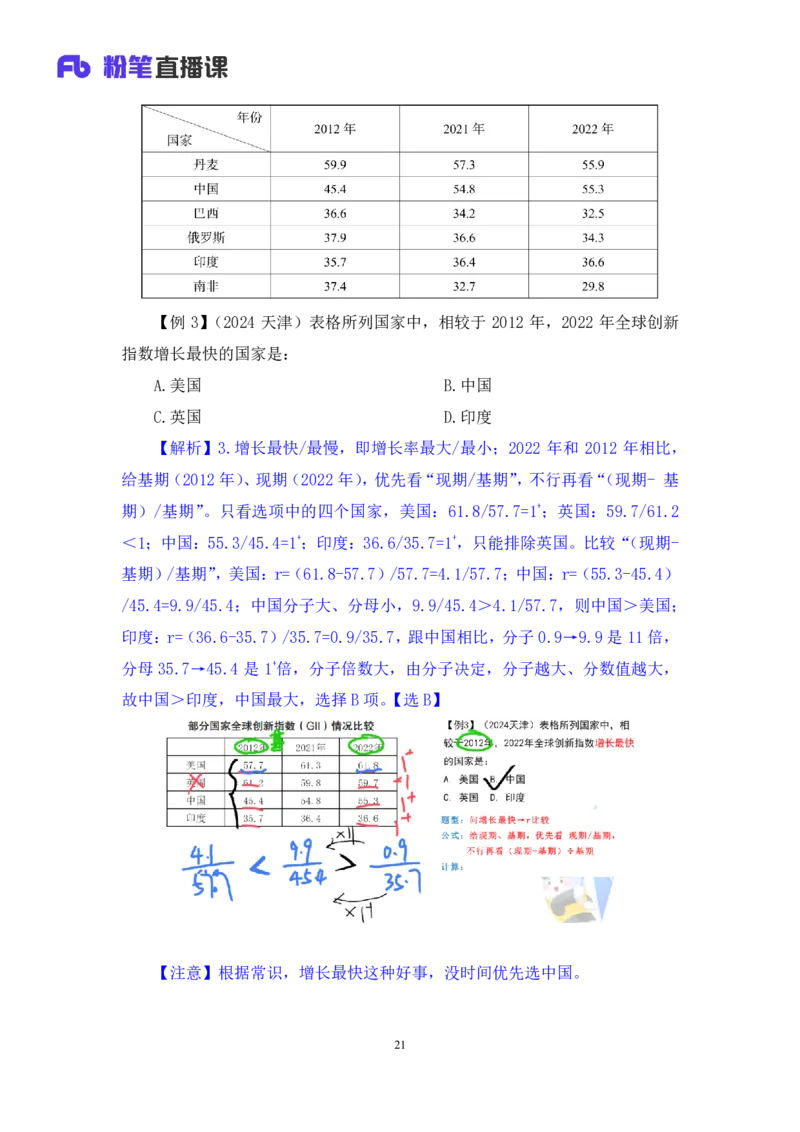
20【例 3】(2024 天津)表格所列国家中,相较于 2012 年,2022 年全球创新
指数增长最快的国家是:
A.美国 B.中国
C.英国 D.印度
【解析】3.增长最快/最慢,即增长率最大/最小;2022 年和 2012 年相比,
给基期(2012年)、现期(2022年),优先看“现期/基期”,不行再看“(现期- 基
期)/基期”。只看选项中的四个国家,美国:61.8/57.7=1+;英国:59.7/61.2
<1;中国:55.3/45.4=1+;印度:36.6/35.7=1+,只能排除英国。比较“(现期-
基期)/基期”,美国:r=(61.8-57.7)/57.7=4.1/57.7;中国:r=(55.3-45.4)
/45.4=9.9/45.4;中国分子大、分母小,9.9/45.4>4.1/57.7,则中国>美国;
印度:r=(36.6-35.7)/35.7=0.9/35.7,跟中国相比,分子 0.9→9.9 是11倍,
分母 35.7→45.4 是 1+倍,分子倍数大,由分子决定,分子越大、分数值越大,
故中国>印度,中国最大,选择B项。【选 B】
【注意】根据常识,增长最快这种好事,没时间优先选中国。
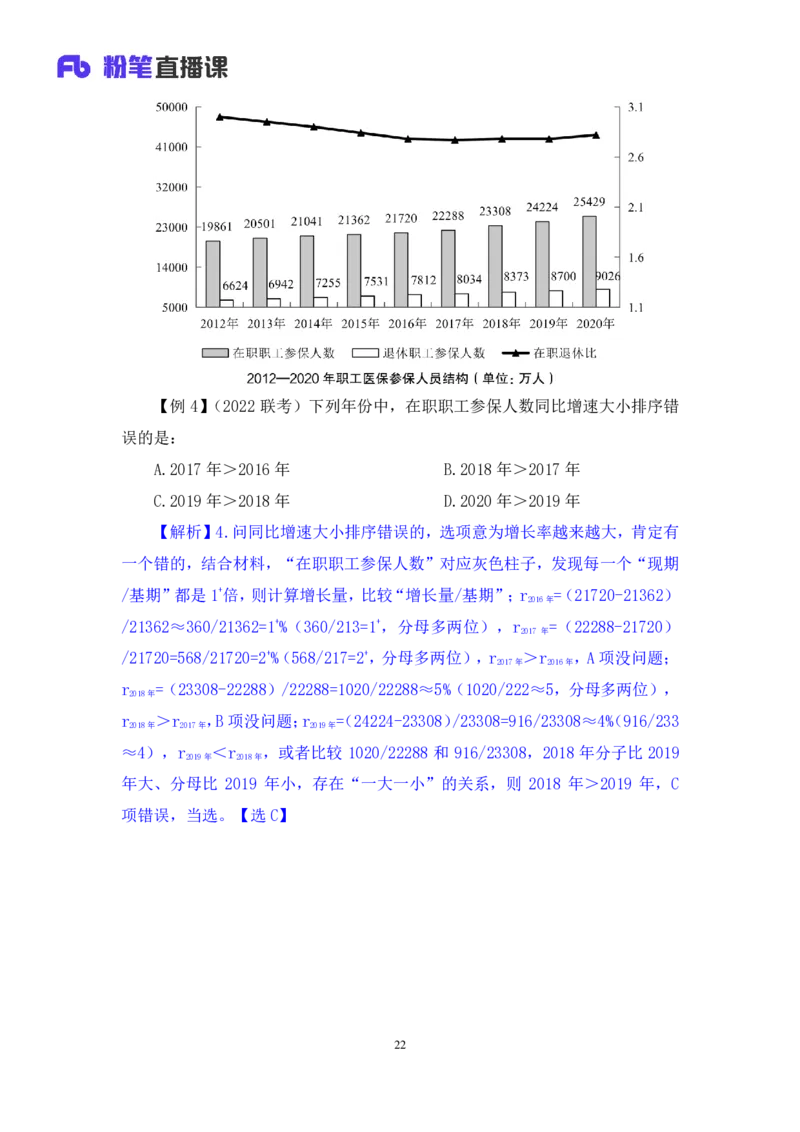
21【例 4】(2022 联考)下列年份中,在职职工参保人数同比增速大小排序错
误的是:
A.2017 年>2016 年 B.2018年>2017年
C.2019 年>2018 年 D.2020年>2019年
【解析】4.问同比增速大小排序错误的,选项意为增长率越来越大,肯定有
一个错的,结合材料,“在职职工参保人数”对应灰色柱子,发现每一个“现期
/基期”都是1+倍,则计算增长量,比较“增长量/基期”;r =(21720-21362)
2016年
/21362≈360/21362=1+%(360/213=1+,分母多两位),r =(22288-21720)
2017 年
/21720=568/21720=2+%(568/217=2+,分母多两位),r >r ,A 项没问题;
2017年 2016年
r =(23308-22288)/22288=1020/22288≈5%(1020/222≈5,分母多两位),
2018年
r >r ,B项没问题;r =(24224-23308)/23308=916/23308≈4%(916/233
2018年 2017年 2019年
≈4),r <r ,或者比较 1020/22288 和 916/23308,2018 年分子比 2019
2019年 2018年
年大、分母比 2019 年小,存在“一大一小”的关系,则 2018 年>2019 年,C
项错误,当选。【选 C】
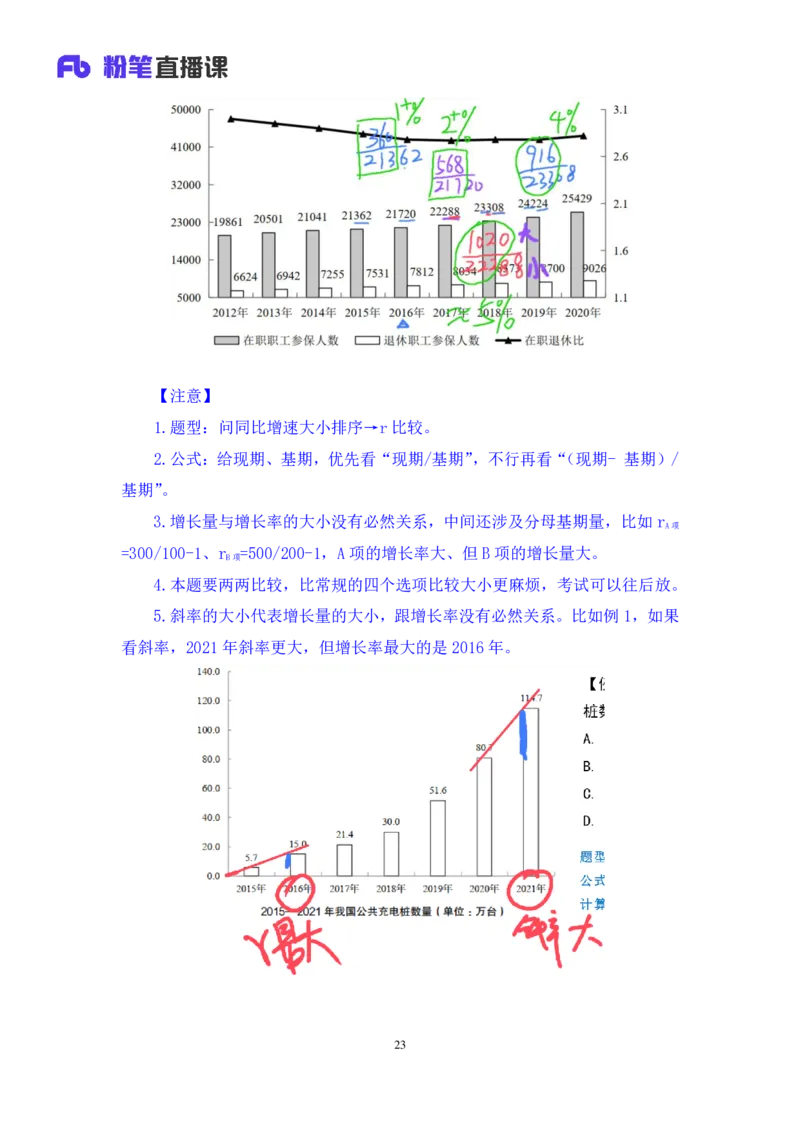
22【注意】
1.题型:问同比增速大小排序→r比较。
2.公式:给现期、基期,优先看“现期/基期”,不行再看“(现期- 基期)/
基期”。
3.增长量与增长率的大小没有必然关系,中间还涉及分母基期量,比如r
A项
=300/100-1、r =500/200-1,A项的增长率大、但 B项的增长量大。
B项
4.本题要两两比较,比常规的四个选项比较大小更麻烦,考试可以往后放。
5.斜率的大小代表增长量的大小,跟增长率没有必然关系。比如例 1,如果
看斜率,2021年斜率更大,但增长率最大的是 2016年。
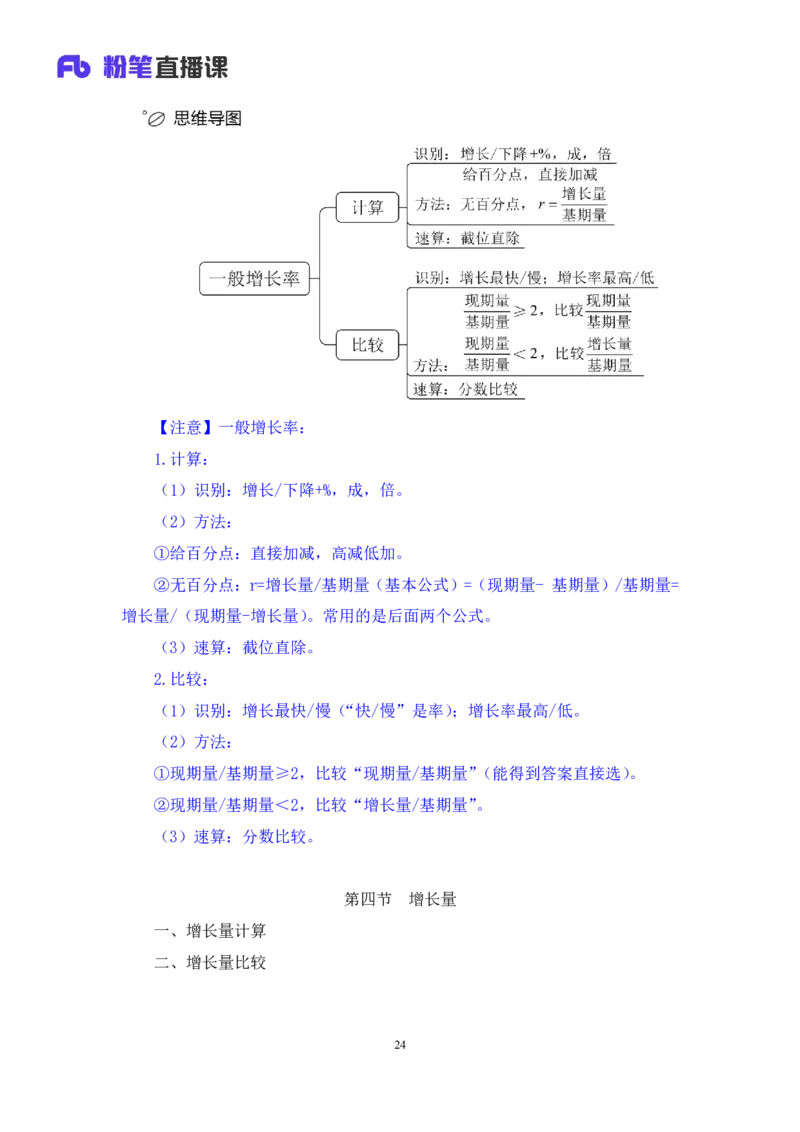
23【注意】一般增长率:
1.计算:
(1)识别:增长/下降+%,成,倍。
(2)方法:
①给百分点:直接加减,高减低加。
②无百分点:r=增长量/基期量(基本公式)=(现期量- 基期量)/基期量=
增长量/(现期量-增长量)。常用的是后面两个公式。
(3)速算:截位直除。
2.比较:
(1)识别:增长最快/慢(“快/慢”是率);增长率最高/低。
(2)方法:
①现期量/基期量≥2,比较“现期量/基期量”(能得到答案直接选)。
②现期量/基期量<2,比较“增长量/基期量”。
(3)速算:分数比较。
第四节 增长量
一、增长量计算
二、增长量比较
24一、增长量计算
题型识别:增长/下降+具体单位
题型 1:给现期量、基期量,求增长量
题型 2:给现期量、基期量,求年均增长量
题型 3:已知现期、增长率,求增长量
【注意】增长量计算:
1.题型识别:增长/下降+具体单位。如增长+人/吨/元/个。
2.根据给的数据不同分成三种题型:
(1)题型1:给现期量、基期量,求增长量。
(2)题型2:给现期量、基期量,求年均增长量。
(3)题型3:已知现期、增长率,求增长量。
题型 1:给现期量、基期量,求增长量
题型识别:增长/下降+具体单位
计算公式:增长量=现期量- 基期量
速算技巧:尾数、估算
【注意】题型 1:给现期量、基期量,求增长量。
1.题型识别:增长/下降+具体单位。
2.计算公式:增长量=现期量- 基期量(普通减法计算)。
3.速算技巧:如果选项是精确值,可以用尾数法;大部分题目是四舍五入后
的结果,可以估算。
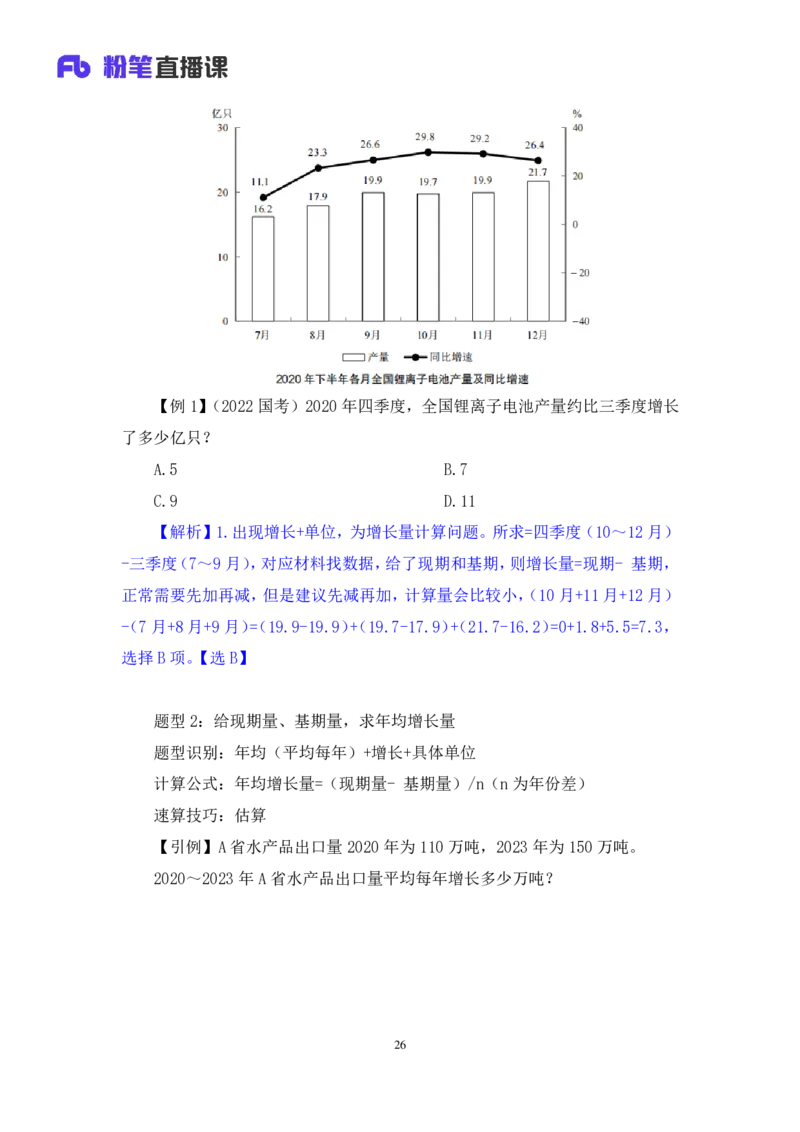
25【例 1】(2022 国考)2020 年四季度,全国锂离子电池产量约比三季度增长
了多少亿只?
A.5 B.7
C.9 D.11
【解析】1.出现增长+单位,为增长量计算问题。所求=四季度(10~12月)
-三季度(7~9月),对应材料找数据,给了现期和基期,则增长量=现期- 基期,
正常需要先加再减,但是建议先减再加,计算量会比较小,(10月+11 月+12月)
-(7月+8月+9月)=(19.9-19.9)+(19.7-17.9)+(21.7-16.2)=0+1.8+5.5=7.3,
选择B项。【选 B】
题型 2:给现期量、基期量,求年均增长量
题型识别:年均(平均每年)+增长+具体单位
计算公式:年均增长量=(现期量- 基期量)/n(n为年份差)
速算技巧:估算
【引例】A省水产品出口量 2020年为110 万吨,2023年为150 万吨。
2020~2023年 A省水产品出口量平均每年增长多少万吨?
26【注意】题型 2:给现期量、基期量,求年均增长量。
1.题型识别:年均(平均每年)+增长+具体单位。
2.计算公式:年均增长量=(现期量- 基期量)/n,n为年份差。
3.速算技巧:估算。
4.引例:A省水产品出口量 2020年为110万吨,2023年为150万吨。2020~
2023年 A省水产品出口量平均每年增长多少万吨?
答:平均每年+增长+单位,为年均增长量问题。2020 年~2023 年增长了 3
次,则 n=3,列式:(150-110)/3=40/3=13+,一个个数比较麻烦,直接用 2023
年-2020 年。
5.年均增长问题中的基期和年份差:
(1)一般情况(除江苏外):
①重点:首(第一个年份)为基期,尾(最后一个年份)为现期。
②举例:2020~2023 年,基期为 2020 年,现期为 2023 年,年份差为 2023
年-2020 年=3。
(2)五年规划(全国都一样):
①重点:年份差为 5,基期往前推一年。
②举例:“十三五”(2016~2020年):基期为 2015年,现期为 2020年,
年份差为5。
27(3)考官规定:
①重点:这 N年,则年份差为 N(往往基期需要往前推一年)。
②举例:2020~2023 年这 4 年,现期为 2023 年,基期往前推一年为 2019
年,年份差=2023年-2019年=4。
(4)江苏:
①重点:基期往前推一年。
②举例:2020~2023 年,基期为 2019 年,现期为 2023 年,年份差为 2023
年-2019 年=4。
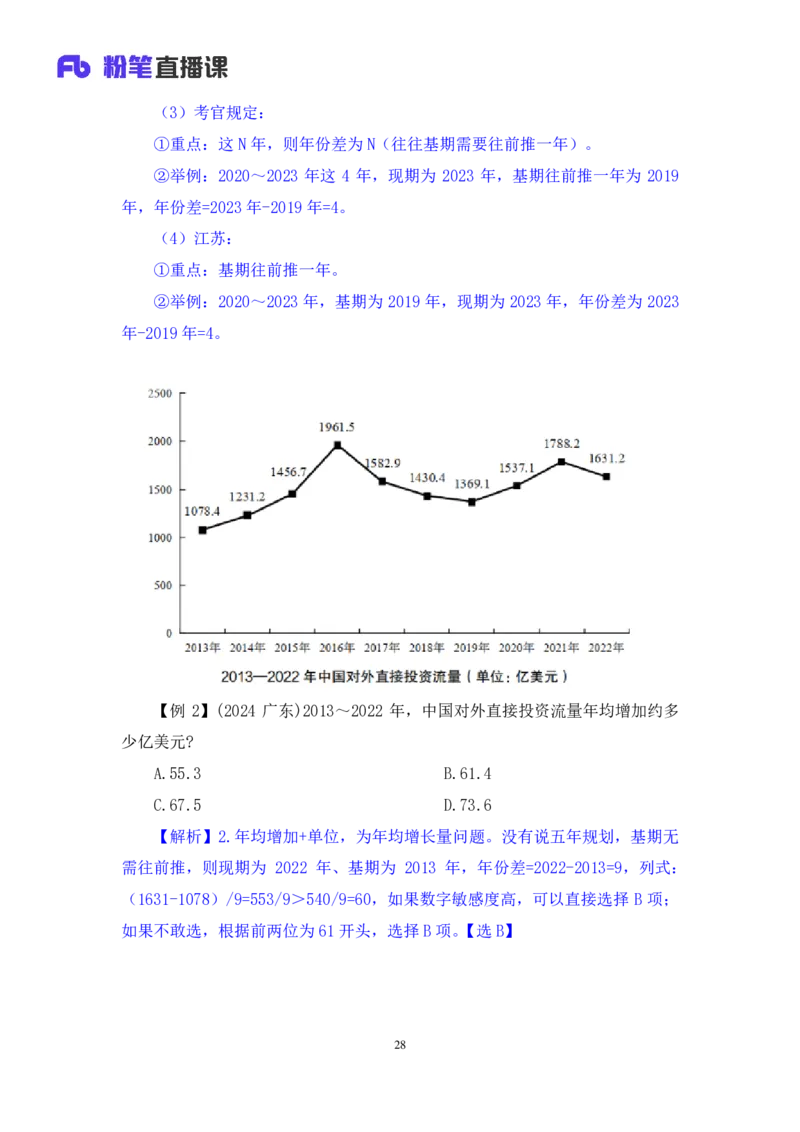
【例 2】(2024 广东)2013~2022 年,中国对外直接投资流量年均增加约多
少亿美元?
A.55.3 B.61.4
C.67.5 D.73.6
【解析】2.年均增加+单位,为年均增长量问题。没有说五年规划,基期无
需往前推,则现期为 2022 年、基期为 2013 年,年份差=2022-2013=9,列式:
(1631-1078)/9=553/9>540/9=60,如果数字敏感度高,可以直接选择 B 项;
如果不敢选,根据前两位为 61开头,选择 B项。【选B】
28【例 3】(2022 江苏)“十三五”时期,我国集成电路出口额的年均增量是:
A.79 亿美元 B.95亿美元
C.111 亿美元 D.139亿美元
【解析】3.本题无需关注题源,问题时间是“十三五”时期,对应 2016~
2020年;求年均增长量,涉及五年规划,基期往前推一年→基期是 2015年、现
期是2020 年;年均增长量=(1166-691)/5=475/5=90+,对应B项。【选 B】
题型 3:给现期量、r,求增长量
题型识别:增长/下降+具体单位
计算公式:增长量=增长量/(1+r)*r
速算技巧:第 1步:r百化分:|r|=1/n
第 2步:计算增长量:增长量=现期量/(n+1)、减少量=现期量/(n-1)
【引例】2023 年A省水产品出口量为150 万吨,比上年增长25%。
2023 年A省水产品出口量比上年增长多少万吨?
【注意】题型 3(考最多):给现期量、r,求增长量。
1.题型识别:增长/下降+具体单位。
2.计算公式:增长量=增长量/(1+r)*r。
3.推导:r=增长量/基期量→增长量=基期量*r,基期量=现期量/(1+r),增
长量=现期量/(1+r)*r。
4.速算技巧:
(1)第1步:r百化分:|r|=1/n。
(2)第2步:计算增长量。
29①增长量=现期量/(n+1)。
②减少量=现期量/(n-1)。
(3)推导:将 r转化为1/n,增长量=现期量÷(1+1/n)*(1/n)=现期量
*(1/n)*[n/(n+1)]=现期量/(n+1)。若 r=1/n,则增长量=现期量/(n+1);
如果增长率为负,则减少量=现期量/(n-1)。
5.例.2023年A 省水产品出口量为150 万吨,比上年增长25%。问2023年A
省水产品出口量比上年增长多少万吨?
答:所求=150/(1+25%)*25%,百化分,r=25%=1/4,增长量=现期量/(n+1)
=150/(4+1)=150/5=30。如果把增长改成减少,r=|-25%|=1/4 则减少量=150/
(4-1)=150/3=50。
【注意】百化分:1/2~1/20这些分数需要记忆。
30【注意】记忆方法:
1.2 倍关系(一半):
(1)1/2=50%,1/4=25%、1/8=12.5%、1/16=6.25%。
(2)33.3%≈1/3、16.7%≈1/6、8.3%≈1/12。
(3)20%=1/5、10%=1/10、5%=1/20。
2.n 和分子互换:
(1)14.3%≈1/7、7.1%≈1/14。
(2)11.1%≈1/9、9.1%≈1/11。
3.失散七夕(1377)、要我录取(1567):7.7%≈1/13、6.7%≈1/15。
4.5.963 对应17、18、19(等差):5.9%≈1/17、5.6%≈1/18、5.3%≈1/19。
【注意】反复练习,直到会操作:
1.方法:
(1)第1步:|r|=1/n。
(2)第2步:增长量=现期量/(n+1);减少量=现期量/(n-1)。
2.例:
(1)例1:现期=100,增速=20%,求增长量。
答:第 1步,|r|=20%=1/5;第2步,增长量=100/(5+1)=100/6=16+。
(2)例2:现期=100,增速=50%,求增长量。
答:第 1步,|r|=50%=1/2;第2步,增长量=100/(2+1)=100/3=33+
31(3)例3:现期=100,增速=-20%,求减少量。
答:第 1步,|r|=|-20%|=1/5;第2步,减少量=100/(5-1)=100/4=25。
国家能源局发布 2022年17月,全社会用电量累计 49303亿千瓦时,同比增
长3.4%。分产业看,……;城乡居民生活用电量 7586亿千瓦时,同比增长 12.5%。
7 月份,全社会用电量 8324 亿千瓦时,同比增长 6.3%。分产业看,……;城乡
居民生活用电量1480 亿千瓦时,同比增长 26.8%。
【例 4】(2023 联考)2022 年 1~7 月份,全国城乡居民生活用电量比 2021
年1~7 月份约多:
A.672 亿千瓦时 B.843亿千瓦时
C.925 亿千瓦时 D.1020亿千瓦时
【解析】4.多+单位,求增长量。主体为“城乡生活用电量”,已知现期和 r,
百化分,|r|=12.5%=1/8;增长量=7586/(8+1)=7586/9=800+,对应B 项。【选B】
2020 年全国人口共 141178万人,比2010 年增长了约5.38%。从地区分布上
看,2020 年东部地区人口占 39.93%,中部地区占 25.83%,西部地区占 27.12%,
东北地区占6.98%。与 2010年相比……
【拓展】(2022 联考)2020 年全国人口比 2010 年全国人口增加的数量位于
以下哪个区间?
A.5000 万~6000 万人 B.6000万~7000万人
C.7000 万~8000 万人 D.8000万~9000万人
【解析】拓展.问增加的数量,即求增长量。主体为“全国人口数量”,已知
现期和r,求增长量,用百化分,|r|=5.38%≈5.3%≈1/19,增长量≈141178/(19+1)
=141178/20,首位商 7,比7大一点点,对应 C项。【选C】
增长率百化分之取中法
如果遇到百分数左右难取舍,且选项接近,取中即可
13.4%≈、9.5%≈
【注意】增长率百化分之取中法:如果遇到百分数左右难取舍,且选项接近,
32取中即可。
1.13.4%:介于 14.3%(1/7)与 12.5%(1/8)之间,如果选项差距非常大,
用1/7、1/8计算都可以;如果选项差距小,用 1/7、1/8计算都有可能出错,可
以取中间值,注意是对分母取中,分母是n,分子一定是1,取中为 1/7.5。
2.9.5%:介于10%(1/10)与9.1%(1/11)之间,几乎是两者之间的平均数,
取中,分母取11与10的中间值,取中为1/10.5,即9.5%≈1/10.5→10.5%≈1/9.5。
增长率百化分之倍数法
利用与背过的百分数的倍数关系,实现百化分
67%≈3.3%≈
【注意】增长率百化分之倍数法:利用与背过的百分数的倍数关系,实现百
化分。
1.67%:67%=33.5%*2≈(1/3)*2=2/3=1/1.5,则n=1.5。
2.3.3%:3.3%=33%/10≈1/3÷10=1/30。
增长率百化分之硬算法 n=100/百分号前面的数字
56%≈
【注意】增长率百化分之硬算法(不推荐,比较慢,要是硬算可以直接现期
*0.56/1.56):n=100/百分号前面的数字。比如 56%:n=100/65≈1.8。
2023 年4月份,我国社会消费品零售总额 34910亿元,同比增长 18.4%。其
中,除汽车以外的消费品零售额 31290亿元,增长 16.5%。
2023 年前 5 个月,汽车出口带动天津口岸整体出口同比增加。汽车出口占
同期天津口岸出口商品总值的 2.2%,较上年同期提升 0.3 个百分点。1~5 月民
营企业出口活力明显,民营企业出口约 10.6 万辆,同比增长 64.3%,占同期天
津口岸汽车出口总量的 61.6%,占比较上年同期提升 13 个百分点。新能源汽车
出口成为新的增长点,出口约 11万辆,同比增长 50.2%。
【例 5】(2024 贵州)2023 年 1~5 月,民营企业出口汽车同比约增加了多
少万辆?
33A.3 B.4
C.5 D.6
【解析】5.增加+多少万辆,即求增长量;主体是民营企业出口汽车,给了
现期和r,用百化分,r=64.3%比较大,可以用倍数转化,64.3%≈32%*2≈(1/3)
*2=1/1.5,则增长量=10.6/2.5≈4,选择B 项。【选B】
2023 年4月份,我国社会消费品零售总额 34910亿元,同比增长 18.4%。其
中,除汽车以外的消费品零售额 31290亿元,增长 16.5%。
【例 6】(2023 河北事业单位)2023年 4月,我国社会消费品零售总额同比
增加:
A.4678 亿元 B.5425亿元
C.6414 亿元 D.7212亿元
【解析】6.增加+单位(亿元),求增长量。主体为“我国社会消费品零售总
额”,已知现期和 r,百化分,r=18.4%,18.4%介于 20%(1/5)与 16.7%(1/6)
之间,取中为1/5.5,r=1/5.5,增长量≈34910/6.5,首位商5,对应 B项。【选
B】
2022 年,我国废钢铁、废有色金属等十个品种再生资源回收总重量约为
37067.7万吨,同比下降2.62%,回收总金额约为13140.6亿元,同比下降4.05%。
2022 年废有色金属中废铅回收重量同比增长 5.56%。2022 年我国报废机动车回
收数量399.1万辆,同比增长 32.9%,回收数量占我国机动车保有量的 9.57‰。
【例 7】(2024 陕西)相比 2021 年,2022 年我国十个品种再生资源回收总
金额同比下降了约:
A.511 亿元 B.532亿元
C.555 亿元 D.578亿元
【解析】7.下降+具体单位,求减少量。主体为“十个品种再生资源回收总
金额”,已知“(2022 年)回收总金额约为 13140.6 亿元,同比下降 4.05%”;给
出现期量、r,考虑百化分。(1)|r|=1/n:|r|=|-4.05%|,有点小,可以先写成
4%=1/25;(2)减少量=现期量/(n-1)≈13140.6/(25-1)=13140.6/24,首位
34商 5、第二位商 4,后面还有余数,最接近 C 项;如果不放心,还可以算出第三
位商7,选择 C项。【选 C】
二、增长量比较
题型识别:增长最多/少,下降最多/少
计算公式:增长量=现期量基期量
速算技巧:有图,看高度差;没图,直接减
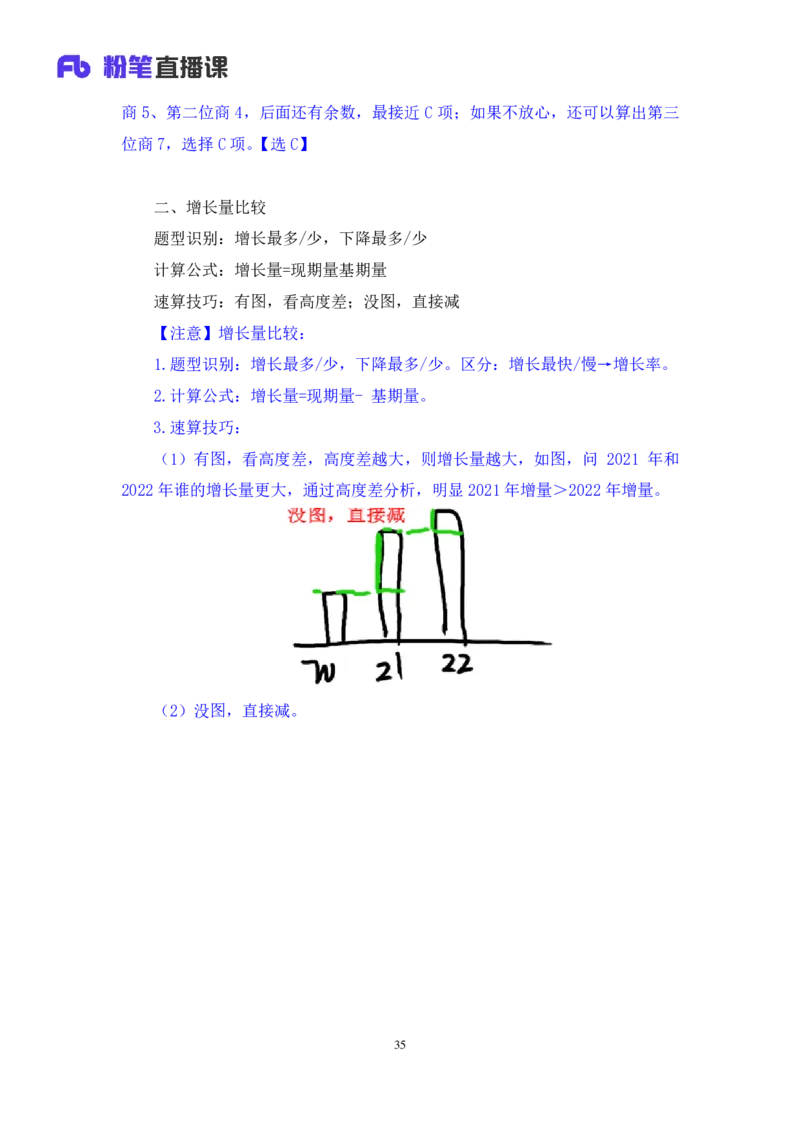
【注意】增长量比较:
1.题型识别:增长最多/少,下降最多/少。区分:增长最快/慢→增长率。
2.计算公式:增长量=现期量- 基期量。
3.速算技巧:
(1)有图,看高度差,高度差越大,则增长量越大,如图,问 2021 年和
2022年谁的增长量更大,通过高度差分析,明显 2021年增量>2022 年增量。
(2)没图,直接减。
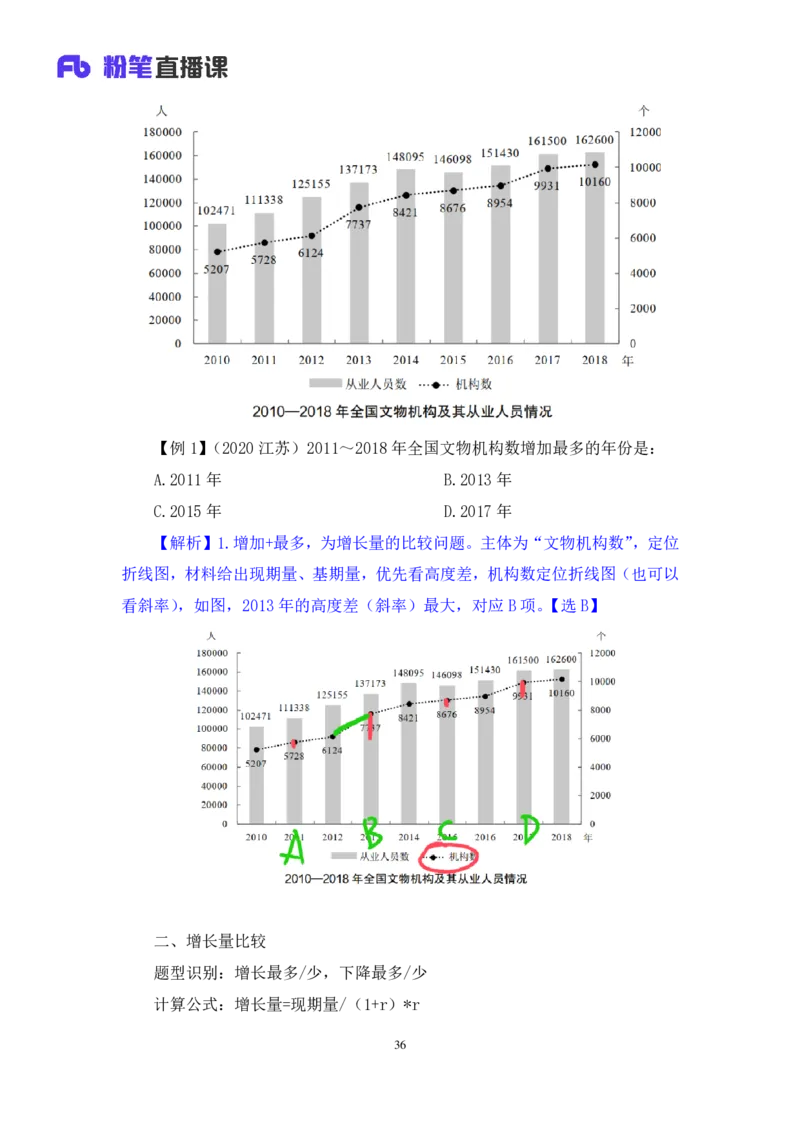
35【例 1】(2020 江苏)2011~2018年全国文物机构数增加最多的年份是:
A.2011 年 B.2013年
C.2015 年 D.2017年
【解析】1.增加+最多,为增长量的比较问题。主体为“文物机构数”,定位
折线图,材料给出现期量、基期量,优先看高度差,机构数定位折线图(也可以
看斜率),如图,2013 年的高度差(斜率)最大,对应B项。【选B】
二、增长量比较
题型识别:增长最多/少,下降最多/少
计算公式:增长量=现期量/(1+r)*r
36速算技巧:第 1步:大大则大(r同号)。
r为正:现期量大,同时 r也大,则其增长量大;
r为负:现期量大,同时|r|也大,则其减少量大。
r有正有负:比较增长量,则正数>负数。
第 2步:百化分
现期量、r一大一小:百化分
【注意】增长量比较:
1.题型识别:增长最多/少,下降最多/少。
2.计算公式:增长量=现期量/(1+r)*r。
3.推导:若 A 项的现期为 200,r=7.7%,B 项的现期为 100,r=7.7%,问 A、
B项谁的增长量更大。增长率相同,现期量不同,而现期量只存在分子上,如果
现期量越大,则增长量越大,A项与B项比较,因为 A项的现期量更大,则 A项
的增量大。若 C 项的现期量为 100,增长率为 6.7%,比较 B、C 项的大小关系,
现期相同,分子、分母同时除以 r→现期量÷[(1+r)/r]→现期量÷[(1/r)
+1],r越大,1/r越小,分母越小,增长量越大,即 r越大,增长量越大,因此
B 项>C 项;A、C 项比较,A 项的现期量和增长率都大,说明 A 项增量>C 项增
量。如果 A 项的现期=888、r=11.1%;B 项的现期=666、r=6.6%,A 项现期大、r
大,则增长量一定大。
4.速算技巧:
(1)第1步:大大则大(r同号)。现期量大、增长率大,则增长量大。
①r 为正:现期量大,同时 r也大,则其增长量大。
②r 为负:现期量大,同时|r|也大,则其减少量大。
③r 有正有负:比较增长量,则正数>负数。
④例:
a.问 A、B项相比谁的增长量更大?
37答:A项的现期量和增长率都大,大大则大,故 A项的增长量更大。
b.问 C、D项相比谁的减少量更大?
答:C项现期量大,增长率的绝对值大,则 C项的减少量更大。
c.在 A、B、C、D项中,问增长量最大的是哪一个?
答:问增长量,当 r 有正有负时,正数>负数,C、D 项是最小的;A、B 项
大大则大,则增长量最大的是 A项,因此A 项>B项>C项、D项。
(2)第 2 步:百化分。现期量、r 一大一小,百化分估算。如果问增长量
的绝对值,有正有负,考虑百化分。
……2018年木家具出口数量增长 5.68%,金额负增长1.6%,木地板出口 26.6
万吨,3.85 亿美元,分别下降 24.8%和下降 25.9%。胶合板出口 1137.8 万立方
米,55.56 亿美元,数量增长 5%,金额增长 9%,纤维板出口 179 万吨,38.35
亿美元,数量下降 14.9%,金额增长6.2%……
【例 2】(2021 新疆兵团)2018年,下列三种产品出口金额增长值从大到小
的顺序排列正确的是:
A.木地板、胶合板、纤维板
B.胶合板、纤维板、木地板
C.木地板、纤维板、胶合板
D.胶合板、木地板、纤维板
【解析】2.“增长值”就是增长的具体数值,即增长量,每个选项给的都是
现期、r,先看有无大大则大,找出口额的增长率,问增长量,增长率有正有负,
正数>负数,只有木地板的增速是负数,则木地板的增量一定是最小的,观察选
项,排除A、C、D项,对应 B项。【选B】
【注意】胶合板:55.56、9%;纤维板:38.35、6.2%,胶合板的现期量大、
r大,根据“大大则大”,则胶合板>纤维板,选择B项。
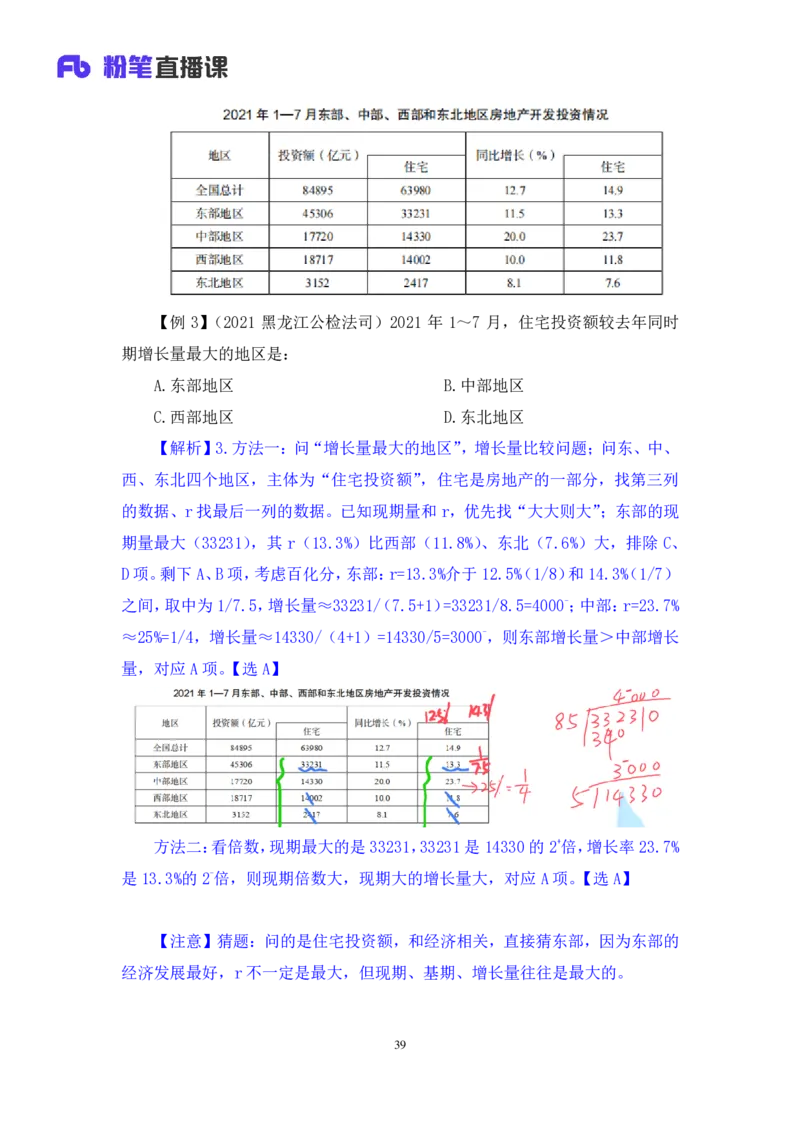
38【例 3】(2021 黑龙江公检法司)2021 年 1~7 月,住宅投资额较去年同时
期增长量最大的地区是:
A.东部地区 B.中部地区
C.西部地区 D.东北地区
【解析】3.方法一:问“增长量最大的地区”,增长量比较问题;问东、中、
西、东北四个地区,主体为“住宅投资额”,住宅是房地产的一部分,找第三列
的数据、r找最后一列的数据。已知现期量和 r,优先找“大大则大”;东部的现
期量最大(33231),其 r(13.3%)比西部(11.8%)、东北(7.6%)大,排除 C、
D项。剩下A、B项,考虑百化分,东部:r=13.3%介于12.5%(1/8)和14.3%(1/7)
之间,取中为1/7.5,增长量≈33231/(7.5+1)=33231/8.5=4000-;中部:r=23.7%
≈25%=1/4,增长量≈14330/(4+1)=14330/5=3000-,则东部增长量>中部增长
量,对应A项。【选 A】
方法二:看倍数,现期最大的是33231,33231 是14330的2+倍,增长率 23.7%
是13.3%的2-倍,则现期倍数大,现期大的增长量大,对应A项。【选 A】
【注意】猜题:问的是住宅投资额,和经济相关,直接猜东部,因为东部的
经济发展最好,r不一定是最大,但现期、基期、增长量往往是最大的。
39按收入来源分,(2019 年)前三季度,全国居民人均工资性收入 13020 元,
增长 8.6%;人均经营净收入 3757 元,增长 9.3%;人均财产净收入 1949 元,增
长12.3%;人均转移净收入 4157元,增长7.2%。
【例 4】(2021 新疆兵团)2019年前三季度,四种收入来源中收入同比增量
最高的是:
A.人均工资性收入 B.人均经营净收入
C.人均财产净收入 D.人均转移净收入
【解析】4.问同比增量最高,为增长量的比较问题。
方法一:定位材料找数据,给了现期和 r,先看“大大则大”,发现人均工
资性收入的现期量最大,人均工资性收入的增长率(8.6%)比人均转移净收入
(7.2%)的 r大,大大则大,人均工资性收入>人均转移净收入,排除 D项。
剩余的三个选项之间不存在“大大则大”,考虑百化分,人均工资性收入:
8.6%≈8.3%≈1/12,增长量≈13020/13=1000+;人均经营净收入:9.3%≈9.1%≈
1/11,增长量≈3757/12=300+;人均财产净收入:12.3%≈12.5%=1/8,增长量≈
1949/9=200+,故同比增量最高的是人均工资性收入,对应A项。
方法二:工资性收入的现期量最大为 13020,其他的现期量最大的是 4157,
现期量是3+倍的关系,增长率之间是 1+倍,现期量之间的倍数更大,则现期量大
的增长量更大,选择 A项。【选A】
拓展:
若 r为正,且现期、r一大一小→看倍数
若现期量倍数更大,则现期量大的,增长量就大(100%正确率);
若 r倍数更大,建议当 r倍数明显大于现期量倍数才用,此时 r 大的,一般
增长量就大(不是 100%正确率)。
【注意】拓展:现期、r一大一小→看倍数:
1.若现期量倍数更大,则现期量大的,增长量就大(100%正确率):比如 A
项的现期量为 188、增长率为 18.8%,B 项的现期量为 89、增长率为 26.6%,两
者之间没有“大大则大”,可以看倍数。现期量之间是 2+倍的关系,增长率之间
是 1+倍的关系,现期量的倍数关系大,则现期量大的增长量大,A 项增长量>B
40项增长量。
2.若 r倍数更大,建议当 r倍数明显大于现期量倍数才用,此时 r大的,一
般增长量就大(不是 100%正确率)。比如 C 项的现期为 128、增长率为 88%,B、
C 项现期和 r 一大一小,依然可以看倍数,现期量之间为 1+倍,增长率之间为 3
倍,此时增长率的倍数大,增长率的倍数关系更大,建议当r倍数明显大于现期
量倍数(比如3+倍和 1+倍、4+倍和2+倍、5+倍和 2+倍)才用,虽然不是 100%正确,
也有 95%的正确率。如果还有 D 项的现期量为 78、增长率为 18%,如果看倍数,
现期量之间为 1+倍,增长率之间为 2+倍,此时有比较大的出错概率,因此 C、D
项就建议用百化分比较。
【拓展】(2020 北京)2017年全国共有各级各类民办学校 17.76万所。其中:
民办幼儿园 16.04 万所,比上年增长4.00%。
民办普通小学 6107所,比上年增长2.21%。
民办初中 5277 所,比上年增长3.78%。
民办普通高中 3002所,比上年增长7.71%。
以下民办学校类型中,2017年学校数量同比增长最多的是
A.民办普通高中 B.民办普通小学
C.民办初中 D.民办幼儿园
【解析】拓展.问同比增长最多的,为增长量的比较问题。大大则大,可以
看倍数,给出四个主体,注意单位,民办幼儿院 16.04万所,其他数据都是几千,
如果用最大的数据(6107)计算,从 6107 到 16.04 万,两者之间是几十倍的关
系,增长率最大不到 2倍,现期量的倍数关系更大,则现期量大的增长量大,对
应D项。【选 D】
41【注意】增长量:
1.计算:
(1)识别:增长/下降+单位(人/元/吨)。
(2)公式:
①增长量=现期力量- 基期量=基期量*r=现期量/(1+r)*r。
②年均增长量=(现期量- 基期量)/年份差。
(3)速算:
①百分数化分数:近似转化、倍数转化、取中转化。
②|r|=1/N,若 r>0,则增长量=现期/(N+1);若 r<0,则增长量=现期/
(N-1)。
2.比较:
(1)识别:增长最多/少。
(2)速算:
①给出每年数据:直接两两相减后比较,柱状图还可用直尺测量。
②给出现期量和 r:两者都大则增长量必然大,否则百化分计算后比较。
③也可以看倍数,只有当现期的倍数更大的时候,才是 100%的正确率,如
果是r的倍数更大,不能保证 100%的正确率,建议百化分。
2020 年,全国职工基本医疗保险(以下简称职工医保)参保人数持续增加,
基金收支规模基本稳定。参加职工医保 34455 万人,比上年同比增加 1530万人。
其中在职职工25429 万人,比上年增长5.0%;退休职工9026万人,比上年增长
423.7%。
【练习 1】(2022 广东)2020年,全国参加职工医保人数同比增长约:
A.4.6% B.5.4%
C.6.2% D.7.1%
【解析】练习1.增长+%,求增长率。主体为“全国参加职工医保人数”,定
位材料找数据,给出现期、增长量,r=增长量/(现期-增长量)=1530/(34455-1530)
=1530/32925,选项差距大,截两位计算,1530/33,首位商 4,商不到 5,选择
A项。【选A】
【练习 2】(2021 广东)2020年前三季度,G省智能机器人产业中,四大行业
总产值的同比增量排序正确的是:
①工业机器人制造业 ②特殊作业工业机器人制造业
③智能无人飞行器制造业 ④服务消费机器人制造业
A.①>③>②>④ B.④>②>①>③
C.③>④>②>① D.③>①>②>④
【解析】练习2.问同比增量排序,为增长量的比较问题。定位材料找数据,
给出现期量和 r,先用“大大则大”,不行再看倍数。观察发现④的增长率是负
的,则增长量也是负的,正的>负的,因此④最小,排除 B、C项;A、D项的区
别在于①和③,没有大大则大,可以看倍数,现期 201是76.88的2+倍,增长率
57.4%是 31.7%的1+倍,现期倍数大,现期大的增长量大,则③>①,选择 D项。
【选D】
4344【答案汇总】
一般增长率计算 1-5:ADDBB
一般增长率比较 1-4:ACBC
增长量计算 1-5:BBBBB;6-7:BC
增长量比较 1-4:BBAA
45遇见不一样的自己
Be your better self
46