文档内容
数学试卷
考生注意:
1.考试时间120分钟;
2.全卷共三道大题,总分120分;
3.所有试题请在答题卡上作答,在试卷上答题无效.
一、单项选择题(本题10个小题,每小题3分,共30分)
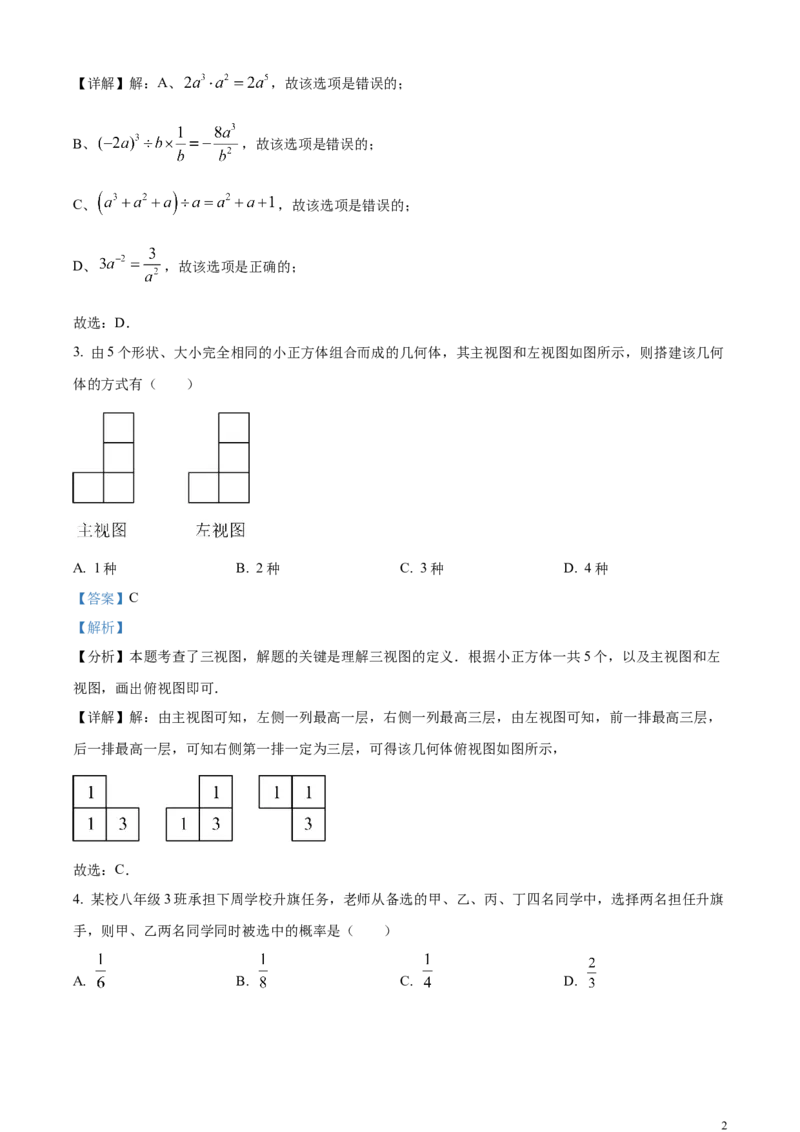
1. 下列图形既是轴对称图形,又是中心对称图形的是( )
A. B. C. D.
【答案】C
【解析】
【分析】本题考查了中心对称图形与轴对称图形的概念,正确掌握中心对称图形与轴对称图形定义是解题
关键.中心对称图形的定义:把一个图形绕某一点旋转180°,如果旋转后的图形能与原来的图形重合,那
么这个图形就叫做中心对称图形;轴对称图形的定义:如果一个图形沿着一条直线对折后两部分完全重台,
这样的图形叫做轴对称图形.根据定义依次对各个选项进行判断即可.
【详解】A、是轴对称图形,不是中心对称图形,故此选项不符合题意;
B、是轴对称图形,不是中心对称图形,故此选项不符合题意;
C、是轴对称图形,是中心对称图形,故此选项符合题意;
D、是轴对称图形,不是中心对称图形,故此选项不符合题意;
故选:C.
2. 下列计算正确的是( )
A. B.
C. D.
【答案】D
【解析】
【分析】本题考查了单项式的乘除法,多项式除以单项式,负整数指数幂,根据运算法则进行逐项计算,
即可作答.
1【详解】解:A、 ,故该选项是错误的;
B、 ,故该选项是错误的;
C、 ,故该选项是错误的;
D、 ,故该选项是正确的;
故选:D.
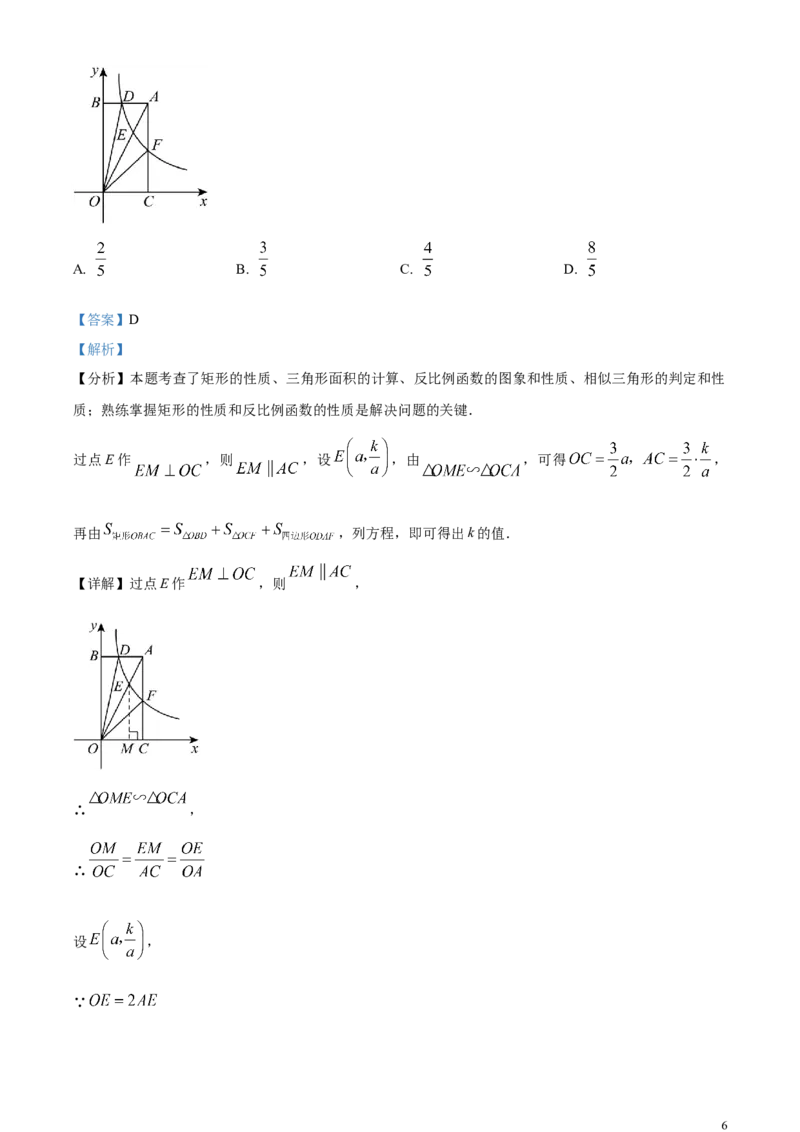
3. 由5个形状、大小完全相同的小正方体组合而成的几何体,其主视图和左视图如图所示,则搭建该几何
体的方式有( )
A. 1种 B. 2种 C. 3种 D. 4种
【答案】C
【解析】
【分析】本题考查了三视图,解题的关键是理解三视图的定义.根据小正方体一共5个,以及主视图和左
视图,画出俯视图即可.
【详解】解:由主视图可知,左侧一列最高一层,右侧一列最高三层,由左视图可知,前一排最高三层,
后一排最高一层,可知右侧第一排一定为三层,可得该几何体俯视图如图所示,
故选:C.
4. 某校八年级3班承担下周学校升旗任务,老师从备选的甲、乙、丙、丁四名同学中,选择两名担任升旗
手,则甲、乙两名同学同时被选中的概率是( )
A. B. C. D.
2【答案】A
【解析】
【分析】本题考查画树状图或列表法求概率,列表适用于两个因素的问题,三个或三个以上因素的问题只
能用树状图.根据列表法或者树状图分析出所有可能的结果,然后根据概率公式求出结果即可.
【详解】解:列表如下:
甲 乙 丙 丁
(甲,
甲 (甲,丙) (甲,丁)
乙)
乙 (乙,甲) (乙,丙) (乙,丁)
(丙,
丙 (丙,甲) (丙,丁)
乙)
(丁,
丁 (丁,甲) (丁,丙)
乙)
由列表可知,共有12种等可能的结果,其中甲、乙两名同学同时被选中的情况有2种,则甲、乙两名同学
同时被选中的概率是 .
故选:A.
5. 如图,四边形 是 的内接四边形, 是 的直径,若 ,则 的度数
为( )
A. B. C. D.
【答案】B
【解析】
【分析】此题考查了圆周角定理、圆内接四边形的性质,连接 ,由 是 的直径得到 ,
3根据圆周角定理得到 ,得到 ,再由圆内接四边形对角
互补得到答案.
【详解】解:如图,连接 ,
∵ 是 的直径,
∴ ,
∵ ,
∴
∴
∵四边形 是 的内接四边形,
∴ ,
故选:B
6. 一种药品原价每盒48元,经过两次降价后每盒27元,两次降价的百分率相同,则每次降价的百分率为
( )
A. B. C. D.
【答案】C
【解析】
【分析】本题考查一元二次方程的实际应用,设每次降价的百分率为 ,根据原价每盒48元,经过两次降
价后每盒27元,列出方程进行求解即可.
【详解】解:设每次降价的百分率为 ,由题意,得:
,
4解得: (舍去);
故选C.
7. 如图是由一些同样大小的三角形按照一定规律所组成的图形,第1个图有4个三角形.第2个图有7个
三角形,第3个图有10个三角形……按照此规律排列下去,第674个图中三角形的个数是( )
A. 2022 B. 2023 C. 2024 D. 2025
【答案】B
【解析】
【分析】此题考查了图形的变化规律,解题的关键是根据图形的排列,归纳出图形的变化规律.根据前几
个图形的变化发现规律,可用含n的代数式表示出第n个图形中三角形的个数,从而可求第674个图形中
三角形的个数.
【详解】解:第1个图案有4个三角形,即 ,
第2个图案有7个三角形,即 ,
第3个图案有10个三角形,即 ,
…,
按此规律摆下去,第n个图案有 个三角形,
则第674个图案中三角形的个数为: (个).
故选:B.
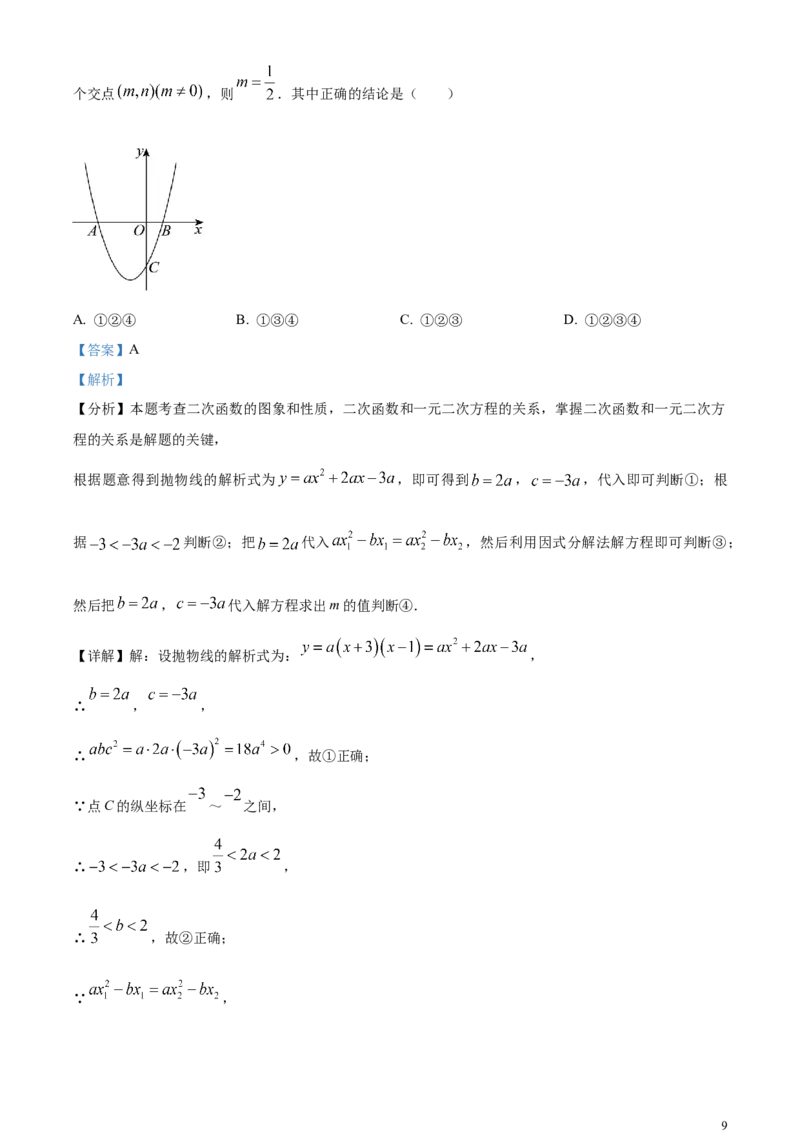
8. 矩形 在平面直角坐标系中的位置如图所示,反比例函数 的图象与 边交于点D,与
边交于点F,与 交于点E, ,若四边形 的面积为2,则k的值是( )
5A. B. C. D.
【答案】D
【解析】
【分析】本题考查了矩形的性质、三角形面积的计算、反比例函数的图象和性质、相似三角形的判定和性
质;熟练掌握矩形的性质和反比例函数的性质是解决问题的关键.
过点E作 ,则 ,设 ,由 ,可得 ,
再由 ,列方程,即可得出k的值.
【详解】过点E作 ,则 ,
∴ ,
∴
设 ,
∵
6∴ ,
∴
∴
即 ,解得:
故选D
9. 小明同学手中有一张矩形纸片 , , ,他进行了如下操作:
第一步,如图①,将矩形纸片对折,使 与 重合,得到折痕 ,将纸片展平.
第二步,如图②,再一次折叠纸片,把 沿 折叠得到 , 交折痕 于点E,则线
段 的长为( )
A. B. C. D.
【答案】B
【解析】
【分析】本题考查了矩形与折叠问题,熟练掌握矩形的性质,折叠的性质,勾股定理是解题的关键.
根据矩形的性质和折叠的性质推出 ,进而得出 ,设 ,则
,根据勾股定理可得: ,列出方程求解即可.
7【详解】解:∵四边形 是矩形,
∴ ,
由折叠可得: , , , ,
∴四边形 是矩形,
∴ ,
∴ ,
∴ ,
∴ ,
设 ,则 ,
在 中,根据勾股定理可得: ,
即 ,
解得: ,
即 ,
故选:B.
10. 在平面直角坐标系中,抛物线 与x轴交于A、B两点, ,与y
轴交点C的纵坐标在 ~ 之间,根据图象判断以下结论:① ;② ;③若
且 ,则 ;④直线 与抛物线 的一
8个交点 ,则 .其中正确的结论是( )
A. ①②④ B. ①③④ C. ①②③ D. ①②③④
【答案】A
【解析】
【分析】本题考查二次函数的图象和性质,二次函数和一元二次方程的关系,掌握二次函数和一元二次方
程的关系是解题的关键,
根据题意得到抛物线的解析式为 ,即可得到 , ,代入即可判断①;根
据 判断②;把 代入 ,然后利用因式分解法解方程即可判断③;
然后把 , 代入解方程求出m的值判断④.
【详解】解:设抛物线的解析式为: ,
∴ , ,
∴ ,故①正确;
∵点C的纵坐标在 ~ 之间,
∴ ,即 ,
∴ ,故②正确;
∵ ,
9∴ ,即 ,
∴ ,
又∵ ,
∴ ,故③错误;
∵令 相等,则
∴ ,解得 (舍), ,
∴ ,故④正确;
故选A.
二、填空题(本题8个小题,每小题3分,共24分)
11. 函数 中,自变量x的取值范围是______________.
【答案】x≥-3且x≠0
【解析】
【分析】根据二次根式的性质和分式的意义,被开方数大于等于0,分母不等于0列不等式组求解.
【详解】解:根据题意得:x+3≥0且x≠0,
解得x≥-3且x≠0.
故答案为:x≥-3且x≠0.
【点睛】本题考查了函数自变量的取值范围.考查的知识点为:分式有意义,分母不为0,二次根式有意
义,被开方数是非负数.
12. 如图, 中,D是 上一点, ,D、E、F三点共线,请添加一个条件______,使得
.(只添一种情况即可)
10【答案】 或 (答案不唯一)
【解析】
【分析】本题考查全等三角形的判定和性质,解答本题的关键是明确题意,利用全等三角形的判定解答.
根据题目中的条件和全等三角形的判定,可以写出添加的条件,注意本题答案不唯一.
【详解】解:∵
∴ , ,
∴添加条件 ,可以使得 ,
添加条件 ,也可以使得 ,
∴ ;
故答案为: 或 (答案不唯一).
13. 将抛物线 向下平移5个单位长度后,经过点 ,则 ______.
【答案】2
【解析】
【分析】此题考查了二次函数的平移,根据平移规律得到函数解析式,把点的坐标代入得到 ,
再整体代入变形后代数式即可.
【
详解】解:抛物线 向下平移5个单位长度后得到 ,
把点 代入得到, ,
得到 ,
∴ ,
故答案为:2
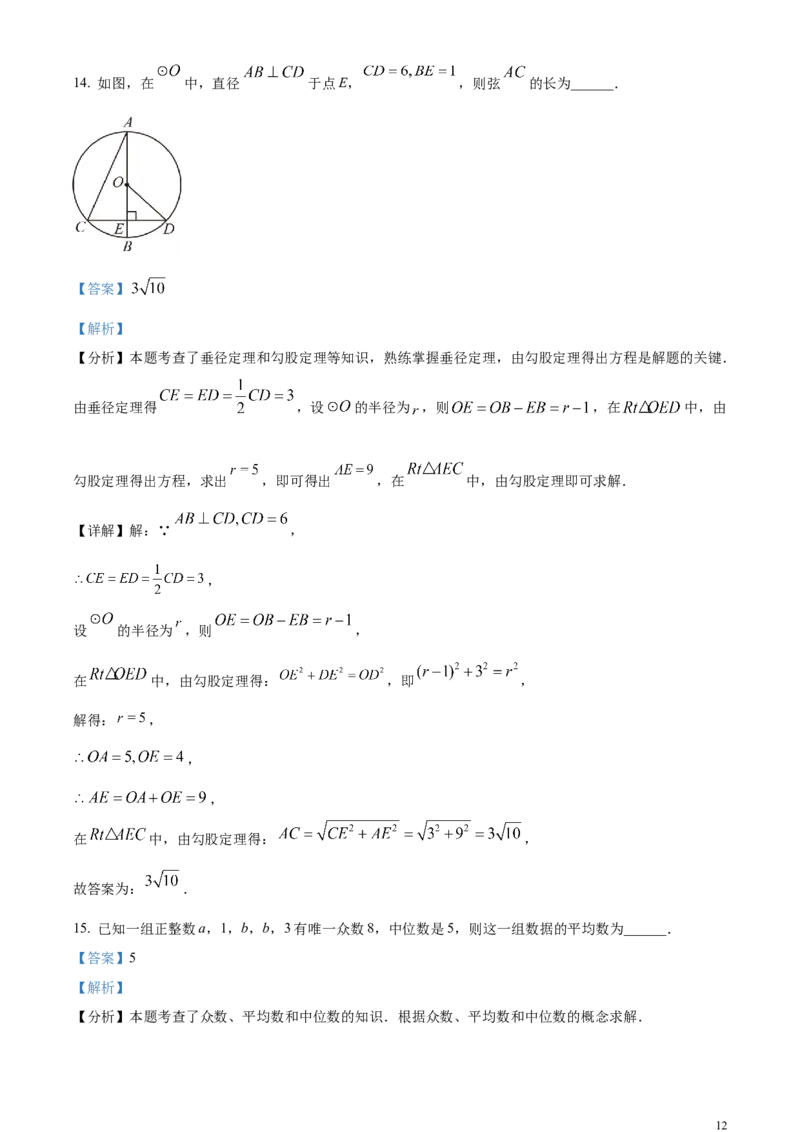
1114. 如图,在 中,直径 于点E, ,则弦 的长为______.
【答案】
【解析】
【分析】本题考查了垂径定理和勾股定理等知识,熟练掌握垂径定理,由勾股定理得出方程是解题的关键.
由垂径定理得 ,设 的半径为 ,则 ,在 中,由
勾股定理得出方程,求出 ,即可得出 ,在 中,由勾股定理即可求解.
【详解】解:∵ ,
,
设 的半径为 ,则 ,
在 中,由勾股定理得: ,即 ,
解得: ,
,
,
在 中,由勾股定理得: ,
故答案为: .
15. 已知一组正整数a,1,b,b,3有唯一众数8,中位数是5,则这一组数据的平均数为______.
【答案】5
【解析】
【分析】本题考查了众数、平均数和中位数的知识.根据众数、平均数和中位数的概念求解.
12【详解】解:∵这组数据有唯一众数8,
为
∴b 8,
∵中位数是5,
∴a是5,
∴这一组数据的平均数为 ,
故答案为:5.
16. 若分式方程 的解为正整数,则整数m的值为______.
【答案】
【解析】
【分析】此题考查了分式方程的解,方程的解即为能使方程左右两边相等的未知数的值.
表示出方程的解,由解是正整数,确定出整数 的值即可.
【详解】解: ,
化简得: ,
去分母得: ,
移项合并得: ,
解得: ,
由方程的解是正整数,得到 为正整数,即 或 ,
解得: 或 (舍去,会使得分式无意义).
故答案为: .
17. 矩形 的面积是90,对角线 交于点O,点E是 边的三等分点,连接 ,点P是
的中点, ,连接 ,则 的值为______.
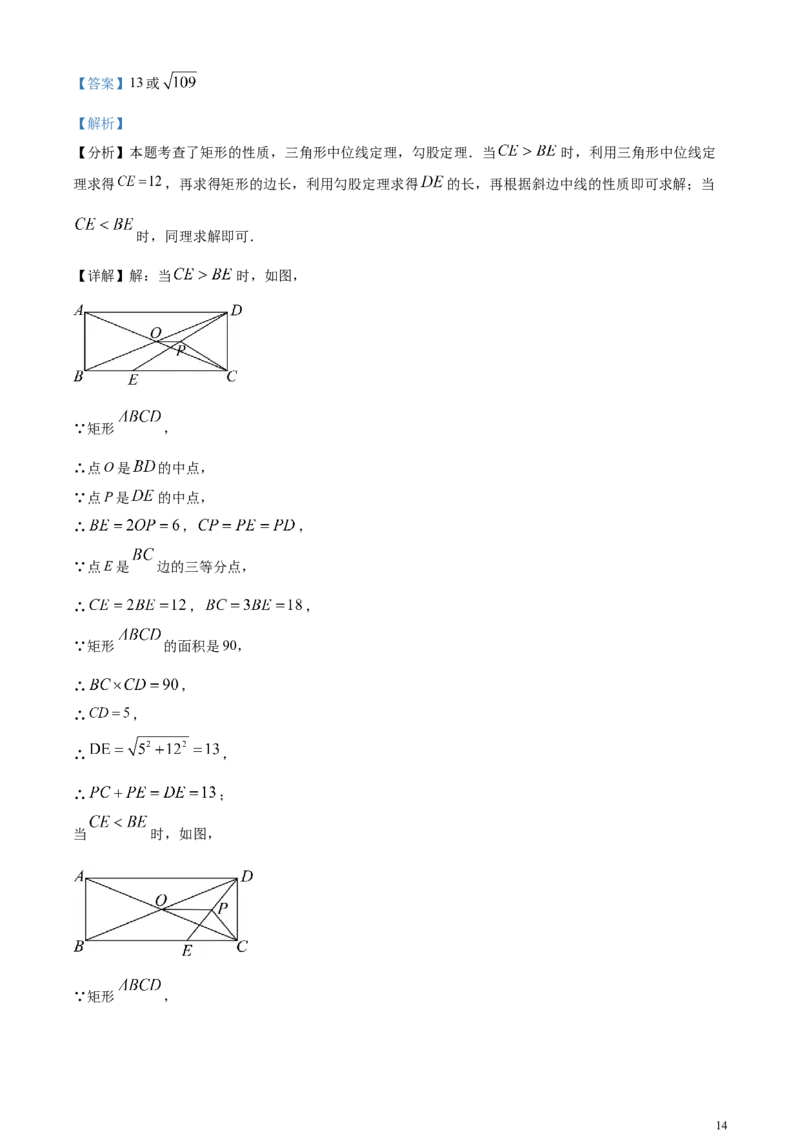
13【答案】13或
【解析】
【分析】本题考查了矩形的性质,三角形中位线定理,勾股定理.当 时,利用三角形中位线定
理求得 ,再求得矩形的边长,利用勾股定理求得 的长,再根据斜边中线的性质即可求解;当
时,同理求解即可.
【详解】解:当 时,如图,
∵矩形 ,
∴点O是 的中点,
∵点P是 的中点,
∴ , ,
∵点E是 边的三等分点,
∴ , ,
∵矩形 的面积是90,
∴ ,
∴ ,
∴ ,
∴ ;
当 时,如图,
∵矩形 ,
14∴点O是 的中点,
∵点P是 的中点,
∴ , ,
∵点E是 边的三等分点,
∴ , ,
∵矩形 的面积是90,
∴ ,
∴ ,
∴ ,
∴ ;
故答案为:13或 .
18. 如图,在正方形 中,E是 延长线上一点, 分别交 于点F、M,过点F作
,分别交 、 于点N、P,连接 .下列四个结论:① ;②
;③若P是 中点, ,则 ;④ ;⑤若
,则 .其中正确的结论是______.
【答案】①②③⑤
【解析】
【分析】如图1,作 于 ,则四边形 是矩形,证明 ,则
15,可判断①的正误;如图2,作 交 于 ,连接 ,证明
,则 , ,由
, ,可得 ,
, ,证明 ,则 ,由勾股定理得,
,由 ,可得 ,可判断
②的正误;如图3,连接 ,由勾股定理得, ,
,可求 ,设 ,则 , ,由
勾股定理得, ,由 ,可得
,整理得, ,可求满足要求的解为 ,则 ,
,由 ,可得 ,可求 ,可判断③的正误;由题意知,
, 不相似, ,可判断④的正误;由设 ,
, ,则 , , ,
16,证明 ,则 ,证明 ,则
,即 ,可求 ,同理, ,则 ,即 ,
同理, ,则 ,即 ,可得 ,将 代入
得, ,整理得, ,可得, ,则
,可判断⑤的正误.
【详解】解:∵正方形 ,
∴ , ,
,
如图1,作 于 ,则四边形 是矩形,
∴ ,
∵ ,
∴ ,
又∵ , ,
∴ ,
∴ ,①正确,故符合要求;
17如图2,作 交 于 ,连接 ,
∴ ,
∴ ,
∵ , , ,
∴ ,
∴ , ,
∵ , ,
∴ ,
∴ ,
∴ ,
∴ ,即 ,
∵ ,
∴ ,
∵ , , ,
∴ ,
∴ ,
由勾股定理得, ,
∵ ,
∴ ,②正确,故符合要求;
∵P是 中点, ,
∴ ,
18如图3,连接 ,
由勾股定理得, , ,
解得, ,
设 ,则 , ,
由勾股定理得, ,
∵ ,
∴ ,整理得, ,
解得, 或 (舍去),
∴ , ,
∵ ,
∴ ,
解得, ,③正确,故符合要求;
由题意知, ,
∴ 不相似, ,④错误,故不符合要求;
19∵ ,
∴ , ,
设 , , ,则 , , ,
,
∵ ,
∴ ,
∴ ,
∵ , ,
∴ ,
∴ ,即 ,
解得, ,
同理, ,
∴ ,即 ,
同理, ,
∴ ,即 ,
∴ ,
将 代入 得, ,整理得, ,
解得, ,
20∴ ,⑤正确,故符合要求;
故答案为:①②③⑤.
【点睛】本题考查了正方形的性质,全等三角形的判定与性质,等角对等边,勾股定理,正弦,余弦,相
似三角形的判定与性质.熟练掌握正方形的性质,全等三角形的判定与性质,等角对等边,勾股定理,正
弦,余弦,相似三角形的判定与性质是解题的关键.
三、解答题(共66分)
19. 先化简,再求值: ,并从 ,0,1,2,3中选一个合适的数代入求值.
【答案】 ,取 ,原式
【解析】
【分析】本题考查了分式的化简求值,熟练掌握分式的运算法则是解题关键.
先计算括号内 的减法,再计算除法,然后根据分式有意义的条件选取合适的值代入计算即可得.
【详解】解:
.
且 ,
或 或 .
当 时,原式 .
21或当 时,原式 .
或当 时,原式 .
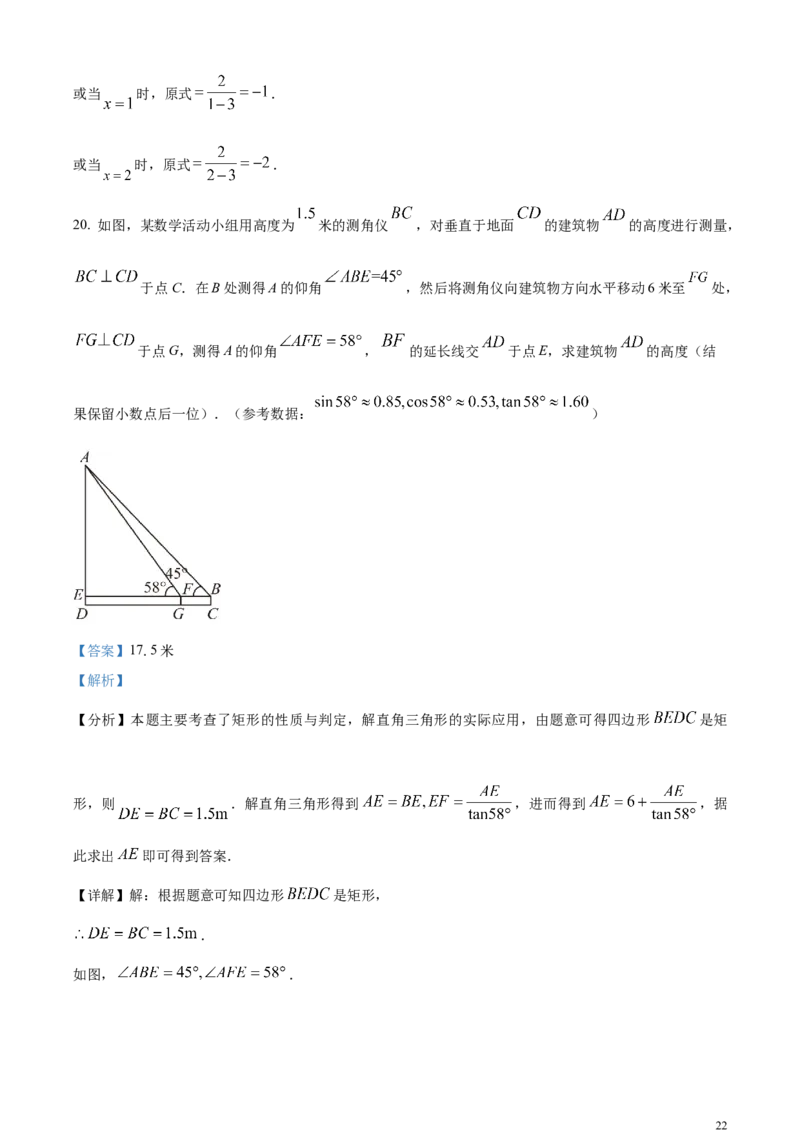
20. 如图,某数学活动小组用高度为 米的测角仪 ,对垂直于地面 的建筑物 的高度进行测量,
于点C.在B处测得A的仰角 ,然后将测角仪向建筑物方向水平移动6米至 处,
于点G,测得A的仰角 , 的延长线交 于点E,求建筑物 的高度(结
果保留小数点后一位).(参考数据: )
【答案】17.5米
【解析】
【分析】本题主要考查了矩形的性质与判定,解直角三角形的实际应用,由题意可得四边形 是矩
形,则 .解直角三角形得到 ,进而得到 ,据
此求出 即可得到答案.
【详解】解:根据题意可知四边形 是矩形,
.
如图, .
22,
.
,
.
(米)
答:建筑物 的高度约为 米.
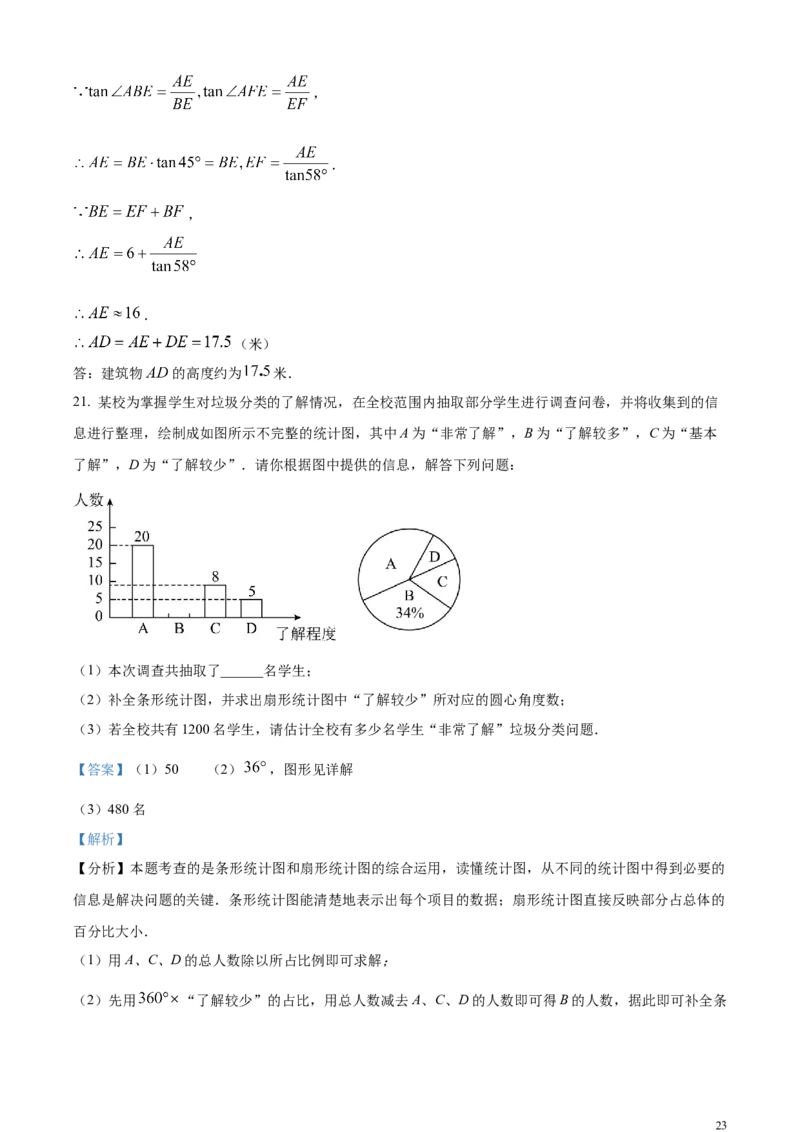
21. 某校为掌握学生对垃圾分类的了解情况,在全校范围内抽取部分学生进行调查问卷,并将收集到的信
息进行整理,绘制成如图所示不完整的统计图,其中A为“非常了解”,B为“了解较多”,C为“基本
了解”,D为“了解较少”.请你根据图中提供的信息,解答下列问题:
(1)本次调查共抽取了______名学生;
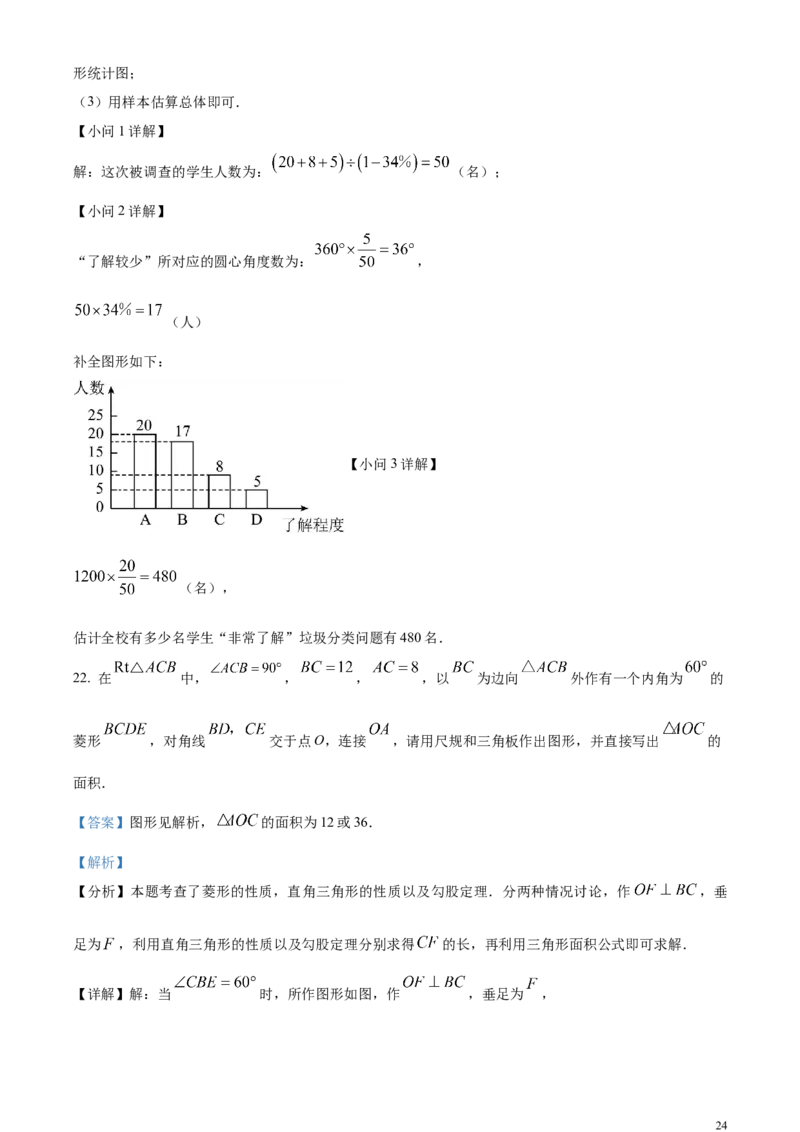
(2)补全条形统计图,并求出扇形统计图中“了解较少”所对应的圆心角度数;
(3)若全校共有1200名学生,请估计全校有多少名学生“非常了解”垃圾分类问题.
【答案】(1)50 (2) ,图形见详解
(3)480名
【解析】
【分析】本题考查的是条形统计图和扇形统计图的综合运用,读懂统计图,从不同的统计图中得到必要的
信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据;扇形统计图直接反映部分占总体的
百分比大小.
(1)用A、C、D的总人数除以所占比例即可求解;
(2)先用 “了解较少”的占比,用总人数减去A、C、D的人数即可得B的人数,据此即可补全条
23形统计图;
(3)用样本估算总体即可.
【小问1详解】
解:这次被调查的学生人数为: (名);
【小问2详解】
“了解较少”所对应的圆心角度数为: ,
(人)
补全图形如下:
【小问3详解】
(名),
估计全校有多少名学生“非常了解”垃圾分类问题有480名.
22. 在 中, , , ,以 为边向 外作有一个内角为 的
菱形 ,对角线 交于点O,连接 ,请用尺规和三角板作出图形,并直接写出 的
面积.
【答案】图形见解析, 的面积为12或36.
【解析】
【分析】本题考查了菱形的性质,直角三角形的性质以及勾股定理.分两种情况讨论,作 ,垂
足为 ,利用直角三角形的性质以及勾股定理分别求得 的长,再利用三角形面积公式即可求解.
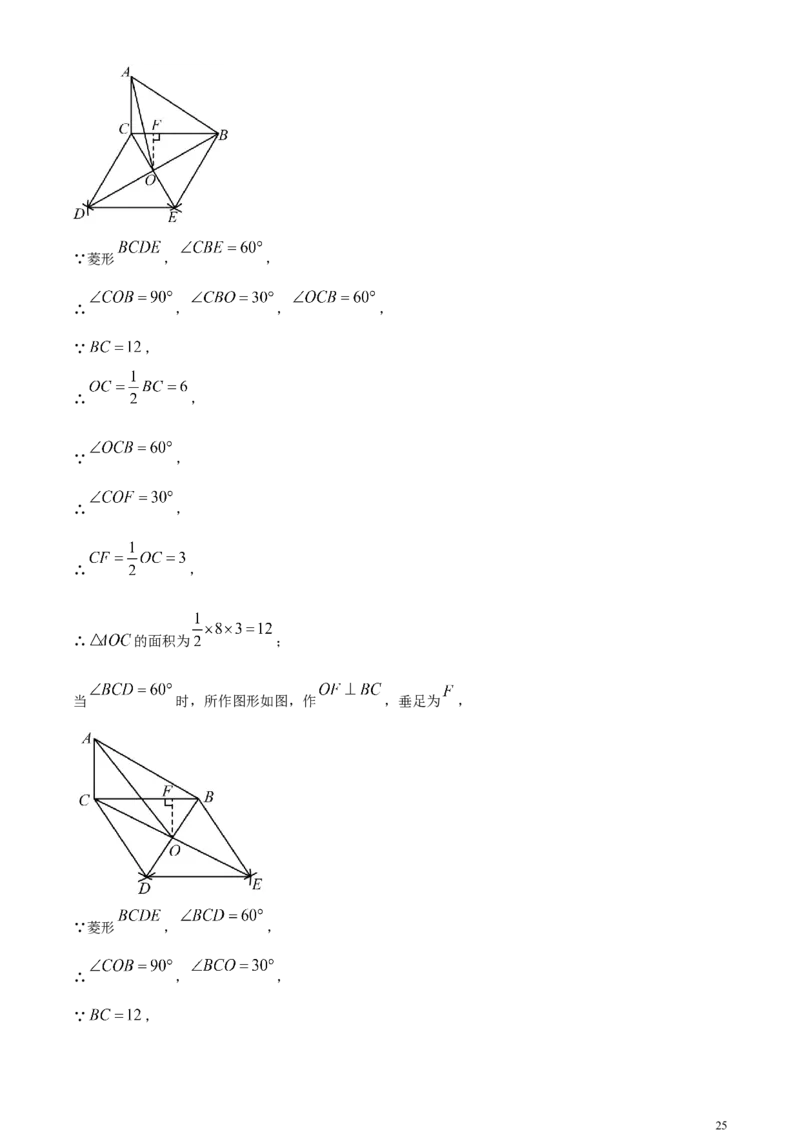
【详解】解:当 时,所作图形如图,作 ,垂足为 ,
24∵菱形 , ,
∴ , , ,
∵ ,
∴ ,
∵ ,
∴ ,
∴ ,
∴ 的面积为 ;
当 时,所作图形如图,作 ,垂足为 ,
∵菱形 , ,
∴ , ,
∵ ,
25∴ , ,
∴ , ,
∴ 的面积为 ;
综上, 的面积为12或36.
23. 如图,二次函数 的图象与x轴交于A、B两点,与y轴交于点C,点A的坐标为
,点C的坐标为 ,连接 .
(1)求该二次函数的解析式;
(2)点P是抛物线在第四象限图象上的任意一点,当 的面积最大时, 边上的高 的值为
______.
【答案】(1)
(2)
【解析】
【分析】本题考查待定系数法求函数解析式,二次函数与图形的面积,掌握待定系数法是解题的关键.
(1)直接利用待定系数法求函数解析式即可;
26(2)先求出直线 的解析式,然后过点 P 作 轴交 于点 D,设点 P 的坐标为
,则点D的坐标为 ,根据 求出面积的最大值,然后求
高 即可.
【小问1详解】
解:把 和 代入得:
,解得 ,
∴二次函数的解析式为 ;
【小问2详解】
解:令 ,则 ,解得: , ,
∴点B的坐标为 ,
∴ ,
设直线 的解析式为 ,代入得:
,解得 ,
∴直线 的解析式为 ,
过点P作 轴交 于点D,
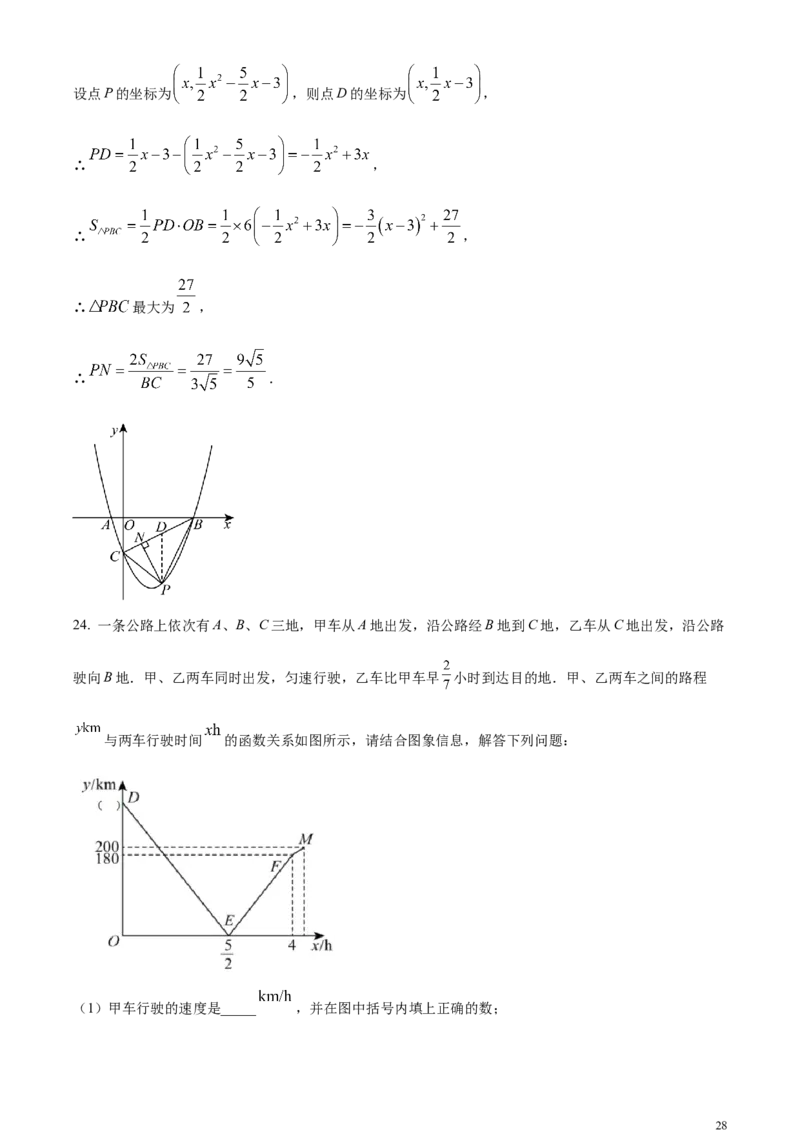
27设点P的坐标为 ,则点D的坐标为 ,
∴ ,
∴ ,
∴ 最大为 ,
∴ .
24. 一条公路上依次有A、B、C三地,甲车从A地出发,沿公路经B地到C地,乙车从C地出发,沿公路
驶向B地.甲、乙两车同时出发,匀速行驶,乙车比甲车早 小时到达目的地.甲、乙两车之间的路程
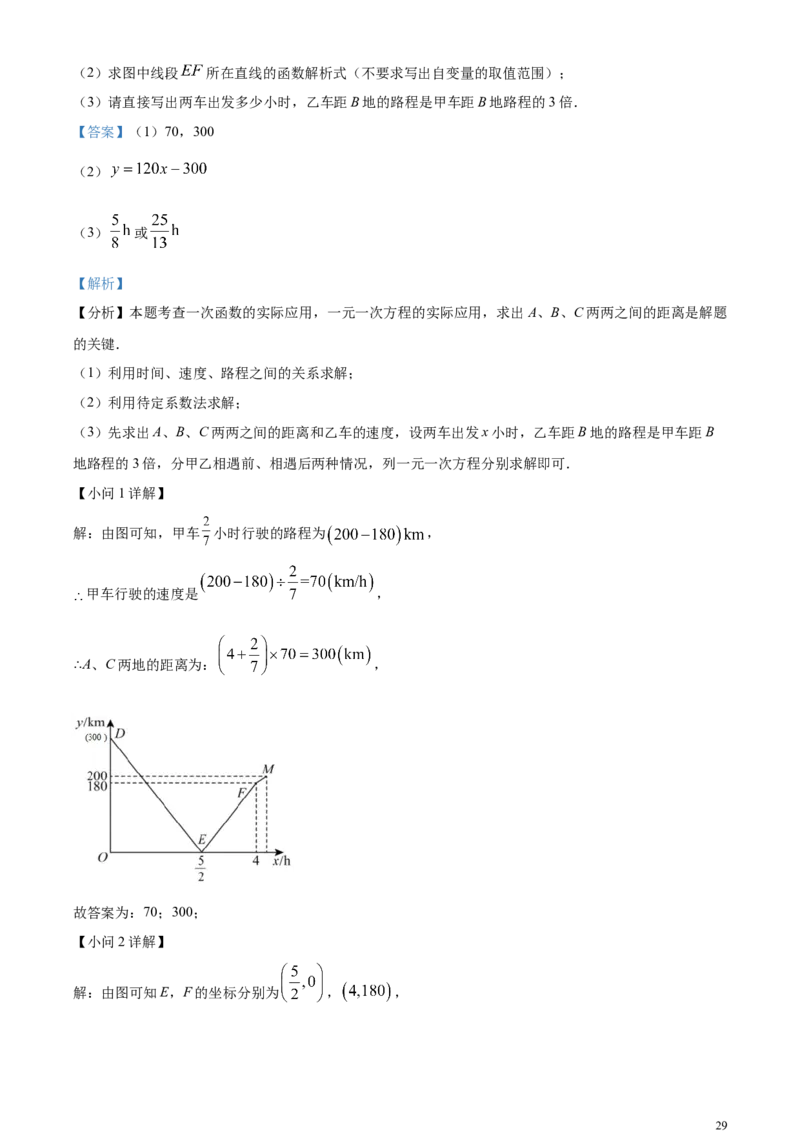
与两车行驶时间 的函数关系如图所示,请结合图象信息,解答下列问题:
(1)甲车行驶的速度是_____ ,并在图中括号内填上正确的数;
28(2)求图中线段 所在直线的函数解析式(不要求写出自变量的取值范围);
(3)请直接写出两车出发多少小时,乙车距B地的路程是甲车距B地路程的3倍.
【答案】(1)70,300
(2)
(3) 或
【解析】
【分析】本题考查一次函数的实际应用,一元一次方程的实际应用,求出A、B、C两两之间的距离是解题
的关键.
(1)利用时间、速度、路程之间的关系求解;
(2)利用待定系数法求解;
(3)先求出A、B、C两两之间的距离和乙车的速度,设两车出发x小时,乙车距B地的路程是甲车距B
地路程的3倍,分甲乙相遇前、相遇后两种情况,列一元一次方程分别求解即可.
【小问1详解】
解:由图可知,甲车 小时行驶的路程为 ,
甲车行驶的速度是 ,
∴A、C两地的距离为: ,
故答案为:70;300;
【小问2详解】
解:由图可知E,F的坐标分别为 , ,
29设线段 所在直线的函数解析式为 ,
则 ,
解得 ,
线段 所在直线的函数解析式为 ;
【小问3详解】
解:由题意知,A、C两地的距离为: ,
乙车行驶的速度为: ,
C、B两地的距离为: ,
A、B两地的距离为: ,
设两车出发x小时,乙车距B地的路程是甲车距B地路程的3倍,
分两种情况,当甲乙相遇前时:
,
解得 ;
当甲乙相遇后时:
,
解得 ;
综上可知,两车出发 或 时,乙车距B地的路程是甲车距B地路程的3倍.
3025. 数学老师在课堂上给出了一个问题,让同学们探究.在 中, ,
点D在直线 上,将线段 绕点A顺时针旋转 得到线段 ,过点E作 ,交直线
于点F.
(1)当点D在线段 上时,如图①,求证: ;
分析问题:某同学在思考这道题时,想利用 构造全等三角形,便尝试着在 上截取
,连接 ,通过证明两个三角形全等,最终证出结论:
推理证明:写出图①的证明过程:
探究问题:
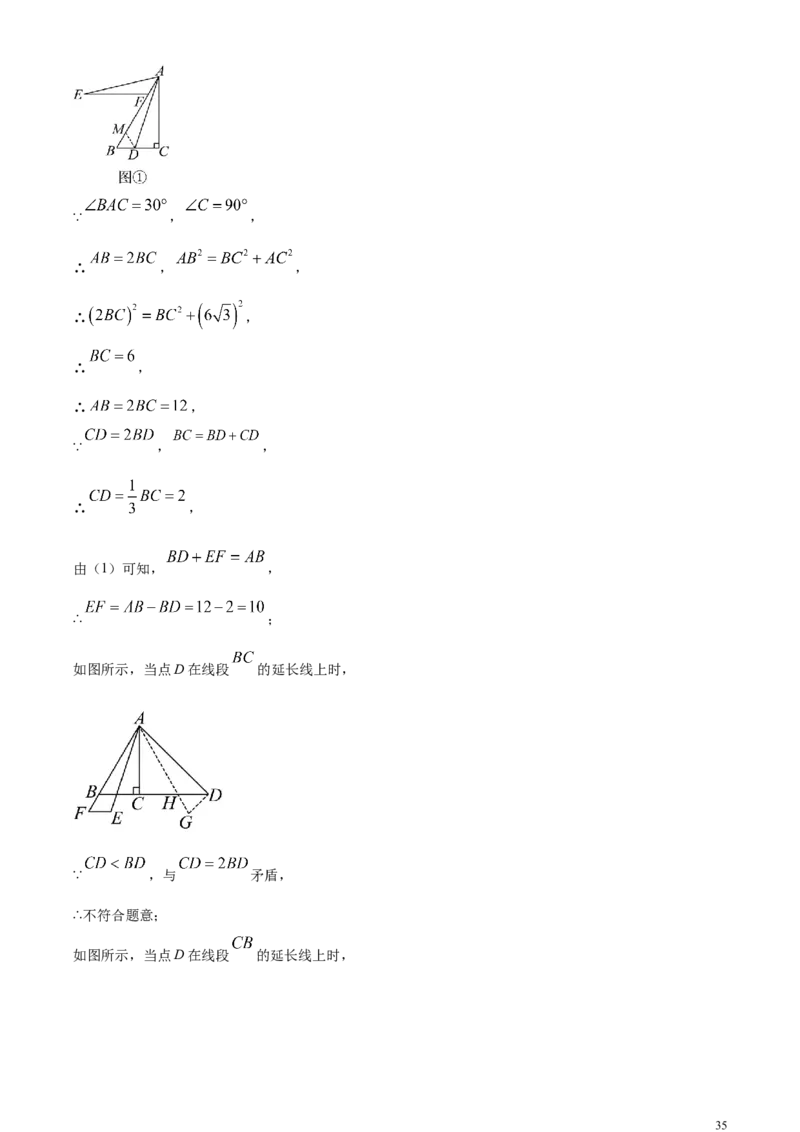
(2)当点D在线段 的延长线上时,如图②:当点D在线段 的延长线上时,如图③,请判断并直
接写出线段 , , 之间的数量关系;
拓展思考:
(3)在(1)(2)的条件下,若 , ,则 ______.
【答案】(1)见解析;(2)图②: ,图③: ;(3)10或18
【解析】
【分析】(1)在 边上截取 ,连接 ,根据题意证明出 ,得到
,然后证明出 是等边三角形,得到 ,进而求解即可;
(2)图②:在 上取点H,使 ,连接 并延长到点G使 ,连接 ,首先证明
出 是等边三角形,得到 ,然后求出 ,然后证明出
,得到 , ,然后证明出 是等边三角形,得到
31,进而求解即可;
图③:在 上取点H使 ,同理证明出 ,得到 , ,
进而求解即可;
(3)根据勾股定理和含 角直角三角形的性质求出 , ,然后结合 ,分别
(1)(2)的条件下求出 的长度,进而求解即可.
【详解】(1)证明:在 边上截取 ,连接 .
在 中, .
,
.
又 ,
.
又 , ,
.
又 ,
.
.
.
.
,
.
是等边三角形.
,
,
;
的
(2)图②:当点D在线段 延长线上时, ,证明如下:
如图所示,在 上取点H,使 ,连接 并延长到点G使 ,连接 ,
32∵ ,
∴ 是等边三角形,
∴ ,
∵线段 绕点A顺时针旋转 得到线段 ,
∴ , ,
∴ ,
∴ ,即 ,
又∵ ,
∴ ,
∴ , ,
∵ ,
∴ ,
∵ ,
∴ 是等边三角形,
∴ ,
∴ ;
图③:当点D在线段 的延长线上时, ,证明如下∶
如图所示,在 上取点H使 ,
33∵ ,
∴ ,
∵ ,
∴ 是等边三角形,
∴ ,
∴ ,
∵将线段 绕点A顺时针旋转 得到线段 ,
∴ , ,
∴ ,
∵ ,
∴ ,
∵ ,
又∵ ,
∴ ,
∴ , ,
∵ ,
∴ ,
∴ ;
(3)如图所示,
34∵ , ,
∴ , ,
∴ ,
∴ ,
∴ ,
∵ , ,
∴ ,
由(1)可知, ,
∴ ;
如图所示,当点D在线段 的延长线上时,
∵ ,与 矛盾,
∴不符合题意;
如图所示,当点D在线段 的延长线上时,
35∵ , ,
∴ ,
由(2)可知, ,
∵ ,
∴ .
综上所述, 或18.
【点睛】此题考查了全等三角形的性质和判定,勾股定理,等边三角形的性质和判定,含 角直角三角
形的性质,解题的关键是掌握以上知识点.
26. 牡丹江某县市作为猴头菇生产的“黄金地带”,年总产量占全国总产量的 以上,黑龙江省发布的
“九珍十八品”名录将猴头菇列为首位.某商店准备在该地购进特级鲜品、特级干品两种猴头菇,购进鲜
品猴头菇3箱、干品猴头菇2箱需420元,购进鲜品猴头菇4箱、干品猴头菇5箱需910元.请解答下列问
题:
(1)特级鲜品猴头菇和特级干品猴头菇每箱的进价各是多少元?
(2)某商店计划同时购进特级鲜品猴头菇和特级干品猴头菇共80箱,特级鲜品猴头菇每箱售价定为50元,
特级干品猴头菇每箱售价定为180元,全部销售后,获利不少于1560元,其中干品猴头菇不多于40箱,
该商店有哪几种进货方案?
(3)在(2)的条件下,购进猴头菇全部售出,其中两种猴头菇各有1箱样品打a(a为正整数)折售出,
最终获利1577元,请直接写出商店的进货方案.
【答案】(1)特级鲜品猴头菇每箱进价为40元,特级干品猴头菇每箱进价为150元
(2)有3种方案,详见解析
(3)特级干品猴头菇40箱,特级鲜品猴头菇40箱
【解析】
【分析】本题考查了二元一次方程组的应用、一元一次不等式组的应用以及一元一次方程的应用,解题的
36关键是:(1)找准等量关系,正确列出二元一次方程组;(2)根据各数量之间的关系,正确列出一元一
次不等式组;(3)正确计算求解.
(1)设特级鲜品猴头菇和特级干品猴头菇每箱的进价分别是x元和y元,根据“购进鲜品猴头菇3箱、干
品猴头菇2箱需420元,购进鲜品猴头菇4箱、干品猴头菇5箱需910元”,列出方程组求解即可;
(2)设商店计划购进特级鲜品猴头菇m箱,则购进特级干品猴头菇 箱,根据“获利不少于1560
元,其中干品猴头菇不多于40箱,”列出不等式组求解即可;
(3)根据(2)中三种方案分别求解即可;
【小问1详解】
解:设特级鲜品猴头菇和特级干品猴头菇每箱的进价分别是x元和y元,
则 ,
解得: ,
故特级鲜品猴头菇每箱进价为40元,特级干品猴头菇每箱进价为150元;
【小问2详解】
解:设商店计划购进特级鲜品猴头菇m箱,则购进特级干品猴头菇 箱,
则 ,
解得: ,
∵ 为正整数,
∴ ,
故该商店有三种进货方案,
分别为:①购进特级鲜品猴头菇40箱,则购进特级干品猴头菇40箱;
②购进特级鲜品猴头菇41箱,则购进特级干品猴头菇39箱;
③购进特级鲜品猴头菇42箱,则购进特级干品猴头菇38箱;
【小问3详解】
解:当购进特级鲜品猴头菇40箱,则购进特级干品猴头菇40箱时:
37根据题意得 ,
解得: ;
当购进特级鲜品猴头菇41箱,则购进特级干品猴头菇39箱时:
根据题意得 ,
解得: (是小数,不符合要求);
当购进特级鲜品猴头菇42箱,则购进特级干品猴头菇38箱时:
根据题意得 ,
解得: (不符合要求);
故商店的进货方案是特级干品猴头菇40箱,特级鲜品猴头菇40箱.
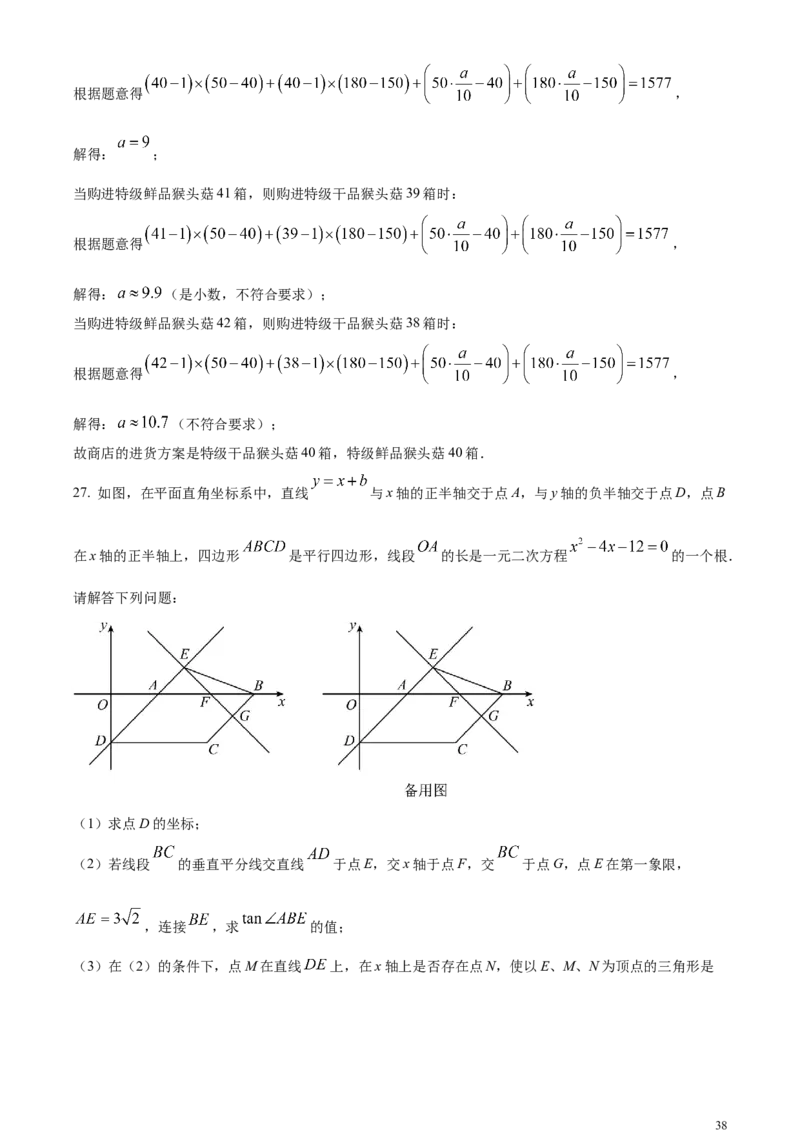
27. 如图,在平面直角坐标系中,直线 与x轴的正半轴交于点A,与y轴的负半轴交于点D,点B
在x轴的正半轴上,四边形 是平行四边形,线段 的长是一元二次方程 的一个根.
请解答下列问题:
(1)求点D的坐标;
(2)若线段 的垂直平分线交直线 于点E,交x轴于点F,交 于点G,点E在第一象限,
,连接 ,求 的值;
(3)在(2)的条件下,点M在直线 上,在x轴上是否存在点N,使以E、M、N为顶点的三角形是
38直角边比为1∶2的直角三角形?若存在,请直接写出 的个数和其中两个点N的坐标;若不存在,
请说明理由.
【答案】(1)
(2)
(3)存在,12个,
【解析】
【分析】(1)先解方程求出 ,然后求出直线解析式即可求得点D的坐标;
(2)过点E作 于点H,求出 ,然后证明 ,即可得到
,然后求出 得正切值即可;
(3)利用分类讨论画出图形,利用勾股定理解题即可.
【小问1详解】
解:解方程 得 , ,
∴ ,即点A的坐标为 ,
把 代入 得 ,
∴ ,点D的坐标为 ;
【小问2详解】
解:过点E作 于点H,
∵ ,
∴ , ,
∴ ,
39又∵ 是平行四边形,
∴ , ,
∵ 是 的垂直平分线,
∴ ,
∵ ,
∴ , ,
∴ ,
∴ ,
∴ ,
∴ ;
【小问3详解】
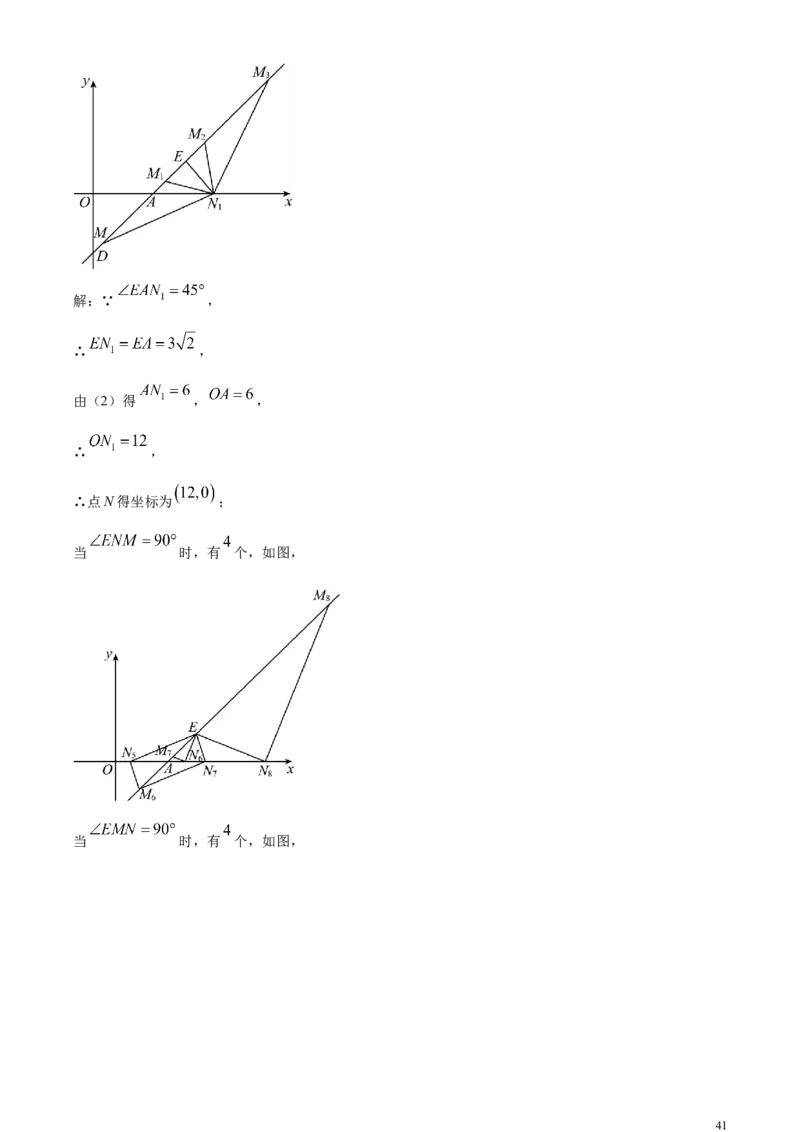
如图,当 时,有 个,
40解:∵ ,
∴ ,
由(2)得 , ,
∴ ,
∴点N得坐标为 ;
当 时,有 个,如图,
当 时,有 个,如图,
41∵ ,
∴ ,
∴ ,
∴点 与O重合,
故点 得坐标为 ,
综上所述,点 的个数为 个,和点N的坐标为 或 .
【点睛】本题考查解一元二次方程,直线的解析式,平行四边形的性质,勾股定理,全等三角形的判定和
性质,解直角三角形等知识,掌握等腰直角三角形的性质是解题的关键.
42