鲁教版物理必修第二册高清教材_4-教培资料-26年最新资料-同步更新_初中高中教资_03科三专项（进去保存报考的学科即可）_02科三专项（笔记真题思维导图教学设计版本二）

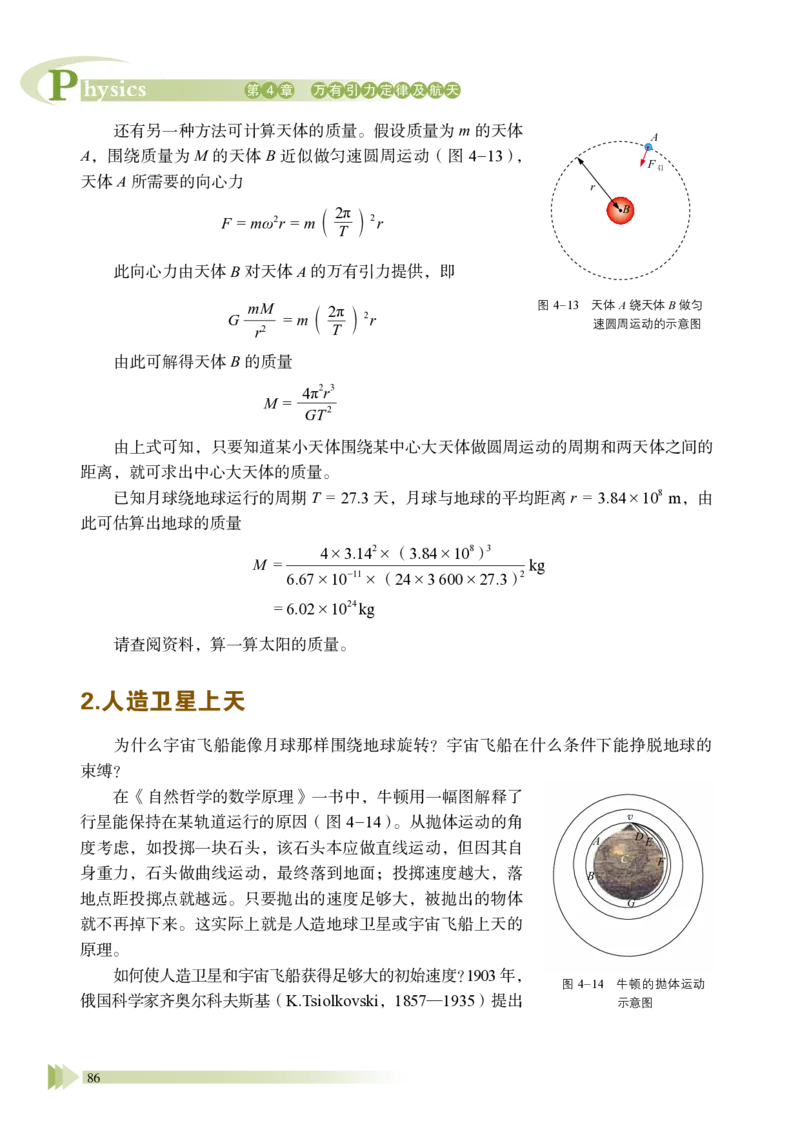
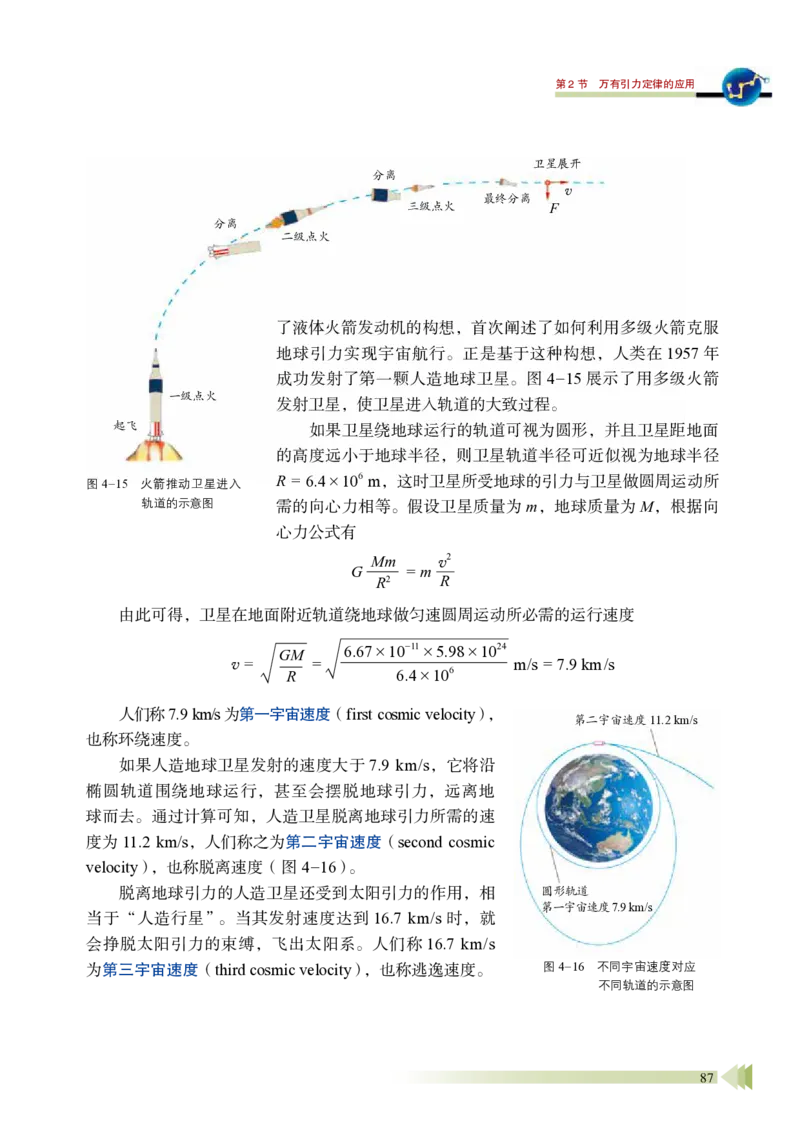
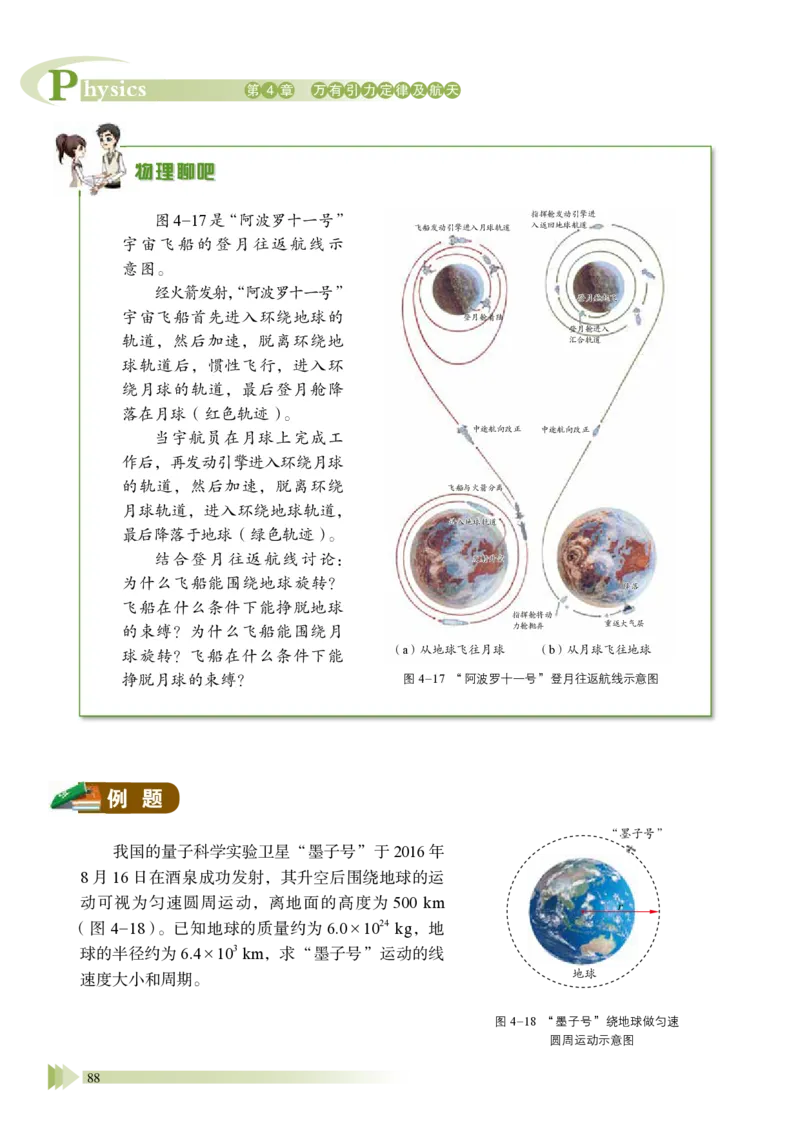
主　　编：廖伯琴 核心编者：林明华　杜明荣　蒋　敏　李洪俊　李太华　廖伯琴 统　　稿：廖伯琴　林明华 定　　稿：廖伯琴 编务联系：李富强　李洪俊 责任编辑：刘大诚　杨文静　刘玉莹 封面设计：孙　佳 版权所有·请勿擅自用本书制作各类出版物·违者必究 如对教材内容有意见、建议或发现印装质量问题，请与山东科学技术出版社联系 电话：0531-82098030　　电子邮箱：sdkjjy@sdcbcm.com 1 目 录 CONTENTS 第1 章　功和机械能 第2 章　抛体运动 第3 章　圆周运动 导　入　神奇之能········································· 2 第1 节　机械功············································ 3 第2 节　功　率············································ 8 第3 节　动能和动能定理 ······························13 第4 节　势能及其改变 ·································18 第5 节　科学验证：机械能守恒定律 ···············23 导　入　更准、更远 ···································· 34 第1 节　运动的合成与分解 ··························· 35 第2 节　平抛运动········································ 40 第3 节　科学探究：平抛运动的特点 ··············· 45 第4 节　生活中的抛体运动 ··························· 48 导　入　生活中的圆周运动 ····························53 第1 节　匀速圆周运动快慢的描述 ···················54 第2 节　科学探究：向心力 ····························60 第3 节　离心现象·········································67 2 第4 章　万有引力定律及航天 第5 章　科学进步无止境 导　入　从嫦娥奔月到“阿波罗”上天 ············78 第1 节　天地力的综合：万有引力定律 ············79 第2 节　万有引力定律的应用 ························85 第3 节　人类对太空的不懈探索 ·····················93 导　入　再次跨越时空的对话 ······················ 102 第1 节　初识相对论 ·································· 103 第2 节　相对论中的神奇时空 ······················ 106 第3 节　探索宇宙的奥秘 ·····························110 1 　 第1 章 导　入　神奇之能 第1 节　机械功 第2 节　功 率 第3 节　动能和动能定理 第4 节　势能及其改变 第5 节　科学验证：机械能守恒定律 能 械 机械 机械 机械 机械 机械 机械 机 和机 和机 和机 功和 功和 功和 功 械 机械 功和 能 械 机 能 械 功和 功 能 和 功 械能 和机 和机 和机械 功 机械能 械能 械能 械 和 械 功 机 和 功和 功和 功和 功和 能 械能 和 能 和 能 械 机 功 能 械能 和 功 械能 机械能 械能 械能 机械能 机械能 机械能 机 功和 功和 功和 功和机 功和机 功和机械 机械 机械 机 本章学业要求 ●能理解功、功率、动能、重力势能及机械 能守恒定律的内涵，定性了解弹性势能； 能用动能定理和机械能守恒定律等分析解 释生产生活中的相关现象，解决一些相关 的实际问题，能体会守恒观念对认识物理 规律的重要性。具有与功和机械能相关的 初步的能量观念。 ——物理观念 ●能在熟悉的问题情境中运用机械能守恒定 律解决问题时建构物理模型，会分析机械 能守恒的条件；能从机械能守恒的角度分 析动力学问题，通过推理，获得结论；能 用与机械能守恒定律等相关的证据说明结 论；能从不同视角解决动力学问题。 ——科学思维 ●能完成“验证机械能守恒定律”等物理实 验。能提出实验中可能出现的物理问题； 能在他人帮助下设计实验方案，获取数 据；能分析数据、验证机械能守恒定律， 能反思实验过程，尝试减小实验误差；能 撰写比较完整的实验报告，在报告中能呈 现实验表格及数据分析过程，能尝试利用 证据进行交流。 ——科学探究 ●通过对机械能守恒定律的验证，能认识科 学规律的建立需要实验证据的检验；有较 强的学习和研究物理的兴趣；能认识机械 能守恒定律对日常生活的影响。 ——科学态度与责任 2 hysics P 第1 章　功和机械能 小小的一颗子弹被抛出 后，人可轻易将其接住。但 是，子弹被高速射出，则可击 穿玻璃、木块甚至石头等。 水能滋润庄稼，也能冲毁 农田。若水被拦蓄在高处，其 能量可以转化为电能，用来取 暖、照明等。 这里面有怎样的奥秘？ 能量，我们既熟悉又陌生。运 动的物体具有动能，被举高的物体 具有势能，物体的动能和势能可 相互转化。这些能量与哪些因素有 关？能量转化遵循怎样的规律？ 通过本章的学习，认识了功和 机械能之间的关系，你就会明白其 中的奥秘。 导　入 神奇之能 水电站泄洪场景 子弹击碎玻璃瞬间 3 第1 节　机械功 用一定的力斜拉购物篮移动时（图1-1），拉力方向 与篮的位移方向有一定的夹角，拉力对篮做功了吗？在初 中物理的基础上，本节我们进一步深化对功的认识，学习 力与位移互成角度时功的计算。 1.机械功的含义 如果施力于某物体，并使该物体在力的方向上移动一段距离，我们就说力对这个物体做 了功。如果作用于某物体的恒力大小为F，该物体沿力的方向运动的位移大小为s，则F 与s 的乘积称为机械功（mechanical work），简称功，用W 表示，其公式为 W = Fs 这个公式只适用于恒力方向与运动方向一致的情况。在生产生活中，我们经常见到类 似斜拉购物篮的情景，这时作用于物体的力与物体的位移成一定夹角。在这个过程中，拉 力做的功是多少呢？我们把斜拉购物篮这类情景转换为物理模型：物体在与水平方向成α 角的恒定拉力F 作用下沿水平方向移动，发生的位移是s，在这个过程中，拉力F 所做的 功是多少？ 如图1-2 所示，可将 F 分解为沿水平方向向 右的分力 F1 和沿竖直方向向上的分力 F2。F1 与物 体位移的方向一致，对物体做了功；F2 与物体位移 的方向垂直，不对物体做功。因此，恒力F 对物 体所做的功 W 就等于分力 F1 所做的功。再结合功 的定义，可得出恒力做功的计算公式 W = Fscos α 第1节 机械功 图1-1　人拉购物篮 图1-2　分析力做功的示意图 F 1 F 2 F s α F α 4 hysics P 第1 章　功和机械能 2.机械功的计算 由功的计算公式可知，当力F 和物体位移s 的大小都一定时，功W 就由F 与s 的夹 角 α 的余弦cos α 决定。 当α = 0°时， cos α = 1， W = Fs，这就是初中物理中作用力与物体位移方向相同的情况。 当α = 90° 时，cos α = 0，W = 0，表示力F 与物体位移的方向垂直时，对物体不做功。 当0° ≤ α < 90° 时，cos α > 0 ，W = Fscos α > 0，表示力F 对物体做正功。 当90° < α ≤ 180° 时， cos α < 0，W = Fscos α < 0，表示力F 对物体做负功，也可说物 体克服这个力做了功。 当 α = 180° 时，cos α = -1， W = -Fs， 表示作用力与物体位移方向相反。例 如，在某些飞机着陆滑跑中，要打开尾 部的减速伞（图1-4）。在这个过程中， 减速伞拉力的方向与飞机位移的方向相 反，对飞机做负功，也可以说飞机克服 这个拉力做了功。 拓展一步 功只有大小没有方向，是标量。在国际单位制中，功的单位是焦耳，用符号J 表示。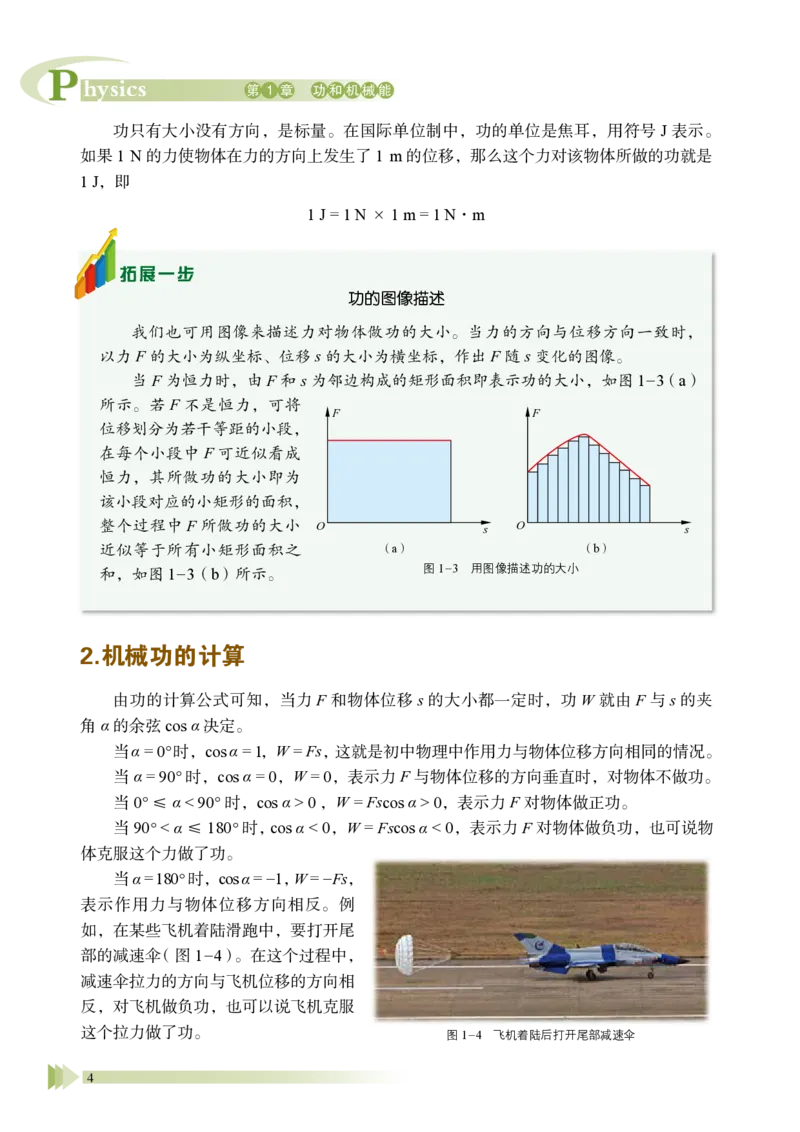 如果1 N 的力使物体在力的方向上发生了1 m 的位移，那么这个力对该物体所做的功就是 1 J，即 1 J = 1 N × 1 m = 1 N·m 功的图像描述 我们也可用图像来描述力对物体做功的大小。当力的方向与位移方向一致时， 以力F 的大小为纵坐标、位移s 的大小为横坐标，作出F 随s 变化的图像。 当F 为恒力时，由F 和s 为邻边构成的矩形面积即表示功的大小，如图1-3（a） 所示。若F 不是恒力，可将 位移划分为若干等距的小段， 在每个小段中F 可近似看成 恒力，其所做功的大小即为 该小段对应的小矩形的面积， 整个过程中F 所做功的大小 近似等于所有小矩形面积之 和，如图1-3（b）所示。 图1-4　飞机着陆后打开尾部减速伞 图1-3　用图像描述功的大小 s s O O F （a） （b） F 5 第1 节　机械功 当物体在多个外力共同作用下运动，求所有外力对物体做的总功时，需要逐个分析 哪些力做功，哪些力不做功，哪些力做正功，哪些力做负功。功是标量，对功的叠加 应采用求代数和的方法。所有外力对物体做的总功，等于各个力分别对物体做功的代数 和，即 W 总= W1 + W2 + W3 + … = F1scos α1 + F2scos α2 + F3scos α3 + … 可以证明，某个物体在多个外力作用下运动时，所有外力对这个物体做的总功，也等 于这些外力的合力对该物体做的功，即 W 总= F合scos α 例 题 一人用平行于斜面的推力把重G = 500 N 的货物从斜面底端推到斜面顶端。已知斜面 的倾角α = 37°，斜面长l = 5 m，斜面与货物间的动摩擦因数 μ = 0.2，推力F = 400 N。求 货物从斜面底端运动到顶端的过程中，所受各力分别对其做的功，以及所有外力对其 做的总功。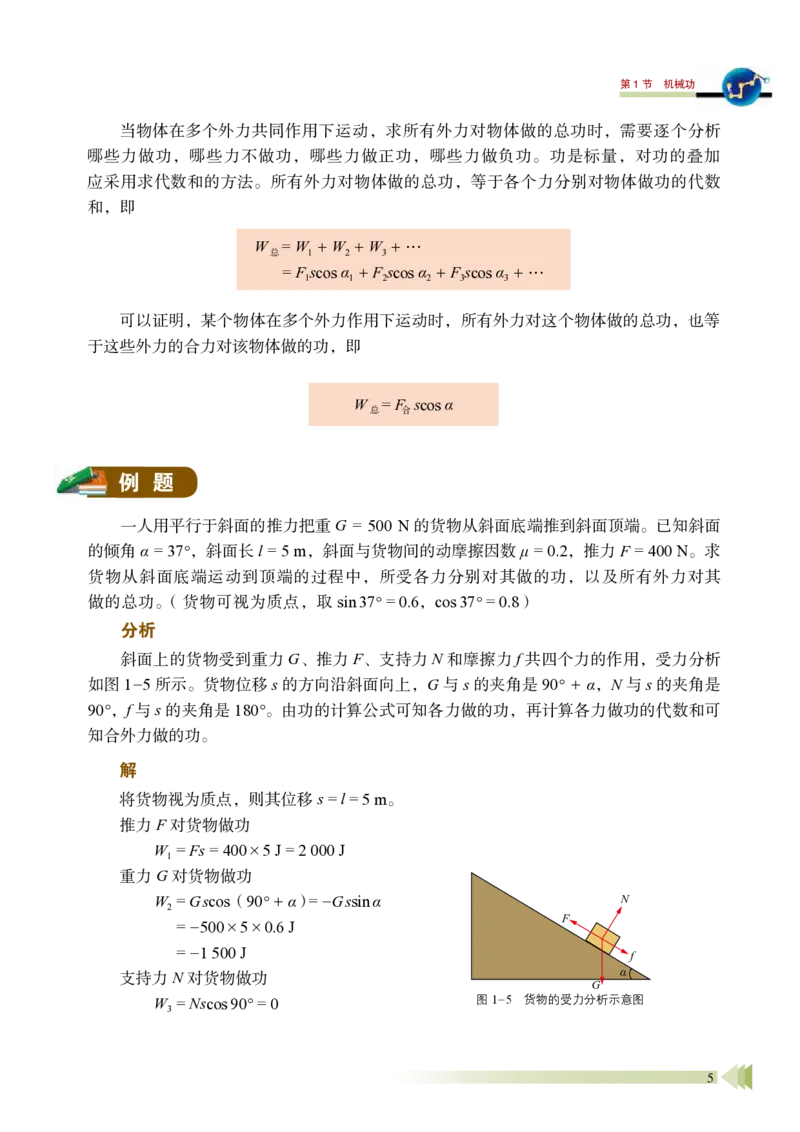（货物可视为质点，取sin 37° = 0.6，cos 37° = 0.8） 分析 斜面上的货物受到重力G、推力F、支持力N 和摩擦力f 共四个力的作用，受力分析 如图1-5 所示。货物位移s 的方向沿斜面向上，G 与s 的夹角是90° + α，N 与s 的夹角是 90°，f 与s 的夹角是180°。由功的计算公式可知各力做的功，再计算各力做功的代数和可 知合外力做的功。 解 将货物视为质点，则其位移s = l = 5 m。 推力F 对货物做功 W1 = Fs = 400×5 J = 2 000 J 重力G 对货物做功 W2 = G scos（90° + α） = -G ssin α = -500×5×0.6 J = -1 500 J 支持力N 对货物做功 W3 = Nscos 90° = 0 图1-5　货物的受力分析示意图 α f G N F 6 hysics P 第1 章　功和机械能 1. 如图所示，若用轻绳拴一物体，使物体以恒定加速度向下做减速运动，则下 列说法正确的是 A. 重力做正功，拉力做负功，合外力做正功 B. 重力做正功，拉力做负功，合外力做负功 C. 重力做正功，拉力做正功，合外力做正功 D. 重力做负功，拉力做负功，合外力做负功 2. 下列选项中，物体所受力F 的大小相等，位移方向向右、大小相同。其中， F 做功最少的是 μ = 0 F μ ≠ 0 F μ = 0 F 30° μ ≠ 0 F 60° 30° A B C D 第1 题 O 上述问题中，能否先求出物体所受的合外力，再求出合外力做的功？试一试，看看计 算结果是否相同。 摩擦力f 对货物做功 W4 = f scos 180° = （μGcos α） scos 180° = -0.2×500×0.8×5 J = -400 J 所有外力对货物做的总功 W总 = W1 + W2 + W3 + W4 =（2 000 - 1 500 + 0 - 400） J 　 = 100 J 讨论 求得所有外力对货物做的总功大于零，表明 货物所受的动力大于阻力。 节练习 策略提炼 计算某力做功时，需先确 定物体在该力的作用下发生 的位移，找出力与位移的夹 角α，再运用W = Fscos α 计 算该力所做的功。 计算合外力所做的功时， 可分别计算每个力所做的功， 再求其代数和；也可先求物体 所受的合外力，然后计算合外 力所做的功。具体采用哪种方 法，应视题目情况而定。 迁 移 7 第1 节　机械功 3. 质量m = 2 kg 的物体，受到与水平方向成37° 角斜向右上方、大小为10 N 的拉力F 的作用，在水 平地面向右移动的距离s = 2 m，物体与地面间的滑动摩擦力f = 4.2 N。取sin37° = 0.6，cos37° = 0.8， 求在此过程中合外力对物体所做的功。 4. 下列说法正确的是 A. 静摩擦力一定不做功 B. 滑动摩擦力一定做负功 C. 滑动摩擦力一定做正功 D. 滑动摩擦力既可以做正功也可以做负功 5. 关于作用力与反作用力做功，有同学认为：当作用力做正功时，反作用力一定做负功。你认为 这种观点正确吗？请说明理由。 6. 以一定的速度竖直向上抛出一小球，小球上升的最大高度为h。假设空气阻力大小恒为F，那么 在小球被抛出至落回出发点的过程中，空气阻力对小球做的功为多少？ 请提问 8 hysics P 第1 章　功和机械能 在生产生活中，人们不仅关注做功的多少， 还关注做功的快慢。例如，借助挖掘机挖土比直 接用人工挖土做功快得多（图1-6）。怎样描述 做功的快慢？本节我们将在初中物理的基础上， 进一步深化对功率的认识。 1.功率的含义 做功的快慢不仅与做功的多少有关，还与做这些功所耗费的时间有关。物理学中将力 所做的功W 与完成这些功所用的时间t 之比，称为功率（power），用符号P 表示，即 P = W t 在国际单位制中，功率的单位是瓦特，简称瓦，用符号W 表示。如果某力在1 s 内 做1 J 的功，它的功率就是1 W。瓦这个单位比较小，在工程技术上常用千瓦（kW）作为 功率的单位。 1 kW = 1 000 W 功率是描述做功快慢的物理量，是标量。 第2节 功　率 2.常见机械的功率 汽车、轮船、火车等交通工具和各种起重机械的动力由内燃机或电动机等动力机械提 供，功率是衡量动力机械性能的重要参数。每一种动力机械都有一个长时间工作的最大允 许功率，这个功率称为机械的额定功率（rated power）。实际工作时，动力机械的功率可 能大于或小于额定功率。例如，汽车爬陡坡时，如果要保持较大速度，实际功率就可能超 过额定功率，这对动力机械有害，要尽量避免。汽车在平直公路上缓慢匀速行驶时，实际 功率就往往小于额定功率。 图1-6　挖掘机挖土 9 第2 节　功　率 3.功率与力、速度的关系 当我们用恒力F 推动书本，让书本在水平桌面上做直 线运动时（图1-7），力F 对书本做功的功率是多大呢？ 力F 的方向和书本位移的方向相同，推力F 所做的功 W = Fs。根据功率的公式P = W t 可得P = Fs t ，而其中s t = v， 因此，推力F 做功的功率 P = Fv 从上面推导可见，公式中的v 是平均速度，对应的功率P 是t 时间内的平均功率。 若时间间隔很小，我们可将平均速度看成瞬时速度，那么此时的功率P 可看成该时刻的 瞬时功率。当物体受力为变力时，在力与速度方向相同的情况下，功率P = Fv 仍然成 立，此时v 为瞬时速度，F 为相应时刻的力，P 则为对应的瞬时功率。 由公式P = Fv 可知，当功率P 一定时，力F 与物体运 动的速度v 成反比。例如，机械正常工作时的功率通常是一 定的，车床在切削硬的工件时需要用较大的力，因此要降低 车床的运转速度。当速度v 一定时，力F 与功率P 成正比。 例如，汽车上坡时（图1-8），司机可通过加大油门，提高 发动机的输出功率来增大牵引力。 一些有特定意义机械的功率 一些常见家用电器的功率 莱特兄弟发明的 “飞行者一号”约9 kW 中国制造的第一辆 汽车约70 kW 电动剃须刀 约1.5 W 波轮式洗衣机 200 ～500 W 第一艘装有螺旋桨推进器的 蒸汽机船“阿基米德号” 约59 kW “和谐号”CRH1 电力动车组 5 300 ～11 000 kW 电风扇 38 ～68 W 家用小定速空调 约800 W 中国制造的第一台蒸汽机车 1 100 kW “辽宁号”航空母舰 的最大功率 约1.5×10 5 kW 冰箱 90 ～200 W 吸尘器 400 ～1 000 W 机械的功率表示其做功的快慢。从表中可以看出，随着社会的发展和技术的进步，一 些同类型机械的功率越来越大，表示其做功越来越快，即在同样的时间里能够做更多的功。 一些机械的功率见下表。 表1-1 一些机械的功率 图1-7　手推书本运动 F v 图1-8　汽车上坡 10 hysics P 第1 章　功和机械能 （2）当F2 = F 阻 时，列车行驶速度最大。 由P = F2vmax 得 　　vmax = P F 阻 = 63.3 m/s 列车的最大行驶速度方向与牵引力方向一致。 讨论 列车的最大行驶速度与其额定功率成正比，与受到的阻力成反比。因此，要提高列车 的最大行驶速度，就需增大发动机的额定功率，并尽量减小阻力。动车组通常由多节动力 车厢相连，且外形被设计成流线型。请解释一下其中的道理。 例 题 一列高速列车总质量m = 465 t，其额定功率P = 5 300 kW，在水平直轨道上行驶时，轨 道对列车的阻力F阻是车重的0.018。列车以额定功率工作，取重力加速度g = 10 m/s 2，求： （1）当行驶速度v = 10 m/s 时，列车的牵引力和加速度； （2）列车在水平直轨道上行驶的最大速度。 策略提炼 运用功率概念和牛 顿第二定律解决列车 行驶等问题时，牵引 力是连接二者的桥梁。 此时，功率公式中的F 是牵引力。 火车或汽车以额定 功率水平行驶，当牵 引力等于阻力时，速度 最大。 分析 由已知的速度和额定功率可求出牵引力，再根据牛 顿第二定律可求出加速度。列车以额定功率工作， 若牵 引力F 大于阻力F 阻（图1-9），列车做加速运动。随 着速度的增大，牵引力F = P v 会逐渐减小，当F = F 阻 时列车的加速度为0，速度达到最大值vmax。 解 由题意可知F 阻 = 0.018 mg。设列车以额定功率工 作，当行驶速度v = 10 m/s 时，牵引力为F1 ；行驶速度 达到最大值vmax 时，牵引力为F2。 （1）由P = F1v 得 F1 = P v = 5.3×10 6 10 N = 5.3×10 5 N 根据牛顿第二定律，有 F1 - F 阻 = ma 解得　 a = 0.96 m/s 2 列车的加速度方向与牵引力方向一致。 图1-9　列车的受力分析 示意图 N F F 阻 G O 11 第2 节　功　率 物理聊吧 前面我们讨论了机械以额定功率工作的问题，那么机械不在额定功率下工作的问题又 该怎样求解呢？试解答下面的问题。 在符合安全行驶要求的情况下，通过减少汽车内放置的物品和控制油箱里的油量等措 施，可实现节能减排。一辆汽车以72 km/h 的速度匀速行驶时，采取以上措施前、后汽车 受到的阻力分别为2 000 N 和1 950 N。试分别求出采取措施前、后汽车的实际功率，并加 以比较。 在本节中，功率与力、速度的关系式P = Fv 是在力的方向与速度的方向一致的 情况下得出的。想想看，如果力与速度的方向相反，或者成任意角度θ 时，功率与 力、速度之间又会有怎样的关系呢？谈谈你的看法，并与其他同学讨论交流。 1. 关于某力做功的功率，下列说法正确的是 A. 该力越大，其功率就越大 B. 该力在单位时间内做的功越多，其功率就越大 C. 功率越大，说明该力做的功越多 D. 功率越小，说明该力做功的时间越少　 2. 一质量为m 的物块沿倾角为θ 的斜面滑下，到达斜面底端时的速度大小为v，此时重力做功的 瞬时功率是 A. mgv B. mgvsin θ C. mgvcos θ D. mgvtan θ 3. 如图所示，某同学的质量为50 kg，自行车的质量为15 kg，设该同学骑自 行车在平直路面上匀速行驶时所受阻力为人车总重的4%，克服阻力做功 的功率为260 W。取重力加速度g = 10 m/s 2，求该自行车匀速行驶的速度 大小。 4. 重量为G 的某汽车，最大功率为Pm，在平直公路上以速度v 匀速行驶时， 汽车发动机的功率为P。 （1）求汽车所受的阻力。 （2）若汽车在倾角为α 的坡路以最大功率匀速向上行驶时，所受路面和空气的阻力大小之和 与（1）中所求阻力大小相等，求此时汽车的速度。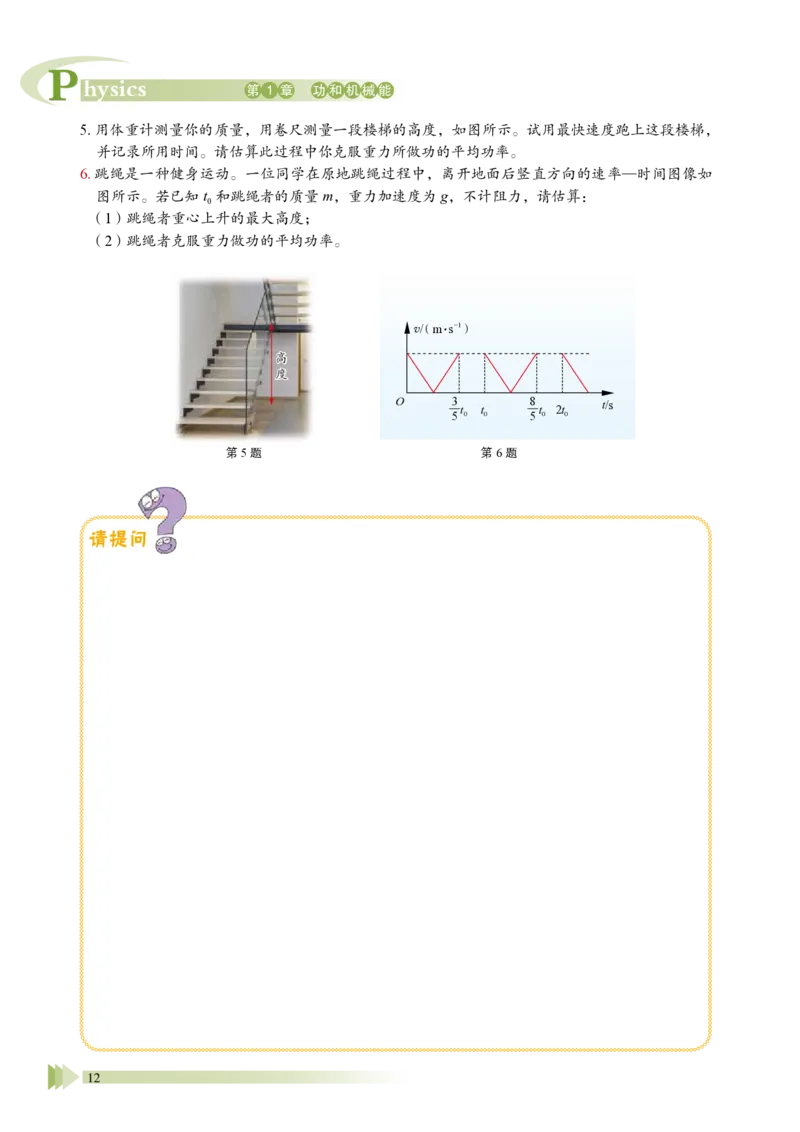 节练习 迁 移 第3 题 12 hysics P 第1 章　功和机械能 5. 用体重计测量你的质量，用卷尺测量一段楼梯的高度，如图所示。试用最快速度跑上这段楼梯， 并记录所用时间。请估算此过程中你克服重力所做功的平均功率。 6. 跳绳是一种健身运动。一位同学在原地跳绳过程中，离开地面后竖直方向的速率—时间图像如 图所示。若已知t0 和跳绳者的质量m，重力加速度为g，不计阻力，请估算： （1）跳绳者重心上升的最大高度； （2）跳绳者克服重力做功的平均功率。 请提问 高 度 第5 题 第6 题 t/s v/ （m·s -1） O t0 2t0 t0 3 5 t0 8 5 13 第3 节　动能和动能定理 迷你实验室 运动的物体可以做功，说明物体运动时具有能 量。例如，台风、龙卷风（图1-10）等强烈的空气 流动具有巨大的能量，可以拔起大树、掀翻汽车甚至 摧毁房屋。运动的物体具有的能量与哪些因素有关？ 其变化与功有着怎样的关系？本节将深入学习动能和 动能定理。 1.动能 物理学中把物体因运动而具有的能量称为动能（kinetic energy）。人类利用动能已有很 长的历史。例如，在船上加挂风帆，利用气流的动能推动帆船前进；制造风车和水车，利 用气流和水流的动能从事各种生产活动。现在，我们能更广泛、更有效地利用气流和水流 的动能来进行发电等活动。 那么，物体动能的大小与哪些因素有关？让我们通过一个小实验来回顾初中物理介绍 过的内容。 影响小车动能大小的因素 如图 1-11 所示，同一小车从斜面的不同高度处 由静止开始下滑，撞击放在水平面上的木块。可以发 现，小车开始下滑时的高度越高，木块被撞击后运动 的距离越大。 质量不同的小车从斜面的同一高度处由静止开始 下滑，撞击放在水平面上的木块。可以发现，小车的 质量越大，木块被撞击后运动的距离越大。 第3节 动能和动能定理 图1-11　实验装置 图1-10 龙卷风 14 hysics P 第1 章　功和机械能 实验与探究 2.恒力做功与动能改变的关系 在“迷你实验室”中，小车通过撞击对木块 做功，使木块从静止开始运动，木块的动能从无到 有。滚动的保龄球具有动能，当其克服球瓶阻力做 功时，动能减小（图1-12）。那么，若外力对物 体做功，该物体的动能总会增大吗？若物体克服外 力做功，该物体的动能总会减小吗？做功与动能的 改变之间究竟有什么关系？ 我们从简单的情况入手，通过实验来探究恒力做功与动能改变的关系。 由以上实验可以看出，动能的大小与物体的质量和运动速度有关。物体的质量m 越 大，速度v 越大，其动能就越大。在物理学中，物体的动能Ek 表示为 Ek = 1 2 mv2 动能是标量。它的单位与功的单位相同，在国际单位制中都是焦耳，符号为J。从上 式也可以看出 1 kg·（m/s） 2 = 1 kg·（m/s 2）·m = 1 N·m = 1 J 恒力做功与动能改变的关系 要研究恒力做功与动能改变的关系，需要测出作用于物体的力、物体的位移， 以及物体的质量和速度，求出恒力所做的功和物体的动能，然后进行比较。 用打点计时器测小车的位移和速度，用天平测小车的质量，用钩码给小车提供 作用力。此实验的装置与“探究加速度与力、质量的关系”的实验装置基本相同。 思考实验中如何平衡摩擦力？如何让小车所受的合力近似等于钩码的重力？为什么？ 如图1-13 所示，用细线通过定滑 轮连接小车与钩码，纸带通过打点计时 器与小车相连。实验中，通过改变钩码 数量来改变小车所受拉力的大小，测出 需要测的物理量，然后算出每次拉力做 的功及相应的小车动能的改变量。比较 二者之间的关系，可以得出什么结论？ 图1-13　实验装置示意图 小车 纸带 打点 计时器 图1-12　保龄球撞击球瓶 15 第3 节　动能和动能定理 3.动能定理 运用牛顿第二定律和匀变速直线运动的规律，可推导出恒力对物体做功与物体动能改 变的关系。 设一个物体的质量为m，初速度为v1，在与其运动方向相同的合外力F 的作用下经过 一段位移s 后，速度增加到v2（图1-14） 。根据牛顿第二定律和匀变速直线运动的规律 　　F = ma 　　s = v2 2 - v1 2 2a 可得　　Fs = 1 2 mv2 2 - 1 2 mv1 2 用W 表示合外力F 在这一过程中所做的功，用Ek1 表示物体的初动能1 2 mv1 2， 用Ek2 表示物体的末动能1 2 mv2 2，于是有 W = Ek2 - Ek1 上式表明，合外力对物体所做的功等于物体动能的变化量。这个结论称为动能定理 （theorem of kinetic energy）。从上式可以看出，当合外力对物体做正功时，物体的末动能 大于初动能，动能增大。例如，在汽车加速的过程中，牵引力和阻力的合力对汽车做正 功，汽车的动能增大。当合外力对物体做负功，或者物体克服合外力做功时，物体的末动 能小于初动能，动能减小。例如，在汽车刹车的过程中，阻力对汽车做负功，汽车的动能 减小。我们可用合外力做功的多少来量度物体动能的变化量。 可以证明，动能定理在物体受到变力作用或做曲线运动的情况下也是成立的。动能定 理是物理学的重要规律。通过它，我们既可用做功的多少来量度动能的变化量，也可用动 能的变化量来确定做功的多少，这为分析力学问题提供了新的思路。 例 题 如图1-15 所示，一辆汽车正以v1 = 72 km/h 的速度匀速直线行驶，司机发现在前方 150 m 处停有一故障车辆，马上进行刹车操作。设司机的反应时间t1 = 0.75 s，刹车时汽车 受到的阻力为重力的 1 2 。取重力加速度g = 10 m/s 2。请计算从发现故障车至停下，汽车在 这段时间内发生的位移，据此判断这两辆车是否会相撞。 图1-14　物体在恒力作用下速度变化的示意图 F v1 v2 F s 图1-15　急刹车情境的示意图 16 hysics P 第1 章　功和机械能 分析 在司机的反应时间内，后车做匀速直线运动，位移s1 = v1t1。后车刹车后，在水平方 向只受到阻力F阻的作用，发生的位移为s2。根据已知条件，运用动能定理即可求出s2， 若s1+ s2 ＜ 150 m ，则两车不会相撞。 解 设后车刹车时所受阻力为F阻；司机反应时间内后车的位移为s1； 从开始刹车到停止，后车的位移为s2。后车受力分析如图1-16 所示。 由题意可知v1 = 72 km/h = 20 m/s，F阻 = 1 2 mg。 由匀速直线运动公式可得 s1 = v1t1 = 20×0.75 m = 15 m 由动能定理得 -F阻 s2 = 0 - 1 2 mv1 2 整理得 s2 = mv1 2 2 F阻 = v1 2 g = 20 2 10 m = 40 m 发现故障车至停下汽车发生的位移为 s = s1+ s2 = 55 m s ＜150 m，故两车不会相撞。 讨论 从计算结果看，后车不会与前车发生追尾。为避免交通事故，汽车在行驶中保持一定 安全距离是很重要的。通常车速越大，需要保持的安全距离也越大。 《中华人民共和国道路交通安全法》规定，机动车在道路上行驶，不得超过限速标志 标明的最高时速。你能从物理学的角度说明该规定的理由吗？ 运用动能定理不仅可以较简便地求解一些恒力做功问题，还可求解一些特殊情况下的 变力做功问题。请你解答下面的问题。 雨滴在空中下落时会受到空气阻力，空气阻力f 的大小与雨滴下落速率v 的二次方成 正比，即f = kv2，其中k 为常数。若质量为m 的雨滴，从高h 处以初速度v0 竖直加速下落， 接近落地前开始做匀速直线运动。已知重力加速度为g，求该雨滴从高处下落到地面的过 程中，空气阻力对其所做的功。 策略提炼 若研究的问题只涉及力、 位移与物体运动的初、末状 态，用动能定理求解通常比用 牛顿运动定律求解简便得多。 对于一些变力做功问题， 利用功的计算公式很难求解， 通常可利用动能定理求解。 迁 移 F阻 mg N 图1-16　受力分析 示意图 17 第3 节　动能和动能定理 1. 若汽车行驶速度增加为原来的2 倍，则该车从开始刹车到停下的距离约将增大为原来的4 倍。 请你从动能定理的角度加以解释。 2. 2017 年5 月5 日，我国自行研制的大型喷气式客机C919 首飞成功，标志着我国大型客机 项目取得重大突破。假设飞机在水平跑道上的滑跑是初速度为0 的匀加速直线运动，当位 移s = 1.6×10 3 m 时才能达到起飞所要求的速度v = 80 m/s。已知飞机质量m = 7.0×10 4 kg，滑 跑时受到的阻力为自身重力的0.1，取重力加速度g = 10 m/s 2 ，求： （1）飞机起飞时的动能； （2）飞机滑跑过程中受到的牵引力。 3. 质量为m 的汽车在平直公路上行驶，发动机的功率P 和汽车受到的阻力均恒定不变。在时间t 内， 汽车的速度由v0 增加到最大速度vmax，则此段时间内汽车沿直线运动的距离为多少？ 节练习 4. 拖把是由拖杆和拖把头构成的清洁工具，如图所示。若某同学保持拖 杆与竖直方向的夹角θ = 37°，并用沿拖杆方向的恒力F = 30 N 推动拖 把头，使其由静止开始在水平地面沿直线运动，位移s = 1 m。已知拖把头 的质量m = 1.6 kg，不计拖杆质量，拖把头与地面间的动摩擦因数 μ = 0.3， 取重力加速度g = 10 m/s 2， sin 37° = 0.6， cos 37° = 0.8，求： （1）摩擦力对拖把头做的功； （2）拖把获得的动能。 5. 如图所示，木块放在光滑水平面上，一颗子弹水平射入木块。已知子弹 受到的平均阻力为F阻，射入深度为d，在此过程中木块的位移为s，求 子弹动能的减少量和木块动能的增加量。 *6. 假设某地强风的风速为v，空气密度为ρ。如果把通过横截面积S 的风的动能转化为电能，转化效率为η，请写出电功率的表达式。 第4 题 θ 拖杆 拖把头 请提问 s d 第5 题 18 hysics P 第1 章　功和机械能 迷你实验室 松软的白雪给人以恬静、美丽的印象。然而 发生雪崩时（图1-17），雪会以排山倒海之势摧 毁沿途的一切，给自然界和人类带来灾难。雪崩 破坏力强大是由于积雪处在一定高度而具有巨大 的能量。这种能量有什么特点？它与积雪所处的 高度有什么关系？与重力又有什么关系？本节将 主要学习与重力势能及其改变有关的内容。 1.重力势能 物理学中，把物体因为处于一定的高度而具有的能量称为重力势能（gravitational potential energy）。例如，高处的石头、打桩时被举高的重锤、水电站储存的水等，都具有 重力势能。 物体重力势能的大小与哪些因素有关？我们先通过一个小实验来回顾初中物理学习过 的内容。 影响小球重力势能大小的因素 准备两个大小相同、质量不同的光滑小球，在一盆中放 入适量细沙。 在沙盆上方同一高度由静止释放两小球，小球落入细沙 时会出现什么现象？是否质量大的小球陷得更深？让同一个 小球分别从不同的高度由静止落下（图1-18），又会出现什 么现象？是否释放位置越高小球陷得越深？对比以上两种现 象，你能得出什么结论？ 第4节 势能及其改变 图1-18　释放小球 图1-17　雪崩 19 第4 节　势能及其改变 2.重力做功与重力势能改变的关系 我们知道，滑雪者靠重力可沿山坡滑下（图1-20）。 下面，我们通过对滑雪者滑雪模型的建构，进一步探索重 力做功与重力势能改变的关系。 首先，建构滑雪者及其滑雪过程的物理模型。如图 1-21 所示，将滑雪者视为质量为m 的物体（质点），物 体从A 点滑向C 点，位移为l，与竖直方向的夹角为θ， A 点的高度为 h1，C 点的高度为 h2。根据功的定义，物体从 A 点到C 点过程中，重力做功为 W = mgl cosθ = mg（h1 - h2）= mgh1 - mgh2 上式的结果正好等于物体从A 点竖直下落到B 点过程中 重力所做的功。这表明，从A 点到B 点和从A 点到C 点，虽 然路径不同，但重力做的功是相同的。其实，理论上可证 明，无论物体沿哪条路径下滑（如图1-21 中的曲线），其 重力做功皆为mgh1 - mgh2。由此可知，重力做功与始末位 置的高度差有关，与路径无关。因此，滑雪者无论沿什么路 线下滑，无论雪坡平缓还是陡峭，只要其始末位置的高度差 由以上实验可知，重力势能的大小与物体的质量和所处的高度有关。物体的质量m 越 大，所处的高度h 越高，重力势能就越大。在物理学中，物体的重力势能Ep 表示为 Ep = mgh 重力势能是标量。它的单位与功的单位相同，在国际单位制中都是焦耳，符号为J。 对同一物体，重力势能的大小由物体所处的高度决定。物体所处的高度总是相对一 定的水平面而言，相对于不同的水平面，物体所处的高度是 不同的。为了便于研究问题，我们一般先选定某一个水平面 作参考。若把这个水平面的高度设为零，则物体在该水平面 的重力势能也为零，这样的水平面称为零势能参考平面。例 如，选定物体放在桌面上时重心所在的水平面B 为零势能参 考平面（图1-19），当质量为m 的物体重心位于该参考平面 以上高度为h1 的水平面A 时，它的重力势能EpA = mgh1 ；当 物体放在桌面上时，它的重力势能EpB = 0 ；当物体放在地面 上时，其重心在水平面C 上，与水平面B 的距离为h2，它的 重力势能则为EpC = -mgh2。 图1-19　零势能参考平面的选择 A B C h1 h2 图1-20　滑雪 图1-21　分析滑雪过程重力做功 的示意图 A C θ B h1 h2 水平面 l 20 hysics P 第1 章　功和机械能 相同，重力做功就相同。 物理聊吧 滑雪者下滑过 程中会受到阻力的 影响，甚至会受到 滑雪杆或滑雪板的 影响。在这种情况 下，重力做功的多 少会受到影响吗？ 图1-22　水力发电站利用水的重力 势能发电 图1-23　拉开的弓存储了弹性势能 由重力做功的特点可知，重力做功与重力势能改变的 关系为 WG = Ep1 - Ep2 = -ΔEp 式中，Ep1 = mgh1，表示物体在初位置时的重力势能；Ep2 = mgh2， 表示物体在末位置时的重力势能。 物体从高处下落的过程中，W G > 0，重力做正功， E p1 > Ep2，重力势能减小；物体被举高的过程中，WG < 0， 重力做负功，即物体克服重力做功，Ep1 < Ep2，重力势能增 大。总之，重力势能的改变是由重力做功决定的：重力对 物体做多少正功，物体的重力势能就减小多少；物体克服 重力做多少功，物体的重力势能就增大多少。物体的重力 势能值与参考平面的选取有关，是相对的；而重力势能的 改变量与参考平面的选取无关。 实际上，高处的物体在下落时对外做功。因此，重力 势能可视为一种被暂时存储起来的潜在能量。在生产生活 中，人们根据需要将重力势能转化成其他形式的能量。例 如，建筑工地常用的打桩机就是把重力势能转化为动能， 从而把桩钉打入地下；在江河中修筑堤坝提高水位，就可 以利用水的重力势能发电（图1-22）。 3.弹性势能及其改变 在射箭比赛中，运动员的手一松开，拉开的弓在恢复 原状的过程中就能把箭发射出去（图1-23）。可见，发生 弹性形变的物体在恢复原状的过程中能够做功，说明它具 有能量。物理学中，把物体因为发生弹性形变而具有的能量 称为弹性势能（elastic potential energy）。拉开的弓弦、上 紧的钟表发条等都具有弹性势能。在弹簧被拉长或被压缩 时，弹簧中就存储了弹性势能；在恢复原状的过程中，弹 簧就对外做功。理论研究表明，物体的弹性形变越大，具 有的弹性势能就越大，恢复原状时对外做的功就越多。 用劲度系数不同的两根弹簧做实验，会发现弹性势能 还与弹簧的劲度系数有关。在同样的形变下，劲度系数越 大的弹簧弹性势能越大。因此，在生产生活中，人们会根 据需要选用不同劲度系数的弹簧。 21 第4 节　势能及其改变 迷你实验室 小纸帽能弹多高 将圆珠笔里的弹簧取出，再用硬卡纸做个小纸帽，套在弹簧 上（图1-24）。用力把小纸帽往下压，使弹簧产生一定的弹性 形变，然后迅速放开手，看看小纸帽能弹多高。 用大小不同的力使弹簧产生大小不同的弹性形变，重复做几 次，看看小纸帽弹起的高度有什么不同。 换用不同劲度系数的弹簧做此实验，看看小纸帽弹起的高度 又有什么不同。 在上面的实验中，弹簧在恢复原状的过程中对小纸帽做功。同时，随着弹簧迅速恢复 到原状，弹性势能也减小到零，弹簧也就不再对外做功。研究表明，与重力做功的情况类 似，弹簧的弹力对外做多少功，弹性势能就减小多少；反之，克服弹力做多少功，弹性势 能就增大多少。 弹性势能和重力势能一样，都与物体间的相对位置有关：重力势能与物体和地球的相 对位置有关，弹性势能与发生弹性形变的物体各部分的相对位置有关。人们把这类由相对 位置决定的能量称为势能（potential energy）。势能是存储于一个物体系统内的能量，不是 物体单独具有的，而是相互作用的物体所共有的。例如，重力势能是物体与地球所组成的 “系统”共有的，没有地球， 就谈不上重力，也谈不上重力势能。关于势能，我们在后面 还将进一步学习。 1. 如图所示，水平桌面距地面0.8 m，一质量为2 kg 的小球放在距桌面 0.4 m 的支架上。小球可视为质点，取重力加速度 g = 10 m/s 2。 （1）以地面为零势能参考平面，计算小球具有的重力势能；若小球由 支架落到桌面，重力势能减小多少？ （2）以桌面为零势能参考平面，计算小球具有的重力势能；若小球由 支架落到桌面，重力势能减小多少？ （3）分析以上计算结果，你能得出什么结论？ 2. 一举重运动员将质量为160 kg 的杠铃从地面举到了1.8 m 的高度。取重力加速度 g = 10 m/s 2。在 此过程中，他对杠铃做了多少功？杠铃的重力势能改变了多少？ 节练习 0.4 m 0.8 m 第1 题 图1-24　实验装置 示意图 22 hysics P 第1 章　功和机械能 3. 质量为m 的物体，在距地面高h 处以2—3 g 的加速度由静止竖直下落到地面。在此过程中，物体 的重力势能和动能的变化量分别是多少？ 4. 以初速度v0 竖直向上抛出一质量为m 的小球。假定小球所受的空气阻力f 大小不变，已知重力 加速度为g，求： （1）小球上升的最大高度； （2）小球返回原抛出点时的速率。 5. 如图所示，质量为M 的物体静止在地面上，物体上面连着一个轻弹簧。用手拉住弹簧上端将物 体缓缓提升高度H，则人做的功 A. 等于MgH B. 小于MgH C. 大于MgH D. 无法确定 *6. 早期人们用不易弯曲的竹竿或金属杆进行撑竿跳高，后来采用了有弹性的玻璃纤维杆，如图所 示，撑竿跳高的世界纪录也因此有了很大的提高。请上网查询，解释为何使用弹性玻璃纤维杆有 助于撑竿跳高成绩的提高。 请提问 第5 题 第6 题 23 第5 节　科学验证：机械能守恒定律 过山车（图1-25）在最高点无动力释放后，会沿 着轨道下滑、爬升、翻转，速度时快时慢，惊险刺激。 过山车在运行过程中既有重力势能，又有动能。高度减 小时，重力势能减小，动能增大；高度增大时，重力势 能增大，动能减小。当重力势能与动能发生变化时，它 们之间遵循着什么规律？本节我们将学习机械能，并研 究动能与势能转化时遵循的规律。 1.机械能守恒定律 运动的物体往往既有动能又有势能，物体的动能与重力势能（弹性势能）之和称为 机械能（mechanical energy）。若用符号E 表示机械能，则物体的机械能为 E = Ep + Ek 在物体运动过程中，不同形式的能量常会相互转化。例如，射箭时，弓的弹性势能减 小，箭的动能增大；蹦极时，重力势能会转化为动能和弹性势能等。大量事实表明，物体 的机械能可从一种形式转化为另一种形式。下面，我们先 从理论上研究只有重力势能与动能发生转化时能量遵循的 规律。 如图1-26 所示，如果小球只在重力作用下自由下落， 从A 到B 的过程中重力做功为WG，根据动能定理可知， 重力做的功等于小球下落过程中动能的增加量，即 WG = 1 2 mv2 2 - 1 2 mv1 2 由重力做功与重力势能改变的关系可知，重力做的功 等于小球下落过程中重力势能的减少量，即 WG = mgh1 - mgh2 第5节 科学验证：机械能守恒定律 图1-26　小球下落示意图 h1 A B h2 v2 v1 图1-25　过山车 24 hysics P 第1 章　功和机械能 由以上两式可得 1 2 mv2 2 - 1 2 mv1 2 = mgh1 - mgh2 即在小球自由下落的过程中，动能的增加量等于重力势能的减少量，说明重力对小球 做了多少功，就有多少重力势能转化为等量的动能。上式移项后得 1 2 mv2 2 + mgh2 = 1 2 mv1 2 + mgh1 即 Ek2 + Ep2 = Ek1 + Ep1 上式表明，在小球自由落体运动中，只有重力做功，小球在A 点的动能与重力势能的 总和等于在B 点的动能与重力势能的总和。由于A、B 两点是任意选定的，故在自由落体 运动中，任何位置（时刻）物体的总机械能保持不变。 同样可以证明， 在只有弹力做功的物体系统内， 动能和弹性势能可相互转化， 总的机 械能保持不变。 大量研究结果表明，在只有重力或弹力这类力 做功的情况下，物体系统的动能与势能相互转化， 机械能的总量保持不变。这个结论称为机械能守恒 定律（law of conservation of mechanical energy）。 事实上，并非只有动能和势能可以相互转化， 任何形式的能量都可以相互转化，但总能量保持不 变，这就是更普遍的能量守恒定律。 2.验证机械能守恒定律 在只有重力或弹力做功的情况下，物体系统的机械能是守恒的。我们已经从理论上推 导出了机械能守恒定律，现在用实验进行验证。 实验目的 （1）验证机械能守恒定律。 （2）进一步熟悉打点计时器的使用。 实验器材 铁架台、打点计时器、交流电源、纸带、重物、天平、砝码、刻度尺。 能在熟悉的问题情境中运用机械 能守恒定律解决问题时建构物理模 型，会分析机械能守恒的条件；能从 机械能守恒的角度分析动力学问题， 通过推理，获得结论；能用与机械能 守恒定律等相关的证据说明结论；能 从不同视角解决动力学问题。　 ——科学思维 素 养 提 升 25 第5 节　科学验证：机械能守恒定律 荡秋千是一种常见的娱乐休闲活动（图1-28）。 若秋千绳的长度l = 2 m，荡到最高点时秋千绳与竖直 方向的夹角θ = 60°。取重力加速度 g = 9.8 m/s 2，求荡 到最低点时秋千的速度大小。（忽略阻力及秋千绳的 质量，且人在秋千上的姿势可视为不变） 例 题 实验原理与设计 实验装置如图1-27 所示。让带有纸带的重物自由下落， 利用打点计时器记录重物下落过程中的运动情况。选取纸带 上的某点作为高度的起点，量出纸带上其他点相对该点的距离 作为高度。用天平称出重物的质量，算出重物经过这些点的 重力势能。再计算重物经过这些点的瞬时速度，算出动能。 最后，通过比较重物经过这些点的机械能，得出实验结论。 实验步骤 （1）使用天平称出重物质量。 （2）纸带一端吊重物，另一端穿过打点计时器。手提纸 带，使重物靠近打点计时器并静止。接通电源，松开纸带， 让重物自由落下。 （3）取下纸带并选其中一个点作为参考点，设打该点时 重物的重力势能为0，计算打该点时重物的动能，它就是重 物下落过程中动能与重力势能的总和。 （4）分别计算纸带上其他各点对应的重物的动能和重力 势能之和。 数据分析 请将测量的数据记入你设计的表格中，并分析数据，形 成结论。 实验结论 请写出实验结论。 讨论 （1）引起实验误差的主要因素有哪些？如何减小实验 误差？ （2）若实验中不测量重物质量，还能验证机械能守恒定 律吗？ （3）你能设计其他实验方案验证机械能守恒定律吗？ 安全警示 使用打点计时器 时注意用电安全。释 放重物时不要让重物 砸到人或实验台。 图1-28　荡秋千 能提出实验中可能出现的 物理问题；能在他人帮助下 设计实验方案，获取数据；能 分析数据、验证机械能守恒定 律，能反思实验过程，尝试减 小实验误差；能撰写比较完整 的实验报告，在报告中能呈现 实验表格及数据分析过程，能 尝试利用证据进行交流。 注意提升提出问题、分析 论证及反思评估的能力。 ——科学探究 素 养 提 升 图1-27　实验装置 26 hysics P 第1 章　功和机械能 分析 秋千绳拉力的大小和方向不断变化，难以直接用牛顿第二定律和运动学公式来求解。 但在摆动过程中，秋千绳拉力不做功，只有重力做功，系统的机械能守恒，可用机械能守 恒定律求解。 下列问题能否运用牛顿运动定律 或机械能守恒定律解答？请试一试。 1924 年，跳台滑雪被列为首届冬 奥会比赛项目。如图1-30 所示，假设 运动员从雪道的最高点A 由静止开始 滑下，不借助其他器械，沿光滑的雪 道到达跳台的B 点时，速度为多少？ 迁 移 策略提炼 运用机械能守恒 定律分析解决问题时， 需要先分析研究对象 在所研究的过程中是 否满足机械能守恒条 件，然后确定研究对象 的初、末状态及其机械 能，最后列式求解。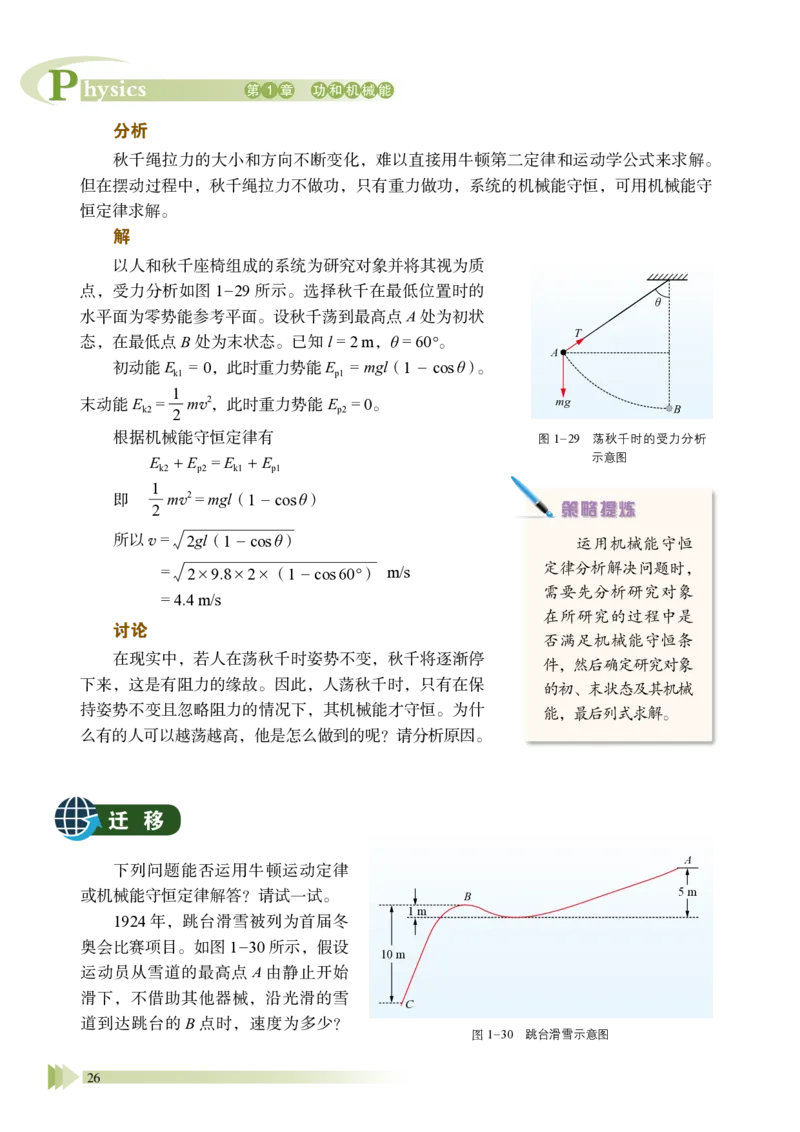 解 以人和秋千座椅组成的系统为研究对象并将其视为质 点，受力分析如图1-29 所示。选择秋千在最低位置时的 水平面为零势能参考平面。设秋千荡到最高点A 处为初状 态，在最低点B 处为末状态。已知l = 2 m，θ = 60°。 初动能Ek1 = 0，此时重力势能Ep1 = mgl（1 - cos θ）。 末动能Ek2 = 1 2 mv2 ，此时重力势能Ep2 = 0。 根据机械能守恒定律有 Ek2 + Ep2 = Ek1 + Ep1 即　 1 2 mv2 = mgl（1 - cos θ） 所以 v = 2gl（1 - cos θ） 　 = 2×9.8×2×（1 - cos 60°） m/s 　 = 4.4 m/s 讨论 在现实中，若人在荡秋千时姿势不变，秋千将逐渐停 下来，这是有阻力的缘故。因此，人荡秋千时，只有在保 持姿势不变且忽略阻力的情况下，其机械能才守恒。为什 么有的人可以越荡越高，他是怎么做到的呢？请分析原因。 图1-30　跳台滑雪示意图 1 m 10 m B C 5 m A 图1-29　荡秋千时的受力分析 示意图 B A T mg θ 27 第5 节　科学验证：机械能守恒定律 1. 请撰写“验证机械能守恒定律”的实验报告，注意在报告中呈现设计的表格及数据分析过程。 第3 题 H h 物理聊吧 跳水运动员在弹离跳板后，先上升到一定的高度，在空中完成一系列复杂而优 美的动作后入水。请你分析一下，从运动员起跳到入水的全过程中，有哪些能量发 生了相互转化。说出你的判断依据，并与同学讨论交流。 节练习 当他落到离B 点竖直高度为10 m 的雪地C 点时，速度又是多少？ （假设这一过程中运动员没有做其 他动作，忽略摩擦力和空气阻力， 取重力加速度g = 10 m/s 2） 能理解功、功率、动能、重力势能及机械能守恒定 律的内涵，定性了解弹性势能；能用动能定理和机械能 守恒定律等分析解释生产生活中的相关现象，解决一些 相关的实际问题，能体会守恒观念对认识物理规律的重 要性。具有与功和机械能相关的初步的能量观念。 ——物理观念 素 养 提 升 v0 第5 题 k 2. 下列说法正确的是 A. 物体的机械能守恒时，一定只受重力作用 B. 物体处于平衡状态时，机械能一定守恒 C. 物体除受重力外，还受其他力时，机械能也可能守恒 D. 物体的重力势能和动能之和增大时，必有重力以外的力对其做功 3. 如图所示，质量为m 的苹果从距地面高度为H 的树上由静止开始下 落，树下有一深度为h 的坑。若以地面为零势能参考平面，则苹果 刚要落到坑底时的机械能为 A. -mgh B. mgH C. mg（H + h） D. mg（H - h） 4. 在水平地面以20 m/s 的速度将一物体竖直上抛。若以水平地面为 零势能参考平面，忽略空气阻力，取重力加速度g = 10 m/s 2，求： （1）物体上升的最大高度； （2）物体在上升过程中其重力势能和动能相等的位置距地面的高度。 5. 如图所示，轻弹簧k 一端与墙相连，质量m = 4 kg 的木块沿光滑水 平面以v0 = 5 m/s 的初速度向左运动。求： （1）弹簧在被压缩过程中的最大弹性势能； （2）木块压缩弹簧后速度减小到3 m/s 时弹簧的弹性势能。 28 hysics P 第1 章　功和机械能 6. 某同学计划通过测量重物自由下落的瞬时速度v 和下落高度h 来验证机械能守恒定律。 （1）以下四种测量方案中，合理的是 　　　　 （填正确选项前的字母），理由是 　　 　 　 　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 　　　　 　　。 A. 直接测量下落高度 h 和下落时间 t，通过 v = gt 算出瞬时速度v B. 直接测量下落高度 h，通过 v2 = 2gh 算出瞬时速度v C. 根据纸带上某点的相邻两点间的平均速度，得到该点的瞬时速度v，再由 v2 = 2gh 算出高度h D. 直接测量下落高度 h，根据纸带上某点的相邻两点间的平均速度，得到该点的瞬时速度v （2）实验中产生系统误差的主要原因是纸带通过打点计时器时存在摩擦阻力，使重物获得的动 能往往 　　　　　　 （选填“大于”“小于”或“等于”）它所减小的重力势能。 （3）如果以v2 —2 为纵轴、h 为横轴，根据实验数据绘出的v2 —2 -h 图线是一条通过坐标原点的倾斜 直线，该直线的斜率是 　　　　　　。 第7 题 0 5 10 15 20 25 30 20 15 10 5 v/（m.s -1） x/m 请提问 7. 研究蹦极运动时，在运动员身上装好传感器， 用于测量他在不同时刻下落的高度及速度。已 知运动员及其所携带的全部设备的总质量为 60 k g，弹性绳原长为10 m。运动员从蹦极台 无初速度下落，根据某次传感器测到的数据， 得到如图所示的速度—位移图像。请据图像 作出初步判断：运动员下落过程中在什么位置 动能最大？该位置受力有什么特点？运动员下 落速度最大时和落到最低点时，绳的弹性势能 分别为多大？请陈述你运用相关定律解决问 题的条件。 29 章末练习 科学认知 1. 竖直向上抛一小球，小球又落回原处。假设空气阻力的大小不变，小球在上升过程中克服重力做功 的平均功率和下降过程中重力做功的平均功率哪个更大？请说明理由。 2. 拖着旧橡胶轮胎跑步是一种训练体能的常用方法。某消防队员在体能训练时拖着轮胎在操场上 以恒定的速率跑了80 m，下列说法正确的是 A. 摩擦力对轮胎做了负功 B. 合外力对轮胎做了正功 C. 拉力对轮胎所做的功等于轮胎动能的改变 D. 支持力对轮胎做了正功 3. 如图所示，质量为m 的小球用长l 的细线悬挂并静止在竖直位置P。 用水平拉力F 将小球缓慢地拉到Q 点的过程中，拉力F 做功为 　A. mgl cos θ　　　　B. mgl（1-cos θ）　　　　C. Fl sin θ　　　　D. Fl 4. 修建高层建筑常用的塔式起重机如图所示。在起重机将质量m = 5×10 3 kg 的重物竖直吊起的过程中，重物由静止开始向上做匀加速直线运动，加 速度a = 0.2 m/s 2。当起重机的输出功率达到其允许的最大值时，保持该 功率不变直到重物做vmax = 1.02 m/s 的匀速运动。取重力加速度g = 10 m/s 2， 不计额外功，求： （1）起重机允许输出的最大功率； （2）重物做匀加速直线运动所经历的时间。 5. 雪车是冬季竞技运动项目之一。如图所示，在一段赛道上，运动员操 控雪车无动力滑行，沿斜坡赛道经A 点至坡底O 点，再沿水平赛道经 B 点滑至C 点。已知运动员与雪车的总质量为m，A 点距水平赛道的 高度为h，OB 距离为s，雪车在A、B 和C 各点的速度 分别为vA 、 vB 和vC ，从B 点滑至C 点所用时间为tBC。 忽略空气阻力，设雪车与赛道表面间的摩擦力大小恒定， 重力加速度大小为g，求： （1）滑行过程中雪车所受摩擦力的大小； （2）雪车与运动员从A 点滑到O 点的过程中机械能的改变量。 6. 某人将质量为0.2 kg 的小球斜向上抛出，抛出点距离地面2.6 m，抛出时速度大小为12 m/s，方向 与水平方向之间的夹角为30°。取重力加速度g = 10 m/s 2。 （1）若不计空气阻力，求小球落地时的速度大小。 （2）若小球落地时的速度为13 m/s，求小球在空中运动过程中克服阻力做的功。 7. “辽宁号”航空母舰的质量为m，以速度v 沿直线匀速驶向某 训练海域，此时多台蒸汽轮机发动机的输出总功率为P。若因 需要临时关闭其中一半的发动机，则 （1）求发动机刚刚关闭时“辽宁号”航空母舰的加速度大小； （2）描述发动机关闭后一段时间内航空母舰的运动速度和加速 度的变化情况。 章末练习 第3 题 P F Q θ 第4 题 第5 题 C B h s O A 第7 题 30 hysics P 第1 章　功和机械能 8. 某海湾面积为1.0×10 7 m 2，涨潮时水深20 m，退潮时水 深降至18 m。现利用此海湾筑水坝建潮汐水力发电站，利 用涨潮和落潮过程中进出海湾的潮水推动水轮发电机组发 电，如图所示。若重力势能转化为电能的效率是10％，每 天有两次涨潮，取海水密度ρ = 1.0×10 3 kg/m 3，重力加速 度g = 10 m/s 2，求该发电站一天能发出多少电能。 科学探究 9. 某同学为了探究书本在下落过程中所受的空气阻力，将一质量为m 的书本放在运动传感器的正下方由静止释放，得到书本落地前下落 的速度—时间图像如图所示。求： （1）书本下落的距离； （2）书本在落地前损失的机械能以及在此下落过程中所受空气阻力 的大小。 温故知新 10. 某航模兴趣小组设计出一架遥控飞行器，质量m = 2 kg，动力系统提供的恒定升力F = 28 N。试飞 时，飞行器从地面由静止开始竖直上升。假设飞行器飞行时所受阻力大小不变，取重力加速度 g = 10 m/s 2。 （1）第一次试飞，飞行器飞行t1 = 8 s 时到达的高度h = 64 m，求飞行器所受阻力f 。 （2）第二次试飞，飞行器飞行t2 = 6 s 时遥控器出现故障，飞行器立即失去升力，求飞行器能到 达的最大高度H。 11. 如图所示，可视为质点的两物块A、B 的质量分别为M、m。A 放在 光滑水平桌面上，一不可伸长的轻绳跨过光滑轻质定滑轮，两端分别 与A、B 相连接，A 和滑轮间的轻绳与桌面平行。现将A 从静止释放， 不计空气阻力，重力加速度为g。请你设计两个问题，使其可应用下 面的物理规律解决。 （1）牛顿第二定律。 （2）动能定理或机械能守恒定律。 12. 请根据第1 章（功和机械能） 的内容，结合你的理解，画出概念图。 第9 题 v1 v t t1 t0 O 第8 题 海水水轮发电机 我的学习总结 A B 第11 题 31 第5 节　科学验证：机械能守恒定律 一、选择题（本题共5 小题。在每小题给出的四个选项中，第1 ～3 题只有一项符合题目要求， 第4、5 题有多项符合题目要求） 1. 如图所示，某同学从一滑坡的顶端由静止开始下滑，然后沿水平面滑动了一段距离后停下来。 在整个运动过程中 A. 支持力对他做正功 B. 他的重力势能一直不变 C. 他的机械能守恒 D. 他的机械能减小 2. 假设摩托艇受到的阻力的大小与它的速率成正比。如果摩托艇发动机的输出功率变为原来的 2 倍， 则摩托艇的最大速率变为原来的 A. 4 倍 B. 2 倍　　　　　　 C. 3 倍 D. 2 倍 3. 某同学骑自行车下坡。已知坡长500 m、高 8 m，人和车的总质量为100 kg。下坡时车的初速度 为4 m/s，在人不踏车的情况下，到达坡底时车速为10 m/s。取重力加速度g = 10 m/s 2，则下坡 过程中阻力做的功为 A. -4 000 J　　　　　B. -3 800 J　　　　　C. -5 000 J　　　　　D. 200 J 4. 如图所示，在粗糙斜面顶端固定一弹簧，弹簧下端挂一物体，物体在 A 点处于平衡状态。现用平行于斜面向下的力拉物体，第一次直接拉 到B 点，第二次将物体先拉到C 点，从静止释放后，再回到B 点。 在这两次到B 点的过程中 A. 物体重力势能的改变量相等 B. 弹簧的弹性势能的改变量相等 C. 摩擦力对物体做的功相等 D. 弹簧弹力对物体做的功相等 5. 一物体静止在粗糙水平地面上。现用一大小为F1 的水平拉力拉动物体，经过一段时间后其速度 为v。若将水平拉力的大小改为F2，物体从静止开始经过同样的时间后其速度为2v。对于上述 两个过程，用WF1、WF2 分别表示拉力F1、F2 所做的功，Wf 1、Wf 2 分别表示物体前、后两次克 服摩擦力所做的功，则 A. WF2 ＞4WF1 　B. WF2 ＜4WF1 C. Wf 2 = 2Wf 1 　D. Wf 2 ＜2Wf 1 二、非选择题 6. 在“验证机械能守恒定律”的实验中，质量为1 kg 的重物自 由下落，在纸带上打出一系列的点，其中O 为第一个点，A、B、C 为从合适位置开始选取的连续三个点，如图所示。相邻计数点 间隔的时间为0.02 s，测量点间距所用单位为cm，取重力加速 度g = 9.8 m/s 2。（计算结果均保留3 位有效数字） （1）打点计时器打下计数点B 时，重物的速度是_________ m/s。 单元自我检测 A B C 第4 题 第6 题 A O B C 15.57 19.20 23.21 C B A O 第1 题 32 hysics P 第1 章　功和机械能 （2）从起点O 到打下计数点B 的过程中，重物重力势能的减少量ΔEp= _________ J，动能的增 加量ΔEk= _________ J。 （3）通过计算可知，在数值上ΔEp __________（选填“＞”“＜”或“ = ”）ΔEk。这是因为 　　　　　　　　　　　　　　　　　　　　　　　。 7. 如图所示，质量为m 的物体，以某一初速度v0 从A 点向下在光滑的轨道中运动。不计空气阻力， 若物体通过B 点时的速度为3 gR ，求： （1）物体在A 点时的速度； （2）物体离开C 点后还能上升的高度。 8. 如图所示，在某些少数民族地区，溜索也是一种交通工具。溜索通常由铁索和滑轮组成，某溜 索的铁索长度为l，等高固定于两岸。若质量为m 的滑行者滑到溜索中央最低点时高度下降了h0， 且滑行者及滑轮在滑行过程中所受阻力大小恒为f，不计滑轮质量，重力加速度为g。 （1）若滑行者初速度为0，当其滑到最低点时，滑行者的速度是多少？ （2）若要到达对岸，滑行者至少要做多少功？ （3）若要架设的溜索在两岸的固定点不等高，请从物理学角度回答架设溜索时应注意哪些问题。 第7 题 A B R 2R C v0 单元自我评价 回顾本单元的学业要求和所学内容，结合本次单元自我检测和平时学习情况进行自我评 价，写一篇“单元自我评价”报告。说说你学会了什么、存在什么问题及今后努力的方向等。 第8 题 33 第5 节　科学验证：机械能守恒定律 第2 章 导　入　更准、更远 第1 节　运动的合成与分解 第2 节　平抛运动 第3 节　科学探究：平抛运动的特点 第4 节　生活中的抛体运动 本章学业要求 ●能了解曲线运动的内涵，知道物体做曲线 运动的条件，能从运动合成与分解角度认 识抛体运动；能综合分析生产生活中的抛 体运动问题，解决一些相关的实际问题。 具有与抛体运动相关的初步的运动观念。 ——物理观念 ●能在熟悉情境中运用抛体运动模型解决问 题；能对平抛运动等问题进行分析推理， 能体会将复杂运动分解为简单运动的物理 思想；能用与抛体运动规律相关的证据说 明结论并作出解释；能从不同角度分析解 决抛体运动问题。 ——科学思维 ●能完成“探究平抛运动的特点”等物理 实验。能有针对性地提出可探究的物理问 题；能在他人帮助下制订相关的探究方 案，有根据器材调整实验方案的意识，获 取数据；能分析数据、提出猜想、形成与 实验目的相关的结论；能撰写比较完整的 实验报告，在报告中能呈现实验表格、数 据分析过程及实验结论，能根据实验报告 进行交流。 ——科学探究 ●通过对平抛运动特点的探究，能认识物理 学是人们有意识探究而形成的对自然现象 的描述与解释；能主动参加科技活动，有 学习物理的内在动力；能体会物理学的技 术应用对日常生活的影响。 ——科学态度与责任 34 hysics P 第2 章　抛体运动 飞镖运动是一项非常有趣 的运动。在一次飞镖比赛中，一 位同学沿水平方向正对飞镖盘的 靶心投出飞镖，飞镖能命中靶心 吗？从物理学的角度看，怎样才 能投得更准？ 导　入 更准、更远 在田径运动会上，运动员投掷 标枪、铅球、铁饼，都会非常注意 投掷的角度。如果要参加学校田径 运动会的投掷比赛，你知道怎样才 能投掷得更远吗？除了力度外，为 何还与投掷角度有关？ 投出的飞镖、掷出的标枪的运动均属于曲线运动。曲线运动有怎样的规律？如何探究 曲线运动的特点？本章将从运动的合成与分解入手，学习平抛运动等内容。 如何投飞镖更准 如何掷标枪更远 35 第1 节　运动的合成与分解 迷你实验室 第1节 运动的合成与分解 我们已经学习了研究某些直线运动的方法，如果物体的运动是较为复杂的曲线运动， 该如何分析呢？本节将学习利用运动的合成与分解的思想，分析和解决曲线运动的相关 问题。 1.认识曲线运动 自然界中物体的运动通常十分复杂。为了便于研 究，可根据研究的问题，将运动简化为直线运动和曲 线运动。 下落的苹果、竖直向上抛出的石子、沿平直公 路行驶的汽车，其运动轨迹都可视为直线，这种轨迹 为直线的运动称为直线运动。水平扔出的飞镖、绕 地球运动的卫星（图 2-1），其运动轨迹都是曲线， 这种轨迹为曲线的运动称为曲线运动（curvilinear motion）。 物体在什么情况下做曲线运动呢？让我们一起来观察下面的实验。 钢珠在磁铁吸引下的运动 首先推动钢珠，让钢珠在水平桌面上做直线运 动，观察其运动轨迹。然后在其运动轨迹旁放一块 磁铁（图2-2），再次推动钢珠，观察其运动轨迹。 解释观察到的现象。 图2-1　绕地球运动卫星的示意图 图2-2　钢珠在磁铁吸引下的 运动轨迹 36 hysics P 第2 章　抛体运动 迷你实验室 2.生活中运动的合成与分解 运动的合成与分解是处理复杂运动的基本方法。如果一个物体同时参与了几个运动， 那么物体实际发生的运动就是这几个运动的合运动，这几个运动就是物体实际运动的分运 动。对于复杂运动，可将其分解为几个简单的直线运动，再运用直线运动规律分别进行研 究。下面我们通过竹筏过小河的运动，来具体探讨运动的合成与分解问题。 曲线运动的速度方向 用笔画一条直线，你会发现，笔尖运动方向保持不变（图2-3）；再用笔画一条曲线， 观察笔尖运动，你会发现，笔尖运动方向不断改变（图2-4）。在图2-4 中，根据 平均速度的定义，笔尖经时间 t 沿曲线从A 点运动到B 点，平均速度的方向与位移AB 的方向相同。t 越短，平均速度越接近A 点的瞬时速度，其方向越接近A 点的切线方 向。因此，物体在某点的速度方向，就是沿曲线在该点的切线方向。 图2-3　画直线时，笔尖运动的 方向不变 B2 B1 B A 图2-4　画曲线时，笔尖运动的 方向不断改变 当物体所受合力的方向跟它的速度方向在同一直线上时，由牛顿第二定律可知，加速 度方向与速度方向在一条直线上，物体做直线运动。当物体所受合力的方向跟它的速度方 向不在同一直线上时，物体做曲线运动。钢珠第一次滚动时受到的阻力与速度方向相反， 做减速直线运动。钢珠第二次滚动时受到阻力和磁铁的吸引力，所受合力的方向与速度方 向不在同一直线上，做曲线运动。水平扔出的飞镖、喷泉口倾斜喷出的水柱，因为所受重 力的方向与速度的方向不在同一直线上，所以都做曲线运动。 速度是矢量，它既有大小，又有方向。做曲线运动的物体在某一点的速度方向，为 沿曲线在该点的切线方向。曲线运动中速度的方向时刻在变化，因此曲线运动是变速 运动。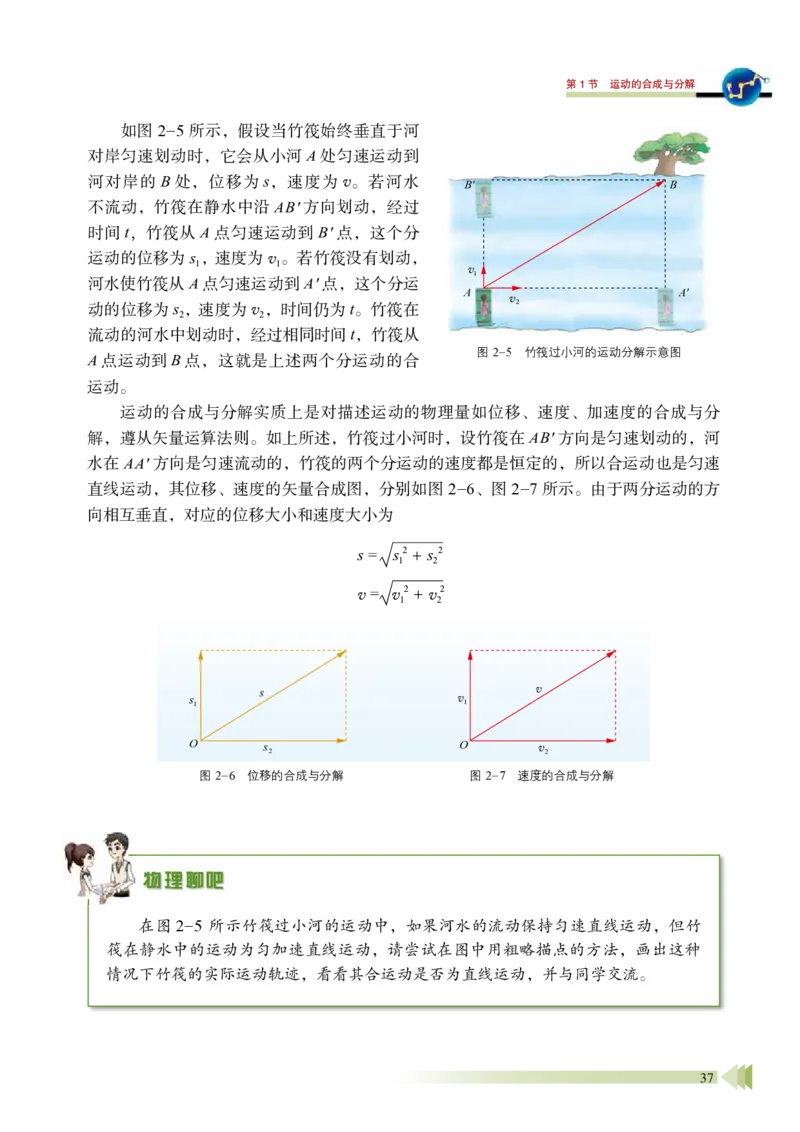 37 第1 节　运动的合成与分解 物理聊吧 如图2-5 所示，假设当竹筏始终垂直于河 对岸匀速划动时，它会从小河A 处匀速运动到 河对岸的B 处，位移为s，速度为v。若河水 不流动，竹筏在静水中沿AB' 方向划动，经过 时间t，竹筏从A 点匀速运动到B' 点，这个分 运动的位移为s1， 速度为v1。若竹筏没有划动， 河水使竹筏从A 点匀速运动到A' 点，这个分运 动的位移为s2， 速度为v2，时间仍为t。竹筏在 流动的河水中划动时，经过相同时间t，竹筏从 A 点运动到B 点，这就是上述两个分运动的合 在图2-5 所示竹筏过小河的运动中，如果河水的流动保持匀速直线运动，但竹 筏在静水中的运动为匀加速直线运动，请尝试在图中用粗略描点的方法，画出这种 情况下竹筏的实际运动轨迹，看看其合运动是否为直线运动，并与同学交流。 运动。 运动的合成与分解实质上是对描述运动的物理量如位移、速度、加速度的合成与分 解，遵从矢量运算法则。如上所述，竹筏过小河时，设竹筏在AB' 方向是匀速划动的，河 水在AA' 方向是匀速流动的，竹筏的两个分运动的速度都是恒定的，所以合运动也是匀速 直线运动，其位移、速度的矢量合成图，分别如图2-6、图2-7 所示。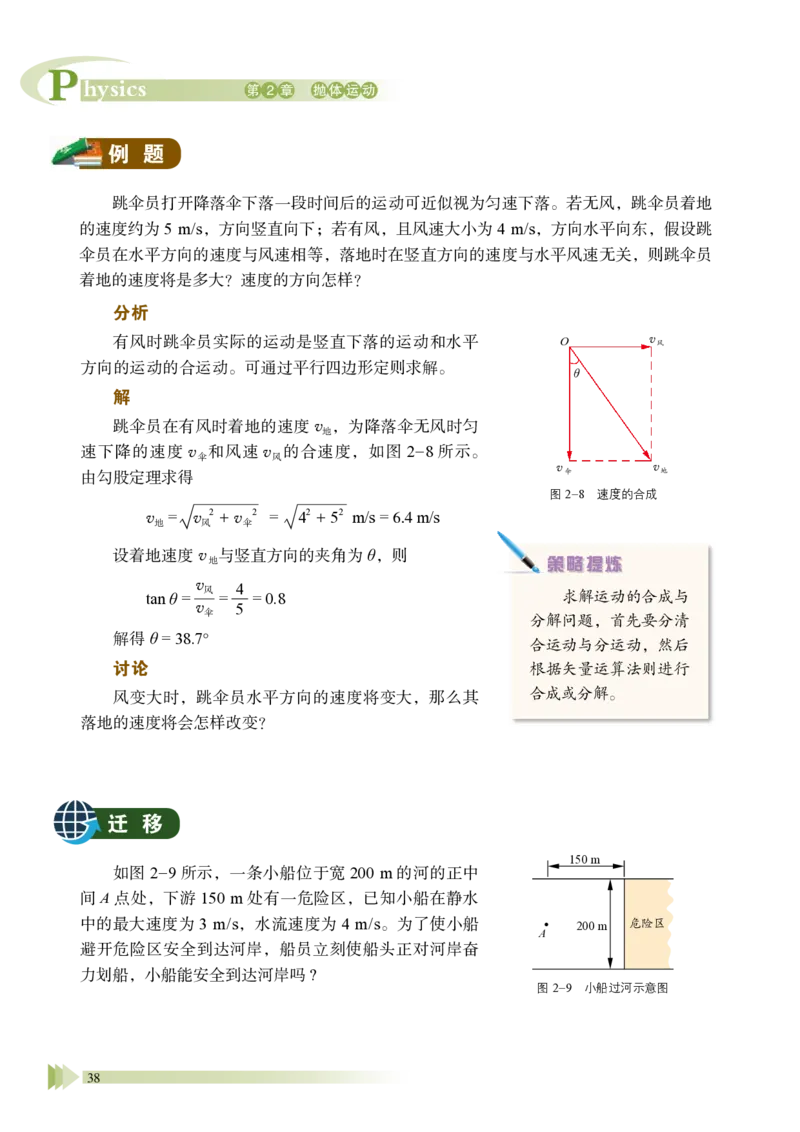由于两分运动的方 向相互垂直，对应的位移大小和速度大小为 s = s1 2 + s2 2 v = v1 2 + v2 2 图2-6　位移的合成与分解 图2-7　速度的合成与分解 s1 s O s2 O v1 v v2 A' A v1 v2 B B' 图2-5　竹筏过小河的运动分解示意图 38 hysics P 第2 章　抛体运动 跳伞员打开降落伞下落一段时间后的运动可近似视为匀速下落。若无风，跳伞员着地 的速度约为5 m/s，方向竖直向下；若有风，且风速大小为4 m/s，方向水平向东，假设跳 伞员在水平方向的速度与风速相等，落地时在竖直方向的速度与水平风速无关，则跳伞员 着地的速度将是多大？速度的方向怎样？ 例 题 如图2-9 所示，一条小船位于宽200 m 的河的正中 间A 点处，下游150 m 处有一危险区，已知小船在静水 中的最大速度为3 m/s，水流速度为4 m/s。为了使小船 避开危险区安全到达河岸，船员立刻使船头正对河岸奋 力划船，小船能安全到达河岸吗? 分析 有风时跳伞员实际的运动是竖直下落的运动和水平 方向的运动的合运动。可通过平行四边形定则求解。 解 跳伞员在有风时着地的速度v地，为降落伞无风时匀 速下降的速度v伞和风速v风的合速度，如图2-8 所示。 由勾股定理求得 v地 = v风 2 + v伞 2 = 4 2 + 5 2 m/s = 6.4 m/s 设着地速度 v 地与竖直方向的夹角为θ，则 tan θ = v风 v伞= 4 5 = 0.8 解得θ = 38.7° 讨论 风变大时，跳伞员水平方向的速度将变大，那么其 落地的速度将会怎样改变？ 图2-8　速度的合成 O v 风 v 伞 v 地 θ 策略提炼 求解运动的合成与 分解问题，首先要分清 合运动与分运动，然后 根据矢量运算法则进行 合成或分解。 迁 移 图2-9　小船过河示意图 A 150 m 200 m 危险区 39 第1 节　运动的合成与分解 1. 设空中的雨滴从静止开始下落，遇到水平方向吹来的风。请分析风速对雨滴下落时间和着地速 度的影响。 请提问 节练习 2. 下列说法正确的是 A. 物体在恒力作用下不可能做曲线运动 B. 物体在变力作用下一定做曲线运动 C. 物体的速度方向与合力方向不在同一条直线上时，物体一定做曲线运动 D. 做曲线运动的物体所受合力的方向一定是变化的 3. 如图所示，炮筒与水平方向的夹角为60°，炮弹从炮筒射出时速度的大小为800 m/s。求炮弹射出时 在竖直方向和水平方向的分速度大小。 4. 如图所示，汽艇在静水中的航行速度是12 km/h。若它在流速为3 km/h 的河水中航行，当船头 与河岸垂直时，求合速度的大小和方向。 5. 在雪地军事演习中，已知子弹射出时的速度是500 m/s，射击者坐在 以10 m/s 的速度向正东方向行驶的雪橇上，要射中位于他正北方的靶 子，必须向什么方向射击？（结果可用三角函数表示） 6. 某趣味物理实验中，在水平桌面上从桌子的一个角A 向B 发射一个乒 乓球，一同学在桌边试着用一支吹管将球由B 处吹进球门C，如图 所示。该同学将吹管对准C 用力吹，但球总是进不了球门。请帮他分 析失败的原因。 第4 题 第3 题 60° 第6 题 A C B 吹管 40 hysics P 第2 章　抛体运动 第2节 平抛运动 多数情况下，抛出去的物体做曲线运动。在射箭运动中，若运动员将箭头正对靶心水 平射出，这支箭在离弦后做直线运动还是曲线运动？最终能否射中靶心？要分析解决这些 问题，需要用到平抛运动的相关知识。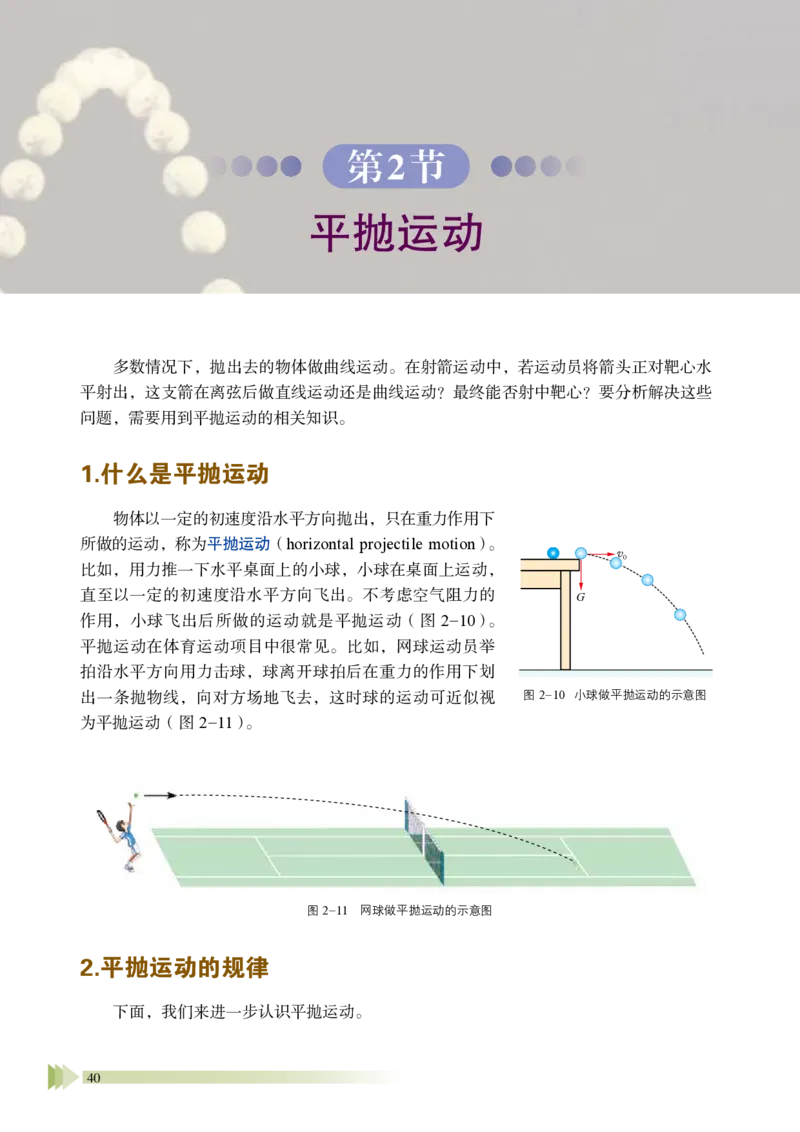 1.什么是平抛运动 物体以一定的初速度沿水平方向抛出，只在重力作用下 所做的运动，称为平抛运动（horizontal projectile motion）。 比如，用力推一下水平桌面上的小球，小球在桌面上运动， 直至以一定的初速度沿水平方向飞出。不考虑空气阻力的 作用，小球飞出后所做的运动就是平抛运动（图2-10）。 平抛运动在体育运动项目中很常见。比如，网球运动员举 拍沿水平方向用力击球，球离开球拍后在重力的作用下划 出一条抛物线，向对方场地飞去，这时球的运动可近似视 为平抛运动（图2-11）。 2.平抛运动的规律 下面，我们来进一步认识平抛运动。 图2-11　网球做平抛运动的示意图 图2-10 小球做平抛运动的示意图 v0 G 41 第2 节　平抛运动 实验与探究 研究平抛运动 （1）通过如图2-12（a）所示的平抛运动演示器来研究平抛运动。用小锤击打弹 性金属片C，球A 沿水平方向飞出，做平抛运动。与此同时，与球A 相同的球B 被 松开做自由落体运动。改变实验装置离地面的高度，多次实验，两球总是同时落地。 在同一高度改变小锤击打的力度，使球A 的平抛初速度大小不同，多次实验，两球 也总是同时落地。这说明做平抛运动的球A 在竖直方向上的运动情况与球B 相同， 为自由落体运动。 （2）在如图2-12（b）所示的装置中，M、N 是两个完全相同的轨道，轨道末端 都与水平方向相切。其中，轨道N 的末端与光滑水平面相切，轨道M 通过支架固定 在轨道N 的正上方。将小铁球P、Q 分别吸在电磁铁C、D 上，然后切断电源，使两 球以相同的初速度v0 同时通过轨道M、N 的末端，发现两球同时到达E 处，发生 碰撞。改变轨道M 在轨道N 上方的高度，再进行实验，结果两球也总是发生碰撞。这 说明做平抛运动的P 球在水平方向上的运动情况与Q 球相同，为匀速直线运动。 为了对平抛运动有更深入的认识，可用频闪照相拍摄小 球的运动。图2-13 是两个小球同时开始分别做自由落体运 动和平抛运动的频闪照片。从照片上可以看出，两个小球在 同一时刻的高度相同，表明做平抛运动的小球在竖直方向上 的运动规律与自由落体运动相同。进一步分析表明，小球在 水平方向上的运动是匀速直线运动。因此，平抛运动可以 分解为沿水平方向的匀速直线运动和沿竖直方向的自由落体 运动。 既然平抛运动可视为水平方向的匀速直线运动与竖直方 向的自由落体运动的合运动，我们就可以运用运动的合成与 分解，确定平抛物体在任一时刻的位置和速度。 图2-13　平抛运动和自由落体 运动的频闪照片 图2-12 研究平抛运动实验装置示意图 v0 v0 P Q C D 同 一 竖 直 线 N E M （b） （a） A B C 42 hysics P 第2 章　抛体运动 以抛出点为坐标原点，初速度方向为x 轴正 方向，重力方向为y 轴的正方向，建立直角坐标系 （图2-14）。在这个坐标系中，加速度方向与y 轴 正方向相同。根据匀速直线运动和自由落体运动的 规律，可以得到物体在任意时刻的位置坐标，即 x = v0t y = 1 2 gt2 　　还可得到物体在任意时刻的分速度和速度，即 vx = v0 vy = gt 　　由此可得　 v = vx 2 + vy 2 = v0 2 + g2t2 设速度的方向与水平分速度vx 的方向成θ 角，则 tan θ = vy vx = gt v0 物理聊吧 图2-15 为一探究小组成员探究平抛运动的情景。他在同一位置以不同的初速度 先后水平抛出三个小球。 请讨论：根据上述探究活动能否得出下列结论？ （1）在相同的高度，以大小不同的初速度水平抛出的小球，初速度越大，抛出 点到落地点的水平距离越远； （2）在高度不变的情况下，水平初速度的大小并不影响平抛物体在竖直方向上 的运动； （3）平抛运动过程经历的时间完全由抛出点到落地点的竖直高度决定，与抛出 时初速度的大小无关。 图2-15　投出的小球做平抛运动的示意图 能在熟悉情境中运用抛体运动模 型解决问题；能对平抛运动等问题进 行分析推理，能体会将复杂运动分解 为简单运动的物理思想；能用与抛体 运动规律相关的证据说明结论并作出 解释；能从不同角度分析解决抛体运 动问题。 ——科学思维 素 养 提 升 v0 vx vy v O P（x，y） x y θ 图2-14　在直角坐标系中分析 平抛运动的示意图 43 第2 节　平抛运动 例 题 在一次军事演习中，一架装载军用物资的飞机，在距地面500 m 的高处以50 m/s 的水平速度飞行。为了把军用物资准确地投掷到地面目标位置，飞行员应在距目标水平 距离多远处投放物资？（取重力加速度g = 10 m/s 2，不计空气阻力） 分析 如图2-16 所示，从飞机上投放的物资在离开飞机 瞬间具有与飞机相同的水平速度。因为其在下落过程中 只受重力作用，所以离开飞机后的物资做平抛运动。题 目中已知水平速度，求水平距离，需要确定物资在水平 方向的运动时间，该时间与竖直方向的运动时间相同， 可根据题目中给出的高度求出。 解 物资在空中飞行的时间t 取决于竖直高度。 由自由落体的位移公式 　H = 1 2 gt2 得　 t = 2H g = 2×500 10 s = 10 s 设投放物资处到地面目标位置的水平距离为s，由 于物资在水平方向做匀速运动，则 　　 s = v0t = 50×10 m = 500 m 即飞行员应在距地面目标位置水平距离为500 m 远 的地方投放物资。 图2-16　投放的物资做平抛运动的示意图 策略提炼 对于平抛运动问题， 一般可从位移关系和速度 关系求解。抓住平抛运动 （合运动）与水平分运动、 竖直分运动经过的时间相 等这一点，往往是解决问 题的关键。 平抛运动的问题中不仅会涉及位移关系，有 时还会涉及速度关系。如图2-17 所示，在摩托车 赛道上，水平路面的前方有一个壕沟，壕沟两侧高 度差为0.8 m，水平间距为5 m。若忽略空气阻力， 取重力加速度g = 10 m/s 2，摩托车水平飞出的速度 至少要多大才能越过这个壕沟？摩托车刚好越过壕 沟时速度方向与水平方向的夹角是多大？ 图2-17　摩托车的速度多大才能越过壕沟 0.8 m 5 m 讨论 要使军用物资准确地落到目标位置，需在飞机到达目标位置上空前投放。提前的时间 和水平距离分别由哪些因素决定？ 若将飞镖或箭正对靶心水平射出，能够命中靶心吗？ 迁 移 44 hysics P 第2 章　抛体运动 1. 取两个形状、大小尽量相同的山楂A、B，将山楂B 夹在 拇指与弯曲的食指之间，山楂A 放在中指上，使两山楂 尽量处于同一高度，如图所示。用食指弹击放在中指上 的山楂A，山楂A 沿水平方向抛出，山楂B 同时被释放， 自由下落。它们是否会同时落地？动手做一做，看看与 你的判断是否相同，并说明其中的道理。 2. 一架飞机沿水平方向匀速飞行，从飞机上每隔1 s 投放 一件物品，先后共投放四件相同的物品。如果不计空气 阻力，这四件物品在空中任何时刻总在飞机正下方的竖直线上，且落地点是等间距的。请判断 这种说法是否正确，并说明理由。 3. 关于平抛物体的运动，下列说法正确的是 A. 平抛运动是物体只在重力作用下的运动 B. 平抛运动是物体不受任何外力作用的运动 C. 做平抛运动的物体在水平方向初速度为0 D. 做平抛运动的物体在竖直方向初速度为0 4. 某实验小组成员站在高处沿水平方向抛出一物体。已知抛出时物体距地面5 m，物体落到地面时 的水平位移为9 m。取重力加速度g = 10 m/s 2，不计空气阻力，求物体抛出时水平速度的大小。 5. 以30 m/s 的初速度水平抛出一个物体，经过一段时间后，物体的速度方向与水平方向成30° 角。 取重力加速度g = 10 m/s 2，不计空气阻力，求此时物体相对于抛出 点的水平位移和竖直位移。 6. 如图所示，两支步枪先后在同一位置沿水平方向各射出一颗子弹， 打在100 m 远处的靶子上，两弹孔在竖直方向相距5 cm，其中A 为 甲枪的子弹孔，B 为乙枪的子弹孔。 （1）哪支枪射出的子弹速度较大？为什么？ （2）若甲枪子弹射出时的速度为500 m/s，取重力加速度g = 10 m/s 2， 不计空气阻力，求乙枪子弹射出时的速度。 节练习 请提问 第6 题 A B h 10 9 8 7 6 5 第1 题 A B 45 第3 节　科学探究：平抛运动的特点 第3节 科学探究：平抛运动的特点 我们经常能够观察到做平抛运动的物体在空中划过一条曲线，这条曲线有什么特点？ 本节我们将用实验的方法记录下做平抛运动物体的运动轨迹，然后根据记录的轨迹对平抛 运动的特点做进一步的探究。 实验目的 （1）描绘物体做平抛运动的轨迹并分析其特点。 （2）根据平抛运动的轨迹求平抛初速度。 实验器材 斜槽、小球、木板、铅垂线、坐标纸、图钉、刻度尺、铅笔（或卡孔）等。 实验原理与设计 将斜槽等器材安装起来，实验装置如图2-18 所示。小球从斜槽上滚下，通过水平槽 飞出后做平抛运动。使小球每次都从斜槽上同一位置由静止释放，小球在空中做平抛运动 的轨迹相同。设法用铅笔描出小球经过的位置。通过多次实验，在坐标纸上记录小球所经 过的多个位置，用平滑的曲线将各点连起来，从而得到小球做平抛运动的轨迹。 根据平抛运动的公式x = v0t 和y = 1 2 gt2，可求出小球做平抛运动的初速度。 安全警示 不随意扔小 球并注意小球落 地过程，避免小 球伤人或损坏实 验室物品。 图2-18　实验装置示意图 O x y 46 hysics P 第2 章　抛体运动 实验步骤 （1）用图钉把坐标纸钉在竖直木板上，在木板的左上角固定斜槽，并使其末端保持 水平。 （2）用悬挂在槽口的铅垂线把木板调整到竖直方向，并使木板平面与小球下落的竖直 面平行且靠近，固定好木板。 （3）把小球放在槽口处，用铅笔记下小球在槽口时球心在木板上的水平投影点O，再 利用铅垂线在纸上画出通过O 点的竖直线。 （4）将小球从斜槽上合适的位置由静止释放，使小球的运动轨迹大致经过坐标纸 的右下角。 （5）把笔尖放在小球可能经过的位置，如果小球运动中碰到笔尖，用铅笔在坐标纸该 位置画上一点。用同样的方法，从同一位置释放小球，在小球运动路线上描下若干点。 数据分析 （1）根据实验记录，在坐标纸上描绘小球平抛运动的轨迹。 （2）在平抛运动轨迹上选取几个水平间距相等的测量点，测出并计算相应物理量填 入你设计的表格中。 （3）观察描出的轨迹，与你熟悉的曲线进行比较，猜想y 与x 的关系，作出y-x2 图像， 验证你的猜想。 实验结论 请写出实验结论。 讨论 在平抛轨迹上依次选取水平方向等间距的 A、B、C、D、E、F 几个点，在竖直方向上测 量并计算yEF-yDE、yDE-yCD、yCD-yBC、yBC-yAB， 在误差允许的范围内，它们有怎样的特点？由 此你能得出小球在竖直方向上的运动性质吗？ 1. 请撰写“探究平抛运动的特点”的实验报告，注意在报告中呈现设计的实验表格以及数据分析 过程和实验结论。 2. 在“探究平抛运动的特点”实验中，下列做法可以减小实验误差的是 A. 使用体积更小的球 B. 尽量减小球与斜槽间的摩擦 C. 使斜槽末端的切线保持水平 D. 使小球每次都从同一高度由静止开始滚下 节练习 能有针对性地提出可探究的物理问 题；能在他人帮助下制订相关的探究方 案，有根据器材调整实验方案的意识， 获取数据；能分析数据、提出猜想、形 成与实验目的相关的结论；能撰写比较 完整的实验报告，在报告中能呈现实验 表格、数据分析过程及实验结论，能根 据实验报告进行交流。 注意提升实验操作能力及猜想验证 能力。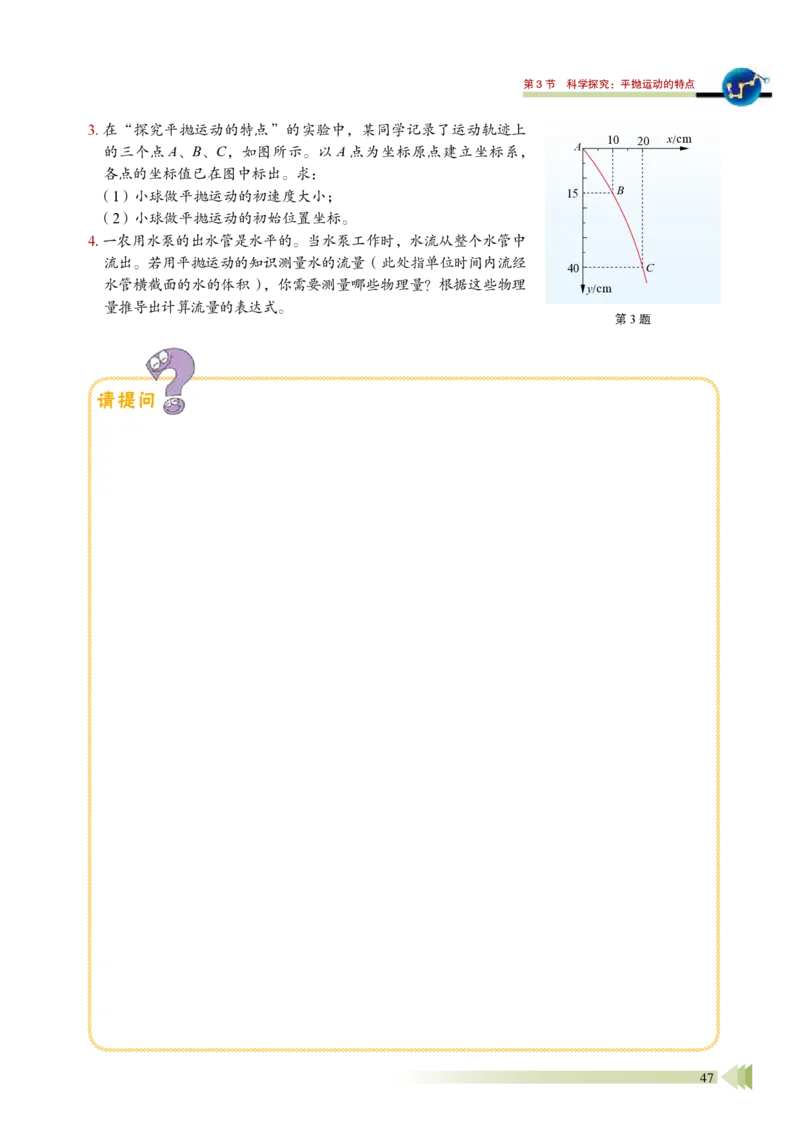 ——科学探究 素 养 提 升 47 第3 节　科学探究：平抛运动的特点 请提问 第3 题 y/cm x/cm 15 10 20 40 A B C 3. 在“探究平抛运动的特点”的实验中，某同学记录了运动轨迹上 的三个点A、B、C，如图所示。以A 点为坐标原点建立坐标系， 各点的坐标值已在图中标出。求： （1）小球做平抛运动的初速度大小； （2）小球做平抛运动的初始位置坐标。 4. 一农用水泵的出水管是水平的。当水泵工作时，水流从整个水管中 流出。若用平抛运动的知识测量水的流量（此处指单位时间内流经 水管横截面的水的体积），你需要测量哪些物理量？根据这些物理 量推导出计算流量的表达式。 48 hysics P 第2 章　抛体运动 田径场上投掷出的链球、铅球、铁饼、标枪以 及杂技表演中抛出去的球在空中的运动（图 2-19） 都可视为抛体运动。以一定的初速度将物体抛出， 物体仅在重力作用下所做的运动，称为抛体运动 （projectile motion）。根据抛出物体的初速度方向， 我们可把抛体运动分为平抛运动、竖直上抛运动、 竖直下抛运动和斜抛运动（斜上抛运动和斜下抛 运动）。 对于抛体运动，我们可用运动的合成与分解的 方法进行分析和研究。以斜抛（斜上抛）运动为 例，我们可建立一个直角坐标系，将坐标系的原点 选择在物体的抛出点，物体运动的水平方向为x 轴 正方向，竖直向上为y 轴正方向，如图 2-20 所示。 物体抛出方向与x 轴正方向之间的夹角称为抛射角， 用θ 表示。在这个坐标系中，物体被抛出的初速度 v0 可分解为水平方向的v0x、竖直方向的v0y。物体 在水平方向没有受到外力的作用，在竖直方向上只 受到竖直向下的重力作用。因此，斜上抛运动可看 成水平方向初速度为v0x 的匀速直线运动和竖直方 向初速度为v0y 的竖直上抛运动的合运动。图2-21 是做斜抛（斜上抛）运动小球的频闪照片。分析可 知，小球运动的轨迹是抛物线。 在图2-20 中，物体能到达的最大高度称为射 高，物体从抛出点到落地点的水平距离称为射程。 研究表明：抛射角一定，初速度增大，射高和射程 都增大。初速度大小一定，当抛射角为45° 时，射 第4节 生活中的抛体运动 图2-19　空中抛球表演 图2-21　做斜抛运动的小球的频闪照片 图2-20　分析斜抛运动的示意图 O θ v0y v0x v0 射高 y x 射程 49 第4 节　生活中的抛体运动 节练习 1. 抛体运动是匀变速运动吗？请说明理由。 2. 如果把物体斜向下抛出，请运用运动合成与分解的方法，说明斜向下的抛体运动可视为哪两个运 动的合运动。 能了解曲线运动的内涵，知道物体做曲线运动的 条件，能从运动合成与分解角度认识抛体运动；能综 合分析生产生活中的抛体运动问题，解决一些相关的 实际问题。具有与抛体运动相关的初步的运动观念。 ——物理观念 素 养 提 升 图2-22　美丽的喷泉 请提问 程最大；当抛射角为90° 时，射高最 大。斜抛运动的射高和射程是实际生 产生活中所关注的问题。 投掷出的链球、铁饼、标枪所做 的运动都可视为斜抛运动，考虑到抛 出点离地面有一段高度，为使它们的 射程最大，抛射角通常可略小于45° （请分析为什么）。有些喷泉喷射出的 水的运动也可视为斜抛运动，控制喷 水的喷射初速度，可使水的射程和射 高不同而形成美景（图2-22）。以上 是忽略空气阻力的情况，若考虑空气 阻力，情况会有所不同。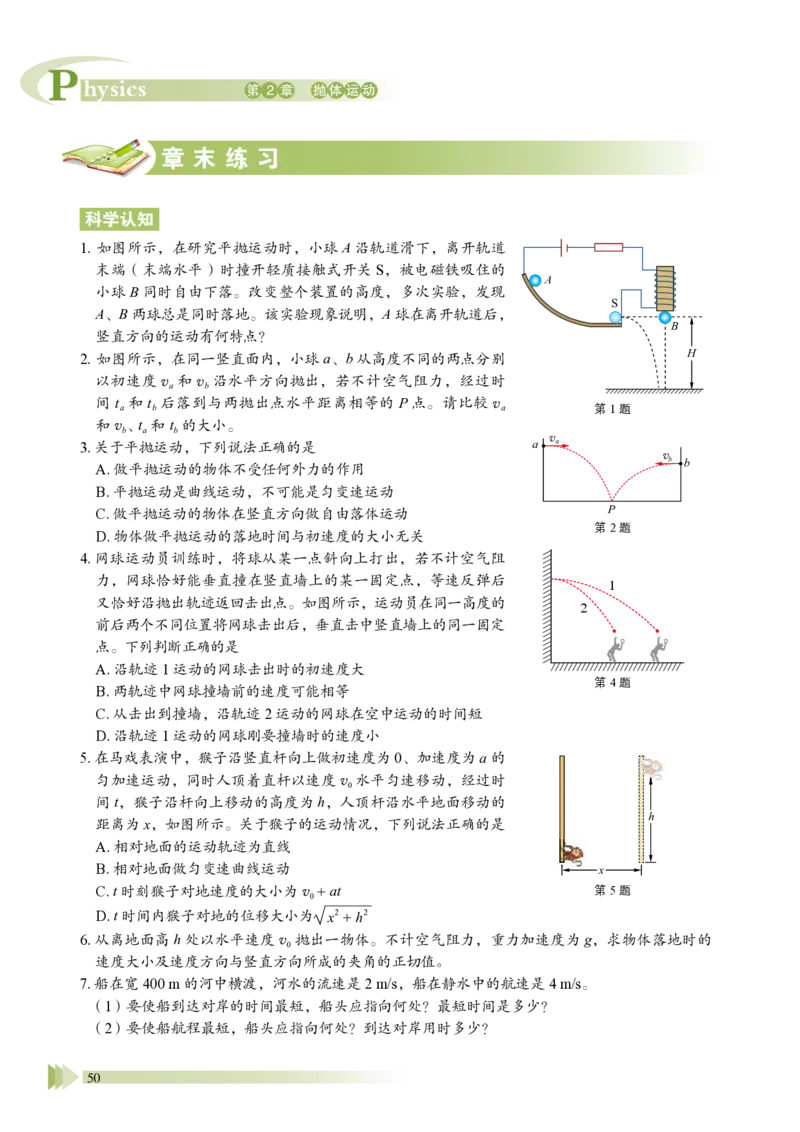 50 hysics P 第2 章　抛体运动 科学认知 1. 如图所示，在研究平抛运动时，小球A 沿轨道滑下，离开轨道 末端（末端水平）时撞开轻质接触式开关S，被电磁铁吸住的 小球B 同时自由下落。改变整个装置的高度，多次实验，发现 A、B 两球总是同时落地。该实验现象说明，A 球在离开轨道后， 竖直方向的运动有何特点？ 2. 如图所示，在同一竖直面内，小球a、b 从高度不同的两点分别 以初速度va 和vb 沿水平方向抛出，若不计空气阻力，经过时 间ta 和tb 后落到与两抛出点水平距离相等的P 点。请比较va 和vb、 ta 和 tb 的大小。 3. 关于平抛运动，下列说法正确的是 A. 做平抛运动的物体不受任何外力的作用 B. 平抛运动是曲线运动，不可能是匀变速运动 C. 做平抛运动的物体在竖直方向做自由落体运动 D. 物体做平抛运动的落地时间与初速度的大小无关 4. 网球运动员训练时，将球从某一点斜向上打出，若不计空气阻 力，网球恰好能垂直撞在竖直墙上的某一固定点，等速反弹后 又恰好沿抛出轨迹返回击出点。如图所示，运动员在同一高度的 前后两个不同位置将网球击出后，垂直击中竖直墙上的同一固定 点。下列判断正确的是 A. 沿轨迹1 运动的网球击出时的初速度大 B. 两轨迹中网球撞墙前的速度可能相等 C. 从击出到撞墙，沿轨迹2 运动的网球在空中运动的时间短 D. 沿轨迹1 运动的网球刚要撞墙时的速度小 5. 在马戏表演中，猴子沿竖直杆向上做初速度为0、加速度为a 的 匀加速运动，同时人顶着直杆以速度v0 水平匀速移动，经过时 间t，猴子沿杆向上移动的高度为h，人顶杆沿水平地面移动的 距离为x，如图所示。关于猴子的运动情况，下列说法正确的是 A. 相对地面的运动轨迹为直线 B. 相对地面做匀变速曲线运动 C. t 时刻猴子对地速度的大小为v0 + at D. t 时间内猴子对地的位移大小为 x2 + h2 章末练习 6. 从离地面高h 处以水平速度v0 抛出一物体。不计空气阻力，重力加速度为g，求物体落地时的 速度大小及速度方向与竖直方向所成的夹角的正切值。 7. 船在宽400 m 的河中横渡，河水的流速是2 m/s，船在静水中的航速是4 m/s。 （1）要使船到达对岸的时间最短，船头应指向何处？最短时间是多少？ （2）要使船航程最短，船头应指向何处？到达对岸用时多少？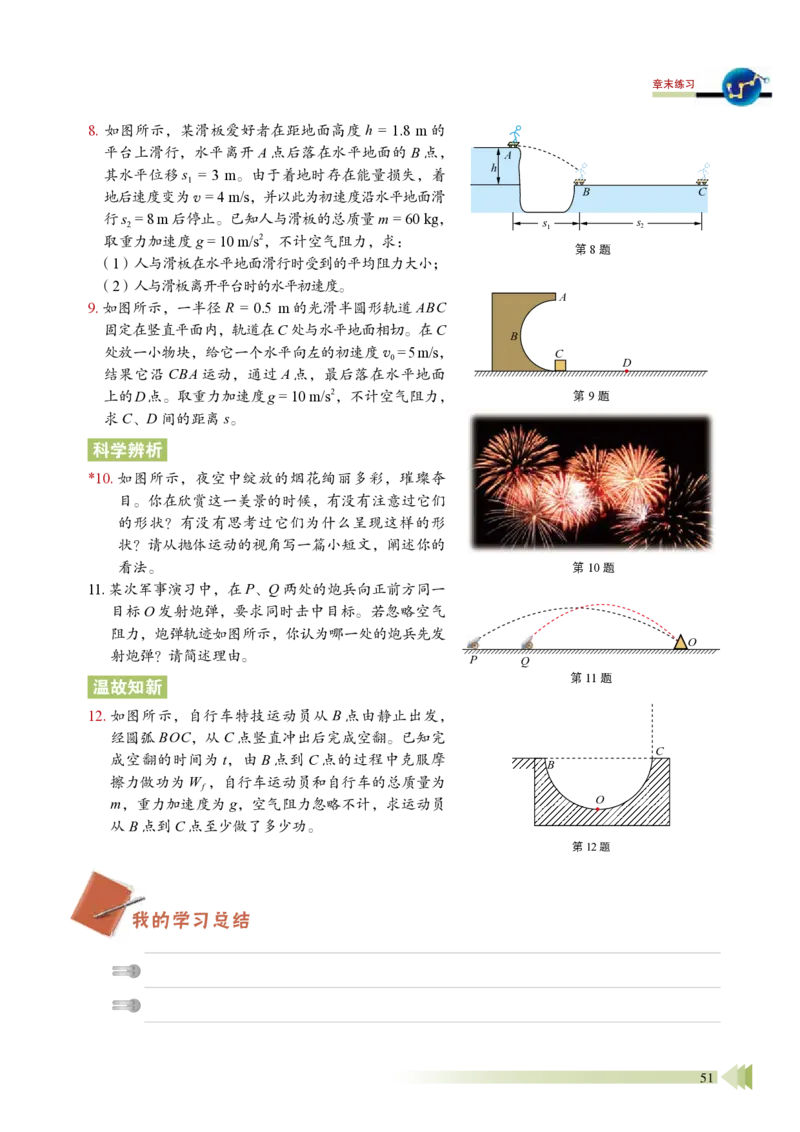 第1 题 A B S H va vb a b P 第2 题 1 2 第4 题 第5 题 x h 51 章末练习 8. 如图所示，某滑板爱好者在距地面高度h = 1.8 m 的 平台上滑行，水平离开A 点后落在水平地面的B 点， 其水平位移s1 = 3 m。由于着地时存在能量损失，着 地后速度变为v = 4 m/s，并以此为初速度沿水平地面滑 行s2 = 8 m 后停止。已知人与滑板的总质量m = 60 kg， 取重力加速度g = 10 m/s 2，不计空气阻力，求： （1）人与滑板在水平地面滑行时受到的平均阻力大小； （2）人与滑板离开平台时的水平初速度。 9. 如图所示，一半径R = 0.5 m 的光滑半圆形轨道ABC 固定在竖直平面内，轨道在C 处与水平地面相切。在C 处放一小物块，给它一个水平向左的初速度v0 = 5 m/s， 结果它沿CBA 运动，通过A 点，最后落在水平地面 上的D点。取重力加速度g = 10 m/s 2，不计空气阻力， 求C、D 间的距离s。 科学辨析 *10. 如图所示，夜空中绽放的烟花绚丽多彩，璀璨夺 目。你在欣赏这一美景的时候，有没有注意过它们 的形状？有没有思考过它们为什么呈现这样的形 状？请从抛体运动的视角写一篇小短文，阐述你的 看法。 11. 某次军事演习中，在P、Q 两处的炮兵向正前方同一 目标O 发射炮弹，要求同时击中目标。若忽略空气 阻力，炮弹轨迹如图所示，你认为哪一处的炮兵先发 射炮弹？请简述理由。 温故知新 12. 如图所示，自行车特技运动员从B 点由静止出发， 经圆弧BOC，从C 点竖直冲出后完成空翻。已知完 成空翻的时间为t，由B 点到C 点的过程中克服摩 擦力做功为Wf ，自行车运动员和自行车的总质量为 m，重力加速度为g，空气阻力忽略不计，求运动员 从B 点到C 点至少做了多少功。 第10 题 第9 题 B C D A h A B C s1 s2 第8 题 第11 题 O P Q 我的学习总结 第12 题 B C O 52 hysics P 第3 章　圆周运动 第3 章 导　入　生活中的圆周运动 第 1 节　匀速圆周运动快慢的描述 第2 节　科学探究：向心力 第3 节　离心现象 本章学业要求 ●会用线速度、角速度、周期描述圆周运 动，知道向心加速度的内涵，能分析匀速 圆周运动的向心力；能用向心力及向心加 速度等解释生产生活中的离心现象及其产 生的原因。具有与匀速圆周运动相关的运 动与相互作用的观念。 ——物理观念 ●能在熟悉情境中运用匀速圆周运动模型解 决问题；能对常见的匀速圆周运动进行分 析推理，获得结论；能用与匀速圆周运动 相关的证据说明结论并作出解释；能从不 同角度分析解决匀速圆周运动问题。 ——科学思维 ●能完成“探究向心力大小与半径、角速 度、质量的关系”等物理实验。能分析 物理现象，提出可探究的物理问题；能在 他人帮助下采用控制变量的方法设计相关 的探究方案，解决问题，能通过向心力演 示仪等器材获得证据；能分析归纳实验信 息、形成与实验目的相关的结论，作出解 释；能撰写比较完整的实验报告，在报告 中能呈现设计的实验步骤、实验表格、分 析过程及实验结论，能根据实验报告进行 交流。 ——科学探究 ●通过对向心力大小影响因素的探究，能认 识物理学研究依赖于实验器材的改进与创 新；有主动将所学知识应用于日常生活的 意识，能在合作中坚持自己的观点，也能 尊重他人；能体会物理学的技术应用对日 常生活的影响。 ——科学态度与责任 53 　 导　入 生活中的圆周运动 在我们周围，与圆周运动有关的事物 比比皆是。例如，钟表的指针、齿轮，电风 扇的叶片等，在转动时，其上的每一点都在 做圆周运动。你坐着不动，其实也在随着地 球自转做圆周运动。从人们拍摄的星空照片 中，你能得到什么启示？ 物体在做圆周运动时，会发生一 些奇特的现象。例如，在游乐场坐过 山车，即使过山车驶过环形轨道顶端 时，也没有竖直下掉的感觉；当乘坐 的车辆转弯时，你会感觉有侧倾的趋 势……物体做圆周运动时受力有什么 特点？物体做圆周运动有什么规律？ 这些规律在生活中有哪些应用？本章 我们将探究这些内容。 梦幻般的星空 充满刺激的过山车 54 hysics P 第3 章　圆周运动 圆周运动是很常见的运动，它有什么特点？我们该如何描述？本节将学习如何用线速 度、角速度、周期、频率和转速等物理量来描述匀速圆周运动的快慢。 1.线速度 物体在做圆周运动时，可能时快时慢，也可能快慢不变。 怎样描述物体做圆周运动的快慢呢？仔细观察钟表指针的转 动，会发现指针上的每一点经过相等时间各自都会转过相等 的弧长。我们把在任意相等时间内通过的弧长都相等的圆周 运动称为匀速圆周运动（uniform circular motion）。匀速圆周 运动是一种最简单的圆周运动。正常工作时，电风扇叶片、 光盘（图3-1）、齿轮等上面每一点的运动都可视为匀速圆 周运动。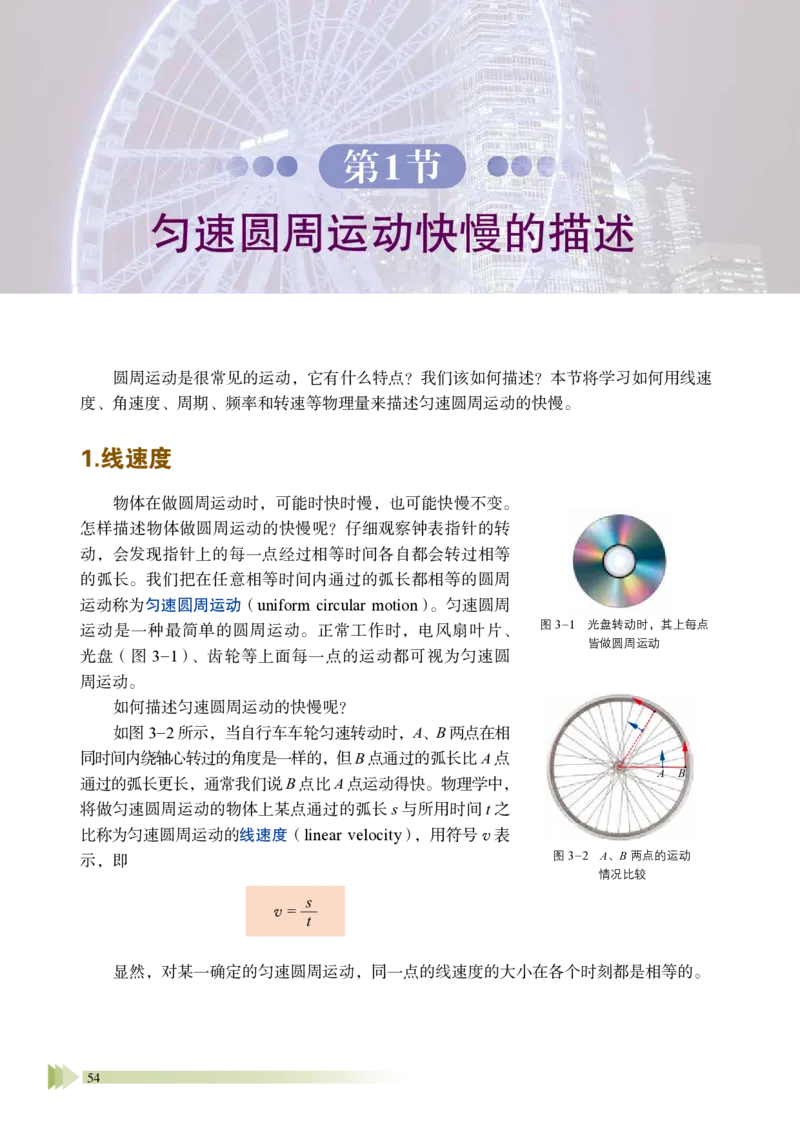 如何描述匀速圆周运动的快慢呢？ 如图3-2 所示，当自行车车轮匀速转动时，A、B 两点在相 同时间内绕轴心转过的角度是一样的，但B 点通过的弧长比A 点 通过的弧长更长，通常我们说B 点比A 点运动得快。物理学中， 将做匀速圆周运动的物体上某点通过的弧长s 与所用时间t 之 比称为匀速圆周运动的线速度（linear velocity），用符号v 表 示，即 v = s t 显然，对某一确定的匀速圆周运动，同一点的线速度的大小在各个时刻都是相等的。 第1节 匀速圆周运动快慢的描述 图3-1　光盘转动时，其上每点 皆做圆周运动 图3-2　A、B 两点的运动 情况比较 B A 55 第1 节　匀速圆周运动快慢的描述 线速度是矢量，不仅有大小，而且有方向。线速度的 方向是怎样的呢？ 我们知道，做曲线运动的物体在某点的速度方向，是 沿曲线在该点的切线方向。因此，圆周运动线速度的方向 总是沿圆周的切线方向。例如，在高速转动的圆盘砂轮上 打磨金属器件时，产生的火星沿着圆周的切线方向飞出 （图3-3）；下雨天转动雨伞时，水滴也是沿着圆周的切线 方向飞出的。 3.周期、频率和转速 物体做匀速圆周运动时，总是每隔一段相等的时间就重复原来的运动，我们称这样的 运动为周期性运动。在自然界中，除了匀速圆周运动，还有一些运动也是周期性运动，如 人的心跳和呼吸、钟摆的摆动、昼夜的更替、潮汐的涨落等。我们把周期性运动每重复一 次所需要的时间称为周期（period），用符号T 表示。匀速圆周运动的周期等于物体运动 一周所用的时间。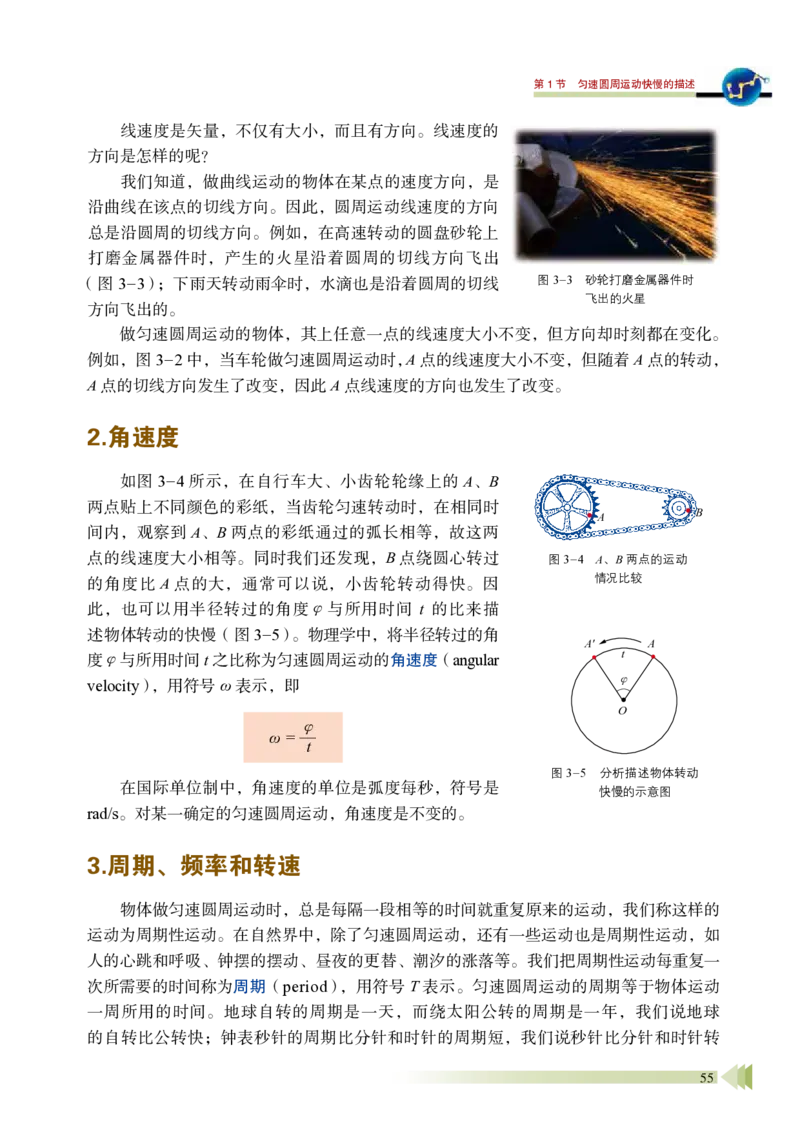地球自转的周期是一天，而绕太阳公转的周期是一年，我们说地球 的自转比公转快；钟表秒针的周期比分针和时针的周期短，我们说秒针比分针和时针转 2.角速度 如图3-4 所示，在自行车大、小齿轮轮缘上的A、B 两点贴上不同颜色的彩纸，当齿轮匀速转动时，在相同时 间内，观察到A、B 两点的彩纸通过的弧长相等，故这两 点的线速度大小相等。同时我们还发现，B 点绕圆心转过 的角度比A 点的大，通常可以说，小齿轮转动得快。因 此，也可以用半径转过的角度φ与所用时间 t 的比来描 述物体转动的快慢（图3-5）。物理学中，将半径转过的角 度φ与所用时间t 之比称为匀速圆周运动的角速度（angular velocity），用符号ω 表示，即 ω = φ t 在国际单位制中，角速度的单位是弧度每秒，符号是 rad/s。对某一确定的匀速圆周运动，角速度是不变的。 图3-4　A、B 两点的运动 情况比较 B A 图3-3　砂轮打磨金属器件时 飞出的火星 做匀速圆周运动的物体，其上任意一点的线速度大小不变，但方向却时刻都在变化。 例如，图3-2 中，当车轮做匀速圆周运动时，A 点的线速度大小不变，但随着A 点的转动， A 点的切线方向发生了改变，因此A 点线 速度的方向也发生了改变。 图3-5 分析描述物体转动 快慢的示意图 φ t A' O A 56 hysics P 第3 章　圆周运动 得快（图3-6）。因此，周期也可用来描述匀速圆周运动的快 慢：周期越短，运动越快；周期越长，运动越慢。 在物理学中，通常也用频率来描述周期性运动的快慢。 在一段时间内，运动重复的次数与这段时间之比称为频率 （frequency），用符号 f 表示。频率的大小等于周期的倒数，即 f = 1 T ，单位是赫兹，符号为Hz。显然，频率越高表示运动越 快，频率越低表示运动越慢。 在生产生活中，还常用转速来描述匀速圆周运动的快慢。 例如，发电机、电动机转动的快慢就是用转速来表示的。转速 是物体一段时间内转过的圈数与这段时间之比，用符号n表示， 单位是转每秒（r/s）或转每分（r/min）。当转速n 以转每秒为 单位时，转速与频率大小相等，即n = f 。转速也是计算机硬 盘（图3-7）和光驱性能的重要指标。你知道现在硬盘和光驱 的最大转速是多少吗？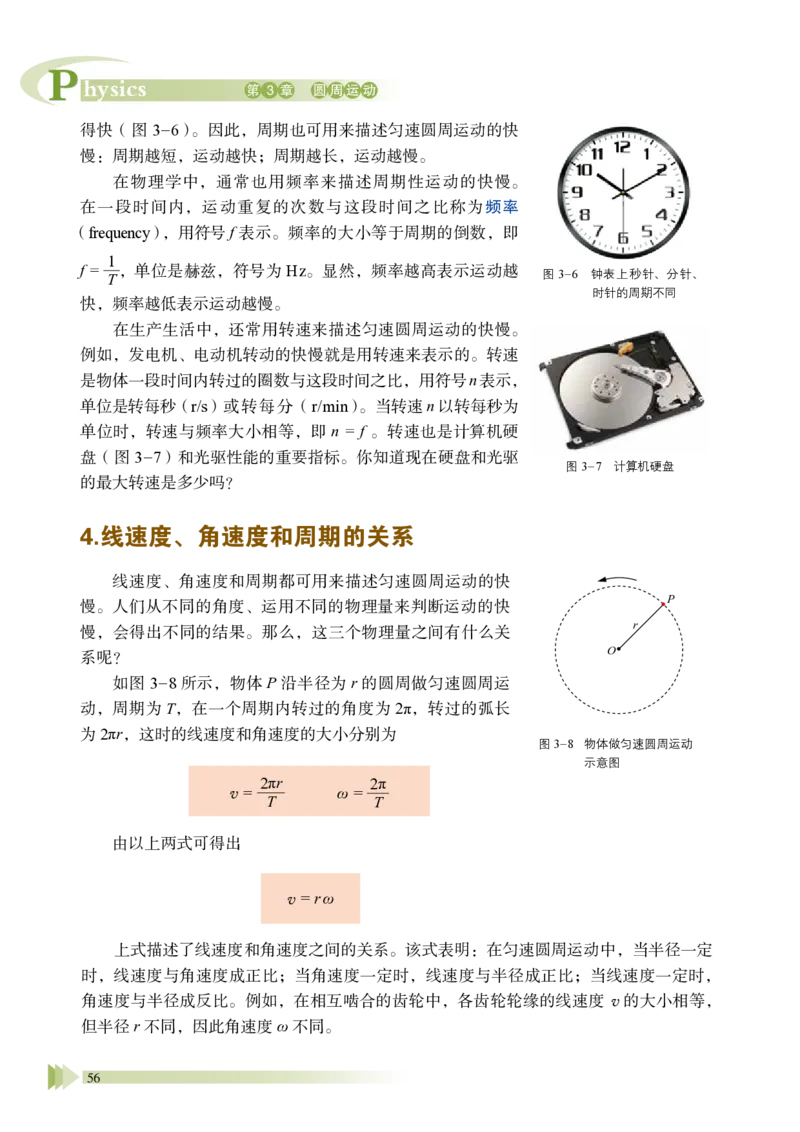 4.线速度、角速度和周期的关系 线速度、角速度和周期都可用来描述匀速圆周运动的快 慢。人们从不同的角度、运用不同的物理量来判断运动的快 慢，会得出不同的结果。那么，这三个物理量之间有什么关 系呢？ 如图3-8 所示，物体P 沿半径为r 的圆周做匀速圆周运 动，周期为T，在一个周期内转过的角度为2π，转过的弧长 为2πr，这时的线速度和角速度的大小分别为 v = 2πr T ω = 2π T 由以上两式可得出 v = r ω 图3-7　计算机硬盘 上式描述了线速度和角速度之间的关系。该式表明：在匀速圆周运动中，当半径一定 时，线速度与角速度成正比；当角速度一定时，线速度与半径成正比；当线速度一定时， 角速度与半径成反比。例如，在相互啮合的齿轮中，各齿轮轮缘的线速度 v 的大小相等， 但半径r 不同，因此角速度 ω 不同。 图3-6　钟表上秒针、分针、 时针的周期不同 图3-8 物体做匀速圆周运动 示意图 P O r 57 第1 节　匀速圆周运动快慢的描述 物理聊吧 在一些机器内部装有很多相互啮合 的大小齿轮（图3-9）。当机器转动时， 有人说小齿轮比大齿轮转得快，也有人 说它们的速度大小实际上是一样的。为 什么会有不同的说法？你怎么看？ 例 题 常见的转动传递方式有皮带传动、链条传动、摩擦传动和齿轮传动。图3-10 是一种 皮带传动装置示意图，A、B 两点分别是两轮轮缘上的点，C 是O2B 连线的中点，大轮与 小轮的半径之比为2 ：1。若皮带不打滑，试分别求出A、B、C 这三个点的线速度、角速 度和周期的比例关系。 图3-10　皮带传动装置示意图 O1 O2 A B C 分析 皮带不打滑，所以两轮轮缘上和皮带接触的A、B 两点具有大小相等的线速度。又因 为B、C 在同一个转轮上绕同一轴转动，所以B、C 两点具有相同的角速度。可从A、B、 C 三点运动的这些联系，结合线速度与角速度的关系求解。 解 A、B 具有大小相等的线速度，即 vA ：vB = 1 ：1。 又因为B 与C 在同一个转轮上，所以B、C 具有相同的角速度，即 ωB ：ωC = 1 ：1。 再由 v = r ω 及 rB = 2rC 可得 　　 vB ：vC = 2 ：1 因此 　　 vA ：vB ：vC = 2 ：2 ：1 图3-9　机器内部的齿轮 58 hysics P 第3 章　圆周运动 策略提炼 挖掘一些隐含条 件，弄清哪些物理量 相等，是解决此类问 题的关键。一般情况 下，皮带传动的轮缘 上各点具有大小相等 的线速度，同轴转动 的转轮上各点具有相 同的角速度。 由rB = 2rA 及 ω = v r 可得 　　 ωA ：ωB = 2 ：1 因此 　　 ωA ：ωB ：ωC = 2 ：1 ：1 由T = 2π ω 可得 　　 TA ：TB ：TC = 1 ：2 ：2 讨论 计算结果表明，小轮的角速度大于大轮的角速度， 小轮转动更快。小轮通过传动装置带动大轮能够降低转 速。例如，电机的转速一般很快，为了得到适当的转速， 通常电机通过传动装置带动大轮降低转速。如果大轮通 过传动装置带动小轮，会怎么样呢？请结合生活中的例 子进行分析。 地球绕地轴自转示意如图3-11 所示。设地球上两点A、 B 的纬度分别是φ1 和φ2，试分别求出这两点的线速度之 比和角速度之比。 1. 在匀速圆周运动中，保持不变的物理量是 A. 速度　　　　　　　B. 速率　　　　　　　C. 角速度　　　　　　　D. 周期 2. 某传动装置如图所示。右轮的半径为r，a 是它边缘上的一点。左侧是一轮轴，大轮的半径为 4r，小轮的半径为2r。b 点在小轮上，到小轮中心的距离为r。c 点和d 点分别位于小轮和大轮 的边缘上。若在转动过程中链条不打滑，下列说法正确的是 A. a 点与b 点的线速度大小相等 B. a 点与d 点的角速度大小相等 C. a 点与c 点的线速度大小相等 D. b 点与d 点的周期相等 节练习 迁 移 第2 题 c d a b r r 2r 4r 图3-11　地球自转示意图 地轴 B A O 赤道 φ1φ2 59 第1 节　匀速圆周运动快慢的描述 3. 如图所示，某变速自行车有多个半径不同的链轮和 多个半径不同的飞轮，链轮与脚踏共轴，飞轮与后 车轮共轴。自行车就是通过改变链条与不同飞轮和 链轮的配合来改变车速的。当人骑该车使脚踏板以恒 定的角速度转动时，若不变换链轮，应如何选择飞轮 才能使自行车行进的速度最大？请说明理由。 4. 若某飞机做匀速圆周运动的轨迹半径为3 000 m，线 速度为150 m/s，则飞机运动的周期、频率、转速和 角速度分别是多少？ 请提问 第6 题 A h R O 第5 题 A B d O φ 链轮 脚踏 飞轮 第3 题 5. 有同学设计了测量玩具枪的子弹速度的方法。如图所示，直径为d 的纸制圆筒以角速度ω 绕轴O 匀速转动，现把枪口对准圆筒，使子弹沿截面直径穿过圆筒。若圆筒旋转不到半周时，子弹在 圆筒上留下A、B 两弹孔，已知OA、 OB 的夹角为φ，不计圆筒对子弹速度的影响，那么子弹的 速度为多大？ *6. 如图所示，半径为R 的水平圆盘绕垂直于盘面的中心轴匀速转动。若在圆心O 正上方h 处沿 与半径OA 平行的方向水平抛出一个小球，要使小球在圆盘上的落点为A，求： （1）小球做平抛运动的初速度； （2）圆盘转动的角速度。 60 hysics P 第3 章　圆周运动 迷你实验室 1.向心力 下面我们通过实验来探究做圆周运动物体的受力特点。 我们知道，物体受到的合外力方向与运动方向不在同一条直线上时，物体将做曲线运 动。圆周运动是一种特殊的曲线运动，那么，做圆周运动的物体受力有什么特点呢？本节 将探究物体做圆周运动时所需的向心力。 上述实验中，小球在桌面上做圆周运动时，受到三个力的作用，即重力G、桌面支持 力N 和绳子的拉力F，合力就是绳子的拉力F。虽然拉力的方向时刻在改变，但它始终指 向圆心，这就是小球做圆周运动的原因。显然，做圆周运动的物体一定受到指向圆心的力 的作用，这个力称为向心力（centripetal force）。 向心力与圆周运动 取一根细绳，一端系一小球，另一端固定在 一枚图钉上。将图钉钉于水平光滑木板上，如图 3-12 所示。 （1） 用手指沿小球与图钉连线的垂直方向轻轻 弹击小球，在细绳未伸直前，小球做什么运动？ （2） 用手指弹击小球，方向同上，加大弹击 力量，使小球运动过程中细绳伸直。细绳伸直后， 小球做什么运动？ 第2节 科学探究：向心力 图3-12　实验装置 小球 图钉 61 第2 节　科学探究：向心力 向心力只改变速度的方向，不改变速度的大小。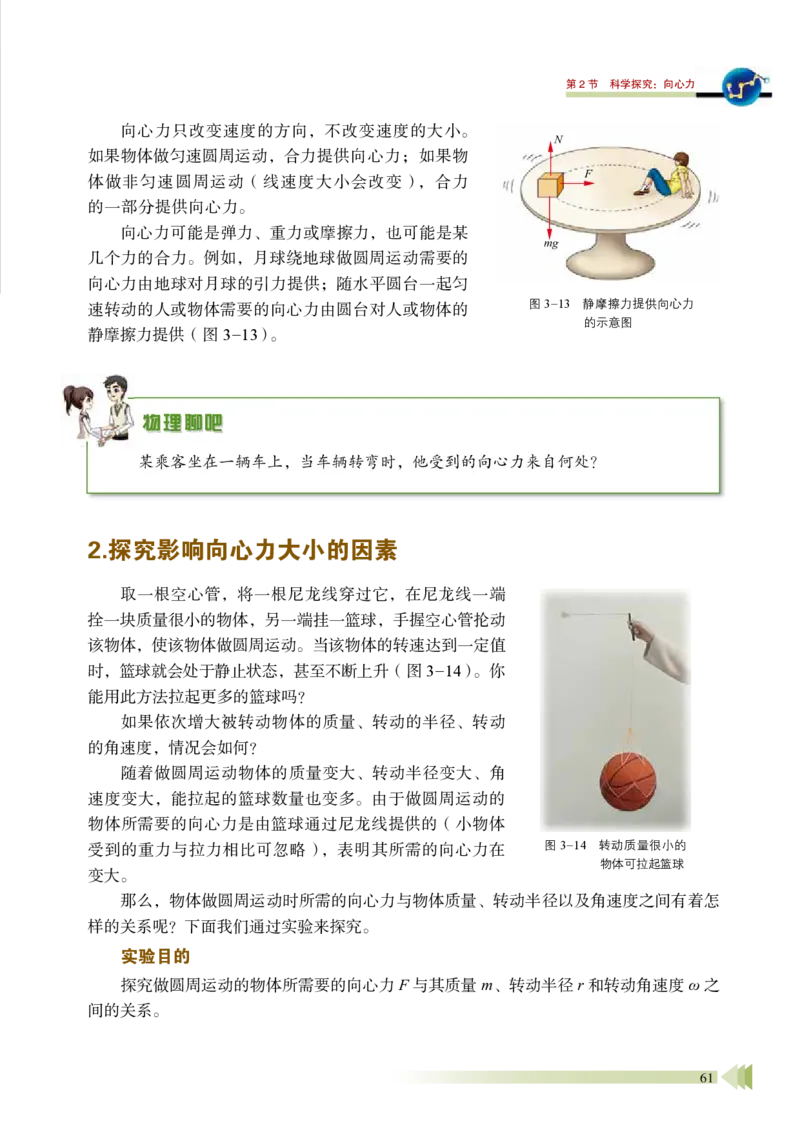 如果物体做匀速圆周运动，合力提供向心力；如果物 体做非匀速圆周运动（线速度大小会改变），合力 的一部分提供向心力。 向心力可能是弹力、重力或摩擦力，也可能是某 几个力的合力。例如，月球绕地球做圆周运动需要的 向心力由地球对月球的引力提供；随水平圆台一起匀 速转动的人或物体需要的向心力由圆台对人或物体的 静摩擦力提供（图3-13）。 物理聊吧 某乘客坐在一辆车上，当车辆转弯时，他受到的向心力来自何处？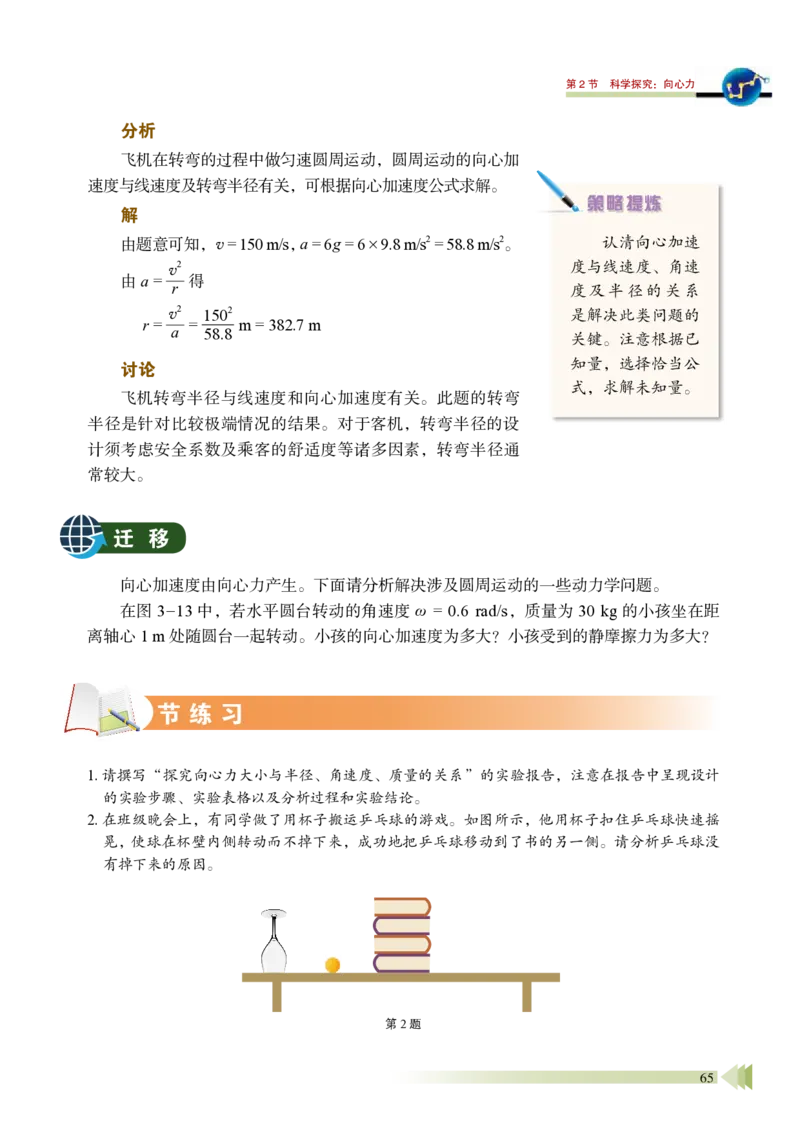 2.探究影响向心力大小的因素 取一根空心管，将一根尼龙线穿过它，在尼龙线一端 拴一块质量很小的物体，另一端挂一篮球，手握空心管抡动 该物体，使该物体做圆周运动。当该物体的转速达到一定值 时，篮球就会处于静止状态，甚至不断上升（图3-14）。你 能用此方法拉起更多的篮球吗？ 如果依次增大被转动物体的质量、转动的半径、转动 的角速度，情况会如何？ 随着做圆周运动物体的质量变大、转动半径变大、角 速度变大，能拉起的篮球数量也变多。由于做圆周运动的 物体所需要的向心力是由篮球通过尼龙线提供的（小物体 受到的重力与拉力相比可忽略），表明其所需的向心力在 变大。 那么，物体做圆周运动时所需的向心力与物体质量、转动半径以及角速度之间有着怎 样的关系呢？下面我们通过实验来探究。 实验目的 探究做圆周运动的物体所需要的向心力F 与其质量m、转动半径r 和转动角速度ω 之 间的关系。 图3-14　转动质量很小的 物体可拉起篮球 图3-13　静摩擦力提供向心力 的示意图 N mg F 62 hysics P 第3 章　圆周运动 实验步骤 （1） 把两个质量不同的小球分别放在长槽和短槽上，调整塔轮上的皮带和小球位置， 使两球的转动半径和角速度都相同。转动手柄，观察向心力的大小与质量的关系。 （2）换两个质量相同的小球，使两球的角速度相同。再增大长槽上小球的转动半径， 使两球的转动半径不同。转动手柄，观察向心力的大小与半径的关系。 （3） 若要研究向心力的大小与角速度的关系，请按照你设计的实验步骤操作。 数据分析 请记录实验现象，分析实验中得到的向 心力大小与物体质量、转动半径及角速度的 关系。 实验结论 请写出实验结论。 讨论 在探究影响向心力大小的因素时，为何 要注意控制变量？请通过日常生活中的案例， 说明控制变量的重要性。 实验器材 向心力演示器、小球等。 实验原理与设计 如图3-15 所示，匀速转动手柄，可使塔轮、长槽和短槽匀速转动，槽内的小球也就 随之做匀速圆周运动。挡板对小球的作用力提供了小球做匀速圆周运动的向心力。同时， 小球挤压挡板的力使挡板另一端压缩测力套筒的弹簧，压缩量可从标尺上读出，该读数即 显示了向心力的大小。如何研究向心力与物体质量、转动半径以及角速度之间的关系？ 方法点拨 实验应采用控制变量法进行探 究。在改变某个因素（如半径）的 同时，必须控制其他因素（如质量和 角速度）不变，以便于找出这个因素 影响向心力变化的规律。 安全警示 快速转动手柄 时，注意扶住实验 装置，以免其倾 覆，同时要防止小 球从槽内甩出。 图3-15　向心力演示器 手柄 长槽 短槽 标尺 变速塔轮 变速塔轮 63 第2 节　科学探究：向心力 DIS实验室 探究影响向心力大小的因素 我们还可用如图3-16 所示的DIS 向心力实验器 来进一步定量探究影响向心力大小的因素。实验中， 通过力传感器测出向心力F 的大小，通过光电门传感 器测量挡光杆的挡光时间，进而求出角速度ω 的大小。 借助DIS 数据采集器以及计算机等工具分析F 与m、r、 ω 之间的定量关系。 3.向心加速度 力是产生加速度的原因。既然做圆周运动的物体受到向心力的作用，那么它必然存在 一个由向心力产生的加速度，这个加速度称为向心加速度（centripetal acceleration）。向心 加速度的方向与向心力的方向一致，始终指向圆心。 根据牛顿第二定律和向心力公式，可以得到向心加速度的大小，即 a = v2 r a = rω2 对于某一确定的匀速圆周运动，向心力和向心加速度的大小恒定不变，但方向却时刻 在改变。因此，匀速圆周运动是加速度方向不断改变的变加速运动。 向心力和向心加速度的公式不仅适用于匀速圆周运动，而且适用于非匀速圆周运动。 一般圆周运动的速度大小变化时，向心力和向心加速度的大小也会发生变化。利用公式求 质点在某时刻或某位置的向心力和向心加速度的大小，其速度必须用该质点在该时刻或该 位置的瞬时速度。 图3-16　DIS 向心力实验器 能分析物理现象，提出可探究的物理问 题；能在他人帮助下采用控制变量的方法设计 相关的探究方案，解决问题，能通过向心力演 示仪等器材获得证据；能分析归纳实验信息、 形成与实验目的相关的结论，作出解释；能撰 写比较完整的实验报告，在报告中能呈现设计 的实验步骤、实验表格、分析过程及实验结 论，能根据实验报告进行交流。 注意提升实验设计能力及分析归纳能力。 ——科学探究 素 养 提 升 进一步研究得出，向心力的大小为 F = mrω2 如果将ω = v r 代入上式，可得 F = m v2 r 64 hysics P 第3 章　圆周运动 一般飞行员能承受的最大向心加速度的大小约为6g。在飞行表演中，飞机某次水平 转弯时，可视为在水平面内做匀速圆周运动。若飞机以150 m/s 的速度飞行，在该次水平 转弯过程中向心加速度为6g，取重力加速度g = 9.8 m/s 2，飞机水平转弯半径至少为多少? 例 题 拓展一步 向心加速度的理论推导 设一质点沿着半径为r 的圆周做匀速圆周运动，如图3-17（a）所示。在某时 刻该质点位于A 点，经过很短一段时间Δt 运动到B 点。在此期间，质点的速度由 vA 变为vB，速度改变量为Δv 。若把速度矢量vB 的始端移到A 点，其矢量关系如图 3-17 （b）所示。 图3-17　匀速圆周运动的速度矢量关系示意图 （a） （b） B A vA vB B A vA vB Δv r r r r O O 从图3-17（b）可以看出，速度矢量三角形与相应的△OAB 是相似三角形，且 vA 和vB 的大小都等于线速度v。用Δs 表示AB 弦长，有 Δv v = Δs r 即 Δv = Δs v r Δt 趋于零时，AB 弦长等于AB 弧长，因此Δs Δt 等于线速度的大小v。 Δt 趋于零时， Δv Δt 表示的就是向心加速度a 的大小，且有Δv Δt = v r ·Δs Δt ，因此 a = v2 r 再由Δt 趋于零时， vA 和vB 的夹角趋于零， Δv 的方向趋于与vA 垂直而指向圆心， 即加速度的方向指向圆心。这样，就通过理论分析得到了向心加速度的大小和方向。 65 第2 节　科学探究：向心力 1. 请撰写“探究向心力大小与半径、角速度、质量的关系”的实验报告，注意在报告中呈现设计 的实验步骤、实验表格以及分析过程和实验结论。 2. 在班级晚会上，有同学做了用杯子搬运乒乓球的游戏。如图所示，他用杯子扣住乒乓球快速摇 晃， 使球在杯壁内侧转动而不掉下来，成功地把乒乓球移动到了书的另一侧。请分析乒乓球没 有掉下来的原因。 节练习 策略提炼 认清向心加速 度与线速度、角速 度及半径的关系 是解决此类问题的 关键。注意根据已 知量，选择恰当公 式，求解未知量。 向心加速度由向心力产生。下面请分析解决涉及圆周运动的一些动力学问题。 在图3-13 中，若水平圆台转动的角速度ω = 0.6 rad/s，质量为30 kg 的小孩坐在距 离轴心1 m 处随圆台一起转动。小孩的向心加速度为多大？小孩受到的静摩擦力为多大？ 分析 飞机在转弯的过程中做匀速圆周运动，圆周运动的向心加 速度与线速度及转弯半径有关，可根据向心加速度公式求解。 解 由题意可知，v = 150 m/s， a = 6g = 6×9.8 m/s 2 = 58.8 m/s 2。 由 a = v2 r 得 　 r = v2 a = 150 2 58.8 m = 382.7 m 讨论 飞机转弯半径与线速度和向心加速度有关。此题的转弯 半径是针对比较极端情况的结果。对于客机，转弯半径的设 计须考虑安全系数及乘客的舒适度等诸多因素，转弯半径通 常较大。 迁 移 第2 题 66 hysics P 第3 章　圆周运动 请提问 第7 题 O C m l 3. 分析图中物体A、B、C 的受力情况，并说明这些物体做圆周运动时由哪些力来提供向心力？ 第3 题 O' O B （b） A O' O （a） O' O C θ （c） 4. 关于匀速圆周运动，下列说法正确的是 A. 匀速圆周运动是匀速运动 B. 匀速圆周运动是匀变速运动 C. 匀速圆周运动是匀速率圆周运动 D. 在任意相等的时间内通过的路程相等 5. 太阳的质量为1.99×10 30 kg，距银河系中心约3 万光年（1 光年≈ 9.46×10 12 km ），以220 km/s 左右的速率绕银河系中心转动。试计算太阳绕银河系中心转动时所需向心力的大小。 6. 在探究向心力大小与半径、角速度、质量的关系的实验中，若用两个质量相等的小球做实验， 且左边小球的轨道半径为右边小球的2 倍，转动时发现右边标尺上读取的向心力的大小是左边 的2 倍。那么，左边小球与右边小球的角速度之比是多少？ 7. 如图所示，长为l 的悬线一端固定在O 点，另一端系一小球。在O 点正下方C 点钉一钉子，O、 C 间距离为l 2 。把悬线另一端的小球拉到跟悬点同一水平面上无 初速度释放，小球运动到悬点正下方时悬线碰到钉子，则小球的 A. 线速度突然增大为原来的2 倍 B. 角速度突然增大为原来的2 倍 C. 向心加速度突然增大为原来的2 倍 D. 悬线拉力突然增大为原来的2 倍 67 第3 节　离心现象 如果你仔细观察高速公路转弯处的路面及铁路转弯处的轨道，会发现这些地方都是 外高内低，这样的设计有什么道理？本节将通过实例分析做圆周运动的物体所需的向 心力。 1.车辆转弯时所需的向心力 汽车在水平路面上转弯时（图3-18），有向外 侧滑的趋势，地面会对汽车产生指向内侧的静摩擦 力。这时在指向圆心的方向上存在静摩擦力f 的作 用，该力提供了汽车转弯所需的向心力。根据向心 力公式 f = m v2 r ，如果弯道半径一定，汽车速度超过 一定限度时，汽车就会向外侧滑。 为了给汽车、火车提供转弯时所需的向心力， 高速公路、铁路的弯道通常都设计成外高内低。这 样，汽车、火车转弯时，可依靠重力与支持力的合力 获得向心力。例如，按限定速度转弯的火车，受到重 力和支持力的作用，此时重力和支持力的合力F 不 为0，而是指向弯道的圆心，合力F 就提供了火车转 弯时做圆周运动的向心力。 如图3-19 所示，假设弯道的倾角为θ，则 F = mgtan θ ，根据向心力公式 mgtan θ = m v2 r ，可得 v = grtan θ 从上式可以看出，通过弯道时限定速度的大小 取决于弯道半径和倾角。 第3节 离心现象 图3-18　汽车转弯需向心力 火车车轮上有突出的轮缘，以保证车轮能行驶在铁轨上。对于半径、倾角都确定的某 个弯道而言，如果车速合适，重力与支持力的合力恰好提供火车转弯时所需的向心力。但 图3-19　重力与支持力的合力提供火 车转弯时的向心力 N F mg θ 68 hysics P 第3 章　圆周运动 如果车速过快，这个合力不足以提供所需的向 心力，外侧车轮轮缘就会与外轨发生挤压，以 补充缺少的向心力，这样会损坏外轨，甚至造 成脱轨。因此，火车转弯时都要限速。飞行中 的飞机要改变飞行方向时，飞机的机身也要倾 斜（图3-20）。与车辆不同的是，飞机转弯时 所需的向心力由重力和空气对它的作用力的合 力提供。 迷你实验室 2.竖直平面内的圆周运动分析 汽车在经过凸形路面和凹形路面时都不宜高速行驶，这是为什么呢？下面我们通过实 验来探究其中的道理。 凹凸桥 （1） 用两根铁丝弯成如图3-21 所示的 凹凸桥。首先，把一个小球放在凹桥底部 A 处，调节两轨间的距离，使球刚好不掉 下去，但稍加一点儿压力，球就会撑开两 轨下落。然后，让球从斜轨滚下。当球经 过凹桥底部A 处时，你观察到了什么？ （2） 把凹桥下面的搭钩扣上，并调整 凸桥顶端B 处两轨间的距离，使小球在B 处放置时，刚好能在此处撑开两轨下落。 然后，让小球从斜轨滚下。当球经过凸桥顶端B 处时，你又观察到了什么？ 图3-21　凹凸桥实验装置示意图 小球 搭钩 A B 铁丝轨道 图3-20　飞机转弯时机身倾斜 通过实验你会发现，小球运动到凹桥底部时从两轨间掉了下去，这说明运动的小球对 凹桥底部的压力大于静止时的压力；小球运动到凸桥顶端时没有落下，而是从桥面掠过， 这说明运动的小球对凸桥顶端的压力小于静止时的压力。 类似地，如图3-22 所示，汽车驶过凸形路面的顶端 时，所受的重力和支持力同在竖直方向，此时汽车行驶所 需的向心力就由这两个力的合力提供。那么，由向心力公 式 G - N = m v2 r 可知，N ＜G。根据牛顿第三定律，汽车 图3-22　汽车驶过凸形路面顶端 的示意图 G N 69 第3 节　离心现象 行驶到凸形路面顶端时对路面的压力小于汽车受到的重力， 此时汽车处于失重状态而不易被控制，并且速度越大越易 失控。因此，汽车在经过凸形路面时不宜高速行驶。 同样的道理，如图3-23 所 示，汽车行驶到凹形路面底部 时，汽车对路面的压力将大于 重力，容易出现超重现象而引 发爆胎。因此，汽车在经过凹 形路面时也不宜高速行驶。 在游乐场里，惊险又有趣的项目之一就是坐过山车。如 图3-24 所示的过山车轨道是由很高的滑轨和环形轨道构成的。 过山车高速驶过环形轨道顶端时，人们不会有从轨道上掉下 来的感觉。我们继续学习下面的内容，就能明白其中的道理。 图3-26　小球经过圆周最高点 的示意图 O mg v N 迷你实验室 图3-24　游乐场的过山车 实验室的“过山车” 用两根铁丝弯成如图3-25 所示的形 状。将小球从斜轨的某一高度释放，然 后逐步改变小球的释放点，看小球能否 越过环形轨道的顶端并继续沿轨道运行 而不掉落。 图3-23　汽车驶过凹形路面底部 的示意图 G N 图3-25　“过山车”实验装置 如图3-26 所示，当小球沿圆环内侧轨道经过最高点时， 向心力 F = mg + N ，根据向心力公式可得mg + N = m v2 r 。 当N = 0 时，mg = m v2 r ，小球恰好能通过最高点，此时，小 球的速度 v = gr ，所需的向心力完全由重力提供。可以 看出，小球能通过最高点的条件是在最高点的速度大小 v ≥ gr 。 现在，你知道为什么过山车到达轨道顶端时，人们不会 有掉下来的感觉了吧？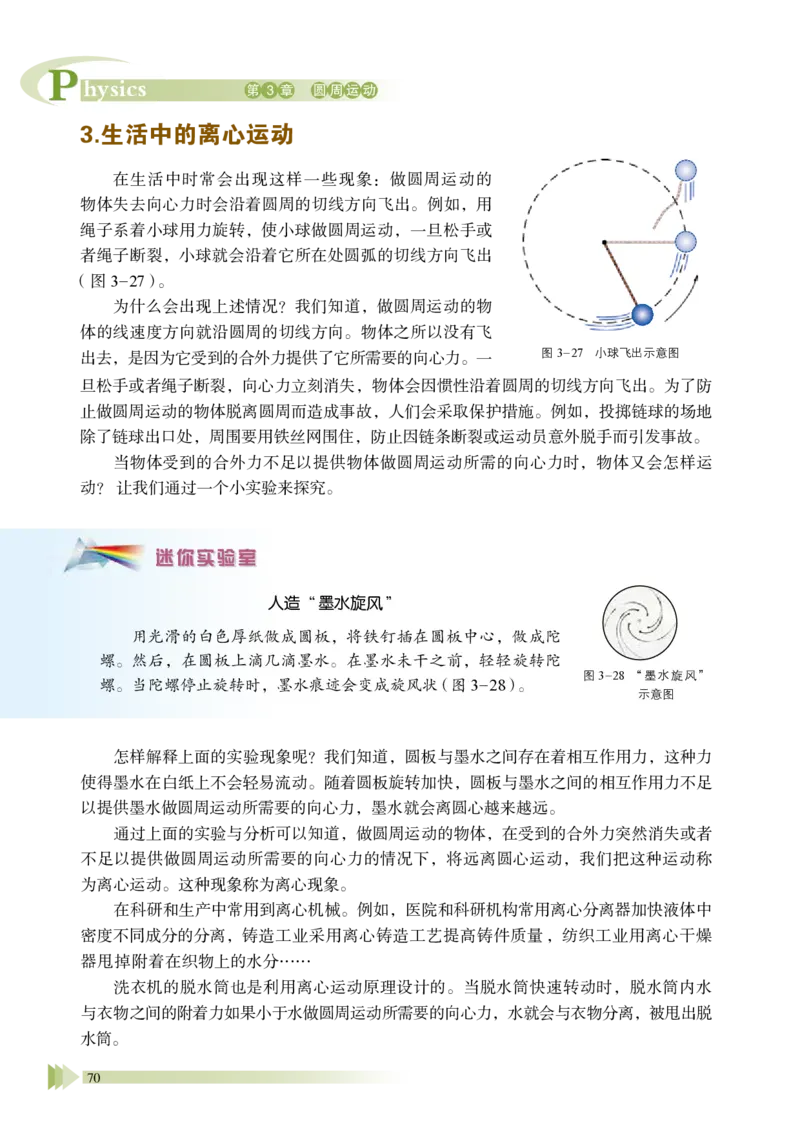 70 hysics P 第3 章　圆周运动 迷你实验室 3.生活中的离心运动 在生活中时常会出现这样一些现象：做圆周运动的 物体失去向心力时会沿着圆周的切线方向飞出。例如，用 绳子系着小球用力旋转，使小球做圆周运动，一旦松手或 者绳子断裂，小球就会沿着它所在处圆弧的切线方向飞出 （图3-27）。 为什么会出现上述情况？我们知道，做圆周运动的物 体的线速度方向就沿圆周的切线方向。物体之所以没有飞 出去，是因为它受到的合外力提供了它所需要的向心力。一 人造“墨水旋风” 用光滑的白色厚纸做成圆板，将铁钉插在圆板中心，做成陀 螺。然后，在圆板上滴几滴墨水。在墨水未干之前，轻轻旋转陀 螺。当陀螺停止旋转时，墨水痕迹会变成旋风状（图3-28）。 图3-28　“墨水旋风” 示意图 怎样解释上面的实验现象呢？我们知道，圆板与墨水之间存在着相互作用力，这种力 使得墨水在白纸上不会轻易流动。随着圆板旋转加快，圆板与墨水之间的相互作用力不足 以提供墨水做圆周运动所需要的向心力，墨水就会离圆心越来越远。 通过上面的实验与分析可以知道，做圆周运动的物体，在受到的合外力突然消失或者 不足以提供做圆周运动所需要的向心力的情况下，将远离圆心运动，我们把这种运动称 为离心运动。这种现象称为离心现象。 在科研和生产中常用到离心机械。例如，医院和科研机构常用离心分离器加快液体中 密度不同成分的分离，铸造工业采用离心铸造工艺提高铸件质量，纺织工业用离心干燥 器甩掉附着在织物上的水分…… 洗衣机的脱水筒也是利用离心运动原理设计的。当脱水筒快速转动时，脱水筒内水 与衣物之间的附着力如果小于水做圆周运动所需要的向心力，水就会与衣物分离，被甩出脱 水筒。 旦松手或者绳子断裂，向心力立刻消失，物体会因惯性沿着圆周的切线方向飞出。为了防 止做圆周运动的物体脱离圆周而造成事故，人们会采取保护措施。例如，投掷链球的场地 除了链球出口处，周围要用铁丝网围住，防止因链条断裂或运动员意外脱手而引发事故。 当物体受到的合外力不足以提供物体做圆周运动所需的向心力时，物体又会怎样运 动？ 让我们通过一个小实验来探究。 图3-27　小球飞出示意图 71 第3 节　离心现象 有些离心运动会对身体造成伤害。例如，飞机翻飞旋转时，离心运动会造成飞行员瞬 间大脑缺血、四肢沉重，这种现象即为过荷。严重时，飞行员会暂时失明甚至昏厥。飞行 员可以通过加强训练来提高抗荷能力。利用离心机可 以研究过荷对人体的影响，测试和训练人体的抗荷能 力。通过训练，可以减轻离心运动对人体的伤害。 有些离心运动会带来危险。如汽车在水平路面 转弯时所需的向心力是由车轮与地面间的静摩擦力 提供的，如果转弯所需的向心力大于最大静摩擦力， 汽车将做离心运动，容易造成事故。为了防止事故 的发生，汽车转弯时应放慢行车速度。 节练习 1. 如图所示，用绳子拴着小球转动。如果使小球越转越快，必须用越来越大的力拉住绳子，同时 绳子也越来越接近水平。分析一下，绳子可能被拉至水平吗？ 2. 铁路的弯道通常都设计成外高内低。若某转弯处的限定速度为v，当火车以该限定速度通过时， 请分析此时火车所需向心力的来源。若火车的实际速度低于限定速度，对铁轨有何影响？ 物理聊吧 （1）游乐场的旋转盘上，开始时有的人离转轴近一些，有的人离转轴远一些 （图3-29）。当旋转盘加速时，哪些人更容易发生滑动？为什么？ （2）握住体温计的顶部用力甩，就能把水银 甩回玻璃泡内。如何解释这个现象？医院每天 要用很多支温度计，如果一支支地甩，是很费 时间的。你能想到简便方法吗？请上网查询，或 者实地调研，然后与同学分享你调研的结果。 图3-29 旋转盘 会用线速度、角速度、周期描 述圆周运动，知道向心加速度的内 涵，能分析匀速圆周运动的向心 力；能用向心力及向心加速度等解 释生产生活中的离心现象及其产生 的原因。具有与匀速圆周运动相关 的运动与相互作用的观念。 ——物理观念 素 养 提 升 第1 题 72 hysics P 第3 章　圆周运动 3. 如图所示，质量相等的甲、乙两物体放在旋转的圆台上，甲物体 到转轴的距离是乙物体到转轴距离的两倍，甲、乙与圆台间的最 大静摩擦力相等。当圆台旋转时，甲、乙均未滑动。请分析当圆 台的转速逐渐增大时哪个物体先滑动，并说明理由。 4. 长为l 的轻绳，其一端固定于O 点，另一端连有质量为m 的小球， 该小球绕O 点在竖直平面内做圆周运动，g 为重力加速度。求： （1）小球刚好到达最高点时的速度； （2）小球到达最高点速度为2 gl 时轻绳受到的拉力。 5. 摩托车通过一座拱形桥顶部时速度为10 m/s，此时车对桥面的压力只有重力的3 4 。如果摩托车 通过该桥顶部对桥面的压力只有重力的1 4 ，则车的速度为多大？ *6. 一把打开的雨伞半径为r，伞边缘距水平地面的距离为h。当该雨伞绕伞柄以角速度ω 水平旋 转时，雨点自边缘甩出下落，在地面上形成一个大圆圈。已知重力加速度为g。试求这个大圆 圈的半径。 请提问 第3 题 乙 甲 73 章末练习 章末练习 科学认知 1. 某质点以恒定的角速度做匀速圆周运动，当轨道半径增大时 A. 周期增大　　　　B. 线速度增大　　　　C. 向心加速度减小　　　　D. 向心力减小 2. 对于匀速圆周运动，下列有关物理量之间关系的描述正确的是 A. 角速度一定与转速成正比 B. 角速度一定与半径成反比 C. 线速度一定与半径成正比 D. 周期一定与半径成正比 3. 如图所示，两个轮通过皮带传动，设皮带与轮之间不打滑，A 是以 O 为圆心、R 为半径的轮缘上的一点，B 是以O' 为圆心、2R 为半 径的轮缘上的一点，C 与B 在同一轮上，且O'C = 2 3 R。当皮带带 动两轮转动时，A、B、C 三点的角速度之比、线速度之比、向心 加速度之比分别是多少？ 4. 汽车在水平圆弧弯道上以恒定速率在2 s 内行驶20 m 的路程后，司机发现汽车速度的方向改变 了30°。请估算弯道的半径大小及汽车的向心加速度大小。（结果保留2 位有效数字） 5. “翻滚过山车”是一种非常刺激的娱乐项目。载有乘客的过山车从轨道的高处沿轨道自由滑下， 由重力势能转化而来的动能使过山车能够冲过一个竖直方向的圆形轨道。设圆形轨道的半径R = 13 m， 如果只有一节车厢（可以视为质点）从高处滑下，不考虑摩擦和空气阻力，要使此车厢能通过 圆形轨道的最高点，车厢开始下滑的位置至少应该比圆形轨道的最高点高出多少？ 6. 如图所示，两个质量相同的小球，用长度不等的细线拴在同一点并在同一水平面内做匀速圆周 运动。它们的 A. 运动周期一样 B. 运动角速度一样 C. 运动线速度大小一样 D. 向心加速度大小一样 7. 高速公路拐弯处的路面通常都是外高内低。如图所示，在某路段汽车向左拐弯，其运动可视为 半径为R 的圆周运动，汽车左侧的路面比右侧的路面低一些，高度差为h，路基的水平宽度为d， 路面的宽度为l。已知重力加速度为g，要使车轮与路面之间的横向（即垂直于前进方向）摩擦 力等于零，汽车转弯时的车速应为多少？ 8. 一体重为68.8 kg 的探险队员欲利用悬挂于树上的攀岩绳索从悬崖一边摆荡至悬崖的另一边。已知 绳索长为18 m，能承受的最大拉力为950 N，人在摆荡过程中竖直下落的最大高度为3.2 m，取重力 加速度 g = 10 m/s 2。在此探险队员摆荡过程中，绳索的最大拉力是多少？绳索会断吗？ 第7 题 l h d 第3 题 B O' C A O 第6 题 O 74 hysics P 第3 章　圆周运动 9. 如图所示，水平转盘上放有质量为m 的物块（可视为质点），当物 块到转轴OO' 的距离为r 时，连接物块和转轴的绳刚好被拉直（绳 上张力为0）。物块和转盘间的最大静摩擦力是物块对转盘压力的μ 倍。求： （1） 当转盘以角速度 ω = μg 2r 旋转时，细绳的拉力T1 ； （2） 当转盘以角速度 ω = 3μg 2r 旋转时，细绳的拉力T2 。 科学辨析 10. 如图所示，游乐场的旋转飞椅非常刺激有趣，随着旋转速度越 来越快，飞椅会逐渐远离圆柱。链球运动员在将链球抛掷出手 之前，总要双手拉着链条加速转动几周，这样可使链球的速 度尽量增大，抛掷出手后球飞得更远。同样，在运动员加速转 动链球过程中，链球会逐渐远离运动员。这两种现象有什么联 系？你能讲出其中的道理吗？ 温故知新 11. 某学校的排球场长为18 m，球网高度为2 m，如图所示。一同 学站在离网3 m 的线上（虚线所示）正对网跳起，将球水平击 出。若球飞行过程中不计阻力，取重力加速度g = 10 m/s 2。 （1）设击球点在3 m 线正上方2.5 m 高度处，击球的速度在什 么范围内才能使球既不触网也不出界？ （2）若击球点在3 m 线正上方的高度小于某个值时，无论水平 击球的速度有多大，球不是触网就是出界，试求这个高度。 3 m 2 m 18 m 第11 题 第10 题 12. 请根据第2 章（抛体运动）和第3 章（圆周运动）的内容，结合你的理解，画出概念图。 我的学习总结 第9 题 r m O' O 75 第3 节　离心现象 一、选择题（本题共5 小题。在每小题给出的四个选项中，第1 ～3 题只有一项符合题目要求， 第4、5 题有多项符合题目要求） 1. 关于运动的合成，下列说法不正确的是 A. 合运动的位移为分运动位移的矢量和 B. 合运动的速度为分运动速度的矢量和 C. 合运动的加速度为分运动加速度的矢量和 D. 合运动的时间为分运动的时间之和 2. 甲、乙两物体都做匀速圆周运动，其质量之比为1 ：2 ，转动半径之比为1 ：2 ，在相等时间内 甲转过60°，乙转过45°。它们所受的合外力之比为 A. 1 ：4 B. 2 ：3 C. 4 ：9 D. 9 ：16 单元自我检测 第5 题 甲 乙 3. 如图所示，半径为r 的圆筒绕竖直中心轴OO′ 旋转，小物块a 靠在 圆筒的内壁上，它与圆筒内壁间的动摩擦因数为μ。若最大静摩擦 力近似等于滑动摩擦力，要使a 不下落，圆筒转动的角速度ω 至少 应为 A. μgr B. μg C. g r D. g μr 4. 如图所示，一固定容器的内壁是光滑半球面，在半球面水平直径的 一端有一质量为m 的质点P。它沿容器内壁由静止下滑到最低点， 已知重力加速度大小为g。设质点P 在最低点时，向心加速度的大 小为a，容器对它的支持力大小为N，则 A. a = 2g B. a = g C. N = 3mg D. N = 2mg 5. 如图所示，甲、乙两人面对面拉着弹簧测力计在冰面上做圆周运动。 已知m 甲 = 80 kg，m 乙 = 40 kg，两人相距0.9 m，弹簧测力计的示数 为96 N。若忽略冰面的摩擦，此时两人的 A. 线速度大小相同，均为4.0 m/s B. 角速度相同，均为2 rad/s C. 运动半径相同，均为0.45 m D. 运动半径不同，甲为0.3 m，乙为0.6 m 二、非选择题 6. 在“探究平抛运动的特点”实验中，可以描绘出小球做平抛运动的 轨迹。实验简要步骤如下： A. 让小球多次从　　 　　 　　 释放，在一张印有小方格的纸上 记下小球碰到铅笔笔尖的一系列位置，如图中a、b、c、d 所示。 B. 按要求安装好器材，注意　 　 　，记下平抛初位置O 点 和过O 点的竖直线位置。 C. 取下白纸，以O 为原点、竖直线为y 轴建立坐标系，用平滑曲 线画出平抛运动物体的轨迹。 （1）将上述步骤补充完整。 a b c d 第6 题 第4 题 P 第3 题 O' O a 76 hysics P 第3 章　圆周运动 7. 如图所示，高台滑雪运动员经过一段滑行后从斜坡上的O 点水 平飞出，落到斜坡上的A 点，A 点与O 点的距离sOA = 12 m。已 知斜坡与水平面的夹角θ = 37°，运动员连同滑雪板的总质 量m = 50 kg，忽略空气阻力的影响，取重力加速度g = 10 m/s 2， sin 37°= 0.6，cos 37°= 0.8。求： （1）运动员在空中飞行的时间； （2）运动员离开O 点时的速度大小。 8. 如图所示，一人在进行杂技表演，表演者手到碗的距离为l，且 手与碗在同一竖直平面内，绳子能够承受的最大拉力是碗和碗内 水重力的8 倍。已知重力加速度为g，要使绳子不断，表演获得 成功，求： （1）碗通过最高点时速度的最小值； （2）碗通过最低点时速度的最大值。 （2）上述实验步骤的合理顺序是　 。 （3）已知图中小方格的边长l = 2.5 cm，取重力加速度g = 10 m/s 2，则小球平抛的初速度 v0 = 　　 　 （用l、g 表示），其值是　 　　　　。 第7 题 A O θ 第8 题 回顾本单元的学业要求和所学内容，结合本次单元自我检测和平时学习情况，根据下表 左列的提示，进行自我评价，在表中填写学会了什么、存在什么问题、今后努力的方向等相 关内容。 所学内容 我学会的 存在问题 努力方向 物理概念 规律及应用 模型建构 科学推理 科学论证 质疑创新 问题 证据 解释 交流 科学本质 科学态度 社会责任 单元自我评价 77 第3 节　离心现象 第4 章 导 入 从嫦娥奔月到“阿波罗”上天 第 1 节 天地力的综合：万有引力定律 第 2 节 万有引力定律的应用 第 3 节 人类对太空的不懈探索 本章学业要求 ●能了解万有引力定律的内涵，会计算人造 卫星的环绕速度，知道第二宇宙速度和第 三宇宙速度；能用万有引力定律解释一些 天体运动问题。具有与万有引力定律相关 的运动与相互作用的观念。 ——物理观念 ●能将一些熟悉天体的运动抽象成匀速圆周 运动模型；能分析一些简单的天体运动问 题，通过推理获得结论；能用与万有引力 定律相关的证据解释一些天象；能对一些 错误认识提出有依据的质疑。 ——科学思维 ●能了解卡文迪许实验的重要性，并能提出 问题；能体会卡文迪许扭秤实验方案设计 的巧妙之处，能感受到科学定律的预测作 用；能认识到测定物理常量在科学研究中 的重要性；能撰写与万有引力定律相关的 调研报告，能与同学交流。 ——科学探究 ●能认识发现万有引力定律的过程及重要意 义，认识科学定律对人类探索未知世界的 作用；知道科学包含大胆的想象和创新； 有探索太空、了解太空的兴趣，能为牛顿 力学对航天技术发展的重大贡献而振奋。 ——科学态度与责任 78 hysics P 第4 章　万有引力定律及航天 远古，人们就梦想能够飞出地球，探索浩 瀚星空的奥秘，各种关于星空的神话流传至今。 “嫦娥奔月”便是我国家喻户晓的古代民间神 话。这美丽神话反映了人们对星辰的崇拜，对 “飞天”的向往。 从嫦娥奔月到“阿波罗”上天 导　入 “嫦娥奔月”的想象画面 斗转星移，岁月如梭。1969 年，“阿波罗 十一号”载着宇航员登上了月球，人类足迹首 次留在月球。2019 年，我国“嫦娥四号”成 功着陆月球，并通过“鹊桥”传回世界第一张 近距离拍摄的月背影像图。举世瞩目的“嫦娥 工程”实现了古老神话中的“嫦娥”“玉兔” 及“鹊桥”的神奇功能。 中国人的探月梦已变为现实 人类借助宇宙飞船，飞向万籁俱寂的茫茫太空，不仅登上了月球，还孜孜不倦地探索 更遥远的星空。为什么宇宙飞船能升空？为何能绕地球旋转？为何还能挣脱地球束缚飞向 月球？学习本章后，你将会找到答案。 79 第1 节　天地力的综合：万有引力定律 自远古时期，人类就开始孜孜不息地探索天体 的运动规律，创作了很多关于星空的神话、史诗。 “仰观吐曜，俯察含章”，浩瀚宇宙中，日月星辰 周而复始地运行（图4-1），它们有着怎样的运动 规律？本节将学习开普勒定律和万有引力定律。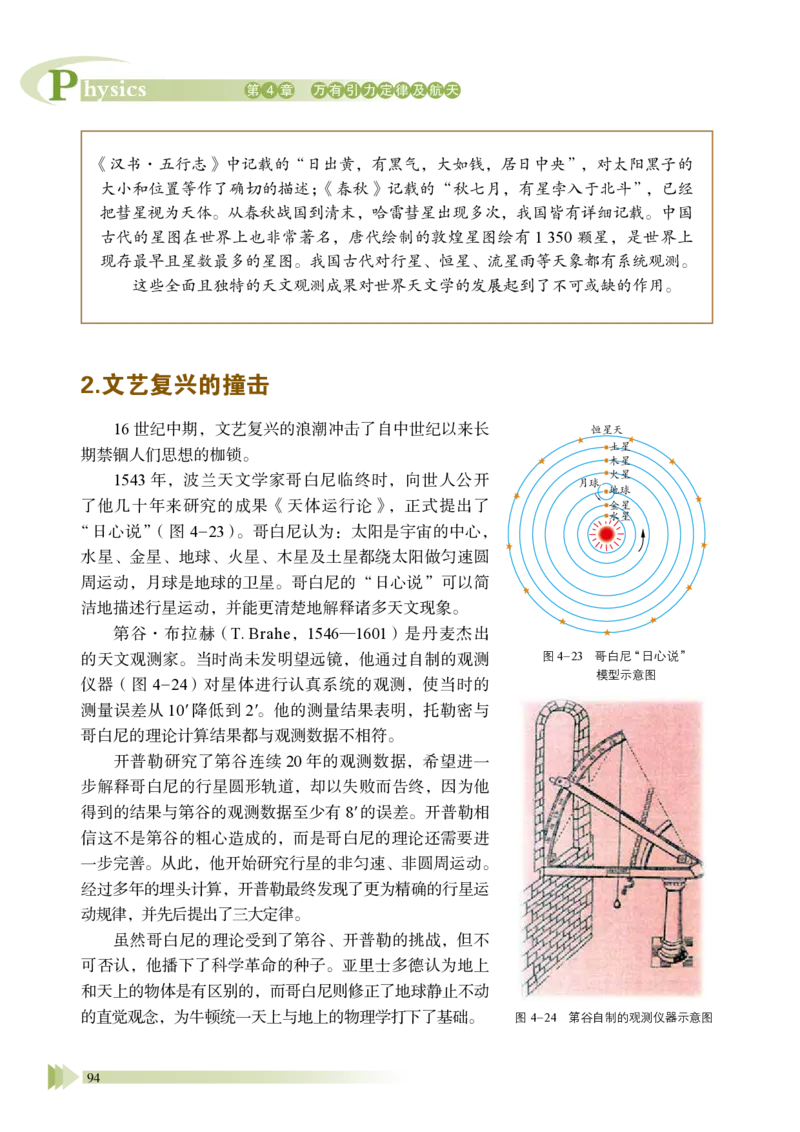 1.行星运动的规律 自古希腊起，人们一直以为太阳、月亮和星星都是围绕地球转动 的，直到波兰天文学家哥白尼（ N. Copernicus，1473—1543）提出“日 心说”。继而，德国天文学家开普勒（J. Kepler，1571—1630，图4-2） 根据前人的观测和研究，于1609 年和1619 年先后提出了太阳系行星 运动的三大定律。 开普勒第一定律：所有行星绕太阳运动的轨道都是椭圆，太阳位 于椭圆的一个焦点上（图4-3）。图中F1、F2 是椭圆的两个焦点。 开普勒第二定律：任何一个行星与太阳的连线在相等的时间内扫 过的面积相等（图4-4）。 开普勒第三定律：行星绕太阳运行轨道半长轴a 的立方与其公转周期T 的平方成正比 （图4-5）。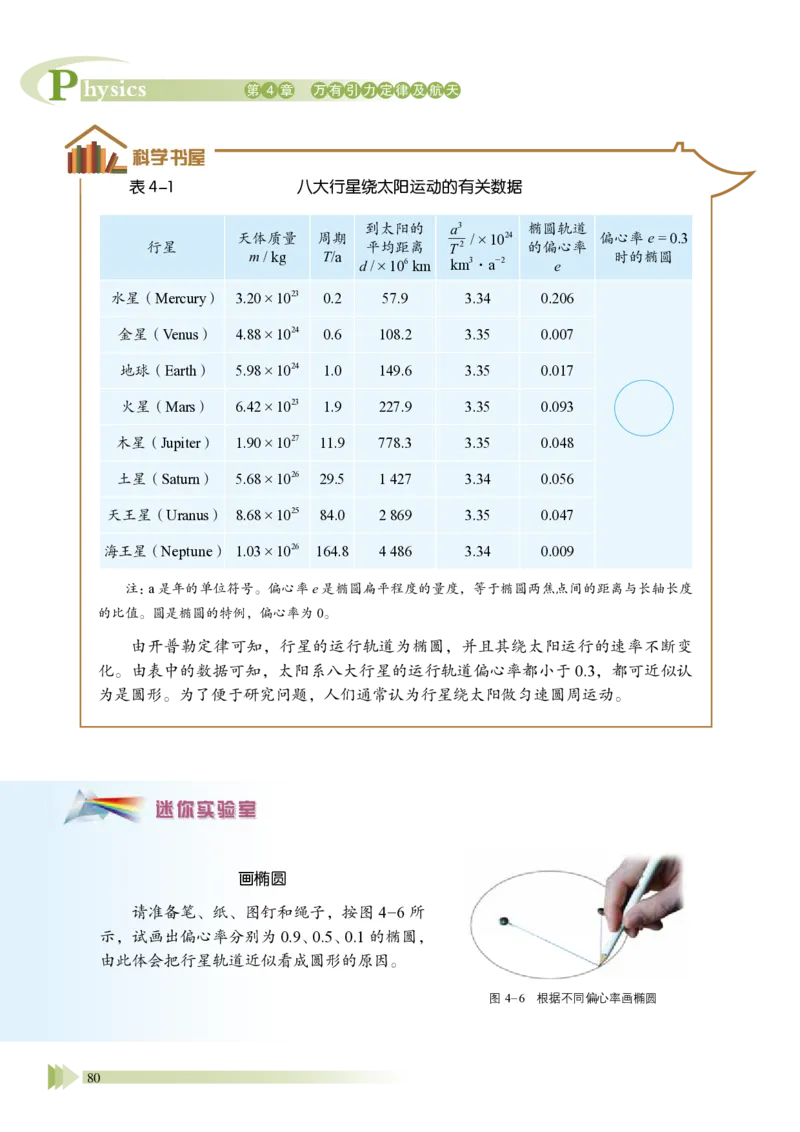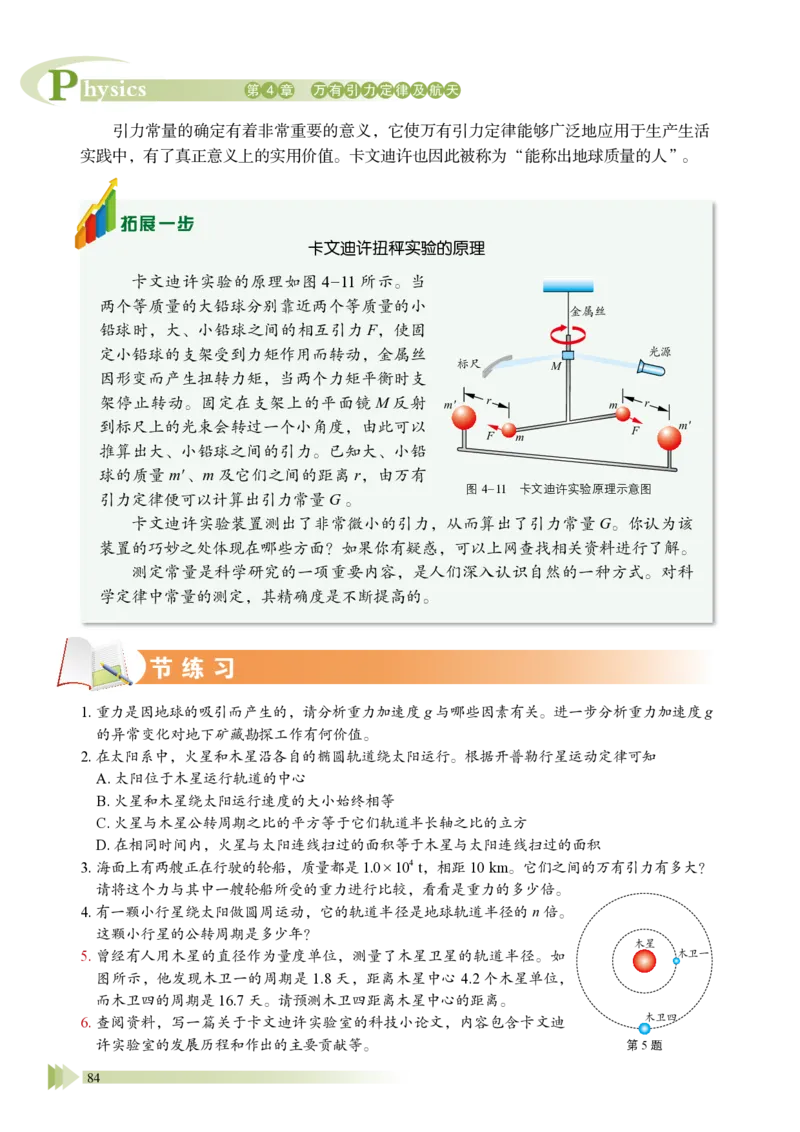 a3 T 2 = k 第1节 天地力的综合：万有引力定律 图4-1 茫茫星空 图4-3 开普勒第一定律示意图 图4-4 开普勒第二定律示意图 行星 F1 F2 太阳 行星 太阳 图4-5 开普勒第三定律示意图 a 太阳 行星 图4-2 开普勒 80 hysics P 第4 章　万有引力定律及航天 迷你实验室 科学书屋 表4-1 八大行星绕太阳运动的有关数据 行星 天体质量 m / kg 周期 T/a 到太阳的 平均距离 d /×10 6 km a3 T 2 /×10 24 km 3·a -2 椭圆轨道 的偏心率 e 偏心率e = 0.3 时的椭圆 水星（Mercury） 3.20×10 23 0.2 57.9 3.34 0.206 金星（Venus） 4.88×10 24 0.6 108.2 3.35 0.007 地球（Earth） 5.98×10 24 1.0 149.6 3.35 0.017 火星（Mars） 6.42×10 23 1.9 227.9 3.35 0.093 木星（Jupiter） 1.90×10 27 11.9 778.3 3.35 0.048 土星（Saturn） 5.68×10 26 29.5 1 427 3.34 0.056 天王星（Uranus）8.68×10 25 84.0 2 869 3.35 0.047 海王星（Neptune）1.03×10 26 164.8 4 486 3.34 0.009 注：a 是年的单位符号。偏心率e 是椭圆扁平程度的量度，等于椭圆两焦点间的距离与长轴长度 的比值。圆是椭圆的特例，偏心率为0。 由开普勒定律可知，行星的运行轨道为椭圆，并且其绕太阳运行的速率不断变 化。由表中的数据可知，太阳系八大行星的运行轨道偏心率都小于0.3，都可近似认 为是圆形。为了便于研究问题，人们通常认为行星绕太阳做匀速圆周运动。 画椭圆 请准备笔、纸、图钉和绳子，按图4-6 所 示，试画出偏心率分别为0.9、0.5、0.1 的椭圆， 由此体会把行星轨道近似看成圆形的原因。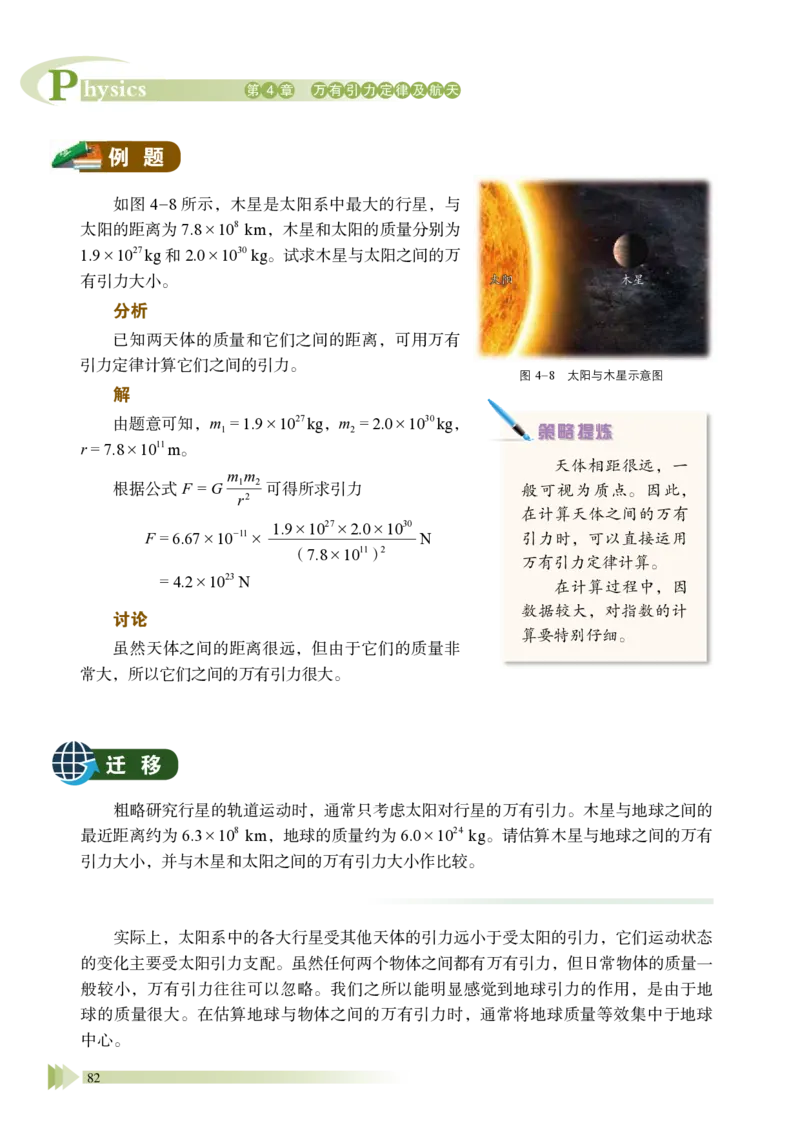 图4-6 根据不同偏心率画椭圆 81 第1 节　天地力的综合：万有引力定律 2.万有引力定律 太阳系的行星在各自基本恒定的轨道上围绕太阳运动，并且遵循一定的运动规律。这 些行星为什么会如此运转？它们为什么既不会脱离太阳，又不会坠向太阳？牛顿总结了前 人的研究成果，运用开普勒三大定律和自己在力学、数学方面的研究成果，于1687 年在 《自然哲学的数学原理》一书中正式提出了万有引力定律（law of universal gravitation）： 自然界中任何两个物体都是相互吸引的，引力的方向沿两 物体的连线，引力的大小F 与这两个物体质量的乘积m1m2 成正 比，与这两个物体间的距离r 的平方成反比（图4-7），即 F = G m1m2 r2 式中，质量的单位用千克（kg），距离（两个物体视为质点时，r 是两质点的距离；若是 两个质量分布均匀的球体， r 则是两球心的距离）的单位用米（m），力的单位用牛顿（N）。 G 为引力常量，在数值上等于两个质量都为1 kg 的物体相距1 m 时相互吸引力的大 小。根据2014 年国际科学技术数据委员会（CODATA）推荐的基本物理常数值， G =（6.674 08 ± 0.000 31）×10 -11 N·m 2/ kg 2，通常取G = 6.67×10 -11 N·m 2/kg 2 。 拓展一步 对万有引力定律公式的推导 如果将行星运行的轨道近似视为圆形，就可由牛顿运动定律和开普勒定律推导 出万有引力定律。 设质量为m 的某行星，以速率v 绕质量为M 的太阳做匀速圆周运动，它们之间 的距离为r。由牛顿第二定律可知，行星所需要的向心力 F = m v2 r 将行星的运转周期T 和速率v 的关系式v = 2πr T 代入上式并加以整理，可得 F = 4π 2 （r 3 T 2） m r2 由开普勒第三定律可知， r 3 T 2 是常量，因此F 与m 成正比，与r 2 成反比。 行星所需要的向心力由太阳对行星的引力提供。根据牛顿第三定律可知，行星 与太阳间的相互引力应大小相等、方向相反、性质相同，这个引力也应与太阳的质 量M 成正比，综上所述，有 F = G Mm r2 G 为引力常量，F 为万有引力，其方向在两物体的连线上。 图4-7 万有引力示意图 m1 m2 F F r 82 hysics P 第4 章　万有引力定律及航天 粗略研究行星的轨道运动时，通常只考虑太阳对行星的万有引力。木星与地球之间的 最近距离约为6.3×10 8 km，地球的质量约为6.0×10 24 kg。请估算木星与地球之间的万有 引力大小，并与木星和太阳之间的万有引力大小作比较。 实际上，太阳系中的各大行星受其他天体的引力远小于受太阳的引力，它们运动状态 的变化主要受太阳引力支配。虽然任何两个物体之间都有万有引力，但日常物体的质量一 般较小，万有引力往往可以忽略。我们之所以能明显感觉到地球引力的作用，是由于地 球的质量很大。在估算地球与物体之间的万有引力时，通常将地球质量等效集中于地球 中心。 如图4-8 所示，木星是太阳系中最大的行星，与 太阳的距离为7.8×10 8 km，木星和太阳的质量分别为 1.9×10 27 kg 和2.0×10 30 kg。试求木星与太阳之间的万 有引力大小。 分析 已知两天体的质量和它们之间的距离，可用万有 引力定律计算它们之间的引力。 解 由题意可知，m1 = 1.9×10 27 kg，m2 = 2.0×10 30 kg， r = 7.8×10 11 m。 根据公式F = G m1m2 r2 可得所求引力 　　F = 6.67×10 -11× 1.9×10 27×2.0×10 30 （7.8×10 11） 2 N 　　 = 4.2×10 23 N 讨论 虽然天体之间的距离很远，但由于它们的质量非 常大，所以它们之间的万有引力很大。 例 题 策略提炼 天体相距很远，一 般可视为质点。因此， 在计算天体之间的万有 引力时，可以直接运用 万有引力定律计算。 在计算过程中，因 数据较大，对指数的计 算要特别仔细。 太阳 木星 图4-8　太阳与木星示意图 迁 移 83 第1 节　天地力的综合：万有引力定律 拓展一步 3.引力常量的测定 万有引力定律是自然界的基本规律之一，在物理学中占 有非常重要的地位。然而，牛顿当时未能给出引力常量的准 确值，如何测量引力常量一时成为物理学界普遍关心的重大 课题之一。 直到1798 年，英国物理学家卡文迪许（H. Cavendish， 1731—1810）利用扭秤实验（图4-10），巧妙地测出了铅球 间的引力，从而证明了万有引力定律的正确性，并得到了当 时精确度很高的引力常量数值。 牛顿的月—地检验 牛顿认为，物体落地是由于地球对物体的吸引，而地球与物体间的引力可能与 天体间的引力具有相同性质。他的证明思路如下（图4-9）： 在地面上质量为m 的物体所受的地球引力遵守万有引力定律，则有 F = G Mm R2 = mg 式中，M 为地球质量，R 为地球半径。 因此，物体在地面处重力加速度的大小 g = G M R2 假设将地面上的物体放到月球绕地球旋转的轨道上，由 于月球轨道半径R1 是地球半径R 的60 倍，则物体受地球引 力作用产生的加速度g′就是它在地面时重力加速度的 1 60 2 ，即 g′= 1 60 2 g = 1 3 600 ×9.8 m/s 2 = 2.7×10 -3 m/s 2 这是根据地球对物体的万有引力计算出的处在月球轨道的物体的加速度，与月 球绕地球公转的向心加速度恰好相等［已知月球绕地球公转的半径约为3.8×10 5 km， 公转周期约为27.3 d（d 是天的单位符号），请自己计算验证］。这表明地球对月球 的引力与地球对地面物体的引力具有相同性质，由此说明了地球对地面物体的引力 与天体之间的引力具有相同性质，遵循同样的规律。 牛顿的月—地检验，将地球对地面物体的引力、行星对卫星的引力统一起来， 证明了它们都遵守万有引力定律。 图4-9 月—地检验示意图 R g g' R1 图4-10 卡文迪许实验装置模型 84 hysics P 第4 章　万有引力定律及航天 拓展一步 1. 重力是因地球的吸引而产生的，请分析重力加速度g 与哪些因素有关。进一步分析重力加速度g 的异常变化对地下矿藏勘探工作有何价值。 2. 在太阳系中，火星和木星沿各自的椭圆轨道绕太阳运行。根据开普勒行星运动定律可知 A. 太阳位于木星运行轨道的中心 B. 火星和木星绕太阳运行速度的大小始终相等 C. 火星与木星公转周期之比的平方等于它们轨道半长轴之比的立方 D. 在相同时间内，火星与太阳连线扫过的面积等于木星与太阳连线扫过的面积 3. 海面上有两艘正在行驶的轮船，质量都是1.0×10 4 t，相距10 km。它们之间的万有引力有多大？ 请将这个力与其中一艘轮船所受的重力进行比较，看看是重力的多少倍。 4. 有一颗小行星绕太阳做圆周运动，它的轨道半径是地球轨道半径的n 倍。 这颗小行星的公转周期是多少年？ 5. 曾经有人用木星的直径作为量度单位，测量了木星卫星的轨道半径。如 图所示，他发现木卫一的周期是1.8 天，距离木星中心4.2 个木星单位， 而木卫四的周期是16.7 天。请预测木卫四距离木星中心的距离。 6. 查阅资料，写一篇关于卡文迪许实验室的科技小论文，内容包含卡文迪 许实验室的发展历程和作出的主要贡献等。 节练习 卡文迪许扭秤实验的原理 卡文迪许实验的原理如图4-11 所示。当 两个等质量的大铅球分别靠近两个等质量的小 铅球时，大、小铅球之间的相互引力F，使固 定小铅球的支架受到力矩作用而转动，金属丝 因形变而产生扭转力矩，当两个力矩平衡时支 架停止转动。固定在支架上的平面镜M 反射 到标尺上的光束会转过一个小角度，由此可以 推算出大、小铅球之间的引力。已知大、小铅 球的质量m′、m 及它们之间的距离r，由万有 引力定律便可以计算出引力常量G 。 卡文迪许实验装置测出了非常微小的引力，从而算出了引力常量G。你认为该 装置的巧妙之处体现在哪些方面？如果你有疑惑，可以上网查找相关资料进行了解。 测定常量是科学研究的一项重要内容，是人们深入认识自然的一种方式。对科 学定律中常量的测定，其精确度是不断提高的。 第5 题 木星 木卫一 木卫四 引力常量的确定有着非常重要的意义，它使万有引力定律能够广泛地应用于生产生活 实践中，有了真正意义上的实用价值。卡文迪许也因此被称为“能称出地球质量的人”。 图4-11 卡文迪许实验原理示意图 M F m r r F m m′ m′ 金属丝 光源 标尺 85 第2 节　万有引力定律的应用 拓展一步 万有引力定律的发现，不仅解决了行星的运行问题，也为人们开启了“飞天”的理 论之路。那么，人造卫星要以多大的速度环绕地球运动才能不落回地面？“嫦娥四号”探 测器又是怎样飞向神秘的月球的？本节我们将运用万有引力定律来研究天体的运动，探讨 人造卫星的发射原理，认识科学定律对人类探索未知世界的作用。 1.天体质量的计算 如何运用引力常量计算出地球的质量？重力的存在主要是因为地球对物体有引力作 用，如果不考虑地球的自转，可以认为在地面附近重力等于万有引力，即 mg = G mM R2 式中， R 为地球的半径， m 为物体的质量，M 为地球的质量。由此可以估算出地球的质量。 第2节 万有引力定律的应用 重力与万有引力的关系 如果考虑地球的自转，物体的重力与万有引力并 不相等。如图4-12 所示，若将地球看成质量分布均匀 的球体，地球对物体的万有引力F 的方向指向地心O； 物体的重力mg 只是万有引力的一个分力，方向竖直 向下；万有引力的另一个分力F′ 提供物体随地球自转 所需要的向心力。进一步计算表明，物体受到的重力 与万有引力相差不大，因此，在粗略计算中可认为重 力近似等于万有引力。 图4-12　重力与万有引力 分析示意图 O O' F' F mg 86 hysics P 第4 章　万有引力定律及航天 A B C D v E F G 图4-14 牛顿的抛体运动 示意图 由上式可知，只要知道某小天体围绕某中心大天体做圆周运动的周期和两天体之间的 距离，就可求出中心大天体的质量。 已知月球绕地球运行的周期T = 27.3 天，月球与地球的平均距离r = 3.84×10 8 m，由 此可估算出地球的质量 M = 4×3.14 2×（3.84×10 8） 3 6.67×10 -11×（24×3 600×27.3） 2 kg = 6.02×10 24 kg 还有另一种方法可计算天体的质量。假设质量为m 的天体 A，围绕质量为M 的天体B 近似做匀速圆周运动（图4-13）， 天体A 所需要的向心力 F = mω2r = m（ 2π T ） 2r 此向心力由天体B 对天体A 的万有引力提供，即 G mM r2 = m（ 2π T ） 2r 由此可解得天体B 的质量 M = 4π 2r 3 GT 2 F 引 r A B 图4-13　天体A 绕天体B 做匀 速圆周运动的示意图 请查阅资料，算一算太阳的质量。 2.人造卫星上天 为什么宇宙飞船能像月球那样围绕地球旋转？宇宙飞船在什么条件下能挣脱地球的 束缚？ 在《自然哲学的数学原理》一书中，牛顿用一幅图解释了 行星能保持在某轨道运行的原因（图4-14）。从抛体运动的角 度考虑，如投掷一块石头，该石头本应做直线运动，但因其自 身重力，石头做曲线运动，最终落到地面；投掷速度越大，落 地点距投掷点就越远。只要抛出的速度足够大，被抛出的物体 就不再掉下来。这实际上就是人造地球卫星或宇宙飞船上天的 原理。 如何使人造卫星和宇宙飞船获得足够大的初始速度？1903 年， 俄国科学家齐奥尔科夫斯基（K.Tsiolkovski，1857—1935）提出 87 第2 节　万有引力定律的应用 F v 卫星展开 最终分离 三级点火 二级点火 一级点火 分离 分离 起飞 图4-15 火箭推动卫星进入 轨道的示意图 G Mm R2 = m v2 R 由此可得，卫星在地面附近轨道绕地球做匀速圆周运动所必需的运行速度 v = GM R = 6.67×10 -11×5.98×10 24 6.4×10 6 m/s = 7.9 km/s 人们称7.9 km/s 为第一宇宙速度（first cosmic velocity）， 也称环绕速度。 如果人造地球卫星发射的速度大于7.9 km/s，它将沿 椭圆轨道围绕地球运行，甚至会摆脱地球引力，远离地 球而去。通过计算可知，人造卫星脱离地球引力所需的速 度为11.2 km/s，人们称之为第二宇宙速度（second cosmic velocity），也称脱离速度（图4-16）。 脱离地球引力的人造卫星还受到太阳引力的作用，相 当于“人造行星”。当其发射速度达到16.7 km/s 时，就 会挣脱太阳引力的束缚，飞出太阳系。人们称16.7 km/s 为第三宇宙速度（third cosmic velocity），也称逃逸速度。 了液体火箭发动机的构想，首次阐述了如何利用多级火箭克服 地球引力实现宇宙航行。正是基于这种构想，人类在1957 年 成功发射了第一颗人造地球卫星。图4-15 展示了用多级火箭 发射卫星，使卫星进入轨道的大致过程。 如果卫星绕地球运行的轨道可视为圆形，并且卫星距地面 的高度远小于地球半径，则卫星轨道半径可近似视为地球半径 R = 6.4×10 6 m，这时卫星所受地球的引力与卫星做圆周运动所 需的向心力相等。假设卫星质量为m，地球质量为M，根据向 心力公式有 图4-16 不同宇宙速度对应 不同轨道的示意图 第二宇宙速度11.2 km/s 圆形轨道 第一宇宙速度7.9 km/s 88 hysics P 第4 章　万有引力定律及航天 物理聊吧 我国的量子科学实验卫星“墨子号”于2016 年 8 月16 日在酒泉成功发射，其升空后围绕地球的运 动可视为匀速圆周运动，离地面的高度为500 km （图4-18）。已知地球的质量约为6.0×10 24 kg，地 球的半径约为6.4×10 3 km，求“墨子号”运动的线 速度大小和周期。 图4-17 是“阿波罗十一号” 宇宙飞船的登月往返航线示 意图。 经火箭发射， “阿波罗十一号” 宇宙飞船首先进入环绕地球的 轨道，然后加速，脱离环绕地 球轨道后，惯性飞行，进入环 绕月球的轨道，最后登月舱降 落在月球（红色轨迹）。 当宇航员在月球上完成工 作后，再发动引擎进入环绕月球 的轨道，然后加速，脱离环绕 月球轨道，进入环绕地球轨道， 最后降落于地球（绿色轨迹）。 结合登月往返航线讨论： 为什么飞船能围绕地球旋转？ 飞船在什么条件下能挣脱地球 的束缚？为什么飞船能围绕月 球旋转？飞船在什么条件下能 挣脱月球的束缚？ 例 题 图4-18　“墨子号”绕地球做匀速 圆周运动示意图 飞船发动引擎进入月球轨道 登月舱起飞 登月舱进入 汇合轨道 中途航向改正 飞船与火箭分离 进入地球轨道 发射升空 降落 重返大气层 指挥舱将动 力舱抛弃 中途航向改正 指挥舱发动引擎进 入返回地球航道 登月舱着陆 图4-17 “阿波罗十一号”登月往返航线示意图 （a）从地球飞往月球 （b）从月球飞往地球 r 地球 “墨子号” 89 第2 节　万有引力定律的应用 分析 卫星绕地球做匀速圆周运动，地球对卫星的万有引力提供向心力。可由向心力公式 求解。 解 由题意可知，“墨子号”距地面高度h = 5.0 ×10 5 m，地球半径R = 6.4×10 6 m，地球 质量M = 6.0×10 24 kg。设m 为“ 墨子号”的质量，r 为地球球心到“ 墨子号”的距离。 由 G Mm r2 = m v2 r 其中 r = R + h 可得 v = GM R + h = 6.67×10 -11×6.0×10 24 6.4×10 6 + 5.0×10 5 m/s = 7.6 ×10 3 m/s 周期 T = 2π（R + h） v = 2×3.14×（6.4×10 6 + 5.0×10 5） 7.6×10 3 s = 5.7×10 3 s 讨论 人造地球卫星绕地球做圆周运动的线速度、角速度、周期和向心加速度与哪些因素 有关？ 策略提炼 当中心天体质量很大，卫星 绕中心天体做匀速圆周运动时， 可认为中心天体不动，卫星所需 要的向心力由中心天体对它的万 有引力提供。由向心力公式建立 关系式G Mm r2 = ma，是解决天 体运动问题的基本思路和方法 之一。 地球同步卫星是相对地面静止的卫星，卫星的运行方向与地球自转方向相同，运行轨 道为位于地球赤道平面上的圆形轨道，运行周期与地球自转周期相等。请定性比较地球同 步卫星与“墨子号”二者的轨道半径、线速度及向心加速度的大小。 迁 移 90 hysics P 第4 章　万有引力定律及航天 科学书屋 人造卫星—人类的“千里眼”“顺风耳” 人造卫星是人类的“千里眼”和“顺风耳”。 人造卫星种类很多、用途各异，有科学卫星、气象 卫星（图4-19）、地球资源卫星、环境检测卫星 和照相侦察卫星等，卫星上的照相机和雷达等设备 可以帮助人们看得更远、更深入。 卫星上的接收器和转发器可以帮助人们接收和 转发信息。例如，通信卫星可以把相距遥远的两地 连接起来，即使是边远地区也可以进入通信网络。 尤其是静止通信卫星（也叫地球同步卫星），为人 类通信带来了极大方便。静止通信卫星绕地球运行一周的时间和地球自转一周的时 间相同，在地球上观察，赤道上方与地球同步运行的通信卫星总是静止不动的。从 理论上来说，发射三颗等距分布在地球同步轨道上的静止通信卫星就几乎可以实现全 球通信了。 图4-19　“风云四号”气象卫星示意图 3.预测未知天体 目前科学家已确认太阳系有八大行星，按距太阳 由近及远的顺序依次为水星、金星、地球、火星、木 星、土星、天王星和海王星。它们在各自的椭圆轨道 上绕太阳运转，如图4-20 所示。 水星、金星、火星、木星及土星都是人们用肉眼 直接观察到的。1781 年，人们第一次通过天文望远镜 发现了新的大行星——天王星。天文学家在观察天王 星时，发现它绕太阳的运行轨道与由万有引力定律 计算出来的轨道不吻合。于是，有些人开始怀疑万 有引力定律的正确性；也有人运用万有引力定律预 测，可能在天王星外还有一颗未知的大行星。 1845 年，英国大学生亚当斯计算出了这颗未知 行星的轨道和质量，但未引起重视。几乎同时，法国 天文爱好者勒维耶也独立计算出了这颗未知行星的位 置。1846 年9 月23 日，德国天文学家伽勒在勒维耶 预测的区域发现了这颗神秘的行星——海王星。 图4-20 太阳系行星运转示意图 能了解万有引力定律的内涵， 会计算人造卫星的环绕速度，知道 第二宇宙速度和第三宇宙速度；能 用万有引力定律解释一些天体运动 问题。具有与万有引力定律相关的 运动与相互作用的观念。 ——物理观念 素 养 提 升 91 第2 节　万有引力定律的应用 科学书屋 方法点拨 利用科学理论不仅能解释已知的现象，还能预言一些未知的事物和现象。例如， 科学家运用万有引力定律成功预测了海王星的存在。后来在天文学领域，基于相对 论，爱因斯坦又预言了一系列重要事件和现象。 1. 同步卫星是与地球自转同步的卫星。请问，能否将同步卫星定点在 北京上空？请说明理由。 2. 为满足不同领域的需要，我国有许多不同轨道高度的人造卫星。如图 所示，在某一轨道平面上有人造卫星A、B 都绕地球做圆周运动，两 颗人造卫星的质量之比为1 ：2，到地球球心的距离之比为2 ：3，则 它们的 A. 周期之比为3 ：2 B. 线速度大小之比为 3 ： 2 C. 向心加速度大小之比为4 ：9 D. 向心力大小之比为1 ：18 节练习 第2 题 A B 地球 哈雷彗星 英国物理学家哈雷（E. Halley，1656—1742）通过观察、计算分析等，认为 1531 年、1607 年和1682 年出现的彗星，实际上是同一颗彗星的三次回归，并预言 这颗彗星将于1759 年再次出现。果然，这颗美丽的彗星在哈雷预计的时间段拖着 长长的尾巴，又一次出现在星空中。 为了纪念哈雷，大家将这颗彗星命 名为哈雷彗星。后来，人们预测这 颗彗星将分别于1835 年、1910 年和 1986 年回归地球，结果它都如期而 至（图4-21）。 人们预测它在2061 年还将回归 地球。让我们共同等待它的出现吧！ 海王星的发现是科学史上的奇迹，因为它是人们通过计算发现的。通过万有引力定律 成功地预测未知的星体，不仅巩固了万有引力定律的地位，也充分展示了科学理论的预 见性。 图4-21 1986 年拍摄到的哈雷彗星 92 hysics P 第4 章　万有引力定律及航天 3. 某卫星在距离地心4R （R 是地球的半径）处，由于地球对它的引力作用而产生的加速度是地球 表面重力加速度的多少倍？ 4. 1970 年，我国发射的第一颗人造地球卫星绕地球运行轨道近似为圆形，运行周期为114 min，轨 道的平均半径为7 782 km。请据此估算地球的质量。 5. 我国发射了绕月运行的探月卫星“嫦娥一号”。该卫星在月面着陆前的轨道近似圆形，且贴近月 球表面运行。已知月球质量约为地球质量的1 81，月球半径约为地球半径的1 4 ，地球的第一宇宙速 度约为7.9 km/s，该探月卫星绕月运行的速率约为 多少？ 6. 火星的质量大约是地球的1 9 。如图所示，卫星M 和 卫星E 分别以等大的轨道半径绕火星和地球做匀速 圆周运动。哪个卫星的周期更短？请说明理由。 7. 下表给出了五颗卫星绕木星运行的数据，这些卫星 的运动可近似视为圆周运动。 卫星 轨道半径r/km 周期T/d 卫星质量m/kg 木卫五 1.814×10 5 0.498 2.08×10 18 木卫一 4.217×10 5 1.77 8.93×10 22 木卫二 6.710×10 5 3.55 4.80×10 22 木卫三 1.070×10 6 7.15 1.48×10 23 木卫四 1.883×10 6 16.7 1.08 ×10 23 （1）请根据表中数据定性描述：卫星运行周期与轨道半径之间的关系，卫星运行周期与卫星质 量之间的关系。 （2）请用物理规律来证明你的上述分析。 8. 某同学在解决一个物理问题的过程中，计算出一颗人造地球卫星绕地球做圆周运动的周期是 80 min。你觉得该同学的答案合理吗？请说明理由。 第6 题 （a） 火星 r M （b） 地球 r E 请提问 93 第3 节　人类对太空的不懈探索 星空如此迷人，周而复始，宁静永恒。人类观察星空，为了耕作，为了远行，为了信 仰，为了探索大自然的奥秘。 1.古希腊人的探索 第3节 人类对太空的不懈探索 毕达哥拉斯（Pythagoras，约公元前 580—约前 500）从美学观念出发，认为宇宙中所 有天体的形状都应该是球形。亚里士多德认为，地球在宇宙的中心静止不动，其他星体绕 地球转动，这很好地解释了天体升落的现象。阿波罗 尼奥斯（Apollonius，约公元前 262—前 190）认为行 星沿某一圆周（本轮）运动，该圆周的圆心沿另一圆 周（均轮）绕地球运动。因此，以地球为中心看行星 时，行星会时而顺行，时而逆行，其亮度也会因与地球 距离的改变而改变。 公元 140 年前后，托勒密（C. Ptolemaeus，约 公元 90—168）对前人的观测成果和理论进行总结， 提出了地心体系（图 4-22）。托勒密的地心体系可以 解释已知天体的运动，在很长的历史时期人们都利用 这一模型预测天体的位置。 图4-22 托勒密“地心说”模型示意图 火星 土星 木星 金星 水星 月球 地球 太阳 恒星球壳 均轮 本轮 科学书屋 中国古代天象观测的成就 中国是天文学发展最早的国家之一。自远古始，人们就对天文现象进行观察， 积累了丰富的天文学知识，形成了系统、独特的天文学体系。中国古代天文学在历 法体系、天文观测等许多领域长期处于世界领先地位。 从甲骨文及古籍等记载看，我国在古代天象观测方面作出了相当的贡献。例如， 殷代的甲骨文中记载的“七日己巳夕，有新大星并火”，是最早的关于新星的记录； 94 hysics P 第4 章　万有引力定律及航天 2.文艺复兴的撞击 16 世纪中期，文艺复兴的浪潮冲击了自中世纪以来长 期禁锢人们思想的枷锁。 1543 年，波兰天文学家哥白尼临终时，向世人公开 了他几十年来研究的成果《天体运行论》，正式提出了 “ 日心说”（图4-23）。哥白尼认为：太阳是宇宙的中心， 水星、金星、地球、火星、木星及土星都绕太阳做匀速圆 周运动，月球是地球的卫星。哥白尼的“日心说”可以简 洁地描述行星运动，并能更清楚地解释诸多天文现象。 第谷·布拉赫（T. Brahe，1546—1601）是丹麦杰出 的天文观测家。当时尚未发明望远镜，他通过自制的观测 仪器（图4-24）对星体进行认真系统的观测，使当时的 测量误差从10′ 降低到2′。他的测量结果表明，托勒密与 哥白尼的理论计算结果都与观测数据不相符。 开普勒研究了第谷连续20 年的观测数据，希望进一 步解释哥白尼的行星圆形轨道，却以失败而告终，因为他 得到的结果与第谷的观测数据至少有8′ 的误差。开普勒相 信这不是第谷的粗心造成的，而是哥白尼的理论还需要进 一步完善。从此，他开始研究行星的非匀速、非圆周运动。 经过多年的埋头计算，开普勒最终发现了更为精确的行星运 动规律，并先后提出了三大定律。 虽然哥白尼的理论受到了第谷、开普勒的挑战，但不 可否认，他播下了科学革命的种子。亚里士多德认为地上 和天上的物体是有区别的，而哥白尼则修正了地球静止不动 的直觉观念，为牛顿统一天上与地上的物理学打下了基础。 图4-24 第谷自制的观测仪器示意图 图4-23 哥白尼“日心说” 模型示意图 恒星天 土星 木星 火星 金星 水星 地球 月球 《汉书·五行志》中记载的 “日出黄，有黑气，大如钱，居日中央”，对太阳黑子的 大小和位置等作了确切的描述；《春秋》记载的“秋七月，有星孛入于北斗”，已经 把彗星视为天体。从春秋战国到清末，哈雷彗星出现多次，我国皆有详细记载。中国 古代的星图在世界上也非常著名，唐代绘制的敦煌星图绘有1 350 颗星，是世界上 现存最早且星数最多的星图。我国古代对行星、恒星、流星雨等天象都有系统观测。 这些全面且独特的天文观测成果对世界天文学的发展起到了不可或缺的作用。 95 第3 节　人类对太空的不懈探索 牛顿在前人研究的基础上，运用开普勒行星运动定律和自己的研究成果，逐步建立了 万有引力定律，并将主要研究成果写入他的著作《自然哲学的数学原理》（图4-25）。他 证明了物体围绕中心运动时需要向心力；沿轨道运行的 每个质点既是被吸引的物体，也是具有吸引力的中心， 继而推广到宇宙中的物体都在彼此吸引。牛顿将地球 对物体的引力扩展到月球，认为地球引力与太阳对行 星的作用力、行星对卫星的作用力是性质相同的力。 在此基础上，牛顿最终给出了具有科学革命价值的万 有引力定律。 牛顿的万有引力定律是物理学的第一次大综合，它 将地上的力学与天上的力学统一起来，形成了以牛顿三 大运动定律为基础的力学体系。 4.人类“飞天”梦的实现 在牛顿力学的基础上，人类对太空的探索取得了丰 硕的成果，实现了自古便有的“飞天”梦。 1957 年10 月4 日，苏联的人造地球卫星上天，震 惊了世界。我国在1970 年发射了第一颗人造地球卫星 “东方红一号”（图4-26），成为世界上第五个发射人 造地球卫星的国家。 1961 年4 月12 日，世界上第一艘载人宇宙飞船发 射升空，苏联宇航员加加林（图4-27）成功完成了人 类第一次环绕地球的飞行。 1969 年7 月20 日，美国的“阿波罗十一号”宇宙 飞船将人类送上了月球。当时，上亿人通过电视注视着 走出登月舱的阿姆斯特朗。他在月球上迈出的一小步， 却是人类迈出的一大步，实现了人类的“飞天”梦。 3.牛顿的大综合 人们在研究天体怎样运动的同时，还在探索天体为什么会这样运动。亚里士多德认 为，天体由“以太”元素组成，它们本来就应围绕地球做匀速圆周运动。到了开普勒时 代，人们才开始寻找天体形成这种运动的动力学原因。开普勒认为，太阳的磁力使天体运 动，并且天体所受太阳的磁力随距离的增加而减弱。笛卡儿认为，是“以太”运载着行 星在巨大的旋涡中运行。胡克、哈雷等人则认为，天体受到遵循平方反比定律的向心力作 用，才进行圆周运动。 图4-25 牛顿著作《自然哲学的 数学原理》 图4-27 第一个“太空人”——加加林 图4-26 “东方红一号” 96 hysics P 第4 章　万有引力定律及航天 1971 年4 月19 日，苏联“礼炮一号”空间站成为人类进入太空的第一个空间站。 1971 年12 月2 日，苏联“火星三号”探测器在火星表面着陆。 1981 年4 月12 日，美国的第一架航天飞机“哥伦比亚号”成功发射。目前，科学家 正在研究一种新型的航天器——空天飞机。 2003 年10 月15 日，“神舟五号”载人飞船成功发射， 中国成为世界上第三个独立掌握载人航天技术的国家。 虽然人类已登上月球，但还没有在除地球外的任何行星 上留下脚印。若实现登陆火星，又将是人类宇宙探索史上的 一大里程碑。 …… 在人类探索太空的过程中，有不少先驱者献出了宝贵的生 命。然而，他们的精神却激励着人们对太空坚持不懈地探索！ 科学书屋 1. 查阅资料，了解空间站中宇航员的衣食住行，并写一篇报告。 *2. 2013 年6 月20 日，“神舟十号”航天员在“天宫一号”上开展了别开生面的太空授课，为我 国青少年讲解并演示失重环境下的基础物理实验。请观看太空授课的视频，尝试设计一种在宇 宙飞船上失重条件下的实验方案，并与同学交流。 节练习 能认识发现万有引力定 律的过程及重要意义，认识 科学定律对人类探索未知世 界的作用；知道科学包含大 胆的想象和创新；有探索太 空、了解太空的兴趣，能为 牛顿力学对航天技术发展的 重大贡献而振奋。 ——科学态度与责任 素 养 提 升 嫦娥工程 2004 年，我国正式开展月球探测工程，并 命名为“嫦娥工程”。探月卫星“嫦娥一号”“嫦 娥二号”已完成“绕”的任务。卫星绕月运行， 获得了月球表面影像、有关物质元素分布等数 据。“嫦娥三号”携“玉兔号”月球车成功实 现月球软着陆，并开展月面巡视勘察以及月表 形貌与地质构造调查等科学探测，实现了“落” 的任务。2019 年1 月，“嫦娥四号”探测器成 功着陆月球背面南极—艾特肯盆地（图 4-28）， 完成了“人类探测器首次实现月球背面软着陆” 的壮举。 图4-28 “嫦娥四号”着陆月球背面 97 章末练习 科学认知 1. 若在太阳系外发现了首颗“宜居”行星，其质量约为地球质量的6.4 倍，一个在地球表面重量为600 N 的人在这个行星表面的重量将变为960 N。由此可推知，该行星的半径与地球半径之比约为 A. 0.5 B. 2 C. 3.2 D. 4 2. 我国“嫦娥二号”可视为在月球表面附近做圆周运动。已知引力常量，要测定月球的密度，仅 仅需要 A. 测定飞船的运行周期 B. 测定飞船的环绕半径 C. 测定月球的体积 D. 测定飞船的运行速度 3. 2012 年1 月9 日，我国成功发射了“资源三号”卫星，同年又成功发射了“中星2A”通信广 播地球同步卫星。在某次实验中，近似做圆周运动的“资源三号”卫星环绕地球飞行24 圈用 时38 h。请比较两颗卫星的周期、速率、加速度和离地面高度这四个物理量的大小。 4. 如图所示，海王星绕太阳沿椭圆轨道运动，P 为近日点，Q 为远日点，M、N 为轨道短轴的两 个端点，运行的周期为T0。若只考虑海王星和太阳之间的相互作用，则海王星在从P 经M、Q 到N 的运动过程中 A. 从P 到M 所用的时间等于T0 4 B. 从Q 到N 阶段，机械能逐渐变大 C. 从P 到Q 阶段，速率逐渐变小 D. 从M 到N 阶段，万有引力对它先做负功后做正功 5. 已知同步卫星与地心的距离为r，运行速率为v1，向心加速度为a1 ；地球赤道上的物体随地球 自转的向心加速度为a2 ；第一宇宙速度为v2，地球半径为R。下列关系式正确的是 A. a1 a2 = r R B. a1 a2 = R r( ) 2 C. v1 v2 = r R D. v1 v2 = R r 6. 荡秋千是深受大家喜爱的一项娱乐活动。随着科学技术的发展，将来我们也许会在其他星球上 享受荡秋千的乐趣。假设你所在星球的质量是M、半径为R，可将人视为质点，秋千质量不计， 摆长不变，摆角小于90°，引力常量为G。 （1）求该星球表面附近的重力加速度g 星。 （2）若你在荡秋千中能上升的最大高度为H，则经过最低点时速度为多大？ 7. 如图所示， A 是地球的同步卫星，另一卫星B 的圆形轨道位于赤道平面内， 离地面高度为h。已知地球半径为R，地球自转角速度为ω，地球表面的 重力加速度为g，O 为地球中心。 （1）求卫星B 的运行周期。 （2）若卫星B 绕行方向与地球自转方向相同，某时刻A、B 两卫星相距最 近，则至少经过多长时间，它们再一次相距最近？ 科学辨析 8. 已知引力常量G、地球半径R、月球和地球之间的距离r、同步卫星距地面的高度h、月球绕地 章末练习 M 太阳 海王星 Q P N 第4 题 第7 题 A B O 98 hysics P 第4 章　万有引力定律及航天 球的运转周期T1、地球的自转周期T2、地球表面的重力加速度g。某同学根据以上条件，提 出一种估算地球质量M 的方法：因同步卫星绕地球做圆周运动，可由G mM h2 = m（ 2π T 2） 2 h 得 M = 4π 2h 3 GT 2 2 。 （1）请判断上面的结果是否正确，并说明理由。若不正确，请给出正确的解法和结果。 （2）请根据已知条件再提出两种估算地球质量的方法，并解出结果。 *9.“嫦娥工程”正在循序渐进地实现中国的航天梦。若“嫦娥一号”和“嫦娥二号”绕月做圆 周轨道运行时，距月球表面的高度分别为h1 和h2，周期分别为T1 和T2，请你推导出月球的 质量和半径，并用必要的方程说明你的理由。若“嫦娥三号”探测器的质量为M，请结合前 面计算的信息，推导出探测器在月球表面附近悬停时其发动机提供的推力大小。如果未来对 从月球返回地球的探测器进行回收，上述发动机是否依然能胜任同质量探测器在地球表面的 悬停任务？请用证据谈谈你的看法。 温故知新 10. 如图所示，一内壁光滑的细管弯成半径R = 0.4 m 的半圆形轨道BC，将其竖直放置并将B 点与 一水平轨道相连。置于水平轨道上的弹簧左端与竖直墙壁相连，B 至墙壁的距离为弹簧的自然 长度。将一个质量m = 0.8 kg 的小滑块放在弹簧的右侧，向左推滑块，压 缩弹簧使弹簧右端至A 处，然后将滑块由静止释放，滑块进入半圆轨道继 续滑行（不计滑块与轨道的碰撞）。已知滑块运动到B 处刚刚进入半圆轨道 时对轨道的压力F1 = 58 N，水平轨道AB 长度l = 0.3 m，滑块与轨道的动摩 擦因数μ = 0.5，取重力加速度g = 10 m/s 2，求： （1）弹簧压缩到A 处时的弹性势能； （2）小滑块运动到轨道最高处C 点时对轨道的压力大小。 11. 请根据第4 章（万有引力定律及航天）的内容，结合你的理解，画出概念图。 我的学习总结 第10 题 B A C 99 第3 节　人类对太空的不懈探索 一、选择题（本题共5 小题。在每小题给出的四个选项中，第1 ～3 题只有一项符合题目要求， 第4、5 题有多项符合题目要求） 1. 要使两物体（可视为质点）间万有引力减小到原来的1 8 ，可采取的方法是 A. 使两物体间的距离变为原来的2 倍，其中一个物体的质量变为原来的1 2 B. 使两物体的质量各减少1 2 ，距离保持不变 C. 使其中一个物体的质量变为原来的1 4 ，距离保持不变 D. 使两物体的质量及它们之间的距离都变为原来的1 4 2. 已知水星绕太阳公转的周期为88 个地球日，水星与地球绕太阳的公转均可视为匀速圆周运动。 可判定 A. 水星的质量大于地球的质量 B. 水星的轨道半径大于地球的轨道半径 C. 水星公转的线速度大于地球公转的线速度 D. 水星的向心加速度小于地球的向心加速度 3. 太空技术的飞速发展使人类登陆其他星球成为可能。假设未来的某一天，宇航员登上某一行星 后，测得该星球表面的重力加速度是地球表面重力加速度的2 倍，而该星球的平均密度与地球 的差不多，则该星球质量大约是地球质量的 A. 1 2 　　　　　　　　B. 2 倍　 C. 4 倍　　　　　　　　D. 8 倍 4. 地球同步卫星常用于通信、气象观测、导弹预警、数据中继等方面。地球同步卫星相对地面静 止不动，犹如悬在空中一样，以实现对同一地区的连续监测。下列说法正确的有 A. 同步卫星处于平衡状态 B. 同步卫星绕地心的角速度与地球自转的角速度相同 C. 同步卫星只能位于赤道上方，且高度和速率是唯一确定的 D. 同步卫星的速率一定大于7.9 km/s 5. 2016 年10 月19 日，“神舟十一号”飞船与“天宫二号”空间实验室成功交会对接。在“神舟 十一号”飞船返回地面的过程中，有一个阶段可视为绕地球做圆周运动，其轨道半径为r1，线 速度大小为v1，周期为T1。此时“天宫二号”的运行轨道也可视为圆形轨道，对应的轨道半径 为r2，线速度大小为v2，周期为T2。下列关系式正确的是 A. v1 v2 = r1 r2 B. v1 v2 = r2 r1 C. T1 T2 = r2 r1 D. T1 T2 = r1 3 r2 3 单元自我检测 100 hysics P 第4 章　万有引力定律及航天 二、非选择题 6. 如图所示，“好奇号”火星探测器于2012 年成功登陆火星表面。在 登陆火星前，“好奇号”在距火星表面高度为h 的轨道上绕火星做匀 速圆周运动，周期为T。已知火星的半径为R，引力常量为G，忽略 其他天体对探测器的引力作用，求： （1）探测器绕火星做匀速圆周运动的线速度大小； （2）火星的质量。 7. 利用宇宙飞船，宇航员可以到太空维修出现故障的人造地球卫星。一颗人造地球卫星在离地高 度一定的圆轨道上运行，飞船接近这颗卫星并与它运行情况基本相同时，速度为6.0 km/s。已知 地球质量M = 6.0×10 24 kg，半径R = 6 400 km，引力常量G = 6.7×10 -11 N·m 2/kg 2，求这颗卫 星离地面的高度。 8. 从地球上发射两颗人造地球卫星A 和B，它们绕地球做匀速圆周运动的半径之比 RA ：RB = 4 ：1， 求它们的线速度大小之比。下面是某同学的一种解法，请判断其是否正确。若是正确的，请你 作出评价；若是错误的，请分析其出错的原因并给出正确的解答方法。 第6 题 解：卫星绕地球做匀速圆周运动所需的向心力　F 向= mg = m v2 R 　设A、B 两颗卫星的质量分别为mA、mB，则 　mA g = mA v2 A RA （1） 　mB g = mB v2 B RB （2） 　由（1） （2）得 v2 A v2 B = RA RB 　所以 vA vB = RA RB = 4 1 = 2 1 单元自我评价 回顾本单元的学业要求和所学内容，结合本次单元自我检测和平时学习情况进行自我评 价，写一篇“单元自我评价”报告。说说你学会了什么、存在什么问题及今后努力的方向等。 101 第3 节　人类对太空的不懈探索 第5 章 科学进步 无止境 导　入　再次跨越时空的对话 第1 节　初识相对论 第2 节　相对论中的神奇时空 第3 节　探索宇宙的奥秘 本章学业要求 ●能初步了解相对论时空观的内涵，初步了 解宇宙起源与演化的研究进展；能运用与 相对论相关的初步知识解释高速世界的一 些特点。尝试建立初步的相对论时空观。 ——物理观念 ●知道研究高速世界需要建构物理模型；知 道科学推理与大胆想象的重要性；能用与 狭义相对论相关的证据尝试说明高速世界 的一些特点；知道创新对科学进步的重要 意义。 ——科学思维 ●能提出与高速世界、宇宙起源与演化相关 的问题；能收集与相对论时空观、宇宙起 源和演化有关的信息；能用收集的信息说 明高速世界的一些特点以及典型恒星的演 化过程；能撰写与相对论初步知识相关 的小论文，能陈述并交流关于高速世界 的认识。 ——科学探究 ●能体会人类对自然界的探索是不断深入的， 能从牛顿力学的局限性体会科学理论既具 有相对持久性和稳定性，也存在局限性， 人类对自然的探索永无止境；具有探索自 然、造福人类的志趣，有关注宇宙起源 与演化研究进展的意愿；能体会科学·技 术·社会存在相互联系，需要协调发展。 ——科学态度与责任 102 hysics P 第5 章　科学进步无止境 导　入 再次跨越时空的对话 物体的运动离不开时间和空间，时间和空间究竟有 怎样的关系？人们对此问题的探索从未间断过。牛顿和 爱因斯坦对时间和空间有着根本不同的认识，如果把他 们的时空观放在一起进行比较，就如同我们再次聆听两 位科学伟人之间跨越时空的“对话”。 牛顿认为，绝对的时间自身在流逝着，因其本性而 在均匀地、与任何外界无关地流逝着；绝对的空间，就 其本性而言，是与外界任何事物无关的，永远是相同和 不动的。时间和空间与物质及其运动无关，并且时间和 空间是完全独立的。 爱因斯坦认为，绝对的时间和绝对的空间是不存在 的，时间、空间与物质及其运动都有着密切的联系；同 时，时间和空间之间也有着紧密的联系。 两位科学伟人的“对话”揭示了人类对时间和空 间认识的不断深入发展的过程。爱因斯坦的时空观揭示 了哪些规律？它对于人类探索宇宙有着怎样的影响？通 过本章的学习，你将体会到人类对基本自然规律孜孜不 倦的探索精神。 牛顿 爱因斯坦 103 第1 节　初识相对论 由伽利略和牛顿等人创立的经典力学体系，到19 世纪末已发展为一个包括力、热、 声、光、电等分支的完整经典物理学体系，对人类的科学认识产生了深远的影响。 1900 年，英国物理学家开尔文踌躇满志地宣告：在已经基本建成的科学大厦中，后辈 物理学家只要做一些零碎的修补工作就行了。但是在这尽善尽美之中，还有一点小小的遗 憾。用开尔文的话说，在物理学晴朗天空的远处，还有两朵小小的令人不安的“乌云”。 正是这两朵“乌云”引发了相对论和量子论的产生。下面我们侧重学习与相对论有 关的内容。在必修第三册中，我们将初步了解量子论的有关内容。 我们知道，水波的传播要有水作为媒介，声波的传播要有空气作为媒介。经典物理学 家曾认为，“以太”是光波的传播介质，这种介质绝对静止、密度极小（几乎为0）、硬 度极大、完全透明，充满宇宙空间，渗透于一切物体。若真存在“以太”，地球在“以 太”的海洋中自转、公转，则一定会有“以太风”迎面扑来。因此，探索“以太风”的 存在，确定地球和“以太”的相对运动，就成为 19 世纪后半叶物理学的一个重要课题。 按照经典时空观的运动合成原理，在以大小为 v1 的速度水平行驶的汽车上，有人相 对于汽车以大小为 v2 的速度将一物体水平抛出。在静止于路边的观察者看来，若物体抛出 时与汽车同向，则物体速度大小为v2 + v1 ；若反向，则物体速度大小为v2 - v1 （图5-1）。 第1节 初识相对论 图5-1　低速世界的速度合成示意图 （a） v1 v2 v2 v1 （b） 104 hysics P 第5 章　科学进步无止境 同样道理，假设光相对“以太”的传播速度为c，地球相对“以太”的运行速度为v， 当光速c与地球速度v 的方向相同时，则静止在地球上的人观测到该光的速度为c' = c - v； 当光速c 与地球速度v 的方向相反时，则此人观测到该光的速度为c' = c + v。如果能通过 实验测量到这种差别，就能够证明“以太”的存在。 1887 年，美国物理学家迈克尔孙（A. Michelson，1852—1931）与莫雷（E. Morley， 1838—1923）合作，进行了著名的迈克尔孙—莫雷实验。实验证 明，不论地球运动的方向同光的射向一致还是相反，测出的光速 都相同，在地球同设想的“以太”之间没有相对运动，找不到 “以太”。这一实验没有支持“以太”说。这便是开尔文所说的 在物理学晴朗天空远处的一朵令人不安的“乌云”，也反映了牛 顿力学的局限性。 爱因斯坦经过不懈的探索加上非凡的抽象思维能力，最终拨开了物理学天空中令人不 安的“乌云”，提出了著名的相对论（relativity）。他于1905 年提出两个基本假设： 相对性原理（principle of relativity）：所有物理规律在一切惯性参考系中都具有相同的 形式。 光速不变原理（principle of constancy of lightspeed）：在一切惯性参考系中，测量到的 真空中的光速c 都一样（c = 3×10 8 m/s）。 相对性原理表明：在某个惯性系中描述某个物理系统的某个物理过程的物理定律，在 其他一切惯性系中对该系统该过程作出描述的物理定律皆保持形式不变。例如，在匀速 飞行的飞机上观测，上抛小球的运动遵循匀变速直线运动的规律，那么在地面上（或在 其他惯性参考系中）观测，上抛小球的运动仍遵循同样形式的匀变速直线运动的规律 （图5-2）。 光速不变原理表明：在一切惯性系中观测真空中传播的光，其传播速度均为c，与光 源或观察者的运动无关。这一结论实际上已被大量的实验（包括迈克尔孙—莫雷实验）证 实。如图5-3 所示，假设在真空环境中，静止在匀速运行列车中的观测者与静立于地面的 观测者，测得手电筒发出的光的速度大小都是c。 基于这两条基本原理，爱因斯坦建立了狭义相对论（special theory of relativity），把物 理学研究推进到高速领域。 图5-3　光速不变原理示意图 s' s c v 图5-2　相对性原理示意图 v 知道研究高速世界 需要建构物理模型；知 道科学推理与大胆想象 的重要性；知道创新对 科学进步的重要意义。 ——科学思维 素 养 提 升 105 第1 节　初识相对论 1. 简述爱因斯坦在狭义相对论中提出的两个基本假设。 2. 查阅资料，比较爱因斯坦的狭义相对性原理与经典力学的相对性原理有什么不同。 节练习 请提问 106 hysics P 第5 章　科学进步无止境 狭义相对论中的两个基本假设包含了不同于经典力学的新时空观，这种新时空观变 革了传统的空间、时间、质量、能量等基本概念，揭示了时空统一性和物质、运动的统一 性，因此会得出不同于“日常”的奇妙结论。 第2节 相对论中的神奇时空 图5-4 在运动火车上的时钟与站台 上的时钟对应的时间不一样 （a） （b） 1.时间延缓效应 经典时空观认为，时间是绝对时间，就像一 条长河，源源不断地从过去到现在直至将来，与 运动无关。而相对论时空观则认为，当时钟相对 于观测者静止时，时钟走得快些； 当时钟相对于 观测者高速运动时，观测者则认为时钟变慢了。 例如，在一列以速度v 做匀速直线运动的火 车中，做一个物理实验的时间是15 min，站台上的 观察者测得该实验花费的时间会更长（图5-4）。 同一个物理过程，乘客测得的时间为τ0，站台上 的观察者测得的时间为τ。可以证明，τ0 与τ 之间 有以下关系 τ = τ0 1 - v2 c2 显然，τ > τ0。这种时间观测效应被称为时间延缓（time dilation）。我们把这一结论形 象地表述为运动的“时钟变慢”。它表明，一个物理过程经历的时间，在不同的参考系中 测量不一定相同。与之相对静止的参考系测得的时间最短，称为固有时；与之有相对运动 的参考系测得的时间变长。相对速度越大，时间延缓效应越明显。在狭义相对论中，时间 不再均匀地流逝，它与物体的运动状态有关，如果不指明参考系就无法回答某一物理过程 经历了多长时间。这充分说明，我们不能脱离物体的运动来理解时间。 107 第2 节　相对论中的神奇时空 科学书屋 验证时间延缓效应存在的实验 由宇宙射线在大气层上方产生的μ子是一种不稳定的粒子，它会自发衰变。据 测试，μ子的平均寿命为2.15×10 -6 s。从测试中得知，在距地球表面6 000 m 的 大气层中，μ子的速度v = 0.998 c，实验室观测到的高速运动的μ子平均寿命为 3.40×10 -5 s。这是证实运动时间延缓效应的实验之一。 2.长度收缩效应 经典时空观认为，空间是绝对空间，与运动无关。例如，一把刻度尺，相对它静止的 观测者测量其长度为1 m，相对它运动的观测者测量其长度仍是1 m。相对论时空观则认 为空间与运动密切相关。若一把刻度尺，相对它静止的观测者测量其长度为 l0（静止长度， 又称固有长度），沿它长度方向相对运动的观测者测量其长度则是 l，它们的关系为 l = l0 1 - v2 c2 由上述关系式可知l < l0。这种长度观测效应被称为长度收缩（length contraction）。被 测物体相对观测者的速度越大，长度收缩效应越明显。 我们平常观察不到这种长度收缩效应，是因为我们生活在比光速低很多的低速世界 中，v << c，l ≈ l0，长度收缩效应可忽略不计。 3.质能关系 在经典物理学中，质量和能量是两个独立的概念。按照相对论及基本力学定律可推出 质量和能量具有以下关系 E = mc2 这就是著名的质能关系式（massˉenergy equivalence）。式中， m 是质量，c 是真空中 的光速， E 是能量。质量和能量是物质不可分离的属性。如果用 Δm 表示物体质量的变化 量， ΔE 表示能量的变化量，则有ΔE = Δmc2。这一关系式表示，随着物体质量的减少，它 会释放出一定的能量。 人类已掌握了这种释放能量的有效方法。1938 年，德国物理学家哈恩的重核裂变反 应使爱因斯坦的质能关系得到了验证。从此，人类进入核能时代。 108 hysics P 第5 章　科学进步无止境 4.奇妙的时空弯曲 爱因斯坦的广义相对论认为，由于物质的 存在，空间和时间会发生弯曲。天体之间的引 力作用是时空弯曲的结果（图5-5）。万有引 力是广义相对论的时空弯曲理论在弱引力场的 近似表述。 当遥远的恒星发出的光经过太阳表面时， 太阳周围的空间弯曲，致使光线发生弯曲。理 论计算星光经过太阳周围空间射向地球后的偏 角为1.75″ （图5-6）。1919 年发生日全食时， 英国派出科考队分赴西非和巴西两地观测，得 到的结果与理论值相当吻合。正是由于这个事 件，相对论才受到人们的重视。 拓展一步 质速关系 在经典物理学中，物体的质量与运动无关。从相对论的角度看，物体的质量则 是变化的。当物体相对于某惯性参考系静止时，它具有最小的质量 m0 ；当物体以速 度 v 相对该惯性参考系运动时，则在该惯性参考系观测它的质量 m = m0 1 - v2 c2 可见，物体的质量会随着它运动速度的增大而增大。这便是相对论的质速关系。 图5-5 巨大质量的物体使时空弯曲的示意图 图5-6 光线在引力场中弯曲的示意图 太阳 地球 来自恒星的光线 1.75'' 能初步了解相对论时空观的内涵； 能运用与相对论相关的初步知识解释高 速世界的一些特点。尝试建立初步的相 对论时空观。 ——物理观念 素 养 提 升 109 第2 节　相对论中的神奇时空 科学书屋 爱因斯坦 爱因斯坦（图5-7）是近现代伟大的物理学家，他出生 在德国西南部古城乌尔姆的一个犹太家庭。 爱因斯坦的主要贡献有：提出光量子说，解释了光电效 应；创立了狭义相对论和广义相对论。1921 年，他因解释了 光电效应而获得诺贝尔物理学奖。 因为担心当时的德国抢先造出原子弹给世界带来灾难， 1939 年，爱因斯坦写信给美国总统罗斯福，建议研制原子弹。 这就是著名的“曼哈顿计划”的起源。爱因斯坦是一位热忱 的和平主义者，他利用一切机会呼吁不要把科学发现变成杀人 武器，并号召全世界科学家团结起来反对核战争。 图5-7　爱因斯坦 1. 也许你会疑惑，为什么在日常生活中未发现长度收缩、时间延缓或质量随速度增大而增加的现 象。请你从长度收缩公式和质速关系式出发，探索牛顿运动定律在宏观低速世界的合理性。 2. 惯性参考系S 中有一边长为l 的正方形。从相对S 系沿x 方向以接近光速匀速飞行的飞行器上测 得该正方形的图像可能是 A B C D y/m y/m y/m y/m l l x/m x/m x/m x/m O l l O l l O l l O 节练习 请提问 110 hysics P 第5 章　科学进步无止境 人类第一次将目光投向太空时，就想知道这浩瀚无垠的宇宙从哪里来，又将去向何 处。本节我们将一起探索宇宙起源和演化的奥秘。 1.宇宙的起源 自古以来，人们通过对日月星辰及周围事物的 观察，设想着宇宙的模样。例如，我国有古人认为 大地是平的，日月星辰在天空中运行，其上方扣着 穹顶（图5-8）。在古希腊，德谟克利特提出了“天 体演化说”，即在原子碰撞等原因形成的原始旋涡 运动中，较大的原子被赶到旋涡的中心相互聚集形 成地球，较小的原子被赶到外围环绕地球做旋转运 动，变得干燥后燃烧，形成各个天体。德国哲学家 康德则提出了“星云假说”， 用引力和斥力的观点描 述天体的形成和运动。 在探索宇宙奥秘的过程中，爱因斯坦发现，根据广义相对论建立的宇宙模型不是静态 的，因此引入宇宙学常数进行修正，提出了“有限无界的静态宇宙”模型。 1929 年，哈勃（E. Hubble，1889—1953）做了一个具有里程碑意义的观测：遥远的恒 星发出的光谱与地球上同种物质的光谱相比，波长变长，即向红光方向偏移（图5-9）。 这一现象说明：不管往哪个方向看，远处的星系都 正在急速地远离我们而去，并且距离我们越远的星 系离开我们的速度越快。 人类从此走出了静态绝对的宇宙观，开始用膨 胀的宇宙观探索宇宙的起源。美国科学家伽莫夫 （G. Gamow，1904—1968）将微观的核物理、化学元 素的起源与宏观的膨胀宇宙联系在一起，提出了描 述宇宙起源和演化的大爆炸宇宙模型，认为宇宙从 一个温度无限高、物质密度无限大的“奇点”爆炸 第3节 探索宇宙的奥秘 图5-9　遥远的恒星发出的光谱朝 红光方向偏移的示意图 图5-8　古人设想的宇宙模型示意图 111 第3 节　探索宇宙的奥秘 科学书屋 而成（图5-10）。大爆炸宇宙模型不仅能解释宇宙光谱的 红移现象，而且预言在大爆炸的特殊宇宙背景下产生的微 波辐射至今存在于宇宙空间中。1965 年，威尔森和彭齐亚斯 观测到了宇宙背景微波辐射，大爆炸宇宙模型得到了有力 的支持。 2.宇宙的演化 宇宙将会一直膨胀下去吗？宇宙的未来将走向何处？根据爱因斯坦广义相对论的预言， 宇宙的未来在很大程度上依赖于宇宙中的物质分布（宇宙物质的平均密度）。如果宇宙物质 的平均密度大于某个临界值，星系间的引力将最终使膨胀停止并使宇宙开始重新收缩，最 终坍缩；如果宇宙物质的平均密度小于该临界值，宇宙将会继续膨胀。但对宇宙物质平均 密度的观测非常困难，因为宇宙中除了可见的发光天体之外，还有大量的暗物质和暗能量。 暗物质是一种不能释放任何电磁辐射的物质，自20 世纪70 年代以来，科学家根据对 星系之间引力效果的观测发现，常规物质不可能产生如此大的引力，因此暗物质的存在理 论被广泛认同。 1998 年，科学家索尔·珀尔马特（S. Perlmutter）、布莱恩·施密特（B. Schmidt）和 亚当·里斯（A. Riess）通过观测遥远的超新星，发现宇宙正在加速膨胀，并且证明了暗 能量的存在，因而获得2011 年诺贝尔物理学奖。通过观测和理论分析，科学家推测宇宙 的大部分都是由暗物质和暗能量组成的，但人类对暗物质和暗能量的本质至今仍不了解， 现有的天文观测资料还不能确定宇宙的未来将走向何处，这有待于人类的进一步探索。 图5-10 宇宙大爆炸设想的示意图 霍金与天体物理 史蒂芬· 霍金（S. Hawking，1942—2018，图5-11）， 出生于英国牛津，17 岁入读牛津大学，毕业后前往剑桥大学 攻读宇宙学。他在21 岁被诊断为患运动神经细胞萎缩症后， 曾一度打算放弃科学研究。但后来他重拾信心，勇敢面对 病痛，继续潜心研究。20 世纪70 年代，他与罗杰·彭罗斯 （R. Penrose）一起提出：爱因斯坦的广义相对论暗示了空间 和时间是从大爆炸“奇点”开始而至黑洞结束。这就是著名 的奇性定理。他们因此在1988 年共获沃尔夫物理学奖。霍金 发现黑洞不完全是“黑”的，而是有向外的辐射，黑洞的温 度会随其辐射而升高，最终会爆炸而消失。这就是著名的“霍 金辐射”。霍金全身瘫痪，蜷缩于轮椅的狭小空间，他的思想 却在无垠宇宙的最深处飞扬，穿越时间与空间，追寻宇宙的源头，探索黑洞的奥秘。 图5-11 霍金 112 hysics P 第5 章　科学进步无止境 3.永不停息的探索 16 世纪初，意大利科学家伽利略用望远镜观测天空，从此人类的视野更加开阔。从 伽利略开始，人类一直在通过不断增加电磁波谱的范围来探索宇宙的奥秘，每一种新的电 磁波谱的拓展都意味着打开一扇通向宇宙的新的窗口。 射电望远镜是主要接收天体射电波段辐射的望远镜。1939 年，美国科学家雷伯利用 世界上第一架专门用于天文观测的射电望远镜接收到了来自银河系中心的无线电波，根 据观测结果绘制了第一张射电图。2016 年，我国落成启用的世界上最大单口径、最灵敏、 具有我国自主知识产权的射电望远镜（图5-12），是人类探索宇宙深处奥秘的神奇“眼 睛”—“中国天眼”。 为了摆脱大气层对天文观测的影响，人类还先后发射了许多人造卫星及宇宙飞行器用 于天文观测。著名的哈勃太空望远镜自1990 年4 月24 日升空以来，为人类源源不断地提 供震撼人心的星际图像，如恒星的诞生和死亡等（图5-13）。人们把它的诞生视为天文 学走向空间时代的一个里程碑。 引力波开启了探索宇宙的新窗口，它可让我们倾听宇宙，了解宇宙。1916 年，爱因 斯坦依据广义相对论预言，大质量天体发生碰撞、恒星爆炸、中子星合并、黑洞合并等 极端天文事件发生时，时空会产生涟漪并产生“ 引力波”，以光速向外扩张。由于产 生引力波的天体离我们过于遥远，引力波 到达地球时就变得极其微弱。2015 年，人 类首次直接探测到引力波的存在。这是 由两个黑洞合并为一个更大黑洞时产生 的持续不到1 s 的引力波信号，被激 光干涉引力波天文台（图5-14）的两个 探测器以7 ms 的时间差先后捕捉到。之 后，人类多次探测到引力波，但信号皆产 生于双黑洞合并。2017 年8 月17 日，人 图5-13　恒星“死亡” 的画面 图5-14　激光干涉引力波天文台（LIGO） 图5-12　世界上最大单口径、最 灵敏的射电望远镜 113 第3 节　探索宇宙的奥秘 们探测到来自双中子星合并所产生的引力波信号， 这标志着天文学进入了一个新时代。雷纳·韦斯 （R. Weiss）、巴里·巴里什（B. Barish）和基普·索 恩（K. Thorne）这三位科学家因对LIGO 探测器和 引力波探测的重大贡献而获得2017 年诺贝尔物理 学奖。 宇宙茫茫无际，人类的探索将永不停歇。人类 这一大自然的精灵，定会把视野扩至宇宙的更深处。 1. 查阅资料，了解关于宇宙起源的理论，说说每种理论的内容及科学依据。 2. 查阅资料，了解典型的恒星演化过程，并与同学们交流。 3. 查阅资料，了解宇宙学的新发展，以小论文或幻灯片等形式进行班级展示。 节练习 章末练习 1. 查阅物理学史的相关资料，了解人类关于时空观念的演变，写一篇心得体会，谈谈你的认识。 2. 查阅资料，了解爱因斯坦创立狭义相对论的过程，写一篇相关的科技小论文。 3. 查阅资料，了解时空弯曲的天文学依据，写一篇相关的科技报道，在班组会上交流。 4. 设计问卷，调研公众对相对论及其对人类影响的了解程度，完成一个相关的调研报告。 5. 与同学合作，发挥想象力，完成一个与经典力学及相对论有关的科幻剧，在班组会上表演。 科学书屋 “中国天眼”与天文学家南仁东 被誉为“中国天眼”的射电望远镜（Five hundred meters Aperture Spherical Radio Telescope，FAST）由主动反射面系统、馈源支撑系统、测量与控制系统、接收机 与终端及观测基地等几大部分构成。从1994 年提出构想到2016 年落成启用，历 时22 年，是我国具有自主知识产权，世界最大单口径、最灵敏的射电望远镜。目前 “中国天眼”已发现若干脉冲星，人们期待其有进一步的天文发现。 “中国天眼”的首席科学家兼总工程师南仁东（1945—2017），为选择最佳台址， 带着300 多幅卫星遥感图，跋涉在中国西南的大山里，先后对比了1 000 多个洼地。 工程建设中，他克服了技术、资金等重重困难，为工程的顺利完成作出了卓越的贡 献。他用人生最后的22 年，精益求精、坚毅执着地实现了一个梦想，用生命铸就了 世人瞩目的“中国天眼”。 能体会人类对自然界的探索是不断 深入的，能从牛顿力学的局限性体会科 学理论既具有相对持久性和稳定性，也 存在局限性，人类对自然的探索永无止 境；具有探索自然、造福人类的志趣， 有关注宇宙起源与演化研究进展的意 愿；能体会科学·技术·社会存在相互 联系，需要协调发展。 ——科学态度与责任 素 养 提 升 后 记 21 世纪初我国启动基础教育课程改革，迄今已十余年。我们根据《普通高中物理课 程标准（实验）》（2003 版）编写的普通高中课程标准实验教科书《物理》在实验区已使 用十余年。随着基础教育课程改革的深入，修订后的《普通高中物理课程标准（2017 年 版）》（以下简称《标准》）已由教育部正式颁布，因此，实验版教科书《物理》也应随之 修订。根据国家大政方针和《标准》的要求，在对一线教师大规模问卷调查及深入访谈的 基础上，基于多年教科书研究、编写和实践的积淀，教科书编写组对实验版教科书进行了 全面修订。 本次修订后的普通高中物理课 程标准修订版教科书的整体架构如 图所示。 总体来看，修订版教科书具有 如下特点： 1. 立意更高，促进学生物理学 科核心素养的达成。不仅继承实验 版教科书注重落实三维课程目标的 特点，而且更加注重体现物理教科 书的育人功能，以“素养提升”“本 章学业要求”等栏目导向，有效促 进教学方式的改进，提升学生物理 学科核心素养。 2. 寓意更深，注重从情境走向 物理，从物理走向社会的内涵。不 仅继承实验版教科书注重联系实际 的特点，而且强调问题情境与物理 内容的相互呼应。通过“以惑为诱、 以问促学”的内容设计，培养学生的物理自然观和建模、推理、论证及质疑能力。 3. 更重实践，强调概念构建过程，注重探究能力的培养。不仅继承实验版教科书的实 验栏目，而且注重凸显物理实验的育人功能。通过“学生必做实验”“实验探究”“迷你 实验室”“DIS 实验室”等实验版块，以“引导、递进、开放”的精巧设计，培养学生在 问题、证据、解释及交流方面的探究能力。 4. 更富逻辑，结构更完善，更符合教育教学规律。不仅继承了实验版教科书结构上注 重逻辑的特点，而且通过“方法点拨”“策略提炼”“拓展一步”等栏目，进一步升华学 114 选择性必修第三册：固体、液体和气体， 热力学定律，原子与原子核，波粒二象性 选择性必修第二册：磁场，电磁感应及其 应用，电磁振荡与电磁波，传感器 选择性必修第一册：动量与动量守恒定 律，机械振动与机械波，光及其应用 必修第三册：静电场，电路及其应用，电 磁场与电磁波初步，能源与可持续发展 必修第二册：机械能及其守恒定律，曲线 运动与万有引力定律，牛顿力学的局限性 与相对论初步 必修第一册：机械运动与物理模型，相互 作用与运动定律 选修第一册： 物理学与社 会发展 选修第二册： 物理学与技 术应用 选修第三册： 近代物理学 初步 选修 必修 选择 性必 修 合 格 性 考 试 等 级 性 考 试 自主 考核 修订后整套教科书的基本架构 习内容，同时注重难点分解、台阶降低、逐步到位，关注了学生的认知特点。 5. 更重评价，发挥习题功能，促进学生全面发展。改进实验版教科书在习题设计方面 的不足，基于物理学科核心素养和学业质量要求，分层设计“节练习”“章末练习”“单 元自我检测”，更好发挥习题的功能，促进对核心素养测试的探索。 6. 更加拓展，反映物理学对人类生活及社会发展的影响。不仅继承实验版教科书从物 理走向社会的特点，而且注重通过“科学书屋”“物理聊吧”等栏目培养学生的学习兴趣、 人文情怀，及节约能源、保护环境的科学态度与社会责任感。 7. 臻于精致，体现“以学生发展为本”的理念。不仅继承实验版教科书图文并茂的 特点，而且更加美观、适用，从结构确定、内容纳入、栏目设计、图片选用到版式推敲等 多方面皆精雕细琢，旨在全力打造高质量的一流物理教科书。 编写组凝聚了高校学科专家、省市物理教研员、中学教学名师、考试评价专家、国际 物理教科书研究者等研究力量，具有高校研究平台与中学教学积累的综合优势。各类课题 研究、理论探索、国际比较等，使教科书修订具有研究基础、国际视野，能让物理教科书 的质量提升到更高的水平。中学各级教学名师丰富的实践经验、珍贵的教学心得，为教科 书修订中落实以学生发展为本的教学理念搭建了接地气的脚手架、扎实的一线平台，让修 订版教科书更符合教学实际。 本教科书编写组主要成员及分工如下：全套教科书主编为廖伯琴；本册核心编者有 林明华、杜明荣、蒋敏、李洪俊、李太华、廖伯琴；本册由廖伯琴、林明华统稿，由廖伯 琴定稿；全套教科书编务联系工作由李富强、李洪俊负责。 教科书的修订是一系统工程，需各方力量支持。参与本次修订版教科书编写、讨论、 审读、组织试教或作出前期贡献的老师还有：李勇、程力、高山、周智良、宋树杰、王 宪收、陈松、林伟庆、罗基鸣、黄晓标、杨燕鸣、梅家烨、谢德胜、吴英、刘林、许华 忠、田序海、杨学切、青春、黄国雄、冯庆、邓磊、蒋小平、刘健智、廖元锡、冯华、张 正严、翟厚岚、洪正平、梁雷、贺晓霞、张修文、梁一平、林钦、李晶晶、王文祥、董茂 寅、宋协俊、邹建光、时玉义、马凤喜、吴新田、侯辰虎、郑玉峰、程美贵、冯连奎、曹 国莹、岳志国、姜妮、欧剑雄、严士线、彭罡、张庆贵、吴双飞、刘新选、黄巧曦、吴寒 平、李勇顺、黄惠菁、赵保钢、朱霞、覃朝玲、张滨等。张书迪女士为本教科书设计图 标，并在版式设计方面提出若干建议。 本次修订得到众多专家、学者、教研员、教师、学生以及家长的热诚帮助，得到了山 东科学技术出版社的鼎力支持。在此，我们特向提供帮助的各方人士表示由衷感谢！修订 后的教科书将很快进入中学课堂，我们恳请各方人士不吝赐教。 挑战与发展共存！我们期待批评，也期待各位的支持。谢谢！ 主编　廖伯琴 2019 年5 月于西南大学荟文楼 115